Abstract
During morphogenesis, various cellular activities are spatiotemporally coordinated on the protein regulatory background to construct the complicated, three-dimensional (3D) structures of organs. Computational simulations using 3D vertex models have been the focus of efforts to approach the mechanisms underlying 3D multicellular constructions, such as dynamics of the 3D monolayer or multilayer cell sheet like epithelia as well as the 3D compacted cell aggregate, including dynamic changes in layer structures. 3D vertex models enable the quantitative simulation of multicellular morphogenesis on the basis of single-cell mechanics, with complete control of various cellular activities such as cell contraction, growth, rearrangement, division, and death. This review describes the general use of the 3D vertex model, along with its applications to several simplified problems of developmental phenomena.
Keywords: 3D vertex model, reversible network reconnection, computational simulation, biomechanics, developmental biology
The morphology of multicellular organisms has a complicated three-dimensional (3D) structure that varies by tissues, organs, individuals, and/or species. The process of constructing these morphologies is accompanied by various cellular activities, such as active cellular deformation, movement, proliferation, and death. Because these cellular activities are spatiotemporally regulated on the background of gene expression and protein interactions, they show characteristic cellular behaviors, which differ between tissue regions and developmental stages. These cellular behaviors drive the autonomous, dynamic process of multicellular morphogenesis.
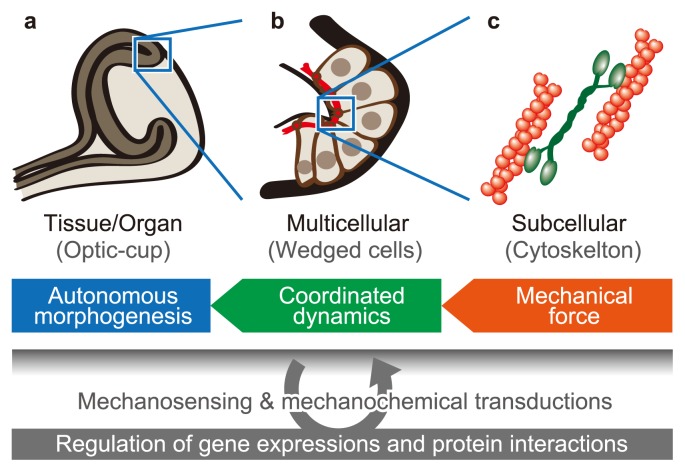
Mechanical force generated by cellular activities has important roles during multicellular morphogenesis, as shown in Figure 1. For example, the dynamics of cytoskeletal and adhesive structures regulate cellular deformations and movements based on mechanical interactions among surrounding cells. These mechanical forces at a subcellular scale are coordinated on the scale of the cell population so as to achieve multicellular morphogenesis on the scale of tissues and organs. Therefore, understanding multicellular morphogenesis requires revealing how mechanical force generates collective cellular behaviors and how they drive the morphogenesis of tissues and organs.
Figure 1.
Mechanical effects of cellular activities on multicellular morphogenesis. Multicellular morphogenesis can be analyzed on several scales, such as (a) the tissue and organ scale, (b) the cell population scale, and (c) the subcellular scale. Mechanical forces generated by cellular activities on the subcellular scale cause cell–cell mechanical interactions on the cell populations scale, which drive morphogenesis on the tissue and organ scale.
Recent studies have identified the key genes and proteins involved in developmental phenomena, and structural and mechanical analyses of these proteins have revealed the molecular mechanisms of mechanosensing and mechanochemical transduction. Notably, these cellular activities cause mechanical interactions among cells during morphogenesis. Hence, to bridge the gap of understanding between molecular dynamics and morphogenesis, we need to understand multicellular dynamics. Such a comprehensive understanding will open the way toward the development of techniques to regenerate 3D organ structures.
Mechanics-based computational simulations have been used to analyze multicellular dynamics. In particular, vertex models have been the focus of efforts because of their versatile descriptions of multicellular dynamics based on single cell mechanics [1–5]. These models have been applied to various realistic and simplified phenomena of epithelia as well as other multicellular tissues.
Based on these research, we have improved the 3D vertex model for simulating multicellular morphogenesis in 3D space. In this model, individual cell shapes are expressed by polyhedrons, and multicellular dynamics are described based on the force balance between vertices comprising these polyhedrons. The 3D modeling enables to express dynamics of the 3D monolayer or multilayer cell sheet like epithelia as well as the 3D compacted cell aggregate, including dynamic changes in layer structures. This model expresses various mechanical effects of cellular activities such as active force generation by cell growth and contraction, changes in cell mechanical properties, and changes in cell number by cell division and death. The expressions describing these cellular activities enable the prediction of their mechanical effects on 3D morphogenesis, based on the interactions among cells. This review describes the general use of the 3D vertex model, along with its applications to several simplified problems of developmental phenomena.
3D vertex model expressing multicellular morphogenesis
Expression of 3D multicellular structure and dynamics
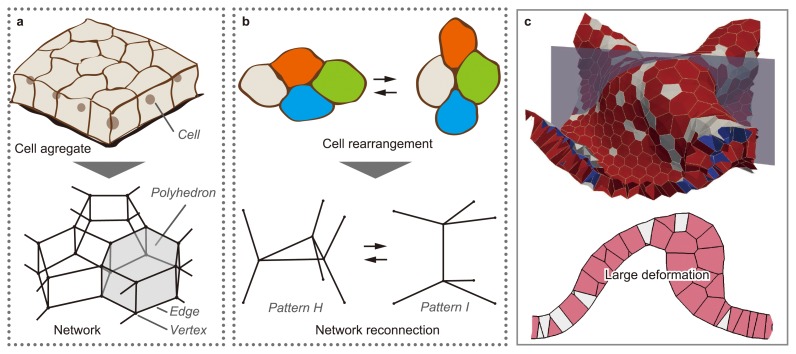
Figure 2 shows an abstract representation of the 3D vertex model. Vertex models are generally based on the geometrical assumption that cells are tightly compacted as an aggregate. Under this assumption, the boundary between two neighboring cells is a polygonal face, and the polyhedron surrounded by boundary faces is a cell. Hence, the morphology of cell aggregate is represented by a single network composed of the vertices and edges of cellular polyhedrons. Moreover, multicellular dynamics are expressed by the movements of vertices.
Figure 2.
Expression of cellular structure, dynamics, and rearrangement in the 3D vertex model. (a) In the 3D vertex model, the shapes of individual cells are expressed by polyhedrons, and the structure of a cell aggregate is expressed as a single network composed of the vertices and edges of these polyhedrons. (b) Cell rearrangement is expressed by reconnecting local patterns of the network according to the topological rule. (c) The model successfully simulates the large deformations of a multicellular sheet, where rearrangements of cells with changes in the layer structure are observed (Modified from [12]).
Cellular dynamics during morphogenesis occur on the order of minutes to hours. Hence, the effects of inertia on cellular dynamics are dispensable, while the effects of viscosity are dominant. According to this assumption, the vertex movements can be calculated by overdamped equation [6] as well as variational methods [7–10]. In case of using overdamped equation, the movement of the iv-th vertex, whose position vector is represented by riv, is described by
| (1) |
The term on the left-hand side of Eq. (1) represents a friction force, where ηiv represents a coefficient of friction and νiv indicates a local velocity vector. Functions ηiv and νiv are determined by viscous properties of tissue components. The right-hand side of Eq. (1) is an effective energy, where U represents an energy function expressing cellular energetic behaviors.
During morphogenesis, cells passively respond to exerted forces according to viscous properties of their components such as cytoplasm, cytoskeleton, cellular cortex, basement membrane and extracellular matrices (ECM). The viscous properties are expressed by friction among the vertices of each geometrical element in the network (edge, polygonal face, and cellular polyhedron) [6]. The viscous friction coefficient ηiv in Eq. (1) is simply defined as follows.
| (2) |
where is the summation overall geometrical elements. The binary function δiv;je is 1 if the je-th geometrical element contains the iv-th vertex and 0 otherwise. The constant ηje is the viscous friction weight of vertices in the je-th geometrical element. To balance the total viscous friction force within each geometrical element, the local velocity vector around the iv-th vertex νiv in Eq. (1) is defined as the mean velocity vector of the surrounding geometrical elements:
| (3) |
In Eq. (3), the vector νje is the velocity of the je-th geometrical element as follows:
| (4) |
where is the number of vertices comprising the je-th geometrical element, and denotes summation overall vertices. The vector is the velocity of extracellular materials in the je-th geometrical element, and weighs the extracellular materials. In the absence of extracellular viscosity ( ), the viscous friction forces at the vertices of each geometrical element are balanced, so that Eq. (1) satisfies the Galilean invariance.
During morphogenesis, cells actively generate mechanical forces during cellular activities such as growth and contraction as well as passively respond. The active energy generation can be expressed using U as a function of cell time tjc, which is defined as the time counted since the jc-th cell was generated. Defining {tjc}={t0c, t1c, t2c, ... tnc}, the potential energy U was introduced as a function of cell time {tjc }. Using cell time {tjc}, potential energy U is expressed by
| (5) |
| (6) |
| (7) |
| (8) |
where the binary function is 1 if the jc-th cell is alive at t=tjc and 0 otherwise. In Eqs. (6), (7), and (8), indicates summations for all cells. Potential energy represents an energy of the jc-th cell, such as volume elasticity, surface elasticity, apical constriction, and other effects of intracellular structures and activities. The potential energy indicates energy between the jc-th and kc-th cells, such as cell-cell adhesions at intercellular junctions. The potential energy indicates energy between the jc-th cell and extracellular components, such as extracellular matrices, basement membranes, and solvent liquids. Therefore, in this model, active cell behaviors are expressed by time-variations in the constants of Eqs. (6), (7), and (8) such as mechanical property, reference state, and energy density.
Expression of 3D cell rearrangement
Multicellular morphogenesis is an irreversible process that appears as sequential, plastic deformations from a continuum viewpoint. The irreversibility is generated by geometrical changes in cell configuration (cell rearrangement). For example, in an epithelium, where cells are aligned on a sheet, cells directionally converge within the sheet, and the sheet extends in the normal direction to the convergence (convergent extension). To express these types of cell rearrangements, the network composed of the edges and vertices of polyhedrons is locally reconnected in the vertex model [11] (Fig. 2b). The network reconnection idea originated from studies of the dynamics of metal crystal grains and soap froth; it has been used as a method for expressing the rearrangements of multiple elements in two-dimensional (2D) and 3D space. Moreover, in recent studies, the reversibility of cell shape, network topology, and total energy has been improved so as to express large deformations during morphogenesis [12] (Fig. 2c).
Expression of 3D cell division and death
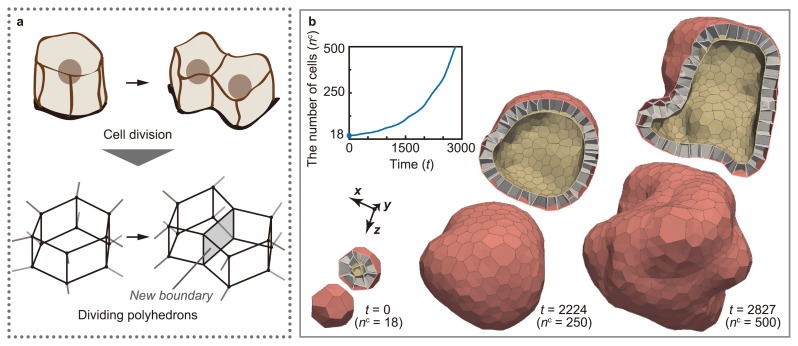
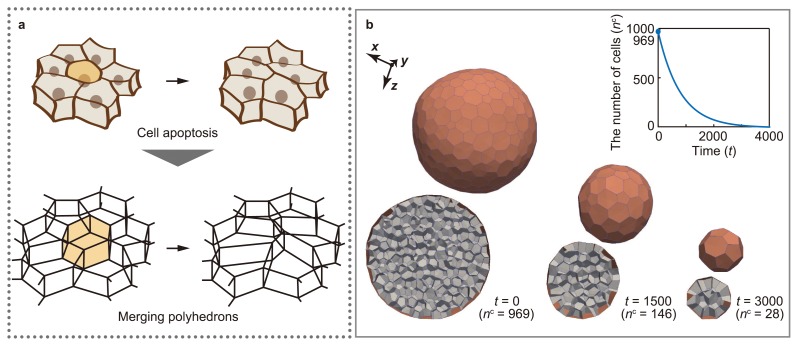
The developmental process of multicellular organisms is accompanied by cell division and death. Cell division and death play important roles in multicellular morphogenesis because they can regulate the local size and shape of tissues by changing the number of cells. The mechanical effects of cell division and death can be expressed in the vertex model. In the 3D vertex model, cell division is expressed by dividing polyhedrons [13] (Fig. 3a). This model enables the analysis of the mechanical effects of the increase in cell number on morphogenesis, while regulating the timing, directionality, and symmetry of cell division (Fig. 3b). Moreover, cell death is expressed by merging polyhedrons [14] (Fig. 4a). This model enables the analysis of the mechanical effects of the decrease in cell number on morphogenesis, while regulating the timing of cell death (Fig. 4b).
Figure 3.
Expression of cell division in 3D vertex model. (a) Cell division is expressed by dividing polyhedrons. (b) The model of cell division successfully expresses the increase in the number of cells while regulating the timing, direction, and symmetry of cell divisions (modified from [13]).
Figure 4.
Expression of cell death in 3D vertex model. (a) Cell death is expressed by merging polyhedrons. (b) The model of cell death successfully expresses the decrease in the number of cells, while regulating the timing of cell death. (refer to [14]).
Coupling intercellular molecular signaling with multicellular deformations
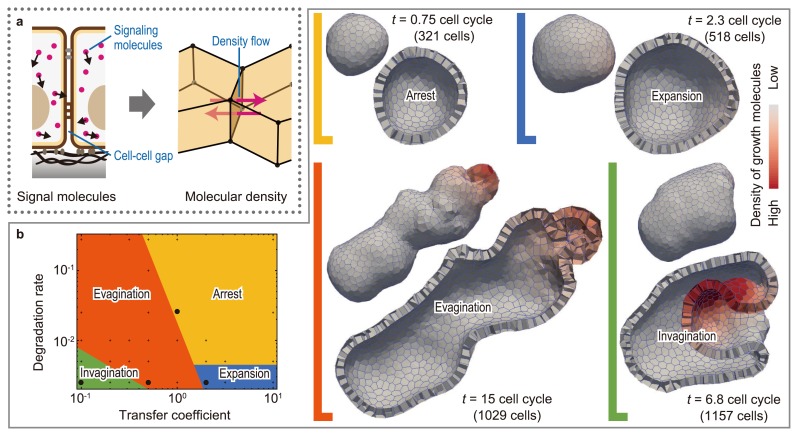
The coordination of 3D multicellular deformations correlates with geometric cell patterns, where individual cells are characterized by their biochemical states, such as protein synthesis, mRNA transcription, and gene methylation. During morphogenesis, this type of cell patterning can be dynamically rearranged because of the regulatory nature of signaling molecules inside and outside cells. Furthermore, the patterning can be physically affected by the geometry of the diffusing passages of signaling molecules, i.e., local cell shapes and configurations and global tissue morphologies. Thus, diffusible molecular signaling causes bidirectional effects between cell patterning and 3D tissue deformations. Such interactions can be expressed in the 3D vertex model by coupling multicellular deformations with intercellular molecular signaling [15] (Fig. 5a and b). This model enables the prediction of the effects of mechanochemical coupling on 3D multicellular morphogenesis (Fig. 5c).
Figure 5.
Coupling intercellular molecular signaling with 3D multicellular deformation. (a) Intercellular molecular signaling is expressed by molecular transport between neighboring polyhedrons. (b) By simulating signal-dependent epithelial growth, we found various types of multicellular morphogenesis, such as arrest, expansion, invagination, and evagination (modified from [15]).
Computational simulations of 3D multicellular morphogenesis
Computational simulations using vertex models enable the prediction of multicellular morphogenesis based on the assumptions of various cellular activities, such as changes in cell viscoelasticity, cell–cell adhesion, active cellular deformations, cell growth, division, and death. By assuming the variance and regulation of these cellular activities over time, dynamic process of cell number, shape, configuration, and the whole tissue shape can be predicted. Moreover, it makes it possible to estimate stress states on the length scale from subcellular to multicellular.
Widely used 2D vertex model
2D vertex models have been widely applied to the analysis of the geometric patterning of the apical surfaces of planar epithelial sheets. For example, in research focusing on mechanical properties, the characteristics of geometric cell patterns are explained by the force balance between cell contractility and cell–cell adhesion [16]. Moreover, in research focusing on the directionality of cell divisions, the effects of the direction of cell division are examined in two cases: with and without cell-shape dependence [17]. Recent research has revealed that the boundary between different cell populations is maintained by the spatial difference in cell contractility and adhesion [18]. These results of analyses performed using 2D vertex models, in terms of the number of neighboring cells, cell shapes, and tension at cell–cell boundaries on apical surfaces, have been verified by comparison with experimental results obtained using drosophila.
2D vertex models have been improved to express a 2D cell sheet in 3D space by reducing the degree of freedom in the direction of epithelial thickness. These pseudo-2D vertex models have been applied to several phenomena, such as rosette formation during migration of the mouse anterior visceral endoderm [19] and the formation of the dorsal appendages of drosophila eggshells [20, 21].
General-purpose 3D vertex model
3D vertex models have been improved and used to analyze the basis of epithelial morphogenesis. The epithelium has a 3D multicellular sheet structure bounded by apical and basal surfaces. It is one of the principal elements comprising the organ structures of multicellular organisms. On the apical surface, neighboring cells adhere to each other using adhesion proteins such as cadherin. On the perimeter of the apical surfaces of individual cells, contractile forces are generated by localized actomyosin activities. Moreover, the basal surface is generally covered by basement membranes, to which cells adhered using adhesion proteins such as integrin. Hence, 3D vertex models have an advantage; the ability to express all the degrees of freedom in 3D space that are involved in changes in the multilayer structures of cell aggregates. 3D vertex models have been applied to several developmental phenomena, such as the polarization of early embryos [22] and the convergent-extension of epithelial sheet [23]. Here we introduce our research.
Apical constriction supports to maintain smooth curvatures of 3D epithelial vesicle
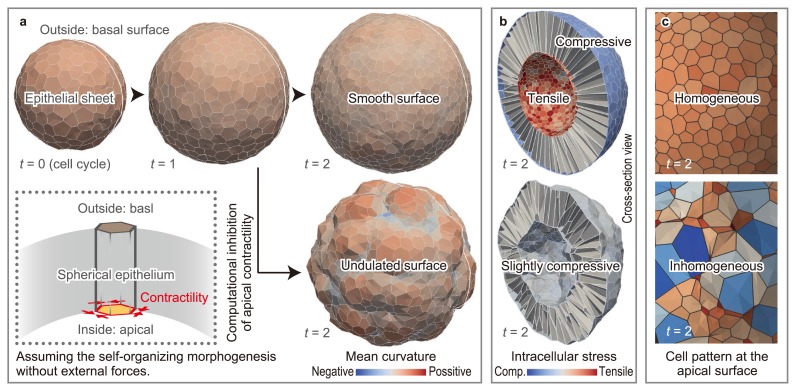
The epithelial sheet regulates its curvature amid the disturbance of frequent cell divisions. This study revealed that apical contractility helps to maintain the homogeneous curvature [24] (Fig. 6a). To analyze the mechanism of this maintenance, we analyzed the distribution of volumetric stresses within the tissue (Fig. 6b). As a result, apical contractility generates a tension on the entire apical surface, which makes individual cell shapes homogeneous. The effects of apical contractility constrain cells within a smooth surface.
Figure 6.
Effects of apical constriction on epithelial curvature. (a) Apical contractility plays a role in the maintenance of the smooth curvature of epithelial sheets amid cell division-induced disturbances. (b) Apical contractility keeps the apical surface tensile under the compressive conditions induced by cell growth. (c) The geometric cell pattern of the apical surface varies according to the presence or absence of apical contractility (modified from [24]).
As the apical contractility increased, the increasing geometric cell pattern of the apical surface approached homogeneity (Fig. 6c). This result is consistent with simulation results obtained using 2D vertex models. The strength of the apical contractility was varied by comparing the cell strain generated by the apical contractility with those obtained in experiments involving the inhibition of apical contractility. These results suggested that the contractility on the scale of single cell helps to maintain the curvature at a scale of tissues beyond the length scale.
Extracellular viscosity leads to buckling, branching, thickening, and twisting of 3D epithelial tubes
The viscous properties of tissues play an important role in passive responses, because they govern the dynamic processes of tissue deformations. Moreover, the viscous properties of tissues are probably spatially inhomogeneous because they should depend on tissue components such as the cytoplasm, cytoskeleton, basement membrane, and extracellular matrix. Crucially, these viscosity-dependent deformations can be regulated by the timing of cellular cues that generate active forces, which are likely to complicate the mechanics of multicellular deformations. To analyze effects of tissue viscosity on morphogenesis, the 3D vertex model has been improved to simulate viscosity-dependent dynamic deformation processes [6].
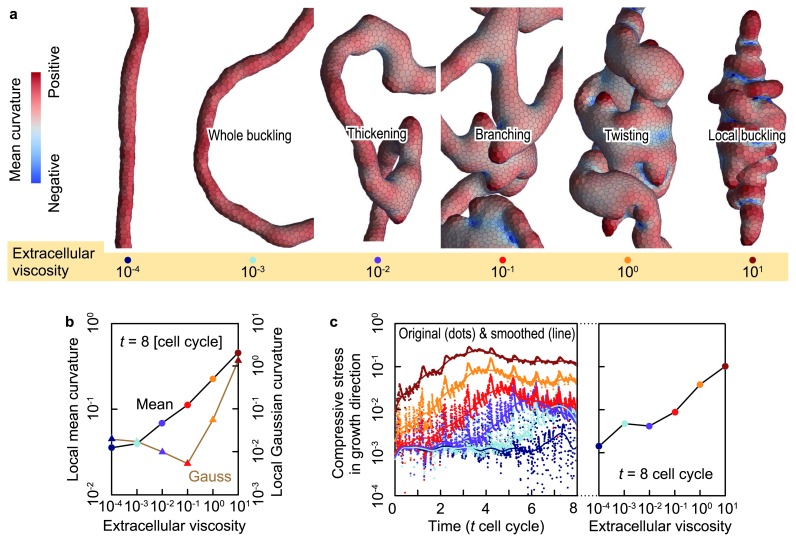
To examine the effects of tissue viscosity in a simple case, the dynamics of directional tissue growth in extracellular matrices were simulated. In simulations using the proposed model, epithelial vesicle deformation was highly sensitive to the viscosity of the extracellular matrix (Fig. 7a). The deformation was quantified using the mean and Gaussian curvatures, as shown in Figure 7b. Different deformations stemmed from the different strengths of the compressive forces generated by viscous frictions between epithelial cells and extracellular materials (Fig. 7c). The strength of the compressive force governed the bending, branching, thickening, and twisting of the epithelial tube.
Figure 7.
The effects of extracellular viscosity on the growing epithelial tube. (a) Enlarged shapes of epithelial vesicles at several extracellular viscosities. Epithelial vesicles are colored by the local mean curvature. (b) The spatial average of the mean and Gaussian curvatures of local epithelial surfaces as a function of the extracellular viscosity. (c) Compressive forces within the epithelial vesicles in the growth direction as a function of time (left) and viscous friction weight (right). Dots and line show original and smoothed data, respectively (modified from [6]).
Future perspectives
Morphogenesis possibly involves mechanical feedback through gene expressions and protein interactions. Herein, individual cells sense their mechanical environments and create responses that drive autonomous morphogenesis. Such mechanical cellular responses could contribute to the successive process of morphogenesis. Moreover, mechanical forces generated by cellular activities affect various cellular behaviors from molecular dynamics to whole tissue deformations. Therefore, morphogenesis is an integrated, multiscale phenomenon caused by mechanical and chemical interactions among multiple cells.
In such morphogenesis, the applicable scales of vertex models are from subcellular components to tissues and organs. This review has described the development of 3D vertex models, involving 3D cellular deformation, rearrangement, division, death, as well as their regulations coupled with intercellular molecular signaling. Because these cellular behaviors are common in various morphogenesis, the model will be useful for exploring a basis of morphogenesis of complicated tissues and organs. Therefore, computational simulations using 3D vertex models will be one of the key tools to analyze mechanics in morphogenesis.
Because morphogenesis is accompanied by a variety of cellular activities, it is one of the challenging problems to develop the model for various cellular activities that have not been established yet, such as epithelial-mesenchymal transition and fission–fusion between epithelial aggregates. Modeling these cellular activities will extend the applicability of vertex models to analyze various morphogenesis. Moreover, coupling multicellular deformation with specific molecular signaling will enable comprehensive analysis from gene expression to morphogenesis, involving mechanochemical transduction.
In conclusion, we have described how to develop a versatile computational model of morphogenesis that includes integrated, multiscale phenomena caused by mechanical and chemical interactions among multiple cells. 3D vertex models have the potential to enable a comprehensive understanding of morphogenesis and to describe the complexity of 3D morphogenesis in a physical manner.
Acknowledgements
We thank Dr. Yoshiki Sasai and Dr. Mototsugu Eiraku from the Center for Developmental Biology (CDB) in RIKEN for their valuable comments. This work was supported by JSPS KAKENHI Grant Number 15K14534.
Footnotes
Conflict of Interest
All the authors declare no conflicts of interests.
Author Contributions
S. O. wrote the manuscript. Y. I. and T. A. reviewed the manuscript and approved the final form.
References
- 1.Odell GM, Oster G, Alberch P.&Burnside B. The mechanical basis of morphogenesis. I. Epithelial folding and invagination. Dev Biol. 1981;85:446–462. doi: 10.1016/0012-1606(81)90276-1. [DOI] [PubMed] [Google Scholar]
- 2.Honda H, Ogita Y, Higuchi S.&Kani K. Cell movements in a living mammalian tissue: long-term observation of individual cells in wounded corneal endothelia of cats. J Morphol. 1982;174:25–39. doi: 10.1002/jmor.1051740104. [DOI] [PubMed] [Google Scholar]
- 3.Fletcher AG, Osborne JM, Maini PK.&Gavaghan DJ. Implementing vertex dynamics models of cell populations in biology within a consistent computational framework. Prog Biophys Mol Biol. 2013;113:299–326. doi: 10.1016/j.pbiomolbio.2013.09.003. [DOI] [PubMed] [Google Scholar]
- 4.Fletcher AG, Osterfield M, Baker RE.&Shvartsman SY. Vertex models of epithelial morphogenesis. Biophys J. 2014;106:2291–2304. doi: 10.1016/j.bpj.2013.11.4498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Honda H.&Nagai T. Cell models lead to understanding of multi-cellular morphogenesis consisting of successive self-construction of cells. J Biochem. 2015;157:129–136. doi: 10.1093/jb/mvu088. [DOI] [PubMed] [Google Scholar]
- 6.Okuda S, Inoue Y, Eiraku M, Adachi T.&Sasai Y. Vertex dynamics simulations of viscosity-dependent deformation during tissue morphogenesis. Biomech Model Mechanobiol. 2015;14:413–425. doi: 10.1007/s10237-014-0613-5. [DOI] [PubMed] [Google Scholar]
- 7.Viens D.&Brodland GW. A three-dimensional finite element model for the mechanics of cell-cell interactions. J Biomech Eng. 2007;129:651–657. doi: 10.1115/1.2768375. [DOI] [PubMed] [Google Scholar]
- 8.Yang J.&Brodland GW. Estimating interfacial tension from the shape histories of cells in compressed aggregates: a computational study. Ann Biomed Eng. 2009;37:1019–1027. doi: 10.1007/s10439-009-9649-6. [DOI] [PubMed] [Google Scholar]
- 9.Hutson MS, Brodland GW, Yang J.&Viens D. Cell sorting in three dimensions: topology, fluctuations, and fluidlike instabilities. Phys Rev Lett. 2008;101:148105. doi: 10.1103/PhysRevLett.101.148105. [DOI] [PubMed] [Google Scholar]
- 10.Brodland GW, Yang J.&Sweny J. Cellular interfacial and surface tensions determined from aggregate compression tests using a finite element model. HFSP J. 2009;3:273–281. doi: 10.2976/1.3175812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nagai T, Ohta S, Kawasaki K.&Okuzono T. Computer simulation of cellular pattern growth in two and three dimensions. Phase Transit. 1990;28:177–211. [Google Scholar]
- 12.Okuda S, Inoue Y, Eiraku M, Sasai Y.&Adachi T. Reversible network reconnection model for simulating large deformation in dynamic tissue morphogenesis. Biomech Model Mechanobiol. 2013;12:627–644. doi: 10.1007/s10237-012-0430-7. [DOI] [PubMed] [Google Scholar]
- 13.Okuda S, Inoue Y, Eiraku M, Sasai Y.&Adachi T. Modeling cell proliferation for simulating three-dimensional tissue morphogenesis based on a reversible network reconnection framework. Biomech Model Mechanobiol. 2013;12:987–996. doi: 10.1007/s10237-012-0458-8. [DOI] [PubMed] [Google Scholar]
- 14.Okuda S, Inoue Y, Eiraku M, Adachi T.&Sasai Y. Modeling cell apoptosis for simulating three-dimensional multicellular morphogenesis based on a reversible network reconnection framework. doi: 10.1007/s10237-015-0724-7. (submitted) [DOI] [PubMed] [Google Scholar]
- 15.Okuda S, Inoue Y, Watanabe T.&Adachi T. Coupling intercellular molecular signaling with multicellular deformation for simulating three-dimensional tissue morphogenesis. Interface Focus. 2015;5:20140095. doi: 10.1098/rsfs.2014.0095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Farhadifar R, Röper JC, Aigouy B, Eaton S.&Jülicher F. The influence of cell mechanics, cell-cell interactions, and proliferation on epithelial packing. Curr Biol. 2007;17:2095–2104. doi: 10.1016/j.cub.2007.11.049. [DOI] [PubMed] [Google Scholar]
- 17.Gibson WT, Veldhuis JH, Rubinstein B, Cartwright HN, Perrimon N.&Brodland GW, et al. Control of the mitotic cleavage plane by local epithelial topology. Cell. 2011;144:427–438. doi: 10.1016/j.cell.2010.12.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Landsberg KP, Farhadifar R, Ranft J, Umetsu D, Widmann TJ.&Bittig T, et al. Increased cell bond tension governs cell sorting at the Drosophila anteroposterior compartment boundary. Curr Biol. 2009;19:1950–1955. doi: 10.1016/j.cub.2009.10.021. [DOI] [PubMed] [Google Scholar]
- 19.Trichas G, Smith AM, White N, Wilkins V, Watanabe T.&Moore A, et al. Multi-cellular rosettes in the mouse visceral endoderm facilitate the ordered migration of anterior visceral endoderm cells. PLoS Biol. 2012;10:e1001256. doi: 10.1371/journal.pbio.1001256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Osterfield M, Du X, Schüpbach T, Wieschaus E.&Shvartsman SY. Three-dimensional epithelial morphogenesis in the developing Drosophila egg. Dev Cell. 2013;24:400–410. doi: 10.1016/j.devcel.2013.01.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Du X, Osterfield M.&Shvartsman SY. Computational analysis of three-dimensional epithelial morphogenesis using vertex models. Phys Biol. 2014;11:066007. doi: 10.1088/1478-3975/11/6/066007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Honda H, Motosugi N, Nagai T, Tanemura M.&Hiiragi T. Computer simulation of emerging asymmetry in the mouse blastocyst. Development. 2008;135:1407–1414. doi: 10.1242/dev.014555. [DOI] [PubMed] [Google Scholar]
- 23.Honda H, Nagai T.&Tanemura M. Two different mechanisms of planar cell intercalation leading to tissue elongation. Dev Dyn. 2008;237:1826–1836. doi: 10.1002/dvdy.21609. [DOI] [PubMed] [Google Scholar]
- 24.Okuda S, Inoue Y, Eiraku M, Sasai Y.&Adachi T. Apical contractility in growing epithelium supports robust maintenance of smooth curvatures against cell-division-induced mechanical disturbance. J Biomech. 2013;46:1705–1713. doi: 10.1016/j.jbiomech.2013.03.035. [DOI] [PubMed] [Google Scholar]