Sensitivity of rat inferior colliculus neurons to frequency distributions

Abstract

Stimulus-specific adaptation refers to a neural response reduction to a repeated stimulus that does not generalize to other stimuli. However, stimulus-specific adaptation appears to be influenced by additional factors. For example, the statistical distribution of tone frequencies has recently been shown to dynamically alter stimulus-specific adaptation in human auditory cortex. The present study investigated whether statistical stimulus distributions also affect stimulus-specific adaptation at an earlier stage of the auditory hierarchy. Neural spiking activity and local field potentials were recorded from inferior colliculus neurons of rats while tones were presented in oddball sequences that formed two different statistical contexts. Each sequence consisted of a repeatedly presented tone (standard) and three rare deviants of different magnitudes (small, moderate, large spectral change). The critical manipulation was the relative probability with which large spectral changes occurred. In one context the probability was high (relative to all deviants), while it was low in the other context. We observed larger responses for deviants compared with standards, confirming previous reports of increased response adaptation for frequently presented tones. Importantly, the statistical context in which tones were presented strongly modulated stimulus-specific adaptation. Physically and probabilistically identical stimuli (moderate deviants) in the two statistical contexts elicited different response magnitudes consistent with neural gain changes and thus neural sensitivity adjustments induced by the spectral range of a stimulus distribution. The data show that already at the level of the inferior colliculus stimulus-specific adaptation is dynamically altered by the statistical context in which stimuli occur.

the ability to adapt to specific aspects of an environment is a crucial feature of neural systems that support perception. Adaptation is important for perceiving environmental changes (Escera and Malmierca 2014; Jääskeläinen et al. 2007; Malmierca et al. 2014; Nelken 2014), anticipating future events (Henry and Herrmann 2014; Large and Jones 1999), and providing perceptual constancy across various contexts (Clifford et al. 2007). With respect to the neural system, two possibly related forms of adaptation are of particular interest to the present study: stimulus-specific adaptation and adaptation to stimulus statistics.

Stimulus-specific adaptation commonly refers to a reduction in the response to a repeatedly presented stimulus that does not generalize (or only partially) to other, rarely presented stimuli (Antunes et al. 2010; Bäuerle et al. 2011; Movshon and Lennie 1979; Nelken 2014; Ringo 1996; Taaseh et al. 2011). Examinations of stimulus-specific adaptation make use of oddball sequences in which the repetition of a standard sound is irregularly interrupted by a deviant sound (Gutfreund 2012; Malmierca et al. 2009; Ruhnau et al. 2012; Ulanovsky et al. 2003). Generally, responses to standard sounds are reduced compared with responses elicited by deviant sounds (Fishman and Steinschneider 2012; Malmierca et al. 2009). Stimulus-specific adaptation occurs throughout the auditory system and has been observed in the inferior colliculus (Duque et al. 2012; Malmierca et al. 2009; Patel et al. 2012; Pérez-González et al. 2005, 2012; Zhao et al. 2011), auditory thalamus (Anderson et al. 2009; Antunes et al. 2010; Bäuerle et al. 2011; Duque et al. 2014), and auditory cortex (Szymanski et al. 2009; Taaseh et al. 2011; Ulanovsky et al. 2003; von der Behrens et al. 2009) of animals as well as in human auditory cortex (Herrmann et al. 2015; May et al. 1999; May and Tiitinen 2004).

Adaptation to stimulus statistics refers to adjustments in the input-output function of a neuron or neural population based on statistical properties of a stimulus distribution, such that an identical sound (input) presented in different contexts elicits different neural responses (output). Statistical adaptation is not specific to one stimulus but instead affects responses to many different input stimuli. Adjustments in the input-output function of neurons can be induced by alterations in the mean as well as the variance of a stimulus distribution, or more complex distribution properties (Brenner et al. 2000; Dahmen et al. 2010; Dean et al. 2005; Hildebrandt et al. 2011; Kvale and Schreiner 2004; Nagel and Doupe 2006). These adjustments might constitute a mechanism by which a neuron maximizes its sensitivity to a particular stimulation context (Fairhall et al. 2001; Wark et al. 2007). Similar to stimulus-specific adaptation, adaptation to stimulus statistics has been observed throughout the auditory system, including the auditory nerve (Wen et al. 2009), inferior colliculus (Dahmen et al. 2010; Dean et al. 2005, 2008), and auditory cortex (Rabinowitz et al. 2011; Watkins and Barbour 2008) of animals as well as in human auditory cortex (Herrmann et al. 2013a, 2014).

One critical aspect of stimulus-specific adaptation relates to the degree to which adaptation is specific to the repeated stimulus. The fact that neurons along the auditory pathway are able to change their response sensitivity (input-output function) depending on the whole stimulation context/history (Hildebrandt et al. 2011; Wen et al. 2009) also allows for the possibility that stimulus-specific adaptation is context dependent and thus relates to stimulus-statistical adaptation (Wark et al. 2007). Indeed, inconsistencies between empirical and modeling data (Hershenhoren et al. 2014; Taaseh et al. 2011), reports of local and global stimulation influences (Ulanovsky et al. 2004; Zhao et al. 2011), as well as context effects in oddball paradigms (Yaron et al. 2012) suggest dynamic variations of stimulus-specific adaptation. Furthermore, recent human electroencephalography recordings offer additional support for dynamic modifications of stimulus-specific adaptation induced by the overall spectral stimulation distribution (Herrmann et al. 2015). In the latter study, it was concluded that the spectral stimulation distribution (i.e., the frequency range of tones within sequences) affects the degree of frequency-specific coadaptation in auditory cortex and in turn modulates stimulus-specific adaptation of individual tones within a sequence (Herrmann et al. 2014, 2015).

Several questions have thus far remained unanswered: 1) The human electroencephalography study showing dynamic modifications of stimulus-specific adaptation by the overall spectral stimulation distribution focused on neural responses at ∼0.1 s after stimulus onset (Herrmann et al. 2015), while traditional examinations of stimulus-specific adaptation concentrate on response magnitudes at ∼0.01–0.04 s using single and multiunit recordings in animals (for a review on the relation between human and animal recordings see Escera and Malmierca 2014). It thus remains to be examined whether context effects similar to those observed in human electroencephalography apply to stimulus-specific adaptation in animal recordings. 2) Neural sensitivity adjustments (i.e., changes in the input-output relation of neurons) to spectral properties of the stimulus distribution and the relation of these adjustments to stimulus-specific adaptation has been reported for auditory cortex responses of human electroencephalographic recordings that reflect the summed activity of many neurons (Briley and Krumbholz 2013; Herrmann et al. 2013a, 2014, 2015; Lanting et al. 2013). It is thus an empirical question whether context effects induced by the overall spectral stimulation distribution affect stimulus-specific adaptation in individual neurons at earlier regions of the auditory hierarchy.

Here we provide evidence from inferior colliculus recordings in rats that stimulus-specific adaptation is affected by the spectral distribution of stimuli. Our data suggest that the sensitivity with which the neural system detects deviations in the sound stimulation is relative to, and thus changes with, the global statistical context in which sounds are presented.

MATERIALS AND METHODS

Ethical approval.

The experimental procedures described in the present investigation were approved by the Institutional Animal Care and Use Committee of Purdue University (PACUC no. 1111000167). The experiments included in this study comply with the policies and regulations described in Drummond (2009). Rats were housed one per cage in accredited facilities (Association for Assessment and Accreditation of Laboratory Animal Care International) with food and water provided ad libitum. The number of animals used was reduced to the minimum necessary to allow adequate statistical analyses.

Surgical procedures.

Seven young (3–6 mo, ∼300 g) male Fischer 344 rats were used in this study. Methods for surgery, sound stimulation, and recording are similar to those described in Rabang et al. (2012). Surgeries and recordings were performed in a 9-ft × 9-ft double-walled acoustic chamber (Industrial Acoustics). Anesthesia was induced in the animals with a mixture of ketamine (VetaKet, 80 mg/kg) and medetomidine (Dexdomitor, 0.2 mg/kg) administered intramuscularly via injection. While anesthesia reduces spontaneous firing in inferior colliculus neurons, stimulus-specific adaptation (Duque and Malmierca 2015) as well as temporal firing precision (Ter-Mikaelian et al. 2007) appear to be largely unaffected by anesthesia. A constant physiological body temperature was maintained with a water-circulated heating pad (Gaymar) set at 37°C with the pump placed outside the recording chamber to eliminate audio and electrical interferences. The animals were maintained on oxygen through a manifold. The pulse rate and oxygen saturation were monitored with a pulse oximeter to ensure that they were within normal ranges during surgery. Supplementary doses of anesthesia (20 mg/kg ketamine, 0.05 mg/kg medetomidine) were administered intramuscularly as required to maintain areflexia and a surgical plane of anesthesia. An initial dose of dexamethasone and atropine was administered prior to incision to reduce swelling and mucosal secretions. A subdermal injection of lidocaine (0.5 ml) was administered at the site prior to first incision. A central incision was made along the midline and the calvaria exposed. A stainless steel headpost was secured anterior to bregma with an adhesive and three screws drilled into the skull to provide structural support for a head-cap constructed of orthodontic resin (Dentsply). A craniotomy was performed from 9 to 13 mm posterior to bregma, which extended posterior to the lambda suture, and 3 mm wide extending from the midline. The dura mater was kept intact, and the site of recording was estimated stereotaxically with a rat atlas (Paxinos and Watson 2006) as well as internal vasculature landmarks and physiological measurements. At the completion of recordings, animals were euthanized with Beuthanasia (200 mg/kg ip). Once areflexive, they were perfused transcardially with 150–200 ml of phosphate-buffered saline followed by 400–500 ml of 4% paraformaldehyde. The brain was then removed and stored or processed further for Nissl or immunohistochemistry.

Stimulus generation.

Sound stimuli were generated with SigGenRP (Tucker-Davis Technologies, TDT) at a 97.64 kHz sampling rate (standard TDT sampling rate) and presented through custom-written interfaces in OpenEx software (TDT). Sound waveforms were generated via a multichannel processor (RX6, TDT), amplified (SA1, TDT), and presented free-field through a Bowers and Wilkins DM601 speaker. The sounds were presented to the animal at azimuth 0° and elevation 0°, calibrated at a distance of 115 cm from speaker to ear, with a Bruel & Kjaer microphone and SigCal software (TDT).

Acoustic stimulation.

Four tones were chosen approximately centered around a unit's best frequency. Stimulus-specific adaptation has been shown to be strongest in the high-frequency edges of a unit's frequency response area (Duque et al. 2012). However, we chose to center the tone frequencies around a unit's best frequency in order to ensure that all four tones elicit a robust response under no-adaptation conditions and that the responses to the four tones do not differ considerably. Spacing between tones was 0.18 octaves to span 0.54 octaves across the four tones. Tone duration was 0.1 s (including 5 ms rise and fall times), and tones were presented at 20–40 dB above the unit's spike threshold. Neuronal activity was recorded in one “no-adaptation” block during which nonadapted responses were measured and in four “adaptation” blocks consisting of oddball sequences in which neuronal response adaptation was probed (Herrmann et al. 2015).

In the “no-adaptation” block, the four tone frequencies were randomly presented with an onset-to-onset interval of 3 s. Each of the four tone frequencies was presented 20 times. Responses to these tones were used to estimate the frequency-specific neural response magnitude for the nonadapted state of the unit.

Stimulation in the four adaptation blocks consisted of oddball sequences that comprised a series of standard tones (83.33%) that were irregularly interrupted by deviant tones (16.67%). A deviant tone was defined as a spectral change from the standard tone frequency and could take on one of three magnitudes within each sequence: small spectral change (Δf = 0.18 octave), moderate spectral change (Δf = 0.36 octave), and large spectral change (Δf = 0.54 octave; Fig. 1). Tones were presented isochronously with an onset-to-onset interval of 0.3 s. Tone presentation was randomized such that at least two standard tones were presented between two deviant tones, with a maximum of eight standard tone presentations between deviant tones. The number of standard tones preceding a deviant tone was counterbalanced across the different types of deviant tones.

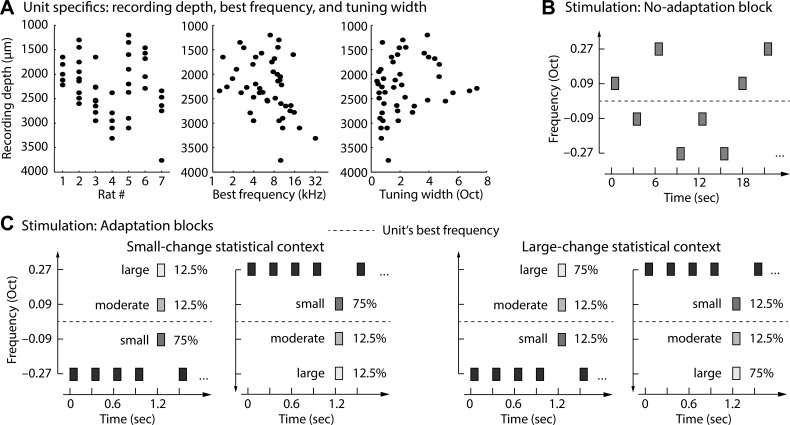
Fig. 1.

Description of units and experimental stimulation. A: recording depth, best frequency, and tuning width for each unit. Note that the graph does not provide information about the number of electrode penetrations within an animal. Dots may be the result of >1 penetration/track. B: a “no-adaptation” block consisted of random presentation of tones that could take on 1 of 4 frequencies. The onset-to-onset interval was 3 s. Responses to these tones were considered to reflect the maximal response amplitude when the neuron is in a nonadapted state. C: stimulus presentation in “adaptation” blocks comprised 2 statistical contexts. In the small-change statistical context the small deviant was presented with highest probability (relative to all deviants), while in the large-change statistical context the large deviant was presented with highest probability (relative to all deviants). Tones in the “adaptation” blocks were presented with an onset-to-onset interval of 0.3 s.

The critical manipulation was the probability of occurrence of a particular deviant tone within a block (Fig. 1C). In one block type (small-change statistical context; Fig. 1C), the deviant tone constituting a small spectral change was presented with 75% probability (relative to all deviant tones), while moderate and large deviants each occurred with 12.5% probability. In a second block type (large-change statistical context; Fig. 1C), the deviant tone constituting a large deviant was presented with 75% probability (relative to all deviant tones), while small and moderate deviants each occurred with 12.5% probability. Note that the moderate deviant was physically and probabilistically identical in both statistical contexts. Within a block, at least two high-probability deviants were presented between low-probability deviants.

Each block started with a period of silence (>5 s) to ensure that neural populations were fully responsive at the beginning of the acoustic stimulation. Then, each block type (small-change statistical context, large-change statistical context) was presented twice. Once the frequency of the standard tone was the lowest of the four frequencies, and once it was the highest frequency; starting block type was randomized across units. (For six units, only two blocks could be used for analysis because of technical problems during recording. None of the statistical results reported below is affected by the inclusion or exclusion of these units.) Within each block, standard tones were presented 1,200 times and deviant tones were presented 240 times. High-probability deviants were presented 180 times, and low-probability deviants were presented 30 times. Ten additional standard tones were presented at the beginning of each block to allow for a clear representation of the standard tone stream, and five were presented at the end to avoid the possibility of a deviant tone at the very end of a block.

Electrophysiological recording procedure.

Neural activity in the inferior colliculus was recorded in vivo (overall 45 units) with a tungsten microelectrode (A-M Systems) encased in a glass capillary that was advanced with a hydraulic microdrive (Narishige). We consider the present recordings to be multiunit activity, although the data set also includes a few clearly isolated neurons. The inferior colliculus was identified based on short-latency driven responses to tone stimuli. The central nucleus of the inferior colliculus was identified using the ascending tonotopy moving in a dorsoventral direction, as well as narrowly tuned responses to pure tones of various frequencies.

Neural signals were acquired with the tungsten microelectrode connected to a headstage (RA4, TDT) and amplified (RA4PA preamplifier, TDT). The digitized waveforms and spike times were recorded with a multichannel recording and stimulation system (RZ-5, TDT) at a sampling rate of 24.41 kHz (standard TDT sampling rate). The interface for acquisition and spike sorting was custom made with OpenEx and RPvdsEx software (TDT). The units acquired were filtered between 300/500 Hz and 5,000 Hz. The acquired spikes were stored in a data tank and analyzed with custom-written software in MATLAB. Local field potentials (LFPs) were simultaneously recorded from the same electrode by sampling at 3,051.8 Hz and band-pass filtering from 3 to 500 Hz. Line noise at 60 Hz was off-line removed from the LFP recordings with an elliptic notch filter (infinite-impulse response; zero-phase lag).

Dependent measures: firing rate, spike latency, and LFP amplitude.

In the present study, neural activity was recorded from 45 units. The analyses concentrated on firing rates, the latency of the first spike after tone onset, and the amplitude of the LFP. Analyses of firing rates focused on the time window from 0.01 to 0.04 s after tone onset, where firing rates were largest in the present (see Fig. 2) and previous (Lakatos et al. 2013; O'Connell et al. 2014; Ulanovsky et al. 2003) studies. The latency of the first spike was extracted from tone presentations eliciting at least one spike within the 0–0.1 s time window (duration of the tone stimulation; Antunes et al. 2010; Heil 2004; Malmierca et al. 2009). Spike latencies reported here include ∼3.4-ms travel time to the ear from the speaker. The amplitude of LFPs was analyzed in the time-frequency domain with wavelet convolution. That is, apart from the initial visualization of LFP time courses and N1 magnitudes (i.e., first major negative deflection at ∼0.015–0.03 s), LFPs were transformed to time-frequency evoked amplitudes. To this end, LFP time courses were averaged across trials, and the resulting time course was convolved with Morlet wavelets using a wavelet family with a constant ratio of f/σf = 6.28 (Tallon-Baudry et al. 1996; Tallon-Baudry and Bertrand 1999). Time-frequency representations were calculated for the −0.05 to 0.15 s time interval and the 2–200 Hz frequencies, and neuronal amplitudes were extracted as the magnitude of the complex wavelet coefficients. Analysis of LFP amplitude focused on the 0–0.04 s time window and the 30–100 Hz frequency area, where LFP responses were strongest (see Fig. 3). Note that the transformation of LFP time courses to time-frequency amplitudes allowed us to capture responses to tone onsets more precisely because deflections in the time domain signal were not clearly identifiable in some units. Furthermore, because time-frequency amplitudes have only positive values, the same analyses (described below) could be carried out for firing rates, spike latency, and LFP amplitude.

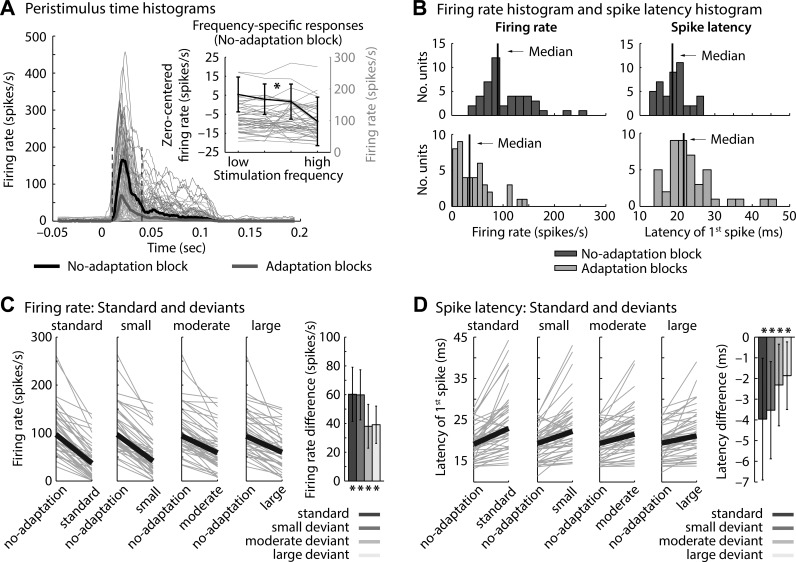
Fig. 2.

Firing rates and spike latencies in “no-adaptation” and “adaptation” blocks. A: peristimulus time histograms (rectangular window: 0.01 s; temporal resolution: 0.001 s) for tones in “no-adaptation” and “adaptation” blocks (thin lines, individual units; thick lines, median across units). Inset: firing rates (0.01–0.04 s) for individual tone frequencies in the “no-adaptation” block. Firing rates were significantly smaller for high compared with low frequencies relative to the unit's best frequency (P = 0.008). B: nonnormally distributed overall firing rates (0.01–0.04 s) and spike latencies. C: firing rates for each stimulus type (standards, small deviants, moderate deviants, and large deviants, irrespective of statistical context) compared with the physically identical stimulus in the “no-adaptation” block (gray lines, individual units, black lines, median across units). Bar graphs show the corresponding firing rate differences. *Significant difference from 0. D: similar to C for the latency of the first spike.

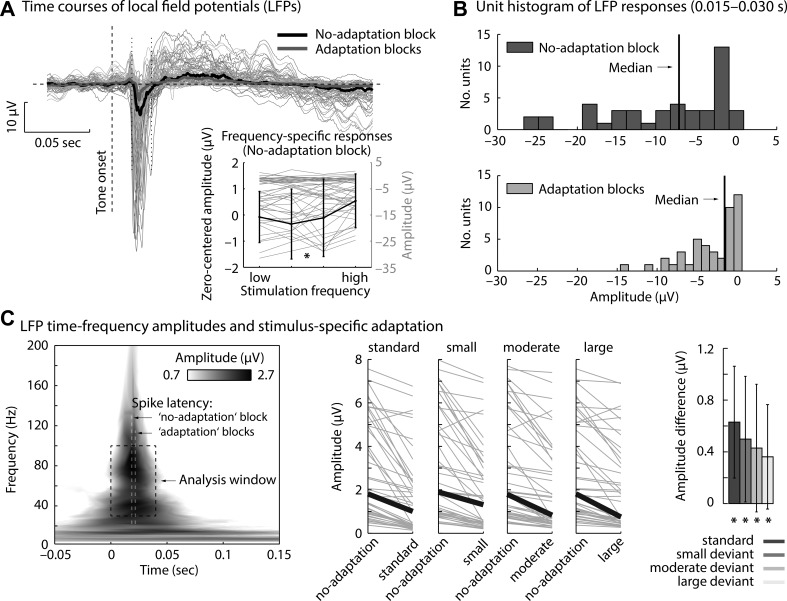
Fig. 3.

Local field potentials (LFPs) in “no-adaptation” and “adaptation” blocks. A: LFP time courses for tones in “no-adaptation” and “adaptation” blocks (thin lines, individual units; thick lines, median across units). Inset: median LFP amplitudes (0.015–0.03 s) for individual tone frequencies in the “no-adaptation” block. LFP amplitudes were significantly smaller (less negative) for high compared with low frequencies relative to the unit's best frequency (P = 0.015). B: nonnormally distributed overall LFP amplitudes (0.015–0.03 s). C, left: time-frequency representation of LFP amplitudes (median across units; responses to tones in the “no-adaptation” block). Rectangle marks the analysis time-frequency window (dashed line). Median spike latencies are displayed for reference. Center: LFP amplitudes (0–0.04 s, 30–100 Hz) for each stimulus type (standards, small deviants, moderate deviants, and large deviants, irrespective of statistical context) compared with the physically identical stimulus in the “no-adaptation” block (gray lines, individual units, black lines, median across units). Right: corresponding amplitude differences. *Significant difference from 0.

Data analysis: overall neural adaptation.

In a first overall analysis of neuronal response adaptation, we focused on contrasting neuronal responses elicited in the “no-adaptation” block with the neuronal responses elicited in the “adaptation” blocks. That is, for the three dependent measures (firing rates, spike latency, LFP amplitude), responses to all tones were separately averaged for the “no-adaptation” block and for the “adaptation” blocks.

We assessed whether the data were normal-distributed across units with Shapiro-Wilk tests. Differences in firing rate, spike latency, and LFP amplitude between the “no-adaptation” and the “adaptation” blocks were tested with nonparametric Wilcoxon signed-rank tests. Significantly larger firing rates and LFP amplitudes as well as shorter spike latencies to tones in the “no-adaptation” block compared with tones in “adaptation” blocks would indicate neural adaptation. Throughout this report, effect sizes are provided as r_equivalent (Rosenthal and Rubin 2003; hereafter referred to simply as r_e).

To investigate for each stimulus type in the “adaptation” blocks (standard, small deviant, moderate deviant, large deviant, irrespective of statistical context) whether neuronal responses showed adaptation, we contrasted firing rates, spike latency, and LFP amplitude of each stimulus type with the responses to the identical stimulus (i.e., tone frequency) in the “no-adaptation” block. That is, for each unit, the difference between the particular stimulus types in the “adaptation” blocks and their respective counterparts in the “no-adaptation block” was calculated. For each stimulus type (standard, small deviant, moderate deviant, large deviant), the median difference was then tested against zero with nonparametric Wilcoxon signed-rank tests.

Data analysis: influence of context on stimulus-specific adaptation.

To investigate the effect of stimulus-specific adaptation within the two statistical contexts, normalization of neuronal responses was necessary. That is, different tone frequencies led to slightly different overall response magnitudes (in the “no-adaptation” block) because of the neuron's frequency tuning; we observed lower firing rates (z = 2.23, P = 0.026, r_e = 0.328) and smaller LFP amplitudes (z = 2.34, P = 0.019, r_e = 0.344) for high-frequency compared with (the averaged) center-frequency tones (relative to the unit's best frequency; no difference was found between responses to low-frequency and center-frequency tones, both P > 0.4; see Fig. 2A and Fig. 3A). These condition-independent differences in overall response magnitude afforded normalization of neuronal response magnitudes across tone frequencies. In detail, we constructed for each unit a vector whose elements weighted the response magnitude for each tone frequency such that all tones elicited the same response magnitude (or spike latency) under no-adaptation conditions. To this end, responses of each of the four tone frequencies in the “no-adaptation” block were divided by the maximum response magnitude across the four tone frequencies:

$$w=\frac{r}{\max \left(r\right)}$$

where r reflects the four-element neuronal response vector corresponding to the four tone frequencies in the “no-adaptation” block and w reflects the frequency-specific weight vector. Responses to tones in the “adaptation” blocks were then normalized by dividing the response to each tone frequency by its respective element in the weight vector w. As a result, if there were no stimulus-specific adaptation, all four tone frequencies in the “adaptation” blocks would have the same response magnitude after normalization. The vector r comprised firing rates (0.01–0.04 s time window), latencies of the first spike after tone onset, or LFP amplitudes (0–0.04 s and 30–100 Hz time-frequency window).

For the statistical analysis, we did not use an analysis of variance to test for statistical differences along the two factors stimulus type (standard, small deviant, moderate deviant, large deviant) and statistical context (small change, large change) because neuronal responses were highly nonnormally distributed across units (see results). Instead, for each unit and separately for each statistical context, a linear function was fitted to neuronal responses as a function of frequency difference from the standard tone (0, 0.18, 0.36, 0.54 for standard, small deviant, moderate deviant, large deviant, respectively). For each statistical context, the median estimated linear coefficient was tested against zero with a Wilcoxon signed-rank test. Stimulus-specific adaptation is indicated by a median linear coefficient that is significantly larger than zero (for firing rate and LFP amplitude) or significantly smaller than zero (for spike latency). Differences between statistical contexts were assessed by testing the median linear coefficient for the small-change statistical context against the median linear coefficient for the large-change statistical context with a Wilcoxon signed-rank test. A significant difference reflects an interaction between stimulus type and statistical context. Finally, for each stimulus type separately, we tested whether neuronal responses differed between statistical contexts with a Wilcoxon signed-rank test.

In an additional analysis, we calculated (separately for each unit) the common stimulus-specific adaptation index (CSI; Antunes et al. 2010; Malmierca et al. 2009; Ulanovsky et al. 2003, 2004; von der Behrens et al. 2009) using the responses normalized for the neuron's frequency tuning. The CSI was calculated separately for each statistical context as the normalized difference between responses to deviant and standard tones:

$${\text{CSI}}_{\text{s}}=\frac{D_2+D_3-S_1-S_4}{D_2+D_3+S_1+S_4};\hspace{0.17em}{\text{CSI}}_{\text{m}}=\frac{D_3+D_2-S_1-S_4}{D_3+D_2+S_1+S_4};\hspace{0.17em}{\text{CSI}}_{\text{l}}=\frac{D_1+D_4-S_1-S_4}{D_1+D_4+S_1+S_4}$$

where CSI ranges from −1 to 1 (subscripts s, m, l refer to small, moderate, and large deviants, respectively) and D reflects the neuronal response magnitude (or spike latency) for a particular deviant tone and S the neuronal response magnitude (or spike latency) for the standard tone in the same statistical context. Subscripts associated with D and S refer to the four tone frequencies (1 = low . . . 4 = high). For each dependent measure (firing rate, spike latency, LFP amplitude), the formula led to a CSI for each deviant type (small, moderate, large) for the two statistical contexts (small change, large change). Statistical differences of the CSI between statistical contexts for each deviant type (small, moderate, large) were assessed with a Wilcoxon signed-rank test.

Spike number histograms and spike-LFP relation.

Single trials (tone presentations) were sorted into 10 bins according to the number of spikes (0–9) that were elicited within the 0.01–0.04 s analysis time window. For each bin, the relative proportion of trials with respect to the overall number of trials was calculated. The aim of this analysis was twofold. First, we aimed to explore the spikes-per-trial distribution underlying stimulus-specific adaptation. Second, we aimed to examine LFP amplitudes between conditions for trials eliciting the same number of spikes. This analysis might provide additional information about the level at which stimulus-specific adaptation and stimulus-statistical adaptation occur.

For this analysis, we first contrasted responses to standards, large deviants, and no-adaptation tones (i.e., we analyzed only those trials comprising lowest and highest tone frequencies) in order to investigate general adaptation effects. Second, we contrasted responses to moderate deviants in the two statistical contexts (small change, large change). Note that both contrast types controlled for the tone frequencies subjected to this analysis, and thus controlled for overall response differences related to the unit's frequency tuning (see above).

RESULTS

Overall neural adaptation: firing rate and spike latency.

Overall neural adaptation (ignoring frequency difference and statistical context) is visualized in Fig. 2, A and B. That is, peristimulus time histograms were separately calculated for tones in the “no-adaptation” block and for tones in “adaptation” blocks. Firing rates (0.01–0.04 s) were nonnormally distributed across units for “no-adaptation” and for “adaptation” blocks (both P < 0.005). The median firing rate (0.01–0.04 s) in the “no-adaptation” block (89.6 spikes/s) was significantly larger than in the “adaptation” blocks (34.7 spikes/s; z = 5.84, P < 0.001, r_e = 0.737; Fig. 2B, left). Furthermore, latencies of the first spike after tone onset were nonnormally distributed across units for “no-adaptation” and for “adaptation” blocks (both P < 0.001). The median first-spike latency was significantly shorter for tones in the “no-adaptation” blocks (18.7 ms) compared with tones in the “adaptation” blocks (21.7 ms; z = 5.03, P < 0.001, r_e = 0.664; Fig. 2B, right).

To investigate whether neuronal responses to standard and deviant tones in the “adaptation” blocks showed adaptation, firing rates for standards and deviants (independent of statistical context) were contrasted with the firing rates observed in the “no-adaptation” block (Fig. 2C). The median firing rate difference between “no-adaptation” and “adaptation” blocks (comparing physically identical tones) was significantly larger than zero for standards as well as for small, moderate, and large deviants (for all, z > 5.70, P < 0.001, r_e > 0.72). Furthermore, the median spike latency difference (between “no-adaptation” and “adaptation” blocks, accounting for specific tone frequencies) was significantly smaller than zero for standards as well as for small, moderate, and large deviants (for all, z = 5.30, P < 0.001, r_e > 0.65; Fig. 2D). Thus tones in the “no-adaptation” block elicited larger firing rates and shorter spike latencies compared with standard and deviant tones in “adaptation” blocks, indicating neural response adaptation.

Overall neural adaptation: local field potential.

Overall neural adaptation of LFPs (ignoring particular stimulus types) is visualized in Fig. 3, A and B. Response time courses for tones in the “no-adaptation” block and for tones in “adaptation” blocks show a negative-going deflection at ∼0.015–0.03 s after tone onset. Amplitudes of the LFP (0.015–0.03 s) were nonnormally distributed across units for “no-adaptation” and “adaptation” blocks (both P < 0.001). The median amplitude (0.015–0.03 s) in the “no-adaptation” block (−7.24 μV) was significantly more negative than in the “adaptation” blocks (−1.53 μV; z = 5.78, P < 0.001, r_e = 0.732; Fig. 3B). Similarly for time-frequency representations (0–0.04 s, 30–100 Hz; Fig. 3C), amplitudes were nonnormally distributed across units for “no-adaptation” and “adaptation” blocks (both P < 0.001) and the median amplitude was larger in “no-adaptation” than in “adaptation” blocks (z = 5.47, P < 0.001, r_e = 0.705).

To investigate whether neuronal responses to standard and deviant tones in the “adaptation” blocks showed adaptation, LFP amplitudes (0–0.04 s, 30–100 Hz) for standards and deviants (independent of statistical context) were contrasted with LFP amplitudes observed for physically identical tones in the “no-adaptation” block (Fig. 3C). The median LFP amplitude difference between “no-adaptation” and “adaptation” blocks was significantly larger than zero for standards as well as for small, moderate, and large deviants (for all, z > 5.30, P < 0.001, r_e > 0.68).

Statistical context affects stimulus-specific adaptation.

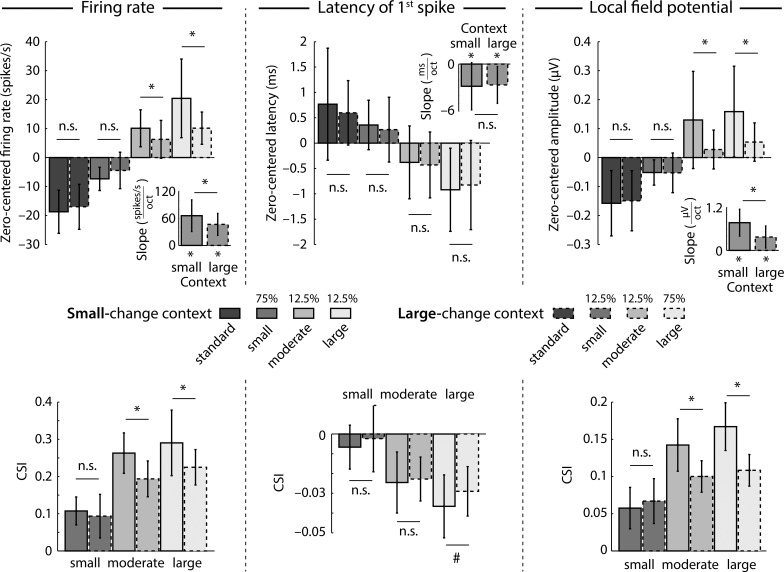
The effects of statistical context on neural response magnitude (firing rate, LFP amplitude) and response latency are depicted in Fig. 4. The influence of statistical context on firing rate was investigated by linear trend analysis. In the small-change as well as the large-change statistical context, slopes (linear coefficients) were significantly larger than zero (small-change context: z = 5.80, P < 0.001, r_e = 0.733; large-change context: z = 5.71, P < 0.001, r_e = 0.726), showing that firing rates increased as a function of deviant magnitude (i.e., degree of spectral change). Furthermore, the slope for the small-change statistical context was larger than that for the large-change statistical context (z = 4.51, P < 0.001, r_e = 0.611), indicating an interaction between stimulus type and statistical context. Direct comparisons between statistical contexts separately for each stimulus type showed significantly larger firing rates for the small-change compared with the large-change context for moderate (z = 3.19, P = 0.001, r_e = 0.457) and large (z = 4.27, P < 0.001, r_e = 0.585) deviants but not for standards (z = 1.55, P = 0.121, r_e = 0.232) and small deviants (z = 1.21, P = 0.225, r_e = 0.182). Consistent with these analyses, examination of the CSI revealed significantly larger indices for the small-change compared with the large-change context for moderate (z = 4.10, P < 0.001, r_e = 0.566) and large (z = 4.48, P < 0.001, r_e = 0.607) deviants but not for small deviants (z = 1.46, P = 0.144, r_e = 0.212).

Fig. 4.

Effects of statistical context on neural responses. Top: median firing rates, latency of 1st spike, and LFP amplitudes for each stimulus type (standard, small deviant, moderate deviant, large deviant) and statistical context (small-change context, large-change context). Separately for each unit, responses were zero-centered by subtracting the mean response across all stimulus conditions from the response of each individual stimulus condition. Insets: slope of the linear fit that reflects the degree of change as a function of tone frequency. Bottom: common stimulus-specific adaptation index (CSI) for each dependent measure (firing rate, spike latency, LFP). Bar graphs reflect the median across units. Error bars reflect the semi-interquartile range. *P < 0.05, ^#P < 0.1. n.s., Not significant.

Similar to the analysis of firing rates, the latency of the first spike was analyzed with linear trend analysis (Fig. 4). For both contexts, slopes were significantly smaller than zero (small-change context: z = 4.53, P < 0.001, r_e = 0.613; large-change context: z = 5.12, P < 0.001, r_e = 0.673), indicating shorter spike latencies for larger spectral changes (i.e., deviant magnitude). The direct comparison of slopes between contexts was not significant (z = 0.62, P = 0.538, r_e = 0.093); neither were the direct comparisons for each stimulus type (for all, z < 1.60, P > 0.10, r_e < 0.25). The analysis of the CSI revealed similar results. There was no difference between contexts for small (z = 1.48, P = 0.138, r_e = 0.222) and moderate (z = 0.19, P = 0.852, r_e = 0.028) deviants and a marginal effect for large deviants (z = 1.95, P = 0.052, r_e = 0.289). We observed, however, that neurons with longer first-spike latencies exhibit larger mean spike CSI values (i.e., more adaptation; Spearman correlation: r = 0.520, P < 0.001).

Linear trend analysis of LFPs revealed significant positive slopes for the small-change (z = 5.51, P < 0.001, r_e = 0.709) and large-change (z = 5.24, P < 0.001, r_e = 0.684) statistical contexts, showing that the LFP amplitude increased as a function of deviant magnitude (i.e., degree of spectral change). Furthermore, a significantly larger slope was observed for the small-change compared with the large-change statistical context (z = 5.45, P < 0.001, r_e = 0.703), indicating an interaction between stimulus type and statistical context. Direct comparisons of LFP amplitudes between statistical contexts independently for each stimulus type showed significantly larger amplitudes for moderate (z = 2.76, P = 0.006, r_e = 0.401) and large (z = 5.46, P < 0.001, r_e = 0.704) deviants, while there was no significant difference for standards (z = 0.03, P = 0.978, r_e = 0.004) and small deviants (z = 0.67, P = 0.502, r_e = 0.102). These results were confirmed by the analysis of the CSI, for which larger indices were observed for the small-change compared with the large-change context for moderate (z = 2.99, P = 0.003, r_e = 0.430) and large (z = 5.45, P < 0.001, r_e = 0.703) deviants but not for small deviants (z = 0.77, P = 0.439, r_e = 0.117).

To summarize, firing rate, spike latency, and LFP amplitude show stimulus-specific adaptation. Neuronal responses increased and spike latencies decreased with increasing frequency difference between standard and deviant stimuli. Critically, we also observed that the statistical stimulation context had a strong influence on firing rate and LFP response magnitudes, while spike latency was unaffected by the statistical context. That is, neural response magnitudes for the moderate deviant were lower in the large-change context than in the small-change context although the moderate deviant was physically and probabilistically identical in both contexts. Our findings thus suggest that neural sensitivity in the inferior colliculus depends on the statistical stimulation context.

Spike number histograms and spike-LFP relation.

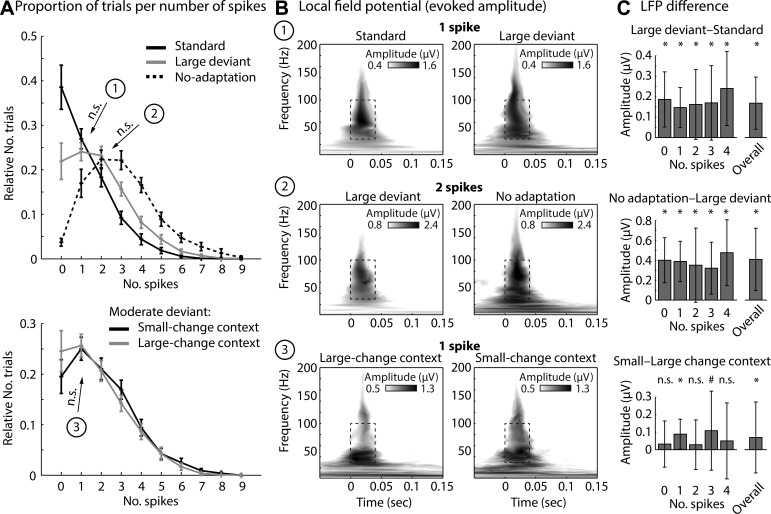
Trial-by-trial analysis of spiking and LFP activity allowed us to evaluate whether synaptic inputs and local activity (LFPs) differed under different stimulus types and statistical contexts for matched spiking output. Trials were sorted into bins according to the number of spikes elicited on individual trials (Fig. 5A). The resulting spike number histograms describe the effects of response adaptation in oddball blocks and in the “no-adaptation” block. That is, the relative number of trials eliciting no spike is largest for tones repeatedly presented (standards) compared with rare spectral changes (large deviants; z = 4.91, P < 0.001, r_e = 0.674) and tones in the “no-adaptation” block (z = 5.37, P < 0.001, r_e = 0.721). Conversely, the relative number of trials eliciting at least one spike is larger for deviants and “no-adaptation” tones compared with standards (Fig. 5A).

Fig. 5.

Relation between spikes and LFPs. A: spike histograms showing the relative number of trials that elicited 1, 2, 3, etc. trials (mean across units; error bars reflect SE). Top: relative number of trials for standards, large deviants, and tones in the “no-adaptation” block. Bottom: moderate deviants in the small-change and large-change contexts. B: time-frequency representations of LFP amplitudes for 3 different contrasts for which no difference between the relative number of trials was observed while keeping the number of spikes constant: standard vs. large deviant (trials eliciting 1 spike); large deviant vs. no-adaptation tones (trials eliciting 2 spikes); moderate deviants in the small-change vs. large-change statistical context (trials eliciting 1 spike). C: difference in LFP amplitude for the 3 contrasts, separately for each spike bin and across all spike bins. *P < 0.05, ^#P < 0.1.

Next, we extracted the LFP amplitude from time-frequency representations for two specific contrasts for which the relative number of trials within a spike bin did not statistically differ (both P > 0.15). In this case, the spiking output was identical, but we wished to compare whether the synaptic and nearby spiking activity was also comparable. For the first contrast, the LFP amplitude for large deviant tones eliciting one spike was significantly larger than the LFP amplitude for standard tones eliciting one spike (z = 3.89, P < 0.001, r_e = 0.577; Fig. 5, B and C). For the second contrast, the LFP amplitude for tones in the “no-adaptation” block that elicited two spikes was significantly larger than the LFP amplitude for large deviant tones eliciting two spikes (z = 3.98, P < 0.001, r_e = 0.593; Fig. 5, B and C). Hence, although the number of spikes elicited was the same across the two conditions, LFPs showed stimulus-specific adaptation.

Finally, we calculated spike number histograms for the moderate deviant tones in the two statistical contexts (small change, large change). Moderate deviants in the large-change context were more likely to elicit no spike compared with moderate deviants in the small-change context (z = 3.19, P = 0.001, r_e = 0.487; Fig. 5A, bottom). The LFP amplitudes from time-frequency representations were then extracted from trials that elicited one spike for the moderate deviants in both statistical contexts, that is, for the spike histogram bin for which the relative number of trials did not differ statistically (z = 0.93, P = 0.350, r_e = 0.152). LFP amplitudes were significantly larger for moderate deviants in the small-change context compared with the large-change context (z = 2.88, P = 0.004, r_e = 0.445; Fig. 5, B and C). Hence, although the number of spikes elicited on a trial was the same, LFP amplitudes for moderate deviants were different between statistical contexts, consistent with the results from Fig. 4.

Recording site.

Previous work has shown that stimulus-specific adaptation is much stronger in nonlemniscal subdivisions of the inferior colliculus (i.e., dorsal and lateral inferior colliculus; Duque et al. 2012; Duque and Malmierca 2015). Our observed CSI values (Fig. 4) are consistent with having recorded from nonlemniscal subdivisions mainly. Although there was a significant number of sharply tuned neurons (Fig. 1A), there was not a significant correlation between tuning sharpness at the sound levels tested (generally 20–40 dB above threshold) and CSI (Spearman correlation: r = −0.141, P = 0.356). Previous studies have demonstrated significant overlap in tone tuning properties between lemniscal and nonlemniscal inferior colliculus (Palombi and Caspary 1996; Syka et al. 2000), with lemniscal inferior colliculus having more sharply tuned and shorter-latency responses on average. Our dorsal approach may have made it more likely to record from dorsal inferior colliculus, and one animal had verified recording sites in dorsal inferior colliculus.

Effects of deviant-to-deviant suppression.

In the present study, deviants occurred pseudorandomly in time such that in some instances the time between two deviants of the same type was shorter and in some instances it was longer. Here we tested whether the interval between two deviant tones of the same type contributes to neural adaptation. For each deviant type (small, moderate, large) and statistical context (small change, large change) we tested whether firing rates were smaller for short compared with long intervals between two deviants of the same type. We selected the 35% of trials with the shortest intervals (≤1.8 s or ≤8.5 s, for high- vs. low-probability deviants, respectively) to the preceding same deviant and the 35% of trials with the longest intervals (≥2.7 s or ≥15 s, for high- vs. low-probability deviants, respectively) to the preceding same deviant. The choice of 35% of trials reflects the balance between maximizing the separation between groups and including a sufficient number of trials per group. Firing rates were calculated, and nonparametric Wilcoxon signed-rank tests compared responses for short vs. long preceding intervals. We observed larger firing rates for long compared with short intervals only for the large deviant in the large-change context (small-change context: z = 1.05, P = 0.294, r_e = 0.158; large-change context: z = 3.75, P < 0.001, r_e = 0.526), while no statistical differences were observed for the small (small-change context: z = 1.19, P = 0.234, r_e = 0.179; large-change context: z = 0.22, P = 0.827, r_e = 0.033) and moderate (small-change context: z = 0.09, P = 0.925, r_e = 0.014; large-change context: z = 0.13, P = 0.896, r_e = 0.020) deviants.

Next, we tested whether the firing rate of moderate deviants is affected by the temporal distance to the other deviants. On this basis, we selected the 35% of the moderate-deviant trials with the shortest intervals (≤1.5 s) to a preceding other deviant and the 35% of moderate-deviant trials with the longest intervals (≥2.1 s) to a preceding other deviant. Firing rates were calculated, and nonparametric Wilcoxon signed-rank tests compared responses for short vs. long preceding intervals. We observed no differences between firing rates elicited by moderate deviants depending on short vs. long time intervals to preceding other deviants (z = 1.08, P = 0.276, r_e = 0.164). Overall, these results show that the time interval between two deviants has only a small impact on neural adaptation in the present study.

Effects of spike history on neural adaptation.

One distinction that has been made is the separation into adaptation that depends on the activation history and adaptation that depends on the stimulus history (Gutfreund 2012). The results above clearly show the relation between stimulation history and neural response adaptation (Fig. 4). Here, we further explored the role of the spike history on neural responses.

We investigated the impact of the last-spike latency of the previous trial on spike latency and firing rate of the subsequent tone presentation. In detail, we tested whether the latency of the last spike of the preceding trial differed depending on whether or not one or more spikes were elicited in the subsequent trial. We did not observe a difference between spike latencies (z = 1.37, P = 0.172, r_e = 0.205). We also tested whether the latency of the last spike on the preceding trial is correlated with the latency of the first spike on the subsequent trial. Separately for each unit, we fitted a linear function to the first-spike latency (i.e., from the subsequent trial) as a function of last-spike latency (i.e., from the preceding trial). The slope of the linear fit was tested against zero, but no significant difference was found (z = 0.90, P = 0.370, r_e = 0.135). We further tested whether the number of spikes elicited on the subsequent trial is affected by the latency of the last spike of the preceding trial. We sorted trials into five bins of 0 to 4 spikes elicited on the subsequent trial and calculated for each bin the mean last-spike latency of the preceding trial. No differences were found in last-spike latencies across the number of spikes elicited on the subsequent trial (all P > 0.3). These analyses show that the spike closest to the subsequent tone presentation did not impact the firing elicited by the tone.

We additionally tested whether the number of spikes elicited on the preceding trial affects the number of spikes elicited on the following trial. We sorted trials into five bins of 0 to 4 spikes elicited on the preceding trial and calculated for each bin the mean number of spikes elicited on the subsequent trial. Here we observed a significant difference that, however, was in the opposite direction of what would be expected based on response history effects. We observed that the number of spikes on the subsequent trial was larger when the preceding trial elicited 4 spikes compared with no spike (z = 3.06, P = 0.002, r_e = 0.441). Notably, this effect was absent when the relation was restricted to standards (preceding trial) and deviants (subsequent trial; z = 0.43, P = 0.667, r_e = 0.065). In the present study, the effects of spike-dependent adaptation were thus negligible over stimulus-dependent adaptation.

DISCUSSION

The present study investigated the degree to which the statistical context in which stimuli are presented affects stimulus-specific adaptation. We observed that neurons in the inferior colliculus of rats adapted depending on the statistical context such that physically and probabilistically identical stimuli in different spectral stimulation contexts elicited different response magnitudes. The present findings show that the way neurons respond depends dynamically on the properties of the whole stimulus distribution.

Stimulus-specific adaptation and adaptation to stimulus statistics.

Stimulus-specific adaptation refers to a reduction in neural response magnitude to a repeatedly presented stimulus that does not generalize (or only partially) to other stimuli (Gutfreund 2012; Movshon and Lennie 1979; Nelken 2014; Ringo 1996). Consistent with stimulus-specific adaptation, we observed larger firing rates and LFP amplitudes as well as shorter spike latencies for rare stimuli (deviants) compared with repeated stimuli (standards). Furthermore, firing rates and LFP amplitudes to deviants increased and spike latencies decreased as a function of increasing frequency distance to the standard stimulus. Similar modulations of firing rate, LFP amplitude, and spike latency have also been reported in previous studies (Antunes et al. 2010; Hershenhoren et al. 2014; Malmierca et al. 2009; Patel et al. 2012; Ulanovsky et al. 2003; von der Behrens et al. 2009; Zhao et al. 2011).

Critically, the present data show that neural response magnitudes (firing rates and LFP amplitudes) are not only related to the probability with which a specific stimulus is presented but in addition are affected by the whole stimulation distribution. In detail, neural responses to deviants of different magnitude were compared between two statistical contexts: In one context, a higher proportion of small spectral changes was presented (small-change statistical context); in the other context, a higher proportion of large spectral changes was presented (large-change statistical context). The paradigm was chosen to increase the neuron's response sensitivity to deviants in the small-change statistical context and to decrease sensitivity in the large-change statistical context based on the spectral properties of the stimulus distributions (Herrmann et al. 2015). We hypothesized that differences in the relative occurrence of large spectral changes would affect neural response magnitudes to all stimuli in the sequence (Herrmann et al. 2013b, 2014, 2015).

Consistent with our hypothesis, the present data suggest a general increase in neural responses to all spectral changes in the small-change statistical context compared with the large-change statistical context (Fig. 4). That is, the probability with which small spectral changes occurred was higher in the small-change compared with the large-change statistical context. Hence, responses to small spectral changes in the small-change context should have been smaller if only the probability of stimulus occurrence would affect response adaptation. However, we observed no difference between contexts for small spectral changes. Furthermore, we observed larger responses to moderate and large deviants in the small-change compared with the large-change statistical context. Specifically, the probability of moderate spectral changes was similar within the two contexts and the difference in response magnitude can thus not be due to a general decrease (or increase) as a function of stimulus probability. Finally, the present observations cannot be due to differences in the timescale of adaptation for different stimuli in a sequence (Ulanovsky et al. 2004; Zhao et al. 2011), because moderate spectral changes were physically and probabilistically identical in both statistical contexts. Indeed, estimating the timescale of adaptation independently for different stimuli of a stimulation distribution (e.g., standards vs. deviants) could be misleading when neural responses are influenced by all stimuli presented.

The present observations are relevant regarding a recently emerging hypothesis that stimulus-specific adaptation might be a dynamic rather than a static phenomenon (Hershenhoren et al. 2014; Taaseh et al. 2011). Inconsistencies between current stimulus-specific adaptation models and empirical data from stimulus-specific adaptation studies further suggest additional contributions to the commonly observed adaptation effects (Nelken 2014). The present results indicate that neurons in the inferior colliculus adjust their response sensitivity based on the differences in the overall spectral stimulation distribution between statistical contexts, similar to what has been observed for human auditory cortex (Herrmann et al. 2013a, 2014, 2015).

Context dependence of neural responses throughout the auditory hierarchy.

The present study was motivated by a recent observation from human electroencephalography that stimulus-specific adaptation in auditory cortex was influenced by the relative probability of large spectral changes within oddball sequences (Herrmann et al. 2015). The data suggested flexible adjustments of coadaptation within tonotopically organized regions of auditory cortex. Here we used the same stimulation paradigm as in our human electroencephalography study, with the exception of a faster stimulus presentation interval (0.3 s vs. 0.5 s) and smaller spectral changes (0.54 octaves vs. 0.95 octaves for the large deviant) in the present compared with the previous study. These differences were mainly motivated by differences between local unit and global population level activities. Similar to the context effects observed for human auditory cortex responses, we show here that neurons in the inferior colliculus of rats exhibit different response sensitivities to tones depending on the statistical context in which stimuli are presented. Hence, context dependence of stimulus-specific adaptation is present at different stages in the auditory hierarchy, including inferior colliculus and auditory cortex.

Previous studies reported local as well as global influences on stimulus-specific adaptation in auditory cortex (Costa-Faidella et al. 2011; Ulanovsky et al. 2004) as well as in inferior colliculus (Zhao et al. 2011). For example, directly preceding stimuli (local history) as well as the overall probability of the spectral change (global history) modulated neural responses to tones. The present study extends those previous reports of global influences on adaptation by showing that the frequency range of the stimulation distribution in oddball sequences affects the neuron's response sensitivity and thus stimulus-specific adaptation. Our results are consistent with previous studies in animals (Hershenhoren et al. 2014; Taaseh et al. 2011) and humans (Herrmann et al. 2013a, 2013b) that have utilized a paradigm in which the frequency of tones randomly varied from trial to trial. In these studies, manipulation of the overall frequency range of the stimulation led to changes in the degree to which neural responses adapted. The combination of evidence from different stimulation paradigms including random frequency sequences and oddball sequences highlights the role of spectral stimulation properties in shaping neural response sensitivity in the auditory system.

More generally, adjustments of a neuron's sensitivity to different statistical properties of a stimulus distribution (e.g., its mean) are present at the earliest stages of the auditory hierarchy including the auditory nerve (Wen et al. 2009, 2012) and neurons that receive direct input from receptor neurons (Hildebrandt et al. 2011). Beyond these early stages, adaptation to statistical properties of a stimulus distribution has been observed for neurons in the inferior colliculus (Dahmen et al. 2010; Dean et al. 2005, 2008; Kvale and Schreiner 2004) and auditory cortex (Herrmann et al. 2014, 2015; Rabinowitz et al. 2011; Watkins and Barbour 2008) (for reviews see Robinson and McAlpine 2009; Willmore et al. 2014). Studies investigating adaptation to the statistics of a stimulus distribution at levels up to the inferior colliculus have mainly used sound intensity as the critical stimulus manipulation (Dean et al. 2005, 2008; Hildebrandt et al. 2011; Wen et al. 2009, 2012) (for adaptation to auditory spatial stimulation distributions see Dahmen et al. 2010). Changes in neural sensitivity to spectral stimulus distributions have thus far only been reported for auditory cortex neurons (Rabinowitz et al. 2011). Here we show that spectral properties of the stimulus distribution also affect the response sensitivity of neurons in the inferior colliculus. Furthermore, we observed effects of statistical context for LFP data, suggesting presynaptic adaptation to stimulus statistics in the inferior colliculus.

Other influences of context.

The present study focused on stimulus-specific and stimulus-statistical adaptation, but other (potentially related) forms of adaptation have been reported. For example, forward masking/suppression refers to an increase in perceptual threshold (Jesteadt et al. 1982; Oxenham and Plack 2000) and to a decrease of neural activity (Bartlett and Wang 2005; Brosch and Schreiner 1997; Calford and Semple 1995; Nelson et al. 2009; Wehr and Zador 2005) of the second tone in a sequential two-tone stimulation paradigm. While previous reports considered forward suppression a stimulus-unspecific form of adaptation (Gutfreund 2012), a recent modeling study suggests a functional link between stimulus-specific adaptation and forward suppression (May et al. 2015). The present data can speak only indirectly to the relation between forward suppression and stimulus-specific adaptation, but our analyses of deviant-to-deviant suppression suggest a limited role of forward suppression in the present study. Previous observations show that forward suppression is strongest for low sound levels of the second tone (Buchsbaum et al. 1971; Scholl et al. 2008), while the sound level was held constant across tones in the present study. Furthermore, effects of forward suppression are often short-lived such that neural responses recover within 300 ms (Brosch and Schreiner 1997; Scholl et al. 2008), although suppression of up to 2 s has been reported (Abolafia et al. 2011), in particular for sounds with longer durations (Bartlett and Wang 2005). However, most of the previous reports on forward suppression investigated neurons in auditory cortex (Abolafia et al. 2011; Bartlett and Wang 2005; Brosch and Schreiner 1997; Calford and Semple 1995; Scholl et al. 2008; Wehr and Zador 2005). Investigations for the inferior colliculus are rare and suggest short-lived forward suppression (Nelson et al. 2009).

In addition to adaptation that is dependent on the stimulation history, neural responses might also be adapted depending on the spike history (Gutfreund 2012). For example, in a forward suppression experiment, response suppression of the second tone seemed to be strongest when the preceding tone elicited a spike (Brosch and Schreiner 1997). Other studies, however, could not find such a relation between the response magnitude of the preceding sound and the response magnitude of the succeeding sound (Bartlett and Wang 2005; Calford and Semple 1995). Similarly, the present analyses of spike latency and number of spikes provided no indication of spike-dependent adaptation of responses elicited by tone stimuli. Hence, stimulus-statistical and stimulus-specific adaptation seem relatively robust to spike-dependent adaptation.

Mechanisms of neural adaptation in spectral context.

The mechanisms underlying stimulus-specific adaptation appear to be multifaceted and may differ between brain regions. For example, stimulus-specific adaptation has been proposed to emerge from a combination of synaptic depression and neural inhibition (Loebel et al. 2007; Ulanovsky et al. 2004). However, the role of GABA_A-mediated inhibition has been further specified in recent studies showing that neural inhibition modulates rather than causes stimulus-specific adaptation (Duque et al. 2014; Pérez-González et al. 2012; but see also Loebel et al. 2007). Longer-lasting GABA_B inhibition has not been investigated thus far. Another likely group of mechanisms that may contribute to adaptation are intrinsic membrane properties. Approximately half of inferior colliculus neurons will adapt their firing rates to sustained currents (Rabang et al. 2012; Sivaramakrishnan and Oliver 2001), due to activation of potassium currents. This has also been observed in the cortex of awake rats in a forward suppression paradigm (Abolafia et al. 2011). Finally, complex network connections have additionally been proposed to play a role in shaping stimulus-specific adaptation (Ulanovsky et al. 2004).

Stimulus-statistical adaptation is commonly associated with adjustments of the gain of a neuron's input-output function (i.e., stimulus-to-response mapping; Hildebrandt et al. 2011). Gain adjustments nonlinearly change the probability of a neuron to elicit a response, in particular for strong and to a lesser degree for weak stimuli. Nonlinear changes in a neuron's input-output function have been linked to neural inhibition (Hildebrandt et al. 2011; Ingham and McAlpine 2005; Olsen and Wilson 2008; Wilson et al. 2012) and synaptic depression (Abbott et al. 1997; Rothman et al. 2009) and might be related to network connections (Willmore et al. 2014) and network states (Reig et al. 2015) (for reviews on neural gain control see Robinson and McAlpine 2009; Salinas and Thier 2000; Silver 2010). Consistent with changes in neural gain, the present results show increased response sensitivity specifically for deviant tones in the small-change context compared with the large-change context.

The apparent overlap of neural mechanisms (synaptic depression, neural inhibition, network of neurons) between the two types of adaptation suggests that stimulus-specific adaptation might reflect a special case of stimulus-statistical adaptation (Wark et al. 2007). Indeed, the present data from inferior colliculus neurons show that stimulus-specific adaptation is not only related to the probability of a particular stimulus in oddball sequences but additionally changes depending on the spectral stimulation distribution.

While our previous human electroencephalography study showed context dependence of stimulus-specific adaptation in auditory cortex (Herrmann et al. 2015), the present study revealed similar effects for neurons in the inferior colliculus. The inferior colliculus is an important brain structure that reflects a major hub for integrating information from ascending and descending pathways (Lee and Sherman 2010; Suga et al. 2000). Whether the release of adaptation for deviant tones and the modulatory change of this release by spectral context emerge within the inferior colliculus is the topic of ongoing research. Stimulus-specific adaptation likely arises within ascending auditory pathways because responses occur early (∼20 ms after stimulus onset) and muting descending connections from auditory cortex leaves stimulus-specific adaptation largely unaffected (Anderson and Malmierca 2013; Antunes and Malmierca 2011; Malmierca et al. 2015). The inferior colliculus is thus far the earliest brain structure for which stimulus-specific adaptation has been observed (Ayala et al. 2013; Malmierca et al. 2009). However, we observed that standards and deviants eliciting the same spike output differed in their respective LFP amplitudes, which raises the possibility that stimulus-specific adaptation emerges already at the synaptic input level of the inferior colliculus neurons.

The likely emergence of stimulus-specific adaptation within ascending auditory pathways does not exclude the possibility that modulatory influences on stimulus-specific adaptation by spectral context rely on, for example, descending pathways from auditory cortex. Adaptation to stimulus statistics requires integrating information over multiple seconds in order to estimate, for example, the frequency range of a stimulation distribution (Herrmann et al. 2014). Adjustments of a neuron's sensitivity to spectral changes in the stimulation could thus reflect the outcome of integration and estimation at a different level of the auditory pathway. Nevertheless, the extent to which the present observations reflect interplay between ascending and descending pathways is subject to future studies.

Conclusions.

The present study investigated stimulus-specific adaptation of inferior colliculus neurons in different statistical contexts. Statistical contexts differed in their relative probability with which a large spectral change occurred within a repetitive sequence. We observed that physically and probabilistically identical stimuli in the two statistical contexts elicited different response magnitudes. Our results show that global characteristics of a stimulus distribution affect responses to individual stimuli. The data suggest that neurons in the inferior colliculus dynamically adjust their response sensitivity using the information about the spectral range in the stimulation.

GRANTS

This research is supported by the Max Planck Society. B. Herrmann and J. Obleser were supported by a Max Planck Research Group grant to J. Obleser. E. L. Bartlett, E. X. Han, and A. Parthasarathy were supported by National Institute on Deafness and Other Communication Disorders Grant DC-0011580.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: B.H., J.O., and E.L.B. conception and design of research; B.H., A.P., E.X.H., and E.L.B. performed experiments; B.H. and E.L.B. analyzed data; B.H., A.P., E.X.H., J.O., and E.L.B. interpreted results of experiments; B.H. prepared figures; B.H., A.P., E.X.H., J.O., and E.L.B. drafted manuscript; B.H., A.P., E.X.H., J.O., and E.L.B. edited and revised manuscript; B.H., A.P., E.X.H., J.O., and E.L.B. approved final version of manuscript.