Counting on dis-inhibition: a circuit motif for interval counting and selectivity in the anuran auditory system

Abstract

Information can be encoded in the temporal patterning of spikes. How the brain reads these patterns is of general importance and represents one of the greatest challenges in neuroscience. We addressed this issue in relation to temporal pattern recognition in the anuran auditory system. Many species of anurans perform mating decisions based on the temporal structure of advertisement calls. One important temporal feature is the number of sound pulses that occur with a species-specific interpulse interval. Neurons representing this pulse count have been recorded in the anuran inferior colliculus, but the mechanisms underlying their temporal selectivity are incompletely understood. Here, we construct a parsimonious model that can explain the key dynamical features of these cells with biologically plausible elements. We demonstrate that interval counting arises naturally when combining interval-selective inhibition with pulse-per-pulse excitation having both fast- and slow-conductance synapses. Interval-dependent inhibition is modeled here by a simple architecture based on known physiology of afferent nuclei. Finally, we consider simple implementations of previously proposed mechanistic explanations for these counting neurons and show that they do not account for all experimental observations. Our results demonstrate that tens of millisecond-range temporal selectivities can arise from simple connectivity motifs of inhibitory neurons, without recourse to internal clocks, spike-frequency adaptation, or appreciable short-term plasticity.

feature extraction by summing excitatory and inhibitory inputs from neurons with different receptive fields is considered a fundamental principle in different modalities (Hubel and Wiesel 1962; Knudsen and Konishi 1978). Much of the information relevant to sound processing, however, involves the time domain and therefore transcends the classical receptive field concept (Mauk and Buonomano 2004). Recognizing speech (Buonomano and Merzenich 1995), bird songs (Konishi 1985), and frog calls (Schwartz 1993) relies on timing information in the tens of millisecond range. What core constituents of the biophysical machinery give rise to temporal-interval selectivities? In the tens of millisecond range and irrespective of the modality, hypotheses abound: interacting and resettable pacemaker cells (Miall 1989) or networks (Ahissar et al. 1997), an array of integration time constants (Grossberg and Schmajuk 1989), a slow ion channel (Hooper et al. 2002), spike-triggered adaptation (Drew and Abbott 2006), and short-term plasticity (Buonomano and Merzenich 1995). Although these hypotheses are biologically plausible, they remain to be put in a close parallel with experimental observations. Recent work has begun to demonstrate how such biologically plausible processes contribute to selectivity for temporal features of sensory signals (Baker and Carlson 2014; Edwards et al. 2008).

Acoustic communication in anurans represents an excellent system in which to uncover neural mechanisms of temporal selectivity in the tens of millisecond range, and how temporal patterns of spikes are decoded in the brain in general. Many species of anurans produce calls that consist of a series of pulses delivered at particular rates; within each call, interpulse intervals (IPIs: the time between onsets of successive pulses) are generally highly regular. Anurans can discriminate between calls that differ in IPIs and pulse number (Gerhardt et al. 2000; Klump and Gerhardt 1987). In some cases, insertion of a short silent gap into a pulse sequence can reduce its attractiveness (Schwartz 1993; Schwartz et al. 2011).

Selectivity for IPIs arises between the auditory nerve and the midbrain (Alder and Rose 2000; Rose and Capranica 1985). In vivo experiments in the anuran IC have revealed cells selective for short IPIs which respond only after a threshold number of sound pulses have occurred. Consistent with behavioral experiments (Schwartz 1993; Schwartz et al. 2011), these cells do not respond when a silent gap is introduced in the pulse sequence (Edwards et al. 2002). Inspection of whole cell recordings from these interval counting neurons (ICNs) led to the hypothesis that the counting process resulted from rate-dependent enhancement of excitation on a background of inhibition (Edwards et al. 2007). Yet, it is not clear how this model can account for the response to calls with short interruptions. Thus, while interplay between excitation and inhibition are clearly important for interval-selectivity and counting, the precise mechanisms for interval-selective counting remain incompletely understood.

What core processes could underlie the selectivities of these ICNs for both IPI and pulse number? In this study, we generated a computational model that can explain experimental observations (Fig. 1). This model incorporates a simple dis-inhibitory network that provides interval selective inhibition to ICNs. We also show that inhibition triggered at every sound pulse is inconsistent with experimental observations, even when excitation undergoes short-term facilitation or when inhibition undergoes short-term depression. Our results predict that dis-inhibitory microcircuits (Chamberland and Topolnik 2012; Jiang et al. 2013) and slow-conductance excitatory synapses are strong candidates for temporal selectivity in the nervous system. We also discuss how a “number sense” (Dehaene 1997) may be an integral part of certain neural systems.

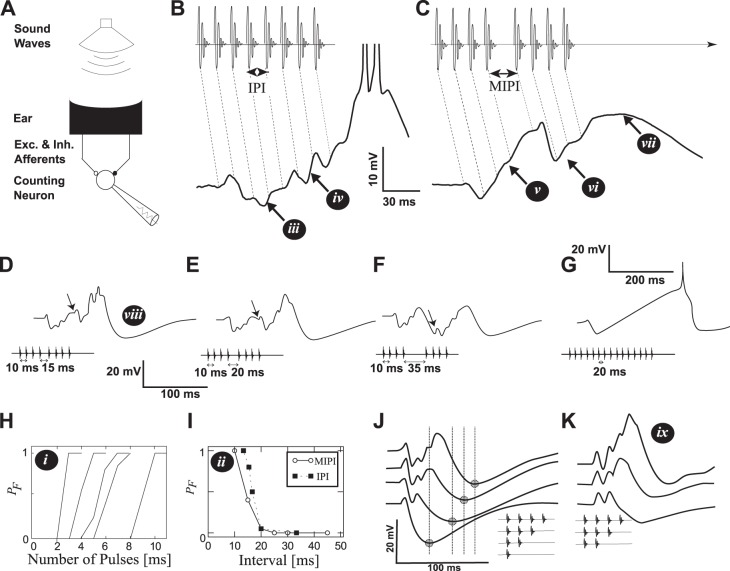
Fig. 1.

Interval-counting neurons in anurans. The white roman numerals in black circles point to a set of 9 main features described in methods. A: a series of sound pulses are produced by a loudspeaker while recording from a cell in the midbrain. B: a pulse sequence made of 8 regular intervals (IPI = 13 ms, top) and the membrane potential response (bottom). The dotted diagonal lines indicate the correspondence between sound pulses and their associated postsynaptic potentials. C: a pulse-sequence interrupted by a longer middle interval MIPI = 25 ms. D–F: recorded membrane potential in response to calls interrupted by increasingly long intervals. G: recorded membrane potential for a cell with a high count threshold. H: the probability P_F of observing a response to a periodic train of pulses as a function of the number of pulses in a call. Each curve corresponds to a different cell. I: dependence of P_F on the baseline IPI (filled squares). Roughly the same dependence is found by increasing only the MIPI (abscissa value) but keeping the baseline IPI fixed to 10 ms (empty circles), when the number of pulses that preceded and followed the MIPI was one less than the count threshold. J: responses to sequences made of 1–4 sound pulses. The minimum membrane potential is marked with a circle and a vertical line. K: responses to sequences made of 2–4 sound pulses when the same cell was hyperpolarized by 12 mV. Same scale as in subplot J. Data from Alder and Rose (1998), Edwards et al. (2002, 2007), and Rose et al. (2011).

METHODS

In this study, model ICNs are constructed to reproduce observed responses to temporal sequences of sound pulses (Fig. 1; Alder and Rose 2000; Edwards et al. 2002, 2007; Leary et al. 2008; Rose et al. 2011). We first review experimental observations and then describe the computational models.

Review of Experimental Observations

ICNs have been recorded (Alder and Rose 2000) in the anuran homolog to the IC (Wilczynski 1988; Wilczynski and Endepols 2006) using extracellular and intracellular methods. The typical experiment consists of a series of sound pulses delivered to a frog while recording from cells in the IC. Whole cell in vivo patch recordings are performed according to previously published methods (Rose and Fortune 1996).

The recordings show a series of features illustrated in Fig. 1: i) the number of sound pulses required to fire, i.e., count thresholds, varies across neurons; ii) short-IPI selectivity for baseline intervals and for the middle interval (MIPI) of an 8-pulse sequence; iii) the first 1–3 pulses cause primarily inhibition (onset-inhibition); iv) the amplitude of excitatory events appears to increase with pulse number; v) after the onset-inhibition, the increase in membrane potential is approximately monotonic, even after 200 ms; vi) with a slightly longer interval between the 4th and 5th pulses (the MIPI), the 5th pulse elicits a small, brief depolarization, followed by a prominent inhibitory event; vii) the cell remains depolarized well after the call has terminated; viii) this is followed by hyperpolarization; and ix) the increase in amplitude and duration of EPSPs with repeated sound pulses is preserved when the neuron is hyperpolarized.

Computational Modeling

Mathematical modeling is based on the integrate-and-fire formalism. Depending on the cell, we include synaptic currents for excitation and inhibition and/or subthreshold ion channel activation. Each model feature is described in detail in the following subsections. We use the fourth-order Runge-Kutta method for numerical integration (0.1 ms time step) of the differential equations.

Auditory afferents.

In vivo experiments have demonstrated that spiking activity of the auditory nerve undergoes phase locking to the amplitude modulation of sound waves (Rose and Capranica 1985). Synchronization coefficients between 0.6 and 0.8 were observed for carrier frequencies representing the spectral peaks in the calls of these animals, when the amplitude of the sound was 10–20 dB above each unit's threshold. Such synchronization is independent of pulse repetition rate between 10 and 100 Hz. Synchronization persists in the first-order central auditory region (dorsal medullary nucleus), which projects prominently to the midbrain. Therefore, we model the main auditory afferents to cells in our models as a temporal sequence of spikes at the times at which the sound pulses reach the ear. Transmission delays from the ear to the interval-selective cells are not modeled explicitly. The afferent spikes trigger excitatory synaptic responses in the interval-selective network.

Membrane potential dynamics.

All neurons are modeled as leaky integrate-and-fire units receiving excitatory and/or inhibitory inputs. To simulate the dynamics of each neuron type, a system of differential equations for the evolution of the membrane potential V(t) and the adaptation current w is integrated numerically. Parameters are used to determine the contribution of different elements in the model. The subthreshold adaptation variable w is used in only one model cell type (see below). The system of differential equations for a single neuron is

$$\begin{array}{l}{\mathrm{\tau }}_m\frac{\mathrm{d}V}{\mathrm{d}t}=-(V-E_L)-{\mathrm{\tau }}_m[g_E(t)(V-E_E)+g_I(t)(V-E_I)-w]/\text{C}\\ {\mathrm{\tau }}_w\frac{\mathrm{d}w}{\mathrm{d}t}=a(V-E_L)-w\end{array}$$ (1)

where g_E is the total excitatory conductance density, E_E its reversal potential, g_I is the total conductance density of inhibitory input, E_I its reversal potential, τ_m the membrane time constant, C the membrane capacitance, E_L the leak reversal potential and w a subthreshold adaptation variable (described below). If the membrane potential reaches a threshold value of V_T a spike is triggered. To simulate an absolute refractory period, V is clamped to 0 mV for 1 ms while keeping w fixed to its value at the threshold crossing. Immediately after, the potential is reset to V = E_L.

The additional current w is introduced here to create post-inhibitory rebound action potentials. During prolonged periods of hyperpolarization, the subthreshold variable w relaxes with time constant τ_w to a negative value proportional to the coupling parameter a. Upon release from inhibition, w results in a net depolarizing current which may be sufficient to trigger a spike. Subthreshold adaptation results from the dynamics of voltage-gated ion channels (Mauro et al. 1970; Richardson et al. 2003; Sabah and Leibovic 1969) or dendritic compartments (Gerstner et al. 2014). When a is set to zero, we recover the leaky integrate-and-fire model.

The single-neuron model used here is a special case of the generalized leaky integrate-and-fire model, which can be tuned to reproduce firing patterns and predict spike timing of many cell types in vitro (Gerstner et al. 2014; Naud et al. 2008). We note that when a spike is fired, the variable for subthreshold adaptation may undergo a small negative jump due to the voltage reset. This spike-triggered effect is sufficiently weak and short that Eq. 1 can be assumed to not produce spike-triggered adaptation. For this reason, our neuron models do not display spike-frequency adaptation.

Synaptic dynamics.

All synaptic dynamics follow an alpha-function. Based on the observation of membrane potential deflections in responses to calls (Fig. 1), we consider three types of synapses: fast inhibitory (subscript I), fast excitatory (subscript E), and slow excitatory (subscript NMDA):

$${\alpha }_x(t)=\{\begin{array}{cc}\frac{k_x}{{\tau }_x}t{e}^{-t/{\tau }_x}\hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>0\hfill \\ 0\hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\le 0\end{array}$$ (2)

where τ_x is the synaptic time constant and t measures elapsed time with respect to the presynaptic action potential. The parameter k_x scales the alpha-function to the appropriate units. It is arbitrarily set to 0.0014 nS for excitatory conductances and 0.1 nS for the inhibitory conductances.

Fast and slow currents contribute to excitatory postsynaptic potentials (EPSPs) triggered at times T_j:

$$I_E(t)={\displaystyle \sum }_j{w}_j^{(E)}{\alpha }_E(t-T_j){+w}_{\text{NMDA}}Z{(V)\alpha }_{\text{NMDA}}(t-T_j)$$ (3)

where the parameters w_E and w_NMDA are the synaptic weights for fast and slow excitation, respectively. The fast excitatory synapse has a time constant of τ_E = 2 ms as observed in IC (Raman et al. 1994), which mimics the alpha-amino-3-hydroxy-5-methyl-5-isoxazole priopionate acid (AMPA) receptors. Typically, the AMPA synaptic weight w_j^(E) has a constant amplitude w_E, but it is allowed to change when we consider the effect of short-term plasticity (below). The slow excitatory synapse has a time constant of τ_NMDA = 100 ms, a value within the range typical for this type of receptor (Attwell and Gibb 2005). Its activation depends on the postsynaptic membrane potential, in accordance with experimental recordings of N-methyl-d-aspartate-activated (NMDA) receptor dynamics. Voltage-dependent removal of the magnesium block is modeled with the activation Z(V) = [1 + cAexp(−BV)]⁻¹, with A and B parametrizing the activation threshold and sensitivity, respectively. Parameter values for A and B are based on experimental data (Gabbiani et al. 1994; Jahr and Stevens 1990) and the concentration c is fixed to 0.92 mM as measured in frog cerebrospinal fluid (Davidoff et al., 1988). All parameters are shown in Table 1 and take values in standard ranges (Gerstner et al. 2014).

Table 1.

Parameter values used in the simulations

	LIN			ICN			Synapses
Name	Value	Unit	Name	Value	Unit	Name	Value	Unit
EL	−65	mV	EL	−65	mV	A	0.28	1/mM
EI	−77	mV	EI	−77	mV	B	0.062	mV
EE	5	mV	EE	5	mV	τNMDA	100	ms
VT	−60	mV	VT	−40	mV	τE	2	ms
C	100	pF	C	100	pF	τI	5	ms
τm	10	ms	τm	20	ms	τF	100	ms
τw	30	ms	a	0	nS	f	0.9
a	8	nS	wE	7.5		τD	10–200	ms
WE	7.5		wI	1		d	0.1–2
WI	2.5		wNMDA	1

See text for definitions of parameters.

Inhibitory postsynaptic potentials (IPSPs) triggered at times T_j follow the conductance changes:

$$g_I(t)=w_I{\displaystyle \sum }_j{\alpha }_I(t-T_j)$$ (4)

where w_I is the synaptic weight of inhibition onto ICN. Equation 4 will also be used but with w_I replaced by W_I for afferents from RI onto LIN (see below). The inhibition unfolds with a time constant of τ_I = 5 ms attributable to GABAergic synapses (Destexhe and Pare 1999; G. J. Rose, unpublished observations). Recent experimental work indicates (G. J. Rose, unpublished observations) that GABA_A receptors mediate much of the inhibition in the anuran IC, consistent with studies of the mammalian IC (Ma et al. 2002). Also, GABA_A receptors mediate much of the inhibition in the mammalian dorsal nucleus of the lateral lemniscus (DNLL; Yang and Pollak 1994).

Dis-inhibitory counting circuit.

We consider two topologies for the afferent circuit. In the first, ICNs receive direct feedforward excitation and inhibition from a simple dis-inhibitory subnetwork. The neural network, shown in Fig. 2A, was suggested by the physiology of the DNLL (Yang and Pollack 1994, 1997) and the pivotal role of inhibition for temporal representation in IC (Casseday et al. 1994; Edwards et al. 2007; Hall 1999). In particular, the temporal firing patterns of cells in the anuran nucleus of the lateral lemniscus (NLL; G. J. Rose, unpublished data) are consistent with a dis-inhibitory circuit of this type.

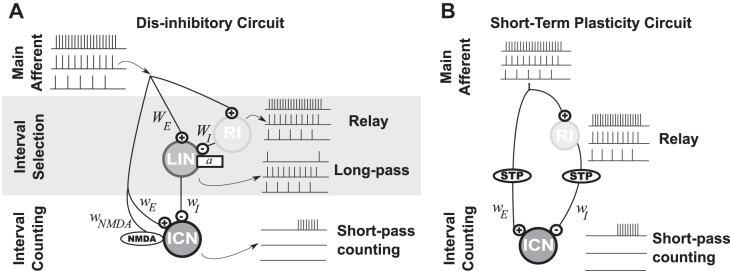
Fig. 2.

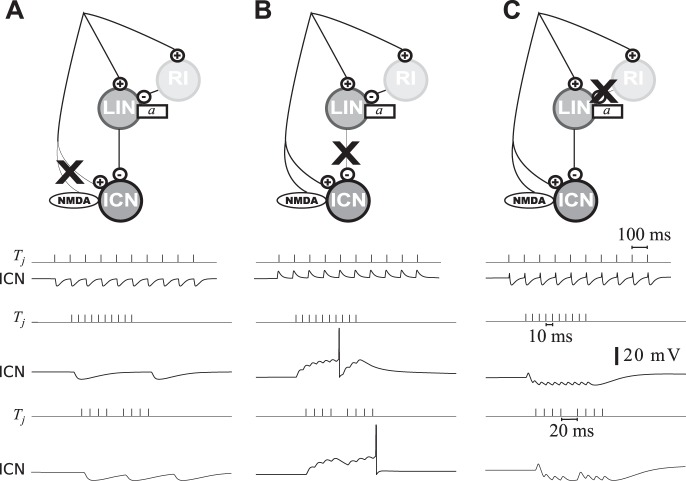
Schematic illustration of the neural architectures considered for short-pass interval counting. A: counting on dis-inhibition circuit motif. From the main afferent, a first layer performs interval selectivity: a relay inhibitory neuron (RI) provides disynaptic inhibition (GABA_A) to a long interval selective neuron (LIN) with subthreshold adaptation strength a. In the second layer, the interval-counting neuron (ICN) combines afferent excitation (AMPA and NMDA) with the interval-selective inhibition from LIN (GABA_A). ICN receives inhibition at every pulse for long IPIs but is dis-inhibited for short IPIs. B: network diagram for a model based on short-term plasticity (STP). Both excitation (AMPA) and inhibition (GABA_A) are triggered at every pulse. Either the excitatory or the inhibitory synapse is dynamic and undergoes substantial short-term plasticity.

In the dis-inhibition model, the ICN receives fast (AMPA-mediated) and slow (NMDA-mediated) excitation as well as fast (GABAergic) inhibition. Both AMPA and NMDA synapses are triggered by the main afferents with a synaptic weight given by w_E and w_NMDA, respectively. The dynamics of an ICN are simulated with Eq. 1 without subthreshold adaptation (a = 0).

To release the ICN from inhibition for short IPIs, the presynaptic inhibitory cell (LIN, for long-IPI transmission neuron) is modeled to fire in response to each pulse at slow pulse rates (long IPIs), but only in a phasic manner at fast pulse rates (short IPIs). The mechanism for long-interval selectivity in LIN is based on the combination of strong excitation with delayed inhibition, as described in centers presynaptic to the IC.

The putative location of LIN is in the anuran homolog of the NLL (Rose and Wilczynski 1984). As observed in mammalian DNLL (Yang and Pollak 1997), LIN receives a combination of strong excitation from the main afferents and disynaptic inhibition through a relay inhibitory neuron (RI). Both excitation and inhibition are triggered at every pulse, but inhibition is delayed with respect to excitation.

The response of LINs corresponds to the “pauser” firing pattern, which has been observed for neurons in the anuran NLL (G. J. Rose, unpublished observations) and DNLL of bats (Yang and Pollack 1994). They respond in a phasic on-off manner to short IPIs; the onset-response results from strong excitation that precedes inhibition, while the offset response is modeled as a postinhibitory rebound. These firing patterns account simultaneously for the initial transient inhibition in the ICN (Fig. 1, feature iii), the reset inhibition (Fig. 1, feature vi) and the inhibition observed after the offset of the pulse sequence (Fig. 1, feature viii). The dynamics of LIN follows Eqs. 1–4, without NMDA synapses (w_NMDA = 0). Relay inhibition is not simulated explicitly, but it is represented by pulse-per-pulse inhibition delayed by 2.5 ms with respect to the afferent excitation.

Note that uppercase W denotes synaptic strength in the interval selection layer (afferents to LIN) and lower case w denotes synaptic strength parameters in the counting layer (afferents to ICN). Also note that in the integrate-and-fire formalism a lower threshold can be compensated by a lower excitatory synaptic weight.

Short-term plasticity.

Previous work (Edwards et al. 2007; Rose et al. 2011) described an alternative, conceptual model of ICNs that involves synaptic plasticity (Fig. 2B). In this second connectivity model, the ICN receives fast inhibition and AMPA-mediated excitation from the primary afferents. The inhibition is delayed with respect to excitation by 5 ms, and excitation undergoes short-term facilitation.

The synaptic efficacy in Eq. 3 [w_j^(E)] was modeled by a constant weight (w_E) times a factor F(t) for the rate dependence. Facilitation of excitation is modeled with a time-dependent function F(t) that modifies multiplicatively the synaptic weights (Varela et al. 1997):

$$w_j^{(E)}=w_E\text{F}(T_j)$$ (5)

$$\frac{\text{d}F}{\text{d}t}=(1-F)/{\tau }_F$$ (6)

where τ_F is the facilitation time constant. The variable F is reset to f + F after a spike arrives at time T_j. The timescale parameter τ_F is fixed to 100 ms, identical to the particular time constant for our model of NMDA synapses (τ_NMDA). The parameter value is in the range observed in L2-3 pyramidal cells of the cortex (Varela et al. 1997). This value was chosen to be sufficiently long to account for the slow membrane potential increase observed in ICNs with high count thresholds.

Analysis Methods

Assessing interval selectivity.

Interval selectivity was determined from the simulated response to periodic pulse-sequences containing ten sound-pulses. We simulated responses of the neural network for different IPIs between 10 and 100 ms. Either for the LIN or ICN, we determined if the cell responded to any of the sound pulses after the third one. If only IPIs greater than a threshold IPI excited the neuron it was classified as long-IPI selective, or “long-pass.” A cell responding only to a range of short IPIs was classified as short-IPI selective or “short-pass.”

LIN firing patterns.

Classifications were based on the responses to an 8-pulse sequence in which a middle interval (MIPI) was twice as long as the other intervals (Fig. 1C). Responses of LINs at various times after the start of a pulse sequence were denoted as “transient-onset” (phasic response at stimulus onset), “resetting” (response after a gap in the pulse sequence), or “rebounding” (response following the end of the pulse train). The term “resetting” relates to the capability of this firing pattern to reset the count in downstream ICNs. None of these categories are exclusive since for some parameter values the LIN can be transient, resetting, and produce a rebound action potential.

ICN count selectivity.

The synaptic weights of excitation regulate the number of sound pulses required for the ICN to elicit an action potential. We determined such count thresholds by simulating the counting neuron model and its presynaptic input from the interval selective layer. When the ICN model produced an action potential, we stopped the simulation and counted the number of sound pulses received up to that time.

Mathematical analysis of STD transients.

The dynamics of short-term depression (STD) were analyzed to determine if the phasic aspect of inhibition can be modeled by STD of pulse-per-pulse inhibition of the ICN. We did not implement STD in a counting network; we only tested if it can account for the type of transient inhibition observed in the experiments (Fig. 1, features iii and vi).

STD of inhibition is assumed to follow a model similar to that for facilitation (Dayan and Abbott 2001). The synaptic weight is controlled by a depression variable D

$$w_j^{(I)}=w_{I}D(T_j)$$ (7)

where the depression variable relaxes to one on a time constant τ_D

$$\frac{\mathrm{d}D}{\mathrm{d}t}=(1-D)/{\tau }_D\mathrm{.}$$ (8)

After a spike at time T_j the dynamics of the depression variable D in Eq. 8 is reset to dD. The depression parameter, d, regulates the level of depression caused by a presynaptic spike. It is varied between 0 and 1, and the time constant τ_D between 0 and 150 ms. Equation 7 determines the effective synaptic weight.

To determine the conditions that enable STD to be reversed during a long interval, we use the discrete map formulation of STP. We solve Eq. 8 for the value of D after a time ρ from an initial condition D₀. This forms the discrete map M_ρ defined as:

$$D(\rho )=1-(1-d{D}_0)e^{-\rho /{\tau }_D}\equiv M_{\rho }(D_0)$$ (9)

The discrete map is used to obtain an expression for the maximal conductance amplitude after each presynaptic spike.

We defined a count reset as “effective” if the inhibitory connection between the LIN and the ICN starts from a depressed state D₀ = 0.5 and recovers to at least 0.9 after a time Δ, such that M_Δ(0.5) > 0.9. Using the discrete map, the effective reset condition can be written in terms of the parameters τ_D and d:

$$d>2-0.2e^{\Delta /{\tau }_D}\mathrm{.}$$ (10)

In a similar way, we defined inhibition as being phasic if, starting from D = 1, a single IPI elicits inhibition that is less than 50% of maximum (M_ρ < 0.5). The relation

$$d<1-0.5e^{\rho /{\tau }_D}$$ (11)

determines the parameters for which short-term depression renders inhibition phasic.

RESULTS

Schematic of the models for counting intervals that are of sufficiently short duration are shown in Fig. 2. In both cases, spikes occur when the number of pulses, presented at optimal intervals, exceeds a threshold value. In the “dis-inhibitory” circuit model (Fig. 2A), afferents make excitatory synapses (AMPA- and NMDA-type) onto ICNs, “long-interval” neurons (LIN) that provide direct inhibition to ICNs and “relay” inhibitory interneurons (RI). The RIs, like their excitatory afferent inputs, faithfully spike in response to each stimulus pulse across the biologically meaningful range of pulse rates (up to ∼100 pulses/s), and provide delayed inhibition of LINs. The delayed inhibition from RI prevents firing in LINs for short intervals, a circuit motif that can perform long-IPI selectivity in centers presynaptic to the inferior colliculus (Yang and Pollak 1997). For short intervals, ICNs are released from inhibition; this dis-inhibition enables a relatively unopposed accumulation of excitatory inputs in the counting neurons. In the second model (Fig. 2B), excitatory and inhibitory synapses undergo short-term plasticity, i.e., facilitation and depression, respectively.

We first describe in more detail how the various response characteristics of short-IPI selective counting neurons (reviewed in methods) can be explained by the short-IPI counting network shown in Fig. 2A.

Short-IPI Selectivity

We propose that short-pass ICNs result from an integration to a threshold that can be vetoed by IPI-dependent inhibition. For long IPIs, this inhibition counteracts and in fact vetoes the summation of excitatory events arising from sound pulses (Fig. 3A). For successive short IPIs, however, inhibition of the ICNs (from LIN) is phasic and is restricted to the onset and offset of the pulse sequence (Fig. 3B), consistent with early and late hyperpolarizations observed experimentally (features iii and viii; Edwards et al. 2007). Consequently, the ICN can fire only between these episodes of inhibition and after a threshold number of pulses have occurred. Thus the network presynaptic to ICN in Fig. 2A simultaneously selects long IPIs and detects stimulus onset and offset. The strength of excitatory connections to the ICN determines the count threshold (Fig. 3C). Small count thresholds require very strong AMPA synapses whereas large count thresholds require weak AMPA synapses and stronger NMDA synapses. This relation is shown in Fig. 3E, where the excitatory parameter space that corresponds to count thresholds of 10–40 are smaller than the regions associated with count thresholds 1–10. This indicates that small count numbers will be encoded more reliably than large count number in the presence of noise, since a small fluctuation of EPSP amplitude can change the count threshold. In principle, variations in the strength of AMPA synapses alone can span all count thresholds but large counts cannot be represented reliably. The long time constant of the NMDA synapse is essential to encode large count-numbers reliably (larger areas for larger w_NMDA in Fig. 3E). Figure 3E also shows that there is a continuous range of parameter values that result in the same count threshold. Since the proportion of NMDA and AMPA components will influence the amplitude of the sustained depolarization after the pulse train, the model can be tuned to produce either marked, as in Fig. 1C, or modest, as for some cells in Rose et al. (2011), sustained depolarization.

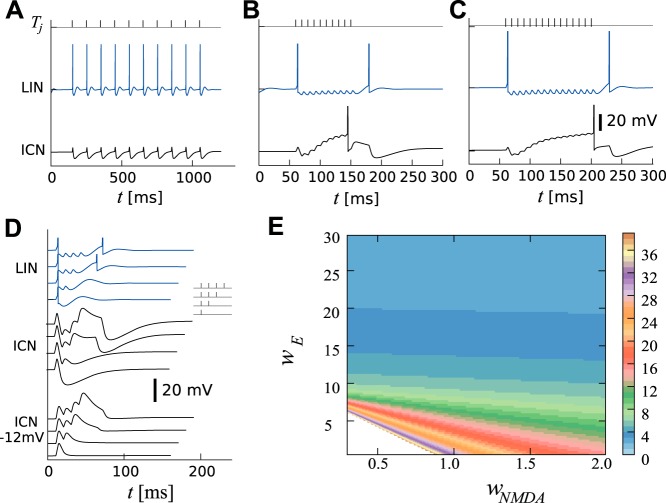
Fig. 3.

Simulated responses of LIN and ICN to uninterrupted calls. A: response to a pulse sequence with long IPIs (top black ticks, IPI = 100 ms) in the ICN (black line) and LIN (blue). B: same as A but for short IPIs (IPI = 10 ms). Note that the rebound spike in LIN causes offset-inhibition in ICN. C: weaker excitatory synapses onto ICN increase the count threshold. D: simulated responses to 1- to 4-pulse stimuli are stacked vertically. Responses of LIN (blue traces) show a rebound for more than two pulses. Responses of ICN when hyperpolarized by 12 mV show an apparent increase in EPSP amplitude (black traces, middle). Responses of ICN (black traces, bottom) reach their minimum with increasing delay as the number of pulses is increased. E: count thresholds between 1 and 40 are shown (colormap on the right) as a function of the excitatory synaptic weights w_E and w_NMDA. The steplike appearance of the boundaries in parameter space is due to the discrete nature of the count thresholds. Simulations were performed with IPI = 10 ms. Parameters are shown in Table 1, except for C, which used a smaller synaptic weight w_E = 5 to increase the count threshold to 15.

Since the synaptic dynamics of AMPA and NMDA synapses implement a low-pass filter (long-IPI selectivity), the short-pass properties of the modeled ICN must be inherited from the inhibition. Therefore, it is mainly the dynamics of the inhibitory input onto ICNs that determines the interval selectivity. Furthermore, since for large count thresholds the inhibition is brief compared with the duration of the pulse-train, the slow increase of the membrane potential results primarily from excitation. The weight and decay time of the excitatory synapses onto ICN strongly influence the count threshold; for example small weights and long decay times result in large count thresholds.

The model is consistent with single-pulse experiments (Figs. 1 and 3D) in which the membrane potential response shows an immediate, brief depolarization that is followed by a longer hyperpolarization. In response to a longer sequence of IPIs in short succession, the transient nature of inhibition from LIN can, in part, explain the increase in both width and amplitude of the EPSPs, even when the cell is hyperpolarized (Fig. 3D and Fig. 1, feature ix). In response to a sequence of pulses presented with optimal intervals, the decline of inhibition and additional excitation result in depolarizing EPSPs that are progressively larger and longer lasting (rounded shape; Fig. 1, feature vii). This incremental augmentation of EPSP amplitude and duration can result from NMDA receptor activation on a background of AMPA-type excitation and residual inhibition.

Interrupted Calls

Remarkably, a gap that is 10–20 ms longer than the optimal IPI can reset the interval counting process (Edwards et al. 2002; Fig. 1, feature vi). In many cases, the time required for resetting the interval-counting process is much shorter than that of the counting itself, e.g., counting more than 10 pulses separated by 20 ms (Rose et al. 2011) would require a time constant on the order of 100 ms. This “dichotomy of time scales” is explained in our model by the distinct patterning of inhibition vs. excitation, i.e., the release from phasic, early inhibition and the slow activation of excitation. As noted in the previous section, larger counting thresholds are associated with a greater role of the slow activation of NMDA synapses. A single long-IPI elicits inhibition from LIN and effectively resets the interval-counting process in the ICN (Fig. 4). As for uninterrupted calls, it is mainly the dynamics of the inhibitory input onto ICNs that determines the time course of resetting the counting process.

Fig. 4.

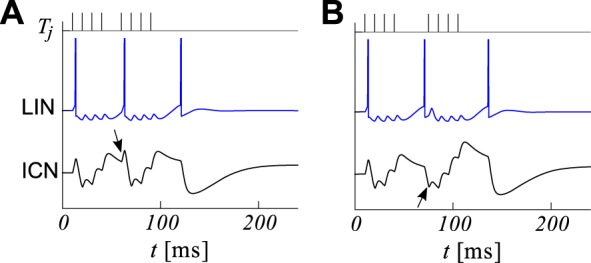
Simulated responses to interrupted calls. A: a short interruption (long interval) in an 8-pulse call (top, each tick corresponds to an excitatory event in the main afferent) causes a spike in LIN (blue) which hyperpolarizes the ICN after the pulses resume, resetting its counting process (black, bottom). Call is made of short intervals (IPI = 10 ms) and a longer middle interval (MIPI = 20 ms). Inhibition is seen after the fifth excitatory event (black arrow). B: for longer silent gaps (MIPI = 35 ms), LIN now fires a rebound spike before the fifth pulse arrives. Accordingly, inhibition in the ICN is seen before the fifth excitatory event (black arrow). Parameter values are shown in Table 1.

Many features of the electrophysiological recordings summarized in Fig. 1 are consistent with the network in Fig. 2A. Simulations show that if a MIPI is too short to produce a rebound spike in the LIN but sufficiently long to release LIN from inhibition, the ICN will receive additional inhibition only after the call resumes, that is after the 5th EPSP (compare Fig. 4A with Fig. 1, feature vi). For longer interruptions, the LIN may fire before the call has resumed (compare Fig. 4B with Fig. 1F), inhibiting the ICN before the fifth EPSP. Thus, our model of presynaptic inhibition reproduces features ii–iv and vi–ix, whereas the features i and v were captured by our model of excitation.

Sensitivity to Model Parameters

To determine if the simulations shown in Figs. 3 and 4 depend on a finely tuned set of parameters, we analyzed the model dynamics in terms of elements critical to short-IPI selectivity. Here, the parameters that regulate the firing patterns are the synaptic weights (W_I and W_E) as well as the subthreshold coupling a; the time constants and reversal potentials remain fixed to typical values (Table 1). Figure 5A shows regions of different firing patterns observed in response to an interrupted pulse-sequence as we change the adaptation coupling parameter a and the inhibitory weight, W_I, of RI onto LIN. Sample traces are shown in Fig. 5B for different parameter combinations. For a restricted portion of the parameter space, LIN fires at the onset, after the interruption, and after the termination of the pulse sequence in a manner consistent with our simulations in Figs. 3 and 4.

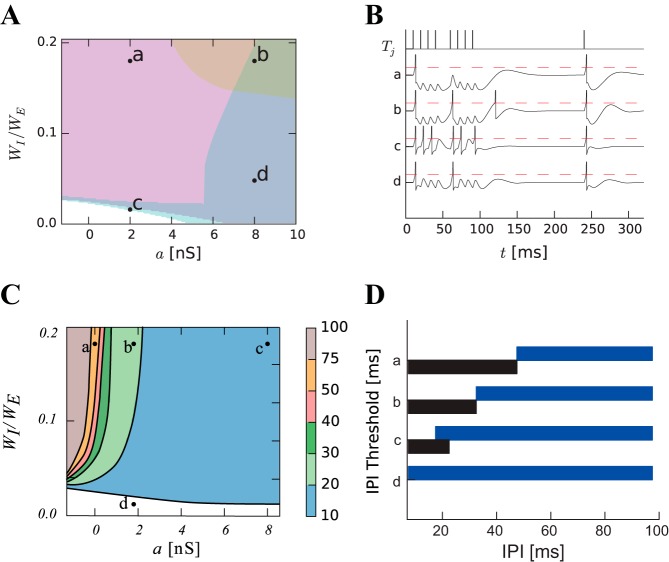
Fig. 5.

Parameter space for the dynamics of LIN. A: parameter space for different subthreshold adaptation a and inhibitory weight. The response to 8-pulse sequences interrupted after the fourth pulse are classified as resetting (cyan, a thin strip at the top of the white region), transient (magenta), resetting and transient (blue), resetting and rebound (peach), or resetting, rebound and transient (green). Parameters labeled b were used to generate Figs. 3 and 4. B: simulated membrane potential (black lines) in response to an interrupted call (IPI = 10 ms, MIPI = 20 ms, black ticks, top) for the four sample parameter sets (a–d) shown in A. Spikes appear as sharp reset after the membrane potential has reached the threshold (red dashed lines). C: parameter space showing the minimum IPI for eliciting a sustained response in the LIN (IPI threshold). D: interval selectivities for the four sample sets of parameter values shown in C. The black (blue) bar shows the IPIs for which 10-pulse sequences elicit a response in the ICN (LIN).

Different values of the coupling parameter, a, and inhibitory weight, W_I, of RI on LIN also determine the range of IPIs that elicit response in LIN. Across the parameter space, LIN responds selectively to intervals shorter than an IPI threshold. Figure 5C shows the contour lines of IPI thresholds 10, 20, 30, 40, 50, and 75 ms in parameter space. Increasing the subthreshold adaptation allows LIN to respond to shorter IPIs (faster pulse rates), thereby restricting responses in the ICN to just the shortest IPIs, i.e., strong selectivity for very fast pulse rates. The regime of long-IPI selectivity (leading to short-IPI selective ICN) is very large and covers most of the parameter space (Fig. 5D). Short-IPI selectivity in ICNs thus appears robust to changes in parameters.

Short-Term Facilitation of Excitation or Depression of Inhibition

Next, we tested the hypothesis that some ICNs receive rate-dependent excitation that interacts with a steady inhibition (Edwards et al. 2007; Rose et al. 2011). This hypothesis was motivated by the potentially crucial role of short-term plasticity for interval selectivity (Buonomano and Merzenich 1995; Buonomano 2000). Here, an ICN receives pulse-per-pulse inhibition and facilitating excitation using a known dynamical model of short-term facilitation (without NMDA, see Computational Modeling; Fig. 2B).

There are only three parameters in this STP model: the baseline synaptic weight w_E, the facilitation time constant τ_F and the facilitation jump f (see methods). The facilitation time constant is fixed to a typical physiological value (100 ms). To generate the onset-inhibition (feature iii), the baseline excitatory synaptic weight must remain small. The facilitation must, therefore, be sufficiently strong to overcome the constant inhibition. For the ICN to reach threshold after 8 pulses, while preserving the initial hyperpolarization, the facilitation jump must be very large (f > 2; Houtman 2012), a parameter value that appears unrealistically large because its measured values are smaller than one (Varela et al. 1997). Importantly, this simple model cannot show repolarization after a long interval has occurred (feature vi), as illustrated in Fig. 6. Taken together, these results suggest that STP is not strongly at play in allowing excitation to overcome inhibition.

Fig. 6.

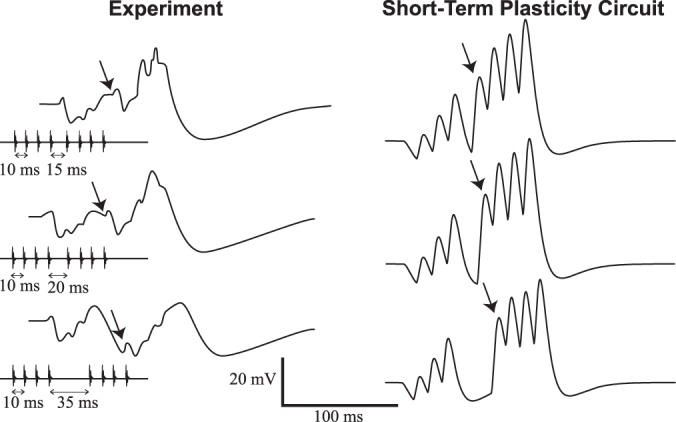
Simulations of STP model (Fig. 2B) compared with experimental recordings. Left column shows membrane potential recordings of ICNs (as in Fig. 1). Right column shows simulations of model depicted in Fig. 2B with short-term facilitation of excitation and pulse-per-pulse inhibition. Calls with IPI = 10 ms are interrupted by MIPI = 15 ms (top), 20 ms (middle), and 35 ms (bottom). The arrows indicate the EPSP associated with the fifth sound pulse. Model parameters are shown in Table 1.

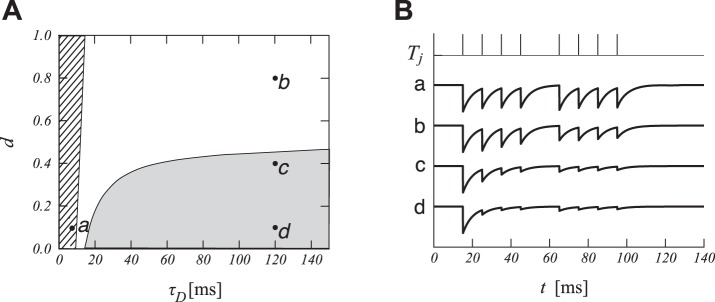
We consider, last, if short-term depression (STD) of pulse-per-pulse inhibition could be sufficient for generating the patterns of membrane potential fluctuations seen in recordings (Fig. 1). Depression of inhibition, coupled with weak excitation, could produce the transient hyperpolarization that is observed (features iii, vi, and viii). However, STD of inhibition fails to account for the hyperpolarization seen after the end of a pulse train (feature viii) because the inhibitory synapses have undergone depression (not shown). Can STD of inhibition alone also explain the inhibitory transient observed after a longer MIPI (feature vi)? We have analyzed STD mathematically (see Analysis Methods) and found that the regions of parameter space associated with an initial transient are markedly separate from the regions for which inhibition could recover after an IPI twice the baseline IPI (Fig. 7). The depression time constant typically observed for inhibitory synapses (τ_D = 30 ms, Hefft et al. 2002; Kramer et al. 2014) can produce transient inhibition but not recovery of inhibition after a short interruption.

Fig. 7.

Short-term depression cannot explain reset inhibition. A: parameter space for short-term depression. The parameters implementing an initial transient correspond to the shaded area (Eq. 11) and the parameters for synaptic recovery after a MIPI correspond to the hatched area (Eq. 10, IPI = 15 ms, MIPI = 30 ms). B: conductance time course g_I from LIN onto ICN simulated with short-term plasticity according to sample parameters shown in A (arbitrary vertical scale). The top row displays synaptic spike times as vertical bars (IPI = 10 ms, MIPI = 20 ms).

Consequently neither STF of excitation nor STD of inhibition captures features vi, vii, and viii. We conclude, therefore, that the model shown in Fig. 2B, when considering STF of excitation or STD of inhibition, is insufficient for generating the experimentally observed results: unconventional types of presynaptic facilitation and depression would be required (Edwards et al. 2007; Houtman 2012). The dis-inhibitory motif of Fig. 2A captures these features.

DISCUSSION

We have presented a novel neural architecture that is able to reproduce experimental observations of interval counting and interval selectivity of ICNs in anuran IC. These results are discussed in three parts. First we consider the neural bases for interval counting. Then we discuss the neural bases for interval selectivity. We close with experimentally testable predictions.

Neural Bases for Interval Counting

The ability of animals to count and integrate events or objects and its underlying mechanisms, including the possible existence of a dedicated “number sense,” is a topic of much recent fascination and research interest (Dehaene 1997; Nieder and Dehaene 2009). For acoustic signals, where elements that are to be counted appear over time, ICNs can encode numerosity of sound pulses.

A neuronal model for encoding numerosity has been proposed for counting static visual objects by Dehaene and Changeux (1993). This McCulloch-Pitts-type network has three layers: one to detect features, another to sum the activity of the first network and compare it to various thresholds, and a third to signal numerosity. Conceptually, ICNs belong to the second layer since they implement a count threshold, not strict numerosity. Combining the interval-counting network motif with the layered structure of Dehaene and Changeux (1993) or Grossberg and Repin (2003) suggests a simple, biologically plausible process for counting objects in space and time. It is also possible that the information relevant for mate selection is decoded directly from the counting neurons, without ever representing numerosity in the strict sense.

Reliably counting a large number of pulses requires an accumulating process with a slow time course. In our model, this slow time course originated from NMDA synapses. Importantly, the contribution of NMDA-type synaptic transmission to late responses in IC neurons is supported by in vitro and in vivo recordings (Kelly and Zhang 2002). Other intrinsic biophysical processes that could contribute to prolonged responses and influence count threshold include T-type calcium currents, slow sodium currents, and network processes. It is well known that a recurrent excitatory network harbors a “reservoir of time constants” (Bernacchia et al. 2011; Buonomano 2003; Buonomano and Maas 2009; Maass et al. 2002), yet it is not clear how recurrent connections would account for the effects of pharmacological removal of inhibition (Edwards et al. 2007) and for onset inhibition (feature iii). Further experiments are required to determine which of these processes underlies the slow accumulation associated with counting in ICNs. Also, further work could determine the robustness of our proposed interval selectivity mechanism to both intrinsic noise and acoustic background.

Neural Bases of Interval Selectivity

Given their central importance in motor planning and speech recognition, the neural mechanisms for processing temporal information have received considerable theoretical attention (Konishi 1985; Mauk and Buonomano 2004). Early theoretical analyses have suggested additional elements such as delay lines (Jeffress 1948; Tank and Hopfield 1987), coincidence detection mechanisms (Poggio and Reichardt 1973), or dedicated timekeeping mechanisms (Braitenberg 1967; Church 1984; Creelman 1962; Meck 2006; Roberts 1981; Treisman 1963). These models do not incorporate inhibition.

We note two instances where feedforward inhibition contributes to temporal feature extraction. We discuss, first, the duration-tuned neurons (DTNs) in auditory midbrain (Aubie et al. 2009, 2012; Casseday et al. 1994; Covey et al. 1996; Leary et al. 2008; Sayegh et al. 2011). Long-pass DTNs are modeled by a sustained excitation overcoming an inhibitory transient. This gradually decreasing but sustained inhibition is modeled by Aubie et al. (2009) with spike-frequency adaptation, which is absent in our model of interval selectivity. Band-pass duration-selectivity, which favors responses to midrange durations, is thought to result from inhibitory rebound combined with a delayed excitation. Short-pass DTNs are thought to elicit a response only when a delayed onset excitation arrives after the termination of sustained inhibition. The inhibition of DTN is constant during the presentation of the stimulus for the short-pass and the mid-pass, but not for the long-pass DTNs. For the long-pass DTNs, inhibition is sustained but gradually decreasing in intensity. Therefore the central role of stimulus-dependent release from inhibition, i.e., dis-inhibition, in our model is distinct from Aubie et al. (2009).

A second type of temporal feature is the interaural time difference (ITD) encoded in the mammalian auditory hindbrain (Grothe 2003). In this case, ipsilateral inhibition hinders response to large ITDs and contralateral inhibition hinders response to small ITDs. Inhibition appears to sharpen the sub-millisecond ITD tuning curve (Grothe 2003). This is similar to the role of inhibition proposed here. One of the predictions of our model is that blocking inhibition to the ICNs should eliminate their IPI selectivity. Together these results suggest a computational role for precisely timed inhibition, a view that arises also in other modalities (Berman and Maler 1998; Taylor et al. 2000).

Our results can be contrasted with the hypothesis of Buonomano and Merzenich (1995) regarding the biophysical basis for interval selectivities in the millisecond range. Their hypothesis contained four central elements: random excitatory connections with Gaussian distribution of weights, layered feedforward excitation, slow disynaptic inhibition [or depressing inhibition as in Buonomano (2000)], and short-term plasticity. Short-term plasticity is crucial to extend the sensitivity of their network from 5–15 ms to hundreds of milliseconds. Without short-term plasticity, excitation combined with disynaptic inhibition can select intervals in the range of 5–15 ms, as shown here. Combining STP with the dis-inhibitory circuit would enhance interval selectivities. Our dis-inhibitory circuit motif explains interval selectivity more parsimoniously, but further work will be needed to determine to what extent short-term plasticity is crucial to the short interval selectivity observed in neurons of the auditory midbrain.

The disynaptic inhibition network motif (Fig. 2A) is a recurring feature of diverse brain areas including neocortex, cerebellum, hippocampus, and amygdala (Bruno 2011). Thalamic input to the cortex, for instance, often consists of volleys of action potentials that provide input to a network motif consistent with our LIN network in Fig. 2A (Beierlein et al. 2003; Bruno 2011). The same network motif was hypothesized to gate the flow of information in recurrent networks (Kremkow et al. 2010; Vogels and Abbott 2009). The new computational properties discussed in this article may contribute to the neural computations outside of the midbrain.

Predictions

In our model, the delayed release of inhibition onto ICNs that occurs for short IPIs (fast pulse rates) is due to the delayed inhibitory action of the RI neurons onto the LINs. This time-dependent release from inhibition at fast pulse rates produces short-IPI selectivity. This patterning of the inhibition is unlike any conceptual models of interval counting or duration selectivity previously proposed.

To test this hypothesis, in vivo pharmacological blockade of excitation in ICNs should reveal a dependence of inhibition on IPI (Fig. 8A). In short-IPI selective ICNs, we predict that this inhibition will be phasic at short IPIs, that is, transient inhibition should be observed at the onset and offset of the pulse-sequence. Furthermore, our model also predicts qualitatively different responses for blockade of excitation onto the ICNs (Fig. 8B) than for blockade of excitation onto LINs (Fig. 8C).

Fig. 8.

Simulated pharmacological blockade of circuit components. A: blockade of excitation onto ICN. Top traces show the responses to long IPIs (IPI = 100 ms). Middle traces show responses to short IPIs (IPI = 10 ms). Bottom traces correspond to a short interruption after the fourth pulse (MIPI = 20 ms). B: as in A but for the blockade of inhibition onto ICN. C: as in A but for the blockade of inhibition onto LIN. Pharmacological blockade is simulated by putting the relevant synaptic weight to zero without altering other parameter values.

Researchers have recorded “pauser”-type neurons in the auditory systems of many animals, including frogs (Condon et al. 1995), but the functional role of this response phenotype has remained mysterious. If the putative LINs are located away from IC, it should be possible to locally block GABAergic or glycinergic synapses. This should alter the inhibition pattern in the ICNs. We predict that locally blocking inhibition to the LINs will result in a tonic firing pattern and inhibition to ICN at fast pulse rates; without the normal rate-dependent release from inhibition, counting and short-IPI selectivity will be precluded (Fig. 8C).

The question of the anatomical localization of the interval-selective network remains open. One possible location for LIN is in the superior olive (SO). Studies in the medial SO of bats show neurons responding at the onset of fast amplitude modulations and at every cycle of slow amplitude modulations (Grothe 1994). Some neurons in the medial SO also signal both the onset and the offset of amplitude modulated sound waves (Grothe 1994). These responses are consistent with those LIN for various strengths of subthreshold adaptation. Another possible location is the nucleus of the lateral lemniscus (NLL). Neurons in the dorsal NLL of bats show response properties similar to those hypothesized for the LINs in our models (Yang and Pollak 1997). In particular, the temporal firing patterns of NLL neurons in anuran (G. J. Rose, unpublished data) are consistent with a dis-inhibitory circuit of this type. The NLL projects directly to the IC and contains neurons that have been immunocytochemically identified as inhibitory.

According to our model for interval counting, we further predict that IPI-number thresholds will increase following pharmacological blockade of NMDA receptors in ICNs. For ICNs with high count-thresholds, removal of the NMDA component should abolish spike responses to long pulse-sequences. Electrophysiological recordings could also reveal that the long-lasting response (Fig. 1, feature vii) and the lengthening of excitatory events with increased number of pulses depend on NMDA receptors. This block will similarly increase the number of IPIs required for response after a pause.

Like delay- and duration-tuned neurons, the ICNs—and particularly their resetting properties—embody a form of temporal receptive field. Our results suggest however that ICNs show two-dimensional temporal receptive fields, with interval length and pulse number contributing to their responses. Duration-selective neurons are thought to arise from a preserved network motif across different species (Aubie et al. 2012). Further experiments could determine if our interval- and count-selectivity model applies to interval-selectivity across vertebrates. Neurons with similar properties have been observed in pulse-type electric fish (Carlson 2009; Pluta and Kawasaki 2010), and possibly in auditory neurons in IC of mice (Geis and Borst 2009). Combined with an investigation of the connectivity structure of inhibitory projections to the ICNs, additional experiments could reveal a firm biological basis for counting and temporal processing on the millisecond time-scale.

GRANTS

This work was supported by an FQRNT scholarship (R. Naud), an NSERC Discovery Grant (A. Longtin), NSERC Discovery Accelerator Grant (A. Longtin) as well as visitor support from the EPFL (A. Longtin) where this work was initiated.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: R.N., G.J.R., and A.L. conception and design of research; R.N. and D.H. analyzed data; R.N., D.H., G.J.R., and A.L. interpreted results of experiments; R.N. prepared figures; R.N. drafted manuscript; R.N., G.J.R., and A.L. edited and revised manuscript; R.N., G.J.R., and A.L. approved final version of manuscript.