A ground truth based comparative study on clustering of gene expression data

Abstract

Given the variety of available clustering methods for gene expression data analysis, it is important to develop an appropriate and rigorous validation scheme to assess the performance and limitations of the most widely used clustering algorithms. In this paper, we present a ground truth based comparative study on the functionality, accuracy, and stability of five data clustering methods, namely hierarchical clustering, K-means clustering, self-organizing maps, standard finite normal mixture fitting, and a caBIG™ toolkit (VIsual Statistical Data Analyzer - VISDA), tested on sample clustering of seven published microarray gene expression datasets and one synthetic dataset. We examined the performance of these algorithms in both data-sufficient and data-insufficient cases using quantitative performance measures, including cluster number detection accuracy and mean and standard deviation of partition accuracy. The experimental results showed that VISDA, an interactive coarse-to-fine maximum likelihood fitting algorithm, is a solid performer on most of the datasets, while K-means clustering and self-organizing maps optimized by the mean squared compactness criterion generally produce more stable solutions than the other methods.

2. INTRODUCTION

High throughput gene expression profiling using microarray technologies provides powerful tools for biologists to pursue enhanced understanding of functional genomics. A common approach for extracting useful information from gene expression data is data clustering, where sample clustering and gene clustering are two main applications. Sample clustering groups samples whose expression profiles exhibit similar patterns (1, 2). Gene clustering groups co-expressed genes together (3, 4). Application of various clustering algorithms in genomic data research has been reported and these methods can be categorized under different taxonomies (5–7). With respect to mathematical modeling, clustering algorithms can be classified as model-based methods like mixture model fitting (4) and VIsual Statistical Data Analyzer (VISDA, a toolkit of caBIG™) (8–11), or “nonparametric” methods such as the graph-theoretical method (12). Regarding the clustering scheme, there are agglomerative methods, such as conventional Hierarchical Clustering (HC) (13), or partitional methods including Self-Organizing Maps (SOM) (1, 3) and K-Means Clustering (KMC) (14). The assignment of data points to clusters can be achieved by either soft clustering methods like fuzzy clustering (15) and mixture model fitting (4), or hard clustering methods like HC and KMC. While most algorithms perform clustering automatically, with even the parameter initialization automated, e.g. random initialization, other recent methods like VISDA attempt to exploit the human gift for pattern recognition by incorporating user-data interactions into the clustering process.

Efforts have been made to evaluate and compare the performance and applicability of various clustering algorithms for genomic data analysis. As Handl et al. stated in (16), external measures and internal measures are two main lines to validate clustering. External assessment approaches use knowledge of the correct class labels in defining an objective criterion for evaluating the quality of a clustering solution. Gibbons and Roth used mutual information to examine the relevance between clustered genes and a filtered collection of GO classes (17, 18). Gat-Viks et al. projected genes onto a line through linear combination of the biological attribute vectors (GO classes) and evaluated the quality of the gene clusters using an ANOVA test (19). Datta and Datta used a biological homogeneity index (relevance between gene clusters and GO classes) and a biological stability index (stability of the gene clusters’ biological relevance with one experimental condition missing) to compare clustering algorithms (20). Loganantharaj et al. proposed to measure both within-cluster homogeneity and between cluster separation of the gene clusters with respect to GO classes (21). Thalamuthu et al. assessed gene clusters by calculating and pooling p-values (i.e. the probability that random clustering generates gene clusters with a certain annotation abundance level) of clustering solutions with different numbers of clusters (22).

When trusted class labels are not available, internal measures serve as alternatives. Yeung et al. compared the prediction power of several clustering methods using an adjusted Figure of Merit (FOM) when leaving one experimental condition out (23). Shamir et al. used a FOM-based homogeneity index to evaluate the separation of obtained clusters (24). Datta and Datta designed three FOM-based consistency measures to assess pair-wise co-assignment of genes, preservation of gene cluster centers, and gene cluster compactness, respectively (25). A resampling based validity scheme was proposed in (26).

In this paper, we report an experimental study comparing the performance of clustering algorithms applied to sample clustering. Our comparison mainly used external measures and evaluated the algorithms’ functionality, accuracy, and stability. We also carefully chose both the competing algorithms and the datasets to assure an informative yet fair comparison; for example, we excluded cases where the algorithms either all succeed or all fail. Acknowledging the difficult, complex nature of the work, we focused on five clustering algorithms, namely distance matrix-based HC, KMC, SOM, Standard Finite Normal Mixture (SFNM) fitting, and VISDA, which covered all the clustering algorithm categories in the taxonomies discussed above. We used seven public and representative microarray gene expression datasets to conduct the comparison and assessed both the bias and variance of the clustering outcomes respective to biological ground truth. In addition to comparing the algorithms’ performance on common objectives, we also report the unique features of some algorithms, for example, hard clustering versus soft clustering, cluster number detection, and learning relational structure among clusters.

There are several major differences between our effort and previously reported works. First, our comparison focused on sample clustering rather than the heavily studied gene clustering. Sample clustering aims to confirm/refine known phenotypes or discover new phenotypes/sub-phenotypes (1). Sample clustering normally has a much higher attribute-to-sample ratio (called “dimension ratio”) than gene clustering, even after front-end gene selection (2, 9, 27), and imposes a unique challenge to many existing clustering algorithms (28). Second, instead of using internal measures (consistency) to evaluate the variance but not the bias of clustering outcome, our comparison used external measures to evaluate both the bias and the stability of the obtained sample clusters respective to the biological categories (29). We also compared our evaluation results with two other popular internal measures (cluster compactness and model likelihood) to study the characteristics and applicability of the internal measures being used. Third, our comparison of clustering algorithms is based on sample clustering against phenotype categories. It is thus more objective and reliable than most reported evaluations, which were based on gene clustering against gene annotations like GO classes. These gene annotations are prone to significant “false positive evidence” when used under biological contexts different from the specific biological processes that produced the annotations in the database. Furthermore, since most GO-like databases only provide partial gene annotations, the comparisons derived from such incomplete truth cannot be considered conclusive.

3. METHODS

Let X={x₁, x₂, …, x_N | x_i∈R^p} denote the p-dimensional vector-point sample set. The general clustering problem is to partition the sample set X into K clusters, such that the samples in the same cluster share some common characteristics or exhibit similarity as compared to the samples in different clusters (5). For the jth cluster in a solution with K clusters, we denote the cluster’s effective size (number of owned samples) by N_j. When soft clustering is applied, the ith sample is assigned with a Bayes posterior probability of belonging to the jth cluster, denoted by z_ij. In the following subsections, we first briefly review the aforementioned five clustering algorithms (5, 8,10, 30–32), and then introduce in detail our comparative study methodology and experimental designs.

3.1. Competing Clustering Algorithms

3.1.1. Hierarchical clustering

As a bottom-up approach, agglomerative HC starts from singleton clusters, one for each data point in the sample set, and produces a nested sequence of clusters with the property that whenever two clusters merge, they remain together at any higher level. At each level of the hierarchy, the pair-wise distances between all the clusters are calculated, with the closest pair merged. This procedure is repeated until the top level is reached, where the whole dataset exists as a single cluster. See (30) for a detailed description of HC methodology. We used a Matlab implementation of HC with the Euclidean distance and average linkage function in the experiment.

3.1.2. K-means clustering

Widely adopted as a top-down scheme, KMC seeks a partition that minimizes the Mean Squared Compactness (MSC), the average squared distance between the center of the cluster and its members. Specifically, KMC performs the following steps. 1) Initialize K cluster centers, with K selected by the user. 2) Assign each sample to its nearest cluster center, and then update the cluster center with the mean of the samples assigned to it. 3) Repeat the two operations in step 2 until the partition converges. See (30) for detailed description of KMC methodology. We used a Matlab implementation of KMC in the experiment.

3.1.3. Self-organizing maps

SOM performs partitional clustering using a competitive learning scheme (32). With its roots in neural computation, SOM maps the data from the high dimensional data space to a low dimensional output space, usually a 1-D or 2-D lattice. Each node (also called a neuron) of the lattice has a reference vector. The mapping is achieved by assigning the sample to the winning node, whose reference vector is closest to the sample. Samples that are mapped to the same neuron form a cluster. In the sequential learning process, when a sample is input, all neurons are updated towards the input sample in proportion to a learning rate and to a function of the spatial distance in the lattice between the winning neuron and the given neuron. The function could be a constant window function or a Gaussian function with a width parameter that defines the spatial “neighborhood”. To reach convergence, the learning rate starts from a number smaller than 1 such as 0.9 or 0.5, and decreases linearly or exponentially to zero during the learning process. The size of the neighborhood also decreases during the learning process (32). We used the conventional, sequential SOM implemented by Matlab in the experiment.

3.1.4. SFNM fitting

The SFNM fitting method uses the Expectation Maximization (EM) algorithm to estimate an SFNM distribution for the data (30, 33). An SFNM model can be described by the following probability density function

$$\mathrm{f}({\mathbf{x}}_i|\mathbf{\theta },\mathbf{\pi })=\sum _{j=1}^K{\pi }_j\mathrm{g}({\mathbf{x}}_i|{\mathbf{\theta }}_j),\text{ and }\sum _{j=1}^K{\pi }_j=1,$$

where g(•) is the Gaussian function, and π_j and θ_j are the mixing proportion and parameters associated with cluster j, respectively. The EM algorithm performs the following two steps alternately until convergence:

E step:	$z_{ij}={\pi }_j\mathrm{g}({\mathbf{x}}_i|{\mathbf{\mu }}_j,{\mathbf{\Sigma }}_j)/\sum _{k=1}^K{\pi }_k\mathrm{g}({\mathbf{x}}_i|{\mathbf{\mu }}_k,{\mathbf{\Sigma }}_k)$,
	${\pi }_j=\sum _{i=1}^N{z}_{ij}/N,{\mathbf{\mu }}_j=\sum _{i=1}^N{z}_{ij}{\mathbf{x}}_i/\sum _{i=1}^N{z}_{ij}$
M step:	${\mathbf{\Sigma }}_j=\sum _{i=1}^N{z}_{ij}({\mathbf{x}}_i-{\mathbf{\mu }}_j){({\mathbf{x}}_i-{\mathbf{\mu }}_j)}^T/\sum _{i=1}^N{z}_{ij}$,

μ_j and Σ_j are the mean and covariance matrix of cluster j, respectively. In the mixture, each Gaussian distribution represents a cluster. We implemented SFNM fitting based on the above algorithm in our experiments.

3.1.5. Visual statistical data analyzer

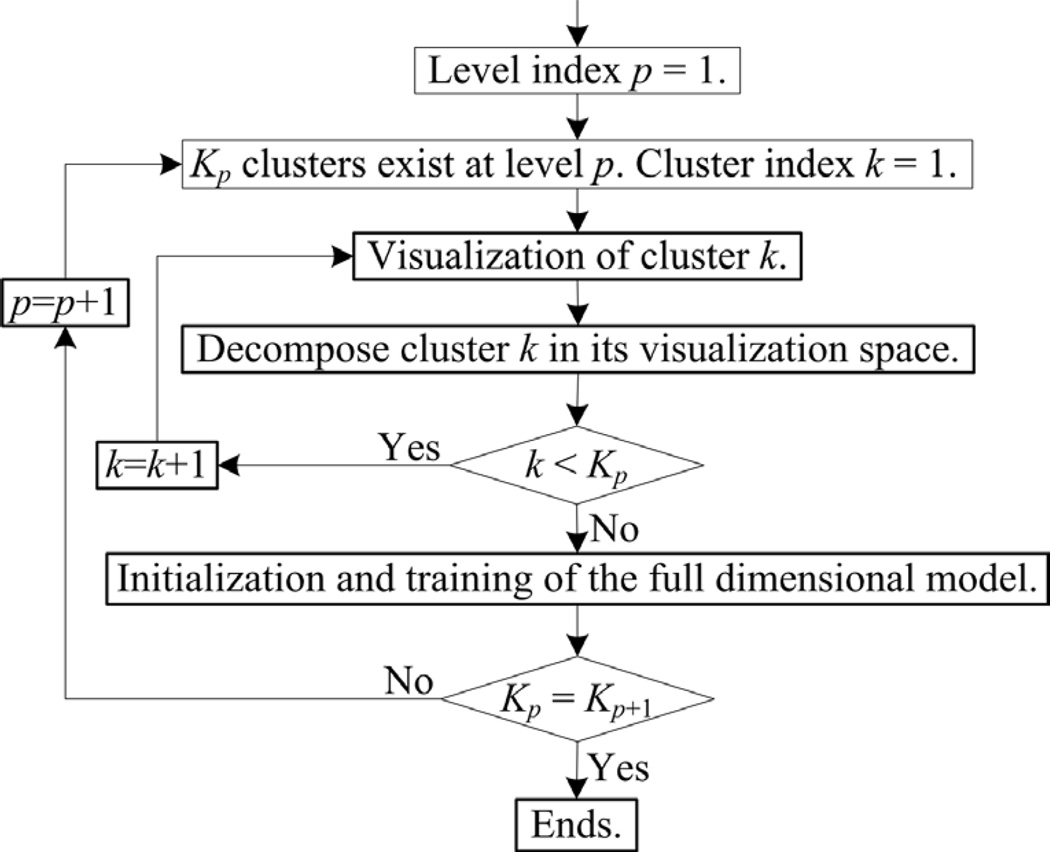
Based on a hierarchical SFNM model, VISDA performs top-down, coarse-to-fine divisive clustering as outlined in Figure 1. At the top level, the entire dataset is split into several coarse clusters that may contain multiple sub-clusters; at lower levels, these composite clusters are further decomposed into finer sub-clusters until no further substructure can be found. For each cluster in the hierarchy, various structure-preserving projection methods are used to visualize the data in the cluster within 2-D projection spaces. Each such space captures distinct characteristics of the cluster’s inner structure. Subsequently, the user can choose the projection that best reveals the data’s structure, and initialize the centers of potential sub-clusters by pinpointing them on the computer screen. A local SFNM distribution for the purpose of decomposing the cluster is then trained by the EM algorithm in the projection space. This procedure is repeated for several competing models with different number of sub-clusters, and the number of sub-clusters in the final model is determined by the Minimum Description Length (MDL) criterion, combined with human justification. Once the optimal local models of all clusters are determined in their projection spaces, their model parameters are transformed back to the original data space to initialize the full-dimensional SFNM model, which will be refined via the EM algorithm. See (8–10) for further description of VISDA. VISDA is freely downloadable from the caBIG™ website (11).

Figure 1.

The flowchart of VISDA.

3.2. Evaluation design

Our evaluation focused on three fundamental characteristics of clustering solutions, namely, functionality, accuracy, and stability. Multiple cross-validation trials on multiple datasets are conducted to estimate the performance.

3.2.1. Functionality

Determining the number of clusters and the membership of data points is the major objective of data clustering. Although model selection criteria have been proposed for use with HC, KMC, SOM, and SFNM fitting algorithms, there is no consensus about the proper model selection criterion. Thus, we simply fixed the cluster number at the true number of classes for these methods. VISDA provides an MDL based model selection module assisted by human justification. We assessed this functionality by its ability to detect the correct cluster number in cross-validation. Furthermore, both SFNM model fitting and VISDA provide soft clustering with confidence values (8); both HC and VISDA perform hierarchical clustering and show the hierarchical relationship among discovered clusters, which may contain biological meaningful information and allows cluster analysis at multiple resolutions, achieved by simply merging clusters according to the tree structure.

3.2.2. Accuracy

A natural measure of clustering accuracy is the percentage of correctly labeled samples, i.e. the partition accuracy. Furthermore, as an unsupervised learning task, data clustering involves both detection and estimation steps, i.e. detection targets the sample labels and estimation targets the class distribution. Note that different clustering solutions with the same partition accuracy may not recover the class distribution equally well. In our study, we evaluate the accuracy of the estimated parametric class distribution against ground truth, i.e. the biases of the estimated class mean and covariance matrix, by taking the cluster mean and covariance matrix as estimates of ground truth class mean and covariance matrix, respectively.

3.2.3. Stability

To test the stability of the clustering algorithms, we calculate the variation of the clustering outcomes using n-fold cross-validation (n = 9~10). In each of the multiple trials, only (n − 1)/n of the samples in each class are used to produce the clustering outcome. Stability of a clustering algorithm is reflected by the resulting standard deviations of partition accuracy, estimated class means, and estimated class covariance matrices.

3.2.4. Additional internal measures

Besides MSC as an internal clustering validity measure, Mean Log-Likelihood (MLL) for mixture model fitting or Mean Classification Log-Likelihood (MCLL) for the hard clustering result measure the goodness of fit between the estimated probability model and the soft or hard partitioned data in terms of average joint log-likelihood.

3.3. Quantitative performance measures

For assessing the model selection functionality of VISDA, cluster number detection accuracy is calculated based on doubled n-fold cross-validation trials, where a detection trial is considered successful if VISDA detects the correct number of clusters, given by

$$\frac{\text{number of successful detection trials}}{2\times n}\times 100\%.$$

A prerequisite for calculating the other aforementioned performance measures is the correct association between the discovered clusters and ground truth classes. To assure the global optimality of the association, all permuted matches between the detected clusters and the ground truth classes are evaluated. For this purpose, after correctly detecting the cluster number, we calculate the consistency between the permuted cluster labels and the ground truth labels over all data points and choose the association whose consistency is the maximum among all permuted matches, given by

$$P_l=\underset{\alpha }{\text{max}}\frac{1}{N_l}\sum _{i=1}^{N_l}1\left\{\alpha \right(L_l({\mathbf{x}}_i)),L^{*}({\mathbf{x}}_i)\}$$

where P_l is the partition accuracy in the lth cross-validation trial, α is the permutation of cluster indices {1, 2, …, K}, N_l is the number of samples used in the lth trial, L_l(x_i) is the clustering label of data point x_i in the lth trial, L^*(x_i) is the true label of x_i, and 1{•, •} is the indicator function, which returns 1 if the two input arguments are equal and returns 0 if not. Using the Hungarian method, the complexity of the search is O(N_l+K³) (34). For soft clustering, we transform the soft memberships to hard memberships via the Bayes decision rule (30) to calculate the optimal association and partition accuracy.

Then, other performance measures are calculated based on 20 cross-validation trials in which the cluster number was correctly detected. The Bias of Class Mean Estimate (BCME) and the Standard deviation of Class Mean Estimate (SCME) are given by

$$\mathrm{B}\mathrm{C}\mathrm{M}\mathrm{E}=\frac{1}{K}\sum _{j=1}^K\Vert \frac{1}{20}\sum _{l=1}^{20}{\hat{\mathbf{m}}}_{lj}-{\mathbf{m}}_j^{*}\Vert$$

$$\mathrm{S}\mathrm{C}\mathrm{M}\mathrm{E}=\frac{1}{K}\sum _{j=1}^K\sqrt{\frac{1}{20}\sum _{l=1}^{20}{\Vert {\hat{\mathbf{m}}}_{lj}-\frac{1}{20}\sum _{q=1}^{20}{\hat{\mathbf{m}}}_{qj}\Vert }^2},$$

where ‖•‖ indicates L₂ norm in this paper, m̂_lj is the mean of cluster j in trial l, and ${\mathbf{m}}_j^{*}$ is the true mean of class j. For soft clustering, m̂_lj is calculated by

$${\hat{\mathbf{m}}}_{lj}=\sum _{i=1}^{N_l}{z}_{lij}{\mathbf{x}}_i/\sum _{i=1}^{N_l}{z}_{lij}.$$

z_lij is the posterior probability of sample i belonging to cluster j in trial l. The Bias of Class Covariance Matrix Estimate (BCCME) and the Standard deviation of Class Covariance Matrix Estimate (SCCME) are given by

$$\mathrm{B}\mathrm{C}\mathrm{C}\mathrm{M}\mathrm{E}=\frac{1}{K}\sum _{j=1}^K{\Vert \frac{1}{20}\sum _{l=1}^{20}{\hat{\mathrm{\Sigma }}}_{lj}-{\mathrm{\Sigma }}_j^{*}\Vert }_F$$

$$\mathrm{S}\mathrm{C}\mathrm{C}\mathrm{M}\mathrm{E}=\frac{1}{K}\sum _{j=1}^K\sqrt{\frac{1}{20}\sum _{l=1}^{20}{\Vert {\hat{\mathrm{\Sigma }}}_{lj}-\frac{1}{20}\sum _{q=1}^{20}{\hat{\mathrm{\Sigma }}}_{qj}\Vert }_F^2},$$

where Σ̂_lj is cluster j’s covariance matrix in trial l, and ${\mathbf{\Sigma }}_j^{*}$ is the true covariance matrix of class j. The subscript ‘F’ denotes the Frobenius norm of a matrix. For soft clustering, Σ̂_lj is calculated by

$${\hat{\mathbf{\Sigma }}}_{lj}=\sum _{i=1}^{N_l}{z}_{lij}({\mathbf{x}}_i-{\hat{\mathbf{m}}}_{lj}){({\mathbf{x}}_i-{\hat{\mathbf{m}}}_{lj})}^T/\sum _{i=1}^{N_l}{z}_{lij},$$

Furthermore, the MSC of hard clustering in the lth cross-validation trial is calculated by

$$\mathrm{M}\mathrm{S}{\mathrm{C}}_l=\frac{1}{N_l}\sum _{j=1}^K\sum _{i=1}^{N_{lj}}{\Vert {\mathbf{x}}_i-{\hat{\mathbf{m}}}_{lj}\Vert }^2$$

where N_lj is the number of samples in the jth cluster in the lth cross-validation trial. The MLL for soft clustering with an SFNM model in the lth cross-validation trial is calculated by

$$\mathrm{M}\mathrm{L}{\mathrm{L}}_l=\frac{1}{N_l}\sum _{i=1}^{N_l}\text{log}\sum _{j=1}^K{\pi }_{lj}\mathrm{g}({\mathbf{x}}_i|{\hat{\mathbf{m}}}_{lj},{\hat{\mathbf{\Sigma }}}_{lj}),$$

where π_lj is the proportion of cluster j in the lth trial. For hard clustering, the MCLL is calculated by

$$\mathrm{M}\mathrm{C}\mathrm{L}{\mathrm{L}}_l=\frac{1}{N_l}\sum _{i=1}^{N_l}\text{log}(\mathrm{g}({\mathbf{x}}_i|{\hat{\mathbf{m}}}_{l{\mathbf{x}}_i},{\hat{\mathbf{\Sigma }}}_{l{\mathbf{x}}_i})),$$

where m̂_lxi and Σ̂_lxi are the mean vector and covariance matrix of the cluster that x_i belongs to in trial l.

3.4. Additional experimental details

For the clustering algorithms that do not have a model selection function, we set the ground truth class number K as the input cluster number. For example, the dendrogram of HC was cut at a threshold that produced a partition with K clusters, and KMC, SOM, and SFNM algorithms were initialized by K randomly chosen samples as cluster centers. We used the best outcome from multiple runs of these randomly initialized clustering algorithms, evaluated using the aforementioned criteria. The KMC was chosen based on MSC. SOM was separately chosen based on both MSC and MCLL. SFNM fitting used MLL as the optimality criterion. Specifically, for each of the 20 cross-validation trials, the clustering procedure was performed 100 times, each with a different random initialization. For SOM, two different neighborhood functions were used 50 times in each cross-validation trial.

3.5. Datasets

We chose a total of seven real microarray gene expression datasets and one synthetic dataset for this ground truth based comparative study, summarized in For example, the datasets cannot be too “simple” (if the clusters are well-separated, all methods perform equally well) or too “complex” (no method will then perform reasonably well). Specifically, each cluster must be reasonably well-defined (for example, not a composite cluster) and contain sufficient data points.

Table 3. For simplicity, Table 4 gives the performance ranks of the algorithms respective to BCME and SCME and Table 5 gives the performance ranks of the algorithms respective to BCCME and SCCME. On each dataset, rank 1 means the best performance among the competing methods, while rank 6 means the worst performance among the competing methods. Table 6 gives the average MSC and average MLL of the obtained clustering solutions. More details, including the exact values of the performance measures, can be found in the supplement.

Table 3.

Mean/standard-deviation of partition accuracy

	VISDA	HC	KMC	SOM(MSC)	SOM(MCLL)	SFNM fitting
Synthetic data	94.89% /0.67%	52.11% /10.37%	92.14% /0.51%	92.14% /0.51%	92.18% /0.49%	94.89% /0.64%
SRBCTs	94.23% /3.01%	46.96% /11.71%	81.52% /5.68%	81.66% /5.65%	94.32% /4.98%	36.74% /2.66%
Multiclass cancer	94.66% /2.08%	66.22% /1.72%	92.28% /11.49%	92.28% /11.49%	94.46% /8.74%	62.33% /10.97%
Lung cancer	79.00% /7.43%	57.43% /2.17%	68.57% /6.73%	68.49% /6.31%	71.78% /4.75%	51.05% /7.99%
UM cancer	94.66% /0.85%	64.14% /5.39%	84.84% /0.49%	84.84% /0.49%	82.20% /7.89%	93.59% /0.88%
Ovarian cancer	65.39% /9.98%	59.83% /4.92%	55.47% /2.53%	55.40% /2.38%	55.07% /2.21%	43.14% /6.24%
MMM-cancer 1	89.36% /3.06%	67.89% /1.74%	81.83% /0.87%	81.83% /0.87%	80.65% /4.16%	79.00% /4.44%
MMM-cancer 2	78.12% /5.03%	56.50% /2.20%	55.08% /3.10%	55.55% /3.09%	64.46% /4.58%	55.05% /6.78%
Average	86.29% /4.01%	58.89%/5.03%	76.47% /3.92%	76.52% /3.85%	79.39% /4.73%	64.47% /5.07%

The highest mean partition accuracy and the smallest standard deviation obtained on each dataset are in bold font.

Table 4.

Rank of BCME/SCME

	VISDA	HC	KMC	SOM (MSC)	SOM (MCLL)	SFNM fitting
Synthetic data	2/1	6/6	4/3	4/3	3/5	1/1
SRBCTs	1/1	6/6	5/3	4/3	2/2	3/5
Multiclass cancer	4/2	5/1	2/4	2/4	1/3	6/6
Lung cancer	1/4	5/5	2/3	3/2	4/1	6/6
UM cancer	1/4	6/6	3/1	3/1	5/5	2/3
Ovarian cancer	1/5	2/6	6/1	3/2	5/3	4/4
MMM-cancer 1	1/3	6/6	4/1	4/1	3/4	2/5
MMM-cancer 2	1/1	6/4	5/5	4/6	3/2	2/3
Average	1.50/2.63	5.25/5.00	3.88/2.63	3.38/2.75	3.25/3.13	3.25/4.13

Bold font indicates the best performance obtained on each dataset.

Table 5.

Rank of BCCME/SCCME

	VISDA	HC	KMC	SOM (MSC)	SOM (MCLL)	SFNM Fitting
Synthetic Data	2/4	6/6	4/1	4/1	3/3	1/5
SRBCTs	1/1	3/5	4/4	4/3	2/2	6/6
Multiclass Cancer	4/3	5/1	2/4	2/4	1/2	6/6
Lung Cancer	1/5	5/4	3/3	4/2	2/1	6/6
UM Cancer	1/4	6/6	3/1	3/1	5/5	2/3
Ovarian Cancer	1/4	2/5	4/1	3/2	5/3	6/6
MMM-Cancer 1	3/4	6/1	4/1	4/1	2/5	1/6
MMM-Cancer 2	1/4	3/1	4/3	4/2	2/5	6/6
Average Rank	1.75/3.63	4.50/3.63	3.50/2.25	3.50/2.00	2.75/3.25	4.25/5.50

Bold font indicates the best performance obtained on each dataset.

Table 6.

Mean MSC/ MLL

	VISDA	HC	KMC	SOM (MSC)	SOM (MCLL)	SFNM fitting	Ground truth
Synthetic data	5.68e+0(4) /−6.19e+0	9.52e+0 (6)	5.52e+0 (1)	5.52e+0 (1)	5.52e+0 (1)	5.68e+0(4) /−6.19e+0	5.78e+0
SRBCTs	5.46e+1(4) /−5.99e−1	7.41e+1 (5)	4.76e+1 (1)	4.76e+1 (1)	5.12e+1 (3)	1.09e+2(6) /−8.33e+1	5.22e+1
Multiclass cancer	1.71e+5(5) /−4.21e+1	1.65e+5 (4)	1.56e+5 (1)	1.56e+5 (1)	1.58e+5 (3)	5.89e+5(6) /−3.88e+1	1.60e+5
Lung cancer	5.02e+5(4) /−7.15e+1	5.49e+5 (5)	4.32e+5 (1)	4.32e+5 (1)	4.33e+5 (3)	1.53e+6(6) /−6.70e+1	5.40e+5
UM cancer	9.07e+7(5) /−6.53e+1	8.99e+7 (4)	5.42e+7 (1)	5.42e+7 (1)	5.68e+7 (3)	9.25e+7(6) /−6.52e+1	8.75e+7
Ovarian cancer	5.10e+7(4) /−1.84e+2	5.87e+7 (5)	4.72e+7 (1)	4.72e+7 (1)	4.73e+7 (3)	8.74e+7(6) /−1.64e+2	5.70e+7
MMM-cancer 1	4.58e+6(5) /−8.98e+1	3.95e+6 (4)	3.01e+6 (1)	3.01e+6 (1)	3.32e+6 (3)	6.26e+6(6) /−8.90e+1	4.72e+6
MMM-cancer 2	2.42e+8(5) /−1.53e+2	1.41e+8 (4)	1.18e+8 (1)	1.18e+8 (1)	1.29e+8 (3)	3.16e+8(6) /−1.50e+2	2.66e+8
Average rank of MSC	4.5	4.63	1	1	2.75	5.75	N/A

Mean MSC is shown with performance rank in parentheses. Best MSC obtained on each dataset is indicated by bold font. Mean MLL is shown only for VISDA and SFNM fitting. Better MLL of VISDA and SFNM fitting method is also indicated by bold font. “Ground truth” indicates the MSC calculated based on the ground truth biological categories.

4. RESULTS

The experimental results are summarized in tables 2–6. Cluster number detection accuracy of VISDA is given in table 2. The mean and standard deviation of partition accuracies are given in table 3. For simplicity, table 4 gives the performance ranks of the algorithms respective to BCME and SCME and table 5 gives the performance ranks of the algorithms respective to BCCME and SCCME. On each dataset, rank 1 means the best performance among the competing methods, while rank 6 means the worst performance among the competing methods. Table 6 gives the average MSC and average MLL of the obtained clustering solutions. More details, including the exact values of the performance measures, can be found in the supplement.

Table 2.

Cluster number detection accuracy of VISDA

	Synthetic dataset	SRBCTs	Multiclass cancer	Lung cancer	UM cancer	Ovarian cancer	MMM cancer (1)	MMM cancer (2)	Average
Detection accuracy	100%	95%	100%	100%	100%	94.44%	90%	100%	97%

4.1. Cluster number detection accuracy

VISDA achieves an average detection accuracy of 97% over all the datasets. This result indicates the effectiveness of the model selection module of VISDA that exploits and combines the hierarchical SFNM model, the structure-preserving 2-D projections, the MDL model selection in projection space, and human-computer interaction (visualization selection, manual cluster center initialization, and cluster number confirmation supported by visualization).

4.2. Partition accuracy

Partition accuracy is considered the most important performance measure. VISDA gives the highest average partition accuracy -- 86.29% over all the datasets. Optimum SOM selected by MCLL ranked second with an average partition accuracy of 79.39%. On the synthetic dataset, both VISDA and SFNM fitting achieve the best average partition accuracy of 94.89%. On SRBCTs dataset, the average partition accuracies of optimum SOM selected by MCLL (94.32%) and VISDA (94.23%) are comparable. Optimum KMC and SOM selected by MSC show similar performance on all the datasets.

On the synthetic data and the majority of the real microarray datasets, HC gives a much lower partition accuracy as compared to all other competing methods. HC is very sensitive to outliers/noise and often produces very small or singleton clusters. On the relatively easy case of the synthetic data, KMC, SOM, VISDA, and SFNM fitting achieve almost equally good partition accuracy, with slightly better performance achieved by using soft clustering. On the two most difficult cases, the ovarian cancer and MMM-Cancer 2 datasets, HC achieves comparable partition accuracies to those of optimum KMC and SOM selected by MSC, while VISDA consistently outperforms all other methods. Interestingly, we have found that the optimum SOM selected by MCLL generally gives a higher partition accuracy than that of optimum SOM selected by MSC. A possible interpretation is that MCLL uses both the first and second order statistics to select the final partition while MSC uses only a first order measure. As a more complex model, SFNM clustering performs well on the datasets with sufficient samples, such as the synthetic dataset and UM cancer dataset. However, when the sample size becomes relatively small and the dimension ratio becomes high, its performance significantly degrades, either because of over-fitting or local optima, which can be seen from the MLL values in table 6.

From the standard-deviation of partition accuracy, we can see that optimum SOM selected by MSC has the most stable partition accuracy, followed by optimum KMC selected by MSC and VISDA. These three methods generate clusters with more stable biological relevance than the other methods.

4.3. Recovery of class distribution

In terms of BCME and BCCME, VISDA outperforms the other methods with an average rank of 1.50 and 1.75, respectively. The two-tier EM algorithm and soft clustering likely contribute to this good performance. We have observed that, on the synthetic dataset and UM cancer dataset, which are the two most data-sufficient cases, soft clustering leads to smaller BCMEs and BCCMEs than hard clustering. This result is consistent with the theoretical expectation that maximum likelihood fitting, which allows a data point to contribute simultaneously to more than one cluster, is least-biased when the clustered data can be well approximated by a mixture model (36). In contrast, when the dimension ratio is high and clusters are not sufficiently well-defined, SFNM fitting gives unsatisfactory clustering outcomes that are possibly due to the increased number of local optima and inaccurate estimation of covariance structure because of the curse of dimensionality. As a non-statistical procedure, HC shows once again its sensitivity to outliers/noise with a high BCME and BCCME.

From the SCME and SCCME, we can see that the optimum KMC and SOM selected by MSC generally provide more stable solutions. Such stability indicates the benefit of using simple optimization criterion (first order statistics) and an ensemble scheme to reduce output variance. VISDA and SFNM fitting utilize second order statistics in their clustering process. As indicated by the bias/variance dilemma (37), for a fixed sample size, with increasing model complexity (measured e.g. by the number of model parameters), the reliability of the parameter estimates decreases. It is theoretically true that some biased estimators could have smaller variance and clustering schemes that exploit higher-order statistics do not necessarily outperform simpler methods with respect to stability (29), as we also can see here from the ranks of SFNM fitting in table 4 and 5. VISDA has a rank of 2.63 and 3.63 for SCME and SCCME, respectively, which are relatively good performances among the competitors, possibly due to the manual model initialization guided/constrained by the operator’s understanding of the data structure and the hierarchical exploration process. It is not surprising that HC exhibits high instability that may be again due to its sensitivity to outliers/noise.

4.4. Additional internal measures

MSC and MLL are two popular internal measures that we also examined (table 6). Since these additional measures do not have a direct relation to the ground truth, although being easily adopted, the conclusions drawn from their values could be misleading and should be used with caution. For example, optimum KMC and optimum SOM selected by MSC consistently achieve the smallest MSC, (somewhat unexpectedly) even smaller than the MSC of the ground truth. Based on the corresponding imperfect partition accuracies, this result indicates that solely minimizing MSC does not constitute an unbiased clustering approach. A similar situation was observed for the MLL criterion with additional issues of inaccurate estimation of the second order statistics and local optima caused by both the curse of dimensionality and covariance matrix singularity. VISDA generally has smaller MLL values than the SFNM fitting method, while VISDA has better partition accuracy and achieves better estimation of the class distribution.

5. SUMMARY AND DISCUSSION

We reported a ground-truth based comparative study on clustering of gene expression data. Five clustering methods, i.e. HC, KMC, SOM, SFNM fitting, and VISDA, were selected as representatives of various clustering algorithm categories and compared on seven carefully-chosen real microarray gene expression datasets and one synthetic dataset with definitive ground truth. Multiple objective and quantitative performance measures were designed, justified, and formulated to assess the clustering accuracy and stability. The outcomes that we observed include both new observations and some established facts. Effort has also been made to interpret the results.

Our experimental results showed that VISDA, a human-data interactive coarse-to-fine hierarchical maximum likelihood fitting algorithm, achieved greater clustering accuracy, on most of the datasets, than other methods. Its hierarchical exploration process with model selection in low-dimensional locally-discriminative visualization spaces also provided an effective model selection scheme for high dimensional data. SOM optimized by the MCLL criterion produced the second best clustering accuracy overall. KMC and SOM optimized by the MSC criterion generally produced more stable clustering solutions than the other methods. The SFNM fitting method achieved good clustering accuracy in data-sufficient cases, but not in data-insufficient cases. The experiments also showed that for gene expression data, solely minimizing mean squared compactness of the clusters or solely maximizing mixture model likelihood may not yield biologically plausible results.

Several important points remain to be discussed. First, our comparative study focused on sample clustering (1, 9, 28), rather than gene clustering (3, 4). Sample clustering in biomedicine often aims to either confirm/refine the known disease categories (28) or discover novel disease subtypes (1). The expected number of “local” clusters of interest is often moderate (1, 38), e.g., 3~5 clusters as presented in our testing datasets. Compared to gene clustering, sample clustering faces much higher dimension ratios and, consequently, a more severe “curse of dimensionality”, which can greatly affect the accuracy of many clustering algorithms. While most existing comparison studies have been devoted to gene clustering, we believe that it is equally important to assess the competence of the competing clustering methods on sample clustering with high dimension ratios. In our comparisons, even after front-end gene selection, some datasets still have much higher dimension ratios than for typical gene clustering. Furthermore, if the competing methods are applied to gene clustering, the comparison of the methods is expected to be similar to what was seen on the synthetic dataset, where the dimension ratio is low.

Second, although VISDA and SFNM fitting methods both utilize a normal mixture model and performed similarly in data-sufficient cases, VISDA outperformed SFNM fitting in the data-insufficient cases. A critical difference between these two methods is that, unlike SFNM fitting, VISDA does not apply a randomly initialized fitting process but performs maximum likelihood fitting guided/constrained by the human operator’s understanding of the data structure. Additionally, the hierarchical data model and exploration process of VISDA apply the idea of “divide and conquer” to find both global and local data structure.

Third, regarding the computational complexity of the competing clustering methods, the batch-mode KMC runs much faster than the sequential SOM and HC, especially when the sample size is large. For mixture model based methods, convergence of the algorithm can be very slow or even fail when the boundary of the parameter space is reached or when singularity of the covariance matrix occurs. Accordingly, in our experiments, for SFNM fitting and VISDA, if the boundary of the parameter space was reached, the mixture model was reinitialized and recomputed; adjustment of the eigenvalues of the covariance matrix was employed to prevent the covariance matrix from becoming singular.

Fourth, among all the compared methods, only VISDA utilizes human-data interaction in the clustering process. Although experienced users and domain experts tend to generate better clustering results, VISDA’s requirement on users’ skill is not high. With a few rounds of practice, all users can gain a good level of experience and produce reasonable clustering outcomes.

Fifth, we selected representative clustering algorithms from various algorithm categories to conduct our comparisons. Some of the selected algorithms may have more sophisticated variants; however, a more complex algorithm does not necessarily lead to stable clustering outcomes, as we observed in the experiments. It is also well known that clustering algorithms always reflect some structural bias associated with the involved grouping principle (5–7). Although, the purpose of this study is to assess which method is most effective for clustering microarray gene expression data, it is recommended that for a new dataset without much prior knowledge one should try several different clustering methods or use an ensemble scheme that combines the results of different algorithms.

Table 1.

Microarray gene expression datasets used in the experiment

Dataset name	Diagnostic task	Biological category (number of samples in the category)	Number of classes/ selected genes	Source
SRBCTs	Small round blue cell tumours	Ewing sarcoma (29), burkitt lymphoma (11), neuroblastoma (18), and rhabdomyosarcoma (25)	4/60	(38)
Multiclass Cancer	Multiple human tumour types	Prostate cancer (10), breast cancer (12), kidney cancer (10), and lung cancer (17)	4/7	(39)
Lung Cancer	Lung cancer sub-types and normal tissues	Adenocarcinomas (16), normal lung (17), squamous cell lung carcinomas (21), and pulmonary carcinoids (20)	4/13	(40)
UM Cancer	Classification of multiple human cancer types	Brain cancer (73), colon cancer (60), lung cancer (91), ovary cancer (119, including 6 uterine cancer samples)	4/8	(41)
Ovarian Cancer	Ovarian cancer sub-types and clear cell	Ovarian serous (29), ovarian mucinous (10), ovarian endometrioid (36), and clear ovarian cell (9)	4/25	(42, 43)
MMM-Cancer 1	Human cancer data from multi-platforms and multi-sites	Breast cancer (22), central-nervous meduloblastoma (57), lung-squamous cell carcinoma (20), and prostate cancer (39)	4/15	(44)
MMM-Cancer 2	Human cancer data obtained multi-platforms and multi-sites	Central-nervous glioma (10), lung-adenocarcinoma (58), lung-squamous cell carcinoma (21), lymphoma-large B cell (11), and prostate cancer (41)	5/20	(44)

Abbreviations

VISDA

visual statistical data analyzer

HC

hierarchical clustering

KMC

K-means clustering

SOM

self-organizing maps

GO

gene ontology

FOM

figure of merit

SFNM

standard finite normal mixture

MSC

mean squared compactness

EM

expectation maximization

MDL

minimum description length

MLL

mean log-likelihood

MCLL

mean classification log-likelihood

BCME

bias of class mean estimate

SCME

standard deviation of class mean estimate

BCCME

bias of class covariance matrix estimate

SCCME

standard deviation of class covariance matrix estimate