Sampling distributions and the bootstrap

We have previously discussed the importance of estimating uncertainty in our measurements and incorporating it into data analysis¹. To know the extent to which we can generalize our observations, we need to know how our estimate varies across samples and whether it is biased (systematically over- or underestimating the true value). Unfortunately, it can be difficult to assess the accuracy and precision of estimates because empirical data are almost always affected by noise and sampling error, and data analysis methods may be complex. We could address these questions by collecting more samples, but this is not always practical. Instead, we can use the bootstrap, a computational method that simulates new samples, to help determine how estimates from replicate experiments might be distributed and answer questions about precision and bias.

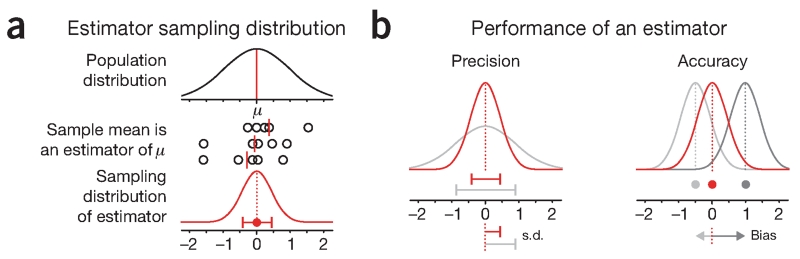
The quantity of interest can be estimated in multiple ways from a sample—functions or algorithms that do this are called estimators (Fig. 1a). In some cases we can analytically calculate the sampling distribution for an estimator. For example, the mean of a normal distribution, μ, can be estimated using the sample mean. If we collect many samples, each of size n, we know from theory that their means will form a sampling distribution that is also normal with mean μ and s.d. σ/√n (σ is the population s.d.). The s.d. of a sampling distribution of a statistic is called the standard error (s.e.)¹ and can be used to quantify the variability of the estimator (Fig. 1).

Figure 1.

Sampling distributions of estimators can be used to predict the precision and accuracy of estimates of population characteristics. (a) The shape of the distribution of estimates can be used to evaluate the performance of the estimator. The population distribution shown is standard normal (μ = 0, σ = 1). The sampling distribution of the sample means estimator is shown in red (this particular estimator is known to be normal with σ = 1/√n for sample size n). (b) Precision can be measured by the s.d. of the sampling distribution (which is defined as the standard error, s.e.). Estimators whose distribution is not centered on the true value are biased. Bias can be assessed if the true value (red point) is available. Error bars show s.d.

The sampling distribution tells us about the reproducibility and accuracy of the estimator (Fig. 1b). The s.e. of an estimator is a measure of precision: it tells us how much we can expect estimates to vary between experiments. However, the s.e. is not a confidence interval. It does not tell us how close our estimate is to the true value or whether the estimator is biased. To assess accuracy, we need to measure bias—the expected difference between the estimate and the true value.

If we are interested in estimating a quantity that is a complex function of the observed data (for example, normalized protein counts or the output of a machine learning algorithm), a theoretical framework to predict the sampling distribution may be difficult to develop. Moreover, we may lack the experience or knowledge about the system to justify any assumptions that would simplify calculations. In such cases, we can apply the bootstrap instead of collecting a large volume of data to build up the sampling distribution empirically.

The bootstrap approximates the shape of the sampling distribution by simulating replicate experiments on the basis of the data we have observed. Through simulation, we can obtain s.e. values, predict bias, and even compare multiple ways of estimating the same quantity. The only requirement is that data are independently sampled from a single source distribution.

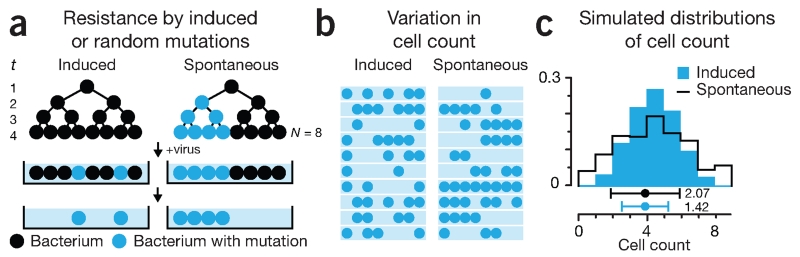
We’ll illustrate the bootstrap using the 1943 Luria-Delbrück experiment, which explored the mechanism behind mutations conferring viral resistance in bacteria². In this experiment, researchers questioned whether these mutations were induced by exposure to the virus or, alternatively, were spontaneous (occurring randomly at any time) (Fig. 2a). The authors reasoned that these hypotheses could be distinguished by growing a bacterial culture, plating it onto medium that contained a virus and then determining the variability in the number of surviving (mutated) bacteria (Fig. 2b). If the mutations were induced by the virus after plating, the bacteria counts would be Poisson distributed. Alternatively, if mutations occurred spontaneously during growth of the culture, the variance would be higher than the mean, and the Poisson model—which has equal mean and variance—would be inadequate. This increase in variance is expected because spontaneous mutations propagate through generations as the cells multiply. We simulated 10,000 cultures to demonstrate this distribution; even for a small number of generations and cells, the difference in distribution shape is clear (Fig. 2c).

Figure 2.

The Luria-Delbrück experiment studied the mechanism by which bacteria acquired mutations that conferred resistance to a virus. (a) Bacteria are grown for t generations in the absence of the virus, and N cells are plated onto medium containing the virus. Those with resistance mutations survive. (b) The relationship between the mean and variation in the number of cells in each culture depends on the mutation mechanism. (c) Simulated distributions of cell counts for both processes shown in a using 10,000 cultures and mutation rates (0.49 induced, 0.20 spontaneous) that yield equal count means. Induced mutations occur in the medium (at t = 4). Spontaneous mutations can occur at each of the t = 4 generations. Points and error bars are mean and s.d. of simulated distributions (3.92 ± 2.07 spontaneous, 3.92 ± 1.42 induced). For a small number of generations, the induced model distribution is binomial and approaches Poisson when t is large and rate is small.

To quantify the difference between distributions under the two mutation mechanisms, Luria and Delbrück used the variance-to-mean ratio (VMR), which is reasonably stable between samples and free of bias. From the reasoning above, if the mutations are induced, the counts are distributed as Poisson, and we expect VMR = 1; if mutations are spontaneous, then VMR >> 1.

Unfortunately, measuring the uncertainty in the VMR is difficult because its sampling distribution is hard to derive for small sample sizes. Luria and Delbrück plated 5–100 cultures per experiment to measure this variation before being able to rule out the induction mechanism. Let’s see how the bootstrap can be used to estimate the uncertainty and bias of the VMR using modest sample sizes; applying it to distinguish between the mutation mechanisms is beyond the scope of this column.

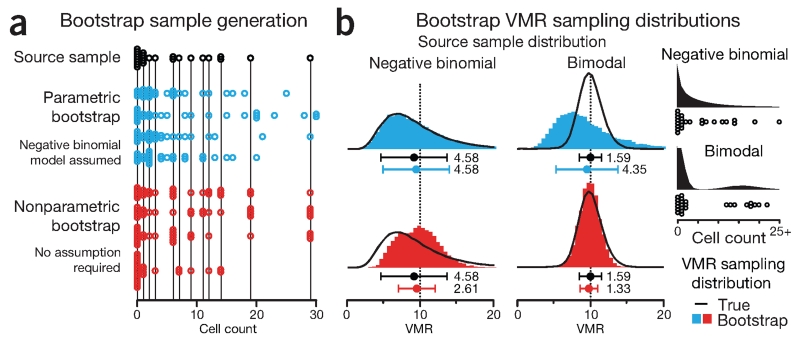
Suppose that we perform a similar experiment with 25 cultures and use the count of cells in each culture as our sample (Fig. 3a). We can use our sample’s mean (5.48) and variance (55.3) to calculate VMR = 10.1, but because we don’t have access to the sampling distribution, we don’t know the uncertainty. Instead of plating more cultures, let’s simulate more samples with the bootstrap. To demonstrate differences in the bootstrap, we will consider two source samples, one drawn from a negative binomial and one from a bimodal distribution of cell counts (Fig. 3b). Each distribution is parameterized to have the same VMR = 10 (μ = 5, σ² = 50). The negative binomial distribution is a generalized form of the Poisson distribution and models discrete data with independently specified mean and variance, which is required to allow for different values of VMR. For the bimodal distribution we use a combination of two Poisson distributions. The source samples generated from these distributions were selected to have the same VMR = 10.1, very close to their populations’ VMR = 10.

Figure 3.

The sampling distribution of complex quantities such as the variance-to-mean ratio (VMR) can be generated from observed data using the bootstrap. (a) A source sample (n = 25, mean = 5.48, variance = 55.3, VMR = 10.1), generated from negative binomial distribution (μ = 5, σ² = 50, VMR = 10), was used to simulate four samples (hollow circles) with parametric (blue) and nonparametric bootstrap (red). (b) VMR sampling distributions generated from parametric (blue) and nonparametric (red) bootstrap of 10,000 samples (n = 25) simulated from source samples drawn from two different distributions: negative binomial and bimodal, both with μ = 5 and σ² = 50, shown as black histograms with the source samples shown below. Points and error bars show mean and s.d. of the respective sampling distributions of VMR. Values beside error bars show s.d.

We will discuss two types of bootstrap: parametric and nonparametric. In the parametric bootstrap, we use our sample to estimate the parameters of a model from which further samples are simulated. Figure 3a shows a source sample drawn from the negative binomial distribution together with four samples simulated using a parametric bootstrap that assumes a negative binomial model. Because the parametric bootstrap generates samples from a model, it can produce values that are not in our sample, including values outside of the range of observed data, to create a smoother distribution. For example, the maximum value in our source sample is 29, whereas one of the simulated samples in Figure 3a includes 30. The choice of model should be based on our knowledge of the experimental system that generated the original sample.

The parametric bootstrap VMR sampling distributions of 10,000 simulated samples are shown in Figure 3b. The s.d. of these distributions is a measure of the precision of the VMR. When our assumed model matches the data source (negative binomial), the VMR distribution simulated by the parametric bootstrap very closely approximates the VMR distribution one would obtain if we drew all the samples from the source distribution (Fig. 3b). The bootstrap sampling distribution s.d. matches that of the true sampling distribution (4.58).

In practice we cannot be certain that our parametric bootstrap model represents the distribution of the source sample. For example, if our source sample is drawn from a bimodal distribution instead of a negative binomial, the parametric bootstrap generates an inaccurate sampling distribution because it is limited by our erroneous assumption (Fig. 3b). Because the source samples have similar mean and variance, the output of the parametric bootstrap is essentially the same as before. The parametric bootstrap generates not only the wrong shape but also an incorrect uncertainty in the VMR. Whereas the true sampling distribution from the bimodal distribution has an s.d. = 1.59, the bootstrap (using negative binomial model) over estimates it as 4.35.

In the nonparametric bootstrap, we forego the model and approximate the population by randomly sampling (with replacement) from the observed data to obtain new samples of the same size. As before, we compute the VMR for each bootstrap sample to generate bootstrap sampling distributions. Because the nonparametric bootstrap is not limited by a model assumption, it reasonably reconstructs the VMR sampling distributions for both source distributions. It is generally safer to use the nonparametric bootstrap when we are uncertain of the source distribution. However, because the nonparametric bootstrap takes into account only the data observed and thus cannot generate very extreme samples, it may underestimate the sampling distribution s.d., especially when sample size is small. We see some evidence of this in our simulation. Whereas the true sampling distributions have s.d. values of 4.58 and 1.59 for the negative binomial and bimodal, respectively, the bootstrap yields 2.61 and 1.33 (43% and 16% lower) (Fig. 3b).

The bootstrap sampling distribution can also provide an estimate of bias, a systematic difference between our estimate of the VMR and the true value. Recall that the bootstrap approximates the whole population by the data we have observed in our initial sample. Therefore, if we treat the VMR derived from the sample used for bootstrapping as the true value and find that our bootstrap estimates are systematically smaller or larger than this value, then we can predict that our initial estimate is also biased. In our simulations we did not see any significant sign of bias—means of bootstrap distributions were close to the sample VMR.

The simplicity and generality of bootstrapping allow for analysis of the stability of almost any estimation process, such as generation of phylogenetic trees or machine learning algorithms.