Abstract
Age and sex can influence brain iron levels. We studied the influence of these variables on deep gray matter magnetic susceptibilities. In 183 healthy volunteers (44.7 ± 14.2 years, range 20-69, ♀ 49%), in vivo Quantitative Susceptibility Mapping (QSM) at 1.5T was performed to estimate brain iron accumulation in the following regions of interest (ROIs): caudate nucleus (Cd), putamen (Pt), globus pallidus (Gp), thalamus (Th), pulvinar (Pul), red nucleus (Rn), substantia nigra (Sn) and the cerebellar dentate nuclei (Dn). We gauged the influence of age and sex on magnetic susceptibility by specifying a series of Structural Equation Models. The distributions of susceptibility varied in degree across the structures, conforming to histologic findings (Hallgren & Sourander, 1958), with the highest degree of susceptibility in the Gp and the lowest in the Th. Iron increase correlated across several ROIs, which may reflect an underlying age-related process. Advanced age was associated with a particularly strong linear rise of susceptibility in the striatum. Nonlinear age trends were found in the Rn, where they were the most pronounced, followed by the Pul and Sn, while minimal nonlinear trends were observed for the Pt, Th, and Dn. Moreover, sex related variations were observed, so that women showed lower levels of susceptibility in the Sn after accounting for age. Regional susceptibility of the Pul increased linearly with age in men but exhibited a nonlinear association with age in women with a leveling off starting from midlife. Women expected to be post menopause (+51 years) showed lower total magnetic susceptibility in the subcortical gray matter. The current report is consistent with previous reports of age related variations of brain iron, but also adds to the current knowledge by reporting age-related changes in less studied, smaller subcortical nuclei. This is the first in-vivo report to show lower total subcortical brain iron levels selectively in women from midlife, compared to men and younger women. These results encourage further assessment of sex differences in brain iron. We anticipate that age and sex are important co-factors to take into account when establishing a baseline level for differentiating pathologic neurodegeneration from healthy aging. The variations in regional susceptibility reported herein should be evaluated further using a longitudinal study design to determine within-person age related changes.
Keywords: quantitative susceptibility mapping, iron, brain aging, sub-cortical nuclei, gender differences, sex differences
1. Introduction
1.1. Aging of the Brain Parenchyma
Brain aging is characterized by a regional shrinkage across multiple gray and white matter regions of the brain parenchyma (Persson et al., 2014; Fjell & Walhovd, 2010), as well as a decline in the dopamine synthesis of subcortical nuclei (Seeman et al., 1987; Severson, Marcusson, Winblad, & Finch, 1982; Wang et al., 1998; Volkow et al., 1998). As the brain ages, non-heme iron accumulates across brain structures (Hallgren & Sourander, 1958).
Iron serves as a cofactor in several neuronal specific functions such as the synthesis of myelin and neurotransmitters (Piñero & Connor, 2000). In particular, iron is required for efficient dopaminergic neurotransmission (Berg & Youdim, 2006; Mills, Dong, Wang, & Xu, 2010), supported by pathways connecting deep subcortical nuclei. The latter are of vital importance for motor- and cognitive functions (Volkow et al., 1998), which are subject to decline with increasing age. A balanced iron level promotes normal cell function of the nervous system, but excessive levels of non-heme iron can cause age related cellular vulnerability (Dixon & Stockwell, 2014). In both aging and neurodegenerative diseases, excessive accumulation of intracellular ferrous iron (Fe2+) gets catalyzed to ferric iron (Fe3+), which may cause reactive oxygen species (ROS), oxidative stress, and cell death (Andersen, Johnsen, & Moos, 2014; Dixon & Stockwell, 2014).
Non-heme iron can only be studied directly postmortem (Hallgren & Sourander, 1958; Morris, Candy, Oakley, Bloxham, & Edwardson, 1992; Ramos et al., 2014; Ward et al., 2014), while in-vivo magnetic resonance imaging (MRI) can estimate iron deposits based on the interplay between its paramagnetic properties and the proton relaxation resonance behavior of tissue water (Schenck, 2003). Most of the non-heme iron in the brain affecting the MRI signal is believed to be consisting of ferritin and hemosiderin (Schenck, 2003; Schenck & Zimmerman, 2004).
1.2. Brain Iron in the Aging Parenchyma
Pioneering post mortem findings, discovered half a century ago, indicate aging related brain iron accumulation with varying degree across brain structures. Iron deposits showed a rapid increase until young adulthood, followed by a smaller rise and, and for some structures even a plateau after midlife (Hallgren & Sourander, 1958). With the progress of MRI techniques, researchers have followed in the footsteps of this landmark work, and both linear and nonlinear age trends of iron distribution were observed (Bilgic, Pfefferbaum, Rohlfing, Sullivan, & Adalsteinsson, 2012; Haacke et al., 2005; Haacke et al., 2010; W. Li et al., 2014; Xu, Wang, & Zhang, 2008). Iron concentrations are greater in the subcortical nuclei relative to the cerebral white matter and cortex among healthy adults (Gelman, 1995; Haacke et al., 2005; W. Li et al., 2014). The nuclei studied the most by far with in-vivo MRI are the striatum and the globus pallidus (Bartzokis et al., 1997; Bartzokis et al., 2011; Bilgic et al., 2012; Cherubini, Peran, Caltagirone, Sabatini, & Spalletta, 2009; Haacke et al., 2005; Haacke et al., 2010; Hagemeier et al., 2013; Pfefferbaum, Adalsteinsson, Rohlfing, & Sullivan, 2009; Xu et al., 2008). The age dependency in MR based iron estimates of the substantia nigra, red nucleus, thalamus, the pulvinar complex and the cerebellar dentate nucleus is studied to a lesser extent, and with greater variability of results (Bilgic et al., 2012; Haacke et al., 2010; W. Li et al., 2014; Pfefferbaum et al., 2009).
1.3. Sex Differences
A far less studied determinant of variability of brain iron levels is sex. Sex differences in the incidence and symptomatology of neurodegenerative diseases have been reported (de Rijk et al., 2000; Taylor, Cook, & Counsell, 2007). Younger male AD and PD patients show greater ferritin iron concentrations, as measured by an increase in the field-dependent relaxation rate, compared to healthy controls (Bartzokis et al., 2007; Bartzokis, Tishler, Shin, Lu, & Cummings, 2004). Compared to women, men showed a steeper decline over time in cognitive abilities tapping basal ganglia functions in adults free of dementia (Persson, Lavebratt, et al., 2013). Females exhibit lower levels of peripheral iron levels (eg. Bartzokis et al., 2007; Fleming et al., 2001; Whitfield, Treloar, Zhu, Powell, & Martin, 2003), and men have shown higher iron concentrations according to changes in MRI contrast in the cortical white matter and subcortical nuclei (Bartzokis et al., 2011; Bartzokis et al., 2007; Hagemeier et al., 2013; Tishler, Raven, Lu, Altshuler, & Bartzokis, 2012). However, a lack of sex related differences in iron levels have also been reported (Xu et al, 2008). Early histologic findings suggest that lower peripheral iron levels may influence brain iron levels, since anemia was found to reduce brain iron postmortem (Hallgren & Sourander, 1958). Pre-menstrual blood loss reduces peripheral iron levels in women and may contribute to sex differences in brain iron accumulation (Tischler et al., 2012; Whitfield et al, 2003). Women had lower levels of brain iron compared to men from midlife to old age according to a recent histologic report (Ramos et al., 2014). Sex steroids, whose levels change post menopause (Al-Azzawi & Palacios, 2009), may also influence sex related variations of brain iron levels (Gu, Xi, Liu, Keep, & Hua, 2010).
1.4. In-vivo Mapping of Susceptibility
Although iron can only be measured directly by histology, it can be estimated in vivo using MRI based on proton relaxation rates or by the effect of the magnetic susceptibility of iron on the MRI signal phase.
The field-dependent relaxation rate increase (FDRI) is defined by the degree by which the MRI field strength affects the measured transverse relaxation rate (R2). The method requires imaging at two field strengths, making it time consuming (eg. Bartzokis et al., 2004; Bartzokis, Aravagiri, Oldendorf, Mintz, & Marder, 1993) and susceptible to between scan variability and differences of orientation, thereby affecting precision.
Both the magnitude signal () (Gorell et al., 1995; Haacke et al., 2005) and the phase signal (Haacke et al., 2007) derived from MRI gradient echo (GRE) data have been used to estimate iron content. GRE phase reflects the magnetic field, which is a weighted sum of all surrounding iron. reflects the phase variance in a voxel and depends on echo time (TE), voxel size, field strength, object orientation and other imaging parameters (Brown et al., 2014). These measures have limitations. Both and phase suffer from non-local field effects. It is also possible to generate a magnetic field correlation (MFC) map to quantify iron, but MFC also depends on imaging parameters such as voxel size and echo time (Jensen et al., 2009).
To address the non-local field effects in the phase information while retaining the quantitative information in the magnetic field, a deconvolution of the magnetic field from the phase data is needed to obtain tissue magnetic susceptibility (see Wang & Liu, 2014 for a review). This method is referred to as Quantitative Susceptibility Mapping (QSM). A recently developed QSM algorithm, morphology enabled dipole inversion (MEDI), calculates the magnetic susceptibility tissue distribution from complex GRE data, incorporating both phase and magnitude information (de Rochefort et al., 2010; Wang & Liu, 2014). QSM has recently been validated by postmortem imaging showing that iron is the dominant source of magnetic susceptibility in the subcortical gray matter (Langkammer et al., 2012).
1.5. Research questions
We aimed at filling the current gaps of knowledge considering age and sex related variations of susceptibility of the deep gray matter nuclei, as outlined above. In particular, we studied age-related susceptibility differences in the smaller nuclei, such as the pulvinar complex, midbrain nuclei, and the cerebellar dentate nucleus, which were studied to a lesser extent in the literature. We have chosen to estimate brain iron using QSM. Previous studies using QSM have applied mixed protocols (W. Li et al., 2014; Bilgic et al., 2012), and we applied MEDI QSM (Wang & Liu, 2014), using the same rigorous scan protocol over a large study cohort (n=183) of healthy adults with a wide age range (20-69 years). We expected, based on the literature, to observe both linear and nonlinear age effects in susceptibility. We also gauged if the level of susceptibility was inter-correlated across the ROIs. Additionally, the influence of sex and the interaction of sex and age as they influenced regional susceptibility were assessed. Differences in total subcortical brain iron from expected menopause onset (51 years) (Al-Azzawi & Palacios, 2009; Cheung et al., 2011; Gold et al., 2001) were also examined. Our regions of interest (ROIs) were: caudate nucleus (Cd), putamen (Pt), globus pallidus (Gp), red nucleus (Rn) and substantia nigra (Sn), thalamus (Th), pulvinar (Pul), and the dentate nucleus (Dn).
2. Methods
2.1. Participants
This study was approved by the first affiliated hospital of Dalian Medical University research ethics committee. Written consent was obtained from each of the subjects. Excluded from the study were participants with a 1) history of neurological, psychiatric, or cardiovascular diseases (diabetes, hypertension, stroke), 2) history of concussion or brain surgery, or 3) drug or alcohol abuse. Two additional subjects were excluded because of image reconstruction failure. A total of 183 volunteers were included. All subjects were right handed. Data from the cerebellar dentate nucleus was only available from a subsection of the sample (n = 88/183), because of the decreased signal to noise ratio due to dephasing by the large inhomogeneous field that typically occurs in this region. This was still considered a large sample in the context of imaging studies, and was therefore included. Table 1 lists these details for each ROI.
Table 1.
Descriptive Statistics for Susceptibility Values (pbb)
| ROI | N | Mean | Std. Deviation | CV | Rank order |
|---|---|---|---|---|---|
| Cd | 183 | 89.221 | 23.941 | .27 | 4 |
| Pt | 181 | 87.953 | 35.593 | .40 | 5 |
| Gp | 181 | 191.055 | 42.193 | .22 | 1 |
| Rn | 179 | 163.232 | 60.279 | .37 | 2 |
| Sn | 179 | 132.390 | 45.006 | .34 | 3 |
| Dn | 81 | 73.819 | 36.930 | .50 | 6 |
| Pul | 177 | 68.363 | 28.693 | .42 | 7 |
| Th | 183 | 11.805 | 11.086 | .93 | 8 |
Note. Cd = caudate nucleus, Pt = putamen, Sn = substantia nigra, Rn = red nucleus, Gp = globus pallidus, Dn = dentate nucleus, Th = thalamus, and Pul = pulvinar; CV = Coefficient of variance, Standard deviation/Mean. Rank-order in col. 6 describes the ordering of susceptibility counts ranging from the highest (1), to the lowest (8).
2.2. MRI protocol
The MRI examination was performed on a 1.5T scanner (GE Signa EXCITE 14.0) equipped with an 8-channel head coil, using a 3D spoiled gradient echo sequence with flow compensation. The radiologists were blinded to the subjects’ age and identity. Routine T1 weighted and fluid-attenuated inversion recovery (FLAIR) images were first obtained on these subjects to confirm the absence of brain resection, infarction, focal lesions or large hyperintensities. Next, a threedimensional flow-compensated gradient echo sequence was applied to acquire the data for quantitative susceptibility mapping. The following imaging parameters were used in the gradient echo sequence: true axial plane, echo time (TE) = 40 ms, repetition time (TR) = 53 ms, flip angle (FA) = 20°, slice thickness = 3 mm, bandwidth = +/−31.25Hz/pixel, field of view (FOV) = 24 cm, matrix size = 512×512×40, and SENSE factor 2. Scan time was 6 min. 28 s. Both the magnitude and phase images were saved for data analysis. Acquisition parameters for the FLAIR images were: TE = 124.8 ms, TR = 9002 ms, TI=2250 ms, FA = 90°, slice thickness = 4 mm, FOV = 256 × 256 mm2, in plane resolution = 1 × 1 × 5 mm3, matrix size = 320 × 256. Acquisition parameters for the T1w images were: TE = 4.2 ms, TR = 9.2 ms, TI = 600 ms, FA = 15°, thickness = 1.0 mm, FOV = 240 × 240 mm2, resolution = 1 × 1 × 1 mm3, matrix size = 256 × 256.
2.3. MRI processing
2.3.1. QSM reconstruction
A quantitative susceptibility map (QSM) for each subject was reconstructed using a modified version of the morphology enabled dipole inversion (MEDI) algorithm (de Rochefort et al., 2010; Wang & Liu, 2014), where the background field was removed bypassing phase unwrapping, skull stripping, and knowledge of the boundary conditions (Liu et al., 2014) . Background field removal was incorporated in the estimation of susceptibility (Dong et al., 2015; Li et al., 2004; Liu et al., 2014; Schweser et al, 2010). QSM values were referenced to CSF to allow comparison across subjects. The inversion algorithm solved the following optimization:
| (1) |
The regularization parameter λ in equation 1 was determined empirically and set to 1000, W was a weighting matrix proportional to the SNR of the complex field in each voxel, to compensate for spatially non-uniform noise in the field map, D was a matrix representing the dipole field convolution, and the gradient mask M was used to allow edges in χ based on where they were likely located. Dong et al. 2015; Liu et al., 2012, 2014). The mask M was computed by filtering the gradient of the magnitude image of the first echo, with a threshold chosen such that 30% of the computed gradients (taken over all three spatial dimensions) were retained The energy minimization in equation 1 has a data fidelity term formulated in the complex plane to account for Gaussian noise and an L1 norm regularization term to encode the prior. In contrast to the original nonlinear MEDI, the energy minimization has an additional Laplacian formula in the data fidelity term. Since the background field is harmonic, the use of the Laplacian eliminates any background fields. The Laplacian term is implemented as a convolution with a kernel equal to the Kronecker delta function minus a sphere with radius 5 mm and unit integral. For efficiency, this convolution is evaluated in Fourier space.
2.3.2. Segmentation protocol
Brain parenchyma regions of interest (ROI), including the caudate nucleus (Cd), thalamus (Th), pulvinar (Pul), dentate nucleus (Dn), putamen (Pt), globus pallidus (Gp), substantia nigra (Sn) and red nuclei (Rn), were segmented manually by experienced radiologists. The segmentation was performed on the QSM images because it provided clearer visual distinction from surrounding tissue compared to the magnitude image. To minimize partial volume effects, each ROI was traced on one axial slice were the structure was the most prominent and its borders well defined. An automatic eroding algorithm was applied to erode the boundary by 2 pixels to further minimize partial volume effects. Cd was traced on a separate slice. Gp and Pt were segmented on the same slice. The Rn and Sn were segmented on the same slice showing hyperintense susceptibility in the ROIs. The slice for Pul was chosen where the greatest contrast was present, separating the group of nuclei from the rest of the thalamus. The thalamus was outlined on the slice showing clear boundaries without showing the subthalamic nucleus. Furthermore, the third ventricle and the white matter (posterior limb) were avoided, and the Rn and Sn were not present on the slice. Figure 1 illustrates an example of the segmentation. Figure 4 presents QSM images showing age-related differences in the Pt. To minimize inter-subject variability, each ROI was segmented by a single radiologist. The region averaged susceptibility was measured for each ROI (Liu et al., 2013) and for each hemisphere.
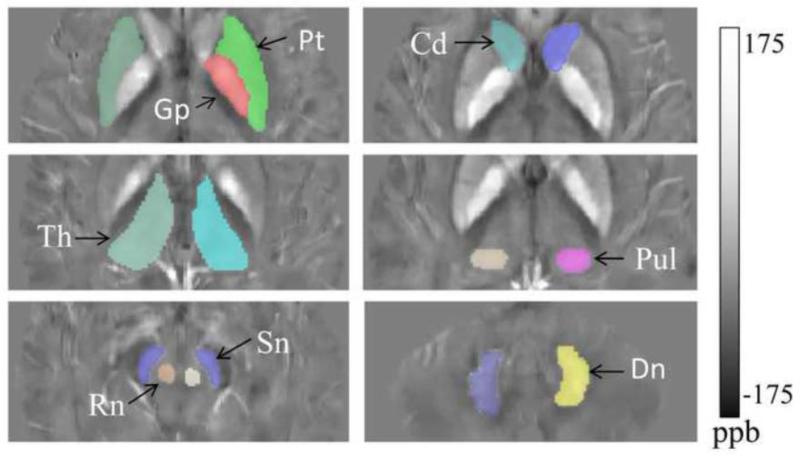
Figure 1.
The manually-traced regions of interest (ROIs): caudate nucleus (Cd), putamen (Pt), globus pallidus (Gp), thalamus (Th), pulvinar nuclei (Pul), the brain stem nuclei; red nucleus (Rn), substantia nigra (Sn), and dentate nucleus (Dn), in the cerebellum. Susceptibility is presented in ppb = parts per billion.
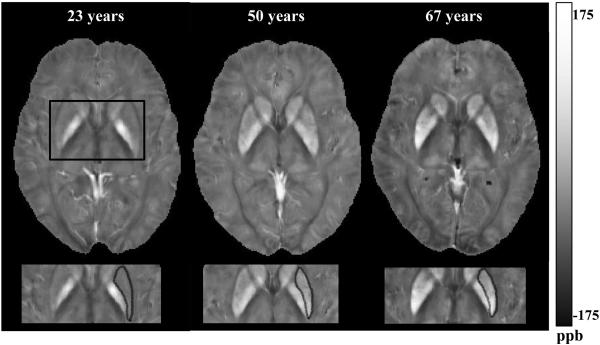
Figure 4.
Distribution of magnetic susceptibility in the putamen (Pt) and globus pallidus (Gp). White indicates a high (paramagnetic) susceptibility. The putamen, marked in black, showing increase of paramagnetic susceptibility expressed in parts per billion (ppb), across participants of 23, 50 and 67 years of age. Gp, on the medial lateral side from the Pt, shows high levels of susceptibility across the three subjects. Susceptibility is presented in ppb = parts per billion.
3. Statistical analyses
3.1. Structural Equation modeling (SEM)
We estimated a series of Structural Equation Models (SEM) to investigate if age and sex could explain variations in subcortical brain iron distribution. SEM was used because it explicitly models the ROI data (referred to as manifest variables) as noisy measurements of the underlying value (referred to as latent variable), reducing the influence of measurement error on the estimated model parameters. In contrast, analysis of variance (ANOVA) and traditional regression techniques are more sensitive to measurement error, and any estimates of effect size are underestimated and prone to bias (Rigdon, 1994). SEM allows us to take into account the measurement error for each manifest variable (the ROI measurements). Each manifest variable reflects both the underlying true score and the measurement error. In other words, the measurement model allows for the unexplained variance in the latent variable to be separated from the measurement error (Jöreskog, 1970; McArdle, 1996).
A second reason for using SEM is the ability to model complex multivariate relationships (e.g., as in our application, multiple dependent variables and interactive processes). We prefer to perform one multivariate analysis instead of multiple univariate analyses, including both separate regressions and correlations, since we have multiple outcome/dependent variables. To use a multivariate model also provides some help in controlling for type 1 error. We also examined inter-correlations between the structures, which can be done in a more elegant fashion using SEM, rather than using multiple subsidiary univariate correlation analyses. The SEM approach gives us the ability of assessing the fit of the mathematical model by various model fit criteria, which can be evaluated using established joint criteria for threshold levels. Estimation in SEM assumes that the latent variables and the residuals are normally distributed (Gregorich, 2006; Jöreskog, 1970).
A SEM comprises of 1) a measurement model (see Fig. 2 for our application), were the latent variables (the underlying ROI values) are represented by various manifest variables (the measured ROI values), and 2) a structural part. The measurement model is first evaluated and can be expressed as follows in matrix form:
| (2) |
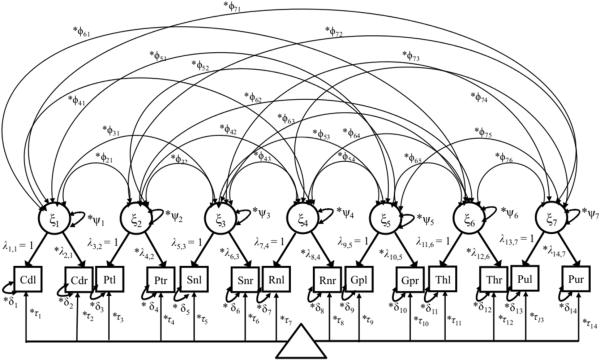
Figure 2.
Path diagram showing the multivariate model fitted to the QSM data for seven ROIs. Squares represent observed variables, circles are latent variables. The triangle indicates that the model has a mean structure (intercepts (τ)/conditional means). Double-headed arrows attached to the same indicator variable, represent the residual variance of the indicator (δ), and those starting and ending at the same latent variable, ψ, represent the variance of the latent variable. The exogenous latent variable is denoted ξ, the factor loadings, or regression coefficients representing ξ are described by λ's. The common factors are inter-correlated by ϕ (double headed arrows). The model is identified with 58 degrees of freedom. The suffixes l and r for each of the ROI refer to the ROI in the left and right hemisphere, respectively.
In equation (2), Xij is the indicator of observed susceptibility in j measures (j = 1,...,14, eg. j = 1 for average susceptibility in the left hemisphere of Caudate nucleus (Cd), and j = 2 for the corresponding right hemisphere) for each latent variable ξmi, eg. m = 1 for the latent representation of susceptibility in Cd as demonstrated in Figure 2) for person i, the average is the intercept of each Xji, are the factor loadings (regression coefficients) of the ROI measurements Xji reflecting the latent or true variable ξi, δji is the residual for the measured susceptibility counts and represents the measurement error in Xji relative to the latent variable. The measurement equation can be written out according to the following formula for seven latent variables (m = 1,...,7), illustrated in Figure 2 were X1i is the susceptibility count for left hemisphere of the Cd, and X14i is the susceptibility counts from the right hemisphere of the pulvinar, and ξ7i is the latent variable representing susceptibility in the ROI pulvinar:
| (2b) |
The value zero indicates that the factors are distinct from one and another (if they were not, the arrows would point from every latent variable to all the manifest indicators in Fig. 2).
The latent variable is here denoted ξ since it is exogenous (not predicted by any other latent variables or covariates) (see Jöreskog, 1979 for a more thorough description of the notation). Covariance was further specified to express inter-relatedness between the seven latent variables (see in line Supplementary material 1, and Fig. 2).
Once the measurement part of the model is verified, the structural part of the model can be evaluated (Brown et al., 2002). The structural part of the model is specified to investigate the causal relationship between covariates (such as age and sex in our application) and the common factor (such as the susceptibility in a certain ROI), which is exemplified by the following measurement (3a), and structural (3b) models:
| (3a) |
| (3b) |
In the measurement equation 3a, were two indicators Yij (j = 1,2...to 13, 14, Fig. 2) are used to measure susceptibility per seven latent variables (ηim, m = 1,...,7) accounting for the measurement error of the indicators (εij) in Yin. This change in notation is done because the latent variables are now themselves dependent on other predictors (endogenous) (in this case age and sex). This follows the traditional notational conventions in the LISREL (linear structural relations) notation (see Jöreskog, 1979). Following the structural equation, 3b is added to let variations in sex and age (n = 7, for regressing 7 latent variables on age and sex), predict level of susceptibility across the latent ROIs ηim with (m = 1, ...,7). κηm, represents the intercept of the regression and ζi denotes the residual error term. We further evaluated the influence of possible nonlinearity in the age effect by regressing the latent variables on linear and quadratic terms of age, as described in equation 4.
| (4) |
Within the SEM modeling framework, multiple group analysis (MGA), where separate parameter estimates are derived across groups, can be applied to evaluate the presence of interactions between categorical and interval scaled variables. In our application these variables are sex and age. Possible moderation (interaction) is evaluated by comparing models with free vs. parallel slopes across groups. We examined if sex could moderate the effect of age on estimates of brain iron. For further information about the algorithms of MGA, please see Gregorich, 2006.
Measurement invariance was first established to secure that the common factors were largely identical across the groups to enable comparison of parameter estimates across sex and to evaluate the influence of sex by age interactions. All models were analyzed under the assumption of strong factorial invariance (Gregorich, 2006; Meredith & Teresi, 2006), so that factor loadings and intercepts were invariant (equal) across men and women. The assumption of measurement equivalence was evaluated through differences in χ2 (Δχ2) after parameter constraints were applied. Δχ2 and difference in degrees of freedom were computed between the models and compared to the central χ2 distribution. Non-significant decrease of model fit (p≥.05) was indicative of strong factorial invariance. Three models with increasing degree of constraints to the model parameters were compared 1) all parameters were estimated freely, 2) factor loadings were invariant (factorial invariance), 3) factor loadings and intercepts were equivalent between the sexes (strong factorial invariance). As outlined below, the model fit was evaluated using joint criteria of goodness of fit indices. Sex by age interactions were assessed by first estimating a free age slope for men and women separately, followed by constraining the regression coefficients to be equal (parallel). If the equality constraint resulted in a significant deterioration of model fit, as measured by change in χ2 (Δχ2) between the unrestricted and restricted models (Δχ2 = χ2restricted - χ2 unrestricted, with df = dfrestricted – dfunrestricted) (see e.g. Little et al, 1997), the equality constraint was considered untenable, thus indicating a difference in age slopes between the groups.
We extended the measurement model from equation 2 to include another hierarchical level in a second order latent variable, reflected by first order latent variables to measure total brain iron levels across all the regions of interest. The second order latent variable is denoted by ξ and the subordinated factors (latent variables), are the latent variables: ηim, m = 1,...,7 representing averaged susceptibility over left and right hemispheres of the ROIs. (see Fig. 3A). The hierarchical factor model can be written as follows:
| (5a) |
| (5b) |
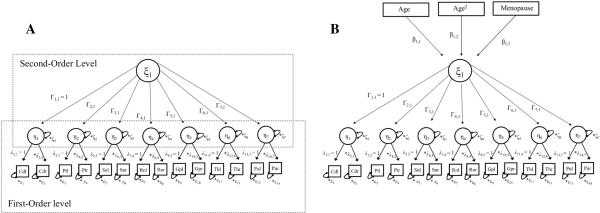
Figure 3.
A. Illustration of the second order factor model. The seven subordinated factors (η1, ...,η7) reflect the susceptibilities of the seven ROIs. λ represents the factor loadings of susceptibilities of left and right hemispheres on to the latent variable η, and ε is the residual error term of each manifest indicator (eg. Cdl). ξ is the second order latent variable reflecting total iron concentration across the subcortical nuclei. Γ denotes the regression coefficient between the second ordered latent variable ξ and the subordinated factors η1, ...,η7. Means and intercepts are omitted for parsimony.
B. Hierarchical factor model with three additional covariates; age, curvilinear age and menopause. This is done to predict total subcortical susceptibilities, adding the regression coefficients β1, β2, and β3. Means and intercepts are omitted for parsimony.
Equation 5 reflects the first-order latent variables and their own factors. Yji denotes the manifest variables (Fig. 3A). In line with equation 2, is the factor loading (regression coefficient) of the Yji reflecting the latent variables ηmi (m = 1, ...,7), the residual εji represents the measurement error in Yji relative to ηmi. Γi in equation 5b is the intercept and the regression coefficient connecting the second order factor ξ to the first order factors ηmi (See Fig. 3 A). ξ explains the covariance (shared variance) among the first-order factors. Following evaluation of fit of the hierarchical measurement model in EQ 5a-b,, we assessed the impact of expected post menopause on total subcortical susceptibility level after accounting for the influence of individual age by fitting the following structural equation to data (see also Fig. 3B).
| (6) |
Women who were expected to be post menopause (51 years and older for Asian and Caucasians: Cheung et al., 2011; Gold et al., 2001), were coded 1, while men and women 50 years or younger (who were expected to be free of menopause) were coded 0, and the variable was assigned the regression coefficient β1,3 to predict total subcortical brain iron, after the influence of individual age was accounted for. For further information about different SEM notation styles and equations, please consult McArdle (1996) and Jöreskog (1979).
We assessed how well the models fitted the data by using several model fit indices: Comparative Fit Index (CFI), Standardized Root Mean Square Residual (SRMR), and Root-Mean-Square Errors of Approximation (RMSEA), in addition to the Chi-Square Test of Model Fit. We used conventional joint criteria: Comparative Fit Index (CFI) > 0.95 and Standardized Root Mean Square Residual (SRMR) < 0.08 and Root-Mean-Square Errors of Approximation (RMSEA) < 0.08 (Browne, Cudeck, & Bollen, 1993; Hu & Bentler, 1998; Hu & Bentler, 1999). All models were identified in terms of degrees of freedom.
Parameter estimates were derived using full information maximum likelihood (FIML) estimation. The alpha level was set to .05, and we performed Bonferroni correction (α′) to adjust for multiple comparisons (Dunn, 1961).
4. Results
4.1. Descriptive statistics & pre-analyses
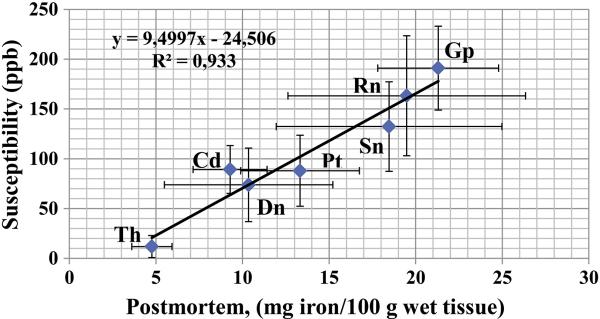
Descriptive statistics for each region of interest (ROI) are presented in Table 1. The sample comprised of 183 healthy volunteers, aged 44.71 ± 14.23 years (range 20-69 years). Forty nine % (90/183) of the subjects were women. To make a brief evaluation of the validity of the QSM estimates, the average susceptibility values were correlated with previously reported distributions in postmortem specimen from a large Swedish sample (Hallgren & Sourander, 1958, Table 1a). Average susceptibility values of the current report showed a very strong correlation (r = .970, p = .000) with the average brain iron levels (mg iron per 100g fresh weight tissue) (See Fig. 5).
Figure 5.
Distribution of iron in the subcortical nuclei reported by Hallgren and Sourander (1958, Fig. 1A), in relation to the average sample distribution of magnetic susceptibility values of the present study. The QSM data reflects means of susceptibility values in ppb, from 183 subjects (20-69 years). The values on the x axis reflects mg iron per 100 gram wet tissue, as reported in Table 1a, p. 43 in the work by Hallgren and Sourander (1958), from subjects aged 30-100 years, (r = .970, p = .000). The error bars represents standard deviations.
Men and women did not differ in their age distribution (t = −0.758, p = .451). See Online Supplementary material Table S2 for descriptive statistics for men and women respectively.
4.2. The Measurement Model
The measurement model in equation 2 (Fig. 2), with 7 latent variables (one for each ROI) showed a good fit to the data by several conventional model fit criteria: CFI = 0.983, SRMR = 0.018, RMSEA = 0.064, (90% CI: 0.043 - 0.085), χ2 (56) = 98.472, p = .0004). The standardized factor loadings of the model were ranging from r = .849 for thalamus to r = .987 for the red nucleus. The factor loadings for the single common factor for susceptibility in the Dn showed strong correlation with r = .852 for the left hemisphere and r = .875 for the right hemisphere. See Online Supplementary Table S3 for inter-correlations between the ROIs. 20 out of 28 correlations were significantly different from zero. The correlations were all positive and indicated an effect size that ranged from medium to large (Cohen, 1992). This suggests a positive manifold of correlations (Spearman, 1904) or, in other words, a pattern of high level of susceptibilities across several ROIs in conjunction.
4.3. Structural Equation Modeling with Covariates
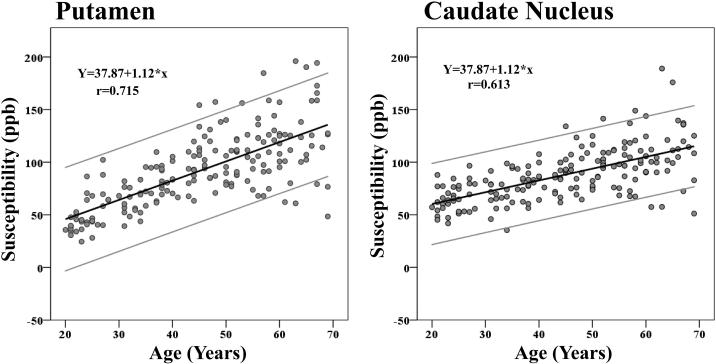
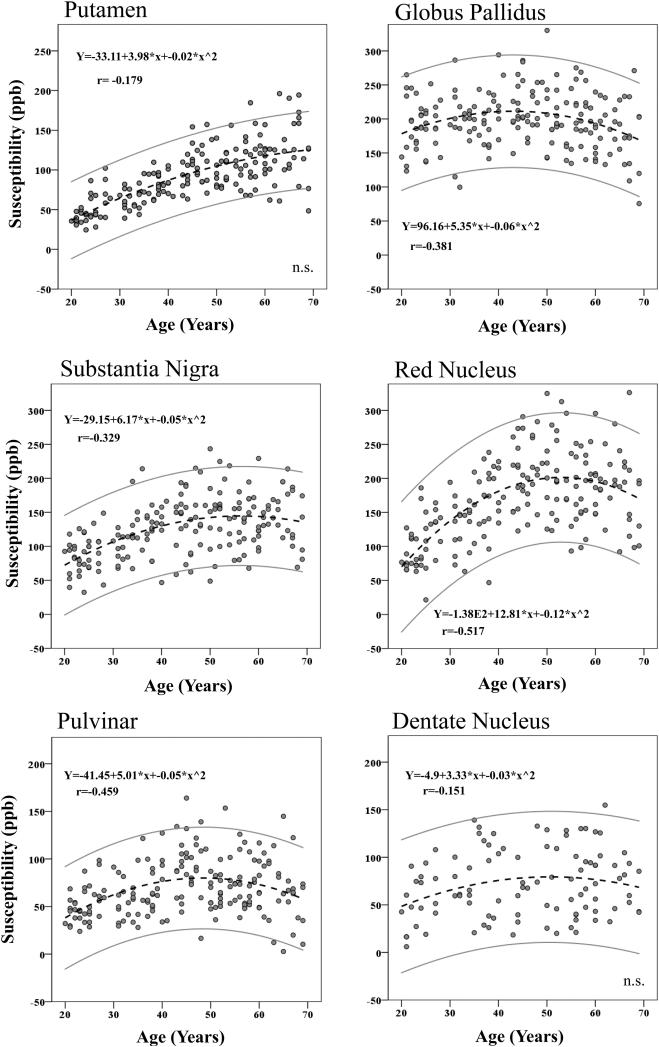
The results from adding age and sex as independent variables to predict susceptibilities across the ROIs (equation 3) are presented in Table 2. A linear increase of susceptibility with advanced age was present in the Cd, Pt (see Fig. 6), Sn, Rn, and Pul, while no reliable age differences were observed for the susceptibility of the Gp, Dn, or Th.
Table 2.
Standardized Parameter Estimates of Covariates Effect on Magnetic Susceptibility Values in the ROIs.
| ROI | Age (β1) | Sex (β2) | R2 (Age, Sex) | R2 (Age) | Cohen's f2 (Age) |
|---|---|---|---|---|---|
| Cd | .613 (.050)*** | −.011 (.063) | .375 (.061)*** | .375 (.061)*** | 0.602 |
| Pt | .716 (.038)*** | −.030 (.054) | .512 (.054)*** | .511 (.054)*** | 1.044 |
| Sn | .442 (.063)*** | −.183 (.070)** | .220 (.058)*** | .188 (.055)** | 0.232 |
| Rn | .507 (.055)*** | −.115 (.064) | .264 (.056)*** | .252 (.056)*** | 0.336 |
| Gp | −.038 (.077) | −.004 (.077) | .001 (.006) | .001 (.006) | 0.001 |
| Pul | .221 (.073)* | −.063 (.073) | .051 (.033) | .047 (.032) | 0.049 |
| Th | .063 (.079) | −.034 (.079) | .005 (.011) | .004 (.010) | 0.004 |
| Dn | .136 (.119) | .066 (.120) | .024 (.037) | .040 (.049) | 0.042 |
Note. The standard errors of the parameter estimates are presented within the parentheses. Cd = caudate nucleus, Pt = putamen, Sn = substantia nigra, Rn = red nucleus, Gp = globus pallidus, Dn = dentate nucleus, Th = thalamus, and Pul = pulvinar; Sex (0 = man, 1 = woman); Age in years; R2 = Proportion of variance. Cohen's f2 = magnitude of the effect (effect size). All significances are Bonferroni-adjusted (α′ = .016)
p< .000
p< .01
p< .016.
Figure 6.
Scatter plots illustrating a linear age dependency of iron concentration as measured by mean QSM susceptibility values, across ROIs. High values are indicative of high iron load. The outer gray lines represent the 95% confidence intervals.
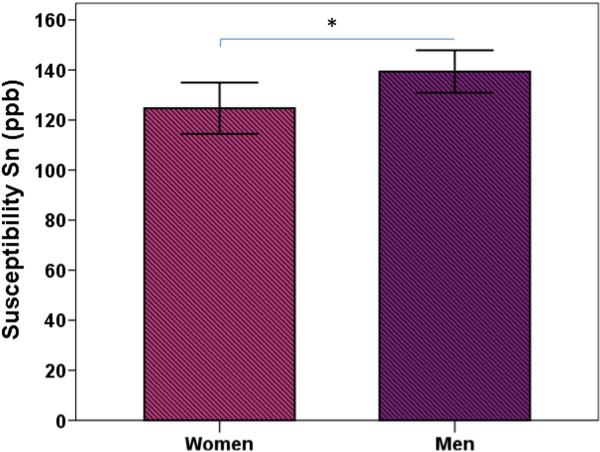
The magnitude of the effect of age is presented in column 6 of Table 2 by means of the Cohen's f2 (f2 = R2 /1 – R2 /) (Cohen, 1992). The effect sizes were large for Cd, Pt, and medium/large for Rn (≥0.35, Cohen, 1992), moderate for Sn (≥0.15: Cohen, 1992), and small for Th, Pul, and Dn. Age explained 37.5% of the variance in mean susceptibility values of the Cd, 51.1 % in the Pt, 18.8% in the Sn, 25.2 % in the Rn, 0.01% in the Gp, 4.7% in the Pul, 0.04 % in the Th, and 4% in the Dn (see column 5 in Table 2). Sex related variations of susceptibility values were reliably different from zero in the Sn, so that women had lower Sn susceptibility values compared to men, after age was accounted for (see column 3 in Table 2 and Fig. 7). A similar trend was observed for the Rn (p =.059). No other ROIs showed significant sex variations in susceptibility. The model fitted the data well: CFI = 0.983, SRMR = 0.017, RMSEA = 0.060, (90 % CI: 0.040 - 0.079), χ2(70) = 116.149, p = .0004.
Figure 7.
Sex differences of QSM susceptibility values in the substantia nigra. The error bars represent the 95% confidence intervals around the means.
4.4. Nonlinearity in the Association between Iron Estimate and Age
Visual inspection of the distributions suggested nonlinear relationships between age and susceptibility in several ROIs. Separate analyses were performed with susceptibility as dependent variable and linear age and quadratic age (age2) as independent variables (equation 4 in Model Specification). For full model results see Online Supplementary material Table S3. Estimates of iron concentrations showed quadratic relationships with age across five ROIs: the Gp, Sn, Rn, Th and Pul. Trends in the same direction was observed for the Pt (p = .024, α’ (Bonferroni correction) =.016), and Dn (p = .072).
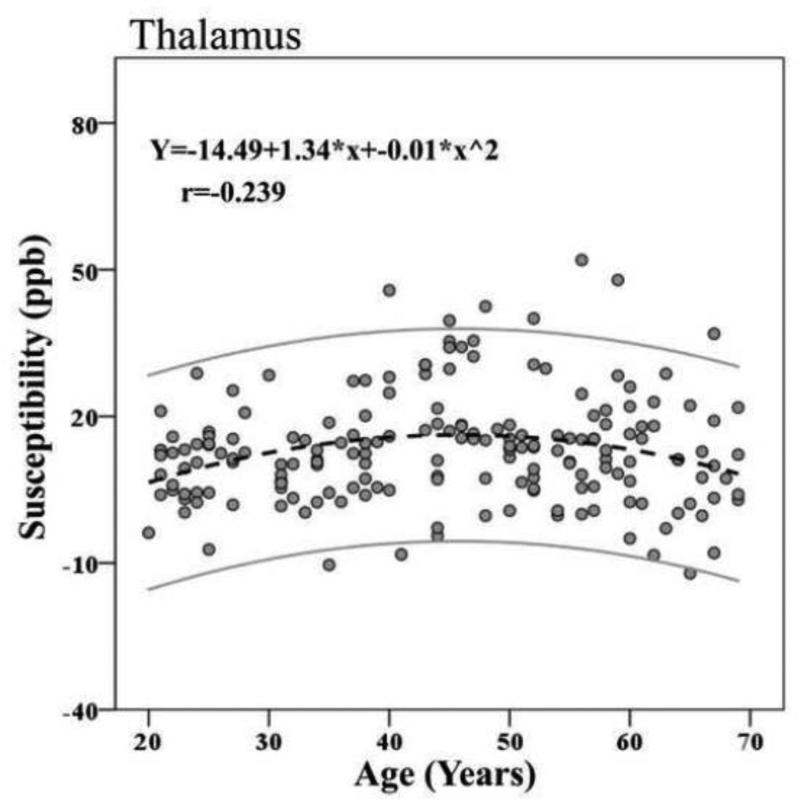
When the difference in effects sizes (f2) of the linear and nonlinear models was considered (see Table S3, columns 6 & 7), the magnitude was large for Rn ( = 0.344) and close to moderate for Pul ( = 0.131), by conventional standards (Cohen, 1992). The effect sizes for the other ROIs were small (<0.15) (see e.g. Fig. 9 for Th). The nonlinear age trend predicted an additional 15.3% of the variance in the Rn susceptibility, (Table S4, columns 4 & 5), 7.2% of the Gp susceptibility, 4.9% of the Sn susceptibility, and 5.4% of the Pul susceptibility, when linear age was accounted for ( – ). The proportions of variance in susceptibility attributed to the curvilinear age term for the Th and Dn were small: 1.8% and 2.2%, respectively. The difference between the linear fit and the nonlinear fit for the Pt was a negligible 0.1%. See Table 3, columns 4 & 5 for complete R2 statistics. The correlations between the curvilinear age term and susceptibilities were strongest for the Rn, followed by the Pul, Sn and Gp in descending order.
Figure 9.
Nonlinear age trends of susceptibility of the Th. The outer gray lines represent the 95% confidence intervals.
Table 3.
Standardized Parameter Estimates of Covariates Effect on Susceptibility Values in the ROIs.
| Women | Men | |||||
|---|---|---|---|---|---|---|
| ROI | Age (β1) | R 2 | Cohen's f2 | Age (β1) | R 2 | Cohen's f2 |
| Cd | .587 (.071)*** | .345 (.083)*** | .526 | .626 (.064)*** | .393 (.081)*** | .647 |
| Pt | .681 (.055)*** | .464 (.075)*** | .866 | .747 (.044)*** | .558 (.066)*** | 1.262 |
| Sn | .455 (.088)*** | .207 (.080)** | .261 | .437 (.089 )*** | .191 (.077)** | .236 |
| Rn | .456 (.083)*** | .208 (.076)** | .262 | .586 (.067 )*** | .344 (.079)** | .524 |
| Gp | −.033 (.109) | .001 (.007 ) | .001 | −.046 (.108) | .002 (.010) | .002 |
| Pul | .057 (.100) | .003 (.012) | .003 | .362 (.093 )*** | .139 (.068)* | .161 |
| Th | .020 (.109) | .000 (.004) | .001 | .115 (.112) | .013 (.026) | .013 |
Note. The standard errors of the parameter estimates are presented within the parentheses. Cd = caudate nucleus, Pt = putamen, Sn = substantia nigra, Rn = red nucleus, Gp = globus pallidus, Th = thalamus, and Pul = pulvinar; Age in years, centered on the grand mean; R2 = Proportion of variance attributed to all covariates; Cohen's f2 = effect size. All significances are Bonferroni-adjusted (α′ = .016)
p< .000
p< .01
p< .016.
Fig. 8 plots the results of the curvilinear fits of ROI susceptibility versus age. The Pt susceptibility showed a linear rise of susceptibility roughly until the 6th decade followed a slight leveling off. As mentioned in the previous paragraph, this trend was rendered non-significant after Bonferroni correction (p = .024, α’ =.016). For the Rn and Sn, gradual increases of susceptibility appeared through midlife, followed by a slight decline from approximately 60 years of age. The estimated iron concentrations vs. age association of the pallidus exhibited an inverted U-shape, reaching a plateau at mid-life, followed by a slight decay. The same U-shape trend was observed for the Pul and Th.
Figure 8.
Scatter plots illustrating nonlinearity in the association between susceptibility and age across ROIs. High values of magnetic susceptibility are indicative of high iron load. The outer gray lines represent the 95% confidence intervals.
4.5 SEM-Multiple Group Analyses (MGA)
Below are the results of performing the MGA in which parameter estimates are simultaneously derived for men and women, in order to evaluate the effects of sex by age interaction on susceptibility.
4..5.1. SEM-Multiple Group Analyses (MGA): Measurement Invariance
Measurement invariance was first established to make certain that the same measurement model (see Fig. 2) held across the two groups (see also the subsections SEM modeling and Model Specification), by comparing a model in which all parameters are estimated freely across groups with two models in which parameters were constrained to be equal across groups. The difference in χ2 and degrees of freedom did not significantly worsen the fit when compared with the χ2 distribution (Δχ2 (5-9) = 5.947-8.9593, p = .311-.441) between the following 1) all parameters estimated freely, 2) invariant factor loadings but free intercepts, 3) both invariant factor loadings and intercepts. This indicated that measurement invariance was established. When the factor loadings and intercepts were constrained to equality across men and women (eg. λ36= 0.913 in men and 0.913 in women) (Fig. 2), a close fit to the data was obtained: CFI = 0.974, SRMR = 0.071, RMSEA = 0.065, (CI 90 % 0.044 - 0.085), χ2 (168) = 233.822, p =.001).
4.5.2. Multiple Group Analysis- Sex by Age Moderation
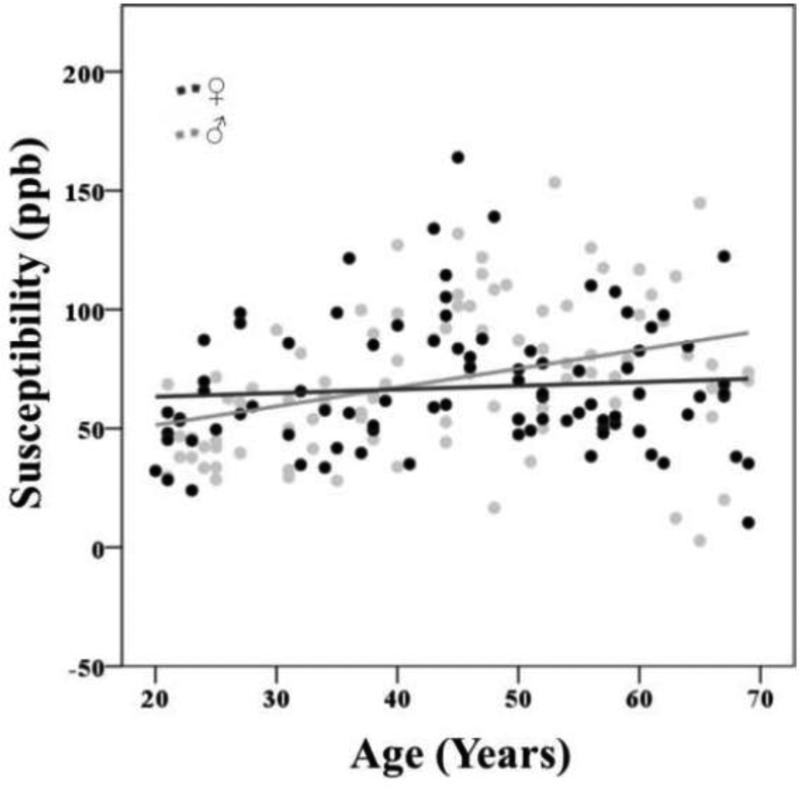
Table 3 presents the results of adding age to the model to predict susceptibility across men and women. Both men and women exhibited a linear raise of iron estimates with advanced age in the Cd, Pt, Sn and Rn. Women, unlike men, showed no linear rise of susceptibility with advanced age in the Pul (>.05) (See column 2 in Table 3). Men showed overall greater proportions of age-related variances in iron concentration, with the greatest difference observed in the Rn, Pt and Pul with an additional 9.4 to 13.6% of the variance attributed to age. Greater effect sizes in men were also reflected in the larger f2 values (columns 4 and 7 in Table 3). In men, age explained 39.3% of the variance in the susceptibility in the Cd, 55.8% in the Pt, 19.1% in the Sn, 34.4% in the Rn, 0.2% in the Gp, 13.9% in the Pul, and 1.3% in the Th in men (see column 6 in Table 3). In women, age explained 34.5% of the variance in the Cd, 46.4% in the Pt, 20.7% in the Sn, 20.8% in the Rn, 0.1% in the Gp, 0.3% in the Pul, and 0.01% in the Th (see column 3 in Table 3).
A significant interaction between sex and age related differences in susceptibility were noted for the Pul. The equality constraint on the age slopes (parallel) showed significant deterioration of model fit (Δχ2(1) = 4.912, p = .025). See Fig. 10 for an illustration of the gradual age related rise of susceptibility in men, while the trend for women is almost constant. The effect size was close to moderate (f3 = 0.15) (Cohen, 1992). The MGA assessing age dependency fitted the data well: CFI = 0.972, SRMR = 0.066, RMSEA = 0.067, (90% CI: 0.047 - 0.086), χ2 (182) = 257.621, p = .0002.
Figure 10.
Show interaction between sex and susceptibility as a linear function of age.
The curvilinear fitting results for susceptibility versus age for men and women are illustrated in Supplementary material 5, Fig. S5. Four of the curvilinear age slopes rendered significant in women, and two in men. As presented in Supplementary Fig. S5, the correlations between the curvilinear age term and susceptibilities of all of the ROIs were stronger in women than men, except for the Th, where the size of the estimate was greater in men (.261 vs. 201, a less than moderate effect size).. Most pronounced were the sex differences of the correlation estimates in the Rn (r = −.507 vs. −.313 in men), the Sn (r = −.346 vs. −.187), the Pul (r = −.359 vs. −.291). Women showed nonlinear susceptibility vs. age change in the Rn (p=.000), and so did men (p=.001). A curvilinear rise of Gp susceptibility was present in women (p=.005) but not in men (p=.024, α′ = .016). Estimates of iron concentration of the Sn showed a curvilinear association with age in women (p=0.005) but not in men (p=.035, α′= .016). Estimates of iron concentration of the Pul showed a curvilinear association with age across women (p=.000) and men (p=.001). Only men exhibited a non-linear age trend in the Th, after Bonferroni correction (p=.010, α′ = .016, women: p = .03). Curvilinear age effects could not be established across the sexes in the Cd and Pt (p ≥ 023, α′ = .016).
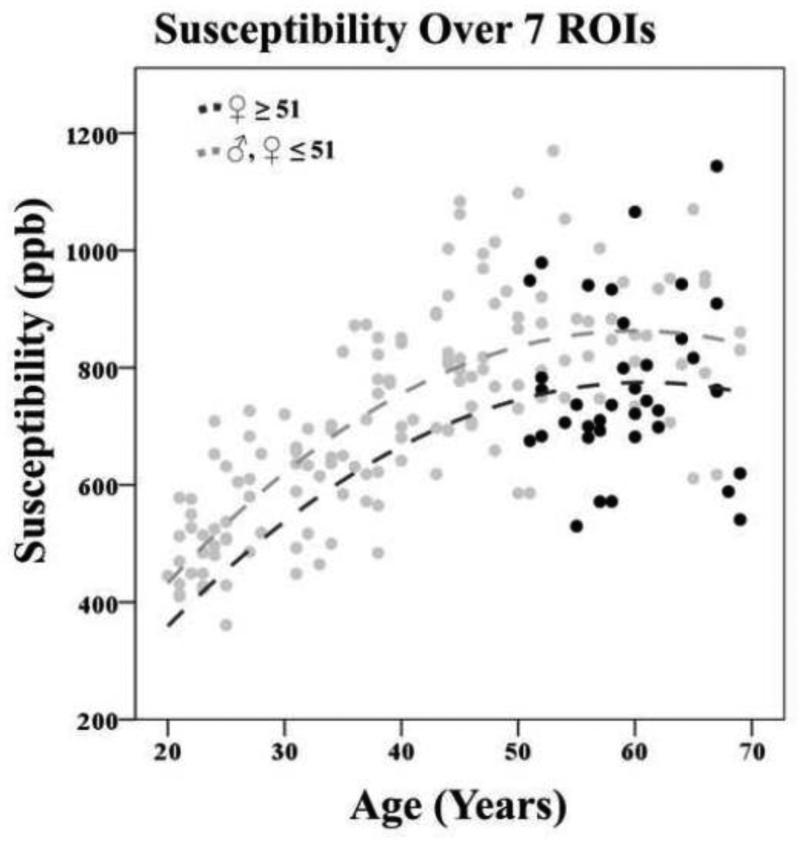
4.6. Change in Total Brain Iron in Women after the Age of 51
As mentioned in section 3, we unraveled potential shifts in susceptibilities in women post menopause, utilizing a binary variable coded 1 for women 51 years or older (n=38) The hierarchical measurement model described in equations 5 a,b and Figure 3a was first fitted to the data. The standardized factor loadings for the second order factors, representing total subcortical iron concentrations, were all significant (p≤.001) with loadings ranging from r=.370 for the Gp to r=.952 for the Rn. Standardized factor loadings for the first-order factors of susceptibilities across the ROIs ranged from r=.847 for the Th to .960 for the Gp. The model showed good fit to the data: CFI = 0.973, SRMR = 0.053, RMSEA = 0.073, (90 % CI: 0.055 - 0.090).
Second was covariates added to the model. The results of the SEM with respect to effects of covariates on susceptibilities (Fig. 3B, EQ 6) are presented in Supplementary material 6. After accounting for age, women who had entered menopause showed lower levels of overall iron deposition (β = −.200, SE = .070, p = .007, α′ = .016) (See Fig. 11). Women at expected post menopause age were 169 ppb lower than the rest of the subjects, according to the unstandardized parameter estimates.
Figure 11.
Decrease of susceptibility in women after the average age of menopause onset (51 years). Total susceptibility is reflected in a second order latent variable represented by the susceptibility of seven ROIs; caudate nucleus (Cd), putamen (Pt), globus pallidus (Gp), thalamus (Th), pulvinar (Pul), red nucleus (Rn), and the substantia nigra (Sn).
5. Discussion
This study demonstrates age and sex related differences of QSM based MRI estimates of brain iron concentration in the deep gray matter in a large study cohort (n=183). This is one of the largest samples of healthy adults to have in-vivo MRI estimates of brain iron concentrations assessed, and the largest thus far using quantitative susceptibility mapping. The distributions of susceptibility varied in degree across the structures conforming to histologic findings (see Fig. 5 and Hallgren & Sourander, 1958), with the greatest iron distribution in the Gp and the lowest in the Th. We report both linear and nonlinear effects of age on susceptibility. Advanced age was associated with a particularly strong linear rise of susceptibility in the striatum (caudate nucleus, putamen). Nonlinearity of age trends were more pronounced in the Rn, followed by Pul, and Sn, while minimal quadratic trends were observed for the Pt, Th and Dn. The current report conforms to previous reports of age related variations of brain iron, but also adds to the current state of affairs by reporting age-related changes in less studied, smaller subcortical nuclei.
Sex differences in susceptibility were present in the deep gray matter structures. Women showed lower levels of susceptibility in the Sn after accounting for age. Regional susceptibility of the Pul increased as a linear function of age in men, while women exhibited curve linearity of age trends, so that susceptibility rise leveled off from midlife. Women expected to be post menopause (age 51 or older) showed lower total magnetic susceptibility in the subcortical brain than younger female subjects and male subjects of any age. This is the first MRI report of lower total subcortical brain iron levels after midlife in women. We discuss the results below.
5.1. Age Dependent Susceptibility in Sub-cortical Gray Matter
5.1.2. Caudate nucleus (Cd)
Our finding of linear age dependency of iron deposition in the Cd confirms the previously reported gradual linear increase between young adulthood to old age, measured post-mortem (Hallgren & Sourander, 1958), between the 4th decade and senescence (Ramos et al., 2014), and between the ages of 19 and 82 years according to FDRI (Bartzokis et al., 2007). A continuing increase in R2* values was reported through the 8th decade (Li et al., 2014). These results are in contrast to another study from the 2nd decade of life on, in which age had little effect on R2* values (Aquino et al., 2009).
5.1.3. Putamen (Pt)
Our finding of an age-related increase of iron concentration in the Pt is consistent with previous reports using iron-sensitive MRI techniques including FDRI, QSM, R2* and phase (Bartzokis et al., 1997; Bilgic et al., 2012; Cherubini et al., 2009; Haacke et al., 2010; W. Li et al., 2014; Pfefferbaum et al., 2009; Ramos et al., 2014; Rodrigue et al., 2011). This, in part, agrees with histology, showing increasing iron levels until old age (Hallgren & Sourander, 1958; Ramos et al., 2014). A steady increase of susceptibility and R2* values into senescence have also been reported (W. Li et al., 2014). The subtle nonlinear age trend was not significant after Bonferroni correction.
5.1.4. Globus pallidus (Gp)
We found no support for a linear age dependency of brain iron accumulation in the pallidus, which is in line with some reports (Cherubini et al., 2009), but not others (Bilgic et al., 2012; Ramos et al., 2014). Other studies have shown a linear decrease of brain iron levels as a function of age (Haacke et al., 2010; Xu et al., 2008).
Instead, we found a curvilinear age trend between the ages of 19 and 69. Susceptibility rose until early middle age, followed by a brief plateau, and subsequent decay from the 6th decade on (see Fig. 8). This partly agrees with early histologic findings from healthy subjects between 1 and 100 years of age, showing a rise in iron concentrations until the late thirties, followed by a plateau (Hallgren & Sourander, 1958). Plateauing susceptibility and R2* values have previously been observed between the ages of 20 and 30 (W. Li et al., 2014), and from the age of 15 (Aquino et al., 2009).
5.1.5. Red nucleus (Rn)
The linear age trends observed in this work confirmed previous findings using phase contrast, R2* and histology (Haacke et al., 2010; Hagemeier et al., 2013; Pfefferbaum et al., 2009; Ramos et al., 2014; Xu et al., 2008). Importantly, we observed a strong nonlinear age trend with a significant effect size (Cohen, 1992), and a strengthened R2 (from 25.2% to 40.5%) using the second degree polynomial fit. A steep increase of susceptibility was noted until mid-life, followed by a brief plateau before a slight decay from the 6th decade on. Similar nonlinear age trends have been reported, in phase values from 6 to 76 years (Hagemeier et al., 2013), in magnetic susceptibility between the ages of 1 and 83, and in R2* (W. Li et al., 2014), although the latter showed a plateau from upper young adulthood. Hallgren and Sourander (1958) could not draw any conclusions about age trends of iron distributions due to technical issues in the samples from the 2nd decade of life.
5.1.6. Substantia nigra (Sn)
Imaging studies in the past have reported differences in susceptibility distributions of the Sn across age groups (Bilgic et al., 2012; Pfefferbaum et al., 2009), and a linear age related change (decrease in average phase) (Hagemeier et al., 2013) which we replicate herein. Previous reports using phase contrast and FDRI (Bilgic et al., 2012; Haacke et al., 2010) have not found an age dependency for the Sn. We also encountered a nonlinear age trend, with a rising susceptibility from the 2nd until the 6th decade of life, followed by a slight decline. This, in part, replicates previous reports of plateauing susceptibility from the 5th decade on (W. Li et al., 2014). Hallgren and Sourander (1958) did not report differences in age slopes after the 2nd decade of life, due to methodological issues in the staining process. We would like to acknowledge that iron may not be the only source of magnetic susceptibility in the Sn. A recent post mortem study found aging related increase of copper, although to a lesser degree than iron (Zecca et al., 2004). We cannot completely out rule that potential copper deposits reflect the magnetic susceptibility, although normal concentrations of copper in the brain have been considered too small to produce a detectable MR contrast (Schenck, 2003).
5.1.7. Thalamus (Th)
We found no support for a linear age related change in iron in the thalamus, which is well in line with some previous studies (Bilgic et al., 2012; Cherubini et al., 2009; Hallgren & Sourander, 1958; Xu et al., 2008), but contradicts others (Haacke et al., 2010; Hagemeier et al., 2013). Differences may in part emerge from the use of gradient echo phase images in the mentioned studies. Divergent adjustments for filter kernel size can change the sensitivity of the measure to detect iron, and have different impact on structures of different size (Haacke et al, 2004; Pfefferbaum et al, 2009). Greater variability of results can be expected with change of kernel size in the high pass filtering procedure, which may in part mediate conflicting findings between studies using phase contrast (e.g. Xu et al., 2008 vs. Haacke et al., 2010; Hagemeier et al., 2013). A recent paper further demonstrates that, when using high-pass filtering, anatomical changes by means of gray matter atrophy may introduce a phase shift seemingly indicative of increased iron concentration, even though the biophysical tissue composition has not changed (Schweser et al., 2013).
A subtle curvilinear rise of susceptibility was present, reaching a plateau in mid-life, followed by a leveling off at older age, which partly mimics previous histologic findings of a decay from the late thirties on (Hallgren & Sourander, 1958). Similar nonlinearities in age trends have also been reported using phase contrast (Hagemeier et al., 2013). As mentioned, the effect size for this curvilinear trend was very small, and explained only an additional 1.8 % of the variance. We encourage, however, further evaluation of such age trends in the thalamus.
5.1.8. Pulvinar nuclei (Pul)
As in previous reports (Haacke et al., 2010; Hagemeier et al., 2013), we found a minimal linear age dependency in the pulvinar complex. We observed a curvilinear effect of age on susceptibility, which is consistent with previous MRI findings (Hagemeier et al., 2013).
5.1.9. Dentate nucleus (Dn)
The lack of a reliable age-dependency of the susceptibility in the Dn is consistent with a previous age group comparison (Bilgic et al., 2012), but is in contrast to a recent study using 3D T1-weighted fast low angle shot (FLASH) echo sequences (Maschke et al., 2004). Previous work has also reported a nonlinear age-related increase of susceptibility in the dentate nucleus (W. Li et al., 2014). A nonlinear trend was reported herein (p=.072). The smaller sample size for the structure (n = 88) may have made this analysis underpowered. As will be discussed further in the Limitations subsection below, the single slice segmentation may in part also suppress the possibility to detect statistical significance.
5.1.10. Mechanisms Behind Age-related Changes
Importantly, the structures showing age related differences of iron concentrations, the basal ganglia and the brainstem nuclei, are of importance for both motoric and cognitive functions through their influence on the dopaminergic system (Volkow et al., 1998; Volkow et al., 1996). The efficiency of dopaminergic pathways depends on iron (see Berg & Youdim, 2006; Mills et al., 2010 for reviews), and the observed findings may have implications for behavioral changes in aging. The change in susceptibility as a function of age can be interpreted as build up or decline in iron deposition (Schenck, 2003). The association between magnetic susceptibility and their estimates using MRI QSM has been validated by phantom experiments (Rochefort, 2010; Liu et al., 2012), and ex vivo imaging (Langkammer et al., 2012; Stuber et al., 2014)
High iron concentrations across several subcortical structures were inter-correlated which may reflect an underlying age-related process. A potential mechanism behind age related changes can be that excessive accumulation of intracellular non-heme iron promotes reactive oxygen species (ROS), oxidative stress, and cell death, resulting in neurodegeneration (Andersen et al., 2014; Dixon & Stockwell, 2014; Floyd & Carney, 1993).
Several structures revealed a nonlinear age dependency of brain iron distribution, following the same inverted U-shape pattern observed in myelination in brain aging (Westlye et al., 2010). Iron is stored in oligodendrocytes (Hallgren and Sourander, 1958) and many of the subcortical gray matter structures both contain and are bordering with deep white matter (see e.g. Bartzokis et al, 1997; Mitrofanis et al., 1993). Myelin breakdown has been associated with ferritin in Alzheimer's disease (Quintana et al., 2006), and late life myelination has been encountered also in phylogenetically older structures (Benes, 1994). Changes in ferritin may follow the same curvilinear shape of myelination through life. Iron is a cofactor in the synthesis of myelin (Piñero & Connor, 2000) and there is evidence that iron undergoes translocation between brain regions (Barkai, Durkin, Dwork & Nelson, 1991; Dwork et al., 1990). Myelin breakdown in the surrounding regions may interplay with the release of ferritin in the subcortical gray matter.
5.2. Sex differences in the susceptibility of deep gray matter
We reported evidence of sex related variations in the distribution of susceptibility. Greater proportions of variance in susceptibility could be attributed to older age in men than in women. Women showed lower levels of magnetic susceptibility in the substantia nigra after accounting for age, and a similar trend was observed for the red nucleus (p = .059). Sex differences have been reported in the past in selective subcortical nuclei, using changes in GRE phase and FDRI (Bartzokis et al., 1997; Bartzokis et al., 2011; Hagemeier et al., 2013; Tishler et al., 2012). Our finding confirms a previous report showing a decrease of phase in the Sn as a function of age in men, interpreted as an increase in iron levels (Hagameier et al, 2013). Sex is an important co-factor to be taken into account by future studies of individual differences in iron accumulation. The current report revealed that only men showed a linear age related increase of susceptibility in the pulvinar (Fig. 10), while the linear age term was non-significant in women. The susceptibility of the pulvinar complex changed as a nonlinear function of age in women, with the susceptibility rise in young age leveling off at midlife. Overall nonlinear age trends where present to a greater degree in women compared to men. However, in the thalamus did men rather than women showed a nonlinear age trend. The reason for that is unknown but sex related variations in transverse relaxation rate (R2) have previously been reported for the thalamus as a main effect, with women showing lower levels of ferritin than men (Bartzokis et al., 2007). To the best of our knowledge, no study has to date compared sex differences in curvilinear age trends of susceptibility rise. As will be discussed in the following paragraph, menopause may in part influence such leveling-off in susceptibility.
Women who were expected to be post menopause (in this work taken to be women 51 years of age or older) showed a lower overall level of susceptibility compared to subjects free of menopause (men of all ages and younger women). This is a novel in vivo finding. Previous post mortem observations show lower global brain iron levels in women compared to men in the 53 to 101 age range (Ramos et al., 2014) and are consistent with the results reported here. Changes in steroid hormones at menopause (Al-Azzawi & Palacios, 2009) may partly explain the lower susceptibility in women post menopause. Sex steroids have been proposed as neuro-protectants (Chen et al., 2010; Rogers & Wagner, 2006), and can mediate the toxic effect of ferrous iron (Gu et al., 2010).
5.3. Strengths
One of the major strength of the present study is the QSM method itself. Convincing evidence from postmortem evaluation of QSM, using mass spectrometry, indicates the validity of using QSM for brain iron estimation by showing that iron is the dominant source of magnetic susceptibility in the deep gray matter (Langkammer et al., 2012). As compared to gradient echo phase images, QSM provides a more correct spatial depiction and a clearer image reconstruction, and suppresses the blooming artefacts observed in phase (Li et al., 2012).
Second, the study is unique in terms of the large sample of healthy subjects with a wide age range and an even gender distribution. This is one of the largest samples of healthy adults to have in-vivo MRI estimates of brain iron concentrations. Decrease of power and subsequent risk of failure in detecting effects is often a major issue for a majority of MR studies that use smaller sample sizes. All subjects were scanned according to the same image acquisition protocol while previous studies that investigated associations of susceptibility and age have used intermixed protocols (Bilgic et al., 2012; W. Li et al., 2014), which adds to the strength of the present study.
5.4. Limitations
The findings of the present study should be interpreted in the context of its limitations. First, we relied on a sample of convenience recruited from hospital personnel and their relatives, which may lead to selection bias and may limit the generalizability of the present findings. For instance, the study sample was highly selected for good health, and is most likely healthier than the general population of its origin. Also, the non-random sample selection per se decreases generalizability. Our aim however, was to study age-related changes in iron accumulation among individuals of good health, not suffering from aging related diseases, and the mentioned drawbacks should not be crucial.
Second, each ROI, was segmented on a single slice (3 mm), exhibiting the region of interest most prominently. Segmentation of the full volume, would have generated a three dimensional representation of each ROI. We cannot rule out that different relationships might have been observed if the neuroanatomical structures were evaluated in their entirety, particularly since the iron distributions may vary across the nuclei. The course of action was taken since the manual segmentation technique, while accurate, is a time-consuming procedure in the relatively large sample of the current report. The manual segmentation, although restricted to a single radiologist per ROI to minimize inter-subject variability, may nonetheless confound the results by subjective error. Further, only one single gradient echo was acquired, and R2* maps could not be calculated. A comparison of QSM with R2* would have been useful to study the age dependency in high iron concentration ROIs. Previous work has shown that R2* and susceptibility yielded similar results regarding the age dependency in estimates of iron deposits in the subcortical gray matter (W. Li et al., 2014).
Recent work found lesser reproducibility in the measurement of susceptibility of the red nucleus and substantia nigra than the structures of the basal ganglia, using the PDF method for background field removal (Lin et al., 2014). Differences in the age dependency of substantia nigra susceptibility have also been reported between L1 and L2 regularizations (Bilgic et al, 2012). A recent publication (Deh et al 2015) has shown good overall reproducibility in QSM using the algorithm employed in this study however, and such limitations should not be crucial.
Such limitations should be taken into account in interpreting the results. The large sample size in the current report may in part help counteract such issues by greater representability of age related differences in adulthood.
Further, GRE images are confounded by other paramagnetic elements besides iron, like manganese, zink and copper causing increasing MR contrast, which poses another concern. Other metals than iron increase with aging (Zecca et al, 2004) and although such paramagnetic properties may have little influence on MRI (Schenck, 2003), this is worth mentioning given the lack of studies evaluating the joint effects of other metals in relation to the measured MRI signal. Magnetic susceptibility of the brain is also influenced by myelin (Langkammer et al., 2012). The latter, is however, a minor concern since smaller amounts of white matter is present in the gray subcortical nuclei (Hallgren & Sourander, 1958; Zecca et al., 2004).
Last, we approximated the onset of menopause by the reported average age according to previous studies (Cheung et al, 2011). Although studies have shown relatively small standard deviations regarding the age of menopause onset in Caucasians and Asians (Cheung et al., 2011; Gold et al., 2001), we do not know the true variance of menopause age among the women in the current study. We lack information on how many women in the study were on hormone replacement therapy (HRT). This should be a minor concern however since large studies report that few Chinese women use HRT (0.8% or less) (Lundberg, Tolonen, Stegmayr, Kuulasmaa, & Asplund, 2004; Yang et al., 2008). Taken together, the mentioned weaknesses may in part bias our results, and the results need further validation from replication.
5.5. Future studies
A repeated measures design would be ideal to study age effects on susceptibility. Aging per se unfolds over time and to the best of our knowledge, inference about age associations of estimates of human brain iron, rely solely on cross sectional studies, while longitudinal studies have been performed only in rodents (Klohs et al, 2013). Cross-sectional design relies on age-related differences between persons that are captured in a snapshot frozen in time, and cannot measure the true dynamic trajectories within a person. As in vivo imaging of susceptibility is improving and already shows good between scan reliability (Deh et al., 2015), repeated measures design becomes feasible.
Further emphasis should be put on unraveling the underlying biochemical mechanisms of the sex differences of brain susceptibility values reported herein. Distributions of sex steroids are of particular interest.
Another interesting avenue is the role of inflammation in relation to individual differences in brain iron. The paradigm of “inflamm-aging” (Franceschi et al., 2000), has recently attracted a great deal of attention in terms of explaining age related changes. Inflammation has been proposed as a key player in mediating cellular death and destruction via poorly liganded iron (Kell, 2009). Observational studies show that risk allelic variants of single-nucleotide polymorphisms (SNPs) regulate pro-inflammatory response, in the IL-1β genetic family (IL-1β C-511T, rs16944), promotes shrinkage in both gray and white matter of the brain parenchyma (Persson et al., 2014; Fornage et al., 2008). This is interesting given recent findings of correspondence between shrinkage in brain volumes and rise of MRI estimates of iron (Hagemeier et al., 2013; Peran et al., 2009), and that poorly liganded iron can cause synchronized inhibition of the genetic expression of 1L-1 β (Small et al., 2011).
The current report sheds light on age related variations in brain iron accumulation and female sex as a potential mitigating factor concerning brain iron concentrations. The findings of age-dependent brain iron accumulation conforms to previous reports, but also adds to the current state of affairs by reporting age-related changes in less studied, smaller subcortical nuclei. QSM, as a mean of quantifying brain susceptibility in-vivo, holds much promise for the detection of age-related iron accumulation, in addition to direct visualization of bleeding in the cerebrum (Liu et al., 2012), calcification (Schweser, Deistung, Lehr, & Reichenbach, 2010), and the study of pathological neurodegeneration (Acosta-Cabronero et al., 2014; Langkammer et al., 2013).
This report is the first to show in vivo that women have lower total subcortical brain iron levels after expected menopause onset. Age related changes in estrogen levels may be a mediating factor of such associations. The current study indicates that age and sex are important co-factors to take into account when establishing a baseline level to differentiate pathologic neurodegeneration from healthy aging. Longitudinal evaluation is necessary to unravel how the age related differences reported herein are related to age related in-person changes over time.
Supplementary Material
Highlights.
The distributions of susceptibility varied in degree across the ROIs.
Strong linear rise of susceptibilities in the striatum with advancing age.
Pronounced curvilinear age trends in the Rn, smaller effects in Pul, Sn, Th & Dn.
Sex differences in susceptibility were present in the Sn and Pul.
Lower total magnetic susceptibility in women expected to be post menopause.
Acknowledgments
This work was supported in part by a grant: R01EB013443, from the National Institute on Aging to YW, Grants FOA11H-349 & FOA13H-090 from the Royal Swedish Society of Sciences, & Solstickan Foundation to NP.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
6. Conflicts of Interest
The authors have no conflict of interest.
References
- Acosta-Cabronero J, Williams GB, Cardenas-Blanco A, Arnold RJ, Lupson V, Nestor PJ. In vivo quantitative susceptibility mapping (QSM) in Alzheimer's disease. PLoS ONE. 2013;8(11) doi: 10.1371/journal.pone.0081093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Al-Azzawi F, Palacios S. Hormonal changes during menopause. Maturitas. 2009;63(2):135–7. doi: 10.1016/j.maturitas.2009.03.009. [DOI] [PubMed] [Google Scholar]
- Benes FM. Myelination of a Key Relay Zone in the Hippocampal Formation Occurs in the Human Brain During Childhood, Adolescence, and Adulthood. Archives of General Psychiatry. 1994;51(6):477. doi: 10.1001/archpsyc.1994.03950060041004. [DOI] [PubMed] [Google Scholar]
- Andersen HH, Johnsen KB, Moos T. Iron deposits in the chronically inflamed central nervous system and contributes to neurodegeneration. Cell Mol Life Sci. 2014;71(9):1607–1622. doi: 10.1007/s00018-013-1509-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aquino D, Bizzi A, Grisoli M, Garavaglia B, Bruzzone MG, Nardocci N, Chiapparini L. Age-related iron deposition in the basal ganglia: quantitative analysis in healthy subjects. Radiology. 2009;252(1):165–172. doi: 10.1148/radiol.2522081399. [DOI] [PubMed] [Google Scholar]
- Barkai AI, Durkin M, Dwork AJ, Nelson HD. Autoradiographic study of iron- binding sites in the rat brain: distribution and relationship to aging. Journal of Neuroscience Research. 1991;29(3):390–5. doi: 10.1002/jnr.490290314. [DOI] [PubMed] [Google Scholar]
- Bartzokis G, Aravagiri M, Oldendorf WH, Mintz J, Marder SR. Field dependent transverse relaxation rate increase may be a specific measure of tissue iron stores. Magnetic Resonance in Medicine : Official Journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 1993;29(4):459–64. doi: 10.1002/mrm.1910290406. [DOI] [PubMed] [Google Scholar]
- Bartzokis G, Beckson M, Hance DB, Marx P, Foster JA, Marder SR. MR evaluation of age-related increase of brain iron in young adult and older normal males. Magn Reson Imaging. 1997;15(1):29–35. doi: 10.1016/s0730-725x(96)00234-2. [DOI] [PubMed] [Google Scholar]
- Bartzokis G, Lu PH, Tingus K, Peters DG, Amar CP, Tishler TA, Connor JR. Gender and iron genes may modify associations between brain iron and memory in healthy aging. Neuropsychopharmacology. 2011;36(7):1375–1384. doi: 10.1038/npp.2011.22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartzokis G, Tishler TA, Lu PH, Villablanca P, Altshuler LL, Carter M, Mintz J. Brain ferritin iron may influence age- and gender-related risks of neurodegeneration. Neurobiol Aging. 2007;28(3):414–423. doi: 10.1016/j.neurobiolaging.2006.02.005. [DOI] [PubMed] [Google Scholar]
- Bartzokis G, Tishler TA, Shin IS, Lu PH, Cummings JL. Brain ferritin iron as a risk factor for age at onset in neurodegenerative diseases. Ann N Y Acad Sci. 2004:224–236. doi: 10.1196/annals.1306.019. [DOI] [PubMed] [Google Scholar]
- Brown RW, Cheng Y-C, Norman Haacke E,M, Thompson MR, Venkatesan R. Magnetic resonance imaging: physical principles and sequence design. John Wiley & Sons; 2014. [Google Scholar]
- Berg D, Youdim MB. Role of iron in neurodegenerative disorders. Top Magn Reson Imaging. 2006;17(1):5–17. doi: 10.1097/01.rmr.0000245461.90406.ad. [DOI] [PubMed] [Google Scholar]
- Bilgic B, Pfefferbaum A, Rohlfing T, Sullivan EV, Adalsteinsson E. MRI estimates of brain iron concentration in normal aging using quantitative susceptibility mapping. Neuroimage. 2012;59(3):2625–2635. doi: 10.1016/j.neuroimage.2011.08.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brewer C, Otto-Duessel M, Wood RI, Wood JC. Sex differences and steroid modulation of cardiac iron in a mouse model of iron overload. Transl Res. 2014;163(2):151–159. doi: 10.1016/j.trsl.2013.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browne MW, Cudeck R, Bollen KA. Alternative ways of assessing model fit. Sage Focus Editions. 1993;154:136–136. [Google Scholar]
- Browne MW, MacCallum RC, Kim C-T, Andersen BL, Glaser R. When fit indices and residuals are incompatible. Psychological Methods. 2002;7(4):403–21. doi: 10.1037//1082-989X.7.4.403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen TY, Tsai KL, Lee TY, Chiueh CC, Lee WS, Hsu C. Sex-specific role of thioredoxin in neuroprotection against iron-induced brain injury conferred by estradiol. Stroke. 2010;41(1):160–165. doi: 10.1161/STROKEAHA.109.562850. [DOI] [PubMed] [Google Scholar]
- Cherubini A, Peran P, Caltagirone C, Sabatini U, Spalletta G. Aging of subcortical nuclei: microstructural, mineralization and atrophy modifications measured in vivo using MRI. Neuroimage. 2009;48(1):29–36. doi: 10.1016/j.neuroimage.2009.06.035. [DOI] [PubMed] [Google Scholar]
- Cheung E, Tsang S, Bow C, Soong C, Yeung S, Loong C, Kung A. Bone loss during menopausal transition among southern Chinese women. Maturitas. 2011;69(1):50–56. doi: 10.1016/j.maturitas.2011.01.010. [DOI] [PubMed] [Google Scholar]
- Cohen J. “A power primer”. Psychological Bulletin. 1992;112(1):155–159. doi: 10.1037//0033-2909.112.1.155. [DOI] [PubMed] [Google Scholar]
- Das SK, Zhabyeyev P, Oudit GY. Role of sex steroids and sexual dimorphism on cardiac iron metabolism in iron-overload cardiomyopathy. Transl Res. 2014;163(2):141–144. doi: 10.1016/j.trsl.2013.09.009. [DOI] [PubMed] [Google Scholar]
- Deh K, Nguyen TD, Eskreis-Winkler S, Prince MR, Spincemaille P, Gauthier S, Wang Y. Reproducibility of quantitative susceptibility mapping in the brain at two field strengths from two vendors. Journal of Magnetic Resonance Imaging : JMRI. 2015 doi: 10.1002/jmri.24943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Rijk MC, Launer LJ, Berger K, Breteler MM, Dartigues JF, Baldereschi M, Hofman A. Prevalence of Parkinson's disease in Europe: A collaborative study of population-based cohorts. Neurologic Diseases in the Elderly Research Group. Neurology. 2000;54(11 Suppl 5):S21–23. [PubMed] [Google Scholar]
- de Rochefort L, Liu T, Kressler B, Liu J, Spincemaille P, Lebon V, Wang Y. Quantitative susceptibility map reconstruction from MR phase data using bayesian regularization: validation and application to brain imaging. Magn Reson Med. 2010;63(1):194–206. doi: 10.1002/mrm.22187. [DOI] [PubMed] [Google Scholar]
- Dixon SJ, Stockwell BR. The role of iron and reactive oxygen species in cell death. Nat Chem Biol. 2014;10(1):9–17. doi: 10.1038/nchembio.1416. [DOI] [PubMed] [Google Scholar]
- Dong J, Liu T, Chen F, Zhou D, Dimov A, Raj A, Wang Y. Simultaneous Phase Unwrapping and Removal of Chemical Shift (SPURS) Using Graph Cuts: Application in Quantitative Susceptibility Mapping. IEEE Transactions on Medical Imaging. 2015;34(2):531–40. doi: 10.1109/TMI.2014.2361764. [DOI] [PubMed] [Google Scholar]
- Dunn OJ. Multiple comparisons among means. Journal of the American Statistical Association. 1961;56(293):52–64. [Google Scholar]
- Dwork AJ, Lawler G, Zybert PA, Durkin M, Osman M, Willson N, Barkai AI. An autoradiographic study of the uptake and distribution of iron by the brain of the young rat. Brain Research. 1990;518(1-2):31–9. doi: 10.1016/0006-8993(90)90950-g. [DOI] [PubMed] [Google Scholar]
- Fjell AM, Walhovd KB. Structural brain changes in aging: courses, causes and cognitive consequences. Reviews in the Neurosciences. 2010;21(3):187–221. doi: 10.1515/revneuro.2010.21.3.187. [DOI] [PubMed] [Google Scholar]
- Fleming DJ, Jacques PF, Massaro JM, D'Agostino RB, Sr., Wilson PW, Wood RJ. Aspirin intake and the use of serum ferritin as a measure of iron status. Am J Clin Nutr. 2001;74(2):219–226. doi: 10.1093/ajcn/74.2.219. [DOI] [PubMed] [Google Scholar]
- Floyd RA, Carney JM. The role of metal ions in oxidative processes and aging. Toxicol Ind Health. 1993;9(1-2):197–214. doi: 10.1177/0748233793009001-214. [DOI] [PubMed] [Google Scholar]
- Fornage M, Chiang YA, O'Meara ES, Psaty BM, Reiner AP, Siscovick DS, Longstreth WT. Biomarkers of Inflammation and MRI-Defined Small Vessel Disease of the Brain: The Cardiovascular Health Study. Stroke; a Journal of Cerebral Circulation. 2008;39(7):1952–9. doi: 10.1161/STROKEAHA.107.508135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franceschi C, Bonafe M, Valensin S, Olivieri F, De Luca M, Ottaviani E, De Benedictis G. Inflamm-aging. An evolutionary perspective on immunosenescence. Ann N Y Acad Sci. 2000;908:244–254. doi: 10.1111/j.1749-6632.2000.tb06651.x. [DOI] [PubMed] [Google Scholar]
- Gelman BB. Iron in CNS disease. J Neuropathol Exp Neurol. 1995;54(4):477–486. doi: 10.1097/00005072-199507000-00001. [DOI] [PubMed] [Google Scholar]
- Gold EB, Bromberger J, Crawford S, Samuels S, Greendale GA, Harlow SD, Skurnick J. Factors associated with age at natural menopause in a multiethnic sample of midlife women. Am J Epidemiol. 2001;153(9):865–874. doi: 10.1093/aje/153.9.865. [DOI] [PubMed] [Google Scholar]
- Gorell JM, Ordidge RJ, Brown GG, Deniau JC, Buderer NM, Helpern JA. Increased iron-related MRI contrast in the substantia nigra in Parkinson's disease. Neurology. 1995;45(6):1138–1143. doi: 10.1212/wnl.45.6.1138. [DOI] [PubMed] [Google Scholar]
- Gregorich SE. Do self-report instruments allow meaningful comparisons across diverse population groups? Testing measurement invariance using the confirmatory factor analysis framework. Med Care. 2006;44(11 Suppl 3):S78–94. doi: 10.1097/01.mlr.0000245454.12228.8f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu Y, Xi G, Liu W, Keep RF, Hua Y. Estrogen reduces iron-mediated brain edema and neuronal death. Acta Neurochir Suppl. 2010;106:159–162. doi: 10.1007/978-3-211-98811-4_29. [DOI] [PubMed] [Google Scholar]
- Haacke EM, Ayaz M, Khan A, Manova ES, Krishnamurthy B, Gollapalli L, Kirsch W. Establishing a baseline phase behavior in magnetic resonance imaging to determine normal vs. abnormal iron content in the brain. J Magn Reson Imaging. 2007;26(2):256–264. doi: 10.1002/jmri.22987. [DOI] [PubMed] [Google Scholar]
- Haacke EM, Cheng NY, House MJ, Liu Q, Neelavalli J, Ogg RJ, Obenaus A. Imaging iron stores in the brain using magnetic resonance imaging. Magn Reson Imaging. 2005;23(1):1–25. doi: 10.1016/j.mri.2004.10.001. [DOI] [PubMed] [Google Scholar]
- Haacke EM, Miao Y, Liu M, Habib CA, Katkuri Y, Liu T, Wu J. Correlation of putative iron content as represented by changes in R2* and phase with age in deep gray matter of healthy adults. J Magn Reson Imaging. 2010;32(3):561–576. doi: 10.1002/jmri.22293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haacke EM, Xu Y, Cheng YC, Reichenbach JR. Susceptibility weighted imaging (SWI). Magn. Reson. Med. 2004;(52):612–618. doi: 10.1002/mrm.20198. [DOI] [PubMed] [Google Scholar]
- Hagemeier J, Dwyer MG, Bergsland N, Schweser F, Magnano CR, Heininen-Brown M, Zivadinov R. Effect of age on MRI phase behavior in the subcortical deep gray matter of healthy individuals. AJNR Am J Neuroradiol. 2013;34(11):2144–2151. doi: 10.3174/ajnr.A3569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallgren B, Sourander P. The effect of age on the non-haemin iron in the human brain. Journal of neurochemistry. 1958;3(1):41–51. doi: 10.1111/j.1471-4159.1958.tb12607.x. [DOI] [PubMed] [Google Scholar]
- Hu L.-t., Bentler PM. Fit indices in covariance structure modeling: Sensitivity to underparameterized model misspecification. Psychological methods. 1998;3(4):424. [Google Scholar]
- Hu L. t., Bentler PM. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling: A Multidisciplinary Journal. 1999;6(1):1–55. [Google Scholar]
- Jensen JH, Szulc K, Hu C, Ramani A, Lu H, Xuan L, Schenck J. Magnetic field correlation as a measure of iron-generated magnetic field inhomogeneities in the brain. Magnetic Resonance in Medicine. 2009;61(2):481–485. doi: 10.1002/mrm.21823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jöreskog KG. A general method for analysis of covariance structures. Biometrika. 1970;57(2):239–251. [Google Scholar]
- Klohs J, Politano IW, Deistung A, Grandjean J, Drewek A, Dominietto M, Rudin M. Longitudinal Assessment of Amyloid Pathology in Transgenic ArcAbeta Mice Using Multi-Parametric Magnetic Resonance Imaging. PLoS One. 2013;(8):e66097. doi: 10.1371/journal.pone.0066097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kell DB. Iron behaving badly: inappropriate iron chelation as a major contributor to the aetiology of vascular and other progressive inflammatory and degenerative diseases. BMC medical genomics. 2009;2(1):2. doi: 10.1186/1755-8794-2-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langkammer C, Ropele S, Pirpamer L, Fazekas F, Schmidt R. MRI for iron mapping in Alzheimer's disease. Neurodegenerative Diseases. 2013;13(2-3):189–191. doi: 10.1159/000353756. [DOI] [PubMed] [Google Scholar]
- Langkammer C, Schweser F, Krebs N, Deistung A, Goessler W, Scheurer E, Fazekas F. Quantitative susceptibility mapping (QSM) as a means to measure brain iron? A post mortem validation study. Neuroimage. 2012;62:3. doi: 10.1016/j.neuroimage.2012.05.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lundberg V, Tolonen H, Stegmayr B, Kuulasmaa K, Asplund K. Use of oral contraceptives and hormone replacement therapy in the WHO MONICA project. Maturitas. 2004;48(1):39–49. doi: 10.1016/j.maturitas.2003.08.006. [DOI] [PubMed] [Google Scholar]
- Li J, Chang S, Liu T, Wang Q, Cui D, Chen X, Wisnieff C. Reducing the object orientation dependence of susceptibility effects in gradient echo MRI through quantitative susceptibility mapping. Magnetic Resonance in Medicine. 2012;68(5):1563–1569. doi: 10.1002/mrm.24135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W, Wu B, Batrachenko A, Bancroft-Wu V, Morey RA, Shashi V, Liu C. Differential developmental trajectories of magnetic susceptibility in human brain gray and white matter over the lifespan. Hum Brain Mapp. 2014;35(6):2698–2713. doi: 10.1002/hbm.22360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin P-Y, Chao T-C, Wu M-L. Quantitative Susceptibility Mapping of Human Brain at 3T: A Multisite Reproducibility Study. AJNR. American Journal of Neuroradiology. 2014 doi: 10.3174/ajnr.A4137. [Epub ahead of print]doi:10.3174/ajnr.A4137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu T, D. Liu T, de Rochefort L, LeDoux J, Zhang Q, Pronce MR, Wu J, Wang Y. Measurement of iron concentration in human brain using Quantitative Susceptibility Mapping (QSM): correlation with age. Proc. Intl. Soc. Mag. Reson. Med. 2010;18 [Google Scholar]
- Liu T, D. Zhou D, Spincemaille P, Wang Y. Differential approach to quantitative susceptibility mapping without background field removal. Proc. 22nd Annu. Meet. ISMRM; Milan, Italy. 2014.p. 0597. [Google Scholar]
- Liu T, Surapaneni K, Lou M, Cheng L, Spincemaille P, Wang Y. Cerebral microbleeds: burden assessment by using quantitative susceptibility mapping. Radiology. 2012;262(1):269–278. doi: 10.1148/radiol.11110251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu T, Xu W, Spincemaille P, Avestimehr AS, Wang Y. Accuracy of the morphology enabled dipole inversion (MEDI) algorithm for quantitative susceptibility mapping in MRI. IEEE Transactions on Medical Imaging. 2012;31(3):816–24. doi: 10.1109/TMI.2011.2182523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maschke M, Weber J, Dimitrova A, Bonnet U, Bohrenkämper J, Sturm S, Diener H-C. Age-related changes of the dentate nuclei in normal adults as revealed by 3D fast low angle shot (FLASH) echo sequence magnetic resonance imaging. Journal of neurology. 2004;251(6):740–746. doi: 10.1007/s00415-004-0420-5. [DOI] [PubMed] [Google Scholar]
- McArdle JJ. Current directions in structural factor analysis. Current Directions in Psychological Science. 1996:11–18. [Google Scholar]
- Meredith W, Teresi JA. An essay on measurement and factorial invariance. Medical care. 2006;44(11):S69–S77. doi: 10.1097/01.mlr.0000245438.73837.89. [DOI] [PubMed] [Google Scholar]
- Mills E, Dong X.-p., Wang F, Xu H. Mechanisms of brain iron transport: insight into neurodegeneration and CNS disorders. Future medicinal chemistry. 2010;2(1):51–64. doi: 10.4155/fmc.09.140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitrofanis J, Guillery RW. New views of the thalamic reticular nucleus in the adult and the developing brain. Trends Neurosci. 1993;16:240–5. doi: 10.1016/0166-2236(93)90163-g. [DOI] [PubMed] [Google Scholar]
- Morris C, Candy J, Oakley A, Bloxham C, Edwardson J. Histochemical distribution of non-haem iron in the human brain. Cells Tissues Organs. 1992;144(3):235–257. doi: 10.1159/000147312. [DOI] [PubMed] [Google Scholar]
- Peran P, Cherubini A, Luccichenti G, Hagberg G, Démonet JF, Rascol O, Sabatini U. Volume and iron content in basal ganglia and thalamus. Human brain mapping. 2009;30(8):2667–2675. doi: 10.1002/hbm.20698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Persson N, Ghisletta P, Dahle CL, Bender AR, Yang Y, Yuan P, Raz N. Regional brain shrinkage over two years: Individual differences and effects of pro- inflammatory genetic polymorphisms. Neuroimage. 2014;28:334–348. doi: 10.1016/j.neuroimage.2014.09.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Persson N, Lavebratt C, Wahlin A. Synergy effects of HbA1c and variants of APOE and BDNFVal66Met explains individual differences in memory performance. Neurobiol Learn Mem. 2013;106:274–282. doi: 10.1016/j.nlm.2013.08.017. [DOI] [PubMed] [Google Scholar]
- Pfefferbaum A, Adalsteinsson E, Rohlfing T, Sullivan EV. MRI estimates of brain iron concentration in normal aging: comparison of field-dependent (FDRI) and phase (SWI) methods. Neuroimage. 2009;47(2):493–500. doi: 10.1016/j.neuroimage.2009.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piñero DJ, Connor JR. Iron in the brain: an important contributor in normal and diseased states. The Neuroscientist. 2000;6(6):435–453. [Google Scholar]
- Qin Y, Zhu W, Zhan C, Zhao L, Wang J, Tian Q, Wang W. Investigation on positive correlation of increased brain iron deposition with cognitive impairment in Alzheimer disease by using quantitative MR R2' mapping. J Huazhong Univ Sci Technolog Med Sci. 2011;31(4):578–585. doi: 10.1007/s11596-011-0493-1. [DOI] [PubMed] [Google Scholar]
- Rigdon EE. Demonstrating the effects of unmodeled random measurement error. Structural Equation Modeling: A Multidisciplinary Journal. 1994;1(4):375–380. [Google Scholar]
- Rodrigue KM, Haacke EM, Raz N. Differential effects of age and history of hypertension on regional brain volumes and iron. Neuroimage. 2011;54(2):750–759. doi: 10.1016/j.neuroimage.2010.09.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogers E, Wagner AK. Gender, sex steroids, and neuroprotection following traumatic brain injury. J Head Trauma Rehabil. 2006;21(3):279–281. doi: 10.1097/00001199-200605000-00008. [DOI] [PubMed] [Google Scholar]
- Ramos P, Santos A, Pinto NR, Mendes R, Magalhães T, Almeida A. Iron levels in the human brain: a post-mortem study of anatomical region differences and age- related changes. Journal of Trace Elements in Medicine and Biology. 2014;28(1):13–17. doi: 10.1016/j.jtemb.2013.08.001. [DOI] [PubMed] [Google Scholar]
- Schenck JF. Magnetic resonance imaging of brain iron. J Neurol Sci. 2003;207(1-2):99–102. doi: 10.1016/s0022-510x(02)00431-8. [DOI] [PubMed] [Google Scholar]
- Schenck JF, Zimmerman EA. High-field magnetic resonance imaging of brain iron: birth of a biomarker? NMR Biomed. 2004;17(7):433–445. doi: 10.1002/nbm.922. [DOI] [PubMed] [Google Scholar]
- Schweser F, Deistung A, Lehr BW, Reichenbach JR. Differentiation between diamagnetic and paramagnetic cerebral lesions based on magnetic susceptibility mapping. Med Phys. 2010;37(10):5165–5178. doi: 10.1118/1.3481505. [DOI] [PubMed] [Google Scholar]
- Schweser F, Dwyer MG, Deistung A, Reichenbach JR, Zivadinov R. Impact of tissue atrophy on high-pass filtered MRI signal phase-based assessment in large-scale group-comparison studies: a simulation study. Frontiers in Physics. 2013;1(14) [Google Scholar]
- Seeman P, Bzowej NH, Guan HC, Bergeron C, Becker LE, Reynolds GP, et al. Human brain dopamine receptors in children and aging adults. Synapse. 1987;1(5):399–404. doi: 10.1002/syn.890010503. [DOI] [PubMed] [Google Scholar]
- Severson JA, Marcusson J, Winblad B, Finch CE. Age-correlated loss of dopaminergic binding sites in human basal ganglia. J Neurochem. 1982;39(6):1623–1631. doi: 10.1111/j.1471-4159.1982.tb07996.x. [DOI] [PubMed] [Google Scholar]
- Small BG, McColl BW, Allmendinger R, Pahle J, Lopez-Castejon G, Rothwell NJ, Kell DB. Efficient discovery of anti-inflammatory small-molecule combinations using evolutionary computing. Nat Chem Biol. 2011;7(12):902–908. doi: 10.1038/nchembio.689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spearman C. “General intelligence” objectively determined and measured. American Journal of Psychology. 1904;15:201–293. [Google Scholar]
- Stüber C, Morawski M, Schäfer A, Labadie C, Wähnert M, Leuze C, Turner R. Myelin and iron concentration in the human brain: a quantitative study of MRI contrast. NeuroImage. 2014;93(Pt 1):95–106. doi: 10.1016/j.neuroimage.2014.02.026. [DOI] [PubMed] [Google Scholar]
- Taylor K, Cook J, Counsell C. Heterogeneity in male to female risk for Parkinson's disease. Journal of Neurology, Neurosurgery & Psychiatry. 2007;78(8):905–906. doi: 10.1136/jnnp.2006.104695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tishler TA, Raven EP, Lu PH, Altshuler LL, Bartzokis G. Premenopausal hysterectomy is associated with increased brain ferritin iron. Neurobiol Aging. 2012;33(9):1950–1958. doi: 10.1016/j.neurobiolaging.2011.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Chan GL, Holden JE, Dobko T, Mak E, Schulzer M, Stoessl AJ. Age-dependent decline of dopamine D1 receptors in human brain: a PET study. Synapse. 1998;30(1):56–61. doi: 10.1002/(SICI)1098-2396(199809)30:1<56::AID-SYN7>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
- Wang Y, Liu T. Quantitative susceptibility mapping (QSM): Decoding MRI data for a tissue magnetic biomarker. Magn Reson Med. 2014;17(10):25358. doi: 10.1002/mrm.25358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward RJ, Zucca FA, Duyn JH, Crichton RR, Zecca L. The role of iron in brain ageing and neurodegenerative disorders. The Lancet Neurology. 2014;13(10):1045–1060. doi: 10.1016/S1474-4422(14)70117-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westlye LT, Walhovd KB, Dale AM, Bjørnerud A, Due-Tønnessen P, Engvig A, Fjell AM. Life-span changes of the human brain white matter: diffusion tensor imaging (DTI) and volumetry. Cerebral Cortex (New York, N.Y. : 1991) 2010;20(9):2055–68. doi: 10.1093/cercor/bhp280. [DOI] [PubMed] [Google Scholar]
- Whitfield JB, Treloar S, Zhu G, Powell LW, Martin NG. Relative importance of female-specific and non-female-specific effects on variation in iron stores between women. British journal of haematology. 2003;120(5):860–866. doi: 10.1046/j.1365-2141.2003.04224.x. [DOI] [PubMed] [Google Scholar]
- Volkow ND, Gur RC, Wang GJ, Fowler JS, Moberg PJ, Ding YS, Logan J. Association between decline in brain dopamine activity with age and cognitive and motor impairment in healthy individuals. Am J Psychiatry. 1998;155(3):344–349. doi: 10.1176/ajp.155.3.344. [DOI] [PubMed] [Google Scholar]
- Volkow ND, Wang GJ, Fowler JS, Logan J, Gatley SJ, MacGregor RR, Wolf AP. Measuring age-related changes in dopamine D2 receptors with 11C-raclopride and 18F-N-methylspiroperidol. Psychiatry Res. 1996;67(1):11–16. doi: 10.1016/0925-4927(96)02809-0. [DOI] [PubMed] [Google Scholar]
- Xu X, Wang Q, Zhang M. Age, gender, and hemispheric differences in iron deposition in the human brain: an in vivo MRI study. Neuroimage. 2008;40(1):35–42. doi: 10.1016/j.neuroimage.2007.11.017. [DOI] [PubMed] [Google Scholar]
- Zecca L, Stroppolo A, Gatti A, Tampellini D, Toscani M, Gallorini M, Zucca FA. The role of iron and copper molecules in the neuronal vulnerability of locus coeruleus and substantia nigra during aging. Proceedings of the National Academy of Sciences of the United States of America. 2004;101(26):9843–9848. doi: 10.1073/pnas.0403495101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou D, Liu T, Spincemaille P, Wang Y. Background field removal by solving the Laplacian boundary value problem. NMR in Biomedicine. 2014;27(3):312–9. doi: 10.1002/nbm.3064. [DOI] [PubMed] [Google Scholar]
- Quintana C, Bellefqih S, Laval JY, Guerquin-Kern JL, Wu TD, Avila J, Patiño C. Study of the localization of iron, ferritin, and hemosiderin in Alzheimer's disease hippocampus by analytical microscopy at the subcellular level. Journal of Structural Biology. 2006;153(1):42–54. doi: 10.1016/j.jsb.2005.11.001. [DOI] [PubMed] [Google Scholar]
- Yang D, Haines CJ, Pan P, Zhang Q, Sun Y, Hong S, Liao W. Menopausal symptoms in mid-life women in southern China. Climacteric : The Journal of the International Menopause Society. 2008;11(4):329–3. doi: 10.1080/13697130802239075. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.