Principal Angle Enrichment Analysis (PAEA): Dimensionally Reduced Multivariate Gene Set Enrichment Analysis Tool

Abstract

Gene set analysis of differential expression, which identifies collectively differentially expressed gene sets, has become an important tool for biology. The power of this approach lies in its reduction of the dimensionality of the statistical problem and its incorporation of biological interpretation by construction. Many approaches to gene set analysis have been proposed, but benchmarking their performance in the setting of real biological data is difficult due to the lack of a gold standard. In a previously published work we proposed a geometrical approach to differential expression which performed highly in benchmarking tests and compared well to the most popular methods of differential gene expression. As reported, this approach has a natural extension to gene set analysis which we call Principal Angle Enrichment Analysis (PAEA). PAEA employs dimensionality reduction and a multivariate approach for gene set enrichment analysis. However, the performance of this method has not been assessed nor its implementation as a web-based tool. Here we describe new benchmarking protocols for gene set analysis methods and find that PAEA performs highly. The PAEA method is implemented as a user-friendly web-based tool, which contains 70 gene set libraries and is freely available to the community.

I. Introduction

The analysis of differential expression with gene sets as opposed to individual genes has developed into a broad array of methods and has become an invaluable tool. Reviews and comparisons between these methods have been reported extensively [1]–[5]. There are two main strengths to this approach. First, it operates on groups of genes which have an associated function so that biological interpretation is integrated. Second, it reduces the dimensionality of the statistical problem by taking the collective differential expression of whole groups of genes into account. This example of dimensionality reduction is a particular case of an important class of methods that are of central significance to data mining. High-dimensional data, consisting of many variables, is often embedded in a high-dimensional space. However, constraints on the system mean that the intrinsic dimensionality of the data is much lower. In terms of gene expression, each genome-wide profile is embedded in a high-dimensional expression space with the expression of each gene corresponding to a coordinate. But since there are dynamic intrinsic and extrinsic constraints on biological systems, genes do not function in isolation but communicate across a complex network, and this results in correlated variations that reduce the intrinsic dimensionality of the data. It is for this reason that Principal Components Analysis (PCA) is often able to give a useful view of the genome-wide variation in expression with only two or three components. By reducing the dimensionality, the data is brought down to its most essential structure and often this can alleviate the over-fitting problem and improve the speed and performance of analysis.

In [6] we introduced a new approach to differential expression that incorporates dimensionality reduction and a multivariate approach that respects the regulatory interactions between genes. This approach characterized differential expression as a direction in gene expression space, which we refer to as the Characteristic Direction. We also showed that this geometrical approach has a natural extension to the analysis of gene sets, which we here refer to as Principal Angle Enrichment Analysis (PAEA). While we were able to benchmark the gene-level differential expression aspect of this approach, the gene set analysis extension has not yet been compared to other methods. In this work we report the benchmarking of the PAEA method, and show that it performs highly. In addition, we present a freely available user-friendly web-based enrichment analysis tool that makes the method readily available to the community.

Comparison of the performance of the various methods of gene set enrichment is complicated by the fact that the truly differentially expressed gene sets are not usually known ab initio. One way of dealing with this is to evaluate the performance of gene set enrichment methods on synthetic data in which the truly differentially expressed gene sets are known by design. However, synthetic data is only a pale imitation of real expression data, lacking the rich, yet poorly understood, structure present in real genome-wide expression data. DeLisi and coworkers [7] highlighted this challenge and devised a method of comparing methods of analysis whereby the degree to which a method is in consensus with other methods is taken as a measure of its performance quality. However, this measure of performance quality depends solely on the relationship of the methods to each other. We propose that a direct method of performance evaluation, which is independent of the relationships between analysis methods, and uses real data, is preferable. In addition, many enrichment methods are not readily available for use by users without advanced computational skills. The enrichment analysis method presented here is implemented as a user-friendly free R Shiny gene set enrichment web-application with over 70 gene set libraries available for enrichment analysis. Canned enrichment analysis for over 700 disease signatures extracted from GEO is provided with the web application that is freely available at: http://amp.pharm.mssm.edu/PAEA.

II. Gene Set Analysis Methods

Here we briefly review the PAEA method as well as a selection of other methods to which we shall compare. We consider a gene expression dataset represented as a matrix, X, with n samples, n_1|2 from sample class 1 and 2 respectively, and p genes. The gene expression level of gene i in sample j is x_ij. The set of all genes on the microarray profile, or for which there are mapped reads in the case of RNA-Seq, is G = {g₁, g₂, …, g_p}. We will examine the collective differential expression of gene sets which are themselves members of a family of sets referred to as a gene set library ℒ = {L^(k) = {g_i}_i∈λk ⊂ G}, where λ_k is the set of indices of the genes in gene set n. Each gene set library typically has some overall theme, for example, common known biological function for gene sets, or target genes for transcription factors based on DNA binding experiments, and each gene set, L^(k), is composed of genes which are associated according to some more specific biological theme, for example L⁽¹⁾ may be composed of genes involved in the bioogical function of oxidative phosphorylation, or genes associated with binding sites of the REST transcription factor.

Each method we review here has the aim of identifying the gene sets from the library that have a significant collective differential expression of its members.

A. PAEA Analysis

The gene expression data are approximated by a reduced-rank matrix via the singular value decomposition,

$$\mathbf{X}\prime =\mathbf{U}.\mathbf{\Sigma }.{\mathbf{V}}^{\mathbf{T}}$$ (1)

where U.Σ is the data projected into the principal component space, which can be projected back to the full gene expression space by the multiplication with the loading matrix V. The rank of the approximating matrix is reduced by truncating the singular values. As in [6] the orientation of the separating hyperplane of a linear classifier for the two classes under consideration, as defined by its normal in principal component space, c′, is used to characterize the differential expression. Furthermore, we employ a quadratic form of regularization by shrinking the covariance matrix, R, to the diagonal,

$$\mathbf{R}\prime =\gamma \mathbf{R}+(1-\gamma )\mathbf{I}$$ (2)

Where γ is the regularization parameter. We use the regularized form of the covariance matrix in a Linear Discriminant Analysis linear classifier. When projected back to the full gene expression space the normal to the separating hyperplane is given by, c = V.c′, and the direction of this vector characterizes the differential expression and its components can be interpreted as the contribution of each corresponding gene to the global differential expression.

[6] also showed that this geometrical conceptualization of the differential expression of genes has a natural extension to the analysis of the differential expression of gene sets. Each gene set in a library is assessed separately, so for simplicity we will drop the index and consider a single gene set L ⊂ ℒ. We take the expression of each gene in G as providing a cartesian coordinate system for expression space and therefore the genes in L span a linear subspace, Ψ. We take the principal angle, θ, between the characteristic direction, c, and Ψ as a measure of the enrichment of the gene set. By comparing to an analytical null distribution of principal angles between Ψ and isotropically distributed directions we can asses the significance of the measure. The null cumulative distribution of principal angle θ is found to take the form,

$$\mathrm{c}\mathrm{d}\mathrm{f}(\theta )=B{\mathit{\text{ Cos}}}^m{}_2{F}_1(\frac{m}{2},\frac{2+m-n}{2},\frac{2+m}{2},{\mathit{\text{cos}}}^2(\theta ))$$ (3)

Where m = |L|, and B is a normalizing constant.

For a given characteristic direction c and gene set subspace Ψ, the principal angle can be expressed in terms of the components as,

$${\mathit{\text{Cos}}}^2\theta =\sum _{i\in \lambda }{c}_i^2$$ (4)

where λ is the set of gene indices for the members of L. Then the one-tailed p value is calculated by evaluating the cumulative null distribution, p = cdf (θ). The one-tailed p value is finally corrected for multiple hypotheses testing over the whole library of gene sets using the Benjamini-Hochberg statistic.

B. Other gene set enrichment methods used for comparison

In order to compare the performance of PAEA to that of other commonly used gene set enrichment methods, we analyzed real data with a sample of commonly applied methods. We used the popular method of Gene Set Enrichment Analysis [8] along with a collection of methods listed by DeLisi and coworkers [7]. These methods are: the χ² test, mean p value test, median p value test, Wilcoxon rank sum test, and the weighed Kolmogorov-Smirnov (WKS) test.

In these methods, the genes are first ranked by their p value for a univariate test of differential expression such that gene g_i has p value p_i. We label the gene set under investigation L and the complementary genes L′, then the order statistics of the set L are labeled y(L). The rank of p_i in the complete list of genes is given by, rank_{L + L′} (p_i). Then, using this notation the, χ² gene set statistic is given by:

$$\sum _{i\in \lambda }{(p_i-<p>)}^2$$ (5)

where < p > is the mean of {p_i∀i ∈ λ}. The mean test gene set statistic is given by,

$$\frac{1}{|L|}\sum _{i\in \lambda }{p}_i$$ (6)

The median test gene set statistic is given by,

$$\{\begin{array}{cc}{y}_{n/2}(L)\hfill & \text{if }n\text{ is odd}\hfill \\ \frac{1}{2}{y}_{n/2}(L)+y_{1+|L|/2}(L)\hfill & \text{if}|L|\text{is even}\hfill \end{array}$$ (7)

The Wilcoxon rank sum test statistic is given by,

$$\sum _{i\in \lambda }{\text{rank}}_{L+L\prime }(p_i)$$ (8)

And the weighted Kolmogorov Smirnov (WKS) test is given by the maximum deviation, taken over i, between,

$$\mathrm{c}\mathrm{d}{\mathrm{f}}_p(i)=\sum _{j\le i,j\in \lambda }\frac{y_j(L+L\prime )}{{\sum }_{k\in L}(L+L\prime )}$$ (9)

and

$$\mathrm{c}\mathrm{d}{\mathrm{f}}_{L\prime }(i)=\sum _{j\le i}\frac{1}{|L\prime |}$$ (10)

These are all as described by Hung et al. [7]. We also compare the performance of these gene set level statistics when using the characteristic direction instead of the t test p values for the gene-level statistics. Each of these statistics are compared to a null disctibution based on random permutations of the class labels.

In addition, a number of other gene set enrichment strategies have been proposed which are global in the sense that they evaluate enrichment of gene sets directly without the univariate gene ranking step [9]–[11]. One example from this class of strategies is the use of Hotelling’s T² test to evaluate the multivariate difference of location of the gene expression values from the gene set under question [9]. The strategy we report here belongs within this class of global approaches of which there are currently relatively few examples in the literature and none are widely used.

III. Benchmarking

The major obstacle in benchmarking gene set analysis methods with real, as opposed to synthetic, data is that there is no reliable ”gold standard” to which we can compare. We typically do not know which are the truly differentially expressed gene sets. We have taken two approaches to benchmarking that use the same basic strategy: firstly we identify a number of controlled experiments, E_i, where our prior knowledge allows us identify a subset of gene sets, S ⊂ ℒ, that we can reasonably expect to be more significant than a randomly sampled set from the gene set library. We then use each gene set analysis method to prioritize all the gene sets in the library by the estimate of the significance of the collective differential expression. Finally we rank the genes sets and examine the cumulative distribution of the ranks of the standard sets S. The degree to which each gene set analysis method prioritizes the standard sets S, as measured by the maximum deviation of the cumulative distribution from a uniform distribution, over the whole set of experiments, is taken as the measure of the performance of the method.

A. Evaluation of the performance of PAEA using TF perturbations

We collected 73 experiments from the gene expression omnibus (GEO) database which contained expression data for control and transcription factor (TF) perturbed human samples with at least three biological replicates. The TF perturbations consisted of knockdowns (32), knockouts (29), over-expressions (5), and other types of single gene genetic perturbations (7) such as mutations. We extracted processed expression values from the Simple Omnibus Format in Text (SOFT) files downloaded from the GEO database.

We used the ChEA [12] gene set library, which contains 327 gene sets each composed of genes associated with ChIP-Seq DNA binding sites of individual transcription factors. The rational of this approach is that genes which are associated with DNA binding sites of the perturbed transcription factor are more likely than others to be differentially expressed upon perturbation of the transcription factor. Therefore, the gene set of ChIP-Seq binding sites for the perturbed transcription factor may be expected to be significantly collectively differentially expressed. The standard gene sets S for each of the 73 experiments is composed of all gene sets from ChEA for the respective perturbed transcription factor.

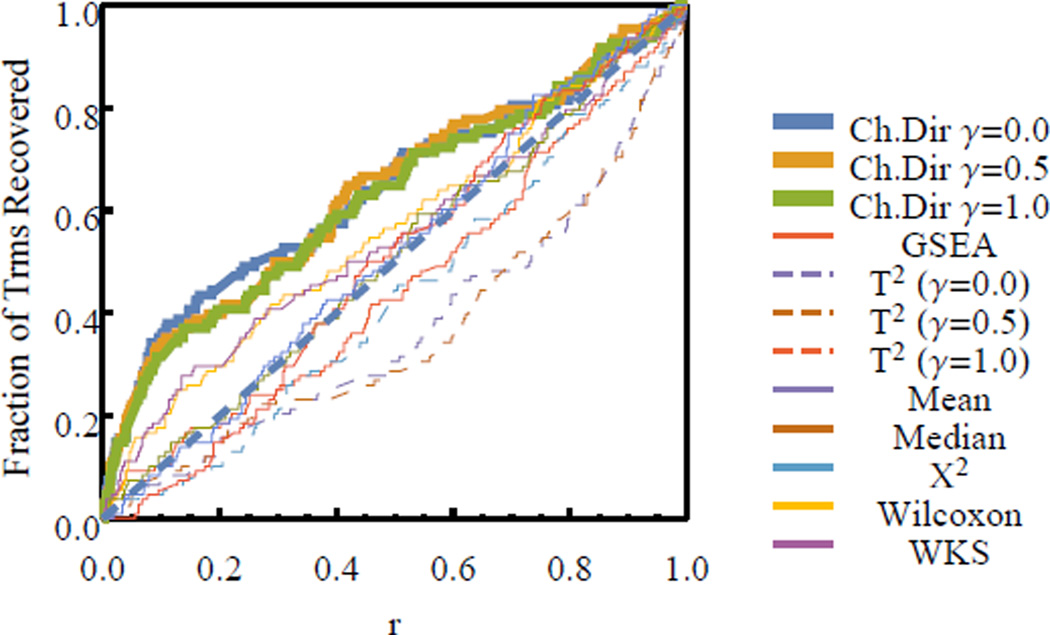
We plot the cumulative distribution of the ranks of the standard gene sets, S, corresponding to the perturbed TF for each of the applied gene set enrichment analysis methods in Fig. 1. It is clear that the PAEA method prioritizes the gene sets associated with the perturbed TF higher than all other methods with the possible exception of the mean and median gene set statistics. The significance of this difference is estimated for each pair-wise comparison by the Kolmogorov-Smirnov test Table I. We note that the closest competing methods to PAEA are the mean and median gene set statistic methods, where the significance of the difference is at 3% and 6% level of confidence for the case of the shrinkage parameter set to γ = 0.5 as described in section II-A. The difference between the remaining methods is significant to at least the 0.3% level of confidence (Kolmogorov-Smirnov). We also note that PAEA outperforms the other multivariate enrichment method, Hoteling T² and one of the most popular methods, GSEA.

Fig. 1.

Benchmarking PAEA using TF perturbations and a ChIP-Seq DNA binding gene set library. The cumulative distribution of the ranks of the standard gene sets are shown (0 corresponds to the most highly ranked and 1 to the lowest ranked gene set).

TABLE I.

Testing the statistical significance of the difference between the cumulative distributions of the standard gene sets. Each meachod is pair-wise compared to all others with the Kolmogorov-Smirnov test. Table elements display the p p values.

	PA (γ = 0.5)	GSEA	T2(γ = 0.5)	Mean	Median	χ2	Wilcoxon	WKS
PA (γ=0.5)	1	0	0	0.062	0.071	0.004	0	0.002
GSEA	0	1	0.02	0.028	0.035	0.291	0.095	0.118
T2 (γ = 0.5)	0	0.016	1	0	0	0.001	0	0
Mean	0.065	0.031	0	1	0.707	0.179	0.028	0.194
Median	0.054	0.033	0	0.723	1	0.168	0.003	0.136
X2	0.002	0.298	0.001	0.153	0.152	1	0.585	0.379
Wilcoxon	0	0.092	0	0.021	0.005	0.588	1	0.709
WKS	0	0.132	0	0.177	0.137	0.375	0.74	1

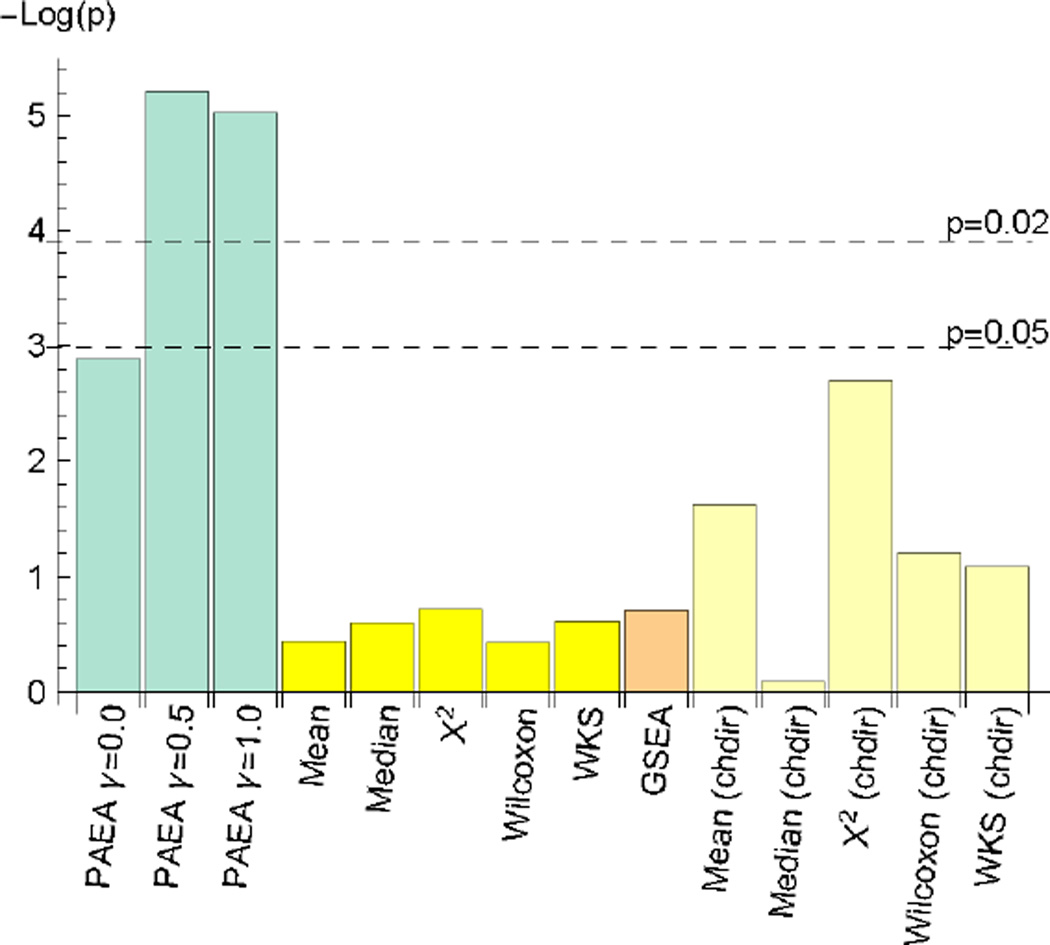
In order to determine if PAEA’s performance advantage derives solely from the use of the Characteristic Direction to prioritize the differentially expressed genes, we analyzed the data using the Characteristic Direction as the gene-level statistic in conjunction with the comparison gene set level statistics (χ², mean p value, etc.) using all other enrichment methods. We calculated the significance of the difference of the cumulative distribution of the ranking of the standard sets S from a uniformly random distribution using the Kolmogorov-Smirnov statistic and compared across all the methods, see Fig. 2. The results indicate that the principal angle measure is an important factor in the performance of PAEA.

Fig. 2.

Performace comparison between all methods as measured by the negative logarithm of the Kolmagorov-Smirnov test p value for the significance of the difference of the cumulative rank distribution from a uniform distribution. The highest and lowest ranked gene sets have the rank value of 0 and 1 respectively.

B. Benchmarking PAEA using data from gene set analysis of Aging

We collected eight experiments from GEO [13]–[15] (listed in Table II) in which aging was the primary independent variable differentiating two classes of samples. For example in experiment, GDS156 [16], gene expression in vastus lateralis skeletal muscle biopsies in healthy young (21–31 year old) and older (62–77 year old) men are compared. We then analyzed gene set enrichment of this data using a gene set library created from the Mouse Genome Informatics (MGI) mouse phenotype ontology. This gene set library consists of a collection of 476 mouse phenotypes and a set of genes which are known to cause each phenotype when knocked out in mice. All of the eight experiments from GEO were applied to human samples so the MGI phenotype genes were converted to their human orthologs using Homologene [17]. We then manually identified a subset of ten MGI mouse phenotypes which are aging-related; these are as follows:

MP0008995	Early Reproductive Senescence
MP0008770	Decreased survivor rate
MP0002081	Perinatal lethality
MP0002080	Prenatal lethality
MP0002083	Postnatal lethality
MP0003786	Premature aging
MP0010770	Preweaning lethality
MP0001661	Extended life span
MP0010779	Abnormal survival
MP0010768	Mortality/aging

TABLE II.

A sample of the MGI Mouse phenotype gene set library

Phenotype	# of Genes	Genes
Anophthalmia	59	PAX6, OTX2, HESX1, …
Amyloidosis	42	CTSL, RELB, IL2, MME, …
Aneurism	27	NTF3, HSPG2, RUNX1, MPG, …
Seizures	325	SOX1, ALPL, SZS1, …
Catelepsy	11	HPIC2, DRD2, ABCB1A, …

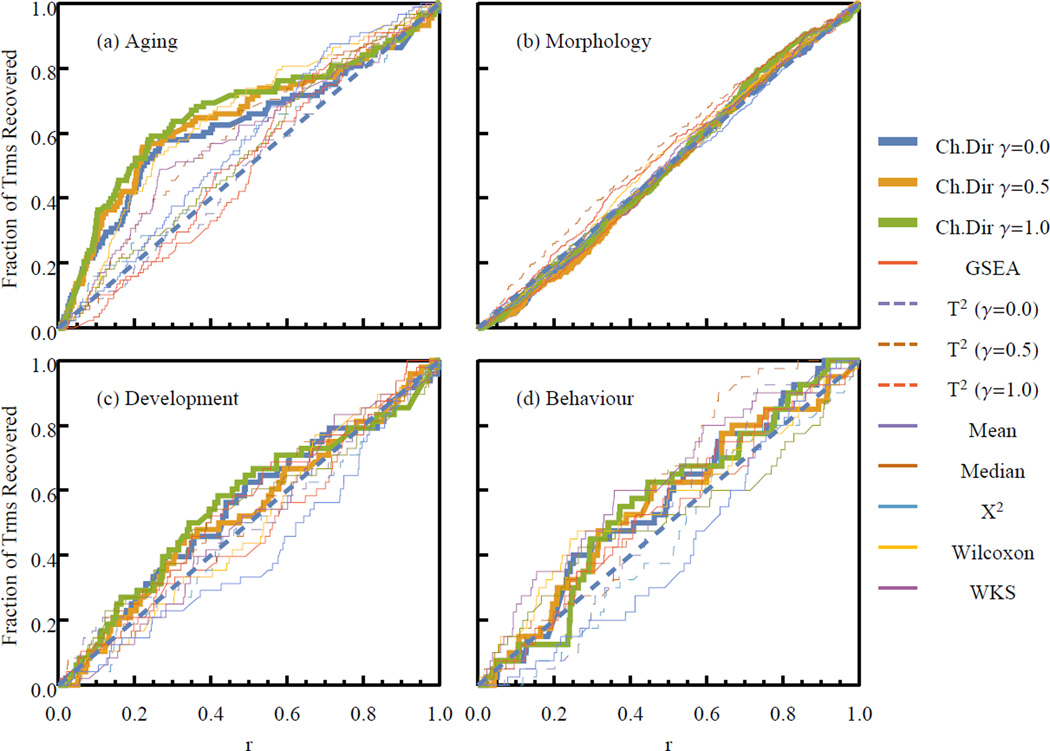
We plot the cumulative distributions of the rankings of mouse phenotype aging related terms for each of the applied analysis methods in Fig.3a. For comparison, in Fig. 3(b–d), we also plot the cumulative distributions for terms associated with Morphology, Development, and Behavior, which are processes we expect to be insignificant. PAEA prioritizes aging terms to a significantly greater degree than the other methods, while all the methods agree that Morphology, Development, and Behavior are irrelevant. The methods that are closest in performance to PAEA are again the mean and median gene set statistics. However with γ = 0.5 the PAEA method significantly prioritizes the aging related gene sets more highly than the other methods at the 1% level of significance (Kolmogorov-Smirnov test).

Fig. 3.

Benchmarking PAEA using data from gene-set analysis of Aging. The cumulative distribution of the ranks of gene set belonging to four biological categories.

IV. The PAEA Shiny R web-based application

The PAEA Shiny web application enables users to analyze and interpret gene/protein expression data by performing Characteristic Direction analysis for computing differential expression, and then PAEA analysis for computing enrichment against 70 gene set libraries. The PAEA Shiny web application also provides canned analysis of over 700 disease signatures which are preloaded and piped to PAEA to find enriched biological terms for the disease signatures.

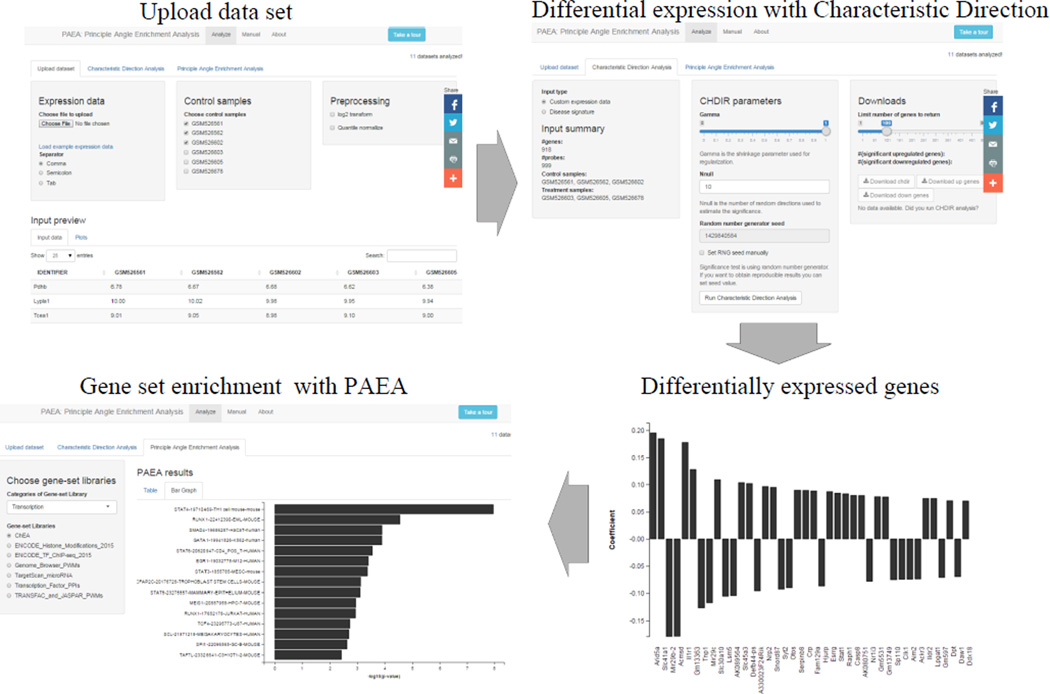
The user interface of the PAEA web application starts by requiring users to upload their expression data tables with genes as the rows and samples as columns. The gene expression data files can be delimited by comma, semicolon or tab. An example gene expression data file is provided to demonstrate to users the desired data format. Once the data is uploaded, users can preview the data and check the overall quality of the data by examining the expression density plot. The application also provides functions to perform log2 transformation and quantile normalization on the uploaded data. Users are required to choose the control and treatment samples before performing the Characteristic Direction analysis for determining differential expression (Fig. 4).

Fig. 4.

Screenshots from the PAEA web-application showing the pipeline for execution of the analysis. The data set is defined using the upload tab. Parameters can be set for the differential gene expression analysis with the Characteristic Direction Analysis tab. The gene-level differential exprsssion results are visualized and exported. Finally, the PAEA gene set analysis parameters are set and the results displayd in the Principal Angle Enrichment Analysis tab.

The Characteristic Direction analysis tab contains widgets and visualization tools for users to perform the Characteristic Direction analysis on their custom data as well as for loading canned and processed disease signatures. The parameters for the Characteristic Direction analysis include: the regularization parameter gamma, a number between 0 and 1 which specifies the degree shrinkage applied to the covariance matrix. The N_null parameter specifies the number of samples in the null distribution for assessing the significance of the components of the Characteristic Direction; and the random number seed needed for generating the null distribution vectors. Users also have the control to select the number of differentially expressed genes the program returns (Fig. 4). After performing the Characteristic Direction analysis or loading a disease signature, the top 40 differentially expressed genes (DEGs) and their Characteristic Direction coefficients are visualized with a bar chart (Fig. 4). The DEGs are also made available for download so they can be analyzed by different programs. The analysis under the PAEA tab enables users to perform PAEA enrichment analyses against 70 gene set libraries divided into several categories: transcription, pathways, ontologies, diseases/drugs, cell types and miscellaneous. Once the user selects a gene set library, PAEA is automatically performing the enrichment and the results are stored in a new session for the user. Enriched biological terms are displayed in a sortable, searchable table and as an interactive bar graph (Fig. 4). The PAEA web application provides an interactive guided tour demonstrating to new users the entire analysis process. The web application has a user manual that describes in details the various features of the software through two case studies.

A. Implementation of the PAEA R Shiny Application

The PAEA R Shiny application is web-based interactive application developed using the R Shiny web development library [18]. PAEA is deployed on an OpenSUSE Linux server with a running Shiny Server. The web application consists of a back-end and a front-end. Both ends are primarily written in R. On the front-end, the R scripts are compiled to HTML DOMs including widgets that help take input data and options from users, as well as data visualization widgets using the ggvis R library which bridges the visualization between R and the JavaScript library, Data Driven Documents (D3) [19]. On the back end, the application uses the dplyr and tidyr R libraries for data preprocessing, for example, transforming the user input to a format that is compatible with the required input format for the GeoDE R library available on CRAN. The GeoDE open source R library implements the PAEA and signatures were collected as part of a crowdsourcing project we conducted in early 2015. The disease signatures were identified manually from GEO datasets and these were reprocessed using the GEO2Enrichr tool [20] to compute differential expression signatures with all the measured genes using the Characteristic Direction method. The gene set libraries used in the PAEA web application are borrowed from Enrichr [21] by directly accessing the Enrichr database.

V. Conclusion

Here we present the first benchmarking results for Principal Anlge Enrichment Analysis method, a dimensionality reduced multivariate approach to gene set enrichment. We devised two approaches to benchmark gene set enrichment in the context of real, as opposed to synthetic data. We find that PAEA outperforms other popular gene set enrichment analysis methods. With PAEA we found a significantly greater degree of apparent consistency between differential gene expression data and ChIP-Seq DNA binding data. Furthermore, comparisons were made in the context of [13]–[16] in which age was the primary independent variable between two classes of microarray samples, and the gene set enrichment analysis was performed against a gene set library created from the MGI mouse phenotype ontology. We found that PAEA identified phenotypes associated with aging in the differential expression to a significantly greater degree than other enrichment analysis methods. While these benchmarking results are encouraging, more studies are needed to make such observations conclusive.

Implementation of the PAEA method is provided as open source free web-based application coded using the R library Shiny. The application enables users to first identify differentially expressed genes using the Characteristic Direction method, and then perform gene set enrichment analysis with PAEA against 70 gene set libraries. Canned analysis of over 700 gene expression signatures extracted manually from studies where disease tissue is compared to normal tissue is provided within the web application. The PAEA R Shiny web-based application available at: http://amp.pharm.mssm.edu/PAEA utilizes the open source R package we developed called GeoDE available within the CRAN repository at: http://cran.r-project.org/web/packages/GeoDE/index.html. This library provides an R implementation of the Characteristic Direction and the PAEA methods.

In summary, accurate and insightful downstream enrichment analysis of differentially expressed genes and proteins is a fundamental data integration strategy for better extracting knowledge from genome-wide expression profiling. PAEA will provide an improvement upon current approaches. PAEA is not only conceptually appealing, by giving a visualizable geometrical formulation to the problem of gene set enrichment, but is also practical to run as a web-service.