Abstract
Introduction
Although accurate diagnosis of deficit of mild intensity is critical, various methods are used to assess, dichotomize and integrate performance, with no validated gold standard. This study described and validated a framework for the analysis of cognitive performance.
Methods
This study was performed by using the GREFEX database (724 controls and 461 patients) examined by 7 tests assessing executive functions. The first phase determined the criteria for the cutoff scores, the second phase, the effect of test number on diagnostic accuracy and the third phase, the best methods for combining test scores into an overall summary score. Four validation criteria were used: determination of impaired performance as compared to expected one, false-positive rate ≤5%, detection of both single and multiple impairments with optimal sensitivity.
Results
The procedure based on 5th percentile cutoffs determined from standardized residuals was the most appropriate procedure. Although AUC increased with the number of scores (p=.0001), the false-positive rate also increased (p=.0001), resulting in suboptimal sensitivity for detecting selective impairment. Two overall summary scores, the average of the seven process scores and the IRT score, had significantly (p=.0001) higher AUCs, even for patients with a selective impairment, and provided higher resulting prevalence of dysexecutive disorders (p=.0001).
Conclusions
The present study provides and validates a generative framework for the interpretation of cognitive data. Two overall summary score met all 3 validation criteria. A practical consequence is the need to profoundly modify the analysis and interpretation of cognitive assessments for both routine use and clinical research.
Keywords: executive functions, mild cognitive impairment, dementia, stroke, sensitivity and specificity, diagnostic accuracy
1. Introduction
Given the importance of cognition in contemporary societies and its impact on health, accurate diagnosis of cognitive ability is critical. Cognitive ability is typically assessed in subjects from heterogeneous backgrounds, using a battery of cognitive tests covering language, visuospatial, memory, executive and general cognitive domains. Each test yields between 1 and 15 performance scores, which are dichotomized (normal vs impaired) according to norms ideally corrected as appropriate for age and education. Next, the dichotomized scores are integrated to form a clinical diagnosis. Despite major progress in this field, a survey of clinical practice in academic memory clinics and rehabilitation centers (Godefroy et al., 2004) and a review of published studies assessing preclinical (Hultsch et al., 2000; Tractenberg et al., 2011; Knopman et al., 2012; Bateman et al., 2012) and mild cognitive impairment (Winblad et al., 2004; Clark et al., 2013), dementia (Dubois et al., 2010), stroke (Tatemichi et al., 1994; Godefroy et al., 2011), cardiac surgery (Murkin et al., 1991; Moller et al., 1998), multiple sclerosis (Rao et al., 1991; Sepulcre et al., 2006) and Parkinson’s disease (Cooper et al., 1994; Dalrymple-Alford et al., 2011; Litvan et al., 2012) showed that various methods are used to assess, dichotomize and integrate performance, with no reference to a validated gold standard (Mungas et al., 1996; Miller et al., 2001; Lezak et al., 2004; Sepulcre et al., 2006; Crawford et al., 2007; Brooks et al., 2010; Dalrymple-Alford et al., 2011). Several carefully designed studies have shown that the use of different criteria for impairment dramatically influences the estimated prevalence of cognitive impairment (Sepulcre et al., 2006; Dalrymple-Alford et al., 2011; Clark et al., 2013). Most importantly, a review of these studies failed to provide a rationale for determining the best criterion in the assessment of cognitive impairment. The absence of a standardized method undermines the reliable determination of cognitive status, which in turn has a major impact on both clinical practice and clinical research. This point is especially important because the objective of cognitive assessment has shifted towards the diagnosis of deficit of mild intensity or of selective deficit.
A systematic review of previous studies, of diagnostic criteria of cognitive impairment (e.g., Winblad et al., 2004; Knopman et al., 2012; Clark et al., 2013) and of available normative data of clinical battery shows that methodology differ in three critical respects: the dichotomization of performance, the integration of several dichotomized scores, and the possible use of a global summary score. The first issue concerns the cutoff criteria used to dichotomize performance. Most cutoffs are based on means and standard deviations (SD) and use varying cutpoints from 1.5 to 1.98 SD. However, the effect of the deviation from normality of most cognitive scores is rarely addressed. Cutoff scores are sometimes based on percentiles, the 10th and 5th percentiles being the most frequently used. Second, cognitive assessment involves multiple tests, thus providing numerous scores. Procedures differ regarding the combination of tests and scores used as criterion of cognitive impairment. Some procedures consider that just one impaired test score is sufficient for classifying a subject as “impaired”, whereas others require “impaired” subjects to have at least two (or more) impaired test scores. Other procedures take into account the cognitive domain (each domain being assessed with one to several scores) and classify as impaired subjects with at least one or two or more impaired domain. In clinical practice, the interpretation is usually based on counting the number of impaired scores. Importantly, the use of multiple tests improves sensitivity but it can also artificially increase the false-positive rate (i.e. lowering the specificity) (Brooks et al., 2009), a concern especially important as the scores are often inter-correlated (Crawford et al., 2007). This well-known redundancy artifact is addressed in trials at the stage of interpretation of statistical analyses using correction for multiple analyses, such as Bonferroni correction. However, this artifact has rarely been examined in the field of test battery interpretation, which typically involves 20 to 50 performance scores (Brooks et al., 2009; Godefroy et al., 2010). Thus, there is currently no rationale for determining the optimal number of tests/scores for diagnostic accuracy (i.e. both sensitivity and specificity). Third, some trials have combined individual test scores into a global summary score. Various types of summary scores have been used: the number of impaired scores, the number of impaired domains, the mean scores for the various cognitive domains (e.g. language, visuospatial, memory, executive functions) and global scores (e.g. average of all cognitive scores after conversion of raw scores into a common metric, such as a z score). However, the influence of the use of a global summary score on diagnostic accuracy (and particularly its ability to detect a selective impairment) has not previously been analyzed. This review emphasizes the importance of examining the effects of various procedures and criteria on diagnostic accuracy and providing a rationale for optimization of these procedures and criteria.
The objective of this study, based on Standards for Reporting of Diagnostic Accuracy (STARD) guidelines (Bossuyt et al., 2003), was to describe the structure and to validate a framework for the analysis and integration of cognitive performance which provides optimal diagnosis accuracy (i.e. both sensitivity and specificity).
2. Methods
2.1 Population
This study was performed using the Groupe de Réflexion sur L’Evaluation des Fonctions EXécutives (GREFEX) database, which assessed executive functions in French-speaking participants (Godefroy et al., 2010). Briefly, the study included 724 controls (mean± SD age: 49.5± 19.8; males: 44%; educational level: primary: 22%; secondary: 34%; higher: 44%) and a group of 461 patients (age: 50.4± 19.4; males: 54%; educational level: primary: 28%; secondary: 40%; higher: 32%) presenting various diseases representative of clinical practice (stroke: n=152, traumatic brain injury: n=112, Alzheimer’s disease: n=73, Mild Cognitive Impairment: n=18, Parkinson’s disease: n=45, multiple sclerosis: n=50, tumor: n=6 and Huntington’s disease: n=5). The study has been approved by institutional review board. Subjects were examined using 7 tests of executive functions, providing a total of 19 scores (Table 1). The complete Cognitive Dysexecutive Battery has been previously detailed (Godefroy et al., 2010) and is briefly presented. It used a French adaptation of seven tests: Trail Making test (Reitan, 1958), Stroop test (Stroop, 1935), Modified Card Sorting test (Nelson, 1976), verbal fluency test (animals and words beginning by letter F in 2 minutes) (Cardebat et al., 1990), Six Elements task (Shallice and Burgess, 1991), Brixton test (Burgess and Shallice, 1996) and a paper and pencil version of the Dual task test (Baddeley et al., 1985). The Six Elements task (Shallice and Burgess, 1991) is a planning test that assesses the ability to time-manage. It consists of 3 simple tasks (picture naming, arithmetic and dictation) repeated once (thus providing 6 elements in all), for which subjects have limited time and have to obey to switching rule. The score is based on the number of tasks attempted with respect to rules. The Brixton test (Burgess and Shallice, 1996) is a rule deduction task where the participant is presented with successive cards, each card displaying 10 circles, one of them being filled. The filled circle moves from one card to the other according to rules (n=9) that have to be found. The score is the number of error. In patients where time-constraint or fatigability precluded the use of the complete battery, investigators were asked to present tests in the following order: verbal fluency, Stroop, Trail Making test, Modified Card Sorting, Dual task, Brixton task and Six Elements task. To be considered as dysexecutive, the disorder should not be more readily explained by perceptuomotor or other cognitive (language, memory, visuospatial) disturbances (Godefroy, 2003). Raw scores have been reported in a previous study (Godefroy et al., 2010) which validates criteria of dysexecutive syndrome using two external criteria, the subject status (patient vs. control) and the disability status (patient with vs. without autonomy loss).
Table 1.
Scores in the battery of executive tests and their combination into 7 executive process scores.
| Tests | 19 scores | Process scores | |
|---|---|---|---|
|
| |||
| Stroop | naming | Time, Error | Initiation1 |
|
|
|||
| reading | Time, Error | Initiation1 | |
|
|
|||
| interference | Time, Error | Inhibition2 | |
|
| |||
| Trail Making | part A | Time, Error | Initiation1 |
|
|
|||
| part B | Time, Error, perseveration | Flexibility3 | |
|
| |||
| Verbal fluency (categorical, letter) | Correct response | Generation4 | |
|
| |||
| Modified Card Sorting | Category | Deduction6 | |
|
| |||
| Error, perseveration | Flexibility3 | ||
|
| |||
| Dual task | Mu | Coordination6 | |
|
| |||
| Brixton | Error | Deduction6 | |
|
| |||
| Six elements | Rank | Planning8 | |
initiation: average of the z scores corresponding to the completion time (corrected for the error rate in each test) in the Trail Making test A and Stroop naming and reading subtests;
inhibition: errors in the interference subtest - errors in the naming subtest of the Stroop test;
flexibility: average of the z scores corresponding to perseveration in the Card Sorting and Trail Making test B;
generation: average of the z scores corresponding to the two fluency tests;
deduction: average of the z scores corresponding to categories achieved in the Card Sorting test and errors in the Brixton test;
coordination: the z scores corresponding to the mu dual task index;
planning: the z scores corresponding to the six elements task (Godefroy et al., 2010).
2.2 Data analysis and statistics
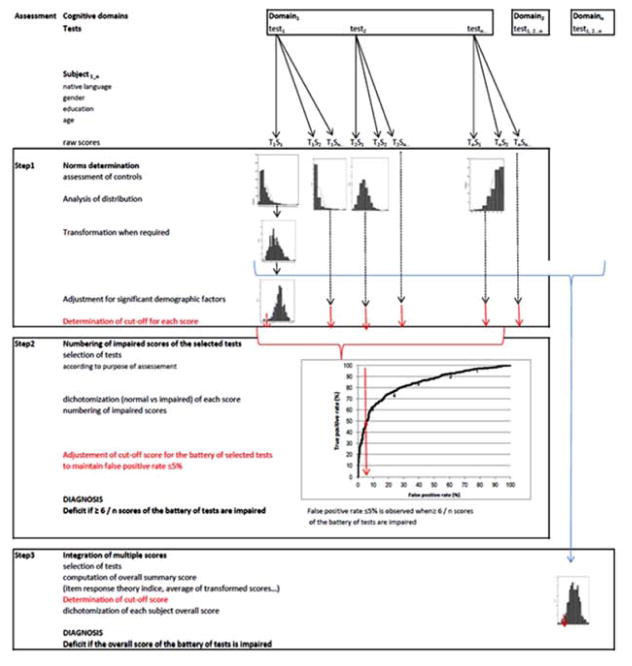
Our overall procedure comprised three phases (Figure 1). The first phase determined the criteria for the cut-off scores used to dichotomize performance (i.e. normal vs. impaired), while controlling for the effects of demographic factors and the variables’ distributions. The second phase determined the effect of the number of tests (and thus the number of scores) on diagnostic accuracy. The third phase examined the integration of multiple scores - which are often inter-correlated (Brooks et al., 2010) - and determined the best methods for combining individual test scores into an overall summary score. Our methodological approach is based on four basic premises which were used as validation criteria: the overall procedure should (1) be able to determine whether a subject’s current performance is worse than that expected on the basis of demographic factors, (2) have a false-positive rate ≤5% and detect both (3) single and (4) multiple impairments with optimal sensitivity. In the absence of a “gold standard”, the choice of a false-positive rate ≤5% was based on two considerations: 5% is frequently used as the upper bound in medical metrology and accurate determination of cut-off scores below the 5th percentile requires a very large sample size. The optimal methods were examined with respect to their accuracy of diagnosis of brain disease (Godefroy et al., 2010).
Figure 1.
The three process phases used to interpret the raw scores obtained in battery of cognitive tests.
Raw scores are obtained on a battery of tests. The first phase determines the cutoff scores used to dichotomize performance while controlling for the effects of demographic factors and the variables’ distributions. The second phase represents the common method based on numbering of impaired scores: it determines the effect of the number of tests (and thus the number of scores) on diagnostic accuracy following selection of tests. The third phase combines individual test scores into an overall summary score and determines its cutoff. Cutoff scores used for the diagnosis of deficit of an individual are represented at each phase in red color.
2.2.1
The first phase concerned the determination of the cutoff scores used to dichotomize performance (i.e. normal vs. impaired). It required us to examine the statistical characteristics of the distribution of all the scores produced by control subjects, apply appropriate transformations (Box and Cox, 1964), assess and control for the effect of demographic factors and determine the appropriate method of cutoff determination. The distributions of scores obtained by controls (n=724) were tested for normality using plot inspection and kurtosis, skewness and Shapiro-Wilk tests. Scores deviating from normality were transformed using either log transformation (for the completion time in the Trail Making and Stroop tests) or Box-Cox transformation (for the other scores) (Box and Cox, 1954). Unless otherwise indicated, the mean was used as measure of center and the standard deviation (SD) was used as a measure of variability. The potential effects of age, gender and educational level on cognitive scores were examined using linear regressions. After each transformed score had been fed into a linear regression analysis with age, educational level, gender and an interaction term, only significant factors were retained. Regression coefficients computed in controls were used to calculate standardized residuals, i.e. z scores. If necessary, variables were reversed so that poor performance corresponded to a negative z score. Three cutoff scores were computed using control data: the 5th percentile and the commonly used 1.5 SD (mean − 1.5 SD) and 1.64 SD (mean −1.64 SD) cutoffs. The subjects’ scores were dichotomized (normal vs. impaired) using cutoff scores. Scores below the corresponding cutoff were considered to be impaired in the corresponding domain. The false-positive rate (i.e. the percentage of controls classified as impaired) was computed for each score.
2. 2.2
The second phase determined the combinations of scores that best discriminated between patients and controls by using a stepwise logistic regression. It also examined the effect of increasing the number of scores on sensitivity and specificity, as this issue remains largely unresolved. Following examination of the diagnostic accuracy (area under the curve (AUC), sensitivity and specificity) of each of the 19 component scores and their intercorrelations, the procedure (1) determined the combination of scores that best discriminated between patients and controls, (2) examined the effect of increasing the number of scores on sensitivity and specificity and (3) adjusted cutoffs in order to keep the false-positive rate ≤5%. The combination of scores that best discriminated between patients and controls was selected using a stepwise, logistic regression analysis with group (patients, controls) as the dependent variable and the 19 dichotomized scores as independent variables (Table 1) (see statistics). As in clinical practice, the analysis was based on counting the number of impaired scores (following dichotomization according to the procedure that had been validated in phase 1). Sensitivity, the false-positive rate, the AUC and the resulting prevalence of dysexecutive disorders were determined for each combination of scores selected at each step of the logistic regression and for the combination of 19 scores. A Monte Carlo simulation was performed using the Crawford et al. method (2007). The parameters of the simulation were the number of scores selected by the stepwise regression (n=8), their correlation matrix and the threshold level was the 5th percentile.
2.2.3
The third phase examined the integration of multiple scores and determined the best methods for combining individual test scores into an overall summary score. We calculated the diagnostic accuracy of the various summary scores that comprised multiple component scores (rather than simply counting the number of impaired scores, as performed in the previous phase) and then determined the corresponding prevalence of dysexecutive disorders. The summary scores were first computed. The large sample of controls in the GREFEX database provided process-level, and global-level reference means and SD. There were 7 process-level summary scores; these correspond to key executive processes (initiation, inhibition, coordination, generation, deduction, planning and flexibility) and have been defined previously (Godefroy et al., 2010). The 7 process summary scores were calculated by taking the average of the component z scores (Table 1). Five global-level summary scores were computed from the process scores: the number of impaired process scores, the average of the 7 process scores, an Item Response Theory (IRT) score, the intra-individual variability across scores of executive processes, and the lowest process score. The number of impaired process scores was the sum of impaired scores at the process level (from 0 to 7). The average of the 7 process scores was computed after ensuring that their respective cut-off values were similar. The 2-parameter IRT score combined scores from each of the seven tests with multidimensional IRT models using Mplus software (version 5) (Muthen et al., 1998 – 2007). These executive function indicators used a variety of response formats, including counts in a pre-specified time span (two fluency tests), completion times (Trails A and B, three Stroop subtests) and the number of errors or items completed (errors in the three Stroop subtests, errors in parts A and B of the Trail Making Test, categories and errors in the Modified Card Sorting test, the mu index in the dual task, errors in the Brixton test and the rank score in the six elements task). The scores were recoded with 10 categories (the maximum allowed by Mplus for ordinal variables), which thus avoids the need to assume that the relationship of a particular test to the IRT score is linear. The IRT models were fitted using Mplus with theta parameterization and the WLSMV estimator. The criteria for model fit were the confirmatory fit index (CFI), the Tucker Lewis Index (TLI) and the root mean squared error of approximation (RMSEA). The thresholds for excellent fit were CFI>.95, TLI >.95, and RMSEA<.05, with an RMSEA of <.08 indicating acceptable fit (Reeve et al., 2007). The final IRT model accounted for residual correlations between the Stroop times, the Modified Card Sorting Test categories and errors, and animal and literal fluency. The model fit was acceptable, with a CFI of .969, a TLI of .98 and an RMSEA of .075. The IRT score assumes that executive function is normally distributed, with a mean of zero and an SD of one. If, for each person, the difference between scores accounting for differential item function (DIF) due to age or educational level and the original score was less than the median standard error of measurement for the IRT score, then the IRT score was determined to be free of salient DIF (Crane et al., 2008). Given that the IRT score was found to be influenced by age (R2=0.267; p=0.0001) and education level (R2=0.09; p=0.0001) in controls, standardized residuals of IRT score (further referred to as the IRT score) were computed using linear regression analysis with age and education as independent variables and transformed IRT score as dependent variable.
The 2 other global scores (the individual SD and the lowest process score) were designed to detect cases with selective impairment of one process because this may be missed by a score based on averaging or counting impaired process scores. We hypothesized that detection of patients with a selective impairment of one component index (which may vary from patient to another: patient 1 may have a selective impairment of the process A, patient 2 may have a selective impairment of the process B, and so on) might be more sensitive when based on the individual SD (which reflects the dispersion around the subject’s own mean, due to an impairment in one component index) than on the average (which is known to smooth the effect of deviation of one index among several others). The same hypothesis prompted us to examine the value of the lowest process score that has not previously been tested. The intra-individual variability across executive processes was analyzed using simply the individual SD of the 7 process scores (i.e., SD of the 7 process scores computed in each subject) as it is a relatively powerful performance summary (Tractenberg et al., 2011). Given that the individual SD was found to be influenced by age (R2=0.06; p=0.0001) and education level (R2=0.02; p=0.0001) in controls, standardized residuals of individual SD (further referred to as individual SD) were computed using linear regression analysis with age and education level as independent variables and transformed individual SD as dependent variable. The lowest process score was the lowest score of the 7 process scores. The cutoff of each global score was determined using the 5th percentile computed in controls. Each overall summary score was dichotomized by a cutoff determined using the controls’ 5th percentile values (as validated in phase 1). Sensitivity, the false-positive rate, the AUC and the resulting prevalence of dysexecutive disorders were determined for each overall score.
2. 2.4 Statistical analyses
We determined whether the various procedures fulfilled the four validation criteria: (1) the ability to determine whether a subject’s current performance is worse than that expected on the basis of demographic factors, (2) a false-positive rate ≤5% and detection of both (3) single and (4) multiple impairments with optimal sensitivity. Given the absence of a previously validated “gold standard”, the diagnostic accuracy of various score analyses was judged according to the scores’ ability to discriminate between patients and controls (Bossuyt et al., 2003) by calculating the area under the receiver operating characteristic (ROC) curves (AUC) with the corresponding 95% confidence interval (CI), sensitivity, specificity, accuracy, positive predictive value (PPV) and negative predictive value (NPV). A false-positive rate ≤5% (i.e. specificity ≥.95) was used as a rule of thumb.
Intergroup comparisons were performed using Student’s t-test for continuous variables and Fisher’s Exact test or Chi-square test for other variables. Multicollinearity was examined by the pairwise correlation of scores computed in controls using z scores to partial out the effects of age and educational level. Furthermore, the number of Pearson correlation coefficients with an absolute value of R>.6 (usually considered as being suggestive of multicollinearity) was determined. The AUC values were compared by applying Delong et al.’s method (DeLong et al., 1988). The extended McNemar test (Hawass, 1997) was used to compare the false-positive rates and the resulting prevalence of dysexecutive disorders (indexed by the true positive rate) provided by the different methods. Unless otherwise indicated, the threshold for statistical significance was set to p ≤.05. Statistical analyses were performed using SAS software (SAS institute, Cary, NC 2006–10).
3. Results
3.1 Phase 1: determination of cutoff scores
All raw cognitive scores in controls deviated from normality (Supplementary Table 1). Most transformed scores were influenced by age, education or both. Using standardized residuals, the 5th percentile was found to provide the most appropriate cutoff point, as it is not influenced by the variation from a normal distribution. This is illustrated by cutoff scores computed from z scores at the 5th percentile level (Supplementary Table 1): most of the scores were above −1.64, which is indeed contrary to what would be expected for a Gaussian distribution. The commonly used 1.5 and 1.64 SD cutoffs resulted in significantly higher false-positive rates (p≤.05 for all comparisons). The procedure based on 5th percentile cutoffs (determined from standardized residuals of controls following the appropriate transformation of raw scores) was the only procedure that achieved a false-positive rate ≤5% (by definition).
In summary, the results of phase 1 indicated that demographic factors and the non-Gaussian distribution of most cognitive scores strongly influence the determination of cutoffs. The frequently used cutoff scores of 1.5 and 1.64 SD were found to inflate the false-positive rate. The use of 5th percentile cutoffs (determined from standardized residuals of controls following the appropriate transformation of raw scores and regression on significant demographic factors) was the only procedure that met two of our validation criteria: a false-positive rate ≤5% and the ability to detect a decline in present performance, relative to that expected on the basis of demographic factors.
3.2 Phase 2: determination of the optimal combination of scores
Each of the 19 component scores (Supplementary Table 2) yielded AUC values ranging from 0.618 to 0.497 and sensitivity values ranging from 2.3% to 30%. The scores were moderately intercorrelated, with an average Pearson R for the 171 pairs of coefficients of .144 (95%CI: .123–.165) and four (2.3%) absolute R values >.6.
The stepwise logistic regression selected 8 scores: Categorical Verbal fluency (OR: 4.64; 95%CI: 2.64–8.15; p=.00001), Stroop Reading time (OR: 4.86; 95%CI: 2.59–9.13; p=. 00001), Stroop Interference error (OR: 3.34; 95%CI: 1.76–6.36; p=.0002), Stroop Interference time (OR: 3.03; 95%CI: 1.52–6.03; p=.002), Six elements task (OR: 2.72; 95%CI: 1.58–4.70; p=.0003), Trail Making test B time (OR: 2.67; 95%CI: 1.48–4.82; p=.001), Trail Making test B error (OR: 2.83; 95%CI: 1.12–7.13; p=.03) and Brixton test error (OR: 2.39; 95%CI: 1.32–4.32; p=.004)
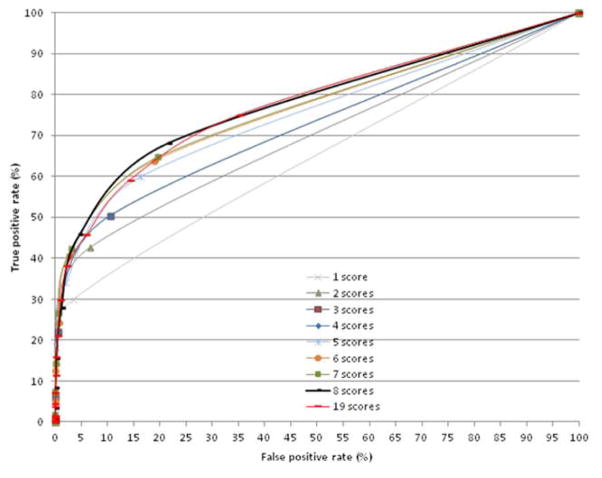
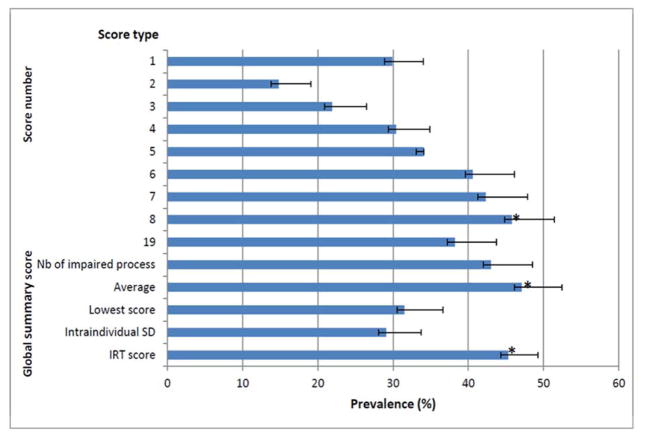
The ROC curves (computed using scores selected at each phase) showed that AUC increased with the number of scores (mean increment for each additional score: .02% increment for each additional score; R2=.9, p=.0001) (Figure 2). The AUC for the 8-score set (Table 2) was higher than those obtained with 7 scores or less (p≤.01, for all comparisons). However, the false-positive rate also increased with the number of scores in the set (mean increment for each additional score: 2.61% increment for each additional score; R2=.97, p=.0001) and reached a value of 21% in the 8-score set. To maintain a 5% false-positive rate, the criterion for the number of impaired scores had to be increased from ≥1 when using the 1-score set to ≥2 when using the 8-score set and ≥4 when using the 19-score set. The resulting determination of the prevalence of dysexecutive disorders (Figure 3) differed (p=.0001). The 8-score set yielded a higher prevalence (p=.0001 for all) than any of the other combinations - including the 19-score set.
Figure 2.
Receiver Operating Characteristic analyses as a function of the number of scores selected by the regression analysis.
Table 2.
Diagnosis accuracy according to the number of scores.
| 1 score | 2 scores | 3 scores | 4 scores | 5 scores | 6 scores | 7 scores | 8 scores | 19 scores | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||||||
| AUC (95% CI) | .632 (.597–.666) | .684 (.652–.717) | .709 (.677–.742) | .726 (.694–.757) | .741 (.711–.772) | .756 (.726–.786) | .759 (.729–.789) | .771* (.741–.799) | .772 (.743–.8) | |||||||||
|
| ||||||||||||||||||
| Impaired scores ≥ | TPR | FPR | TPR | FPR | TPR | FPR | TPR | FPR | TPR | FPR | TPR | FPR | TPR | FPR | TPR | FPR | TPR | FPR |
|
| ||||||||||||||||||
| 0 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 1 | 29.9 | 3.6 | 42.7 | 6.8 | 50.3 | 10.5 | 54.4 | 12.3 | 59.9 | 16.3 | 63.8 | 18.9 | 64.6 | 19.6 | 68.1 | 21.5 | 75 | 35 |
| 2 | .0 | .0 | 14.8 | .3 | 21.9 | .6 | 30.4 | 1.7 | 34.1 | 2.1 | 40.6 | 2.8 | 42.3 | 3.2 | 45.8 | 4.7 | 59 | 14 |
| 3 | .0 | .0 | 6.1 | .0 | 14.1 | .3 | 18.2 | .3 | 24.3 | .7 | 26.5 | .7 | 27.8 | 1.2 | 46 | 6.1 | ||
| 4 | .0 | .0 | 4.1 | .0 | 7.6 | .0 | 12.6 | .1 | 14.1 | .3 | 15.4 | .3 | 38.2 | 2.35 | ||||
|
| ||||||||||||||||||
| Sensitivity | 29.9 | 14.8 | 21.9 | 30.4 | 34.1 | 40.6 | 42.3 | 45.8 | 38.2 | |||||||||
| Specificity | 96.4 | 99.7 | 99.4 | 98.3 | 97.9 | 97.2 | 96.8 | 95.3 | 97 | |||||||||
| Accuracy | 73.9 | 66.6 | 66.6 | 68.3 | 66.9 | 67.3 | 67.5 | 67.4 | 74.6 | |||||||||
| Positive PV | 81.0 | 96.5 | 95.3 | 90.4 | 89.4 | 88.3 | 87.2 | 83.3 | 86.7 | |||||||||
| Negative PV | 72.9 | 69.5 | 71.3 | 73.4 | 74.3 | 76.1 | 76.6 | 77.4 | 75.4 | |||||||||
AUC: Area Under Curve; CI: confidence interval; TPR: True positive rate; FPR: false-positive rate; PV: predictive value. Underlined bold rates: False-positive rate ≤5% and corresponding true positive rate;
the AUC for the 8-score set was higher than those obtained with 7 scores or less (p≤.01 for all comparisons in an extended McNemar test).
Figure 3. Resulting prevalence of dysexecutive disorder using selected scores (from 1 to 8), the 19 scores of the battery (phase 2) and global summary scores (phase 3).
Results expressed as percent and 95%CI (confidence interval) *: the prevalence computed using the average of the 7 process score, IRT (item response theory) score and the 8-score set was higher (extended McNemar test, p=.0001) than that computed other overall summary scores and set-score.
The Monte Carlo simulation provided similar false-positive rate: the estimated population was 31% with ≥1 impaired score, 7% with ≥2 impaired scores, 1.3% with ≥3 impaired scores and .2% with ≥4 impaired scores. The simulation also indicated that the number of impaired scores must be ≥2 if a false-positive rate ≤5% is to be achieved.
In summary, our results indicate that the increased sensitivity achieved by combining several scores is obtained at the cost of specificity, since the false-positive rate also increases with the number of scores in the set. This major result reflects statistical laws as shown by the fact that Monte Carlo simulation yielded exactly the same findings. This suggests that in order to maintain a 5% false-positive rate, the impairment criterion have to be adjusted as a function of the number of scores in the set. The procedure for selecting the optimal combination of scores, counting the number of “impaired” scores and adjusting the impairment criterion accordingly met only two of the four validation criteria, i.e. a false-positive rate ≤5% and sensitive detection of the impairment of multiple scores. However, another major finding was that adjustment of the impairment criterion decreases sensitivity and thus the estimated prevalence of an impairment. Furthermore, this type of adjustment prevents the detection of patients with impairment in a single score - indicating that the “ability to detect a single impairment” criterion was not met. One way of circumventing this issue is the use of an overall summary score that combines the scores for several tests; this approach was explored in the third phase of the study
3.3 Phase 3: the integration of multiple cognitive scores
All process scores and all overall summary scores (Table 3) were impaired in the patient group. All summary scores had a false-positive rate ≤5%, with the exception of the number of impaired processes because 19% of the controls displayed an impairment in one or more process scores. The cutoff of ≥2 impaired process scores kept the false-positive rate below 5%.
Table 3.
Process (top) and global (bottom) scores (mean ± SD) and impairment frequency (%).
| Patients (%) | Controls | P¥ | |
|---|---|---|---|
| Process score | |||
| Initiation | −1.0 ± 1.2 (34.1)* | .1 ± .8 (4.8) | .0001 |
| Inhibition | −2.1 ± 6.8 (22.2)* | .0 ± .8 (2.5) | .0001 |
| Coordination | −.4 ± 1.1 (10.7)* | .0 ± 1.0 (5.0) | .0001 |
| Generation | −.7 ± 1.1 (27.8)* | .1 ± .8 (2.4) | .0001 |
| Planning | −1.1 ± 1.6 (25)* | .0 ± 1.0 (5.0) | .0001 |
| Deduction | −.8 ± 1.5 (22)* | .1 ± 1.0 (4.4) | .0001 |
| Flexibility | −.9 ± 1.8 (26.2)* | .0 ± .8 (5.0) | .0001 |
|
| |||
| Global score | |||
| Impaired process scores (0/1/2/≥3) | −.7 ± .7 (32/ 25/ 18/ 25)* | −.3 ± .5 (76/ 19/ 3/ 2) | .0001 |
| Average | −1.0 ± 1.4 (47.3)* | .0 ± .5 (5.0) | .0001 |
| IRT score | −1.6 ± 1.4 (45.3)* | .0 ± 1.0 (5.0) | .0001 |
| Individual SD | −1.1 ± 1.4 (29)* | .0 ± 1.0 (5.0) | .0001 |
| Lowest score | −3.7 ± 5.9 (31.5)* | −1.2 ± 1.2 (4.8) | .0001 |
Fisher’s exact test p≤ .005;
t test;
IRT: Item Response Theory; SD: standard deviation Godefroy et al. 21
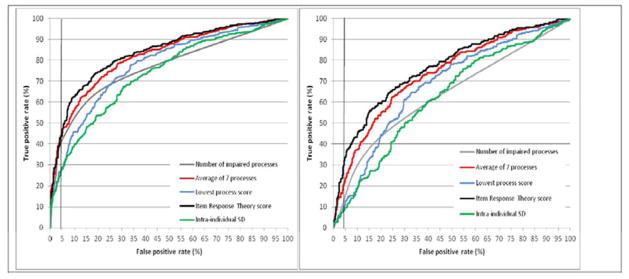
The ROC curve analysis (Figure 4a) showed that the average of the seven process scores and the IRT score had significantly higher AUCs (p=.0001 for all comparisons) than all summary scores other than the lowest process score. This influenced the resulting prevalence of dysexecutive disorders (Figure 3), which was higher (p=.0001 for all comparisons) for the average of the seven process scores, the IRT score and the 8-score set determined in the second phase.
Figure 4. Receiver operating characteristic analysis of the overall summary scores for executive processes in all subjects (4a, left) and in subjects with no more than 1 impaired executive process (4b, right).
SD: standard deviation
Impairment of one executive process was more frequent (p=.0001) in patients (114 out of 261; 44%) than in controls (139 out of 682; 20%). The ROC curve analysis (Figure 4b) showed that both the average of the 7 process scores and the IRT score had significantly higher AUCs (p=.0001 for all comparisons) than the other overall summary scores.
In summary, this analysis showed that two overall summary scores (the average of the component z scores and the IRT score) were better able to discriminate between patients and controls - even when the impairment concerned just one cognitive process. In turn, these two summary scores provided a more accurate determination of the prevalence of cognitive impairment. By integrating component scores into an overall summary score, controlling for the effect of demographic factors and determining cutoff scores according to the procedure validated in phase 1, this approach met all four validation criteria: a false-positive rate ≤5%, detection of both single and multiple impairments with high sensitivity and ability to determine whether a subject’s current performance is worse than that expected on the basis of demographic factors.
4. Discussion
This study reports on comprehensive, comparative analyses of methods of key importance in the field of cognition. Our framework provides a generative, integrated methodology for the analysis and integration of cognitive performance and yields important, practical conclusions on the assessment of cognitive ability in both clinical practice and research. Although several studies have previously addressed each of the three above-described phases separately, there has been no assessment or validation of the whole processes required to interpret and integrate the raw scores obtained in batteries of cognitive tests. This framework also validates the integrative processes required to interpret the raw scores obtained in batteries of cognitive tests by controlling for confounding factors and providing optimal diagnostic accuracy for all types of impairment (including selective impairments). This study addresses the methodology of performance analysis and is not aimed at determining the optimal battery for the diagnosis of a given disease, which would be nonsensical in view of the range of diseases present in the patient group. Thus, sensitivity and accuracy values are only given as a means of comparing the results provided by various methods of performance analysis.
One of the present study’s major findings is that the analyses and interpretations of cognitive scores commonly performed in routine clinical practice and research settings are not based on valid methods. These analyses and interpretations tend to inflate the false-positive rate, which has major consequences for both clinical practice and research. Here, the false-positive rate refers to the proportion of healthy controls with impaired performance, regardless of the mechanism. It does not directly address the reasons for false-positive errors (such as malingering), in contrast to some statistical analysis of intra-individual variability (Larrabee, 2012). Even when a given procedure had a false-positive rate below 5%, we found that the use of differing methods to analyze cognitive data has a major impact on sensitivity and therefore biases estimation of the prevalence of cognitive disorders, with as much as a three-fold difference between one procedure and another. This wide observed range of prevalence values emphasizes the urgent need for a standardized method for detecting cognitive impairment in both clinical practice and research.
A key output of this study is its generative methodology, which may be useful for all neuropsychological assessments that integrate raw performance data and interpret a subject’s cognitive ability. Our methodology provides a basis for standardizing the analysis of cognitive performance. The first phase determines cut-off scores. Our results indicated that demographic factors and the non-Gaussian distribution of most cognitive scores strongly influence the determination of cut-off scores. The frequently used cut-off scores of 1.5 and 1.64 SD were found to inflate the false-positive rate. The present procedure combines score transformation, a check for significant demographic factors (using standardized residuals) and the determination of cut-off scores based on the 5th percentile, it therefore satisfactorily addresses this major issue. Likewise, use of percentiles is preferable when operationalizing diagnostic criteria for cognitive impairment. The second phase addresses the trade-off between sensitivity and specificity as a function of the number of tests. The combination of tests previously selected according to a controlled procedure does improve sensitivity but also dramatically increases the false-positive rate. This outcome was also observed in Monte Carlo simulations in the present study and in previous studies (Crawford et al., 2007). Consequently, there is a need to check that the false-positive rate has not been inflated, which requires the integration of component scores.
The third phase deals with the integration of component scores. When the outcome measure is based on the number of “impaired” scores (as in clinical practice), the “number of impairments” criterion should be adjusted according to the number of tests. However, this adjustment decreases sensitivity, prevents the detection of selective impairments and thus argues in favor of the use of an overall summary score. We found that two overall summary scores (derived from either an average z-score or an IRT analysis) were better able to discriminate between patients and controls - even when the impairment concerned only one cognitive process. This was unexpected and contrasts with the common view in which global assessment (such as that performed with the Wechsler Adult Intelligence Scale, for example) is likely to miss selective impairment. Furthermore, our results showed that the best sensitivity is obtained using a global summary score based on tests selected for the assessment of a specific disease. Interestingly, the individual SD (which detects dispersion across tests (Hultsch et al., 2000; Tractenberg et al., 2011)) and the lowest process summary scores were not the best parameters for detecting selective impairment whereas they were designed to detect such situation. Very few studies have shown that the individual’s SD varies with the overall severity of cognitive impairment, with higher individual SD at mild levels of impairment (Hill et al., 2013) and lower individual SD in severe impairment, close to that of normal controls (Reckess et al., 2013). It remains to be determined whether the individual SD and the lowest process summary scores may be useful in detecting selective impairment in some specific situations. The choice of global summary score to be used is likely to depend on statistical characteristics of performance scores. The average z-score is easy to compute and is frequently used. However, we observed that it is very sensitive to deviation from normal distribution and to differences in the cut-off values of the component scores (e.g., 5% cutoff of score1=1.2, 5% cutoff of score2=2.5…). An IRT score requires more complex computation and it has the advantage of avoiding the assumption that each test is equally difficult, as the difficulty of each item is incorporated in scaling items. The use of IRT assumes that tests (or inventory) assess a unidimensional latent trait. The assumption of unidimensionality often does not hold in neuropsychology as cognitive domains include multiple modules and levels of information that are separable. The development of a multidimensional extension of standard IRT (Kelderman et al., 1994; Adams et al., 1997; Hoijtink et al., 1999; Briggs et al., 2003) has partly addressed this difficulty, although it remains a concern.
Overall, our study results show that the best sensitivity is obtained using a global summary score based on tests selected for the assessment of a specific disease. This finding indicates that domain-specific impairment can be investigated after impairment of a global summary score has been detected. In routine practice, few cognitive batteries (Wechsler, 1944; Reitan et al., 1993; Randolph, 1998; Jurica et al., 2001) are based on a global summary score. Miller and Rohling (2001) have suggested a method for interpreting multiple cognitive scores obtained in an individual patient. It shares some features with our present approach, such as the conversion of raw scores into a common metric (the T score), the use of summary scores (based on averaging T scores within each domain) and the interpretation of summary scores based on statistical probabilities. Although this approach certainly improves the interpretation of deviating scores and selective impairment, it does not address the three phases as in the present study.
Our study has several limitations. The study population is heterogeneous and thus differs from that found in diagnostic accuracy studies that seek to determine the sensitivity and specificity of a test for a given disease. We purposely included patients with different diseases, in order to decrease colinearity between scores (a single pattern of impairments artificially increases colinearity). This is critical for the validity of the study results, since the false-positive rate increases with intercorrelation between scores (Crawford et al., 2007). The fact that we analyzed data on executive function raises the issue of whether our conclusions can be generalized to other cognitive domains. The characteristics of cognitive scores may vary according to (1) the cognitive domain assessed by the test battery, (2) correlations between tests and (3) the frequency of selective impairment. However, previous studies were confronted with similar characteristics and difficulties when analyzing neuropsychological data in the domain of language (Godefroy et al., 1994; Godefroy et al., 2002), working memory (Roussel et al., 2012), attention (Godefroy et al., 1994b; Godefroy et al., 1996) and episodic memory (Godefroy et al., 2009). This feature has also been observed for battery of tests covering multiple domains (Tatemichi et al., 1994a; Godefroy et al., 2011; Mungas et al., 1996) and was found to have major influence on the resulting prevalence of Mild Cognitive Impairment (diagnosed using the conventional criterion of one test score <1.5 SD below normal) (Clark et al., 2013) and mild cognitive deficit in multiple sclerosis (Sepulcre et al., 2006) and Parkinson disease (Dalrymple-Alford et al., 2011).
The generative methodology proposed here is relevant for all types of neuropsychological assessment and may provide a basis for the adoption of common procedures and the operationalization of criteria for cognitive impairment. Our study also provides a rationale for calculation of sample sizes of normative populations, defined here as the size required to provide a 95%CI of 5th percentile below a given value. Our findings may well indicate a need for extension of the STARD statement (Bossuyt et al., 2003), which does not address this major methodological issue.
Supplementary Material
Supplementary Table 1. Distribution characteristics of 11 raw scores (upper part), the effect of demographic factors on transformed scores (middle part), values of cut-off scores at the 5th percentile and false-positive rates using the 1.5 and 1.64 SD cut-offs (lower part).
Supplementary Table 2. The sensitivity, false-positive rate (FPR) and area under the curve (AUC) (95% confidence interval (CI)) for the 19 individual scores (ranked by decreasing sensitivity).
Supplementary Table 3. The area under the curve (AUC) and 95% confidence interval (CI) obtained using the seven process scores and the overall scores in the overall population (left) and using the overall scores in the subgroup with no more than one impairment of a process score (right).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adams RJ, Wilson Mark, Wang Wen-chung. The Multidimensional Random Coefficients Multinomial Logit Model. Appl Psych Meas. 1997;21:1–23. [Google Scholar]
- Baddeley AD, Logie RH, Bressi S, Della Sala S, Spinnler H. Dementia and working memory. Quart J Exp Psychol. 1986;38A:603–618. doi: 10.1080/14640748608401616. [DOI] [PubMed] [Google Scholar]
- Bateman RJ, Xiong C, Benzinger TL, Fagan AM, Goate A, Fox NC, Marcus DS, Cairns NJ, Xie X, Blazey TM, Holtzman DM, Santacruz A, Buckles V, Oliver A, Moulder K, Aisen PS, Ghetti B, Klunk WE, McDade E, Martins RN, Masters CL, Mayeux R, Ringman JM, Rossor MN, Schofield PR, Sperling RA, Salloway S, Morris JC Dominantly Inherited Alzheimer Network. Clinical and biomarker changes in dominantly inherited Alzheimer’s disease. N Engl J Med. 2012;367:795–804. doi: 10.1056/NEJMoa1202753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bossuyt PM, Reitsma JB, Bruns DE, Gatsonis CA, Glasziou PP, Irwig LM, Lijmer JG, Moher D, Rennie D, de Vet HC. Standards for Reporting of Diagnostic Accuracy. Towards complete and accurate reporting of studies of diagnostic accuracy: the STARD initiative. BMJ. 2003;326:41–4. doi: 10.1136/bmj.326.7379.41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Box GEP, Cox DR. An analysis of transformations. J R Stat Soc B. 1964;26:211–252. [Google Scholar]
- Briggs DC, Wilson M. An Introduction to Multidimensional Measurement using Rasch Models. J Appl Meas. 2003;4:87–100. [PubMed] [Google Scholar]
- Brooks BL, Iverson GL. Comparing Actual to Estimated Base Rates of “Abnormal” Scores on Neuropsychological Test Batteries: Implications for Interpretation. Arch Clin Neuropsych. 2010;25:14–21. doi: 10.1093/arclin/acp100. [DOI] [PubMed] [Google Scholar]
- Burgess PW, Shallice T. Bizarre responses, rule detection and frontal lobe lesions. Cortex. 1996;32:241–259. doi: 10.1016/s0010-9452(96)80049-9. [DOI] [PubMed] [Google Scholar]
- Cardebat D, Doyon B, Puel M, Goulet P, Joanette Y. Évocation lexicale formelle et sémantique chez des sujets normaux: Performances et dynamiques de production en fonction du sexe, de l’âge et du niveau d’étude. Acta Neurol Belg. 1990;90:207–217. [PubMed] [Google Scholar]
- Clark LR, Delano-Wood L, Libon DJ, McDonald CR, Nation DA, Bangen KJ, Jak AJ, Au R, Salmon DP, Bondi MW. Are empirically-derived subtypes of mild cognitive impairment consistent with conventional subtypes? J Int Neuropsychol Soc. 2013;19:635–45. doi: 10.1017/S1355617713000313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper JA, Sagar HJ, Tidswell P, Jordan N. Slowed central processing in simple and go/no-go reaction time tasks in Parkinson’s disease. Brain. 1994;117:517–29. doi: 10.1093/brain/117.3.517. [DOI] [PubMed] [Google Scholar]
- Crane PK, Narasimhalu K. Composite scores for executive function items: demographic heterogeneity and relationships with quantitative magnetic resonance imaging. J Int Neuropsychol Soc. 2008;14:746–759. doi: 10.1017/S1355617708081162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crawford JR, Garthwaite CH, Gault CB. Estimating the percentage of the Population with abnormally low scores (or Abnormally Large Score Differences) on Standardized Neuropsychological Test Batteries: A generic method with applications. Neuropsychology. 2007;21:419–430. doi: 10.1037/0894-4105.21.4.419. [DOI] [PubMed] [Google Scholar]
- Dalrymple-Alford JC, Livingston L, MacAskill MR, Graham C, Melzer TR, Porter RJ, Watts R, Anderson TJ. Characterizing mild cognitive impairment in Parkinson’s disease. Mov Disord. 2011;26:629–36. doi: 10.1002/mds.23592. [DOI] [PubMed] [Google Scholar]
- DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics. 1988;44:837–45. [PubMed] [Google Scholar]
- Dubois B, Feldman HF, Jacova C, Cummings JL, DeKosky ST, Barberger-Gateau P, Delacourte A, Frisoni G, Fox NC, Galasko D, Gauthier S, Hampel H, Jicha GA, Meguro K, O’Brien J, Pasquier F, Robert P, Rossor M, Salloway S, Sarazin M, de Souza LC, Stern Y, Visser PJ, Scheltens P. Revising the definition of Alzheimer’s disease: a new lexicon. Lancet Neurol. 2010;9:1118–27. doi: 10.1016/S1474-4422(10)70223-4. [DOI] [PubMed] [Google Scholar]
- Gibbons LE, Carle AC, Mackin RS, Harvey D, Mukherjee S, Insel P, Curtis SM, Mungas D, Crane PK Alzheimer’s Disease Neuroimaging Initiative. A composite score for executive functioning, validated in Alzheimer’s Disease Neuroimaging Initiative (ADNI) participants with baseline mild cognitive impairment. Brain Imaging Behav. 2012;6:517–27. doi: 10.1007/s11682-012-9176-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Godefroy O. Frontal syndrome and disorders of executive functions. J Neurol. 2003;250:1–6. doi: 10.1007/s00415-003-0918-2. [DOI] [PubMed] [Google Scholar]
- Godefroy O et Groupe de Réflexion sur L’Evaluation des Fonctions EXecutives. Syndromes frontaux et dysexécutifs. Rev Neurol. 2004;160:899–909. doi: 10.1016/s0035-3787(04)71071-1. [DOI] [PubMed] [Google Scholar]
- Godefroy O, Azouvi P, Robert P, Roussel M, LeGall D, Meulemans T on the behalf of the GREFEX study group. Dysexecutive syndrome: diagnostic criteria and validation study. Ann Neurol. 2010;68:855–64. doi: 10.1002/ana.22117. [DOI] [PubMed] [Google Scholar]
- Godefroy O, Rousseaux M, Pruvo JP, Cabaret M, Leys D. Neuropsychological changes related to unilateral lenticulostriate infarcts. J Neurol Neurosurg Psychiatry. 1994a;57:480–5. doi: 10.1136/jnnp.57.4.480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Godefroy O, Cabaret M, Rousseaux M. Vigilance and effects of fatigability, practice and motivation on simple reaction time tests in patients with lesion of the frontal lobe. Neuropsychologia. 1994b;32:983–90. doi: 10.1016/0028-3932(94)90047-7. [DOI] [PubMed] [Google Scholar]
- Godefroy O, Lhullier C, Rousseaux M. Non-spatial attention disorders in patients with frontal or posterior brain damage. Brain. 1996;119:191–202. doi: 10.1093/brain/119.1.191. [DOI] [PubMed] [Google Scholar]
- Godefroy O, Dubois C, Debachy B, Leclerc M, Kreisler A. Vascular aphasias: main characteristics of patients hospitalized in acute stroke units. Stroke. 2002;33:702–5. doi: 10.1161/hs0302.103653. [DOI] [PubMed] [Google Scholar]
- Godefroy O, Roussel M, Leclerc X, Leys D. Deficit of episodic memory: anatomy and related patterns in stroke patients. Eur Neurology. 2009;61:223–229. doi: 10.1159/000197107. [DOI] [PubMed] [Google Scholar]
- Godefroy O, Fickl A, Roussel M, Auribault C, Bugnicourt JM, Lamy C, Canaple S, Petitnicolas G. Is the Montreal Cognitive Assessment superior to the Mini-Mental State Examination to detect post-stroke cognitive impairment? A study with neuropsychological evaluation. Stroke. 2011;42:1712–16. doi: 10.1161/STROKEAHA.110.606277. [DOI] [PubMed] [Google Scholar]
- Hawass NED. Comparing the sensitivities and specificities of two diagnostic procedures performed on the same group of patients. Br J Radiol. 1997;70:360–6. doi: 10.1259/bjr.70.832.9166071. [DOI] [PubMed] [Google Scholar]
- Hill BD, Rohling ML, Boettcher AC, Meyers JE. Cognitive intra-individual variability has a positive association with traumatic brain injury severity and suboptimal effort. Arch Clin Neuropsychol. 2013;28:640–8. doi: 10.1093/arclin/act045. [DOI] [PubMed] [Google Scholar]
- Hoijtink H, Rooks G, Wilmink FW. Confirmatory factor analysis of items with a dichotomous response format using the multidimensional Rasch model. Psychol Methods. 1999;4:300–314. [Google Scholar]
- Hultsch DF, MacDonald SWS, Hunter MA, Levy-Bencheton J, Strauss E. Intraindividual variability in cognitive performance in older adults: comparison of adults with mild dementia, adults with arthritis, and healthy adults. Neuropsychology. 2000;14:588–598. doi: 10.1037//0894-4105.14.4.588. [DOI] [PubMed] [Google Scholar]
- Jurica PL, Leitten CL, Mattis S. Professional Manual for the Dementia Rating Scale – 2. Lutz, Florida: Psychological Assessment Resources Inc; 2001. [Google Scholar]
- Kelderman H, Rijkes C. Loglinear multidimensional IRT models for polytomously scored items. Psychometrika. 1994;59:149–176. [Google Scholar]
- Knopman DS, Jack R, Wiste HJ, Weigand SD, Vemuri P, Lowe V, Kantarci K, Gunter JL, Senjem ML, Ivnik RJ, Roberts RO, Boeve BF, Petersen RC. Short-term clinical outcomes for stages of NIA-AA preclinical Alzheimer disease. Neurology. 2012;78:1576–1582. doi: 10.1212/WNL.0b013e3182563bbe. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larrabee GJ. Performance validity and symptom validity in neuropsychological assessment. J Int Neuropsychol Soc. 2012;18:625–30. doi: 10.1017/s1355617712000240. [DOI] [PubMed] [Google Scholar]
- Lezak MD, Howieson DB, Loring DW. Neuropsychological Assessment. 4. New York (NY): Oxford University Press; 2004. [Google Scholar]
- Litvan I, Goldman JG, Tröster AI, Schmand BA, Weintraub D, Petersen RC, Mollenhauer B, Adler CH, Marder K, Williams-Gray CH, Aarsland D, Kulisevsky J, Rodriguez-Oroz MC, Burn DJ, Barker RA, Emre M. Diagnostic criteria for mild cognitive impairment in Parkinson’s disease: Movement Disorder Society Task Force guidelines. Mov Disord. 2012;27:349–56. doi: 10.1002/mds.24893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller LS, Rohling ML. A statistical interpretive method for neuropsychological test data. Neuropsychol Rev. 2001;11:143–69. doi: 10.1023/a:1016602708066. [DOI] [PubMed] [Google Scholar]
- Moller JT, Cluitmans P, Rasmussen LS, Houx P, Rasmussen H, Canet J, Rabbitt P, Jolles J, Larsen K, Hanning CD, Langeron O, Johnson T, Lauven PM, Kristensen PA, Biedler A, van Beem H, Fraidakis O, Silverstein JH, Beneken JE, Gravenstein JS. Long-term postoperative cognitive dysfunction in the elderly ISPOCD1 study. ISPOCD investigators. International study of post-operative cognitive dysfunction. Lancet. 1998;351:857–61. doi: 10.1016/s0140-6736(97)07382-0. [DOI] [PubMed] [Google Scholar]
- Mungas D, Marshall SC, Weldon M, Haan M, Reed BR. Age and education correction of Mini-Mental State Examination for English and Spanish-speaking elderly. Neurology. 1996;46:700–706. doi: 10.1212/wnl.46.3.700. [DOI] [PubMed] [Google Scholar]
- Murkin JM, Newman SP, Stump DA, Blumenthal JA. Statement of consensus on assessment of neurobehavioral outcomes after cardiac surgery. Ann Thorac Surg. 1995;59:1289–95. doi: 10.1016/0003-4975(95)00106-u. [DOI] [PubMed] [Google Scholar]
- Muthén LK, Muthén BO. Mplus: statistical analysis with latent variables. Los Angeles, CA: Muthén & Muthén; 1998–2007. [Google Scholar]
- Nelson HE. A modified card sorting test sensitive to frontal lobe defects. Cortex. 1976;12:313–324. doi: 10.1016/s0010-9452(76)80035-4. [DOI] [PubMed] [Google Scholar]
- Randolph C. Manual for the Repeatable Battery for the Assessment of Neuropsychological Status. New York, USA: The Psychological Corporation; 1998. [Google Scholar]
- Rao SM, Leo GJ, Bernardin L, Unverzagt F. Cognitive dysfunction in multiple sclerosis: frequency, patterns, and prediction. Neurology. 1991;41:685–91. doi: 10.1212/wnl.41.5.685. [DOI] [PubMed] [Google Scholar]
- Reckess GZ, Varvaris M, Gordon B, Schretlen DJ. Within-Person Distributions of Neuropsychological Test Scores as a Function of Dementia Severity. Neuropsychology. 2013 doi: 10.1037/neu0000017. [DOI] [PubMed] [Google Scholar]
- Reeve BB, Hays RD, Bjorner JB, Cook KF, Crane PK, Teresi JA, Thissen D, Revicki DA, Weiss DJ, Hambleton RK, Liu H, Gershon R, Reise SP, Lai JS, Cella D PROMIS Cooperative Group. Psychometric evaluation and calibration of health-related quality of life item banks: plans for the Patient-Reported Outcomes Measurement Information System (PROMIS) Med Care. 2007;45(Suppl 1):S22–31. doi: 10.1097/01.mlr.0000250483.85507.04. [DOI] [PubMed] [Google Scholar]
- Reitan R, Wolfson D. The Halstead-Reitan Neuropsychological Test Battery: Theory and Clinical Interpretation. Tucson, Arizona: Neuropsychology Press; 1993. [Google Scholar]
- Reitan RM. Validity of the Trail Making test as an indicator of organic brain damage. Percept Mot Skills. 1958;8:271–276. [Google Scholar]
- Roussel M, Dujardin K, Hénon H, Godefroy O. Is the frontal dysexecutive syndrome due to a working memory deficit? Evidence from patients with stroke. Brain. 2012;135:2192–201. doi: 10.1093/brain/aws132. [DOI] [PubMed] [Google Scholar]
- Sébille V, Hardouin JB, Le Neel T, Kubis G, Boyer F, Guillemin F, Falissard B. Methodological issues regarding power of Classical Test Theory (CTT) and Item Response Theory (IRT)-based approaches for the comparison of Patient-Reported Outcomes in two groups of patients - A simulation study. BMC Medical Research Methodology. 2010;10:24. doi: 10.1186/1471-2288-10-24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sepulcre J, Vanotti S, Hernández R, Sandoval G, Cáceres F, Garcea O, Villoslada P. Cognitive impairment in patients with multiple sclerosis using the Brief Repeatable Battery-Neuropsychology test. Mult Scler. 2006;12:187–95. doi: 10.1191/1352458506ms1258oa. [DOI] [PubMed] [Google Scholar]
- Shallice T, Burgess PW. Deficits in strategy application following frontal lobe damage in man. Brain. 1991;114:727–741. doi: 10.1093/brain/114.2.727. [DOI] [PubMed] [Google Scholar]
- Stroop JR. Studies of interference in serial verbal reaction. J Exp Psycho. 1935;18:643–662. [Google Scholar]
- Tatemichi TK, Desmond DW, Stern Y, Paik M, Sano M, Bagiella E. Cognitive impairment after stroke: Frequency, patterns, and relationship to functional abilities. J Neurol Neurosurg Psychiatry. 1994;57:202–207. doi: 10.1136/jnnp.57.2.202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tractenberg RE, Pietrzak RH. Intra-Individual Variability in Alzheimer’s Disease and Cognitive Aging: Definitions, Context, and Effect Sizes. PLOS One. 2011;6:e16973. doi: 10.1371/journal.pone.0016973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wechsler D. The measurement of adult intelligence. Baltimore, USA: The Williams and Wilkins Company; 1944. [Google Scholar]
- Winblad B, Palmer K, Kivipelto M, Jelic V, Fratiglioni L, Wahlund LO, Nordberg A, Bäckman L, Albert M, Almkvist O, Arai H, Basun H, Blennow K, de Leon M, DeCarli C, Erkinjuntti T, Giacobini E, Graff C, Hardy J, Jack C, Jorm A, Ritchie K, van Duijn C, Visser P, Petersen RC. Mild cognitive impairment--beyond controversies, towards a consensus: report of the International Working Group on Mild Cognitive Impairment. J Intern Med. 2004;256:240–6. doi: 10.1111/j.1365-2796.2004.01380.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Table 1. Distribution characteristics of 11 raw scores (upper part), the effect of demographic factors on transformed scores (middle part), values of cut-off scores at the 5th percentile and false-positive rates using the 1.5 and 1.64 SD cut-offs (lower part).
Supplementary Table 2. The sensitivity, false-positive rate (FPR) and area under the curve (AUC) (95% confidence interval (CI)) for the 19 individual scores (ranked by decreasing sensitivity).
Supplementary Table 3. The area under the curve (AUC) and 95% confidence interval (CI) obtained using the seven process scores and the overall scores in the overall population (left) and using the overall scores in the subgroup with no more than one impairment of a process score (right).