Abstract
Here we examine a new task to assess working memory for visual arrays in which the participant must judge how many items changed from a studied array to a test array. As a clue to processing, on some trials in the first two experiments, participants carried out a metamemory judgment in which they were to decide how many items were in working memory. Trial-to-trial fluctuations in these working memory storage judgments correlated with performance fluctuations within an individual, indicating a need to include trial-to-trial variation within capacity models (through either capacity fluctuation or some other attention parameter). Mathematical modeling of the results achieved a good fit to a complex pattern of results, suggesting that working memory capacity limits can apply even to judgments that involve an entire array rather than just a single item that may have changed, thus providing the expected conscious access to at least some of the contents of working memory.
In the past few years, we have seen an explosion of research on visual working memory, following an article by Luck and Vogel (1997) that introduced a procedure in which, on each trial, a briefly-studied array of objects is followed by a probe display testing memory of one or more features of at least one object from the studied array (see also Phillips, 1974; Sperling, 1960). The recent research has addressed a variety of interlocking issues, including the basis of individual and group differences in capacity (e.g., Cowan, Morey, AuBuchon, Zwilling, & Gilchrist, 2010; Gold et al., 2006; Vogel, McCollough, & Machizawa, 2005), the role of feature binding in working memory (e.g., Allen, Hitch, Mate, & Baddeley, 2012; Cowan, Blume, & Saults, 2013; Logie, Brockmole, & Jaswal, 2011; Oberauer & Eichenberger, 2013), the sharing of capacity between different modalities and codes (e.g., Fougnie & Marois, 2011; Morey & Mall, 2012; Saults & Cowan, 2007; Stevanovski & Jolicoeur, 2007; Vergauwe, Barrouillet, & Camos, 2010), the proper expression of capacity limits in terms of discrete items versus a continuous resource (e.g., Anderson, Vogel, & Awh, 2011; Bae & Flombaum, 2013; Bays & Husain, 2008; Cowan, 2001; Donkin, Nosofsky, Gold, & Shiffrin, 2013; Rouder et al., 2008; Thiele, Pratte, & Rouder, 2011; van den Berg, Shin, Chou, George, & Ma, 2012; Zhang & Luck, 2008), and processes that are used to manage the information in one’s working memory (Barrouillet, Portrat, & Camos, 2011; Camos, Mora, & Oberauer, 2011).
Most tests of working memory for arrays have involved memory probes with at most one change in an item compared to the studied array (but see Gibson, Wasserman, & Luck, 2011; Wilken & Ma, 2004, Experiments 4–6). This limitation in method, however, has been for convenience rather than as a reflection of what is supposedly most interesting or important in the world. Many real-world comparisons of two displays do involve multiple differences between them; this is the case, for example, when one compares two paintings by the same artist to discern their similarities and differences, compares two mobile phones to determine which one has better features, or compares before-and-after pictures.
As an initial foray into the topic of multi-change detection, we examine relatively small displays with 5, 7, or 9 objects; a real-world analogue might be the comparison of two recipes to estimate how many of their ingredients they have in common. After describing our task and theoretical analysis of it, but before reporting data, we discuss additional background concerning two topics: 1) literature on change detection for scenes, and 2) literature related to auxiliary tasks that we used to assess some individual differences in memory and metamemory (in particular, awareness of one’s working memory) in the present study.
The Present Multi-Change-Detection Task
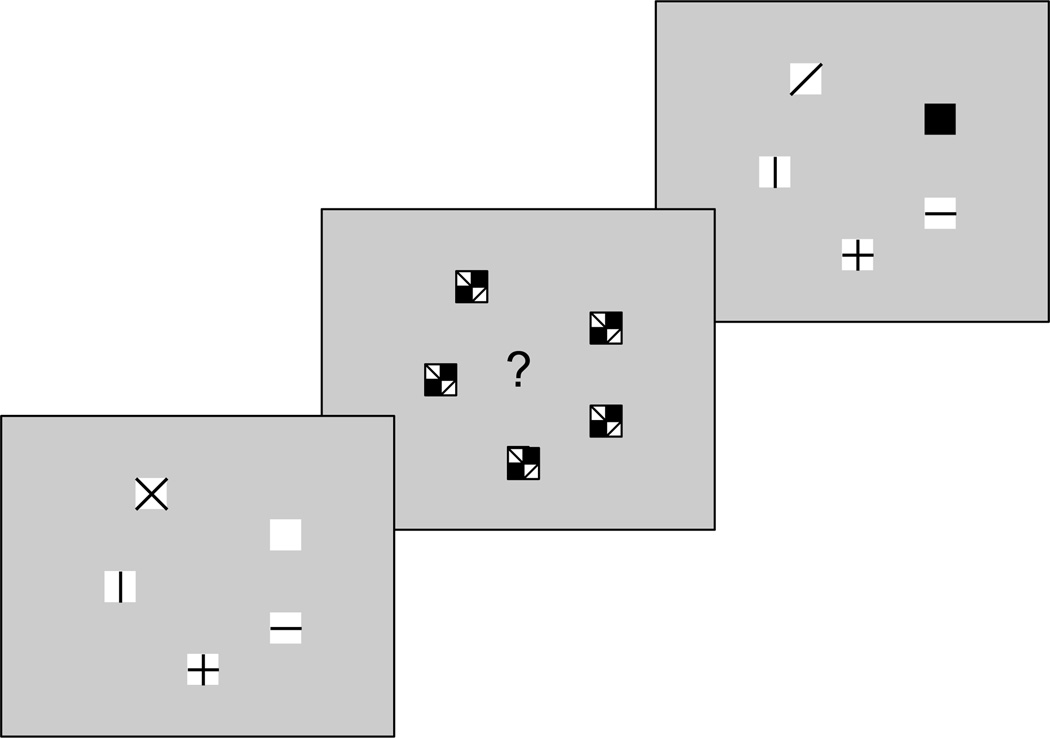
Our basic procedure was as shown in Figure 1. A probe array of N colored squares was presented (in Experiments 1 and 2, N=5 and 7, respectively; in Experiment 3, N=5, 7, or 9). This was followed by a masking display to eliminate any contribution of lingering sensory memory (cf. Saults & Cowan, 2007). The mask was sometimes accompanied by a cue for a metamemory task that we will discuss shortly. Last, a test array was presented that was identical to the first or included 1 to N changes in color compared to the squares in the original array. The task following the test array was to indicate the number of changes from the first array.
Figure 1.
Schematic illustration of the method of Experiment 1. Patterns shown on the squares represent colors in the actual experiment. The participant responds to the question mark within the display of multicolored masks by estimating by keypress the number of items stored in mind. The response to the probe in this experiment is to indicate by keypress how many items changed color from the original array. In this example, 2 items changed; across trials, from 0 to all 5 items could change. In half the trials, the question mark seen here was replaced by an X and no storage judgment was to be made.
To analyze data from such a procedure we introduce a new method that is a spinoff of what has been done with change-detection procedures (Cowan, 2001; Pashler, 1988). These investigators introduced mathematical models in which the participant either answers correctly because the queried or changed item is present in working memory, or else guesses randomly. The model of Cowan (2001) is appropriate when one item is singled out for the test, and the model of Pashler (1988) is appropriate when all items in the original array must be compared with a test array for which it is not indicated which item may have changed (Rouder, Morey, Morey, & Cowan, 2011). The models yield an estimate of k, the number of items held in working memory for a particular array size. If these estimates approach an asymptotic level as the array size increases, the asymptote is said to approximate the individual’s working memory capacity.
Zhang and Luck (2008) introduced a procedure from which one supposedly can estimate not only k, but also the precision of the working memory representation, based on a task in which a variable stimulus property has to be reproduced as precisely as possible (cf. Wilken & Ma, 2004). We, however, circumvent the need for that by using stimuli with colors that differ categorically, for which failure to detect a difference seems unlikely to be due to imprecision of the representation (Awh, Barton, & Vogel, 2007). In this regard we also wish to emphasize that the difficult issue of whether capacity might be best described as a continuous resource limit that can be spread out among all items, rather than as a discrete item limit, will not be addressed here in detail, and need not be addressed, though we favor the discrete item limit. (To read about this debate see, for example, Anderson et al., 2011; van den Berg, Awh, & Ma, 2014; Suchow, Fougnie, Brady, & Alvarez, 2014; Zhang & Luck, 2011.) When we find that participants have X items in working memory, or when we find that participants think they have Y items in working memory, this could reflect the number of items that are remembered with a precision high enough to detect a change from one color to a categorically different one. Performance for categorically different colors is known to be almost as high as when one tests a change from one type of object, such as a face, to another type of object, such as a cube (Awh et al., 2007; Scolari, Vogel, & Awh, 2008); that is, almost the largest possible change, requiring minimal precision. Thus, one can benefit from our k measure to examine working memory in multi-change-detection situations even if a commitment to a discrete-item capacity ultimately proves to be unwarranted. Similarly, Gibson et al. (2011, p. 980) suggested the following: “It is important to note that this model assumes that observers store high-quality representations of all K items and have no information about the remaining items…However, it is possible to avoid this assumption by treating K as the number of items’ worth of information stored in VSTM [visual short-term memory] (Vogel, Woodman, & Luck, 2001).”
The studies with the manipulations closest to ours were conducted by Gibson et al. (2011) and Wilken & Ma (2004). As in our study, anywhere between none and all of the items in an array could change between the studied array and the following probe array. In these studies, however, the task was to determine whether there was at least one change, a task that became easier as the number of changes increased. Wilken & Ma also collected confidence ratings. In contrast, our task was to estimate how many items changed, which of course affords more information about the number of changes detected. We also measured awareness of one’s own memory with a judgment of number of array items in mind, rather than using confidence ratings.
Multi-change Detection and Working Memory for Scenes
Unlike the finding of a fixed capacity measured on an item-by-item basis in single-change-detection procedures (e.g., Anderson, Vogel, & Awh, 2011; Cowan, 2001; Luck & Vogel, 1997; Rouder et al., 2008), there has been other work on whole-field working memory, some of which suggests broad judgment in which the items are not just examined separately in working memory. For example, Hollingworth (2004) presented natural scenes with a dot indicating which item should be fixated. Memory for the last few items fixated was especially good, but there was also a long-term memory component that did not diminish with interpolated material. Chong and Treisman (2005) probed memory for characteristics of the array taken as a whole, such as the average size of items. Such averages can be abstracted from arrays of many items at once, even though capacity appears limited to just a few items. Other work has shown that information about any one object in a large array is remembered in a way that is biased by the statistics of the ensemble (Brady & Alvarez, 2011), and Brady and Tenenbaum (2013) showed how it will be necessary to combine item-level information with higher-level conceptual structural information to explain memory for natural scenes.
The present work is not designed to examine scenes, but the methods developed here could be modified in the future to gain a better understanding of the role of item information in working memory for scenes. It remains possible that an item capacity limit applies to large ensembles; for example, the average size of an item in a large array might be abstracted not from all items in the scene, but from a random subsample of items or groups of items that are few enough to be held in working memory. Consistent with the general suggestion that perception of scenes requires active encoding of elements into working memory, Cohen, Alvarez, and Nakayama (2011) showed that distraction during perception of a scene resulted in inattentional blindness for items in the scene.
We do not attempt to deal with scenes but note that a characteristic of scenes is that comparisons between them generally reveal multiple differences. We develop methods to examine the role of a limited-capacity working memory in relatively small arrays of separate items. Subsequent research then could seek to determine whether similar processes operate in the case of large arrays or scenes.
An Auxiliary, Metamemory Measure in the Multi-Change-Detection Task
Although metamemory, or knowledge of what information is in one’s own memory, has been extensively investigated in long-term memory procedures (e.g., Koriat & Helstrup, 2007; Lachman, 1979; Maki, 1999), it has hardly been investigated in working memory procedures (though see Bunnell, Baken, & Richards-Ward, 1999; and for subjective judgments about the efficacy of participants’ working memory see Kane et al., 2007). Rademaker, Tredway, and Tong (2012) investigated it with confidence ratings and found that more confident ratings corresponded to trials with more precise memory. Instead of asking for confidence ratings, we sometimes asked for direct estimates of the number of items in working memory and, importantly, did so before rather than after an objective judgment was made. This is important because participants’ subjective ratings collected after an objective probe is presented could be influenced by the participant’s ability or inability to retrieve the information to respond to that probe.
We did not know in advance whether subjective ratings would correspond to objective responses. One could imagine that participants might make a judgment about the number of items that have changed on the basis of a holistic stance in which the array is perceived without individuating the items in memory. That is, multi-item patterns and regularities might be found (Brady & Tenenbaum, 2013; Jiang, Chun, & Olson, 2004) and used to encode the array in such a way that the judged number of changes in the array would have little to do with knowledge of the individual items.
We added the metamemory task on half of the trials in Experiments 1 and 2, yielding an auxiliary measure of working memory, namely the number of items the participant thought he or she had in mind during the retention interval. On trials in which the metamemory response was to be made, the masking array included a question mark as shown in Figure 1. The participant was to indicate the number of items’ colors that she (or he) thought she had in mind. There was a fixed time for this activity that did not lengthen the time between the original studied array and the test array. The participant was then to go on to indicate how many items changed, as in the trials with no metamemory judgment.
The metamemory judgments are useful for examining several issues. First, they can be used to assess whether individuals have knowledge of trial-to-trial fluctuations in the number of items in working memory. There has been some suggestion that an individual’s number of items in working memory is not always fixed (van den Berg, Awh, & Ma, 2014) or that attention to the array varies between trials (Rouder et al., 2008), and this general hypothesis of variability would be strengthened if it could be shown that trial-to-trial fluctuation in the participant’s conception of how many items are known correlates with objective performance. A positive result would also suggest that at least some faculties used to remember arrays are open to introspection, as one would expect if the attention system is used for retention of information in one way or another (e.g., Baars & Franklin, 2003) as a number of investigators have suggested (e.g., Cowan, 1995, 2001; Cowan, Saults, & Blume, 2014; Barrouillet et al., 2011; Oberauer, 2013).
On the other hand, an individual’s apparent failure of insight on a particular trial could occur for reasons other than insufficient capacity. For example, an individual who is especially vulnerable to interference might have been correct that he or she had all of the array items in working memory during the retention interval, but might lose them due to interference from the probe array (cf. Wheeler & Treisman, 2013; Woodman & Luck, 2003). According to at least one view, visual working memory may operate on the basis of a mechanism that does not tax attention as measured, in particular, by the efficiency of visual search (Woodman, Vogel, & Luck, 2001). Cowan, Saults, and Blume (2014) acknowledged that information in working memory may be off-loaded and held outside of attention during at least part of the maintenance period which might result in a tenuous relationship between awareness and working memory.
Second, the metamemory judgments could be used to assess whether individuals know something about the capacity of their own working memory relative to other people. A good knowledge of one’s own cognitive strengths and weaknesses, including one’s working memory capability, seems important because it could be relevant to career choices. Understanding of the cognitive demands of a particular working memory task seems important because it is relevant to how one manages the task; one might choose to devote more attention control for a task that one expects to be more demanding. A correlation between metamemory judgments and array memory across individuals would seem likely only if participants have some understanding of both the task demands and their own level of capability on this kind of task relative to other individuals in the participant pool. Given the complex reasons why a correlation could fail, this issue can be examined here only for exploratory purposes.
Modeling of working memory capacity in change-detection tasks
One contribution of the present work is to show how it is possible to model capacity limits in working memory in the multi-change-detection task. As a preview, the task yielded an intricate pattern of results and modeling of that pattern provided insight into processes that may be involved in multi-change detection.
Our initial model in an earlier draft of this article was based on the assumption that a separate decision was made by the participant about each item in the array, based either on information in working memory or, for those items not included in the working memory representation, on guessing. That model did a good job of fitting the mean judged number of changes as a function of the actual number changed; mean responses within both the model and the data were at least approximately related to the number of array changes in a linear manner, with a slope approaching 1 as the number of items in working memory approached the number of items in the array. However, this sort of model did a poor job of fitting the more detailed pattern of data. Specifically, for trials with x changes out of n array items (0<x<n), the number of times that the participants judged that 0, 1, 2…n items changed was not well predicted. The obtained patterns included much more use of the extremes of the judgment scale than the model predicted.
In our final models of performance, the participant is said to observe c changes and must make a decision about what actual states of affairs could produce this observed number of changes.1 This class of models assumes that the participant is aware of how many items he or she has in working memory. The participant also is assumed to use the knowledge that, in the experiment, there is an equal likelihood of receiving 0, 1, 2…n changes. As an example of why that assumption is important, suppose a participant with a capacity of 3 items (k=3) saw a 5-item array (n=5) and detected 3 changes in the comparison array (c=3). This outcome could occur in several ways according to these models. It could be that there actually were 3 changes and none of them was missed; 4 changes and 1 of them was missed; or 5 changes and 2 of them were missed (x=3, 4, or 5). Given that there were equal numbers of trials in the experiment with each possible number of changes, the last possibility is most likely because it should happen on all, and not just some, of the 5-change trials. In contrast, for example, when there are only 4 changes out of 5 items, a participant with k=3 will sometimes detect only 2 changes.
The model can take the form of either a discrete slot model or a continuous resource model. For 5-item lists, a continuous resource model with variable precision fit the data well, but so did a discrete slots model with two assumptions added. One was the assumption that after the participant implicitly computed the probabilities of various numbers of changes, the response did not consistently reflect the most probable case, but rather a probability match to the various possible cases. Probability matching has been well supported in previous research on human judgment and decision-making (e.g., Shanks, Tunney, & McCarthy, 2002; Vulkan, 2000). Second, we allowed the estimate of the number of items in working memory to conform to a distribution rather than being identical across trials.
For 7- and 9-item lists, there was an asymmetry in the data that caused an important misfit to even these models. Specifically, people were a lot more willing to indicate that no or few items changed than they were to indicate that many or all items changed. We were able to fit these data, with the added assumption that participants did not know how many items they truly had in working memory, but judged the number of items in working memory in a manner that was estimated from our metamemory judgments of the number of items in mind. When the number of detected changes surpassed the number of items the participant thought to be in working memory, the estimate was assumed to be revised upward. It might have been possible to form a comparable model for continuous resources based on the assumption that the distribution of precisions that participants think they have does not match the distribution that they actually have, and instead matches the metamemory results. That endeavor, however, seemed complex enough to be outside of the scope of our modeling effort. It is our aim simply to begin to make sense of the processes taking place in multi-change procedures, and we leave it for follow-up work to adjudicate between discrete and continuous models or to try out additional alternative possibilities. Both discrete and continuous models predict the data by estimating the number of items that are present in working memory with enough precision to allow discrimination between a changed and an unchanged item. We delay the more detailed presentation of the model until results from three experiments have been presented.
Other Auxiliary Tasks
In the first two experiments (with 5 and 7 array items, respectively), we collected two other, independent measures of capacity that have been useful in that they have been shown to correlate with one another and with array memory: the running span and operation span tasks. Both tasks provide estimates in a range similar to what is obtained with array memory tasks. They involve sequential presentations of verbal and symbolic items, a method quite different from the simultaneous presentation of nonverbal objects that occurs within visual arrays; yet they are not very amenable to covert verbal rehearsal (Cowan et al., 2005). They may draw on partly different faculties (e.g., Shipstead, Redick, Hicks, & Engle, 2012) and correlations between them are based at least partly on rather general, attention-related components of working memory maintenance (e.g., Kane et al., 2004). We included them in order to compare array multi-change detection and metamemory to very different, but often-used, measures of working memory functioning. In the third experiment, to allow for the inclusion of 3 set sizes (5, 7, and 9), we omitted the metamemory measure and the running and operation spans.
Experiment 1: 5-Item Arrays
Method
Participants
Participants were introductory psychology students who received course credit for their participation. There were 69 participants (48 female) but 9 were eliminated: 7 because they did not make storage judgments or only made them on 1 or 2 trials, and 1 because of experimenter error. An additional participant always gave a storage judgment of 5 and in fact performed well, with a slope of change responses across actual changes of .88. This participant was excluded from further analysis because it was impossible to appraise the participant’s awareness of fluctuations from trial to trial. The 60 participants used in the analyses included 43 females and 17 males, and each used 3 or more of the storage judgment categories.
Apparatus, stimuli, and procedure
All tests were completed in a sound-attenuated booth with computer-controlled stimuli. We carried out a running span procedure, an operation span procedure, and the array change-detection task that included storage judgments on half of the trials.
Running span
In the running span procedure (taken from Cowan et al., 2005), on every trial 12 to 20 spoken, digitally-compressed digits were presented through loudspeakers at the rapid rate of 4 digits per second. The digits were easily intelligible. The determination of list length was random so the list ended at a point that was unpredictable to the participant. When the list ended, the task was to use the number keys to enter the last seven digits from the list, or as many of these digits as the participant believed he or she could recall, in the presented order. The response was right-justified so that the last digit entered by the participant was considered to be the recall of the final list item. Guessing was allowed. Credit was given for the number of digits that were recalled in the correct serial position within the right-justified response.
Operation span
Next, each participant completed the operation span procedure using a program described by Unsworth, Heitz, Schrock, and Engle (2005). On every trial, sets of arithmetic equations were shown, with the correctness of each equation to be verified by the participant, and each equation was followed by a letter to be remembered. After a list of equation-letter pairs was completed, all of the letters in the list were to be recalled. The list length varied randomly between 3 and 7 equation-letter pairs, with three lists per set size. Operation span was defined as the total number of letters recalled within all perfectly-recalled lists (the first measure described by Unsworth et al., p. 501, which is their traditional measure).
Array memory
Finally, each participant completed the array-memory multi-change-detection task illustrated in Figure 1. A special keyboard was used that only included the needed keys. Participants made responses with their right hand by pressing one of 6 keys arranged in two rows, with the keys labeled 0, 1, 2, 3, 4, and 5. On each trial, a screen indicated whether there would be a storage judgment. When ready, the participant would press the Enter key to begin each trial. A fixation cross was presented for 1000 ms followed by the array of 5 colored squares for 500 ms. A blank screen then appeared for 500 ms, followed by the mask display that also contained a prompt indicating whether a storage judgment should be made (?) or not (X). The mask and storage judgment response period lasted 4000 ms. A probe array was then presented in which 0 to 5 of the items’ colors differed from those in the otherwise identical first array. (The items did not change locations.) The task was to indicate how many of the colored squares on the second array had changed, again by key press. Following the participant-paced response, two feedback screens were provided. The first indicated memory accuracy (including the response as well as the correct response, i.e., how many colored squares actually had changed). The second feedback screen provided storage judgment feedback. It was made clear in the instructions that each possible color could appear only once in an array and that any change between the studied and probe arrays would be changes of one or more items to colors that had not been in the studied array.
When a storage judgment was to be made the participant was to indicate, before the mask ended, the number of colors from the target array (0–5) that were still held in mind. It was emphasized that it was the color, not the location, of an object that had to be remembered in order for that object to be included in this judgment of the number of items in mind. It was further pointed out that it was not the number of colors presented (always 5) that was to be reported, but the number remembered.
The spatial arrangement of the experimental materials was as follows. Participants were seated about 50 cm away from the computer screen. The 5 squares in the target array were drawn on a grey background. They were differently colored, with the square colors randomly drawn without replacement from the set black, white, red, blue, green, yellow, brown, cyan, purple, and dark-blue-green. These colors are defined by RGB values in the in-line object 'DefineColorsAsRGB' in the E-Prime program. Standard RGB values for the colors in every experiment are shown in Table 1. The target squares were each 6 mm on a side (0.7 degrees of visual angle), arranged within a 74 mm wide × 56 mm high area (8.5 × 6.4 degrees of visual angle). The locations of squares were restricted so that there was at least 17.5 mm between their centers and they were at least 17.5 mm from the center of the display area. The mask array included 5 multicolored squares in the same spatial arrangement as the target array, overwriting the colors while preserving location information.
Table 1.
Names and RGB Values of the Colors Used in the Arrays in Each Experiment
| Color | RGB Values | Experiments |
|---|---|---|
| brown* | 204,102,0 | 1 |
| dark-blue-green* | 0,102,102 | 1 |
| black | 0,0,0 | 1,2,3 |
| white | 255,255,255 | 1,2,3 |
| red | 255,0,0 | 1,2,3 |
| lime | 0,255,0 | 1,2,3 |
| blue | 0,0,255 | 1,2,3 |
| magenta | 255,0,255 | 1,2,3 |
| yellow | 255,255,0 | 1,2,3 |
| cyan | 0,255,255 | 1,2,3 |
| fluorescent green* | 0,230,115 | 2 |
| orange* | 255,128,0 | 2 |
| navy | 0,0,128 | 2,3 |
| purple | 128,0,128 | 2,3 |
| dark green | 0,100,0 | 2,3 |
| saddle brown | 139,69,19 | 2,3 |
| light pink | 255,182,193 | 3 |
| burly wood | 222,184,135 | 3 |
| dark orange | 255,140,0 | 3 |
| silver | 192,192,192 | 3 |
| olive drab | 107,142,35 | 3 |
| teal | 0,128,128 | 3 |
Note. All color names are standard in HTML code except for the ones marked with an asterisk.
The session began with 12 practice trials followed by 13 blocks of 12 test trials. Within each block, 6 trials were designated as “Storage Judgment” while the rest were “No Storage Judgment” trials. Within the 6 trials of each designation per block, one of each of the possible number of changed items (0–5) was selected. Thus, each block of 12 trials consisted of exactly one example of all possible trial types.
Results
The included participants erroneously made judgments on how much information was in working memory on 4% of trials when they had not been instructed to do so, and they erroneously omitted judgments on 6% of trials in which they had been instructed to make them. These trials were excluded from the analyses.
Mean response function
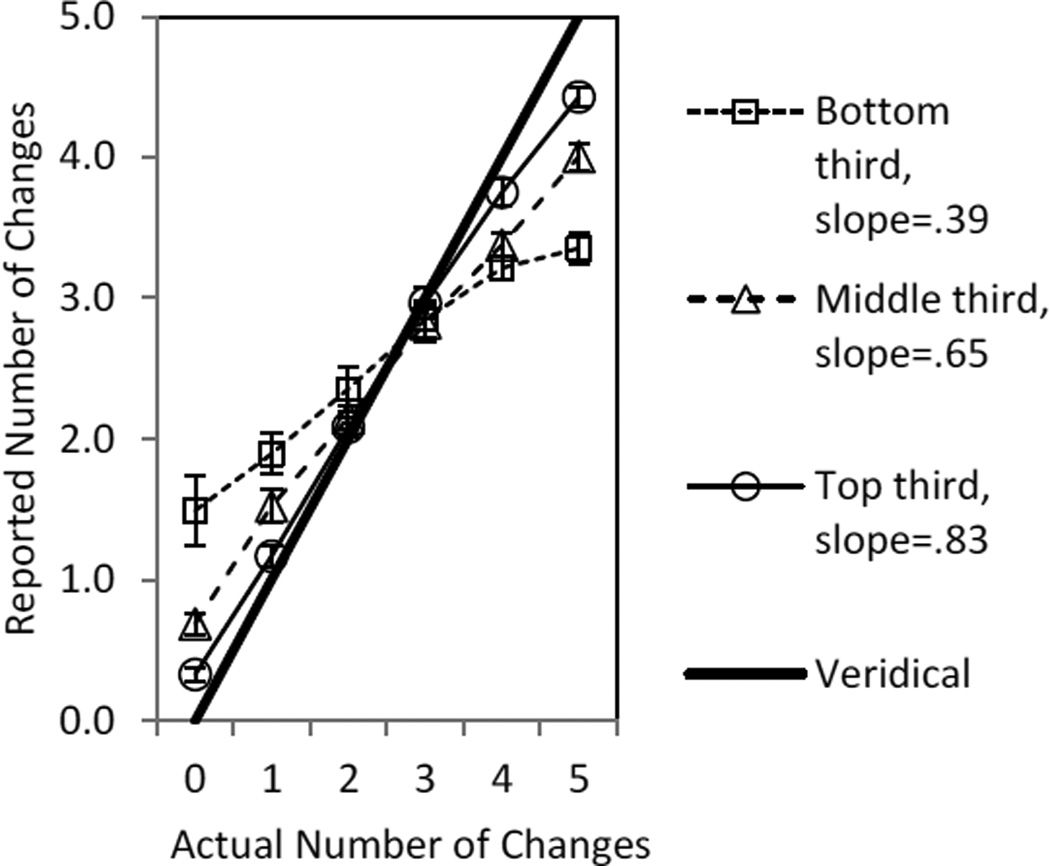
Figure 2 shows the mean number of reported changes for each number of actual changes. To give a rich picture of performance, these means were calculated separately for the thirds of the participants with the poorest performance, intermediate performance, and best performance. The figure also shows perfect or veridical performance, for which the slope would be 1.0.
Figure 2.
For performance thirds of the sample in Experiment 1, the mean reported number of changes in the array for each number of actual changes in the array. The functions approximate straight lines and the reported slopes are the average individual slopes for these performance thirds. Error bars are standard errors. Veridical performance (thick line) would yield a slope of 1.0.
Performance levels
Mean performance in terms of the discrimination slopes and metamnemonic judgments are shown in Table 2. The discrimination slopes based on the mean judgments shown were slightly but significantly higher on trials without storage judgments (M=.66, SD=.16) than on trials with them (M=.62, SD=.17), F(1,56)=4.84, p<.05, ηp2=.08, The metamnemonic judgment mean (2.71) is roughly comparable to capacity estimates from limited capacity models meant for single-change tasks (e.g., Cowan, 2001; Rouder et al., 2008) and from production tasks (Anderson et al, 2011; Luck & Vogel, 2008), typically about 3 items. It is even closer to the capacity estimate for the present study (2.69) that is based on our best mathematical model of the results, to be described after Experiment 3.
Table 2.
Number of Participants (N), Mean Performance Levels, and Standard Errors of the Mean (SEM) for Various Measures in Experiment 1 (5-item Arrays)
| N | Mean | SEM | |
|---|---|---|---|
| Trials with no Metamemory Judgment Task | |||
| Judged changes when 0 changed | 60 | 0.84 | 0.11 |
| Judged changes when 1 changed | 60 | 1.53 | 0.08 |
| Judged changes when 2 changed | 60 | 2.19 | 0.06 |
| Judged changes when 3 changed | 60 | 2.88 | 0.07 |
| Judged changes when 4 changed | 60 | 3.45 | 0.06 |
| Judged changes when 5 changed | 60 | 3.93 | 0.07 |
| Trials with Metamemory Judgment Task | |||
| Judged Items Stored | 60 | 2.71 | 0.08 |
| Judged changes when 0 changed | 60 | 1.06 | 0.11 |
| Judged changes when 1 changed | 60 | 1.82 | 0.09 |
| Judged changes when 2 changed | 60 | 2.49 | 0.08 |
| Judged changes when 3 changed | 60 | 2.96 | 0.07 |
| Judged changes when 4 changed | 60 | 3.57 | 0.08 |
| Judged changes when 5 changed | 60 | 3.97 | 0.08 |
| Slope with storage judgment 0 | 15 | .47 | .17 |
| Slope with storage judgment 1 | 47 | .45 | .05 |
| Slope with storage judgment 2 | 54 | .56 | .04 |
| Slope with storage judgment 3 | 60 | .62 | .03 |
| Slope with storage judgment 4 | 48 | .59 | .05 |
| Slope with storage judgment 5 | 29 | .66 | .07 |
| Auxiliary Tasks | |||
| Operation Span Score | 60 | 39.47 | 2.15 |
| Running Span Score | 60 | 2.70 | 0.12 |
Note. Slope refers to increases in the reported number of changes in the array as a function of increases in the actual number of changes. The estimate of items in working memory based on the winning model, summed over the probabilities of different numbers of items in working memory, was 2.69. The proportions of trials with 0 through 5 items in working memory according to the model are .03, .08, .18, .58, .13, and .00, respectively.
Trial-to-trial metamnemonic awareness
We asked whether participants were aware of remembering fewer items on some trials and more items on others. Inspection of Table 2 informally illustrates such a trend in terms of participants with data at each possible metamemory storage judgment. These data could not be analyzed statistically given that different participants used different judgment categories. In order to ask whether participants were aware of remembering fewer items on some trials and more items on other trials, we examined the proportion correct for every participant separately for trials in which each metamnemonic category was used. We calculated the regression slope of discrimination slopes across the five categories. A mean slope greater than zero indicates an improvement in performance across increasing numbers of items judged to be in working memory. The mean regression slope (M=.06, SEM=.02) was indeed significantly above zero, t(59)=3.31, p<.01, indicating metamnemonic awareness.
Individual differences
As shown in Table 3, there was a very high correlation between discrimination slopes obtained from trials with versus without metamemory judgments but, otherwise, the different indices of working memory and knowledge of it did not correlate. One concern with these results is that there was an outlier who had a discrimination slope near zero, yet had a metamemory judgment mean of nearly 4 items. Without that misguided outlier, there was a significant correlation of metamemory judgments with discrimination slope on trials with no storage judgments, r=.44, and on trials with storage judgments, r=.40. It appears, then, that many participants do have some idea of where they stand in terms of array memory information relative to other individuals. Still, the absence of correlation between discrimination slope and the working memory composite based on other tasks persisted, suggesting that array memory here does not necessarily tap the same characteristics as the other working memory tasks. This issue will be revisited in Experiment 2.
Table 3.
Summary of Correlation and Results
| Measure | |||||
|---|---|---|---|---|---|
| Measure | 1 | 2 | 3 | 4 | 5 |
| 1. Discrim. slope (with no metamemory judgment) | --- | .81* | .14 | .10 | .16 |
| 2. Discrim. slope (with metamemory judgment) | .82* | --- | .09 | .03 | .06 |
| 3. metamemory judgment | −.17 | −.04 | --- | −.01 | .16 |
| 4. Change in d. slope across metamemory judgments | .16 | .12 | −.15 | --- | .04 |
| 5. working memory composite | .31* | .37* | .04 | .28* | --- |
Note. In the table, the correlations shown above the diagonal are from Experiment 1 (5-item arrays); below the diagonal, from Experiment 2 (7-item arrays). Discrimination (or d.) slope refers to increases in the reported number of changes in the array as a function of increases in the actual number of changes. Working memory composite based on running span and operation span scores.
p<.05.
Discussion
A priori, it might have been expected that the assessment of working memory capacity in terms of number of items in working memory (Cowan, 2001; Luck & Vogel, 1997; Pashler, 1988) might be irrelevant when the judgment pertains to the entire array. Indeed, participants seem able to make conjoint judgments based on the average of a feature value (e.g., size) across an entire array of many items (Chong & Treisman, 2005). The present experiment shows, however, that the new, multi-change-detection method of determining the used capacity of working memory is viable. Our modeling result will show that it yields estimates rather comparable to the standard, single-change-detection method. This result shows that the limited capacity of working memory appears to be an important factor in understanding responses even when they pertain to the entire array rather than a single item that may have changed from the studied array to the test array.
One possible problem with this experiment is that participants appeared to do rather well. A difference between a capacity of 4 and a perfect score might be difficult to observe. Perhaps this functional ceiling limited the individual-score reliabilities, in which case the multi-change-detection task could be more reliable with a larger set size. Accordingly, in Experiment 2, we retested the multi-change-detection model with 7 items per array.
Experiment 2: 7-item Displays
Method
Participants
We ran 65 college students (36 female). We excluded the data from 10 participants who had incomplete data or almost always failed to make storage judgments, 2 others who used only two storage judgment categories (described below), and 1 other who appears to have reversed the scale, indicating how many items stayed the same rather than how many changed. The final sample of 52 included 29 females.
The participants who used only 2 storage judgment categories were excluded from most analyses because it was considered difficult to compare trial-to-trial fluctuations in memory with metamemory. One of them used metamnemonic categories 2 and 3 (M=2.34) and had near-average performance, with a slope of reported changes across actual changes of .52. The other used categories 3 and 4 (M=3.60) and did very well, with a slope of .93.
Apparatus, stimuli, and procedure
The method was similar to Experiment 1 (including the auxiliary tasks) except that, in the main task, there were 7 items in each array instead of 5, and the response scales were adjusted accordingly. Participants completed a total of 160 experimental trials: 10 blocks of 16 (with storage judgments in 8 of the 16 per block). Each of the possible array change values (0–7) occurred once in each block for storage-judgment trials, and once for no-storage-judgment trials. The color set was expanded to include those in the former set of 10 except for dark-blue-green (excluded in order to split up the green category), and also included fluorescent green, dark green, navy, violet, and orange.
Results
The included participants erroneously made judgments of how much information was in working memory on 2% of trials when they had not been instructed to do so, and they erroneously omitted judgments on 3% of trials in which they had been instructed to make them. These trials were excluded from the analyses.
Mean response function
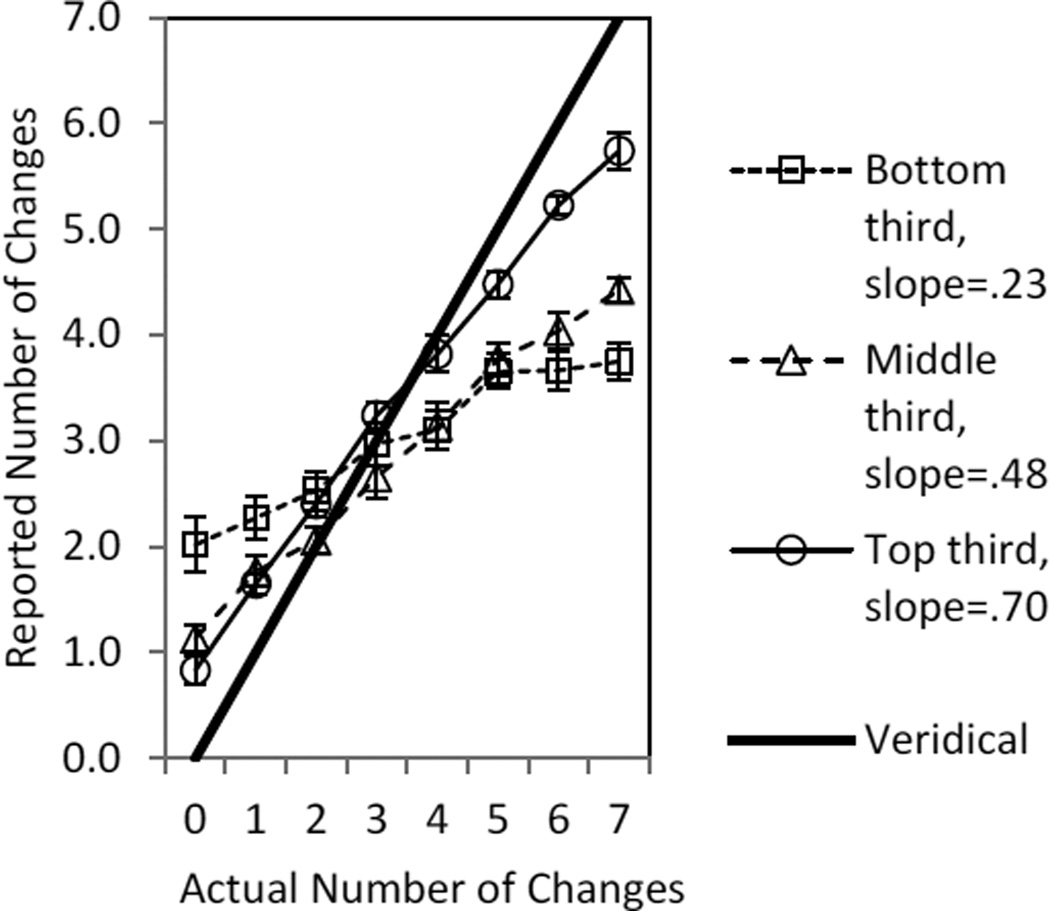
Figure 3 shows the mean response function for Experiment 2, separately for individuals in the bottom, middle, and top third of performance. It can be seen that even the top third of the participants was further from the veridical line than was the case in Experiment 1 (Figure 2), indicating that increasing the set size from 5 to 7 items successfully removed any problem of ceiling effects in some participants.
Figure 3.
For performance thirds of the sample in Experiment 2, the mean reported number of changes in the array for each number of actual changes in the array. The functions approximate straight lines and the reported slopes are the average individual slopes for these performance thirds. Error bars are standard errors. Veridical performance (thick line) would yield a slope of 1.0.
Performance levels
Mean performance in terms of discrimination slopes and metamnemonic judgments are shown in Table 4. These means are generally similar to Experiment 1. One difference is that the discrimination slope for trials with no metamnemonic judgment (M=.49, SD=.20) did not significantly differ from trials with a metamnemonic judgment (M=.46, SD=.19), F(1,51)=3.19, p=.08, ηp2=.06. The metamnemonic judgment mean (2.76 items) was somewhat higher than the mean number of items in working memory according to the winning mathematical model (2.28 items).
Table 4.
Number of Participants (N), Mean Performance Levels, and Standard Errors of the Mean (SEM) for Various Measures in Experiment 2 (7-item Arrays)
| N | Mean | SEM | |
|---|---|---|---|
| Trials with no Metamemory Judgment Task | |||
| Judged changes when 0 changed | 52 | 1.31 | 0.11 |
| Judged changes when 1 changed | 52 | 1.89 | 0.08 |
| Judged changes when 2 changed | 52 | 2.33 | 0.08 |
| Judged changes when 3 changed | 52 | 2.96 | 0.11 |
| Judged changes when 4 changed | 52 | 3.36 | 0.12 |
| Judged changes when 5 changed | 52 | 3.97 | 0.10 |
| Judged changes when 6 changed | 52 | 4.32 | 0.13 |
| Judged changes when 7 changed | 52 | 4.66 | 0.14 |
| Trials with Metamemory Judgment Task | |||
| Judged Items Stored | 52 | 2.76 | 0.09 |
| Judged changes when 0 changed | 52 | 1.56 | 0.12 |
| Judged changes when 1 changed | 52 | 2.07 | 0.13 |
| Judged changes when 2 changed | 52 | 2.61 | 0.11 |
| Judged changes when 3 changed | 52 | 2.97 | 0.11 |
| Judged changes when 4 changed | 52 | 3.43 | 0.10 |
| Judged changes when 5 changed | 52 | 3.92 | 0.11 |
| Judged changes when 6 changed | 52 | 4.33 | 0.13 |
| Judged changes when 7 changed | 52 | 4.81 | 0.14 |
| Slope with storage judgment 0 | 11 | .40 | .17 |
| Slope with storage judgment 1 | 38 | .41 | .05 |
| Slope with storage judgment 2 | 50 | .41 | .04 |
| Slope with storage judgment 3 | 52 | .50 | .04 |
| Slope with storage judgment 4 | 44 | .48 | .04 |
| Slope with storage judgment 5 | 12 | .57 | .16 |
| Slope with storage judgment 6 | 4 | .67 | .22 |
| Slope with storage judgment 7 | 3 | .00 | .00 |
| Auxiliary Tasks | |||
| Operation Span Score | 52 | 41.81 | 2.34 |
| Running Span Score | 52 | 3.13 | 0.09 |
Note. Slope refers to increases in the reported number of changes in the array as a function of increases in the actual number of changes. The estimate of items in working memory based on the winning model, summed over the probabilities of different numbers of items in working memory, was 2.28. The proportions of trials with 0 through 7 items in working memory according to the model are .04, .04, .51, .40, .00, .00, .00, and .00, respectively.
Trial-to-trial metamnemonic awareness
Once again we asked whether participants were aware of remembering fewer items on some trials and more items on other trials. Inspection of Table 4 informally illustrates such a trend in terms of all participants who had data for each possible storage judgment (0–7). Once more in a more formal measure, a mean regression slope across judgment categories greater than zero indicates awareness. The mean slope (.06, SEM=.02) was indeed significantly above zero, t(51)=2.74, p<.01, indicating that participants again did show some metamnemonic awareness of their trial-to-trial knowledge, as in the other experiments.
Individual differences
The present experiment shows a stronger pattern of correlations (Table 4) than we obtained in Experiment 1. Not only is there a strong correlation between the two measures of discrimination slope; there also are strong correlations between these measures of items in working memory and the working memory composite score. Thus, there seems to be some evidence in favor of the need to use larger set sizes for the multi-change-detection task in order to obtain an ideal set of correlations, probably because of ceiling effects for some participants in 5-item arrays. The change in the function of discrimination slope across storage judgments, indicating trial-by-trial knowledge of the contents of working memory, also was correlated with the working memory composite score in this experiment, so that higher-span individuals seem to have more knowledge of their current mental state.
As in Experiment 1, metamemory storage judgments were not correlated with discrimination slope. Unlike Experiment 1, this lack of correlation was not the result of an outlier. Instead, it appears that with this more difficult task, participants are unable to assess reliably how good their memory capacity is overall.
Discussion
The present experiment, like Experiment 1, showed that there is considerable usefulness in a method in which any number of items in the field can change. The use of a larger array set size in the present experiment (7 instead of 5 colored items) produced results that did not suggest any ceiling effect, but still are similar to those of Experiment 1 in key ways. The estimates of discrimination slope were similar though slightly higher in the present experiment, probably because there is no longer a ceiling effect for the more capable participants.
Both experiments also produced similar evidence that participants are aware of trial-to-trial fluctuations in the number of items in working memory. Specifically, in both experiments, the slope of performance (items in working memory) as a function of the assigned storage judgment was positive, indicating awareness of trial-to-trial differences. There were mixed indications of the presence or absence of between-individual correlations between working memory tasks and metamnemonic knowledge, indicating that there was not very consistent awareness of the quality of one’s own working memory compared to other participants.
Experiment 3
In this experiment we tested the generality of the pattern of results obtained in the first two experiments by examining 5-, 7-, and 9-item arrays intermixed in the same trial blocks. In order to allow time for this broader set of trials in an experiment, we omitted the storage judgments and the auxiliary working memory tasks. This experiment therefore should provide a pure measure of multi-change detection unaffected by any additional task requirements. It also serves as a good basis for mathematical modeling of the results.
Method
Forty-six introductory psychology students participated (27 male, 19 female). The stimulus set was expanded to 18 colors, chosen to be maximally discriminable from one another (Table 1). In order for the objects to fit in the display, they could be separated by only 13.7 mm, compared to 17.5 mm in Experiments 1 and 2. Ten practice trials were followed by 216 test trials, with an equal number of trials for each combination of set size and number of changes. Given that there were 6 trial types for 5-item trials (0–5 changes), 8 trial types for 7-item trials, and 10 trial types for 9-item trials, there were 24 experimental conditions. Each condition occurred 3 times within a block of 72 trials, and there were 3 of these experimental trial blocks with breaks in between the blocks. Because there were no storage judgments, we were able to reduce the retention interval from 4s previously to 1s in this experiment, decreasing the test time.
Results and Discussion
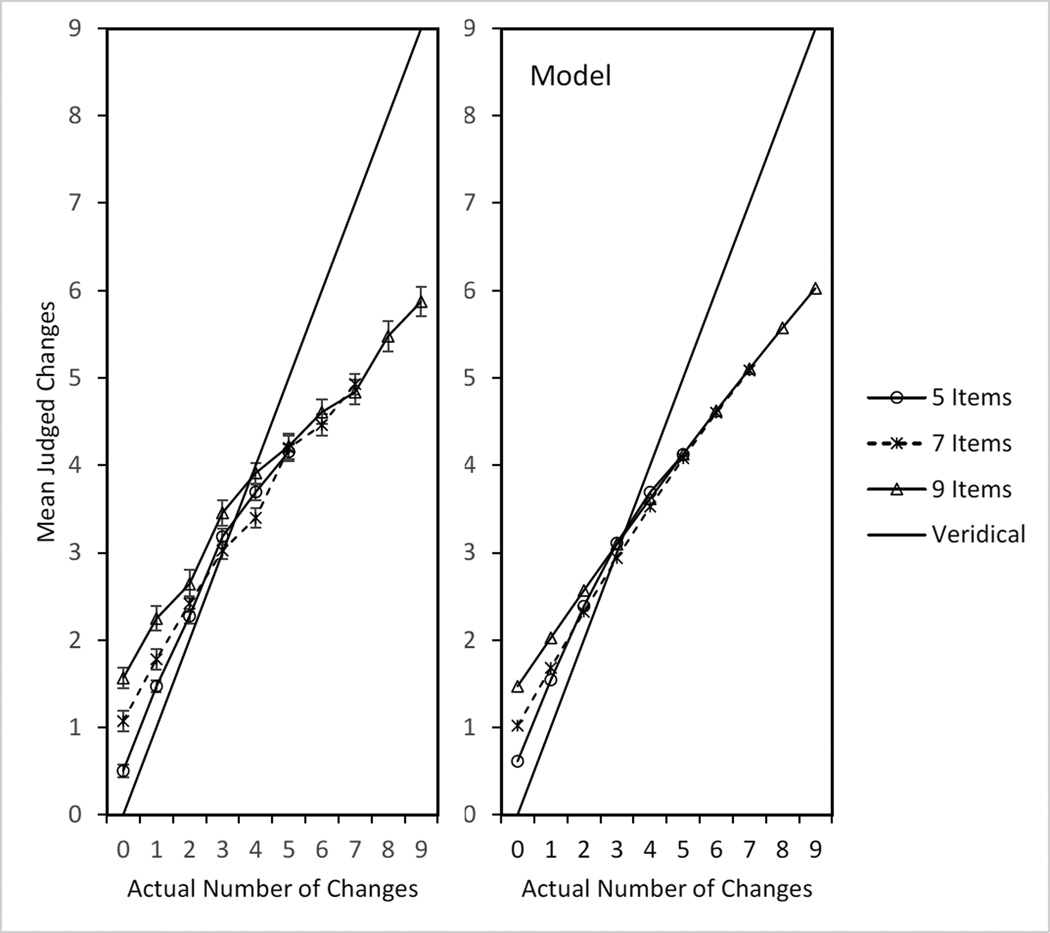
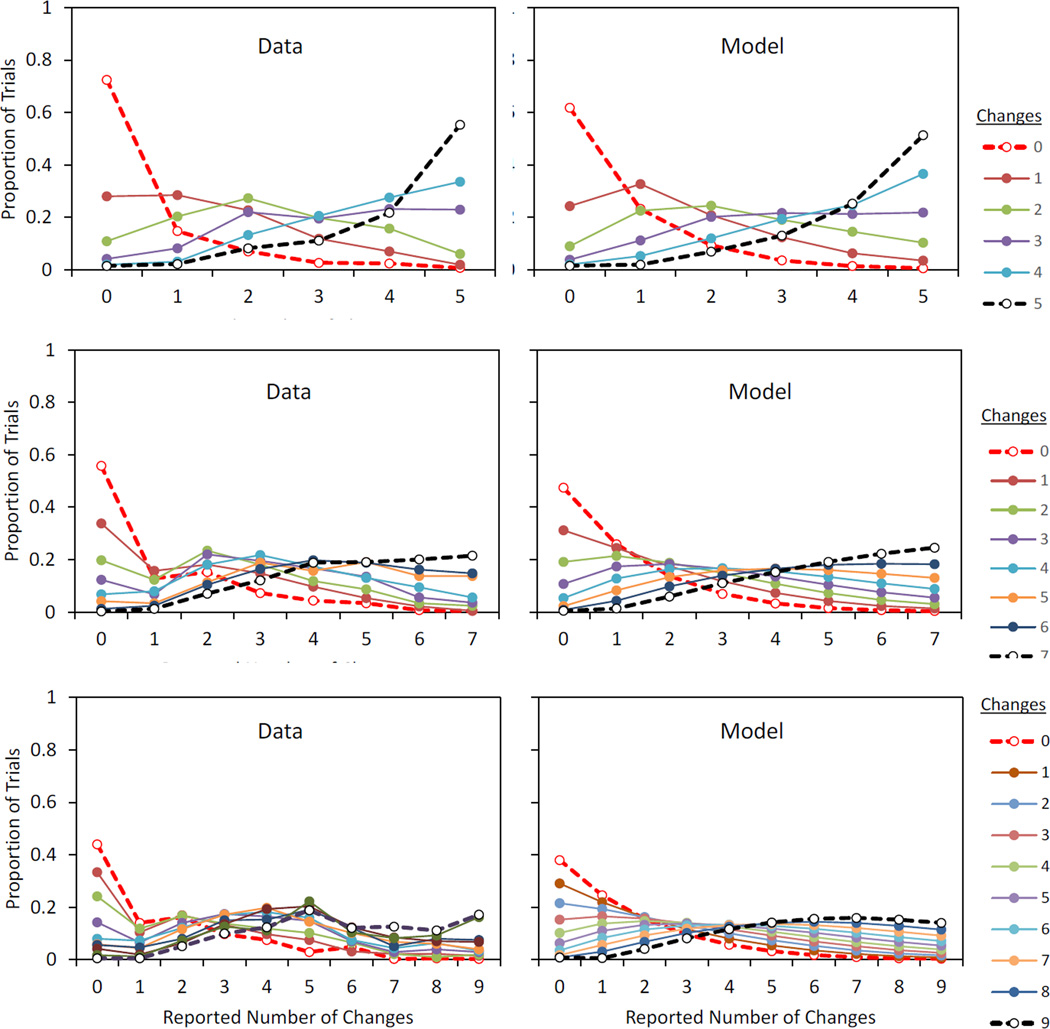
The left-hand panel of Figure 4 shows the mean performance function (mean reported number of changes as a function of the actual number of changes) for each set size. Interestingly, the functions stay separate by set size up to 4 changes and then converges, suggesting that sensitivity to the number of changes may have a different basis after this point.
Figure 4.
In Experiment 3, the mean number of reported changes for each number of actual changes, separately for each set size (graph parameter). Veridical performance (thick line) would yield a slope of 1.0. Left panel, actual data (error bars are standard errors); right panel, winning model.
Mathematical Models of Performance
The usefulness of the multi-change-detection procedure may hinge in part on whether the appropriate model of performance in that procedure can be developed. We do not claim to have the final word on that issue but have had considerable success in finding at least one model that appears to account for a complex pattern of results.
So far, the results of the experiments have been presented in terms of mean reported number of changes for each actual number of changes (Figures 2, 3, & 4). We have found that it is fairly easy for a variety of models to fit these means, whereas a more detailed pattern of responding is harder to fit and provides much better discrimination between possible models. The detailed pattern involves the entire distribution of responses for each actual number of changes.
Failure of an independent-decisions model
In the first model that fit the linear shape of the means rather well, but failed in modeling the detailed pattern, was one in which a decision was made independently for each item in the array. The decision was made based on the item’s representation in working memory or, if that representation was not present, on guessing. For a given set size a given change would have the same probability of being detected regardless of how many other items changed; thus, the reported number of changes increased as a linear function of the actual number of changes, the slope of the function was determined by the number of items in working memory, and the intercept was determined by the guessing rate. This kind of model failed, however, in explaining the detailed pattern of results, which is shown for Experiments 1 and 2 in the left-hand panels of Figure 5 and for Experiment 3 in the left column of panels in Figure 6. Whereas the pattern increases at the extreme responses, the model just described showed a dramatic downturn at the extreme responses.
Figure 5.
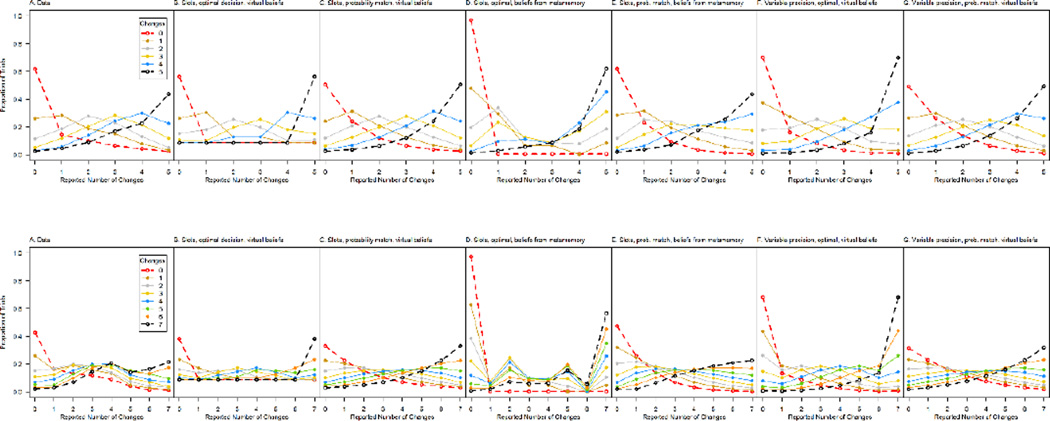
Pattern of responding in Experiment 1 (top left figure) and Experiment 2 (bottom left figure) along with the predictions of a number of viable or nearly-viable models. Each panel shows the proportion of responses with each reported number of changes (x axis) for each actual number of changes (graph parameter). The models differ in whether they are based on limited slots (B–E) or precision (F–G), whether the decision basis is optimal (B, D, F) or according to probability matching (C, E, G), and whether the belief about the number or precision of items in working memory is virtual (B, C, F, G) or based on the metamnemonic judgments (D, E). We did not develop precision models with an alternative belief so the results do not rule out precision models. For the data, the maximum standard error of the mean for any one data point shown is 0.02 in Experiment 1 (top left panel) and 0.03 in Experiment 2 (bottom left panel).
Figure 6.
In Experiment 3, the proportion of trials yielding each reported number of changes (x axis) for each actual number of changes (graph parameter). Left panels, data; right panels, winning model. The top, middle, and bottom rows of panels represent arrays with 5, 7, and 9 items, respectively. The maximum standard error of the mean for any given data point shown (left-hand panels) is 0.04, with the same maximum found for each set size examined separately.
Success of overall-decision models
In the remaining models, which were compared more formally, the general shape of the detailed pattern of responses was reproduced better. These models were based on the premise that performance involves several components. First, a number of changes is detected. The number detected on a particular trial depends on chance but also on the current capacity of working memory. Second, the participant has and employs beliefs about what his or her working memory capability is. Third, based on these first two components and some mental, undoubtedly implicit use of the laws of probability, the participant constructs a distribution of probabilities for the various scenarios (0 changed, 1 changed, etc.). Fourth, a response is determined based on the application of a decision rule to this distribution of probabilities.
Given limitations in the amount of data per individual, we modeled group data. In the first model we tried, capacity was set to a fixed number of items, k, and it was supposed that c changes were detected on a trial. The participant was assumed to be aware of the k value and, therefore, the rules of probability yielded the likelihood of observing c changes given various numbers of actual changes, according to a hypergeometric distribution. The decision rule was to select the most likely scenario to produce the observed number of changes. This model failed badly because when all items changed, k changes were observed and the participant should always indicate that the most likely basis of this result was that all items changed. Similarly, when no changes were detected, the most likely option should always be that no items changed. It can be seen in Figures 5 and 6 that participants were not so severe in their judgments.
Formal modeling
In Figure 5, one can see the modified models that were formally considered, as applied to Experiments 1 and 2. Table 5 shows the outcomes of various models according to 4 fit indices: log likelihood of the fit (Fisher, 1922), the residual sum of squares (Draper, 1998), AIC (Akaike, 1974), and BIC (Schwarz, 1978). In the first model that was considered, the only change that was made was that capacity (k) was said to vary from trial to trial. The proportion of trials with 0, 1, 2…n items in working memory were allowed to vary independently as parameters of the model (Nelder & Mead, 1965). As shown in Panel B of the top and bottom rows of Figure 5, the result was encouraging though still a bit severe at the extremes. Moreover, for the 7-item arrays of Experiment 2, there was an asymmetry in the results that was not picked up by the model.
Table 5.
Parameters of each mathematical model tested
| Expt. | Premise | Items | Rule | Meta | Proportion of Trials with Number of Items in Working Memory As Shown (slot models) | Precision | Scale | LL | ssResid | BIC | AIC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| -- | -- | -- | -- | -- | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | -- | -- | -- | -- | -- | -- |
| 1 | slots | 5 | optimal | virtual | 0.52 | 0.00 | 0.21 | 0.05 | 0.16 | 0.06 | -- | -- | -- | -- | -- | -- | −830.46 | 0.10 | 1678.83 | 1670.92 |
| 1 | slots | 5 | match | virtual | 0.17 | 0.17 | 0.29 | 0.27 | 0.07 | 0.04 | -- | -- | -- | -- | -- | -- | −238.27 | 0.04 | 494.47 | 486.55 |
| 1 | slots | 5 | optimal | actual | 0.02 | 0.05 | 0.31 | 0.62 | 0.00 | 0.00 | -- | -- | -- | -- | -- | -- | −3709.68 | 0.56 | 7437.27 | 7429.35 |
| 1 | slots | 5 | match | actual | 0.03 | 0.08 | 0.18 | 0.58 | 0.13 | 0.00 | -- | -- | -- | -- | -- | -- | −383.94 | 0.04 | 785.80 | 777.88 |
| -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 2 | slots | 7 | optimal | virtual | 0.71 | 0.00 | 0.09 | 0.09 | 0.00 | 0.10 | 0.02 | 0.00 | -- | -- | -- | -- | −1216.97 | 0.18 | 2463.06 | 2447.95 |
| 2 | slots | 7 | match | virtual | 0.24 | 0.24 | 0.24 | 0.24 | 0.06 | 0.00 | 0.00 | 0.00 | -- | -- | -- | -- | −656.97 | 0.11 | 1343.05 | 1327.94 |
| 2 | slots | 7 | optimal | actual | 0.01 | 0.14 | 0.26 | 0.56 | 0.00 | 0.00 | 0.02 | 0.00 | -- | -- | -- | -- | −5491.84 | 1.13 | 11012.80 | 10997.69 |
| 2 | slots | 7 | match | actual | 0.04 | 0.04 | 0.51 | 0.40 | 0.00 | 0.00 | 0.00 | 0.00 | -- | -- | -- | -- | −543.54 | 0.07 | 1116.19 | 1101.07 |
| -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 3 | slots | 5 | optimal | virtual | 0.38 | 0.00 | 0.33 | 0.14 | 0.13 | 0.02 | -- | -- | -- | -- | -- | -- | −290.05 | 0.11 | 598.01 | 590.09 |
| 3 | slots | 5 | match | virtual | 0.05 | 0.18 | 0.34 | 0.33 | 0.09 | 0.00 | -- | -- | -- | -- | -- | -- | −160.70 | 0.09 | 339.32 | 331.41 |
| 3 | slots | 5 | optimal | actual | 0.01 | 0.02 | 0.25 | 0.66 | 0.07 | 0.00 | -- | -- | -- | -- | -- | -- | −684.02 | 0.34 | 1385.95 | 1378.04 |
| 3 | slots | 5 | match | actual | 0.03 | 0.04 | 0.22 | 0.33 | 0.38 | 0.01 | -- | -- | -- | -- | -- | -- | −114.85 | 0.04 | 247.63 | 239.71 |
| -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 3 | slots | 7 | optimal | virtual | 0.61 | 0.00 | 0.10 | 0.11 | 0.12 | 0.04 | 0.03 | 0.00 | -- | -- | -- | -- | −620.94 | 0.25 | 1270.99 | 1255.88 |
| 3 | slots | 7 | match | virtual | 0.02 | 0.35 | 0.35 | 0.15 | 0.12 | 0.00 | 0.00 | 0.00 | -- | -- | -- | -- | −350.45 | 0.17 | 730.01 | 714.90 |
| 3 | slots | 7 | optimal | actual | 0.00 | 0.08 | 0.41 | 0.41 | 0.10 | 0.00 | 0.00 | 0.00 | -- | -- | -- | -- | −1686.92 | 0.90 | 3402.96 | 3387.84 |
| 3 | slots | 7 | match | actual | 0.01 | 0.05 | 0.47 | 0.47 | 0.00 | 0.00 | 0.00 | 0.00 | -- | -- | -- | -- | −261.01 | 0.08 | 551.12 | 536.01 |
| -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 3 | slots | 9 | optimal | virtual | 0.68 | 0.00 | 0.10 | 0.06 | 0.10 | 0.00 | 0.06 | 0.00 | 0.00 | 0.00 | -- | -- | −898.94 | 0.30 | 1839.32 | 1815.87 |
| 3 | slots | 9 | match | virtual | 0.06 | 0.47 | 0.00 | 0.47 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -- | -- | −679.79 | 0.25 | 1401.02 | 1377.57 |
| 3 | slots | 9 | optimal | actual | 0.00 | 0.20 | 0.41 | 0.16 | 0.18 | 0.00 | 0.05 | 0.00 | 0.00 | 0.00 | -- | -- | −2800.86 | 1.40 | 5643.16 | 5619.72 |
| 3 | slots | 9 | match | actual | 0.02 | 0.00 | 0.82 | 0.16 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | -- | -- | −470.84 | 0.14 | 983.12 | 959.68 |
| -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 1 | precision | 5 | optimal | virtual | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | 2.25 | 0.78 | −789.06 | 0.16 | 1585.28 | 1582.12 |
| 1 | precision | 5 | match | virtual | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | 2.95 | 1.32 | −298.11 | 0.05 | 603.39 | 600.23 |
| -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 2 | precision | 7 | optimal | virtual | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | 1.79 | 1.26 | −2049.80 | 0.56 | 4107.91 | 4103.59 |
| 2 | precision | 7 | match | virtual | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | 1.45 | 1.47 | −650.65 | 0.11 | 1309.62 | 1305.30 |
| -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 3 | precision | 5 | optimal | virtual | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | 2.42 | 0.84 | −163.20 | 0.07 | 333.56 | 330.39 |
| 3 | precision | 5 | match | virtual | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | 3.22 | 0.30 | −162.53 | 0.09 | 332.22 | 329.05 |
| -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 3 | precision | 7 | optimal | virtual | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | 1.80 | 0.98 | −663.51 | 0.47 | 1335.33 | 1331.01 |
| 3 | precision | 7 | match | virtual | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | 2.04 | 1.23 | −361.13 | 0.17 | 730.57 | 726.25 |
| -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 3 | precision | 9 | optimal | virtual | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | 1.43 | 1.75 | −1245.28 | 0.79 | 2499.78 | 2494.57 |
| 3 | precision | 9 | match | virtual | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | 1.39 | 1.34 | −683.02 | 0.25 | 1375.26 | 1370.05 |
Note. Optimal refers to the decision that reflects the maximum likelihood scenario, whereas match refers to a probability-matching decision policy. Virtual refers to the assumption that the participant knows what is in working memory, whereas actual refers to an atheoretical estimation of what the participant knows about what is in working memory based on the metamnemonic judgments. Precision refers to mean precision and scale refers to theta, two parameters of a gamma distribution of precisions such that precision/scale=shape. LL=log likelihood. In bold: the best model for each of four fit parameters for each comparison. Notice that, except for Experiment 1, the winning model was consistently the slots model with probability matching and actual metamnemonic data forming decision policy. This finding should not be taken as evidence for the slots model because it might be possible to construct a model in which the metamnemonic judgments are converted to an assumed distribution of precisions.
Different modifications of the model were found to overcome these two limitations. In many studies of behavior, as mentioned earlier, participants do not consistently select the optimal choice from a distribution, but rather probability match (Shanks et al., 2002; Vulkan, 2000). For example, if the participant must choose which of two responses yields a reward and Response A yields the reward 60% of the time in an unpredictable manner, winnings would be optimized by always choosing Response A but, instead, participants tend to choose Response A only about 60% of the time. Use of a probability-matching principle to select the response made the pattern of predictions much more gradual, like the actual results.
What probability matching did not do was produce the asymmetry seen for the 7-item arrays in Experiment 2 (later replicated in the 7- and 9-item arrays of Experiment 3). We found that what did produce the asymmetry was a situation in which the participant misjudged his or her own working memory capacity. At first, we despaired because of the large number of ways in which capacity could be misperceived. Then we realized that a theoretical description of that misperception was not needed, given that we had actual data on participants’ metamnemonic judgments in Experiments 1 and 2. We assumed that the distribution of metamnemonic judgments reflected the distribution of perceived values of capacity. To model Experiment 3, we applied the metamnemonic judgments for the same set sizes in Experiments 1 and 2. The metamnemonic judgment almost never went up to 7, so to model 9-item arrays we assumed probabilities of 0 for believing that there were 8 or 9 items in memory, as well.
Winning model
Figure 5 and Table 5 show that both of these innovations, probability matching and metamnemonic judgments, are needed in order to produce the gradual and asymmetric patterns that were obtained. For 5-item arrays the asymmetry was not very severe, so the use of metamnemonic judgments was not very important for them, but these judgments were essential for a good account of the 7- and 9-item array results. Thus, the model depicted as Panel E in the top and bottom rows of Figure 5 was the winning model. Figure 6 shows that this model provides an excellent fit to the results of Experiment 3, as well. In the model, it is assumed that the belief about k that is used in the inferential process is generally the one yielded by the metamnemonic process, distributed as that process is over trials. Whenever the detected number of changes is higher than the belief about k, the assumption is that the belief is modified upward. (For example, one might think something like the following, implicitly or explicitly: “I believed that I knew only 2 of the items but I have detected three changes, so now I know that I must have had 3 items in working memory.”) Appendix A provides a formal expression of this model.
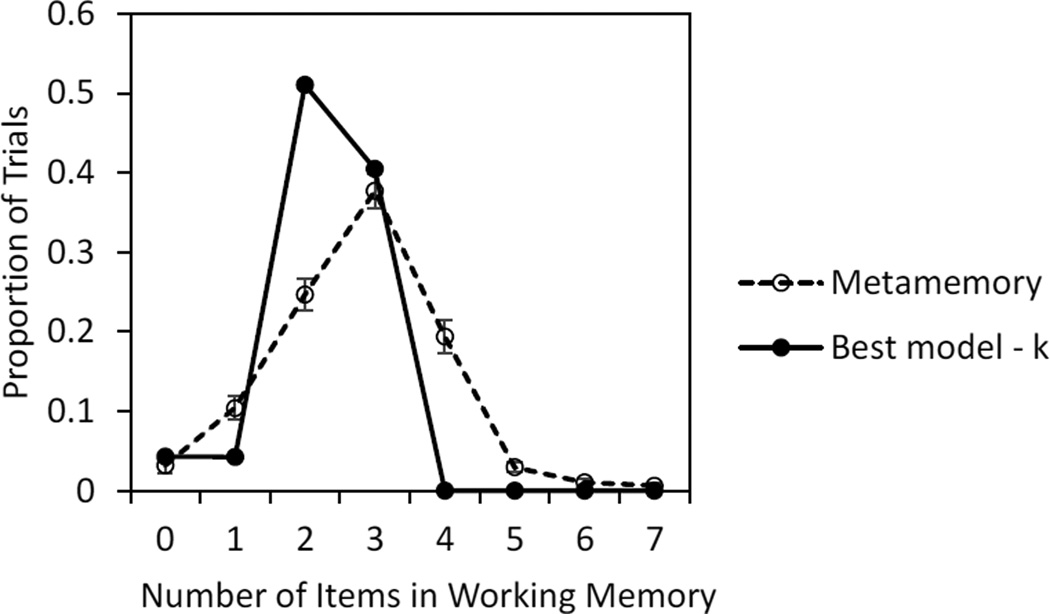
Discrepancies between k and the beliefs about k produce the asymmetry in the detailed pattern of data. The likely reason can be gleaned from Figure 7, which depicts the distribution of metamemory judgments in Experiment 2 along with the theoretical distribution of items in working memory according to the best model. Participants on many trials observe few or no changes in part because they have few opportunities to observe changes (because they only remember 3 items), but think they have more opportunities (because they think they remember 4 or 5 items). On these trials, too much weight is then placed on the absence of detected changes, and the inference is made that there must have been few or no items that changed. The converse is not true because the model is based on the assumption that items must be in working memory in order for a change to be observed; detecting few no-changes (i.e., many changes) presumably happens only with a large number of items in working memory, but there are rarely more than 4 items in working memory according to the model.
Figure 7.
For Experiment 2, the distribution of metamemory judgments in the data (error bars are standard errors) and the distribution of items in working memory according to the best model.
Precision-based models
It is also possible to account for some key aspects of the results under the assumption that all of the array items are represented in working memory, but that some of them are represented at a level that is too imprecise to allow the participant to notice a change from one color to another (e.g., Bays & Husain, 2008; van den Berg et al., 2012). As explained in Appendix A, the two parameters of that model determine a probability distribution of precisions for various items in the arrays, assuming a gamma distribution. This kind of approach elegantly produces the gradually changing patterns that we have observed. If the precision model is allowed to use a probability-matching rule rather than always choosing the optimal response within the confines of the observed changes in the array, the fit generally improves further (see Table 5 and the rightmost two panels of both rows in Figure 5).
What the precision approach cannot easily do is produce the asymmetry that we see in the data, especially at the larger set sizes. In the slot models, we have not used a theoretical principle to create the discrepancy between the actual and assumed number of items in working memory; we have used the metamnemonic judgments. To implement a precision approach with this discrepancy included, it would be necessary to make an assumption about the believed distribution of precisions that differs from the real distribution. That would be possible and might well produce the desired result, but we see little point in carrying out the exercise. If we failed to find a satisfactory solution we would still wonder whether we had just not hit upon the best distribution, so in any case we cannot claim that the slot approach outweighs the precision approach for these data. We claim only to have found a reasonable account of the data making explicit the inferential process, based on the number of items in working memory; the account could be modified to be based on the number of items in working memory with sufficient precision.
General Discussion
Our new multi-change-detection procedure addresses a question that at least potentially is ecologically different from the more conventional one of single-change detection, reflecting a different collection of real-world concerns. For example, the single-change-detection procedure might be like comparing a set list of objects on a table, such as wares to be sold, to the same set a moment later to make sure that no item has been moved or stolen and there has been no substitution. In contrast, the multi-change-detection procedure might be like comparing one peddler’s collection of goods on display to another’s, to decide which one to do business with. The data from three experiments show that participants carry out multiple-change detection as if they base their responses on a limited memory for some of the items in the array. Figures 4–6 show that the results are similar to a simple model based on the notion of comparing the number of detected changes to the different scenarios that could result in that kind of detection and responding with probability matching between the observed and to-be-expected probabilities. It is unclear if the same psychological processes would operate for arrays of a very large numbers of items, as in the comparison of photographs of scenes from a geographic setting before and after a natural disaster has hit.
Despite task differences, both tasks can be assessed to determine whether they display the properties desired of working memory tasks. Previous results indicate that array change-detection task results correlate well with other measures of working memory, including the presently-used operation span and running span measures (Cowan et al., 2005). It is true of the new multi-change-detection procedure also, but only if the number of items in the array is sufficiently beyond the capacity limit. The correlations between performance and composite working memory scores were substantial in Experiment 2, in which 7-item arrays were used, but not in Experiment 1 with its 5-item arrays.
We also collected informative data on participants’ knowledge of their own working memories. It is theoretically important that we found metamemory that correlates with actual memory in terms of trial-to-trial fluctuations. Participants appear to know something about how good or bad their working memory contents are on a particular trial, as one would predict, for example, if the relevant contents of working memory were at least partly held in the focus of attention (Cowan, 1988, 1995). If it turns out that all items are in working memory but just not at sufficient precision, the metamemory judgments still tell us about participants’ manner of converting their precision to a likely number of items usefully precise for the task.
Regardless of the reason for the correlation between working memory performance and metamemory, it provides evidence of trial-to-trial fluctuations that are due not to chance, but to variation in memory or attention from trial to trial that can be indexed to some extent by the storage judgment response. This fluctuation does not occur in most extant models, though it has been included as a fluctuation in memory resources (van den Berg et al., 2012) or attention (Rouder et al., 2008). Most importantly, the metamnemonic results proved to be important in providing a possible reason for the asymmetries in the detailed pattern of responding especially for the large (7- and 9-item) arrays; participants often overestimated the items in working memory according to the model, and this discrepancy accounted for the asymmetries.
It has been difficult in the working memory literature to discriminate between slots and resources as a basis for working memory, in our opinion, because alternative assumptions can make either model viable. A parallel exists in the literature on multi-object tracking. Tripathy, Narasimham, and Barrett (2007) varied the number of moving dots that changed direction and found that the ability to determine whether they turned clockwise or counter-clockwise varied with the angle of the change. Ma and Huang (2009) found that these data were best fit with a model in which there is no attentional capacity limit, but rather a fluid resource that monitors all dots. We note that the slots model might have an improved fit, though, if attention is shifted at least once during the display period and smaller angles of change require more time for a change to be noticed. According to this revised limited-slots explanation, participants may sample certain dots and then shift to other dots, sometimes shifting too soon to observe small-angle changes. Alternative versions of models will undoubtedly likewise prove relevant to finding the best account of multi-object-change detection in working memory.
In sum, the present results and analyses generalize the notion of same-different comparisons based on working memory, to situations in which the extent of change in an array is to be assessed. It remains to be seen how the model suggested here might be modified to account for more complex data sets (e.g., objects that can change in more than one feature), and whether the model can be applied in any form to very large set sizes or natural scenes. The research also combines objective and subjective measures of working memory as a way to understand the capacity of working memory and the processing of its contents. Finally, the study illustrates the importance of examining converging measures across working memory tasks, which induce different processing biases and require different theoretical models.
Acknowledgments
This research was supported by NIH grant R01-HD21338. Some of the work was completed while Cowan was a Professorial Fellow at the University of Edinburgh. M. Sunday is now at the University of South Carolina. We thank Gordon Logan and Geoffrey Woodman for helpful comments and Jacob T. Nicholson and Suzanne Redington for assistance. Wei Ji Ma was especially helpful in providing extensive guidance for mathematical modeling. Among the authors, K. Hardman carried out the mathematical modeling. R code for the models is available from the authors.
Appendix A
Definitions of the Models
Slots Models
The losing slots models form the basis of the winning slots model, so the losing model will be described first, followed by the final adjustment that creates the winning model out of the losing model. The slot models assume that on each trial, a participant loads k items from the sample array into WM. Therefore, k represents the number of items in WM on a given trial, not an asymptotic capacity for items. We assume that k follows some distribution, but we do not specify a shape for the distribution but rather freely estimate the proportion of time that k took on each value from 0 to the array size. Due to limited data at the individual participant level, the k were estimated based on the data from all participants, so it is impossible to tell whether the distribution of k represents within-participant variability, between-participant variability, or some combination of the two. When the test array is shown, the participant compares the k items that are in WM to the corresponding items in the test array, with the correspondence determined by item location. In this comparison process, all of the k items that are in WM that changed from sample to test will be detected, resulting in the participant knowing that there were D detected changes. It is natural to use a hypergeometric distribution to describe this process. The hypergeometric distribution applies to a case in which there is a finite population, the members of which have one of two possible states, and a sample is taken from that population and the number of sampled items with each of the states counted. In our case, the finite population is the array of items, with size N, the sample is the contents of WM, with size k, and D is the number of changes detected in the sample. Because changes are detected without error, we can speak as though the N members of the population are changes or non-changes, k of which are sampled.
At this point, a participant has all of the information they are able to obtain. They know how many changes they have observed, but now they must make an inference about the number of changes in the population in order to make their response. This can be done by hypothesizing various numbers of changes in the population, denoted C, and using the hypergeometric distribution to calculate the probability of having observed D changes out of k sampled items from a population of size N for each hypothesized C. The resulting distribution gives the relative probability of each C having given rise to the observed number of changes. For example, if N=5, k=3, and D=2, the participant would hypothesize that there were 0 to 5 changes in the population. Because 2 changes were detected, both C=0 and C=1 are impossible, so they have 0 probability. Similarly, 1 non-change was detected, so C=5 is impossible. Finally, by the hypergeometric distribution, the probability of 2, 3, or 4 changes are 0.2, 0.4, and 0.4, respectively.
In a rudimentary model that was unsuccessful, we assumed that the most likely response would be used, in this case the participant makes a random choice between 3 and 4 changes. This model was clearly inadequate (Figure 5, top-B and bottom-B) so, in a subsequent model that still is not the winning model, the participant was said to assume a probability match (Figure 5-C). In our example, they would respond that 2, 3, or 4 changes occurred with probability 0.2, .0.4, and 0.4, respectively.
A final adjustment to the model allows us to incorporate the metamemory judgments and reach the winning slots model (when applied along with probability matching as in Figure 5, top and bottom Panel E, and in Figure 6). Instead of assuming that participants know that they have k items in mind, we will have the model say that participants have a subjective belief about how many items they have in mind (in a task that occurred on some trials, before the probe array), denoted B. In this version of the model, when calculating the probability of each true number of changes, the participant uses B instead of k. On each trial, B is initially sampled from the distribution of metamemory judgments given by participants, with the probability of sampling each B dependent of how often participants endorsed the belief that they had that amount of information in WM. That B is independent of k and D, with one exception. It was assumed that a participant who observed more changes than the initially-believed number of items in working memory would adjust their belief upward, resulting in B=D on those trials. In this version of the model, it must be assumed that participants do not detect non-changes, as otherwise they would know k exactly by adding up the number of detected changes and non-changes. There is previous evidence of this asymmetry in which participants dwell on changes in a change-detection task (Gilchrist & Cowan, 2014; Hyun, Woodman, Vogel, Hollingworth, & Luck, 2009).
Variable Precision Models
The variable precision models take a different approach. They assume that all of the items in the sample array are encoded with some variable precision. Each item in the array is either a non-change, in which case it has a true value of 0, or a change, in which case it has a true value of 1. The participant observes these true values for all of the items in the array, but with error. This error is assumed to follow a normal distribution with mean 0 and variance equal to the inverse of the precision. The precision of measurement (i.e. the inverse of how much error there is in the measurement) is assumed to follow a gamma distribution parameterized as having a mean and a scale. In this model, only two parameters are estimated: the mean and scale of the gamma distribution of precisions, which are assumed to be the same across all participants and trials. This was done because we had limited data per participant, not because we believe that all participants and trials are the same.
Given that participants have measured the change state of each of the items in the array, they must then decide how many changes they believe to have occurred. If they measured the items without error, this would be trivial because they have information about all of the items. However, because of the measurement error, they are not easily able to come to an unambiguous decision about how many changes they believe to have occurred. Like the slots models, in the variable precision model, the participants are assumed to hypothesize a true number of changes, C, which varies from 0 to N. For each C, each possible configuration of which items could have changed is enumerated and the observed measurements are compared with each possible configuration. The likelihood of obtaining the observed measurements given each configuration and knowledge of the precision of each measurement is calculated by the participant. Note that it is assumed that participants know on an item-by-item basis the precision with which that item’s state was measured. These likelihoods are then averaged across all configurations that have the same number of changes. This results in a distribution of belief about the probability of each number of changes producing the observed measurements.
In one version (Figure 5, top and bottom F), participants always choose the most likely response. In a further version of the model that proved to be slightly superior (Figure 5, top and bottom G), participants were assumed to probability-match rather than choosing the optimal solution. They were assumed to respond that each number of changes occurred with some probability that depended on the distribution of probabilities.
The parameters of the models were estimated using the Nelder-Mead simplex (Nelder and Mead, 1965), a numerical search algorithm, as implemented by the “optim” function in R (R Core Team, 2014). The R code is available from the authors.
Footnotes
We are indebted to Wei Ji Ma, who made us aware of this possible basis of modeling and formulated both the basic model that assumes continuous resources and the rudimentary slots model upon which we elaborated (by adding probability matching and a perceived k distribution based on the metamemory results) to form what we term the winning model.
Contributor Information
Nelson Cowan, Department of Psychological Sciences, University of Missouri.
Kyle Hardman, Department of Psychological Sciences, University of Missouri.
J. Scott Saults, Department of Psychological Sciences, University of Missouri.
Christopher L. Blume, Department of Psychological Sciences, University of Missouri
Katherine M. Clark, Department of Psychological Sciences, University of Missouri
Mackenzie A. Sunday, Department of Psychological Sciences, Vanderbilt University
References
- Akaike H. A new look at the statistical model identification. IEEE Transactions on Automatic Control. 1974;19:716–723. [Google Scholar]
- Allen RJ, Hitch GJ, Mate J, Baddeley AD. Feature binding and attention in working memory: A resolution of previous contradictory findings. Quarterly Journal of Experimental Psychology. 2012;65:2369–2383. doi: 10.1080/17470218.2012.687384. [DOI] [PubMed] [Google Scholar]
- Anderson DE, Vogel EK, Awh E. Precision in visual working memory reaches a stable plateau when individual item limits are exceeded. The Journal Of Neuroscience. 2011;31:1128–1138. doi: 10.1523/JNEUROSCI.4125-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Awh E, Barton B, Vogel EK. Visual working memory represents a fixed number of items regardless of complexity. Psychological Science. 2007;18:622–628. doi: 10.1111/j.1467-9280.2007.01949.x. [DOI] [PubMed] [Google Scholar]
- Baars BJ, Franklin S. How conscious experience and working memory interact. Trends in Cognitive Sciences. 2003;7:166–172. doi: 10.1016/s1364-6613(03)00056-1. [DOI] [PubMed] [Google Scholar]
- Bae GY, Flombaum JI. Two items remembered as precisely as one: How integral features can improve visual working memory. Psychological Science. 2013 doi: 10.1177/0956797613484938. online ahead of print. [DOI] [PubMed] [Google Scholar]
- Barrouillet P, Portrat S, Camos V. On the law relating processing to storage in working memory. Psychological Review. 2011;118:175–192. doi: 10.1037/a0022324. [DOI] [PubMed] [Google Scholar]
- Bays PM, Husain M. Dynamic shifts of limited working memory resources in human vision. Science. 2008;321:851–854. doi: 10.1126/science.1158023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brady TF, Alvarez GA. Hierarchical encoding in visual working memory: Ensemble statistics bias memory for individual items. Psychological Science. 2011;22:384–392. doi: 10.1177/0956797610397956. [DOI] [PubMed] [Google Scholar]
- Brady TF, Tenenbaum JB. A probabilistic model of visual working memory: Incorporating higher order regularities into working memory capacity estimates. Psychological Review. 2013;120:85–109. doi: 10.1037/a0030779. [DOI] [PubMed] [Google Scholar]
- Bunnell JK, Baken DM, Richards-Ward LA. The effect of age on metamemory for working memory. New Zealand Journal of Psychology. 1999;28:23–29. [Google Scholar]
- Camos V, Mora G, Oberauer K. Adaptive choice between articulatory rehearsal and attentional refreshing in verbal working memory. Memory & Cognition. 2011;39:231–244. doi: 10.3758/s13421-010-0011-x. [DOI] [PubMed] [Google Scholar]
- Chong SC, Treisman A. Statistical processing: computing the average size in perceptual groups. Vision Research. 2005;45:891–900. doi: 10.1016/j.visres.2004.10.004. [DOI] [PubMed] [Google Scholar]
- Cohen MA, Alvarez GA, Nakayama K. Natural-scene perception requires attention. Psychological Science. 2011;22:1165–1172. doi: 10.1177/0956797611419168. [DOI] [PubMed] [Google Scholar]
- Cowan N. Evolving conceptions of memory storage, selective attention, and their mutual constraints within the human information processing system. Psychological Bulletin. 1988;104:163–191. doi: 10.1037/0033-2909.104.2.163. [DOI] [PubMed] [Google Scholar]
- Cowan N. Oxford Psychology Series (No. 26) New York: Oxford University Press; 1995. Attention and memory: An integrated framework. [Google Scholar]
- Cowan N. The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behavioral and Brain Sciences. 2001;24:87–185. doi: 10.1017/s0140525x01003922. [DOI] [PubMed] [Google Scholar]
- Cowan N. Working memory capacity. Hove, East Sussex, UK: Psychology Press; 2005. [Google Scholar]
- Cowan N, Blume CL, Saults JS. Attention to attributes and objects in working memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2013;39:731–747. doi: 10.1037/a0029687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, Elliott EM, Saults JS, Morey CC, Mattox S, Hismjatullina A, Conway ARA. On the capacity of attention: Its estimation and its role in working memory and cognitive aptitudes. Cognitive Psychology. 2005;51:42–100. doi: 10.1016/j.cogpsych.2004.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, Morey CC, AuBuchon AM, Zwilling CE, Gilchrist AL. Seven-year-olds allocate attention like adults unless working memory is overloaded. Developmental Science. 2010;13:120–133. doi: 10.1111/j.1467-7687.2009.00864.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, Saults JS, Blume CL. Central and peripheral components of working memory storage. Journal of Experimental Psychology: General. 2014;143:1806–1836. doi: 10.1037/a0036814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donkin C, Nosofsky RM, Gold JM, Shiffrin RM. Discrete slot models of visual working-memory response times. Psychological Review. 2013;4:873–902. doi: 10.1037/a0034247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Draper NR, Smith H. Applied Regression Analysis. 3rd ed. John Wiley; 1998. [Google Scholar]
- Fisher RA. On the mathematical foundations of theoretical statistics. Philosophical Transactions of the Royal Society A. 1922;222:309–368. [Google Scholar]
- Fougnie D, Marois R. What limits working memory capacity? Evidence for modality-specific sources to the simultaneous storage of visual and auditory arrays. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2011;37:1329–1341. doi: 10.1037/a0024834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibson B, Wasserman E, Luck SJ. Qualitative similarities in the visual short-term memory of pigeons and people. Psychonomic Bulletin & Review. 2011;18:979–984. doi: 10.3758/s13423-011-0132-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilchrist AL, Cowan N. A two-stage search of visual working memory: Investigating speed in the change-detection paradigm. Attention, Perception, & Psychophysics. 2014;76:2031–2050. doi: 10.3758/s13414-014-0704-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gold JM, Fuller RL, Robinson BM, McMahon RP, Braun EL, Luck SJ. Intact attentional control of working memory encoding in schizophrenia. Journal of Abnormal Psychology. 2006;115:658–673. doi: 10.1037/0021-843X.115.4.658. [DOI] [PubMed] [Google Scholar]
- Hollingworth A. Constructing visual representations of natural scenes: The roles of short- and long-term visual memory. Journal of Experimental Psychology: Human Perception and Performance. 2004;30:519–537. doi: 10.1037/0096-1523.30.3.519. [DOI] [PubMed] [Google Scholar]
- Hyun J-S, Woodman GF, Vogel EK, Hollingworth A, Luck SJ. The comparison of visual working memory representations with perceptual inputs. Journal of Experimental Psychology: Human Perception and Performance. 2009;35:1140–1160. doi: 10.1037/a0015019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang Y, Chun MM, Olson IR. Perceptual grouping in change detection. Perception & Psychophysics. 2004;66:446–453. doi: 10.3758/bf03194892. [DOI] [PubMed] [Google Scholar]
- Kane MJ, Brown LH, McVay JC, Silvia PJ, Myin-Germeys I, Kwapil TR. For whom the mind wanders, and when: An experience-sampling study of working memory and executive control in daily life. Psychological Science. 2007;18:614–621. doi: 10.1111/j.1467-9280.2007.01948.x. [DOI] [PubMed] [Google Scholar]
- Kane MJ, Hambrick DZ, Tuholski SW, Wilhelm O, Payne TW, Engle RE. The generality of working memory capacity: A latent-variable approach to verbal and visuospatial memory span and reasoning. Journal of Experimental Psychology: General. 2004;133:189–217. doi: 10.1037/0096-3445.133.2.189. [DOI] [PubMed] [Google Scholar]
- Koriat A, Helstrup T. Metacognitive aspects of memory. In: Magnussen S, Helstrup T, editors. Everyday memory. Hove, UK: Psychology Press; 2007. pp. 251–274. [Google Scholar]
- Lachman JL. Metamemory through the adult life span. Developmental Psychology. 1979;15:543–551. [Google Scholar]
- Lewis-Peacock JA, Drysdale AT, Oberauer K, Postle BR. Neural evidence for a distinction between short-term memory and the focus of attention. Journal Of Cognitive Neuroscience. 2012;24:61–79. doi: 10.1162/jocn_a_00140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logie RH, Brockmole JR, Jaswal S. Feature binding in visual short-term memory is unaffected by task-irrelevant changes of location, shape, and color. Memory &Cognition. 2011;39:24–36. doi: 10.3758/s13421-010-0001-z. [DOI] [PubMed] [Google Scholar]
- Luck SJ, Vogel EK. The capacity of visual working memory for features and conjunctions. Nature. 1997;390:279–281. doi: 10.1038/36846. [DOI] [PubMed] [Google Scholar]
- Ma WJ, Huang W. No capacity limit in attentional tracking: Evidence for probabilistic inference under a resource constraint. Journal of Vision. 2009;3(11):1–30. doi: 10.1167/9.11.3. [DOI] [PubMed] [Google Scholar]
- Maki RH. The Roles of competition, target accessibility, and cue familiarity in metamemory for word pairs. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1999;25:1011–1023. [Google Scholar]
- Morey CC, Mall JT. Cross-domain costs during concurrent verbal and spatial serial memory tasks are asymmetric. Quarterly Journal of Experimental Psychology. 2012;65:1777–1797. doi: 10.1080/17470218.2012.668555. [DOI] [PubMed] [Google Scholar]
- Nelder JA, Mead R. A simplex algorithm for function minimization. Computer Journal. 1965;7:308–313. [Google Scholar]
- Oberauer K. The focus of attention in working memory—from metaphors to mechanisms. Frontiers in Human Neuroscience. 2013;7:1–16. doi: 10.3389/fnhum.2013.00673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oberauer K, Eichenberger S. Visual working memory declines when more features must be remembered for each object. Memory & Cognition. 2013 doi: 10.3758/s13421-013-0333-6. E-publication ahead of print. [DOI] [PubMed] [Google Scholar]
- Pashler H. Familiarity and visual change detection. Perception & Psychophysics. 1988;44:369–378. doi: 10.3758/bf03210419. [DOI] [PubMed] [Google Scholar]
- Phillips WA. On the distinction between sensory storage and short-term visual memory. Perception & Psychophysics. 1974;16:283–290. [Google Scholar]
- R Core Team. R Foundation for Statistical Computing. Austria: Vienna; 2014. R: A language and environment for statistical computing [Computer software] URL http://www.R-project.org/. [Google Scholar]
- Rademaker RL, Tredway CH, Tong F. Introspective judgments predict the precision and likelihood of successful maintenance of visual working memory. Journal of Vision. 2012;21(13):1–13. doi: 10.1167/12.13.21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouder JN, Morey RD, Cowan N, Zwilling CE, Morey CC, Pratte MS. An assessment of fixed-capacity models of visual working memory. Proceedings of the National Academy of Sciences (PNAS) 2008;105:5975–5979. doi: 10.1073/pnas.0711295105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouder JN, Morey RD, Morey CC, Cowan N. How to measure working-memory capacity in the change-detection paradigm. Psychonomic Bulletin & Review. 2011;18:324–330. doi: 10.3758/s13423-011-0055-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz Gideon E. Estimating the dimension of a model. Annals of Statistics. 1978;6:461–464. [Google Scholar]
- Scolari M, Vogel EK, Awh E. Perceptual expertise enhances the resolution but not the number of representations in working memory. Psychonomic Bulletin & Review. 2008;15:215–222. doi: 10.3758/pbr.15.1.215. [DOI] [PubMed] [Google Scholar]
- Shanks DR, Tunney RJ, McCarthy JD. A re-examination of probability matching and rational choice. Journal of Behavioral Decision Making. 2002;15:233–250. [Google Scholar]
- Shipstead Z, Redick TS, Hicks KL, Engle RW. The scope and control of attention as separate aspects of working memory. Memory. 2012;20:608–628. doi: 10.1080/09658211.2012.691519. [DOI] [PubMed] [Google Scholar]
- Sperling G. The information available in brief visual presentations. Psychological Monographs. 1960;74 (Whole No. 498.) [Google Scholar]
- Stevanovski B, Jolicoeur P. Visual short-term memory: Central capacity limitations in short-term consolidation. Visual Cognition. 2007;15:532–563. [Google Scholar]
- Suchow JW, Fougnie D, Brady TF, Alvarez GA. Terms of the debate on the format and structure of visual memory. Attention, Perception, & Psychophysics. 2014 doi: 10.3758/s13414-014-0690-7. [DOI] [PubMed] [Google Scholar]
- Thiele JE, Pratte MS, Rouder JN. On perfect working-memory performance with large numbers of items. Psychonomic Bulletin & Review. 2011;18:958–963. doi: 10.3758/s13423-011-0108-7. [DOI] [PubMed] [Google Scholar]
- Tripathy SP, Narasimham S, Barrett BT. On the effective number of tracked trajectories in normal human vision. Journal of Vision. 2007;72(6):1–18. doi: 10.1167/7.6.2. [DOI] [PubMed] [Google Scholar]
- Unsworth N, Heitz RP, Schrock JC, Engle RW. An automated version of the operation span task. Behavior Research Methods. 2005;37:498–505. doi: 10.3758/bf03192720. [DOI] [PubMed] [Google Scholar]
- van den Berg R, Shin H, Chou W-C, George R, Ma WJ. Variability in encoding precision accounts for visual short-term memory limitations. Proceedings of the National Academy of Sciences. 2012;109:8780–8785. doi: 10.1073/pnas.1117465109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Berg R, Awh E, Ma WJ. Factorial comparison of working memory models. Psychological Review. 2014;121:124–149. doi: 10.1037/a0035234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vergauwe E, Barrouillet P, Camos V. Do mental processes share a domain general resource? Psychological Science. 2010;21:384–390. doi: 10.1177/0956797610361340. [DOI] [PubMed] [Google Scholar]
- Vogel EK, McCollough AW, Machizawa MG. Neural measures reveal individual differences in controlling access to working memory. Nature. 2005;438:500–503. doi: 10.1038/nature04171. [DOI] [PubMed] [Google Scholar]
- Vogel EK, Woodman GF, Luck SJ. Storage of features, conjunctions, and objects in visual working memory. Journal of Experimental Psychology: Human Perception and Performance. 2001;27:92–114. doi: 10.1037//0096-1523.27.1.92. [DOI] [PubMed] [Google Scholar]
- Vulkan N. An economist’s perspective on probability matching. Journal of Economic Surveys. 2000;14:101–118. [Google Scholar]
- Wheeler ME, Treisman AM. Binding in short-term visual memory. Journal of Experimental Psychology: General. 2002;131:48–64. doi: 10.1037//0096-3445.131.1.48. [DOI] [PubMed] [Google Scholar]
- Wilken P, Ma WJ. A detection theory account of change detection. Journal of Vision. 2004;4:1120–1135. doi: 10.1167/4.12.11. [DOI] [PubMed] [Google Scholar]
- Woodman GF, Luck SJ. Dissociations among attention, perception, and awareness during object substitution masking. Psychological Science. 2003;14:605–611. doi: 10.1046/j.0956-7976.2003.psci_1472.x. [DOI] [PubMed] [Google Scholar]
- Woodman GF, Vogel EK, Luck SJ. Visual search remains efficient when visual working memory is full. Psychological Science. 2001;12:219–224. doi: 10.1111/1467-9280.00339. [DOI] [PubMed] [Google Scholar]
- Zhang W, Luck SJ. Discrete fixed-resolution representations in visual working memory. Nature. 2008;453:23–35. doi: 10.1038/nature06860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W, Luck SJ. Sudden death and gradual decay in visual working memory. Psychological Science. 2009;20:423–428. doi: 10.1111/j.1467-9280.2009.02322.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W, Luck SJ. The number and quality of representations in working memory. Psychological Science. 2011;22:1434–1441. doi: 10.1177/0956797611417006. [DOI] [PMC free article] [PubMed] [Google Scholar]