Meta‐analysis of genome‐wide association from genomic prediction models

Summary

Genome‐wide association (GWA) studies based on GBLUP models are a common practice in animal breeding. However, effect sizes of GWA tests are small, requiring larger sample sizes to enhance power of detection of rare variants. Because of difficulties in increasing sample size in animal populations, one alternative is to implement a meta‐analysis (MA), combining information and results from independent GWA studies. Although this methodology has been used widely in human genetics, implementation in animal breeding has been limited. Thus, we present methods to implement a MA of GWA, describing the proper approach to compute weights derived from multiple genomic evaluations based on animal‐centric GBLUP models. Application to real datasets shows that MA increases power of detection of associations in comparison with population‐level GWA, allowing for population structure and heterogeneity of variance components across populations to be accounted for. Another advantage of MA is that it does not require access to genotype data that is required for a joint analysis. Scripts related to the implementation of this approach, which consider the strength of association as well as the sign, are distributed and thus account for heterogeneity in association phase between QTL and SNPs. Thus, MA of GWA is an attractive alternative to summarizing results from multiple genomic studies, avoiding restrictions with genotype data sharing, definition of fixed effects and different scales of measurement of evaluated traits.

Introduction

The recent availability of high‐density single nucleotide polymorphism (SNP) genotyping platforms has stimulated the development and implementation of genomic selection in animal breeding (Meuwissen et al. 2001; Goddard & Hayes 2007). Genomic selection permits estimation of genomic breeding values, or GEBV, for economically relevant traits (González‐Recio et al. 2008; De los Campos et al. 2009; Hayes et al. 2009; VanRaden et al. 2009). A common practice after estimation of GEBV from a genomic evaluation consists of performing genome‐wide association (GWA) analyses (Wang et al. 2012, 2014; Gualdrón Duarte et al. 2014). In GWA, the goal is to identify genomic regions that explain a substantial portion of the genetic variation in complex traits (Hirschhorn & Daly 2005; Visscher et al. 2007). Because GWA does not assume a priori knowledge of genomic location of associated segments, it constitutes an unbiased search procedure regarding the function or location of causal genes (Hirschhorn & Daly 2005).

A limitation of many GWA applications in animal breeding is that the effect sizes of tests of association between SNP and phenotype are extremely small, and detection of signals requires a large number of individuals (Minozzi et al. 2012). However, increasing sample size is difficult in the context of animal production due to difficulties in having populations with comparable phenotypes and the limited availability of samples from commercial production systems (Houlston et al. 2010). Furthermore, animal populations contain stratification that, if ignored, can result in spurious associations between markers and traits of interest (Rabinowitz 1997; Hirschhorn & Daly 2005). In order to increase sample size, mapping precision and power of detection of variants with small effects and, subsequently, to decrease false‐positive associations, data from different populations can be pooled in a joint analysis (JA) (Allison & Heo 1998; Skol et al. 2006). If well applied, this approach increases power of detection of QTL that cannot be found through individual population analyses (Lander & Kruglyak 1995). However, a challenge that appears under this methodology is to deal with different phenotype and model definitions and also with qualitative and quantitative differences in variance components across populations (Minozzi et al. 2012). Furthermore, the implementation of JA requires availability of original data from target populations, which can be limited in commercial populations due to specific interests and restrictions to sharing genotypes. One alternative is to perform a meta‐analysis of GWA (MA‐GWA). First mentioned by Glass (1976), MA is a statistical methodology that combines, in a single statistic, summary results from different studies or populations, accounting for population structure and population‐specific covariates (Willer et al. 2010; Evangelou & Ioannidis 2013). According to Minozzi et al. (2012), MA provides more accurate estimates of SNP effects derived from population‐specific GEBVs, improving the power to detect genomic associations that are consistent across populations.

In human and model organism genetics research, MA‐GWA has been widely used (Begum et al. 2012; Evangelou & Ioannidis 2013). However, applications of MA are just starting in animal breeding. For instance, Wood et al. (2006) implemented a MA using Bayesian hierarchical models to evaluate consistence of associations between the thyroglobulin gene (TG) and marbling in beef cattle. Silva et al. (2010) applied MA to linkage analysis results to find QTL for three different categories of production traits (fatness, carcass composition and growth traits), considering independent studies. Porto Neto et al. (2010) used MA to combine results from GWA and gene expression studies related to the study of tick resistance. Furthermore, one of the most commonly used whole‐genome regression methods to predict phenotypes from thousands of SNPs is GBLUP (Meuwissen et al. 2001; Misztal et al. 2009; Aguilar et al. 2010), which has been recently adapted to perform GWA (Wang et al. 2012, 2014; Gualdrón Duarte et al. 2014). Therefore, implementation of a MA‐GWA from several GBLUP analyses is an attractive approach to increase power of detection of variants with small but consistent effects across populations.

Consequently, the goal of this study was to describe methods for the implementation of MA‐GWA, combining results from multiple independent GBLUP evaluations while accounting for population structure and heterogeneity of variance components. In particular, we show how to properly weight estimates of SNP effects from multiple populations and how to perform the significance testing. We illustrate the proposed method with real data from three pig populations.

Materials and methods

Due to the importance of pork quality traits in the meat industry, the proposed methodology was applied to objective measurements of redness or CIE a* (CIE International 1976) on the longissimus muscle surface after chilling. Records from three pig populations were used, as described below.

Pig populations

Michigan State University Pig Resource Population

A population was developed at the Michigan State University Swine Teaching and Research Farm, East Lansing, MI (Edwards et al. 2008). To establish this population, four F₀ unrelated Duroc sires were mated to 15 Pietrain sows by artificial insemination to produce the F₁ generation. From all resulting F₁ animals, 50 females and six males (sons of three F₀ sires) were kept as parents to produce 1259 F₂ pigs born alive from 142 l of 11 farrowing groups, avoiding full‐ and half‐sib matings. Growth, carcass composition and pork quality traits were measured in the F₂ offspring. The experimental population was genotyped using two SNP panels. First, 411 animals, including four F₀ Duroc boars, 15 F₀ Pietrain sows, six F₁ males, 50 F₁ females and 336 F₂ pigs, were genotyped (Gualdrón Duarte et al. 2013) with the PorcineSNP60 BeadChip (Illumina, Inc.), designed by Ramos et al. (2009). Then, 612 F₂ animals were genotyped with the 9K tagSNP set and the GeneSeek Genomic Profiler for Porcine LD (version 1) (GGP‐Porcine LD; Badke et al. 2013) imputation of genotypes for animals genotyped at low density was performed, as described by Gualdrón Duarte et al. (2013).

Meat Animal Research Center Population

A population was created from the mating of Yorkshire–Landrace females with Duroc or Landrace sires. Sires were assigned randomly (12 sires of each breed) to Yorkshire–Landrace females (n = 220). The next generations of matings were as follows: Duroc‐sired pigs were mated with Landrace‐sired pigs. Further matings were performed at random, avoiding those within the sire line. The Meat Animal Research Center (MARC) population consists of 1237 phenotyped animals that were sampled in generations 4 (531 gilts), 6 (223 barrows and gilts) and 7 (483 barrows and gilts) sired by 13, 12 and 14 boars respectively. This population was developed at the US Meat Animal Research Center (USMARC) in Clay Center, Nebraska. Animals, as well as their sires, were genotyped using the Illumina PorcineSNP60 BeadChip (Ramos et al. 2009). Records of carcass composition and pork quality traits were collected, as described by Nonneman et al. (2013).

Commercial population

Boneless, center‐cut pork loins were obtained from the left side of each carcass from four large‐scale processing facilities at approximately 24 h postmortem, as described by King et al. (2011) and Shackelford et al. (2012). Loins were sampled for three different studies, two of which attempted to span the typical variation observed in an average production day and another which assessed all pigs from a production unit. Boneless loins were vacuum‐packaged, boxed and transported at 1 °C to USMARC. At 14 days postmortem, a 2.54‐cm‐thick chop was obtained from the 14th rib region and, within 1 min of cutting, color was determined objectively from the exposed surface of the loin using a colorimeter (Minolta ColorTec PCM; color‐tec.com). In this population, 480 loins, sampled across all three studies, were genotyped using the PorcineSNP60 BeadChip (Illumina, Inc.) and 1440 loins were genotyped using the GGP‐Porcine LD and imputed following procedures described by Badke et al. (2012). CIE a* (CIE International 1976) was measured in all loins.

Data editing

In all datasets, individuals with low genotyping rate (< 90%) as well as SNPs with low minor allele frequency (MAF < 0.05) and more than 10% of missing data were discarded. These editing criteria were the same as those used by Badke et al. (2012), and they were implemented independently in each dataset, resulting in different number of SNPs retained in each population (Table 1). A total of 36 879 markers segregated in all three populations. We further discuss the implications of this filtering strategy when discussing SNP weighting and MA z‐score computation. The initial number of markers and individuals genotyped in high density and the final number of SNP and individuals after applying edit criteria are shown in Table 1.

Table 1.

Summary of genotypic information for commercial, MARC and MSUPRP

	Population
	Commercial	MARC	MSUPRP
Initial number of SNPsa	61565	61565	62163
Initial number of individuals at HDb	480	1237	398
Final number of SNPs after filteringc	45688	44020	40569
Final number of individuals at HDd	474	1234	324
Final number of individuals at LowDe	1418	0	604
Total number of individualsf	1892	1234	928
Imputation accuracyg	0.97	—	0.99

Commercial, samples from four large‐scale processing facilities; MARC, Meat Animal Research Center population; MSUPRP, Michigan State University Pig Resource Population.

^aNumber of SNPs before quality editing.

^bNumber of individuals before quality editing.

^cFinal number of SNPs after filtering by minor allele frequency < 0.05 and more than 10% missing data.

^dFinal number of animals in high density after filtering out animals with > 10% of SNPs missing.

^eFinal number of animals in low density after filtering out animals with > 10% of SNPs missing.

^fTotal number of animals for each dataset.

^gImputation accuracy of missing genotypes quantified as squared correlation between observed and imputed allelic dosages (Badke et al. 2013; Gualdrón Duarte et al. 2013).

Genome‐wide association for CIE a*

To perform a GWA for measure of redness CIE a* in all populations, variance components and breeding values were estimated following an animal‐centric model for genomic evaluation given by:

$$\mathit{y}=X\mathit{\beta }+a+e$$ (1)

where y is the vector of records of CIE a*; X is the incidence matrix relating records to the vector of fixed effects β;a is the vector of random breeding values with incidence matrix equal to Identity, assuming that all animals with genotypes have phenotypic records, with a ~ N(0, G ${\mathit{\sigma }}_a^2$); and G is the genomic relationship matrix (n × n), with n being the number of genotyped and phenotyped animals. The G matrix is scaled to be analogous to the numerator relationship matrix A and obtained as G = Z Z’. In this case, Z (n × m) (where m is equal to the number of SNPs available within each population after quality edit) is the matrix containing normalized allelic dosages (counts of allele ‘B’ minus its expected value divided by the expected standard deviation). For instance, the element of Z for animal i and SNP j was calculated as:

$$\frac{{\mathit{Z}}_{\mathit{i}\mathit{j}}={\mathit{M}}_{\mathit{i}\mathit{j}}-2p_j}{\sqrt{2p_j\left(1-p_j\right)}}$$ (2)

where M _ij is the ij ^th element of the SNP matrix M, with dimensions (n × m). This matrix contains genotypes in the interval [0, 2] (counts of B allele), normalized according to the frequency for SNP j and with p _j, calculated from the F₀ generation in the Michigan State University Pig Resource Population (MSUPRP) (19 animals) and from all animals in the remaining populations.

In addition, e is the vector of residual effects, with e ~ N(0,$I{\mathit{\sigma }}_e^2$), and ${\mathit{\sigma }}_a^2$ and ${\mathit{\sigma }}_e^2$ representing additive genetic variance and residual variance respectively. For each population, different fixed effects were included in the model, that is, the contemporary group effect in commercial and MSUPRP populations, whereas the model for the MARC data also included sex and age at slaughter.

Estimation of SNP effects and variances

It has been shown that the model presented in (1) is equivalent to a SNP‐centric model given by:

$$\mathit{y}=X\mathit{\beta }+Zg+e,$$ (3)

where, in addition to previously defined elements in (1), g corresponds to the vector of SNP effects (Strandén & Garrick 2009; Badke et al. 2014; Gualdrón Duarte et al. 2014). In this context, SNP effects $\widehat{g}$ can be estimated from a linear transformation of estimated breeding values $\widehat{a}$ for genotyped individuals using:

$$\widehat{\mathbf{g}}={\mathbf{Z}}^{\prime }{\mathbf{G}}^{-\mathbf{1}}\widehat{\mathbf{a}},$$ (4)

with Z and G defined previously. Also, Gualdrón Duarte et al. (2014) have shown that variance of SNP effects can be obtained as

$$\mathrm{Var}\left(\widehat{g}\right)={\mathbf{Z}}^{\prime }{G}^{-1}Z{\mathit{\sigma }}_a^2-Z^{\prime }{G}^{-1}{C}^{aa}{G}^{-1}Z,$$ (5)

where ${\mathit{\sigma }}_a^2$ is the genetic variance and C ^aa is the portion of the inverse of the mixed‐model equations associated with the breeding values.

P‐values for significance of SNP effects

To identify significant associations for CIE a*, P‐values were obtained as follows:

$$p-\mathrm{valu}{\mathrm{e}}_{ij}=2\left[1-\mathrm{\Phi }\left(\frac{|{\widehat{\mathbf{g}}}_{ij}}{\sqrt{\text{Var}\left({\widehat{\mathbf{g}}}_{\mathbf{ij}}\right)}|}\right)\right],$$ (6)

where P‐value_ij is the P‐value associated with the j ^th SNP in population i and ɸ(•) is the standard normal cumulative distribution (Gualdrón Duarte et al. 2014).

Population structure analysis

Two types of population structure may be present in this dataset. First, within‐population structure is likely to exist. Second, between‐population structure is almost guaranteed considering the heterogeneity in breed origin of the ancestors of each population. A common approach to account for population structure is to include principal components of the relationship matrix as fixed effects (Price et al. 2010). However, it has been reported that including the whole G matrix through a pertinent random animal effect may account for all structure, making it unnecessary to fit individual components (Lans et al. 2012). To confirm this, we compared SNP effects estimated from GBLUP models including and ignoring the principal components as fixed effects but keeping the background additive effect with the variance–covariance matrix proportional to G , following Lans et al. (2012). To determine the number of principal components, we factorized G using the eigenvalue decomposition given by G = UDU’, where U (n × n, with n the number of genotyped animals) is a matrix of eigenvectors of G and D is a diagonal matrix with elements equal to eigenvalues. Eigenvectors explaining a substantial portion of genomic variance (in this case two‐first principal components; Fig. S1a–d) were included as fixed effects in the model, leading to:

$$\mathit{y}=X\mathit{\beta }+U_1{\mathrm{\alpha }}_1+U_2{\mathrm{\alpha }}_2+a+e,$$ (7)

where, in addition to those elements defined in (1), α_i (i = 1, 2) are the coefficients for the two‐first principal components U ₁ and U ₂. In particular, the first two principal components explained 0.57%, 0.2%, 0.85% and 0.7% of genomic variance for commercial, MARC, MSUPRP and JA GWA respectively. We estimated variance components and SNP effects from model (7) and from model (1), and we found that the inclusion of principal components did not result in noticeable changes in results (Fig. S2a–d). For this reason, we did not include principal components in our analyses, either in individual population analyses or in the JA.

Equivalence to fixed SNP effect model

It can be shown that the model presented in (1) is equivalent to a model fitting one SNP at a time as a fixed effect while accounting for random background polygenic effects using the genomic relationship matrix G (Appendix S1). In particular, P‐values and test statistics obtained with equation (6) are identical to those from the Efficient Mixed‐Model Association eXpedited (EMMAX; Kang et al. 2010; Zhang et al. 2010). EMMAX is a well‐known algorithm, computationally efficient and with known statistical properties (Price et al. 2010; Wu et al. 2011). Specifically, consider the model given by:

$$\mathit{y}\mathbf{=}\mathit{X}\mathit{\beta }\mathbf{+}{\mathit{z}}_{\mathit{i}\mathit{j}}{b}_{ij}+\mathit{a}\mathbf{+}\mathit{e}\mathbf{,}$$ (8)

where all components are defined as in (1) except for b _ij, which is the fixed effect related to SNP j in population i. Also, elements z _ij are columns of the Z matrix. For this model, the test statistic given by $b_{ij}=\frac{{\widehat{b}}_{ij}}{\sqrt{\text{Var}\left({\widehat{b}}_{ij}\right)}}$ is equivalent to the statistic derived from (1) through proportional numerators and denominators. An important result for the purposes of this paper is that the variance in the denominator of the fixed effects test can be expressed as:

$$\text{Var}\left({\widehat{\mathbf{b}}}_{\mathbf{ij}}\right)=\frac{{\left({\mathit{\sigma }}_{\mathbf{a}}^{\mathbf{2}}\right)}^{\mathbf{2}}}{\mathbf{\text{Var}}\left({\widehat{\mathbf{g}}}_{\mathbf{ij}}\right)}.$$ (9)

Meta‐analysis of genome‐wide association studies (MA‐GWA)

Statistical procedures in MA are based on the estimation of average effect sizes from a set of primary studies, considering alternative weighting procedures (Evangelou & Ioannidis 2013). One of the most common approaches is the Hedges and Vevea's estimator (Hedges & Vevea 1998), in which weights are based on the estimation of the inverse variance of each effect size. Hedges (1983) and Hedges & Olkin (1985) showed that this is the optimal weight for averaging a set of q independent effect sizes when estimation is carried out under a fixed SNP effects model. Alternatively, the Hunter and Schmidt's estimator (Hunter & Schmidt 1990), which consists of weighting by sample size as an approximation to the optimal weights defined previously, can be implemented.

Suppose that the GWA analysis protocol represented by equations (3), (4), (5) and (6) is applied to k independent populations. To implement MA, we combine results from k GWA studies into a single z‐score, using two weighting alternatives.

Computation of z‐scores

Estimated effects of each SNP (j) in each population (i) were standardized to obtain population‐specific SNP z‐scores:

$$\frac{z_{ij}={\widehat{\mathbf{g}}}_{\mathbf{ij}}}{\sqrt{\text{Var}\left({\widehat{\mathit{g}}}_{ij}\right)}}.$$ (10)

One advantage of this approach is that it takes into account the direction of the effect, and it is rather straightforward to introduce weights (Evangelou & Ioannidis 2013).

Weighting by inverse variance of SNP effects

It has been demonstrated that the optimal weighting criterion for combining test statistics for fixed SNP effect tests is $\text{Var}\left({\widehat{b}}_{ij}\right)$. Also, we have shown that our test statistic is identical to the fixed SNP effect test but that their numerators and denominators are not identical. Consequently, to optimally weight our z‐scores, we need to compute the variance of the fixed SNP effect estimate from the variance of the random effect in our model using expression (9). The weight for inverse‐variance criteria is:

$$w_{ij}=\frac{1}{\text{Var}\left(\mathbf{1}{\widehat{\mathbf{b}}}_{\mathbf{ij}}\right)}.$$ (11)

According to Willer et al. (2010), the inverse‐variance approach requires that estimated effect sizes and their variances be in the same units across populations. If a trait in several populations is measured in different scales, all measurements should be transformed into a common scale. Alternatively, a weighting scheme that is not necessary optimal, but that does not require equal units of measure, is based on sample size.

Weighting by sample size

As mentioned, an alternative weight for SNP effect ${\widehat{g}}_{ij}$ will be given by the sample size of population i (N _i), that is, w _ij = N _i. In this case, populations with more records could count more in the MA‐GWA (that is, have larger weights). This weighting approach is independent of the scale of measurement and can be used with a MA involving different units for the same phenotype, for example, body condition scores from multiple production systems. Also, with homogeneity of variances across populations, the two weighting schemes should produce very similar results.

Combined z‐score

Once weights for MA have been computed, an estimate of SNP effects across populations $z_j^{*}$ is given by a weighted combination of the z _ij obtained in (10) multiplied by the selected weighing scheme, that is:

$$z_j^{*}=\sum _{i=1}^k\left[z_{ij}\left(\frac{\sqrt{w_{ij}}}{\sqrt{\sum _{i=1}^k{w}_{ij}}}\right)\right],$$ (12)

where z _ij is the z‐score obtained using (10) and w _ij represents the respective non‐negative inverse‐variance or sample‐size weight for j ^th SNP effect on population i. Finally, P‐values for association were computed as presented in (6). Equations (11) and (12) show the problem posed by SNPs that segregate in only a subset of the populations. If a SNP does not have an associated z‐score and weight in a population (because the SNP is monomorphic), it cannot be included in the summation of equation (12). A possible solution could be to implement equation (12) by summing over the populations for which the jth SNP is segregating, but this could lead to the extreme case in which a SNP is segregating in only one population and the MA‐GWA z‐score would be based on only one population‐specific estimate. This solution may not be desirable with small datasets. Thus, we take a conservative approach of including only SNPs that segregate in all populations.

Comparison with joint analysis

Traditionally, to increase power and resolution of detection of significant QTL and to evaluate population differences, joint analysis (JA) has been performed, pooling data from different populations and analyzing them as a single dataset (Walling et al. 2000; Kim et al. 2005). To compare results obtained from MA‐GWA and taking advantage of availability of source data, a JA was also performed for CIE a*, following an animal‐centric model as in (1) but with some different specifications. First, a unique genotype file was created, keeping only animals with available genotypes and phenotypes for CIE a* (n = 3358) and common SNPs after quality checks within datasets (m = 36 876). Also the incidence matrix X, related to the vector of fixed effects β, was constructed previously for each population and then built as a block diagonal matrix in order to incorporate the same fixed effects accounted for in population GWA. Although the G matrix was also obtained as G = ZZ’, the Z matrix was constructed considering common SNPs across datasets and, consequently, allelic frequencies across populations. Data were then pooled to estimate homogeneous genetic and residual variances ${\mathit{\sigma }}_a^2$ and ${\mathit{\sigma }}_e^2$, SNP effects and their variances as well as P‐values for association as in population‐specific GWAs and MA‐GWAs. Notice that the JA model used here does not account for heterogeneous additive and residual variances. A model accounting for such heterogeneity would produce estimates that are identical to the individual population analysis (see Fig. S3). If such a model were to be used, population‐specific effects would be obtained and the question of how to combine those into a single value would still persist. However, because the goal of our work is to find those SNPs with a consistent effect across populations, rather than focus on the SNP × population interaction, we used the homoscedastic joint association model.

Results

Phenotypic variation and variance components

Descriptive statistics for the longissimus muscle color trait CIE a*, as well as genetic parameters and heritabilities across populations, are shown in Table 2. Standard errors of heritability estimates were obtained following Visscher & Goddard (2015). A lower number of records were available for the MARC and MSUPRP populations, in contrast to the commercial population, which had the highest sample size. Mean values ranged between 6.75 and 17.26 and were lower in the MARC population than in the commercial and MSUPRP datasets. These differences are consistent with the contrasting genetic background in each population. For instance, MARC animals have a higher percentage of Landrace than do the other two populations and thus are expected to show lower CIE a* values. Genetic variances were in the range of 0.131 (MARC) to 0.899 (commercial) with an intermediate estimate of 0.552 for the MSUPRP. Residual variances were higher than genetic variances in the commercial and MARC populations, ranging between 0.363 (MSUPRP) and 1.103 (commercial). Moreover, heritabilities estimated fitting population‐specific GBLUP models showed a wide range of variation (h ² MARC = 0.160, h ² commercial = 0.449 and h ² MSUPRP = 0.603). Thus, the heterogeneity observed in these results supports the importance of modeling separate variance components and fitting different genomic evaluation models for the populations under study.

Table 2.

Summary statistics of phenotypic records, variance components and heritability estimates for CIE a* across populations

	Population
	Commercial	MARC	MSUPRP
No. recordsa	1780	704	874
Mean (SD)b	14.49 (1.495)	6.746 (1.428)	17.26 (1.827)
Min–maxc	9.238–19.360	2.525–10.960	13.23–23.55
CV (%)d	10.32	21.16	10.58
Genetic var. (SE)e	0.899 (0.129)	0.131 (0.049)	0.552 (0.075)
Residual var. (SE)f	1.103 (0.079)	0.688 (0.050)	0.363 (0.030)
Heritability (hb) (SE)g	0.449 (0.044)	0.160 (0.055)	0.603 (0.045)

Commercial, samples from four large‐scale processing facilities; MARC, Meat Animal Research Center population; MSUPRP, Michigan State University Pig Resource Population.

^aNumber of records.

^bMean and standard deviation for CIE a* (CIE International 1976).

^cMinimum and maximum values for CIE a* (CIE International 1976).

^dCoefficient of variation (%).

^eGenetic variance and standard error.

^fResidual variance and standard error.

^gHeritability for CIE a* within population and standard error (Visscher & Goddard 2015).

Population‐specific GWA

Manhattan plots for CIE a* in commercial, MARC and MSUPRP are shown in Fig. 1(a–c) respectively. Although peaks were present on SSC6 across populations and also on SSC12 for MSUPRP, none of them reached the genome‐wide significance threshold. Specifically, a Bonferroni correction for multiple testing of 1.094 × 10⁻⁶, 1.1359 × 10⁻⁶ and 1.2325 × 10⁻⁶ was considered in the commercial, MARC and MSUPRP respectively.

Figure 1.

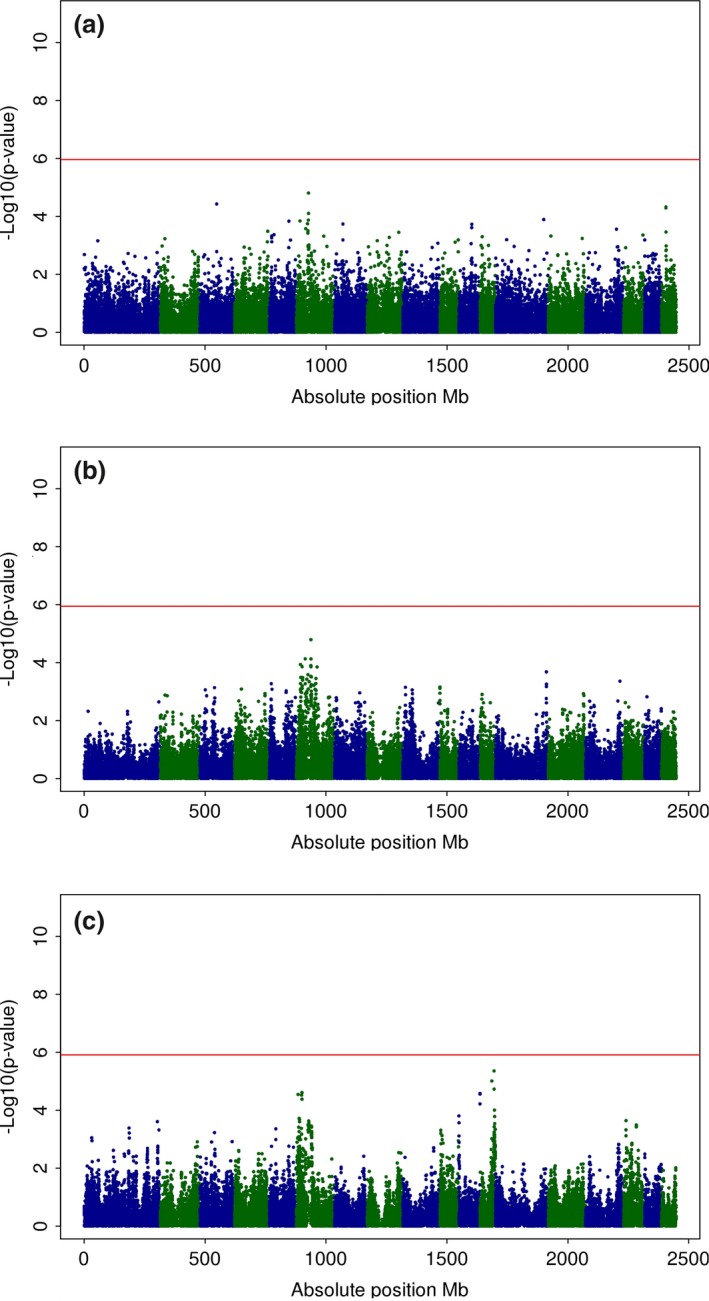
Manhattan plots for CIE a* across populations. Manhattan plots for SNP associations with CIE a* in: (a) commercial (samples from four large‐scale processing facilities), (b) MARC (Meat Animal Research Center population) and (c) MSUPRP (Michigan State University Pig Resource Population). −Log₁₀(P‐value) (y‐axis) vs. absolute SNP position in Mb (x‐axis); horizontal line marks the significance threshold of genome‐wide P < 0.05.

Meta‐analysis of GWA

Manhattan plots for MA‐GWA using inverse‐variance and sample‐size weights are presented in Fig. 2a and 2b respectively. Additionally, detailed information of SNPs associated with CIE a* using both approaches is included in Table S1. First, results from the MA‐GWA obtained with both weighting schemes were quite similar. However, sample‐size MA detected an additional SNP on SSC6 (H3GA0017949, P‐value < 4.4449 × 10⁻⁷) that was not significant under inverse‐variance MA. Inverse‐variance and sample‐size MA identified a significant QTL on SSC1 at 308.9 Mb (ALGA0103022, inverse‐variance and sample‐size P‐values < 4.349 × 10⁻⁸ and 3.5164 × 10⁻⁸ respectively) and also a significant region on SSC6 ranging between 48.5 Mb and 63.1 Mb. In this region, a peak was detected at 49.8 Mb following both weighting approaches (DIAS0000492, inverse‐variance and sample‐size P‐value < 1.353 × 10⁻⁹ and 2.1432 × 10⁻⁹ respectively). Also, comparing P‐values resulting from both MA approaches, as shown in Fig. 3, reveals that P‐values from inverse‐variance MA were highly correlated to P‐values obtained from sample‐size MA (R ² = 0.964), mainly in the case of smaller P‐values (−log₁₀ P‐value ≥ 6).

Figure 2.

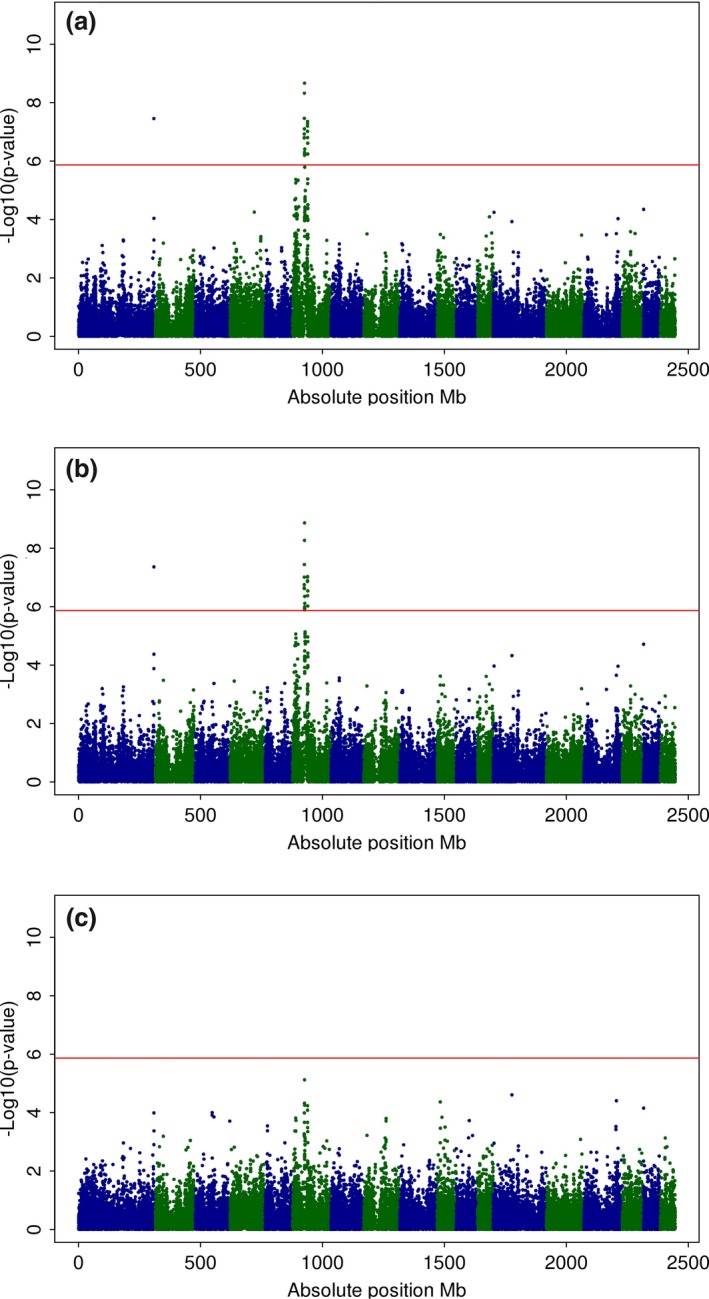
Manhattan plots for CIE a* from meta‐analysis (MA) and joint analysis (JA). Manhattan plots for SNP associations with CIE a* considering: (a) inverse‐variance MA, (b) sample size MA and (c) JA. −Log₁₀(P‐value) (y‐axis) vs. absolute SNP position in Mb (x‐axis); horizontal line marks the significance threshold of genome‐wide P < 0.05.

Figure 3.

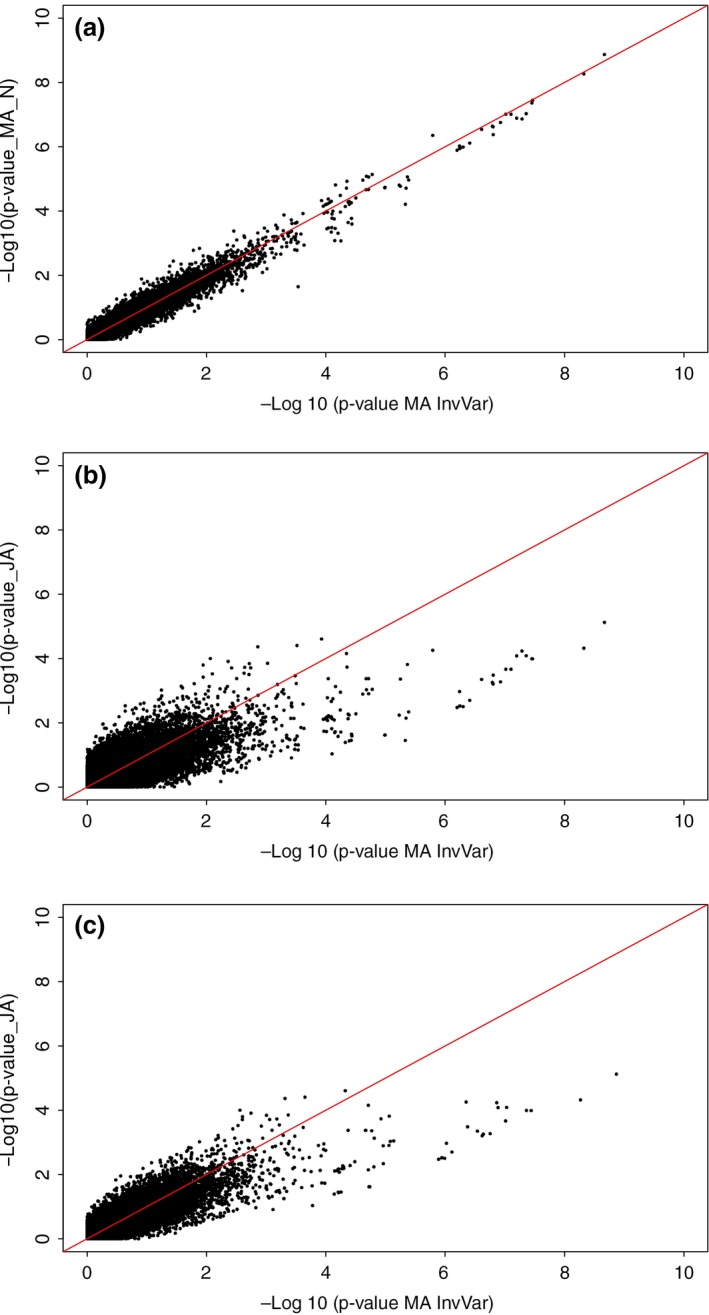
Comparison of P‐values obtained under meta‐analysis (MA) and from joint analysis (JA). Q–Q plot for comparison of P‐values obtained from: (a) Inverse‐variance MA (x‐axis) vs. sample size MA (y‐axis), (b) inverse‐variance MA (x‐axis) vs. JA (y‐axis) and (c) sample size MA (x‐axis) vs. JA (y‐axis).

Joint analysis

Taking into account that no differences were observed between estimates from a JA with or without principal components (Fig. S2d), Fig. 2c shows the Manhattan plot resulting from implementation of JA for CIE a*, assuming homogeneous genetic and residual variances across datasets and without the inclusion of principal components in the GBLUP model. Even though a peak was observed on SSC6 as in population‐specific GWA, it did not reach the genome‐wide significance threshold established as 1.356 × 10⁻⁶. Considering these results, we compared them with those P‐values obtained from MA‐GWA. Thus, according to Fig. 3b and 3c, JA produced larger P‐values than did both MA‐GWA, with more dispersion around the 1–1 line when the inverse variance was used as weighting scheme (R ² = 0.726) in comparison with the use of sample‐size weights (R ² = 0.831).

Discussion

In the present paper, we show how to perform a MA‐GWA study based on multiple and independent genomic evaluations, and we compare its results with those obtained from a JA. Our method can be applied to situations in which the SNP effects are estimated by back transformation of animal effects estimated with GBLUP models. The method is general enough to accommodate additional random effects of herds, permanent environments and even diagonal residual matrices that arise when using de‐regressed breeding values (Garrick et al. 2009). Furthermore, the models used across populations do not need to be identical or include the same effects as long as the correct mixed‐model equations are used to compute SNP effects and associated variances [equations (4) and (5) of this paper]. We illustrate the procedure using the trait CIE a* due to its economic importance (Cannon et al. 1996; Ovilo et al. 2002) and the presence of heteroskedasticity across populations, as shown in Table 2. Moreover, we believe that the heterogeneity of residual and genetic variances displayed in Table 2 is representative of prospective MA studies. For instance, the commercial population spanned a large number of animals and the associated variance components were larger than those in the experimental populations derived from a small set of animals that are descendants of reduced base populations (MSUPRP and MARC).

A main contribution of this paper is the proper computation of weights for MA derived from animal‐centric GBLUP models. In our previous work (Gualdrón Duarte et al. 2014), we showed the numerical equivalence between the proposed SNP test, derived from GBLUP models, and a fixed SNP test derived from a model with a background random polygenic effect called EMMAX (Kang et al. 2010; Zhang et al. 2010). Consequently, the test used in this paper is not a random SNP test but a fixed SNP test, which is shown in Appendix S1 of this paper by including an analytical proof of equivalency between the two tests. We also show in Appendix S1 that, although the numerator and denominator of our test are not equal to the quantities used to build the fixed SNP test, the quotients (z‐scores) are indeed identical. Such proof is essential to deriving the correct inverse‐variance weights proposed in this paper. Moreover, inverse‐variance weights are optimal for fixed SNP MA (Cochran 1954; Hedges & Olkin 1985; Lipsey & Wilson 2001; Zhou et al. 2011) and, given that our test statistic is identical to the fixed SNP test, the optimal weights are the inverse variance of the fixed SNP effect estimate. Such variance estimates are easily obtained from the random SNP variance, as shown in equation (9). Another important point of our proposed MA implementation is that any weighting should be applied on z‐scores and not on SNP effect estimates, because our SNP effect estimates are not identical to those from a fixed SNP effect model, but they are shrunk toward zero. On the other hand, z‐scores are identical to those from fixed SNP effect models and thus are amenable to a weighted linear combination into MA z‐scores.

Similar to other MA implementations (Stankowich & Blumstein 2005; Akanno et al. 2013), we also consider sample‐size weighting. Sample‐size‐based weights are potentially suboptimal with respect to inverse‐variance weights because they do not incorporate imputation accuracies (Jiao et al. 2011) and they do not consider population‐specific heteroskedasticity that are incorporated in inverse‐variance weights (Hedges & Olkin 1985; Marin‐Martinez & Sanchez‐Meca 2010; Akanno et al. 2013). However, sample‐size weights are easier to implement when the variable is measured in different related scales across populations (Willer et al. 2010). In the particular case of our dataset, we obtained almost identical results with both weighting schemes.

In addition to proper definition of weights for MA, we put substantial effort into correctly modeling within‐population GWA. This is important because the population‐specific GWA model constitutes the first step in the implementation of MA, required to account for all within‐population systematic variation. Thus, we incorporated fixed and random effects to model all known sources of variation. We also explored the need to include covariates to account for within‐population genetic structure. In particular, we followed the approach proposed by Lans et al. (2012), which consists of including eigenvectors of the G matrix as covariates. After studying the variance explained by the principal components of G (Fig. S1), we included the two eigenvectors as fixed effects in population GWA (equation (7)). We also considered an animal effect with variance covariance matrix proportional to G. However, we found no differences between the SNP P‐values derived from the models with (equation (7)) and without (equation (1)) eigenvectors of G as fixed covariates (Fig. S2). These results are in agreement with Lans et al. (2012), who suggested that, when eigenvectors are included in the GBLUP model, a ‘double counting’ is observed given that the effect of the eigenvector is already included in the genomic relationship matrix used to estimate the variance components and subsequent SNP effects (Lans et al. 2012). Consequently, we dropped the eigenvectors of G and kept the model represented by equation (1) throughout the analysis.

Despite careful modeling of between‐ and within‐population sources of variation, single population GWA did not detect significant SNP associated with CIE a* because the association peaks (Fig. 1) failed to reach the genome‐wide significance threshold. This is a typical situation in many GWA, which, regardless of the existence of some suggestive peaks, fail to reach genome‐wide significance after adjusting for multiple testing (Hang et al. 2009; Roberts et al. 2010). A possible criticism is that the Bonferroni correction used in this study is extremely conservative because it overestimates the number of independent tests (Hirschhorn & Daly 2005). An alternative could be using the false discovery rate (FDR, Benjamini & Hochberg 1995). In our case, setting FDR < 0.01 produced practically the same significant QTL for CIE a* on chromosomes 1 and 6 as did Bonferroni correction at 5% (Fig. S4). This is not surprising considering that a FDR < 0.01 is equivalent to a P‐value < 1.285 × 10⁻⁶, which corresponds to a Bonferroni significance threshold of 0.05 with 38 900 independent tests (which is very close to our 36 879 SNP). We defer to the user of these MA methods the computation of an appropriate significance threshold, but we highlight the fact that, regardless of the chosen significance threshold, the increased power of MA compared to population‐level GWA is evident.

For instance, with a FDR < 0.01 or a Bonferroni‐corrected P‐value < 0.05, MA detects significant association at SSC1 (P‐value < 4.349 × 10⁻⁸) and SSC6 (P‐value < 2.1433 × 10⁻⁹). Similar results were observed by Bolormaa et al. (2014) in beef cattle, where multitrait MA increased the power with respect to single‐trait GWA for growth, reproduction and production traits, allowing the validation of a larger number of SNPs than in independent population GWA. These results show that MA has the potential of detecting more associated SNPs than does single population GWA while requiring minimal data sharing and accounting for variance heterogeneity if the model for population GWA has been well specified.

A possible criticism of the MA presented in this study is the lack of modeling of population‐specific SNP effects. The point is well taken, because to some researchers, studying the SNP by population interaction could be a reasonable research goal. However, in our case we focused on studying additive effects across all populations. An implicit assumption in the way we compute the MA z‐score is that a consistent sign of all population z‐scores should be observed for a SNP to be significant; otherwise, large z‐scores with opposite signs across populations would cancel each other out. This is a common assumption for human and model organism GWA (Smith et al. 2011; Qayyum et al. 2012). For livestock, however, there is a potential for violations of this assumption when medium density chips are used in low LD populations. Under those circumstances, the persistence of phase will be low, to the point of being negative (Badke et al. 2012). To relax this assumption, the absolute value of the z‐scores can be combined, but it is important to remember that the MA z‐score will not follow a standard normal distribution under the null hypothesis. Instead, the null distribution will correspond to the linear combination (according to the used weights) of as many folded normals as populations are included in the MA. To the best of our knowledge, such distribution has a complicated form and estimation of parameters will be challenging (Chakraborty & Chaterjee 2013). We did not pursue such an endeavor in the illustration used in this paper. Noteworthy is the fact that Monte Carlo approximation of the null hypothesis of sample‐size weighted MA would be much more straightforward than the approximation of variance weighted MA results that required a specific simulation for every SNP in the GWA, because each SNP has a different weight under inverse‐variance linear combinations.

We observed quantitative and qualitative similarities between the results from the two weighting schemes for MA, which is reflected in the correlation between −log(P‐values) obtained from both weighting schemes (R ² = 0.964; Fig. 2a). All significant association peaks resulting from inverse‐variance MA were also observed using sample‐size weights, which detected an additional SNP on SSC6 (H3GA0017949, P‐value < 4.4449 × 10⁻⁷). Thus, power of detection of both weighting approaches was virtually the same. This result is similar to the one reported by Akanno et al. (2013), who compared the inverse‐variance and sample‐size weights in a MA for production and reproduction traits in pigs, obtaining similar‐weighted mean heritability under both approaches.

Finally, we compared MA results to its natural alternative, JA, where all data are pooled and analyzed together (Bravata & Olkin 2001). In this paper, access to original data allowed the implementation of JA. However, this is not a common situation in livestock populations, especially when data come from commercial sources where transference of genotypes involves conflict of economic interests. Contrastingly, implementation of MA only required sharing estimates of SNP effects and their standard errors, which are more likely to be available from commercial sources. A further difficulty in implementing this model is the construction of a genomic relationship matrix. If relationships across populations are modeled, base population allelic frequencies should be computed, that is, the allelic frequencies before the populations diverged. Of course, such estimates are not available. One alternative would be to use population‐specific allelic frequencies. A second challenge is presented by the modeling of heteroskedasticity across populations. For example, if a population‐specific variance is modeled while zero covariance is assumed between populations, similar to approaches presented by Reverter et al. (2004) and Möhring & Piepho (2009), JA produced the same results as population‐specific GWA (Fig. S3). However, this model produces population‐specific SNP effect estimates and tests. Consequently, an important question that arises is how to combine the results into single SNP scores. In the other extreme, if pooled population allelic frequencies are used to estimate within‐ and between‐population genomic relationships, the resulting G matrix typically fits a single genomic variance component. When we assumed a JA based on homogeneous variances across datasets, implementation of JA did not identify significant SNPs associated with CIE a*. Furthermore, although P‐values from JA and from MA were highly correlated with MA P‐values (R ² = 0.8308 and 0.7264 for sample‐size and inverse‐variance MA respectively), JA yielded more conservative tests than did MA, especially for extreme test statistics. Thus, JA led to larger P‐values than did MA, which is reflected in the larger number of points under the diagonal line in Figs S2b and S2c). These results are similar to those obtained by Walling et al. (2000) and Zhou et al. (2011), who reported more significant tests in MA compared to JA. According to Zhou et al. (2011), the observed differences are related to the ability of MA to account for SNP effect‐size heterogeneity across populations, thus modeling the important sources or variation better.

Noteworthy, the closer agreement between JA and sample‐size MA, R ² = 0.8308 (compared to JA vs. inverse‐variance MA, R ² = 0.7264), is not surprising because pooling of datasets for a JA basically favors the population with the larger sample size, which mimics sample‐size weighted MA (Walling et al. 2000; Kim et al. 2005).

Altogether, the results of this paper encourage the use of MA to combine multiple genomic evaluations into a single GWA scan. Given the widespread implementation of GWA in livestock genetics research (Hayes et al. 2009; Snelling et al. 2010; Bolormaa et al. 2011; Fan et al. 2011; García‐Gámez et al. 2012; Nonneman et al. 2013), this is a timely contribution. Moreover, as a legacy to the widespread use of MA in human GWA, there are a number of programs available to perform these types of analysis that share common features (metaqtl, Veyrieras et al. 2007; metal, Willer et al. 2010; metabel, Aulchenko et al. 2007; gwama, Mägi & Morris 2010). Moreover, Bayesian approaches to MA of GWA have been proposed (Han & Eskin 2012). Most of these programs require the specification of population‐specific SNP effects or z‐scores and weights. In this paper, we show that for GBLUP‐based SNP tests, z‐scores should be combined based on specific weights, and we also show the correct way to compute the optimal weights assuming a fixed SNP test derived from recently published work on transforming animal evaluations into SNP effects (Wang et al. 2012, 2014; Gualdrón Duarte et al. 2014). Illustrative data and code implemented in the r programming language (RDC Team 2013) is available at http://tinyurl.com/BLUPMA.

Supporting information

Figure S1. Proportion of variance explained by principal components. Proportion of genomic variance explained by the first 20 eigenvectors, obtained after eigenvalue decomposition of G matrix in: a. Commercial population (0.57); b. MARC population (0.2); c. MSUPRP; d. Joint analysis. First two principal components explained 0.57% (commercial), 0.2% (MARC), 0.85% (MSUPRP) and 0.7% (Joint analysis) of genomic variance.

Figure S2. Comparison of P‐values between models including and ignoring principal components. Q–Q plot for comparison of P‐values after including (x‐axis) and ignoring (y‐axis) principal components in: a. GWA commercial population; b. GWA MARC population; c. GWA MSUPRP; d. Joint analysis.

Figure S3. Comparison of P‐values between heteroskedastic joint analysis and population GWA. Q–Q plot for comparison of P‐values obtained from: a. Joint analysis (x‐axis) vs. GWA in commercial population (y‐axis); b. Joint analysis (x‐axis) vs. GWA in MARC population (y‐axis); c. Joint analysis (x‐axis) vs. GWA in MSUPRP (y‐axis).

Figure S4. Manhattan plot for CIE a* considering false discovery rate 1% for multiple testing correction. Manhattan plot for CIE a* considering estimated q‐values < 0.01 on the P‐values resulting from MA‐GWA using: a. Sample size weights; b. Inverse variance weights. −Log10(P‐value) (y‐axis) vs. absolute SNP position in Megabases (x‐axis); Horizontal line marks the significance threshold according to false discovery rate 1%.

Table S1. SNP associations with CIE a* using meta‐analysis. SNP associations obtained under inverse‐variance and sample size meta‐analysis.

Appendix S1. Showing equivalence between a test based on an animal‐centric model and a test based on SNP effects fixed model.