Abstract
Background
The second Chargaff’s parity rule and its extensions are recognized as universal phenomena in DNA sequences. However, parity of the frequencies of reverse complementary oligonucleotides could be a mere consequence of the single nucleotide parity rule, if nucleotide independence is assumed. Exceptional symmetry (symmetry beyond that expected under an independent nucleotide assumption) was proposed previously as a meaningful measure of the extension of the second parity rule to oligonucleotides. The global exceptional symmetry was detected in long and short genomes.
Results
To explore the exceptional genomic word symmetry along the genome sequences, we propose a sliding window method to extract the values of exceptional symmetry (for all words or by word groups). We compare the exceptional symmetry effect size distribution in all human chromosomes against control scenarios (positive and negative controls), testing the differences and performing a residual analysis. We explore local exceptional symmetry in equivalent composition word groups, and find that the behaviour of the local exceptional symmetry depends on the word group.
Conclusions
We conclude that the exceptional symmetry is a local phenomenon in genome sequences, with distinct characteristics along the sequence of each chromosome. The local exceptional symmetry along the genomic sequences shows outlying segments, and those segments have high biological annotation density.
Keywords: Exceptional symmetry, Genome, Chargaff’s second parity rule, Window analysis
Background
Chargaff’s first parity rule states that, in any sequence of double-stranded DNA molecules, the total number of complementary nucleotides is exactly equal [1]. Chargaff’s second parity rule states that those quantities are almost equal in a single strand of DNA [2–4], and this phenomenon holds in almost all living organisms.
The extension to the second parity rule is also known as single strand symmetry phenomenon. The single strand symmetry states that, in each DNA strand, the proportion of an oligonucleotide should be similar to that of its reverse complement [5–8]. There is no knowledge about why the parity is needed and there is no consensual explanation for the occurrence of the single strand phenomenon. There are some attempts to explain the phenomenon related with the species evolution process, for example: stem-loops hypothesis [9]; duplication followed by inversion hypothesis [10]; inversions and inverted transposition hypothesis [11]; no strand bias [12]; original trait of the primordial genome [8].
Powdel and others [13] studied the symmetry phenomenon in non-overlapping regions of DNA of specific size. They analysed the frequency distributions of the local abundance of oligonucleotides along a single strand of DNA, and found that the frequency distributions of reverse complementary oligonucleotides tend to be statistically similar. Afreixo et al. [14] introduced a new symmetry measure, which emphasizes that the frequency of an oligonucleotide is more similar to the frequency of its reverse complement than to the frequencies of other equivalent composition oligonucleotides. They also identified several word groups with a strong exceptional symmetry. Here, we have applied this measure to find genomic regions with very strong exceptional symmetry effect and to characterize their non-uniform behaviour. We observed exceptional symmetry throughout the human genome. Moreover, some regions showed outlying exceptional symmetry, and those are enriched in protein-coding annotated genes.
Methods
Materials
We analysed the whole human genome, reference assembly build 37.3, available from the website of the National Center for Biotechnology Information. In our data processing, the chromosomes were processed as separate sequences, words were counted with overlap. We also produced and used random control experiments. Those experiments tried to mimic some features of each human chromosome and contained the same number of base pairs of the corresponding chromosome (see ‘Control experiments’ subsection).
We obtained the coding sequences (cds file) for all the transcripts of the human genome (release 75) from Ensembl (http://www.ensembl.org/), to use in coding vs non-coding region classification.
Exceptional genomic word symmetry
In a previous work, we proposed the concept of exceptional genomic word symmetry in equivalent composition groups (ECG), and globally [14]. Exceptional symmetry is a refinement of Chargaff’s second parity rule that highlights the words whose frequencies of occurrence are similar to those of their reversed complements, but are dissimilar to the frequencies of occurrence of other words with equivalent composition. Words of equal length are defined to have equivalent composition if they contain the same number of nucleotides A or T.
Some words are equal to their reverse complement. We denote these as self symmetric words (SSW). We also define a symmetric word pair as the set composed by one word w and the corresponding reverse complement word w′, with (w′)′=w.
Let Gm denote a set of words with equivalent composition, i.e. words containing the same number (m) of As + Ts. For words of length k=2, the ECGs are: G0={CC,CG,GC,GG}; G1={AC,AG,CA,GA,CT,GT,TC,TG} and G2={AA,AT,TA,TT}. The proposed exceptional symmetry measure for Gm is given by
| (1) |
where is used to evaluate the discrepancy between the frequencies of symmetric words in Gm, and to evaluate the variability within Gm words (discrepancy from uniformity). To define those measures we establish the following notation
Nm the number of elements in Gm.
the number of elements in Gm which are self symmetric words.
the number of symmetric word pairs in Gm, excluding the SSWs, such that both words in the pair are absent from the nucleotide sequence under study.
nw the frequency of occurrence of word w in a nucleotide sequence.
Nm the frequency of occurrence of words from group Gm in a nucleotide sequence.
The discrepancy measures for equivalent composition group Gm can be described by
Taking into account that an SSW has no discrepancy from symmetry, we introduce here an adjustment to the degrees of freedom proposed in [14],
and
According to the exceptional symmetry concept, if VR(Gm)≈1, there is no exceptional symmetry, but if VR(Gm)≫1, there is exceptional symmetry.
To measure the global exceptional symmetry, we use
| (2) |
where , and i∈{s,u}.
The exceptional genomic word symmetry values were determined in all non-overlapping sub-chromosomal regions (windows) of several specific sizes (1000 bp, 2000 bp, 5000 bp and corresponding multiples of 10, up to the size of the chromosomes). The starting window size (1000 bp) was established taking into account the maximum word size under study (k = 10) and the expected number of words in each ECG assuming uniform word distribution: as expected value we fixed at least one word in the smallest ECGs, G0 and Gk. However, note that for large k, the shorter windows (1000 bp and 2000 bp) may not include enough ocurrences in the smallest ECGs to provide a good estimate of VR(Gm).
Control experiments
To produce a negative control (without exceptional symmetry) we generated two types of random scenarios
-
random (rnd): assuming independence and using the human chromosome nucleotide composition as input. There are small differences between the frequencies of occurrence of complementary nucleotides. Moreover, in this scenario the expected probabilities of the reverse complements are not equal but there are words in an ECG (e.g. ATT, TAT, TTA) with equal expected probabilities.
Input: nucleotide probabilities (πA, πC, πG, πT, where πw denotes the probability of w).
-
random symmetric (sym): assuming independence and using the same composition for complementary nucleotides as input. In this scenario the expected probabilities of ECG words are the same.
Input: nucleotide probabilities (πA, πC, πG, πT, subject to with w∈{A,C,G,T}).
To produce a positive control (with exceptional symmetry for k=2) we generated two types of random scenarios
-
random with first-order dependence (mrnd): assuming first order Markov structure using the human chromosome nucleotide and dinucleotide composition as inputs.
Input: matrix of nucleotide transition probabilities ( with K1, K2∈{A,C,G,T}) and initial probabilities (πA, πC, πG, πT).
-
random exceptional symmetric with first-order dependence (msym): assuming first order Markov structure using the human chromosome nucleotide and dinucleotide composition and using the same composition for inverted complement dinucleotides as inputs.
Input: matrix of nucleotide transition probabilities ( with K1, K2∈{A,C,G,T}, subject to with w∈{AA,AC,…,TT}) and initial probabilities (πA, πC, πG, πT, subject to with w∈{A,C,G,T}).
Coding region classification
We extracted the start and end positions of all known coding sequences from the Ensembl cds file whose gene biotype was “protein coding”. For genes with multiple transcripts, the gene start position was considered as the minimum start position of all the transcripts of that gene, and the end position as the maximum end position of the same transcripts. For each chromosome, for a given word length k and window size, windows that intercept a gene were labeled as coding neighbourhood windows, windows that do not intercept any gene were labeled as non-coding windows.
Isochores region classification
We used the IsoSegmenter program [15] with the default parameters, to classify the human genome in isochore families: L1, L2, H1, H2, H3. For each chromosome, for a given word length k and window size, windows fully included in an isochore were labeled with the corresponding isochore family. Windows spanning more than one isochore were discarded.
DNA segmentation procedure
In order to evaluate the association between the local exceptional symmetry values and their biological relevance we propose a threshold based method to perform DNA segmentation into high and low exceptional symmetry regions.
To perform the DNA segmentation on the exceptional symmetry profile (the sequence of exceptional symmetry values, also referred to as VR sequences), we need to choose an adequate window size and word length. The window size and the word length which show the widest diversity of local behaviours along the sequence have the potential to perform a good sequence segmentation. So, to explore the variability of local behaviours we evaluate the strict stationarity using the Kolmogorov Smirnov (KS) statistic.
To explore the stationarity, and find the window size and the word length which show the highest lack of stationarity, we propose the following procedure:
the VR chromosome sequence (the sequence of VR values in each chromosome) is divided in successive non-overlapping subsequences (VR subsequences) with a fixed length (50, 100, 200);
for each word length and for each window size, we compute the KS statistic between the VR distribution of each subsequence and the VR distribution of its complete chromosome sequence;
to characterise the lack of stationarity in each exceptional symmetry experiment (defined by the window size and the word length) we compute the average of all KS statistics obtained from VR subsequences.
the window size and word length of the exceptional symmetry experiment with the highest average of KS values are chosen.
To perform the DNA segmentation
we determined the quartiles of the VR chromosome sequence;
we calculated the outlier threshold as the third quartile (Q3) plus 1.5 times the interquartile range (IQR): Q3+1.5∗IQR;
we identified the windows with VR≥Q3+1.5∗IQR as the regions with very high local exceptional symmetry (outlying regions) and the other regions with VR<Q3+1.5∗IQR as the regions without very high local exceptional symmetry (non-outlying regions).
Functional annotation enrichments
Using BioMart, we extracted the annotation information for Homo sapiens genes (GRCh37.p13) dataset from the Ensembl Genes database. To examine the functional annotation enrichments of outlying regions vs non-outlying regions we computed the annotation density ratio (ADR) for each chromosome, defined by
| (3) |
where denotes the number of annotations in the subset S. We used the chi-square test to evaluate if the annotations are equally distributed in the two subsets. To better evaluate the diferences between both subsets, we used the adjusted residual analysis. Under the homogeneity hypothesis the adjusted residuals have a standard normal distribution [16].
Results and discussion
In this study, we analysed local exceptional word symmetry in the complete human genome. In particular, we analysed words of lengths up to 10 in all human chromosomes. We performed a sliding window analysis in terms of exceptional symmetry (VR). We obtained, when possible, results for the following window sizes: 10l, 2×10l, 5×10l base pairs, with l∈{3,4,5,6,7,8}.
We performed our analysis using five ACGT sequence types: real human chromosomes, and corresponding simulated sequences generated according to four distinct random scenarios. For each fixed window size and word length we determined the exceptional symmetry (VR) and symmetry values. Each of these experiments is characterized by median and median absolute deviation values.
To evaluate the effect of chromosome type, window size and word length on the local exceptional symmetry behaviour, we considered the window VR median values of each ACGT sequence (chromosomes or corresponding random chromosomes).
Figure 1 shows five boxplots; one for each sequence type. The local exceptional symmetry in the human genome is clearly higher than in the random scenarios produced without exceptional symmetry (rnd and sym), but globally the effect is similar to random sequences generated with first order Markov models (mrnd and msym).
Fig. 1.
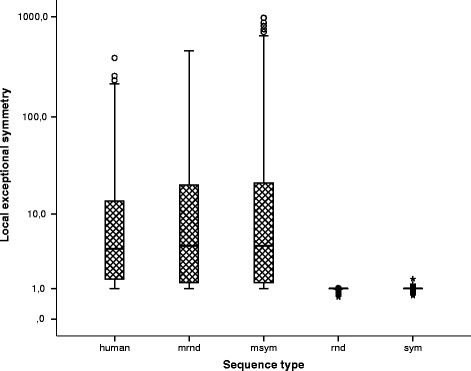
Local exceptional symmetry by sequence type in the human genome. Box plots comparing the local exceptional symmetry values (V R median) using all chromosomes, window length, and word length results, separated by: human chromosomes (human), random scenarios with first order structure (without exact symmetry: mrnd, and with exact symmetry for k = 2: msym), and random scenarios assuming nucleotide independence (without exact symmetry: rnd, and with exact symmetry for k = 1: sym). The local exceptional symmetry in the human genome and positive control experiments (mrnd and msym) is higher than in the random scenarios produced without exceptional symmetry (rnd and sym)
Local exceptional symmetry has no significant differences between chromosomes (Kruskal-Wallis test p≫0.1). Figure 2 presents the results of the local exceptional symmetry using boxplots for comparing the various human chromosomes. The similarity of the chromosomes results is easily observed in the plot.
Fig. 2.
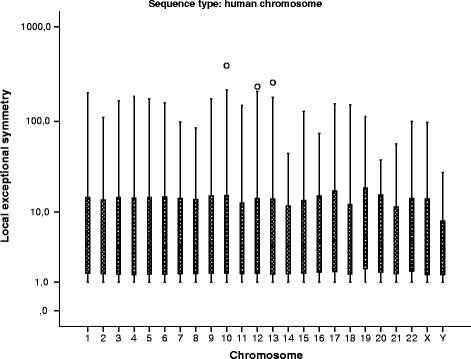
Local exceptional symmetry by human chromosome. Box plots comparing the local exceptional symmetry values (V R median) by human chromosomes for all window and word lengths. The results are similar across all chromosomes
Figure 3 plots the median of the local exceptional symmetry values by word length using all chromosomes and all window size data. Excluding k=2, the local exceptional symmetry and the corresponding dispersion decrease with increasing word length. The effect of word length in local exceptional symmetry has significantly different behaviours in human and random scenarios (random and symmetric random). As was expected, for shorter word lengths we obtain higher local exceptional symmetry values in random scenarios with first order dependence structure, but for k≥7 the human chromosomes surpass the random values. In Fig. 3 all chromosomes results are combined, but the local exceptional behaviour is also present in each chromosome.
Fig. 3.
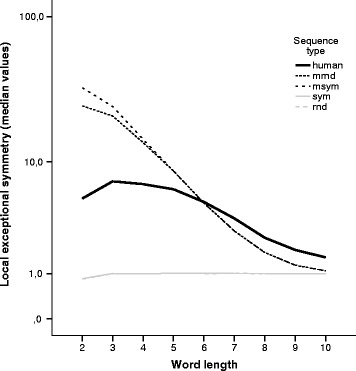
Local exceptional symmetry by word length. Line plot comparing the median of local exceptional symmetry values (V R median) by word length, for human and random scenarios. The sym and rnd scenarios overlap. The local exceptional symmetry in the human genome decreases with increasing word length, excluding k=2. The effect of word length in local exceptional symmetry is significantly different in human and random scenarios. For k≥7 the local exceptional symmetry in the human genome surpasses that obtained by positive control scenarios
Window size effect
Figure 4 shows the local exceptional symmetry values by window size. In the presence of exceptional symmetry, the local exceptional symmetry values increase with the window size, as was expected.
Fig. 4.
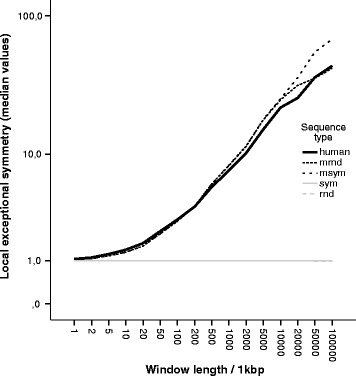
Local exceptional symmetry by window length. Line plot comparing the median of local exceptional symmetry values (V R median) by window length, for human and random scenarios. The local exceptional symmetry increases with increasing window length, except for the negative control scenarios (sym and rnd)
The random sequences msym and mrand were generated with forced exceptional symmetry under stationary behaviour, and an increasing tendency was observed on their local exceptional symmetry values as a function of the window size. For the random sequences without exceptional symmetry (sym and rnd) the local VR values are nearly constant (see Fig. 4).
All human chromosomes exhibit increased exceptional symmetry with increasing window lengths. In general, the behaviour is similar to the random sequences with first order Markov structure. However, we can observe higher values in the first order Markov sequences than in the human sequences.
Local exceptional symmetry stationarity
In order to find the window size and the word length with the highest potential to show distinct local behaviour along the sequence, we explored the stationarity using the procedure described previously. Figure 5 presents a heat map of the results of the Kolmogorov-Smirnov statistic by word length and by window size in the human genome, obtained with VR subsequences with length 200. The results obtained with VR subsequences with length 50 and 100 are similar to these (not shown). The human genome shows non stationary local exceptional symmetry behaviour. Local results are distinct from the global. We observe the maximum value for k=7 and for window size equal to 20,000 base pairs. The second highest value is obtained for k=6 and window size equal to 10,000 base pairs.
Fig. 5.
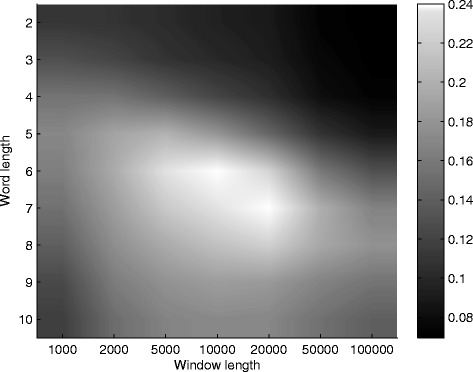
Heat map for Kolmogorov-Smirnov statistics. Kolmogorov-Smirnov statistics by word length and window size, using V R subsequences of length 200, for the complete human genome. The human genome shows non-stationary local exceptional symmetry behaviour, with maximum value for k=7 and window length equal to 20,000 bp
Local exceptional ECG symmetry
As G0 and Gk are the sets with fewer elements, higher variability in VR results is expected, and this was confirmed in all sequences under study (results not shown). We verified that almost all human ECGs have higher VR values than the random scenarios.
Figure 6 shows the comparison of the human and random local ECG exceptional symmetry results for word length 7 and window length 20,000. In the human genome, the ECG G7 has the highest local exceptional symmetry values (and dispersion). Surprisingly, the human G0 has lower median VR values than the random sequences that incorporate exceptional symmetry.
Fig. 6.
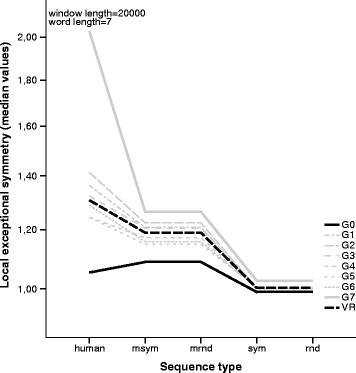
Local exceptional symmetry by ECG. Line plot comparing local exceptional symmetry median values by ECG for k=7 and 20,000 bp window length in the human genome and random scenarios. ECG G 7 has the highest local exceptional symmetry values and G 0 has the lowest
Segmentation
We have observed exceptional symmetry throughout the genome, including coding and non-coding regions. Figure 7 shows the chromosome median exceptional symmetry values for k=7 and window length 20,000, divided in two sets: the coding neighbourhood windows (70,646 VR subsequences), and the non-coding windows (72,543 VR subsequences). The coding neighbourhood windows show significantly higher VR values than non-coding windows (p<0.001, z-test). However, the effect size of the difference is small (Cohen’s d≈0.2). Figure 8 presents box plots comparing the local exceptional symmetry median values for k=7 and 20,000 bp window length in the five isochore families: L1, L2, H1, H2, H3. The exceptional symmetry effect between H and L isochores show strong and significant diferences (p<0.001, d>0.8).
Fig. 7.
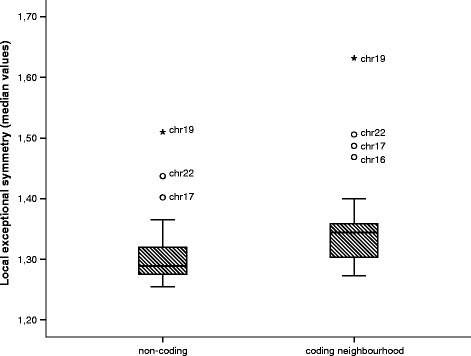
Chromosome median exceptional symmetry values. Box plots comparing the local exceptional symmetry median values by chromosome in coding neighbourhood windows and in non-coding windows. The analysis was performed with k=7 and 20,000 bp window length. Chromosome 19 has the highest median V R value in both window sets. The coding neighbourhood windows show significantly higher V R values than non-coding windows
Fig. 8.
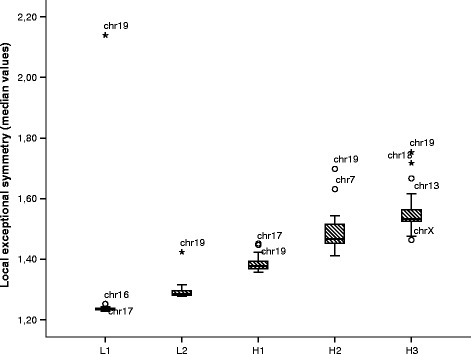
Chromosome median exceptional symmetry values. Box plots comparing the local exceptional symmetry median values by chromosome in five isochore families: L1, L2, H1, H2 and H3. The analysis was performed with k=7 and 20,000 bp window length. Chromosome 19 has outlying median V R values in all isochore families. The H isochores show significantly higher V R values than L isochores
Additionally, there are several windows with strong outlying behaviour. We applied the outlier detection procedure described previously. As an example, Fig. 9 shows the local symmetry results for chromosome 1. Table 1 shows the percentage of outlying segments by chromosome. In all chromosomes, the percentage of outliers is less than 10 %.
Fig. 9.
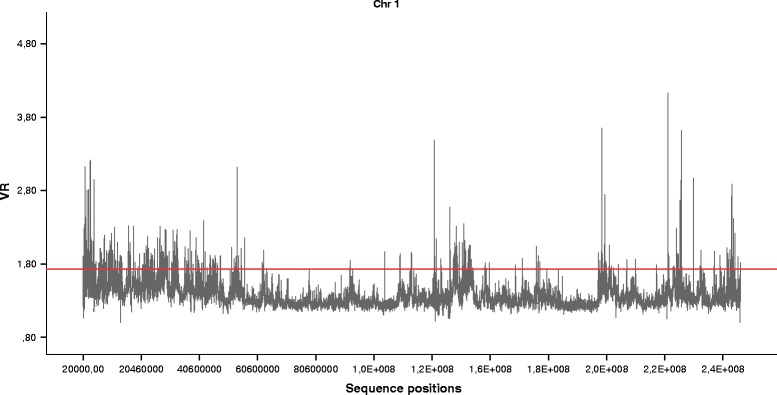
Chromosome 1 segmentation. Chromosome 1 V R results for k=7 and 20,000 bp window size. The horizontal line shows the threshold for segmentation into very high local exceptional symmetry regions (outliers) and complementary regions (non-outliers)
Table 1.
Outlying segments description by human chromosome for k=7 and 20,000 window size
| Chr | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Outlying segments % | 4.8 | 6.1 | 6.4 | 7.6 | 7.7 | 6.5 | 9.1 | 6.8 | 4.7 | 5.3 | 6.0 | 6.5 |
| A D R | 3.5 | 3.9 | 4.1 | 4.3 | 3.8 | 3.6 | 2.9 | 3.5 | 4.0 | 3.3 | 3.3 | 6.9 |
| χ 2 test (p-value) | ** | ** | ** | ** | ** | ** | ** | ** | ** | ** | ** | ** |
| ϕ∗100 % | 9 | 9 | 10 | 14 | 13 | 14 | 12 | 14 | 13 | 12 | 13 | 12 |
| Chr | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | X | Y |
| Outlying segments % | 5.6 | 4.5 | 4.4 | 3.5 | 3.0 | 6.7 | 1.5 | 5.5 | 5.0 | 2.6 | 8.6 | 7.0 |
| A D R | 5.5 | 4.3 | 3.8 | 3.1 | 2.2 | 4.5 | 1.2 | 2.5 | 5.2 | 2.5 | 3.8 | 1.5 |
| χ 2 test (p-value) | ** | ** | ** | ** | ** | ** | ** | 0.003 | ** | 1 | ** | 0.038 |
| ϕ∗100 | 16 | 15 | 11 | 7 | 6 | 14 | 8 | 9 | 15 | 8 | 14 | 19 |
The p-values are adjusted for Holm–Bonferroni method
**means that the p-value is lower than 0.001
A D R - annotation density ratio; χ 2 test - p-value of chi-square test; ϕ - phi measure
Annotation results
To characterize the chromosome features associated with the outlying segments of local exceptional symmetry, we have performed annotation enrichment analyses. Table 1 presents the annotation density ratio (ADR, Eq. 3) of the outlying segments vs non-outlying segments by chromosome, as defined by the DNA segmentation procedure described in the ‘Methods’ section. We observe that in the human genome the ADR values are higher than 1 for all chromosomes, which means that the density of annotation in outlying segments is higher than in non-outlying segments (average value equal to 3.6 and standard deviation equal to 1.2). Table 1 also shows the p-values of the chi-square test for homogeneity of annotation types between outlying and non-outlying segments. The p-values were adjusted using the Holm–Bonferroni method [17]. Almost all chromosomes display significant diferences in annotation between segment types (outlying vs non-outlying). In chromosome 22, however, the difference was not considered significant, perhaps due to the low percentage of outlying segments and chromosome size. Still, the dissimilarity effect between outlying and non-outlying annotations is present in all chromosomes (phi measure (ϕ) range between 0.06 to 0.19).
Figure 10 presents a heat map with the adjusted residuals of the homogeneity in gene type annotation using all chromosome sequences. The counts of protein-coding gene annotations in outlying segments are significantly larger than expected (adjusted residual equal to 37.7), whereas in non-outlying segments long intergenic non-coding RNAs (lincRNA), microRNAs (miRNAs), antisense and pseudogene annotations predominate (adjusted residuals equal to 22.0, 9.6, 15.5 and 20.3, respectively).
Fig. 10.

Association residual analysis between gene type annotation and segment type. Heat map of adjusted residuals by each gene and segment type for all human chromosomes data. The counts of protein-coding gene annotations in outlying segments are significantly larger than expected, whereas in non-outlying segments long intergenic non-coding RNAs (lincRNA), microRNAs (miRNAs), antisense and pseudogene annotations predominate
Conclusion
The local exceptional symmetry profile provides a numerical signature along genomic sequences. The proposed procedure to analyse local exceptional symmetry in the human genome can be applied to any genomic sequence as a segmentation procedure and also as a genomic signature. The results obtained in this work suggest that for the human genome there is an optimal word length and window size to explore the local exceptional symmetry (7 and 20,000 bp, respectively).
The local exceptional symmetry in the human genome is very dissimilar from random scenarios (both with independent symbols or first order Markov structure) showing, as expected, a non-stationary behaviour. Globally, the human genome exhibits high local exceptional symmetry values, which for some word lengths are lower than the values for positive control experiments, but higher than the values for negative control experiments.
The global statistical pattern (location and dispersion values), which is obtained from the exceptional symmetry profiles, is present in all chromosomes of the human genome. The local profile is chromosome specific and the regions with very high exceptional symmetry values are strongly associated with the presence of protein coding genes, although non-coding regions also present exceptional symmetry. Additionally, the local exceptional symmetry values are positively correlated with the GC content as defined by isochore families.
Acknowledgements
This work was supported by Portuguese funds through the iBiMED - Institute of Biomedicine, IEETA - Institute of Electronics and Telematics Engineering of Aveiro and the Portuguese Foundation for Science and Technology (“FCT–Fundação para a Ciência e a Tecnologia”), within projects: COMPETE/FEDER UID/BIM/04501/2013 and PEst-OE/EEI/UI0127/2014.
Footnotes
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
VA idea for study conception/procedures, statistical analysis of local exceptional symmetry values, BioMart data acquisition, interpretation of data results and writing paper. JMOSR coding and optimization of programming procedures to obtain local exceptional symmetry values and critically revising the paper. CACB critically discussing the procedures presented, generating random sequences and critically revising the paper. RMS critically discuss the use of genomic annotation to evaluate the local exceptional symmetry profiles, critically revising the paper. All authors read and approved the final manuscript.
Contributor Information
Vera Afreixo, Email: vera@ua.pt.
João M. O. S. Rodrigues, Email: cbastos@ua.pt
Carlos A. C. Bastos, Email: cbastos@ua.pt
Raquel M. Silva, Email: raquelsilva@ua.pt
References
- 1.Chargaff E. Chemical specificity of nucleic acids and mechanism of their enzymatic degradation. Experientia. 1950;6(6):201–9. doi: 10.1007/BF02173653. [DOI] [PubMed] [Google Scholar]
- 2.Rudner R, Karkas JD, Chargaff E. Proc Nat Acad Sci USA. 1968; 60(2):630–5. [DOI] [PMC free article] [PubMed]
- 3.Karkas JD, Rudner R, Chargaff E. Separation of B, subtilis DNA into complementary strands. II. template functions and composition as determined by transcription with RNA polymerase. Proc Nat Acad Sci USA. 1968;60(3):915–20. doi: 10.1073/pnas.60.3.915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Rudner R, Karkas JD, Chargaff E. Proc Nat Acad Sci USA. 1968; 60(3):921–2. [DOI] [PMC free article] [PubMed]
- 5.Forsdyke DR. Evolutionary Bioinformatics. New York: Springer; 2011. [Google Scholar]
- 6.Qi D, Cuticchia AJ. Compositional symmetries in complete genomes. Bioinformatics. 2001;17(6):557–9. doi: 10.1093/bioinformatics/17.6.557. [DOI] [PubMed] [Google Scholar]
- 7.Kong SG, Fan WL, Chen HD, Hsu ZT, Zhou N, Zheng B, et al. Inverse symmetry in complete genomes and whole-genome inverse duplication. PLoS ONE. 2009;4(11):7553. doi: 10.1371/journal.pone.0007553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zhang SH, Huang YZ. Limited contribution of stem-loop potential to symmetry of single-stranded genomic DNA. Bioinformatics. 2010;26(4):478–85. doi: 10.1093/bioinformatics/btp703. [DOI] [PubMed] [Google Scholar]
- 9.Forsdyke DR, Bell SJ. Purine loading, stem-loops and Chargaff’s second parity rule: a discussion of the application of elementary principles to early chemical observations. Appl Bioinformatics. 2004;3(1):3–8. doi: 10.2165/00822942-200403010-00002. [DOI] [PubMed] [Google Scholar]
- 10.Baisnée PF, Hampson S, Baldi P. Why are complementary DNA strands symmetric? Bioinformatics. 2002;18(8):1021–33. doi: 10.1093/bioinformatics/18.8.1021. [DOI] [PubMed] [Google Scholar]
- 11.Albrecht-Buehler G. Inversions and inverted transpositions as the basis for an almost universal “format” of genome sequences. Genomics. 2007;90:297–305. doi: 10.1016/j.ygeno.2007.05.010. [DOI] [PubMed] [Google Scholar]
- 12.Lobry JR, Lobry C. Evolution of dna base composition under no-strand-bias conditions when the substitution rates are not constant. Mol Biol Evol. 1999;16:719–23. doi: 10.1093/oxfordjournals.molbev.a026156. [DOI] [PubMed] [Google Scholar]
- 13.Powdel B, Satapathy S, Kumar A, Jha P, Buragohain A, Borah M, et al. A study in entire chromosomes of violations of the intra-strand parity of complementary nucleotides (chargaff’s second parity rule) DNA Res. 2009;16:325–43. doi: 10.1093/dnares/dsp021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Afreixo V, Rodrigues JAMOS, Bastos CAC. Analysis of single-strand exceptional word symmetry in the human genome: new measures. Biostatistics. 2015;16(2):209–21. doi: 10.1093/biostatistics/kxu041. [DOI] [PubMed] [Google Scholar]
- 15.Cozzi P, Milanesi L, Bernardi G. Segmenting the human genome into isochores. Evol Bioinformatics. 2015;11:253–61. doi: 10.4137/EBO.S27693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Agresti A. Categorical Data Analysis. New York: Wiley; 2002. [Google Scholar]
- 17.Holm S. A simple sequentially rejective multiple test procedure. Scand J Stat. 1979;6(2):65–70. [Google Scholar]


