Multi-Diffusion-Tensor Fitting via Spherical Deconvolution: A Unifying Framework

Abstract

In analyzing diffusion magnetic resonance imaging, multi-tensor models address the limitations of the single diffusion tensor in situations of partial voluming and fiber crossings. However, selection of a suitable number of fibers and numerical difficulties in model fitting have limited their practical use. This paper addresses both problems by making spherical deconvolution part of the fitting process: We demonstrate that with an appropriate kernel, the deconvolution provides a reliable approximative fit that is efficiently refined by a subsequent descent-type optimization. Moreover, deciding on the number of fibers based on the orientation distribution function produces favorable results when compared to the traditional F-Test. Our work demonstrates the benefits of unifying previously divergent lines of work in diffusion image analysis.

1 Introduction

The diffusion tensor model [1] is widely used for analyzing data from diffusion weighted magnetic resonance imaging (DW-MRI), but is inadequate in situations of partial voluming and fiber crossings. Multi-compartment models provide a natural extension by combining multiple diffusion tensors. They have been used to study the effects of partial voluming [2], and to analyze the diffusion weighted signal in voxels with multiple fiber contributions [3].

Fitting multi-tensor models requires nonlinear optimization, for which previous work has used descent-type algorithms [3–6]. However, these methods only find the global optimum when provided with an initial guess that is sufficiently close to the final solution. At the state of the art, numerous randomized re-starts are tried to reach a suitable optimum with high probability [3, 7, 6], which incurs an excessive computational cost. Alternatively, regularization over spatial neighborhoods [8] requires numerical solution of a partial differential equation.

We present a novel way of applying spherical deconvolution [9] to “kick-start” model fitting, as summarized in Figure 1. We derive a deconvolution kernel to approximate the ball-and-stick model [10, 11], a common variant of the multi-tensor model. The deconvolution result is analyzed by a recent method for fitting discrete models to continuous orientation distribution functions [12]. This decides the number of fibers and provides a starting point to make subsequent optimization [13, 4–6] more reliable and efficient.

Fig. 1.

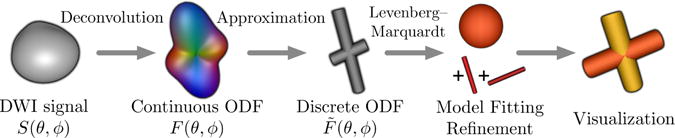
In our framework, deconvolution and ODF approximation make Levenberg-Marquardt fitting of ball-and-stick models faster and more reliable.

Diffusion image analysis approaches based on spherical deconvolution have generally been distinct from those involving explicit fitting of multi-fiber models. Our main contribution is showing how these two approaches can be adapted and combined to create a unified algorithmic solution that offers advantages of both.

2 Related Work

2.1 Multi-Tensor Models

Multi-tensor models assume k diffusion compartments with little or no exchange during measurement time [2], each parametrized by a symmetric 3 × 3 diffusion tensor D_i per compartment, with eigenvalues λ₁ ≥ λ₂ ≥ λ₃ ≥ 0. The signal fractions f_i ε [0, 1] sum to unity. With this, the signal S(g) is predicted as

$$S(\mathbf{g})=S_0={\displaystyle \sum _{i=1}^k{f}_i{\mathrm{e}}^{-b{\mathbf{g}}^{\mathrm{T}}{\mathrm{D}}_i\mathbf{g}}},$$ (1)

where k is the number of compartments, S₀ is the non diffusion-weighted signal, b is the diffusion weighting, and g is the diffusion-sensitizing gradient.

A full k-tensor model has 7k−1 degrees of freedom, but additional constraints are imposed in practice. When a single non-zero b-value is used, a mathematical indeterminacy prevents simultaneous estimation of the isotropic part of D_i and its volume fraction f_i [7]. Most authors constrain the isotropic part, for example by assuming equal eigenvalues on all D_i [3, 14, 5], but some prefer to fix the f_i instead [7, 15]. A very common assumption is axial symmetry (λ₂ = λ₃) [3, 7, 8, 10, 14–16]. In many cases, k is limited to k ≤ 2 [3, 7, 16, 5].

In this work, we focus on the ball-and-stick model [10], which assumes that all D_i have equal λ₁; a single “ball” compartment is completely isotropic (λ₁ = λ₂ = λ₃), the remaining “stick” compartments are perfectly linear (λ₂ = λ₃ = 0). For n fiber terms, this leads to k = n + 1 compartments and 3n + 1 degrees of freedom. We consider the model up to n = 3.

2.2 Spherical Deconvolution

Rather than assuming a fixed number of compartments, spherical deconvolution reconstructs an orientation distribution function (ODF) F(θ, ϕ), which specifies a continuous density of volume fractions on the unit sphere. The predicted signal S(θ, ϕ) is then defined as the convolution of the ODF F(θ, ϕ) with an axially symmetric single-fiber response function R(γ),

$$S(\theta ,\varphi )={\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_0^{\mathrm{\pi }}F({\theta }^{\prime },{\varphi }^{\prime })R({\gamma }^{\prime })\text{sin}({\theta }^{\prime })d{\theta }^{\prime }}d{\varphi }^{\prime }}$$ (2)

where γ′ is the angle between directions given by (θ, ϕ) and (θ′, ϕ′). Typically, S(θ, ϕ) and R(γ) are estimated from the data and modeled in spherical harmonics and rotational harmonics, respectively. This reduces spherical deconvolution to simple scalar division, and yields F(θ, ϕ) [9].

It has been pointed out [10] that Equation (2) describes a continuous version of the ball-and-stick model when substituting

$$R(\gamma )=S_0{\mathrm{e}}^{-bd{\text{cos}}^2\gamma }$$ (3)

and adding S₀f_iso exp(−bd) outside the integral, where f_iso is the volume fraction of the ball compartment. We use this relation to compute an ODF F(θ, ϕ) that corresponds to the continuous ball-and-stick model. FORECAST [14] has followed a similar goal, though corresponding to a multi-tensor model with nonzero perpendicular diffusivity (λ₂ = λ₃ > 0) in the individual compartments.

2.3 Discrete Approximations of Continuous ODFs

From a continuous ball-and-stick model, the discrete case is recovered by replacing the continuous function F(θ, ϕ) with a discrete ODF $\stackrel{\sim }{F}\left(\theta ,\varphi \right)$ that is a finite sum of weighted delta peaks. Even though it is common to recover discrete directions by locating maxima in F(θ, ϕ) [9, 17], this is not accurate. It ignores the fact that delta peaks represented by finite-order spherical harmonics no longer have negligible width, so the individual peaks interfere with each other.

Therefore, we employ nonlinear optimization based on higher-order tensor representations to find a discrete approximation $\stackrel{\sim }{F}\left(\theta ,\varphi \right)$, as described in [12]. Selecting the maximum spherical harmonics order involves a tradeoff between increasing peak sharpness and reducing the influence of noise. Unlike maximum extraction, the optimization in [12] explicitly accounts for the blurring of ODF peaks at low orders. We found that because of this, a good tradeoff is already achieved at maximum order four.

3 Using Spherical Deconvolution for Model Fitting

3.1 Fitting the Ball-and-Stick Model

The previous section described how fitting the ball-and-stick model can theoretically be formulated as a deconvolution problem with a discrete ODF $\stackrel{\sim }{F}\left(\theta ,\varphi \right)$. We now describe an efficient and reliable algorithm based on this insight.

Initial per-voxel estimates of the diffusivity d and the isotropic volume fraction f_iso of the ball-and-stick model are obtained from the maximum apparent diffusion coefficient d_max and the average diffusion-weighted intensity $\overline{S}$

$$d_{max}=-\frac{1}{b}\underset{i}{min}\text{log}\frac{S_i}{S_0}\overline{S}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{S}_i},$$ (4)

where S_i are the diffusion-weighted values. Integrating Equation (1) over the unit sphere shows that $\overline{S}$ varies linearly with f_iso between $\overline{S}=S_0\sqrt{\mathrm{\pi }/(4bd)}\text{erf}(\sqrt{bd})$ (at f_iso = 0) and $\overline{S}$ = S₀ exp(−bd) (at f_iso = 1), where erf is the Gauss error function. Assuming that d ≈ d_max, this allows us to compute f_iso from $\overline{S}$. These initial estimates are refined further as part of the final descent-based fitting.

Now, the predicted isotropic part S₀f_iso exp(−bd) is subtracted from S_i, and a spherical harmonics representation of S(θ, ϕ) is fit to the remainder. Like [12], we deconvolve to a non-ringing cosine power lobe (cos⁴ γ) instead of a truncated delta peak. Using computer algebra software, the order-four coefficients of the deconvolution kernel that corresponds to R(γ) in Equation (3) are found as:

$$\begin{array}{c}{R}_0=\frac{5\sqrt{\mathrm{\pi }}{S}_0}{2\sqrt{bd}}\text{erf}(\sqrt{bd});R_2=\frac{-35S_0}{32\sqrt{{(bd)}^3}}\left(6\sqrt{bd}{\mathrm{e}}^{-bd}+\sqrt{\mathrm{\pi }}(2bd-3)\text{erf}(\sqrt{bd})\right)\\ R_4=\frac{105S_0}{512\sqrt{{\left(bd\right)}^5}}\left(-30\sqrt{bd}\left(2bd+21\right){\mathrm{e}}^{-bd}+9\sqrt{\mathrm{\pi }}\left(4bd\left(bd-5\right)+35\right)\text{erf}\left(\sqrt{bd}\right)\right)\end{array}$$ (5)

Dividing the order-n spherical harmonics coefficients of S(θ, ϕ) by R_n gives F(θ, ϕ) [9], which is then approximated by a discrete ODF $\stackrel{\sim }{F}\left(\theta ,\varphi \right)$ with the algorithm in [12]. This involves nonlinear optimization, but it is much simpler than fitting Equation (1) directly: Instead of fitting to 50–100 DWI values, it considers only 15 coefficients of F(θ, ϕ) (at maximum order four). Moreover, both the objective function and its derivatives involve only additions and multiplications.

The peaks in $\stackrel{\sim }{F}\left(\theta ,\varphi \right)$ approximate fiber directions, their weights provide relative volume fractions. In a final step, these estimates are refined by fitting Equation (1) to the original DWI data, using Levenberg-Marquardt (LM)¹ [13].

3.2 Selecting the Number of Sticks

For best quality, the correct number of compartments needs to be selected in the multi-tensor model: If it is chosen too low, the model might indicate fiber directions that do not align with any true tract. On the other hand, overestimating the true number reduces the accuracy of the result due to overfitting.

In spherical deconvolution, it is common to estimate the number of fiber compartments from the maxima in the ODF F(θ, ϕ) [17]. Since our framework uses deconvolution, we explore a similar strategy based on the discrete ODF $\stackrel{\sim }{F}\left(\theta ,\varphi \right)$. We use a three-stage test with thresholds t_{0,1,2}: If f_iso > t₀, no fiber is detected. Otherwise, F (θ, ϕ) is normalized to integrate to unity and a discrete ODF with two delta peaks is extracted, whose weights are w₁ > w₂. If w₂ < t₁, a single fiber is used. Otherwise, a three-peak approximation is found with w₁ > w₂ > w₃. If w₃ < t₂, we assume two fibers, else three compartments are used.

4 Results

4.1 Synthetic Data

Synthetic diffusion-weighted data with 60 directions, b = 3000 s/mm², and Rician noise at SNR₀ = 30 was created from a multi-cylinder model with non-zero λ₂ = λ₃. Eigenvalues were sampled from Gaussian distributions with parameters according to estimates from real DW-MRI data. Principal eigenvectors and volume fractions were sampled uniformly at random. Cases in which any volume fraction was below 0.2 or any pair of vectors was closer than 30° were rejected.

We created 5000 one-, two-, and three-fiber configurations each and used Levenberg-Marquardt with 100 random restarts, sampled in analogy to data generation, to find the global optimum for the predetermined, correct number of compartments. We then counted the number of times a single randomized run and a run that was kick-started by spherical deconvolution found the correct optimum. Table 1 shows that in the two- and three-fiber cases, the prediction raised the chances of finding the optimum by around 10%. On average, the cost of deconvolution, finding the discrete ODF, and final refinement by LM, is about half the computational cost of finding the optimum by LM alone.

Table 1.

Percentage of cases in which the global optimum was found by a single randomized run of LM, versus our kick-start method, with “speed” in voxels per second.

	1 Fiber		2 Fibers		3 Fibers
	% Found	Speed	% Found	Speed	% Found	Speed
Randomized Run	99.9	3430	90.3	1496	82.6	805
Kick-Started Run	100	5635	98.6	3264	93.1	1527

Table 2 lists the mean and median angular deviation of the individual stick compartments, sorted by volume fraction, from the ground truth. It confirms that spherical deconvolution comes close enough to the final result to be a useful seed, but subsequent optimization still improves upon its accuracy, especially in the three-fiber case. To validate our choice of [12] over ODF peak finding, we also list the most accurate result we were able to achieve using that more traditional technique (order 6, truncated delta peak, Laplace-Beltrami regularization [17]).

Table 2.

Mean and median (in parentheses) of angular deviation from ground truth confirms that spherical deconvolution seeds the optimization close to the final result.

	1 Fiber	2 Fibers		3 Fibers
	Angle	Angle 1	Angle 2	Angle 1	Angle 2	Angle 3
Kick-Started Run	1.2 (1.0)	2.3 (1.9)	5.9 (3.9)	3.9 (3.0)	6.8 (4.9)	8.8 (6.3)
Prediction alone	1.3 (1.1)	3.0 (2.3)	7.5 (5.0)	5.8 (4.4)	9.5 (7.3)	12.0 (9.6)
ODF Peaks	1.5 (1.3)	3.5 (2.6)	12.4 (6.3)	5.7 (4.2)	12.4 (8.1)	16.2 (11.1)

Finally, we used the synthetic data to compare our criterion for selecting the fiber number to two statistical tests previously applied to diffusion model selection, the Bayesian Information Criterion (BIC) [18], and the F-Test [19, 6, 18]. Automatic relevance determination [11] is not included in our comparison, since it aims at Bayesian model averaging rather than at making a hard decision. As shown in Table 3, the parameter-free BIC exhibited a strong bias towards selecting two or three fibers. The thresholds t_{0,1,2} of the other two tests were set to balance sensitivity and specificity at each stage. The deconvolution-based test achieved best results for all ground truth configurations.

Table 3.

In synthetic data, our deconvolution-based test for the number of fiber compartments produces better results than standard statistical tests

Truth	BIC				Prediction F-Test				Our Test
	0	1	2	3	0	1	2	3	0	1	2	3
No Fiber	98%	2%	0%	0%	98%	2%	0%	0%	100%	0%	0%	0%
1 Fiber	0%	29%	43%	28%	0%	82%	6%	12%	0%	94%	5%	1%
2 Fibers	0%	5%	74%	21%	0%	15%	53%	32%	0%	5%	83%	12%
3 Fibers	0%	5%	23%	73%	2%	31%	13%	54%	0%	0%	16%	84%

We also repeated all experiments with b = 1000 s/mm². Without providing the quantitative results, we qualitatively state that the probability of finding the correct optimum increased, but average accuracy with respect to ground truth decreased. Our test for model selection became less reliable, while results of the F-Test improved. Apparently, the F-Test benefits from a low effective noise level, while the deconvolution-based test requires the better separation of the individual compartments afforded by higher b values.

4.2 Real Data

In order to identify the voxels in a real dataset (60 directions, b = 1000 s/mm², isotropic voxel size 1.72 mm) in which the individual tests are most likely to use two- and three-fiber models, we calibrated the F-Test and our deconvolution-based test to generate 25% no-fiber, 40% one-fiber, 25% two-fiber, and 10% three-fiber voxels within a brain mask.

A detail of the result is shown in Figure 2, the intersection of corpus callosum and corticospinal tract on a coronal slice. For visualization, we map the stick compartments to tensors whose perpendicular diffusivity is scaled by the volume fraction of the ball compartment (λ₂ = λ₃ = f_isod). The fiber fractions are renormalized to unity and color-coded. In (a), standard single diffusion tensors are shown for reference. We found that the F-Test tends to fit multiple stick compartments to voxels that likely just contain a single bending or spreading bundle, e.g., in the body of the corpus callosum (CC). The deconvolution-based test is more robust to such cases, as long as they lead to a clear single ODF peak. We expect that this will allow us to track through crossings like the one presented in Figure 2, while avoiding spurious tracts. However, design of a tractography method that makes use of our novel framework is left as future work.

Fig. 2.

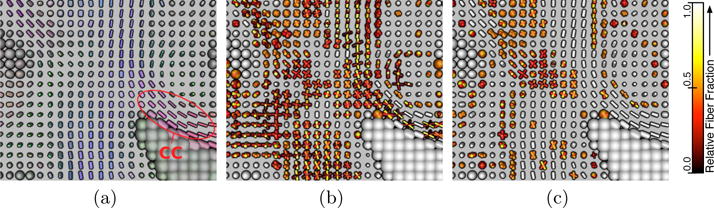
In real data (a), our deconvolution-based test (c) produced more plausible results than the F-Test (b), which frequently fits multiple sticks in regions that are generally thought to contain a single bending or spreading compartment.

With the deconvolution-based test, Levenberg-Marquardt is only run once per voxel, which provides an additional speedup. Our complete pipeline, including testing and fitting the final result, processed 1050 voxels per second with the F-Test, 2950 voxels per second with the deconvolution-based test, on a single CPU core of a 2.7 GHz workstation. Finally, 20 randomized restarts of Levenberg-Marquardt improved upon the optimum found by our method in less than 0.2% of all voxels. Therefore, we conclude that our pipeline offers a reliable and efficient solution for fitting ball-and-stick models.

5 Conclusion

Traditionally, multi-fiber models and spherical deconvolution are used as competing methods, each with its own set of advantages and disadvantages: Linear spherical deconvolution is extremely fast and does not require pre-specification of an expected number of fibers. On the other hand, multi-tensor models offer higher accuracy for applications like multi-fiber streamline tractography [4, 7, 17, 15], where it is the primary goal to estimate the most likely fiber directions.

We have presented a framework that combines the best of both worlds: Based on spherical deconvolution, a plausible number of fiber compartments is found automatically. Initializing the fitting with the deconvolution result doubles the speed of the computation, while at the same time increasing the probability of finding the global optimum to more than 95% in the two-fiber case and to more than 90% for three fibers. As a result, we achieve a fully integrated, reliable and efficient algorithmic solution for multi-tensor fitting.