Cation–Anion Interactions within the Nucleic Acid Ion Atmosphere Revealed by Ion Counting

Abstract

The ion atmosphere is a critical structural, dynamic, and energetic component of nucleic acids that profoundly affects their interactions with proteins and ligands. Experimental methods that “count” the number of ions thermodynamically associated with the ion atmosphere allow dissection of energetic properties of the ion atmosphere, and thus provide direct comparison to theoretical results. Previous experiments have focused primarily on the cations that are attracted to nucleic acid polyanions, but have also showed that anions are excluded from the ion atmosphere. Herein, we have systematically explored the properties of anion exclusion, testing the zeroth-order model that anions of different identity are equally excluded due to electrostatic repulsion. Using a series of monovalent salts, we find, surprisingly, that the extent of anion exclusion and cation inclusion significantly depends on salt identity. The differences are prominent at higher concentrations and mirror trends in mean activity coefficients of the electrolyte solutions. Salts with lower activity coefficients exhibit greater accumulation of both cations and anions within the ion atmosphere, strongly suggesting that cation–anion correlation effects are present in the ion atmosphere and need to be accounted for to understand electrostatic interactions of nucleic acids. To test whether the effects of cation–anion correlations extend to nucleic acid kinetics and thermodynamics, we followed the folding of P4–P6, a domain of the Tetrahymena group I ribozyme, via single-molecule fluorescence resonance energy transfer in solutions with different salts. Solutions of identical concentration but lower activity gave slower and less favorable folding. Our results reveal hitherto unknown properties of the ion atmosphere and suggest possible roles of oriented ion pairs or anion-bridged cations in the ion atmosphere for electrolyte solutions of salts with reduced activity. Consideration of these new results leads to a reevaluation of the strengths and limitations of Poisson–Boltzmann theory and highlights the need for next-generation atomic-level models of the ion atmosphere.

Introduction

DNA and RNA—biological macromolecules with central roles in information storage, gene expression, and function—are polyelectrolytes. Thus, an understanding of their structural and functional properties requires an accounting of their electrostatic properties.^1–4

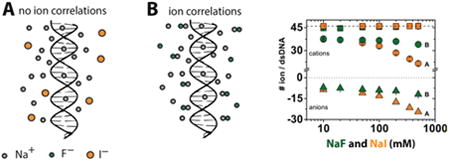
While there are important examples of specifically bound ions that are required for folding and function of nucleic acids,^5,6 the vast majority of interacting ions are present in an ion atmosphere, dynamically associated in a sheath that surrounds these polyelectrolytes (Figure 1A).^7–12 Unlike specifically bound ions that can be investigated by X-ray crystallography and other static structural techniques, ^13–17 the dynamic ions present in the ion atmosphere are refractory to most traditional experimental methods.^1,5,18 For this reason, and because of the general importance of nucleic acids and their electrostatic behavior, there is a long history of theoretical approaches developed for understanding the ion atmosphere.^7,8,11

Figure 1.

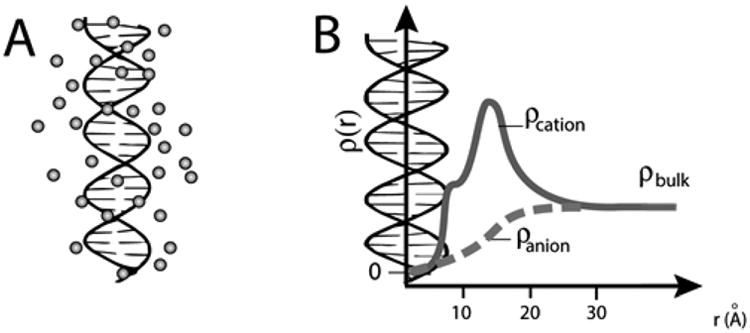
Nucleic acid ion atmosphere. (A) Schematic representation of the cation excess surrounding a nucleic acid. (B) Schematic representation of ion concentrations as a function of distance from a nucleic acid estimated by Poisson–Boltzmann (PB) theory; PB predictions adapted from ref 31. The cation concentration is the highest near to the nucleic acid and equal to the bulk concentration far from the nucleic acid; the anion concentration is lower near the nucleic acid relative to the bulk concentration. The number of ions associated with the ion atmosphere is calculated by integrating the excess ion density $({\rho }_{\text{ion}}^{\text{DNA}}-{\rho }_{\text{ion}}^{\text{bulk}})$ around the nucleic acid; eq 2).

Manning counterion condensation theory provided an early, critical step toward understanding the formation of the ion atmosphere and remains a useful conceptual guide.^7,8,19 Its intentional oversimplification of nucleic acid–ion interactions highlighted the need for more rigorous electrostatic models. Poisson–Boltzmann (PB) theory emerged as the approach of choice for studies of the electrostatic properties of macro-molecules, in part because it is easily implementable, computationally tractable, and conceptually straightforward.^20–25 Nevertheless, its mean-field approximation and treatment of ions as point charges renders it insufficient to fully account for the complexity of nucleic acid-ion interactions.^1,26–31

Given these limitations, there has been an increasing interest in atomic-level theories to describe the ion atmosphere.^31–40 In principle, these computational approaches can provide a thorough and deep understanding of ion–nucleic acid interactions, solvent–nucleic acid interactions, and the dynamic and energetic consequences of these interactions.^{31,39,41–44} Nevertheless, the reliability of theoretical results must be tested through comparison to experiments. Further, while existing experimental data can provide powerful benchmarks to guide the development of theoretical approaches, blind predictions are required to provide unbiased tests.

Early experiments, studying duplex formation and other physical transitions, have revealed dependences of the structural behavior of nucleic acids on the identity and concentration of ions present.^6,45,46 However, it is difficult to use such data to benchmark or test electrostatic theories, because the molecular behaviors followed are typically complex (e.g., even for duplex formation, there is a large and changing ensemble of single-stranded DNA conformers as the ion identity and concentration changes, see ref 47). For this reason we adopt herein a reductionist approach in which we study the composition of the ion atmosphere, specifically the number of associated ions, around stable, rigid nucleic acids duplexes.

The number of associated ions, commonly expressed in terms of ion preferential interaction coefficients (Γ_i), can be characterized by means of so-called ion counting experiments (Figure 2 and eq 3).^12,48,49 Importantly, these methods provide a unique opportunity for testing existing models since Γ_i can be readily computed, without further assumptions, using theoretical methods that calculate ion densities around nucleic acids solutes (Figure 1B and eq 2).^{12,28,31,39,44,50–54} Ion counting studies have confirmed the theoretical expectation of charge neutrality, i.e., that the sum of the charges from ions surrounding a nucleic acid (eq 1) must be equal and opposite to that of the nucleic acid.¹² In particular, these studies have shown that charge neutrality is realized by a combination of an accumulation of cations and an exclusion of anions from the ion atmosphere.¹² Ion counting studies have also provided a clear demonstration of the inability of PB theory to quantitatively account for the preferential attraction of divalent metal cations over monovalent cations to DNA.^12,50 The inability of PB theory to quantitatively account for divalent cation behavior has been suggested to derive, at least in part, from the lack of cation–cation correlations in the model.^1,28,55–57

Figure 2.

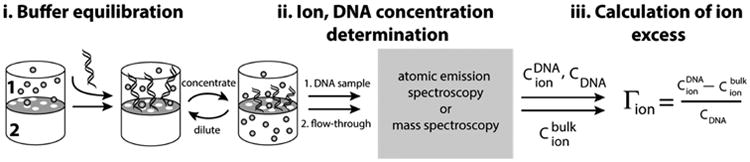
Scheme of the buffer equilibration-atomic emission/mass spectroscopy experiment, referred to as “ion counting” herein. The scheme is adapted from ref 12. For a detailed description of the ion counting methodology, see the Experimental Methods and ref 60.

Because of the anionic nature of nucleic acids, nearly all studies have focused on characterizing the attractive interactions between the nucleic acid and cations.^{5,6,12,49,58,59} Nevertheless, as mentioned above, the ion atmosphere also contains a deficit of anions relative to the concentration in bulk solution. To date, the details of how anion exclusion contributes to the overall ion atmosphere formation has not been addressed in either experimental or theoretical treatments. In this work, we investigated anion exclusion from the ion atmosphere and explored possible effects of anion identity. Our initial expectation was that the identity of the anion would have little or no influence on the number of ions within the ion atmosphere. To our surprise, the results revealed a variation in the number of anions and cations associated with the nucleic acid that depends on both the identity of the anion and that of the accompanying cation. Further, single-molecule fluorescence resonance energy transfer (smFRET) studies of P4–P6, a domain of the Tetrahymena group I intron RNA, showed that anion identity affects RNA folding kinetics and thermodynamics.

Experimental Methods

Reagents

DNA oligonucleotides were purchased from Integrated DNA Technologies, USA. The following sequences were used: S1, _5′GGT GAC GAG TGA GCT ACT GGG CGG_3′, and S2, _5′CCG CCC AGT AGC TCA CTC GTC ACC_3′. All salts were of the highest purity (TraceSELECT or BioXtra, Sigma-Aldrich USA). All solutions were prepared in high-purity water, ultra-low TOC biological grade (Aqua Solutions, USA).

Preparation of DNA Samples

Ion counting was carried out on 24-bp DNA (24bp) duplexes assembled from chemically synthesized oligonucleotides, identical to the construct used in previous ion counting studies.¹² Prior to assembly, oligonucleotides were purified by ion-exchange HPLC (Dionex, CA) and after assembly were desalted using centrifugal Amicon Ultra-3K filters. Equimolar complementary strands (0.1–0.5 mM) were annealed in 20 mM Na-EPPS (sodium 4-(2-hydroxyethyl)piperazine-1-propanesulfonic acid), pH 8.4: samples were incubated at 70 °C for 5 min and gradually cooled down to ambient temperature over 1 h. Non-denaturing polyacrylamide gel electrophoresis (PAGE) (DNA stained by Stains-All) showed no detectable single-stranded DNA in samples, corresponding to >90% duplex.

Buffer Equilibration–Inductively Coupled Plasma Atomic Emission Spectroscopy (BE-ICP AES) and Buffer Equilibration– Inductively Coupled Plasma Mass Spectroscopy (BE-ICP MS)

Buffer equilibration for DNA with the appropriate buffer was carried out using Amicon Ultracel-30K filters (Millipore, MA), replacing Microcon YM-30 (Millipore, MA) used previously. Samples were prepared in 2 mM Na-EPPS, Rb-EPPS, or Cs-EPPS, pH 8.5; Rb-cacodylate was prepared by titrating RbOH (1 M, Aldrich, USA) with cacodylic acid (0.5 M in 2 mM Rb-EPPS buffer, Sigma, USA) to pH 8.5. The concentration of 24bp was varied from 0.2 to 2 mM. As the accuracy of the ion counting method at high salt concentrations depends on the dsDNA concentration, higher DNA concentrations were used at these salt concentrations, and experiments were carried out to demonstrate that final ion counting values were independent of the experimental DNA concentration (Figure S1).

DNA-containing samples (500 μL) were spun down to ∼100 μL at 7000g in Amicon Ultracel-30K filters (Figure 2, i). To minimize solution evaporation, experiments were conducted at 4 °C.⁶⁰ Equilibration between ions associated with DNA and the bulk ions was shown to be complete after five rounds of the buffer exchange (Figures S2 and S3). dsDNA remained in the top chamber (Figure 2) throughout the equilibration buffer process; no DNA was detected in flow-through samples.

Ion Counting

ICP AES ion counting measurements were carried out using an iCAP 6300 Duo View Spectrometer (Thermo Scientific, USA) and ICP MS measurements were carried out using a XSERIES 2 ICP-MS (Thermo Scientific, USA).

Sodium salt solutions were analyzed by ICP AES or, when bromide ions were also being measured, by ICP MS. Sodium detection by ICP AES and ICP MS was identical, within experimental error (Table S1). ICP MS was used to analyze rubidium and cesium. Phosphorus (to determine DNA concentration) and arsenic (to determine cacodylate anion concentration) were analyzed by both methods with similar detection precision (Table S1). Several anions studied herein (F⁻, Cl⁻, ClO₄⁻, and I⁻) are not detected by either method with our current instrumentation. In these cases, the number of depleted anions was calculated from the measured number of accumulated cations and the total DNA charge based on charge neutrality for this system (eq 1), as established by prior results¹² and additional results herein.

$$\sum q_i{\mathrm{\Gamma }}_i=-q_{\text{DNA}}$$ (1)

In eq 1, q_i indicates the charge of ionic species i, Γ_i is the preferential interaction coefficient (i.e., the number of associated ion), and q_DNA the charge of the DNA, which is equal to −46 for the 24bp studied herein. Calculated anion counts are represented by open instead of closed triangles in figures throughout the text.

Samples were analyzed as follows. Aliquots (2.5–20 μL) of DNA-containing sample, the flow-through from the final equilibration, and the equilibration buffer were diluted to 5 mL in 15 mL Falcon tubes (BD Falcon, USA) with 50 mM ammonium acetate buffer (pH 5.0) for ICP AES, or water for ICP MS. Dilution factors, the ratio of diluted to total sample volume, were used to maintain sample concentrations within the linear dynamic range of detection (Figure S4).¹² Controls varying the dilution factor within the linear range demonstrated that the dilution factor did not alter the final results (Table S2). Calibrations were carried out using standards from SpexCertiPrep (USA). Quality control samples, containing each element of interest at 100 μM, were assayed every 10 samples to estimate measurement precision and to ensure that there was no significant instrument drift.

For each data point reported, at least three measurements were made on three different days with independently prepared samples. Errors are the standard deviation of all measurements.

P4–P6 RNA Preparation and Single-Molecule Fluorescence Resonance Energy Transfer Experiments

A P4–P6 RNA construct (smP4-P6), derived from a domain of the Tetrahymena group I ribozyme, was prepared as previously reported⁶¹ via in vitro transcription from DNA templates, splinted ligation of fluorescently labeled (Cy5 and Cy3) synthetic and transcribed oligonucleotides, and PAGE purification. Purified smP4-P6 was annealed to the DNA oligonucleotide T2b (biotin, _5′TGT GTA AGT TTT AGG TTG ATT TTG GT_3′) by incubating eluted smP4-P6 with 2 nM T2b, 100 mM Na-MOPS, pH 7.0, and 1 mM EDTA at 50 °C for 15 min. The sample was then diluted to a concentration of ∼50 pM and flowed onto quartz slides for surface attachment and imaging. smFRET experiments were carried out in 50 mM Na-MOPS, pH 7.0, 0.1 mM EDTA with the salt of interest, and with an oxygen scavenging system of 2 mg/mL glucose, 1.8 mM Trolox, 100 units/mL glucose oxidase, and 1000 units/mL catalase. Image data were taken at 50 frames per second using a custom total internal reflection setup with image acquisition by Andor iXon Ultra camera and the Nikon Elements software. The FRET traces of individual molecules displayed transitions between two FRET states: a high FRET state of ∼0.95, corresponding to the folded states, and a low FRET state of ∼0.2, corresponding to the unfolded state.⁶² Rate and equilibrium constants for folding were determined by analyzing FRET traces with the SMART analysis package, which uses a hidden Markov model-based algorithm, and fitting to a two-state model with a single unfolded (low FRET) and a single folded (high FRET) state.⁶³

Nonlinear Poisson–Boltzmann Calculations

The B-form 24bp duplex was constructed with the Nucleic Acid Builder package.⁶⁴ Charges were assigned using the PDB 2PQR routine²⁴ with the CHARMM parameter set. Nonlinear PB calculations were carried out using the Adaptive Poisson–Boltzmann Solver (version 1.4.1)²² on a 405 × 405 × 578 ų grid with a grid spacing of 1.8 Å and the ion size equal 4 Å (the approximated radius of the hydrated ions; ^12,65 see also comment (66)). Varying the grid spacing in the range 1.5–2.5 Å and changing the box size by ±30% gave identical results within 1% relative error. As ion counting experiments were carried out at 4 °C, the simulation temperature was set to 277.15 K, and the dielectric constant of the solvent was set to 86, characteristic of water at 4 °C.⁶⁷ The internal dielectric of the DNA was set to 2; control calculations with the DNA dielectric set to 4 and 10 gave identical results to within 0.5% relative error (Figure S14). The solvent-excluded volume of the DNA molecules was defined with a solvent probe radius of 1.4 Å. Boundary conditions were obtained by Debye–Hückel approximation.

The preferential interaction coefficient of ions i of valence z_i associated with the DNA was computed by integrating the excess ion density:^12,68,69

$${\mathrm{\Gamma }}_i={\rho }_{\mathrm{b},i}\int (\lambda (r)e^{-z_{i}e\phi (r)/kT}-1)\mathrm{d}r$$ (2)

where ρ_b,i is the bulk ion density, λ(r) is an accessibility factor that defines the region in space that is accessible to ions (where λ(r) = 1 and λ(r) = 0 for the solvent-excluded region—i.e., inside the macromolecule), e is the elementary charge, φ(r) is the electrostatic potential, k is the Boltzmann constant, and T is the temperature.

The integration volume was defined as the entire volume of a simulation box including the solvent-excluded region in the DNA interior. ³¹ This approach matches the conditions for the experimental measurement, as the experiments employ equal total volumes for the DNA and bulk reference samples. Numerical integration of eq 2 was carried out using a custom-written routine in C++, which is available from the authors upon request.

Background

The number of associated ions around 24bp is reported here as a preferential interaction coefficient,⁷⁰ Γ_i (i = C⁺ or A⁻, indicating cation or anion, respectively). Γ_i is the difference in the ion concentration between a DNA-containing sample $(C_{\text{ion}}^{\text{DNA}})$ and a sample containing only ions, which represents the bulk solution $(C_{\text{ion}}^{\text{bulk}})$, divided by the concentration of the DNA (C_DNA):

$${\mathrm{\Gamma }}_i=\frac{C_{\text{ion}}^{\text{DNA}}-C_{\text{ion}}^{\text{bulk}}}{C_{\text{DNA}}}$$ (3)

Thus, this value corresponds to the preferentially associated ions per DNA molecule. For DNA, the cation preferential interaction coefficient, Γ_C⁺, is expected to be greater than zero, indicating its accumulation around the negatively charged polyelectrolyte; for an anion, Γ_A⁻ is expected to be less than zero due to repulsive interactions with the DNA.

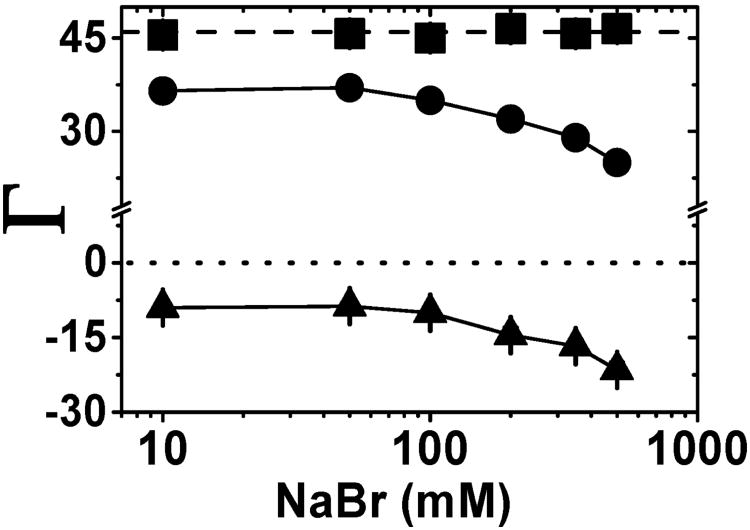
Figure 3 shows the number of ions associated with 24bp over a range of bulk NaBr concentrations. The values of Γ_i are positive for Na⁺ and negative for Br⁻. As previously observed,^12,60 the total ionic charge of the ion atmosphere is equal magnitude and opposite in charge to the 24bp charge (eq 1). The observed total ionic charge of +46.0 ± 1.0 matches the total DNA charge of −46 across the range of NaBr concentrations investigated in Figure 3 (squares vs dashed line).

Figure 3.

Neutralization of a 24-bp DNA (charge −46) by NaBr. The number of associated Na⁺ ions (●) and the excluded Br⁻ ions (▲) give the total charge of the ion atmosphere (■, Γ_i, eq 1). The dashed line at +46 represents charge neutrality and the dotted line at zero represents the absence of an ion excess. The solid line connecting data points are provided as guides. Each data point is the average of 3–5 independent repeats. Error bars are shown when not smaller than the symbols. See Table S3 for raw data.

The ionic charge within the ion atmosphere around 24bp is not equally distributed between cations and anions, consistent with general expectations from the polyelectrolyte effect.^20,71,72 At low salt concentrations (i.e., up to 50 mM) there is in average of 37 ± 1 associated Na⁺ and an average of −9 ± 1 depleted anions. As the bulk salt concentration is increased, the number of accumulated cations decreases and the number of excluded anions increases. Absolute values of Γ_Na⁺ and Γ_Br⁻ are near equal at the highest NaBr concentration investigated herein (|Γ_Na⁺| = +24.6 ± 1 and |Γ_Br⁻| = 21.5 ± 1.5 at 500 mM NaBr; Figure 3 and Table S3). The decrease in cation accumulation and increase in anion exclusion seen as the concentration of bulk salt arise because of the presence of the DNA duplex. The DNA takes up space that then cannot be occupied by solvent and its ions, resulting in fewer cations and anions in the sample containing the DNA^31,73 (see Figure S16). One can correct for this excluded volume effect;⁷⁴ however, herein we report the values that include the volume occupied by the DNA as these values most directly reflect the experimental measurement and our analyses predominantly involve comparison of the behavior of different salt solutions (see also comment (75)).

Results

Cation Accumulation Depends on the Anion Identity

We carried out ion counting experiments for 24bp with a total charge of −46 with the following cations: Na⁺, Rb⁺, and Cs⁺ and the following anions: F⁻, (CH₃)₂AsO₂⁻ (cacodylate anion), ClO₄⁻, Cl⁻, Br⁻, and I⁻. Figure 4 shows results for the NaX, RbX, and CsX series over a range of concentrations. When both the cation and anion could be directly measured (see Experimental Methods), the calculated total charge agrees well with the charge of 24bp (+46; squares vs dashed line), in accord with the charge neutrality principle.¹² When the anion could not be directly assayed, we assumed overall charge neutrality to calculate the anion depletion (and represent these values as open triangles). The number of accumulated cations is in reasonable agreement with previous measurements with NaO₂As(CH₃)₂ and RbCl (Table S6).^12,49,51

Figure 4.

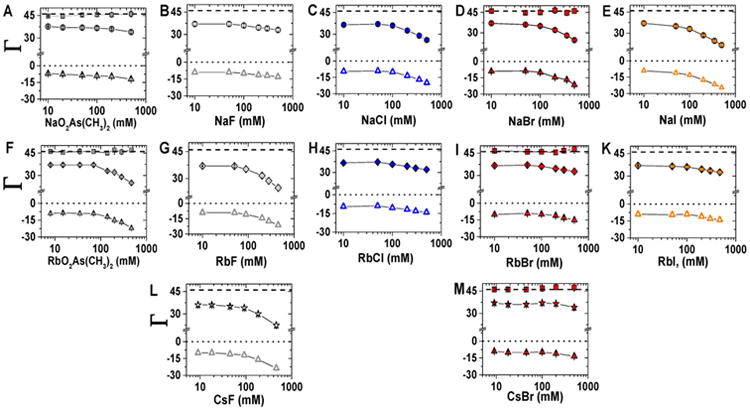
Preferential association of ions with a 24-bp DNA over a range of bulk ion concentrations (10–500 mM). Accumulated cations Na⁺, Rb⁺, and Cs⁺ are shown by filled circles, diamonds, and stars, respectively; triangles indicate depleted anions. Filled triangles represent anion counts determined experimentally and open triangles show number of anions estimated based on electroneutrality (eq 1). Salts with the same cation are organized by rows: Na⁺ (circle) top row, Rb⁺ (diamonds) middle row, and Cs⁺ (stars) bottom row. Salts with the same anion are organized by column and are represented by common color: As(CH₃)₂O₂⁻ (dark gray), F⁻ (light gray), Cl⁻ (blue), Br⁻ (red), and I⁻ (orange). Dotted and dashed lines and error bars are as in Figure 3. Each data point is the average of 3–5 independent repeats. See Tables S3–S5 for raw data.

At low salt concentrations, the number of excess cations and excluded anions does not change with anion identity, but at higher salt concentrations anion-specific effects emerge for each cation. Figure 5 shows the cation excess (Γ_C⁺) for Na⁺, Rb⁺, and Cs⁺ with 10 and 500 mM total salt. (Comparisons across all salt concentrations are shown in Figure S5.) With 10 mM NaX, all anions gave an excess of 37 ± 1.0 Na⁺ ions, but at 500 mM the Na⁺ excess varied from 33–34 with F⁻ or (CH₃)₂AsO₂⁻ to 24 with Br⁻ and 21 with I⁻ (Figure 5A and Table S3). The same number of Rb⁺ ions accumulated at low salt as for Na⁺, and this number was not affected by the anion identity. High concentrations of Rb⁺, like high concentrations of Na⁺, show an anion-dependent effect. This dependence followed an opposite trend as that for Na⁺, with (CH₃)₂AsO₂⁻ and F⁻ giving fewer Rb⁺ ions (25–24) and Br⁻ and I⁻ giving more Rb⁺ ions (33–32; Figure 5B and Table S4). Additionally, cesium salts were tested with fluoride and bromide and gave a trend that mirrored that for the rubidium salts (Figure 5B,C, Table S5). Physical models for this behavior are presented in the Discussion.

Figure 5.

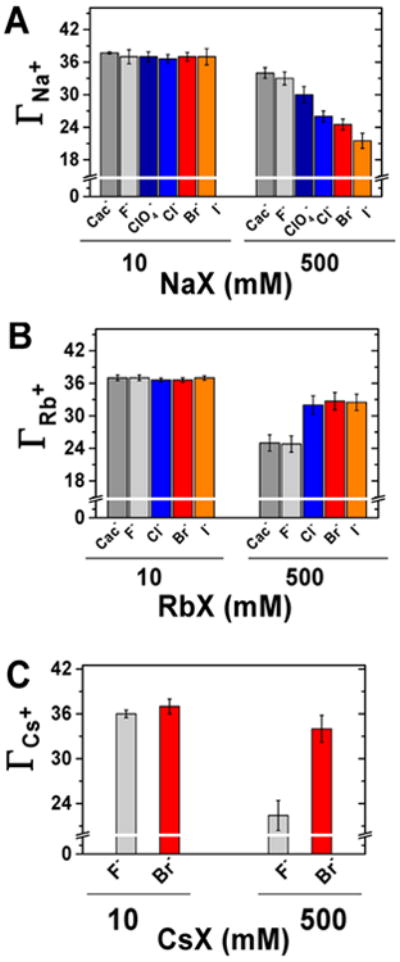
Number of accumulated cations around a 24-bp DNA at two selected salt concentrations (10 and 500 mM) for Na⁺ (A), Rb⁺ (B), and Cs⁺ (C) in the presence of different anions.

RNA Folding Energetics Depend on Anion Identity

Intrigued by the differences in ion atmosphere observed with different anions, we decided to test if there were analogous effects on the energetics of RNA tertiary folding. For this we turned to the folding kinetics and thermodynamics of P4–P6 RNA, an independently folding and well-studied RNA derived from the Tetrahymena group I intron (Figure 6A).^65,76–79 The folding and unfolding rate constants and the equilibrium folding constant were determined in NaX and RbX salts, using a previously developed smFRET assay (Figure 6B, Figures S6 and S7, Table S7).^61–63 As observed before, P4–P6 RNA has an equilibrium folding constant of approximately 1 in 1 M monovalent salt solutions.⁷⁸ This monovalent cation concentration is much higher than the Mg_1/2 for P4–P6 folding (Mg_1/2 ≈ 1 mM) because one of the stabilizing tertiary interactions requires divalent metal ions (i.e., the metal core/metal core receptor that requires Mg²⁺; Figure 6A) and because monovalent cations are much less effective in polyelectrolyte charge screening than divalent cations.^{11,14,26,78,80}

Figure 6.

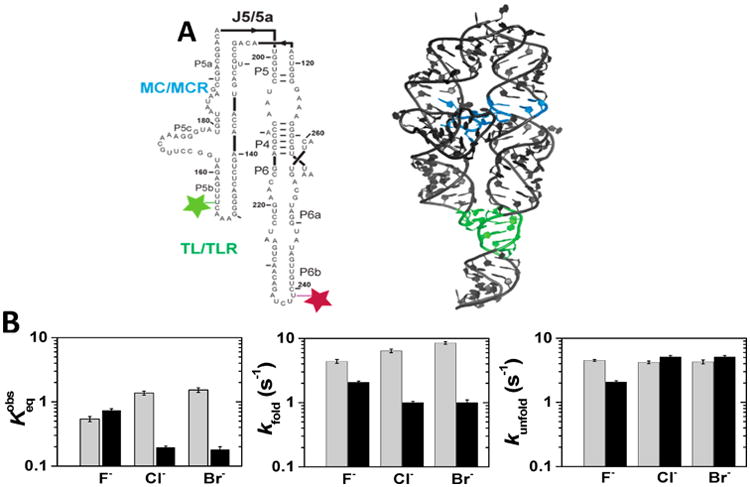
P4–P6 folding kinetics and thermodynamics as a function of the cation and anion identity. (A) Secondary (left) and crystallographic (right) structure of the P4–P6 domain of the Tetrahymena group I intron. Tertiary contacts are colored as follows: the tetraloop/tetraloop receptor TL/TLR (green), and the metal core/metal core MC/MCR receptor (blue). Dye placements used for smFRET are shown: Cy3 (light green) and Cy5 (maroon).^62,65 The P4–P6 crystallographic structure has both tertiary contacts formed, but the experiments herein were carried out in the absence of Mg²⁺, and thus the MC/MCR is not formed.⁸⁰ (B) Folding and unfolding rate constants and the equilibrium constant for P4–P6 RNA folding at 1 M NaX (in gray) and 1 M RbX (in black). The folding equilibrium is defined as the ratio of the folding rate constant to unfolding rate constant: $K_{\text{eq}}^{\text{obs}}=([\text{Fold}]/[\text{unfold}])=(k_{\text{fold}}/k_{\text{unfold}})$. Error bars correspond to the bootstrap-estimated 95% confidence intervals (SD = 2σ bootstrap).

For both NaX and RbX salts, the anion identity affected the folding equilibrium, with effects of up to ∼5-fold. These changes in equilibrium constant across the different anions for Na⁺ or Rb⁺ salts were almost entirely due to changes in the folding rate constants; the anion identities had only minor effects on the unfolding rate constants (Figure 6). The salts that gave greater accumulation of cations (accompanied by lesser anion depletion) in the DNA ion atmosphere gave lower equilibria for P4–P6 RNA folding (Figure S8). The more favorable folding in Na⁺ relative to Rb⁺ (when each is present with its preferred anions) presumably reflects stabilization by specific Na⁺ binding to the tetraloop/tetraloop receptor tertiary interaction in folded P4–P6.^65,81–83

Discussion

We also observed that the identity of the anion present in solution significantly alters the number of cations and anions in the DNA ion atmosphere (Figure 4, cf. top and middle rows for Na⁺ and Rb⁺, respectively, with a series of anions). The effect depends on the concentration of the salt and the accompanying cation. For example, at 500 mM NaX or RbX salt, up to 40% more Na⁺ ions were found in the ion atmosphere with F⁻ as the accompanying anion than with Br⁻ or I⁻; conversely, much more Rb⁺ and Cs⁺ ions were found with Br⁻ than with F⁻ (Figure 5). These differences were not observed at lower salt concentrations (Figures 5 and S5).

We observed that the identity of the anion and cation affect RNA folding kinetics and thermodynamics. The equilibrium and rate constants for P4–P6 RNA folding varied by ∼5-fold depending on the anion–cation combination used, with anions that gave increased cation and anion accumulation in the ion atmosphere giving less favorable P4–P6 folding (Figures 8C and S8). One of the possible explanation for this behavior could be specific interactions between the RNA and cations or anions present in the solution, i.e., Hofmeister effects.^72,84 It has been shown that ions of the Hofmeister series affect formation of an oligomeric DNA duplex.⁸⁵ However, in our opinion the observed salts effects on RNA folding kinetics and thermodynamics arise from ion correlation effects between cations and anions of matching size rather than Hofmeister (specific) effects; see comment (86).

Figure 8.

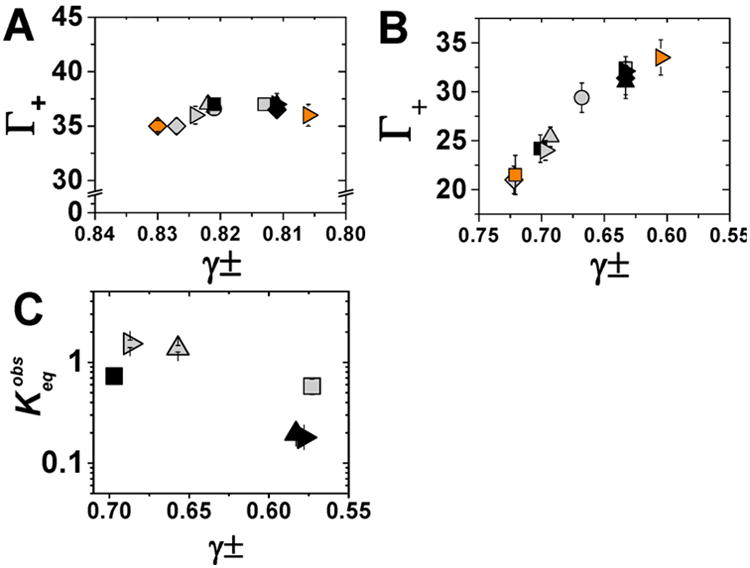
Dependence of ion preferential interaction coefficients for 24bp and RNA folding on the mean activity coefficient of a series of electrolyte solutions.⁸⁷ The number of associated cations as a function of mean activity coefficients at 50 mM (A) and 500 mM (B) bulk ion concentration. NaX salts are represented in gray, RbX salts in black and CsX salts in orange. Salts with the same anion are represented by common symbol: NaF, RbF, and CsF (■: gray, black, and orange, respectively); NaCl, RbCl (▲: gray and black, respectively); NaBr, RbBr, and CsBr (▶: gray, black, and orange, respectively), NaI and RbI (◆: gray and black, respectively). Note the different x-axis scales in (A) and (B). (C) Equilibrium constant of P4–P6 folding at 1 M NaX (gray) or RbX (black) with the following symbols for anions F⁻ (■), Cl ⁻ (▲), and Br⁻ (▶) as a function of mean activity coefficients for the given salt. Error bars correspond to the bootstrap-estimated 95% confidence intervals (SD = 2σ bootstrap).

Our results reveal new properties of the ion atmosphere and, as discussed below, lead to a reevaluation of the strengths and limitations of PB theory and highlight the need for next-generation atomic-level models of the ion atmosphere.

Cation–Anion Interactions within the Ion Atmosphere

The differential ion content of the ion atmosphere depends on the identity of the combination of the cation and anion that is present (Figures 4 and 5 and Table S3). We noticed that salt solutions consisting of cations and anions that are similar in size seemed to behave similarly to one another and distinct from salt solutions with one large and one small ion. Notably, this trend is also reflected in activity coefficients of salt solutions.^87,88 As a result, we explored a possible relationship between activity coefficients and the number of cations and anions in the ion atmosphere. Figure 7A divides salt solutions into two, well-separated groups: those that exhibit a smaller (solid symbols) or larger (open symbols) decrease in activity coefficients with increasing salt concentration. At high concentrations (500 mM), the salts with lower activity coefficients gave more cations in the DNA ion atmosphere (and correspondingly more anions thereby maintaining charge neutrality) (Figure 7B, open symbols, and Figure S9). In contrast, at low concentrations, where all of the salt solutions have similar activity coefficients, the ion excesses were indistinguishable (Figure 7B).

Figure 7.

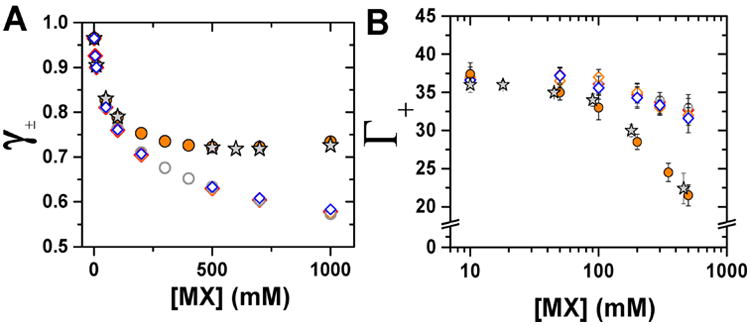
Relationship between mean activity coefficients of monovalent salt solutions and the ion excess around 24bp. Dependence of mean activity coefficient (A) and the number of associated cations (B) on salt concentration. Solutions are placed in two groups: low activity coefficient (open symbols: NaF, gray ○; RbCl, blue ◊; RbBr, red ◊; RbI, orange ◊) and high activity coefficient (closed symbols: NaI, orange ●; CsF, gray ★). Activity coefficients in (A) are from ref 87. In (B), each data point is the average of 3–5 independent repeats, and error bars are as in Figure 3. For clarify, experimental results are presented only for cations and for selected salts. Comparisons of all salt solutions are shown in Figure S9.

The relationship between activity coefficients and ion excess is further demonstrated in Figure 8. At a low salt concentration (50 mM, Figure 8A), there is little spread in activity coefficients (from 0.83 to 0.80), and all tested salt solutions gave the same number of excess cations, within error (36 ± 1). At a high salt concentration (500 mM, Figure 8B), the salts have a wider spread in activity coefficients (from 0.72 to 0.605), and there is a strong trend in cation excess with ∼21 for the highest activity coefficient salt solution, 32–34 for the lowest activity coefficient solution, and intermediate cation excesses for salt solutions with intermediate activity coefficients (see also Figure S10).

Why might a lower activity coefficient correlate with a larger excess of cations and a lesser deficit of anions? Based on the seeming concordance of activity coefficients and the atmosphere effects, we considered the physical origins for the differential ion atmosphere content related to factors causing activity coefficient effects; mainly ion-ion correlations. Activity coefficients of less than one represent a deviation from an ideal solution due to correlated behavior between the ion constituents (see also “Correlation between ion preferential interaction coefficients, solution activity coefficients, and activity” in Supporting Information).⁸⁸ These correlations can, in principle, be direct physical interactions—the formation of contact or solvent-separated ion pairs—or indirect, via perturbation of the solvent. ^88–92

The activity coefficient expresses a macroscopic average of the excess interactions in the solutions and does not provide a direct picture of the molecular level mechanisms. On empirical grounds, it has been suggested that the strength of ion-pairing depends on the relative strength of the ion–water interactions compared to water–water interactions.^93,94 Ions have been classified into two groups: kosmotropes, strongly hydrated ions such as Li⁺, Na⁺, or F⁻ and chaotropes, weakly hydrated ions such as K⁺, Rb⁺, Cs⁺, Cl⁻, Br⁻, or I⁻. According to Collins's “law of matching water affinities”,^93,94 two ions form a contact ion-pair (CIP) when their hydration shells are similar. Empirically one observes that two kosmotropes or two chaotropes readily associated e.g., NaF, RbCl, RbBr, or RbI, whereas CIPs are not formed between kosmotropes and chaotropes, e.g., NaCl, NaI, or RbF.

The thermodynamic effect of ion-pair formation is the removal of a certain number of free ions from solution.⁸⁸ Thus, effective concentrations, i.e., activity, should be considered rather than the total concentration of ions in comparing different salt solutions. If the sole factor responsible for the observed salt-dependent differences in ion atmosphere cation accumulation (and anion depletion) was the concentration of free cation and anions, then the simplest expectation would be that a plot of ion excess (Γ_i) versus activity would give a single line for all salt solutions. However, the salts remain in distinct groups (Figure S11), with more cations (and anions) in the ion atmosphere for salts with lower activity coefficients and greater propensities to ion-pair.⁹⁰ These observations are consistent with preferential pairing or association of cations and anions within the ion atmosphere,⁹⁵ and we present simplest models, which are consistent with presented results, that will require testing. We also note that changes in local solvent^{34,96,97,31,90,94,98} and dielectric properties could influence the ion atmosphere content in addition to or instead of ion-pairing or related effects.

Figure 9A presents a schematic ion atmosphere model for a salt solution with minimal ion-pairing (i.e., the salts represented by closed symbols in Figures 7 and S9). This ion atmosphere has a predominance of excess cations and a deficit of anions. For ions that exhibit lower activities and thus correlations, ion pairs are more prevalent, and in the model of Figure 9B these ion pairs preferentially orient to give a favorable electrostatic interaction with the DNA and thereby preferentially occupy the ion atmosphere; this effect increases, equally, the number of cations and anions in the ion atmosphere (Figure 7B, open versus closed symbols).

Figure 9.

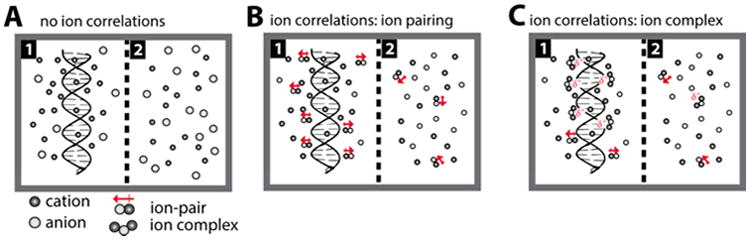
Models representing differences in ion association around a dsDNA as a function of salt propensity for cation–anion correlations. (A) Salts with high γ_± such as NaI or CsF show little or no ion–ion correlations. Salts with low γ_± such as NaF, RbCl, or CsBr show ion–ion correlations leading to formation of ion-pairs (B) or higher ion complexes (C). Cation–anion correlations are greater in the presence of a nucleic acid (compartment 1) and near to the nucleic acid compared to the bulk solution (compartment 2).

In a second model (Figure 9C), two (or more) cations can make favorable electrostatic interactions with the DNA and the barrier for their close approach is mitigated by an intervening anion that (partially) screens their charge repulsion and forms a 2:1 cation: anion complex that is akin to two ion pairs.⁹⁹ Both models qualitatively predict, as is observed, increased cation–anion excess at higher salt concentrations, as mass action will provide a stronger driving force for their association and more cations and anions in an ion atmosphere in solutions with cation–anion combinations that more readily form ion pairs— i.e., have lower activity coefficients.

Reevaluating the Strengths and Limitations of Poisson–Boltzmann Theory

PB theory only takes into account ion valence and, therefore, cannot account for different effects from solutions with ions of the same valence but different identities. Although adjustments can be made to PB in an attempt to account for size, such efforts are ad hoc and have had limited success.^27,100 Further, it is generally recognized that PB does not account well for the properties of divalent and higher valence cations in the ion atmosphere. This failure has been attributed to the fact that—as a mean field theory—PB does not account for cation–cation correlations, which are thought to be more significant for higher valence cations compared to monovalent ions.

Our observation of correlations between monovalent cations and monovalent anions in the ion atmosphere raises the question of how well PB and other mean-field theories can account for the ion atmosphere of monovalent salts. Most simply, the observation that the same cation at the same concentration (or activity) can give ion atmospheres with significantly different numbers of accumulated cations, depending on the anion present (Figure 5), indicates a need to go beyond mean field and take into account at least some correlations and atomic-level properties.

We briefly review prior results, as there have been conflicting prior conclusions and prior mistakes by us, and others, in the choice of standard states used for comparison of experiment and theory. For example, Bai et al. provided a full accounting of all ions within a polyelectrolyte ion atmosphere.¹² They observed good agreement between experiment and PB calculations for the number of accumulated Na⁺ ions and excluded cacodylate anions around a DNA duplex across a range of salt concentrations (Figure S13A and ref 12). However, they, and others, have carried out the integration of eq 2 only over the solute volume,^12,101 which leads to an overestimated predicted number of ions (both cations and anions) (see Figures S12 and S13B).³¹

PB theory predicts well the ion preferential interaction coefficients at low concentration regime where ion correlation effects are weak, as presented herein and by others.^102–104 But, when the correct comparison of the experimental data with PB theory is used, it is revealed that PB theory does not match the experimentally determined ion atmosphere content for sodium cacodylate above 50 mM (Figure 10A).³¹ We observe herein that sodium cacodylate follows the behavior of low activity coefficient salts (Figures 4 and 10A, and comment (105)), so that deviation from a PB prediction would be expected and its deviation cannot be used to invalidate PB theory for non-interacting or low-interacting salts.

Figure 10.

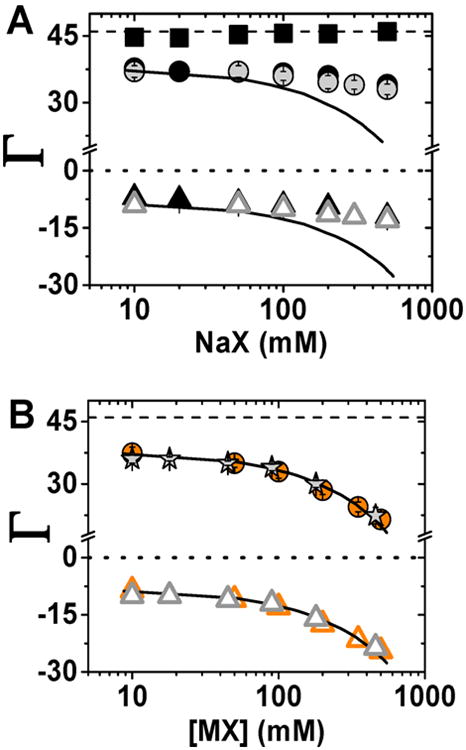
Comparison between the experimentally determined ion preferential interaction coefficients (Γ) and theoretical estimate of these counts from PB model. (A) Comparison between experimental Γ for NaF (gray ●) and NaO₂As(CH₃)₂ (Na⁺ (black ●), As(CH₃)₂O₂⁻ (black▲), and total ionic charge (black ■)) and PB predictions (solid black line). (B) Comparison between experimental Γ for NaI (orange ●) and CsF (gray stars) and PB predictions (solid black line). In both plots open triangles represent anion counts that were estimated on the basis of charge neutrality (eq 1). Error bars as in Figure 3.

We therefore turn to salts with small activity effects (i.e., high activity coefficients) for comparison to PB predictions (Figure 10B). Ion counting data for NaI and CsF agree remarkably well with PB predictions across a wide range of salt concentrations, suggesting that PB does an excellent job of accounting for the overall content of the ion atmosphere for monovalent salts in the absence of complicating ion-pairing and correlation effects. While this agreement is remarkable, there is no guarantee—or evidence—that PB leads to an accurate prediction of the dynamic placement of ions within an ion atmosphere and tests of energetic consequences need to be reevaluated considering possible activity coefficient effects. Indeed, PB and molecular dynamics (MD) simulations give considerably different predicted ion positions.³¹

Ion Atmosphere Models beyond Mean Field

Prior computational work used sodium cacodylate to benchmark MD and three-dimensional reference interaction site model (3D-RISM) estimates of preferential interaction coefficients of Na⁺ and Cl⁻ ions.³¹ The assumption that the identity of the anion does not influence the ion atmosphere composition was based on experimental comparisons of sodium salt solutions with cacodylate and chloride ions. However, these experimental tests were made only up to 100 mM, whereas the deviations revealed herein are most evident at higher NaX concentrations (Figure 4). Subtle differences at these lower concentrations would not have been evident in the earlier experiments due to their lower precision.

Figure 11 compares the observed NaCl ion atmosphere data with the ion atmosphere composition calculated by 3D-RISM using different closure relationships with the ff10 AMBER force field for nucleic acids and SPC/E water by Giambasu et al.³¹ (See comment (106) for a brief explanation of the closure relations, and refs 107 and 108.) Whereas some of these models match the newly acquired data well over limited concentration ranges, none of them provide a good match across the entire NaCl concentration range. Estimates of the ion atmosphere content from MD simulations at two NaCl concentrations agreed well when using the TIP3P water model, but not with the TIP4P water model (Figure 11; ion parameters used in this studies were taken from Joung and Cheatham¹⁰⁹). Overall, the fortuitous agreement between 3D-RISM NaCl calculations and experimental data for sodium cacodylate (but not the newer NaCl data) underscores the need for multiple independent rounds of experimental tests of new predictions made based on computational or experimental models, as has been carried out herein.

Figure 11.

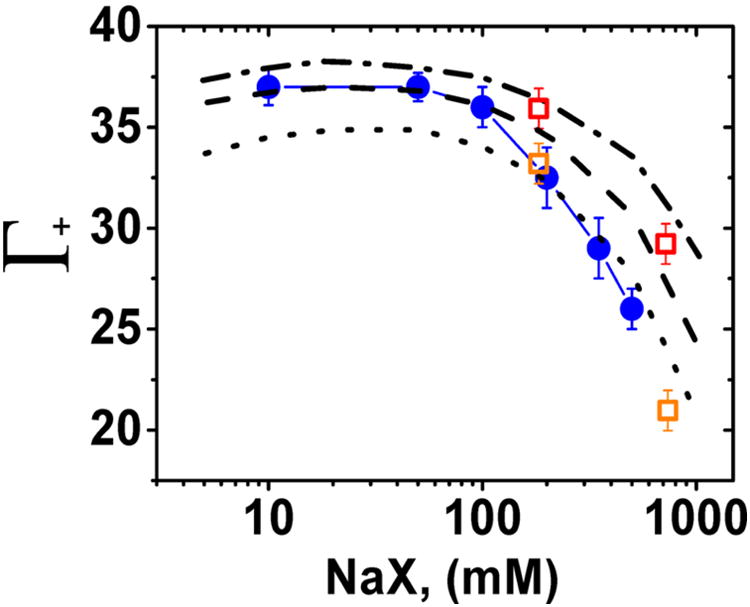
Comparison between the experimentally determined ion preferential interaction coefficients (Γ) of NaCl and theoretical estimates of these ion counts from 3D-RISM and MD calculations. Experimental Γ for NaCl (blue ●), 3D-RISM predictions with following closures: PSE-4 (dotted-dashed line), PSE-3 (dashed line), and PSE-2 (dotted line). SPE/E water model was used for all 3D-RISM calculations. MD predictions with different water models: TIP3P (orange □) and TIP4P (red □). Computational data are from ref 31.

Summary and Implications

We have shown that the composition of the ion atmosphere in terms of the number of cations and anions around a nucleic acid depends not only on the type of cation present, as is commonly discussed, but also on the anion identity. Importantly, we have shown that the identity of the anion has consequences for the stabilization of RNA tertiary structure. Our smFRET experiments suggest that these effects arise mostly from differences in folding rate constants, consistent with the idea that electrostatic forces and the ion atmosphere are important factors in the energetics of transition state formation for RNA folding.^1,5,59 Although we only show this effect for the folding of the model P4–P6 RNA, the polyelectrolyte nature of nucleic acids and the ubiquity of the ion atmosphere around nucleic acids suggest that deeper understanding of the ion atmosphere and its consequences will be broadly relevant for biological processes in which electrostatic interactions between nucleic acids and other macro-molecules and other charged species are involved. These include the folding of structured RNAs, the assembly of RNA/protein complexes, the packing of viral DNA, and the assembly of chromatin.^{4,5,110–112}

We have shown that the anion effect on ion-atmosphere composition correlates remarkably well with the activity coefficient of the salt solution, suggesting that the observed effects are caused by correlations between anions and cations in the ion atmosphere.

We present two models that could account for the observed ion counting data: (i) an ion atmosphere enriched in ion pairs through charge–dipole interactions with the DNA (Figure 9B), and (ii) ion clusters between cations and anions with overall positive net charge within the ion atmosphere (Figure 9C). In addition, our data helps to reveal strengths and limitations of current state-of-the art computational models.

There has been extensive discussion of the possibility of ion-pairing between cations and the phosphoryl groups of nucleic acids,^48,94,113 but much less consideration has been given to the possibility of enhanced ion-pairing between cations and accompanying anions within the ion atmosphere.^41,42,44,97 Our results provide experimental support for this phenomenon and highlight the importance of developing more complex atomic-level (and possibly quantum) theories to account for cation–anion correlations within the nucleic acid atmosphere. These results also provide new experimental constraints to develop and test computational models for the ion atmosphere and its properties and effects.