Automatic Segmentation of Mechanically Inhomogeneous Tissues Based on Deformation Gradient Jump

Abstract

Variations in properties, active behavior, injury, scarring, and/or disease can all cause a tissue’s mechanical behavior to be heterogeneous. Advances in imaging technology allow for accurate full-field displacement tracking of both in vitro and in vivo deformation from an applied load. While detailed strain fields provide some insight into tissue behavior, material properties are usually determined by fitting stress-strain behavior with a constitutive equation. However, the determination of the mechanical behavior of heterogeneous soft tissue requires a spatially varying constitutive equation (i.e. one in which the material parameters vary with position). We present an approach that computationally dissects the sample domain into many homogeneous subdomains, wherein subdomain boundaries are formed by applying a betweenness based graphical analysis to the deformation gradient field to identify locations with large discontinuities. This novel partitioning technique successfully determined the shape, size and location of regions with locally similar material properties for: (1) a series of simulated soft tissue samples prescribed with both abrupt and gradual changes in anisotropy strength, prescribed fiber alignment, stiffness, and nonlinearity, (2) tissue analogs (PDMS and collagen gels) which were tested biaxially and speckle tracked (3) and soft tissues which exhibited a natural variation in properties (cadaveric supraspinatus tendon), a pathologic variation in properties (thoracic aorta containing transmural plaque), and active behavior (contracting cardiac sheet). The routine enables the dissection of samples computationally rather than physically, allowing for the study of small tissues specimens with unknown and irregular inhomogeneity.

I. Introduction

Tissues are often mechanically inhomogeneous due to variations in properties (e.g., supraspinatus tendon [1], [2]; pulmonary artery [3]; left recurrent laryngeal nerve [4]), variations in active behavior (e.g., myocardial shortening [5]), injury (e.g., whiplash [6]), myocardial [7]–[9] or dermal [10]–[12] scarring), or disease (coronary artery disease [13]; idiopathic pulmonary fibrosis [14], [15]; or cancer [16], [17]). The imaging of soft tissues to identify regional variations in mechanical properties, known as elastography, has become a major focus for medical imaging (reviewed by [18]–[21]). The main goal of elastographic studies has traditionally been the identification of high-stiffness regions (e.g. tumor, vascular plaque, liver fibrosis) within a compliant soft tissue. For example, Goenezen et al. [16] identified the size, shape, and location of varying shear modulus regions within a tissue with exceptional clarity in a study of breast cancer tumors. If only broad differences in stiffness are of interest, then the simplifying assumptions of isotropy and linearity (infinitesimal deformation) are justified. In order to capture more completely the complex material properties of the tissue, however, a more robust method is needed. The intrinsic complexity of soft tissues presents a tremendous challenge in constitutive modeling. In particular, the fibrous structural constituents of a tissue typically have orientations and concentrations unique to the tissue’s anatomy and physiology, causing strong anisotropy in the mechanical behavior of the tissue. In addition, the stress-strain response of soft tissues is often markedly nonlinear; the tissue is initially very compliant, but as the strain is increased, it becomes much stiffer.

A few elastographic inverse techniques have been employed which account for the anisotropic, nonlinear behavior exhibited by soft tissues. However, in order to employ these techniques and retain a heterogeneous analysis the sample domain must be divided into homogeneous subdomains which are tested or analyzed separately. The methods developed to approach the problem fall into two broad categories: (1) distributing local tests on the tissue sample, and (2) computationally dividing the sample into presumably homogenous subdomains. As an example of the distributed testing method, Cox et al. [22], developed an indentation method capable of capturing anisotropy by combining force and deformation gradient data. They utilized repeated indentation to quantify the inhomogeneous nature of heart valve leaflet [23], which they coupled with inverse finite element analysis and a nonlinear, anisotropic constitutive equation [24] to determine local material properties. Chai et al. [13], [25] further utilized the methods of Cox to characterize the heterogeneous properties of atherosclerotic plaques, and other approaches have also been developed [26], [27]. In order to determine regional differences, indentation must be applied repeatedly to a tissue specimen, requiring either some a priori knowledge of the regions of interest or an extensive blanket testing protocol.

Inflation and extension are often preferred as more relevant for in-vivo tissue function, usually in conjunction with the homogenous subdomain approach. The work of Seshaiyer & Humphrey [28] is an excellent example of this strategy, applying a hyperelastic constitutive equation to each homogeneous subdomain within a heterogeneous sample. The method was utilized successfully to quantify the material properties of the lens capsule [29] but was limited to small regions of interest within the tissue and has yet to be applied to full-field vessel inflation. Kroon and Holzapfel [30], [31] proposed a different homogenous subdomain method for the estimation of the nonlinear elastic properties of anisotropic membranes during inflation of cerebral and aortic aneurysms with particular emphasis on determination of the anisotropy distribution within the material. Using a hierarchical approach, they successively grouped elements into smaller and smaller locally similar subgroups based on sample geometry. Girard et al. [32] used a similar approach to partition the sclera focusing on shell anatomy. Tomographic approaches, like that presented by Liu et al. [33] for the identification of anisotropic tumors also require the partitioning on the sample domain into homogenous subregions. Again, partitioning was determined based on the tissue geometry.

From this brief survey, certain essential themes emerge: (1) A spatially varying constitutive equation (i.e. material parameters vary with position) is often, if not always, necessary to capture the behavior of a complex tissue. (2) The most common way to implement such variation is by partitioning the sample into homogeneous subdomains. (3) The best approach to identifying partitions, particularly in the absence of anatomical information as a guide, remains an open question and may in fact be the greatest impediment to regional mechanical characterization. This last point is critical - inverse methods per se have advanced to the point where they are significantly better than the subdomain determination methods on which they rely, presenting both a challenge and an opportunity for our community as a whole. Before turning to our approach, we review briefly previous work specifically on the identification of suitable subdomains.

Subdomain determination often requires extensive experimental interrogation, a computationally intensive iterative approach, or a priori information concerning tissue structure. Extensive testing allows true local interrogation of material properties, but the testing mode may not load the tissue in a physiologically relevant manner (i.e. indentation for ventricular or bladder tissue), it may threaten tissue integrity, and it is difficult to execute in-vivo. Various computationally intensive iterative approaches have arisen for the inverse measurement of tissue properties. While these methods are promising, they often require a prohibitively large number of model parameters resulting in both long computation times and concerns about parameter uniqueness. Structural measurements [34]–[41] can inform the partitioning process, but are limited in application to samples suitable for both structural and mechanical characterization if material properties are to be determined.

Strain is an attractive alternative to structural or anatomical variation as a basis for defining partitions, because it can be measured readily and is intimately tied to the mechanical properties of a tissue. For example Plewes et al. [42] showed that partitions determined by strain imaging were as robust as those determined by structural measurement in the identification of breast cancer tumors. MR and ultrasound have produced full 3D reconstructions of displacement fields within tissues from multiple slices of 2D displacement information, induced by harmonic excitations (e.g. [43]). MR elastography is widely used to detect tumors in the breast, prostate, liver, etc. [44]–[46]. Vascular plaques are assessed with intravascular ultrasound by measuring vessel area change in response to applied pressure [47], [48]. Speckle tracking echocardiography [49]–[51], sonomicrometry [52], cardiovascular magnetic resonance tagging [53], and color-coded tissue Doppler echocardiography [54] have all been used to assess regional ventricular function through the measurement of local deformation [55]. Skeletal muscle contraction has been characterized with sonoelastography, which tracks internal tissue displacements following an externally applied perturbation [56]. Full-field strain tracking is also utilized extensively for tissue characterization for experimentation in vitro (as reviewed in [57], [58]). For example, Nielsen and colleagues [59] built a one-of-a-kind multiaxial tester to capture the mechanical behavior of anisotropic, heterogeneous tissues and verified their deformation measurement technique on both an inhomogeneous rubber membrane and sheep diaphragm. Regions with varied mechanical properties were identified through a full-field strain analysis. For some tissue types, the surface of the tissue itself may provide enough unique texture to be tracked without the application of any agent. However, the sample can also be textured through the application of a paint or stain (e.g. [60]) or the dispersion of small particles (e.g. [61]) to achieve a fine, random texture. Additional techniques have also been developed to track surface movement using the microstructure of the tissue such as polarized light (e.g. [62]) and optical coherence tomography [63], [64]. The success of these approaches creates an opportunity for a novel, sequential strategy: the strain field can be used first to partition the sample into regions of with homogeneous or nearly homogeneous properties, and then it can be used as part of an inverse method to determine those properties.

If the strain field is to be used for partitioning, the next issue is how to implement the strain-based segmentation process efficiently and effectively. Manual thresholding [59], [60] is common, but an automated scheme capable of determining partitions from a strain field would be attractive. In particular, Wu and Leahy [65] challenge the use of thresholds in the segmentation of MR images, suggesting instead a segmentation algorithm based on graph theory. Automated image segmentation is challenging, but significant progress has been made (reviewed in [66]). In this work, the concept of network clustering is adapted to the identification of mechanically similar regions within a heterogeneous sample based on a measured displacement field. Two observations inform the process: (1) the normal components of the stress tensor must be continuous across any interface by Newton’s third law, but the deformation gradient need not be so; (2) a displacement field represented by a finite-element grid results in a discontinuous deformation gradient even if the field is smooth in the continuous limit. Thus, the jump in the deformation gradient across an element boundary is a measure of the local change in material properties. Large jumps indicate the element boundary is a good target for segmentation. In some cases, when viewing deformation gradient field there are obvious visual choices for boundary selection. In other cases, however, these boundaries are less clear. Thus, a third critical observation is that the set of finite elements and interelement deformation gradient jumps can be analyzed using graph theory to identify optimal subpopulations (i.e., partitions). The novelty of our approach is combining the two separate existing methods in a new way to create a relatively rapid, simple-to-use, automatic method for segmenting a soft tissue from the tracking without presuming a constitutive equation or seed points (as in the case of a random walking algorithm). Thus, the objective of this work was to combine betweenness based graphical analysis [67], [68] with measured deformation gradient jumps to segment a tissue into homogeneous subregions of different mechanical properties.

II. METHODS: ANALYSIS AND SEGMENTATION SCHEME

A. Full-Field Displacement Tracking

Accurate estimation of full-field displacements from motion capture of soft tissue deformation is crucial for tissue segmentation. Accordingly, high-resolution digital video was captured of various tissue equivalent and soft tissue samples during deformation and digital image correlation was utilized to determine full-field displacement per Raghupathy [69], [70]². The video was synchronized and downsampled to construct grayscale image sequences corresponding to the loading curves of each extension. The image of the sample before the start of test was used as the reference configuration. Using Abaqus™ (6.11, Simulia, Inc., Providence, RI), the tissue boundary was sketched on top of the reference image and meshed with quadrilateral elements. Successive pairs of images were correlated to track the movement of the mesh throughout the loading sequence. Displacement fields were constructed from movement of the mesh and smoothed to reduce noise.

B. Deformation Gradient Jump Calculations

The deformation gradient tensor at the midpoint of each element edge (Fig. 1) was calculated from the bilinear isoparametric representation of the displacement field. For each element edge, the deformation gradient tensor was calculated as follows:

$$F=\left[\begin{array}{cc}\frac{\partial x}{\partial X}& \frac{\partial x}{\partial Y}\\ \frac{\partial y}{\partial X}& \frac{\partial y}{\partial Y}\end{array}\right]=\left[\begin{array}{cc}\frac{\partial x}{\partial \xi }& \frac{\partial x}{\partial \eta }\\ \frac{\partial y}{\partial \xi }& \frac{\partial y}{\partial \eta }\end{array}\right]\ast {\left[\begin{array}{cc}\frac{\partial X}{\partial \xi }& \frac{\partial X}{\partial \eta }\\ \frac{\partial Y}{\partial \xi }& \frac{\partial Y}{\partial \eta }\end{array}\right]}^{-1}$$ (1)

where (X, Y) is the initial position, (x, y) is the final position, and (ξ, η) is the computational coordinate. The deformation gradient tensor for each element edge point, j, was

$$F=\left({\displaystyle {\sum }_{j=1}^4\left[\begin{array}{c}{x}^j\\ y^j\end{array}\right]\left[\begin{array}{cc}\frac{\partial {\phi }^j}{\partial \xi }& \frac{\partial {\phi }^j}{\partial \eta }\end{array}\right]}\right)\ast {\left({\displaystyle {\sum }_{j=1}^4\left[\begin{array}{c}{X}^j\\ Y^j\end{array}\right]\left[\begin{array}{cc}\frac{\partial {\phi }^j}{\partial \xi }& \frac{\partial {\phi }^j}{\partial \eta }\end{array}\right]}\right)}^{-1}$$ (2)

where φ is the bilinear function and j is the index variable looping through the four basis functions for a given element. All shared edges were identified (Fig. 1), and the deformation gradient jump was defined as the double contraction of the difference between the deformation tensors across the edge with itself,

$${\mathrm{\Delta }}_{\mathrm{k}}={\displaystyle {\sum }_{\mathrm{i}=1}^4}{({{\mathrm{F}}_{\mathrm{i}}}^{\text{element}1}-{{\mathrm{F}}_{\mathrm{i}}}^{\text{element}2})}^2$$ (3)

where elements 1 and 2 are the two elements sharing the edge k and i is the index variable looping through the four components of the deformation gradient tensor.

Fig. 1.

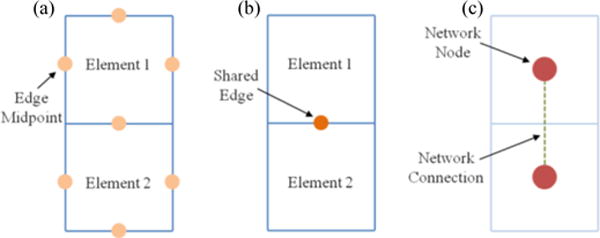
(a) Schematic showing two finite elements indicating the midpoint of each element edge. A deformation gradient tensor was determined for every edge midpoint within the finite element (FE) mesh. (b) Schematic showing two finite elements indicating their shared edge. A deformation gradient jump was calculated for every shared edge. (c) Schematic showing two finite elements and indicating how the FE mesh geometry is converted into a network. The deformation gradient jump was utilized when weighting the network connection.

C. Tissue Segmentation

The flow chart in Fig. 2 summarizes the tissue segmentation scheme. In order to segment the tissue into homogeneous subregions, the finite element geometry for a sample was converted into an equivalent unweighted network. A network node was created for each finite element and if two elements shared an edge, their corresponding network nodes were considered connected (Fig. 1). Once the unweighted network was constructed, it was analyzed to determine the shortest path between each pair of network nodes. Then, a betweenness value for each connection was determined using a breadth-first search algorithm (per [68]). The betweenness value for a connection, as defined by Newman [67], [68], is the number of shortest paths between any given pair of nodes that run along that connection. If there was more than one geodesic path joining a pair of network nodes, then each path contributed a fractional amount to the betweenness. Next, the network connection betweenness values were multiplied by the deformation gradient jump for the corresponding finite element edge. Thus, the final weighted value of betweenness for each network connection was determined both by the sample geometry and by the deformation gradient jump. Following [67], [68], the network connection with the largest value of weighted betweenness was removed. The new, less-connected network was then reanalyzed to determine the new set of shortest paths and the process was repeated. When the network split into disconnected subnetworks, communities were formed, and the network modularity was calculated. Modularity [67] is defined to be the difference between the fraction of connections that fall within communities and the expected value of the same quantity if connections are assigned at random.

Fig. 2.

Flow chart summarizing tissue segmentation scheme.

III. Methods: Testing and Application of the Segmentation Scheme

A. Simulated Experiments

To test the tissue segmentation method in silico, equibiaxial and strip biaxial extensions were simulated using a closed-form nonlinear fiber-based structural model (NFSM) for soft tissues [71]. Briefly, the fiber contribution is described by a bidirectional von Mises distribution, and the fiber stretch ratio is related to the second Piola-Kirchhoff stress through an exponential stress-strain law [72]. The model uses four parameters; the direction (μ) and degree (κ) of fiber orientation and the small-strain stiffness (A) and nonlinearity (B) of the fibers. Simulation parameters were selected based on previous fits of the NFSM to data from rat myocardium [73] and cadaveric bladder wall [69]. For the first set of simulations, a cruciform sample was generated with a central triangular shaped inclusion; the inclusion varied from the bulk sequentially in prescribed fiber orientation (μ_bulk =20° and μ_inclusion =80°), strength of alignment (κ_bulk =1.5 and κ_inclusion = 6.0), stiffness (A_bulk = 5 kpa and A_inclusion = 20 kpa), and nonlinearity (B_bulk = 12 kpa and B_inclusion = 48 kpa). For the second set of simulations, more gradual changes were studied. First, sample orientation was set with anisotropy vectors radially aligned about the sample center. Next, sample anisotropy strength, stiffness, and nonlinearity were maximized in the center of the sample and reduced with radial distance from the center (κ, A, B ~1/1(1 + radial distance)) sequentially. Fig. 3 shows the sample geometry and anisotropy as well as full-field deformation gradient for the equibiaxial extension for both simulations for the condition in which the prescribed fiber orientation was allowed to vary, (strip biaxial extension deformation gradient fields are in the supplementary material).

Fig. 3.

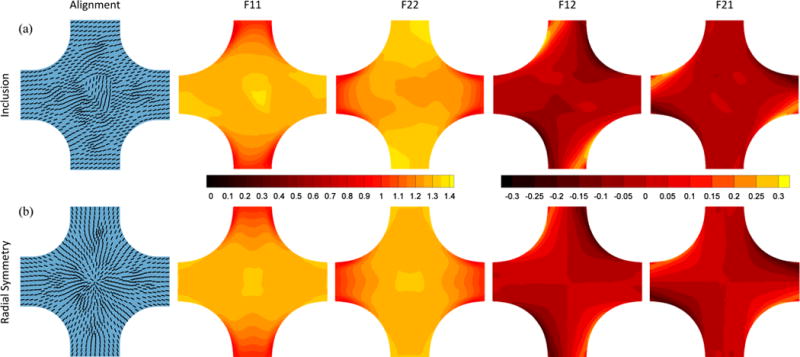
Fiber alignment and full-field deformation gradient tensor components for equibiaxial extension of (a) simulated sample with inclusion for which the inclusion varies only in prescribed fiber orientation (80° vs. 20°) and (b) simulated radially symmetric sample for which the prescribed fiber orientation varied.

Any image segmentation technique is vulnerable to reduced performance in the presence of noise, but for our automated segmentation scheme, noise in the displacement field is amplified in the calculation of deformation gradient, making it a particular concern. To assess the role of noise, we performed additional calculations on the simulated data with various levels of noise introduced into the simulated displacement field. Specifically, the noise amplitude ranged from 0.1% to 5.0% of the maximum displacement for the simulation involving the inclusion with fiber alignment different from the bulk. For each noise level, random error chosen from a uniform distribution was added to the displacements and the sample was partitioned. If one assumes an average strain of 20% on an image that is 1024 pixels wide, the maximum displacement would be 205 pixels, so the error introduced would be roughly equivalent to 0.2 – 10 pixels. Ten replications were performed at each noise level.

B. Experiments on Artificial and Natural Tissues

Strain tracking was performed on experimental data collected from the following samples to provide a wide range of tissue type, heterogeneity, nonlinearity, and anisotropy for the tissue segmentation scheme:

• A heterogeneous polydimethysiloxane (PDMS) sample [70],

• Two compacted collagen tissue-equivalents with different geometries [70],

• A segment of cadaveric human aorta containing a large plaque,

• A segment of a supraspinatus tendon, and

• A sheet of beating cardiac cells [74].

Heterogeneous PDMS

Deformation data from equibiaxial and two strip biaxial extensions performed on a heterogeneous PDMS cruciform, presented previously in the context of inverse methods [69], [70], was analyzed. Briefly, a PDMS solution (Sylgard® 184 Silicone Elastomer Kit; Dow Corning) was created by mixing the curing agent and base (1:10). Since the clear polymer is difficult to image, rice flour was added to opacify the sample. The solution was poured into a custom aluminum mold with a step in the center and was cured at room temperature overnight. The resulting sample was 2.1 mm thick except for the central depression, which was 0.2 mm thick. The thickness difference led to a compliant central region surrounded by a stiffer outer region. Spray paint was used to texture the sample surface for measurement of full-field displacement. The sample was tested at room temperature on an Instron planar biaxial test machine (Instron, Norwood, MA). A pre-load was applied (0.01 N) to each of the four arms, and the sample was preconditioned with nine equibiaxial extension cycles (7.5% stretch). Subsequently, a series of mechanical tests was performed. During testing, digital video of the textured sample surface was obtained with a spatial resolution of ~30 pixels/mm. Full-field displacement tracking was done on the equibiaxial and strip biaxial extensions. The Green strain, which is a direct function of the deformation gradient, for the equibiaxial extension was reported previously [69] and is markedly higher in the central region of the sample. To assess the effect of mesh spacing on the results, we performed a mesh refinement study using ~250 to 4200 elements to discretize the sample geometry. For each case, we determined the number of partitions needed to identify the central depression and the accuracy of the depression area (partitioned area vs. actual area).

Collagen Tissue-Equivalents

Deformation data from equibiaxial and two strip biaxial extensions performed on collagen tissue-equivalent cruciforms, presented previously in the context of inverse methods [69], [70], were analyzed. The samples were created by seeding neonatal human dermal fibroblasts in a collagen gel-forming solution, detailed in Raghupathy et al. [69], [70]. Briefly, the samples were cast in cruciform-shaped Teflon molds such that one sample had vertical arms that were twice as wide as the horizontal, producing moderate vertical alignment in the sample center, and the other sample had arms of equal width, producing a large isotropic zone in the sample center. The samples were incubated for 11 days to allow for cell-induced contraction and remodelling of the collagen network. Prior to biaxial testing, quantitative polarized light imaging (QPLI) was used to quantify the localized direction and strength of fiber alignment in each collagen tissue equivalent sample. Verhoeff’s stain was used to texture the sample surface for measurement of full-field displacement. The sample was immersed in 1% phosphate buffered saline (PBS) and tested at room temperature on a planar biaxial testing machine. Again, a pre-load was applied (0.01 N) to each of the four arms, and the sample was preconditioned with nine equibiaxial extensions (7.5% stretch), followed by a series of extension tests. During testing, digital video of the textured sample surface was obtained with a spatial resolution of ~25 pixels/mm. Full-field displacement tracking was done on the equibiaxial and strip biaxial extensions and Green strain was reported previously [69] for the equibiaxial extension.

Arteriosclerotic Plaque

A segment of fresh diseased thoracic human aorta was obtained from the Anatomy Bequest Program at the University of Minnesota. A portion of the ascending thoracic aorta was cut into a cruciform such that a large transmural arteriosclerotic plaque resided in the central region of the sample, and the circumferential and axial orientations of the aorta coincided with the cruciform axes. Verhoeff’s stain was used to texture the luminal surface sample for optical strain tracking. The textured sample was attached to a biaxial test machine and immersed in 1% PBS for the duration of the test. After a slight preload, the sample was preconditioned with 7 equibiaxial extensions of 15% grip strain at a rate of 3 mm/min. Following preconditioning, the sample underwent an equibiaxial extension and two strip biaxial extensions of 15% grip strain. During testing, digital video of the luminal surface of the tissue sample was obtained at 24 fps, 1080p HD resolution and spatial resolution of ~45 pixels/mm. Full-field displacement tracking was done on each extension, and deformation gradient fields are shown in the supplementary material for the equibiaxial extension.

Supraspinatus Tendon

A whole supraspinatus tendon (SST) specimen, one of the four tendons comprising the rotator cuff of the shoulder, was obtained from the Anatomy Bequest Program at the University of Minnesota and dissected per Lake et al. [1], [2]. A portion of the SST was cut into a cruciform shape such that the transverse and longitudinal orientations coincided with the cruciform axes. The orientation of the sample was noted prior to testing, and Verhoeff’s stain was applied to texture the bursal surface for optical strain tracking. The sample was attached to a biaxial test machine and immersed in 1% PBS at room temperature for the duration of testing. A pre-load was applied (~1 N) to each of the four arms, and the sample was preconditioned with nine equibiaxial extensions (5% stretch). Subsequently, a series of mechanical tests was performed. During testing, digital video of the textured sample surface was obtained with a spatial resolution of ~15 pixels/mm. Full-field displacement tracking was done on the equibiaxial and strip biaxial extensions (deformation gradient fields for equibiaxial extension are in the supplementary material).

Beating Cardiac Sheet

We analyzed the motion of a beating cardiac tissue model using video generously provided by the Healy Group at the University of California, Berkley. Their methods are described elsewhere [74] and are summarized here. Cardiomyocytes were differentiated from healthy human iPS cells per the small molecule WNT-mediated protocol developed by Lian et al. [75]. Single cells were seeded and grown as a monolayer in defined mTeSR1 medium on Matrigel-coated plates at 37°C and 5% carbon dioxide. The cardiomyocytes formed spontaneously contracting sheets (without pacing) of cells 10 days after the WNT-mediated differentiation protocol. A video of the cells was obtained for multiple beats with a spatial resolution of ~0.8 pixels/μm. Full-field displacement tracking was done on grayscale images of the deformation from three successive beats.

IV. Results

A. Simulated Experiments

Full-field displacement was determined for both simulations for all conditions. For brevity, results are presented only for the simulation of the sample containing the inclusion with fiber alignment different from the bulk (μ_bulk = 20°, μ_inclusion = 80°,) and the radially symmetric sample with varied alignment (results from other simulations are provided in the supplementary material). Fig. 4a and d show the sum of the normalized deformation gradient jumps from all three extensions (equibiaxial, vertical strip biaxial, and horizontal strip biaxial) for each simulation. For the sample containing the inclusion, the inclusion boundary can be determined visually from the sum of the deformation gradient jumps alone. For the radially symmetric sample, however, the boundaries are not obvious from the sum of the normalized deformation gradient jumps alone. The partitions are overlaid on each sample in Fig. 4b and e with vectors representing the prescribed fiber orientation. All simulations involving the sample containing the inclusion identified the inclusion as a separate material (supplementary material). The partitions determined for the simulated sample with radial symmetry of prescribed fiber orientation show a distinct pinwheel-shaped pattern at the sample center. Similarly, all the simulations involving the radially symmetric sample created a circular pattern of partitions at the sample center (supplementary material). Fig. 4c and f shows the modularity for the partitioning scheme as a function of the connections removed. The scheme was allowed to continue until 400 connections were removed and the modularity at which communities formed were recorded. While step changes in modularity do correspond with cluster formation, there is no consistent range of modularity values at which the manually determined optimal number of clusters is formed. Fig. 6 shows the inclusion area error as a function of added noise. The errors in the calculated inclusion error vs. the real inclusion area that resulted were averaged over 10 replicates for each noise level. In all cases, the true inclusion area was encompassed by that determined by the segmentation scheme. The inclusion area was identified perfectly for all noise levels of 1% or less.

Fig. 4.

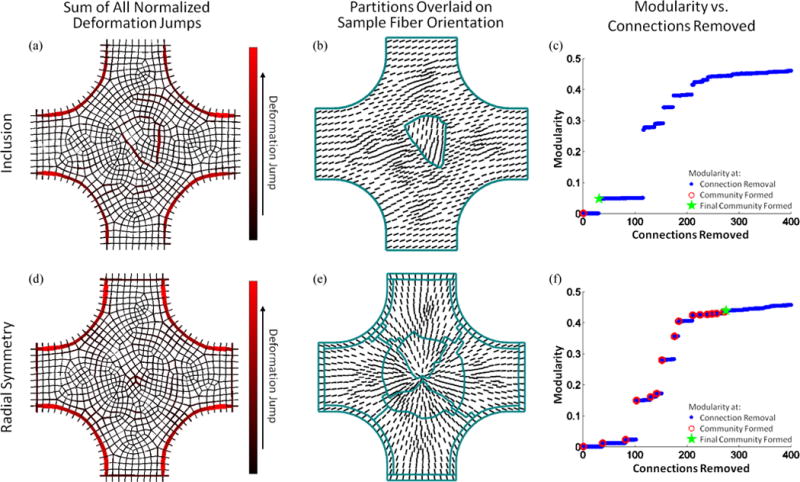
Sum of normalized deformation gradient jumps for all three extensions for the simulated sample containing the inclusion with fiber alignment different from the bulk (μ_bulk = 20°, μ_inclution = 80°) (a) and for the radially aligned simulated sample with varied fiber alignment (d). Partitions, overlaid on sample geometry with prescribed fiber alignment indicated by vectors, identified inclusion (b) and radial symmetry (e), respectively. Modularity as a function of connections removed for both the simulated sample containing the inclusion (c) and the radially aligned simulated sample (f). Blue dots indicate values when a connection is removed, open red circles indicate when a community is formed, and the green star mark when the final community formed.

Fig. 6.

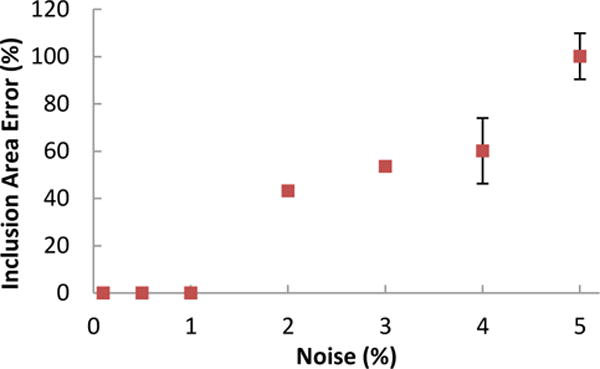
Effect of noise on identification of an inclusion. As the noise level increased, the size of the partition associated with the inclusion increased as well. There was no error in the calculation for noise levels of 1% or less. Each point is the average ± standard deviation of ten replications.

B. Experiments on Artificial and Natural Tissues

Heterogeneous PDMS

The sum of the normalized deformation gradient jumps for the three extensions (equibiaxial, vertical strip biaxial, and horizontal strip biaxial) and the partitions resulting from the automatic segmentation scheme for the PDMS sample are shown in Fig. 5. It is readily apparent from Fig. 5a that the 3-D nature of the modification and the deformation leads to a thick ring of high deformation gradient jumps around the compliant central region rather than a sharp, well-defined boundary as would occur in a purely 2-D experiment. The partitioning scheme immediately and compellingly identified the compliant central region of the sample, Fig. 5b. Fig. 5c shows the modularity for the partitioning scheme as connections are removed. For this sample, we stopped the partitioning scheme after two communities had been formed.

Fig. 5.

(a) Sum of normalized deformation gradient jumps for all three extensions for the heterogeneous PDMS sample. (b) Partitions, overlaid on sample geometry, strongly mirror sample heterogeneity. (c) Modularity as a function of connections removed. Blue dots indicate values when a connection is removed and the green star mark when the final community formed.

Results from the mesh refinement study are shown in Fig. 7. For very coarse and very fine meshes, the image correlation software did not converge, so no data could be generated. For meshes with ~250 – 4200 elements, however, partitions were obtained. Ideally, only two partitions should be needed to describe the sample geometry: one partition for the central depression and one for the outer area. As can be seen in Fig. 7a, for at least 1800 elements, the algorithm was able to identify the more compliant central region using 2 or 3 partitions, one for the central region and one or two in the outer part of the sample. The central region was captured poorly by the coarse meshes (Fig. 7b), with the central partition too large compared to the actual size of the depression. As the mesh was refined, the central partition became more accurate and tended to be slightly smaller than the central depression, perhaps because of the 3D effects near the rim. This error decreased as the mesh was further refined.

Fig. 7.

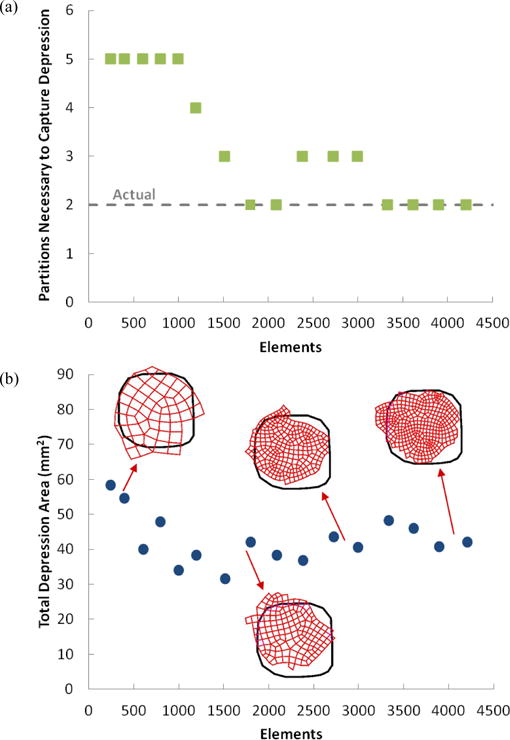
Effect of mesh refinement on identification of the depression area. (a) Number of partitions necessary to capture central depression. (b) Total depression area determined by partitioning scheme for meshes of various sizes.

Collagen Tissue-Equivalents

Fig. 8a and d show the sum of the normalized deformation gradient jumps from all three extensions for both the collagen tissue-equivalent sample with arms of equal width and the sample with vertical arms twice as wide as horizontal arms. Note how in comparison to the PDMS sample, the graph showing the sum of the normalized deformation gradient jumps no longer gives obvious visual cues of partition boundaries. Quantitative polarized light imaging results indicating fiber alignment degree (contour and length of vector) and direction (vector orientation) are shown in Fig. 8b and e, with the partitioning results overlaid. For the equal arm sample, the large isotropic central area is well-identified as are the strongly-aligned arms. In addition, there is preferential partitioning along the edges of the central region, which exhibited strong off-axis alignment. The partitioning scheme was allowed to generate more communities for the sample with unequal arms as a result of its more complex alignment field. In this case, the scheme had some difficulty identifying the two isotropic zones present away from the center and towards the smaller arms. However, a large partition was placed within the moderately aligned sample center, and preferential partitioning was present along the edges of the sample that exhibited strong off-axis alignment. Fig. 8c and f show the modularity for the partitioning scheme as connections are removed.

Fig. 8.

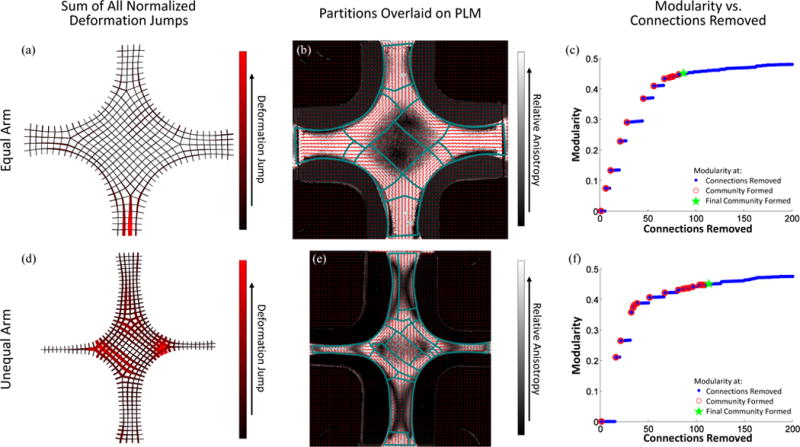
Sum of normalized deformation gradient jumps for all three extensions for both the equal (a) and unequal (d) arm collagen cruciform samples. Partitions are overlaid on the QPLI for both the equal (b) and unequal (e) arm collagen cruciform samples. The modularity for both the equal (c) and unequal (f) arm collagen cruciform samples, respectively. Blue dots indicate values when a connection is removed, open red circles indicate when a community is formed, and the green star mark when the final community was allowed to form.

Arteriosclerotic Plaque

The sum of the normalized deformation gradient jumps from all three extensions for the sample containing the large arteriosclerotic transmural plaque is shown in Fig. 9a. The partitioning results are overlaid on an image of the intimal surface sample taken prior to testing in which visible location of the plaque was noted, arrow in Fig. 9b. The sample was segmented into 10 separate partitions. Of the resulting partitions, one encompasses the plaque with little extraneous tissue. In addition, other partitions seem to identify visually similar regions of the tissue. Fig. 9c shows the modularity for the partitioning scheme as connections are removed.

Fig. 9.

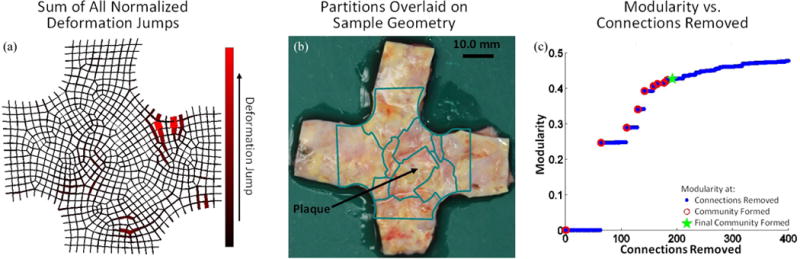
(a) Sum of normalized deformation gradient jumps for all three extensions for the aortic sample containing a large arteriosclerotic transmural plaque. (b) Partitions are overlaid on an image of the sample taken prior to testing in which the plaque was identified. (c) The modularity as a function of connections removed. Blue dots indicate values when a connection is removed, open red circles indicate when a community is formed, and the green star mark when the final community was allowed to form.

Supraspinatus Tendon

The sum of the normalized deformation gradient jumps from all three extensions are shown for the SST sample in Fig. 10a. The partitioning results are overlaid on an image of the bursal surface of the sample taken immediately prior to testing, Fig. 10b. The sample was segmented into 9 separate partitions. Partitions agree with previous results [1], [2] suggesting significant mechanical and organizational heterogeneity including horizontal banding along the anterior-posterior axis and increased vertical banding towards the humeral insertion. Fig. 10c shows the modularity for the partitioning scheme as connections are removed.

Fig. 10.

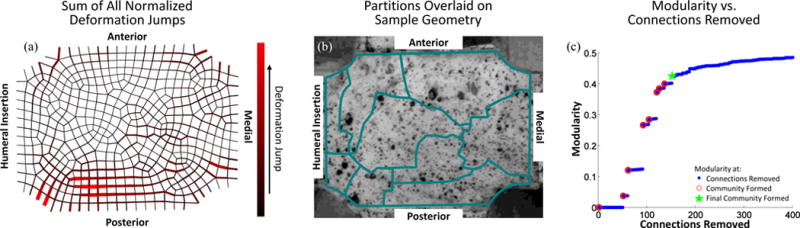
(a) Sum of normalized deformation gradient jumps for all three extensions for the SST sample. (b) Partitions are overlaid on an image of the sample taken immediately prior to testing. c) The modularity as a function of connections removed. Blue dots indicate values when a connection is removed, open red circles indicate when a community is formed, and the green star mark when the final community was allowed to form.

Beating Cardiac Sheet

The sum of the normalized deformation gradient jumps from three beats of the spontaneously beating cardiac sheet are shown overlaid on an image of the cardiac sheet taken immediately prior to beat one, Fig. 11a. The partitioning results, Fig. 11b, are overlaid on the maximum displacement field for beat 1 of the cardiac sheet. The partitions each contain regions of cells that were visually identified by our collaborator Dr. P. Loskill of the Healy Group as beating in unison- both in terms of the magnitude and phase. Fig. 11c shows the modularity for the partitioning scheme as connections are removed.

Fig. 11.

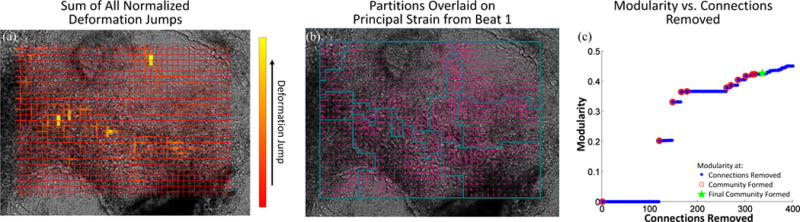
(a) Sum of normalized deformation gradient jumps for all three beats of the cardiac sheet. (b) Partitions are overlaid on an image of the sample taken immediately prior to beat 1 with the principal strain indicated by pink vectors. c) The modularity as a function of connections removed. Blue dots indicate values when a connection is removed, open red circles indicate when a community is formed, and the green star mark when the final community was allowed to form.

V. Discussion

The tissue segmentation routine determined both the location and size of different materials within a single sample based solely on displacement tracking results for simulated samples, tissue equivalents, and native tissue. It was able to capture regional changes in tissue properties due to pathology, as in the case of the sample containing the large transmural plaque, and natural variation, as in the case of the SST, and was able to describe heterogeneous cell contraction in a cardiac sheet. Although the modularity tended to jump when a new partition was formed, we did not find it to be a useful metric to determine the optimal stopping point of the clustering scheme as has been found previously [67]. While the stopping metric did not always suspend partitioning at the time point in agreement with manual partitions, community formation typically identified regions of interest early in the partitioning process (e.g. PDMS sample). Therefore, if one is subsequently analyzing the mechanical properties, an overpartitioned material should give similar mechanics between adjacent regions. Alternative stopping metrics are a potential area of improvement for the algorithm.

Separately, there is our choice of a betweenness based algorithm, which is but one of many options. The random walker algorithm [76], for example, is generally faster than betweenness-based segmentation and has clear stopping criteria but requires user-defined seed points within each partition to be identified a priori. We explored a random walker scheme, but found that it required an unacceptably large number of seed points. For the simulated experiment with the sample containing the inclusion, 12 seed points were required (8 in the bulk and 4 in the inclusion) to identify the inclusion properly. Additionally, segmentation was very sensitive to the location of each seed point, yielding poor results when seed points were close to one another. Therefore, in this context a random walker may be useful to finalize or refine segmentation boundaries but does not appear to be an acceptable stand-alone scheme.

Both the segmentation process and displacement tracking itself are limited by the speckling technique used to texture the sample surface. The coarseness of the FE mesh is dictated by the speckling technique and in turn affects the size and shape of the partitions formed. When the sample surface is discretized into finite elements, they must contain regions with a unique texture in order for DIC to capture surface deformation accurately. The finer a texture is applied to the sample surface, the more refined the mesh can be and therefore the more detailed the displacement tracking and partitioning. In a mesh refinement study (Fig. 7), we found that the performance of the method, in terms of ability to capture a region known to have different properties, improved with mesh refinement. When the mesh becomes too refined relative to the resolution of the image correlation code, however, noise effects pollute the results. Tracking techniques based on inherent image texture [77], measured fiber alignment [62], [78], [79], or natural speckle in an ultrasound image [80], [81] can all provide the potential for better resolution.

Noise in the displacement field is particularly troublesome to the automated segmentation scheme presented because noise error is amplified in the calculation of deformation gradient. In the noise assessment study, when noise was added to displacements from simulated experiments (Fig. 6), it was determined that noise levels less than 1% did not affect partitioning choices. For example, if one assumes an average strain of 20% on an image that is 1024 pixels wide, then 1% of maximum displacement would be 2.0 pixels, which is well above the normal error levels (typically < 0.1 pixels) for the strain-tracking algorithm used. Therefore, even though in the automated segmentation scheme noise in the displacement field is amplified in the calculation of deformation gradient the method can tolerate relatively high levels of noise. It must also be recognized that smoothing the displacement field, which is almost always necessary in DIC-based methods, intrinsically reduces any jumps in the deformation gradient and could reduce the effectiveness of the segmentation scheme. While we used a full-field displacement tracking code developed by Raghupathy et al. [69], [70], any displacement tracking scheme could be used with the automatic segmentation presented, and we would expect similar performance and noise sensitivity.³

In applying inverse methods and complicated constitutive equations to heterogeneous tissues, a major stumbling block is the segmentation of the tissue into discrete homogenous zones. Many inverse methods (e.g., [28], [30], [33], [60], [82]–[85]), which are applied to soft tissues employ full-field displacement measurements from more than one homogenous loading condition, providing information that can help guide the partitioning process. The jump in the deformation gradient across a finite element boundary is a measure of the local change in material properties. Our method takes advantage of the displacement data by applying a betweenness-based graph theory to the deformation gradient to identify mechanically similar regions within a heterogeneous sample, and it has the advantage of segmenting the same finite element mesh that will be used for the inverse calculation. We also note that the approach could, in principle, be applied to any finite element mesh, such as one might obtain from a thermal map of a tissue [86], [87] (using the jump in temperature gradient), and that although only two-dimensional fields were analyzed in the current work, three-dimensional data could be segmented via the same algorithm.

Nondestructive structural characterization (i.e. polarized light, small angle light scattering, optical coherence tomography, etc.) of heterogeneous tissues is not feasible for many tissue types. In addition, it is often the tissues with unique heterogeneity, such as those that are damaged or diseased which are of particular interest. Thus, studies on the mechanical properties of soft tissues that consider regional variability and often involve cutting multiple samples from a single intact tissue specimen present a dilemma: without a priori knowledge of regional variability, how should the sample be cut? The proposed method suggests instead mechanically testing the entire specimen and applying the automated computational dissection routine to the full-field deformation after testing. Thus, dissection is done computationally rather than physically, allowing for the study of tissues with unknown heterogeneity.