Macromolecular crowding develops heterogeneous environments of gene expression in picoliter droplets

Abstract

Understanding the dynamics of complex enzymatic reactions in highly crowded small volumes is crucial for the development of synthetic minimal cells. Compartmentalised biochemical reactions in cell-sized containers exhibit a degree of randomness due to the small number of molecules involved. However, it is unknown how the physical environment contributes to the stochastic nature of multistep enzymatic processes. Here, we present a robust method to quantify gene expression noise in vitro using droplet microfluidics. We study the changes in stochasticity in cell-free gene expression of two genes compartmentalised within droplets as a function of DNA copy number and macromolecular crowding. We find that decreased diffusion caused by a crowded environment leads to the spontaneous formation of heterogeneous micro-environments of mRNA as local production rates exceed diffusion rates of macromolecules. This heterogeneity leads to a higher probability of the molecular machinery to stay in the same microenvironment, directly increasing the system’s stochasticity.

Noise is present in all living cells. It has been studied in prokaryotes and eukaryotes¹, as well as stem^2,3 and cancer cells⁴, and cells expressing viruses⁵. Gene expression is a key example of a complex stochastic enzymatic process. Careful analysis of variations in mRNA and protein levels has revealed the importance of both amplitude and typical decay time of noise and the ability of cells to exploit or suppress noise in gene expression^6-9. Unlike deterministic models of gene expression, which are used to predict dynamics over large populations, stochastic models can correctly predict the dynamics of gene expression at the single cell level¹⁰. Recently, it has become apparent that the stochastic nature of many biochemical processes cannot be ignored in vivo and in vitro: The two-reporter system, developed by Elowitz¹¹ as a reliable method to estimate¹² the magnitude of variation in gene expression, has been used to study noise both in vivo and in vitro^12-14. Because reaction networks inside the cell involve numerous components each at very low concentration, an important degree of randomness is expected^15-18. It is generally accepted that stochasticity is due to both low concentrations of reacting molecules and the random nature of molecular collisions due to diffusion. However, this inherent stochastic nature of chemical reactions is typically ignored when studying chemical reactions in dilute, well-stirred reactors. In contrast, the cell’s interior is an inhomogeneous, crowded environment. In bacteria for example, ~30% of the cell volume is occupied by macromolecules resulting in highly reduced diffusion^19,20. Such a crowded environment can lead to spontaneous spatial organisation due to severely limited diffusion of mRNA molecules²¹. Moreover macromolecular crowding affects the dynamics and thus reaction rates of cellular processes²². Additional studies have shown that prokaryotic cells are less fluid-like than originally anticipated and can exhibit dynamical heterogeneity and glassy features^23,24. Most studies thus far have dealt with either the quantification of noise²⁵, or how cells exploit or suppress noise^1,26. It has previously been shown in silico²⁷ that diffusivity plays a role in gene expression noise, yet no experimental work has estimated the magnitude of the effect of cellular composition or crowded environment within a cell-sized compartment on the stochasticity of biochemical reactions.

To quantify various contributions to noise in in vitro gene expression, we study transcription and translation of cyan fluorescent protein (CFP) and yellow fluorescent protein (YFP) in picoliter droplets^14,28,29. Picoliter droplets are ideally suited to study biochemical reactions involving very small numbers of reactants^30,31. The microfluidic approach allows for precise control over droplet volume, producing a large number of monodisperse water-in-oil droplets at rates up to 500 droplets per second (Supplementary Fig. 1). The large number of identical droplets provides high reproducibility. We can therefore measure stochasticity in gene expression as a function of DNA copy number and macromolecular crowding. Our results emphasise the complex interplay between the cellular environment and the dynamics of cellular processes.

Uncorrelated noise increases with decreasing DNA copy number

One typically distinguishes two types of noise: extrinsic and intrinsic noise¹¹. When comparing the expression of two identical yet independent genes in vivo, fluctuations in the amounts or states of cellular material lead to correlated fluctuations in expression of both proteins, and this is considered extrinsic noise. On the other hand, the stochasticity of a biochemical process or other factors leading to uncorrelated fluctuations in the numbers of either protein is considered intrinsic noise. In line with these explanations, but to avoid confusion with other in vivo experiments and taking into account our experimental setup, we make the distinction between uncorrelated and correlated noise (Fig. 1a and 1b)^8,32,33. Correlated noise arises from the inhomogeneous Poisson distribution of molecules among different bio-reactors leading to droplet-to-droplet variation in expression, but within one bio-reactor CFP and YFP levels are correlated. Correlated noise can be calculated from the covariance between normalised CFP (I_CFP) and YFP (I_YFP) intensities over all droplets. Uncorrelated noise can be seen as the extent to which the output of two reactions in the same confined space differs²⁵ and, is calculated as the normalised root mean square distance from the line CFP = YFP. Various physical and biochemical factors contribute to the uncorrelated noise in our experiments (Fig. 1c): first, as a result of our experimental design using plasmids, our uncorrelated noise is influenced by differences in the relative Poisson distributions of CFP and YFP plasmids. This contribution is not present in the original approach taken by Elowitz and co-workers, and the uncorrelated noise we discuss here should therefore not be confused with their intrinsic noise¹¹. Second, uncorrelated noise arises from the randomness inherent to biochemical reactions and increases with decreasing numbers of reacting molecules. Third, there is a possible contribution from differences in the maturation time of CFP and YFP. Finally, as we demonstrate in this paper, the physical environment within one droplet, reflected for instance by limited diffusion or crowding, can lead to an enhancement of the variations in reaction rates, and makes an additional contribution to uncorrelated noise.

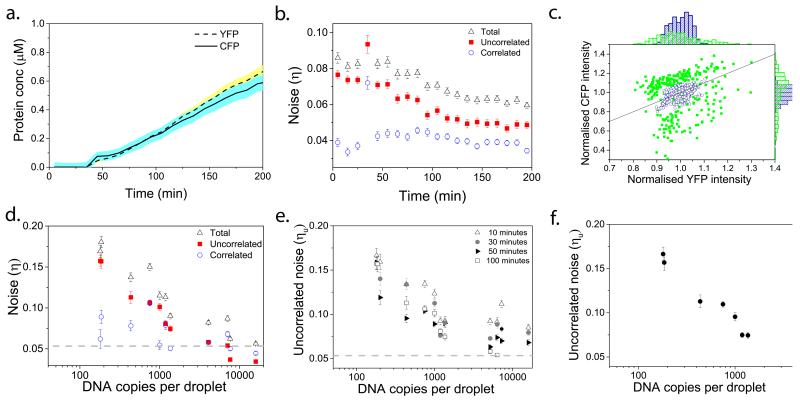
Figure 1. Correlated versus uncorrelated noise.

a, Correlated noise is dominated by the Poisson distribution of reactants over the population of droplets, causing differences of CFP and YFP levels between droplets, i.e. CFP and YFP levels within a droplet are correlated. b, Uncorrelated noise is the noise orthogonal to the line CFP=YFP. c, Uncorrelated noise is caused by relative differences in the Poisson distributions of plasmids, stochasticity of the biochemical reactions, differences in the maturation time of CFP and YFP and the effect of a crowded environment with limited diffusion.

By measuring the fluorescence intensity of YFP (pRSET-YFP) and CFP (pRSET-CFP) (Supplementary Fig. 2) for a population of 300 droplets every 10 minutes (Fig. 2a, Supplementary Fig. 3) and thus following the expression of both proteins per droplet, we can calculate the time evolution of uncorrelated, correlated and total noise in our system (Fig 2b.). There is a constant increase in protein concentrations, because we have no observable protein degradation (Supplementary Fig. 4). Figure 2b shows that the noise levels decrease over time, which is in agreement with the observed increase in protein concentration over time (See Supplementary Fig. 5 for all expression and noise curves). We first varied the DNA concentration from 16,000 copies to 100 copies per droplet of both the CFP and YFP plasmid; the concentrations of all other components were kept constant throughout these experiments. Plotting the normalised fluorescence intensities of CFP and YFP in each droplet with either high (16,000) or low (190) plasmid copy numbers 100 minutes after the start of fluorescence increase (Fig. 2c), we can clearly observe a significant increase in uncorrelated noise (the spread of data points orthogonal to the axis CFP=YFP) as the copy number decreases. These experiments were repeated for a wide range of initial plasmid concentrations. The correlated noise, i.e. distribution of components over the droplets, (Fig. 2d, blue open circles) shows no statistically significant correlation (−0.393 Spearman’s rho correlation) with plasmid concentration. Uncorrelated noise however shows a clear negative correlation (−0.929 significant at the 0.01 level) with plasmid concentration (Fig. 2d), which can be due to gene expression becoming increasingly stochastic with lower numbers of molecules involved. This is in line with the theory of stochasticity, stating that there is an increased relative importance of the fluctuations involved as reactant number decrease¹⁵. This trend is also visible 10, 30 and 50 minutes after the start of expression (Fig. 2e and Supplementary Fig. 7), indicating that it is independent of the moment the image was taken. We chose to calculate noise 100 minutes after the start of fluorescence increase as this yielded higher signal-to-background ratios and thus more reliable data. Furthermore, we plotted uncorrelated noise at 0.2 μM of average protein production over the population of droplets for all DNA copy numbers (Fig. 2f and Supplementary Fig. 8) to confirm that noise increases as we decrease copy number.

Figure 2. Effect of decreased copy number on inherent stochasticity of gene expression in pico-reactors.

a, Average CFP and YFP expression over all droplets. b, Uncorrelated (red full squares), correlated (blue empty circles) and total noise (black empty triangles) values over time for 7600 copies of each plasmid per droplet. c, Normalised CFP versus normalised YFP intensities of the whole population of droplets at 100 minutes after the start of fluorescence increase for 190 (green full squares), and 16,000 copies (blue empty circles) of each plasmid per droplet. Each point represents one droplet. The line is the axis X = Y. d, Uncorrelated (red full squares), correlated (blue empty circles) and total noise (black empty triangles) at 100 minutes after start of fluorescence increase for a range of DNA concentrations. The dotted line represents the background noise due to imaging and analysis (Supplementary Fig. 6). e, Uncorrelated noise values for the DNA range at 10 (empty triangles), 30 (full circles), 50 (full triangles) and 100 (empty squares) minutes after start of fluorescence increase. f, Uncorrelated noise values for the DNA range at different time points where the total protein concentration had reached 0.2 μM. d-f, Error bars show 95% confidence intervals, which were calculated by bootstrapping from the original distribution.

Macromolecular crowding enhances uncorrelated noise

After exploring the range of copy numbers that can be studied reliably, we added Ficoll 70, a common macromolecular crowding agent, to mimic the crowded conditions inside cells^34,35. Remarkably, the addition of 90 mg ml⁻¹ of Ficoll leads to strikingly different production levels of CFP and YFP over the population of droplets (i.e. the uncorrelated noise significantly increases) (Fig. 3a and b, Supplementary Fig. 9).

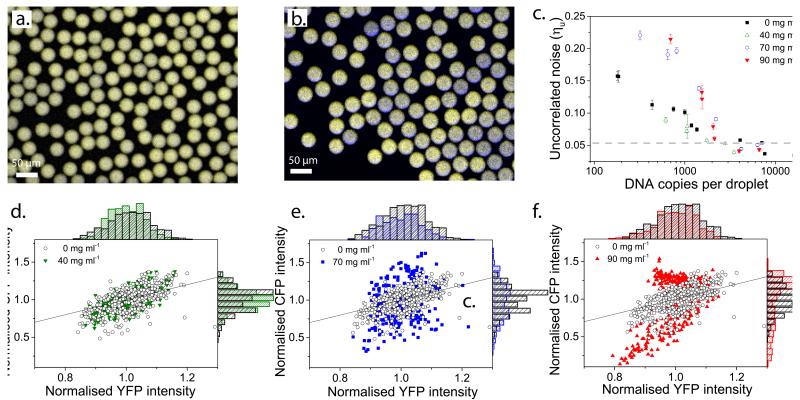
Figure 3. Enhancement of uncorrelated noise in the presence of Ficoll.

a, Superimposed false colour images; CFP and YFP levels are similar in dilute droplets, approximately 600 copies of each plasmid per droplet. b, Super-imposed false colour images; CFP and YFP levels show high variability over a population of droplets, due to differences in CFP and YFP expression within the same droplet at 90 mg ml⁻¹ of Ficoll, approximately 600 copies of each plasmid per droplet. c, Uncorrelated noise at 100 minutes after start of expression for a range of DNA concentrations at different Ficoll concentrations, 0 mg ml⁻¹ (black full squares), 40 mg ml⁻¹ (green empty triangles), 70 mg ml⁻¹ (blue empty circles) and 90 mg ml⁻¹ (red full triangles). The dotted line represents the background noise due to imaging and analysis (Supplementary Fig. 6) and error bars show 95% confidence intervals, which were calculated by bootstrapping from the original distribution. d-f, Normalised CFP versus normalised YFP intensities of the whole population of droplets at 100 minutes after the start of expression, 0 mg ml⁻¹ Ficoll (black empty circles) and 40 mg ml⁻¹ Ficoll (green full triangles), 70 mg ml⁻¹ Ficoll (blue full squares), 90 mg ml⁻¹ Ficoll (red full triangles), for approximately 600 copies of plasmid per droplet. Each point represents one droplet.

We performed cell-free gene expression in the presence of 40, 70 and 90 mg ml⁻¹ Ficoll for a range of DNA concentrations and compared the uncorrelated noise values to results from experiments using 0 mg ml⁻¹ Ficoll (Fig. 3c, see Supplementary Fig. 10). Cell-free gene expression in the presence of 40 mg ml⁻¹ Ficoll shows similar levels of uncorrelated noise as in the absence of Ficoll (Fig. 3d), yet results from both 70 (Fig. 3e) and 90 mg ml⁻¹ (Fig. 3f) Ficoll show enhancement of uncorrelated noise. At approximately 600 copies of each plasmid uncorrelated noise values are 0.11, 0.10, 0.19 and 0.21 for 0, 40, 70 and 90 mg ml⁻¹ of Ficoll respectively.

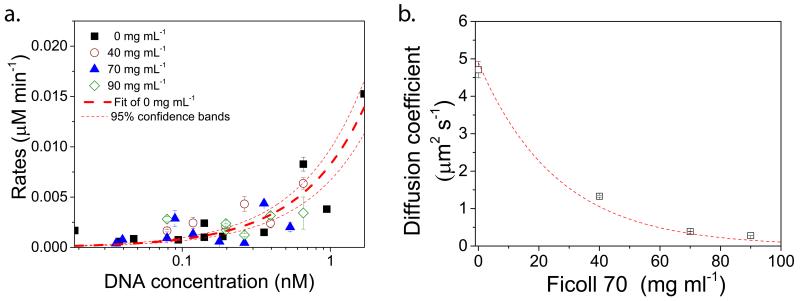
The average protein expression rates (Supplementary methods) in droplets upon the addition of Ficoll are comparable to droplets without Ficoll (Figure 4a and Supplementary Fig. 11), confirming that the increase in uncorrelated noise with increasing Ficoll concentrations was not due to lower protein production. Furthermore the uncorrelated noise at the same protein concentration shows the same trend for all Ficoll concentrations (Supplementary Fig. 12). To understand how crowding leads to enhanced levels of uncorrelated noise in cell-free protein expression we probed the influence of the physical environment on molecular processes. We used fluorescent recovery after photo-bleaching (FRAP) to determine the diffusion coefficient of Alexa 647-labelled 70S ribosomes (Supplementary Fig. 13 and Supplementary methods). As expected the diffusion coefficients decreases as the Ficoll concentration is increased (Fig. 4b). We find a diffusion coefficient of 4.7 ± 0.215 μm² s⁻¹ in the absence of Ficoll and 0.4 ± 0.001 μm² s⁻¹ in the presence of 90 mg ml⁻¹ of Ficoll.

Figure 4. Protein expression rates and ribosomal diffusion coefficients.

a, CFP expression rates for 0, 40, 70 and 90 mg mL⁻¹ with linear fit for 0 mg mL⁻¹ showing 95% confidence bands. b, Diffusion coefficients of ribosomes over a range of Ficoll concentrations determined using fluorescence recovery after photo bleaching experiments. The dashed line is a Stokes-Einstein fit of the diffusion coefficient D ~ 1/μ, with μ the concentration-dependent dynamic viscosity of Ficoll (Supplementary methods).

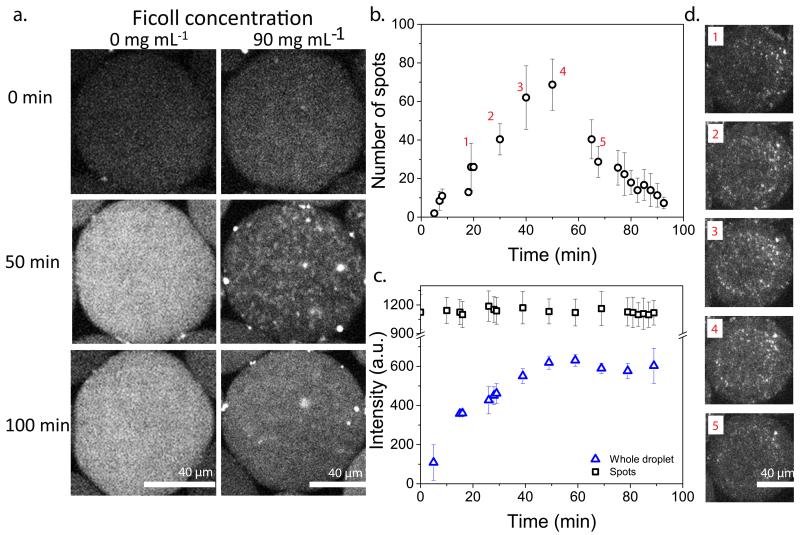
Noting these significantly lower diffusion constants for ribosomes in crowded solutions, we decided to study the spatial distribution of mRNA. Limited diffusion induced by macromolecular crowding could potentially hinder the homogeneous distribution of in situ synthesized mRNA molecules^21,36 thereby increasing heterogeneity and consequently uncorrelated noise. To investigate the distribution and localisation of the mRNA in crowded and dilute solutions, we studied an in vitro transcription-only system using a DNA sequence encoding for a 32 repeat sequence (pET-32xBT) of a hybridisation target for a molecular beacon (Supplementary Fig. 14 and Supplementary methods). This method has previously been used successfully in vivo³⁷, and allows visualisation of mRNA production using confocal microscopy. In vitro transcription was performed in droplets in the absence of Ficoll and in the presence of 90 mg ml⁻¹ of Ficoll (Fig. 5a). Without Ficoll there is a homogeneous distribution of mRNA molecules and gradual increase in fluorescence in the droplets, while droplets with crowding agent show the appearance of spots over time indicating local areas of high concentrations of mRNA. These spots disappear when transcription stops, indicating that they are not aggregates of mRNA. We followed the number of spots over time for two separate experiments (Fig, 5b and Supplementary Fig. 15) and in both cases observed an increase in the number of detectable spots for approximately the first 50 minutes followed by a decrease. We note that the absolute number of spots detected is quite low; we can see many more very small spots, but they fall below our signal-noise threshold. The spots have constant average fluorescence intensity over time (Fig. 5c) indicating that there is equilibrium between production and dissipation of mRNA. However, the fluorescence intensity of the whole droplet increases for the first 50 minutes, which supports the argument that mRNA is constantly dissipating from its production point. As spots started disappearing after 50 minutes the average intensity of the droplet reaches a plateau, the spots disappear because as production of mRNA seizes, only dissipation occurs. The number of spots scale linearly with the DNA copy number (Supplementary Fig. 15). These results imply that the spots are local production sites of mRNA. These spots were absent when no DNA was added and we verified that they did not result from aggregation of mRNA and molecular beacon induced by Ficoll (Supplementary Fig. 16). In other words, transcription in crowded droplets leads to a heterogeneous distribution of mRNA molecules over the time course of mRNA expression, similar to the limited diffusion of mRNA molecules observed in E.coli cells²¹. The formation of high local concentrations of mRNA can be explained by an imbalance in production rates and diffusion rates, the latter dropping significantly in crowded solutions (Fig. 4b). We note that the inhomogeneous production of proteins cannot be observed, as they will have distributed homogeneously over the droplet volume before their fluorophore have matured.

Figure 5. Inhomogeneous distribution of mRNA over one droplet at high Ficoll concentrations.

a, In vitro transcription only experiments with 0.6 nM pET-32×BT showing mRNA expression with 0 mg mL⁻¹ (left) and 90 mg mL⁻¹ (right) of Ficoll, in the presence of molecular beacon (MB) b, Average number of spots over time from three separate droplets (circles) with error bars showing standard deviations. c, Average fluorescence intensity over time of the detected spots (squares) and the whole droplets (triangles). Error bars are standard deviations of three separate droplets. d, Representative fluorescence images corresponding to the labelled time points in b.

Crowding causes spontaneous formation of microenvironments

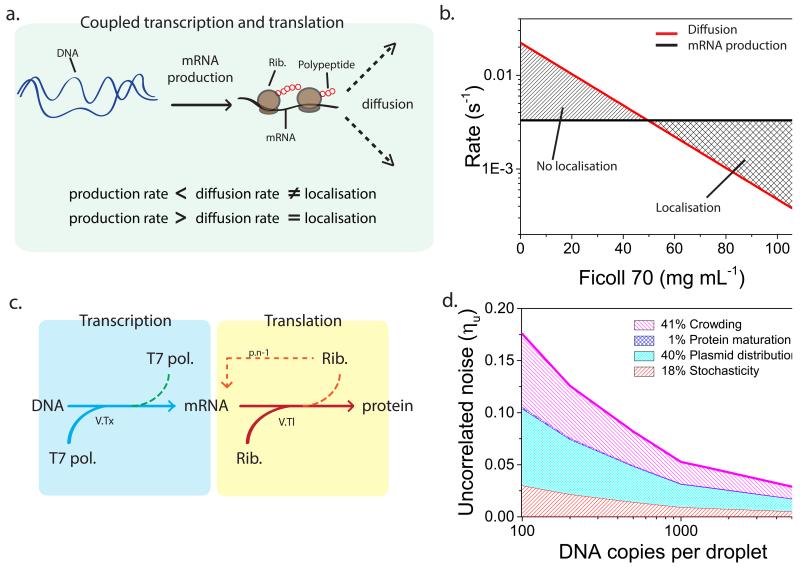
To understand under what conditions the mRNA will be distributed heterogeneously, in other words, at what point the local synthesis rate of mRNA exceeds the local diffusion rate of mRNA (Fig. 6a), in a coupled transcription translation reaction, we calculated the time it would take for one mRNA to be produced (Fig. 6b Black line) using Michaelis Menten kinetics with a typical K_m of 0.5 nM and V_max of 0.1 nM min⁻¹ (derived experimentally, see Supplementary Fig. 17). Newly produced mRNA becomes bound by ribosomes, multiple ribosomes interacting with one mRNA can associate into a polysome and diffusion coefficients for these polysomal complexes were estimated using Stokes-Einstein equation (Supplementary Fig. 18). We assume that the plasmids are distributed homogeneously (Supplementary Fig. 19) with an average distance d ~ c^−1/3. We thus calculated the average rate (in s⁻¹) for a polysome to diffuse over a distance d/2 (Fig. 6b Red line). We found that below 50 mg mL⁻¹ of Ficoll the diffusion is typically higher than mRNA production resulting in no localisation, and above 50 mg mL⁻¹ the inverse is the case resulting in localisation. Not much is known about the exact mechanism of localised transcription and translation in bacterial cells, though there has been much speculation that slower diffusion plays a role^38,21. Our results indicate that the decreased diffusion caused by molecular crowding could indeed play a prominent role in localised gene expression.

Figure 6. Theoretical modelling of gene expression noise.

a, During in vitro transcription and translation all the biologically active machinery is unlikely to localise at the production site if the production rate is smaller than the diffusion rate, and is likely to localise at the production site if the production rate is larger than diffusion rate. b, Theoretical model predictions of mRNA production (black line) and polysome diffusion over half the average distance between two plasmids (red line). The crossover between both rates indicates the transition between a homogeneous distribution of mRNA and an overall localization of mRNA, therefore showing the Ficoll concentrations at which we would see localisation and which not. c, Schematic illustration of the stochastic transcription-translation model used in crowded droplets. Due to the formation of microenvironments ribosomes preferentially rebind to previous mRNA (n-1). d, Simulation results showing the contributions of all factors to the total uncorrelated noise. Stochasticity shown in red, plasmid distribution in light blue, protein maturation in dark blue, and crowding in violet.

To estimate the relative contribution of the different factors influencing uncorrelated noise we simulated the stochastic cell-free gene expression in 200 droplets using Gillespie’s Direct Method algorithm (Supplementary methods) (Fig. 6c). Again we used the same K_m and V_max values for transcription previously established. For translation, a K_m value from Stögbauer and co-workers was used³⁹ and V_max was estimated from our experimental results. We measured protein maturation times (Supplementary Fig. 20) at different Ficoll concentrations and included these in the model. The uncorrelated noise versus plasmid copy number is plotted by taking the uncorrelated noise values after 100 minutes. First we simulated transcription and translation with stochasticity as the only contributing factor, thereby excluding Poisson distribution of plasmids, protein maturation and crowding. Later, the other factors were included in the model one by one to determine the contribution of each factor separately (Fig. 6d and Supplementary Fig. 21). The crowded droplets were simulated using a 10 times higher probability for a ribosome to rebind to the same mRNA (p.n-1). An enhanced rebinding probability is supported by the observation and explanation of mRNA localisation discussed above. The translationally active machinery must be co-localised with the mRNA, and this creates local microenvironments with higher concentrations of biologically active transcription and translation machinery, i.e. accumulation of ribosomes at plasmids. Due to lower diffusivity this machinery has a higher probability of rebinding than anticipated from a homogeneous distribution of all components.

The results from the stochastic simulation show a decrease of uncorrelated noise with increasing copy number which is consistent with our experimental data. Importantly, the model also shows that the trend of uncorrelated noise over plasmid copy number is not due to population differences in mean (CFP and YFP concentration) over the range of DNA copy numbers, which is also consistent with our experimental findings (Supplementary Fig. 22 and 12). We find that CFP and YFP maturation time has almost no effect on uncorrelated noise (mean of 1% over the plasmid copy numbers) while the average contributions over the plasmid copy numbers of stochasticity, Poisson distributions of plasmids and crowding are 18%, 40% and 41% respectively (Supplementary Fig. 20).

Conclusions

By studying gene expression in picoliter droplets, we can reliably analyse the uncorrelated and correlated noise of protein expression of low copy numbers of DNA under different physical conditions. Surprisingly, we find that an increase in macromolecular crowding, leading to an order-of-magnitude decrease of diffusion coefficients of RNA and proteins, leads to significantly enhanced uncorrelated noise. At the same time, we observe that mRNA becomes distributed heterogeneously over the droplet creating local microenvironments where gene expression occurs. Due to the formation of large polysomes, biologically active machinery will be less likely to diffuse away from these microenvironments. This lack of diffusion maintains the heterogeneous environment and enhances any already existing stochasticity caused by transcription and translation of low copies of DNA. Theoretical modelling strongly supports this theory, showing that heterogeneous display of mRNA is caused by a fine balance between mRNA production rates and diffusion times. Furthermore the results of the stochastic simulations suggest that any existing bias towards one of the two fluorescent proteins is strongly enhanced by preferential rebinding of ribosomes to the same mRNA, which we believe is the cause of our observed enhanced uncorrelated noise in crowded droplets.

These results are the first to show that the stochasticity of biochemical reactions is governed by the interplay between the rate of the reaction and its environment. Our experimental finding of heterogeneous mRNA distributions in crowded in vitro transcription systems and the concomitant increase in uncorrelated noise in similarly crowded cell-free expression systems has important implications for our understanding of living cells. It is very much conceivable that the synthesis of macromolecules (mRNA and proteins) in vivo leads to locally heterogeneous systems, as production rates will often be larger than diffusion rates²¹. This might explain the findings in literature on localisation of mRNA in E. coli^21,38, but also helps to explain the origin of experimentally determined uncorrelated noise in gene expression⁴⁰. Finally, our experiments enable us not only to take into account, but also predict the magnitude of stochasticity when designing synthetic chemical pathways similar to artificial cell-like systems.

Methods

Device fabrication

The design of the microfluidic devices was made in AutoCAD. These wafers contain a negative relief in SU-8 photoresist on a silicon wafer substrate. The channels for the droplet production are 25 μm. To make the microfluidic devices, crosslinker and PDMS were added together at a ratio of 1:10 crosslinker:PDMS and the solution was poured on the wafers (which were cleaned with isopropanol). Air bubbles were removed using a desiccator. Thereafter, the devices were put in the oven at 65 °C for at least two hours. After preparing the PDMS layer, the device was bonded on a glass slide by activating the PDMS and glass surfaces using the plasmacleaner (Femto) after which the surfaces were bonded together. Air between the surfaces was removed by gently applying pressure. The device was incubated for at least 3 hours at 100 °C after which the device was coated with a 2% silane solution.

Device and set-up operation

Liquids were pumped into microfluidic devices using adjustable pumps (Harvard apparatus, PHD 2000 infusion) connected to syringe via PTFE tubing (inner diameter: 0.056mm outer diameter 1.07 mm). Droplets in microfluidics were stabilised using a 2% of biocompatible Krytox-based tri-block copolymer surfactant, in Fluorinert FC-40 oil (from Sigma-Aldrich) or Hydrofluoroether (HFE).

Data acquisition and analysis

The devices were mounted on the inverted microscope (Olympus IX81) equipped with a motorised stage (Prior, Optiscan II). Fluorescence images were taken with the sensitive EMCCD camera (iXon, Andor) using illumination from the mercury lamp. Analysis of images was done by home-written Matlab routine.

Plasmids

The pET plasmids with CFP and YFP sequence at the multiple clone sites were a kind gift of R.Y. Tsien. The sequences for CFP and YFP production in the pET plasmids were inserted into pRSET vectors (Life Technologies) with Nco-I at the 5’end of the coding sequence (CDS) and a Xho-I restriction site at the 3’end of the CDS. The plasmids were purified and purity was analysed using gel electrophoresis and sequencing analysis (GATC Biotech, Germany). Concentration of plasmids was determined using a Nanodrop N1000 spectrophotometer. The pRSET vector has T7 RNAP promoter and terminator regions.

Lysate preparation

E. coli Rosetta2 cells were grown at 37°C to an OD₆₀₀ = 1.5 in 2YTPG broth. After cell growth all the subsequent steps were kept on ice. The cells were collected (3000 g, 10 minutes, 4°C), thoroughly dissolved in ice-cold 20% sucrose solution (16 ml for 3 g wet pellet weight) and incubated on ice for 10 minutes. Cells were then collected (3000 g, 10 minutes, 4°C), resuspended in ice cold MQ (4 × wet pellet weight) and immediately spun down (3000 g, 10 minutes, 4°C). Next cells were again resuspended in ice cold MQ (4 × wet pellet weight), allowed to incubate on ice for 10 minutes and spun down (3000 g, 10 minutes, 4°C). Pellet was then carefully washed twice with ice-cold MQ (1.5 × volume). The spheroplast pellet was stored at −80°C.

The spheroplasts were thawed and resuspended in ice-cold MQ (0.8 × volume). Cells were lysed by 10 cycles of sonication (10 s at 10 μm amplitude followed by 30 s on ice). Cell debris was collected (30000 g, 30 min, 4°C) and dialysed 1 × against 50% dialysis buffer (5 mM Tris, 30 mM potassium glutamate, 7 mM magnesium glutamate, 0.5 mM DTT), and 3 × 100% dialysis buffer (10 mM Tris, 60 mM potassium glutamate, 14 mM magnesium glutamate, 1 mM DTT).

IVTT mixture

For transcription-translation systems the reaction mixtures consisted of one third of cell lysate from BL21 (DE3) host strain (approximately 25 mg ml⁻¹) and of two thirds of reaction buffer. The final reaction mixture contained 50 mM Hepes (pH 8.0), 2.4 mM Guanosine Triphosphate (GTP), 1 mM Adenosine Triphosphate (ATP) and Cytidine Triphosphate (CTP) and Uridine Triphosphate (UTP) each, 0.66 mM Spermidine, 0.5 mM cyclic adenosine monophosphate (cAMP), 0.22 mM Nicotinamide adenine dinucleotide (NAD), 0.17 mM coenzyme A, 20 mM 3-phosphoglyceric acid (3-PGA), 0.045 mM folinic acid, 0.13 mg ml⁻¹ transfer ribonucleic acid (tRNA), 1 mM of each amino acid, 10 mM magnesium glutamate, and 66 mM potassium glutamate, T7 RNA polymerase (130 U), and cell lysate (8.3 mg ml⁻¹), contributing an additional 5 mM magnesium glutamate and 20 mM potassium glutamate. Plasmids were added last to initialise transcription.