Fourier phase in Fourier-domain optical coherence tomography

Abstract

Phase of an electromagnetic wave propagating through a sample-of-interest is well understood in the context of quantitative phase imaging in transmission-mode microscopy. In the past decade, Fourier-domain optical coherence tomography has been used to extend quantitative phase imaging to the reflection-mode. Unlike transmission-mode electromagnetic phase, however, the origin and characteristics of reflection-mode Fourier phase are poorly understood, especially in samples with a slowly varying refractive index. In this paper, the general theory of Fourier phase from first principles is presented, and it is shown that Fourier phase is a joint estimate of subresolution offset and mean spatial frequency of the coherence-gated sample refractive index. It is also shown that both spectral-domain phase microscopy and depth-resolved spatial-domain low-coherence quantitative phase microscopy are special cases of this general theory. Analytical expressions are provided for both, and simulations are presented to explain and support the theoretical results. These results are further used to show how Fourier phase allows the estimation of an axial mean spatial frequency profile of the sample, along with depth-resolved characterization of localized optical density change and sample heterogeneity. Finally, a Fourier phase-based explanation of Doppler optical coherence tomography is also provided.

1. INTRODUCTION

Phase is a manifestation of an electromagnetic wave propagating through a medium [1]. In microscopic imaging, where the media are often cells and tissue samples with low intrinsic contrast under bright-field imaging conditions, phase contrast [2,3] and differential interference phase contrast [4,5] microscopes are extensively used to noninvasively visualize the structure and dynamics of these unlabeled biological samples. Over time, research efforts have focused on developing microscopes with the ability to both visualize and quantify this phase contrast [6–12] and applying them to characterize cellular dynamics and pathology [13–19]. The phase in these transmission-mode quantitative phase microscopes is well understood in wave optics. It is the integral of the sample refractive index along its depth—that is, the optical path length (OPL)—with respect to the surrounding medium and couples together the refractive index and the sample thickness.

In the past decade, Fourier-domain optical coherence tomography (FD-OCT) [20,21] has been utilized to successfully extend the idea of quantitative phase from transmission-mode to reflection-mode [22–24], generating significant interest in the research community [25–41]. Unlike the transmission phase, however, the phase measured through FD-OCT—either using spectral-domain OCT (SD-OCT) or swept-source OCT (SS-OCT) configurations—is the phase of the Fourier transform of the spectral interference between the depthwise coherently integrated back-reflected waves from within the sample and a reference (preferably a common mode). This Fourier phase, therefore, involves an explicit recharacterization of the phase associated with the propagating electromagnetic wave and carries distinctly different information than the OPL in transmission-mode quantitative phase microscopy (QPM). While studying cellular dynamics at a strong interface, the authors of [23] showed that Fourier phase at the interface estimates the subresolution change in its optical depth location. They named their FD-OCT-derived approach for measuring Fourier phase changes at strong interfaces as spectral-domain phase microscopy (SDPM). In our own work, we have been interested in extending the measurement of Fourier phase to fixed-depth locations within the sample without any strong interfaces. This has led to the development of depth-resolved spatial-domain low-coherence quantitative phase microscopy (dr-SLQPM) [42,43]. During its development, we realized that both SDPM and dr-SLQPM are special cases of a more general and richer theory of Fourier phase. This general theoretical framework is the focus of this paper.

We show that Fourier phase in the context of FD-OCT is an estimate of the otherwise inaccessible (based on Fourier amplitude) structural information about the sample refractive index within the implicit coherence gating enforced by the limited spectral bandwidth of the light source. This structural information characterizes the subresolution offset and mean spatial frequency of the coherence-gated refractive index at the optical depth being probed.

Subresolution offset, first introduced in [23] for a special case, is in general a measure of the subresolution deviation between the optical depth where the measurement is made and the optical depth corresponding to the weighted-center of the coherence-gated refractive index around the probed optical depth. In the particular case of a strong interface, it can be used to measure the subresolution change in the optical depth location of the interface [23]. (Also see Eq. (9) and the related discussion, and Section 4).

The mean spatial frequency is a measure of the average rate-of-change of refractive index within the coherence gate at the optical depth being probed. It is, therefore, a measure of the intrinsic structural property of the coherence-gated refractive index. It quantifies not only the changing (increasing or decreasing) optical density within the gate but also its mean heterogeneity.

Fourier phase is a joint estimate of these two characteristics of the coherence-gated sample refractive index. We show why this is so and derive analytical expressions for this joint estimate from first principles. We additionally show that under specific sample and measurement conditions, SDPM and dr-SLQPM are special cases of this joint estimate. To bring the theoretical framework full circle, we further show that for an ideal source with unrestricted spectral bandwidth, all structural information is carried in the Fourier amplitude of FD-OCT and the Fourier phase is zero. The theoretical results presented here are illustrated and verified throughout by plotting the derived analytical expressions and performing numerical simulations.

These analytical expressions and numerical simulations have interesting implications. Using them we estimate the axial mean spatial frequency profile of the sample, along with providing depth-resolved characterization of localized heterogeneity of the sample refractive index and density changes in the sample refractive index. We also show that they provide a Fourier-phase-based explanation of the principle of Doppler OCT (D-OCT), a functional extension of FD-OCT [44].

The paper is structured as follows. In Section 2, we present how Fourier phase originates and derive its general expression by introducing the concept of structural information. Section 3 explains Fourier phase in the context of a slowly varying refractive index and presents the corresponding analytical expression. This expression is used to establish the validity of dr-SLQPM. In Section 4, the refractive index profile with a strong interface is considered, and the general expression for Fourier phase is used to derive the specific measurement made by SDPM. In Section 5, Fourier phase is discussed for an ideal source with infinite spectral bandwidth. Simulation-based results along with Fourier phase applications and a Fourier phase-based explanation of the D-OCT principle are presented in Section 6. We conclude in Section 7. For ease of explanation, detailed derivations associated with the above sections have been collected in the appendices.

2. GENERAL THEORY

Consider an FD-OCT optical setup that either uses a coherent source with point scanning or a spatially incoherent source with full-field illumination. In the latter case, the van Cittert–Zernike theorem [1] along with the light source properties can be utilized to design optical setups (see, for example, [45]) that decompose the sample illumination beam into mutually incoherent light channels. In either case, if the illumination angle is small, the back-reflected sample field at an en face location (x′, y′) is characterized by a one-dimensional (1D) axial refractive index profile n_s(z′), with z′ denoting the physical depth [46]. This 1D characterization is also used in developing the principle of SDPM [23,24] and FD-OCT itself [20].

Assuming that the sample being probed satisfies the Born approximation [1], the reflection profile corresponding to n_s(z′) is given by [47,48]

$$r_s(z^{\prime })=\frac{1}{2}\frac{d\log n_s(z^{\prime })}{d{z}^{\prime }}.$$ (1)

We note that the concept of Born approximation is typically associated with describing the scattering potential of a weakly scattering sample in the setting of diffraction tomography to reconstruct the three-dimensional (3D) refractive index distribution of the sample via far-field measurements of the scattering amplitude [49]. There, the scattering potential F(r) characterizes the refractive index distribution of the sample n_s(r) with respect to the surrounding medium n_m(r) through the relation $F(\mathbf{r})=-k_0^2(\frac{n_s^2(\mathbf{r})}{n_m^2(\mathbf{r})}-1)$ [1,47,50], where $k_0=\frac{2\pi }{{\lambda }_0}$ is free-space wavenumber corresponding to wavelength λ₀. However, in the context of Fourier phase, the gradient of the refractive index within the sample is of primary interest as it is the change in the refractive index within the sample that gives rise to the back-reflected sample field. It has been shown that the validity of the Born approximation also allows the scattering potential of an object to be described in terms of the gradient of the 3D refractive index [47]. The restriction of the gradient to the 1D setting is given by Eq. (1).

For the purpose of explication, we adopt a common-path reflection-mode geometry, while noting that it is not a requirement. (Methods have been developed to remove phase noise arising in optical setups, where the reference is generated using a mirror placed in a separate reference arm [51].) In common-path geometry, the reference wave generated by reflection from the substrate–sample interface spectrally interferes with the back-scattered waves from all sample depths (see Fig. 1) resulting in a spectrally interfered signal given by [50]

$$\begin{array}{l}P(k)=S(k)(r_r^2+{\displaystyle {\int }_0^L{r}_s^2(z^{\prime })\mathrm{d}{z}^{\prime }}\\ +2{\displaystyle {\int }_0^L{r}_s(z^{\prime })r_r\cos (4\pi k{z}_{\mathrm{opl}}(z^{\prime }))}\mathrm{d}{z}^{\prime }).\end{array}$$ (2)

Here, S(k) is the source spectrum, and the integration upper limit L represents the sample thickness. Equation (2) states that for every wave number k=1∕λ (we use the spectroscopic wave number notation), the last term on the right-hand side is the coherent integration of interference between the reference and reflections from all depths, modulated by the source spectrum. The strength of the sample reflection from physical depth z′ is given by the reflection profile r_s(z′) and that of the reference by r_r. The self-interference of the reference and within-sample scattering gives rise to the first two terms. In this expository development of Fourier phase, we ignore the first two terms. In practice, ancillary background measurements are used to separately measure and remove $r_r^2$. Furthermore, typical experimental conditions ensure r_s(z′) ≪ r_r, and we can ignore the second term ${\displaystyle {\int }_0^L{r}_s^2(z^{\prime })\mathrm{d}{z}^{\prime }}$. (In SS-OCT dual balanced detection is used to mitigate the effect of the first two terms.) We, therefore, simplify Eq. (2) to

$$P(k)=2S(k){\displaystyle {\int }_0^L{r}_s(z^{\prime })\cos (4\pi k{z}_{\mathrm{opl}}(z^{\prime }))\mathrm{d}{z}^{\prime }},$$ (3)

where, the reflection term has been normalized to remove r_r.

Fig. 1.

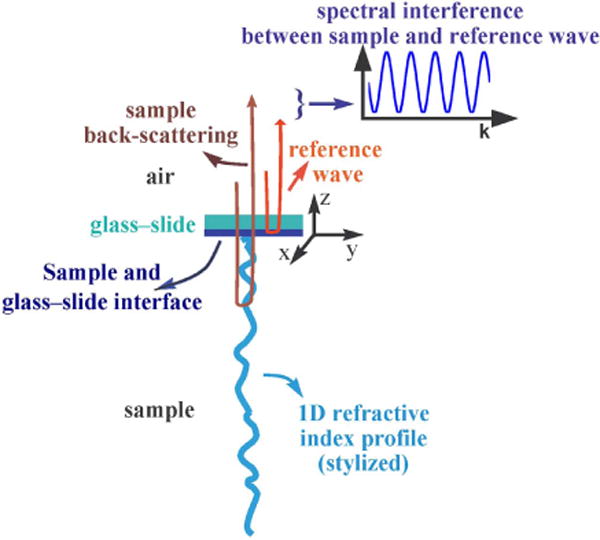
Stylized depiction of spectral interference due to sample back-scattering and common-path reference.

In reflection-mode geometry shown in Fig. 1, the illumination and back-scattered wave vectors corresponding to the wave number k, respectively, are ${\mathbf{k}}_i=-k\widehat{\mathbf{z}}$ and ${\mathbf{k}}_{bs}=k\widehat{\mathbf{z}}$. The resulting axial spatial frequency, therefore, is given by $\mathbf{K}={\mathbf{k}}_{bs}-{\mathbf{k}}_i=[k-(-k)]\widehat{\mathbf{z}}=2k\widehat{\mathbf{z}}=K\widehat{\mathbf{z}}$. We note that throughout this paper spatial frequency will exclusively refer to axial spatial frequency. Incorporating it in Eq. (3) and transforming to the optical-space where Fourier measurements are made, we reformulate Eq. (3) as (see Appendix A)

$$P(K)=2S(K){\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{r}_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))\cos (2\pi K{z}_{\mathrm{opl}}(z^{\prime }))\mathrm{d}}{z}_{\mathrm{opl}}(z^{\prime }),$$ (4)

where

$$z_{\mathrm{opl}}(z^{\prime })={\displaystyle {\int }_0^{z^{\prime }}n(z^{″})\mathrm{d}{z}^{″}},$$ (5)

is the optical depth corresponding to the physical depth z′ and

$$r_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))=\frac{r_s(z_{\mathrm{opl}}(z^{\prime }))}{n_s(z_{\mathrm{opl}}(z^{\prime }))},$$ (6)

defines the mapping of the reflection profile r_s(z′) to the optical-space. Equation (4) now expresses the coherent integration of interference between the reference and reflections from all depths within the sample as a function of the optical depth instead of the physical depth. We emphasize that this mapping from physical-space to optical-space is imperative with the use of Fourier transform in FD-OCT, as the Fourier transform allows access only to the latter and not the former.

The spectral source S(K) we controls the resolution with which can recover r_opl(z_opl(z′)) through the virtual coherence gating enforced by its correlation function in the optical-space. If the source spectrum had infinite bandwidth, we would have ideal resolution allowing for exact measurement of real-valued r_opl(z_opl(z′)) with Fourier phase being zero. (We prove this in Section 5.) In practice, however, only a finite spectral bandwidth can be realized, with an attendant loss in resolution. The resulting Fourier transform of the spectral interference has both amplitude and phase, with both carrying distinct information about the refractive index profile within the coherence gate.

The amplitude of the Fourier transform has been well understood within the context of FD-OCT. It captures the coherence-gated average of r_opl(z_opl(z′)) and therefore is a point estimate of the average strength of coherence-gated r_opl(z_opl(z′)) at the optical depth being probed. Fourier phase, on the other hand, is a point estimate of two distinct structural characteristics of the refractive index profile within the coherence gate.

The first structural characteristic is the subresolution offset. We denote it by δz_opl(z), where z_opl(z) indicates the optical depth being probed. Subresolution offset estimates the subresolution deviation of the optical depth associated with the weighted-center $z_{\mathrm{opl}}^{wc}(z)$ of the refractive index profile within the coherence gate, from z_opl(z). (Note that the coherence gate is centered at z_opl(z).) Mathematically, the subresolution offset is given by

$$\delta z_{\mathrm{opl}}(z)=z_{\mathrm{opl}}(z)-z_{\mathrm{opl}}^{wc}(z),$$ (7)

where

$$\begin{array}{l}{z}_{\mathrm{opl}}^{wc}(z)={\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{z}_{\mathrm{opl}}(z^{\prime })}\\ \times \frac{r_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))\mathrm{\Gamma }(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z))\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime })}{{\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{r}_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))\mathrm{\Gamma }(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z))\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime })}}.\end{array}$$ (8)

Here, Γ(z_opl(z′)− z_opl(z)) is the correlation function centered at the probing depth z_opl(z) that ensures the integration is performed only at those depths that lie within the coherence gate centered at z_opl(z). The weighting by the normalized reflection profile r_opl(z_opl(z′)) emphasizes those depths where the reflection are strong relative to other depths, resulting in $z_{\mathrm{opl}}^{wc}(z)$ being the weighted-center of the refractive index profile. Although no assumption about a strong interface is made, and in fact none is required, we do note that for a strong interface located at z_opl(z₀), r_opl(z_opl(z′)) → r_iδ(z_opl(z′)−z_opl(z₀))—a Dirac-delta at z_opl(z₀) with reflection coefficient r_i—and Eq. (7) reduces to

$$\delta z_{\mathrm{opl}}(z)=z_{\mathrm{opl}}(z)-z_{\mathrm{opl}}(z_0).$$ (9)

Thus, for a strong interface, δz_opl(z) describes the subresolution offset of z_opl(z₀), the optical depth where the strong interface is located, from z_opl(z), the optical depth being probed. Although a strong interface is easy to identify, δz_opl(z) provides additional accuracy in estimating the correct optical depth location of the interface, when there is only a subresolution deviation of the optical depth being probed from the actual optical depth location of the interface. This is the basis for SDPM [23]. Figure 2(a) is a visual illustration of subresolution offset using a simple refractive index profile model. (Note that a strong interface is not assumed.) Later, in Section 3.A, we present a parametric model for this simple refractive index profile, where the subresolution offset is modeled through the subresolution shift parameter. We will effectively employ this model to validate our results.

Fig. 2.

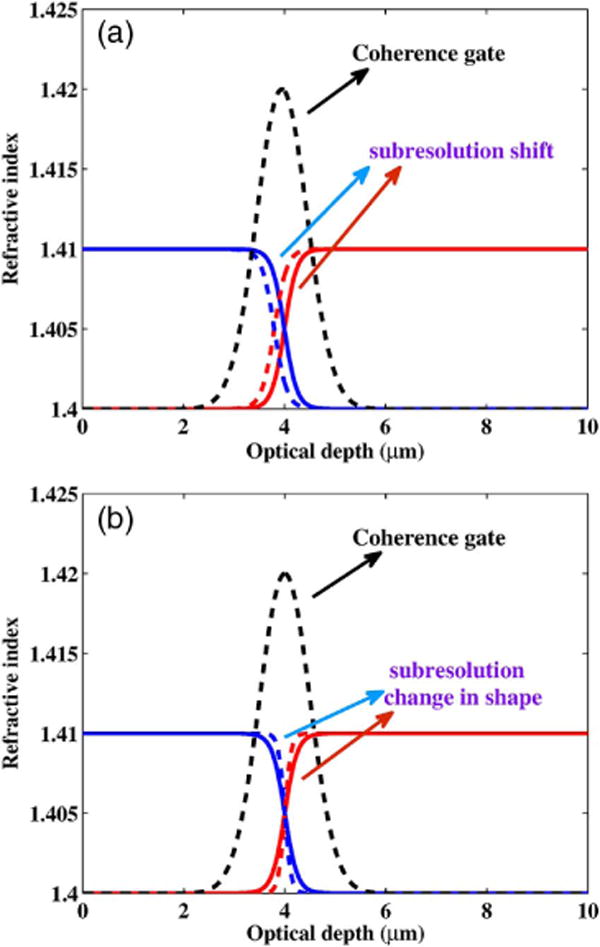
Behavior of the refractive index profile within the coherence gate. (a) Subresolution shift within the coherence gate (indicated by the difference between the solid and dashed lines) for increasing (red) and decreasing (blue) refractive index profiles. It is the parameter used to model subresolution offset. (b) Subresolution change in shape within the coherence gate (indicated by dashed and solid lines) for increasing (red) and decreasing (blue) refractive index profiles. It is the parameter used to model mean spatial frequency.

The second structural characteristic is the mean spatial frequency of the coherence-gated refractive index. We denote it by s_i(z_opl(z)), where z_opl(z) is again the optical depth where the refractive index profile is being probed. Mean spatial frequency estimates the average rate at which change in refractive index occurs within the coherence gate centered at z_opl(z). (As we will show, the averaging is a direct consequence of the coherence gate.) For example, for an increasing or decreasing refractive index profile within the coherence gate, it characterizes how fast or slow that subresolution change occurs. More generally, it is a characterization of the refractive index heterogeneity within the coherence gate. (Details are in Sections 3 and 6.H.) A simple illustration of mean spatial frequency is depicted in Fig. 2(b), where small changes in the shape of the refractive index model are used to indicate the increasing or decreasing rates-of-change in optical density. The parametric modeling of mean spatial frequency is done through the subresolution shape parameter.

Having described what structural characteristics Fourier phase estimates, we next show how and why this is the case.

A. Structural Information

Consider the spectral interference P(K) in Eq. (4) in its generalized complex form,

$$\begin{array}{l}P(K)=2S(K){\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}\Re (r_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))e^{i2\pi K{z}_{\mathrm{opl}}(z^{\prime })})\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime })}\\ =2S(K)\Re \left({\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{r}_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))e^{i2\pi K{z}_{\mathrm{opl}}(z^{\prime })}\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime })}\right),\end{array}$$ (10)

with ℜ representing the real part of its argument. Here, for a given K, we interpret the integrand of Eq. (10) as a phasor rotating with angular frequency 2πz_opl(z′). The amplitude of this phasor is the real-valued reflection profile r_opl(z_opl(z′)). Probing r_opl(z_opl(z′)) at optical depth z_opl(z) corresponding to the physical depth z does not return r_opl(z_opl(z)) but its weighted average over the coherence gate around z_opl(z). Using the phasor representation, we explicitly incorporate this loss in resolution by extending the phasor amplitude to its general complex form

$$r_{\mathrm{opl}}^c(z_{\mathrm{opl}}(z^{\prime }))=r_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))e^{i2\pi I(K,z_{\mathrm{opl}}(z))},$$ (11)

where I(K, δz_opl(z)) controls the division of r_opl(z_opl(z′)) between the quadrature cosine and sine components. It is the cosine component that we have access to through Eq. (10). The imaginary sine component represents the resolution loss due to the coherence gate. Therefore, a nonzero value of I(K, z_opl(z)) results in a leakage of r_opl(z_opl(z′)) from the real in-phase component to the imaginary quadrature component. This loss will naturally be greater for refractive index profiles with greater structural content within the coherence gate. Therefore, we refer to I(K, z_opl(z)) as structural information reflecting the subresolution structural content of the coherence-gated refractive index profile. We choose I(K, z_opl(z)) to be a function of both spatial frequency K and the optical depth z_opl(z) at which the refractive index is being probed. The dependence on the latter is natural because the measurement is being made at that optical depth. The dependence on the former is because the measurement is being made in the spectral domain where the sample is being probed by waves with wave numbers $k=\frac{K}{2}$.

To characterize the nature of the dependence of I(K, z_opl(z)) on K and z_opl(z), we note that when we probe the refractive index at z_opl(z), the Fourier amplitude is the coherence-gated average of r_opl(z_opl(z′)). We denote it as |p(z_opl(z))|. If we were to place an actual coherence gate, corresponding to the correlation function of the light source at the probing depth z_opl(z), then the corresponding coherence-gated average of r_opl(z_opl(z′)) would be

$$r_{\mathrm{avg}}={\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{r}_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))\mathrm{\Gamma }(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z))\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime })},$$ (12)

where we have exploited the symmetry of the correlation function to write the convolution as a correlation. This coherence-gated average has an associated weighted-center where the optical depth of the structural content of the refractive index profile within the coherence gate is centered. This weighted-center is precisely given by $z_{\mathrm{opl}}^{wc}(z)$ [defined in Eq. (8)]. If this weighted-center and the probing depth z_opl(z) coincide, then |p(z_opl(z))|=r_avg. If, however, the two are offset from each other, then the deviation manifests as δz_opl(z) given by Eq. (7) and can be accounted for in the following way. The reflection profile within the coherence gate centered at z_opl(z) is given by the equivalent reflection profile $r_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))=r_{\mathrm{avg}}\delta (z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}^{wc}(z))$ Equation (10) then tells us that the spectral interference signal corresponding to the back-reflected waves from this equivalent profile is

$$P(k)=2S(K)\Re (r_{\mathrm{avg}}{e}^{i2\pi K{z}_{\mathrm{opl}}^{wc}(z)}),$$ (13)

which can be rewritten as

$$\begin{array}{l}P(k)=2S(K)\Re (r_{\mathrm{avg}}{e}^{i2\pi K{z}_{\mathrm{opl}}^{wc}(z)}(e^{-i2\pi K{z}_{\mathrm{opl}}(z)}{e}^{i2\pi K{z}_{\mathrm{opl}}(z)}))\\ =2S(K)\Re (r_{\mathrm{avg}}{e}^{-i2\pi K(z_{\mathrm{opl}}(z)-z_{\mathrm{opl}}^{wc}(z))}{e}^{i2\pi K{z}_{\mathrm{opl}}(z)})\\ =2S(K)\Re (r_{\mathrm{avg}}{e}^{-i2\pi K\delta z_{\mathrm{opl}}(z)}{e}^{i2\pi K{z}_{\mathrm{opl}}(z)}),\end{array}$$ (14)

where $\delta z_{\mathrm{opl}}(z)=z_{\mathrm{opl}}(z)-z_{\mathrm{opl}}^{wc}(z)$ is the subresolution offset and for reflection profile $r_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))=r_{\mathrm{avg}}\delta (z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}^{wc}(z))$ is exactly given by Eq. (7). On comparing the complex phasor amplitudes in Eqs. (11) and (14), we define the structural information as

$$I(K,z_{\mathrm{opl}}(z))=-K\delta z_{\mathrm{opl}}(z).$$ (15)

This bilinear—in K and δz_opl(z)—characterization of information-loss in conjunction with Eq. (11) bounds I(K, δz_opl(z)) to the range (−1, 1). For values outside this range, the structural behavior will manifest in the Fourier amplitude—the amplitude of p(z_opl(z)) defined in Eq. (18).

Incorporating Eq. (15) in Eq. (11), we get

$$r_{\mathrm{opl}}^c(z_{\mathrm{opl}}(z^{\prime }))=r_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))e^{-i2\pi K\delta z_{\mathrm{opl}}(z)},$$ (16)

which simplifies the spectral interference P(K) in Eq. (10) to (see Appendix B)

$$\begin{array}{l}P(K)=2S(K){\displaystyle {\int }_0^{(L)}{r}_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))}\\ \times \cos (2\pi K(z_{\mathrm{opl}}(z^{\prime })-\delta z_{\mathrm{opl}}(z)))d{z}_{\mathrm{opl}}(z^{\prime }).\end{array}$$ (17)

Thus, the phasor representation of resolution loss allows us to express spectral interference in terms of structural information. We next show that an estimate of this structural information I(K, z_opl(z)) is accessible to us through Fourier phase.

B. Fourier Phase

Fourier phase at the optical depth z_opl(z) is the phase of the Fourier transform of the spectral interference P(K),

$$p(z_{\mathrm{opl}}(z))={\displaystyle {\int }_{B}P(K)e^{-i2\pi K{z}_{\mathrm{opl}}(z)}}\mathrm{d}K.$$ (18)

Appendix C details the expansion of p(z_opl(z)) in Eq. (18) to p(z_opl(z))

$$\begin{array}{l}=({\displaystyle \sum _{j=0}^{\infty }\frac{{\left(\delta z_{\mathrm{opl}}(z)\right)}^{2j}}{2j!}\Re ({(r_{\mathrm{opl}}^{2j})}^{K_c}\ast \mathrm{\Gamma })(z_{\mathrm{opl}}(z))})\\ +i\left(\delta z_{\mathrm{opl}}(z){\displaystyle \sum _{j=0}^{\infty }\frac{{\left(\delta z_{\mathrm{opl}}(z)\right)}^{2j}}{(2j+1)!}\mathfrak{J}({\left(r_{\mathrm{opl}}^{2j+1}\right)}^{K_c}\ast \mathrm{\Gamma })(z_{\mathrm{opl}}(z))}\right),\end{array}$$ (19)

with ℑ representing the imaginary part of its argument and * denoting the convolution operation. ℜ, as before, represents the real part of its argument. As explained in Appendix C, Eq. (19) is the baseband representation of the Fourier transform of the spectral interference whose carrier frequency corresponds to the central frequency of the source

$$K_c={\displaystyle {\int }_{B}K\frac{S(K)}{{\displaystyle {\int }_{B}S(K)\mathrm{d}K}}\mathrm{d}K.}$$ (20)

In Eq. (19), ${\left(r_{\mathrm{opl}}^{(\ell )}\right)}^{K_c}(z_{\mathrm{opl}}(z^{\prime }))$, ℓ = 0, 1, 2, … is the baseband representation of the (ℓ) th derivative of reflection profile, and Γ(z_opl(z)) is the baseband representation of the correlation function corresponding to the source spectrum centered at K_c. Note that ℓ is a general representation for both 2j and 2j + 1.

The baseband signal holds the entirety of the information content—both amplitude and phase—of the back-scattered signal. A closer look at Eq. (19) reveals that $\frac{{\left(r_{\mathrm{opl}}^{(\ell )}\right)}^{K_c}(z_{\mathrm{opl}}(z^{\prime }))}{\ell !}$, ℓ = 0, 1, 2, …, are the coefficients of the Taylor expansion of the baseband reflection profile ${\left(r_{\mathrm{opl}}\right)}^{K_c}(z_{\mathrm{opl}}(z^{\prime }))$, about z_opl(z), and therefore characterize the reflection profile in optical-space. The convolution with the correlation function ensures that only their coherence-gated structural characterization about z_opl(z) is reflected in p(z_opl(z)).

Equation (19) shows that Fourier phase is given by

$$\varphi (z_{\mathrm{opl}}(z))={\tan }^{-1}\left(\delta z_{\mathrm{opl}}(z)\frac{{\displaystyle {\sum }_{j=0}^{\infty }\underset{\mathfrak{J}\left({\left(r_{\mathrm{opl}}^{(2j+1)}\right)}^{K_c}\ast \mathrm{\Gamma }\right)(z_{\mathrm{opl}}(z))}{\frac{{\left(\delta z_{\mathrm{opl}}(z)\right)}^{2j}}{(2j+1)!}}}}{{\displaystyle {\sum }_{j=0}^{\infty }\underset{\Re \left({\left(r_{\mathrm{opl}}^{(2j)}\right)}^{K_c}\ast \mathrm{\Gamma }\right)(z_{\mathrm{opl}}(z))}{\frac{{\left(\delta z_{\mathrm{opl}}(z)\right)}^{2j}}{2j!}}}}\right),$$ (21)

where the odd and even order derivatives, respectively, appear in the numerator and denominator of the fraction. Taken with their respective imaginary and real parts, the separation of odd and even coherence-gated Taylor coefficients, respectively, to the numerator and denominator characterizes the structure in a manner that is consistent with tangent phase notation.

Equation (21) states that the Fourier phase measured at z_opl(z) jointly estimates two structural features of the coherence-gated refractive index profile. The first is the aforementioned subresolution offset, δz_opl(z). The second feature is characterized by the fraction

$$\frac{{\displaystyle {\sum }_{j=0}^{\infty }\frac{{\left(\delta z_{\mathrm{opl}}(z)\right)}^{2j}}{(2j+1)!}\mathfrak{J}\left({\left(r_{\mathrm{opl}}^{(2j+1)}\right)}^{K_c}\ast \mathrm{\Gamma }\right)(z_{\mathrm{opl}}(z))}}{{\displaystyle {\sum }_{j=0}^{\infty }\frac{{\left(\delta z_{\mathrm{opl}}(z)\right)}^{2j}}{2j!}\Re \left({\left(r_{\mathrm{opl}}^{(2j)}\right)}^{K_c}\ast \mathrm{\Gamma }\right)(z_{\mathrm{opl}}(z))}}.$$

Despite its rich information content, this fraction is difficult to interpret apart from noting that it is some form of structural characterization of the reflection profile. However, there are two specific scenarios, where the fraction and therefore Eq. (21) reduce to simpler forms. Fortunately, these are the two scenarios of most interest in the context of FD-OCT. The first is when the refractive index profile is dominated by a strong interface and the Fourier phase measurement is made at this interface. SDPM and its derivatives fall in this category. The second arises when there are no strong interfaces within the sample and the sample is well-matched with the medium that it is immersed in. In this scenario, the refractive index profile has a small gradient so that the Born approximation is satisfied. Here, the Fourier phase measurements do not track a particular interface but are made at fixed depth locations. dr-SLQPM falls under this latter category.

It was in anticipation of the second category that we developed the general theory under the assumption that the Born approximation was satisfied. For the first category, certain specific considerations need to be satisfied to ensure the validity of Eq. (21). We detail them in Section 4, where we re-establish the validity of Eq. (21) and its simplification in the presence of a strong interface. We, however, first present the Fourier phase for a slowly varying refractive index profile.

3. FOURIER PHASE ALONG A SLOWLY VARYING REFRACTIVE INDEX PROFILE

Samples with slowly varying refractive index profiles have small gradients. Consequently, their corresponding reflection profiles, given by Eq. (6), have even smaller derivatives. As a result, higher-order derivatives of the reflection profile can be neglected, allowing the simplification of Fourier phase in Eq. (21) as

$$\varphi (z_{\mathrm{opl}}(z))={\tan }^{-1}\left(\delta z_{\mathrm{opl}}(z)\frac{\mathfrak{J}\left({\left({r^{\prime }}_{\mathrm{opl}}\right)}^{K_c}\ast \mathrm{\Gamma }\right)(z_{\mathrm{opl}}(z))}{\Re \left({\left(r_{\mathrm{opl}}\right)}^{K_c}\ast \mathrm{\Gamma }\right)(z_{\mathrm{opl}}(z))}\right),$$ (22)

where only the reflection profile (zeroth-order derivative) and its gradient (first-order derivative) are considered. For notational ease, we define

$$s_i(z_{\mathrm{opl}}(z))=\frac{\mathfrak{J}\left({\left({r^{\prime }}_{\mathrm{opl}}\right)}^{K_c}\ast \mathrm{\Gamma }\right)(z_{\mathrm{opl}}(z))}{\Re \left({\left(r_{\mathrm{opl}}\right)}^{K_c}\ast \mathrm{\Gamma }\right)(z_{\mathrm{opl}}(z))},$$ (23)

and rewrite Eq. (22) succinctly as

$$\varphi (z_{\mathrm{opl}}(z))={\tan }^{-1}(\delta z_{\mathrm{opl}}(z)s_i(z_{\mathrm{opl}}(z))).$$ (24)

Equation (24) shows that the Fourier phase for a slowly varying refractive index profile is a joint estimate of δz_opl(z) and s_i(z_opl(z)). To characterize the structural information estimated by the latter, we express s_i(z_opl(z)) in terms of the refractive index profile itself. Using Eqs. (1) and (6), we expand Eq. (23) to

$$\begin{array}{r}{s}_i(z_{\mathrm{opl}}(z))=\frac{1}{2}\frac{f({n^{″}}_s(z_{\mathrm{opl}}(z))/n_s^2(z_{\mathrm{opl}}(z)))}{f({n^{\prime }}_s(z_{\mathrm{opl}}(z))/n_s^2(z_{\mathrm{opl}}(z)))}\\ -\frac{f({n^{\prime }}_s(z_{\mathrm{opl}}(z))/n_s^3(z_{\mathrm{opl}}(z)))}{f({n^{\prime }}_s(z_{\mathrm{opl}}(z))/n_s^2(z_{\mathrm{opl}}(z)))},\end{array}$$ (25)

where f(·) represents the convolution of its argument with the correlation function and therefore enforces the coherence gating. Equation (25) reveals that for a slowly varying refractive index, the Fourier phase at some optical depth of interest is a manifestation of the interplay between the coherence-gated refractive index profile n_s(z_opl(z)) and its first two derivatives ${n^{\prime }}_s(z_{\mathrm{opl}}(z))$ and ${n^{″}}_s(z_{\mathrm{opl}}(z))$ at the optical depth z_opl(z). We refer to the two derivatives, respectively, as the gradient and curvature of n_s(z_opl(z)). The ratio between the coherence-gated curvature and the coherence-gated gradient is the first term of Eq. (25), with both derivatives having been first normalized by $n_s^2(z_{\mathrm{opl}}(z))$. (This normalization is due to the measurement being performed in optical-space.) In the slowly varying refractive index regime, both the curvature and the gradient are well-defined and so is the ratio. Furthermore, the first term of Eq. (25) has a simple interpretation: it is an estimate of the mean spatial frequency of the coherence-gated refractive index profile. To see this, first observe that for a slowly varying refractive index the contribution of $n_s^2(z_{\mathrm{opl}}(z))$ effectively cancels out, therefore simplifying the first term to $\frac{1f({n^{″}}_s(z_{\mathrm{opl}}(z)))}{2f({n^{″}}_s(z_{\mathrm{opl}}(z)))}$. The effect of canceling the contribution of $n_s^2(z_{\mathrm{opl}}(z))$ from the numerator and the denominator of the first term is illustrated in Fig. 3(a), which shows a scatter plot of the first term and its simplified form for a range of slowly varying refractive index profiles at a fixed probing z_opl(z). The refractive index model used to generate the scatter plot is defined in Eq. (26) (see the following section), and the refractive index variation is controlled through the subresolution shape parameter that varies from −3 to −2.3 in the log-scale (also explained in the next section). This is the range of slow changes in the shape of the refractive index. As can be seen, the scatter plot aligns along the 45° line showing close correspondence between the first term and its simplification. This simplified form is a ratio of the coherence-gated curvature and gradient of the refractive index profile within the coherence gate. The former is a measure of the mean gradient of the refractive index within the coherence gate, while the latter measures the net change in the refractive index within the coherence gate. The ratio of the two, therefore, is an estimate of the mean spatial frequency of the coherence-gated refractive index profile. This can be easily understood by considering the analogy with a car equipped with an accelerometer and a speedometer. For a fixed time interval Δt, the average velocity of the car is $\overline{v}={\displaystyle {\int }_{\mathrm{\Delta }t}a(t)\mathrm{d}t}$, while the average traveled distance is $\overline{s}={\displaystyle {\int }_{\mathrm{\Delta }t}v(t)\mathrm{d}t}$. Here, a(t) and v(t) respectively, denote the instantaneous acceleration and velocity of the car measured, respectively, by the accelerometer and the speedometer. The ratio $\frac{\overline{s}}{v}$ gives the average time the car takes to travel distance $\overline{s}$. The ratio $\frac{\overline{s}}{v}$, on the other hand, gives the average number of times the car can travel the distance $\overline{s}$ in one unit of time, that is, it gives the mean temporal frequency of car motion. On relating acceleration with curvature of the refractive index, speed with the gradient of the refractive index, and the time interval with the coherence gate, it is easy to see that the first term of Eq. (25) in the slow-varying regime estimates the mean spatial frequency of refractive index change within the coherence gate around z_opl(z). This mean spatial frequency describes the average rate at which the spatial change in the refractive index occurs within the coherence gate. This change can be an increasing or a decreasing refractive index within the coherence gate and is described by the subresolution shape of the refractive index profile illustrated in Fig. 2(b). This change can also be an increase (or a decrease) in subresolution heterogeneity, which will manifest as an increase (or a decrease) in spatial frequency. (See Section 6.H.) Finally, to complete the discussion of the first term of Eq. (25) we note that the normalization by $n_s^2(z_{\mathrm{opl}}(z))$ need not be neglected as it naturally results from making the measurements in the optical-space. Even with normalization, the first term of Eq. (25) is an estimate of the mean spatial frequency in optical-space. The simplification was primarily done to explain this first term without being encumbered by the normalization factor.

Fig. 3.

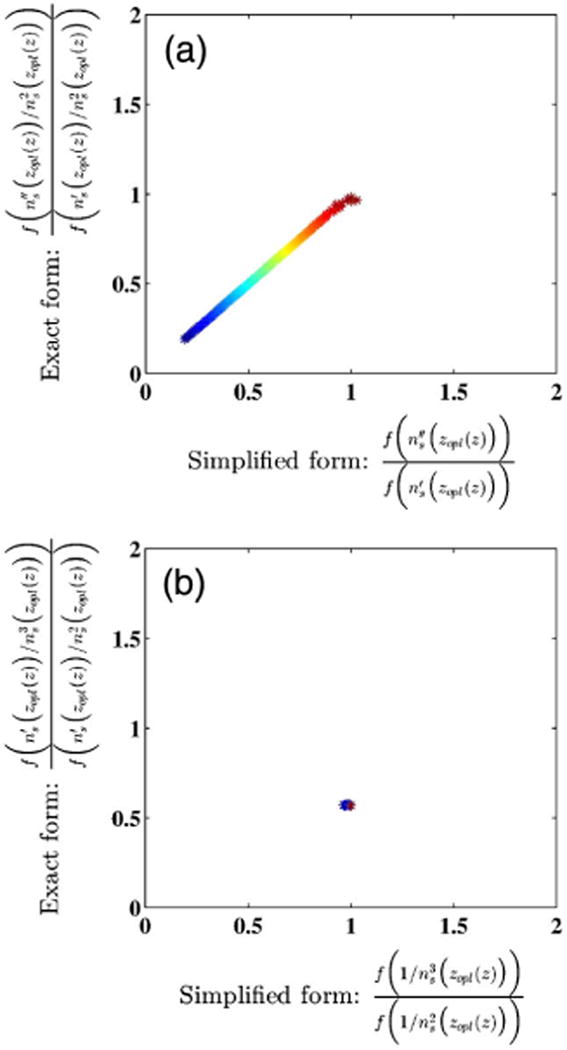
Correlating the behavior of the exact and simplified forms of each term in Eq. (25) at optical depth z_opl(z) = 4 μm, using the refractive index model defined in [Eq. (26)]. The parameters of the refractive index model are n₀ = 1.4, Δn = 0.01, and s ranging from −3 to −2.3 in the log-scale, indicating a slowly varying refractive index profile. (a) Normalized scatter plot of the first term of Eq. (25) along the y-axis and its simplification along the x-axis. The normalization factor for both axes is 1.019 × 10⁷ m⁻¹. (b) Normalized scatter plot of the second term of Eq. (25) along the y-axis and its simplification along the x-axis. The normalization factor for both axes is 0.0025 m⁻¹.

The second term of Eq. (25), also well-defined for a slowly varying refractive index, is unresponsive to the slow variation. Figure 3(b) shows the scatter plot between it and its simplified form $\frac{f(1/n_s^3(z_{\mathrm{opl}}(z)))}{f(1/n_s^2(z_{\mathrm{opl}}(z)))}$, where the effect of the gradient of the slowly varying refractive index profile is neglected in the numerator and the denominator. First, it can be seen that the scatter plot has no spread illustrating the unresponsiveness of the second term to the variation in refractive index. Second, the location of the scatter points shows that the effect of the gradient of the refractive index profile is to reduce the contribution of the second term to s_i(z_opl(z)) in Eq. (25).

In absolute terms, the factors used to normalize the scatter plots for the first and second terms of Eq. (25), respectively, are 1.019 × 10⁷ m⁻¹ and 0.0025 m⁻¹. Since the former is much greater than the latter, the second factor can be neglected, resulting in s_i(z_opl(z)) itself being an estimate of mean spatial frequency. It is also worth noting that the value of the subresolution shape parameter for which s_i(z_opl(z)) 1.019 × 10⁷ m⁻¹ in the log-scale is −2.3. In the linear-scale the log-scale value corresponds to 1 × 10⁷ m⁻¹, illustrating that s_i(z_opl(z)) is indeed an estimate of the mean spatial frequency. Finally, we note that s_i(z_opl(z)) is not defined in the impractical scenario of the refractive index gradient being zero, that is, when the reflection profile is zero and there is no back-scattered light.

Therefore, we can now state that the Fourier phase jointly estimates the structural information given by δz_opl(z) the subresolution offset, and s_i(z_opl(z)), the mean spatial frequency.

A. Subresolution Shape and s_i(z_opl(z))

Consider the refractive index model given by the modified sigmoidal function

$$n_s(z^{\prime })=n_0+\frac{\mathrm{\Delta }n}{1+{\ell }^{-2s(z^{\prime }-z_0)}},$$ (26)

where an isolated change in shape is modeled at a physical depth z₀. Figure 4 provides the illustration. A small change in z₀ will shift the physical depth where the isolated change occurs. We refer to this change in z₀ as the subresolution shift in the location of the isolated change in the refractive index profile. In Section 6, we decompose z₀ as z₀ = z_ℓ + Δz₀. We perform our Fourier measurement at optical depth z_opl(z_ℓ) corresponding to physical depth z_ℓ. Δz₀ models the subresolution offset. Since z_ℓ is kept fixed, the subresolution shift parameterizes the subresolution offset. The structural characteristic δz_opl(z₀) is an estimate of Δz₀ in optical-space.

Fig. 4.

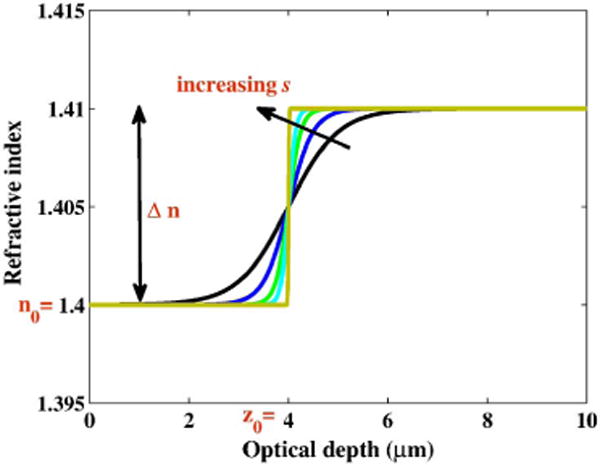
Simple refractive index profile model with an increasing value of the shape parameter.

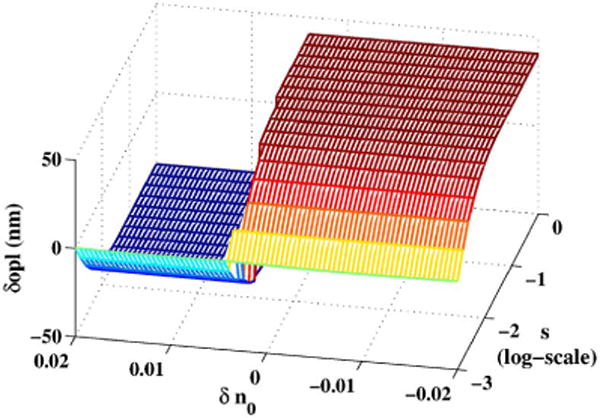
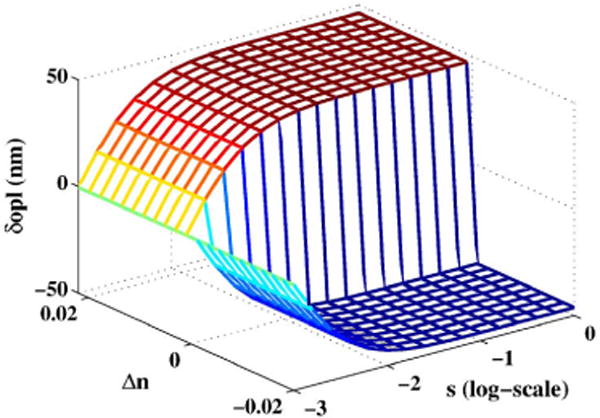
The parameter n₀ is the baseline refractive index, and Δn is the net change in refractive index around physical depth z₀. Noting that the refractive index of vacuum is one, we set n₀ ≥ 1. The shape parameter s controls how the net change Δn manifests itself. For a given Δn, small values of s indicate a slowly varying refractive index, while the limit s → ∞ indicates a strong interface, where the net change Δn occurs in a single discontinuous step. This range of shapes of the refractive index profile is shown in Fig. 4. We refer to this shape parameter as subresolution shape as its effect is primarily localized within the coherence gate. We note that for the refractive index model in Eq. (26), the subresolution shape s controls the rate at which the isolated change occurs. For increasing s, the rate-of-change increases. This notion can be made precise by considering the Fourier transform of a sigmoidal function. The Fourier pair is given by $\frac{1}{1+e^{-2sz\prime }}\stackrel{ℱ\mathcal{T}}{\leftrightarrow }\frac{i}{2}\sqrt{\frac{\pi }{2}}\mathrm{cosech}\left(\frac{\pi w}{2s}\right)$. It can be seen in the amplitude of the Fourier transform that the frequency spread of cosech away from zero is controlled by the subresolution shape s. As s increases, the rate at which the isolated change occurs increases, and the Fourier pair shows that the higher spatial frequencies are present in the refractive index model in proportion to s. Therefore, we use s as a measure of spatial frequency of the refractive index profile within the coherence gate. The unit of s is meter⁻¹.

Based on this model and using Eq. (25), we can analytically compute the value of s_i(z_opl(z)). Additionally, if for the sake of simplicity, we assume δz_opl(z) to be some constant c, we can qualitatively isolate the effect of s_i(z_opl(z) on Fourier phase ϕ(z_opl(z)) through the simplified relation ϕ(z_opl(z)) = tan⁻¹ (cs_i(z_opl(z))). Figures 5(a), 5(b), and 5(c) plot this effect of s_i(z_opl(z)) on Fourier phase, respectively, due to changes in s, n₀ and Δn. We express the shape parameter in log-scale by transforming s to log₁₀ (sd∕2), where d = 1 nm. The shape parameter of this transformed representation changes from −3 to 0 as the refractive index changes from a slowly varying profile (0.002∕d) to one with a strong interface (2∕d). We note that to approximately ensure that the parameter-based changes in the refractive index profile can be reasonably described as subresolution changes, we consider a small range of values for the three parameters.

Fig. 5.

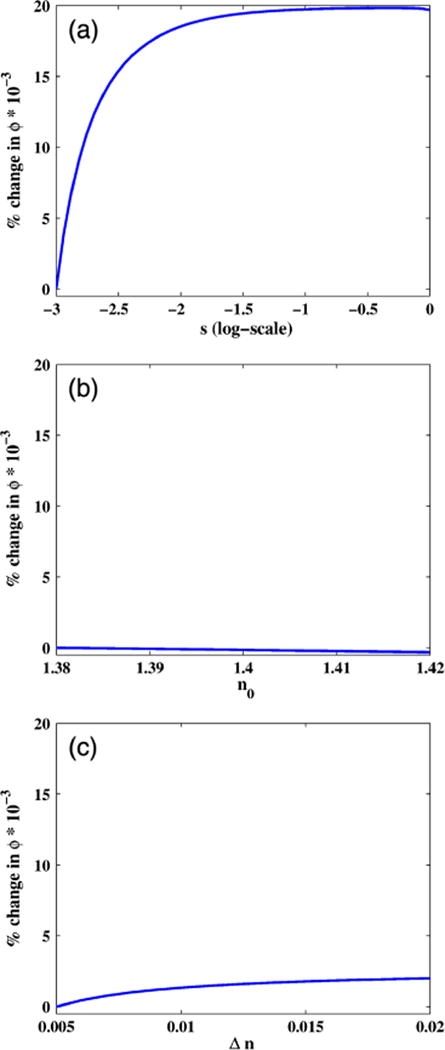
Effect of s_i(z_opl(z)) on Fourier phase for changing values of the s, n₀, and Δn parameters. The shape parameter s is expressed in the log-scale. (a) Increasing s for n₀ = 1.4, Δn = 0.01, and z₀ = 2.85 μm. (b) Increasing n₀ for s = −2.3, Δn = 0.01, and z₀ = 2.85 μm. (c) Increasing Δn for n₀ = 1.4, s = −2, and z₀ = 2.85 μm.

Figure 5 shows that the Fourier phase responds most strongly to change in subresolution shape and most weakly to change in n₀. The Fourier phase eventually becomes unresponsive to increasing subresolution shape because these are higher-order changes not captured by the curvature and gradient of the refractive index. Fourier phase has a moderate response to Δn primarily through the indirect effect of Δn on the subresolution shape for any given value of the s parameter. Δn itself does not directly affect the Fourier phase because it is the common term in both the curvature and gradient of the refractive index profile and therefore its effect is canceled out [in the first term Eq. (25)], while its effect on the second term is weak.

B. Depth-Resolved Spatial-Domain Low-Coherence Quantitative Phase Microscopy

In dr-SLQPM, the sample satisfying the Born approximation is embedded in a well-matched medium, making it ideally suited to the Fourier phase approximation in Eq. (22) for volumetric structural characterization. Utilizing an approximately collimated and spatially incoherent white light source, dr-SLQPM decomposes the 3D physical-space into lateral x, y-space, with each en face location x, y associated with an axial z channel (with the associated z-space), which is mutually incoherent with channels corresponding to other lateral locations. The standard FD-OCT principle allows dr-SLQPM to map each z-space refractive index profile to optical-space z_opl, allowing dr-SLQPM to operate in the hybrid space (x, y, z_opl). For all en face locations, the z_opl space is sampled at fixed optical depths (note, not interfaces) with the sampling interval a small fraction of the width of the coherence gate. This oversampling mimics the action of a sliding window along the axial refractive index profile. Oversampling has two benefits. First, the small sampling step ensures that any change in Fourier phase results in a two-dimensional (2D) Fourier phase-based map that washes out the effect of δz_opl(z)—the reason and the extension to 3D is discussed in Section 6.C—allowing the map to characterize the mean spatial frequency of the axial refractive index.

4. FOURIER PHASE AT A STRONG INTERFACE

In 2005, two groups independently proposed spectral-domain phase microscopy (SDPM) where they measured the Fourier phase ϕ(z_opl(z)) to, respectively, study subresolution motion in living cells and perform quantitative phase-contrast imaging in the reflection-mode. In both of these works, Fourier phase measurements were performed at a strong interface. One of the groups was also the first to provide a physical interpretation of their results (see Eq. (2) in [23]) by establishing a relation between the Fourier phase measurement at a strong interface and the subresolution offset δz_opl(z) between the optical depth the measurement was made and the optical depth where the interface was actually located. We now show that their result is a special case of the Fourier phase defined in Eq. (21).

A. Establishing the Validity of the Born Approximation

Our derivation of Fourier phase required the validity of the Born approximation which assumes a sample with a slowly varying refractive index profile [1]. Such a profile decouples the Cartesian components of the complex light wave $\mathbf{E}(z^{\prime },k)=E_{x^{\prime }}(z^{\prime },k)\widehat{x}+E_{y^{\prime }}(z^{\prime },k)\widehat{y}+E_{z^{\prime }}(z^{\prime },k)\widehat{z}$ as it travels through the sample by ensuring that the last term of the wave equation

$$\begin{array}{l}{\nabla }^2\mathbf{E}(z^{\prime },k)+4{\pi }^2{k}^2{n}^2(z^{\prime })\mathbf{E}(z^{\prime },k)\\ +2\nabla (\mathbf{E}(z^{\prime },k)\cdot \nabla \log (n(z^{\prime })))=0,\end{array}$$ (27)

is negligible, thereby allowing a one-to-one far-field correspondence between K and k_bs − k_i. However, when the refractive index profile is defined by a strong interface, the gradient of the refractive index can no longer be neglected. Nevertheless, for normal source illumination where the sample can be decomposed into an en face representation of 1D refractive index profiles—a condition typically satisfied by FD-OCT setups— the decoupling is valid despite the strong interface, under the strict condition that the number of strong interfaces is restricted to one.

Consider the general case of a plane-polarized light wave incident on the interface at an angle θ_i. (See Fig. 6.) Assuming the parallel and perpendicular polarization of the light wave at the interface be the complex-valued amplitudes E_p and E_s, respectively—the polarizations are described with respect to the plane of incidence—the Cartesian components of the incident wave are given by $E_{x^{\prime }}=E_s,E_{y^{\prime }}=E_p\cos {\theta }_i,$ and $E_{z^{\prime }}=E_p\sin {\theta }_i.$ When the angle of incidence is normal, that is, ${\theta }_i=0,E_{z^{\prime }}$ is zero. As the gradient of the refractive index profile is along the z-direction with its lateral components zero, the last term of Eq. (27) is zero. Furthermore, a single strong interface does not violate the assumptions of negligible multiple-scattering events and negligible depth distortion effects due to the refractive index gradient required for the Born approximation to hold. As a result, both Eq. (1) [47,48,52] and Eq. (21) remain valid, however, Eq. (22) is not.

Fig. 6.

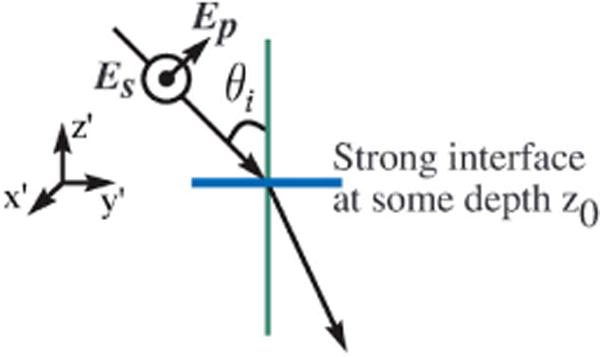
Plane-polarized light incident on a strong interface at an angle θ_i. The plane of incidence is in the y′–z′ plane. Parallel and perpendicular polarization of only the incident illumination is shown.

B. Invalidity of Eq. (22) at a Strong Interface

Corresponding to the refractive index profile model of $n_s(z^{\prime })$ in Eq. (26), the reflection profile in the optical-space is

$$\begin{array}{l}{r}_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))=\frac{r_s(z_{\mathrm{opl}}(z^{\prime }))}{n_s(z_{\mathrm{opl}}(z^{\prime }))}[\text{See Eq}.(6)]\\ =\frac{\mathrm{\Delta }ns{e}^{-2s(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z_0))}}{{(n_0+\mathrm{\Delta }n+n_0{e}^{-2s(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z_0))})}^2}.\end{array}$$ (28)

In the limit s → ∞, the refractive index is approximated by a Heaviside function, while the reflection profile in Eq. (28) approaches (see Fig. 7) a Dirac-delta

$$r_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))=r_i\delta (z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z_0)),$$ (29)

where $r_i=\frac{\mathrm{\Delta }n}{(n_0+(n_0+\mathrm{\Delta }n))}\frac{1}{(n_0+(n_0+\mathrm{\Delta }n))}$ is the reflection coefficient at the optical depth z_opl(z). It is interesting to note that this reflection strength corresponds to the reflection coefficient $\frac{\mathrm{\Delta }n}{(n_0+(n_0+\mathrm{\Delta }n))}$ obtained using the Fresnel equations for normal illumination [1], after accounting for the optical-space transformation factor $\frac{1}{(n_0+(n_0+\mathrm{\Delta }n))}.$

Fig. 7.

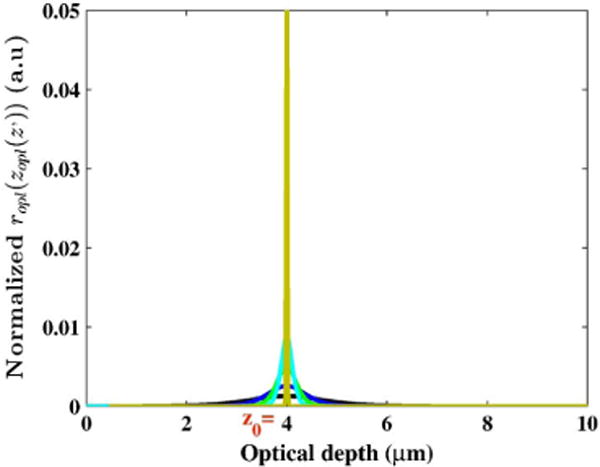
Optical-space reflection profile expressed in Eq. (28), corresponding to the refractive index model in Eq. (26) and plotted in Fig. 4, for increasing values of the shape parameter.

Incorporating Eq. (29) in Eq. (21), we rewrite the Fourier phase at z_opl(z₀) as

$$\varphi (z_{\mathrm{opl}}(z_0))={\tan }^{-1}\left(\delta z_{\mathrm{opl}}(z_0)\frac{\begin{array}{c}\frac{{(\delta z_{\mathrm{opl}}(z_0))}^{2j}}{(2j+1)!}\\ {\displaystyle {\sum }_{j=0}^{\infty }\mathfrak{J}({({\delta }^{(2j+1)})}^{K_c}\ast \mathrm{\Gamma })(z_{\mathrm{opl}}(z_0))}\end{array}}{\begin{array}{c}\frac{{(\delta z_{\mathrm{opl}}(z_0))}^{2j}}{2j!}\\ {\displaystyle {\sum }_{j=0}^{\infty }\Re ({({\delta }^{(2j)})}^{K_c}\ast \mathrm{\Gamma })(z_{\mathrm{opl}}(z_0))}\end{array}}\right),$$ (30)

where

$$\begin{array}{l}{({\delta }^{(\ell )})}^{K_c}(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z_0))\\ =e^{i2\pi K_c(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z_0))}{\delta }^{(\ell )}(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z_0)).\end{array}$$

Here, ℓ denotes the order of Dirac-delta derivative. We note that since r_i is common to both the numerator and the denominator, it cancels out.

Equation (30) shows that unlike the slowly varying refractive index profile, higher-order derivatives of the refractive index profile are not negligible, thereby invalidating Eq. (22). However, as we now show, under a mild condition, we get a simple closed form for the Fourier phase at a strong interface that matches the result in [23]. We note that this Fourier phase is derived under more general conditions than those in [23].

C. SDPM: General Development

We begin by restating the Fourier phase in Eq. (30) as (see Appendix D for details)

$$\varphi (z_{\mathrm{opl}}(z_0))={\tan }^{-1}\left(\frac{\mathrm{\Gamma }(0)\mathrm{\Delta }\left(1-\frac{{\mathrm{\Delta }}^2}{3!}+\frac{{\mathrm{\Delta }}^4}{5!}\right)+\gamma (0)\left(\frac{3\mathrm{\Delta }}{3!}-\frac{10{\mathrm{\Delta }}^3}{5!}\right)+10{\gamma }^2(0)\frac{\mathrm{\Delta }}{5!}+\mathrm{H}.\mathrm{O}.\mathrm{T}.}{\mathrm{\Gamma }(0)\left(1-\frac{{\mathrm{\Delta }}^2}{2!}+\frac{{\mathrm{\Delta }}^4}{4!}\right)+\gamma (0)\left(\frac{1}{2!}-\frac{6{\mathrm{\Delta }}^2}{4!}\right)+\frac{{\gamma }^2(0)}{4!}+\mathrm{H}.\mathrm{O}.\mathrm{T}.}\right),$$ (31)

where

$${\mathrm{\Delta }}^{\ell }={(2\pi K_c\delta z_{\mathrm{opl}}(z_0))}^{\ell },\ell \in {\mathbb{Z}}^{+},$$

and

$${\gamma }^{\ell }(0)={\mathrm{\Gamma }}^{(2\ell )}(0){(\delta z_{\mathrm{opl}}(z_0))}^{2\ell },\ell \in {\mathbb{Z}}^{+}.$$

The abbreviation H.O.T. stands for “higher-order terms” with respect to γ(0).

Simplification of Eq. (31) requires that the condition $\left|\gamma (0)\right|\ll 1$ be satisfied. We know from Eq. (11) and the discussion thereafter that $\left|K_c\delta z_{\mathrm{opl}}(z_0)\right|<1$. Therefore, for the condition $\left|\gamma (0)\right|=\left|{\mathrm{\Gamma }}^{(2)}(0){(\delta z_{\mathrm{opl}}(z_0))}^2\right|\ll 1$ to be valid, we only need to show $\left|\frac{{\mathrm{\Gamma }}^{(2)}(0)}{K_c^2}\right|\ll 1$, that is, the ratio of the second-order derivative of the correlation function evaluated at its center of symmetry, and the square of the center frequency of the source is much less than one. For a typical Gaussian correlation function with standard deviation σ, the magnitude of Γ⁽²⁾(0) is $\frac{1}{{\sigma }^2}$. Therefore, the condition $\left|\gamma (0)\right|\ll 1$ is satisfied when $\frac{1}{{(\sigma K_c)}^2}\ll 1$. For a standard deviation σ, the corresponding full width at half-maximum of the coherence gate is ${\ell }_c=2\sqrt{2\ln 2\sigma }$. Furthermore, the central wavelength of the source spectrum ${\lambda }_c=\frac{2}{K_c}$. Figure 8 plots $\frac{1}{{(\sigma K_c)}^2}$ as a function of ℓ_c and λ_c. As can be clearly seen, for a majority of ℓ_c and λ_c combinations typical for OCT setups, $\frac{1}{{(\sigma K_c)}^2}\ll 1$. For these combinations $\left|\gamma (0)\right|\ll 1$, and Eq. (32) simplifies to

$$\varphi (z_{\mathrm{opl}}(z_0))={\tan }^{-1}\left(\frac{\mathrm{\Gamma }(0)\mathrm{\Delta }\left(1-\frac{{\mathrm{\Delta }}^2}{3!}+\frac{{\mathrm{\Delta }}^4}{5!}\right)}{\mathrm{\Gamma }(0)\left(1-\frac{{\mathrm{\Delta }}^2}{2!}+\frac{{\mathrm{\Delta }}^4}{4!}\right)}\right)$$ (32)

$$={\tan }^{-1}\left(\mathrm{\Delta }\frac{\left(1-\frac{{\mathrm{\Delta }}^2}{3!}+\frac{{\mathrm{\Delta }}^4}{5!}\right)}{\left(1-\frac{{\mathrm{\Delta }}^2}{2!}+\frac{{\mathrm{\Delta }}^4}{4!}\right)}\right),$$ (33)

as the higher powers of γ^ℓ(0) can be neglected. For $\left|\mathrm{\Delta }\right|=\left|2\pi K_c\delta z_{\mathrm{opl}}(z_0)\right|<1$, the ratio $\frac{\left(1-\frac{{\mathrm{\Delta }}^2}{3!}+\frac{{\mathrm{\Delta }}^4}{5!}\right)}{\left(1-\frac{{\mathrm{\Delta }}^2}{2!}+\frac{{\mathrm{\Delta }}^4}{4!}\right)}$ in Eq. (33) is upper bounded by 1.554, and the Fourier phase is given by

$$\varphi (z_{\mathrm{opl}}(z))={\tan }^{-1}(1.554(2\pi K_c\delta z_{\mathrm{opl}}(z))).$$ (34)

For even smaller values of Δ, the ratio approaches one, and the Fourier phase is given by

$$\varphi (z_{\mathrm{opl}}(z))={\tan }^{-1}(2\pi K_c\delta z_{\mathrm{opl}}(z)).$$ (35)

For $\left|\mathrm{\Delta }\right|=\left|2\pi K_c\delta z_{\mathrm{opl}}(z_0)\right|\ll 1$, Fourier phase is simply approximated by

$$\varphi (z_{\mathrm{opl}}(z))=2\pi K_c\delta z_{\mathrm{opl}}(z_0).$$ (36)

This result is identical to that obtained in [23].

Fig. 8.

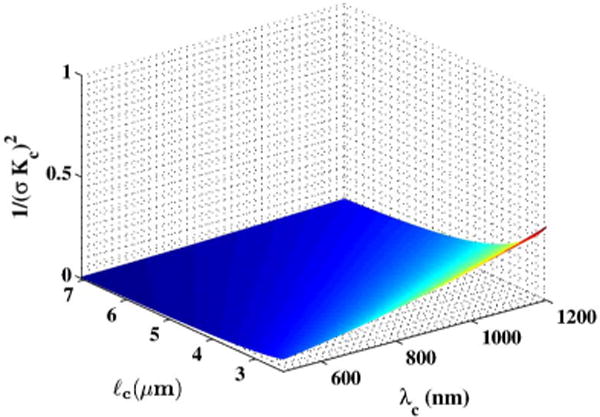
Behavior of $\frac{1}{{\left(\sigma K_c\right)}^2}$ as a function of full width at half-maximum coherence length, ℓ_c, and central wavelength of the source spectrum, λ_c.

5. FOURIER PHASE FOR AN IDEAL CONDITION: INFINITE SPECTRAL BANDWIDTH

For infinite spectral bandwidth, the correlation function approaches a Dirac-delta, $\mathrm{\Gamma }(z_{\mathrm{opl}}(z^{\prime }))\to \delta (z_{\mathrm{opl}}(z^{\prime }))$, with ℓ_c → 0. As a consequence, the integral on the right-hand side of Eq. (8) approaches z_opl(z), resulting in δz_opl(z) → 0. It then follows from Eq. (21) that the Fourier phase approaches zero if the fraction $\frac{{\displaystyle {\sum }_{j=0}^{\infty }\frac{{(\delta z_{\mathrm{opl}}(z))}^{2j}}{(2j+1)!}\mathfrak{J}({(r_{\mathrm{opl}}^{\left(2j+1\right)})}^{K_c}\ast \mathrm{\Gamma })(z_{\mathrm{opl}}(z))}}{{\displaystyle {\sum }_{j=0}^{\infty }\frac{{(\delta z_{\mathrm{opl}}(z))}^{2j}}{2j!}\Re ({(r_{\mathrm{opl}}^{\left(2j\right)})}^{K_c}\ast \mathrm{\Gamma })(z_{\mathrm{opl}}(z))}}$ remains well-defined. To verify that this indeed is the case, we first note that K_c is no longer the center frequency. In fact, the concept of center frequency becomes meaningless for an ideal source with infinite spectral bandwidth. It follows that the baseband and the passband representations of the derivatives of the reflection profile are the same because downshifting the ideal source by any amount has no effect. As a result, ${(r_{\mathrm{opl}}^{\left(\ell \right)})}^{K_c}(z_{\mathrm{opl}}(z^{\prime }))=r_{\mathrm{opl}}^{\left(\ell \right)}(z_{\mathrm{opl}}(z^{\prime })),\ell =0,1,2,3,\dots ,$ and each imaginary term in the numerator is

$$\mathfrak{J}\left({(r_{\mathrm{opl}}^{\left(2j+1\right)})}^{K_c}\ast \delta \right)\left(z_{\mathrm{opl}}(z_0)\right),j=0,1,2,3,\dots$$ (37)

$$=\mathfrak{J}\left((r_{\mathrm{opl}}^{\left(2j+1\right)})\ast \delta \right)\left(z_{\mathrm{opl}}(z_0)\right),j=0,1,2,3,\dots$$ (38)

$$=\mathfrak{J}\left({\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{r}_{\mathrm{opl}}^{\left(2j+1\right)}(z_{\mathrm{opl}}(z^{\prime }))}\delta (z_{\mathrm{opl}}(z_0)-z_{\mathrm{opl}}(z^{\prime }))\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime })\right),j=0,1,2,3,\dots$$ (39)

$$=\mathfrak{J}((r_{\mathrm{opl}}^{\left(2j+1\right)})(z_{\mathrm{opl}}(z_0))),j=0,1,2,3,\dots$$ (40)

$$=0.$$ (41)

We note that $((r_{\mathrm{opl}}^{\left(\ell \right)})(z_{\mathrm{opl}}(z_0)))$ is always a real-numbered value. Equations (37) through (41) show that all the summation terms in the numerator of Eq. (21) are zero and therefore so is the numerator.

The denominator, on the other hand, reduces to

$$\begin{array}{l}{\displaystyle \sum _{j=0}^{\infty }\frac{{(\delta z_{\mathrm{opl}}(z))}^{2j}}{2j!}}\Re ({(r_{\mathrm{opl}}^{\left(2j\right)})}^{K_c}\ast \mathrm{\Gamma })(z_{\mathrm{opl}}(z)\\ ={\displaystyle \sum _{j=0}^{\infty }\frac{{(\delta z_{\mathrm{opl}}(z))}^{2j}}{2j!}}((r_{\mathrm{opl}}^{\left(2j\right)})\ast \delta )(z_{\mathrm{opl}}(z))\end{array}$$ (42)

$$=(r_{\mathrm{opl}}\ast \delta )(z_{\mathrm{opl}}(z))+\left({\displaystyle \sum _{j=1}^{\infty }\frac{{(\delta z_{\mathrm{opl}}(z))}^{2j}}{2j!}}((r_{\mathrm{opl}}^{\left(2j\right)})\ast \delta )(z_{\mathrm{opl}}(z))\right)$$ (43)

$$=(r_{\mathrm{opl}}\ast \delta )(z_{\mathrm{opl}}(z)),$$ (44)

and consequently, the fraction reduces to $\frac{0}{(r_{\mathrm{opl}}\ast \delta )(z_{\mathrm{opl}}(z))}=0$. Therefore, it is indeed well-defined and is in fact zero and so is the Fourier phase. Equations (41) and (44) further show that the Fourier transform of the spectral interference given in Eq. (19) is

$$p(z_{\mathrm{opl}}(z))=(r_{\mathrm{opl}}\ast \delta )(z_{\mathrm{opl}}(z))=r_{\mathrm{opl}}(z_{\mathrm{opl}}(z)).$$ (45)

Thus, for an ideal source with infinite spectral bandwidth, the Fourier transform of the spectral interference between the reference wave and the back-reflected sample field is a real signal, equal to the actual reflection profile of the sample.

6. RESULTS AND DISCUSSION

Having presented the theoretical development of how the Fourier phase jointly estimates subresolution offset and mean spatial frequency, we present simulations based on the parametric model of the refractive index profile given in Eq. (26) to support our theoretical predictions, illustrate the suitability of Fourier phase for dr-SLQPM, and highlight its distinct characterization of coherence-gated structural information with respect to Fourier amplitude. We also present multiple applications of Fourier phase and describe flow velocity in D-OCT in terms of Fourier phase.

A. Parametric Modeling of the Refractive Index Profile

We use Eq. (26) to model the refractive index profile. This profile is parameterized by z₀, n₀, Δn, and s. Parameter z₀ is the depth location around which the change in the refractive index profile occurs with respect to the baseline refractive index characterized by n₀. Parameters Δn and s control the nature of this change. The former specifies the increase (Δn > 0) or decrease (Δn < 0) in refractive index, while the latter specifies how this increase or decrease is realized. For small values of s, the rise is gradual and spread over a range of depths around z₀. This spread implies that back-reflected waves are coming from a range of depths, corresponding to greater structural complexity and higher structural information. It is in this range of smaller values of s that the Fourier phase is most responsive, as is shown in the results presented below.

For s → ∞, the rise is sharp and localized at z₀, corresponding to a strong interface. Here, based on our discussion in Section 4, we expect the Fourier phase to primarily estimate δz_opl(z). This is indeed the case. As a side point, we note that Δn contributes to the strength of the interface. A sharp change might not imply a strong interface if Δn is small. This is especially true in experimental settings, where the refractive index profile with a sharp change can only be approximated by a Heaviside function. In such settings, for the sharp change to qualify as a strong interface, Δn should be large enough that it relatively dominates the slow-varying changes in the refractive index at other depths. However, in the simulations presented here, the interface with a sharp change and strong interface coincide.

Each of the above four parameters define the following four behaviors:

1. Behavior 1: subresolution shift controlled by z₀. [See Fig. 2(a).] As noted in Section 3.A, for a fixed z_ℓ, change in z₀ parameterizes subresolution offset Δz₀.

2. Behavior 2: subresolution shape controlled by s. [See Fig. 2(b).]

3. Behavior 3: baseline shift controlled by n₀. [See Fig. 9(a).]

4. Behavior 4: interface increment controlled by Δn. [See Fig. 9(b).]

Fig. 9.

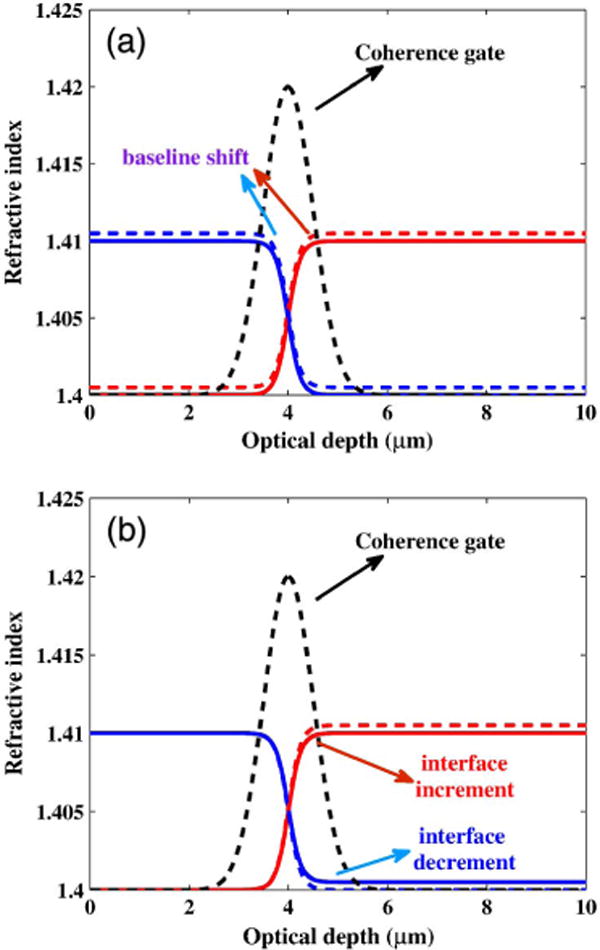
Behavior of the refractive index profile within the coherence gate in addition to those shown in Fig. 2. (a) Baseline shift (indicated by solid and dashed lines) for increasing (red) and decreasing (blue) refractive index profiles. (b) Interface increment (indicated by solid and dashed lines) for increasing (red) and decreasing (blue) refractive index profiles.

The first two have already been discussed in the context of δz_opl(z) and s_i(z_opl(z)). Simulation results presented below validate those connections. The last two behaviors are included for a complete description of Fourier phase response to all model parameters.

In Sections 6.C, 6.D, and 6.E we, respectively, present Fourier phase simulations for Behaviors 1 and 2, 3 and 2, and 4 and 2. The reason for including Behavior 2 in all the three cases is that we have presented theoretical details for the refractive index profile that is either slowly varying or has a strong interface, and the demarcation between these two regimes is controlled by s. We begin by detailing our simulation methodology.

B. Simulation Methodology

To simulate the Fourier phase measurement, we consider a white light spectral source S(k) with spectral bandwidth B (500–800 nm), center frequency K_c= 3.25 MHz, and ℓ_c = 1.5 μm corresponding to a Gaussian-shaped S(k), and mean refractive index of 1.4. The refractive index profile n_s(z′), defined by Eq. (26), is implemented as a multilayer system with the unit layer thickness taken to be d = 1 nm. The implementation requires constructing a transfer matrix [53] to mimic wave propagation through the refractive index profile. This is done for each K = 2k = 2∕λ. The back-reflected waves from all depths are interfered with a reference that is implemented in the common mode, by defining a substrate and refractive index profile interface. These interferences from all depths are integrated to get the spectral interference curve, P(K), as a function of spatial frequency K. (We note that unlike the experimental implementation, where phase noise can be greatly minimized by common-mode geometry, it is not important in the context of this simulation. It suffices to simply set the reference reflection-coefficient to one.) The self-interference of the reference and back-reflected sample waves is ignored. The Fourier transform of the spectral interference curve is the complex Fourier signal p(z_opl(z)) as a function of optical depth. The Fourier transform is implemented as a discrete-time Fourier transform. The phase of the Fourier transformed spectral interference is

$$\varphi (z_{\mathrm{opl}}(z))=\arctan \left(\frac{\mathfrak{J}(p(z_{\mathrm{opl}}(z)))}{\Re (p(z_{\mathrm{opl}}(z)))}\right).$$ (46)

This phase is wrapped and modulated by the center frequency K_c. Therefore, it is first unwrapped along the optical depth, followed by subtracting −2πK _cz_opl(z) from it to remove the phase ramp associated with the K_c-centered passband of the source spectrum. The resulting phase is the unwrapped Fourier phase. This, however, is not the final result as the unwrapped Fourier phase, by definition, accumulates Fourier phase along the depth due to the unwrapping. Therefore, at any optical depth, it is affected by all depths preceding it. We resolve this conflict by computing the gradient ${\varphi }^{\prime }(z_{\mathrm{opl}}(z^{\prime }))=\frac{d\varphi (z_{\mathrm{opl}}(z^{\prime }))}{d{z}_{\mathrm{opl}}(z^{\prime })}$ and integrating it within the coherence gate around the optical depth z_opl(z) to get the correct Fourier phase. Note that this coherence-gated integration of the phase gradient is not providing any additional information. It is only retrieving the coherence-gated unwrapped Fourier phase information—associated with p(z_opl(z))—otherwise difficult to access due to phase wrapping. Furthermore, since ϕ′(z_opl(z′)) is the instantaneous frequency, it cannot exceed the bandwidth of the source spectrum. Therefore, we use it to filter out those depths where the instantaneous spatial frequency exceeds the source bandwidth.

The phase obtained after the filtering is expressed in units of length by multiplying it by $\frac{{\lambda }_c}{2\pi }$, where λ_c is the wavelength corresponding to K_c. We denote it by δopl. As an illustration, Fig. 10 shows Fourier phase as a function of optical depth computed using the method outlined above for refractive index profile modeled by Eq. (26) with increasing values of s. This method to extract Fourier phase is used in all results presented below.

Fig. 10.

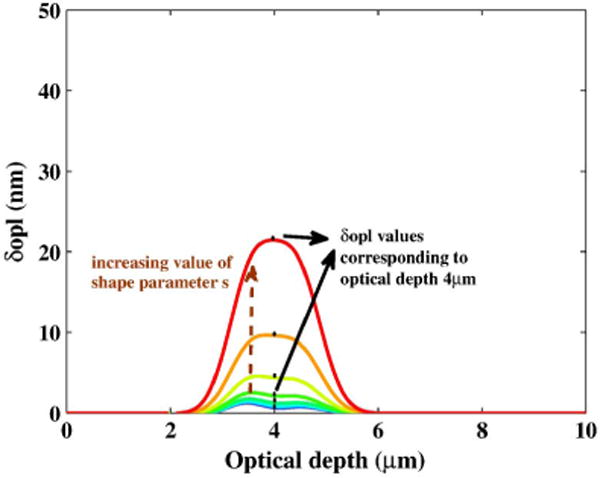
Fourier phase profiles for fixed refractive index model parameters z₀ = 2.85 μm, Δn = 0.01, and n₀ = 1.4 and increasing shape parameter s. The optical depth corresponding to physical depth z₀ = 2.85 μm is 4 μm.

C. Fourier Phase: Estimating Subresolution Offset and Subresolution Shape

We consider a 7 μm refractive index profile and set n₀ = 1.4 and Δn = 0.01. The corresponding OPL is roughly 10 μm. Parameter n₀ fixes the baseline refractive index, and Δn fixes the net increment in the refractive index with respect to the baseline. The two parameters z₀ and s are varied:

1. A Fourier phase measurement is made at z_ℓ, and Δz₀ is varied from −20 through 20 nm. We set z_ℓ = 2.85 μm, resulting in a subresolution shift in z₀ = Δz_ℓ + Δz₀ ranging from 2.83 through 2.87 μm.

2. The shape parameter s is varied from 0.002∕d to 2∕d, which changes the shape at the interface from slowly varying to strong. To avoid cluttering the figures, s is plotted in a log-scale (from −3 to 0). The transformation to log-scale was discussed in Section 3.A.

For each of the pairwise values of z₀ and s, the Fourier phase is measured at z_opl(z_ℓ) = 4 μm. Figure 11(a) shows the 2D plot of the resulting Fourier phase as a function of Δz₀ and s. In the slowly varying refractive index regime, Fourier phase increases with the increasing value of s just as theoretically predicted by Eq. (25), shown in Fig. 5(a). Fourier phase, therefore, captures increasing optical density. Comparing Eq. (24) with Eqs. (34) and (35) shows that s_i(z_opl(z_ℓ)) is approximately bounded by 2πK_c. Therefore, as the value of s approaches the strong interface regime, its value approaches or exceeds 2πK_c, and Fourier phase dependence on s ceases. As a result, for strong interfaces Fourier phase primarily depends on δz_opl(z_ℓ) in accordance with theoretical results in Eqs. (34)–(36). Figure 11(b) shows this dependence through the marginal representation extracted from the 2D plot. As can be seen, Fourier phase captures the subresolution offset δz_opl(z_ℓ). For Δz₀ < 0, z_opl(z₀) < z_opl(z_ℓ), and in conjunction with Eq. (7), implies $z_{\mathrm{opl}}^{wc}(z_{\ell })<z_{\mathrm{opl}}(z_{\ell })$ and δz_opl(z_ℓ) > 0. Similarly, for Δz₀ > 0, δz_opl(z_ℓ) < 0. It should, however, be noted that in the simulation δz_opl(z_ℓ), underestimates the subresolution offset Δz₀, partly because of the correlation function weighting in Eq. (8) skews the weighted-center toward z_opl(z_ℓ) and partly by the action of tan⁻¹. We note that Fourier phase estimation of δz_opl(z_ℓ) for a strong interface makes it suitable for measuring subresolution dynamic changes in optical depth of the interface via SDPM.

Fig. 11.

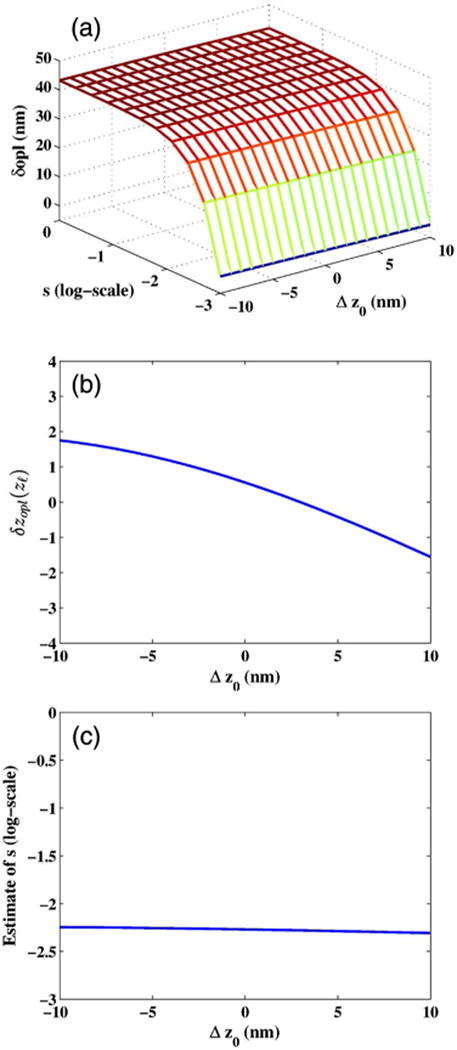
Behavior of Fourier phase by varying the subresolution offset and shape for a fixed baseline shift and interface increment. Fourier phase is plotted in units of length and the shape parameter s is expressed in the log-scale. (a) Fourier phase as a 2D function of subresolution offset and shape. (b) Isolating the effect of subresolution offset on Fourier phase. (c) Estimating the subresolution shape from Fourier phase and subresolution offset for true shape parameter value of −2.7 in the log-scale.

In our theoretical development of a slowly varying refractive index profile, we showed in Eq. (24) that tan (ϕ(z_opl(z_ℓ))) = δz_opl(z_ℓ)s_i(z_opl(z_ℓ)). From our simulation we know the value of Fourier phase ϕ(z_opl(z_ℓ)), and also δz_opl(z_ℓ), allowing us to estimate the mean spatial frequency, which for the model we have used is parameterized by the subresolution shape. Figure 11(c) shows the estimate of subresolution shape corresponding to the actual s = −2.7 in the log-scale as function of Δz₀. First, the estimate of s is approximately −2.27 and is constant for all values of subresolution offsets, thereby illustrating that _si(z_opl(z_ℓ)) captures the intrinsic structural characteristic of the refractive index profile. Second, the value of s is slightly over-estimated primarily because the value of δz_opl(z_ℓ) is under-estimated.

In the slowly varying refractive index regime, the symmetry of Fourier phase dependence on δz_opl(z_ℓ) can be used to remove its effect by performing Fourier phase measurements at multiple optical depths with subresolution sampling intervals. Given the symmetry, a depthwise average of the Fourier measurements will wash out the dependence of Fourier phase on δz_opl(z_ℓ) and only capture the effect of s [or more generally _si(z_opl(z_ℓ))] as desired. Moreover, it is not even necessary that the Fourier phase average be taken for the entire sample depth. A window, the size of the coherence gate, can be moved over the Fourier phase profile. Averaging within the window will remove the effect of δz_opl(z_ℓ), while also providing a depth-resolved estimate of s. (See Section 6.H below.) When performed at all lateral locations, we get a 3D characterization of s.

Fourier phase and Fourier amplitude: can Fourier amplitude estimate either δz_opl(z_ℓ) or s_i(z_opl(z_ℓ)) unambiguously? The answer is no. In Figs. 12(a) and 12(b), we show the Fourier amplitude profiles, respectively, for different values of Δz₀ and s. For the former, the subresolution offsets of the order of 10 nm do not substantially change the amplitude profile. For the latter, although the amplitude does change with changing s, it is difficult to ascertain the cause. This causal ambiguity—whether the amplitude change is due to a slowly varying refractive index or simply due to a smaller interface increment Δn for a sharp interface—is not present in Fourier phase. For a slowly varying refractive index, a fast increase in Fourier phase, as shown in Fig. 11, can happen only due to an increasing _si(z_opl(z_ℓ)). (This point is further emphasized by the results in the next two sections.) On the other hand, for refractive index profiles with a strong interface, the change in Fourier phase is only due to subresolution offset δz_opl(z_ℓ).

Fig. 12.

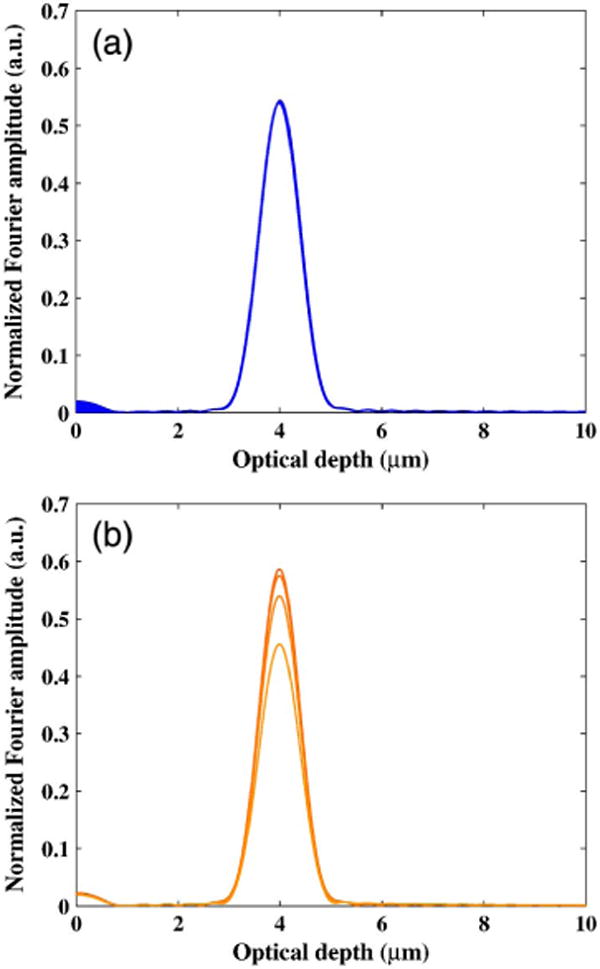
Fourier amplitude profiles as a function of optical depth for (a) Δz₀ ranges from −11 to 9 nm for s = −2.2 and (b) changing subresolution shape from −2.4 through −1.8 for Δz₀ = −11 nm.

D. Fourier Phase: Estimating Baseline Shift and Subresolution Shape

Here, we set z₀ = z_ℓ and define the baseline refractive index to be n₀ = z_ℓ + δn₀, with z_ℓ = 1.4 and δn₀ (Behavior 3) varying between −0.02 and 0.02. As in Section 6.C above, shape parameter s is varied from 0.002∕d through 2∕d, corresponding to −3 through 0 in the log-scale. For each pairwise value of δn₀ and s, the Fourier phase is computed. Figure 13 shows the 2D plot of Fourier phase as a function of δn₀ and s. The plot shows that Fourier phase captures the subresolution shape of the refractive index profile but very weakly depends on the baseline shift, which is in line with the theoretical prediction of Eq. (25) shown in Fig. 5(b). The primary discrepancy between theory and simulation is that when the baseline shift is large enough for the same measurement location of z_opl(z_ℓ), the weighted-center $z_{\mathrm{opl}}^{wc}(z_{\ell })$ moves from one side of z_opl(z_ℓ) to the other, thereby inducing a change in sign. Specifically, when the baseline increases, that is δn₀ > 0, the optical depth z_opl(z₀) where the interface is located also increases for the same physical depth z₀, and at some combinations of s and δn₀ it exceeds z_opl(z_ℓ) and δz_opl(z_ℓ) becomes negative. This can be seen in Fig. 13, where the change from positive to negative is not centered at n₀ = 0 but deviates from it depending on what s is. This is not an issue in the practical scenario. If one ensures that the mean refractive index of the medium in which the cell or tissue sample is embedded is less than the mean refractive index of the sample, δn₀ will effectively be less than zero, resulting in our operating in the positive regime. Given this regime, the Fourier phase dependence on |δn₀| is weak.

Fig. 13.

Behavior of Fourier phase by varying the baseline shift and subresolution shape for fixed subresolution offset and interface increment. Fourier phase is plotted in units of length and the shape parameter s is expressed in the log-scale.

E. Fourier Phase: Estimating Interface Increment and Subresolution Shape

We set n₀ = z_ℓ, z₀ = z_ℓ, and vary interface increment Δn (Behavior 4) and subresolution shape s, respectively, between −0.02 and 0.02, and −3 and 0 (log-scale). Figure 14 shows that as in the previous two cases, Fourier phase reliably estimates structural information corresponding to subresolution shape parameter s in the slowly varying refractive index regime. However, unlike the theoretical prediction in Fig. 5(c), where the dependence of Fourier phase on interface increment is moderately weak, the simulation shows that the dependence of Fourier phase on interface increment is even weaker. This discrepancy primarily arises because the interface increment indirectly affects the shape of the increment. This indirect effect is easily captured in the plot of the analytical expression. In the case of simulation, however, this effect is subsumed by the changing shape parameter.

Fig. 14.

Behavior of Fourier phase by varying the interface increment and shape for fixed baseline shift and subresolution offset. Fourier phase is plotted in units of length and the shape parameter s is expressed in the log-scale.

We note that Fourier phase distinctly captures one characteristic of Δn, and that is the direction of change. For negative values of Δn, Fourier phase becomes more negative with increasing values of s until it enters the strong interface regime, where it stops responding to changes in s. The opposite happens for positive Δn.

F. Application: Fourier-Phase-Based Estimation of the Axial Mean Spatial Frequency Profile

The parametric model of the refractive index profile helped illustrate the nature of structural information carried by Fourier phase. In practice, however, such an ideal profile has modest relevance. Therefore, we turn our attention to a more realistic refractive index profile (with n₀ = 1.4) depicted in Fig. 15(a). Fourier phase measurements are performed on this refractive index profile using the simulation methodology outlined in Section 6.B above. These measurements are performed at fixed oversampled optical depths in accordance with the strategy discussed in Section 3.B. The resulting optical phase profile ϕ(z_opl(z)) is convolved with a Gaussian window W—mimicking the coherence gate imposed by the spectral source described in Section 6.B above—to suppress the effect of subresolution offset δz_opl(z) due to its local symmetry and obtain ϕ_W(z_opl(z)). (See Section 6.C above.) The estimate of the optical-space axial mean spatial frequency profile is then given by ${\widehat{s}}_i(z_{\mathrm{opl}}(z))=|{\varphi }_W(z_{\mathrm{opl}}(z))|/{\ell }_c$, where the coherence ℓ_c as the normalization factor.

Fig. 15.

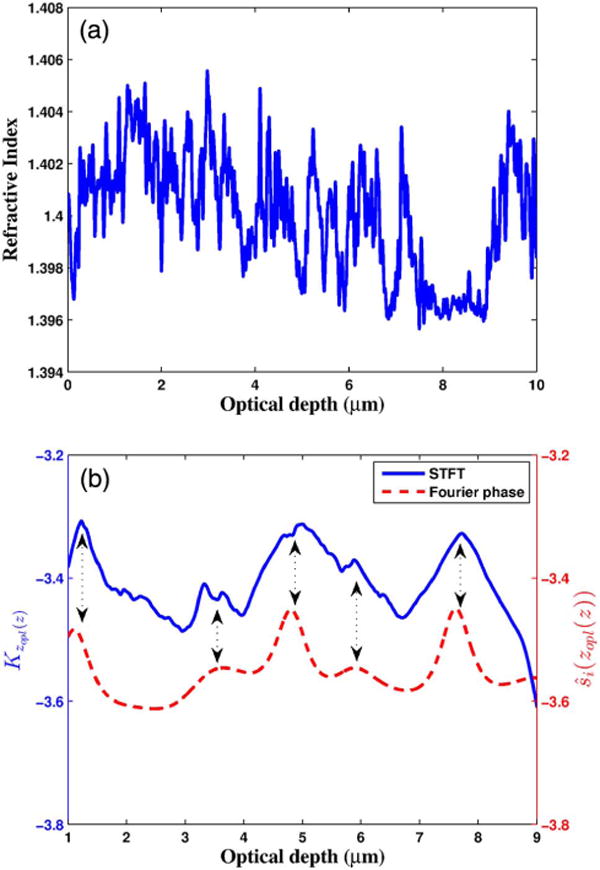
(a) Refractive index profile mapped to the optical-space, and (b) Fourier phase and STFT-based estimates of the axial mean spatial frequency profile corresponding to the refractive index profile. Both are expressed in the log-scale. The optical depth range is limited to (1μm, 9μm) to avoid simulation-based boundary artifacts.

To show that ${\widehat{s}}_i(z_{\mathrm{opl}}(z))$ does indeed carry axial mean spatial frequency information, we also estimate the axial mean spatial frequency directly from the refractive index profile by performing a short-time Fourier transform (STFT) along n_s(z′) after mapping it to the optical-space z_opl(z′). The STFT window is chosen to be the same window W used to compute ${\widehat{s}}_i(z_{\mathrm{opl}}(z))$. The STFT window scans the refractive index profile at all those optical depth locations z_opl(z) for which the phase profile was computed. At each optical depth z_opl(z) the amplitude $\left|F_{z_{\mathrm{opl}}(z)}^W(K)\right|$ of the Fourier transform of the windowed refractive index profile $n_s^W(z_{\mathrm{opl}}(z))$ centered at z_opl(z) gives its axial spatial frequency distribution over the spatial frequency range defined by the spectral source baseband bandwidth. This distribution is used to calculate the STFT-based mean spatial frequency $K_{z_{\mathrm{opl}}(z)}$ at that optical depth using the relation $K_{z_{\mathrm{opl}}(z)}=\frac{{\displaystyle {\int }_{B}K|K_{z_{\mathrm{opl}}(z)}^W(K)|\mathrm{d}K}}{{\displaystyle {\int }_B|K_{z_{\mathrm{opl}}(z)}^W(K)|\mathrm{d}K}}$. Figure 15(b) plots the Fourier phase and STFT-based estimates of the axial mean spatial frequency of the refractive index profile in Fig. 15(a) as a function of optical depth. These mean spatial frequency profiles are plotted in the log-scale. The figure clearly shows that both approaches result in similar behavior, although Fourier phase in this example underestimates the mean spatial frequency.

G. Application: Fourier Phase-Based Depth-Resolved Characterization of Change in Optical Density

For the same refractive index profile as above, we now include a small local decrement (minimum Δn = −0.001) in the refractive index around optical depth z_opl(z₀) = 5.3 μm. Figure 16(a) illustrates the refractive index profiles with and without this decrement. The corresponding Fourier phase profiles ϕ(z_opl(z)) are plotted in Fig. 16(b). They show that Fourier phase is able to provide a depth-resolved characterization of this decrement. As discussed in Section 6.E above, however, this characterization is the indirect effect of the local refractive index decrement on ${\widehat{s}}_i(z_{\mathrm{opl}}(z))$. We note that we have not computed ϕ_W(z_opl(z)) because, first, the decrement occurs in a window smaller than the coherence gate, and second, it gives us an opportunity to illustrate the phase profile itself.

Fig. 16.

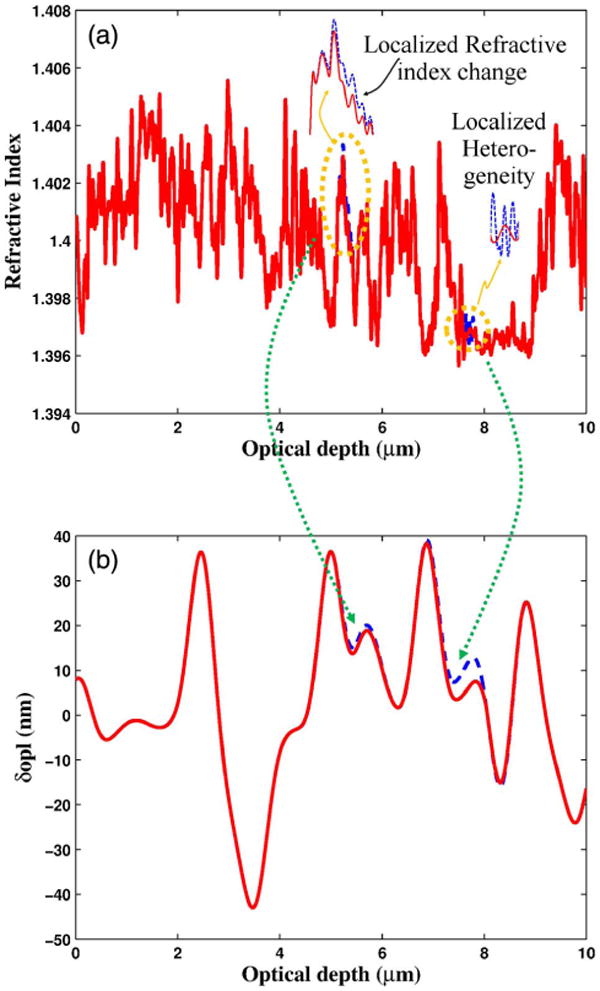
(a) Refractive index profile in optical-space with localized refractive index change and heterogeneity, respectively at optical depths z_opl(z₀) = 5.3 μm and z_opl(z₀) = 7.7 μm, and (b) corresponding depth-resolved changes in Fourier phase. Fourier phase is plotted in units of length.

H. Application: Fourier Phase-Based Depth-Resolved Characterization of Heterogeneity

Heterogeneity is a well-established statistical characteristic in many biological processes, such as cancer development. Here we indicate the presence of heterogeneity by considering two refractive index profiles with a localized difference in the rate of variation of the refractive index around the optical depth z_opl(z₀) = 7.7 μm. This localized heterogeneity is shown in Fig. 16(a), and the corresponding Fourier phase profiles are shown in Fig. 16(b). It can be seen that the phase value increases with an increase in heterogeneity.

In practice, it is difficult to separate local change (increment or decrement) in the refractive index from refractive index heterogeneity, and in a real scenario Fourier phase will manifest the combined effect of the two. This is only natural because they both affect the mean spatial frequency s_i(z_opl(z)).

I. Doppler OCT in the Context of Fourier Phase

A different scenario arises when we consider, for example, blood flow through static tissue. Here, the flow of blood primarily affects the weighted-center $z_{\mathrm{opl}}^{wc}(z)$ within the coherence gate resulting in the subresolution offset δz_opl(z) between it and the probing depth z_opl(z). For a fixed probing depth z_opl(z₀), the phase difference ΔΦ between the Fourier phase at two adjacent A-scans, therefore, captures the net axial subresolution offset. If the time t between the two A-scans is known, the axial flow velocity is given by $v=\frac{\mathrm{\Delta }\Phi }{2\pi K_{c}t}$. Strictly speaking, this is the axial optical flow velocity. To estimate the axial flow velocity itself, v should be divided by the average refractive index of the sample.

7. CONCLUSION

Despite being enthusiastically received by the research community, the scope and physical meaning of Fourier phase within the framework of FD-OCT has not been fully studied. This paper is an attempt to fill that gap. We have shown that Fourier phase is a direct consequence of finite spectral bandwidth of the source that results in a loss of structural information into the quadrature component of the complex spectral interference. Phasor representation allowed us to reveal that Fourier phase is, in fact, able to access an estimate of this structural information. We showed that this joint estimate characterizes subresolution offset and mean spatial frequency of coherence-gated refractive index profile, and derived an analytical expression precisely showing how and why this is the case. We also showed that both dr-SLQPM and SDPM are special cases of this general theoretical framework of Fourier phase and look at complementary aspects of Fourier phase. The former focuses on measuring mean spatial frequency, while the latter measures subresolution offset. Both have the advantage associated with any derivative of FD-OCT that they quantify the coherence-gated depth-resolved structure of the sample without being confounded by its thickness as in transmission-mode QPM.

Based on the general framework of Fourier phase, we further showed that Fourier phase can be applied to estimate axial mean spatial frequency profile and characterize localized change in the refractive index and heterogeneity. These characterizations play an important role in early cancer detection and risk assessment [43]. Finally, we utilized the principle of Fourier phase to derive axial flow velocity in D-OCT.

APPENDIX A: SPECTRAL INTERFERENCE

Starting with Eq. (3), and noting that $\mathbf{K}=2k\widehat{\mathbf{z}}$, we have

$$\begin{array}{l}P(K)=2S\left(\frac{K}{2}\right){\displaystyle {\int }_0^{L}r(z^{\prime })\cos \left(4\pi \frac{K}{2}{z}_{\mathrm{opl}}(z^{\prime })\right)}\mathrm{d}{z}^{\prime }\\ =2S\left(\frac{K}{2}\right){\displaystyle {\int }_0^{L}r(z^{\prime })\cos \left(2\pi K{z}_{\mathrm{opl}}(z^{\prime })\right)}\mathrm{d}{z}^{\prime },\end{array}$$ (A1)

implying a dilation of the source spectrum under the transformation from wave number to spatial frequency. We denote the source spectral density in the spatial frequency basis by $S_1(K)=S\left(\frac{K}{2}\right)$. As this representation is purely notational, we redefine S(K) = S₁K without any loss in generality or accuracy because dilation, though made implicit, is not ignored. Therefore, we rewrite Eq. (A1) as

$$P(K)=2S(K){\displaystyle {\int }_0^{L}r(z^{\prime })\cos \left(2\pi K{z}_{\mathrm{opl}}(z^{\prime })\right)}\mathrm{d}{z}^{\prime }.$$ (A2)

The OPL is a monotonically increasing function of physical depth for any given refractive index profile. This definition, expressed in Eq. (5), is used in Eq. (A2) to get

$$P(K)=2S(K){\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}r(z^{\prime })\cos \left(2\pi K{z}_{\mathrm{opl}}(z^{\prime })\right)}\frac{\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime })}{n(z^{\prime })}$$ (A3)

$$=2S(K){\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}\cos \left(2\pi K{z}_{\mathrm{opl}}(z^{\prime })\right)}\frac{r(z^{\prime })}{n(z^{\prime })}\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime }),$$ (A4)

where the substitution $d{z}^{\prime }=\frac{d{z}_{\mathrm{opl}}(z^{\prime })}{n(z^{\prime })}$ follows from the Leibniz theorem. Equation (A4) states that when the integration is performed in the optical-space z_opl(z′), the reflection profile is modified from r(z′), to $\frac{r(z^{\prime })}{n(z^{\prime })}$. The normalization by the refractive index accounts for mapping of the reflection profile from the physical-space to optical-space. The mapping z_opl(z′) from physical-space to optical space defines a homeomorphism between the two spaces that preserves the topological structure of the two spaces. As a result, the value of the modified reflection profile at z′ is the same as that at z_opl(z′). Therefore, we denote the modified reflection profile at the optical depth z_opl(z′) (corresponding to physical depth z′) by $r_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))=\frac{r(z_{\mathrm{opl}}(z^{\prime }))}{n(z_{\mathrm{opl}}(z^{\prime }))}$

$$P(K)=2S(K){\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{r}_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))\cos (2\pi K{z}_{\mathrm{opl}}(z^{\prime }))\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime })}.$$ (A5)

It is helpful to think of r_opl(z_opl(z′)) as a distribution acting on cos(2πKz_opl(z′) through integration, because it allows the modeling of interfaces within the reflection profile that otherwise are difficult to handle mathematically. (See Section 4.B for an example.) This interpretation is feasible because cos(2πKz_opl(z′)) is a smooth function with compact support over [0, z_opl(L).

APPENDIX B: SIMPLIFYING SPECTRAL INTERFERENCE

Starting with generalized representation of the spectral interference

$$P(K)=2S(K)\Re \left({\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{r}_{\mathrm{opl}}^c}(z_{\mathrm{opl}}(z^{\prime }))e^{i2\pi K{z}_{\mathrm{opl}}(z^{\prime })}\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime })\right)$$ (B1)

and substituting Eq. (11) we get

$$\begin{array}{c}P(K)=2S(K)\Re ({\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{r}_{\mathrm{opl}}}(z_{\mathrm{opl}}(z))e^{-i2\pi K\delta z_{\mathrm{opl}}(z)}\\ \times e^{i2\pi K{z}_{\mathrm{opl}}(z^{\prime })}\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime }))\end{array}$$ (B2)

$$\begin{array}{c}=2S(K)({\displaystyle {\int }_0^L{r}_{\mathrm{opl}}}(z_{\mathrm{opl}}(z^{\prime }))\cos (2\pi K(z_{\mathrm{opl}}(z^{\prime })\\ -\delta z_{\mathrm{opl}}(z)))\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime })).\end{array}$$ (B3)

APPENDIX C: FOURIER TRANSFORM OF THE SPECTRAL INTERFERENCE

Starting with Eq. (18),

$$p(z_{\mathrm{opl}}(z))={\displaystyle {\int }_{B}P(K)e^{-2\pi K{z}_{\mathrm{opl}}(z)}\mathrm{d}K}$$ (C1)

and substituting Eq. (17), we get

$$\begin{array}{c}p(z_{\mathrm{opl}}(z))=2{\displaystyle {\int }_{B}S(K)}({\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}r(z_{\mathrm{opl}}(z^{\prime }))\cos (2\pi K(z_{\mathrm{opl}}(z^{\prime })}\\ -\delta z_{\mathrm{opl}}(z)))\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime }))e^{-i2\pi K{z}_{\mathrm{opl}}(z)}\mathrm{d}K.\end{array}$$ (C2)

Due to finite spectral-bandwidth, finite sample-depth, and real samples, Fubini’s theorem applies, allowing for the interchange of integrals. This, in conjunction with Euler representation of the cosine term, results in

$$\begin{array}{c}p(z_{\mathrm{opl}}(z))={\displaystyle {\int }_0^{L}r(z_{\mathrm{opl}}(z^{\prime }))}({\displaystyle {\int }_{B}S(K)(e^{-i2\pi K(z_{\mathrm{opl}}(z)-z_{\mathrm{opl}}(z^{\prime })+\delta z_{\mathrm{opl}}(z))}}\\ +e^{-i2\pi K(z_{\mathrm{opl}}(z)+z_{\mathrm{opl}}(z^{\prime })-\delta z_{\mathrm{opl}}(z))})\mathrm{d}K)\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime }).\end{array}$$ (C3)

Rearranging Eq. (C3) allows us to express p(z_opl(z)) as a sum of

$$\begin{array}{l}{p}_1(z_{\mathrm{opl}}(z))={\displaystyle {\int }_0^{L}r(z_{\mathrm{opl}}(z^{\prime }))}({\displaystyle {\int }_{B}S(K)}\\ \times e^{-i2\pi K(z_{\mathrm{opl}}(z)-z_{\mathrm{opl}}(z^{\prime })+\delta z_{\mathrm{opl}}(z))}\mathrm{d}K)\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime }),\end{array}$$ (C4)

and

$$\begin{array}{l}{p}_2(z_{\mathrm{opl}}(z))={\displaystyle {\int }_0^{L}r(z_{\mathrm{opl}}(z^{\prime }))}({\displaystyle {\int }_{B}S(K)}\\ \times e^{-i2\pi K(z_{\mathrm{opl}}(z)+z_{\mathrm{opl}}(z^{\prime })-\delta z_{\mathrm{opl}}(z))}\mathrm{d}K)\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime }).\end{array}$$ (C5)

1. Baseband Represenation of p₁(z_opl(z))

To simplify Eq. (C4), we rewrite it as

$$\begin{array}{l}{p}_1(z_{\mathrm{opl}}(z))\\ ={\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{r}_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))}({\displaystyle {\int }_{B}S(K)}{e}^{-i2\pi K\delta z_{\mathrm{opl}}(z)}\\ \times e^{-i2\pi K(z_{\mathrm{opl}}(z)-z_{\mathrm{opl}}(z^{\prime }))}\mathrm{d}K)\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime })\\ ={\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{r}_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))}({\displaystyle {\int }_{B}S(K)}{\displaystyle \sum _{j=0}^{\infty }\frac{{\left(-i2\pi K\delta z_{\mathrm{opl}}(z)\right)}^j}{j!}}\\ \times e^{-i2\pi K(z_{\mathrm{opl}}(z)-z_{\mathrm{opl}}(z^{\prime }))}\mathrm{d}K)\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime })\end{array}$$ (C6)

$$={\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{r}_{\mathrm{opl}}(z_{\mathrm{opl}}(z^{\prime }))\left({\displaystyle {\int }_{B}S(K)}\left({\displaystyle \sum _{j=0}^{\infty }\frac{{(i2\pi K\delta z_{\mathrm{opl}}(z))}^{2j}}{2j!}}-{\displaystyle \sum _{j=0}^{\infty }\frac{{(i2\pi K\delta z_{\mathrm{opl}}(z))}^{2j+1}}{(2j+1)!}}\right)\times e^{-i2\pi K(z_{\mathrm{opl}}(z)-z_{\mathrm{opl}}(z^{\prime }))}\mathrm{d}K\right)\mathrm{d}{z}_{\mathrm{opl}}}(z^{\prime }),$$ (C7)

where Eq. (C6) employs the power series representation of the analytic exponential function $e^{i2\pi K\delta z_{\mathrm{opl}}(z)}$, and Eq. (C7) decomposes the power series into its even and odd powers. Denoting them, respectively, by h_e(Kδz_opl(z)) and h_o(Kδz_opl(z)), we write Eq. (C7) as

$$p_1(z_{\mathrm{opl}}(z))={\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{r}_{\mathrm{opl}}\left(z_{\mathrm{opl}}\left(z^{\prime }\right)\right)}\left({\displaystyle {\int }_{B}S(K)(h_e(K\delta z_{\mathrm{opl}}(z))}-h_0(K\delta z_{\mathrm{opl}}(z)))e^{-i2\pi K(z_{\mathrm{opl}}(z^{\prime }))}\mathrm{d}K\right)\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime }).$$ (C8)

The inner integrals are the Fourier transforms of S(K)h_e(Kδz_opl(z)) and S(K)h_o(Kδz_opl(z)), evaluated at (z_opl(z)−z_opl(z′)). Considered together with the outer integrals, they reduce Eq. (C8) to a convolution between the reflection profile, the correlation function of the light source, and Fourier transforms of h_e(K δz_opl(z)) and h_o(K δz_opl(z)). The transforms of latter, respectively, are

$$ℱ\mathcal{T}\left\{h_e(K\delta z_{\mathrm{opl}}(z))\right\}={\displaystyle \sum _{j=0}^{\infty }\frac{{\delta }^{(2j)}\left(z_{\mathrm{opl}}(z)\right){\left(\delta z_{\mathrm{opl}}(z)\right)}^{2j}}{2j!}},$$ (C9)

$$ℱ\mathcal{T}\left\{h_0(K\delta z_{\mathrm{opl}}(z))\right\}=-\delta z_{\mathrm{opl}}(z){\displaystyle \sum _{j=0}^{\infty }\left(\frac{\frac{{\delta }^{(2j+1)}\left(z_{\mathrm{opl}}(z)\right)}{{\left(\delta z_{\mathrm{opl}}(z)\right)}^{2j}}}{(2j+1)!}\right),}$$ (C10)

where the notation δ(^ℓ) (z_opl(z)) denotes the (ℓ)th derivative of the Dirac-delta, δ. The convolution of the outer integral then simplifies to

$$p_1\left(z_{\mathrm{opl}}(z)\right)={\displaystyle \sum _{j=0}^{\infty }\frac{{\left(\delta z_{\mathrm{opl}}(z)\right)}^{2j}}{2j!}}\left(r_{\mathrm{opl}}^{(2j)}\ast {\mathrm{\Gamma }}_c\right)\left(z_{\mathrm{opl}}(z)\right)+\delta z_{\mathrm{opl}}(z){\displaystyle \sum _{j=0}^{\infty }\frac{{\left(\delta z_{\mathrm{opl}}(z)\right)}^{2j}}{(2j+1)!}\left(r_{\mathrm{opl}}^{(2j+1)}\ast {\mathrm{\Gamma }}_c\right)\left(z_{\mathrm{opl}}(z)\right)},$$ (C11)

where $r_{\mathrm{opl}}^{(2j)}\left(z_{\mathrm{opl}}(z)\right)$ is the (2j)th derivative of the reflection profile, * indicates the convolution operation, and ${\mathrm{\Gamma }}_c\left(z_{\mathrm{opl}}(z)\right)=e^{-i2\pi K_c{z}_{\mathrm{opl}}(z)}\mathrm{\Gamma }\left(z_{\mathrm{opl}}(z)\right)$ is the correlation function corresponding to the source spectrum centered at K_c. $\mathrm{\Gamma }\left(z_{\mathrm{opl}}(z)\right)$ itself is its baseband representation. We assume that the source spectral range is [K₁, K₂] and its center frequency K_c is as defined in Section 2.B.

There is a second interpretation of Eq. (C11). To see it, we focus on the convolution operation $\left(r_{\mathrm{opl}}^{(\ell )}\ast {\mathrm{\Gamma }}_c\right)\left(z_{\mathrm{opl}}(z)\right)$ in Eq. (C11),

$$\left(r_{\mathrm{opl}}^{(\ell )}\ast {\mathrm{\Gamma }}_c\right)\left(z_{\mathrm{opl}}(z)\right)={\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{r}_{\mathrm{opl}}^{(\ell )}\left(z_{\mathrm{opl}}(z^{\prime })\right)\mathrm{\Gamma }\left(z_{\mathrm{opl}}(z)-z_{\mathrm{opl}}(z^{\prime })\right)e^{-i2\pi K_c\left(z_{\mathrm{opl}}(z)-z_{\mathrm{opl}}(z^{\prime })\right)}\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime })}$$ (C12)

$$=e^{-i2\pi K_c{z}_{\mathrm{opl}}(z)}{\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{r}_{\mathrm{opl}}^{(\ell )}\left(z_{\mathrm{opl}}(z^{\prime })\right)e^{i2\pi K_c{z}_{\mathrm{opl}}(z^{\prime })}}\times \mathrm{\Gamma }\left(z_{\mathrm{opl}}(z)-z_{\mathrm{opl}}(z^{\prime })\right)\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime })$$ (C13)

$$=e^{-i2\pi K_c{z}_{\mathrm{opl}}(z)}{\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{\left(r_{\mathrm{opl}}^{(\ell )}\right)}^{K_c}\left(z_{\mathrm{opl}}(z^{\prime })\right)\mathrm{\Gamma }\left(z_{\mathrm{opl}}(z)-z_{\mathrm{opl}}(z^{\prime })\right)\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime })}$$ (C14)

$$=e^{-i2\pi K_c{z}_{\mathrm{opl}}(z)}\left({\left(r_{\mathrm{opl}}^{(\ell )}\right)}^{K_c}\ast \mathrm{\Gamma }\right)\left(z_{\mathrm{opl}}(z)\right),$$ (C15)

where ${\left(r_{\mathrm{opl}}^{(\ell )}\right)}^{K_c}\left(z_{\mathrm{opl}}(z)\right)=r_{\mathrm{opl}}^{(\ell )}\left(z_{\mathrm{opl}}(z)\right)e^{i2\pi K_c{z}_{\mathrm{opl}}(z)}$ is the baseband representation of the (ℓ)th derivative of the reflection profile. As mentioned above, Γ(z_opl(z)) is the baseband representation of Γ(z_opl(z)) which is the correlation function corresponding to the source. Substituting Eq. (C15) in Eq. (C11), we get the final form of p₁(z_opl(z)) as

$$\begin{array}{l}{p}_1\left(z_{\mathrm{opl}}(z)\right)\\ =e^{-i2\pi K_c{z}_{\mathrm{opl}}(z)}({\displaystyle \sum _{j=0}^{\infty }\frac{{\left(\delta z_{\mathrm{opl}}(z)\right)}^{2j}}{2j!}\left({\left(r_{\mathrm{opl}}^{(2j)}\right)}^{K_c}\ast \mathrm{\Gamma }\right)}\left(z_{\mathrm{opl}}(z)\right)\\ +\delta z_{\mathrm{opl}}(z){\displaystyle \sum _{j=0}^{\infty }\frac{{\left(\delta z_{\mathrm{opl}}(z)\right)}^{2j}}{(2j+1)!}\left({\left(r_{\mathrm{opl}}^{(2j+1)}\right)}^{K_c}\ast \mathrm{\Gamma }\right)\left(z_{\mathrm{opl}}(z)\right)}),\end{array}$$ (C16)

which decomposes p₁(z_opl(z)) into its baseband representation (the term in the parentheses) and the carrier signal (the exponential before the parentheses) with carrier frequency K_c. The Fourier phase depends only on the baseband representation. Therefore, in the main text we exclusively use the baseband representation of p₁(z_opl(z)).

2. Baseband Representation of p₂(z_opl(z))

Following the same approach as above, p₂(z_opl(z)) simplifies to p₂(z_opl(z))

$$\begin{array}{c}{p}_2(z_{\mathrm{opl}}(z))\\ =e^{-i2\pi K_c{z}_{\mathrm{opl}}(z)}({\displaystyle \sum _{j=0}^{\infty }\frac{{\left(\delta z_{\mathrm{opl}}(z)\right)}^{2j}}{2j!}}\left({\left(r_{\mathrm{opl}}^{(2j)}\right)}^{K_c^{\ast }}\ast \mathrm{\Gamma }\right)(z_{\mathrm{opl}}(z))\\ -\delta z_{\mathrm{opl}}(z){\displaystyle \sum _{j=0}^{\infty }\frac{{\left(\delta z_{\mathrm{opl}}(z)\right)}^{2j}}{(2j+1)!}}\left({\left(r_{\mathrm{opl}}^{(2j+1)}\right)}^{K_c^{\ast }}\ast \mathrm{\Gamma }\right)(z_{\mathrm{opl}}(z))),\end{array}$$ (C17)

where we have exploited the symmetry of the correlation function. The notations ${\left(r_{\mathrm{opl}}^{(2j)}\right)}^{K_c^{\ast }}$ and ${\left(r_{\mathrm{opl}}^{(2j+1)}\right)}^{K_c^{\ast }}$ denote the complex conjugation of ${\left(r_{\mathrm{opl}}^{(2j)}\right)}^{K_c}$ and ${\left(r_{\mathrm{opl}}^{(2j+1)}\right)}^{K_c}$, respectively.

Summing Eqs. (C16) and (C17) gives us the Fourier transform p(z_opl) of spectral interference P(K) as

$$\begin{array}{l}p(z_{\mathrm{opl}}(z))\\ =p_1(z_{\mathrm{opl}}(z))+p_2(z_{\mathrm{opl}}(z))\\ =2e^{-i2\pi K_c{z}_{\mathrm{opl}}(z)}({\displaystyle \sum _{j=0}^{\infty }\frac{{\left(\delta z_{\mathrm{opl}}(z)\right)}^{2j}}{2j!}}\Re \left({\left(r_{\mathrm{opl}}^{(2j)}\right)}^{K_c}\ast \mathrm{\Gamma }\right)(z_{\mathrm{opl}}(z))\\ +i\delta z_{\mathrm{opl}}(z){\displaystyle \sum _{j=0}^{\infty }\frac{{\left(\delta z_{\mathrm{opl}}(z)\right)}^{2j}}{(2j+1)!}\mathfrak{J}\left({\left(r_{\mathrm{opl}}^{(2j+1)}\right)}^{K_c}\ast \mathrm{\Gamma }\right)(z_{\mathrm{opl}}(z))}),\end{array}$$ (C18)

with ℜ and ℑ representing the real and imaginary parts of their respective arguments. We emphasize that in the main text the baseband representation of p(z_opl(z)) is used. Also, the leading is dropped as p(z_opl(z)) can be normalized by it.

APPENDIX D: SIMPLIFYING FOURIER PHASE REPRESENTATION AT A STRONG INTERFACE

We start by evaluating the first three convolutions in both the numerator and denominator of the Fourier phase expression in Eq. (30).

First convolution in the denominator of Eq. (30):

$$\begin{array}{c}\Re ({\delta }^{K_c}\ast \mathrm{\Gamma })z_{\mathrm{opl}}(z_0)\\ =\Re ({\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}\delta (z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z_0))\mathrm{\Gamma }(z_{\mathrm{opl}}(z_0)-z_{\mathrm{opl}}(z^{\prime }))}\\ \times e^{i2\pi K_c(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z_0))}\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime }))\end{array}$$ (D1)

$$=\Re (\mathrm{\Gamma }(0))$$ (D2)

$$=\mathrm{\Gamma }(0).$$ (D3)

First convolution in the numerator of Eq. (30):

$$\begin{array}{c}\mathfrak{J}\left({\left({\delta }^{(1)}\right)}^{K_c}\ast \mathrm{\Gamma }\right)z_{\mathrm{opl}}(z_0)\\ =\mathfrak{J}({\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{\delta }^{(1)}(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z_0))\mathrm{\Gamma }(z_{\mathrm{opl}}(z_0)-z_{\mathrm{opl}}(z^{\prime }))}\\ \times e^{i2\pi K_c(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z_0))}\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime }))\end{array}$$ (D4)

$$=\mathfrak{J}(i2\pi K_c\mathrm{\Gamma }(0)+{\mathrm{\Gamma }}^{(1)}(0))$$ (D5)

$$=2\pi K_c\mathrm{\Gamma }(0).$$ (D6)

Second convolution in the denominator of Eq. (30):

$$\begin{array}{c}\Re ({\left({\delta }^{(2)}\right)}^{K_c}\ast \mathrm{\Gamma })z_{\mathrm{opl}}(z_0)\\ =\Re ({\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{\delta }^{(2)}(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z_0))\mathrm{\Gamma }(z_{\mathrm{opl}}(z_0)-z_{\mathrm{opl}}(z^{\prime }))}\\ e^{i2\pi K_c(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z_0))}\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime }))\end{array}$$ (D7)

$$=\Re (-{\left(2\pi K_c\right)}^2\mathrm{\Gamma }(0)+i2(2\pi K_c){\mathrm{\Gamma }}^{(1)}(0)+{\mathrm{\Gamma }}^{(2)}(0))$$ (D8)

$$=-{\left(2\pi K_c\right)}^2\mathrm{\Gamma }(0)+{\mathrm{\Gamma }}^{(2)}(0).$$ (D9)

Second convolution in the numerator of Eq. (30):

$$\begin{array}{c}\mathfrak{J}\left({\left({\delta }^{(3)}\right)}^{K_c}\ast \mathrm{\Gamma }\right)z_{\mathrm{opl}}(z_0)\\ =\mathfrak{J}({\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{\delta }^{(3)}(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z_0))\mathrm{\Gamma }(z_{\mathrm{opl}}(z_0)-z_{\mathrm{opl}}(z^{\prime }))}\\ \times e^{i2\pi K_c(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z_0))}\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime }))\end{array}$$ (D10)

$$\begin{array}{l}=\mathfrak{J}(-i{\left(2\pi K_c\right)}^3\mathrm{\Gamma }(0)-3{\left(2\pi K_c\right)}^2{\mathrm{\Gamma }}^{(1)}(0)\\ +i3(2\pi K_c){\mathrm{\Gamma }}^{(2)}(0)+{\mathrm{\Gamma }}^{(3)}(0))\end{array}$$ (D11)

$$=-{\left(2\pi K_c\right)}^3\mathrm{\Gamma }(0)+3\left(2\pi K_c\right){\mathrm{\Gamma }}^{(2)}(0)).$$ (D12)

Third convolution in the denominator of Eq. (30):

$$\begin{array}{c}\Re ({\left({\delta }^{(4)}\right)}^{K_c}\ast \mathrm{\Gamma })z_{\mathrm{opl}}(z_0)\\ =\Re ({\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{\delta }^{(4)}(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z_0))\mathrm{\Gamma }(z_{\mathrm{opl}}(z_0)-z_{\mathrm{opl}}(z^{\prime }))}\\ \times e^{i2\pi K_c(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z_0))}\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime }))\end{array}$$ (D13)

$$\begin{array}{l}=\Re ({\left(2\pi K_c\right)}^4\mathrm{\Gamma }(0)-i4{\left(2\pi K_c\right)}^3{\mathrm{\Gamma }}^{(1)}(0)-6{\left(2\pi K_c\right)}^2{\mathrm{\Gamma }}^{(2)}(0)\\ +i4(2\pi K_c){\mathrm{\Gamma }}^{(3)}(0)+{\mathrm{\Gamma }}^{(4)}(0))\end{array}$$ (D14)

$$={\left(2\pi K_c\right)}^4\mathrm{\Gamma }(0)-6{\left(2\pi K_c\right)}^2{\mathrm{\Gamma }}^{(2)}(0)+{\mathrm{\Gamma }}^4(0).$$ (D15)

Third convolution in the numerator of Eq. (30):

$$\begin{array}{c}\mathfrak{J}\left({\left({\delta }^{(5)}\right)}^{K_c}\ast \mathrm{\Gamma }\right)z_{\mathrm{opl}}(z_0)\\ =\mathfrak{J}({\displaystyle {\int }_0^{z_{\mathrm{opl}}(L)}{\delta }^{(5)}(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z_0))\mathrm{\Gamma }(z_{\mathrm{opl}}(z_0)-z_{\mathrm{opl}}(z^{\prime }))}\\ \times e^{i2\pi K_c(z_{\mathrm{opl}}(z^{\prime })-z_{\mathrm{opl}}(z_0))}\mathrm{d}{z}_{\mathrm{opl}}(z^{\prime }))\end{array}$$ (D16)

$$\begin{array}{l}=\mathfrak{J}(i{\left(2\pi K_c\right)}^5\mathrm{\Gamma }(0)+5{\left(2\pi K_c\right)}^4{\mathrm{\Gamma }}^{(1)}(0)-i10{\left(2\pi K_c\right)}^3{\mathrm{\Gamma }}^{(2)}(0)\\ -10(2\pi K_c){\mathrm{\Gamma }}^{(3)}(0)+i5\left(2\pi K_c\right){\mathrm{\Gamma }}^{(4)}(0)+{\mathrm{\Gamma }}^{(5)}(0))\end{array}$$ (D17)

$$={\left(2\pi K_c\right)}^5\mathrm{\Gamma }(0)-10{\left(2\pi K_c\right)}^3{\mathrm{\Gamma }}^{(2)}(0)+5\left(2\pi K_c\right){\mathrm{\Gamma }}^{(4)}(0).$$ (D18)

Substituting Eqs. (D3), (D6), (D9), (D12), (D15), and (D18) in Eq. (30), the Fourier phase becomes

$$\angle p(z_{\mathrm{opl}}(z_0))={\tan }^{-1}\left(\begin{array}{c}\mathrm{\Gamma }(0)\mathrm{\Delta }\left(1-\frac{{\mathrm{\Delta }}^2}{3!}+\frac{{\mathrm{\Delta }}^4}{5!}\right)+\\ \frac{\gamma (0)\left(\frac{3\mathrm{\Delta }}{3!}-\frac{10{\mathrm{\Delta }}^3}{5!}\right)+10{\gamma }^2(0)\frac{\mathrm{\Delta }}{5!}+\mathrm{H}.\mathrm{O}.\mathrm{T}}{\mathrm{\Gamma }(0)\left(1-\frac{{\mathrm{\Delta }}^2}{2!}+\frac{{\mathrm{\Delta }}^4}{4!}\right)}\\ +\gamma (0)\left(\frac{1}{2!}-\frac{6{\mathrm{\Delta }}^2}{4!}\right)+\frac{{\gamma }^2(0)}{4!}+\mathrm{H}.\mathrm{O}.\mathrm{T}\end{array}\right),$$ (D19)

where Δ^ℓ = (2πK_cδz_opl(z₀))^ℓ, ℓ ∈ ℤ⁺; and γ^ℓ(0) = Γ^(2ℓ)(0)(δz_opl(z₀))^2ℓ, ℓ ∈ ℤ⁺. Again, the abbreviation H.O.T. stands for “higher-order terms” with respect to γ(0).