Shear Brillouin light scattering microscope

Abstract

Brillouin spectroscopy has been used to characterize shear acoustic phonons in materials. However, conventional instruments had slow acquisition times over 10 min per 1 mW of input optical power, and they required two objective lenses to form a 90° scattering geometry necessary for polarization coupling by shear phonons. Here, we demonstrate a confocal Brillouin microscope capable of detecting both shear and longitudinal phonons with improved speeds and with a single objective lens. Brillouin scattering spectra were measured from polycarbonate, fused quartz, and borosilicate in 1-10 s at an optical power level of 10 mW. The elastic constants, phonon mean free path and the ratio of the Pockels coefficients were determined at microscopic resolution.

1. Introduction

Brillouin scattering spectroscopy is a useful technique for noncontact and nondestructive measurements in material sciences [1–4], mineralogy [5,6] and biology [7]. The acoustic and thermodynamic properties of a material can be determined from the spectrum of Brillouin light scattering resulting from the phase-matched interaction of an incident light and the acoustic phonons in the sample [8–10]. The complete stiffness tensor of a material can be characterized by measuring Brillouin scattering from both longitudinal and shear phonons along the principal axis of symmetry of a material [11]. The technique has been used to characterize various polymers and optical glass [12–15].

In previous studies, multi-pass Fabry-Perot interferometers [16], optical beating instruments [17], or scanning-grating monochromators [18] are employed due to their high spectral resolution and extinction ratio. However, a single spectral analysis of shear Brillouin light scattering typically requires more than a few minutes due to the slow data acquisition speeds of these instruments. Faster acquisition of a few seconds was demonstrated by the use of angle-dispersive Fabry-Perot interferometry at an optical power of 100-200 mW in quartz [19–21]. However, this approach achieves the data acquisition speed only at the expense of the spectral resolution, as the throughput efficiency is inversely proportional to the Finesse (F).

We have previously demonstrated a non-scanning Brillouin spectrometer using virtually-imaged phased array (VIPA) etalons [9,22,23]. The ability to acquire all spectral components simultaneous with minimal incident loss owing to the special coating of VIPA tremendously increased data acquisition speed without the loss of spectral resolution. This innovation has enabled measurement of the age-related stiffening in the crystalline lens [24], in situ and in vivo mapping of the longitudinal modulus of the human cornea [25,26]. However, the instruments based on this parallel spectrometer have so far been configured to collect near 180° back scattering. With the back scattering measurement, the magnitude of Brillouin scattering from shear phonons in isotropic materials vanishes. Therefore, the previous Brillouin microscopes are suited only for the measurements of longitudinal phonons.

Here, we describe an off-axis confocal microscope that is capable of measuring both longitudinal and shear Brillouin scattering and offers high acquisition speed by employing a two-stage VIPA spectrometer. The off-axis beam geometry allows a single objective lens with high numerical aperture (NA) to be used for both illumination and collection. In comparison with traditional approaches using two lenses to achieve a 90° scattering angle between the input and scattered beams, our approach offers a more simple and convenient approach that is well-suited for high-resolution microscopy. The polarization state of the scattered light from shear phonons is orthogonal to the input polarization state where as the longitudinal Brillouin scattering maintains the polarization state. Therefore, polarization-based filtering allowed us to discriminate shear and longitudinal Brillouin signals. We achieved a reduction in data acquisition time by more than an order-of-magnitude compared to previous measurement of shear phonons using scanning Fabry-Perot interferometers.

2. Theoretical background

Spontaneous Brillouin scattering is a process in which light is inelastically scattered via phase-matched interaction with acoustic phonons: either by receiving energy from thermally activated acoustic waves (Stokes) or by giving energy to acoustic waves (anti-Stokes). The acoustic waves (phonons) in a medium cause local fluctuations of density and pressure, and the resulting spatial variation of refractive index causes light scattering. Because such waves are not static but propagate inside the material, the scattered light also experiences a frequency shift ${\Omega }_B$ given by

$${\Omega }_B=\frac{2nv}{\lambda }\sin (\frac{\theta }{2})$$ (1)

where n is the refractive index of the medium, v is the velocity of the acoustic wave, λ is the wavelength, and θ is the angle between the incident and scattered beams. The Brillouin shifts are in the order of a few GHz for visible light in backward (θ = 180°) or right-angle (θ = 90°) scattering.

The acoustic velocity can be related to the mechanical properties of the material. The mechanical properties of the material are generally described by a stiffness tensor, C_ijkl commonly written as a 6 × 6 matrix C_mn. In the case of isotropic materials, the stiffness tensor reduces to two independent components: longitudinal modulus M = c₁₁ and shear modulus G = c₄₄. Similarly, the acoustic modes of isotropic solids are either longitudinal (velocity v_L) or shear (velocity v_S). The acoustic velocities and elastic constants are related by:

$$\rho v_L^2=M, \rho v_S^2=G.$$ (2)

where $\rho$ is the density. Therefore, the Brillouin spectrum of a homogeneous isotropic material has two peaks corresponding to the longitudinal and shear phonons, respectively.

The magnitude of shear Brillouin scattering in isotropic materials is zero in back-scattering angle of θ = 180°. To observe shear Brillouin peaks, an appropriate scattering angle, θ ≠180° is required.

For 90° scattering, the differential scattering cross section [27] is expressed as:

$${\frac{d\sigma }{d\Omega }|}_{VV}=\left(\frac{k_{B}T{\pi }^2{\epsilon }^4{V}_s}{2{\lambda }^4\rho }\right)\frac{p_{12}^2}{v_L^2}$$ (3)

for the longitudinal acoustic phonons, and

$${\frac{d\sigma }{d\Omega }|}_{VH}=\left(\frac{k_{B}T{\pi }^2{\epsilon }^4{V}_s}{2{\lambda }^4\rho }\right)\frac{p_{44}^2}{2v_S^2}$$ (4)

for the shear phonons, where $k_B$ is Boltzmann’s constant, T is the absolute temperature, $\in$ is the dielectric permittivity, V_s is the scattering volume, and p_ij are the Pockels elasto-optic coefficients. Here, the subscript VV indicates that the polarization states of the input and scattered waves are both vertical to the scattering plane (i.e. s-pol), and VH indicates that the polarization state of the scattered wave is horizontal (p-pol)—orthogonal to the input polarization. From (3) and (4), the magnitude ratio of shear and longitudinal Brillouin scattering is given by

$$\frac{I_S}{I_L}={\left(\frac{v_S}{v_L}\right)}^2{\left(\frac{p_{44}}{p_{12}}\right)}^2$$ (5)

The ratio of the Pockels coefficients, (p₄₄/p₁₂)², ranges from 0.01 in solid materials with high mechanical strength to 0 in liquids. Since (p₄₄/p₁₂)² <<1, the magnitude of Brillouin scattering from the shear phonons is typically much weaker than that from the longitudinal phonons.

3. Instrumentation

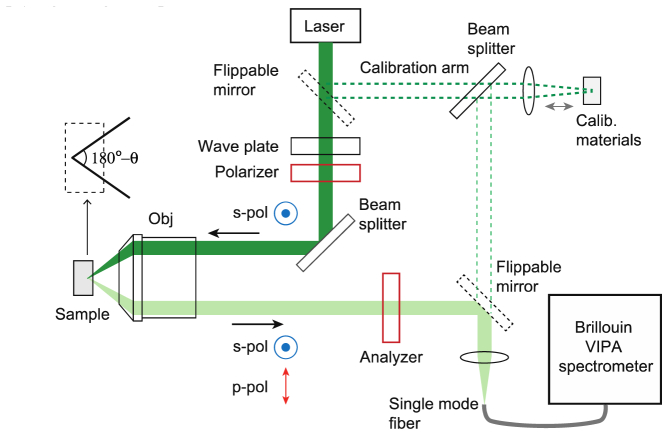
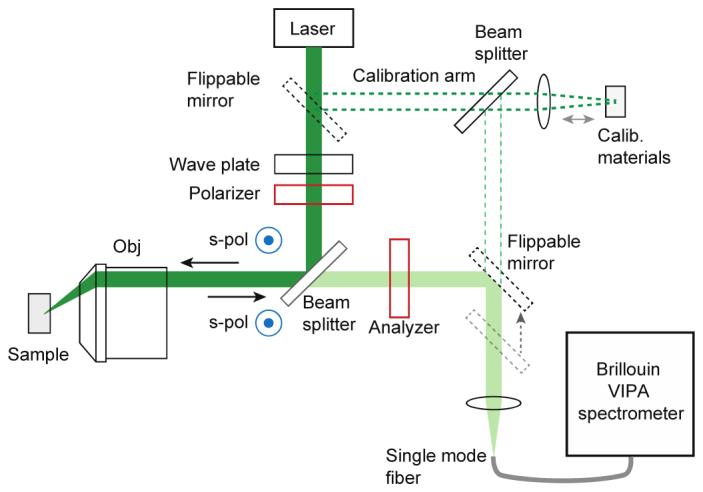
A schematic of the Brillouin confocal microscope is shown in Fig. 1. A single-frequency frequency-doubled Nd:YAG laser at 532 nm (Torus, Laser Quantum) was used as a light source. Laser light passing through a waveplate and a polarizer was partially reflected by a beam splitter. At the objective lens (OLYMPUS, UPlanSApo, 60XW/1.2NA), the probe beam was off-centered by 3 mm and was focused to the sample. The laser power at the sample plane was about 10 mW. In order to maximize the detection efficiency of shear phonons, the microscope objective was underfilled and only part of the scattered light within a narrow solid angle centered at θ≈107° (See Section A1) was collected and coupled into a single-mode optical fiber. The effective NA of the illumination was 0.27, computed from the input beam size of 1.7 mm and the 7.6 mm back-aperture size of the objective lens. The effective collection NA was 0.28, calculated from the numerical aperture (NA = 0.1) of the fiber and the focal length (18 mm) of the fiber-coupling lens (OLYMPUS, UPlanFL, 20X, 0.5NA). The light coupling in the single mode fiber was delivered to a two-stage VIPA spectrometer [23]. The spectrally dispersed beam after two VIPA etalons were imaged on an electron-multiplying charge-coupled-device (CCD) camera (Andor, iXon 897).

Fig. 1.

Schematic of the off-axis Brillouin confocal microscope. Flip-mirrors are used to choose from the sample arm or calibration arm. Obj: objective lens (UPLSAPO, 60XW, 1.2 NA).

Utilizing a single objective lens is practically advantageous, however, light loss can be increased at high angles because of the limited NA of the objective lens. In order to verify that the collection efficiency of the off-axis confocal microscope was optimized, we compared the signal strength of quasi right-angle Brillouin scattering with that of 180° (back-scattered) Brillouin scattering (See Section A1.). The signal strength at the quasi right-angle configuration was 8.6 ± 0.6% of that in the back-scattering configuration. This agrees with the theoretically predicted factor of 12.1% (See Section A2.). The small discrepancy is likely due to the aberration and diffraction of the beam clipped at the aperture of the objective lens.

To measure the spatial resolution, we recorded the Brillouin scattering while moving the position of a cover glass, laterally and axially and analyzed edge response functions. The spatial resolution of the microscope was 1.2 µm × 1.2 µm × 1.2 µm. In addition, we measured the spatial resolution using another objective lens (Leica PLAPO 100XO, 1.4 NA) to enlarge the NA and reduce aberrations. In this case, the resolution was 0.8 µm × 0.8 µm × 0.8 µm.

The polarization of the incident wave was perpendicular to the scattering plane (TE mode, s-pol, or Vertical polarization). Longitudinal and shear Brillouin scattering can be selectively observed by choosing the appropriate polarization of detection using a polarizer (analyzer) in the collection path. When the horizontal (vertical) polarization was selected, scattering from shear (longitudinal) phonons was analyzed.

The setup also has a flip-mirror that directed the laser beam to a calibration arm for frequency calibration. A polystyrene cuvette containing water was used as standard. The Brillouin frequency shifts of polystyrene and water are known to be 14.2 GHz and 7.46 GHz, respectively, at 18 °C. An objective lens (OLYMPUS, PlanN, 4X, 0.1NA) was used to focus the laser beam at the interface between the water and the polystyrene cuvette and collects the back-scattered light from both materials. At this interfacial layer, the spectrogram showed four distinct peaks corresponding to two Brillouin peaks (Stokes and anti-Stokes scattering) from water (a pair of inner peaks) and polystyrene (a pair of outer peaks) (Fig. 2). The free-spectral range (FSR) and spectral dispersion (SD) which is a conversion ratio from frequency to pixel were determined from the following formulas:

$$SD=\frac{{\Omega }_{PS-S}-{\Omega }_{W-S}}{2\left|P_{PS-S}-P_{W-S}\right|}+\frac{{\Omega }_{PS-AS}-{\Omega }_{W-AS}}{2\left|P_{PS-AS}-P_{W-AS}\right|}$$ (6)

$$FSR=\left|P_{PS-S}+P_{PS-AS}\right|\times SD$$ (7)

where P_PS-S, P_PS-AS, P_W-S, P_W-AS are the measured pixel position of Brillouin peaks in the spectrum profile, and ${\Omega }_{PS-S}$ = 14.2 GHz and ${\Omega }_{W-S}$ = 7.46 GHz.

Fig. 2.

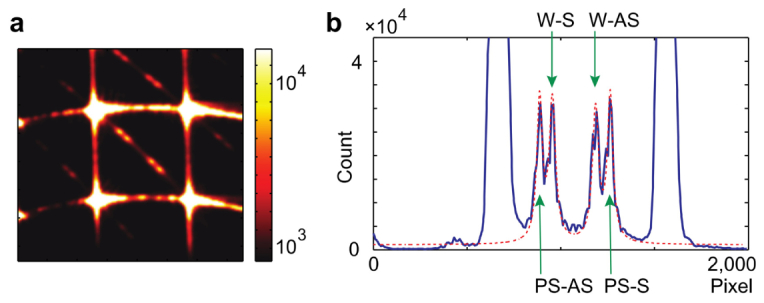
Water-Polystyrene optical spectra acquired with the two-stage VIPA spectrometer. (a) Spectrogram of two calibration materials (water and polystyrene cuvette). Color bar, number of photons. (b) 1-D plot of the Brillouin spectrum. Blue line: measured data, red dotted line: Lorentzian curve fit to the measured data.

4. Results

4.1 Brillouin scattering in polycarbonate

Amorphous polycarbonate (Lexan) is a polymer material widely used for engineering applications because of its high mechanical strength. Its shear modulus at hypersonic frequency has been previously measured by Brillouin spectroscopy and is in the range of 1 GPa at room temperature [28,29]. The transverse and longitudinal Brillouin scattering spectrum measured by our instrument are reported in Fig. 3. From these spectra, the Brillouin shift for the longitudinal and shear phonons is calculated by:

$${\Omega }_{PC-S}=\frac{FSR}{2}\pm \frac{\left|P_{PC-S}-P_{PC-AS}\right|}{2}\times SD$$ (8)

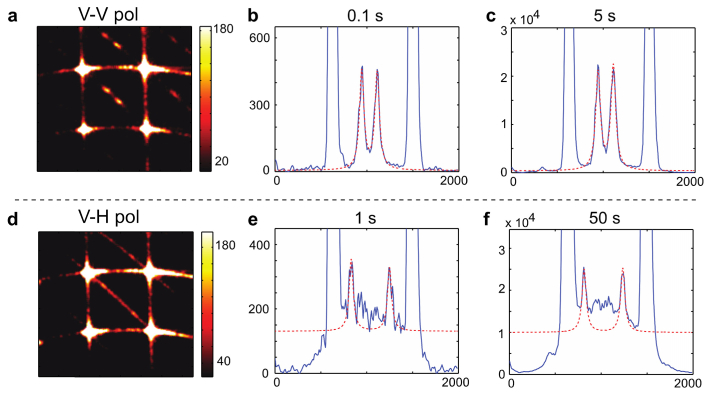
where the positive (negative) sign in ± is applied to longitudinal and shear phonons in polycarbonate when the magnitude of the Stoke and anti-Stoke shifts is larger (smaller) than the half of the FSR. For longitudinal Brillouin scattering, we used the positive sign because the Stokes peak appears on the right side of the anti-Stokes peak, whereas the negative sign applies to Shear Brillouin scattering. The spectrometer clearly resolved both peaks of the longitudinal and shear components (Figs. 3(a) and (d)) at an integration time of 0.1 s and 1 s, respectively. The frequency shifts were 11.67 ± 0.03 GHz for longitudinal phonons (Fig. 3(b)), and 5.16 ± 0.07 GHz for shear phonons (Fig. 3(e)).

Fig. 3.

Brillouin spectra of polycarbonate for VV input-output polarization (a-c) and VH polarization (d-f). (a), (d): Spectrograms at 0.1 s and at 1 s, respectively. Color bar, number of photons (counts) (b), (c) 1-D plot of the spectra at 0.1 s and at 5 s, respectively. The measured Brillouin frequency shifts and linewidths are 11.68 ± 0.03 GHz and 0.36 GHz. (e), (f) 1-D plot of the spectra at 1 s and at 50 s, respectively. The measured Brillouin frequency shifts and linewidths are 5.16 ± 0.07 GHz and 0.68 GHz. (Blue line: measured data. Sampling points are interpolated by ten times. Red dotted line: Lorentzian curve fit to the measured data, x axis: pixel index, y axis: number of photons (counts) in (b), (c), (e) and (f)).

The measured linewidths directly from the full-width at half-maximum (FWHM) of the raw data were 1.50 GHz for the longitudinal phonons and 1.29 GHz for the shear phonons. The Brillouin linewidths were broadened by both the finite resolution of the instrument and the linear phonon dispersion due to the collecting angle. To correct these factors, the dispersion broadening was subtracted after the instrumental linewidth of 0.4 GHz was removed by deconvolution [30]. The corrected linewidths were 0.36 GHz for the longitudinal phonons and 0.68 GHz for the shear phonons. All the measured linewidths referred hereinafter are broadening-corrected values. The magnitude of signal increased linearly with the data integration time and, therefore, the signal to noise ratio (SNR) (Fig. 3(c) and (f)). Nonetheless, the integration time of 1 s was sufficient to analyze both longitudinal and shear Brillouin spectral shifts and linewidth with reasonable accuracy.

4.2 Brillouin scattering in fused quartz and borosilicate glass

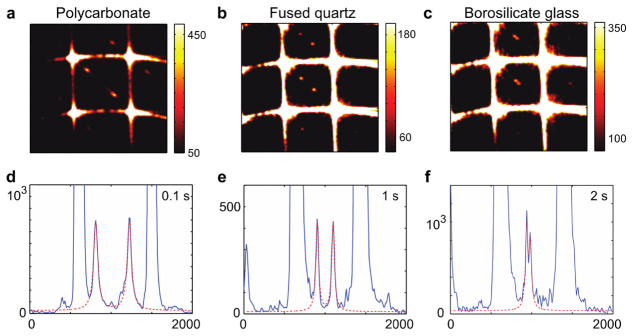
Elastic properties of optical glasses have been investigated in several studies [12–15]. We measured Brillouin scattering in fused quartz (Fig. 4) and Pyrex borosilicate glass (Fig. 5). Figures 4(a) and 4(c) display the spectrograms from longitudinal and shear phonons measured at an integration time of 1 s and 10 s, respectively. Longer exposure times were required to compensate for the lower scattering magnitudes in both fused quartz and borosilicate glass in comparison to polycarbonate. Under these conditions, both peaks of the longitudinal and shear components were clearly resolved.

Fig. 4.

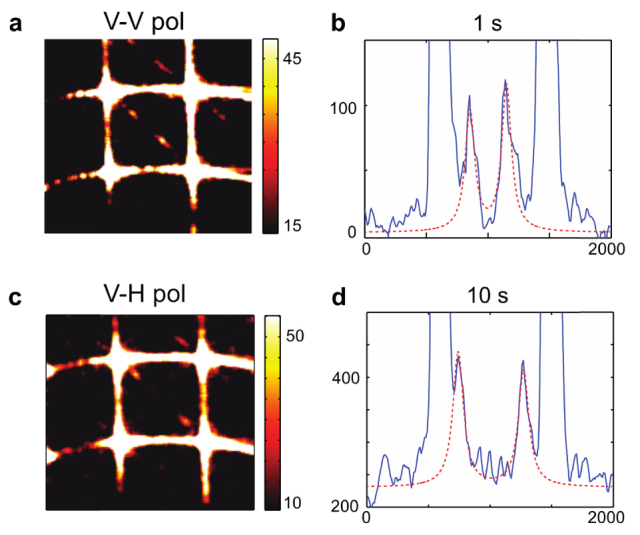
Brillouin spectra of fused quartz for VV (a-b) and VH (c-d). (a), (c): Spectrograms at 1 s and at 10 s, respectively. Color bar, number of photons (counts) (b): 1-D plot of the spectra of (a). The measured Brillouin frequency shifts and linewidths are 26.03 ± 0.15 GHz and 0.18 GHz. (d): 1-D plot of the spectra of (c). The measured Brillouin frequency shifts and linewidths are 15.9 ± 0.11 GHz and 0.57 GHz.

Fig. 5.

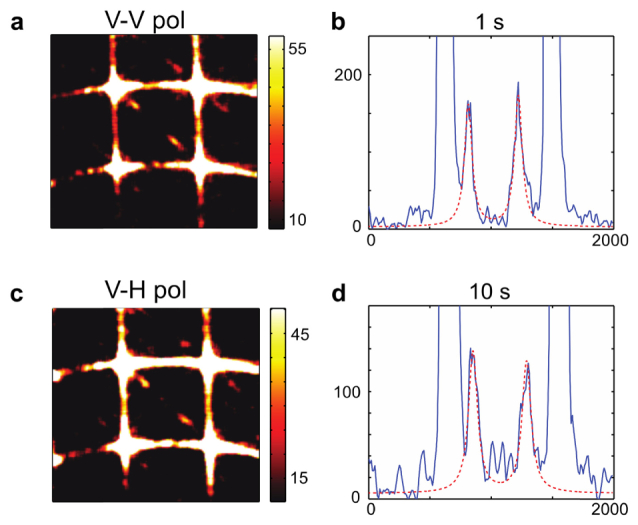
Brillouin spectra of borosilicate glass for VV (a-b), and VH (c-(d). (a), (c): Spectrograms at 1 s and at 10 s, respectively. Color bar, number of photons (counts) (b): 1-D plot of the spectra of (a). The measured Brillouin frequency shifts and linewidths are 24.47 ± 0.11 GHz and 0.11 GHz. (d): 1-D plot of the spectra of (c). The measured Brillouin frequency shifts and linewidths are 14.73 ± 0.13 GHz and 0.68 GHz.

4.3 Summary of the measured data

From the measured Brillouin spectral shifts, we determined the hypersonic velocities (Table 1 ) using Eq. (1) and the elastic constants (Table 2 ) from Eq. (2). From the linewidth $\delta v$, the attenuation coefficients, $\alpha =\pi \delta v/\upsilon$, and the phonon mean free path, l = 1/(2α), were calculated (Table 1).

Table 1. The measured Brillouin frequency shifts, hypersonic velocities, linewidths (FWHM), attenuation coefficient, phonon mean free paths, and intensity at longitudinal and shear phonons. The intensity means the number of photons in FWHM of one Brillouin peak.

	Polarization	Brillouin Shift (GHz)	Hypersonic Velocity (km/s)	Linewidth (GHz)	Attenuation (μm−1)	Phonon Mean Free Path (μm)	Intensity (photons/s)
Polycarbonate	VV	11.68	2.43	0.36	0.47	1.07	2.2 × 104
	VH	5.16	1.08	0.68	1.97	0.25	1.2 × 103
Fused Quartz	VV	26.03	5.91	0.18	0.10	5.24	7.1 × 102
	VH	15.90	3.63	0.57	0.49	1.01	1.4 × 102
Borosilicate Glass	VV	24.47	5.50	0.11	0.06	7.96	1.1 × 103
	VH	14.73	3.32	0.68	0.65	0.77	1.0 × 102

Table 2. The elastic constants and the ratio of Pockels coefficients. E: Young’s modulus, G: Shear modulus, K: Bulk modulus, M: Longitudinal modulus, ν: Poisson’s ratio. Unit (GPa).

	E	G	K	M	ν	(p44/p12) 2
Polycarbonate	3.83	1.39	5.26	7.12	0.38	1.09 × 10−2
Fused Quartz	69.47	29.03	38.14	76.85	0.20	7.26 × 10−2
Borosilicate Glass	59.60	24.53	34.84	67.54	0.21	3.43 × 10−2

The measured hypersonic velocities in polycarbonate were 2.43 km/s and 1.08 km/s for longitudinal and shear phonons, respectively. The signal strengths of the Brillouin peak were 2.2 × 10⁴ photons/s for the longitudinal phonons and 1.2 × 10³ photons/s for the shear phonons. From the measured intensity ratio and Eq. (5), we determined (p₄₄/p₁₂)² = 0.01. This agrees well with the previously reported value of 0.01 [28]. For fused quartz, we measured (p₄₄/p₁₂)² = 0.0726, which is in excellent agreement with the known value of 0.0729 [28]. This value is one of the highest among all known materials. The measured Brillouin linewidths were 0.18 GHz and 0.57 GHz for longitudinal and shear phonons, respectively. The linewidth of the longitudinal phonons in the fused quartz is known to vary from 0.05 GHz to 0.3 GHz at the room temperature [14,30–32]. Table 2 summarizes the measured ratio of Pockels coefficients.

5. Conclusion

The Brillouin off-axis confocal microscope enabled us to measure both the longitudinal and shear acoustic phonons with a high spatial resolution of 0.8-1.2 µm. The Brillouin spectra of polycarbonate, fused quartz, and borosilicate glass were recorded with an acquisition time of 1-10 s at an input power of 10 mW. This measurement speed represents at least an order of magnitude improvement over previous Brillouin spectroscopy based on two objective lenses and scanning interferometers. The en face Brillouin microscope demonstrated here may be useful for non-destructive, non-invasive microscopic measurement of mechanical properties in various materials with anisotropic mechanical properties or micro-structured heterogeneous materials.

Appendix.

A1. Measurement at backscattering configuration

In order to verify the collection efficiency of the off-axis confocal microscope, we modified the setup into the back-scattering configuration as depicted in Fig. 6

Fig. 6.

Schematic of the confocal microscope reconfigured for back-scattering measurement. The flippable mirror in front of the single mode fiber is shifted 6mm along the direction of the arrow to change the beam path. Note that this configuration allows only the longitudinal phonons to be characterized.

. The instrument is transformed from the off-axis angle configuration, as shown in Fig. 1, to a backscattering configuration by shifting the flip mirror in front of the single mode fiber (Fig. 6).

The spectrometer outputs of polycarbonate, fused quartz and borosilicate glass revealed longitudinal Brillouin frequency shifts of 14.55, 32.37, 30.56 GHz, respectively (Fig. 7

Fig. 7.

Optical spectra acquired with two-stage VIPA spectrometer. (a), (b), (c): Spectrograms of polycarbonate (0.1 s), fused quartz (1 s), borosilicate glass (2 s) for VV scattering, respectively. Color bar, number of photons (counts) (d), (e), (f): 1-D plot of the spectra of (a), (b), and (c), respectively experimental data (blue line); The curve fit based on Lorentzian functions (red dotted line); The measured Brillouin frequency shifts and linewidths are 14.55 GHz and 0.61 GHz for (d), 32.37 GHz and 0.18 GHz for (e), 30.56 GHz and 0.12 GHz for (f). (x axis: pixel index, y axis: number of photons (counts) in (d), (e) and (f)).

). The shear Brillouin peaks were not observed as theoretically expected. Comparing the Brillouin shifts at θ=180° and those measured in the quasi right-angle configuration allowed us to determine the scattering angle to be 107°, more precisely than geometrical estimations.

A2. Comparison of the scattered-light collection depending on the beam geometry

We derived the theoretical prediction of comparing the detected light intensity at right-angle scattering configuration (Fig. 1) to that at back-scattering configuration (Fig. 6). The detected energy of the scattered wave from the volume V at the intensity of the incident wave I_ill is described as

$$E={\displaystyle \iiint I_{ill}}N{A}_s^2{f}_{c}dV$$ (9)

where NA_s is the NA of the scattered light, f_c is cut-off function determined by coupling fraction into the optical fiber. The detected energy from the backscattering can be described by the weighted integral of disk-shape overlap volume between illumination beam and collection beam, which has the radius $r_s(z)=0.61\lambda /N{A}_s(z)$and thickness dz at depth $z=n\lambda /2N{A}_s^2(z)$, generating the single-mode beam through the objective lens and is expressed as

$$\begin{array}{l}{E}_B={\displaystyle {\int }_{-zo}^{zo}{P}_{0}N{A}_c^2}dz+2{\displaystyle {\int }_{zo}^{\infty }\frac{P_0}{\pi r_o^2(z)}\pi r_s^2(z)N{A}_s^2(z)\frac{N{A}_s^2(z)}{N{A}_c^2}dz}\\ =n{P}_0\lambda +\frac{{1.22}^2}{2n}{P}_0\lambda \end{array}$$ (10)

where P₀ is the power of the illumination beam, r_o(z) is the radius of the illumination beam, $f_c(z)=N{A}_c^2/N{A}_s^2(z) (for z<zo), N{A}_s^2(z)/N{A}_c^2 (for z>zo)$.

On the other hand, for the case of right-angle scattering the overlap volume of the illumination and collection beam can be approximated into a sphere of the radius $r_o=0.61\lambda /N{A}_c$. Then, the detected energy from the right-angle scattering becomes

$$E_R=\frac{4}{3}\times 0.61P_0\lambda N{A}_c$$ (11)

For the comparison, the ratio γ of the detected energy between right-angle scattering E_R and back-scattering E_B is

$$\gamma =\frac{0.81N{A}_c}{(n+0.74/n)}$$ (12)

The theoretically expected detection ratio γ between right-angle scattering and backscattering is 12.1% for NA_c = 0.28, and n = 1.33 (refractive index of water). Ideally, if NA_c is increased, the collection intensity at right-angle scattering can be increased. However, NA_c is optimized at 0.28 in our experimental setup since the NA of the objective lens is limited. In the case of the conventional right-angle configuration using two objective lenses arranged at orthogonal directions, NA_c can be increased by using long working distance objective lenses.