Neural Mechanisms of Post-error Adjustments of Decision Policy in Parietal Cortex

SUMMARY

Humans often slow down after mistakes (post-error slowing, PES), but the neural mechanism and adaptive role of PES remains controversial. We studied changes in the neural mechanisms of decision-making after errors in humans and monkeys that performed a motion-direction discrimination task. We found that PES is mediated by two factors: a reduction in sensitivity to sensory information and an increase in the decision bound. Both effects are implemented through dynamic changes in the decision-making process. Neuronal responses in the monkey lateral intraparietal area (LIP) revealed that bound changes are implemented by decreasing an evidence-independent urgency signal. They also revealed a reduction in the rate of evidence accumulation, reflecting reduced sensitivity. These changes in the bound and sensitivity provide a quantitative account of choices and response times. We suggest that PES reflects an adaptive increase of decision bound in anticipation of maladaptive reductions in sensitivity to incoming evidence.

INTRODUCTION

The ability to change strategies when our actions fail to produce desired outcomes is fundamental to flexible behavior and survival in a complex, varying environment. Following errors, humans often slow down to respond on subsequent decisions, a phenomenon known as post-error slowing (Rabbitt and Rodgers, 1977). PES is a prime example of flexible changes in decision-making and is widely assumed to play an adaptive role by preventing future errors (Botvinick et al., 2001; Dutilh et al., 2013; Goldfarb et al., 2012; Holroyd et al., 2005; Laming, 1979). However, the increased response times (RTs) in PES are rarely accompanied with tangible improvements in accuracy, suggesting the phenomenon is more complex than a simple change in decision criterion (Danielmeier and Ullsperger, 2011; Gehring et al., 1993; Notebaert et al., 2009; Schroder and Moser, 2014). Understanding the mechanisms of PES and its role in adaptive decision-making requires a systematic and quantitative study of the behavior and neural mechanisms involved in the decision-making process.

Previous investigations into the neural mechanisms of PES have focused almost exclusively on one aspect of this process: error detection and performance monitoring by medial frontal cortex (Schall et al., 2002). Error-related signals from medial frontal cortex correlate with slowing on the next trial (Gehring et al., 1993), and inactivation or lesions of medial frontal cortex can reduce or eliminate PES (di Pellegrino et al., 2007; Narayanan et al., 2013). However, far less is known about how the detection of errors in medial frontal regions impacts future decision-making processes. Neuroimaging studies have revealed a diversity of changes in BOLD responses across cortex following errors (Danielmeier and Ullsperger, 2011; King et al., 2010), but the limited spatial and temporal resolution of these techniques precludes model-based hypothesis testing for changes in the neural mechanisms of decision-making at the level of single neurons.

Intra-cortical recordings in non-human primates have excellent temporal and spatial resolution and, thus far, have revealed a network of posterior parietal, lateral prefrontal, and subcortical brain areas that work in concert to form decisions by integration of sensory information over time toward a criterion level (decision bound) (Hanes and Schall, 1996; Kiani et al., 2014b; Ratcliff et al., 2003; Roitman and Shadlen, 2002). Medial frontal cortex sends projections to several areas in this network (Huerta and Kaas, 1990), but does not directly represent the evidence accumulation process (Purcell et al., 2012; Stuphorn et al., 2010). Recent studies have demonstrated that integration of sensory evidence in this network is influenced by the behavioral state of the animal to adjust decision speed and accuracy (Hanks et al., 2014; Heitz and Schall, 2012), but it is unclear whether similar mechanisms extend to PES. Particularly, no previous study has quantified changes of neural responses following perceptual errors in these areas.

We measured PES in humans and monkeys trained to perform a motion direction discrimination task, establishing a non-human primate model for studying neural mechanisms of PES. By using quantitative models of the decision-making process we hypothesized that PES in both species arises from a mixture of two effects: an increase in the decision bound and a decrease in the signal-to-noise ratio (SNR) of incoming sensory evidence. Together, these effects explain why PES may or may not be accompanied by changes in accuracy. We tested this hypothesis by recording from responses of single neurons in the lateral intraparietal area (LIP) of monkeys performing the task. Consistent with our model predictions, neural responses in LIP revealed both decreased sensitivity and an increase in decision bound after errors. Neural responses also showed that both factors were implemented through changes in the dynamics of decision formation. Sensory and motor delays, sensory and accumulation noise, and static components of neural responses (start and end points) remained unchanged, ruling out competing hypotheses that could not be distinguished based solely on the behavior and computational models. These results indicate that changes of neural response dynamics after errors implement rapid adjustments of the decision policy by elongation of decision time in order to mitigate reduction of accuracy.

RESULTS

Humans and monkeys (Macaca mulatta) were trained to perform a reaction-time version of a motion direction discrimination task (Fig. 1A). On each trial the subject viewed a dynamic random dots stimulus (Britten et al., 1992) and, when ready, reported the perceived motion direction with a saccadic eye movement. We manipulated task difficulty by varying the percentage of coherently moving dots (motion strength) on a trial-by-trial basis (see Experimental Procedures).

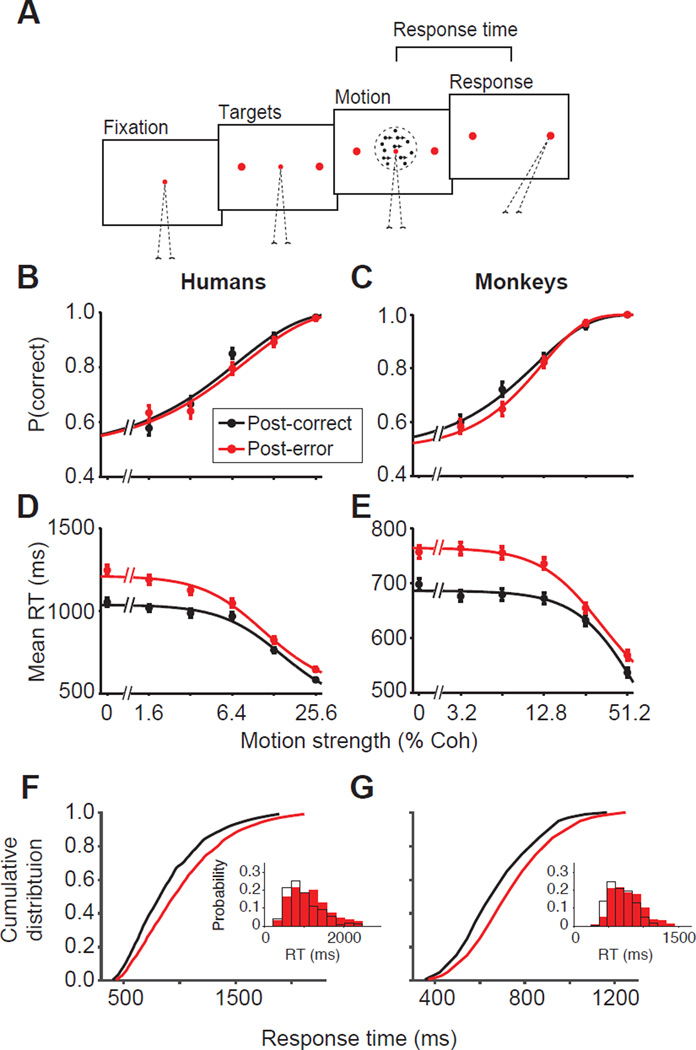
Figure 1. Post-error slowing in humans and monkeys during perceptual decision-making.

(A) Motion discrimination task. Subjects initiated a trial by fixating on a central point. The targets appeared after a short delay, followed by the random dot stimulus. When ready, subjects indicated the motion direction with a saccadic eye movement to a choice target. The motion strength (percentage of coherently moving dots, %Coh) varied randomly across trials.

(B–C) Psychometric functions did not show appreciable change following negative feedback. Mean proportion correct as a function of motion strength for post-correct (black) and post-error (red) trials for six humans (B) and two monkeys (C) who exhibited PES. Smooth curves are fits to a logistic function. Error bars are SEM. See Figs. 8, S2, and S5 for behavioral data from subjects that did not exhibit PES. (D–E) Response times (RTs) are longer following errors. Smooth curves are fits to a hyperbolic tangent function.

(F–G) RT distributions show heavier upper tails following errors. Cumulative RT distributions for post-correct (black) and post-error (red) trials averaged across motion strengths demonstrate greater slowing for long RTs compared to short RTs. Insets show the RT probability density for an example motion strength (3.2% coherence) following correct (black open bars) and error (red solid bars) trials. Similar changes were evident for other motion strengths.

All subjects exhibited improved accuracy for stronger motion (Table S1; Fig. 1B–C; Eq. 1, Humans, β₁ = 20.85 ± 1.01, p < 10⁻¹⁰; Monkeys, β₁ = 11.91 ± 0.46, p < 10⁻¹⁰), compatible with previous studies (Roitman and Shadlen, 2002). Also as expected, RTs decreased sharply for stronger motion (Table S1; Fig. 1D–E; Eq. 2, Humans β₁ = −2,005 ± 104.56, p < 10⁻¹⁰; Monkeys β₁ = −267 ± 15.00, p < 10⁻¹⁰). All subjects were trained to a high level of performance as evidenced by their low psychophysical thresholds (range = 8.2% – 13.0% for monkeys; 4.6% – 9.9% for humans). On average, monkeys were faster than humans (mean RT = 604 ± 0.9 ms for monkeys; 915 ± 3.6 ms for humans), but humans had lower thresholds than monkeys. Therefore, we used a slightly more difficult stimulus set for humans to approximately match the error rates across species (mean percent correct = 77.2 ± 0.20 for monkeys; 74.8 ± 0.33 for humans).

Because the motion strength and direction were independent across trials, the optimal strategy was to make the decision solely based on the sensory information provided on each trial. Nonetheless, both humans and monkeys were influenced by the outcome of previous trials. The majority of subjects (73%, six humans and monkeys O and N) exhibited longer RTs on trials following error feedback (Table S1; mean human ΔRT = 117.0 ± 14.82 ms; Monkey O and N mean ΔRT= 59.5 ± 6.75 ms), compatible with past studies on PES. To maintain our focus, we will first report results from this majority group that exhibited clear PES. Later in this paper we will report results from the minority that responded differently to errors.

Quantitative hypotheses of PES

Electrophysiological recordings of neural responses from parietal cortex, frontal cortex, basal ganglia, and superior colliculus of monkeys engaged in perceptual decisions have shown that integration of noisy sensory evidence over time toward a decision bound underlies the choice and RT (Hanes and Schall, 1996; Kiani et al., 2014b; Ratcliff et al., 2003; Roitman and Shadlen, 2002). Many of the recorded neurons represent the integral of evidence in favor of the target in their response fields (RF). Further, their firing rates reach a common threshold shortly before a saccade toward RF. A simple process model that closely approximates these responses consists of accumulators that integrate noisy evidence toward a decision bound (Gold and Shadlen, 2007). The accumulator that reaches its bound first dictates the choice and the time to bound indicates the decision time. Variants of this “bounded accumulation” model have been shown to provide quantitative explanations of behavior across a large array of decisions (Bogacz et al., 2006; Busemeyer and Townsend, 1993; Link, 1992; Usher and McClelland, 2001). To study the mechanisms of PES quantitatively, we used a simple variant of this model, the drift-diffusion model (DDM), in which the two competing accumulators are replaced with a single accumulator with an upper and a lower bound that correspond to the two options (Gold and Shadlen, 2007; Link, 1992). We adopted the DDM because of its simplicity, but other variations of the bounded-accumulator framework will produce identical conclusions.

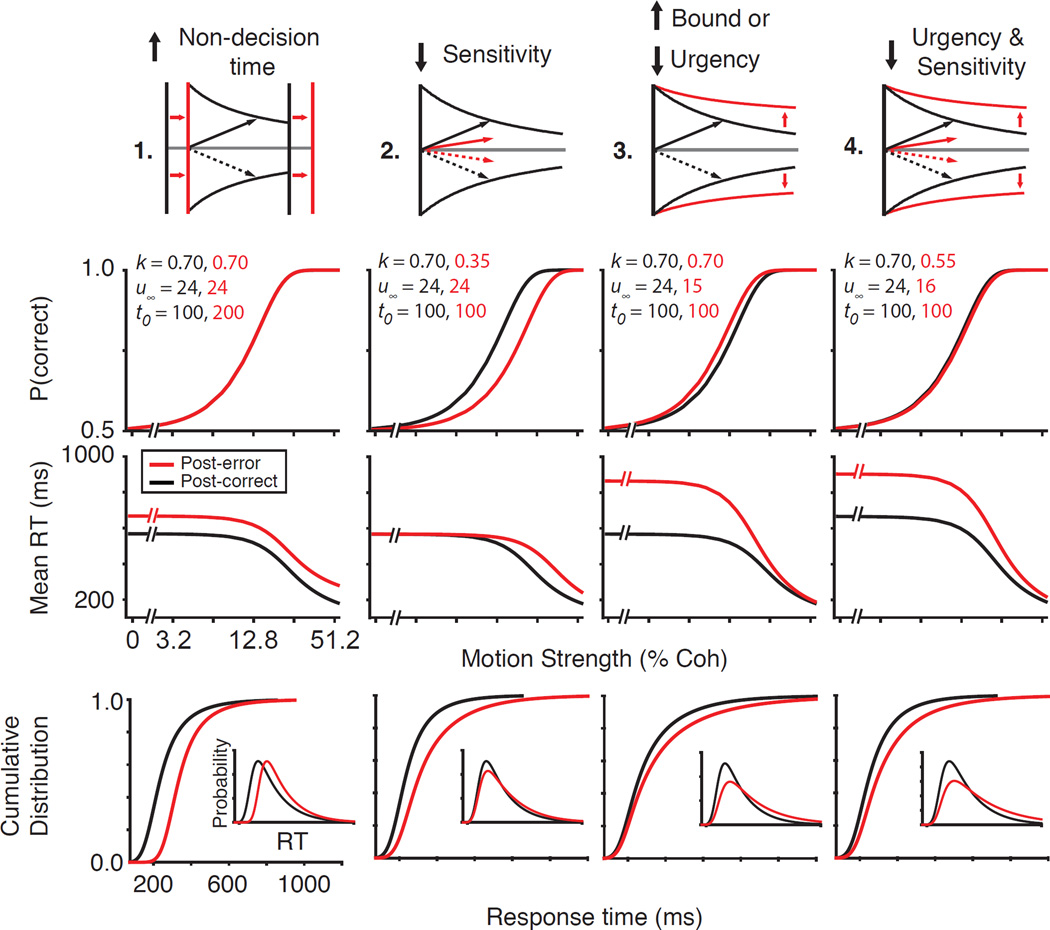
Our model offers a tool to formalize longstanding hypotheses about the neural mechanisms of PES (Fig. 2). A first hypothesis is that PES occurs because subjects postpone the onset of evidence accumulation in order to recover from the error (Laming, 1979; Pouget et al., 2011; Rabbitt and Rodgers, 1977). In the DDM, this would be captured by the non-decision time parameter that reflects the sum of sensory and motor delays. If PES arises from error-induced elongation of non-decision time, slowing would be equivalent at all motion strengths and the proportion correct would remain unchanged (Fig. 2; first column). Furthermore, the RT distributions should shift in time but maintain their shape for each motion strength.

Figure 2. Hypothesized mechanisms of PES and their behavioral predictions.

We used a drift-diffusion model to predict expected changes in post-error behavior under different hypotheses for the mechanism of PES. Each column shows one of these hypotheses, which can be distinguished based on changes in the psychometric and chronometric functions, and the shape of the RT distributions. The first row shows a schematic of these hypotheses. The second and third rows illustrate predictions for psychometric and chronometric functions, respectively. The final row shows predicted changes in cumulative RT distributions (insets show the probability density function for an example motion strength). The sensitivity (k), urgency (u_∞, Eq. 4), and non-decision time (t₀) parameters used for the model simulations are shown in row two. All other parameters were constant for post-correct and post-error conditions.

A second hypothesis is that PES arises from impairment of the subject’s sensitivity to incoming evidence following errors, perhaps because the negative feedback or unexpected outcome distracts and diverts attention (Notebaert et al., 2009) by influencing either sensory cortex (Treue and Martinez Trujillo, 1999) or transmission of information from sensory cortex to decision-making areas (Green et al., 2010). This hypothesis is plausible because accuracy rarely increases, and occasionally decreases following errors (Danielmeier and Ullsperger, 2011). In the DDM, this is captured by a sensitivity parameter that defines how the evidence that the decision maker extracts from the stimulus scales with stimulus strength (Gold and Shadlen, 2007). Lower sensitivity reduces available evidence per unit time and slows down evidence accumulation, causing longer RTs (Fig. 2; second column). The increased RTs, however, are also associated with reduced accuracy due to the reduced reliability of evidence (Fig. 2; second column). Moreover, slowing of RTs should be maximal for higher motion strengths because the rate of evidence accumulation (sensitivity × motion strength) is changed more for those stimuli. Finally, the RT distribution should be shifted and only modestly skewed for each motion strength.

A third hypothesis is that PES is caused by an adaptive increase in the decision bound, which increases the total evidence that must be accumulated before a choice is made. This hypothesis, which is favored by many leading models of executive control and adaptive behavior (Holroyd et al., 2005; Laming, 1979), predicts increased accuracy at the cost of longer RTs (Hanks et al., 2014; Heitz and Schall, 2012). Changes in bound height also predict larger effects on RT when the rate of evidence accumulation is low, causing maximal slowing at low motion strengths (Fig. 2; third column) and skewing the RT distribution of each motion strength by creating a heavier upper tail.

A change in decision bound could be implemented through different neural mechanisms. Two obvious possibilities include changes in the final firing rate or the initial firing rate of the neurons that represent evidence accumulation. A less obvious but computationally effective alternative is to adjust the total evidence needed to reach the bound through a dynamic stimulus-independent rise of the accumulators, referred to as urgency (Churchland et al., 2008; Standage et al., 2011; Thura et al., 2014). Because urgency equally increases the firing rates of neurons representing all potential choices, it reduces the total evidence that must be accumulated for committing to a choice, as if the bound had changed although the start- and end-points remain fixed. In the DDM, changes in the start and end points are represented by static shifts in bound heights but urgency is implemented with a dynamic collapse of the bounds (Hanks et al., 2014). Note that the DDM bound collapse in this paper is solely a mathematical shortcut to capture urgency in a simplified model that accumulates evidence along a single dimension. Also note that both static bound changes and changes in urgency make qualitatively similar predictions about accuracy and RTs in PES (Fig. 2; third column). In our initial modeling, we use a DDM with urgency, and later we will distinguish changes in urgency from static changes in start and end points through quantitative model comparisons and, more importantly, analyses of neural responses.

The aforementioned mechanisms are not mutually exclusive. In fact, it is likely that PES results from changes in multiple components of the decision-making process. For example, sensitivity may be reduced by unexpected negative feedback, and simultaneously the decision bound is raised to compensate. The model can disentangle these mixed effects into a combination of reduced urgency and sensitivity (Fig. 2; fourth column). The opposite effects of the two changes on accuracy could balance out, leading to little or no change in psychometric functions. However, the RT distributions develop a heavier tail and the mean RTs increase for all stimuli, especially on trials with lower motion strengths.

Post-error slowing is due to decreased urgency and sensitivity

To distinguish different PES mechanisms we characterized the post-correct and post-error performance of our subjects. Human and monkey behavior after errors exhibited common trends suggesting that PES in both species reflects a common set of neural mechanisms (Fig. 1). The increase in mean RT following errors was significantly larger for lower motion strengths, both for humans (Fig. 1D, Fig. S1, Table S1, Eq. 2, β₃ = −512.9 ± 144.06, p = 3.7 × 10⁻⁴) and monkeys (Fig. 1E; Eq. 2, β₃ = −94.4 ± 26.31, p = 3.4 × 10⁻⁴). Also, for each motion strength, post-error slowing was maximal for longer RTs, causing a heavier upper tail in the RT distribution (humans, Fig. 1F, Eq. 3, β₂ = 21.95 ± 2.92, p < 10⁻¹⁰; monkeys, Fig. 1G; Eq. 3, β₂ = 5.88 ± 1.31, p = 1.6 × 10⁻⁵). Finally, despite the RT changes, accuracy did not show an appreciable difference following errors, either for humans (Fig. 1B, Fig. S1, Table S1, Eq. 1, β₂ = −2.31 ± 1.37, p = 0.09) or for monkeys (Fig. 1C, Eq. 1, β₂ = −0.63 ± 0.99, p = 0.53). The pattern of RT changes together with the constancy of accuracy rules out isolated changes in sensory-motor delays, sensitivity, and bound height as the cause of PES. Rather, PES appears to be caused by a mixture of changes in the decision-making processes.

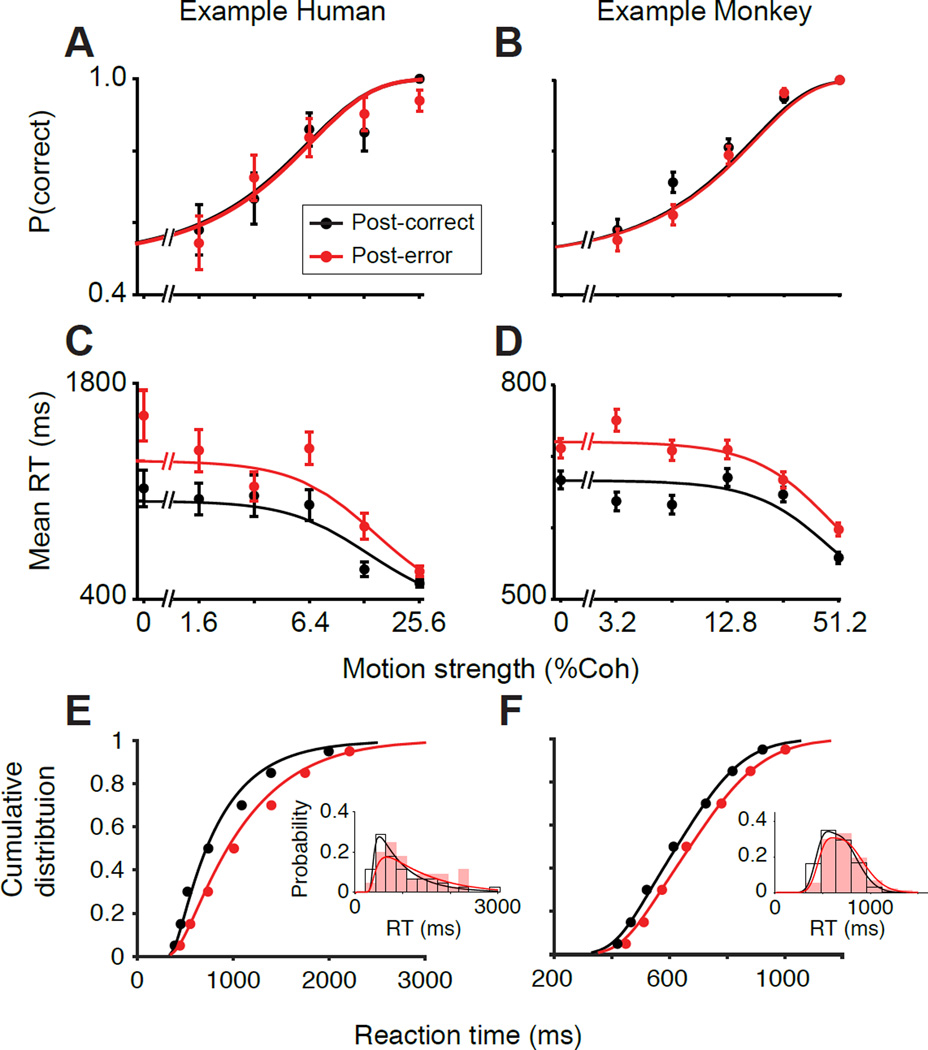
To pinpoint the mechanisms underlying PES, we fit a drift-diffusion model to the RT distributions of individual subjects following correct and error feedback (see Experimental Procedures). Figures 3 and S1 demonstrate that the model reproduces all key aspects of PES. The fits successfully accounted for the full RT distributions across all motion strengths (Fig. S1, third and fourth columns, R² values for the match between the model and data for individual subjects ranged from 0.86–0.98). They also captured the properties of PES, showing increased slowing at lower motion strengths (Fig. 3C–D; Fig. S1, first column) and also increased skewness (heavier tail) in RT distributions of each motion strength (Fig. 3E–F and Fig. S1, comparison of third and fourth columns).

Figure 3. The drift-diffusion model fit to RT distributions explains PES and predicts no change in accuracy.

Model fits and predictions for one representative human subject (left) and one representative monkey subject (right). See Figures S1 and S2 for detailed summary of model results for all subjects.

(A–B) Observed (solid points) and predicted (lines) proportion correct as a function of motion strength for a representative human (S6; first column) and monkey (O; second column). (C–D) Observed and expected mean RT as a function of motion strength. (E–F) Observed (solid points) and fitted (lines) cumulative RT distributions averaged across motion strengths. Insets show the corresponding observed (bars) and fitted (lines) RT probability density functions for an example motion strength (3.2% coherence). For both species, the model fits the heavier upper tail (greater slowing at larger RTs compared to short RTs), ruling out pure non-decision time changes (Fig. 2; column 1). Similar results were obtained for all motion strengths. Error bars are SEM.

The model can be independently verified by its ability to predict choices. Because we optimized the model parameters based solely on RTs and irrespective of choice, we could generate predictions about the probability of each choice. Those predictions accurately matched individual subjects’ choice probabilities (R² range: 0.81–0.98 for psychometric functions), in line with the experimental observation that accuracy is unchanged following errors although this was not forced by the model (Fig. 3A,B; Fig. S1, second column). This successful prediction supports that the model is a reliable approximation of the neural mechanisms that underlie choice and RT.

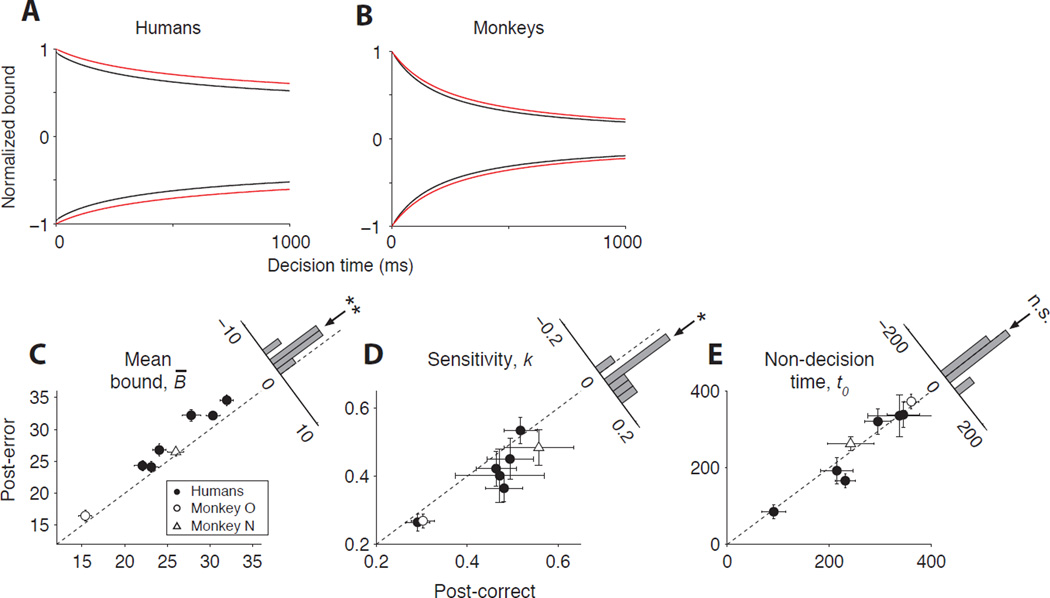
The best fitting model parameters offer strong predictions about the neural mechanisms of PES. Figure 4 illustrates those predictions by comparing the model parameters for post-error and post-correct trials (see Table S2 for all model parameters). First, urgency was reduced following errors for all humans (Fig. 4A) and monkeys (Fig. 4B) that exhibited PES. This reduction resulted in a significant elevation of the mean bound height (Fig. 4C, Eq. S2, β = 1.91 ± 0.402, p = 2.1 × 10⁻³). Second, the stimulus sensitivity decreased for both monkeys and humans (Fig. 4D, Eq. S2, β = −0.038 ± 0.013, p = 2.1 × 10⁻²). Third, there was no systematic tendency for increased non-decision time following errors (Fig. 4E, Eq. S2, β = −10.4 ± 11.80, p = 0.41). Therefore, we hypothesized that PES emerges from a combination of changes in the decision-making processes: a decrease in urgency and sensitivity. Below we will evaluate this hypothesis using LIP neural responses.

Figure 4. Joint reductions in urgency and sensitivity explain PES.

(A–B) Decision bound for post-correct (black) and post-error (red) trials averaged across humans (A) and monkeys (B) that exhibited PES. To ensure all subjects contributed equally to the averages, we normalized the bound heights by dividing by each subject’s maximum across all conditions and times. Urgency is reduced after errors for both species, resulting in an overall greater bound height.

(C–E) Mean bound height (C), sensitivity (D), and non-decision time (E) for post-error trials versus post-correct trials. Mean bound height was computed for each subject as the average bound over the middle 95% of the decision time distribution. Error bars are SE. Histograms show the distribution of the difference of post-error and post-correct model parameters across subjects. Arrows over the histograms indicate the mean difference (Eq. S2, ** for p<0.01; * for p<0.05; n.s. for not significant).

Dynamics of LIP neural responses change with PES

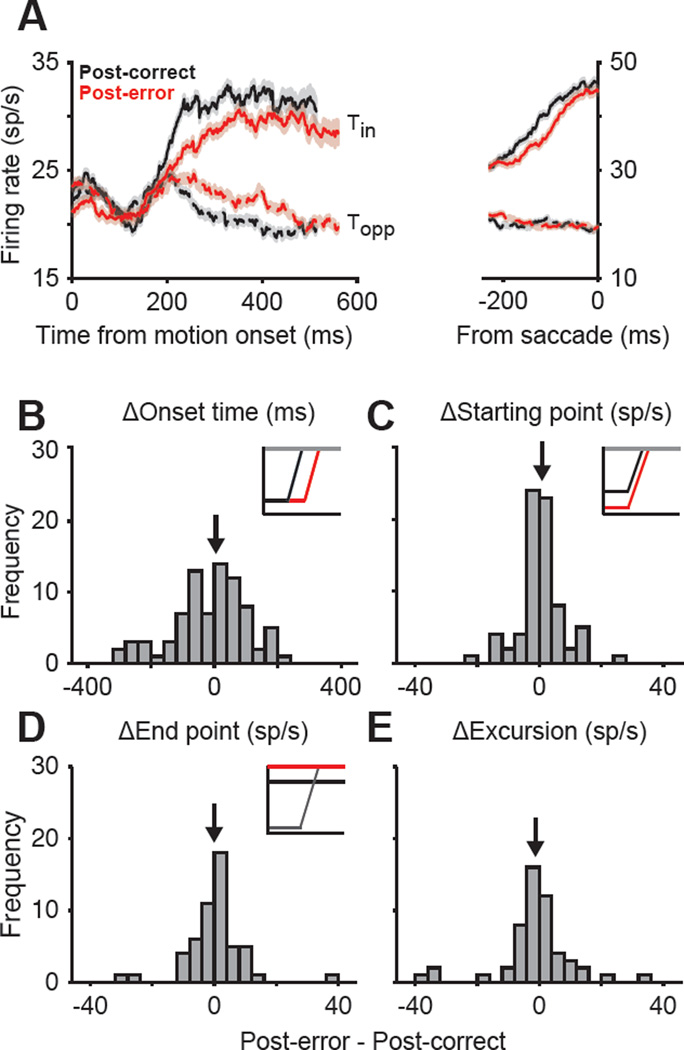
Figures 5A and S3 show the mean firing rates of 114 neurons from monkeys O and N. After the stimulus onset, there was a gradual ramping of firing rates. Responses increased when the monkey ultimately chose the target in the RF (T_in), or declined when the choice was in the opposite direction (T_opp). The “buildup rate” depended on the motion strength; stronger motion toward T_in increased buildup rates (Fig. S3; Eq. 5, β₂ = 1.6 ± 0.13, p < 10⁻¹⁰) and stronger motion toward T_opp decreased buildup rates (Eq. 5, β₃ = −0.4 ± 0.13, p = 8.6 × 10⁻⁴), consistent with the accumulation of different levels of sensory evidence. Also, as expected by the model, the firing rates reflected the decision commitment by converging to a common level at the end of the ramp ~70ms prior to the T_in saccade (Fig. S3). The start and end points of the ramp represent, respectively, the start point of evidence accumulation and the span over which the firing rates change during decision formation.

Figure 5. The static components of the decision-making mechanism do not change with PES.

(A) Average responses of LIP neurons for monkeys O and N on post-correct (black) and post-error (red) trials. Solid and dashed lines show trials in which the choice was made to the target inside (T_in) or opposite (T_opp) the neuron’s response field. (B–E) There was no change in the static components of the LIP responses. The histograms show the difference between post-correct and post-error trials for the onset time of ramping responses (B), magnitude of neural responses at the beginning of evidence accumulation (C), magnitude of neural responses at the end of accumulation, prior to the saccade (D), and total excursion between the start point and end point (E). Insets illustrate schematic changes in activity that would be expected if the static components of the decision-making process explained PES. Black arrows indicate the mean of the distribution.

LIP responses did not show any change in the static features of the ramp: onset time, start point firing rate, and end point firing rate. The mean onset time of the ramp was indistinguishable for post-error (120 ± 21.3 ms) and post-correct trials (119 ± 17.6 ms, p = 0.66, Wilcoxon signed-rank test; Fig. 5B), ruling out increased sensory delay as a main cause for PES. LIP neurons also showed similar firing rates at the beginning of the integration process following errors (Fig. 5C; F = 0.01, p = 0.91, mixed-measures ANOVA), and achieved the same common level before the saccade (Fig. 5D; F = 0.15, p = 0.70). Finally, we verified that the total excursion (end point - start point) was indistinguishable for post-correct and post-error trials (Fig. 5E; F = 0.15, p = 0.69). Identical trends were evident in the normalized responses, which reduced across-neuron variation in total excursion (see Experimental Procedures). Overall, the onset time and the range of the ramp remained stable.

However, PES was associated with a change in the dynamics of neural responses between the start and end points. This change consisted of two components: a stimulus-independent component that corresponded to a reduced urgency, and a stimulus-dependent component that corresponded to a reduced sensitivity to stimulus strength. Below we expand on these components.

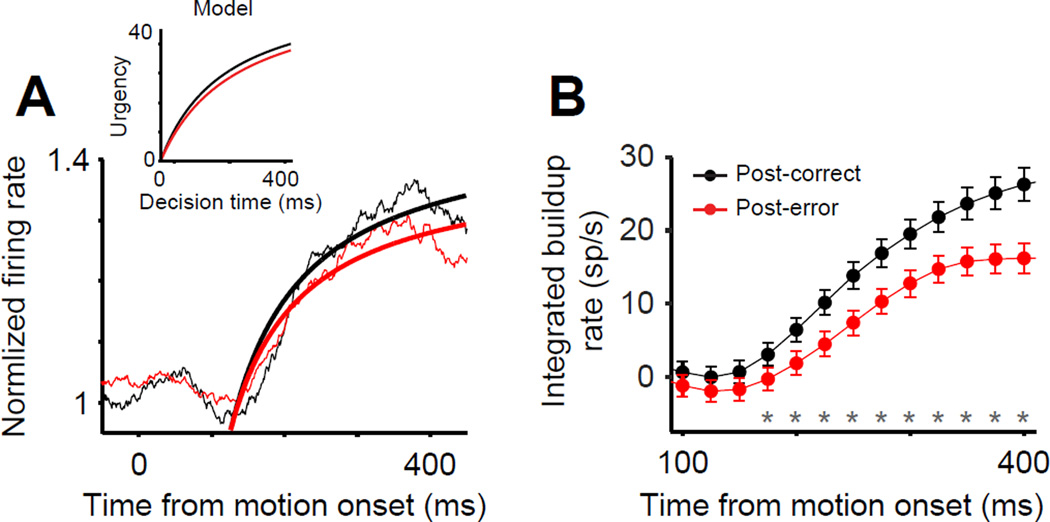
Following Churchland et al. (2008), we estimated the form of the urgency signal by averaging firing rates across T_in and T_opp trials. Because we combined trials in which evidence is for and against a particular response, the effect of incoming evidence cancels out, and only the nonspecific urgency modulation remains. Figure 6A shows these neurally-derived estimates, confirming the presence of a rising urgency signal that was well characterized by the same hyperbolic function used in the DDM. It also shows that the urgency was reduced following errors. Across individual neurons, there was a significant reduction in urgency following errors as captured by a decrease in the asymptote of the best-fitting hyperbolic function (Eq. S3, Δu_∞ = −0.60 ± 0.20, p = 1.7 × 10⁻², Wilcoxon signed-rank test), while the rise time and start point did not change (Δτ_1/2 = −6.9 ± 50.41, p = 0.84; Δβ₀ = 0.016 ± 0.012, p = 0.99). A similar difference in post-error and post-correct urgency was observed when the dynamic component of the urgency signal was estimated using an alternative method developed by Hanks et al (2011) (Fig. 6B; see Supplemental Experimental Procedures). Put together, the unchanged start-and end-point firing rates and the reduced urgency in LIP responses implemented a dynamic increase in the decision bound and augmented the overall evidence that subjects accumulated for decisions. We found further support for this conclusion through nested model testing. Replacing the dynamic urgency (bound collapse) in the model with a static change in bound height significantly reduced the quality of the fits in the majority of subjects (p < 0.05, likelihood-ratio test in 7/8 subjects exhibiting PES).

Figure 6. LIP responses reflect a reduction of urgency following errors.

(A) LIP responses averaged across all choices (T_in and T_opp) and stimuli from monkeys O and N on post-correct (black) and post-error (red) trials. Averaging across choices cancels out the effect of incoming sensory evidence such that only an evidence-independent urgency signal remains (Churchland et al., 2008). Smooth curves are fits of a hyperbolic function (Eq. S3). Inset shows the average urgency signal based on the best fitting drift-diffusion model parameters for the two monkeys (see Fig. 4B).

(B) Neurally-derived estimate of urgency based on the mean buildup rates computed during decision formation (Hanks et al., 2011). The mean buildup rate was computed in a running window (width = 150ms, 25ms steps) 100 – 400ms after motion onset to obtain a piecewise estimate of the first derivative of the urgency function. The integral of the piecewise buildup rates provides an estimate of the dynamic urgency signal. The urgency signal was estimated independently for post-correct (black) and post-error (red) trials. Asterisks indicate time bins in which the urgency signals on post-correct and post-error trials were significantly different (p < 0.05; parametric bootstrap, 1000 samples). Error bars are SEM.

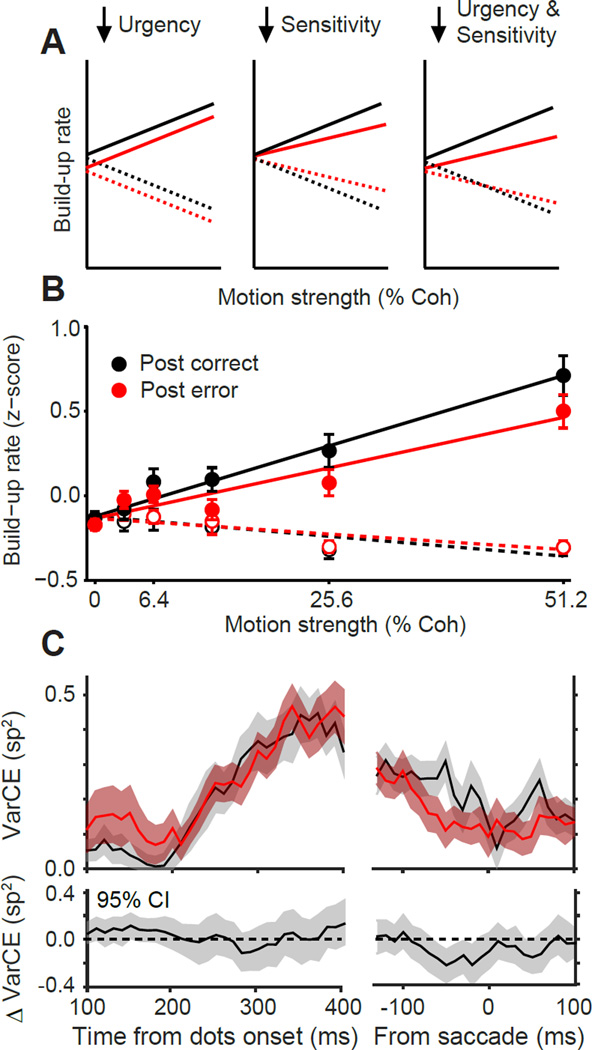
LIP neural responses also reflected the reduction of stimulus sensitivity. Recall that our model suggested reduced sensitivity as one of the two factors that induced PES. A combination of urgency and sensitivity reductions makes specific predictions for changes in the buildup rate of LIP neurons (Fig. 7A): an overall reduction of buildup rates for T_in motion directions, smaller or no effects for T_opp motion directions, and shallower dependency of buildup rates on motion strength. LIP responses were consistent with this prediction (Fig. 7B). The lack of change in the T_opp buildup rates could potentially be due to a floor effect (firing rates cannot go below zero). Importantly, however, we found that the slope of buildup rate as a function of motion strength for T_in motion directions was significantly shallower following errors (Fig. 7B; Eq. 5; β₄ = −0.46 ± 0.18, p = 9.0 × 10⁻³). This effect was still clear even when we regressed out the relationship of RT and buildup rate (Eq. 5; β₄= −0.35 ± 0.17, p = 3.9 × 10⁻²), indicating that RT differences alone cannot explain the result. Altogether, LIP responses are most consistent with a model in which both evidence-dependent (sensitivity) and evidence-independent (urgency) inputs to the accumulation mechanism are reduced following errors.

Figure 7. Sensitivity, not noise, changes with PES.

(A) Schematic changes in buildup rate under different hypotheses of PES. Reduction of urgency alone (left) reduces buildup rate for all motion strengths. Reduction of sensitivity alone (middle) induces stimulus strength-dependent reduction of buildup rate for T_in motions and increase of buildup rate for T_opp motions. The combination of reduced urgency and sensitivity (right) predicts a distinct pattern that combines the abovementioned trends.

(B) Measured buildup rates of LIP responses for monkeys O and N during decision formation as a function of motion strength for T_in (solid circles) and T_opp (open circles) directions. Changes of buildup rates following errors are consistent with a combined change in urgency and sensitivity (panel A, right). Error bars are SEM.

(C) Variance of the firing rates that underlie spiking activity is unchanged following errors. This variance indicates a combination of stimulus and neural noise and can be quantified with the variance of conditional expectation (VarCE; Eq. S4). The top panel shows VarCE for T_in for post-correct (black) and post-error (red) trials. Shaded regions are ± SE. The bottom panel shows a 95% confidence interval (CI) around the post-error minus post-correct VarCE.

Decreased SNR with PES is not explained by elevated noise

From a theoretical perspective the combined reduction of urgency and sensitivity could be replaced with a combination of reduced urgency and increased noise without affecting the quality of RT fits. Note that the critical factor in the model is the ratio of signal to noise (SNR). Traditionally, noise is assumed constant and drift rate and decision bound are expressed in units of noise (Link, 1992). Assuming fixed noise, our model predicted a reduction of sensitivity. A more general conclusion from the model would be a reduced SNR, which could be implemented by reduced sensitivity, elevated noise, or both. To formally establish this point we fit an alternative model in which we fixed sensitivity and allowed noise to vary across post-correct and post-error trials (equal number of free model parameters). For all eight subjects exhibiting PES, the quality of the fit was statistically unchanged (bootstrap test of model log-likelihoods, p > 0.46 for all subjects). An examination of the best fitting parameters revealed that PES could be equally well explained with a mixture of reduced urgency and elevated noise (Fig. S4; Eq. S2; B̄: β = 3.96 ± 1.239, p = 1.5 × 10⁻²; σ: β = 0.12 ± 0.038, p = 1.6 × 10⁻²; t₀: β = −0.12 ± 7.923 ms, p = 0.98). Thus, these two models (noise change and sensitivity change) are indistinguishable based solely on behavioral data, but we can turn to physiology to resolve this apparent model mimicry.

The LIP responses confirmed that reduced SNR is at least partly due to reduced sensitivity (above). They also enabled us to directly test whether PES could be partially attributed to elevated noise. Elevated noise manifests itself as increased trial-to-trial fluctuations of the rate function that underlies spiking activity. We quantified this rate fluctuation by computing the variance of conditional expectation (VarCE), a statistic that parses true across-trial variability in response rate from point-process variability (Eq. S4; Churchland et al., 2011). For both post-correct and post-error trials, VarCE gradually increased over time following motion onset, consistent with the accumulation of noisy evidence, and reached nadir around the time of saccade, consistent with convergence to a bound. However, there was no significant increase in VarCE for post-error relative to post-correct trials (Fig. 7C; bootstrap, p > 0.05 for all comparisons 100–400ms after motion onset). Results were identical when we analyzed the Fano factor (spike count variance/spike count mean; Eq. S5). Altogether, our data demonstrate that decreased SNR with PES is primarily due to reductions in sensitivity rather than elevated noise.

Post-error speeding is associated with reduced sensitivity and reduced decision bound

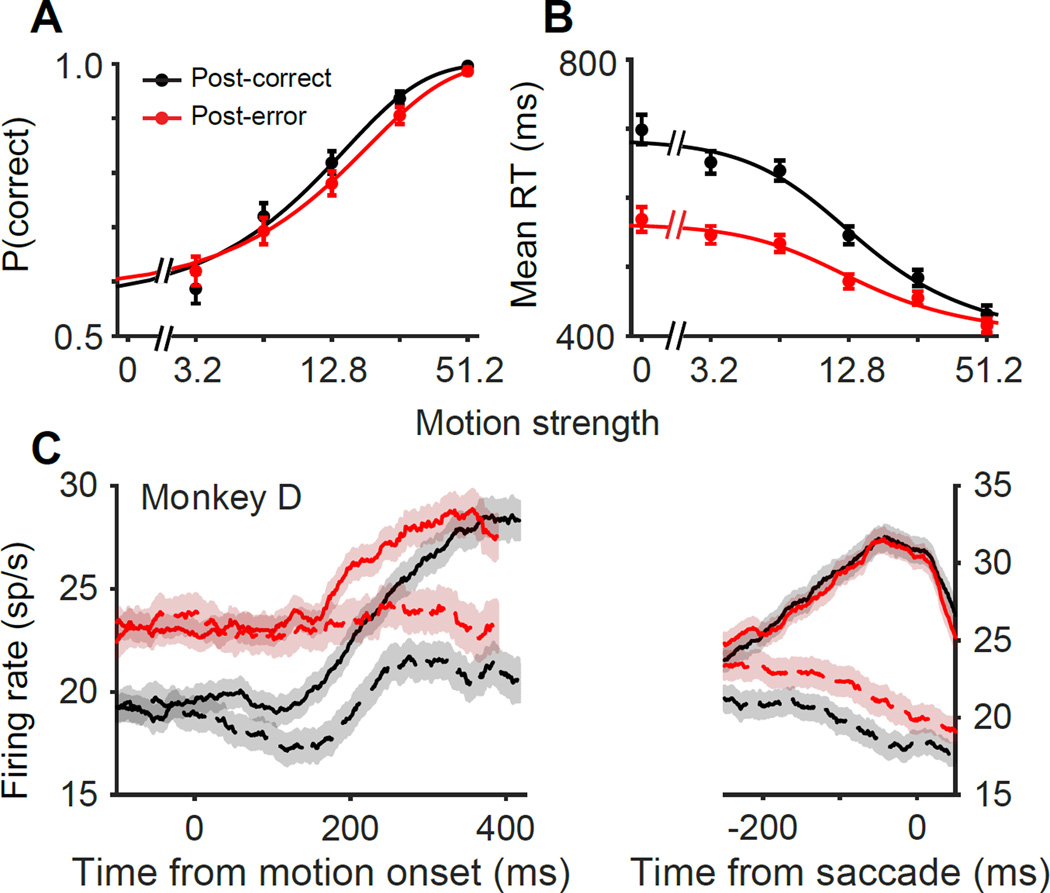
In the previous sections we focused on the majority of subjects who exhibited clear PES. Here, we explore the remaining minority. Two subjects (One human, S7, and one monkey, D) consistently decreased their RTs following errors (Fig. 8 and Fig. S2; Table S1). “Post-error speeding” has been previously reported, especially in fast-response regimes when subjects emphasize speed over accuracy (King et al., 2010; Notebaert et al., 2009). Our two subjects with post-error speeding presented an opportunity to contrast the mechanism of post-error speeding and slowing. For both subjects, the slope of the psychometric function was significantly reduced after errors (Fig. 8A and Fig. S2; Eq. 1; β₂ = −2.02 ± 0.82, p = 0.01) and post-error speeding was maximal at lower coherences (Eq. 2; β₃ = 161 ± 52.77, p = 2.3 × 10⁻³). This pattern of behavior was best explained with a combination of decreased sensitivity and, importantly, decreased decision bound (Table S2), perhaps to rush through trials with impaired sensitivity. Our nested behavioral models indicated the necessity of bound changes to explain post-error speeding for both subjects (Monkey D, p = 8.9 × 10⁻⁸; Subject S7, p < 10⁻¹⁰), but could not distinguish between static bound changes or dynamic changes in urgency.

Figure 8. Post-error speeding is associated with a change in start point.

(A–B) Psychometric and chronometric functions of subjects that exhibited post-error speeding (monkey D and subject S7). Conventions are similar to Figure 1B–E. (C) Average responses of the population of LIP neurons recorded from monkey D. The start point of the integration was higher after errors, compatible with a static reduction of effective decision bound height. Conventions are the same as in Figure 5A.

The responses of 37 LIP neurons of monkey D indicated a strong increase in the start point of integration (Fig. 8C; F = 8.89, p = 3.1 × 10⁻³, mixed-measures ANOVA) and no change in the end point (F = 0.04, p = 0.83), leading to an overall reduction of the neural response excursion for this monkey (F = 4.36, p = 3.7 × 10⁻²). This large increase in start point obscured our ability to reliably compare neural urgency signals across conditions. Therefore, we cannot rule out changes in urgency in addition to changes in start point. Regardless of its origin, it seems clear that a reduced decision-bound is highly likely to play a central role in shaping post-error speeding. A stronger conclusion about the underlying neural mechanism of this bound reduction must await data from additional monkeys.

Our last subject, Monkey B, did not show noticeable changes of behavior following errors (Fig. S5A,B; Table S1), offering a control to test whether the aforementioned changes in neural responses following errors were associated with behavioral changes, or were merely incidental to negative feedback. Post-correct and post-error responses of 52 neurons recorded from this monkey were largely identical (Fig. S5C). The buildup rates (Eq. 5, β₄ = 0.34 ± 0.48, p = 0.48), urgency (Δu_∞ = 0.27 ± 0.43, p = 0.63; Δt_1/2 = −42.87 ± 60.07, p = 0.35, Wilcoxon signed-rank test), and overall excursion (F = 0.002, p = 0.96, mixed-measures ANOVA) were unchanged following errors. Altogether, these results indicate that changes in neuronal responses are specific to the type of post-error behavioral adjustment.

DISCUSSION

Seminal work by Laming (Laming, 1979) has formed the basis for numerous computational frameworks that explain PES through adjustments in the decision bound (Goldfarb et al., 2012; Holroyd et al., 2005), and has led various clinical and neurophysiological studies to interpret PES as a direct index of adaptive behavior (e.g., Sergeant and van der Meere, 1988). However, a pure bound-change makes a strong prediction that accuracy increases following errors (Fig. 2)—a prediction that has been contradicted by many studies, including this one (e.g., King et al., 2010). This has lead some researchers to question whether PES reflects any adaptive process whatsoever or whether this interpretation should be exclusively reserved for the rare cases in which post-error accuracy is also elevated (Schroder and Moser, 2014).

Through a detailed analysis of behavior we demonstrated that increases in decision bound are necessary to explain PES, even in the absence of elevated accuracy. The key experimental observations are more slowing at low stimulus strengths and heavier tails in the RT distribution. This pattern is best explained by a reduction in urgency that effectively raises the decision bound. Although our results support adaptive theories of PES we note that this explanation is necessarily incomplete; some additional mechanism is needed to explain why accuracy rarely increases with PES.

The additional mechanism is a concurrent reduction in sensory SNR, which eliminates expected gains in accuracy with increased decision bound. Decreased SNR is maladaptive for the goals of the task – it reduces the reward rate by making responses both slower and less accurate, and therefore cannot reflect a strategic adjustment. Rather, decreased SNR must reflect an unavoidable reaction to the occurrence of negative feedback. Such maladaptive responses are not unprecedented. Several previous studies have reported declines in performance after negative feedback, particularly when it is unexpected (Notebaert et al., 2009; Rabbitt and Rodgers, 1977).

Our results suggest a new interpretation of PES as an attempt to adaptively compensate for a maladaptive consequence of negative feedback. This conjunction explains why RT and accuracy appeared unrelated in many past studies of PES (Danielmeier and Ullsperger, 2011). When the reduction of urgency and sensitivity are balanced, RTs will increase without appreciable changes in accuracy (King et al., 2010; Rabbitt and Rodgers, 1977). When the reduction of urgency (increase of decision bound) overcompensates, PES will be accompanied with increased accuracy, as observed in some studies (Danielmeier and Ullsperger, 2011; Laming, 1979). An imbalance in the opposite direction will result in reduced accuracy as observed in our post-error speeding subjects and a minority of previous studies (Rabbitt and Rodgers, 1977). We suggest that the key to understanding the diversity of PES behavior is the balance between changes of decision criterion and changes of stimulus sensitivity.

This new hypothesis generates several testable predictions. One prediction is that increasing the delay following feedback facilitates recovery of sensitivity from negative feedback, thereby mitigating the need to slow down. We tested this prediction through a follow-up study in which we manipulated the delay between feedback and the start of the next trial (i.e., the intertrial interval, ITI; 0.35–3.2 s, see Supplemental Experimental Procedures). We observed that for longer ITIs, PES was reduced (Fig. S6), compatible with previous studies (e.g., Danielmeier and Ullsperger, 2011).

The effect of negative feedback on sensitivity also suggests a link between the subject’s expectations and PES, leading to a second prediction: unexpected negative feedback should produce larger declines in sensitivity and a larger PES. We tested this prediction by fitting a modified version of the model with an additional parameter that scaled post-error sensitivity by error-trial motion strength. The results indicated a larger decline in sensitivity when subject received negative feedback on trials with stronger motion (Eq. S2, β = −0.86 ± 0.345, p = 0.03), compatible with our prediction because negative feedback is less expected on those trials (Kiani et al., 2014a). Our prediction is partially consistent with theories that assume error detection and PES are driven by differences between predicted and actual outcomes (Holroyd et al., 2005). However, our results suggest that this component of PES is not necessarily adaptive. Distinguishing whether expectations drive adaptive or maladaptive components of PES could be addressed through experiments that explicitly probe subjects’ expectations before feedback delivery (Purcell and Kiani, Society for Neuroscience Meeting 2015).

Neural mechanisms of PES

A complete understanding of PES requires us to understand (i) how errors are detected and (ii) how they impact future sensory processing and decision strategies. The role of medial frontal cortex in error-detection is well known. Medial frontal neurons discharge immediately after erroneous responses or feedback (Purcell et al., 2012; Schall et al., 2002), contributing to error-related negativity in extracranial EEG signal (Gehring et al., 1993) and BOLD responses associated with performance monitoring (King et al., 2010). Further, artificial inactivation of medial frontal cortex eliminates PES in rodents (Narayanan et al., 2013), and medial frontal lesions in humans reduce or eliminate PES (di Pellegrino et al., 2007), indicating a critical connection between performance monitoring processes and PES.

Studies on medial frontal cortex, however, do not tell us how errors impact sensory processing and decision strategies. Previous studies have reported correlations between medial frontal cortex and decision-related frontal and parietal areas during PES (King et al., 2010), but the nature of this interaction is unclear at a single neuron level. Anatomically, medial frontal cortex is not well positioned to accumulate sensory evidence because it receives relatively sparse inputs from sensory areas (Huerta and Kaas, 1990). During perceptual decision-making, medial frontal neurons may not exhibit choice-selective signals (Purcell et al., 2012), and firing rates do not converge at a fixed bound prior to response execution (Stuphorn et al., 2010). In contrast, LIP is a node in a larger network of brain areas involved in integration of sensory inputs to plan eye movements. In the direction discrimination task, LIP neurons represent integration of sensory evidence to a decision bound (Gold and Shadlen, 2007). Our recordings from LIP provide crucial new insights into the mechanisms by which errors modify future decisions.

Neural responses that provide access to the dynamics of the integration process are key to distinguish hypotheses that could not be differentiated based on behavior alone. Below, we expand on three components of the decision-making process that have been implicated in PES by past studies.

Delays in decision onset

Our observation that the onset of evidence accumulation is indistinguishable for post-correct and post-error trials is inconsistent with theories of PES that hypothesize delays in the start of evidence accumulation following errors (Laming, 1979; Rabbitt and Rodgers, 1977). We cannot directly rule out delayed activation of motor processes downstream of LIP; for example, slowing following countermanded saccades has been shown to produce delayed activation in oculomotor neurons (Pouget et al., 2011). However, the non-uniform slowing across RTs and absence of increased non-decision time in the model indicate that delayed motor activation is not sufficient to explain PES and is unlikely to be a core component of increased RTs.

Quality of evidence and efficiency of accumulation

Although the DDM indicated that reduction of SNR was a core component of PES, the model could not separately quantify the role of sensitivity and noise. The inadequacy of DDM is an inherent feature shared by all bounded accumulation models. To provide intuition about this inadequacy, we note that fitting a model in which bound, sensitivity, and noise are all free to vary does not generate a unique solution. Broadly speaking, to achieve a unique fit one must fix at least one of the three factors and express the remaining two in the units of the fixed one. It is, therefore, implausible to use the pattern of choices and RTs to independently assess post-error changes of sensitivity and noise in the presence of bound changes.

LIP responses addressed this conundrum by showing no change in VarCE following errors. VarCE reflects the sum of sensory and accumulation noise (Churchland et al., 2011) and its constancy suggests that elevated neural noise is not a major contributor to PES. On the other hand a reduction of sensitivity shows clearly in the buildup rates of LIP neurons. In our task, sensory evidence for direction discrimination is provided by extra-striate visual cortical areas, MT and MST (Britten et al., 1992; Ditterich et al., 2003; Fetsch et al., 2014). Reduction of sensitivity in parietal neurons may reflect a reduction in the quality of the sensory representation in MT and MST (Treue and Martinez Trujillo, 1999), or the readout of sensory information by the decision-making network (Green et al., 2010). Based on past fMRI studies we speculate that the former is less likely (Danielmeier and Ullsperger, 2011; King et al., 2010), but distinguishing these two possibilities requires electrophysiological recordings from MT and MST.

Decision bound

Bound adjustments in PES are likely implemented through modulation of a dynamic urgency signal—an evidence-independent input that equally drives all choice-selective neural populations (Churchland et al., 2008; Hanks et al., 2014). Decreased urgency causes neural responses to rise more slowly, increasing the evidence required to reach the bound. Similar changes in LIP and prefrontal neurons have been shown to implement changes of decision bound for speed-accuracy tradeoff (Hanks et al., 2014; Heitz and Schall, 2012). Thus, our results contribute to mounting evidence that changes in decision bound are not implemented through elevated end-point as one might expect, but instead through mechanisms that directly accelerate or decelerate accumulation of evidence toward a fixed threshold (Hanks et al., 2014; Lo et al., 2015).

Post-error reduction of urgency increases the accumulated evidence for the decision and neutralizes the reduction of SNR. In theory, such effective increase of decision bound could also have been implemented by a static reduction of the start point of the accumulation process. There is, however, a limitation to this alternative. Because firing rates are bounded at zero, decreasing the start point has an inherently restricted range. A similar limitation, however, does not apply if one’s goal is to reduce the effective bound height to respond faster following errors, as did monkey D in our experiment (Fig. 8).

A dynamic modulation of decision bound may be computationally advantageous, compared to a static change of the bound. Note that the difference of post-correct and post-error urgency signals grows with time (Fig. 6). The effective increase in the decision bound is, therefore, largest for longer RTs, which are associated with intermediate and weak motion stimuli (Fig. 1). For the same stimuli, accuracy is most susceptible to a reduction of SNR and also can improve the most with an increase of decision bound. In contrast, for the strongest stimuli, accuracy tends to be high and is unlikely to significantly benefit from increasing the decision bound. Manipulating decision bound through urgency ensures the increase of decision time happens where it matters the most.

The origin of urgency signal is unknown, but it may be shaped by the cost of acquiring evidence (Drugowitsch et al., 2012) and implemented by mechanisms that encode elapsed time (Jazayeri and Shadlen, 2015). The post-error changes of urgency, however, are likely to originate from structures involved in error detection (Purcell et al., 2012; Schall et al., 2002). While it is tempting to conclude that these error-related signals directly furnish changes of decision bound in the following trials, it is important to note that these signals are limited to the period immediately after the error and rarely overlap with the following decisions. Most likely, the effect on urgency is mediated through mechanisms that store long-term history of past behavior (e.g., Kiani et al., 2015; Tsujimoto et al., 2010). Future studies will shed light on this issue.

The changes of urgency in LIP responses can be part of a more widespread effect in the decision-making and action-planning network. For example, pre-supplementary motor area is inhibited (Danielmeier and Ullsperger, 2011; King et al., 2010) and corticospinal excitability is reduced in PES (Amengual et al., 2013). Such inhibitions, if also present in our task, are unlikely to be a purely motor (i.e., post-decisional) effect because they would predict equal elongation of RT for all stimulus strengths, incompatible with our experimental observations (Figs. 1, 3, S1). Rather, they are likely to be part of the decision-making process itself. Mounting evidence suggests that the decision-making process is distributed in a network that includes motor areas (Cisek and Kalaska, 2010; Gold and Shadlen, 2000; Hanes and Schall, 1996; Noorbaloochi et al., 2015; Ratcliff et al., 2003; Selen et al., 2012). From this perspective, we view our parietal recordings as a window onto the activity of this distributed network, and so the reductions in motor activity likely reflect another manifestation of the reduced urgency that we observe in our parietal neurons.

Conclusions

The neural mechanisms of PES have been hotly debated, but different hypotheses have been difficult to distinguish using only behavioral data or noninvasive methods for monitoring neural activity. Using quantitative modeling and electrophysiology, we provide a new account of PES as an active reduction of response urgency to balance reductions of sensitivity and maintain performance. This dual mechanism quantitatively explains post-error behavior and offers a parsimonious description for its diversity in past studies.

EXPERIMENTAL PROCEDURES

Behavioral task

Seven humans (four female, three male, ages 18–30) and four rhesus monkeys (two male, two female, ages 4–12) were trained to perform a motion direction discrimination task. All subjects were naïve to the purpose of the experiment. Informed written consent was obtained from all human subjects. Experimental procedures for humans were approved by the Institutional Review Board at New York University. Experimental procedures for monkeys conformed to the National Institutes of Health Guide for the Care and Use of Laboratory Animals and were approved by the animal care committees at the University of Washington (monkeys N and B) and Stanford University (monkeys O and D). Data from monkeys N and B have been previously published (Roitman and Shadlen, 2002).

Subjects were seated in a semi-dark room in front of a CRT monitor (frame rate, 75 Hz) with their heads stabilized (surgically implanted headpost for monkeys, chin and forehead support for humans). They began each trial by fixating a small red point at the center of the screen (FP, 0.3° diameter). After a variable delay (truncated exponential distribution; mean = 300–700 ms), two red targets (0.5°) appeared on opposite sides of the screen equidistant from the FP. After another random delay, the dynamic random dots stimulus (Britten et al., 1992) appeared within a 5–7° circular aperture centered on the FP. The stimulus consisted of three independent sets of moving dots shown in consecutive frames. Each set of dots was shown for one video frame and then replotted three frames later (Δt = 40 ms; density, 16.7 dots/deg²/s). When replotted, a subset of dots were offset from their original location (speed, 5 deg/s) while the remaining dots were placed randomly. The percentage of coherently displaced dots determined the strength of motion. Subjects reported their perceived direction of motion with a saccadic to the choice target in the direction of motion. Subjects were free to indicate their choice any time after motion onset. RT was defined as the difference between saccade initiation time and motion onset. See Supplemental Experimental Procedures for additional task details.

Behavioral data analyses

For all analyses, post-error refers to trials following an error feedback, and post-correct refers to trials that followed a correct feedback. In addition, we used only post-correct trials that are also pre-error to guard against slow fluctuations in behavioral state (see Supplemental Experimental Procedures).

We used a logistic regression to assess the effects of motion strength and errors on accuracy on the subsequent trial:

$$\text{logit}[P(\mathit{\text{correct}})]={\beta }_{1}C+{\beta }_2\mathit{\text{CI}}$$ (Eq. 1)

where logit(p) is log $\text{log}(\frac{p}{1-p})$, C is the motion strength on the current trial, I indicates the outcome of the previous trial (0 = correct; 1 = error), and β_i are the regression coefficients. β₁ tests for the effect of motion strength on choice, β₂ tests for the effect of previous-trial outcome on the slope of the psychometric function.

Similarly, we assessed the effects of motion strength and errors on RT with the following linear regression:

$$T={\beta }_0+{\beta }_{1}C+{\beta }_{2}I+{\beta }_3\mathit{\text{CI}}$$ (Eq. 2)

where T is the RT on the current trial. We obtained identical results using a nonlinear regression analysis (hyperbolic tangent).

We tested whether post-error slowing was greatest at shorter or longer RTs using a linear regression model of the following form:

$$\mathrm{\Delta }T={\beta }_0+{\beta }_{1}C+{\beta }_{2}D$$ (Eq. 3)

where ΔT indicates the mean RT difference between post-error and post-correct trials for coherence, C, and RT decile, D. Deciles were computed separately for each coherence and trial type (post-correct or post-error). Positive β₂ indicates maximal slowing at longer RTs (H₀: β₂ = 0). We obtained similar results using different numbers of quantiles.

Drift-diffusion model

We fit a drift-diffusion model to each subject’s behavior following correct and error trials to evaluate alternative hypotheses about the mechanisms responsible for PES. Choice and RT result from integration of noisy sensory evidence over time to a decision criterion or bound. The model parameters are as follows. The sensitivity parameter, k, determines the linear scaling of the mean rate of accumulation (i.e., drift rate) with motion strength (C). Therefore, µ = kC is the mean of the distribution of momentary evidence per time unit. The standard deviation of the momentary evidence, σ, is fixed to 1 in the majority of model fits. For one variation of the model we compared the standard model with the effect of varying signal-to-noise ratio of sensory evidence by changing the noise (σ) and fixing k. The non-decision time parameter, t₀, determines the mean time necessary for sensory processing and motor delays before and after the decision process. We further assume that non-decision time is normally distributed with standard deviation, s_t0. The bound height, B(t), determines the amount of evidence that must be accumulated for a choice at decision time t. We modeled evidence-independent response urgency as a collapsing bound over time (Hanks et al., 2014). A hyperbolic function was chosen for the shape of the bound collapse (Churchland et al., 2008):

$$|B(t)|=b-u_{\infty }\frac{t}{t+{\tau }_{1/2}}$$ (Eq. 4)

where b is the initial bound height, u_∞ is the asymptotic reduction in bound height, and τ_1/2 is the time to reach 50% reduction. Similar results were obtained with other functional forms for urgency. Finally, an offset in the start point of the accumulation, z, and a bias in the duration of non-decision time for right/left choices, t_0bias, accounted for choice biases and choice-dependent RT difference that are occasionally observed in both human and nonhuman primates. See Supplemental Experimental Procedures for details of model fitting. Briefly, we fit the full RT distributions, irrespective of choice, using a maximum likelihood procedure. In most fits we allowed four model parameters (k, t₀, u_∞, τ_1/2) to vary between post-error and post-correct conditions.

Neural analyses

Single neuron responses were recorded from area LIP of four rhesus monkeys while they performed the motion discrimination task (see Supplemental Experimental Procedures). Peristimulus time histograms (PSTHs) were created by averaging neural responses aligned to different task events. For illustration purposes they were smoothed by convolution with a 100 ms boxcar filter. We divided trials according to whether the chosen target was inside (T_in) or opposite (T_opp) the response field (RF) of the neuron, and whether the trial was post-correct or post-error as defined above.

We estimated the start time of evidence integration based on PSTHs of trials ending with a T_in saccade. A 40 ms window moved backward along the PSTH from the saccade onset toward motion onset in 1 ms steps. The onset of integration was defined as the first time when (1) activity made a transition from a ramp to a stable state (ramp was defined with a significant Spearman correlation for 10 consecutive steps, p < 0.01), and (2) firing rate showed at least a 20% drop compared to 100 ms before the saccade onset (Pouget et al., 2011). Other methods for measuring activity onset (e.g., dip time, see below) produced similar conclusions. Also, similar results were obtained for individual neurons and the population.

The firing rates associated with the beginning and end of the evidence accumulation process were measured in two distinct time windows. For the start-point firing rate we used a 50ms window centered on the post-stimulus dip in LIP activity. The dip is hypothesized to reflect a reset of the integration process and happens 50–150 ms after motion onset. We defined the dip as the minimum firing rate for each neuron in that period (mean dip time = 107 ± 3.34 ms). The dip time closely corresponds with the accumulation onset time estimated above. Thus, similar results were obtained by using the firing rate around the onset time. Using other measurements of start-point firing rate (e.g., the baseline period 0 to 200 ms before motion onset) led to identical conclusions. We estimated the end point of accumulation as the mean firing rate 75 to 25 ms before the saccade onset; a time period at which firing rates converge to a common level irrespective of RT and motion strength (Fig. S3; Churchland et al., 2008; Roitman and Shadlen, 2002). Only trials in which the T_in target was chosen were included in this analysis. We also tested for differences in the overall excursion; that is, the difference between the start-point and end-point firing rate of each neuron. We assessed the significance of activity changes in each epoch using a mixed-measures ANOVA with motion strength and previous trial outcome as fixed effects and cell identity as a random effect.

We quantified the urgency signal using two different methods: averaging neural responses across all motion directions, motion strength, and choices (Churchland et al., 2008), and piecewise estimation of the derivative of the urgency signal (Hanks et al., 2011). See Supplemental Experimental Procedures for details. Parameterization of post-correct and post-error urgency signals was done by fitting a hyperbolic function (Eq. S3) in the epoch from the response dip until 450ms after motion onset (Fig. 6A).

We computed the buildup rate of LIP neurons on a trial-by-trial basis by convolving the spike train with a Gaussian kernel (SD=25ms) to estimate the smoothed rate function and then by applying a linear regression to this rate function. The analysis was performed on an epoch starting at the characteristic dip and ending 100 ms before saccade initiation. To combine the buildup rates across neurons we standardized them for each neuron (z-score). We tested for post-error changes of buildup rate using the following linear regression:

$$\nu ={\beta }_0+{\beta }_{1}I+{\beta }_{2}C{J}_1+{\beta }_{3}C{J}_2+{\beta }_{4}C{J}_{1}I+{\beta }_{5}C{J}_{2}I$$ (Eq. 5)

where ν indicates the normalized buildup rate and C is the motion strength on each trial. I is an indicator variable for the previous trial outcome. J₁ and J₂ are indicator variables for motion direction: J₁ is 1 for motion toward the neuron’s RF, 0 otherwise; J₂ is 1 for motion away from RF, 0 otherwise. β₂ and β₃ indicate the change of buildup rate with motion strength toward T_in and T_opp (i.e., the neural sensitivity), and β₄ and β₅ indicate the change of sensitivity following errors. The null hypothesis is no change in sensitivity (H₀: β₄= 0 and β₅ = 0).

We also tested whether the variation in buildup rate following errors can be entirely accounted for by changes in RTs. First, we removed the covariation with RT using a regression model:

$$\nu ={\beta }_0+{\beta }_{1}T$$ (Eq. 6)

Then the residual buildup rate that could not be explained by RT variations (ν_r = ν – β₀ – β₁T) was used in Eq. 5.

To test for changes in neural variance during PES, we measured the across-trial firing rate variability as the variance of conditional expectation (VarCE) (Churchland et al., 2011). See Supplemental Experimental Procedures for details. Briefly, the analysis assumes that the spike count in each epoch is a stochastic realization of a point process governed by a rate parameter, which itself is randomly drawn from a distribution. VarCE estimates the variance of this rate distribution at each moment by subtracting from the total spike count variance an estimate of the point-process variance.

HIGHLIGHTS.

1. Humans and monkeys slow down after perceptual errors (post-error slowing).

2. Post-error slowing arises from reduced sensitivity and increased decision bound.

3. Changes in sensitivity and bound are implemented in parietal response dynamics.

4. A balance of these dynamics stabilizes post-error accuracy at the expense of time.