Abstract
Geometric frustration and quantum fluctuations may prohibit the formation of long-range ordering even at the lowest temperature, and therefore liquid-like ground states could be expected. A good example is the quantum spin liquid in frustrated magnets. Geometric frustration and quantum fluctuations can happen beyond magnetic systems. Here we propose that quantum electric-dipole liquids, analogues of quantum spin liquids, could emerge in frustrated dielectrics where antiferroelectrically coupled electric dipoles reside on a triangular lattice. The quantum paraelectric hexaferrite BaFe12O19 with geometric frustration represents a promising candidate for the proposed electric-dipole liquid. We present a series of experimental lines of evidence, including dielectric permittivity, heat capacity and thermal conductivity measured down to 66 mK, to reveal the existence of an unusual liquid-like quantum phase in BaFe12O19, characterized by itinerant low-energy excitations with a small gap. The possible quantum liquids of electric dipoles in frustrated dielectrics open up a fresh playground for fundamental physics.
 In magnetic materials, geometry-defined competing interactions between spins combined with quantum fluctuations can present the possibility of quantum liquid states which do not order even as 0K is approached. Here, the authors present an analogue built from electric dipoles on a triangular lattice.
In magnetic materials, geometry-defined competing interactions between spins combined with quantum fluctuations can present the possibility of quantum liquid states which do not order even as 0K is approached. Here, the authors present an analogue built from electric dipoles on a triangular lattice.
Geometric frustration arises on various triangle-based lattices such as one-dimensional (1D) trestle lattice, two-dimensional (2D) triangular and kagome lattices and three-dimensional (3D) B-site spinel and pyrochlore lattices, and are typically investigated in spin systems1,2,3. It has become well known that the introduction of quantum fluctuations in geometrically frustrated magnets gives rise to a rich variety of interesting quantum phases3,4,5, as discussed with both the transverse Ising models6,7,8,9 and Heisenberg models10,11. Especially, exotic quantum spin liquids (QSLs), characterized by either gapped or gapless itinerant excitations3,4, have been theoretically predicted to show extremely intriguing phenomena. Compared with the impressive progress and diversity in theory, nevertheless, a clear identification of QSLs in real materials has proved challenging, with a very limited number of candidates reported so far12,13,14,15,16.
Similar to the situation of spin lattices in magnets, geometric frustration can occur in lattices made of electric dipoles in dielectrics. In the case of small electric dipoles with significant quantum fluctuations persisting down to T=0 K, exotic disordered quantum phases, such as a quantum electric-dipole liquid (QEL), could emerge in certain conditions. In fact, some theoretical models proposed for ultracold dipolar particles trapped on 2D frustrated optical lattices have predicted topological quantum phases with fractional excitations17. In a QEL, the electric dipoles are highly entangled with one another in a form of quantum dimers (pairs of antiparallel dipoles) and continue to fluctuate in the resonating valence bond state, a picture qualitatively similar to a QSL. However, we must emphasize that the QEL should have distinctive features from QSLs because electric dipole and spin have important differences18. For instance, electric dipole neither has intrinsic angular momentum nor exhibits quantum precession as magnetic dipole (spin) does. Moreover, the nature of short- and long-range interactions between electric dipoles is very different from that of spins19. This could lead to a very different phase diagram between QSLs and QELs.
Frustration in dielectrics has been previously studied in materials with competing ferroelectric (FE) and antiferroelectric (AFE) constituents such as the KH2PO4/NH4H2PO4 (KDP-ADP) family or containing random-site impurities such as KTaO3:Li, which usually result in electric-dipole glasses similar to spin glasses20,21. However, the geometric origin of frustration and cooperative liquid-like quantum phases has been largely ignored in the studies of dielectrics. On the other hand, the role of quantum fluctuations in dielectrics has been noticed since 1970s when people were studying the abnormal dielectric behaviour of SrTiO3 (ref. 22). It was proposed that quantum fluctuations in SrTiO3 prevent the onset of long-range FE order so that a quantum paraelectric state persists down to zero temperature23. Since then, quantum paraelectricity has been reported in a number of perovskite oxides with similar structures to SrTiO3, such as CaTiO3, EuTiO3 and KTaO3. The quantum paraelectrics provide a new playground for the study of quantum critical phenomena18; however, it seems hopeless to search for the QELs in those perovskite quantum paraelectrics because their crystalline structures and FE interactions usually do not introduce geometric frustration.
In this work, we demonstrate that both geometric frustration and strong quantum fluctuations can be simultaneously achieved in a unique quantum paraelectric hexaferrite BaFe12O19 in which small electric dipoles that originated from the off-centre displacement of Fe3+ in the FeO5 bipyramids constitute a 2D triangular lattice. Our experiments including dielectric permittivity, heat capacity and thermal conductivity measured down to 66 mK suggest the existence of a very unusual liquid-like ground state, characterized by itinerant low-energy excitations with a small gap. We consider this nontrivial quantum phase as a possible candidate of the QELs. The quantum liquids of electric dipoles in frustrated dielectrics provide a new playground for fundamental physics and may find applications in quantum information and computation as well.
Result
Geometric frustration in BaFe12O19
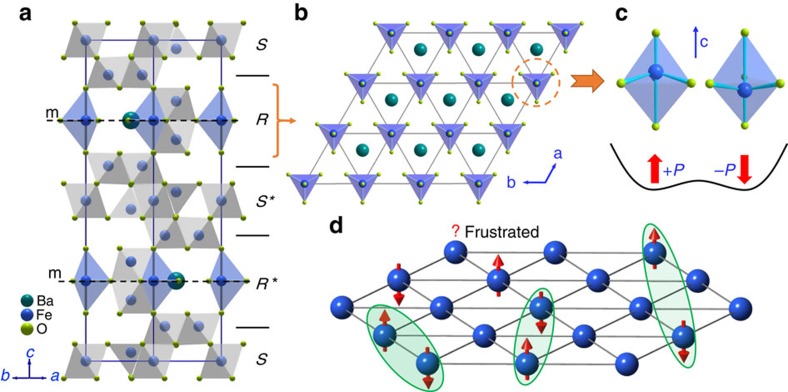
Recently, we have discovered that the M-type hexaferrites, such as BaFe12O19, belong to a completely new family of quantum paraelectrics24. Other hexaferrites containing the FeO5 bipyramids in their crystal structures, such as the W-, Z-, X- and U-type hexaferrites, are also likely candidates of quantum paraelectrics24. The M-type hexaferrite BaFe12O19 is one of the most popular magnetic materials with a wide use in magnetic credit cards, bar codes, small motors and low-loss microwave devices25 because of its superior properties of ferrimagnetic ordering with a strong ferromagnetic moment and a very high Néel temperature (∼720 K), high resistivity, as well as low cost of synthesis. The crystal structure of BaFe12O19 is shown in Fig. 1a. It can be described by a periodically stacking sequence of two basic building blocks—S block and R block along the c axis. The Fe3+ ions occupy three different kinds of sites: octahedral, tetrahedral and bipyramidal sites. In particular, the FeO5 bipyramids only exist in the middle of the R/R* blocks and form a triangular lattice in the ab plane (Fig. 1b).
Figure 1. Uniaxial electric dipoles on a triangular lattice in BaFe12O19.
(a) Crystal structure of the M-type hexaferrite BaFe12O19. It consists of alternate stacks of S and R blocks along the c axis. The asterisk symbols indicate that the corresponding blocks rotate about the c axis by 180°. The Fe3+ ions occupy three different sites: octahedral, tetrahedral and bipyramidal (blue) sites. A mirror plane (m) bisects equally the bipyramids in the R/R* blocks. (b) The 2D triangular lattice of FeO5 bipyramids in each R/R* block. (c) Illustration of Fe3+ off-equator displacements in the FeO5 bypyramid. The upward or downward displacements at two 4e sites give rise to small electric dipoles along the c axis. Quantum fluctuations between two 4e sites persist to T=0 K. (d) Frustrated electric dipoles on a triangular lattice. Each site contains an Ising-type electric dipole (red arrow), while the neighbouring interactions favour anti-alignment. Quantum dimers (marked by green ovals) with either short-range or long-range entanglement continue to fluctuate and result in a QEL.
Previous experiments including Mössbauer spectroscopy26, X-ray diffraction27 and neutron diffraction28 have revealed the existence of off-equatorial displacements for Fe3+ at Wyckoff position of 2b site inside the FeO5 bipyramids to minimize the total energy, which results in two adjacent Wyckoff positions of 4e sites with a lowered symmetry (Fig. 1c). The off-equatorial displacement (4e–4e distances are 0.176(5) Å at 4.2 K and 0.369(5) Å at room temperature)26 would induce a small local electric dipole P along the c axis in each FeO5 bipyramid (Fig. 1c). A dynamic displacement persists down to the lowest temperature because of the significant quantum tunnelling between two 4e sites and the weak dipole–dipole coupling along the c axis. Consequently, a quantum paraelectric behaviour without long-range electric ordering has been observed in BaFe12O19 (ref. 24).
More importantly, these electric dipoles associated with the FeO5 bipyramids reside on a triangular lattice in each R/R* block. Because the R/R* blocks are well separated by the S/S* blocks, this triangular lattice thus has a 2D feature. Consequently, a dielectric system with uniaxial (Ising-type) electric dipoles on a 2D triangular lattice is practically achieved in BaFe12O19 (Fig. 1c). If the neighbouring dipole–dipole interaction favours anti-alignment, the system confronts frustration and has a very large degeneracy of ground states. In this sense, BaFe12O19 is a very unique quantum paraelectric system compared with those previously known perovskite quantum paraelectrics: first, it has uniaxial electric dipoles, whereas perovskite SrTiO3 is pseudocubic with multiple easy axis; second, it experiences geometrical frustration, whereas there is no evidence of geometrical frustration in SrTiO3 and other perovskite quantum paraelectrics. Thus, the quantum paraelectric BaFe12O19 sets up a promising candidate to search the proposed QELs, where an assembly of quantum dimers (pairs of dipoles) with long-range entanglement continues to fluctuate (Fig. 1d). We then employ a series of experimental techniques to resolve the ground state of BaFe12O19.
Dielectric permittivity
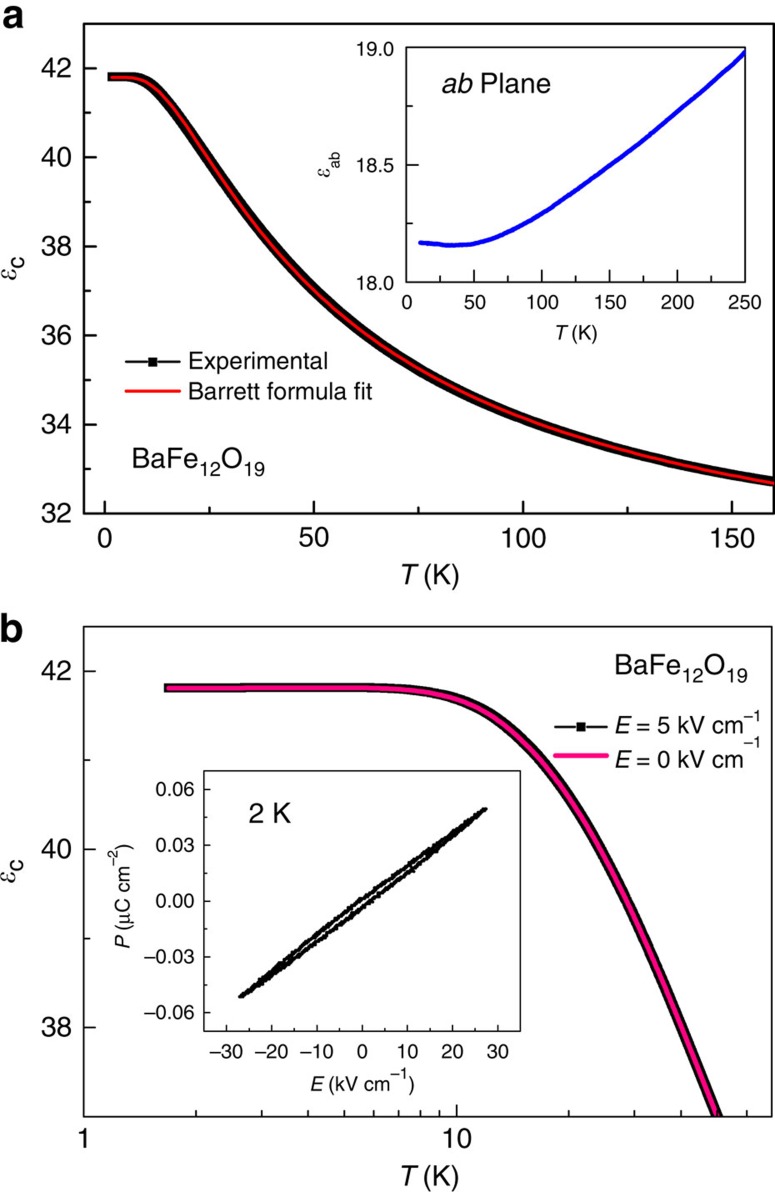
A prerequisite of a QEL is the AFE interaction between neighbouring dipoles. To confirm the AFE coupling in BaFe12O19, we have made a careful analysis on the low-temperature dielectric permittivity. As shown in Fig. 2a, the dielectric permittivity along the c axis (ɛc) of BaFe12O19 increases steadily with decreasing temperature but remains nearly constant below ∼5.5 K. No dielectric phase transition is observed down to 1.5 K. This dielectric behaviour evidences a quantum paraelectricity, similar to that in SrTiO3. The quantum paraelectric behaviour can be well described by the mean-field Barrett formula29:
Figure 2. Dielectric permittivity of BaFe12O19.
(a) The temperature dependence of c axis dielectric permittivity ɛc. The red solid line is the fitting curve to the Barrett formula. The negative fitting parameter T0=−22.9(1) K suggests the AFE interaction. The inset shows the dielectric permittivity measured along the [100] direction in the ab plane. (b) The temperature dependence of dielectric permittivity ɛc measured with d.c. bias electric fields. A bias electric field of 5 KV cm−1 has no detectable influence on the quantum paraelectric behaviour. The inset shows the P–E loop at 2 K. The nearly linear response and the low values of P imply the AFE coupling.
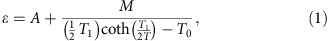 |
where A is a constant, T0 is proportional to the effective dipole–dipole coupling constant and the positive and negative values correspond to FE and AFE interactions, respectively. T1 represents the tunnelling integral and is a dividing temperature between the low-temperature region where quantum fluctuation is important and the high-temperature region where quantum effect is negligible. M=nμ2/kB, where n is the density of dipoles, μ denotes the local dipolar moment and kB is the Boltzmann constant.
After fitting the ɛc below 160 K to the Barrett formula, we obtained T0=−22.9(1) K and T1=47.3(1) K. The negative T0 confirms the AFE coupling between electric dipoles. We note that recent first-principle calculations30 also predicted the AFE interaction with frustration in BaFe12O19. The relative strength of quantum fluctuations can be estimated by ∼|T1/T0|=2.06, which is likely high enough to favour a liquid ground state rather than an ordered or glass phase. The uniaxial anisotropy is evidenced by comparing the dielectric permittivity along the c axis with that in the ab plane. As seen in the inset of Fig. 2a, the in-plane ɛ decreases slowly with decreasing temperature (less than 1 for a temperature interval of 250 K). The absence of a paraelectric behaviour in the ab plane is consistent with the uniaxial electric dipoles along the c axis.
Further lines of evidence of the AFE coupling in BaFe12O19 are presented in Fig. 2b. For those perovskite quantum paraelectrics with FE coupling, such as SrTiO3, a moderated electric field is able to drive the quantum paraelectric state into a long-range ordered FE state31. In strong contrast, for BaFe12O19, an external electric field of 5 KV cm−1 applied along the c axis has no detectable influence on the dielectric permittivity. This inertness to external electric fields may indicate the AFE interaction in BaFe12O19. Moreover, the P–E loop at 2 K (the inset of Fig. 2b) shows a nearly linear response with quite small polarization up to a high electric field of 30 kV cm−1, further implying the AFE coupling. It should be clarified that the magnetic moments of Fe3+ at the bipyramidal sites are all parallel along the c axis in the R/R* blocks (see Supplementary Fig. 1) so that there is no magnetic frustration on the triangular lattice.
Heat capacity and thermal conductivity
The thermodynamic studies at temperatures as low as possible are crucial to identify the conjectured quantum liquid state, as they provide the key information on the spectrum of low-energy elementary excitations. Heat capacity and thermal transport measurements can probe the low-energy density of states as well as determine whether these low-energy excitations are localized or itinerant, and have been indispensably employed in the study of QSLs32,33,34.
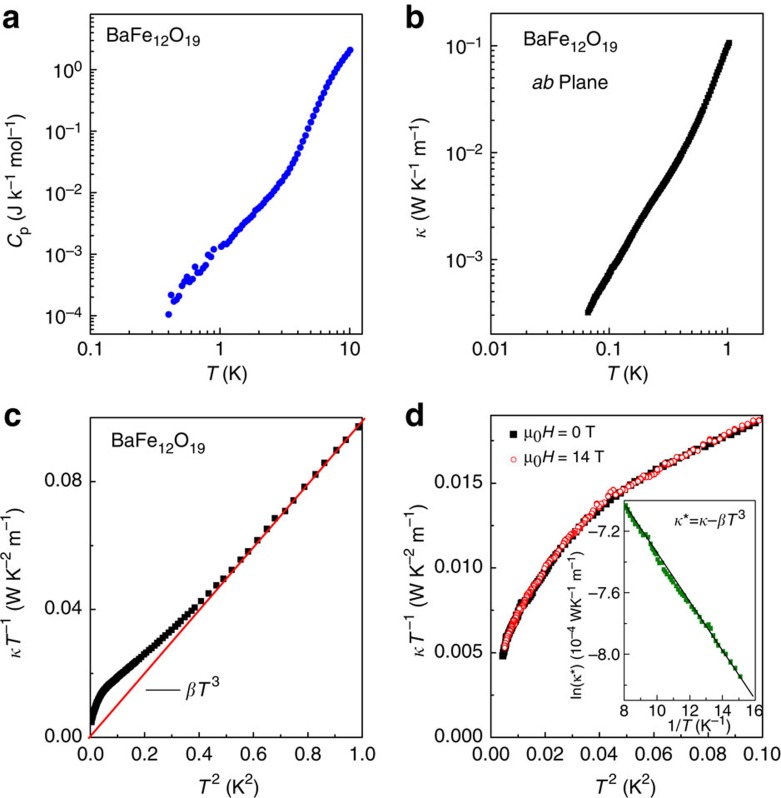
Since BaFe12O19 is a good insulator (see Supplementary Fig. 2) with long-range collinear ferrimagnetic ordering (TN=720 K), both the electronic and magnon contributions to the thermal dynamics become negligible at very low temperatures35. Therefore, its thermodynamics at low enough temperatures should be dominated by the lattice contribution only, and the well-known T3 dependence would be expected for both the heat capacity and thermal conductivity. Figure 3a shows the heat capacity (CP) of BaFe12O19 at low temperatures (T<10 K). No sharp anomaly due to a phase transition could be detected down to 0.4 K, in accordance with the quantum paraelectric behaviour. Unfortunately, the heat capacity data become scattered and noisy below ∼1 K, possibly because of the very small values that reach the resolution limit of our equipment. Thus, a quantitative analysis of the heat capacity data is not possible.
Figure 3. Heat capacity and thermal conductivity of BaFe12O19.
(a) Heat capacity Cp as a function of temperature. No phase transition is detected down to 0.4 K. (b) Thermal conductivity κ measured in the ab plane as a function of temperature. No anomaly due to a phase transition is observed down to 66 mK. (c) The ab plane thermal conductivity divided by temperature plotted as a function of T2 below ∼1 K. The red solid line represents the expected thermal conductivity of phonons, κ=βT3, with β=0.098 WK−4 m−1. Apparently, there is an extra contribution beside the phonon thermal conductivity below ∼650 mK. (d) The κT−1 versus T2 plot in the lowest temperature region. κ/T tends to vanish at the T→0 K limit. An applied magnetic field of 14 T along the c axis has no influence on the ab plane thermal conductivity in this low-temperature region. The inset shows the Arrhenius plot of κ*=κ−βT3 below ∼125 mK. The good linearity suggests gapped excitations with a small gap ∼0.16 K.
The thermal conductivity provides more reliable and critical information on the low-lying elementary excitations because it is sensitive exclusively to itinerant excitations and is totally insensitive to localized entities that may cause the nuclear Schottky contribution and plague the heat capacity measurements at low temperatures33,34. For example, although the heat capacity study32 suggested a gapless QSL in the frustrated triangular magnet κ-(BEDT-TTF)2Cu2(CN)3, the thermal conductivity measurements33 carried out down to 80 mK clarified instead a gapped QSL in the same material. We then have devoted a great effort to measure precisely the thermal conductivity of BaFe12O19 down to 66 mK.
Figure 3b shows the thermal conductivity κ measured in the ab plane as a function of temperature below ∼1 K. κ decreases rapidly with cooling, with a change more than 2 orders from 1 to 100 mK. No anomaly due to a phase transition is observed down to 66 mK. The thermal conductivity divided by temperature as a function of T2 is plotted in Fig. 3c. The data between 0.65 and 1 K exactly follow a linear relation with an extrapolation to the origin, in a good agreement with what expected for the phonon thermal conductivity, κ=βT3, with β=0.098 WK−4 m−1. Nevertheless, there is apparently an extra contribution below ∼650 mK in addition to the normal phonon term, strongly suggesting the existence of abundant itinerant low-energy excitations other than phonons. Moreover, the thermal transport behaviour at the zero temperature limit provides the key information on the nature of these low-lying excitations. As seen in Fig. 3d, κT−1 in the T→0 K limit tends to vanish rather than having a finite residual value, immediately implying the absence of gapless excitations. Instead, the data at the lowest temperature regime (T<125 mK) can be fitted to
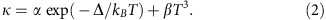 |
The inset of Fig. 3 shows an Arrhenius plot of κ*=κ−βT3 in the lowest temperature region. The good linearity confirms the validity of equation (2). The best fit gives Δ=0.16(1) K, which is much smaller than the effective dipole–dipole interaction constant T0 (∼23 K). The exponential behaviour of thermal conductivity at the zero temperature limit is very similar to that observed in the frustrated triangular magnet κ-(BEDT-TTF)2Cu2(CN)3, where a QSL with gapped excitations (Δ=0.46 K) was identified32. Therefore, the thermal transport behaviour excludes a frozen dipole glass or a classical paraelectric phase but strongly suggests an exotic liquid-like ground state.
To exclude the possibility that these itinerant low-lying excitations may have a magnetic origin, we further studied the influence of magnetic field on the thermal conductivity behaviour. As seen in Fig. 3d, a high magnetic field of 14 T applied along the easy c axis has no influence on the in-plane thermal conductivity in the lowest temperature range. The inertness of these low-lying excitations to external magnetic fields supports our argument that they stem from electric dipoles rather than spins.
Discussion
We think that the above experimental observations, especially the thermal conductivity at the zero temperature limit, strongly indicate the existence of a nontrivial ground state of electric dipoles in BaFe12O19 that is a very unique dielectric system because both geometrical frustration and strong quantum fluctuations play an important role, a situation similar to frustrated antiferromagnets where people are looking for QSLs. This unusual ground state is characterized by itinerant low-energy excitations with a tiny gap (Δ=0.16 K) that is 140 times smaller than the effective dipole–dipole interaction constant T0 (∼23 K), a feature against a dipole glass or a classical dipole liquid. Thus, we consider it as a possible candidate of an exotic QEL. As current theoretical models proposed for frustrated spin systems, such as the transverse Ising models on a triangular lattice, are inadequate for the frustrated electric dipoles because the long-range dipole–dipole interactions are quite different from the short-range spin exchange interactions, a quantitative comparison between experiments and theories is not available at this stage. We expect that our experimental findings will stimulate theoretical efforts towards this interesting subject in the future. The present work serves as a start point to draw attention on frustrated quantum electric dipoles in dielectric materials where an abundance of exotic phenomena could be awaiting ahead.
Methods
Sample preparation
The single-crystal samples of BaFe12O19 were prepared with the flux method and were characterized with X-ray diffraction, as shown in Supplementary Fig. 3. Powders of BaCO3, Fe2O3 and fluxing agent Na2CO3 were weighed to a molar ratio of 1:1:1, and then were mixed and well ground. The ground raw powder was put in a Pt crucible and heated to 1,250 °C for 24 h in the air, and then cooled down to 1,100 °C at a rate of 3 °C min−1 and finally quenched to room temperature.
Dielectric measurements
The dielectric measurements were carried out in a Cryogen-free Superconducting Magnet System (Oxford Instruments, TeslatronPT) down to 1.5 K. To measure the dielectric permittivity, silver paste was painted on the surfaces of a thin plate of crystal and annealed at 150 °C for ∼30 min to make good electrodes. An Agilent 4980A LCR meter was used to measure the dielectric permittivity with the frequency f=1 MHz.
Heat capacity and thermal transport measurements
Heat capacity measurements were performed down to 0.4 K in a commercial Physical Properties Measurement System (Quantum Design) using a 3He refrigerator. A thin-plate-shaped sample with mass of 12.7 mg was used for this measurement. The contribution of attendant was measured separately and subtracted from the raw data. Thermal conductivity was measured between 60 mK and 1 K using the conventional steady-state ‘one heater, two thermometers' technique in a 3He–4He dilution refrigerator36,37. A parallelepiped-shaped sample with size of 2.0 × 0.57 × 0.11 mm3 was cut from the as-grown crystals for thermal conductivity measurements. A chip heater and two RuO2 chip sensors are attached to the sample with gold wires. The temperature difference between the two thermometers was controlled to be typically 3% of the sample temperature. To minimize heat leak, superconducting NbTi wires with 15 μm diameter are used as the leads of the chip sensors.
Additional information
How to cite this article: Shen, S.-P. et al. Quantum electric-dipole liquid on a triangular lattice. Nat. Commun. 7:10569 doi: 10.1038/ncomms10569 (2016).
Supplementary Material
Supplementary Figures 1-3
Acknowledgments
This work was supported by the National Basic Research Program of China (Grant No. 2015CB921201), the National Natural Science Foundation of China (Grant Nos. 11227405, 11534015, 11374347, 11174263 and U1532147) and the Opening Project of Wuhan National High Magnetic Field Center (Grant No. PHMFF2015021). Y.S. also acknowledges the support from Chinese Academy of Sciences (Grants No. XDB07030200 and KJZD-EW-M05).
Footnotes
Author contributions Y.S. conceived the study and designed experiments with X.F.S. S.-P.S. prepared the sample and carried out dielectric and magnetic measurements. J.-C.W. and J.-D.S. performed heat capacity and thermal conductivity measurements. Y.-F.Y., Y.-S.C., D.-S.S., S.-G.W. and J.F.S. contributed to the data analysis and discussions. Y.S. and Y.-F.Y. wrote the paper, and all authors reviewed the paper.
References
- Ramirez A. P. Strongly geometrically frustrated magnets. Annu. Rev. Mater. Sci. 24, 453–480 (1994). [Google Scholar]
- Moessner R. & Ramirez A. P. Geometrical frustration. Phys. Today 59, 24–29 (2006). [Google Scholar]
- Balents L. Spin liquids in frustrated magnets. Nature 464, 199–208 (2010). [DOI] [PubMed] [Google Scholar]
- Wen X.-G. Quantum orders and symmetric spin liquids. Phys. Rev. B 65, 165113 (2002). [Google Scholar]
- Sachdev S. Quantum magnetism and criticality. Nat. Phys. 4, 173–185 (2008). [Google Scholar]
- Moessner R., Sondhi S. L. & Chandra P. Two-dimensional periodic frustrated Ising models in a transverse field. Phys. Rev. Lett. 84, 4457–4460 (2000). [DOI] [PubMed] [Google Scholar]
- Moessner R. & Sondhi S. L. Ising models of quantum frustration. Phys. Rev. B 63, 224401 (2001). [Google Scholar]
- Moessner R. & Sondhi S. L. Resonating valence bond phase in the triangular lattice quantum dimer model. Phys. Rev. Lett. 86, 1881–1884 (2001). [DOI] [PubMed] [Google Scholar]
- Jiang Y. & Emig T. String picture for a model of frustrated quantum magnets and dimers. Phys. Rev. Lett. 94, 110604 (2005). [DOI] [PubMed] [Google Scholar]
- Capriotti L., Trumper A. E. & Sorella S. Long-range Néel order in the triangular Heisenberg model. Phys. Rev. Lett. 82, 3899–3902 (1999). [Google Scholar]
- Suzuki N., Matsubara F., Fujiki S. & Shirakura T. Absence of classical long-range order in an S=1/2 Heisenberg antiferromagnet on a triangular lattice. Phys. Rev. B 90, 184414 (2014). [Google Scholar]
- Shimizu Y. et al. Spin liquid state in an organic Mott insulator with a triangular lattice. Phys. Rev. Lett. 91, 107001 (2003). [DOI] [PubMed] [Google Scholar]
- Lee S. H. et al. Quantum-spin-liquid states in the two-dimensional kagome antiferromagnets ZnxCu4−x(OD)6Cl2. Nat. Mater. 6, 853–857 (2007). [DOI] [PubMed] [Google Scholar]
- Okamoto Y. et al. Spin-liquid state in the S=1/2 hyperkagome antiferromagnet Na4Ir3O8. Phys. Rev. Lett. 99, 137207 (2007). [DOI] [PubMed] [Google Scholar]
- Han T. H. et al. Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet. Nature 492, 406–410 (2012). [DOI] [PubMed] [Google Scholar]
- Clark L. et al. Gapless spin liquid ground state in the S=1/2 vanadium oxyfluoride kagome antiferromagnet [NH4]2[C7H14N][V7O6F18]. Phys. Rev. Lett. 110, 207208 (2013). [DOI] [PubMed] [Google Scholar]
- Sun K., Zhao E. & Liu W. V. Topological phases of dipolar particles in elongated Wannier orbitals. Phys. Rev. Lett. 104, 165303 (2010). [DOI] [PubMed] [Google Scholar]
- Rowley S. E. et al. Ferroelectric quantum criticality. Nat. Phys. 10, 367–372 (2014). [Google Scholar]
- Baranov M., Dalmonte A., Pupillo M. G. & Zoller P. Condensed matter theory of dipolar quantum gases. Chem. Rev. 112, 5012–5061 (2012). [DOI] [PubMed] [Google Scholar]
- Courtens E. Vogel-Fulcher scaling of the susceptibility in a mixed-crystal proton glass. Phys. Rev. Lett. 52, 69–72 (1984). [Google Scholar]
- Vugmeister B. E. & Glinchuk M. D. Dipole glass and ferroelectricity in random-site electric dipole systems. Rev. Mod. Phys. 62, 993–1026 (1990). [Google Scholar]
- Müller K. A. & Burkhard H. SrTiO3: an intrinsic quantum paraelectric below 4 K. Phys. Rev. B 19, 3593–3602 (1979). [Google Scholar]
- Prosandeev S. A., Kleemann W., Westwanski B. & Dec J. Quantum paraelectricity in the mean-field approximation. Phys. Rev. B 60, 14489–14491 (1999). [Google Scholar]
- Shen S. et al. Magnetic-ion-induced displacive electric polarization in FeO5 bipyramidal units of (Ba,Sr)Fe12O19 hexaferrites. Phys. Rev. B 90, 180404 (2014). [Google Scholar]
- Pullar R. C. Hexagonal ferrites: a review of the synthesis, properties and applications of hexaferrite ceramics. Prog. Mater. Sci 57, 1191–1334 (2012). [Google Scholar]
- Albanses G., Deriu A. & Cabrini D. The dynamics of iron ions in pseudotetrahedral (bipyramidal) sites of BaFe12O19 and SrFe12O19 hexagonal ferrites. Hyperfine Interact. 70, 1087–1090 (1992). [Google Scholar]
- Obradors X., Collomb A., Pernet M., Samaras D. & Joubert J. C. X-ray analysis of the structural and dynamic properties of BaFe12O19 hexagonal ferrite at room temperature. J. Solid State Chem. 56, 171–181 (1985). [Google Scholar]
- Cao H. B. et al. High pressure floating zone growth and structural properties of ferrimagnetic quantum paraelectric BaFe12O19. APL Mater. 3, 062512 (2015). [Google Scholar]
- Barrett J. H. Dielectric constant in perovskite type crystals. Phys. Rev. 86, 118–120 (1952). [Google Scholar]
- Wang P. S. & Xiang H. J. Room-temperature ferrimagnet with frustrated antiferroelectricity: promising candidate toward multiple-state memory. Phys. Rev. X 4, 011035 (2014). [Google Scholar]
- Hemberger J., Nicklas M., Viana R., Lunkenheimer P., Loidl A. & Bohmer R. Quantum paraelectric and induced ferroelectric states in SrTiO3. J. Phys. Condens. Matter 8, 4673–4690 (1996). [Google Scholar]
- Yamashita S. et al. Thermodynamic properties of a spin-1/2 spin-liquid state in a κ-type organic salt. Nat. Phys. 4, 459–462 (2008). [Google Scholar]
- Yamashita M. et al. Thermal-transport measurements in a quantum spin-liquid state of the frustrated triangular magnet κ-(BEDT-TTF)2Cu2(CN)3. Nat. Phys. 5, 44–47 (2009). [Google Scholar]
- Yamashita M. et al. Highly mobile gapless excitations in a two-dimensional candidate quantum spin liquid. Science 328, 1246–1248 (2010). [DOI] [PubMed] [Google Scholar]
- Hess C. et al. Magnon heat transport in doped La2CuO4. Phys. Rev. Lett. 90, 197002 (2003). [DOI] [PubMed] [Google Scholar]
- Zhao Z. Y. et al. Thermal conductivity of IPA-CuCl3: evidence for ballistic magnon transport and the limited applicability of the Bose-Einstein condensation model. Phys. Rev. B 91, 134420 (2015). [Google Scholar]
- Sun X., Segawa K. & Ando Y. Metal-to-insulator crossover in YBa2Cu3Oy probed by low-temperature quasiparticle heat transport. Phys. Rev. Lett. 93, 107001 (2004). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figures 1-3