Formant measurement in children’s speech based on spectral filtering

Abstract

Children’s speech presents a challenging problem for formant frequency measurement. In part, this is because high fundamental frequencies, typical of a children’s speech production, generate widely spaced harmonic components that may undersample the spectral shape of the vocal tract transfer function. In addition, there is often a weakening of upper harmonic energy and a noise component due to glottal turbulence. The purpose of this study was to develop a formant measurement technique based on cepstral analysis that does not require modification of the cepstrum itself or transformation back to the spectral domain. Instead, a narrow-band spectrum is low-pass filtered with a cutoff point (i.e., cutoff “quefrency” in the terminology of cepstral analysis) to preserve only the spectral envelope. To test the method, speech representative of a 2–3 year-old child was simulated with an airway modulation model of speech production. The model, which includes physiologically-scaled vocal folds and vocal tract, generates sound output analogous to a microphone signal. The vocal tract resonance frequencies can be calculated independently of the output signal and thus provide test cases that allow for assessing the accuracy of the formant tracking algorithm. When applied to the simulated child-like speech, the spectral filtering approach was shown to provide a clear spectrographic representation of formant change over the time course of the signal, and facilitates tracking formant frequencies for further analysis.

1 Introduction

The formant frequencies present in a speech signal are regions of spectral prominence for which acoustic energy has been enhanced, and provide cues for the perception of both vowels and consonants. Formants are the resultant effect of the interaction of vocal tract resonances with a source of sound, and thus provide an “acoustic window” to the shape of the vocal tract, albeit indirect. For adult speech, wide-band spectrography and linear prediction (LP) techniques (e.g., Makhoul, 1975; Markel & Gray, 1976) can provide reasonably accurate measurements of the formants (Monsen & Engebretsen, 1983; Vallabha & Tuller, 2002). In part, this is because the ample harmonics produced by the voice source adequately sample the vocal tract transfer function and express it clearly as the envelope of the speech spectrum. On the other hand, children’s speech is typically characterized by high fundamental frequencies (e.g., 250–600 Hz) that generate widely spaced harmonic components, producing an apparent undersampling of the vocal tract transfer function (c.f., Lindblom, 1962; Kent, 1976). It then becomes difficult to measure the formant frequencies from the spectral envelope because the envelope peaks are strongly influenced by individual harmonic amplitudes rather than by a collective effect of many closely-spaced harmonics. In addition, children may produce a breathy voice quality characterized by low amplitude upper harmonics and a significant noise component due to glottal turbulence (Glaze et al., 1988; Ferrand, 2000).

The problem of estimating formants from speech with high fundamental frequencies (f_o) is well known (cf. Lindblom, 1962, 1972; Fant, 1968; Kent, 1976) and has been addressed with a variety of techniques and methods. With wide-band spectrography, for example, the effective filter bandwidth can be increased to obscure individual harmonic components such that broad formant peaks can be observed (Eguchi & Hirsh, 1969; Lindblom, 1972; Kent, 1976; Bennett, 1981), but potentially with considerable error as pointed out by Lindblom (1972). Modifications to linear prediction methods have also been proposed to deal with formant measurement in high-f_o speech (cf., Hermansky et al., 1984; El-Jaroudi & Makhoul, 1991; Ma et al., 1993). More recently, Alku et al. (2013) proposed a weighted linear prediction technique in which the main points of excitation within each glottal cycle are attenuated. This has the effect of giving more weight to the portions of each cycle that contain information about vocal tract resonances rather than the voice source, and results in better estimates of formant frequencies. Liu and Shimamura (2015) reported a similar technique but without the need to identify glottal closure epochs.

Undersampling the vocal tract transfer function in high-f_o speech can be mitigated to some degree by varying the fundamental frequency over the time course of an utterance. This has the effect of sweeping the f_o and associated harmonic components through the resonance peaks in the transfer function, thus producing a more complete excitation of the formant structure, albeit over an adequately long temporal window. White (1991) reported a formant measurement technique in which 11 year-old children were asked to produce a vowel, either spoken or sung, while simultaneously shifting their f_o from low to high frequency. The duration of the recordings was 1–2 seconds and formants were identified from a narrow-band spectrogram as the points at which the harmonic amplitudes were highest; these coincided with the points in time at which a particular harmonic passed through a resonance peak in the vocal tract transfer function. This is perhaps a useful method, but relies on the ability of the talker to perform the unusual task of maintaining a static vocal tract configuration during a pitch glide, and does not lend itself to analysis of time-varying speech. Wang and Quatieri (2010) similarly exploited f_o changes to develop a signal processing technique for detecting the vocal tract resonances in high-f_o speech, but relied on the natural variation of f_o in human speech rather than deliberately asking talkers to produce f_o glides. Using localized 2D Fourier transforms of the temporal-spatial variation of speech, they showed an improved separation of the voice source and vocal tract filter when the f_o was changing.

Cepstral analysis is an alternative approach to measuring formants in high-f_o speech. The envelope of the log spectrum of a speech segment can be considered analogous to a low frequency modulation of a waveform, whereas the individual harmonics or noise components can be regarded as an analogy to a carrier signal. Thus, calculation of the log spectrum of the initial log spectrum results in yet another kind of spectrum, called the cepstrum (Bogert et al., 1963), that separates the envelope from the harmonics and higher frequency noise. The cepstrum can be modified such that only the portion related to the envelope is retained, and then transformed back to the spectral domain. The result is an estimate of the spectral envelope, the peaks of which are representative of the formants (cf. Childers et al., 1977). As has been shown Fort and Manfredi (1998), cepstral filtering can be enhanced by allowing the filter (or “lifter”) length to be dependent on the fundamental frequency within a given time frame, and using a chirp Z-transform to improve the resolution for finding spectral peaks. Rahman and Shimamura (2005) have also improved formant tracking in high-f_o signals by applying linear prediction to the portion of the cepstrum related to the vocal tract impulse response.

The purpose of this study was to develop and test a technique for visualizing and measuring formants in children’s speech with a wide range of variation of f_o, vocal tract resonances, and distribution of harmonic and noise-like energy. The method is conceptually based on cepstral analysis (Bogert et al., 1963), but does not require modification of the cepstrum itself or transformation back to the spectral domain. Instead, the narrow-band spectrum over any given time-window is low-pass filtered with a selected cutoff point (i.e., cutoff “quefrency” in the terminology of cepstral analysis), determined by the time-dependent f_o, to preserve only the spectral envelope. Formants are then measured by applying a peaking-picking algorithm to the spectral envelope.

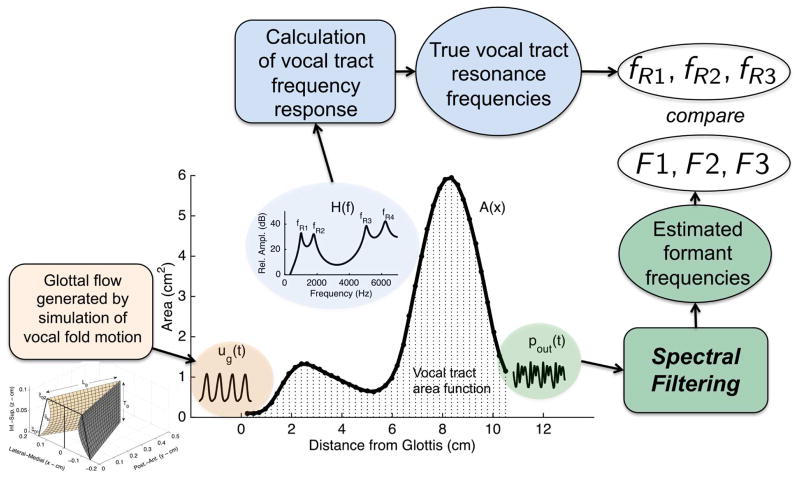
Assessing the accuracy of formant tracking algorithms applied to natural (recorded) speech can be problematic because the “true” answer is typically unavailable. That is, an algorithm will deliver measurements of the formant frequencies but whether they are reasonable estimates of the vocal tract resonances produced by the talker is unknown. A typical paradigm for testing is to apply the algorithm to synthetic speech for which the resonance frequencies are known a priori and compare them to the formant values determined by the algorithm. As illustrated in Fig. 1, a similar paradigm was used here by applying the spectral filtering method to artificial speech samples, representative of a 2–3 year-old child talker, that were produced with a computational model such that resonance frequencies could be calculated independently of the spectral filtering algorithm. The model allows for time-dependent variations in vocal tract shape, f_o, and degree of vocal fold adduction. In addition, the glottal flow signal is produced interactively with the propagating acoustic pressures in the vocal tract, and contains noise that emulates the effects of glottal turbulence. Thus, the generated audio samples include characteristics similar to those observed in children’s speech and provide reasonably challenging cases for testing the algorithm (or any other algorithm designed to track formants).

Figure 1.

Vocal tract area function of an /ɑ/-like vowel for a 2–3 year-old talker. A kinematic model vocal fold vibration coupled to the aerodynamics and acoustics of the vocal tract generates the glottal flow, u_g(t). The excitation signal is propagated through the vocal tract with a wave-reflection algorithm and terminates into a radiation impedance to generate the output sound pressure, p_out(t). The frequency response H(f) is calculated with an impulse response technique separately from the simulation of the vowel and yields values for the vocal tract resonances f_Rn independent from measurements of the formants F_n based on the spectral filtering algorithm.

The specific aims of the paper are to 1) describe the model used to simulate child-like speech samples, 2) describe the spectral filtering algorithm, and 3) apply the algorithm to the simulated speech samples and compare results to the known values of vocal tract resonances. In addition, the spectrographic representation provided by the spectral filtering algorithm will be compared to that given by a conventional linear prediction algorithm.

2 Simulation of child-like speech

The speech production model depicted in Fig. 1 consists of two main components: 1) a kinematic representation of the medial surfaces of the vocal folds, and 2) a vocal tract airway defined by an area function. The vocal fold medial surfaces can be controlled to modulate the glottal airspace on a slow time scale for adduction and abduction maneuvers, as well as on a more rapid time scale to emulate vocal fold vibration at speech-like fundamental frequencies (Titze, 2006). When supplied with a subglottal pressure the modulation of the glottis produces a glottal airflow signal, u_g(t), that provides the acoustic excitation of the vocal tract. Propagation of acoustic waves through the vocal tract shape, represented as an area function, is calculated with a wave-reflection algorithm that includes energy losses due to yielding walls, fluid viscosity, heat conduction, and acoustic radiation at the lip termination (Liljencrants, 1985; Story, 1995). Because the glottal flow and acoustic waves in the vocal tract are calculated in time-synchrony, their nonlinear interaction is simulated. Thus, unlike a linear source-filter synthesizer (e.g., Klatt, 1980), the glottal flow signal may contain ripples or other features that result from its dependence on both the glottal area and the resonances of a given vocal tract shape (cf. Rothenberg, 1986; Titze, 2008). The output of the model is the radiated acoustic pressure, p_out(t), which is analogous to a pressure signal recorded with a microphone from a real talker. The sampling frequency of this signal is f_s = 44100 Hz.

The model used in this study was identical to the description given in Story (2013) except that the vocal fold surfaces and vocal tract were scaled to be roughly representative of a two-year old child. This age was chosen to provide reasonably difficult test cases with regard to high f_o and resonance frequencies, but not to the extreme degree infant sound production might present. Specifically, the vocal fold rest length and thickness were set to L₀ = 0.4 cm and T₀ = 0.15 cm, respectively (Eckel, 1999; Eckel et al. 2000), the surface bulging parameter was ξ_b = 0.04 cm, and the superior distance of the vocal processes from the glottal midline was set to ξ₀₂ = 0.12 cm. The latter parameter setting ensures incomplete glottal closure during vibration in order to produce a moderately breathy quality that is often characteristic of child-like speech. Other settings include the respiratory driving pressure P_L = 15000 dyn/cm² (Stathopoulos & Sapienza, 1997) and a turbulence noise generator that adds band-limited noise (500–5000 Hz) to the glottal flow signal when a Reynold’s number threshold is exceeded (see Story, 2013, p. 995). Although a subglottal airway system can be incorporated into the model, it was not used in this study to ensure that, at this stage, tracheal resonances would not be present in the simulated signals.

The time-dependent configuration of the vocal tract area function was controlled by two shaping patterns called modes that can be combined with an underlying neutral tract shape to generate a wide range of static or time-varying vowel-like area functions (Story, 2005; 2013). The model is written mathematically as,

$$A(i,t)=\frac{\pi }{4}{[\mathrm{\Omega }(i)+q_1(t){\varphi }_1(i)+q_2(t){\varphi }_2(i)]}^{2}i=[1,N_{vt}]$$ (1)

where the sum of the terms in brackets represents a set of N_vt = 44 diameters extending from the glottis to the lips, as indexed by the variable i. The squaring operation and scaling factor of π/4 convert the diameters to areas. The variable Ω(i) is the neutral diameter function and ϕ₁(i) and ϕ₂(i) are the modes. The time-dependent parameters q₁(t) and q₂(t) are coefficient values that, when multiplied by the corresponding mode and added to the neutral diameter function as in Eq. (1), construct a specific vocal tract shape. The overall vocal tract length was set to be L_vt = 10.5 cm, approximately the value reported by Vorperian et al. (2009) for two year-old children based on anatomical growth curves. Thus, the length of each ith section of the area function is ΔL = 10.5/N_vt = 0.2386 cm. Because there are essentially no measured vocal tract area functions available for children¹, the Ω(i), ϕ₁(i), and ϕ₂(i) functions for this study were heuristically derived with an acoustic perturbation technique. A detailed description of the method is outside the scope of this article but was essentially the same as reported in Story (2006, 2007) where an area function representing a “neutral” vowel was perturbed by linear combinations of acoustic sensitivity functions to generate a family of new area functions from which Ω(i), ϕ₁(i), and ϕ₂(i) were derived with Principal Components Analysis (PCA). The three derived functions are presented in tabular form in the Appendix (Table A.1) and can be used in Eq. (1) to generate vowels and vowel transitions based on the [q₁, q₂] coefficient values given in Table A.2. Calculated resonance frequencies based this vocal tract model are in the ranges of measured formants reported for two-year old talkers (Vorperian & Kent, 2007).

Along with calculations of glottal flow and acoustic pressure signals, the frequency response, H(f), of the vocal tract at any given instant of time was also calculated. This was carried out by introducing an ideal flow impulse at the vocal tract entrance and determining the DFT spectrum of the pressure response at the lip termination. In Fig. 1, the frequency response, H(f), for the /ɑ/-like area function is shown in the inset plot. The resonance peaks are denoted as f_R1 − f_R4². When the area function is time-varying, H(f) can be calculated for each incremental change in vocal tract shape to generate time-dependent resonance frequencies.

2.1 Description of simulation cases

To test the spectral filtering algorithm (described in the next section), eight simulations were generated in which several different f_o contours were combined with both static and time-varying area functions to provide a range of cases from which to extract formant frequencies. The simulations are grouped into two sets as described below.

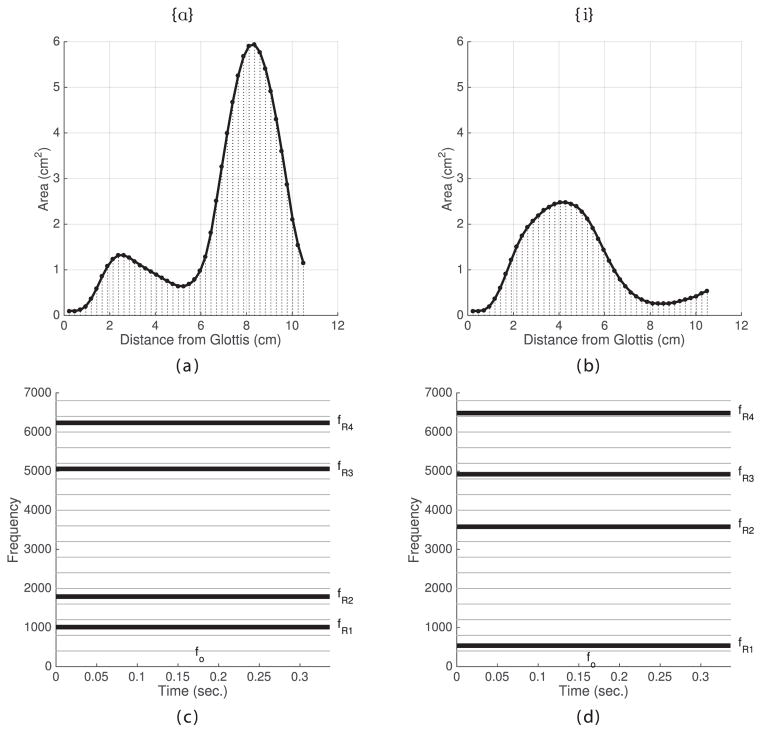
• Set 1: Two area functions representative of the static vowels {ɑ} and {i} were constructed with Eq. (1) (the IPA symbols set within the unconventional curly brackets are used to denote that these samples are constructed with a vocal tract model where the intent is to produce acoustic characteristics similar to the vowels specified by the IPA symbols, but are not phonetic transcriptions of either the target of a real talker, or the perceived sound produced by the simulations). For the {ɑ} [q₁, q₂] = [3.60, −1.26], and for {i}, [q₁, q₂] = [−4.03, −0.41]. Each vowel was simulated with a duration of 0.34 seconds. In both cases, the fundamental frequency was held constant at f_o = 400 Hz. The area functions of the two vowels are shown in the top row of Fig. 2. The dots along each function denote a section i, where i = [1 … 44]. The second row of the figure shows an idealized spectrographic display of the simulations of each vowel in which the calculated resonances frequencies (thick black lines) are superimposed on the f_o and harmonic frequencies (gray). The vocal tract shapes and value of f_o were chosen such that the first resonance frequency was not aligned with any of the harmonics. This was done so that the ability of the spectral filtering algorithm to find a formant peak between harmonics could be evaluated, potentially a more difficult case than when harmonics are aligned with resonance peaks.

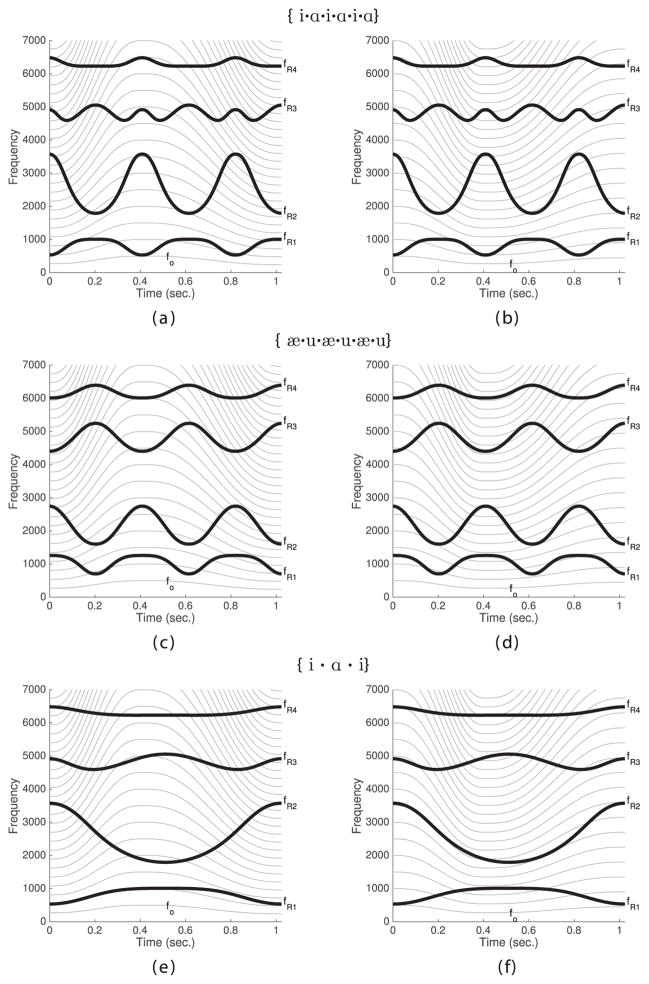
• Set 2: This set of six simulations was comprised of three time-varying vocal tract shapes combined with two different time-dependent variations of f_o. The duration of each simulation was 1.03 seconds³. The first time-varying vocal tract was configured to move back and forth from {i} to {ɑ} three times during the simulation. The temporal variation of [q₁(t), q₂(t)] was produced with a cosine interpolation of the coefficients specified for these same two vowels in Set 1. The points in time at which the interpolation passes through the {i} coefficients were t = [0, 0.4, 0.8], and for the {ɑ}, t = [0.2, 0.6, 1.03]. The second time-varying vocal tract was similarly moved back and forth with the same interpolated temporal variation, but from {æ} to {u}, where the coefficients were set to [q₁, q₂] = [2.26, 2.10] and [q₁, q₂] = [3.0, −2.6] for the two vowels, respectively. In the third case, the vocal tract was more slowly transitioned from {i} to {ɑ} and back to {i}. Each time-varying vocal tract shape was combined with two f_o contours. The first contour started at 270 Hz, increased to 500 Hz within 0.4 seconds, and then decreased to 240 Hz at the end, whereas the second contour began at 500 Hz, dropped to 270 Hz by 0.4 seconds, and then rose to 450 Hz by the end of the simulation. Idealized spectrographic plots can be seen for all six simulations in Fig. 3. These cases were constructed to produce a variety of harmonic sampling situations that are combined with time-dependent variations of resonance frequencies.

Figure 2.

Area functions and corresponding idealized spectrographic plots for child-like {ɑ} and {i} vowels in “Set 1.” The dots along each area function (a & b) represent the i^th consecutive section ordered from glottis to lips. The spectrographic plots include the calculated resonance frequencies, f_Rn, as thick black lines and the f_o and harmonic components as thin gray lines.

Figure 3.

Idealized spectrographic plots for the six time-varying simulations in “Set 2.” In each panel, the calculated resonance frequencies, f_Rn, are shown as thick black lines, and the f_o and harmonic components are plotted as thin gray lines. Note the figure is arranged such that each column corresponds to one of the two f_o contours, and each row corresponds to one of three time-varying vocal tracts.

All eight simulations are included with this article as a set of audio files in “.wav” format, and the resonance frequencies for each of the time-varying cases are provided in tabular form in the Appendix (Table A.3).

3 Spectral filtering algorithm

The spectral filtering algorithm will first be described with reference to a static vowel, where the steps in the process are shown by example. Application to the time-varying case then follows, along with a brief description of a conventional linear prediction method used for comparison.

3.1 Spectral envelope for a static vowel

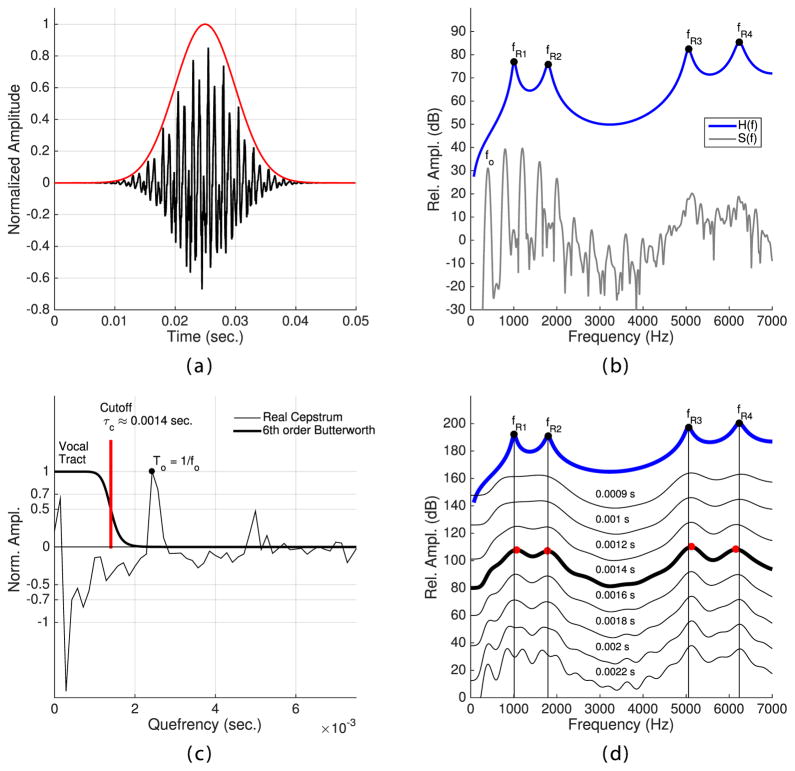
A time segment, 0.05 seconds in duration, taken from the mid-portion of the simulated signal for the static {ɑ} vowel (Fig. 2a) is shown in Fig. 4a. The segment was preemphasized⁴, and then modified with a Gaussian window whose amplitude was less than 0.04 outside the middle 0.025 seconds of the time frame (Boersma & Weenink, 2015). A spectrum for the windowed segment was calculated with a zero-padded 8820 point⁵ DFT so that the frequency resolution was 5 Hz (with f_s = 44100 Hz). The resulting DFT spectrum is shown in gray in Fig. 4b. It can be seen that the first five harmonics are relatively high in amplitude, but energy in the upper harmonics drops off with frequency and gives way to noise. The calculated frequency response of the vocal tract area function is also plotted in Fig. 4b and indicates the location of the resonance frequencies. Although the third and fourth resonances are apparent in the DFT spectrum due the noise excitation, the first two resonances appear to form a only single broad band of energy due to their close proximity and the wide spacing of the harmonics.

Figure 4.

Design of the spectral filter. (a) 0.05 second segment of the simulated signal, preempha-sized and modified with a Gaussian window. (b) Calculated frequency response of the vocal tract shape in Fig. 4a (blue) and the DFT spectrum of the segment in (a). (c) Real cepstrum (thin line) and quefrency response of a 6th order Butterworth filter (thick line). (d) Calculated frequency response along with spectral envelopes obtained with a range of cutoff quefrency settings.

The spectral filtering algorithm is based on applying a low-pass filter to the DFT spectrum to obtain an estimate of the spectral envelope. Because the filtering is applied to a spectrum rather than a waveform, the characteristics of the filter must be specified with respect to the spectrum of the DFT spectrum, which is the well-known cepstrum (cf. Childers et al., 1977). Shown in Fig. 4c is the real cepstrum (obtained by computing the inverse DFT of the spectrum) of the spectrum from Fig. 4b. The cepstrum separates contributions of the vocal tract resonances from those of the voice source along a time axis referred to as quefrency in cepstral terminology (Bogert et al., 1963; Oppenheim & Schafer, 2004). The cepstral peak located at a quefrency of 0.0025 seconds is the reciprocal of the 400 Hz fundamental frequency in the spectrum, whereas information regarding the spectral envelope produced by the vocal tract resonances is found in the leftmost portion of the cepstrum, well below this quefrency.

A low-pass spectral filter that preserves the vocal tract contribution and removes the source excitation can be realized with a Butterworth design where the cutoff point is located at just over half the fundamental period. Experimentation during development of the algorithm indicated that a sixth-order Butterworth filter with a cutoff quefrency set to 0.56/f_o provides the desired filtering effect. For the case here, the cutoff quefrency is 0.56/400 Hz = 0.0014 seconds as indicated by the red vertical line in Fig. 4c; the quefrency response of the filter is shown as the black line. The filter is applied to a spectrum in both the forward and reverse directions along the frequency axis to realize a zero-phase response (Kormylo & Jain, 1974; Oppenheim, Schafer, & Buck, 1999); i.e., the filtering is performed in the forward direction first, and then the output of the first pass is filtered in the reverse direction. This has the effect of preserving phase (and consequently the envelope shape), squaring the magnitude of the filter transfer function (hence, the cutoff quefrency is aligned 0.5 amplitude in Fig. 4c), and effectively doubling the filter order. The zero-phase filter is, in turn, applied to a given spectrum twice, once in the forward direction from low to high frequency, and once in reverse direction from high to low frequency (after filtering, the order of the second spectrum is reversed). This results in two spectra that are then averaged in the linear domain and converted back to the log domain. The combination of the zero-phase filter and the latter averaging operation minimizes spectral “transients” at the two ends of the spectrum that could be confused as formants by an automatic tracking algorithm.

When applied to the DFT spectrum in Fig. 4b, the complete filtering process produces the spectral envelope plotted as the thick black line in Fig. 4d. The other envelope curves demonstrate the effect of a series of different cutoff quefrencies ranging from 0.0009–0.0022 seconds, and at the top of the plot is the calculated frequency response. If the cutoff is too large, harmonic information leaks into the spectral envelope, and when it is too small the formants are obscured.

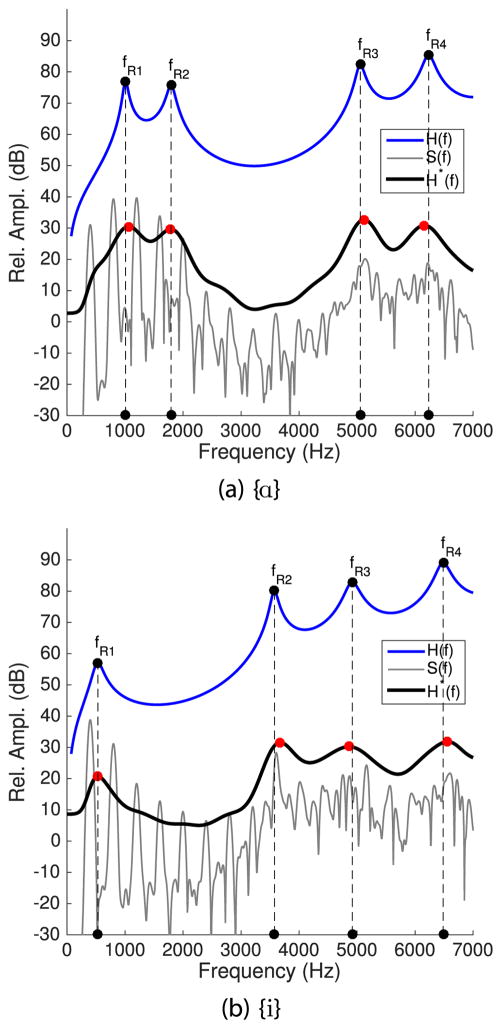
Spectral envelopes determined for the simulated {ɑ} vowel, as well as the {i} from Fig. 2, are plotted in Fig. 5 along with the calculated frequency response curves and DFT spectra. Formants were measured for each spectral envelope by finding the frequency of all peaks with a three-point parabolic interpolation (Titze et al., 1987). The four peaks with the highest amplitudes were chosen as candidates for the formants and their frequencies were sorted in ascending order to yield values for F1, F2, F3 and F4. The black dots and vertical dashed lines denote the calculated resonance frequencies, whereas the red dots are the formants. Table 1 provides frequency values of resonances and formants, directional percent error of the formant measurements relative to the calculated resonances, ε_n = 100(Fn −f_Rn)/f_Rn, as well as the absolute error, Δ_n = |Fn − f_Rn|. The largest percent error was 5.4 percent for F1 of the {ɑ} vowel; the errors of the other measurements were all less than three percent. When absolute error is considered, the largest deviation of 101 Hz occurs for F2 of the {i} vowel, whereas the others are all less than 75 Hz. It is encouraging that, even though the spectral shape of the {ɑ} vowel does not visually provide much indication of two separate peaks for F1 and F2, the spectral envelope produced by the filter does reveal their presence. Similarly, for the {i} an F1 peak is present in the spectral envelope that is aligned with the calculated f_R1 and not f_o as might be expected from visual inspection of the spectrum.

Figure 5.

DFT spectra, calculated frequency response functions, and spectral envelopes based on filtering the simulated {ɑ} and {i} vowels in “Set 1.’

Table 1.

Calculated resonance frequencies, f_Rn, and measured formants, Fn, for simulated {ɑ} and {i} vowels where f_o = 400 Hz. Percent error for each measurement is shown in the third row and calculated as 100(Fn − f_Rn)/f_Rn. The absolute errors, calculated as Δ_n = |Fn − f_Rn|, are given in the bottom row.

	{ɑ}				{i}
n	1	2	3	4	1	2	3	4
fRn(Hz)	1009	1793	5056	6234	533	3576	4918	6484
Fn(Hz)	1063	1789	5120	6161	534	3677	4860	6562
εn (% error)	5.4	−0.2	1.3	−1.2	0.2	2.8	−1.2	1.2
Δn(Hz)	54	4	64	73	1	101	58	78

3.2 Time-varying spectral envelope

To analyze a time-varying signal, the spectral envelope must be determined for consecutive waveform segments that are overlapped in time. The segment length was set to 0.05 seconds, and consecutive segments were shifted by 0.002 seconds giving approximately a 96 percent overlap factor. The spectral filtering method also requires that the f_o be determined for each time segment in order to set the cutoff point of the Butterworth filter. Although this could be accomplished by finding harmonics in the computed DFT spectrum, utilizing an autocorrelation method applied directly to the segmented waveform tended to be more robust for signals with noise present. Once the f_o was determined for any given segment, the normalized cutoff point, W_n, was calculated as,

$$W_n=\frac{0.56/f_o}{\frac{1}{2\mathrm{\Delta }f}}=1.12\frac{\mathrm{\Delta }f}{f_o}$$ (2)

where Δf is the “sampling interval” (i.e., the frequency resolution) of the DFT spectrum, and the scaling coefficient of 1.12 assures that the cutoff will be set to slightly greater than half the fundamental period, as discussed in the previous section. The spectral envelope for a given segment can then be obtained by applying the filter.

After the spectral envelopes have been calculated in sequence over the time course of an utterance, each envelope in the sequence was normalized to its own maximum value. The time-dependent amplitude values along each frequency bin were then smoothed with a second-order Butterworth filter set to a cutoff frequency of 15 Hz, again applied as a zero-phase formulation. This was done to enhance the visual representation as well as to facilitate tracking formants. Formants were measured for each spectral envelope with the same method described for the static case. The resulting formant tracks are an estimate of the temporal variation of the vocal tract resonances produced during an utterance.

3.3 Linear prediction

For purposes of comparison, a linear prediction algorithm was also configured to extract time-varying spectral envelopes from a speech signal. Each signal was first downsampled to f_s = 14000 Hz, and then segmented into overlapping 0.05 second windows; the amount of overlap and Gaussian window were identical to those used in the spectral filtering method. An autocorrelation LP algorithm (Jackson, 1989; Mathworks, 2015) with 12 coefficients was used to produce an estimate of the spectral envelope. Formants were tracked with the same peak-picking technique described in the previous subsection for the spectral filtering method.

3.4 Implementation

All components of the spectral filtering and linear prediction algorithms were written in Matlab (Mathworks, 2015) and made use of many of the built-in functions available for signal processing and graphical display.

4 Results

The spectral filtering and LP algorithms were applied to each of the six time-varying cases illustrated in Fig. 3, and the results are presented in Figs. 6, 7, and 8. Each figure shows results from one of the three time-varying vocal tracts, and is arranged such that each of the two columns corresponds to the two different f_o contours.

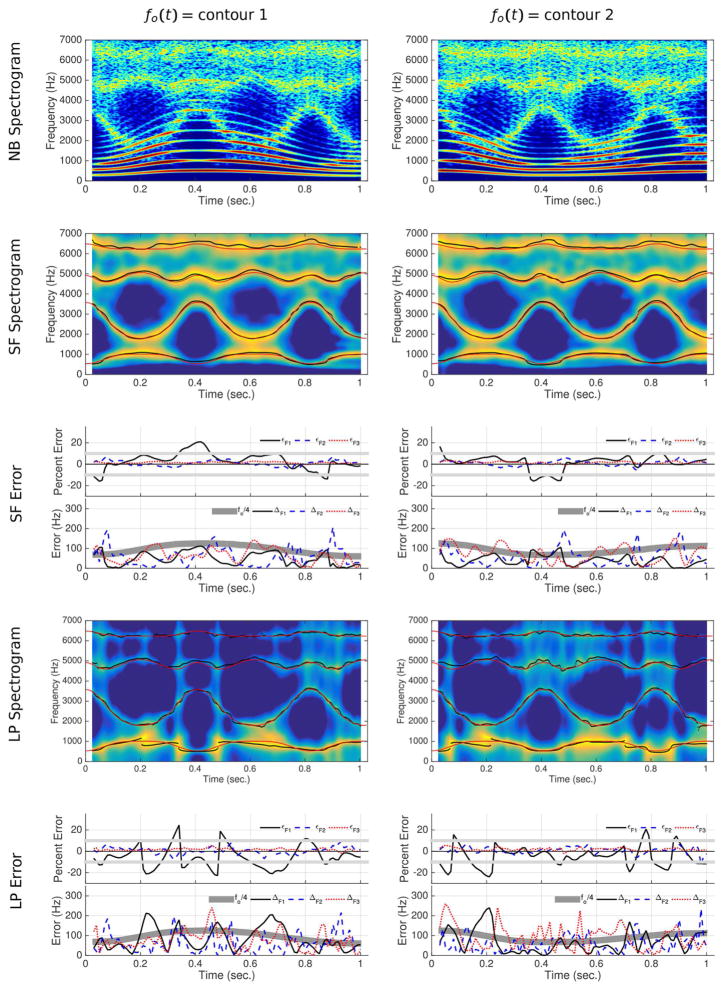
Figure 6.

Results of spectral filtering and linear prediction analysis for two simulations of {i·ɑ·i·ɑ·i·ɑ}. (Top row) Narrowband (NB) spectrograms. (Second row) Spectrographic display of the time-varying envelopes obtained with the spectral filtering (SF) method. Black dotted lines show formant tracking, and red lines are calculated resonances. (Third row) Two types of error calculations for the first three formants tracked with the spectral filtering (SF) relative to the calculated resonance frequencies. (Fourth row) Spectrographic display obtained with linear prediction (LP). Black dotted lines show formant tracking and manual correction, and red lines are the calculated resonances. (Bottom row) Error calculations for the first three LP formants (corrected) relative to the calculated resonance frequencies.

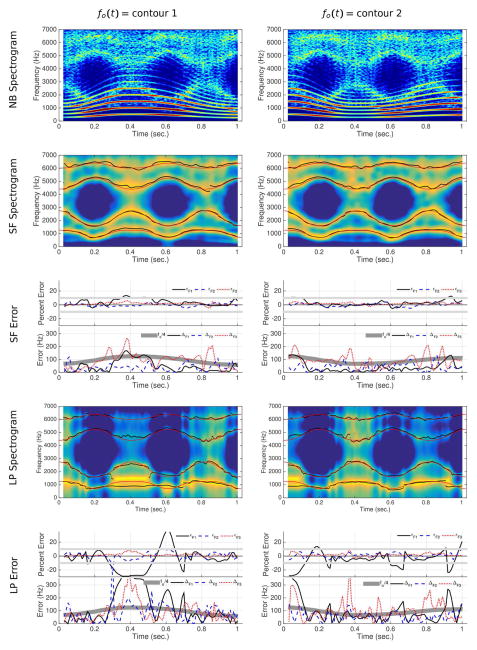
Figure 7.

Results of spectral filtering and linear prediction analysis for two simulations of {æ·u·æ·u·æ·u}. The arrangement of the plots is identical to Fig. 6.

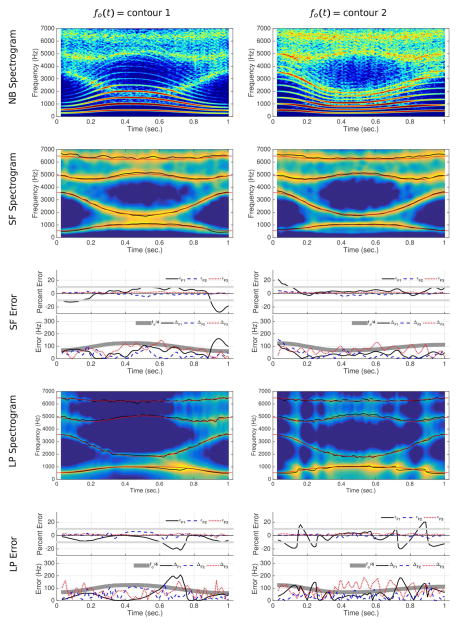
Figure 8.

Results of spectral filtering and linear prediction analysis for two simulations of {i · ɑ · i}. The arrangement of the plots is identical to Figs. 6 and 7.

In the first row of Fig. 6 are narrow-band spectrograms of the speech signals for {i·ɑ·i·ɑ·i·ɑ}, where variation of the f_o, harmonics, and noise due to turbulence combined with the vocal tract resonances can be seen. A spectrographic display of the time-varying envelopes obtained with spectral filtering are shown in the second row of the figure for each of two f_o contours. The formant tracks, Fn(t), in each of these panels are shown with black dots and the true (calculated) resonance frequencies, f_Rn(t), are plotted as red lines.

Visually, the formants observed in these spectrographic plots follow the calculated resonances fairly closely, but with some amount of deviation. The tracking error was assessed with the same two calculations used for the static vowels but in time-dependent form: 1) the directional percent error ε_n(t) = 100(Fn(t) − f_Rn(t))/f_Rn(t), and 2) the absolute error Δ_n(t) = |Fn(t) − f_Rn(t)|. Both error functions are plotted for each of the two simulations in the third row of Fig. 6 (because of relative importance of F1, F2, and F3, and to maintain clarity in the plots, errors for only the n = 3 formants are shown). The percent error functions are shown with superimposed gray lines that bracket ±10 percent. Although 10 percent is greater than difference limens reported for formants (Flanagan, 1955), it is adopted here as a reasonable level of error considering the nature of the high f_o signal. For F1, the percent error exceeds 10 percent in either the positive or negative direction during a few short segments of each simulation when the frequency of F1 is very low, but otherwise is mostly constrained within the gray lines. For F2 and F3, the percent error is well within the gray lines, and is considerably lower than the F1 error. Regardless of the f_o, F1 percent error tends to increase as F1 moves downward in frequency because the formant peak may become only partially defined (Monson & Engebretson, 1983), and any given number of Hz deviation contributes a larger percentage to the measurement error for low frequency formant values than at higher frequencies. In addition, preemphasis will slightly attenuate the amplitude of the f_o component (Klatt, 1986) resulting in a change of the relative weighting provided by the first few harmonic amplitudes that define the shape of the F1 formant peak (Lindblom, 1962) (the advantages of preemphasis for measuring the higher formants, however, outweigh the slight disadvantage for F1). Absolute error functions are plotted along with a thick gray line that denotes the fundamental frequency at each point in time divided by four, i.e., f_o(t)/4. Lindblom (1962, 1972) suggested this value as the hypothetical error that could be expected in formant measurements. It is shown here as another rough criterion for judging the success of formant tracking. With the exception of few spurious points, the absolute error of F1 is less than f_o/4 across the time course of each simulation, whereas for F2 and F3, there are slightly more instances where the error exceeds f_o/4.

Spectrographic displays of the spectral envelopes obtained with the LP algorithm are shown in the fourth row of Fig. 6. Results of formant tracking are again shown with black dots, along with a red line indicating the calculated vocal tract resonances. A striking feature of both plots is that, in the F1 range, the LP algorithm appears to be tracking the harmonic component that is closest to the first vocal tract resonance. For example, in the left panel, where f_o rises then falls, F1 is equal to 3f_o from the beginning until about 0.2 seconds, drops to 2f_o from 0.2–0.35 seconds, and drops down to f_o for the period from 0.35–0.5 seconds. In the latter half of the simulation, F1 closely follows 2f_o until near the end. In addition, between 0.5–0.65 seconds, the tracked F2 is nearly identical to 4f_o. Similar effects can be seen in the right panel, where F1 jumps from one harmonic to another, but in opposite order because the f_o starts high, falls, and then rises again.

For signals with high f_o, automatic measurement of formants with the LP-based envelopes was prone to generating mistracks (e.g., assigning a peak to F2 when it should be F1, etc.). Hence, the formant tracks initially obtained with the LP algorithm for each of the two simulations in Fig. 6 were manually corrected⁶(these are the versions plotted in the spectrographic displays) so that the percent and absolute error functions could be calculated, and are plotted in the bottom row of Fig. 6. The percent error of F1 rises and falls above and below ±10 percent across the duration of each simulation, reflecting the discontinuous nature of jumping from one harmonic to another. The percent error for F2 and F3 is relatively small and comparable to the error calculated for the spectral filtering approach. The absolute error functions show that all three formants exceed the f_o/4 criterion for much of the duration of each utterance, but this is particularly apparent for F1 and F3.

Fig. 7 displays results for the two {æ·u·æ·u·æ·u} simulations in exactly the same format as the previous figure. For the first f_o contour (left column), the largest amount of error in tracking formants occurs between 0.35–0.6 seconds. This is expected since the f_o is rising to its maximum value during this time segment. For the second simulation, the errors are largest near the beginning and end, again because these are the portions where f_o is highest. The percent error functions for both simulations are mostly contained within the ±10 percent brackets, and, with the exception of F3, the absolute errors are generally less than f_o/4. The LP analyses in the bottom row also indicate considerable error when the f_o is high. In fact, during the segment between 0.35–0.5 seconds the LP spectrogram of the simulation with the first f_o contour clearly finds the second and third harmonics as spectral peaks, rather than the actual resonance located between these harmonics. This caused a large number of misidentified formants, which were manually corrected to the form shown in the LP spectrogram so that the error calculations could be performed. Not surprisingly, both types of errors are quite large and extend beyond the range set for these plots (to maintain consistency across figures the ranges were maintained), especially for F1. For the second simulation, similar error is present in the beginning and ending portions since these are at the high points of the f_o contour.

Results for the two {i·ɑ·i} simulations are shown in Fig. 8. The spectrographic displays of the spectral envelopes (second row) again provide a clear representation of the formants as indicated by superimposed formant tracks and calculated resonance frequencies. The error functions show that in both simulations, the largest amount of error in tracking F1 occurs near the beginning and end, where the first formant frequency is very low. These errors occur for the same reasons discussed in regard to the simulations in Fig. 6. Otherwise, the percent errors are less than 10 percent and the absolute errors are largely constrained to be less than f_o/4.

The spectrographic display based on the LP algorithm (bottom row) also provides a fairly clear visual representation of the formants in the first simulation (left panel), except around 0.7 seconds where the f_o is rapidly decreasing. It also can be noted that, for F1, both types of error approach zero during the time between 0.3–0.5 seconds. Although this gives the appearance of successful formant tracking, it is during this time that the first resonance is almost perfectly aligned with the second harmonic 2f_o, hence the small error is correct, but also coincidental. For the second simulation (right panel), the upper formants are again well represented, but for F1 there are clearly jumps from one harmonic to another as the f_o falls and then rises over the duration of the utterance. The percent error calculations reflect the discontinuities in tracking F1 but are relatively small for F2 and F3. The absolute errors also indicate points in time where F1 exceeds the f_o/4 criterion, as does F3 during the middle portion of utterance.

5 Discussion

Using simulated speech to test formant tracking algorithms as a precursor to analysis of real speech has the advantage of providing an ideal “recording” without any effects of room acoustics, microphone characteristics, recording levels, or background noise, as well as a priori knowledge of the true values of the vocal tract resonance frequencies. Thus, the first aim of this study was to generate simulations of child-like speech that can be used as test material for any formant tracking algorithm. The simulation model included time-dependent parametric control of the vocal fold surfaces and the vocal tract area function, both of which were scaled to be representative of a two-year old child. As the vocal folds vibrate, glottal flow is computed in time synchrony with wave propagation in the vocal tract, thus allowing sound production to be based on a “Level 1” nonlinear interaction of source and filter (Titze, 2008). This is perhaps a more realistic situation for child-like speech than the more conventional linear source-filter approach to synthesis for which the glottal flow characteristics are entirely independent of the vocal tract. The eight simulations generated for this study are linked to this article as supplementary material, and the time-varying resonance frequencies corresponding to the latter six simulations are provided in Table A.3.

The second and third aims were concerned with development and testing of the spectral filtering algorithm. The implementation is fairly straightforward, requiring only that a zero-phase low-pass filter be applied to a DFT spectrum in order to extract the spectral envelope. The cutoff point of the filter, however, is set relative to the fundamental frequency present in any given time window, and based on concepts of cepstral analysis. The spectral filtering approach produced a reasonably clear visual representation of the time-varying vocal tract resonance pattern, as shown in spectrographic form, when applied to the simulated child-like speech samples. Improved visualization could be particularly useful for spectrographic analysis of children’s speech where an investigator wants to interactively select the location of formants in time and frequency. It was also shown that, for a wide range of both fundamental frequency and resonance frequencies, formants could be automatically tracked with less overall error than that of conventional linear prediction. With both algorithms, the largest amount of error was in estimating the first formant. This is expected due to the dominance of the most intense harmonic in the low frequency portion of the spectrum (Klatt, 1986). The LP algorithm, however, was particularly susceptible as evidenced by the ambiguity of whether F1 or individual harmonics were being tracked when the f_o was high (i.e., the F1 track was observed to jump from one harmonic to another for high f_o). Although results were reported here for only the child-like speech, the spectral filtering method could be applied to adult speech too. There is likely little advantage, however, over conventional linear prediction when the f_o is lower than about 250 Hz, since both methods should provide similar results.

It is recognized that applying the spectral filtering algorithm to a small number of limited simulations of child-like speech is not a comprehensive test of the method. Further testing needs to include a wider range of simulation conditions such as scaling the vocal folds and vocal tract for different ages, removing or modifying the noise added to the glottal flow, and incorporating a self-oscillating model of vocal fold vibration. In addition, a subglottal system could be incorporated into the model (c.f. Lulich, 2009; Ho, Zanartu, & Wodicka, 2011) so that tracheal resonances would be coupled to the voice source and vocal tract. Such resonances interact with the glottal flow, and have the effect of producing spectral zeroes (anti-formants) that may shift frequencies of the vocal tract resonances and modify their bandwidths (Stevens, 1998). Implementation of a nasal system would similarly add side-branch resonances that modify the frequencies of the main vocal tract resonances (Fant, 1960; Pruthi, Espy-Wilson, & Story, 2007) when a vowel is nasalized. The effects of both the subglottal and nasal systems are important to study with respect to how they affect formant analysis because they will be present in some segments of natural speech.

In addition, the cosine interpolation used to produce the temporal variation of the vocal tract may not adequately represent actual speech movements. It was used here to ensure that the spectral filtering algorithm was tested on a wide range of time-dependent variations of resonance frequencies combined with a variety of voice source spectra. Other interpolation schemes could be implemented that are based developmental speech movement data (e.g., Riley & Smith, 2003; Green, Moore, Higashikawa, and Steeve, 2000; Smith & Zelaznik, 2004; Vick et al., 2012), or with a technique like that reported in Story (2007) that derives the time-dependent change of the q₁(t) and q₂(t) parameters (see Eq. 1) from articulatory fleshpoint data. The effect of consonantal constrictions also needs to be incorporated into the simulations (c.f., Story, 2005; 2013) in order to test the accuracy of measuring rapid changes in the formants. In any case, designing the parameter variation based on speech movement data is a next step toward enhancing the physiologic relevance of the simulations.

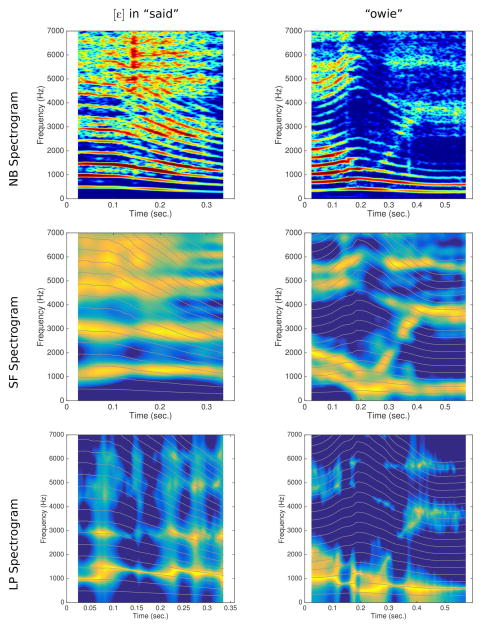
Even with these limitations, the analysis of the simulated speech samples in this study does provide some degree of confidence that the technique will allow for accurate formant measurements when applied to recordings of natural speech. As a demonstration, two audio samples spoken by a two year-old talker from the Arizona Child Acoustic Database (Bunton & Story, 2014) were analyzed with the same spectral filtering and linear prediction algorithms used with the simulated speech. Spectrographic plots similar to those in Figs. 6, 7, and 8 are shown for these two samples in Fig. 9. The plots in left column are based on the vowel [ε] extracted from the word “said,” and those in the right column are analyses of the colloquial children’s word “owie.” The narrowband spectrograms of both samples indicate time-varying, and relatively high f_o that results in wide harmonic spacing along with a visible noise component due to turbulence-generated sound. In the first sample, the f_o falls from 487 Hz to 285 Hz in about 0.24 seconds, whereas in the second sample the f_o starts at 345 Hz, rises to 420 Hz, and drops to 295 Hz at the end of the word. The spectrographic plots based on spectral filtering, shown in the middle row of the figure, present a fairly clear view of the formants over time. The first sample is essentially a static vowel as indicated by the relatively constant position of the formant bands, whereas in the word “owie” the formants change rapidly. Plots based on linear prediction are shown in the bottom row, where the formants exhibit a discontinuous pattern due to jumping from one harmonic to another, much like was demonstrated with the analyses of simulated speech. The f_o contours for each of the two samples, which were tracked during the spectral filtering analysis, and the associated harmonic frequencies are superimposed (gray lines) on the spectrograms based on both spectral filtering and linear prediction. This allows for a visual check of whether the formants appear to be dominated by any particular harmonic frequencies. In the spectral filtering cases, there is no obvious interaction of the visible formants with harmonic frequencies. For linear prediction, however, there are several time segments in each sample where a formant frequency coincides with a specific harmonic, and then jumps to a new harmonic as the f_o changes.

Figure 9.

Results of spectral filtering and linear prediction analysis of audio recordings of a two year-old child. The left column shows the NB spectrogram, SF spectrogram, and LP spectrogram for the vowel [ε] portion of the word “said.” In right column are the same plots but for the word “owie” ([ɑwi]).

In these two demonstration cases, the spectral filtering algorithm provided a clear view of the formant frequencies over the time course of each utterance. This is certainly an advantage over the LP algorithm (or a traditional wide-band spectrogram of high f_o speech), and would allow a user to interactively determine and measure formants at select points in time. Automatically tracking the formants, however, is likely to remain a challenge even with the enhanced visualization. Children’s speech can be expected to contain periods of time where 1) two or more formants merge together (c.f., at about 0.35 seconds in the spectrograms for “owie” in Fig. 9), 2) a formant amplitude may drop drastically and then return to its former level, or 3) the source excitation is simply absent in parts of the spectrum such that formants are not expressed, and thus cannot be measured. Furthermore, recording children’s speech sometimes necessitates less than ideal conditions. For example, microphone-to-mouth distance may be variable due to movement by the child, generating amplitude variations unrelated to speech, or recordings may need to be obtained in observation rooms or classrooms rather than a sound treated environment. Any of these events compromise the clarity of the spectral representation and could lead to mistracking time-varying formants by an automated system.

6 Conclusion

The acoustic resonances of the vocal tract can be thought of as a modulation of the voice source spectrum, much like a high-frequency carrier signal in the time domain may be modulated by lower frequency signals. The idea implemented in this study was to apply a low-pass filter to a DFT spectrum to extract the spectral envelope imposed by the vocal tract. The characteristics of the filter are based on considerations informed by cepstral methods. When applied to a signal with time-varying f_o and vocal tract resonances, the spectral filtering approach provides a clear spectrographic representation of formant change over the time course of the signal, and facilitates tracking formant frequencies for further analysis.

Highlights.

• Children’s speech presents a challenging problem for formant frequency measurement.

• A spectral filtering technique is proposed for analysis of children’s speech.

• The method was tested with child-like simulated speech samples.

• The new approach produced less error than a linear prediction algorithm.

Appendix

The functions needed for the vocal tract model specified by Eq. (1) (Ω(i), ϕ₁(i), and ϕ₂(i)) are given in Table A.1. The index i = 1 corresponds to a point just above the glottis and i = 44 is located at the lip termination. In Table A.2 are [q₁, q₂] coefficient values that can be used with Eq. (1) to generate area functions representative of i, æ, ɑ, and u. Table A.3 contains the calculated vocal tract resonance frequencies for each of the time-varying cases presented in Fig. 3. The temporal resolution is 0.02 seconds.

Table A.1.

Neutral diameter function, Ω(i), and two modes, ϕ₁(i) and ϕ₂(i), used to generate vocal tract area functions with Eq. (1). The index i represents consecutive sections of an area function ordered from glottis to lips. The length of each section is ΔL = 0.2386 cm.

i	Ω(i)	ϕ1(i)	ϕ2(i)
1	0.353	0.000	−0.004
2	0.353	0.000	−0.003
3	0.382	−0.000	−0.005
4	0.479	−0.001	−0.009
5	0.634	−0.002	−0.018
6	0.810	−0.005	−0.033
7	0.976	−0.010	−0.052
8	1.115	−0.018	−0.068
9	1.224	−0.026	−0.072
10	1.300	−0.035	−0.070
11	1.342	−0.044	−0.062
12	1.363	−0.055	−0.049
13	1.376	−0.065	−0.033
14	1.387	−0.075	−0.015
15	1.394	−0.082	0.002
16	1.395	−0.089	0.019
17	1.390	−0.095	0.036
18	1.378	−0.100	0.051
19	1.359	−0.103	0.065
20	1.333	−0.105	0.077
21	1.303	−0.104	0.085
22	1.272	−0.096	0.086
23	1.243	−0.081	0.079
24	1.221	−0.059	0.063
25	1.212	−0.029	0.039
26	1.223	0.008	0.006
27	1.257	0.053	−0.036
28	1.306	0.101	−0.083
29	1.351	0.146	−0.120
30	1.392	0.187	−0.147
31	1.428	0.223	−0.164
32	1.462	0.252	−0.170
33	1.491	0.274	−0.166
34	1.515	0.288	−0.149
35	1.533	0.295	−0.121
36	1.546	0.294	−0.081
37	1.554	0.287	−0.029
38	1.556	0.274	0.034
39	1.550	0.256	0.107
40	1.535	0.233	0.189
41	1.509	0.205	0.279
42	1.467	0.173	0.376
43	1.439	0.141	0.459
44	1.414	0.115	0.531

Table A.2.

Coefficient values that, when used in Eq. (1), will generate area functions representative of the four corner vowels. These values were used in both simulation Sets 1 and 2.

	q1	q2
i	−4.03	−0.41
æ	2.26	2.10
ɑ	3.60	−1.26
u	3.00	−2.60

Table A.3.

Time-varying vocal tract resonance frequencies calculated for each of the simulations specified in Set 2. The temporal resolution is 0.02 seconds.

	{i·ɑ·i·ɑ·i·ɑ}				{æ·u·æ ·u·æ·u}				{i · ɑ · i}
t	fR1	fR2	fR3	fR4	fR1	fR2	fR3	fR4	fR1	fR2	fR3	fR4
0.00	533	3576	4918	6484	1259	2745	4403	6010	533	3576	4918	6484
0.02	555	3515	4856	6461	1257	2712	4419	6015	536	3567	4908	6480
0.04	616	3329	4721	6403	1249	2619	4467	6029	546	3539	4879	6469
0.06	707	3033	4618	6339	1227	2477	4543	6054	563	3492	4834	6452
0.08	805	2701	4595	6288	1187	2305	4647	6094	585	3425	4781	6431
0.10	890	2404	4644	6255	1120	2119	4772	6149	613	3338	4727	6406
0.12	951	2171	4740	6238	1027	1941	4908	6214	645	3234	4677	6380
0.14	986	2000	4854	6232	915	1791	5039	6281	682	3116	4637	6355
0.16	1002	1882	4959	6231	806	1684	5149	6340	720	2988	4610	6331
0.18	1008	1814	5032	6233	729	1622	5221	6380	759	2857	4595	6310
0.20	1009	1792	5056	6234	703	1603	5246	6394	797	2727	4593	6291
0.22	1008	1804	5043	6234	717	1613	5232	6387	834	2603	4603	6276
0.24	1004	1860	4982	6232	783	1664	5172	6352	867	2487	4623	6263
0.26	991	1965	4883	6231	886	1760	5070	6297	897	2380	4651	6253
0.28	962	2122	4768	6235	999	1899	4942	6232	923	2283	4686	6245
0.30	908	2339	4665	6249	1099	2072	4806	6165	945	2196	4726	6239
0.32	828	2620	4601	6278	1173	2258	4677	6107	963	2119	4770	6235
0.34	732	2948	4604	6324	1219	2436	4567	6063	976	2051	4815	6233
0.36	637	3261	4689	6387	1244	2586	4484	6034	987	1992	4860	6231
0.38	567	3480	4824	6448	1255	2694	4428	6017	995	1941	4904	6231
0.40	535	3572	4914	6482	1258	2743	4404	6011	1001	1898	4944	6231
0.42	536	3566	4907	6480	1258	2740	4405	6011	1004	1862	4980	6232
0.44	575	3456	4804	6440	1255	2681	4435	6019	1006	1834	5009	6232
0.46	650	3220	4671	6377	1242	2567	4494	6037	1008	1813	5032	6233
0.48	747	2898	4599	6316	1214	2411	4582	6068	1009	1800	5048	6234
0.50	842	2575	4607	6273	1164	2230	4695	6115	1009	1793	5055	6234
0.52	918	2303	4678	6247	1086	2045	4826	6174	1009	1793	5055	6234
0.54	967	2095	4785	6234	983	1876	4962	6242	1009	1798	5049	6234
0.56	994	1946	4899	6231	869	1743	5087	6306	1008	1811	5035	6233
0.58	1005	1849	4993	6232	770	1654	5184	6359	1007	1831	5013	6233
0.60	1009	1800	5048	6234	712	1609	5237	6390	1005	1858	4984	6232
0.62	1009	1793	5055	6234	704	1603	5245	6394	1001	1892	4950	6231
0.64	1007	1821	5024	6233	738	1628	5214	6376	996	1934	4910	6231
0.66	1001	1897	4945	6231	821	1697	5135	6332	988	1984	4867	6231
0.68	982	2021	4837	6232	932	1811	5021	6272	979	2042	4822	6232
0.70	944	2201	4724	6240	1042	1966	4888	6204	965	2108	4777	6235
0.72	879	2444	4633	6259	1132	2146	4752	6140	948	2184	4733	6238
0.74	791	2749	4593	6294	1194	2331	4630	6087	927	2269	4692	6244
0.76	692	3081	4628	6348	1232	2501	4530	6049	901	2364	4656	6251
0.78	605	3364	4741	6413	1250	2636	4458	6026	872	2470	4627	6261
0.80	549	3532	4872	6467	1257	2721	4415	6014	839	2584	4606	6274
0.82	533	3577	4919	6484	1259	2746	4403	6010	803	2708	4594	6289
0.84	547	3537	4877	6469	1257	2724	4413	6013	765	2837	4594	6307
0.86	601	3375	4748	6416	1251	2641	4455	6025	726	2968	4607	6328
0.88	687	3096	4632	6351	1233	2508	4526	6048	687	3097	4632	6351
0.90	786	2765	4593	6297	1197	2340	4625	6085	651	3217	4670	6376
0.92	876	2458	4629	6260	1135	2155	4746	6137	617	3324	4719	6402
0.94	941	2212	4718	6240	1047	1974	4881	6201	589	3413	4773	6427
0.96	981	2029	4831	6232	937	1817	5015	6268	566	3483	4827	6449
0.98	1000	1902	4940	6231	826	1701	5130	6330	548	3533	4873	6467
1.00	1007	1824	5021	6233	741	1631	5211	6374	537	3564	4905	6479
1.02	1009	1793	5055	6234	704	1603	5245	6394	533	3576	4918	6484