Retrospective Correction for Induced Magnetic Field Inhomogeneity in Measurements of Large-Vessel Hemoglobin Oxygen Saturation by MR Susceptometry

Abstract

MR susceptometry-based blood oximetry relies on phase mapping to measure the difference in magnetic susceptibility between intravascular blood and surrounding tissue. The main source of error in MR susceptometry is the static field inhomogeneity caused by an interface between air and tissue or between adjacent tissue types. High-pass filtering has previously been used in conjunction with shimming to reduce the effect of low spatial-frequency modulations of the phase caused by large-scale induced magnetic fields. We demonstrate that high-pass filtering is not optimum for MR susceptometry because the results are sensitive to filter size. We propose an alternative method that acquires data without scanner-implemented default shimming, and fits, after appropriate weighting and masking, the static field inhomogeneity to a second-order polynomial. Compared to shimming the retrospective correction technique improved agreement between hemoglobin saturations measured in different segments of a vessel (femoral versus popliteal artery and vein) from three standard errors to less than one.

Determination of oxygen saturation is of great importance in assessing a number of clinical conditions, including ischemia in various organs (e.g., peripheral arterial disease), hypoxemias as in chronic obstructive pulmonary disease (1), apneas of various kinds (2,3), and chamber mixing in congenital heart disease (4). MR susceptometry-based oximetry (5–7) takes advantage of the relative magnetic susceptibility between intravascular blood and surrounding tissue, which is directly proportional to deoxyhemoglobin concentration (1 – HbO₂), the source of paramagnetism in blood. Whole-blood oximetry based on a measurement of blood paramagnetic susceptibility has several advantages over T₂-based methods (8), including self-calibration, equal sensitivity to all oxygenation levels, relatively straightforward implementation, and excellent temporal and spatial resolution. High temporal resolution makes time-course measurement of oxygenation possible during reactive hyperemia in response to exercise or cuff-induced ischemia; measurements of key parameters such as recovery rate and washout delay can be exploited to obtain detailed information on vascular pathophysiology. Further, the high spatial resolution, inherent to the method, allows targeting of medium- to large-sized vessels such as the femoral artery or vein.

MR susceptometry is based on field mapping and its main source of error is static field inhomogeneity caused by susceptibility mismatch at the interface between the object and the surrounding air. High-pass filtering (e.g., see Ref. 9 for details) is commonly implemented to reduce the effect of the static field inhomogeneity characterized by low spatial-frequency modulations in phase difference images. High-pass filtering suppresses low spatial-frequency components from k-space indiscriminately while also affecting the phase to be quantified in a manner dependent on filter size. Therefore, fundamentally the high-pass filter cannot separate static or background field inhomogeneity from the field offset we desire to quantify as resulting from the relative susceptibility difference between intravascular blood and surrounding tissue.

For phantoms with simple geometry, automatic shimming implemented by the scanner is often sufficient because the remnant field inhomogeneity can be further reduced by averaging the phase of reference medium surrounding the region of interest (ROI). However, in vivo, where the surrounding tissue serves as a reference, the field inhomogeneity becomes a more serious problem. Often, muscle tissue does not completely surround the vessels of interest, or a region of the image may be obscured by pulsatile flow artifacts. The field variation also limits the area of the reference tissue, therefore introducing a bias in the phase measurement in that the position of the reference tissue section can affect oxygen saturation by as much as 5–10 %HbO₂.

Here we propose a weighted least-squares fitting method to reduce the effect of static field inhomogeneity in the phase images, required for deriving the intravascular susceptibility. This postprocessing method acquires the data without shimming and approximates the field inhomogeneity with a second-order polynomial after appropriate weighting and masking. Masking and weighting are important steps that ensure that the phase discontinuity at the vessel boundary remains unperturbed, a critical improvement over high-pass filtering. The proposed method is evaluated with phantom and in vivo studies. For the phantom study the magnetic susceptibilities of various concentrations of Gd-doped water in an array of cylindrical vials embedded in distilled water were measured. For the in vivo study, blood oxygenation measurements in femoral and popliteal vessels provide a constraint that can be used to compare the two postprocessing methods at 3T field strength.

MATERIALS AND METHODS

MR Susceptometry-Based Oximetry

An object of uniform susceptibility placed into a homogeneous magnetic field becomes magnetized, which in turn produces a typically inhomogeneous induced field that depends on the shape of the object and its orientation with respect to the external field. The induced field is homogeneous inside ellipsoids and can be calculated analytically (see, e.g., Refs. 10–12). The field outside an ellipsoid, however, is in general inhomogeneous. Examples of ellipsoids are spheres and infinitely long cylinders. The latter geometry is an excellent approximation for segments of blood vessels since l ≫ d, where l and d represent vessel length and diameter, respectively. For a long cylinder at some angle θ relative to the applied field B₀, the incremental field, ΔB, inside, when including the sphere of Lorentz correction (13,14), is given as

$$\mathrm{\Delta }B=\frac{1}{6}\mathrm{\Delta }\mathrm{\chi }{B}_0(3{\text{cos}}^2\mathrm{\theta }-1),$$ [1]

where Δχ is the susceptibility difference (in SI units) between the medium inside the cylinder and that of its surroundings. Lorentz correction takes into account the inhomogeneous distribution of sources near the point of interest. The spherical region around the point of interest is referred to as a Lorentz sphere; its radius is macroscopic compared to atomic scales but microscopic compared to the size of the object immersed in the external field. For a blood vessel Δχ = Δχ_doHct · (1 − HbO₂), i.e., the source of paramagnetism in blood is deoxyhemoglobin, giving:

$$\mathrm{\Delta }B=\mid B_i-B_s\mid =\frac{1}{6}\mathrm{\Delta }{\mathrm{\chi }}_{do}\mathit{Hct}·(1-{\mathit{HbO}}_2)·B_0(3{\text{cos}}^2\mathrm{\theta }-1)$$ [2]

B_i and B_s is the field inside a vessel and in the surrounding (diamagnetic) tissue, respectively, Δχ_do = 4π · (0.27 ± 0.02) ppm (15) is the susceptibility difference in SI units between fully deoxygenated and fully oxygenated erythrocytes, hematocrit (Hct) is the fractional volume of the packed erythrocytes in the whole blood, and HbO₂ represents the fraction of the oxygenated hemoglobin (Hb). For women, Hct typically ranges from 0.37–0.47, whereas for men the range is 0.40–0.54. The weighted averages are 0.39 and 0.44 for women and men, respectively (16). It is further assumed that the reference tissue is muscle and its susceptibility is equal to that of fully oxygenated blood. As long as the above assumptions are met, %HbO₂ can be measured from a phase difference image between two echoes separated by ΔTE, Δϕ_map = γΔBΔTE, once Hct is known, i.e.:

$$\%H_b{O}_2=\left[1-\frac{2\mathrm{\Delta }\mathrm{\varphi }/\mathrm{\Delta }T}{\mathrm{\gamma }\mathrm{\Delta }{\mathrm{\chi }}_{do}\mathit{Hct}·B_O({\text{cos}}^2\mathrm{\theta }-1/3)}\right]\times 100.$$ [3]

In the above expression, Δϕ is the absolute difference between the phases measured inside of a vessel and its surrounding tissue from a phase difference images. The last step ensures MR oximetry to be calibration-free. For this investigation we used 0.39 and 0.44 for the Hct values for female and male volunteers, respectively.

Weighted Least-Squares Fit

We propose to remove the large-scale field inhomogeneity by fitting the phase difference images to a second-order polynomial, similar to phase correction reported in other applications (17,18), i.e., we assume that the macroscopic field variation in phase difference images Δϕ_map can be approximated as a linear combination of 1,X,Y… and Y², i.e.:

$$\mathrm{\Delta }{\mathrm{\varphi }}_{\text{inhom}}\approx c_{1}1+c_{2}X+c_{3}Y+c_{4}XY+c_5{X}^2+c_6{Y}^2,$$ [4]

where c_i’s are the coefficients to be determined through the weighted least-squares fit and the matrices 1,X,Y… represent the constant matrix, linearly varying matrix along the x- and y-direction, respectively, etc. Before fitting the field inhomogeneity to a second-order polynomial, tubes or the vessels are masked out, and the background is suppressed by multiplying each pixel in the phase map with the corresponding value in the magnitude image. Setting a threshold is a convenient way to mask out the vessels since their magnitude is substantially larger than that of the surrounding muscle tissue due to flow-related enhancement. In fact, thresholding is superior to manual masking as it allows suppression of the tissue near the air/tissue interface where the field inhomogeneity is most severe (and should not be corrected!). Otherwise, fitting the surface regions may overcompensate field inhomogeneity correction near the vessels where local field inhomogeneity is more moderate due to buffering provided by the muscle tissue.

In order to estimate the field inhomogeneity with least-squares fit technique, Eq. [4] is recast into a well-known form Ax ≈ B. B represents 128² × 1 columnized vector of Δϕ_inhom and the right-hand side of Eq. [4] is decomposed as a matrix multiplication of A and x, where x is a 6 × 1 column matrix of c_i’s and A is a 128² × 6 matrix constructed by concatenating columnized matrices of 1,X,Y… and Y₂. Matrices are columnized by taking the transpose of each row and concatenating them along a column. c_i’s are found by minimizing |Ax – B|², or (Ax – B)^T(Ax – B) which leads to the following expression: x ≈ (A^TA)^–1A^TB. The same expression will result by solving for x in Ax ≈ B. Inverse of A does not exist because it is not a square matrix; however, A^TA is a square matrix and we assume that its inverse is nonsingular. The solution will provide the coefficients c_j’s to approximate the static field inhomogeneity with a second-order polynomial, which is the simplest nontrivial fit. Other functions can be used, which, however, will not be pursued here. The corrected phase difference image is then given by Δϕ_corr = Δϕ_map − Δϕ_inhom.

Sequence

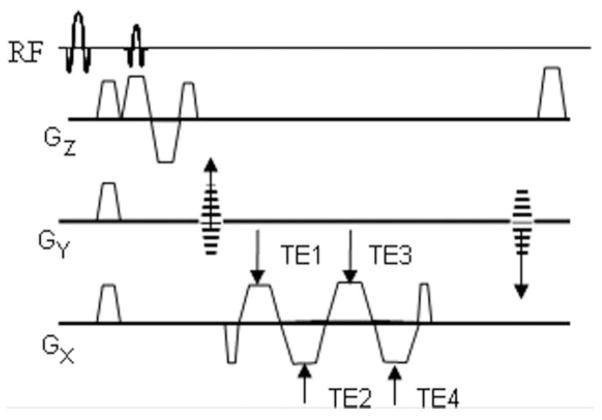
Images were acquired with a multiecho RF-spoiled gradient- recalled echo (GRE) sequence (Fig. 1) programmed with SequenceTree v. 3.1 (19). The pulse sequence includes fat suppression and first-moment nulling along the slice (i.e., blood flow) direction. The phase difference is taken from the echoes having the same polarity to minimize off-resonance errors. The first moment of the readout gradient at echo center is equal among the same polarity echoes. Hence, in the event of vessel obliquity the phase imparted by the read gradient will not cause any error in the phase difference attributed to blood Hb as long as the phase difference is computed between echoes of the same polarity. Images were acquired with the following parameters: voxel size = 1 × 1 × 5 mm³, FOV = 128 × 128 mm², BW = 488 Hz/pixel, TE1 = 4.5 ms, interecho spacing = 2.5 ms, TR = 39 ms, and flip angle = 13°. For in vivo measurements pulsatile flow artifacts were minimal (see Fig. 5a,d) and cardiac gating was not used in order to achieve higher temporal resolution since the pulse sequence was developed to quantify reactive hyperemia in response to cuff-induced ischemia.

FIG. 1.

Multiecho spoiled GRE sequence with fat saturation and flow compensation along the slice direction. Two phase difference images are constructed and averaged, one for each equal-polarity pair of echoes.

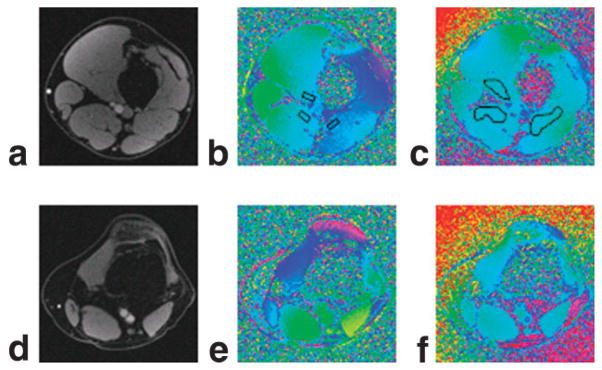
FIG. 5.

a: In vivo magnitude image of an axial slice containing the femoral artery and vein. b: Corresponding phase difference image with shimming. c: Shimming disabled but with weighted least-squares fit correction. d–f: Corresponding axial magnitude and phase images containing popliteal artery and vein.

Phantom Experiments

The phantom (6) consisted of six cylindrical vials filled with doped water of increasing concentrations of Gd- DTPA. The concentration of the Gd ranged from 0–3 mM, covering the range of susceptibility differences (0– 1.02 ppm in SI) found between venous blood and tissue. The assembly of vials was held in a cylinder filled with distilled water and placed with its axis parallel to the static field inside the bore of a Siemens (Erlangen, Germany) Trio scanner. The k-space data were acquired with and without shimming and the data were processed offline. A phase difference image between successive echoes was then constructed (20) as Δϕ_map = arg(Z₃,Z₁*) where Z₁ and Z₃ represent complex values of a particular pixel in the images of first and third echo (positive readout gradients), respectively, and the asterisk denotes complex conjugate. Phase difference images with short echo-spacing reduce phase wraps that can confound the data analysis. For each tube a surrounding annulus was chosen as the reference medium and its average phase difference subtracted from the average phase difference in the circular region encompassing the tube. The susceptibility difference was then calculated for data obtained with and without shimming using Δχ (3Δϕ)/(B₀γΔTE), where Δϕ is the absolute phase difference between the tube and its surrounding reference medium and ΔTE is the interval between equal-polarity echoes. In the case of shimmed data the susceptibility calculation was repeated for several high-pass filter sizes by varying the Hanning window from 2 × 2 to 30 × 30 pixels to investigate the effectiveness of filtering.

For the unshimmed data a weighted least-squares fit correction was applied to the average phase difference image after appropriate masking and weighting. The fitted surface was then subtracted from the phase difference image and the susceptibility difference derived from the corrected phase difference image as described above.

In Vivo Measurement of Oxygenation in Femoral and Popliteal Vessels

The same experimental setup was used for the in vivo measurements. Written informed consent was obtained prior to all human studies following an Institutional Review Board-approved protocol.

An eight-channel knee array coil (Invivo, Pewaukee, WI) was used to acquire axial images containing the popliteal and femoral vessels from five volunteers with and without shimming for comparison. The raw k-space data were processed analogous to that of the phantom data. The local vessel tilt angle θ (Eq. [2]) was measured with a 10-slice localizer set of images. Phase difference images constructed from shimmed data limited area of reference tissue sections around the vessels. Regions directly anterior and posterior (phase-encoding direction) were excluded to avoid interference with pulsatile flow artifacts. The weighted average phase of several surrounding reference tissue sections was then subtracted from the intravascular phase measurement in the artery and vein for deriving the oxygen saturation levels. The intravascular phase was measured as the average in an ROI placed at the center of the cross-sectional area of the vessel. High-pass filtering and weighted least-squares fitting were compared with blood oxygenation measurement in the femoral and popliteal vessels. Measurement of hemoglobin saturation in the femoral and popliteal artery or vein provides a simple consistency check since these are merely successive segments of the same vessel and no oxygen extraction takes place between; therefore, HbO₂ levels should be the same.

Error Analysis

The precision of the derived hemoglobin saturation levels is largely determined by the uncertainty of phase measurement, which depends on the signal-to-noise ratio (SNR) of the magnitude image (21). The SNR of the blood is always enhanced as a result of the in-flow effect (flow-related enhancement) but tissue SNR is considerably lower at the short TR dictated by the required temporal resolution (39 ms and 5 sec, respectively). Therefore, the surrounding muscle tissue is the largest contributor to the uncertainty in the phase measurement. The errors associated with vessel tilt and minor deviation from circularity were ignored (estimated at ≈ 1%). Straightforward error propagation leads to the following expression for the uncertainty of the hemoglobin oxygenation:

$${\mathrm{\sigma }}_{\%{\mathit{HbO}}_2}=(2{\mathrm{\sigma }}_{\mathrm{\Delta }\mathrm{\varphi }}/\mathrm{\Delta }TE)/(\mathrm{\gamma }\mathrm{\Delta }{\mathrm{\chi }}_{do}\mathit{Hct}·B_o({cos}^2\mathrm{\theta }-1/3))\times 100,$$ [5]

where σ_Δϕ represents the error associated with the phase measurement, which is equal to the inverse of voxel SNR in the corresponding magnitude image. The SNR of magnitude images was determined according to Ref. (22). For the 8-channel knee array coil an additional factor of about 3.14 needs to be multiplied along with the usual factor of 1.25; for N-channels, 1 · 3 · 5 · …(2N–1)/(2 · 4 · 6 · …(2N–2)). This additional factor was derived by equating the noise mean of the background region of an N-channel sum-of-squares reconstruction image to the mean root-squares sum of 2N independent Gaussian variables, i.e.:

$$M(N)={\left(\frac{1}{\sqrt{2\mathrm{\pi }}}\right)}^{2N}\int \sqrt{x_1^2+x_2^2+\cdots x_{2N}^2}exp[-(x_1^2+x_2^2+\cdots x_{2N}^2)/2]{dx}_1{dx}_2\cdots {dx}_{2N}$$ [6]

where x_i’s represent either real or imaginary components of the signal from each of the N quadrature coils.

RESULTS

Phantom Experiment

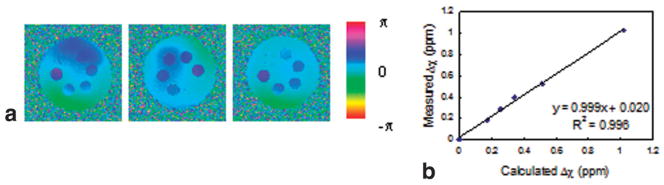
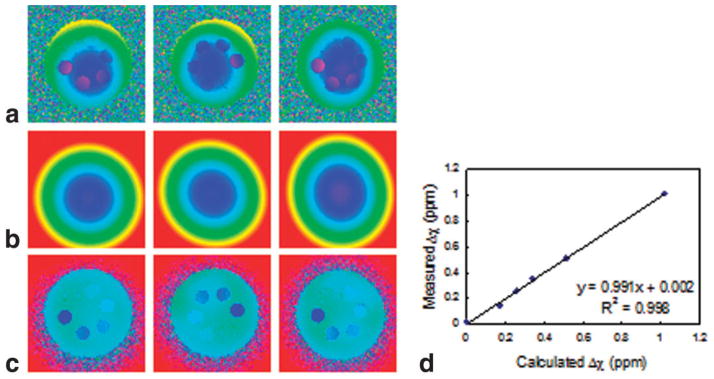
The effect of scanner-implemented shimming is shown in the phase difference images of Fig. 2a; the phantom was rotated 180° clockwise between scans. The static field inhomogeneity is still visible. Even though the data were acquired during the same session, auto-shimming did not produce consistent phase difference images. Nevertheless, the resulting volume magnetic susceptibilities of the gadolinium solutions (6) were accurate (Fig. 2b). High-pass filtering reduced the residual low spatial-frequency phase variation in the above phase difference images. Sample images of filtered phase difference images of the first image from Fig. 2a are displayed in Fig. 3a. The field inhomogeneity is less apparent but the phase differences between samples and background are reduced, leading to erroneous susceptibility values. The adverse effect of indiscriminate filtering on the measured susceptibility values is illustrated in Fig. 3b; only four of the six susceptibility values are plotted for clarity. The derived susceptibility of vial 1 containing distilled water did not significantly depend on the size of the Hanning window (Fig. 3a) since there is virtually no phase difference relative to its immediate surrounding, which serves as a reference. The same behavior will be observed between artery and adjacent reference tissue, which has nearly the same magnetic susceptibility. Corresponding phase difference images of Fig. 2a in the absence of shimming are shown in Fig. 4a. The radial variations in induced field are commensurate with the geometry of the phantom, which is more apparent in Fig. 4b, the weighted least-squares fit to the static field inhomogeneity. Compared to the images of Fig. 2a, the retrospectively corrected phase difference images derived from images obtained without shimming (Fig. 4c) are noticeably more uniform. Figure 4d quantitatively shows improvement in the accuracy of the derived magnetic susceptibility as evidenced by the lower y-intercept. The improvement is less noticeable in the phantom study because shimming is relatively effective but is more dramatic in the in vivo oxygen saturation measurements described below. In summary, residual field inhomogeneity after scanner-implemented shimming was not reproducible. Thus, shimming was disabled in order to acquire and process the data in a systematic manner. Evidence for the poor performance of shimming only is that no consistent blood oxygenation values could be derived at two different locations in the same vessel segment from “shimmed” data, as discussed in more detail below.

FIG. 2.

a: Phase difference images of the phantom after auto-shimming implemented by the scanner. Residual field inhomogeneity is mild but not reproducible from scan to scan. b: The measured susceptibility values are usually in good agreement with the calculated values. Slope and y-intercept are significant to two decimal places.

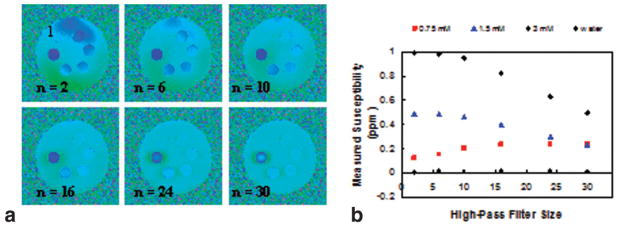
FIG. 3.

a: Series of high-pass filtered phase difference images of the phantom. Field inhomogeneity is reduced with increasing filter size from n = 2 to n = 30. However, contrast is gradually lost among the vials containing different concentrations of Gd with increasing filter size resulting different susceptibility dependence on filter size (b).

FIG. 4.

a: Resulting phase difference images of the phantom without the default shimming. b: Weighted least-squares fit of the static field inhomogeneity. c: Retrospectively corrected phase difference images. d: Correlation between the measured and calculated values.

In Vivo Blood Oxygen Saturation Measurements

Typical magnitude and phase difference images of axial slices at the level of femoral and popliteal vessels are shown in Fig. 5. In general, the static field inhomogeneity has no effect on the magnitude images (Fig. 5a,d). SNR on the order of 45 at TE1 = 4.5 ms and 35 at TE4 = 12 ms was achieved (75 and 55 in veins; 75 and 70 in arteries) in reference tissues. In the phase difference images the severity of the static field inhomogeneity is apparent even with shimming (Fig. 5b,e). Due to significant remnant field inhomogeneity small reference tissue sections (indicated by black rectangles in Fig. 5b) near the vessels must be chosen and their ROI pixel values averaged, analogous to the phantom study. The limited area of the reference section can introduce bias since even minute changes in size or position can affect the derived HbO₂ values by as much as 5–10%. In contrast, the effects of the static field inhomogeneity are considerably less after retrospective correction (Fig. 5c,f), which allows larger areas of surrounding reference tissue to be chosen (Fig. 5c), therefore reducing bias because the average phase of the reference section is less sensitive to its location. Measured oxygenation levels in femoral and popliteal vessels and their uncertainties from both methods are summarized in Tables 1 and 2. We note that the average discrepancies between blood oxygenation measurements in femoral and popliteal vessels are smaller by more than two times the standard error when shimming is disabled and retrospective weighted least squares fit correction is implemented on the phase images. The effect of filter size in high-pass filtered images (derived from the data of Fig. 5b) is illustrated in Fig. 6 and the resulting hemoglobin saturation levels are given in Table 3. The data show that the venous saturation measurement is critically dependent on filter size. The choice of filter size is determined by the desired level of uniformity in phase images. However, uniformity itself is subjective and after a critical filter size images become visually indistinguishable (Fig. 6 with filter size n > 10). Furthermore, the “critical” size is dataset-dependent and the extent to which the images are visually distinguishable depends on the window level.

Table 1.

Hemoglobin Oxygen Saturation Level and Its Uncertainty for Five Healthy Volunteers Computed from Axial Images Taken with Shimming Implemented by the Scanner

Subject	Femoral A. (SAO2±σSO2) %HbO2	Popliteal A. (SAO2±σSO2) %HbO2	Femoral V. (SVO2±σSO2) %HbO2	Popliteal V. (SVO2±σSO2) %HbO2
1	99 ± 3	93 ± 3	59 ± 3	67 ± 3
2	98 ± 3	97 ± 3	56 ± 3	79 ± 3
3	92 ± 4	97 ± 4	54 ± 4	63 ± 4
4	91 ± 4	99 ± 4	54 ± 4	64 ± 4
5	97 ± 4	99 ± 3	68 ± 4	58 ± 3

The average difference in venous saturation is greater than 10% HbO₂.

Table 2.

Same as Table 1 Except That the Oxygenation Values Were Computed from the Unshimmed Images Which Were Corrected Retrospectively as Described

Subject	Femoral A. (SAO2±σSO2) %HbO2	Popliteal A. (SAO2±σSO2) %HbO2	Femoral V. (SVO2±σSO2) %HbO2	Popliteal V. (SVO2±σSO2) %HbO2
1	93 ± 3	93 ± 3	61 ± 3	60 ± 3
2	99 ± 3	99 ± 3	61 ± 3	63 ± 3
3	98 ± 4	95 ± 4	67 ± 4	62 ± 4
4	99 ± 4	97 ± 4	62 ± 4	64 ± 4
5	93 ± 4	96 ± 3	64 ± 4	61 ± 3

Variation in the measured oxygenation values is significantly lower between femoral and popliteal vessels. It is also noted that the measured oxygenation values are in excellent agreement with values reported in the literature.

FIG. 6.

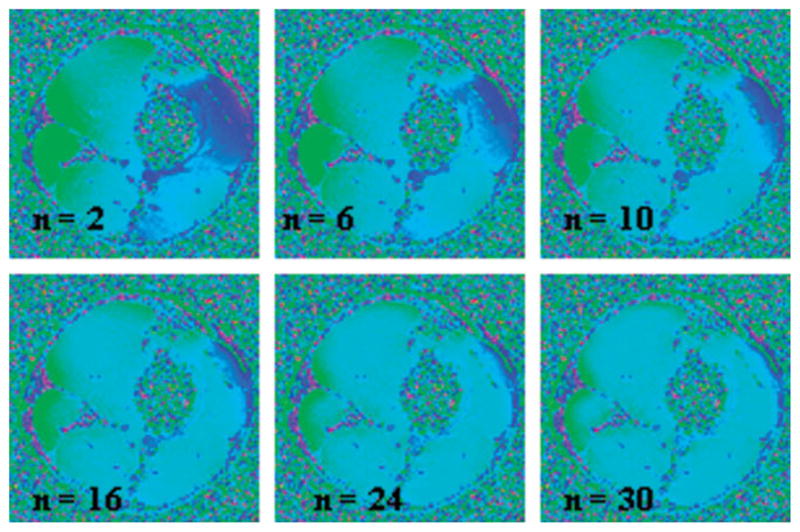
High-pass filtered images of the data of Fig. 5b. As expected, the contrast between artery and vein is lost as the Hanning window size is increased, resulting in increased apparent oxygenation values in the venous blood.

Table 3.

Effect of Filter Size on the Measured Blood Oxygenation

Filter Size	SaO2 (%HbO2)	SvO2 (%HbO2)
2	98	62
6	97	60
10	96	61
16	98	64
24	98	69
30	97	74

DISCUSSION AND CONCLUSIONS

Hemoglobin saturation is an important physiologic parameter that is difficult to measure, especially in deep-lying vessels. High spatial resolution gives MR oximetry the ability to pinpoint vessels noninvasively. At the same time, high temporal resolution allows monitoring of oxygenation levels under various physiologic challenges such as cuff-induced ischemia or exercise to assess peripheral arterial disease. However, in order to realize the clinical potential of MR oximetry static field inhomogeneity must be dealt in a systematic manner.

In this work we have demonstrated a retrospective correction method to reduce the detrimental effects of static field inhomogeneity with a retrospective image-processing technique. The weighted least-squares fit method removes the low spatial-frequency variations in phase images while the phase of interest remains unperturbed. Figure 3b and Table 3 illustrate that high-pass filtering, which removes low-frequency variations indiscriminately without generally applicable criteria for choosing filter size, is not suited for this purpose.

Compared to high-pass filtering, shimming was more accurate in the phantom experiment (Fig. 2b) but failed in the in vivo studies where the average discrepancy of hemoglobin saturation between femoral and popliteal veins was found to be too large (≈ 10% HbO₂) to be clinically practical. In contrast, the oxygen saturation levels in the corresponding femoral and popliteal vessels differed, on the average, by less than 3% HbO₂, using the weighted least-squares fitting method. This degree of variability is reasonable and comparable to the precision of the method itself.

Initial concerns about the effectiveness of shimming arose from irreproducible phase data in the phantom experiments even when data were taken during the same session (Fig. 2a). Shimming adds certain degree of randomness that is detrimental. Our results therefore suggest that auto-shimming be disabled and replaced by the proposed retrospective correction technique.

Here, we chose Δχ = 0.27 ppm between fully deoxygenated and fully oxygenated erythrocytes (instead of 0.18 ppm (23) prompted by the work of Spees et al. (15)). Spees et al. support their 0.27 ppm value with a detailed model and measurements made with two independent techniques (MRI and SQUID magnetometry). Two measurements were identical within their uncertainties and their blood samples were stirred in order to avoid erythrocytes from settling. For these reasons, we have greater confidence in the 0.27 ppm value. This particular choice of susceptibility, however, does not affect our fundamental results showing that retrospective correction gives consistent measurement of blood oxygenation, whereas shimming does not. We note that a 0.18 ppm value would lead to unrealistically low blood oxygenation, i.e., below 90 and 45 %HbO₂ in artery and vein, respectively.

The least-squares fit is susceptible to errors associated with interpolation across voids in the image. Figure 5d shows a dark region between the medial and lateral gastrocnemius resulting from fat suppression. This area is suppressed by the weighted fit due to its low signal magnitude; therefore, phase correction in this area requires interpolation based on separate fits of the medial and lateral gastrocnemius regions. However, interpolation may result in poor fit to the field inhomogeneity in this region where vessels are located. For this reason it might be preferable to measure the hemoglobin saturation in the femoral vessels since at this level there is less adipose tissue surrounding the vasculature and hence interpolation will be minimal. On the other hand, in the absence of fat saturation, an adipose region could potentially be used as a reference tissue.

The chemical shift displacement artifact which could obscure a small portion of the vessel is less than one pixel at the currently used sampling frequency bandwidth of 488 Hz/pixel. Sufficient contrast between fat and tissue will be provided while avoiding phase wraps by selecting an interecho spacing that is an odd-integer multiple of 2.39 ms. High contrast will aid automatic implementation of separating and subsequent phase matching of fat and muscle tissue. In short, the weighted least-squares fit method will be optimized by reducing interpolation in the regions occupied by adipose fat that surround the vessels.

Phase aliasing is a legitimate concern in MR susceptometry. However, no aliasing has been observed for the targeted application of hemoglobin oxygenation measurement in the peripheral vessels. The phase difference images with relatively short echo spacing of 5 ms avoid large phase accumulation; the largest being in the vein, typically ranging from 0.3–0.6 radians. Furthermore, the field inhomogeneity due to the air/tissue interface is less severe near the centrally located vessels due to buffering provided by the surrounding tissue. It is noted that MR susceptometry-based oximetry may also be useful for estimating the cerebral metabolic rate of oxygen by combining blood flow and blood oxygenation measurements in carotid arteries and internal jugular veins as described in Ref. (6). However, in this particular application static field inhomogeneity is expected to be more severe because of the additional field gradients caused by the air present in the trachea and other air spaces in the neck. The measurements of the two carotid arteries and jugular veins provides excellent opportunity to further test the robustness of MR susceptometry in conjunction with the retrospective correction (by measuring HbO₂ in both left and right vessels serves as a consistency check).

In T₂-based oximetry (8) no reference tissue is needed and the method is accessible to all large vessels. However, its implementation is involved and requires extensive individual calibration. MR susceptometry-based oximetry, on the other hand, is a self-calibrating technique in which sensitivity and accuracy do not scale with the oxygenation level, and the data acquisition is robust due to the simplicity of the pulse sequence, which is not much more involved than a basic GRE scout sequence. Lastly, a single measurement including postprocessing requires less than 10 sec.