Effect of Zn²⁺ binding and enzyme active site on the transition state for RNA 2′-O-transphosphorylation interpreted through kinetic isotope effects

Abstract

Divalent metal ions, due to their ability to stabilize high concentrations of negative charge, are important for RNA folding and catalysis. Detailed models derived from the structures and kinetics of enzymes and from computational simulations have been developed. However, in most cases the specific catalytic modes involving metal ions and their mechanistic roles and effects on transition state structures remains controversial. Valuable information about the nature of the transition state is provided by measurement of kinetic isotope effects (KIEs). However, KIEs reflect changes in all bond vibrational modes that differ between the ground state and transition state. QM calculations are therefore essential for developing structural models of the transition state and evaluating mechanistic alternatives. Herein, we present computational models for Zn²⁺ binding to RNA 2′O-transphosphorylation reaction models that aid in the interpretation of KIE experiments. Different Zn²⁺ binding modes produce distinct KIE signatures, and one binding mode involving two zinc ions is in close agreement with KIEs measured for non-enzymatic catalysis by Zn²⁺ aquo ions alone. Interestingly, the KIE signatures in this specific model are also very close to those in RNase A catalysis. These results allow a quantitative connection to be made between experimental KIE measurements and transition state structure and bonding, and provide insight into RNA 2′O-transphosphorylation reactions catalyzed by metal ions and enzymes.

1 Introduction

Divalent metal ions play critical roles in RNA folding and catalysis.^1–8 The ability of divalent ions to stabilize high concentrations of negative charge in transphosphorylation reaction centers via electrostatic interactions, direct coordination or acid-base chemistry empowers them with potential mechanisms to assist in catalysis. However, unraveling the specific role of metal ions is extremely challenging due to the difficulty in discerning the catalytically active metal ion binding mode and its connection with the transition state (TS) structure and bonding,^2–4 which also exists as the major barrier in the investigation of enzyme catalysis mechanisms.

A powerful strategy to resolve mechanistic ambiguity is to rationally design and study simplified model reaction systems using a joint experimental/theoretical approach. Perhaps the most sensitive experimental mechanistic probe is the measurement of kinetic isotope effects (KIEs) that compare the relative reaction rate constants between isotopologues. KIEs arise from subtle quantum effects associated with the changes in structure and bonding that occur in proceeding from the reactant state (RS) to rate-controlling TS.^9–14 However, meaningful interpretation of KIE measurements requires the use of computational models. Computational modeling of KIEs has been extensively applied to study RNA transphosphorylation catalyzed by enzyme,¹⁵ specifically designed metal catalyst^16,17 and without catalyst.^18–20 In a recent work,²¹ Zhang et. al. measured the primary and secondary kinetic isotope effects for catalysis by Zn²⁺ ions and by specific base alone, and compared results with preliminary calculations. In the present work, we extend the scope of these calculations to explore 9 distinct, alternative Zn²⁺ ion binding modes (Figure 2) in the TS and characterize the resulting KIE signatures. Comparison across different model reactions are also performed and analyzed.

Figure 2.

TS structures located from all 9 Zn²⁺ binding models and comparison with the baseline model B1. Model IX matches best with experimental KIEs and has been highlighted. Key bond lengths in Å are labeled. All Zn²⁺ are saturated to hexacoordination by water but only key water molecules are shown for clarity.

2 Results and Discussion

2.1 Building a baseline model for un-catalyzed RNA 2′-O-transphosphorylation

In order to understand the effect of Zn²⁺ binding on TS structure, it is necessary to first characterize the reaction mechanism and TS in the absence of Zn²⁺. The transition states for a series of non-enzymatic baseline models (B1-B3) in the absence of Zn²⁺ are shown in Figure 1, and their calculated KIEs are compared with experimental values¹⁵ for a UpG dinucleotide in Table 1. As the models progress from the minimal model (B1) to the full dinucleotide (B3), the agreement between the calculated and experimental ¹⁸k_LG values significantly improves, while for ¹⁸k_NUC and ¹⁸k_NPO it improves slightly in B3 but not B2. The notable decrease in the calculated ¹⁸k_LG value from 1.0416 in B1 to 1.0358 in B2 mainly arises from the addition of a sugar ring to the leaving group, which enhances the leaving group activity since the pK_a of tetrahydro-2-furanmethanol (14.68²²) is lower than that of of ethanol (16.47²²). The addition of the full guanosine leaving group (B3) further reduces the ¹⁸k_LG value to 1.0322 that is very close to the experimental value of 1.034. This is due to coupling of vibrational modes of the nucleobase, in addition to the overall greater effective mass of the leaving group that damps the frequency of certain key modes. It is noteworthy to mention that when the leaving group is a methoxide, which is even lighter than the ethoxide group of B1, the calculated ¹⁸k_LG value increases to 1.0649, despite having a pK_a value roughly 0.5 units lower.²⁰

Figure 1.

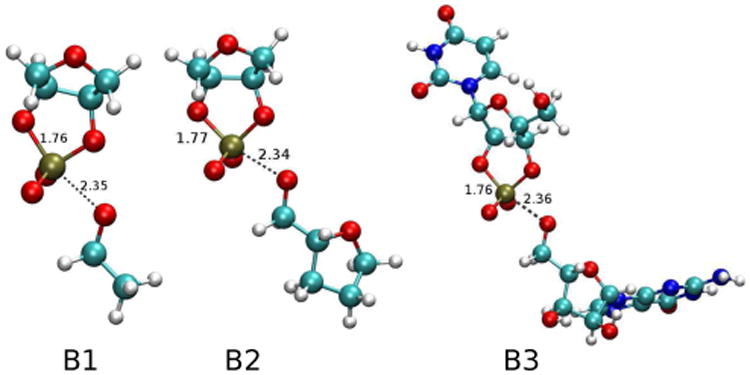
TS structures of baseline models for un-catalyzed RNA transphosphorylation. Key bond lengths in Å are labeled.

Table 1.

Comparison of calculated and experimental KIE values and the effect of catalysts for UpG dinucleotide 2′-O transphosphorylation model reactions in solution.

Condition	18kLG	18kNUC	18kNPO
Model B1 calc.	1.0416	1.0016	1.0029
Model B2 calc.	1.0358	1.0038	1.0032
Model B3 calc.	1.0322	1.0011	1.0025
Baseline expt.18	1.034(3)	0.997(1)	0.999(1)
Zn model IX calc.	1.0276	0.9950	1.0028
Zn2+-catalyzed expt.21	1.015(2)	0.986(4)	1.0007(2)
(kCat/kBL)Calc.	0.986	0.993	1.000
(kCat/kBL)Expt.	0.982	0.989	1.002
RNase A calc.20	1.0272	0.9973	1.0060
RNase A expt.15	1.014(3)	0.994(2)	1.001(1)
(kCat/kBL)Calc.	0.986	0.996	1.003
(kCat/kBL)Expt.	0.981	0.997	1.002

All KIE values were measured/calculated at the temperature of 90°C except for ¹⁸k_NPO in the baseline models, where the only available experimental value was at 37°C (from Ref. 18). Therefore, the corresponding calculations were also performed at 37°C. k^Cat/k^BL quantifies the effect of the catalyst on the KIEs, which is the ratio between KIEs in the catalyzed and uncatalyzed reactions, where the BL refers to the baseline model B1.

Although the full dinucleotide baseline model (B3) is in best agreement with experiment, it is too computationally intensive to be practical as a departure point from which to exhaustively explore multiple Zn²⁺ binding modes that add many more electrons to the quantum system and degrees of freedom to the optimization procedure. The goal of the present work is to determine the effect of Zn²⁺ binding on the TS structure of the UpG dinucleotide. As seen in Table 1, while the absolute values of the calculated KIEs for catalyzed and uncatalyzed reactions deviate modestly from the experimental values, their relative values are very consistent. Our comparison focuses on the relative KIEs for the catalyzed and uncatalyzed (baseline) models in order to maximize the cancellation of systematic errors in order to obtain quantitative agreement of the relative calculated and experimental KIE values. It has been suggested²³ to use isotope-effect-minus-one (KIE - 1) instead of KIE itself when comparing heavy atom isotope effects as these values are usually very close to unity. Here since we're focusing on the ratio between catalyzed and un-catalyzed KIEs, subtracting by one will make the magnitudes of both numerator and denominator much smaller, which will make the result a lot more sensitive to the computational errors and experimental uncertainties because both numerator and denominator are now in similar orders of magnitude with the uncertainties. It might also blow up because the denominator could be very close to zero. With an understanding of the deviations of the minimal baseline model (B1) relative to the dinucleotide baseline model (B3), it is reasonable to expect that comparison of Zn²⁺ binding in the context of the minimal model (which is computationally tractable even with multiple hydrated Zn²⁺ ions bound) would be transferable to the dinucleotide. Consequently, in what follows, we use the minimal baseline model (B1) as a framework from which to calculate the effect of Zn²⁺ binding on the TS and KIE values.

2.2 Exploration of Zn²⁺ catalytic modes

Comparison of experimental KIEs for un-catalyzed (baseline) and Zn²⁺-catalyzed reactions (Table 1) indicate that both primary ¹⁸k_LG and ¹⁸k_NUC values decrease considerably (by 0.019 and 0.011) upon Zn²⁺ binding. Examination of the experimental ratio of the KIE values for Zn²⁺-catalyzed and baseline reactions [(k^Cat/k^BL)Expt.] indicates the largest deviation from unity occurs for the leaving group (1.8%). The large normal ¹⁸k_LG value for the uncatalyzed reaction (1.034) suggests a late transition state characterized by a small bond order to the leaving group and high degree of accumulated charge at the O5′ position. The significant reduction of the ¹⁸k_LG value upon Zn²⁺ binding (1.015) suggests a TS that is not as late,²⁰ has greater bonding to the leaving group and less charge at the O5′ position. The effect of Zn²⁺ binding on the ¹⁸k_NUC value is also significant (1.1%), but less pronounced than for ¹⁸k_LG, and indicates a slightly higher degree of bond formation of the nucleophile to phosphorus for the Zn²⁺-bound TS compared to the un-catalyzed reaction. There is little effect of Zn²⁺ binding on the secondary KIE (¹⁸k_NPO) values (0.2%). The overall effect of Zn²⁺ binding is to produce a generally tighter TS bonding environment.

In order to establish a molecular electronic structure model that explains the effect of Zn²⁺ binding on the KIE values relative to the uncatalyzed reaction, we examined a series of 9 plausible Zn²⁺ binding modes (Figure 2), the results for which are shown in Table 2. Agreement between calculated and experimentally measured KIE values can be quantified by examination of the percent deviation (%D) in the KIE ratios defined as %D = [(k^Cat/k^BL)_Calc. – (k^Cat/k^BL)_Expt.] × 100%. Further, the character of the TS can be quantified by a reaction coordinate ξ defined as ξ = R₂ – R₁, where R₁ and R₂ are the P-O2′ and P-O5′ bond lengths, respectively (Table 2). Negative values of ξ indicate an early TS, whereas positive values indicate a late one.

Table 2.

Comparison of calculated KIEs and reaction coordinate ξ values in the TSs from models I to IX.

Model	ξ (Å)	18kLG (%D)	18kNUC (%D)	18kNPO (%D)
B1	0.59	1.0416	1.0016	1.0029
Expt. w/o Zn	N/A	1.034(3)	0.997(1)	0.999(1)
I	0.79	1.0466 (2.3)	0.9986 (0.8)	1.0017 (-0.3)
II	0.74	1.0441 (2.1)	0.9986 (0.8)	1.0029 (-0.2)
III	0.90	1.0517 (2.8)	1.0040 (1.3)	1.0007 (-0.4)
IV	0.67	1.0417 (1.8)	1.0012 (1.1)	1.0031 (-0.2)
V	-0.53	1.0063 (-1.6)	1.0463 (5.6)	1.0015 (-0.3)
VI	-0.49	1.0051 (-1.7)	1.0484 (5.8)	1.0029 (-0.2)
VII	0.47	1.0324 (1.0)	1.0054 (1.5)	1.0017 (-0.3)
VIII	0.48	1.0080 (-1.4)	1.0079 (1.7)	1.0005 (-0.4)
IX	0.42	1.0276 (0.5)	0.9950 (0.4)	1.0028 (-0.2)
Expt. w. Zn	N/A	1.015(2)	0.986(4)	1.0007(2)

Model numbering is the same as in Figure 1. Temperature is 90°C for all calculations and experiment. Reaction coordinate ξ is defined as ξ = R₂ – R₁, where R₁ and R₂ are the P-O2′ and P-O5′ bond lengths, respectively. Percentage deviation %D is defined as %D = [(k^Cat /k^BL)_Calc – (k^Cat /k^BL)_Expt.] × 100%, where BL is the baseline model (B1) consistent with the series of Zn²⁺ calculations. The numbers in parentheses following the experimental values are the experimental uncertainties.

We first explored a series of representative single Zn²⁺ binding modes to ascertain the effects on the predicted KIE values. In models I and II, Zn²⁺ are placed near the non-bridging oxygens to stabilize the negatively-charged phosphorane TS. However, the TSs are too late (ξ ∼ 0.7-0.8 Å, Table 2) and have ¹⁸k_LG values that are considerably larger than the experimental value. The difference between models I and II involves direct versus indirect Zn²⁺ coordination and does not substantially alter the KIE values. For model III and IV in which Zn²⁺ binds directly and indirectly to the nucleophile O2′, the ¹⁸k_NUC becomes slightly normal, and the ¹⁸k_LG values remain large. Models V and VI explore direct and indirect Zn²⁺ binding to the leaving group oxygen, which leads to an early TS (ξ ∼ -0.5 Å) with considerably underestimated ¹⁸k_LG and overestimated ¹⁸k_NUC values. This can be explained by recognizing that this Zn²⁺ binding mode has a similar effect as that of an enhanced leaving group²⁰ to shift the TS from late to early in character, with limited bond cleavage and charge accumulation at the O5′ position.

The inability for the single Zn²⁺ binding models (I-VI) to reproduce the experimental KIEs lead us to explore dimetal Zn²⁺ binding modes. Models VII and VIII explore direct and indirect Zn²⁺ binding, respectively, at both the nucleophile and leaving group positions. Model VII produces a late transition state (ξ = 0.47 Å) that is much earlier than models I-IV and has a considerably improved ¹⁸k_LG value (%D = 1.0), but has a normal ¹⁸k_NUC value with greater deviation (%D = 1.5). Model VIII has a similar late transition state (ξ = 0.48 Å) to model VII, but has a nucleophile KIE value that is even more normal, and considerably underestimates the leaving group KIE, resulting from a partial proton transfer from a Zn²⁺-coordinated water to leaving group oxygen.

Interestingly, each different Zn²⁺ binding model has a distinct set of predicted KIE values, however, only model IX corresponds closely with what is observed experimentally. Model IX involves one Zn²⁺ making direct coordination to the leaving group, and another that makes direct coordination to the non-bridge phosphoryl oxygen while maintaining indirect coordination with the nucleophile (Figure 2). In this model, the dimetal binding mode provides three distinct elements of TS stabilization—leaving group stabilization, negative charge redistribution and potentially assistance in proton transfer. The nucleophile and leaving group KIE deviations are 0.4% and 0.5%, respectively, a reduction in deviation by a factor of 2 with respect to the next smallest deviations in the series of models. The ¹⁸k_NUC value is slightly inverse and the ¹⁸k_LG value normal. Excellent agreement is obtained between calculated and experimental (k^Cat/k^BL) ratios (Table 1) for the leaving group (0.986 and 0.982, respectively) and nucleophile (0.993 and 0.989, respectively). We've also expanded the leaving group in model IX with a sugar ring as in model B2, but the KIE values calculated from corresponding optimized structures are not significantly different from the original model IX (¹⁸k_LG = 1.0268 vs 1.0276, ¹⁸k_NUC = 0.9963 vs 0.9950). Therefore we did not attempt to further expand the model to full UpG as in B3, as these are very large calculations that become more difficult to converge with more degrees of freedom. The general effect of Zn²⁺ binding is to create an earlier TS with an overall stiffer bonding environment that leads to a less pronounced normal leaving group KIE and slightly more inverse nucleophile KIE. The very close agreement of this model with recently measured KIE values, in stark contrast to that of a series of 8 other models tested, provides strong evidence that it can be used to provide an experimental interpretation of the TS structure and bonding for Zn²⁺-catalyzed RNA 2′O-transphosphorylation.

2.3 Comparison between Zn²⁺ catalysis and enzyme catalysis

The transition state for RNA 2′-O-transphosphorylation catalyzed by RNase A exhibits a primary KIE signature, both from experiment and computation, that is very close to that produced upon Zn²⁺ binding (Table 1). This is evident by analyzing the normalized k^Cat/k^BL values for the Zn²⁺ and RNase A transition states which are all within 1% of one another. The baseline normalized computational values are very close to the experimental values, but particularly striking is the internal consistency for the ¹⁸k_LG values between Zn²⁺ and RNase A systems as determined from either theory or experiment. The most straight forward interpretation is that the Zn²⁺ ions produce a local TS bonding environment that is similar to that of the RNase A active site: one Zn²⁺ ion stablizes the negatively charged reaction center in transition state similar to a protonated His12 in RNase A, while another Zn²⁺ ion enhances the leaving group departure analogous to the role of His119 (Figure 3). This analysis sheds light on general principles involved in RNA catalysis.

Figure 3.

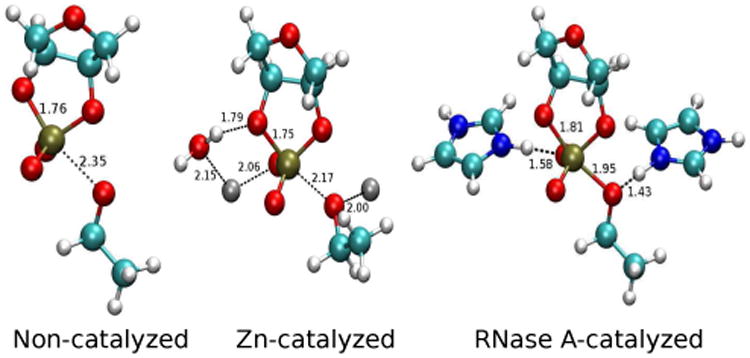
Comparison of TS structures in baseline, Zn²⁺-catalyzed and RNase A-catalyzed model reactions. The two imidazole rings in the RNase A model represents His12 (left) and His119 (right) residues in RNase A.

3 Conclusion

In conclusion, we explored the effect of different Zn²⁺ binding modes on the ¹⁸O kinetic isotope effects for Zn²⁺-catalyzed RNA 2′O-transphosphorylation. Different Zn²⁺ binding modes yield distinct KIE signatures that can be connected to TS structure and bonding and used to aid in the interpretation of experimental measurements to give insight into mechanism. A unique binding mode was identified as being very closely aligned with recent experimental measurements. This mode involved two zinc ions, one directly coordinating the leaving group and the other directly coordinating a non-bridge phosphoryl oxygen while interacting with the nucleophile at solvent separation. This catalytic mode produces a KIE signature very close to that observed for the TS in RNase A, and leads to model TS structure that is also quite similar. We also identified the origin of the systematic overestimation of the ¹⁸k_LG KIE value relative to experiment noted previously^15,19–21 which herein was shown to be corrected by inclusion of more realistic leaving group models. This work provides a predictive framework for the identification of Zn²⁺ ion binding modes in RNA 2′O-transphosphorylation reactions from KIE measurements that will advance our understanding of the role of divalent metal ions in mechanisms of RNA catalysis.

Computational Methods

DFT calculations were performed using the B3LYP^24,25 functional which has been demonstrated to be reliable for zinc complexes.²⁶ The 6-31+G(d) basis set was used for H, C, N, O and P, while the SDD effective core potential²⁷ was applied to Zn. Solvation effects were treated with the polarizable continuum model²⁸ (PCM) using specialized atomic cavity radii for RNA catalysis adopted from previous work.^15,19 Water solvent with a dielectric constant of 78.4 is used in all PCM calculations. Kinetic isotope effects were calculated from the Bigeleisen equation⁹ using the vibrational frequencies obtained from normal mode analysis of the optimized reactant and transition state geometries. All electronic structure calculations were carried out in Gaussian 09 package.²⁹

Scheme 1.

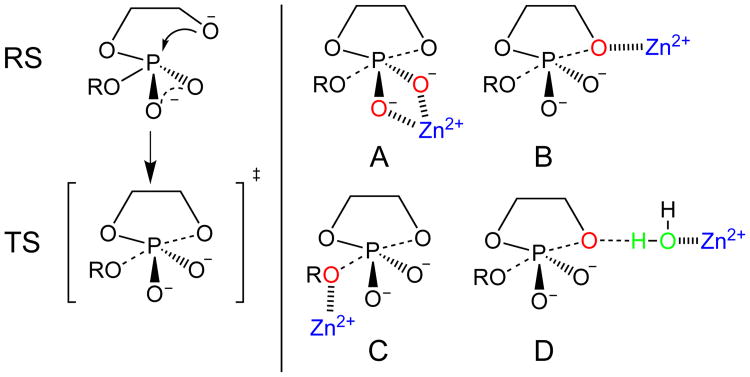
(Left) Schematic description of the reactant state and rate-limiting transition state in the RNA transphosphorylation reaction model. (Right) Illustration of three different Zn²⁺ binding sites (non-bridging oxygens in A, nucleophile oxygen in B, leaving group oxygen in C) and two interaction modes (direct coordination in A, B and C, indirect binding via a solvent water molecule in D).