Using Classification and Regression Trees (CART) and Random Forests to Analyze Attrition: Results From Two Simulations

Abstract

In this article, we describe a recent development in the analysis of attrition: using classification and regression trees (CART) and random forest methods to generate inverse sampling weights. These flexible machine learning techniques have the potential to capture complex nonlinear, interactive selection models, yet to our knowledge, their performance in the missing data analysis context has never been evaluated. To assess the potential benefits of these methods, we compare their performance with commonly employed multiple imputation and complete case techniques in 2 simulations. These initial results suggest that weights computed from pruned CART analyses performed well in terms of both bias and efficiency when compared with other methods. We discuss the implications of these findings for applied researchers.

A counterfactual is something that is contrary to fact. In an experiment, we observe what did happen when people received a treatment. The counterfactual is knowledge of what would have happened to those same people if they simultaneously had not received treatment. An effect is the difference between what did happen and what would have happened (Shadish, Cook, & Campbell, 2002, p. 5).

As Shadish et al. (2002) observed in their classic text, counterfactual reasoning is fundamental to causal inference. The focus of this article is on counterfactual inferences in a different context: that of missing data caused by attrition. Although the parallel is not typically made transparent, inferences about missing data take a near-identical form to the more familiar causal inferences described above. Paraphrasing Shadish et al., in the case of missing data, what we observe is the sample data, which may contain incompleteness. The counterfactual is what the data—and particularly our model(s) of interest—would have looked like if there was no incompleteness; that is, if we had access to all of the data. The effect of incompleteness is the difference between the results we obtain from our actual sample and the results we would have obtained with access to the complete data.

Viewed in this way, it seems evident that thinking about the effects of missing data requires the same set of inferential skills that researchers confidently deploy in a variety of other contexts on a regular basis. The major difference is that, unlike an experimental treatment condition, researchers do not have access to an alternative set of complete data that could foster such a comparison with the incomplete sample in order to assess the effects of incompleteness. As a result, it is not possible to observe what our model(s) would have looked like if there was no incompleteness. Instead, this needs to be estimated.

In this article, we assess a new method of estimation under missing data: the use of inverse probability weights derived from an exploratory classification tree analysis (cf. McArdle, 2013). The potential utility of this method comes from the promise of exploratory data mining techniques to uncover and account for complex relationships in the data that other linear methods might overlook. To evaluate whether this method lives up to its promise, we compare it with (a) weights derived from logistic regression analysis, and (b) multiple imputation (MI) methods (Rubin, 1976, 1987). Further, we extend McArdle’s (2013) logic by comparing these methods with probability weights computed using random forest analysis (Breiman, 2001).

We begin by reviewing two well-known methods of handling missing data: complete case methods and MI. We then describe the logic of using inverse sampling weights to address incomplete data. Although inverse probability weighting (IPW) has a long history in survey research (Kish, 1995; Potthoff, Woodbury, & Manton, 1992) and in the analysis of attrition (Asparouhov, 2005; McArdle, 2013; Stapleton, 2002), coupling this technique with an exploratory data mining analysis of the probability of incompleteness is a recent and novel idea (McArdle, 2013). We present three alternative methods for computing these weights: conventional logistic regression, classification and regression trees (CART), and random forest analysis. We then attempt to answer our questions about the relative benefits of these methods using data from two simulation studies.

Methods for Handling Incomplete Data

Complete Case Analyses

The simplest thing to do about missing data is, of course, nothing at all,¹ and this is the basis for complete case methods. In listwise deletion, any rows in the data set that contain incompleteness are deleted prior to analysis and only complete cases are analyzed. In pairwise deletion, the data set is subsetted to include only those variables relevant to a particular analysis, and then listwise deletion is performed on each pair of variables in the subsetted data set (that is, cases are not deleted if they contain incompleteness on variables not relevant to the analysis at hand, with the standard example being correlation tables computed from the complete cases on each pair of variables). Complete case methods implicitly assume that the data are missing completely at random (Rubin, 1976)²—that is, unrelated to both the missing and observed portions of the data set—and unless this assumption is met, these methods will result in biased parameter estimates. Even when incompleteness is caused by a completely random process, however, deleting cases reduces statistical power, and the extent of this problem increases as the amount of incompleteness becomes more severe. In a world in which methods for addressing incompleteness are widely available and easily implemented in common software packages, complete case analysis should never be the only analysis performed. However, these methods can serve as a useful baseline (or control) against which to compare the effects of statistical adjustments for incompleteness.

Multiple Imputation (MI)

Instead of simply ignoring missing data, researchers might apply an analysis method that effectively adjusts for the effects of incompleteness. One such method is MI (Rubin, 1987). MI functions exactly as its name implies: this method imputes new values in place of missing cases, and it does this multiple times.

Concretely, MI is a simulation-based method that consists of three steps: (a) imputing m data sets, in which m is typically between 3 and 10,³ (b) performing the data analysis of interest on each of the m imputed data sets, and, finally, (c) using simple arithmetic formulas to pool the parameter estimates and standard errors resulting from the m analyses. By analyzing and aggregating the results from each of the m data sets, MI produces estimates that are less biased and standard errors that are smaller than those produced by a single imputation alone (for more information on MI see, e.g., Graham & Schafer, 1999; Rubin, 1987).

Handling Missing Data Using Inverse Probability Weights

An alternative strategy to address incompleteness frames missing data as a sample selection problem (Asparouhov, 2005; Kish, 1995; McArdle, 2013; Potthoff et al., 1992; Stapleton, 2002). Understood in this way, missing data results from undersampling the members of certain subpopulations. For example, perhaps individuals in a certain age group, say individuals with age greater than 58 years, are less likely to return to the study at Time 2. In this scenario, individuals in the >58 age group are undersampled relative to individuals with age <58. In practice, these probabilities might be estimated from an exploratory analysis, such as a logistic regression, decision tree analysis, or ensemble method (see the section on “Random forest analysis”) predicting a variable coded 0 for dropout (missing) at Time 2, and 1 for returning (nonmissing) at Time 2. In order to correct the analysis for these uneven selection probabilities, researchers can utilize IPW (cf. Kish, 1995; McArdle, 2013; Potthoff et al., 1992; Stapleton, 2002). If p_i represents the probability of selection—that is, the probability of returning to the study (not dropping out)—for person i at time t + 1, then the inverse probability weight, w_i is equal to 1/p_i.

Because estimates of the weighted sample variance are not invariant to scaling, it is important to choose an appropriate scale for the sample weights. One technique that fits well with the goals of the current situation is weighting to the relative sample size (Stapleton, 2002).⁴ This scaling is accomplished by multiplying the raw weights, w_i, by a scaling factor, λ, where

$$\mathrm{\lambda }=\frac{n}{{\displaystyle \sum _{i=1}^n{w}_i}}.$$ (1)

This transformation scales the raw weights so that the scaled weights sum to the actual sample size, n. Weights can readily be incorporated into structural equation models by maximizing

$$\text{ln}\left(L\right)={\displaystyle \sum _{i=1}^n{w}_i\text{ln}\left(L_i\right)},$$ (2)

the weighted log likelihood (Asparouhov, 2005). Here, w_i indicate the weights, which may be rescaled using Equation 1 (that is, w_i here may refer to λw_i if relative weights are used). Weighted maximum likelihood (WML) estimation is the computational equivalent of fitting a model to the weighted sample means and covariances using standard maximum likelihood estimation. When w_i is a vector of unit weights (that is, when w_i = 1 for all i), this equation reduces to regular maximum likelihood and is equivalent to listwise deletion with every case receiving the same weight. Thus, it is evident that researchers cannot ignore or avoid missing data issues by adopting program defaults; even the most basic of these defaults carries tacit assumptions about the equal probability of selection into the sample.

However, WML has been shown to produce overly short standard errors and confidence intervals. Instead of WML, pseudomaximum likelihood (PML) is preferred, using the Huber-White sandwich estimator to generate the asymptotic covariance matrix (Asparouhov, 2005). PML is calculated by several robust maximum likelihood estimators offered in Mplus (Muthén & Muthén, 2011), including maximum likelihood with robust standard errors (MLR), used in the demonstration below.

Modeling Selection Probabilities

Logistic regression

The standard way to assess the relationship between the variables in a data set and the probability of incompleteness is by using logistic regression. Logistic regression relates a set of categorical, ordinal, or continuous predictors to a binary response variable—in this case, an incompleteness indicator variable, in which 0 = dropout and 1 = return at time t + 1. If one’s goal is to identify correlates of incompleteness to include as auxiliary variables in an imputation model, one might opt to select those variables that display significant relationships to incompleteness. If one’s goal is to compute sample weights, however, the predicted log odds can be converted to predicted probabilities using a standard formula, and the predicted probabilities can then be inverted to form sampling weights.

The logistic regression approach assumes that the predictors exhibit a linear relationship to the logged odds of the binary response variable, and therefore provides a useful way of assessing the significance of such linear relationships. Alternatively, it is possible that predictors in the data set may exhibit complex, unconventional interactions and/or may be related to incompleteness in a nonlinear fashion. Although it is possible to specify multiplicative linear interactions and polynomial functions in the regression framework, specifying all such interactions and nonlinearities among many predictors could result in multicollinearity issues and may miss important predictive relationships that do not conform to these specified functional forms. Even if the true relationship could be well captured by linear interactions and polynomial terms, finding the correct model specification may be difficult to approximate manually. If the analyst fails to specify the correct relationship among the covariates and the missing data indicator, the logistic regression approach may fail to capture important relationships among predictors and important nonlinear predictors of incompleteness. What is needed, then, is a technique to identify such interactions and nonlinearities in a systematic, automated manner. CART provides such a technique.

CART analysis

To identify a model of incompleteness is, by definition, to attempt to discover a set of auxiliary covariates that may be unimportant with respect to one’s a priori substantive model of interest but that are related in important ways to the probability of attrition (Enders, 2010; Rubin, 1976). One analytic technique that is particularly well suited to these exploratory goals is CART (Berk, 2009; Breiman, Friedman, Olshen, & Stone, 1984; Morgan & Sonquist, 1963; see also Strobl, Malley, & Tutz, 2009, for an excellent, readable introduction aimed at psychologists). In the context of attrition, a CART analysis seeks to find the values of the predictor variables that separate the data into groups of people who either (a) dropout, or (b) return to the data set at time t + 1.⁵

As an example, imagine that the dependent variable is an indicator of incompleteness, coded 0 for missing and 1 for not. Imagine, further, that one particular predictor is the highest level of education that a participant has achieved, coded with four ordered categories: (a) high school diploma or GED, (b) bachelor’s degree, (c) master’s degree, and (d) doctoral degree. The first thing a CART analysis does is to search for the “split” on this variable that will partition the data into two homogenous groups—a group of mostly 1s (people who returned to the study) and a group of mostly 0s (people who dropped out). With four ordinal categories, there are 4−1 = 3 possible splits: high school education versus bachelor’s, master’s, and doctoral; high school and bachelor’s versus master’s and doctoral; and high school, bachelor’s, and master’s versus doctoral education. CART iteratively tries out each of these potential cut points, subdividing the data at each possible split and choosing as the best split the split that produces the most homogenous subgroups.⁶

Once the best split has been identified for every variable, the CART algorithm partitions the data using the best overall split among these best splits and assigns a predicted class to each subgroup by majority vote (i.e., a predicted class of 1 for a subgroup containing mostly 1s). CART repeats this same process on each predictor in the model, identifying the best split by iteratively trying out all possible splits and settling on the split that produces the greatest reduction in impurity (or, equivalently, the most homogenous partitions).

CART proceeds recursively in this fashion until some stopping criterion is reached. Examples of stopping criteria include creating a prespecified number of nodes, or reaching a point at which no further reduction in node impurity is possible. If the algorithm is allowed to proceed indefinitely, the model will eventually find splits that are completely or nearly completely homogenous but that may have trivial sample sizes. For example, the final split might create two subgroups of only three people each. Because CART assigns predicted classes by majority vote, the results of such splits are highly unstable and unlikely to generalize to new samples—it would only require changing a single case to overturn a majority of two and change the predicted class for that node. Therefore, it is advisable to curb this algorithmic tendency to overfit these fine-grained idiosyncrasies in the observed data. One might consider accomplishing this using one of two broad strategies. First, one could consider stopping the tree from growing too large (and thereby preventing, in theory, the tendency to overfit in response to trivial, unstable partitions in the data) by setting a minimum sample size, a priori (e.g., all final splits must have at least 20 people in each node).

Alternatively, one may instead grow a very large tree and subsequently prune it back using cost-complexity pruning, which tempers the number of partitions by adding a parameter that penalizes larger, more unstable trees. In the binary classification context, cost-complexity pruning seeks to identify the nested subtree that minimizes the sum of (a) the risk associated with a tree of size T, and (b) the penalty for complexity assigned to a tree of size T. Here, risk is defined in terms of the proportion of misclassified observations of class 0 or 1 (e.g., in a node or entire tree) weighted by the cost parameters assigned to each type of misclassification, and a nested subtree is defined as a tree with fewer of the initial partitions than the original large tree. Hence, the optimal subtree chosen by cost-complexity pruning is a function of the costs of misclassification errors (the risk) qualified by the penalty associated with tree complexity. Cost-complexity methods employ crossvalidation to set the optimal penalty parameter for pruning, trying out various values for the parameter and computing the associated risk on the validation portion(s) of the data set.

Which of these two strategies—stopping or pruning—should researchers prefer? Some methodologists are equivocal, stating that “in practice, whether one determines tree complexity by using [penalty parameter] α … or an explicit argument to the CART procedure determining the minimum terminal node sample size, seem to make little difference” (Berk, 2009, p. 130). Others (e.g., Louppe, 2014), however, caution against employing stopping criteria, such as minimum node size, arguing that there may be cases in which further splits below the enforced minimum (e.g., minimum node sizes of less than a stopping rule of N = 20) could potentially provide benefits in decreasing generalization error. Because this argument is both intuitive and persuasive, and because investigating the effects of different choices of minimum node size is tangential to the aims of the present research, in the simulations described here we employ cost-complexity pruning rather than minimum node size.

The results of a CART analysis are displayed as a tree diagram, as shown in Figure 1. At the top of the diagram is the “root node,” which contains the entire data set. In this example, after trying out every possible split on all variables, CART chose to partition the data at cut point c₁ on predictor x. If x ≥ c₁, we proceed visually to the right of the diagram, reaching a new node. Because CART chose to further partition this subgroup of the data, this interim node is referred to as an “internal node.” This new split occurred on variable z at cut point c₃. If x ≥ c₁ and z < c₃, we reach Node 3, which is a “terminal node”—that is, a final node that was not split further. Because the majority of cases in this node were 0s (e.g., dropouts), this node receives a predicted class of 0. Similarly, if x ≥ c₁ and z ≥ c₃, we reach terminal Node 4, in which the majority of individuals were 1s (e.g., returners) and the predicted class is 1.

Figure 1.

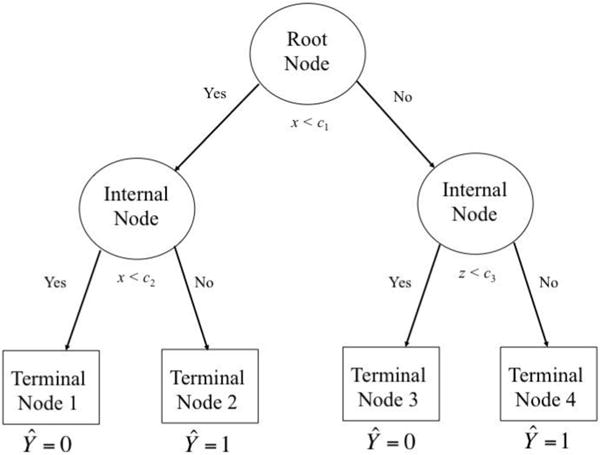
Example tree diagram from classification and regression tree (CART) analysis (cf. Berk, 2009).

Splitting the data on both x and z represents an interaction effect—the effect of x on the predicted probability of returning to the study depends on z. Yet this interaction may be quite different from those modeled by the usual regression techniques (Aiken & West, 1991). In this case, z interacts with x only above cut point c₁ and it does so not by modifying the simple slope of a line, but instead by splitting the values of x ≥ c₁ into two distinct subgroups (nodes) with different predicted outcomes.

If, instead, CART had partitioned the subgroup using a different cut point on x, the result would be a nonlinear step function (Berk, 2009). This pattern can be seen on the left side of the diagram: If x < c₁ but ≥ c₂, the predicted class is 1; if x < c₁ and < c₂, the predicted class is 0. In this way, by testing each possible split on every variable, the CART algorithm tests all possible nonlinearities and interactions among all cut points on the predictors.

In addition to assigning a class to each node, CART also computes a predicted probability of “success” (i.e., being classified as a 1, or, in the case of attrition, returning to the study) using the proportion of 1s in each terminal node. For example, if only 25% percent of individuals in a certain terminal node returned to the study, the predicted probability for this node would be .25. These predicted probabilities can be inverted to create sample weights that might be used to give greater weight to individuals from high-dropout groups who actually returned to the study.

Random forest analysis

Although CART has many virtues, it has some limitations. One such limitation is high variance across samples. This means that the tree structure and resulting estimates (e.g., predicted classes and probabilities) are not necessarily stable in new samples. As we have seen, pruning is one method that may address this issue. An alternative is to employ bootstrap methods that repeatedly create new data sets by sampling from the observed data with replacement, fitting the CART model to each bootstrap sample and aggregating the results to determine the most stable features of the tree. Because of their low variance and high predictive accuracy, in many domains the use of CART has largely been supplanted by resampling (“ensemble”) methods that address CART’s potential instability by averaging the results of many trees.

Bootstrap methods take many repeated samples from the data with replacement, each time recording the predicted classification for each case. The resulting predicted probabilities are computed as the proportion of times a given case is classified as a 0 or a 1 across the bootstrap samples. For example, if Case 1 in the data set is classified as a 1 in 900 out of 1,000 bootstrap samples, the predicted probability of this case being assigned a value of 1 is .9. Similarly, the predicted class for the case is assigned by majority vote as 1. This is the basis for bagging (short for “bootstrap aggregation”; Breiman, 1996), an early resampling-based method.⁷ Random forest analysis (Breiman, 2001) provides an additional benefit: For each split on each bootstrap tree, the algorithm randomly samples a subset of the predictors to be used as candidates for the split. When the predictors in the data set are highly correlated, this procedure addresses potential collinearity issues by giving each of the correlated predictors a chance to be used in different bootstrap trees. As in CART and logistic regression, the predicted probabilities from a random forest analysis can be inverted and scaled to create weights for use in further analyses (Asparouhov, 2005; Kish, 1995; McArdle, 2013; Potthoff et al., 1992; Stapleton, 2002).

The biggest disadvantage of random forests is that the analysis, which aggregates over the results of many bootstrap trees, does not produce a single, easily interpretable tree diagram. However, this method does provide variable importance measures derived from the contribution of each variable to prediction or fit across the bootstrap trees. As a result, variables with high variable importance scores in a missing data analysis may be considered as important missing data correlates.

The Present Research

The promise of using CART and random forest methods to model missing data is the potential of these methods to better capture complex selection models than traditional linear methods such as logistic regression. Yet the relative performance of these methods has not been assessed in the missing data context. As a result, whether and when these methods will provide gains over traditional techniques is unknown. Therefore, in order to assess the performance of these methods, we conducted two statistical simulations. The first, large-scale simulation study assessed the effects of selection model (linear vs. tree with one, two, or three splits) and percent attrition (30% or 50%) on parameter estimates returned by a cross-lagged path model.

Simulation A

Simulation design

Template model

As a template model, we simulated a crosslagged factor model with two time points as our template model for all analyses. This model is displayed in Figure 2a, which also displays the true population parameters for the structural part of the model. For the sake of simplicity, we set the correlation between X₁ and Y₁ to zero in the population. We used this factor model to simulate indicators with varying degrees of reliability. In all cases, once the data were generated at a given level of reliability, we averaged the indicators to form composite variables, yielding the analysis model shown in Figure 2b. This analysis model was then fitted using each of the techniques (e.g., MI, CART weights) assessed in the simulation.⁸

Figure 2.

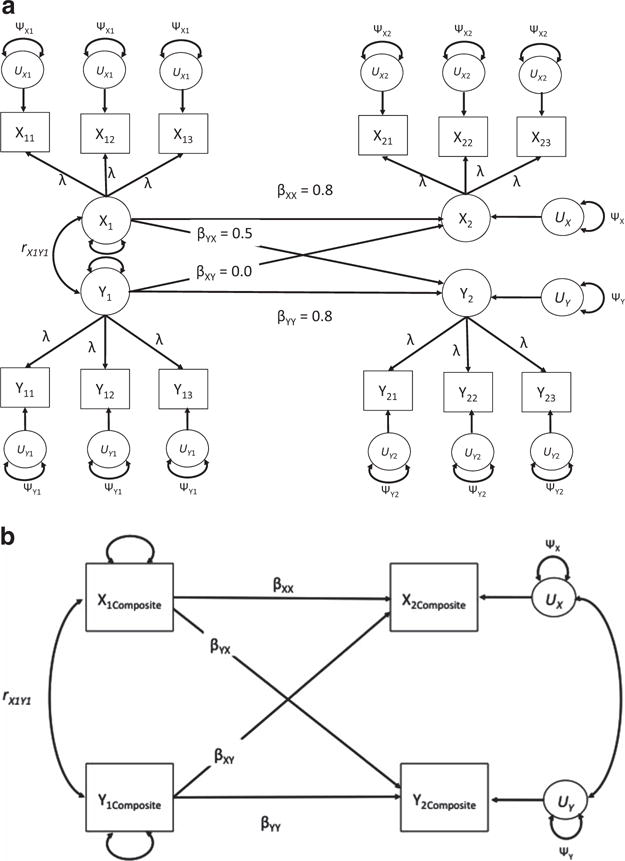
Template models used in Simulation A. (a) Population factor model. (b) Composite model used for actual analyses.

Simulated missing data covariates

In addition to this template model, we simulated three missing data covariates, v, z, and w. These three covariates were uncorrelated with each other and were set to be correlated with both time one variables at r_COV,X1 = r_COV,Y1 =.4. Given the structural expectations of the template model, this resulted in expected correlations of .32 between each covariate and X₂ (because the cross between Y₁ and X₁ was zero) and expected correlations of .52 between each covariate and Y₂.

Approach to modeling attrition

In this simulation, we were interested in modeling participant attrition rather than other types of missing data (e.g., selective nonresponse to certain surveys or items). Specifically, we modeled a situation in which participants showed up at Time 1 and then either did or did not return at Time 2. Thus, if a participant dropped out at Time 2, both variables—X₂ and Y₂—were missing.

Factors varied in the simulation

Primary factors in the simulation

The two key factors in the present simulation were the selection model and the percent attrition generated. For each simulation cell, we generated j = 200 simulation data sets from a multivariate normal distribution.

Selection model

The most crucial factor varied in the simulation was the structure of the selection model. Once we generated complete data sets from the template model, we generated attrition using either a linear selection model or a tree with one, two, or three splits. Figure 3, Panels a, b, and c, display the structures of these tree-based selection models, respectively. Note that, particularly in the case of the three-split model (Panel c), these figures represent conceptual, missing data generation models for the simulation, and the order of the splits may not necessarily be the same when analyzed using decision tree methods (e.g., the first split on variable v may not result in the biggest partition, and may therefore not be the first split returned by the analysis, despite this data generation model).⁹

Figure 3.

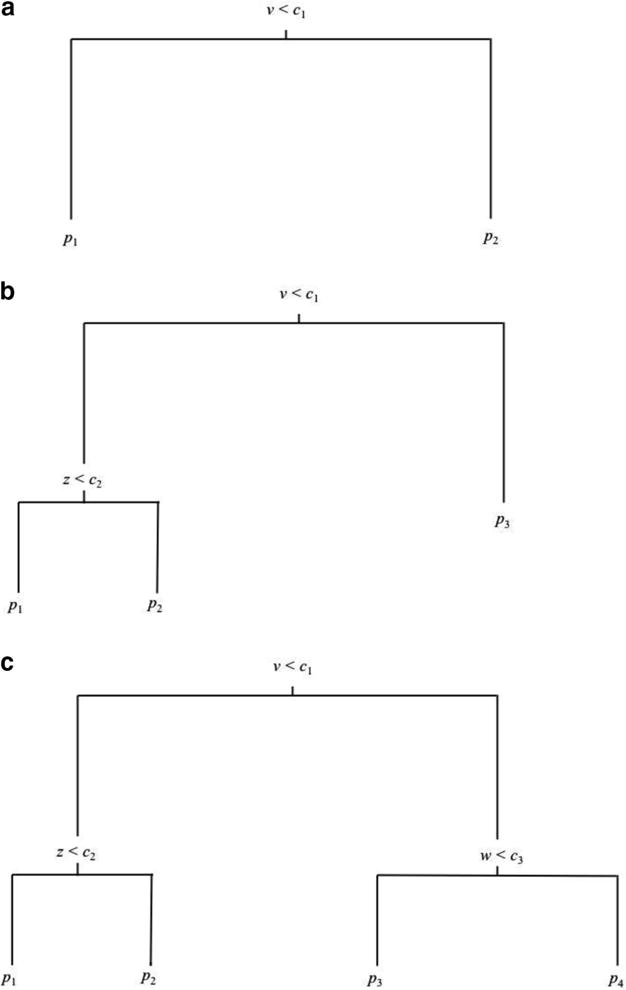
Tree structures used to generate attrition in the simulations: (a) one-split condition; (b) two-split condition; (c) three-split condition.

Percent attrition

The percent of attrition modeled in this simulation was varied to be either 30% or 50% at Time 2 in the manner described in the next section.

Choice of cut points and methods of simulating selection models under different percentages of attrition

In the linear selection conditions, attrition was predicted by variable v using a smooth function. To simulate linear selection, we simulated the log odds of attrition using the linear model:

$$\mathit{LogOdds}\left(\mathit{Miss}\right)={\mathrm{\beta }}_0+{\mathrm{\beta }}_{1}v.$$

We then converted these log odds to probabilities using conventional formulas and used these resulting probabilities to generate missing data. For example, if a certain case had a predicted probability of .6, this case would have a 60% chance of receiving a missing value in the data set and a 40% chance of not receiving a missing value in the data set.

In the 30% attrition condition, the coefficients used to generate the log odds were β₀ = −0.85 and β₁ = 0.3. In the 50% attrition condition, the coefficients used to generate the log odds were β₀ = 0.03 and β₁ = −0.86. These values were chosen based on simulation pretests because of their ability to reliably lead to 30% and 50% missing cases, respectively. We simulated linear attrition in this way, rather than a more conventional manner (e.g., monotonically increasing the probability of attrition in each quartile of the missing data indicator, as in Collins, Schafer, & Kam, 2001), because we wanted the linear selection conditions to truly represent, rather than merely approximate, the kind of smooth, linear function that would be easily captured by logistic regression analysis (but not necessarily by decision tree methods).

The cut points and probabilities displayed in Table 1 correspond to the tree-based selection models from Figure 3. Importantly, the values displayed for the cut points are percentiles of the splitting variable. For example, cut point c₁ occurred at the 75th percentile of variable v in the one-split, 30% attrition condition, and at the 50th percentile (median) in the one split, 50% attrition condition, and so on. We generated these cut points and probabilities of attrition by first hypothesizing tree structures that might generate 30% or 50% attrition among the uncorrelated covariates and then empirically adjusting these values based on simulated pretests.

Table 1.

Simulation Parameters for Tree-Based Selection Models

Percent missing:	One split		Two splits		Three splits
	30%	50%	30%	50%	30%	50%
Cut points
c1	.75	.50	.80	.60	.40	.50
c2	—	—	.15	.30	.65	.40
c3	—	—	—	—	.70	.60
P(Return)
p1	.87	.70	.40	.30	.88	.75
p2	.20	.30	.89	.85	.40	.30
p3	—	—	.60	.25	.90	.70
p4	—	—	—	—	.30	.25

Note. Cut point values represent percentiles (quantiles) of the observed covariates.

Secondary factors in the simulation

In addition to these primary factors, we varied two secondary factors in this simulation: the sample size, N, and the reliability of the covariates.

Sample size, N

In each simulation cell, we generated data sets of three different sizes, N = {100, 250, and 500}.

Reliability of the indicator variables

Rogosa (1995) suggests that the more reliable variable is often chosen as a cause in cross-lagged models. In order to investigate this phenomenon in the present missing data context, we varied how reliable the X and Y measures were in our simulated data. In order to simulate different reliabilities among the X and Y variables, we set α_X = {.7, .9} and α_Y = {.7, .9}. Fully crossing these factors resulted in four conditions: (a) α_X = α_Y = .7; (b) α_X = .7 and α_Y = .9; (c) α_X =.9 and α_Y = .7; and (d) α_X = α_Y = .9. We chose these values because α = .9 is generally acknowledged as a high degree of reliability, whereas α = .7 is generally acknowledged to be a minimum acceptable level of reliability. Thus, these conditions were designed to represent high and minimum acceptable reliability conditions, reflecting reliability levels typically reported in practice.

We generated these reliabilities by varying the size of the uniquenesses in the template factor model (Figure 2a). All factor loadings for all indicators in the template model were set to λ = .8 and the values of the uniquenesses were calculated to return either .7 or .9 reliability among the indicators. Specifically, ψ was set equal to .82 when α = .7, and .21 when α = .7. Note that reliabilities refer to indicators of all factors related to a given measure, such that when α_X = .9, the indicators of both X₁ and X₂ are set at a reliability of .9, and the same is true for indicators of both Y₁ and Y₂ when the reliability of Y is varied.

Models tested in the simulation

Models applied to the simulated data

Because of the way we simulated attrition, in which participants either returned or not at Time 2, we were not able to include full information maximum likelihood (FIML; Anderson, 1957; Arbuckle, 1996) among the missing data estimators tested in this simulation. This is because when data are missing only on the dependent (endogenous) variables, Mplus (Muthén & Muthén, 2011) automatically applies listwise deletion to these cases.¹⁰ Therefore, we used only six missing data methods to analyze each simulated data set: listwise deletion, MI, and weights generated from (a) logistic regression, (b) CART, (c) CART with cost-complexity pruning, and (d) random forest analysis. We ran CART analyses using R package rpart (Therneau, Atkinson, & Ripley, 2014). In pruned CART conditions, we implemented cost-complexity pruning using the onestandard-error rule, which essentially recognizes that values falling within one standard error of the minimum risk are statistically equivalent and chooses the complexity parameter that produces smallest, most parsimonious subtree falling within this range (see package documentation). Random forest analyses were conducted using package randomForest (Liaw & Wiener, 2002) with default settings. In passing, we note that these were the same packages and setting employed by Lee, Lessler, and Stuart (2010) in their simulations of machine learning techniques in the propensity-score matching context, although it is unclear whether these authors used the onestandard-deviation rule for pruning or simply the minimum crossvalidated risk.

In all models besides CART and pruned CART (in which we chose the first single tree and best nested subtree, respectively), we took an inclusive approach to choosing missing data covariates for analysis, as previous research has shown that including more covariates often tends to improve the results of missing data methods (Collins et al., 2001). For this reason, we included all missing data covariates in each of these models in order to enhance their performance as much as possible. That is, we modeled logistic regression weights and imputed data using all three covariates, v, z, and w. Similarly, we used the results of random forest analyses modeling all covariates to create probability weights. That is, although we recorded which variables were flagged as statistically significant and predictively important in the simulation, we utilized all covariates in all final missing data models, regardless of which were flagged in the selection analyses.

With each of these methods, we estimated the full cross-lagged regression model displayed in Figure 2b and assessed each method’s performance in recovering the true parameter values. All structural models were run in Mplus (Muthén & Muthén, 2011) via the MplusAutomation package in R (Hallquist & Wiley, 2014).

Overall design

Given these factors, the overall design of the simulation consisted of a fully crossed 4 (selection: linear, one split, two splits, three splits) × 2 (percent attrition: 30%, 50%) × 2 (α_Y = .7, .9) × 2 (α_X = .7, .9) × 3 (N = 100, 250, 300) design, resulting in 96 unique simulation cells. Because each cell was resampled 200 times, this resulted in 96 × 200 = 19,200 simulated data sets.

Dependent measures assessed in the simulation

Methods used to assess the selection model

In the first part of the simulation, we tested the performance of several methods for assessing the selection model: (a) t tests of missing versus nonmissing cases performed on each covariate, (b) logistic regression analysis predicting the missing-data indicator from all covariates, (c) CART analysis, (d) pruned CART analysis, and (e) random forest analysis. The performance of these methods in determining the true selection model was assessed using two methods: (a) by recording which variables each selection analysis flagged as statistically significant or predictively important, and (b) by recording the classification accuracy returned by each method.

Selection variables flagged

To assess the accuracy of these techniques in recovering the true selection model, we captured whether or not each analysis flagged each covariate as (a) statistically significant (for t tests and logistic regression), (b) a split variable in a tree (for CART and pruned CART analyses), or (c) an important predictor in the random forest analysis, using the standardized classification accuracy measure available in the importance() function in the randomForest package (Liaw & Wiener, 2002). Additionally, we assessed effect size measures (e.g., Cohen’s d) for the t tests and variable importance for the CART models, respectively.

Classification accuracy

For the logistic regression, CART/pruning, and random forest analyses, we recorded the classification accuracy returned by each method. Because CART-based methods are prone to overfitting, we hypothesized that these methods would likely return higher classification accuracy rates than all other methods, regardless of selection model. Conversely, because random forest analysis is designed to undercut CART’s tendency to overfit, we hypothesized that this method might be likely to return lower classification accuracy, regardless of selection model (and regardless of random forest’s actual performance).

Dependent measures used to assess the performance of missing data estimators

To assess the performance of missing data techniques in recovering model parameters, we used four primary measures taken from the prior simulation literature on incomplete data (Enders, 2001; Enders & Bandalos, 2001): percent bias, mean squared error (MSE), efficiency, and statistical rejection rates.

Percent bias

Consistent with Enders’s work (Enders, 2001; Enders & Bandalos, 2001), percent bias was measured using the formula

$$\text{\%}\mathit{Bias}=\left[\frac{{\widehat{\theta }}_{ij}-{\theta }_i}{{\theta }_i}\right]\ast 100$$ (3)

where ${\widehat{\theta }}_{ij}$ indicates the value of the estimated statistic on the jth iteration and θ_i indicates the true population parameter. The overall bias for a given parameter in a given simulation cell is the average percent bias across the j iterations. Following Muthén and colleagues (Muthén, Kaplan, & Hollis, 1987), values greater than 15% are considered problematic.

Efficiency

Efficiency was simply computed as the empirical standard deviation of the estimates of each model parameter for each analysis method across the simulated iterations in each simulation cell.

MSE

In contrast to percent bias, MSE is simply computed as the average squared difference of each estimate from the corresponding parameter. As noted by others (Collins et al., 2001; Enders, 2001; Enders & Bandalos, 2001), MSE incorporates both bias and efficiency, making it a rough proxy for the “overall accuracy” of a given method.

Statistical rejection rates

Finally, for all parameters, statistical rejection rates were recorded in the simulation.

Simulation Results

Selection variables flagged

Based on the selection models included in this simulation, a given technique is considered accurate to the extent that, on average, it (a) flags variable v, but not variables z and w, as an important missing data covariate in the linear and one-split conditions; (b) flags variables v and z, but not w, as important missing data covariates in the two-split conditions; and (c) flags all three covariates as important predictors of missing data in the three-split conditions.

Table 2 displays results for missing data t tests, logistic regression analysis, and CART-based methods. For the t tests and logistic regression, the table displays the average rate at which each variable was flagged as a significant predictor of incompleteness. For the CART methods, the table indicates the average rate at which each variable was included as a split variable in the chosen tree.

Table 2.

Selection Model Identification by Sample Size and Selection Model, Simulation A

	Covariate flagged as significant (rejection rate)						Covariate used in tree
	t tests			Logistic			CART			CART + Prune
	v	z	w	v	z	w	v	z	w	v	z	w
N = 100
Linear	.612	.041	.052	.611	.054	.042	.914	.710	.698	.876	.396	.387
One split	.944	.052	.058	.943	.049	.047	.997	.428	.408	.989	.065	.063
Two splits	.892	.539	.056	.926	.049	.620	.991	.903	.219	.964	.699	.055
Three splits	.044	.371	.593	.046	.616	.393	.848	.796	.943	.576	.597	.828
N = 250
Linear	.786	.050	.054	.783	.064	.053	.996	.924	.912	.97	.482	.483
One split	.999	.051	.048	.999	.047	.041	1.000	.545	.539	1.000	.033	.034
Two splits	1.000	.922	.044	1.000	.052	.958	1.000	.997	.518	.993	.838	.081
Three splits	.048	.734	.884	.054	.896	.777	.999	.996	1.000	.902	.804	.964
N = 500
Linear	.929	.053	.052	.928	.048	.054	.978	.811	.816	.966	.477	.482
One split	1.000	.053	.060	1.000	.054	.042	1.000	.306	.316	1.000	.018	.018
Two splits	1.000	.996	.044	1.000	.044	.999	1.000	1.000	.484	.999	.911	.070
Three splits	.076	.959	.989	.078	.991	.972	1.000	1.000	1.000	.993	.901	.998

Note. CART = classification and regression trees; Prune = pruned CART analysis. Table entries indicate the percentage of simulated iterations that each variable was either flagged as statistically significant (t-tests, logistic regression) or included as a split variable (CART, CART + Prune).

Overall, the results are encouraging for all selection model assessment methods. In general, all methods flagged variable v as more important than variables z and w in the linear and one-split models, although the rates for t tests and logistic regression improved with increased sample size in the linear condition. Similarly, all methods seemed to flag variables v and z, but not w, as important missing data correlates in the two-split conditions. Once again, however, the rates at which t tests and logistic regressions flagged w as significant improved with increased sample size. Finally, all methods performed well in identifying the role of z and w in the three-split conditions, but the t tests and logistic analyses performed poorly in recognizing the role of variable v in this selection model.

The CART and pruning methods performed consistently better than t tests and logistic regressions in all but the linear selection model conditions. Whereas CART tended to overfit the data and flag all three variables as predictors of attrition in the linear selection model conditions, implementing pruning seemed to curb this tendency, cutting rates of falsely identifying z and w as important split variables down by roughly a half for all sample sizes. Pruning also substantially reduced the rates of flagging incorrect variables as split variables (e.g., flagging w in the two-split condition or z in the one-split condition) in virtually all other conditions. One exception to this trend is that pruning did not perform quite as well as single-tree CART in flagging all three covariates in the three-split, N = 100 conditions.

Statistical significance of t tests and logistic regression coefficients and inclusion as split variables in tree models are not the only criteria for flagging important predictors. Alternative approaches include examining effect size estimates and extracting variable importance measures. One potential benefit of these approaches is their potential to obviate some of the sample-size dependence found for t tests and logistic regression when decisions were based purely on statistical significance. To examine the merits of these alternative approaches, Table 3 displays mean values of Cohen’s d, McFadden’s pseudo R² (as an effect size measure of the overall logistic regression model), and variable importance for CART, pruned CART, and random forest analyses.

Table 3.

Effect Size Measures and Variable Importance by Sample Size and Selection Model, Simulation A

	Mean effect size measures				Mean variable importance
	t test |Cohen’s d|			Logistic regression	CART			CART + Prune			RF
	v	z	w	McFadden’s pseudo-R2	v	z	w	v	z	w	v	z	w
N = 100
Linear	.563	.167	.170	.086	8.199	3.656	3.703	6.871	2.706	2.722	7.391	−.106	−.112
One split	.940	.175	.173	.177	15.224	3.431	3.257	13.903	1.729	1.687	23.271	.024	−.054
Two splits	.732	.470	.169	.155	11.125	8.117	2.065	10.667	7.485	1.423	20.075	11.71	−.147
Three splits	.166	.366	.508	.093	5.502	5.662	7.591	4.335	4.601	6.613	6.067	6.533	11.192
N = 250
Linear	.548	.105	.108	.070	18.810	8.242	7.85	14.412	5.141	5.007	12.175	−.055	−.037
One split	.927	.107	.105	.155	35.932	6.077	5.835	32.604	1.965	1.969	40.284	.157	−.141
Two splits	.731	.473	.105	.141	26.257	19.352	3.301	24.228	17.860	1.609	36.120	22.149	−.073
Three splits	.106	.354	.496	.077	15.179	13.58	17.005	11.488	10.093	14.539	13.759	12.736	20.681
N = 500
Linear	.546	.075	.074	.065	28.434	8.512	8.618	23.614	5.960	5.998	17.546	−.010	.052
One split	.920	.075	.078	.147	65.234	4.773	4.850	63.561	2.485	2.499	58.864	.011	−.010
Two splits	.737	.467	.074	.137	48.704	35.515	3.732	46.384	33.936	1.609	53.898	33.001	−.045
Three splits	.084	.355	.503	.074	26.227	22.838	29.152	21.728	17.958	26.093	22.843	20.421	31.863

Note. Cohen’s d indicates the mean of the absolute d values across simulated iterations. Random forest variable importance calculated using classification accuracy. CART = classification and regression trees; Prune = pruned CART analysis; RF = random forests.

Examining Table 3, we see that the true missing data predictor(s) reliably showed much larger effect sizes than the other covariates. Based on these effect size measures, which covariates would an analyst likely include in the missing data model? If anything, these results suggest that use of Cohen’s d rather than statistical significance may result in inclusion of all the covariates. Based on standard cutoffs (e.g., flag any covariate with a |d| > .10), all covariates would be included, on average, in every condition except for the N = 500 cells. However, past research indicates that adopting an inclusive covariate selection strategy is generally not harmful and, in fact, often carries many benefits (Collins et al., 2001).

Interestingly, McFadden’s pseudo R² was small across all logistic regression models, despite the inclusion of the true predictor(s) in each case. Here again, one would be well-advised to use an inclusive approach to predictor selection here, rather than dismissing the logistic regression results because of the small overall R².

Additionally, variable importance measures proved to be a sound alternative method for covariate selection when using tree-based methods. In each case, the average importance of the true predictor(s) was much larger than the average importance of the other covariates. This was especially true for the random forest method, in which only the true predictor(s) received high importance scores and the other covariates’ scores were uniformly near zero.

Classification accuracy

As expected, CART and Pruning methods consistently returned higher classification accuracy values than logistic regression or random forest analysis across all selection models and missing data percentages. These results indicate that classification accuracy measures lack diagnostic value in identifying the true selection model. Based on these results, one cannot claim that “the CART model had a higher classification accuracy than the logistic regression analysis; therefore, the true selection model is most likely a tree.” As we suspected, this measure says more about the classifier used (in particular, its tendency to overfit the data or not) than the data being classified. To conserve space, further details concerning this result are omitted here. However, a full table of classification accuracy rates is presented in Online Supplement B.

Percent bias

Surprisingly, given the complexity of the selection models employed in the simulation and the high percentages of missing data induced, percent bias was low, overall, among the majority of the parameter estimates. Tables of percent bias relative to the population structural parameters are included in Online Supplement B. To summarize, the most notable results from these tables are as follows: (a) In general, the regression coefficients show negligible bias; and (b) the most bias, however, is observed in the estimate of the Y₂ residual.

To provide a broad illustration of these results, Figure 4 displays the marginal means of percent bias for each method under each selection model, aggregated across parameters. Although this figure loses information by collapsing over the different parameters, it is evident that all of the missing data methods display low amounts of bias in all conditions (including, unfortunately, listwise deletion).

Figure 4.

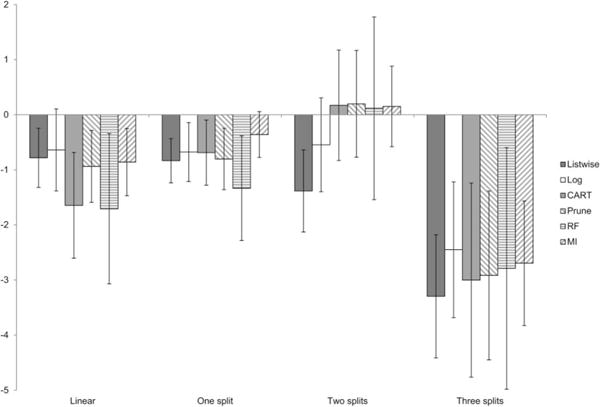
Marginal means of percent bias for parameters in Simulation A.

Relative efficiency

Table 4 presents the relative efficiency of each missing data estimator compared with pruned CART analysis. This ratio is formed by taking the empirical standard deviation of the estimates returned by measure X across the simulated iterations and dividing it by the empirical standard deviation of the pruned CART estimates, that is, SD_MethodX/SD_Prune (cf. Enders & Bandalos, 2001). Using this metric, values > 1 indicate instances in which a given method is less efficient than pruned CART (i.e., pruned CART is more efficient), whereas values < 1 indicate the opposite. Because these results were similar across conditions, we present results for the α_X = α_Y = .9, N = 500 cells only. Further, we average results across parameters, because efficiency, unlike bias, did not seem to be parameter-specific. In general, pruned CART was more efficient than either single tree CART or random forest analysis. Listwise deletion and MI, however, consistently outperformed pruning in terms of efficiency. When comparing the efficiency of pruned CART with logistic regression-weighted analyses, the results were more mixed. In the N = 100 conditions, logistic weighting was more efficient across the board, whereas pruning was more efficient in several cells of the N = 250 and N = 500 conditions, especially when the selection models were trees and the percent attrition was high. In general, however, these methods (logistic and pruned weights) displayed similar degrees of efficiency. To the extent that these ratios rose above or sunk below 1, it was rarely far, indicating (perhaps surprisingly) that these methods often do not represent a significant tradeoff in terms of efficiency.

Table 4.

Average Relative Efficiency Across Parameters, Simulation A

	Listwise deletion		Log weights		CART weights		RF weights		MI
	30%	50%	30%	50%	30%	50%	30%	50%	30%	50%
N = 100
Linear	.955	.886	.954	.958	1.006	1.053	.994	1.075	.942	.885
One split	.788	.896	.893	.959	1.010	1.095	1.001	1.197	.790	.887
Two splits	.880	.821	.931	.982	1.016	1.049	1.032	1.168	.887	.822
Three splits	.893	.884	.935	.943	1.018	1.073	1.006	1.081	.900	.881
N = 250
Linear	1.006	.970	1.009	1.074	1.085	1.179	1.057	1.233	1.009	.971
One split	.895	.971	1.069	1.072	1.152	1.167	1.331	1.348	.896	.976
Two splits	.902	.902	.978	1.103	1.121	1.131	1.227	1.395	.910	.911
Three splits	.945	.957	1.009	.998	1.135	1.171	1.102	1.191	.948	.946
N = 500
Linear	.940	.917	.948	1.036	1.010	1.051	1.012	1.281	.937	.933
One split	.816	.932	1.005	1.037	1.007	1.019	1.360	1.327	.828	.937
Two splits	.883	.858	.955	1.042	1.052	1.019	1.208	1.507	.89	.872
Three splits	.867	.873	.909	.899	1.040	1.009	1.076	1.276	.868	.883

Note. Relative efficiency is computed as the efficiency of measure X over the efficiency of pruned CART. Log = logistic regression; CART = classification and regression trees; RF = random forests; MI = multiple imputation.

MSE ratios

Table 5 displays the ratio of each estimator’s MSE over that of pruned CART (cf. Enders, 2001) for each parameter estimated in the model. In this case, values > 1 indicate that pruned CART was more accurate than the comparison method, whereas values < 1 indicate that pruned CART was less accurate than the comparison method. Once again, because of similarity in results across conditions, we display results for the α_X = α_Y = .9, N = 500 cells here. One result that is worth highlighting is the superior performance of pruned CART to random forest analyses on virtually all measures. The performance of pruned CART compared with listwise deletion and logistic regression is more mixed. Pruned CART does appear to have an advantage over logistic regression weights in some conditions, particularly when the percentage of attrition is 50%. Finally, MI performed particularly well here. Although many of the ratios were close to 1, indicating near-identical performance to pruned CART, a few the ratios were substantially smaller (between .6 and .8), indicating an overall advantage of MI in these conditions.

Table 5.

MSE Ratios, Simulation A

	Listwise		Log		CART		RF		MI
	30%	50%	30%	50%	30%	50%	30%	50%	30%	50%
BX2Y1
Linear	.869	.907	.898	1.101	1.007	1.104	1.027	1.500	.880	.922
One split	.695	.837	1.198	1.011	1.006	.968	1.945	1.738	.682	.863
Two splits	.803	.781	.958	1.132	1.087	1.071	1.660	2.203	.762	.832
Three splits	.752	.777	.831	.816	1.081	1.021	1.124	1.574	.754	.810
BY2X1
Linear	.999	.944	.975	.979	1.015	.998	.95	1.228	1.012	.860
One split	1.054	1.043	1.021	.953	.994	1.034	1.162	1.250	.897	.939
Two splits	1.201	1.232	1.249	1.234	1.063	1.023	1.120	1.236	.936	.932
Three splits	1.117	.992	1.009	.986	1.039	1.002	1.096	1.372	.985	.892
BX2X1
Linear	1.004	.971	1.006	.996	1.013	1.019	1.004	1.276	1.020	.985
One split	1.004	.977	1.036	.967	1.012	1.008	1.287	1.100	.933	1.003
Two splits	1.108	1.065	1.129	1.077	1.062	1.028	.989	1.266	1.007	.973
Three splits	1.039	.972	.986	.968	.993	.981	1.012	1.070	.956	.994
BY2Y1
Linear	1.009	1.022	.994	1.013	1.002	1.008	1.001	1.096	.984	.957
One split	1.076	.987	1.035	.972	.995	1.020	1.070	1.116	.938	.947
Two splits	1.151	1.202	1.156	1.198	.996	1.020	.969	1.243	.969	.966
Three splits	1.090	1.014	1.018	.967	1.018	.999	1.017	1.225	.989	.971
rY2X2
Linear	.983	.963	.997	1.042	.993	1.059	1.017	1.340	.961	.987
One split	.861	.984	.951	1.056	1.039	1.007	1.209	1.295	.899	.995
Two splits	.904	.869	.926	1.002	1.042	.986	1.138	1.266	.937	.924
Three splits	.926	.898	.977	.943	1.013	.991	1.084	1.185	.936	.902
Resid (X2)
Linear	.902	.901	.917	1.047	1.025	1.043	1.016	1.538	.944	.843
One split	.733	.921	.930	1.092	1.060	1.019	1.847	1.470	.697	.855
Two splits	.850	.697	.946	.961	1.062	1.034	1.332	2.128	.807	.684
Three splits	.840	.754	.890	.751	1.051	1.068	1.131	1.367	.788	.746
Resid (Y2)
Linear	1.004	.998	1.006	1.009	1.001	1.010	1.014	1.005	1.018	1.059
One split	.962	.979	.965	1.018	.999	1.001	1.008	.963	.994	1.035
Two splits	1.018	.959	.996	.963	1.005	.996	.975	1.044	1.054	1.030
Three splits	.985	.964	.990	.970	.99	.999	1.000	1.030	1.004	1.022

Note. α_X = α_Y = .9, N = 500. MSE ratio is computed as MSE_MeasureX/MSE_Prune. MSE = mean squared error; Log = logistic regression; CART = classification and regression trees; RF = random forests; MI = multiple imputation.

Statistical rejection rates for β_X2Y1

Finally, Table 6 presents statistical rejection rates of β_X2Y1 by sample size, selection, and percent attrition. We display β_X2Y1 rather than the β_Y2X1 cross because β_Y2X1 was (correctly) flagged as significant nearly 100% of the time in all conditions. Interestingly, the reliability of X and Y exerted negligible effects on rejection rates, and this factor is therefore not discussed further. MI exhibited slightly higher rejection rates (> .1) under 50% attrition in the N = 100 and N = 250 conditions.

Table 6.

Statistical Rejection Rates for B_X2Y1, Simulation A

	Full data		Listwise deletion		Log weights		CART weights		Prune weights		RF weights		MI
	30%	50%	30%	50%	30%	50%	30%	50%	30%	50%	30%	50%	30%	50%
N = 100
Linear	.045	.055	.060	.070	.055	.095	.040	.070	.050	.080	.050	.075	.040	.115
One split	.035	.050	.035	.050	.055	.085	.035	.060	.070	.075	.075	.095	.060	.120
Two splits	.095	.045	.045	.040	.075	.100	.060	.055	.090	.140	.085	.140	.110	.135
Three splits	.095	.045	.095	.055	.095	.095	.095	.050	.075	.105	.075	.115	.095	.170
N = 250
Linear	.045	.035	.025	.050	.040	.050	.045	.060	.050	.050	.050	.075	.040	.075
One split	.055	.075	.055	.065	.100	.085	.080	.085	.095	.100	.090	.105	.110	.105
Two splits	.060	.060	.040	.035	.055	.065	.050	.060	.080	.065	.100	.075	.095	.125
Three splits	.075	.035	.085	.075	.075	.085	.060	.065	.110	.085	.095	.105	.085	.105
N = 500
Linear	.025	.055	.045	.040	.050	.050	.055	.055	.055	.045	.055	.055	.055	.055
One split	.050	.075	.030	.040	.065	.065	.060	.045	.050	.065	.050	.050	.070	.065
Two splits	.070	.055	.090	.050	.085	.045	.085	.065	.085	.050	.095	.055	.095	.055
Three splits	.035	.060	.060	.060	.070	.055	.060	.090	.055	.070	.065	.065	.055	.085

Note. Log = logistic regression; CART = classification and regression trees; Prune = pruned CART analysis; RF = random forests; MI = multiple imputation.

Discussion

Several important conclusions can be drawn from the present study. In brief, (a) all methods performed admirably in correctly identifying the population selection model, but CART, pruned CART, and random forest analyses were especially strong; (b) classification accuracy was not especially useful in discriminating between selection models; and (c) of all methods considered here, pruned CART and MI performed extremely well. Perhaps surprisingly to many readers, pruned CART outperformed traditional CART and random forest analysis in terms of both MSE and efficiency.

This study was not without limitations. One troubling fact was the low amounts of bias observed for nearly all parameters. This may be indicative of the resilience of regression coefficients, specifically to missing data in this type of cross-lagged model under these conditions. Nonetheless, the lack of bias observed in many of the parameters assessed in the present simulation undercuts any claims we could make about the benefits of these methods for alleviating bias in the present scenario.

In light of these results, we wondered whether the relatively strong performance of pruned CART over random forest analysis would replicate when estimating different parameters from the regression coefficients modeled in this study. Perhaps point estimates of means and variances would be more affected by the attrition induced by these selection models, and, if so, this could alter the observed pattern of results. We reasoned that even if the direction and strength of a straight regression line proved resilient to missing data, the specific values of item means and variances may not be. This intuition is in line with the results found by Collins et al. (2001), who noted that the effects of their simulated missing data on estimated regression coefficients “appear[ed] surprisingly robust in many circumstances,” whereas “the situation [was] different for the estimate of [the mean under missing data], which was affected … in every condition” (p. 341). These authors further noted that variances in their simulations were most affected by their nonlinear selection model, leading us to believe that the same might be true for variable variances under our nonlinear tree-based selection models. Therefore, we decided to conduct a smaller scale simulation to follow up on these lingering questions.

Simulation B

Simulation B extended the logic of Simulation A to a different scenario: Rather than estimating regression coefficients in a path model, we sought to estimate point estimates of the sample statistics at Time 2. In so doing, we extend our results from a model-based framework, in which the missing data estimators are employed to estimate a particular structural model, to a model-free framework. This is reminiscent of large scale survey research, for which researchers might apply imputation or weighting methods to adjust the estimates of item means, variances, and covariances.

Simulation Design

The design of Simulation B was identical to the previous simulation, with three important changes. First, in this smaller scale simulation, we did not vary the reliability of the indicators, as this factor did not seem to interact with selection or percent attrition in the prior study and was ultimately tangential to our present focus. Instead of simulating the structural model of Figure 2a, then, we directly simulated the covariance structure corresponding to the path model in Figure 2b. Despite the fact that we did not intend to fit a structural model to this data set, we used the expected covariance structure from this model to generate the same correlation structure as the prior simulation (i.e., r_COV,X2 = .32, r_COV,Y2 = .52, as before).

Second, instead of setting the means equal to zero, we employed an expected mean vector that set the means of X equal to 0.5 at both time points, and the means of Y equal to 1 at both time points. After generating structural model expectations, this resulted in expected means of ${\overline{X}}_2=0.90$ and ${\overline{Y}}_2=2.05$. More important than the specific parameter estimates was the fact that these nonzero values were now more easily amenable to the standardized percent bias measures to be employed in the study (inasmuch as division by 0 was no longer an issue). Additionally, we again set the var(X₂) = var(Y₂) = 1, and, once again, the observed correlation between X₂ and Y₂ was set to 0.4.

Finally, rather than sending models to Mplus, we estimated all sample statistics in R. We estimated the weighted statistics using the weighted.mean and cov.wt functions. Additionally, we conducted MI using the mice package in R (van Buuren & Groothuis-Oudshoorn, 2011) with default settings. Imputed means, variances, and covariances were computed as the arithmetic mean of the estimates from five imputed data sets.

Results

The effect of sample size on MI estimates

In general, the methods employed here were robust to differences in sample size, and therefore only tables from the N = 500 conditions are displayed. One exception is worth mentioning, however. MI proved to be the one estimator that improved steadily from the N = 100 condition to the N = 250 and N = 500 conditions. Although MI displayed minimal bias in estimating the means of X₂ and Y₂ across sample sizes, the estimates of var(Y₂), and especially cov(X₂, Y₂), dramatically improve in the N = 250 condition compared with the N = 100 condition, with the smallest amount of bias observed in the N = 500 cells. In the interest of space, tables of percent bias can be found in Online Supplement C.

Percent bias

Like Figure 4, Figure 5 displays the marginal means of bias across parameters in Simulation B. This figure illustrates several key points about the overall trends in the data. Most importantly, in this simulation, the tree-based selection models succeeded in introducing a greater amount of bias in listwise estimates than Simulation A. This circumvents the problematic low-bias “floor” effects observed in the prior study. Here, the beneficial effects of the missing data estimators are in clear evidence: Listwise methods display greater bias across all conditions and all missing data estimators substantially reduce this bias.

Figure 5.

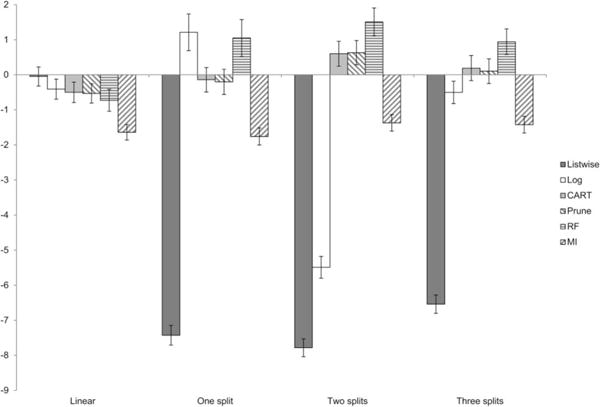
Marginal means of percent bias for parameters in Simulation B.

To examine these results in greater detail, Table 7 displays the percent bias for the N = 500 conditions. Once again, random forest analyses perform well here, but often not quite as well as pruned CART, which tends to often (though not always) display lower bias. MI shows similarly strong results in the N = 500 cells (but see the note concerning smaller sample sizes in the previous section, “The effect of sample size on MI estimates”). Pruned CART performs a bit better in many of the var(Y₂) and cov(X₂, Y₂) cells. In the end, though, all of these missing data methods undercut the bias observed among the listwise estimates, and, indeed, these differences largely represent the difference between “strong” and “stronger,” rather than the difference between “strong” and “weak” performances.

Table 7.

Percent Bias, N = 500, Simulation B

	Listwise		Log		CART		Prune		RF		MI
	30%	50%	30%	50%	30%	50%	30%	50%	30%	50%	30%	50%
${\overline{X}}_2$
Linear	−3.539	13.265	−.561	−.300	−1.206	1.504	−1.277	3.017	−.268	−2.303	−.602	.549
One split	−11.009	−11.891	−.066	1.011	−.228	−.056	−.196	−.148	4.392	3.425	−.466	−.723
Two splits	−2.615	−4.019	−.524	−.675	.466	−.450	.902	−.377	1.752	1.151	−.075	−.416
Three splits	−9.912	−12.207	−.781	−.836	−.067	−.204	−.019	−.686	1.328	1.498	−.429	−1.130
${\overline{Y}}_2$
Linear	−2.029	9.398	.117	.073	−.248	1.113	−.276	2.176	.431	−1.748	.050	.351
One split	−7.623	−8.479	.501	.878	.324	−.137	.365	−.212	3.427	2.248	−.291	−.371
Two splits	−1.598	−2.848	−.166	−.102	.411	−.291	.848	−.232	1.555	1.384	.188	−.226
Three splits	−6.520	−8.206	.027	.100	.393	.226	.421	−.108	1.322	1.821	.081	−.325
${\mathrm{\sigma }}_{X_2}^2$
Linear	−1.399	−1.511	−1.201	.163	−1.306	.025	−1.391	−.415	−.449	−.760	−1.694	−1.706
One split	−3.089	−1.447	−.135	.660	−.307	.227	−.488	−.097	.496	−.257	−1.070	−1.998
Two splits	−3.605	−4.119	−3.287	−2.269	.217	1.774	.100	1.877	.763	2.117	−.376	−1.016
Three splits	−2.389	−.929	−.341	.081	.710	−.298	.765	−.665	1.086	−.832	−.598	−1.057
${\mathrm{\sigma }}_{Y_2}^2$
Linear	−1.528	−4.661	−1.059	−.999	−.758	−2.315	−.572	−3.221	.904	−3.285	−2.132	−3.859
One split	−8.056	−4.375	2.089	1.924	.766	−1.429	.848	−1.383	.799	−2.195	−2.469	−3.490
Two splits	−10.246	−12.876	−9.938	−9.393	.827	.327	−.005	1.113	2.925	−1.016	−1.796	−3.497
Three splits	−6.431	−2.683	−1.089	.974	1.053	.362	1.470	−.183	2.164	.956	−1.693	−2.439
${\mathrm{\sigma }}_{X_2,Y_2}$
Linear	−1.257	−7.225	−.426	.079	.039	−1.873	.172	−3.549	2.414	−2.223	−2.283	−5.073
One split	−12.295	−6.004	2.036	3.234	.923	−1.500	.976	−1.685	1.942	−3.757	−2.415	−4.309
Two splits	−16.170	−19.752	−15.135	−13.396	1.429	1.317	−.051	2.142	3.808	.652	−1.479	−5.027
Three splits	−10.144	−5.970	−2.461	−.719	1.393	−1.654	1.905	−1.877	2.766	−2.675	−1.766	−4.876

Note. Log = logistic regression; CART = classification and regression trees; Prune = pruned CART analysis; RF = random forests; MI = multiple imputation.

Relative efficiency

Table 8 displays the results for relative efficiency, once again comparing each method to pruned CART. Here again, pruned CART outperforms random forest analysis and single-tree CART in virtually all cells. The comparisons with logistic regression weights are more thoroughly mixed, with logistic estimates displaying greater efficiency in many cases. Consistent with Simulation A, these results are rarely severe in their discrepancies: In a few cells, pruned CART is substantially more efficient, whereas in a few other cells, the reverse is true. On the balance, however, these methods are often in the same range, with values between .9 and 1.10 abounding.

Table 8.

Relative Efficiency, N = 500, Simulation B

	Listwise		Log		CART		RF		MI
	30%	50%	30%	50%	30%	50%	30%	50%	30%	50%
${\overline{X}}_2$
Linear	1.020	.924	.985	.984	1.022	1.038	1.057	1.340	.954	.816
One split	.855	.930	1.158	.961	1.010	1.021	2.135	1.395	.813	.811
Two splits	.924	.823	.925	.99	.990	.997	1.177	1.650	.805	.764
Three splits	.912	.858	.892	.824	1.017	.975	1.056	1.102	.825	.727
${\overline{Y}}_2$
Linear	.972	.907	.945	.893	1.024	.985	1.020	1.226	.945	.728
One split	.833	.979	1.297	.869	.982	.942	1.813	1.187	.729	.691
Two splits	.920	.887	.809	.815	.960	.982	1.205	1.597	.749	.669
Three splits	.921	.955	.854	.793	1.019	.937	1.019	1.272	.801	.714
${\mathrm{\sigma }}_{X_2}^2$
Linear	.925	.819	.952	1.042	1.034	1.055	1.037	1.301	.889	.785
One split	.752	.931	1.166	1.048	1.022	1.019	1.843	1.268	.735	.85
Two splits	.858	.769	.916	.993	1.089	1.037	1.294	1.408	.867	.725
Three splits	.792	.855	.900	.956	1.096	1.049	1.138	1.096	.792	.830
${\mathrm{\sigma }}_{Y_2}^2$
Linear	.971	.971	.985	1.176	1.030	1.083	.976	1.206	.809	.814
One split	.694	.897	1.834	1.179	.983	.953	1.167	1.070	.631	.678
Two splits	.736	.681	.794	.921	1.023	.962	1.173	1.015	.729	.610
Three splits	.757	.773	.909	.948	1.008	.998	1.011	1.098	.707	.649
${\mathrm{\sigma }}_{X_2,Y_2}$
Linear	.936	.887	.965	1.128	1.022	1.116	1.023	1.331	.848	.774
One split	.695	.900	1.575	1.098	1.016	.962	1.576	1.077	.689	.723
Two splits	.789	.727	.835	.939	1.037	.975	1.151	1.218	.794	.635
Three splits	.733	.838	.853	.967	1.026	1.036	1.001	1.108	.741	.685

Note. Relative efficiency ratios computed over SD_Prune. Log = logistic regression; CART = classification and regression trees; RF = random forests; MI = multiple imputation.

Listwise estimates display greater efficiency than pruned CART in all cells but one. The benefit of this efficiency is diminished, of course, by the fact that these parameter estimates were, in general, biased when compared with those returned by other methods. Finally, MI displays the greatest efficiency of all methods. This is similar to the results of Simulation A.

MSE ratios

Finally, Table 9 displays the MSE ratios of each estimator compared with pruned CART. Several results are worth noting. First, the superior performance of pruned CART to random forest analysis is not only evident here, but even stronger than it appeared in Simulation A. Second, pruned CART once again outperforms single tree CART in the majority of cells, although there are exceptions to this rule. Third, once again the comparisons with logistic regression weights are mixed. Logistic weights seem to do a particularly good job of recovering the item means, whereas pruned CART seems to excel in recovering the variances and covariance of the two variables, particularly under 50% attrition. Fourth, pruned CART outperforms listwise deletion in the majority of cells. When listwise appears superior, we can surmise that this is likely because of the greater efficiency of the estimates. However, in light of the bias displayed in the listwise estimates, it would be ill-advised to dub listwise methods “more accurate” in these cells. Finally, MI, as instantiated by the mice package, excels in all simulation cells. As we have seen, this is likely aided by the method’s high efficiency.

Table 9.

MSE Ratios, N =500, Simulation B

	Listwise		Log		CART		RF		MI
	30%	50%	30%	50%	30%	50%	30%	50%	30%	50%
${\overline{X}}_2$
Linear	1.359	3.478	.933	.832	1.038	.960	1.066	1.624	.877	.576
One split	3.044	3.713	1.341	.943	1.021	1.042	4.923	2.183	.664	.668
Two splits	.979	.931	.847	.986	.968	.996	1.424	2.738	.638	.585
Three splits	3.344	2.837	.811	.685	1.035	.945	1.160	1.237	.686	.543
${\overline{Y}}_2$
Linear	1.565	5.940	.884	.569	1.047	.766	1.057	1.257	.883	.385
One split	6.089	8.160	1.685	.829	.963	.885	4.340	1.909	.533	.489
Two splits	1.044	1.500	.610	.662	.873	.967	1.590	2.708	.524	.450
Three splits	6.295	8.569	.713	.629	1.035	.882	1.238	1.994	.629	.522
${\mathrm{\sigma }}_{X_2}^2$
Linear	.860	.694	.901	1.084	1.063	1.112	1.046	1.696	.810	.645
One split	.666	.887	1.357	1.101	1.044	1.039	3.392	1.607	.551	.760
Two splits	.933	.711	1.002	.999	1.186	1.070	1.682	1.963	.754	.519
Three splits	.704	.736	.805	.910	1.199	1.096	1.301	1.204	.628	.697
${\mathrm{\sigma }}_{Y_2}^2$
Linear	.981	1.069	.985	1.241	1.066	1.101	.961	1.410	.736	.748
One split	1.155	.984	3.386	1.400	.966	.911	1.357	1.171	.458	.575
Two splits	1.831	1.544	1.843	1.419	1.056	.918	1.482	1.029	.571	.449
Three splits	.978	.655	.820	.905	1.005	.997	1.048	1.212	.518	.469
${\mathrm{\sigma }}_{X_2,Y_2}$
Linear	.884	.921	.933	1.221	1.045	1.207	1.078	1.718	.747	.656
One split	.889	.892	2.484	1.223	1.031	.925	2.488	1.187	.489	.564
Two splits	1.534	1.372	1.496	1.263	1.082	.946	1.375	1.470	.638	.454
Three splits	.860	.782	.738	.929	1.046	1.070	1.015	1.236	.553	.523

Note. MSE ratios computed over MSE_Prune. MSE = mean squared error; Log = logistic regression; CART = classification and regression trees; RF = random forests; MI = multiple imputation.

Discussion

Simulation B replicated and extended the key results of Simulation A in a different analysis context—that of accurately recovering observed sample statistics rather than fitting a structural model. In this context, listwise estimates displayed evident, albeit modest, bias that was successfully reduced by the missing data estimators. In this study, like Simulation A, pruned CART once again outperformed random forest analysis and, in most cases, single-tree CART methods. The benefits over logistic regression weights were once again varied, with each method outperforming the other in different cells. By applying these estimators in a different analysis context (e.g., retrieving sample statistics rather than model estimates), we can feel more confident that these results are not idiosyncratic to the conditions simulated in Simulation A. By applying these estimates in a different software package (using weighted mean and variance functions in R rather than weighted structural equation modeling using MLR estimation in Mplus), we can feel assured that these results are properties of the weights themselves, not simply of the program used to implement them.

General Discussion

Two simulation studies demonstrated the strong performance of using machine learning techniques to compute missing data weights. In both studies, these methods performed comparably with and/or exceeded the performance of more traditional methods, such as logistic regression weights and MI. Across both simulations, pruned CART outperformed single-tree and random forest methods in terms of efficiency and MSE. Though more simulation research is needed on this topic, several preliminary conclusions can be drawn from these results.

All Methods, But Especially Pruned CART and Random Forests, Excel in Identifying the True Selection Model

One exciting finding from Simulation A is the strong performance of nearly all selection model identification methods (t tests, logistic regression, CART, pruning, and random forest analysis) in identifying the true selection variables. The performance of t tests and logistic regression was not quite as high as the other methods when using significance testing as the main criterion, and the performance of these analyses also depended more highly on sample size. Using effect size measures (e.g., Cohen’s d) alleviated this tendency, but could lead to overoptimism concerning how many covariates to include in the selection model. Pruning seemed to alleviate some of CART’s tendency to overfit, and mainly seemed to cut spurious selection variables from the tree models. Finally, random forest’s variable importance measures were remarkably consistent in prioritizing the true selection variables in the model.

The Performance of Tree-Based Weights Under a Smooth, Linear Selection Model

It is important to draw attention to one thing that did not happen in the simulations: The performance of CART, pruned CART, and random forests did not, in general, deteriorate when the selection model was a smooth linear function. This was not a foregone conclusion; to quote Berk (2009, p. 150), “Even under the best of circumstance, unless the f(X) is a step function, there will be biases in any CART estimates. The question is how serious the biases are likely to be.” Although the results of CART may be biased in the sense of approximating rather than capturing the true function, the present simulations suggest that pruned CART weights may be fairly robust under smooth, linear selection models, making this a surprisingly viable candidate as a useful all-purpose method (but see Lee et al., 2010, whose quadratic functions proved problematic for tree-based methods in a different context).

The Performance of Logistic Regression Weights

Throughout many of the simulation cells, pruned CART and logistic regression were “neck and neck,” with each method taking turns outperforming the other. One notable exception was in estimating the variances and, especially, the covariance of X₂ and Y₂ in Simulation B (see Table 7). Under these conditions, logistic regression weights performed considerably worse than pruned CART weights, suggesting that, although logistic weights performs very well under many circumstances, there may be instances in which this does not hold true. Further simulation research is needed to clarify which moderators affect the relative performance of logistic weights over pruned CART weights.

The Surprisingly Small Impact of Sample Size

The present simulations seem to suggest that these methods are useful in modeling attrition even in very small samples. This helps to clarify a misconception some practitioners may carry concerning the uses of decision tree methods. Although CART and random forest methods are often invoked in the context of “big data,” this reflects the methods’ usefulness for the types of prediction problems commonly found in big data scenarios and does not imply that “big” data sets are required to profitably employ tree-based methods (see also Strobl et al., 2009, who make a similar point). As mentioned, MI was the one exception to this rule, performing most strongly in the N = 500 conditions in Simulation B.

Pruned CART Versus Random Forest Weights

It may seem surprising to find that pruned CART’s overall performance exceeded that of random forest analysis. In light of a large body of research suggesting that random forest should nearly always be a preferred method (Hastie, Tibshirani, & Friedman, 2009; Lee et al., 2010), how might these results be understood? We believe that there are (at least) three potential explanations of these results.

First, an important difference between these methods lies in the random forest algorithm’s superior ability to handle collinearity among the model predictors. In the present simulations, we included only three covariates that were kept uncorrelated for computational reasons (this helped us more easily generate tree structures that reliably returned 30% and 50% missing cases). In real-world contexts, however, researchers may have many, highly intercorrelated covariates in their data sets. In such contexts, random forest analysis could provide an advantage because of its ability to address collinearity through resampling predictors. Therefore, it is important to extend the present research by simulating data sets with more numerous, correlated missing data covariates in order to examine whether the present results hold or change under these conditions.

Second, in these simulations, we predominantly used tree models to generate missing data. CART and pruned CART are ideal for detecting these piecewise, linear step functions. By contrast, by averaging across the results of many bootstrap trees, random forest methods actually create a smoothed functional form and may not perform as well when the true function is a step function.¹¹ It is possible, then, that random forest methods could outperform CART and pruned CART when nonlinear and interactive selection models exhibit smooth rather than piecewise step functional forms. Future work should compare the performance of these methods when the missing data correlates exhibit smooth, multiplicative linear interactions (e.g., v * z) and smooth nonlinear functions (such as, e.g., quadratic, cubic).

Third, it is possible that these results speak, at least in part, to the specific goals and aims of the missing data analysis, which differ from many common data analysis situations in crucial ways. In most data analysis contexts, researchers hope that their substantive model of interest will generalize to future samples. This ability to generalize is one strength of random forest analysis. By classifying cases using majority vote, resampling methods like random forest analysis are designed to capture information that is true across the majority of repeated samples. In so doing, these methods “average out” the parts of each model that are idiosyncratic to each particular sample. This is how resampling methods reduce the variance of CART results: by retaining only those elements of the model that vary the least across repeated samples from the data.

But in missing data analysis, researchers are typically concerned with addressing incompleteness in their own sample, not maximizing their ability to forecast what sorts of people are most likely to have missing data in future samples. In this way, missing data analysis may represent an atypical inferential case. In this context, we do not care whether the observed tree that caused incompleteness in our data will be equally predictive of incompleteness in a future data set, nor do we especially care how closely the chosen split variables resemble those in the population, so long as they help us weight our model estimates in an effective manner. Thus, if the goal is to try to make inferences about what this sample would have looked like without incompleteness, rather than which cases are likely to be incomplete in the next sample, then averaging out idiosyncratic, sample-specific information may impede the true goal. In this case, the priority should be to accurately model correlates of incompleteness in the sample at hand, however idiosyncratic those correlates happen to be.

Pruned CART may be particularly suited to these goals. Although cost-complexity pruning employs cross-validation, a technique commonly used to assess the generalizability of a model to new data, it does this to determine the optimal nested subtree that is a subset of the original, larger, overfit tree produced by CART. Thus, this technique may serve to curb CART’s tendency to overfit in response to trivial blemishes in one’s data (e.g., by pruning back nodes based on small numbers of observations) while still utilizing a good amount of sample-specific information. In this way, pruning may represent an optimal middle ground between CART and random forest that serves our purposes well in the missing data context.

Future research is needed to disentangle these three potential explanations. Specifically, simulating covariates that are (a) more highly correlated with one another, as well as (b) related to attrition in a smooth interactive/nonlinear manner, would help determine whether random forest methods excels under these conditions. It would be ideal to conduct these simulations both with a highly controlled design with smaller number of predictors, as we have done here, as well as a larger, more real-world design in which many predictors compete for inclusion in the missing data model. Therefore, strength of covariate intercorrelations (low, moderate, high), smoothness of selection functions (smooth vs. step functions), and number of covariates (many vs. few) are three factors worth exploring in future studies.

Important Future Directions

Although these initial results are promising, it is important for future research to build on this work in several key ways. First, it would be beneficial to simulate covariates that are more strongly correlated with model response variables. In the present study, the greatest degree of correlation was between the covariates and Y₂, set at r = .52. In line with previous research, we believe that simulating greater covariate-outcome correlations would result in higher amounts of bias and a greater need for missing data techniques (see, e.g., Collins et al., 2001, who found correlations of .9 between the covariates and Y to be particularly deleterious).

Additionally, we note that although in our simulation we (like Lee et al., 2010) only included main effects in our logistic regression analyses in order to most accurately model what researchers typically do in practice, we agree with those (including our reviewers) who argue for the importance of assessing the performance of this method when interactions and nonlinearities are included in the model. This is a logical and important next step in comparing these two methods. In practice, however, even if this method performs well, there is one obvious and debilitating drawback: Including all interactions and nonlinear terms will undoubtedly be cumbersome for researchers who, in many software packages, would have to compute these numerous multiplicative and exponential terms manually. Combined with the potential collinearities that could result in such analyses, this may relegate this approach to the category of “possible but infeasible,” giving the automated tree algorithms an edge in terms of practical utility.

Another extension of this work would be to simulate longitudinal data with t > 2 time points. We began with t = 2 in the present studies in order to form missing data weights in the most straightforward way: modeling incompleteness at only one time point (Time 2). With a greater number of time points, more complex patterns of incomplete data are possible, necessitating decisions about which time point should be predicted and how the weights might be formed (e.g., predicting Time 2 vs. the final time point; averaging weights across time points; or using a multivariate extension of CART, as in Brodley & Utgoff, 1995; De’ath, 2002). In addition to providing an avenue to explore CART and random forest weights in a multivariate context, such simulations would also afford the possibility of simulating more complex patterns of incompleteness and incorporating FIML (see, e.g., Arbuckle, 1996; Enders & Bandalos, 2001) among the missing data estimators assessed.

Finally, two additional extensions are required to assess the performance of these techniques in a comprehensive manner: (a) examining these methods when the data are missing not at random (Rubin, 1987; that is, when incompleteness is determined by individuals’ scores on the endogenous variables themselves), and (b) examining these methods when the data are non-normal. This latter condition may be especially interesting, given that weighting methods, unlike FIML and MI, do not require an assumption of normality. Thus, it would be interesting to compare these methods with other missing data techniques previously studied under nonnormality (see e.g., Enders, 2001).

Conclusion and Recommendations for Researchers

We close by attempting to answer what may be the most important question of all: What can applied researchers take away from these results? Which methods should they prefer and how will they know what to use to address their missing data issues?

The present research can offer several suggestions for researchers, particularly when dealing with missing data at two time points, as investigated here: First, although many techniques (i.e., t tests, logistic regressions) can be successfully used to assess the true selection model, pruned CART and random forest analysis appear to perform particularly well. Second, of the machine learning techniques studied here, pruned CART seems like a strong choice under the various selection models, sample sizes, and amounts of incomplete data considered here. Although random forest performed well, the current simulations suggest that this computationally intensive technique may be overkill in the missing data analysis context, at least when employing a smaller number of uncorrelated (or lowly correlated) missing data covariates. This being said, it is rare in psychology to have sample sizes so large as to make random forest substantially slower than CART, despite its larger computational demands. Because the cost of trying random forest analysis tends to be minimal in these practical situations, and because it is possible that random forest may perform better under selection models other than the ones simulated here (e.g., smooth linear interactions; smooth, polynomial functions), it is still worth trying this method. As one reviewer pointed out, an added benefit of this technique is that it unburdens the user from having to make decisions about whether (and how much) to prune. Third, MI’s overall strong performance depended somewhat on sample size. This method seems to be a particularly strong choice when dealing with larger samples, especially with N ≥ 500. The usual caveats apply, however, and MI may be more cumbersome than other methods when specifying analysis models with explicit or implicit interactions, multiple group structural models, or hierarchical linear models (see Enders, 2010, for a very readable discussion).

Finally, an additional major theme of these simulations is that sometimes selection models exert greater influence on the performance of missing data techniques than others. Therefore, in practice, we recommend that researchers remember the counterfactual inference discussed in the beginning of this article. Thus, rather than asking which of several complicated methods for handling missing data is the one that should be used, researchers can ask themselves “How stable are my model estimates and results across analyses that address incompleteness in different ways, under different but related assumptions?” We believe this is a vastly better question. Although it would be impractical to try out every possible missing data technique on every data set, comparing estimates from one or two recommended methods with estimates from listwise deletion can be illuminating. For example, when working with N = 100 and two time points, comparing listwise with pruned CART estimates may be a worthwhile assessment. For N = 500, comparing listwise with pruned CART and MI might be helpful. In each case, such comparisons can shed important light on whether the data are relatively affected (as in the means, variances, and covariances assessed in Simulation B) or relatively unaffected by attrition (as in the case of the regression coefficients assessed in Simulation A).

This suggestion should not be misconstrued as an endorsement of running many tests and selectively reporting desirable-looking results. Rather, we believe such comparisons should be shared, not hidden, from your readers, even if only parenthetically or in technical footnotes (e.g., “The results of missing data Method 1 were near-identical to the results of missing data Method 2. Therefore, Method 2 is relegated to the appendix”). Used responsibly in concert with recommendations from empirical simulation research, we believe this strategy provides a straightforward and incisive way to assess the effects of incompleteness on one’s data.