Test of Martin’s overkill hypothesis using radiocarbon dates on extinct megafauna

Significance

Coincident with the human colonization of the Western Hemisphere, dozens of genera of Pleistocene megafauna were lost to extinction. Following Martin, we argue that declines in the record of radiocarbon dates of extinct genera may be used as an independent means of detecting the first presence of humans in the New World. Our results, based on analyses of radiocarbon dates from Eastern Beringia, the contiguous United States, and South America, suggest north to south, time, and space transgressive declines in megafaunal populations as predicted by the overkill hypothesis. This finding is difficult to reconcile with other extinction hypotheses. However, it remains to be determined whether these findings will hold with larger samples of radiocarbon dates from all regions.

Abstract

Following Martin [Martin PS (1973) Science 179:969–974], we propose the hypothesis that the timing of human arrival to the New World can be assessed by examining the ecological impacts of a small population of people on extinct Pleistocene megafauna. To that end, we compiled lists of direct radiocarbon dates on paleontological specimens of extinct genera from North and South America with the expectation that the initial decline of extinct megafauna should correspond in time with the initial evidence for human colonization and that those declines should occur first in eastern Beringia, next in the contiguous United States, and last in South America. Analyses of spacings and frequency distributions of radiocarbon dates for each region support the idea that the extinction event first commenced in Beringia, roughly 13,300–15,000 BP. For the United States and South America, extinctions commenced considerably later but were closely spaced in time. For the contiguous United States, extinction began at ca. 12,900–13,200 BP, and at ca. 12,600–13,900 BP in South America. For areas south of Beringia, these estimates correspond well with the first significant evidence for human presence and are consistent with the predictions of the overkill hypothesis.

Just over 42 y ago, Paul Martin (1) proposed that humans entered the contiguous United States via the Ice Free Corridor at ∼13,500 BP and there encountered almost three dozen genera of now-extinct megafaunal mammals. Hunting of these naïve prey fueled rapid human population growth, he argued, resulting in both the colonization of the landmass stretching from the southern terminus of the North American ice sheets to the far tip of South America in 1,000 y, and the extinction of the mammoths, mastodons, camels, horses, ground sloths, and other large mammal taxa that had inhabited the Western Hemisphere for hundreds of thousands to millions of years before human arrival. Martin (p. 973) closed his paper with the statement, “Should the model survive future findings, it will mean that the extinction chronology of the Pleistocene megafauna can be used to map the spread of Homo sapiens through the New World.”

Central to this hypothesis is the idea that small numbers of humans can have large ecological impacts and that those impacts should be directly observable in the paleontological record. If we accept that premise as true, then as Martin argues, it is possible to assess the timing of human arrival independently of direct archaeological evidence by examining when megafaunal decline occurred across time and space. In this paper, we use databases of radiocarbon dates on extinct megafauna from Eastern Beringia (EB), the contiguous United States (CUSA), and South America (SA) to estimate the timing of initial population declines that ultimately resulted in extinction. We intend this exercise to be both a direct test of the timing of extinction as proposed by Martin (1) and as an independent means of estimating the timing of human arrival to each region. Similar approaches using paleoecological proxy records as possible indicators of human arrival have been applied elsewhere, particularly on islands (2–7).

From this premise, we make two complementary arguments pertaining to New World colonization. First, we expect initial megafaunal declines for each region to correspond temporally with the first evidence of human presence. Second, we expect that the timing of megafaunal declines should be geographically patterned according to Martin’s (1) model in which the founding population moved through EB and then south into the CUSA and SA. When Martin published his classic work, radiocarbon calibration was not possible, so by necessity, he worked within the radiocarbon time scale. For the CUSA, Martin estimated a mean colonization age of ca. 11,200 ¹⁴C y BP, or ca. 13,100 BP, and for SA, ca. 10,700 ¹⁴C y BP, or ca. 12,700 BP. Martin did not specify a human arrival date for EB, except to suggest his model required that “the time of human entry into Alaska need be no older than 11,700 [radiocarbon] years ago,” or roughly 13,600 BP.

Importantly, the expectation of a north to south spatiotemporal extinction trend across the Western Hemisphere should be largely unique to the overkill hypothesis. There is no single climatic (8, 9) or catastrophic (10) extinction hypothesis that shares this prediction. Therefore, this kind of analysis is not only capable of testing the overkill hypothesis, but of posing legitimate challenges to other extinction hypotheses, with the possible exception of multifactor models that also invoke “first contact” effects, such as the keystone herbivore (11), habitat modification (12), and hyperdisease hypotheses (13).

We use two analytical techniques to identify dates of initial megafaunal decline: for technical precision, an approach based on spacings (time lags between consecutive ordered dates), and, for simple understanding, an approach based on histograms of observed dates. The key property of spacings is that mean spacings are inversely proportional to population levels. For spacings, individual spacing values are regressed onto the midtime (t_i+1 + t_i)/2 of the spacing interval using a generalized linear model with estimated breakpoints (representing times of onset of extinction). Decline dates are identified as the time before extinction for which waiting times between dates begin to increase, implying population declines. This method produces both a likely date for extinction onset and an associated approximate 95% CI (confidence interval). For histogram creation, we first apply a jackknife method to identify optimal binning parameters for histogram creation (14) to create frequency distributions of calibrated radiocarbon dates, which are then corrected for taphonomic bias following Surovell et al. (15). Taphonomic correction adjusts frequency distributions of radiocarbon dates to account for the loss of sedimentary contexts through time due to erosion and weathering. Decline dates are estimated as occurring within the last mode before extinction. Spacings are also taphonomically corrected (SI Materials and Methods).

Both spacings and frequency analyses rest on three assumptions: (i) our radiocarbon datasets are representative of the relative frequencies of megafauna in the paleontological records of each region; (ii) after taphonomic correction, temporal frequency distributions positively correlate with population densities of megafaunal taxa through time; and (iii) the same taphonomic correction model characterizes each region.*

Results

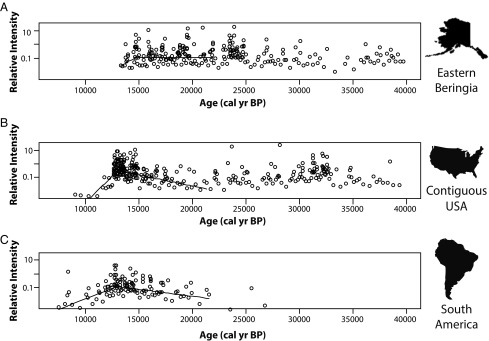
Spacings analyses (Fig. 1 and Table 1) are consistent with a north to south trend in initial megafaunal decline dates. For EB, our best estimate for the date of initial megafaunal decline is 14,661 BP; because EB spacing between dates are fairly consistent from ca. 20,000 to 13,400 BP, there is a very wide 95% CI associated with that estimate, ranging from 13,613 to 19,958 BP. For CUSA, the most likely decline date is 13,001 BP, with a 95% CI of 12,861–13,232 BP, and the estimated decline date for SA is 12,967 BP, with a 95% CI of 12,595–13,921 BP.

Fig. 1.

Comparison of estimated dates of initial megafaunal decline using generalized linear model analyses of taphonomically corrected spacing lengths for (A) EB, (B) the CUSA, and (C) SA. Inverse spacings (°) and inverse estimated mean lengths (—) are on a scale proportional to frequency of occurrence and are labeled as relative intensity. Times of descent (EB = 14,661; CUSA = 13,001; SA = 12,967 BP) correspond to estimated onset of decline for each region.

Table 1.

Estimated dates of decline for EB, the CUSA, and SA using gap and binning analysis methods

Region	Gap analysis		Binning analysis
	Best fit age (yr BP)	95% CI (yr BP)	Median age (yr BP)	Bin range (yr BP)
EB	14,661	13,613–19,958	14,714	14,440–14,988
CUSA	13,001	12,861–13,232	13,473	12,819–14,127
SA	12,967	12,595–13,921	13,480	12,021–14,939

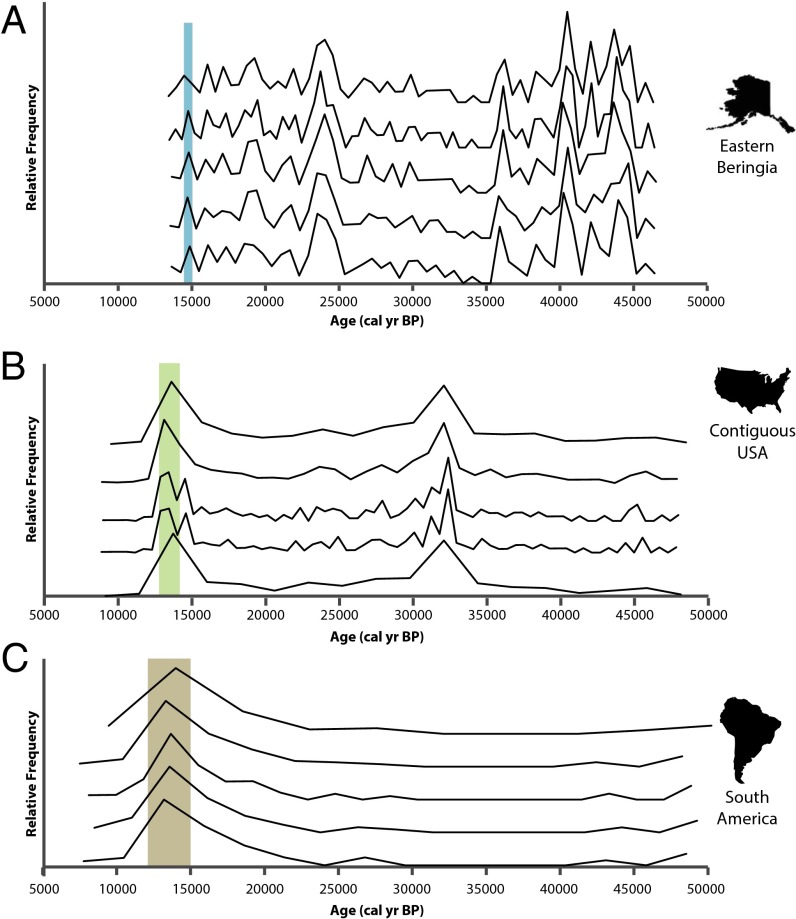
Best-fit histograms for all radiocarbon dates yield estimates of extinction onset that are very similar to those derived using spacings, but with smaller observed uncertainty for EB and more uncertainty for CUSA and SA (Fig. 2 and Table 1). The analysis produces distinct bin widths and ranges among regions (Table S1). The precision with which we are able to estimate the initial date of decline by date binning correlates somewhat with sample size and with the extent to which date distributions are uniformly distributed or skewed. For binning results, there is considerable ambiguity with respect to the relative timing of events in CUSA and SA, and their median dates for final modes before extinction are virtually identical (Table 1).

Fig. 2.

Taphonomically corrected calibrated radiocarbon frequency polygons for (A) EB, (B) the CUSA, and (C) SA. For each region, the optimal binning solution is presented for five histograms varying bin number with the highest likelihood values using the Hogg method. Colored rectangles represent the mean location of the final mode preceding extinction.

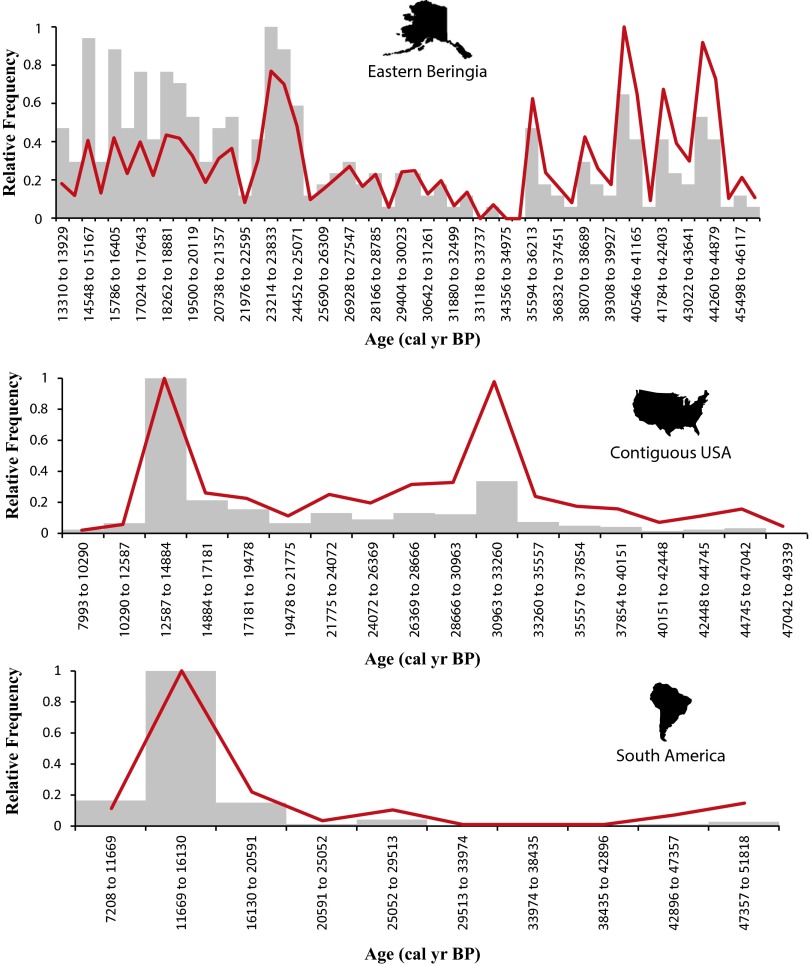
Table S1.

Optimal histogram binning for the three study regions using the Hogg (14) method

Bin number	Bin width (yr)	Bin 1 start date (yr BP)	α	Likelihood rank
EB
54	619	13,310	1.7	1
57	587	13,237	1.9	2
58	577	13,343	1.9	3
78	428	13,249	1.7	4
63	531	13,146	1.9	5
CUSA
18	2,297	7,993	1.4	1
69	574	8,574	1.2	2
71	558	8,692	1.1	3
38	1,055	8,373	1.4	4
20	2,055	8,484	1.4	5
SA
16	2,723	7,323	1.1	1
17	2,553	7,128	1.1	2
23	1,857	7,096	1.1	3
15	2,917	5,955	1.1	4
10	4,538	7,115	1.1	5

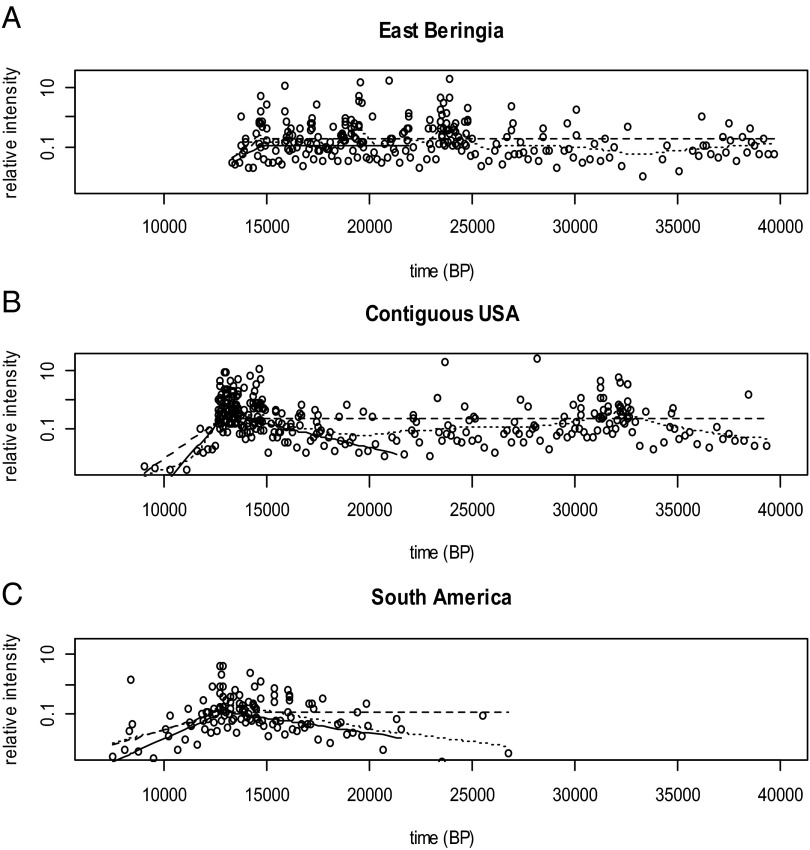
Both analyses are consistent with the hypothesis that declines first began in EB followed in order by the CUSA and SA. The commencement of extinction in EB appears to have preceded those in the CUSA by about 1,600 y, and the extinction event in EB may have been completed before it even began in CUSA. By comparison, initial megafaunal declines in the CUSA and SA appear to have been very closely spaced in time, probably separated by at most a few centuries. These conclusions are essentially the same for both spacing and binning analyses and are also robust to alternate approaches to data analysis (Fig. S1 and Table S2).

Fig. S1.

Comparison of estimated dates of initial megafaunal decline using generalized linear model analyses, approximate AR analyses, and optimized loess fits of taphonomically corrected spacing lengths for (A) EB, (B) the CUSA, and (C) SA. Inverse spacings (°) and inverse estimated mean lengths are on a scale proportional to frequency of occurrence and are labeled as relative intensity. Fits are distinguished as GLMs (—), approximate AR (- - -), and loess (......).

Table S2.

Spacings-based estimated dates of decline and 95% CIs for EB, the CUSA, and SA using the generalized linear model and the approximate AR model and estimates for the optimized nonparametric loess fit

Region	GLM		AR		Loess (estimate only)
EB	14,661	13,613–19,958	14,652	13,308–40,000	14,702
CUSA	13,001	12,861–13,232	12,727	11,749–13,636	13,027
SA	12,967	12,595–13,921	12,712	10,816–13,635	12,937

One pattern that emerges from comparative analyses of these three regions is that the shape of the EB frequency distribution is distinct from those of the CUSA and SA (Fig. 2). Given the progressive loss of materials through time, radiocarbon ages are expected to decrease nonlinearly with age from recent modes, producing a heavily right-skewed distribution (15, 16). Even after correction for taphonomic bias, the CUSA and SA datasets form curves typical of this phenomenon. Potentially, loss should be even greater for these datasets than for others due to these dates having been derived from bone and organic materials (e.g., dung), which may progressively be lost to weathering and/or dissolution even if site sediments are not lost to erosion. Quite distinctly, there appears to be considerably less loss of bone through time in the EB dataset. We expect that this is due to a combination of excellent bone preservation in periodically frozen “muck” deposits (17) and the sampling of extensive exposures of Pleistocene deposits due to gold mining activities (18). This pattern suggests that unique taphonomic corrections are preferable for each region, but natural cycles in populations and sampling concerns are confounding factors that make such unique corrections impracticable. However, it is important to note that the taphonomic corrections we applied have little effect on estimating dates of megafaunal decline (Fig. S2).

Fig. S2.

Optimal histogram binning for EB (54 bins), the CUSA (18 bins), and SA (10 bins) comparing raw date frequencies (gray bars) and taphonomically corrected frequencies (red lines). Over long time scales, the taphonomic correction process can have major effects on the shapes of curves, but over short time scales (<4,000 y), the effects are minimal. Therefore, unless adjacent bin frequencies are very similar, taphonomic correction does not affect the position of the last major mode before extinction.

The curve for EB suggests that megafaunal population levels remained relatively constant from ∼45,000 to 15,000 BP with a few minor periods of increase, most notably around the Last Glacial Maximum (LGM; Figs. 1A and 2A). This peak may imply that glacial climatic conditions are particularly favorable for extinct megafauna in arctic regions, when the so-called “Mammoth Steppe” flourished (19, 20). This pattern conforms well to Guthrie’s (21) hypothesis that size diminution among Alaskan Pleistocene horses was linked to post-LGM climatic and ecological change. Unlike the curves for the CUSA and SA, there is no major mode in date frequencies that precedes extinction. However, all five best fit histograms estimate that the final mode before extinction, or the onset of population decline in EB, occurred between ∼14,440 and 14,990 BP. The spacings-based 95% CI is much wider, but an early date of onset with constant exponential rate of decline is inconsistent with the observed rapid arrival of extinction at the end of record. An alternative reading of data should be mentioned, although it requires speculation beyond the information in the data as observed. As stated above, early estimates of onset in the 95% CI for EB imply a precipitous population decline at the end of record, and even the best estimate of 14,661 BP leads to a more rapid than expected break in data time-adjacent to the most recently observed fossils. Thus, there may have been a catastrophic extinction event around 13,300–13,400 BP, probably but not certainly preceded by a more gradual onset of extinction ca 14,660 BP.

In contrast to the Beringian curve, the dataset from the CUSA suggests two major periods of megafaunal population increase, both associated with climatic warming (Figs. 1B and 2B). High frequencies of radiocarbon dates occur at ∼32,000 BP toward the end of the Marine Isotope Stage 3 interstadial and correlating well with Heinrich Event 3 (22, 23), although this peak could be a sampling artifact. The second period of increase occurs in the terminal Pleistocene, just before extinction. Onset of extinction is estimated with a 95% CI between 12,861 and 13,232 BP, and, notably, the younger range of this estimate is very close to the terminal date of many extinct taxa, which most researchers place at ∼12,800 BP (24–26), implying a very rapid extinction event likely occurring within 1,000 y, consistent with Alroy’s simulation results (27). Finally, we note that in histogram solutions with finer binning (Fig. 2B), a temporary decline in date frequencies occurs at ca. 14,000 BP, a phenomenon that has been observed by others (28, 29), but date frequencies increase over the next 500 y or so, suggesting that whatever forcing factor caused this decline was not long lasting.

Taphonomically corrected data for SA suggest relatively low population levels of megafauna persisting throughout the Late Pleistocene with population expansion occurring in post-LGM times, but, as stated above, this curve is also typical of temporal frequency distributions that have been affected by taphonomic bias, suggesting that a unique taphonomic correction would also be desirable for the South American record. A sharp shift in spacings and a major mode in date frequencies are nonetheless evident (Figs. 1C and 2C), with a 95% CI between 12,595 and 13,921 BP, entirely overlapping our age estimates for CUSA.

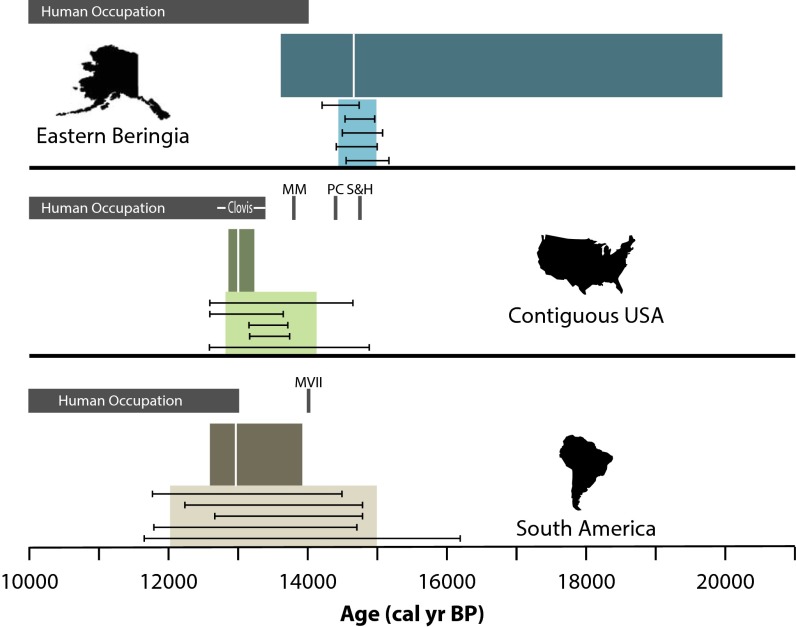
In Fig. 3, we summarize our estimates for the timing of megafaunal decline for all three regions in comparison with archaeological evidence of human colonization. In EB, the evidence for overlap between human and megafaunal populations lasts for ∼600 y. The youngest megafaunal dates occur around 13,400 BP and the oldest archaeological sites, in the Tanana River Valley of central Alaska, date to around 14,000 BP (30–32). The earliest evidence for human occupation of EB overlaps with the wide 95% CI from our spacings analysis, but it does not overlap with our estimate from binning. Relevant to this possible temporal incongruity is that most, if not all of the evidence for interaction between humans and extinct megafauna in EB can be attributed to the scavenging of old ivory or bones for tool production and fuel (31, 33). Therefore, it is possible that initial megafaunal declines in Beringia are not explained by human occupation or that with a larger archaeological sample, the date of initial colonization of this region by humans will be pushed back several centuries. Notably, the estimated timing of megafaunal decline in EB correlates well with the Bolling Interstadial and a major human population expansion event into northeast Asia (31, 34, 35).

Fig. 3.

Comparison of estimated dates of initial megafaunal decline (colored rectangles) with earliest archaeological evidence for each region (gray bars). Lighter colored bars indicate estimated decline dates based on binning, and horizontal error bars indicate the minimum and maximum values for the final mode preceding extinction for the five optimal histogram solutions for each region. Darker colored bars indicate the 95% CI for the gap analysis and vertical white lines indicate the best fit decline date. MM, Manis Mastodon; PC, Paisley Cave; S&H, Schaefer and Hebior; MVII, Monte Verde, Component 2.

In the CUSA, the evidence for overlap between human and megafaunal populations lasts for almost 6,000 y, but much of that time is accounted for by a few Holocene megafaunal dates and temporally isolated pre-Clovis sites. Our estimated dates of megafaunal decline from the spacings and binning analyses overlap with the age range for Clovis (36). Various sites have been argued to date considerably earlier than the oldest dates for the Clovis complex, perhaps as early as 15,500 BP (37–40). If there was a significant human presence in North America before the onset of Clovis, pre-Clovis foragers had no measurable impact on megafaunal populations, despite the fact that they were apparently hunting these species (37, 39, 40). However, we would suggest that these few early sites need not dictate our view of the colonization event. We must not assume that these few spatio-temporally isolated sites are indicative of an extensive, as yet undiscovered and hemisphere-wide pre-Clovis record. In other words, it is possible that they resulted from occasional dispersal events that did not result in true colonization. It is interesting to note that much of the strongest evidence for a pre-Clovis population occurs in close proximity to the southern margin of the continental ice sheets (37–39, 40, 41). What is clear is that abundant, continuous, and widespread archaeological evidence in CUSA does not occur until after ca. 13,200 BP, about 200 y before estimated onset of extinction, and if people were present at earlier times, their numbers were not large.

In SA, the evidence for overlap between human and megafaunal populations also lasts for close to 6,000 y, but, again, much of that time is accounted for by 10–12 Holocene megafaunal dates (42) and a single, possible archaeological component at Monte Verde in Chile (43). Permanent human occupation of SA began around 13,000 BP (44–46), within the range of our estimated date of initial megafaunal decline as estimated by both spacing and binning analysis methods. The abundance of Holocene dates on megafauna from South America may suggest that even though the extinction process may have been initiated around the time of human arrival, it was considerably more prolonged than in North America (42).

In comparison with Martin’s (1) estimates for the timing of human colonization and megafaunal decline, the evidence cited above from EB is considerably earlier than Martin anticipated. Human occupation begins by at least 14,000 BP, compared with Martin’s estimate of 13,600 BP, and megafaunal decline likely commenced earlier, around 14,600 BP. We note, however, that extinction itself ca. 13,300–13,400 BP occurred very rapidly, which is concurrent with human occupation. For the CUSA and SA, our analyses of radiocarbon date frequency distributions and spacings are unambiguously similar to Martin’s predictions. For CUSA, our 95% bounds are 12,861 and 13,232 BP in comparison with Martin’s estimate of 13,100 BP. For SA, our 95% bounds are 12,595 and 13,921 BP in comparison with Martin’s estimate of 13,100 BP.

Conclusion

Paul Martin’s classic model of New World colonization and Pleistocene extinctions stands as an iconic work in Quaternary studies. For more than 40 y, it has stood as a caricature of not only the Clovis-first paradigm, but also the idea that human hunting was the primary driver of Pleistocene extinctions in the Western Hemisphere. In that regard, it has regularly served as a target of researchers who have proclaimed that both of these ideas have long since gone the way of the Columbian mammoth and Shasta ground sloth (47, 48). It is indeed a rare phenomenon in science for such large-scale ideas to have lifespans of more than four decades. Nonetheless, using only temporal patterns of radiocarbon dates for extinct Pleistocene fauna, our estimates for the initial dates of megafaunal declines leading to extinction are consistent with Martin’s predictions. If Martin’s model was seriously flawed, no doubt by today, it would be little more than a curious artifact of the state of Quaternary science in the late 1970s. That it continues to be a matter of discussion and debate in and of itself may speak to its lasting value.

Initial megafaunal declines do appear to correlate with the first evidence for permanent human occupation in much of the Americas and are time-space transgressive in the manner predicted by Martin’s model, except that megafaunal declines in Beringia began much earlier than Martin expected, unless the real decline was the abrupt drop at the end of our fossil record. With the exception of the wide error range for SA and the consequent overlap between CUSA and SA, the north to south time-transgressive pattern is striking, and, barring significant new data, it would be difficult to reconcile this pattern with extinction hypotheses that invoke a single climatic, ecological, or catastrophic extinction mechanism across the entirety of the Americas. We do not mean to suggest that the issue is fully resolved. First, there remains a possible temporal incongruity between initial megafaunal declines and human colonization of EB. Given the small population of people that initially colonized EB and the small number of archaeologists looking for them, maybe we are seeing the impact of their presence before the appearance of their archaeological remains. Only more extensive investigations of terminal Pleistocene deposits in EB will resolve this issue. Second, we need to understand what exactly pre-Clovis sites represent. In our view, these sites may represent pulses of population expansion that failed to result in permanent colonization, paleontological sites mistaken for archaeological sites, poorly dated archaeological sites, or a combination of these. Regardless, based on our results, we must question whether they represent the presence of a permanent and widespread pre-Clovis population in the New World.

Finally, we would like to reassert the value of using paleoecological data to study the human past. The heavy ecological footprint of human societies throughout prehistory is becoming increasingly apparent through a variety of environmental proxies independent of the archaeological record. Past human societies have disrupted ecological communities in dramatic ways for many tens, if not hundreds of thousands, of years. In some ways, the record of ecological disruption marked by the arrival of a small founding human population may be more evident in the paleoecological record on a large scale than in the archaeological record itself. If archaeologists come to accept paleoecological proxies as also a record of human ecological disruption, rather than as solely a proxy for human boundary conditions, we believe that many new areas of research will emerge.

Materials and Methods

For each study region, we compiled radiocarbon dates on extinct megafauna from published sources (Datasets S1–S3). For EB and SA, we draw heavily from Guthrie (49) and Barnosky and Lindsey (44), respectively. We vetted these dates following the criteria of Barnosky and Lindsey (44) to isolate only the highest quality radiocarbon associations. We averaged statistically-indistinguishable dates on individual specimens to eliminate the problem of overrepresentation following Long and Rippeteau (50). We excluded specimens from archaeological contexts to isolate demographic trends of fauna independent of archaeological research. We expected that the inclusion of dates from archaeological contexts (e.g., dozens of Clovis sites) would introduce a degree of sample bias into the dataset because these contexts are often more thoroughly dated, and have played a central role in determining terminal dates for extinct taxa (11, 12). Our interest is not in estimating extinction dates, but rather in determining the timing of initial declines that lead to extinction. We calibrated all dates using OxCal v. 4.2 using the Intcal14 calibration curve to produce 2σ contiguous age ranges. We used the median age of the contiguous 2σ age range for the age of each specimen. For spacings analyses, in the presence of duplicate medians ages were adjusted to median $\pm 1/2$ ·(expected range) (SI Materials and Methods).

To examine demographic trends in extinct taxa over the Late Pleistocene, we created temporal frequency distributions of radiocarbon dates. During initial analyses, it became clear that arbitrary decisions made in histogram creation (i.e., choices of histogram bin boundaries and widths) had dramatic effects on results. Accordingly, we turned to a jackknife algorithm developed by David Hogg (14) for histogram creation that results in objectively chosen bin widths and boundaries that best fit the underlying distribution. In Hogg’s method, each histogram is characterized by a likelihood value that describes the degree of fit between the histogram and underlying distribution (SI Materials and Methods, Dataset S4). For each set of histograms of n = 2–101 bins, we identified the solution with the greatest likelihood of fit resulting in 100 histograms of variable bin width. Of those 100, we chose the five bin width solutions with the greatest likelihood values and corrected each for taphonomic bias following Surovell et al. (15). We determined the bin in which initial megafaunal population declines occurred as the last major mode before extinction. Finally, for each region, we identified the most likely date of decline as the average of the minimum and maximum boundaries for the five modal bins.

We also analyzed temporal patterns using spacings, i.e., times between consecutive ordered dates. The expected size of a spacing is inversely proportional to the concurrent population intensity, so spacings can indirectly lead to estimates of when populations change. Use of spacings avoids the need to select bin boundaries and uses a finer time scale than is used with binning, but it does pose other challenges. T₀, the initial time of movement toward extinction, is the parameter of interest in Martin's hypothesis, and we modeled μ_t, the mean for the taphonomically corrected spacing for (t₂ - t₁) at t = (t₂ + t₁)/2 as

$$\log \left({\mu }_t\right)=\left\{\begin{array}{cc}{\beta }_1\left(t-T_0\right)+C\hspace{0.17em}\hspace{0.17em}& \hspace{0.17em}t\le T_0\\ {\beta }_2\hspace{0.17em}\left(t-T_0\right)+C& \hspace{0.17em}t>T_0\end{array}\right\}.$$

For each $T_0$ this model was fit as a gamma-family generalized linear model (GLM) with log link (51). The model as given is nonlinear in T₀, and we evaluated GLMs at yearly fixed values of T₀ to select the estimate of T₀ based on the maximum profile likelihood. Patterns in the distant past effectively introduce excess noise into likelihood calculations unless models are simple, and for spacings analysis we restricted data to dates post-LGM for estimating change points in GLMs. Details of spacing-based estimation and confidence interval specification, including taphonomic correction, are described in SI Materials and Methods, and R code is provided in Dataset S5.

SI Materials and Methods

Radiocarbon Datasets.

The large majority of the SA and EB datasets are derived from Barnosky and Lindsey (44) and Guthrie (49), respectively. However, we made several edits to these data. Some dates in Guthrie’s supplementary table were either duplicates or individual laboratory numbers had distinct radiocarbon ages. In these cases, we either deleted one date, or threw them both out, respectively. The supplementary table for Barnosky and Lindsey (44) differs from the table in print by several dates, the latter possessing more. To maximize the number of dates from this region, we used the printed dataset. We also added 10 dates to SA and 11 to EB.

We compiled the dataset for the CUSA from a large number of sources, but the dataset is overwhelmingly dominated by remains from two areas, Ranch la Brea and Colorado Plateau cave sites, from which dates were derived from megafaunal dung. We used another large sample of dates from Boulanger and Lyman (28) for the northeast United States.

We vetted radiocarbon dates according to the method presented in Barnosky and Lindsey (44) and included only those dates that ranked an 11 or 12. For the North American dataset, we added several categories of material, which are listed in Dataset S2. Around 40 of the dates provided in Guthrie’s (49) dataset are from previously published studies by that author. We did not rank these dates, but assumed that they would all score 11 or higher on this scale because they were included in Guthrie’s (49) study. All of the dates listed as new in Guthrie’s study rank a 12.

Binning Analysis.

One critical measurement we make in this work concerns the peak of a histogram of binned data. The final major peak of the histogram before extinction is our best estimate for the initial date of decline of megafaunal populations. Measuring the peak of a histogram is a procedure fraught with choices that could potentially bias our result. Most obviously, the choice of binning for a histogram is subjective. If one chooses a binning that is too wide, the measured decline date may approach the mean of the range of measured data. If one chooses a binning that is too narrow, the histogram becomes noisy. With either (bad) choice, the overall shape of the distribution becomes poorly constrained.

Rather than arbitrarily selecting a histogram binning, a more defensible choice is to allow the data to inform us of the optimal binning for the histogram. This method is the approach we take in this paper. We adopt the formalism of Hogg (14), which uses a jackknife, or “leave-one-out” approach to infer the correct histogram binning. Broadly, the procedure is to create a series of all possible histogram bin sizes, each of which will have a different number of bins over the range of the data. Variation in boundaries can also be explored. Within a given one of this series of bin sizes and edges, each of the individual datum are looped through and discarded in turn. With this datum missing, the fraction (compared with the total across all bins) of the remaining objects contributing in their bin is calculated for each remaining datum. These fractions are summed in logarithmic space to create a likelihood for that choice of bin size and boundaries in the series. Typically a small positive value is added to the numerator of each bin fraction, to smooth the data by preventing zero values from corrupting the likelihood sum.

In this manner, a single likelihood can be constructed for each possible choice in the series of bin sizes and boundaries, and the maximum value among these likelihoods represents the optimal binning choice. This procedure allows the data to inform us of how we should bin it, in the sense that every time a datum is discarded, the remaining data have been used to test the question “what was the likelihood of a new datum populating a particular bin”? The resulting histogram is then defensible in that it is the choice that best predicts where any new set of data would fall if we were to continue to probe the paleontological record reflected by the histogram, and if we did so repeatedly using a consistent experiment.

The Hogg method was applied using a macro written in Visual Basic for Microsoft Excel. Bin number was varied from 2 to 101. Starting bin boundaries were varied in 10-y increments. The smoothing variable, α, was varied from 0.9 to 3.0 in increments of 0.1. In the case of α ≤ 1 for histograms with empty bins, negative fractions result, meaning that likelihood cannot be calculated because it would require taking the logarithm of a negative value. When such histograms were encountered, they were discarded.

The Microsoft Excel Visual Basic code used to find optimal histogram solutions is provided in Dataset S4. To use this code, a spreadsheet should be set up with the following specifications. Column A should contain mean radiocarbon ages beginning in row 2, with row 1 reserved for a header label. The list of dates should have no gaps or empty rows. Cell D1 should contain the maximum radiocarbon age [e.g., the formula =MAX(A:A)]. Cell D2 should contain the minimum radiocarbon age [e.g., the formula =MIN(A:A)]. Cell D3 should contain the number of radiocarbon dates [e.g., the formula =COUNT(A:A)]. Summary histogram statistics are outputted in columns F through K, starting on row 2. The following headers should be placed in cells F1 to K1: Bin Min, n Bins, Alpha, Likelihood, Bin Width, and Good Solution. All histograms for which a value of NO occurs in column K should be discarded.

Analysis of Spacings between Observations.

Although Hogg's procedure provides automatic selection of bin numbers and boundaries, any histogram analysis ultimately depends on the bins selected. An analysis at the finest possible scale of time is possible by looking at time lags between dates—long lags correspond to infrequent events and short lags correspond to frequent events.

Time lags can be conceptualized either as spacings between the order statistics for a sample of dates or as waiting times in a temporal point process (such as a Poisson process), with occurrences in the process being observations at some specified date. In an idealized setting over a period of demographic stability, the frequency of randomly obtained dates in a unit interval is Poisson distributed with intensity λ, and spacings are exponentially distributed with mean μ = $1/\lambda$. The present setting is not quite ideal, and accommodations made are described below.

A few independent samples gave duplicate dates (one pair in the CUSA and six pairs in EB), even though the theoretical chance of exact duplication is zero. Zero spacings cause problems for formal analysis, but it would be inappropriate to simply discard duplicates. The fact that all calibrated dates are reported as medians within a 2σ interval suggests a way to replace duplicate pairs by alternate nonduplicate estimates. For two independent observations (t₁, t₂) from normal distributions with the same mean and respective variances ${\sigma }_1^2$ and ${\sigma }_2^2$ the expected range is r = $\sqrt{\left({\sigma }_1^2+{\sigma }_2^2\right)\hspace{0.17em}2/\pi }$, suggesting using date substitutions median $\pm 1/2$ range = median $\pm$ $\sqrt{\left({\sigma }_1^2+{\sigma }_2^2\right)/2\pi }$.

Once a set of unique dates t₁, t₂, …,t_m is found for each region, dates are sorted, and ordered values t_(i) are used to create baseline spacings t_(i+1) − t_(i) for i = 1, 2,…, m − 1.

Because of taphonomic bias, observed spacings are longer than would be expected without loss of sedimentary contexts through time. The average spacing over a block of time is the inverse frequency over that block, so the desired taphonomic correction is based on the inverse taphonomic correction formula for frequencies. Over the observed time interval [t₁, t₂], the correction is ${{\displaystyle \int }}_{t_1}^{t_2}n\left(t\right)dt$, where n(t) $\propto {(t+2\text{,}176.4)}^{-1.3925309}$ is the taphonomic bias in Surovell et al. (15). The integral is easily solved to be proportional to ${(t_1+2\text{,}176.4)}^{-0.3925309}-\hspace{0.17em}{(t_2+2\text{,}176.4)}^{-0.3925309}$. For purposes of detecting onset of decline, the proportionality constant does not matter.

We note that using uncorrected spacings instead of corrected spacings in our data could change relative values between early and late spacings by a factor greater than six, so taphonomic adjustment is recommended. Nonetheless, we compared results using uncorrected values and found similar estimates for onset of extinction but generally wider confidence intervals. This comparison helps alleviate possible concerns about the quality of the standard taphonomic correction for data in this study.

Because interest is in population changes over time, and adjusted time lags are indirect measures of population levels, we associate spacing lengths with particular times. For simplicity, each taphonomically deflated spacing is linked to the midpoint of the original spacing interval, t = $\left(t_1+t_2\right)/2$ . Spacing data thus consist of m – 1 pairs $(t,\hspace{0.17em}{y}_t$), where $y_t$ is the value of the integral above. The taphonomically corrected value y_t is the actual response used in generalized linear model analyses, not the raw spacing t₂ − t₁.

According to Martin's hypothesis, population levels before $T_0$ (time of onset of extinction) are easiest to envision as varying about a smooth curve of unspecified shape over time or else as a stationary correlated time series with some fixed mean. Spacings correspond to measures of inverse population levels, so these same modeling structures apply for spacings. We found that a simple parametric model for spacings over times post-LGM gave the most coherent information about $T_0$ and the best goodness of fit. For CUSA and SA, we observed population increases post-LGM and before extinction, so we chose a model that admitted different nonzero rates of change before and after extinction onset. For EB, frequencies and spacings were very stable before onset, and we set the preonset slope to zero. We also considered that rates of population decline leading to extinction should be close to exponential. These facts motivate the choice of model for spacings post-LGM (defined as younger than 22,000 BP)

$$\log \left({\mu }_t\right)=\left\{\begin{array}{cc}{\beta }_1\left(t-T_0\right)+C\hspace{0.17em}\hspace{0.17em}& \hspace{0.17em}t\le T_0\\ {\beta }_2\hspace{0.17em}\left(t-T_0\right)+C& \hspace{0.17em}t>T_0\end{array}\right\}.$$

Here ${\mu }_t$ is the expected value of spacing $y_t$. In a Poisson process spacings are exponentially distributed, and exponential distributions are generalized by the family of gamma distributions, so a gamma distribution model for spacings is sensible. For a known value of $T_0$, the above model can be fit using a generalized linear model (glm) with a gamma family and a log link function (51, 52), but the parameter $T_0$ is nonlinear with respect to other parameters. It is possible to fit generalized nonlinear models, but the delicacy of the EB data, in particular, relative to Martin's hypothesis, motivated us to estimate $T_0$ not from purely asymptotic behavior at the optimum but based on profile likelihoods obtained for a broad grid of values of $T_0$. Further information about generalized linear models may be found in McCullagh and Nelder (51) and in Dobson and Barnett (52). 95% CIs are given as likelihood ratio confidence intervals: any onset time producing −2 log likelihood values within ${\chi }_{0.95;1}^2=3.8415$ of the optimum value is considered to be within the confidence region. Autocorrelations of model residuals were assessed approximately by treating spacings as though they occurred at regular time lags. Using the above models, observed approximate autocorrelations at lags greater than zero were small and statistically insignificant. All programming and analyses for spacings were done using R (53).

Alternative approaches to modeling with spacings were also considered. Approximate autoregressive time series models for log ($y_t$) can be fit if we treat observed spacings as though they were regularly spaced. Following this approach, EB and SA data fit first-order AR (autoregressive) models and CUSA data fit a fifth-order AR model. We also considered a nonparametric smoother (loess fit optimized via generalized cross-validation) (54). These models were fit over the entire time series of taphonomically corrected spacings. In both cases, estimates for onset of extinction were similar relative to conclusions about Martin’s hypothesis, but confidence intervals and diagnostics for goodness of fit for these methods were either inferior or not easily obtained. (Table S2, Fig. S2, and Dataset S5).