Abstract
Ultrasound and microbubble optimization studies for therapeutic applications are often conducted in water/saline, with a fluid viscosity of 1 cP. In an in vivo context, microbubbles are situated in blood, a more viscous fluid (~4 cP). In this study, ultra-high speed microscopy and passive cavitation approaches were employed to investigate the effect of fluid viscosity on microbubble behavior at 1 MHz subject to high pressures (0.25 – 2 MPa). The propensity for individual microbubble (n=220) fragmentation was shown to significantly decrease in 4 cP fluid as compared to 1 cP fluid, despite achieving similar maximum radial excursions. Microbubble populations diluted in 4 cP fluid exhibited decreased wideband emissions (up to 10.2 times), and increasingly distinct harmonic emission peaks (e.g. ultraharmonic) with increasing pressure as compared to 1 cP fluid. These results suggest that in vitro studies should consider an evaluation using physiologic viscosity perfusate before transitioning to in vivo evaluations.
Keywords: microbubbles, ultrasound, fluid viscosity, fragmentation, stable cavitation, inertial cavitation, high-speed imaging
Introduction
Microbubbles are currently clinically employed as an intravascular contrast agent for diagnostic ultrasound imaging. In addition to diagnostic applications, ultrasound stimulated microbubbles have been recently employed to elicit therapeutic benefit. Sonothrombolysis, namely the use of ultrasound and microbubbles to non-invasively dissolve blood clots and restore flow, has been shown to be a feasible strategy both in vitro (Acconcia et al. 2014; Leeman et al. 2012; Tachibana and Tachibana 1995) and in vivo (Birnbaum et al. 1998; Culp et al. 2011; Pacella et al. 2015), and is also the first therapeutic application of microbubbles to enter clinical trials (Molina et al. 2006). Ultrasound and microbubbles have also been employed as an emerging strategy for enhanced drug and gene delivery for the treatment of cancer and vascular disease. Indeed, the delivery of chemotherapeutic drugs (Escoffre et al. 2013; Kang et al. 2010; Kotopoulis et al. 2013; Tinkov et al. 2010), DNA (Carson et al. 2011; Christiansen et al. 2003) and siRNA (Carson et al. 2012; Kinoshita and Hynynen 2005) has been shown in both in vitro and in vivo contexts. In addition to these applications, studies have shown that ultrasound stimulated microbubbles can transiently and locally disrupt the blood brain barrier (BBB) in order to facilitate drug delivery for the treatment of brain disorders (Park et al. 2012; Tung et al. 2011; Wang et al. 2015; Weber-Adrian et al. 2015).
Central to all these applications is the interaction between microbubbles and ultrasound, namely microbubble oscillation dynamics. The precise microbubble behavior required to elicit therapeutic benefit, however, remains unclear. For sonothombolysis applications, previous studies have suggested that microbubble disruption (i.e. inertial cavitation) is required for effective treatment (Leeman et al. 2012), while others conclude that non-inertial cavitation (i.e. stable cavitation) is necessary (Datta et al. 2008). These types of microbubble cavitation regimes have also been observed in drug/gene delivery applications, whereby some authors conclude that inertial cavitation is required to induce a therapeutic effect (Fan et al. 2013; Hallow et al. 2006), and others indicate stable cavitation as the primary mechanism (Forbes et al. 2008). In brain disorder applications, it is stable, nonlinear emissions that play an important role in the detection of BBB disruption (McDannold et al. 2006), however the physical mechanisms responsible for this disruption remain unknown (Burgess and Hynynen 2014).
Aside from the ultrasound parameters, including transmit frequency, acoustic pressure and pulse duration, several physical factors are known to affect microbubble behaviour. These include the intrinsic properties of the bubble (e.g. core gas and encapsulation properties), the presence of nearby boundaries (Garbin et al. 2007; Helfield et al. 2014), and the properties of the surrounding fluid environment (e.g. density, viscosity). The majority of studies designed to optimize ultrasound stimulated microbubbles for the aforementioned therapeutic applications are conducted with agent diluted in gas-equilibrated water or saline, a fluid that is characterized by a viscosity of 1 cP (0.001 Pa s). However, in an in-vivo context microbubbles circulate within the blood pool to which they are confined. Although the viscosity of blood is dependent on shear rate and hematocrit percentage (Walker et al. 1976), it is typically ≈ 4 cP at 37 °C, approximately four times greater than that of water/saline. Such an increase in viscosity may alter microbubble behavior by dampening oscillations or altering thresholds for bubble disruption (i.e. inertial cavitation regimes). Indeed, both experimental work with polystyrene beads (Deng et al. 1996) and simulation work (Allen et al. 1997) have been previously conducted on the effect of fluid viscosity on inertial cavitation thresholds.
The objective of the present study was to therefore investigate the effect of fluid viscosity on microbubble behavior. Specifically, the behavior of individual microbubbles and microbubble populations situated in either a 1 cP fluid (to compare with previous microbubble characterization studies) or a 4 cP fluid (to further simulate in-vivo conditions) were investigated under ultrasound exposure conditions relevant to therapeutic applications. The motivation for this study was to determine whether microbubble optimization studies conducted in water/saline for use into subsequent in-vivo studies need to be interpreted judiciously. This study employed an ultra-high speed imaging system to investigate individual microbubble behavior and the propensity for microbubble fragmentation, and a passive cavitation detection apparatus to record the acoustic emissions from microbubble populations, associated with both stable and inertial cavitation.
Materials and Methods
Agent Preparation
In-house phospholipid encapsulated microbubbles were prepared from a lipid aqueous dispersion composed of polyoxyethylene (40) stearate (Sigma-Aldrich; St. Louis, MO), 1,2-distearoyl-sn-glycero-3-phosphocholine (DSPC) and 1,2-distearoyl-sn-glycero-3-phosphoethanolamine-N-[methoxy( (polyethylene glycol)-2000] (DSPE-mPEG2000; Avanti Polar Lipids; Alabaster, AL), as previous described elsewhere (Weller et al. 2002). Briefly, polyoxyethylene (40) stearate, DSPC and DSPE-mPEG2000 (1: 2: 1, w/w/w) were dissolved in chloroform. The chloroform was evaporated by flushing with argon and followed by an overnight vacuum-dry. The dried lipid film was rehydrated in saline (0.9% NaCl) with a final lipid concentration of 10 mg/ml for 4 hours at room temperature. After a brief sonication to dissolve any lipid debris, the lipid dispersion was sonicated with a 20 kHz probe (Heat Systems Ultrasonics, Newtown, CT) at a power level of 5 in the presence of perfluorobutane gas (FluoroMed, L.P.; Round Rock, TX). After sonication, the microbubbles were washed twice with 20 ml of saline by incubation at room temperature for 30 min to allow for microbubble floating. The washed microbubble solution was then re-suspended in saline saturated with perfluorobutane. The resulting in-house agent is characterized by a concentration of 2×109 bubbles/ml and a mean microbubble diameter of 3.3 μm as assessed by a Coulter Counter (Multisizer™ 3, Beckman Coulter Inc., Fullerton, USA) with a 30 μm aperture. In addition, the zeta potential of this agent was determined to be −(12.8±1.5) mV (Malvern Instruments, Zetasizer Nano ZS90, Worcestershire, UK).
Viscosity Measurements
Fluid viscosity adjustments were performed by dissolving polyvinylpyrrolidone (PVP; #PVP360-100g, Sigma-Aldrich, St Louis, MO, USA), a biologically inert polymer, in phosphate-buffered saline (PBS; #17-516F, Lonza, Walkersville, MD, USA). In this manner, fluid with different fluid viscosities can be achieved (Bolten and Turk 2011). Pure PBS and a 1.25% PVP solution at room temperature were employed to achieve fluid viscosities of 1.05±0.01 cP and 4.02±0.01 cP, respectively, as measured using a capillary viscometer (model C445, Cannon Instrument Company, State College, PA). Measurements were repeated four times and the means and standard deviations are presented.
Optical-Acoustical Apparatus
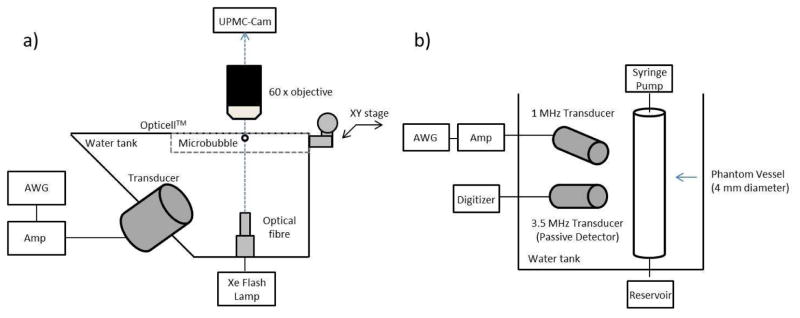
A water tank was constructed in order to house both a single element transducer (f=1 MHz, f#=1.67; −6 dB beam width of 2.5 mm; model A302S-SU-F1.63-PTF, Olympus NDT, Waltham, MA) at an angle of 45 degrees from below and a white light illumination fiber optic (Figure 1a). The tank was filled with de-ionized water and placed under a 60x water-coupled objective lens (LUMPLFLN, 60x/w, Olympus) and coupled to the UPMC Cam, an ultrafast frame microscopy imaging system capable of recording up to 25 million frames per second (Mfps) for 128 frames (Chen et al. 2013). Optical-acoustical co-alignment was performed with a pulse-echo approach, employing a pulse-receiver (5073PR, Olympus NTD, Waltham, MA) and a false objective lens as detailed in Chen et al 2013. Once co-alignment was achieved, suspensions of microbubbles were diluted in either 1 cP or 4 cP fluid and injected in an Opticell™ chamber placed on an XY positioning stage. At least 8 hours prior to experiments, the Opticell™ was pre-treated with 2% bovine serum albumin (BSA; Sigma Aldrich #A2153, ST. Louis, MO, USA) dissolved in de-ionized water in order to mitigate any potential bubble adhesion to the polystyrene layer. The BSA solution was subsequently removed, and the Opticell™ was washed with PBS immediately prior to experiments. Individual microbubbles were insonicated with a 1 MHz, 8-cycle Tukey-windowed pulse (α=0.25), generated from an arbitrary function generator (model AFG3252, Tektronix, Beaverton, OR) and amplified by a gated RF power amplifier (model 250A250AM8, Amplifier Research, Souderton, PA). The transmit pulses were sent over a peak negative pressure range of 0.5 to 2 MPa, as measured in water in a separate tank with a hydrophone (HGL-0200, Onda Corp, Sunnyvale, CA). Under the assumption that the attenuation coefficient is proportional to the fluid viscosity (Stokes-Kirchhoff’s equation, e.g. (Shutilov 1988)), KZK simulations (Soneson 2009) were conducted and confirm only negligible differences (<1%) in peak negative pressure and propagation harmonic amplitudes between a 1 cP and a 4 cP fluid (data not shown).
Figure 1.
Schematic diagrams of the experimental apparatuses employed in this study. (a) Ultra-high speed microscopy setup, consisting of a single element 1 MHz transducer, fibre optic light source and Opticell™ phantom within a 2-D translational stage. (b) Passive cavitation detection arrangement, consisting of a 1 MHz transmit transducer and a 3.5 MHz passive cavitation detector transducer. See text for further details.
An offline analysis in MATLAB (The Mathworks, Natick, MA, USA) was performed in order to extract the dynamic behaviour of individual microbubbles from the ultra-high-speed recordings. This was accomplished by employing a minimum cost algorithm based on pixel intensity gradients (Sonka et al. 1998) in order to estimate the microbubble radius (i.e. for a given frame), as a function of time, a method previously employed on still frames (Helfield et al. 2012).
Passive Cavitation Detection
Passive cavitation detection was performed in order to assess the effect of fluid viscosity on the microbubble acoustic emissions from within a 4 mm diameter wall-less rubber phantom (Leeman et al. 2012). Briefly, microbubbles were diluted (2×106 microbubbles/ml) in either a 1 cP or 4 cP fluid and infused within the phantom vessel at a flow rate of 1.5 ml/min (approximately 2mm/sec flow velocity). A single element transducer (model A302S-SU-F1.63-PTF, Olympus NDT, Waltham, MA) was employed to insonicate the microbubble population with a 1 MHz, 5000 cycle pulse at a pulse repetition frequency (PRF) of 0.33 Hz over a peak negative pressure range of 0.25–1.5 MPa. A second, co-localized transducer (f=3.5 MHz, f#=2.67; −6 dB beam width of 1.2 mm; model V383-SU-F1.00IN-PTF, Olympus NDT) was employed as a passive cavitation detector at an approximate angle of 45 degrees with respect to the ultrasound delivery transducer (Figure 1b). The received signal was pre-amplified by 10 dB with an ultrasound pulse/receiver (model 5073PR, Olympus NTD, Waltham, MA) in receiver mode, and digitized with a high resolution digitizer (12 bits, sampling frequency of 100 MHz, Acqiris DP310, Agilent, Santa Clara, CA). The frequency dependent transfer function was not determined for the receive transducer, as all quantitative results are comparative between the two fluids employed.
Joint time-frequency analysis of the cavitation signals was performed with a window size of 2000 points (corresponding to 20 μs) with a 500-point increment step size resulting in 75% overlap. A Hamming window was applied to the RF signal before digital Fourier transformation, and the power spectrum P(f) was calculated by averaging the spectrogram for all samples in each experimental group (n=4). The integrated power Pn at a given frequency fn was defined in the following manner:
| (1) |
where Δf=0.05 MHz. The integrated power was calculated at the subharmonic (f0.5=0.5 MHz), fundamental (f1=1 MHz), first order ultraharmonic (f1.5=1.5 MHz), second-harmonic (f2=2 MHz) and third harmonic (f3=3 MHz) frequencies, as well as at a wideband frequency band around the operating frequency of the passive cavitation detector (which is 3.5 MHz), defined here at f3.15=3.15 MHz in order to avoid the third order ultraharmonic. In addition to the frequency dependent integrated power, in order to extract a stable cavitation metric SCn from the passive cavitation results, the integrated power as calculated from Eq. (1) was normalized to an average of the surrounding wideband emission on either side of a given harmonic peak:
| (2) |
The above metric was employed in order to estimate the amount of energy at a given harmonic that was produced from microbubbles exhibiting stable cavitation versus the contribution to the spectrum from microbubble disruption (performed in linear units), a similar methodology to that which has been conducted previously (Datta et al. 2008).
Results
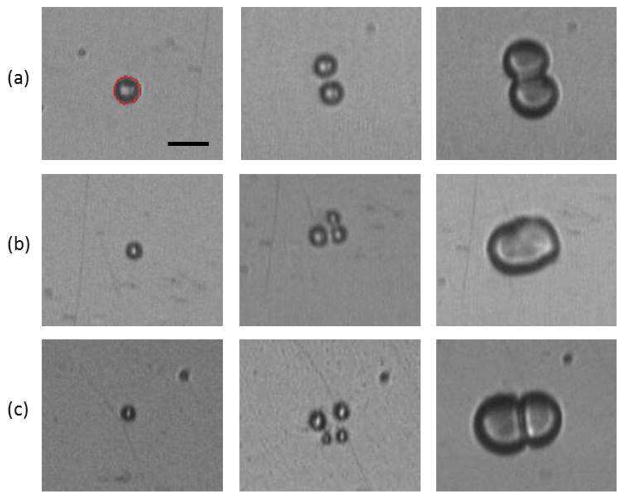
The dynamic behavior of individual microbubbles was recorded via ultra-high speed microscopy at approximately 10.5 Mfps for microbubbles situated in either 1 cP (n=111) or 4 cP (n=109) fluid. At the acoustic pressures employed in this study, microbubbles in 1 cP fluid were shown to undergo fragmentation; namely the fission of a microbubble into N (where N>1) smaller bubbles (Postema et al. 2004). Figure 2 displays frame selections from three ultra-high speed recordings in 1 cP fluid at (a) 0.5 MPa and (b & c) 1.0 MPa, depicting examples of (a) N=2, (b) N=3 and (c) N=4 fragmentation. In this figure, the first column represents a frame recorded prior to ultrasound exposure from which the initial bubble diameter can be extracted. The second column displays a frame chosen to highlight bubble fragmentation, where multiple, smaller bubbles can be distinctly observed. Finally, the frames highlighted in the third column display microbubbles coalescence, namely the merging of multiple bubbles back into a larger microbubble.
Figure 2.
Selected frames from three ultra-high speed recordings at approximately 10.5 Mfps of microbubble fragmentation into (a) 2, (b) 3 and (d) 4 bubbles and subsequent coalescence. The first column depicts a frame before ultrasound exposure, in which the initial microbubble diameter was extracted (3.6 μm, 2.6 μm and 2.4 μm). The microbubble in panel (a) was recorded under a 0.5 MPa exposure, while those in panels (b) and (c) experienced 1 MPa. All the microbubbles are situated in 1 cP fluid. Scale bar is 5 μm, and each panel is 21.90 × 18.45 μm. Microbubble size information was extracted by an edge detection algorithm (minimum cost algorithm based on pixel intensity gradients generated in-house in MATLAB), an example of which is shown in red on the first frame of panel (a).
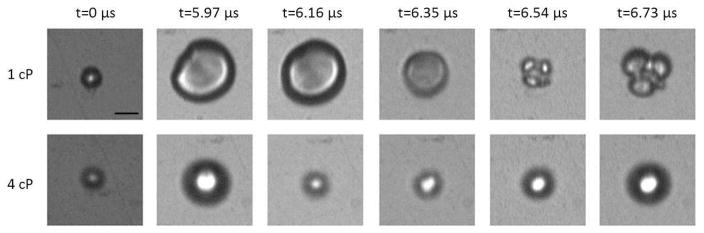
In 4 cP fluid, however, microbubble fragmentation was observed much less frequently. Figure 3 displays a representative example of the oscillation behavior in both fluid environments. Six selected frames from an ultra-high speed recording of an individual microbubble sonicated at 1 MPa in 1 cP fluid (top panels; 4.3 μm) and 4 cP fluid (bottom panels; 4.8 μm) are shown. It can be seen in this example that for two similar sized microbubbles under the same acoustic stimulus, the microbubble situated in 1 cP fluid underwent fragmentation, in this example N=3. However, in a 4 cP fluid environment the microbubble oscillated in a spherical manner and does not fragment; that is to say remained intact. Figure 4 summarizes the effect of liquid viscosity on the propensity of microbubble fragmentation for all microbubbles interrogated in this study, highlighting the percentage of microbubbles undergoing fragmentation as a function of the transmit pressure in either fluid. Error bars denote the 95% confidence interval (Clopper-Pearson interval) and the stars denote statistical significance (p<0.002) as determined by Fisher’s exact test. At pressures of 0.5 MPa, 1.0 MPa and 1.5 MPa respectively, all microbubbles interrogated in 1 cP fluid were shown to exhibit fragmentation (n=36; n=36; n=28) over similar size ranges (2.1–4.3 μm; 1.9–5.1 μm; 1.9–5.6 μm). In 4 cP fluid, 3.1% (n=32), 21.9% (n=32) and 70.9% (n=31) of bubbles were shown to fragment in 4 cP fluid over a similar size range (1.8–4.8 μm; 2.2–5.0 μm; 2.2–5.8 μm). Finally, at 2.0 MPa, all bubbles in either liquid environment underwent fragmentation (n=11; n=14).
Figure 3.
A representative example of the effect of fluid viscosity on microbubble oscillation characteristics at 1 MPa. Six selected still frames from an ultra-high speed recording at approximately 10.5 Mfps for (top) a 4.3 μm diameter microbubble in 1 cP liquid and (bottom) a 4.8 μm diameter microbubble in 4 cP liquid. Each panel is 18.70 × 17.85 μm.
Figure 4.
Summary of the effects of liquid viscosity on microbubble behavior at high transmit pressures, displaying the percentage of microbubbles that undergo fragmentation as a function of pressure for microbubbles residing in (gray bars) 1 cP or (black bars) 4cP liquid. See text for microbubble size range details. Error bars denote the 95% confidence intervals (Clopper-Pearson interval), and stars denote statistical significance (p<0.002) as determined by Fisher’s exact test.
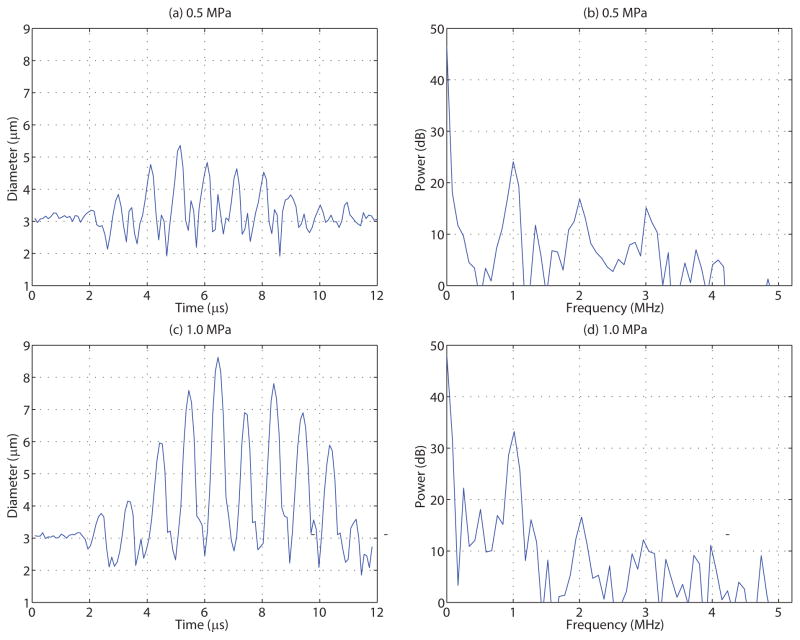
In addition to determining whether a given microbubble has undergone fragmentation, individual microbubble radial dynamics can be extracted from the ultra-high speed recordings. For microbubbles that exhibited fragmentation, a complete diameter versus time trace cannot be extracted. However, the maximum diameter Dmax achieved before fragmentation can indeed be determined. For microbubbles that underwent stable cavitation, specifically in 4 cP fluid, the complete microbubble diameter versus time trace can be extracted. Figure 5 depicts one such example of an individual microbubble diameter versus time trace and its corresponding Fourier spectrum at (top) 0.5 MPa and (bottom) 1.0 MPa for individual microbubbles situated in 4 cP fluid. From this figure, it can be seen that microbubbles exhibited highly asymmetrical oscillations, consistent with the presence of higher order harmonics in their associated power spectra.
Figure 5.
The diameter versus time trace and corresponding Fourier transform of similarly sized individual microbubbles situated in a 4 cP fluid and insonicated at either (top) 0.5 MPa or (bottom) 1 MPa peak negative pressure. Microbubbles situated in 1 cP fluid did not remain intact at these pressures – see Figure 4.
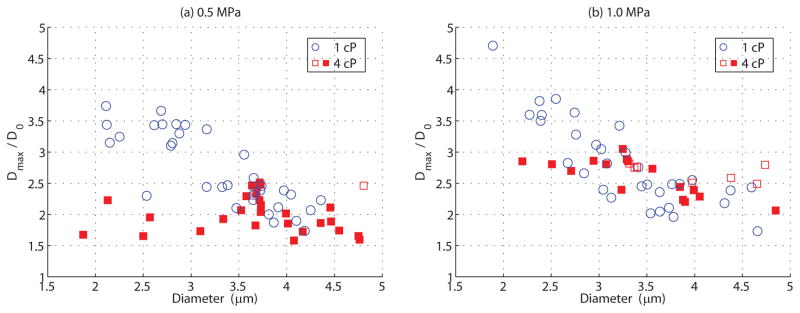
Regardless of whether or not fragmentation occurred, the maximum relative microbubble expansion, defined as the maximum diameter Dmax normalized to its initial diameter D0, can be measured from the ultra-high speed recordings. Figure 6 summarizes the results of the maximum relative expansion as a function of initial diameter at (a) 0.5 MPa and (b) 1.0 MPa for all microbubbles interrogated at these pressures in both 1 cP (circles) and 4 cP (squares) fluid. Note that the open symbols denote fragmentation, and for these bubbles the maximum relative expansion is calculated from the maximum diameter prior to fragmentation, while the closed symbols denote intact bubbles (see Figure 3). A small subset of microbubbles was excluded from this analysis due to their position within the UPMC-Cam field of view. Radiation forces, especially at larger pressure amplitudes (> 1.5 MPa), can result in a partial clipping of the microbubble image, and therefore subsequent analysis may extract an inaccurate estimate of microbubble diameter for that frame.
Figure 6.
Maximum relative microbubble expansion, defined as the normalized maximum diameter (Dmax/D0), as a function of initial diameter D0 for individual microbubbles insonicated at (a) 0.5 MPa and (b) 1.0 MPa, situated in either (circles) 1 cP or (squares) 4 cP fluid. Open symbols refer to microbubbles that have fragmented into smaller microbubbles, and in this case the relative expansion is calculated from the maximum diameter prior to fragmentation. Closed symbols denote microbubbles that do not fragment. Note that all microbubbles situated in 1 cP fluid undergo fragmentation at these pressures (see Figure 4).
It can be seen from Figure 6 that for 1 cP fluid, the maximum relative expansion prior to fragmentation increased for decreasing microbubble sizes, reaching a maximum of 3.7 at 2.11 μm and 4.7 at 1.89 μm for pressures of 0.5 MPa and 1.0 MPa, respectively. At 0.5 MPa (Figure 6a), microbubbles in 4 cP fluid did not generally fragment, and the maximum relative expansion did not significantly correlate with initial bubble diameter as determined by a Pearson’s test (r=−0.09, p=0.59). As compared to that within 1 cP fluid, microbubbles smaller than 3.5 μm in diameter exhibited considerably smaller oscillation amplitudes in 4 cP fluid at 0.5MPa (p=9.6×10−6). However, microbubbles larger than 3.5 μm did indeed oscillate with comparably similar maximum relative expansions to those in 1 cP fluid (p=0.07), yet generally remain intact. At 1.0 MPa (Figure 6b), the maximum expansions in 4 cP fluid significantly correlated with diameter (r=−0.77, p=4×10−4), and this panel shows that fragmentation in 4 cP fluid does not entirely depend on achievable oscillation amplitude. Similar to panel a), as compared to 1 cP microbubbles below 3.0 μm underwent smaller oscillation amplitudes in 4 cP (p=0.03), while the oscillation amplitudes above 3.0 μm exhibited no statistical difference (p=0.19).
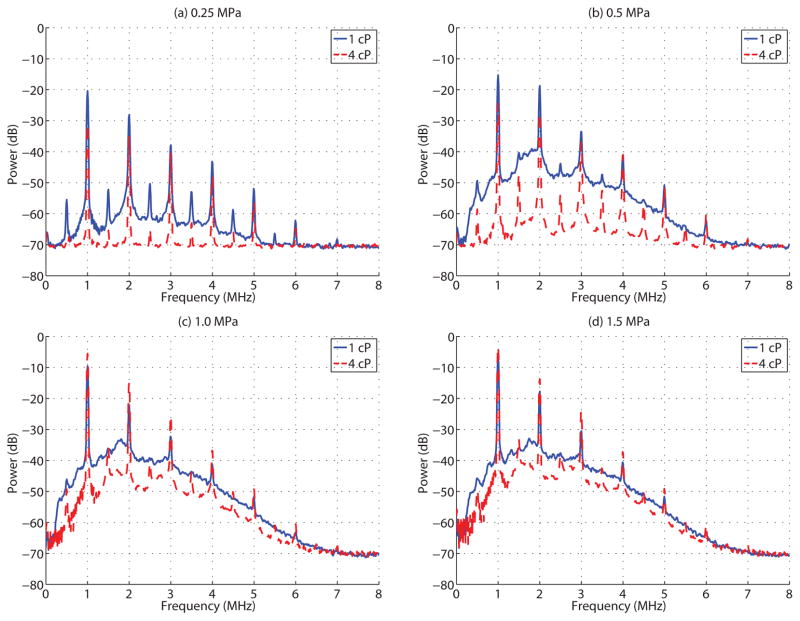
The results from passive cavitation detection (PCD) experiments were consistent with the ultra-high speed microscopy data. Figure 7 depicts the cavitation power spectra over the first 1 ms of insonication for a population of bubbles in either a (solid) 1 cP or (dashed) 4 cP fluid environment at (a) 0.25 MPa, (b) 0.5 MPa, (c) 1.0 MPa and (d) 1.5 MPa. Under the acoustic conditions employed in this study, PCD measurements were consistent with microbubbles that underwent either stable or inertial cavitation, as indicated by the distinct harmonic content (stable) and the presence of wideband emissions (inertial). At 0.25 MPa (Figure 7a), the emission spectrum in a 1 cP fluid environment exhibited distinct harmonic (mf, m=1,2,…6) and subharmonic (mf/2 with m=1,3,5,…11) emissions. In addition, a significant amount of wideband emission occurred, suggesting microbubble inertial cavitation (i.e. microbubble disruption). As the pressure was increased to 0.5 MPa, the subharmonic signals became less distinct, confounded by the disproportionally increasing wideband emissions. At 1.0 MPa and 1.5 MPa, the subharmonic components became enveloped by the wideband emissions, consistent with the majority of microbubbles undergoing inertial cavitation. Microbubbles situated in a 4 cP fluid, however, exhibited less wideband emissions at a given pressure level, suggesting a higher pressure threshold for the onset of inertial cavitation. Indeed, even at 1.5 MPa, distinct subharmonic signals were clearly observed, highlighting that there existed a subset of microbubbles that were undergoing stable cavitation at this pressure amplitude.
Figure 7.
Microbubble cavitation spectra, averaged over the first 1 ms, for insonication pressures of (a) 0.25 MPa, (b) 0.5 MPa, (c) 1.0 MPa and (d) 1.5 MPa within a 1 cP (solid) and 4 cP (dashed) fluid.
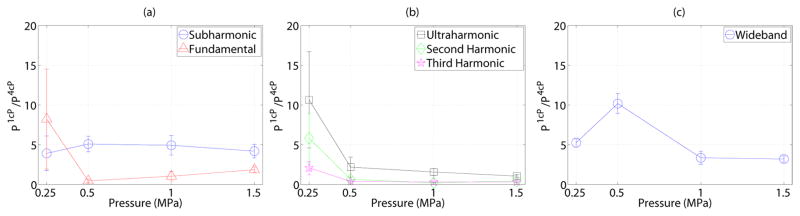
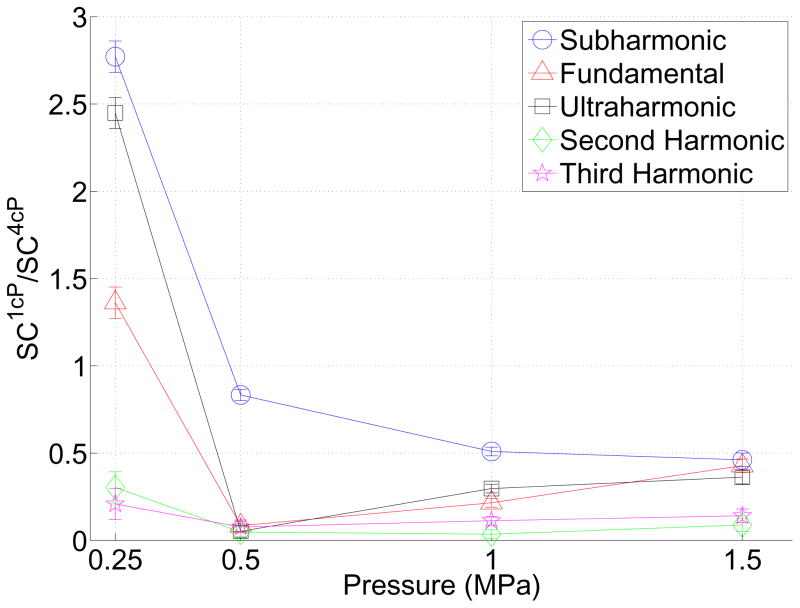
Figure 8 further quantifies the effect of viscosity on the emission spectra (Eq. 1) over the full 5 ms duration in the (a) subharmonic and fundamental, (b) ultraharmonic, second and third harmonic and (c) wideband frequency bands. In this figure, the ratio of the integrated power from the acoustic emissions in 1 cP fluid to that in 4 cP fluid is displayed as a function of transmit pressure amplitude. A value larger than 1 in this figure indicates that the emissions in the given frequency band are larger in magnitude in 1 cP fluid than in 4 cP fluid. This ratio significantly differs from 1 (indicating an effect of fluid viscosity) in every instance except the fundamental response at 1 MPa, the ultraharmonic at 1.5 MPa and second-harmonic at 0.5 MPa (p<0.02). The relative subharmonic emission power (Figure 8a) reached a maximum of 5.1 at 0.5 MPa, however did not generally exhibit pressure dependence. Integrated power over the other frequency bands exhibited similar behavior; a value decreasing with increasing pressure and exhibiting a maximum of 8.23, 10.65, 5.82, 2.10 at 0.25 MPa for the fundamental, ultraharmonic, second and third harmonic respectively. The wideband emission power (sampled at f=3.15±0.05MHz) achieved a maximum of 10.2 at 0.5 MPa. Given that there exists contributions from broadband content in the fundamental, ultraharmonic, second and third harmonics (Figure 7), Figure 9 depicts the relative stable cavitation metric (Eq. (2)) in 1 cP fluid to that of 4 cP fluid in order to gain insight into the physical origins of the received scattered emission spectrum. This figure suggests that for pressures ≥ 0.5 MPa, populations of microbubbles in 1 cP fluid exhibited less stable cavitation than in 4 cP fluid (p<0.02). For the lowest pressure, where microbubble disruption was less prevalent, subharmonic, fundamental and ultraharmonic scattering in 1 cP fluid due to stable cavitation was greater than in 4 cP fluid (p<0.02).
Figure 8.
The relationship between transmit pressure amplitude and the ratio of the integrated power from passive cavitation emissions in 1 cP to that in 4 cP, as calculated from Eq. 1. Mean and standard deviations for all sonications at each pressure amplitude are shown.
Figure 9.
The ratio of the stable cavitation metric defined in Eq. (2) in 1 cP fluid to that in 4 cP fluid. A value less than 1 suggests that emissions from microbubble populations due to sable cavitation may be larger in 4 cP fluid than in 1 cP fluid. Mean and standard deviations for all sonications at each pressure amplitude are shown.
Discussion
Microbubble Fragmentation and Inertial Cavitation
This study investigates the effect of the fluid viscosity on microbubble behaviour at high acoustic pressures. For the transmit pressures employed, ultra-high speed recordings have shown that individual microbubbles in 1 cP fluid undergo fragmentation (Figure 2). Direct optical evidence of bubble fragmentation has been previously observed for microbubbles situated with saline (1 cP), both for albumin (Bouakaz et al. 2005) and lipid (Chomas et al. 1999, 2001; Postema et al. 2004) encapsulated agents. Microbubble fragmentation is often considered as the result of surface instabilities; namely perturbations in microbubble shape from spherical symmetry with an amplitude that either abruptly increases (Storey 2001) or increases unabated with time against the stabilizing effects of surface tension and viscous forces (Brenner et al. 2002). Indeed, under small forcing amplitudes such that the amplitudes of non-spherical components remain small relative to D0, stable, non-spherical oscillations for un-encapsulated (Versluis et al. 2010) and encapsulated (Dollet et al. 2008; Vos et al. 2011) bubbles in 1 cP fluid have been observed. At larger pressure amplitudes, as in the present study, these parametric instabilities can quickly become more unstable, in some instances due to the re-bounding of a bubble that has previously undergone an initial explosive growth and violent collapse; consistent with the inertial cavitation framework (Apfel 1986; Flynn 1975a). It should be noted that in the present study, distinct, stable non-spherical shape oscillations were not observed, suggesting that a sudden surface instability on the order of nanoseconds (Rayleigh-Taylor instability) (Hilgenfeldt et al. 1996) may be the mechanism for bubble fragmentation.
Motivated primarily by sonoluminescence applications, there have been theoretical investigations into the effect of fluid viscosity on non-spherical bubble oscillations, indicating that the pressure threshold between stable and unstable perturbations (i.e. whether or not a bubble may fragment) can be significantly altered by fluid viscosity (Hao and Prosperetti 1999; Wu and Roberts 1998). For example, the pressure threshold for an un-encapsulated air bubble of D0=20 μm driven at 26.4 kHz in 4 cP fluid increases by approximately 30% as compared to that in 1 cP fluid (Wu and Roberts 1998). Encapsulated microbubbles driven in the MHz frequency range will likely result in more complex behavior, however the hypothesis that an increase in fluid viscosity serves to help stabilize non-spherical shape instabilities remains a plausible explanation for the observed differences in microbubble fragmentation propensity in the current study. Future studies on stable microbubble shape modes in both fluid environments, however, may help shed some insight into the interpretation of the results presented here.
For microbubbles in 4 cP fluid, much less fragmentation was observed (Figure 4). For sizes smaller than a given threshold diameter (D0<3.5 μm at 0.5 MPa and D0<3.0 μm at 1 MPa), the maximum relative expansion in 4 cP liquid is smaller than in the less viscid fluid (Figure 6), suggesting that these bubbles do not expand to large enough sizes to initiate fragmentation. However, the relative expansion exhibited above this threshold is similar in either fluid, and given that microbubbles fragment in 1 cP fluid and remain intact within 4 cP despite comparable relative expansions, this implies that Dmax/D0 may not be the only governing metric for fragmentation, and in particular that there may a size-dependency to its potential use as a threshold indicator for this behavior. Furthermore, the threshold diameter shifts towards a smaller diameter with increasing pressure – potentially due to nonlinear resonance phenomena (e.g. strain-softening system). In Vos et al. (Vos et al. 2011), the oscillation dynamics of microbubbles adjacent to a cellulose tube were examined with ultra-high speed imaging in two orthogonal imaging planes. It was shown that for large relative excursions (Dmax/D0 > 1.3), microbubbles may exhibit non-spherical oscillations perpendicular to the boundary. These perpendicularly-orientated non-spherical shape modes are not detectable in the present study, but may contribute to the propensity for a given bubble to fragment.
Aside from bubble fragmentation, microbubble disruption can also be achieved via ultrasound-induced gas diffusion (Chomas et al. 2001), a process that takes longer than a single ultra-high speed recording. The passive cavitation data highlights that for a given acoustic pressure, the amount of wideband emissions is substantially affected by fluid viscosity. This data is consistent with the high-speed study; however, as the passive cavitation data reflect emissions over a longer pulse (5000 cycles) than that used for the high speed recordings (8 cycles), it is also possible that gas diffusion mechanisms for bubble disruption were operative and affected by the surrounding fluid viscosity, for example, by affecting the likelihood of lipid shedding (Pu et al. 2006).
The effect of fluid viscosity on microbubble fragmentation (Figures 4 and 6) and inertial cavitation (Figure 7 and 8c) has implications on therapeutic applications that have been suggested to be initiated by such violet phenomena. Early work on un-encapsulated cavitation defines a minimum expansion criterion of after which bubble collapse is expected (Flynn 1975b; Leighton 1994). In considering Figure 6, it can be observed that for a fixed pressure and particular size range (e.g. D0>3.5 μm), a microbubble can exhibit similar maximum relative expansions while undergoing fragmentation in 1 cP fluid and remaining intact within 4 cP fluid. A study concluding successful drug/gene delivery, for example, as initiated from a bubble in this regime would consider the event due to inertial cavitation in an in-vitro setup. It may, however, be primarily a function of the maximum diameter achieved (Dmax/D0); a mechanism that has indeed been previously proposed to induce sonoporation (van Wamel et al. 2006). As such, this drug/gene delivery event would be correlated to stable cavitation in an in-vivo environment. It is therefore conceivable that the results gleaned from in-vitro studies on payload delivery efficiency with respect to the identification of stable or inertial cavitation as the dominant mechanism may be misinterpreted. In addition, the optimization of acoustic parameters for therapeutic studies as determined in-vitro may not represent the physical situation in a more viscid fluid. Figure 6 highlights, for example, that for the same acoustic conditions, a smaller microbubble (e.g. D0<3.5 μm) can exhibit a difference between 50–100% in maximum relative expansion for a given bubble situated in 1 cP fluid (inertial) to that in 4 cP fluid (stable). As shown in Figures 7 and 8c, the inertial cavitation threshold is significantly altered by the surrounding fluid viscosity, and therefore the optimal ultrasound conditions required to achieve such an oscillation regime may not translate readily.
Microbubble Stable Cavitation
In addition to inertial cavitation, these results show that stable cavitation is also affected by fluid viscosity at the transmit pressures employed. As indicated by the scattered power (Figure 8), under most of the acoustic conditions employed, the scattered emissions typically associated with stable cavitation were less in magnitude in 4 cP fluid than in 1 cP fluid. Indeed, linearized theory (i.e. low-pressure) predicts that an increase in the fluid viscosity is expected to dampen microbubble oscillations, primarily near resonance (Leighton 1994). At larger pressures, the effect of fluid viscosity on oscillation amplitude (fundamental and/or harmonic oscillations) becomes more complicated due to nonlinear resonance phenomena. It should be noted here that the integrated cavitation power as defined in Eq. (1) calculates the total scattered emission in a given frequency band over a specified time duration (Figure 7 and 8). While the presence of distinct peaks at the sub/super harmonics is often associated with stable cavitation, a portion of the energy contained within these bands can also be due to wideband emissions (when present) from a subset of microbubbles exhibiting inertial cavitation. It is conceivable that a significant portion of microbubbles in 1 cP fluid are exhibiting inertial cavitation (emissions over all frequencies) which, in addition to the subset that are exhibiting stable cavitation, results in a larger emission magnitude at a given frequency as compared to those situated in 4 cP fluid. In an attempt to isolate emissions due to stable cavitation, Figure 9 suggests that for larger pressures (≥ 0.5 MPa), microbubble populations exhibit stable cavitation to a greater degree in 4 cP fluid as compared to 1 cP fluid, consistent with ultra-high speed imaging results. Another aspect in this regard is revealed from Figure 2. The process of microbubble fragmentation is a subset of those that elicit inertial cavitation; however the resulting “daughter” bubbles may themselves undergo stable cavitation. Indeed, these daughter bubbles are often of comparable size to the original microbubble (second column in Figure 2). Furthermore, the resulting coalesced microbubble (third column in Figure 2) is often larger in size than the original microbubble, and may also undergo stable oscillations and contribute to the scattered emissions. Recent ultra-high speed recordings investigating microbubble dynamics in 1 cP fluid over long, therapeutic transmit pulses (e.g. 5 ms pulse duration at 1 MHz) has revealed that microbubble aggregates can persist throughout the insonication pulse, and were indeed shown to oscillate (Wang et al. 2012). The details of how microbubble aggregates and/or coalesced microbubbles respond to ultrasound remains unclear, for example whether these cavitation nuclei are encapsulated; however the aforementioned study highlights that cavitation nuclei do persist and therefore likely contribute to the scattered emissions recorded from PCD measurements. In order to robustly characterize the effects of viscosity on the stable cavitation regime, further investigation of individual microbubble dynamics situated in different viscous environments is warranted; and is indeed the subject of future work.
These stable cavitation results from Figures 7 and 9 have implications on therapeutic applications that may rely on stable microbubble activity. In drug and gene delivery studies for brain disease applications, for example, it has been determined through PCD experiments that stable cavitation, particularly the ultraharmonic (O’Reilly and Hynynen 2012) and second/third harmonic (McDannold et al. 2006) emissions, can correlate with successful BBB disruption. Many optimization studies have been performed in water/saline in vitro setups (O’Reilly et al. 2014) and animal models including mice (Choi et al. 2007), rats (O’Reilly et al. 2011), and non-human primates (Marquet et al. 2011); all of which contain microbubble populations diluted in a host liquid characterized by a different viscosity (Windberger et al. 2003). For payload delivery applications in cancer and/or vascular disease, previous studies have shown a transient increase in cell membrane permeability by use of microbubbles oscillating in a non-inertial regime (Kooiman et al. 2011; van Wamel et al. 2006). Sonothrombolysis studies have also suggested that stable cavitation, including ultraharmonic emissions, may play an important role in clot lysis (Borrelli et al. 2012; Datta et al. 2008). It is therefore important to interpret results from such studies with the surrounding fluid environment taken into account, as opposed to simply replicating optimal acoustic parameters obtained in one fluid medium to another.
Limitations
It should be noted here that the ultra-high speed microscopy recordings were performed on microbubbles adjacent to a polystyrene membrane. Microbubble radial oscillations (Garbin et al. 2007), scattered emissions (Helfield et al. 2014), and propensity to initiate surface mode oscillations (Dollet et al. 2008) can be altered by the presence of a boundary. An acknowledged limitation is the fact that the boundary effects themselves may be a function of fluid viscosity (i.e. the effects of fluid viscosity on a microbubble within an infinite medium may not equal the effects of fluid viscosity on a microbubble adjacent to a boundary). Indeed, in the limiting case of a rigid boundary, a microbubble adjacent to a boundary can be modeled through the method of images (Leighton 1994). Microbubble radial response is therefore altered by the scattered emissions from the “image” bubble, and these scattered emissions are itself a function of fluid viscosity. The extent to which the observed differences in microbubble behaviour within 1 cP and 4 cP are due to fluid viscosity-dependent microbubble behaviour (i.e. differences in fluid viscosity-based pressures at the bubble wall present in the Rayleigh-Plesset equation) versus due to fluid viscosity-dependent boundary effects (i.e. differences due to the scattered emissions from an image bubble) is not known.
The ultra-high speed imaging system recorded individual microbubble response over an 8-cycle pulse, while the passive cavitation detection studies were conducted on bubble populations over 5000 cycles. The direct link between datasets is therefore not straightforward; however general consistencies can be made, for example between propensity for fragmentation and wideband acoustic signatures.
Furthermore, the average apparent viscosity of blood in arterioles and venules is approximately 4 cP(Papaioannou and Stefanadis 2005; Rosenson et al. 1996), however in microvascular flow where the hematocrit percentage is low, the apparent viscosity may be adequately approximated by the viscosity of the plasma, approximately 1.5 cP(Pries et al. 1992).
Conclusions
The effect of viscosity on microbubble behavior subject to acoustic pressures from 0.25–1.5 MPa was investigated. Ultra-high speed recordings of individual microbubbles revealed that microbubble fragmentation propensity was lower in 4 cP fluid as compared to bubbles in 1 cP fluid. Passive cavitation detection on microbubble populations determined that as compared to 1 cP fluid, the pressure threshold for inertial cavitation was much higher in 4 cP fluid, and that stable cavitation emissions were generally higher in 4 cP fluid, potentially due to the decrease in bubble disruption. This study suggests that translating the results from in vitro studies conducted with microbubbles suspended in water/saline (1 cP) for use in vivo (4 cP) should be interpreted judiciously, both in terms of the optimization of ultrasound parameters and in the interpretation of the mechanisms of action.
Acknowledgments
This work was partly funded by the National Institutes of Health (R01EB016516), the Fonds de Recherche Natures et Technologies in Quebec, Canada, and the Center for Ultrasound Molecular Imaging and Therapeutics, University of Pittsburgh Medical Center, Pittsburgh, PA.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Acconcia C, Leung BYC, Manjunath A, Goertz DE. Interactions between individual ultrasound-stimulated microbubbles and fibrin clots. Ultrasound Med Biol. 2014;40:2134–2150. doi: 10.1016/j.ultrasmedbio.2014.03.008. [DOI] [PubMed] [Google Scholar]
- Allen JS, Roy RA, Church CC. On the Role of Shear Viscosity in Mediating Inertial Cavitation from Short-Pulse, Megahertz-Frequency Ultrasound. IEEE Trans Ultrason Ferroelectr Freq Control. 1997;44:743–751. [Google Scholar]
- Apfel RE. Possibility of microcavitation from diagnostic ultrasound. IEEE Trans Ultrason Ferroelectr Freq Control. 1986;33:139–42. doi: 10.1109/t-uffc.1986.26805. [DOI] [PubMed] [Google Scholar]
- Birnbaum Y, Luo H, Nagai T, Fishbein MC, Peterson TM, Li S, Kricsfeld D, Porter TR, Siegel RJ. Noninvasive in vivo clot dissolution without a thrombolytic drug: recanalization of thrombosed iliofemoral arteries by transcutaneous ultrasound combined with intravenous infusion of microbubbles. Circulation. 1998;97:130–134. doi: 10.1161/01.cir.97.2.130. [DOI] [PubMed] [Google Scholar]
- Bolten D, Turk M. Experimental study on the surface tension, density, and viscosity of aqueous poly( vinylpyrrolidone) solutions. J Chem Eng Data. 2011;56:582–588. [Google Scholar]
- Borrelli MJ, O’Brien WD, Hamilton E, Oelze ML, Wu J, Bernock LJ, Tung S, Rokadia H, Culp WC. Influences of microbubble diameter and ultrasonic parameters on in vitro sonothrombolysis efficacy. J Vasc Interv Radiol. 2012;23:1677–1684. doi: 10.1016/j.jvir.2012.08.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouakaz A, Versluis M, de Jong N. High-speed optical observations of contrast agent destruction. Ultrasound Med Biol. 2005;31:391–9. doi: 10.1016/j.ultrasmedbio.2004.12.004. [DOI] [PubMed] [Google Scholar]
- Brenner MP, Hilgenfeldt S, Lohse D. Single-bubble sonoluminescence. Rev Mod Phys. 2002;74:425–484. doi: 10.1103/PhysRevLett.77.3467. [DOI] [PubMed] [Google Scholar]
- Burgess A, Hynynen K. Drug delivery across the blood-brain barrier using focused ultrasound. Expert Opin Drug Deliv. 2014;11:711–721. doi: 10.1517/17425247.2014.897693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carson AR, McTiernan CF, Lavery L, Grata M, Leng X, Wang J, Chen X, Villanueva FS. Ultrasound-targeted microbubble destruction to deliver siRNA cancer therapy. Cancer Res. 2012;72:6191–6199. doi: 10.1158/0008-5472.CAN-11-4079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carson AR, McTiernan CF, Lavery L, Hodnick A, Grata M, Leng X, Wang J, Chen X, Modzelewski RA, Villanueva FS. Gene therapy of carcinoma using ultrasound-targeted microbubble destruction. Ultrasound Med Biol. 2011;37:393–402. doi: 10.1016/j.ultrasmedbio.2010.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Wang J, Versluis M, de Jong N, Villanueva FS. Ultra-fast bright field and fluorescence imaging of the dynamics of micrometer-sized objects. Rev Sci Instrum. 2013;84:063701. doi: 10.1063/1.4809168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi JJ, Pernot M, Small SA, Konofagou EE. Noninvasive, transcranial and localized opening of the blood-brain barrier using focused ultrasound in mice. Ultrasound Med Biol. 2007;33:95–104. doi: 10.1016/j.ultrasmedbio.2006.07.018. [DOI] [PubMed] [Google Scholar]
- Chomas J, Dayton P, Morgan K, Allen J, Ferrara K. Optimization of microbubble destruction. IEEE Ultrason Symp Proceedings Int Symp (Cat No99CH37027) 1999;2:1689–1692. [Google Scholar]
- Chomas JE, Dayton P, May D, Ferrara K. Threshold of fragmentation for ultrasonic contrast agents. J Biomed Opt. 2001;6:141–50. doi: 10.1117/1.1352752. [DOI] [PubMed] [Google Scholar]
- Christiansen JP, French Ba, Klibanov AL, Kaul S, Lindner JR. Targeted tissue transfection with ultrasound destruction of plasmid-bearing cationic microbubbles. Ultrasound Med Biol. 2003;29:1759–1767. doi: 10.1016/s0301-5629(03)00976-1. [DOI] [PubMed] [Google Scholar]
- Culp WC, Flores R, Brown AT, Lowery JD, Roberson PK, Hennings LJ, Woods SD, Hatton JH, Culp BC, Skinner RD, Borrelli MJ. Successful microbubble sonothrombolysis without tissue-type plasminogen activator in a rabbit model of acute ischemic stroke. Stroke. 2011;42:2280–5. doi: 10.1161/STROKEAHA.110.607150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Datta S, Coussios C-C, Ammi AY, Mast TD, de Courten-Myers GM, Holland CK. Ultrasound-enhanced thrombolysis using definity as a cavitation nucleation agent. Ultrasound Med Biol. 2008;34:1421–33. doi: 10.1016/j.ultrasmedbio.2008.01.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng C, Apfel RE, Holland CK. Inertial cavitation produced by pulsed ultrasound in controlled host media. J Acoust Soc Am. 1996;10:1199–1208. doi: 10.1121/1.416304. [DOI] [PubMed] [Google Scholar]
- Dollet B, van der Meer SM, Garbin V, de Jong N, Lohse D, Versluis M. Nonspherical oscillations of ultrasound contrast agent microbubbles. Ultrasound Med Biol. 2008;34:1465–73. doi: 10.1016/j.ultrasmedbio.2008.01.020. [DOI] [PubMed] [Google Scholar]
- Escoffre JM, Novell A, Serriere S, Lecomte T, Bouakaz A. Irinotecan Delivery by Microbubble-Assisted Ultrasound: In Vitro Validation and a Pilot Preclinical Study. Mol Pharm. 2013;10:2667–75. doi: 10.1021/mp400081b. [DOI] [PubMed] [Google Scholar]
- Fan Z, Chen D, Deng CX. Improving ultrasound gene transfection efficiency by controlling ultrasound excitation of microbubbles. J Control Release. 2013;170:401–13. doi: 10.1016/j.jconrel.2013.05.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flynn HG. Cavitation dynamics. I. A mathematical formulation. 1975a;57:1379–1396. [Google Scholar]
- Flynn HG. Cavitation dynamics. II. Free pulsations and models for cavitation bubbles. J Acoust Soc Am. 1975b;58:1160–1170. [Google Scholar]
- Forbes MM, Steinberg RL, O’Brien WD. Examination of inertial cavitation of optison in producing sonoporation of chinese hamster ovary cells. Ultrasound Med Biol. 2008;34:2009–18. doi: 10.1016/j.ultrasmedbio.2008.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garbin V, Cojoc D, Ferrari E, Di Fabrizio E, Overvelde MLJ, van der Meer SM, de Jong N, Lohse D, Versluis M. Changes in microbubble dynamics near a boundary revealed by combined optical micromanipulation and high-speed imaging. Appl Phys Lett. 2007;90:114103. [Google Scholar]
- Hallow DM, Mahajan AD, McCutchen TE, Prausnitz MR. Measurement and correlation of acoustic cavitation with cellular bioeffects. Ultrasound Med Biol. 2006;32:1111–22. doi: 10.1016/j.ultrasmedbio.2006.03.008. [DOI] [PubMed] [Google Scholar]
- Hao Y, Prosperetti A. The effect of viscosity on the spherical stability of oscillating gas bubbles. Phys Fluids. 1999;11:1309–1317. [Google Scholar]
- Helfield BL, Cherin E, Foster FS, Goertz DE. Investigating the subharmonic response of individual phospholipid encapsulated microbubbles at high frequencies: a comparative study of five agents. Ultrasound Med Biol. 2012;38:846–63. doi: 10.1016/j.ultrasmedbio.2012.01.011. [DOI] [PubMed] [Google Scholar]
- Helfield BL, Leung BYC, Goertz DE. The effect of boundary proximity on the response of individual ultrasound contrast agent microbubbles. Phys Med Biol. 2014;59:1721–1745. doi: 10.1088/0031-9155/59/7/1721. [DOI] [PubMed] [Google Scholar]
- Hilgenfeldt S, Lohse D, Brenner MP. Phase diagrams for sonoluminescing bubbles. Phys Fluids. 1996;8:2808–2826. [Google Scholar]
- Kang J, Wu X, Wang Z, Ran H, Xu C, Wu J, Wang Z, Zhang Y. Antitumor effect of docetaxel-loaded lipid microbubbles combined with ultrasound-targeted microbubble activation on VX2 rabbit liver tumors. J Ultrasound Med. 2010;29:61–70. doi: 10.7863/jum.2010.29.1.61. [DOI] [PubMed] [Google Scholar]
- Kinoshita M, Hynynen K. A novel method for the intracellular delivery of siRNA using microbubble-enhanced focused ultrasound. Biochem Biophys Res Commun. 2005;335:393–9. doi: 10.1016/j.bbrc.2005.07.101. [DOI] [PubMed] [Google Scholar]
- Kooiman K, Foppen-Harteveld M, van der Steen AFW, de Jong N. Sonoporation of endothelial cells by vibrating targeted microbubbles. J Control Release. 2011;154:35–41. doi: 10.1016/j.jconrel.2011.04.008. [DOI] [PubMed] [Google Scholar]
- Kotopoulis S, Dimcevski G, Gilja OH, Hoem D, Postema M. Treatment of human pancreatic cancer using combined ultrasound, microbubbles, and gemcitabine: A clinical case study Treatment of human pancreatic cancer using combined ultrasound, microbubbles, and gemcitabine: A clinical case study. 2013:072902. doi: 10.1118/1.4808149. [DOI] [PubMed] [Google Scholar]
- Leeman JE, Kim JS, Yu FTH, Chen X, Kim K, Wang J, Chen X, Villanueva FS, Pacella JJ. Effect of acoustic conditions on microbubble-mediated microvascular sonothrombolysis. Ultrasound Med Biol. 2012;38:1589–98. doi: 10.1016/j.ultrasmedbio.2012.05.020. [DOI] [PubMed] [Google Scholar]
- Leighton TG. The Acoustic Bubble. Academic Press; San Diego: 1994. [Google Scholar]
- Marquet F, Tung Y-S, Teichert T, Ferrera VP, Konofagou EE. Noninvasive, transient and selective blood-brain barrier opening in non-human primates in vivo. PLoS One. 2011;6:e22598. doi: 10.1371/journal.pone.0022598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDannold N, Vykhodtseva N, Hynynen K. Targeted disruption of the blood-brain barrier with focused ultrasound: association with cavitation activity. Phys Med Biol. 2006;51:793–807. doi: 10.1088/0031-9155/51/4/003. [DOI] [PubMed] [Google Scholar]
- Molina CA, Ribo M, Rubiera M, Montaner J, Santamarina E, Delgado-Mederos R, Arenillas JF, Huertas R, Purroy F, Delgado P, Alvarez-Sabin J. Microbubble administration accelerates clot lysis during continuous 2-MHz ultrasound monitoring in stroke patients treated with intravenous tissue plasminogen activator. Stroke. 2006;37:425–9. doi: 10.1161/01.STR.0000199064.94588.39. [DOI] [PubMed] [Google Scholar]
- O’Reilly MA, Hynynen K. Feedback-controlled focused ultrasound disruption by using an acoustic emissions – based controller. Radiology. 2012;263:96–106. doi: 10.1148/radiol.11111417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Reilly MA, Jones RM, Hynynen K. Three-dimensional transcranial ultrasound imaging of microbubble clouds using a sparse hemispherical array. IEEE Trans Biomed Eng. 2014;61:1285–94. doi: 10.1109/TBME.2014.2300838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Reilly MA, Waspe AC, Ganguly M, Hynynen K. Focused-ultrasound disruption of the blood-brain barrier using closely-timed short pulses: influence of sonication parameters and injection rate. Ultrasound Med Biol. 2011;37:587–594. doi: 10.1016/j.ultrasmedbio.2011.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pacella JJ, Brands J, Schnatz FG, Black JJ, Chen X, Villanueva FS. Treatment of microvascular micro-embolization using microbubbles and long-tone-burst ultrasound: an in vivo study. Ultrasound Med Biol. 2015;41:456–464. doi: 10.1016/j.ultrasmedbio.2014.09.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papaioannou TG, Stefanadis C. Vascular Wall Shear Stress: Basic Principles and Methods. Hell J Caridology. 2005;46:9–15. [PubMed] [Google Scholar]
- Park E, Zhang Y, Vykhodtseva N, Mcdannold N. Ultrasound-mediated blood-brain / blood-tumor barrier disruption improves outcomes with trastuzumab in a breast cancer brain metastasis model. J Control Release. 2012;163:277–284. doi: 10.1016/j.jconrel.2012.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Postema M, van Wamel A, Lancee CT, de Jong N. Ultrasound-induced encapsulated microbubble phenomena. Ultrasound Med Biol. 2004;30:827–40. doi: 10.1016/j.ultrasmedbio.2004.02.010. [DOI] [PubMed] [Google Scholar]
- Pries AR, Neuhaus D, Gaehtgens P. Blood viscosity in tube flow: dependence on diameter and hematocrit. Am J Physiol - Hear Circ Physiol. 1992;263:H1770–H1778. doi: 10.1152/ajpheart.1992.263.6.H1770. [DOI] [PubMed] [Google Scholar]
- Pu G, Borden Ma, Longo ML. Collapse and shedding transitions in binary lipid monolayers coating microbubbles. Langmuir. 2006;22:2993–9. doi: 10.1021/la0530337. [DOI] [PubMed] [Google Scholar]
- Rosenson RS, McCormick A, Uretz EF. Distribution of blood viscosity values and biochemical correlates in healthy adults. Clin Chem. 1996;42:1189–1195. [PubMed] [Google Scholar]
- Shutilov VA. Fundamental Physics of Ultrasound 1988. Gordon and Breach Science Publishers; Amsterdam: [Google Scholar]
- Soneson JE. A User-Friendly Software Package for HIFU Simulation. AIP Conference Proceedings, 8th International Symposium on Therapeutic Ultrasound; 2009; pp. 165–169. [Google Scholar]
- Sonka M, Hlavac V, Boyle R. Border detection as dynamic programming. Imaging Processing, Analysis and Machine Vision 1998; Cengage Learning [Google Scholar]
- Storey B. Shape stability of sonoluminescence bubbles: Comparison of theory to experiments. Phys Rev E. 2001;64:017301. doi: 10.1103/PhysRevE.64.017301. [DOI] [PubMed] [Google Scholar]
- Tachibana K, Tachibana S. Albumin microbubble echo-contrast material as an enhancer for ultrasound accelerated thrombolysis. Circulation. 1995;92:1148–1150. doi: 10.1161/01.cir.92.5.1148. [DOI] [PubMed] [Google Scholar]
- Tinkov S, Coester C, Serba S, Geis NA, Katus HA, Winter G, Bekeredjian R. New doxorubicin-loaded phospholipid microbubbles for targeted tumor therapy: in-vivo characterization. J Control Release. 2010;148:368–72. doi: 10.1016/j.jconrel.2010.09.004. [DOI] [PubMed] [Google Scholar]
- Tung Y, Vlachos F, Feshitan JA, Borden MA, Konofagou EE. The mechanism of interaction between focused ultrasound and microbubbles in blood-brain barrier opening in mice. J Acoust Soc Am. 2011;130:3059–3067. doi: 10.1121/1.3646905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Wamel A, Kooiman K, Harteveld M, Emmer M, ten Cate FJ, Versluis M, de Jong N. Vibrating microbubbles poking individual cells: drug transfer into cells via sonoporation. J Control Release. 2006;112:149–155. doi: 10.1016/j.jconrel.2006.02.007. [DOI] [PubMed] [Google Scholar]
- Versluis M, Goertz DE, Palanchon P, Heitman IL, van der Meer SM, Dollet B, de Jong N, Lohse D. Microbubble shape oscillations excited through ultrasonic parametric driving. Phys Rev E. 2010;82:026321. doi: 10.1103/PhysRevE.82.026321. [DOI] [PubMed] [Google Scholar]
- Vos HJ, Dollet B, Versluis M, de Jong N. Nonspherical shape oscillations of coated microbubbles in contact with a wall. Ultrasound Med Biol. 2011;37:935–48. doi: 10.1016/j.ultrasmedbio.2011.02.013. [DOI] [PubMed] [Google Scholar]
- Walker A, Naylor GP, Humphries WV. Measurement of blood viscosity using a conicylindrical viscometer. Med Biol Eng. 1976;14:551–557. doi: 10.1007/BF02478056. [DOI] [PubMed] [Google Scholar]
- Wang J, Chen X, Pacella JJ, Villanueva FS. Therapeutic potential of long ultrasound tone bursts in microbubble-ultrasound mediated therapeutics: mechanistic insights using high speed imaging. American Heart Association Scientific Sessions and Resuscitation Science Symposium; 2012. [Google Scholar]
- Wang S, Olumolade OO, Sun T, Samiotaki G, Konofagou EE. Noninvasive, neuron-specific gene therapy can be facilitated by focused ultrasound and recombinant adeno-associated virus. Gene Ther. 2015;22:104–110. doi: 10.1038/gt.2014.91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber-Adrian D, Thevenot E, O’Reilly M, Oakden W, Akens M, Ellens N, Markham-Coultes K, Burgess A, Finkelstein J, Yee A, Whyne C, Foust K, Kaspar B, Stanisz G, Chopra R, Hynynen K, Aubert I. Gene delivery to the spinal cord using MRI-guided focused ultrasound. Gene Ther. 2015;22:568–577. doi: 10.1038/gt.2015.25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weller GER, Villanueva FS, Klibanov AL, Wagner WR. Modulating targeted adhesion of an ultrasound contrast agent to dysfunctional endothelium. Ann Biomed Eng. 2002;30:1012–1019. doi: 10.1114/1.1513565. [DOI] [PubMed] [Google Scholar]
- Windberger U, Bartholovitsch A, Plasenzotti R, Korak KJ, Heinze G. Whole blood viscosity, plasma viscosity and erythrocyte aggregation in nine mammalian species: reference values and comparison of data. Exp Physiol. 2003;88:431–440. doi: 10.1113/eph8802496. [DOI] [PubMed] [Google Scholar]
- Wu CC, Roberts PH. Bubble shape instability and sonoluminescence. Phys Lett A. 1998;250:131–136. [Google Scholar]