Bayesian Approach for Flexible Modeling of Semicompeting Risks Data

Summary

Semicompeting risks data arise when two types of events, non-terminal and terminal, are observed. When the terminal event occurs first, it censors the non-terminal event, but not vice versa. To account for possible dependent censoring of the non-terminal event by the terminal event and to improve prediction of the terminal event using the non-terminal event information, it is crucial to model their association properly. Motivated by a breast cancer clinical trial data analysis, we extend the well-known illness-death models to allow flexible random effects to capture heterogeneous association structures in the data. Our extension also represents a generalization of the popular shared frailty models that usually assume that the non-terminal event does not affect the hazards of the terminal event beyond a frailty term. We propose a unified Bayesian modeling approach that can utilize existing software packages for both model fitting and individual specific event prediction. The approach is demonstrated via both simulation studies and a breast cancer data set analysis.

1. Introduction

Semicompeting risks data arise when two types of events, a non-terminal event and a terminal event are observed. When the terminal event occurs first, it censors the non-terminal event. Otherwise the terminal event can still be observed when the non-terminal event occurs first [1, 2]. This is in contrast to the well-known competing risks setting where occurrence of either of the two events precludes observation of the other (effectively censoring the failure times) so that only the first-occurring event is observable. More information about the event times is therefore contained in semicompeting risks data than typical competing risks data due to the possibility of continued observation of the terminal event after the non-terminal event. Consequently, this allows for modeling of the association between the non-terminal and terminal events without making unverifiable assumptions. Adequate modeling of the association is important to address the issue of dependent censoring of the non-terminal event by the terminal event [3, 4]. It also can allow modeling of the influence of the non-terminal event on the hazard of the terminal event and thus improve prediction of the terminal event [3].

Semicompeting risks data are frequently encountered. In oncology clinical trials, time to tumor progression and time to death of cancer patients from the date of randomization are typically recorded. It is generally expected that the two event times are strongly correlated. Main objectives of the trials usually include estimation of treatment effects on both of these events. When the time to death is the primary endpoint, there may also be great interest in predicting the overall survival based on disease progression to facilitate more efficient interim decisions in subsequent clinical trials [3]. It is therefore crucial to model the association between the two types of events adequately. Another semi-competing data example arises in AIDS treatment studies where the non-terminal event is first virologic failure and the terminal event is treatment discontinuation [5].

Semicompeting risks data have been popularly modeled using copula models [1, 2, 4, 6-14]. The copula model includes nonparametric components for the marginal distributions of the two types of events and an association parameter to accommodate dependence. However one contentious feature of the copula models is that the non-terminal event is specified as a latent failure time for any subject experiencing the terminal event first. Such a supposition is often considered unnatural in the classical competing risks setting [15], and those concerns carry over to the semi-competing risks setting. Xu et al. [15] suggested the well-known illness-death models to tackle both of these issues. Their approach not only allows for easy incorporation of covariates but also is based only on observable quantities; no latent event times are introduced. Their general illness-death models differentiate three types of hazards: hazard of illness, hazard of death without illness, and hazard of death with illness. Incorporation of covariates is achieved through proportional hazards modeling. Nonparametric maximum likelihood estimation (NPMLE) based on marginalized likelihood is used for inference.

Our research is motivated by randomized breast cancer clinical trial B-14 conducted by the National Surgical Adjuvant Breast and Bowel Project (NSABP) comparing the effect of tamoxifen with placebo on cancer recurrence [16, 17]. For each subject, the first recurrence at any anatomic site—be it local (or regional) or distant—is recorded. If a local recurrence occurs first, patients will continue to be followed up for the first recurrence at the distant location and hence both types of events may be observed. If distant metastasis was the first event, then reporting of additional local failure is not required; indeed, owing to likely clinical intervention upon detection of distant recurrence, the natural history of the local disease process would be interrupted. As such, local recurrence after distant recurrence will have a different biological and clinical interpretation than it will in the absence of distant recurrence. For these reasons, the data follow a semicompeting risks structure where the local failure is considered as non-terminal and distant failure as terminal [16]. Age and tumor size at baseline were also collected and are known prognostic factors for cancer recurrence. Our objectives are two-fold. The first is to estimate the effects of baseline variables treatment, age and tumor size on both local and distant recurrences. It is likely that the treatment effect may be quite different on local and distant recurrences. It is also conceivable that the treatment effects may be different on direct distant recurrences and on distant recurrences after local recurrences. As such, the second objective is to predict distant recurrences using baseline prognostic factors and, as time progresses, local recurrences as well. The association between local and distant recurrences may depend on patient's age and tumor characteristics. Proper modeling of such association can lead to improvement both in terms of estimation efficiency and prediction accuracy.

Xu et al. [15] used a single gamma frailty term to model the association between the non-terminal and terminal events mainly for mathematical convenience, as it leads to close-form expressions of the marginal likelihood. In addition to the restriction of using a single variable to capture all associations, it is also hard to extend the gamma frailty framework to incorporate covariates or random effects into modeling the association structure [18, 19]. For our purpose, we will extend the gamma frailty model to multivariate log-normal frailty models to analyze the motivating data set. The log-normal frailty models can easily incorporate covariates [18, 20-25]. Whereas our extension is theoretically straight-forward, our goal and contribution is to deal with multiple challenges arising in semi-competing risks and in our motivating example in a unified way.

Our extension also represents a generalization of the popular shared frailty models for joint modeling of non-terminal and terminal events [18, 19]. These shared frailty models can be restrictive because they usually assume that the effect of the non-terminal event on the terminal event hazard is captured solely by frailty terms. As a result, shared frailty models tend to put strong assumptions on the association structure and may be inadequate to capture relationships in the data due to time-varying processes leading to the non-terminal and terminal events, similar to the longitudinal data analysis setting [26]. In contrast, our general model assumes that the terminal event hazard function is possibly changed after experiencing the non-terminal event beyond what is accounted for by the frailty terms.

With the log-normal frailty model, it is unfortunately impossible to derive the marginal likelihood function in an explicit form, and as such, parameter estimation and inference relies on numerical algorithms [25]. In this paper, we propose using Bayesian Markov Chain Monte Carlo methods (MCMC) that have previously been applied in frailty models [23, 27-30]. The Bayesian paradigm provides a unified framework for carrying out estimation and predictive inferences. In particular, we show that computation and modeling can be simply implemented using existing software packages such as WinBUGS [31], JAGS [32], and Stan [33]. In section 2 we describe the model formulation. In section 3, we present details of the Bayesian analysis including prior specification, implementation of the MCMC, and computation using existing software packages. In section 4, we discuss individual specific prediction of the terminal event. In section 5, we present results from some simulation studies. In section 6, we conduct a thorough analysis of the motivating dataset. We end the article with a brief discussion.

2. Model and likelihood

Let T₁ be the time to the non-terminal event, e.g., disease progression (referred to as illness hereafter), T₂ be the time to the terminal event (referred as death hereafter), and C be the time to the censoring event (e.g. the end of a study or last follow-up assessment status). Observed variables consist of X₁ = T₁ ∧ T₂ ∧ C, X₂ = T₂ ∧ C, δ₁ = 1(T(₁ ≤ T₂ ∧ C), and δ₂ = 1(T₂ ≤ C). Note that T₂ can censor T₁ but not vice visa, whereas C can censor both T₁ and T₂, just T₂, or neither. In addition, a vector of covariates Z is observed. We assume that C is independent of the joint distribution of T₁ and T₂ given Z.

2.1 Models for semicompeting risks data

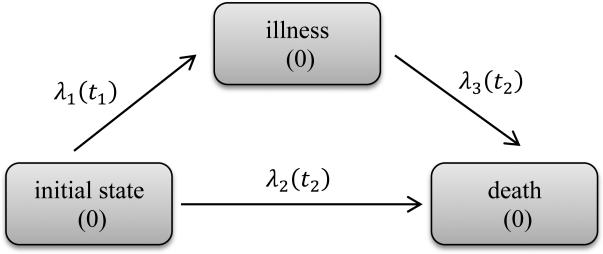
Semicompeting risks data such as these can be conveniently modeled using illness-death models [15]. These models assume individuals begin in an initial healthy state (state 0) from which they may transition to death (state 2) directly or may transit to an illness state (state 1) first and then to death (state 2) (see Figure 1). As in [15], the hazards or transition rates are defined as follows:

$$\mathrm{d}{\Lambda }_1\left({\mathrm{t}}_1\right)={\lambda }_1\left({\mathrm{t}}_1\right){\mathrm{dt}}_1=\mathrm{Pr}({\mathrm{t}}_1\le {\mathrm{T}}_1\le {\mathrm{t}}_1+{\mathrm{dt}}_1\mid {\mathrm{T}}_1\ge {\mathrm{t}}_1,{\mathrm{T}}_2\ge {\mathrm{t}}_1),{\mathrm{t}}_1>0$$ (1)

$$\mathrm{d}{\Lambda }_2\left({\mathrm{t}}_2\right)={\lambda }_2\left({\mathrm{t}}_2\right){\mathrm{dt}}_2=\mathrm{Pr}({\mathrm{t}}_2\le {\mathrm{T}}_2\le {\mathrm{t}}_2+{\mathrm{dt}}_2\mid {\mathrm{T}}_1\ge {\mathrm{t}}_2,{\mathrm{T}}_2\ge {\mathrm{t}}_2),{\mathrm{t}}_2>0$$ (2)

$$\mathrm{d}{\Lambda }_3({\mathrm{t}}_2\mid {\mathrm{t}}_1)={\lambda }_3({\mathrm{t}}_2\mid {\mathrm{t}}_1){\mathrm{dt}}_2=\mathrm{Pr}({\mathrm{t}}_2\le {\mathrm{T}}_2\le {\mathrm{t}}_2+{\mathrm{dt}}_2\mid {\mathrm{T}}_1={\mathrm{t}}_1,{\mathrm{T}}_2\ge {\mathrm{t}}_2),0<{\mathrm{t}}_1<{\mathrm{t}}_2$$ (3)

Equations (1) and (2) are the hazard functions for illness and death without illness, which are the competing risks part of the model. Equation (3) defines the hazard for death following illness. In general, λ₃(t₂|t₁) can depend on both t₁ and t₂. These equations define a semi-Markov model. When λ₃(t₂|t₁) = λ₃(t₂), the model becomes Markov. The ratio λ₃(t₂|t₁)/λ₂(t₂) partly explains the dependence between T₁ and T₂. When this ratio is 1, the occurrence of T₁ has no effect on the hazard of T₂. We refer models that force λ₃(t₂|t₁) = λ₂(t₂) as “restricted models” and models without this assumption as “general models”.

Figure 1.

Illness-death model framework

To account for the dependency structure between T₁ and T₂, Xu (2010) introduced a single shared gamma frailty term γ to capture association among λ₁(t₁), λ₂(t₂) and λ₃(t₂|t₁). Here we extend the association model using multivariate random effects. In particular, we specify the following conditional transition functions:

$${\lambda }_1({\mathrm{t}}_1\mid \mathrm{z},\mathrm{b})={\lambda }_{01}\left({\mathrm{t}}_1\right)\exp ({\mathrm{z}}^{\prime }{\beta }_1+{\tilde{\mathrm{z}}}^{\prime }\mathrm{b}),{\mathrm{t}}_1>0$$ (4)

$${\lambda }_2({\mathrm{t}}_2\mid \mathrm{z},\mathrm{b})={\lambda }_{02}\left({\mathrm{t}}_2\right)\exp ({\mathrm{z}}^{\prime }{\beta }_2+{\tilde{\mathrm{z}}}^{\prime }\mathrm{b}),{\mathrm{t}}_2>0$$ (5)

$${\lambda }_3({\mathrm{t}}_2\mid {\mathrm{t}}_1,\mathrm{z},\mathrm{b})={\lambda }_{03}({\mathrm{t}}_2\mid {\mathrm{t}}_1)\exp ({\mathrm{z}}^{\prime }{\beta }_3+{\tilde{\mathrm{z}}}^{\prime }\mathrm{b}),0<{\mathrm{t}}_1<{\mathrm{t}}_2$$ (6)

where λ₀₁(t₁), λ₀₂(t₂) and λ₀₃(t₂|t₁) are the unspecified baseline hazards; β₁, β₂ and β₃ are vectors of regression coefficients associated with each hazard; z̃ usually consists of 1 and a subset of covariates from z, and b represents random effects that account for possible associations among the three hazards λ₁(t₁|z, b), λ₂(t₂|z, b) and λ₃(t₂|t₁, z, b). For simplicity, hereafter we adopt the setting where the baseline hazard λ₀₃(t₂|t₁) does not depend on t₁. We assume a normal distribution for the random effects, b~N(0, Σ). The zero mean constraint is imposed so that the random effects represent deviations from population averages. The covariance matrix Σ is assumed to be unconstrained.

Models (4) - (6) allow multivariate random effects with arbitrary design matrix in the log relative risk. In its simplest form, when z̃ = 1, the frailty term b is reduced to a univariate random variable that accounts for the subject-specific dependency of three types of hazards. The models in Xu et al. (2010) belong to this simple case where they assume that exp(b) follows a gamma distribution. However, in many cases, random effects models that incorporate covariates such as clinical center may better account for the correlation structure in the data. Then the term z̃′b can be used to incorporate these random effects. For example, clustered semicompeting risks data frequently arise from oncology trials evaluating efficacies of different treatments. A typical model for this type of data is to have both subject-level and cluster-level frailty terms [23, 30].

Note that the general models allow much flexibility in model specification in case of prior scientific knowledge or data sparsity. For example, we can set λ₀₂(t₂) = λ₀₃(t₂) but still allow different coefficients for the fixed covariates in (5) and (6). The models can also easily incorporate time-dependent covariates. For example, if drug or behavioural interventions were administered to a subset of subjects after illness onset at t₁, then an intervention indicator can be incorporated into λ₃(t₂|t₁) in (6). However care must be given to identifiability issues. If all subjects receive the intervention immediately after illness, then the intervention effect is confounded with the baseline hazard λ₀₃(t₂). In this case, we need to put constraints on λ₀₃(t₂), e.g. λ₀₂(t₂) = λ₀₃(t₂), in order to estimate the drug effect.

2.2 Likelihood

For a subject i, we observe (x_1i, x_2i, δ_1i, δ_2i, z_i). Let N_1i(t) = 1(x_1i ≤ t, δ_1i = 1), N_2i(t) = 1(x_2i ≤ t, δ_1i = 0, δ_2i = 1), and N_3i(t) = 1(x_2i ≤ t, δ_1i = 1, δ_2i = 1) be the counting processes for the three event patterns. Correspondingly, let dN_ki(t) be the jump size of N_ki(t) at time t. Let R_1i(t) = 1(x_1i ≥ t), R_2i(t) = 1(x_1i ≥ t, x_2i ≥ t), and R_3i(t) = 1(x_2i ≥ t > x_1i) be the at-risk processes for the three event patterns. With the proportional hazards assumptions (4)-(6) the corresponding conditional (on b) likelihood is proportional to

$${\prod }_{\mathrm{i}=1}^{\mathrm{n}}{\prod }_{\mathrm{k}=1}^3\left\{{\prod }_{\mathrm{t}\ge 0}{\lambda }_{\mathrm{ki}}{(\mathrm{t}\mid \mathrm{z},\mathrm{b})}^{{\mathrm{dN}}_{\mathrm{ki}}\left(\mathrm{t}\right)}\exp \left[-{\int }_{\mathrm{t}=0}^{\infty }{\mathrm{R}}_{\mathrm{ki}}\left(\mathrm{t}\right){\lambda }_{\mathrm{ki}}(\mathrm{t}\mid \mathrm{z},\mathrm{b})\mathrm{dt}\right]\right\}$$ (7)

where ${\lambda }_{1\mathrm{i}}(\mathrm{t}\mid \mathrm{z},\mathrm{b})={\lambda }_{01}\left(\mathrm{t}\right)\exp ({\mathrm{z}}_{\mathrm{i}}^{\prime }{\beta }_1+{\tilde{\mathrm{z}}}_{\mathrm{i}}^{\prime }\mathrm{b})$, ${\lambda }_{2\mathrm{i}}(\mathrm{t}\mid \mathrm{z},\mathrm{b})={\lambda }_{02}\left(\mathrm{t}\right)\exp ({\mathrm{z}}_{\mathrm{i}}^{\prime }{\beta }_2+{\tilde{\mathrm{z}}}_{\mathrm{i}}^{\prime }\mathrm{b})$, and ${\lambda }_{3\mathrm{i}}(\mathrm{t}\mid \mathrm{z},\mathrm{b})={\lambda }_{03}\left(\mathrm{t}\right)\exp ({\mathrm{z}}_{\mathrm{i}}^{\prime }{\beta }_3+{\tilde{\mathrm{z}}}_{\mathrm{i}}^{\prime }\mathrm{b})$. Likelihood (7) follows from direct counting process formulation. We can view (7) as comprising Poisson kernels for the jumps of the counting processes dN_ki(t) with means of λ_ki(t)dt. That is dN_ki(t) ~ Poisson(λ_ki(t)dt). Note that with the restricted model where λ_3i(t|z, b) = λ_2i(t|z, b), the likelihood reduces to

$$\mathrm{L}=\prod _{\mathrm{i}=1}^{\mathrm{n}}{\left[{\lambda }_{01}\left({\mathrm{x}}_{1\mathrm{i}}\right){\mathrm{e}}^{{\mathrm{z}}_{\mathrm{i}}^{\prime }{\beta }_1+{\tilde{\mathrm{z}}}_{\mathrm{i}}^{\prime }{\mathrm{b}}_{\mathrm{i}}}\right]}^{{\delta }_{1\mathrm{i}}}\exp [-{\mathrm{e}}^{{\mathrm{z}}_{\mathrm{i}}^{\prime }{\beta }_1+{\tilde{\mathrm{z}}}_{\mathrm{i}}^{\prime }{\mathrm{b}}_{\mathrm{i}}}{\Lambda }_{01}\left({\mathrm{x}}_{1\mathrm{i}}\right)]\times \prod _{\mathrm{i}=1}^{\mathrm{n}}{\left[{\lambda }_{02}\left({\mathrm{x}}_{2\mathrm{i}}\right){\mathrm{e}}^{{\mathrm{z}}_{\mathrm{i}}^{\prime }{\beta }_2+{\tilde{\mathrm{z}}}_{\mathrm{i}}^{\prime }{\mathrm{b}}_{\mathrm{i}}}\right]}^{{\delta }_{2\mathrm{i}}}\exp \left[-{\mathrm{e}}^{{\mathrm{z}}_{\mathrm{i}}^{\prime }{\beta }_2+{\tilde{\mathrm{z}}}_{\mathrm{i}}^{\prime }{\mathrm{b}}_{\mathrm{i}}}{\Lambda }_{02}\left({\mathrm{x}}_{2\mathrm{i}}\right)\right]$$ (8)

The baseline hazard functions λ_0k(t) are left unspecified. Similar to Zeng and Lin (2007) [18], we take λ_0k(t) as a discrete function, or Λ_0k(t) as a step function, with increments or jumps occurring at the corresponding observed distinct failure time points. In other words, for Λ₀₁(t), its jump points are at those x_1i with δ_1i = 1; for Λ₀₂(t), its jump points are at those x_2i with δ_1i = 0 and δ_2i = 1; and for Λ₀₃(t), its jump points are at those x_2i with δ_1i = 1 and δ_2i = 1. The jump sizes are treated as parameters. When the sample sizes are small or the number of events is low, the need to estimate such a large number of parameters may lead to computational instability. In this case we can also model the baseline hazards from parametric distributions such as the exponential, Weibull, lognormal, etc. However, these parametric assumptions can be too restrictive. An attractive compromise is to adopt piecewise constant (PWC) baseline hazards models to approximate the unspecified baseline hazards, which may significantly reduce computational time [34]. For k = 1, 2, 3, the follow-up times are divided into J_k intervals with break points at s_k,0, s_k,1, ... , s_k,Jk where s_k,Jk equals or exceeds the largest observed times and s_k,0 = 0. Usually, s_k,j can be chosen according to percentiles of the observation period from the study design or according to the observed event times [35]. The baseline hazard function then takes values h_0k,j in the intervals (s_k,j–1, s_k,j] for j = 1, ... , J_k.

3. Bayesian approach

Estimation for frailty models can usually be conducted using either the expectation-maximization (EM) algorithm [18, 36-39] or MCMC methods [23, 27, 39-46]. When the EM algorithm is used, the unobserved random effects are treated as ‘missing values’ in the E step, which often involves intractable integrals. Monte Carlo methods have been used to approximate the integrals [19, 25, 39] but their implementation is not straightforward and usually needs to be treated on a case-by-case basis. For semi-competing risks data, involvement of different event types will make programming a daunting task that can easily discourage ordinary users. In addition, for prediction of future events, high order integration involving complicated functions of random effects is needed under the EM algorithm.

We propose Bayesian approaches for computation. The Bayesian framework is naturally suited to our setting with conditionally independent observations and hierarchical models. The Bayesian approach allows us to use existing software packages like WinBUGS [31], JAGS [32], and Stan [33] in which model fitting becomes very accessible to any user. For example, the program for WinBUGS only involved tens of lines of code (see the Supporting Web Materials).

In order to carry out the Bayesian analysis, we specify the prior distributions for various parameters as follows. Following Kalbfleisch [47], the priors for Λ_0k(t) are assigned as gamma processes with means ${\Lambda }_{0\mathrm{k}}^{\ast }\left(\mathrm{t}\right)$ and variances ${\Lambda }_{0\mathrm{k}}^{\ast }\left(\mathrm{t}\right)∕\mathrm{c}$, for k=1, 2, 3. The increments dΛ_0k(t) are distributed as independent gamma variables with shape and scale parameters $\mathrm{c}\times \mathrm{d}{\Lambda }_{0\mathrm{k}}^{\ast }\left(\mathrm{t}\right)$ and c, respectively. Here ${\Lambda }_{0\mathrm{k}}^{\ast }\left(\mathrm{t}\right)$ can be viewed as an initial estimate of Λ_0k(t). The scale c reflects the degree of belief in the prior specification with smaller values associated with higher levels of uncertainty. In our computation, we take c = 0.0001. For univariate censored survival data without any frailty term, the prior for Λ₀(t) has the virtue of being conjugate and the Bayes estimator (given β) for Λ₀(t) is a shrinkage estimator between the maximum likelihood estimate and the prior mean ${\Lambda }_0^{\ast }\left(\mathrm{t}\right)$ [27]. In our computation, we take the mean process ${\Lambda }_{0\mathrm{k}}^{\ast }\left(\mathrm{t}\right)$ to be proportional to time, that is, ${\Lambda }_{0\mathrm{k}}^{\ast }\left(\mathrm{t}\right)=\mathrm{rt}$ with r = 0.1. With this formulation, r can be considered as the mean baseline hazard rate. In actual fitting, we used gamma distribution priors as a result of the gamma process discretized on a pre-specified partition of the time interval [35, 48]. While it is common and popular to create the partition based on observed data, it is not fully legitimate within the Bayesian setting. The choices had minimal impact on our simulation studies.

For regression parameters, independent normal prior distributions are assigned ${\beta }_{\mathrm{k}}\sim \mathrm{N}(0,{\sigma }_{{\beta }_{\mathrm{k}}}^2{\mathrm{I}}_{\mathrm{k}})$ with I_k as the corresponding identity matrices for k = 1, 2, 3. Usually, large values of ${\sigma }_{{\beta }_{\mathrm{k}}}^2$ are used so that the prior distributions bear negligible weights on the analysis results. However relevant historical information about regression parameters can be incorporated into the prior distribution to enhance the analysis results.

Finally, we specify an inverse Wishart prior distribution for the unconstrained covariance matrix, Σ~ W⁻¹(V, d). The scale matrix V is often chosen to be an identity matrix multiplied by a scalar ν. The choice of ν is fairly arbitrary. The sensitivity of the results to changes of ν needs to be examined to ensure the prior distribution can leave considerable prior probabilities for extreme values of the variances terms. If we have evidence to assume no correlation among the random effects, diffuse priors can be directly specified on the diagonal elements of $\Sigma :{\sigma }_{\mathrm{g}}^2\sim \mathrm{G}({\mathrm{a}}_{\mathrm{g}},{\mathrm{b}}_{\mathrm{g}})$ for g = 1, ... . , d. With minimum prior information, we can choose a_g = 0.01 and b_g = 0.01.

For the piecewise constant baseline models, diffuse gamma distribution priors can be specified for h_0k,j, h_0k,j~G(a_j, b_j) for j = 1, ... . , J_k. With minimum prior information, we can choose a_j = 0.01 and b_j = 0.01.

Because the posterior distributions involve complex integrals and are computationally intractable, MCMC methods are used. The existing packages WinBUGS, JAGS, and Stan all led to similar results in our simulation studies. Our analysis was based on Stan version 1.1.0 [33], an open-source generic BUGS-style [49] package for obtaining Bayesian inference using the No-U-Turn sampler [50], a variant of the Hamiltonian Monte Carlo [51]. For complicated models with correlated parameters, the Hamiltonian Monte Carlo avoids the inefficient random walks used in simple MCMC algorithms such as the random-walk Metropolis [52] and Gibbs sampling [53] by taking a series of steps informed by first-order gradient information, and hence converges to high-dimensional target distributions more quickly. However we provide the WinBUGS program codes for the general models with Cox and PWC types of baseline hazards in the Supporting Web Materials due to the long-standing status of WinBUGS. Program codes for other packages are available upon request.

4. Prediction for terminal events

Within the Bayesian framework, it is straightforward to predict an individual's survival, which is often of great interest to both patients and physicians. Denote β = (β₁, β₂, β₃). The survival probability at time t* for a patient i with illness at x_1i < t* and still alive at x_2i < t* is

$$\int \mathrm{Pr}({\mathrm{T}}_{2\mathrm{i}}>{\mathrm{t}}^{\ast }\mid {\mathrm{T}}_{2\mathrm{i}}>{\mathrm{x}}_{2\mathrm{i}},{\mathrm{T}}_{1\mathrm{i}}={\mathrm{x}}_{1\mathrm{i}},{\mathrm{z}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}},\beta )\mathrm{f}({\mathrm{b}}_{\mathrm{i}},\beta \mid {\mathrm{T}}_{2\mathrm{i}}\ge {\mathrm{x}}_{2\mathrm{i}},{\mathrm{T}}_{1\mathrm{i}}={\mathrm{x}}_{1\mathrm{i}},{\mathrm{z}}_{\mathrm{i}}){\mathrm{db}}_{\mathrm{i}}\mathrm{d}\beta$$ (10)

The first term in the integrand of (10) is given in the Appendix. Direct evaluation of (10) can be very computationally challenging even when the dimension of b_i and β are only moderately high. Because we have draws of b_i and β from the posterior distribution, ${\mathrm{b}}_{\mathrm{i}}^{\left(\mathrm{m}\right)}$ and β^(m) for m = 1, ... , M, however, a straightforward approximation of (10) arises via a simple average with the following form: ${\mathrm{M}}^{-1}{\sum }_{\mathrm{m}=1}^{\mathrm{M}}\mathrm{Pr}({\mathrm{T}}_{2\mathrm{i}}>{\mathrm{t}}^{\ast }\mid {\mathrm{T}}_{1\mathrm{i}}={\mathrm{x}}_{1\mathrm{i}},{\mathrm{T}}_{2\mathrm{i}}\ge {\mathrm{x}}_{2\mathrm{i}},{\delta }_{1\mathrm{i}}=1,{\delta }_{2\mathrm{i}}=0,{\mathrm{z}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}}^{\left(\mathrm{m}\right)},{\beta }^{\left(\mathrm{m}\right)})$. Similarly the survival probability for terminal event at time t* for a patient i who is censored for both illness and death events at x_1i = x_2i is

$$\int \mathrm{Pr}({\mathrm{T}}_{2\mathrm{i}}>{\mathrm{t}}^{\ast }\mid {\mathrm{T}}_{2\mathrm{i}}\ge {\mathrm{x}}_{2\mathrm{i}},{\mathrm{T}}_{1\mathrm{i}}\ge {\mathrm{x}}_{1\mathrm{i}},{\mathrm{z}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}},\beta )\mathrm{f}({\mathrm{b}}_{\mathrm{i}},\beta \mid {\mathrm{T}}_{2\mathrm{i}}\ge {\mathrm{x}}_{2\mathrm{i}},{\mathrm{T}}_{1\mathrm{i}}\ge {\mathrm{x}}_{1\mathrm{i}},{\mathrm{z}}_{\mathrm{i}}){\mathrm{db}}_{\mathrm{i}}\mathrm{d}\beta$$ (11)

The first term in the integrand of (11) is also given in the Appendix. Again (11) may be approximated by ${\mathrm{M}}^{-1}{\sum }_{\mathrm{m}=1}^{\mathrm{M}}\mathrm{Pr}({\mathrm{T}}_{2\mathrm{i}}>{\mathrm{t}}^{\ast }\mid {\mathrm{T}}_{1\mathrm{i}}\ge {\mathrm{x}}_{1\mathrm{i}},{\mathrm{T}}_{2\mathrm{i}}\ge {\mathrm{x}}_{2\mathrm{i}},{\delta }_{1\mathrm{i}}=0,{\delta }_{2\mathrm{i}}=0,{\mathrm{z}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}}^{\left(\mathrm{m}\right)},{\beta }^{\left(\mathrm{m}\right)})$.

5. Simulation study

To evaluate the performances of the various proposed models, we generated simulated datasets with various sample sizes (n = 100, 250, 600) based on either the restricted or the general models. The simulated datasets were then analysed using proposed models. In particular, we generated data according to models (4) - (6) with various baseline models or regression coefficients. Weibull distributions were used to generate the baseline hazard functions to represent non-uniform baseline hazards that may be encountered in practice. Specifically, for simulating data from general models, we chose λ₀₁(t) = λ₀₂(t) = 1.25t^0.25 and λ₀₃(t) = 2.5t^0.25. For simulating data from the restricted models, we chose λ₀₁(t) = λ₀₂(t) = λ₀₃(t) = 1.25t^0.25. Following Xu et. al. [15], the censoring time C was simulated from a 50:50 mixture distribution of a uniform distribution on (1.5, 3) and a point mass at 3.

A fixed covariate Z₁~ unif(0, 2) was applied to all three types of hazards, with corresponding coefficients β₁ = β₂ = 1.0 and β₃ = 0.5 for simulating data from general models, and β₁ = 1.0, β₂ = β₃ = 0.8 for simulating data from the restricted models, respectively. Random effects were incorporated using Z₂ = 1 and Z₃~ unif(0, 3) with the corresponding random effects generated independently using normal distributions with variances ${\sigma }_1^2=1.0$ and ${\sigma }_2^2=2.0$ respectively. With such simulation settings, around 50% patients will experience illness, death before illness, or death after illness by the end of study.

Data analyses were conducted using the general models with Cox-type and PWC baseline hazards and the restricted models with Cox-type baseline hazards. With gamma process priors, we refer to these models as the Cox general model, the PWC general model, and the Cox restricted model respectively. We report results from 500 replications. The results are summarized in Table 1. The average posterior mean (Mean), the standard deviation (SD) of the posterior mean, the average standard deviation of the posterior distribution (ESE), and the coverage probabilities of the 95% credible intervals (CP) are listed in the table.

Table 1.

Simulation results comparing various models

True model	n	parameter	Truth	General PWC model				General Cox model				Restricted Cox model
				Mean	SD	ESE	CP	Mean	SD	ESE	CP	Mean	SD	ESE	CP
Restricted model	250	β 1	1	1.01	0.26	0.27	0.95	1.05	0.29	0.29	0.95	1.02	0.26	0.26	0.94
		β 2	0.8	0.81	0.28	0.28	0.95	0.84	0.31	0.30	0.95	0.81	0.24	0.23	0.94
		β 3	0.8	0.79	0.31	0.31	0.95	0.83	0.34	0.33	0.94	0.81	0.24	0.23	0.94
		${\sigma }_1^2$	1	1.16	0.69	0.66	0.91	1.29	0.86	0.79	0.91	1.10	0.56	0.49	0.91
		${\sigma }_2^2$	0.8	0.77	0.27	0.27	0.94	0.90	0.38	0.35	0.92	0.83	0.25	0.24	0.95
General model	100	β 1	1	1.04	0.43	0.43	0.94	1.21	0.55	0.55	0.93	1.11	0.47	0.47	0.93
		β 2	1	1.04	0.45	0.43	0.95	1.22	0.57	0.55	0.94	0.97	0.45	0.42	0.96
		β 3	0.5	0.58	0.51	0.49	0.94	0.75	0.62	0.60	0.94	0.97	0.45	0.42	0.77
		${\sigma }_1^2$	1	1.36	1.07	1.03	0.92	2.33	2.10	1.96	0.93	1.71	1.23	1.13	0.90
		${\sigma }_2^2$	0.8	0.77	0.40	0.40	0.93	1.26	0.89	0.83	0.93	1.05	0.60	0.53	0.92
	250	β 1	1	1.02	0.27	0.28	0.96	1.07	0.31	0.31	0.94	1.08	0.28	0.28	0.94
		β 2	1	1.01	0.28	0.28	0.95	1.06	0.32	0.31	0.93	0.90	0.27	0.25	0.91
		β 3	0.5	0.49	0.32	0.31	0.94	0.55	0.35	0.34	0.93	0.90	0.27	0.25	0.62
		${\sigma }_1^2$	1	1.19	0.75	0.70	0.94	1.40	1.02	0.88	0.89	1.49	0.70	0.62	0.87
		${\sigma }_2^2$	0.8	0.77	0.27	0.28	0.94	0.94	0.43	0.39	0.91	0.95	0.29	0.29	0.93
	600	β 1	1	1.00	0.18	0.19	0.96	1.01	0.19	0.19	0.95	1.04	0.18	0.18	0.95
		β 2	1	0.99	0.18	0.19	0.96	1.01	0.20	0.19	0.95	0.89	0.17	0.16	0.87
		β 3	0.5	0.49	0.20	0.21	0.95	0.52	0.22	0.21	0.95	0.89	0.17	0.16	0.31
		${\sigma }_1^2$	1	1.06	0.49	0.46	0.94	1.14	0.57	0.51	0.93	1.38	0.37	0.36	0.81
		${\sigma }_2^2$	0.8	0.79	0.20	0.20	0.95	0.86	0.25	0.23	0.93	0.94	0.18	0.18	0.88

For data generated from the restricted model with n = 250, we can see that the Cox restricted model fitted well with very small biases for both regression coefficients and variance estimates of the random effects. When analysed using the Cox and 10-piece PWC general models, the fitted values from all models agreed well with the true values. Unsurprisingly, the magnitudes of SD or ESE were larger for ${\sigma }_1^2$, ${\sigma }_2^2$, β₂, and β₃ when compared with those from the Cox restricted models.

For data generated from the general model with n = 250 and n = 600, the general models fitted well with very small biases for both regression coefficients and variance parameters of two random effects. Compared with the PWC general model, the Cox general model had larger ESEs and SDs. When analysed using the Cox restricted model, relatively larger biases were observed. Because the Cox restricted model used the same hazard parameter for the two types of terminal hazards, the resulting average posterior mean of the regression coefficient fell between the true values of β₂ and β₃. On the other hand, the biases for β₁ were small. We think this was likely due to factorization of the likelihood into a part that involves only β₁ and another part involving both β₂ and β₃. The β₁ part takes the same form in both the restricted and the general models.

We further simulated data under the general model with sample size n = 100. In this small sample size setting, the general model still performed relatively well, especially when the 5-piece PWC model was used. The biases were larger, especially for the variance components under the Cox model. The main reason for this was the sparsity of events with such small sample sizes and the complexity of the Cox model. When 10-piece PWC models were used, biases of similar magnitudes to Cox model were observed (data not shown).

We used Stan to perform all the simulations. With 10,000 posterior samples and 2,000 burn-in iterations, it took an average of 7.3 minutes for the PWC models with 20 pieces and 39.5 minutes for the Cox models to fit each replicate with n=600 on a Linux server with 2.40GHz Intel Xeon(R) E7340 CPU and 4.0 GB RAM. Three multiple chains were run in parallel and the method of Gelman-Rubin was used for convergence diagnosis [54].

6. Application to the breast cancer data

Between 1982 and 1988, 2892 women with estrogen receptor-positive breast tumors and no auxiliary node involvement were enrolled in NSABP Protocol B-14, a double-blind randomized trial comparing 5 years of tamoxifen (10 mg b.i.d.) with placebo [16, 17]. Among 2850 patients with follow-up times of at least 6 months before any events, 1424 and 1426 patients received placebo and tamoxifen, respectively. A total of 237 patients had local recurrence and 93 of these patients further developed distant metastasis. An additional 428 patients experienced distant recurrence without prior local failure for a total of 521 patients with distant metastasis events. Second primary cancers and non-cancer deaths are treated as independent censoring on recurrence. This dataset was previously analyzed using missing data approach for semicompeting risks data [16], where the occurrence of non-terminal event was assumed not to change the hazard of the terminal event. We report results from model fitting using Cox type baseline hazards. Corresponding PWC baseline hazards gave very similar results.

6.1 Results from restricted models

We first fitted a Cox restricted model with random intercept to compare the effect of the treatment. Covariates considered were age and tumor size at randomization. The results are summarized in Table 2. As compared with placebo, tamoxifen significantly reduced both local and distant recurrences with estimated log hazard ratios of −1.274 (95% credible interval (CI): −1.642, −0.938) and −0.713 (95% CI: −1.019, −0.012), respectively. Our results confirmed substantial effect of tamoxifen from [16]. There also seem to be differential effects of the treatment on the two types of recurrence.

Table 2.

NSABP B-14 data analysis based on various restricted models

	Local occurrence				Distant occurrence
	Mean	SD	2.5%	97.5%	Mean	SD	2.5%	97.5%
Random intercept Cox restricted model
Regression coefficients
Age	−0.04	0.008	−0.056	−0.024	−0.026	0.007	−0.039	−0.012
Treat	−1.274	0.183	−1.642	−0.938	−0.713	0.145	−1.019	−0.443
Tumor size	0.037	0.007	0.025	0.051	0.042	0.006	0.03	0.053
Variance of random effect
Intercept	4.36	0.676	3.223	5.887
Multivariate random effects Cox restricted model
Regression coefficients
Age	−0.036	0.013	−0.061	−0.01	−0.02	0.013	−0.046	0.005
Treat	−1.425	0.214	−1.874	−1.023	−0.843	0.175	−1.175	−0.504
Tumor size	0.041	0.011	0.021	0.063	0.043	0.01	0.024	0.062
Variances of random effects
Intercept	4.264	0.813	2.676	5.899
Age	0.024	0.003	0.018	0.032
Tumor size	0.018	0.003	0.014	0.024

According to Table 2, both age and tumor size had substantial effects on recurrences. Younger women had greater chance of recurrence. It is known that younger women usually have worse prognosis, as younger age at onset is associated with more aggressive tumor types. Every increase of 10 years in age led to a reduction of local recurrence with an estimated log hazard ratio of −0.4 (95% CI: −0.56, −0.24) and of distant failure with an estimated hazard ratio of −0.26 (95% CI: −0.39, −0.12). An increase in the tumor size also resulted in significant increases of hazard rates for both recurrence types. The estimated variance of the frailty term is 4.360 (95% CI: 3.223, 5.887), indicating a strong association between the local and distant recurrences. This is consistent with a large observed percentage of distant recurrences among patients with local recurrences. There were 39.2% of patients with local failures further developed distant failures whereas 16.4 % of patients without local failures developed distant failures.

We next fitted a Cox restricted model that incorporated intercept, age and tumor size to the random effects. The results are also shown in Table 2. An unstructured matrix was used for the variance-covariance of the random effects. The posterior means of covariance were found to be rather close to zero (data not shown), indicating minimum correlation among the random effects. The variances for the random intercept, age and tumor size were 4.264, 0.024 and 0.018, respectively, with 95% CIs of (2.676, 5.899), (0.018, 0.032), and (0.014, 0.024) respectively. The posterior means of the log-hazard ratios of the treatment were −1.425 and −0.843 for the local and distant recurrences respectively.

6.2 Results from general models

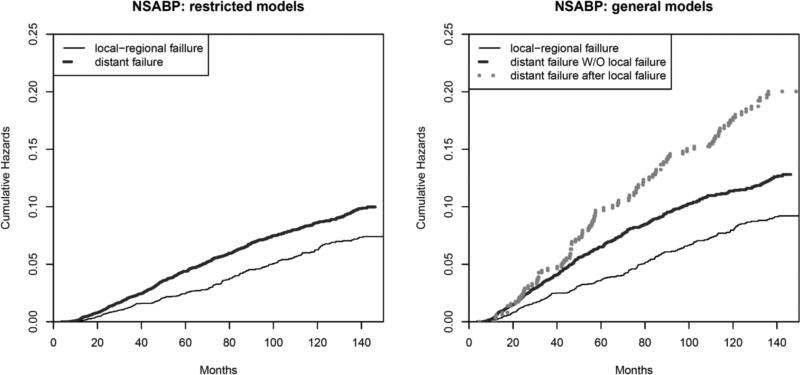
We fitted the random intercept Cox and the multivariate random effects Cox general models with results presented in Table 3. Based on the random intercept Cox model, the estimated cumulative baseline hazards are plotted in Figure 2. In addition, for comparison, the estimated cumulative baseline hazards based on restricted models are plotted in the same figure. Notice that the restricted models do not distinguish the two types of hazards for the terminal events while the general models do. The cumulative hazards for distant failure with and without local recurrence are quite similar before 40 months, but then diverge from each other. The variance of the random intercept is 2.617 with a standard deviation of 1.143, which is smaller than that from the restricted model, possibly because the dependence of T₂ on T₁ may partly be captured by the different baseline hazard functions λ₀₂(t₂) and λ₀₃(t₂).

Table 3.

NSABP B-14 data analysis based on various general models

					Distant Recurrence
	Local Recurrence				Without local recurrence				After local recurrence
	Mean	SD	2.5%	97.5%	Mean	SD	2.5%	97.5%	Mean	SD	2.5%	97.5%
Random intercept Cox general model
Regression coefficients
Age	−0.035	0.008	−0.051	−0.018	−0.022	0.007	−0.037	−0.010	−0.007	0.015	−0.036	0.023
Treat	−1.130	0.181	−1.512	−0.802	−0.616	0.153	−0.949	−0.340	0.051	0.332	−0.571	0.705
Tumor size	0.03	0.008	0.017	0.046	0.035	0.007	0.024	0.049	0.028	0.013	0.004	0.055
Variance of random effect
Intercept	2.617	1.143	1.025	5.353
Multivariate random effects Cox general model
Regression coefficients
Age	−0.043	0.017	−0.077	−0.012	−0.029	0.016	−0.063	0.001	−0.005	0.023	−0.050	0.041
Treat	−1.723	0.252	−2.242	−1.236	−1.190	0.223	−1.648	−0.766	−0.563	0.416	−1.370	0.215
Tumor size	0.052	0.014	0.025	0.079	0.055	0.014	0.028	0.083	0.05	0.019	0.010	0.087
Variances of random effects
Intercept	8.733	1.693	5.753	12.619
Age	0.032	0.006	0.022	0.044
Tumor size	0.023	0.004	0.017	0.031

Figure 2.

The estimated baseline cumulative hazards for the NSABP B-14 dataset based on the random intercept Cox restricted (left) and the random intercept Cox general models (right).

Based on the random intercept Cox general model, tamoxifen significantly reduced the local recurrence with an estimated log hazard ratio of −1.130 (95% CI: −1.512, −0.802). Tamoxifen also had a significant effect on distant recurrence without local failure with an estimated log hazard ratio of −0.616 (95% CI: −0.949, −0.340). However, tamoxifen showed no effect in reducing distant recurrence following local failure. This is possibly because once a tumor has demonstrated ability to recur locally despite tamoxifen, then the treatment is also less likely to reduce risk of distant failure. The increase in tumor size had comparable effects of increased risk on all three types of recurrences. On the other hand, age had significant effects on both local and distant failure without local recurrence, but no significant effect on distant recurrence following local failure, indicating an age-independent metastatic rate after local failure.

For the multivariate random effects Cox general model, the standard deviations (SDs) for the posterior distribution of the variance of random effects are relatively small, as compared with the mean estimate (mean/SD ratio is larger than 5). The correlations among the three random effects were negligible. There were noticeable changes for the mean and SD values of the regression coefficients due to the inclusion of different random effects in the two models. To determine which model is preferred, we used the Deviance Information Criteria (DIC) [55] which is defined as the sum of the posterior expectation of deviance function D̄, and the effective number of parameters p_D. Smaller values of D̄ indicate better fit and smaller values of p_D indicate more parsimonious model. Models with smaller values of DIC are preferred. With the Bayesian approach, DIC can be easily calculated from posterior distributions. Table 4 reports these quantities for various Cox models. For both restricted and general models, including random effects for age and tumor size resulted in reduction of the DIC. In addition, general models have smaller DIC than the corresponding restricted models. In particular, the multivariate random effects Cox general model yielded smallest DIC and is therefore preferred.

Table 4.

Bayesian model selection based on DIC

Model	Random effects	D̄	pD	DIC
Restricted	Intercept only	11593.6	1507.02	13100.6
	Intercept, age, tumor size	11154.2	1555.14	12709.3
General	Intercept only	11620.9	1431.46	13051.7
	Intercept, age, tumor size	10378.2	1631.73	12009.9

6.3 Predicting distant recurrences

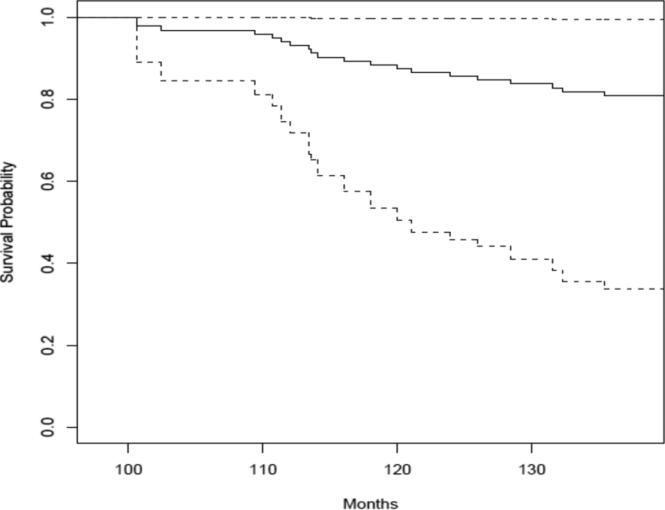
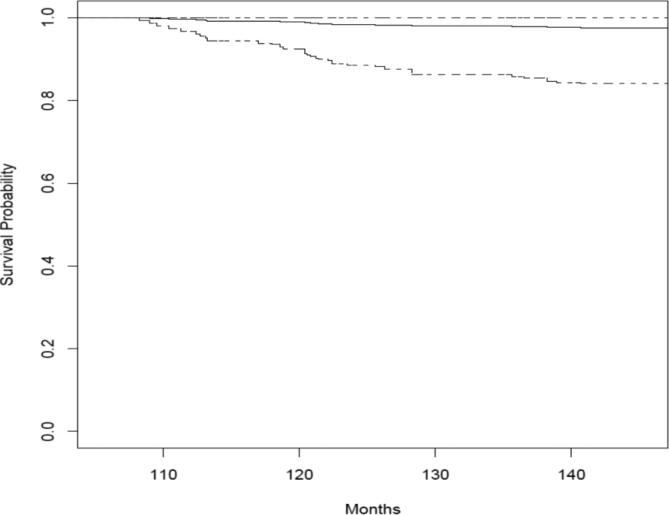
With posterior samples for regression parameters and frailty terms, the prediction of future events for subjects that are censored for local and/or distant recurrence is straightforward. Based on formulae (10) and (11), we illustrate the predictions of the survival probabilities for distant recurrence using two selected individuals, one with δ_li = 1 and δ_2i = 0, the other with δ_1i = δ_2i = 0. The prediction was based on the multivariate random effects Cox general model. The results are in Figures 3 and 4. Figure 3 is for a patient treated with tamoxifen, aged 35 at the time of randomization with a tumor size of 20 mm. The patient experienced local recurrence at 49 month and censored at 100.6 month for distant recurrence. Figure 4 is for a patient treated with placebo, aged 61 at the time of randomization with a tumor size of 33 mm. The patient was censored at 107.9 months.

Figure 3.

Prediction of the distant recurrence survival probability for a patient who experienced the local failure. The prediction was based on the multivariate random effects Cox general model. The posterior mean is the solid line while the 2.5% and 97.5% quartiles are dashed lines.

Figure 4.

Prediction of the distant recurrence survival probability for a patient who did not experience the local failure. The prediction was based on the multivariate random effects Cox general model. The posterior mean is the solid line while the 2.5% and 97.5% quartiles are the dashed lines.

7. Discussion

We have developed flexible frailty models for semicompeting risks data. Our models can incorporate different covariates into the frailty terms for three different types of hazard functions corresponding to the illness, death without illness, and death after illness. Our methods extended the gamma frailty models by Xu et al. (2010) which used a single frailty term to correlate the events and did not consider covariates for the frailty term. In clinical trial settings, this model will help address important questions such as whether continuing treatment is still beneficial for the terminal event after the occurrence of the non-terminal event. We used Bayesian methods for estimation. Our choice over the EM algorithm was mainly computational. With the development of general purpose software packages such as WinBUGS, JAGS and Stan, implementation of the Bayesian approach and model based predictions became very straightforward. Our models will also work with clustered data [23, 40]. Further they can be extended to other frailty models such as correlated frailty models [23]. We are also adapting our approach to the joint modeling of semicompeting risks data with longitudinally observed biomarker data.

APPENDIX Prediction of survival probability for individual patients

With Bayesian framework, it is straightforward to predict an individual's future event on the basis of his or her event history. First we prove the following two formulae that are generally true for the illness-death hazard models based on (1)-(3).

$$\mathrm{P}({\mathrm{T}}_{1\mathrm{i}}\ge {\mathrm{x}}_{1\mathrm{i}},{\mathrm{T}}_{2\mathrm{i}}\ge {\mathrm{x}}_{1\mathrm{i}})={\mathrm{e}}^{-{\Lambda }_1\left({\mathrm{x}}_{1\mathrm{i}}\right)-{\Lambda }_2\left({\mathrm{x}}_{1\mathrm{i}}\right)}$$ (A.1)

$$\mathrm{P}({\mathrm{T}}_{1\mathrm{i}}={\mathrm{x}}_{1\mathrm{i}},{\mathrm{T}}_{2\mathrm{i}}\ge {\mathrm{x}}_{2\mathrm{i}})={\lambda }_1\left({\mathrm{x}}_{1\mathrm{i}}\right){\mathrm{e}}^{-{\Lambda }_1\left({\mathrm{x}}_{1\mathrm{i}}\right)-{\Lambda }_2\left({\mathrm{x}}_{1\mathrm{i}}\right)-{\Lambda }_3({\mathrm{x}}_{2\mathrm{i}}\mid {\mathrm{x}}_{1\mathrm{i}})+{\Lambda }_3({\mathrm{x}}_{1\mathrm{i}}\mid {\mathrm{x}}_{1\mathrm{i}})}.$$ (A.2)

For (A.1), we can add (1) and (2) evaluated at a particular time point t to obtain

$$\mathrm{d}{\Lambda }_1\left(\mathrm{t}\right)+\mathrm{d}{\Lambda }_2\left(\mathrm{t}\right)=\mathrm{Pr}(\mathrm{t}\le {\mathrm{T}}_1\Lambda {\mathrm{T}}_2\le \mathrm{t}+\mathrm{dt}\mid {\mathrm{T}}_1\ge \mathrm{t},{\mathrm{T}}_2\ge \mathrm{t})$$

So the hazard function of T₁ ∧ T₂ is dΛ₁(t) + dΛ₂(t) which immediately leads to (A.1). Now from (1), we can further obtain

$$\mathrm{P}({\mathrm{T}}_1=t,{\mathrm{T}}_2\ge t)={\lambda }_1\left(t\right){\mathrm{e}}^{-{\Lambda }_1\left(t\right)-{\Lambda }_2\left(t\right)}.$$ (A.3)

From (3), we can obtain

$$\mathrm{P}({\mathrm{T}}_1={\mathrm{t}}_1,{\mathrm{T}}_2\ge {\mathrm{t}}_2)=\mathrm{P}({\mathrm{T}}_1={\mathrm{t}}_1,{\mathrm{T}}_2\ge {\mathrm{t}}_1){\mathrm{e}}^{-{\Lambda }_3({\mathrm{t}}_2\mid {\mathrm{t}}_1)+{\Lambda }_3({\mathrm{t}}_1\mid {\mathrm{t}}_1)}.$$ (A.4)

From (A.3) and (A.4) we have (A.2).

Now denote β = (β₁, β₂, β₃). The conditional survival probability at time t* for a patient with illness at x_1i < t* and censored for death at x_2i < t* is

$$\mathrm{Pr}({\mathrm{T}}_{2\mathrm{i}}>{\mathrm{t}}^{\ast }\mid {\mathrm{T}}_{1\mathrm{i}}={\mathrm{x}}_{1\mathrm{i}},{\mathrm{T}}_{2\mathrm{i}}\ge {\mathrm{x}}_{2\mathrm{i}},{\delta }_{1\mathrm{i}}=1,{\delta }_{2\mathrm{i}}=0,{\mathrm{z}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}},\beta )=\frac{\mathrm{Pr}({\mathrm{T}}_{1\mathrm{i}}={\mathrm{x}}_{1\mathrm{i}},{\mathrm{T}}_{2\mathrm{i}}>{\mathrm{t}}^{\ast }\mid {\mathrm{z}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}},\beta )}{\mathrm{Pr}({\mathrm{T}}_{1\mathrm{i}}={\mathrm{x}}_{1\mathrm{i}},{\mathrm{T}}_{2\mathrm{i}}\ge {\mathrm{x}}_{2\mathrm{i}}\mid {\mathrm{z}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}},\beta )}={\mathrm{e}}^{-{\Lambda }_3({\mathrm{t}}^{\ast }\mid {\mathrm{x}}_{1\mathrm{i}},{\mathrm{z}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}},\beta )+{\Lambda }_3({\mathrm{x}}_{2\mathrm{i}}\mid {\mathrm{x}}_{1\mathrm{i}},{\mathrm{z}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}},\beta )}$$

Here the last equality used (A.2). By plugging the frailty model (6), we have

$$\mathrm{Pr}({\mathrm{T}}_{2\mathrm{i}}>{\mathrm{t}}^{\ast }\mid {\mathrm{T}}_{1\mathrm{i}}={\mathrm{x}}_{1\mathrm{i}},{\mathrm{T}}_{2\mathrm{i}}\ge {\mathrm{x}}_{2\mathrm{i}},{\delta }_{1\mathrm{i}}=1,{\delta }_{2\mathrm{i}}=0,{\mathrm{z}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}},\beta )=\exp \left[-\{{\Lambda }_{03}\left({\mathrm{t}}^{\ast }\right)-{\Lambda }_{03}\left({\mathrm{x}}_{2\mathrm{i}}\right)\}{\mathrm{e}}^{{\mathrm{z}}_{\mathrm{i}}^{\prime }{\beta }_3+{\tilde{\mathrm{z}}}_{\mathrm{i}}^{\prime }{\mathrm{b}}_{\mathrm{i}}}\right]$$

This leads to a formula for (10). The survival probability for death at time t* for a patient censored at x_1i = x_2i < t* for both illness and death is

$$\mathrm{Pr}({\mathrm{T}}_{2\mathrm{i}}>{\mathrm{t}}^{\ast }\mid {\mathrm{T}}_{1\mathrm{i}}\ge {\mathrm{x}}_{1\mathrm{i}},{\mathrm{T}}_{2\mathrm{i}}\ge {\mathrm{x}}_{2\mathrm{i}},{\delta }_{1\mathrm{i}}=0,{\delta }_{2\mathrm{i}}=0,{\mathrm{z}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}},\beta )=\frac{\mathrm{Pr}({\mathrm{T}}_{1\mathrm{i}}\ge {\mathrm{x}}_{1\mathrm{i}},{\mathrm{T}}_{2\mathrm{i}}>{\mathrm{t}}^{\ast }\mid {\mathrm{z}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}},\beta )}{\mathrm{Pr}({\mathrm{T}}_{1\mathrm{i}}\ge {\mathrm{x}}_{1\mathrm{i}},{\mathrm{T}}_{2\mathrm{i}}\ge {\mathrm{x}}_{2\mathrm{i}}\mid {\mathrm{z}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}},\beta )}=\frac{\mathrm{Pr}({\mathrm{t}}^{\ast }>T_{1\mathrm{i}}\ge {\mathrm{x}}_{1\mathrm{i}},{\mathrm{T}}_{2\mathrm{i}}>{\mathrm{t}}^{\ast }\mid {\mathrm{z}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}},\beta )+\mathrm{Pr}({\mathrm{T}}_{1\mathrm{i}}>{\mathrm{t}}^{\ast },{\mathrm{T}}_{2\mathrm{i}}>{\mathrm{t}}^{\ast }\mid {\mathrm{z}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}},\beta )}{\mathrm{Pr}({\mathrm{T}}_{1\mathrm{i}}\ge {\mathrm{x}}_{1\mathrm{i}},{\mathrm{T}}_{2\mathrm{i}}\ge {\mathrm{x}}_{2\mathrm{i}}\mid {\mathrm{z}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}},\beta )}$$

The denominator and the second term of the numerator can be obtained directly using (A.1). For the first term of the numerator,

$$\mathrm{Pr}({\mathrm{t}}^{\ast }>T_{1\mathrm{i}}\ge {\mathrm{x}}_{1\mathrm{i}},{\mathrm{T}}_{2\mathrm{i}}>{\mathrm{t}}^{\ast }\mid {\mathrm{z}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}},\beta )={\int }_{{\mathrm{x}}_{1\mathrm{i}}}^{{\mathrm{t}}^{\ast }}\mathrm{Pr}({\mathrm{T}}_{1\mathrm{i}}=\mathrm{s},{\mathrm{T}}_{2\mathrm{i}}>{\mathrm{t}}^{\ast }\mid {\mathrm{z}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}},\beta )\mathrm{ds}={\int }_{{\mathrm{x}}_{1\mathrm{i}}}^{{\mathrm{t}}^{\ast }}{\lambda }_1\left(\mathrm{s}\right){\mathrm{e}}^{-{\Lambda }_1\left(\mathrm{s}\right)-{\Lambda }_2\left(\mathrm{s}\right)-{\Lambda }_3({\mathrm{t}}^{\ast }\mid \mathrm{s})+{\Lambda }_3(\mathrm{s}\mid \mathrm{s})}\mathrm{ds}$$

By plugging in the frailty models (4)-(6), we can obtain a formula for (11).