Accurate measurement of ³J_HNHα couplings in small or disordered proteins from WATERGATE-optimized TROSY spectra

Abstract

Provided that care is taken in adjusting the WATERGATE element of a ¹H-¹⁵N TROSY-HSQC experiment, such that neither the water magnetization nor the ¹H^α protons are inverted by its final 180° pulse, ³J_HNHα couplings can be measured directly from splittings in the ¹H dimension of the spectrum. With band-selective ¹H decoupling, very high ¹⁵N resolution can be achieved. A complete set of ³J_HNHα values, ranging from 3.4 to 10.1 Hz was measured for the 56-residue third domain of IgG-binding protein G (GB3). Using the H-N-C^α-H^α dihedral angles extracted from a RDC-refined structure of GB3, ³J_HNHα values predicted by a previously parameterized Karplus equation agree to within a root-mean-square deviation (rmsd) of 0.37 Hz with the experimental data. Values measured for the Alzheimer's implicated Aβ^1-40 peptide fit to within an rmsd of 0.45 Hz to random coil ³J_HNHα values.

³J_HNHα values have long been recognized as important parameters for defining the backbone torsion angles, ϕ, in peptides and proteins (Bystrov 1976)(Pardi et al. 1984). Parameterization of best-fitting Karplus curves typically has been carried out using ³J_HNHα couplings measured for small proteins and dihedral angles taken from the corresponding high resolution X-ray structures, yielding root-mean-square deviations (rmsd's) in the 0.8–1.0 Hz range (Pardi et al. 1984)(Ludvigsen et al. 1991)(Vuister and Bax 1993). Considering that in such X-ray structures, the electron density of the hydrogens is often ill defined, these atoms are typically model-built into the structure, assuming idealized geometry. Alternatively, the H-N-C^α-H^α dihedral angles needed as input to the Karplus equation are directly calculated from ϕ_i − 60°, where ϕ_i is the backbone torsion angle of residue i, defined by the backbone atoms C′_i−1, N_i, C^α_i, and C′_i. The residual rmsd in the fit was initially believed to result from difficulties in measuring ³J_HNHα at an accuracy better than about 0.8 Hz, but a large number of conceptually rather different methods, ranging from addition and subtraction of in-phase and anti-phase ¹H^N-{¹H^α} doublets (Ludvigsen et al. 1991), E.COSY measurements (Griesinger et al. 1987)(Wang and Bax 1996)(Montelione and Wagner 1989), quantitative J correlation methods (Vuister and Bax 1993)(Lohr et al. 1999), fitting of J_HH-modulated 2D HSQC and HMQC spectra (Billeter et al. 1992)(Kuboniwa et al. 1994), to multiple quantum methods (Rexroth et al. 1995), were unable to go significantly below this 0.8 Hz threshold. Only when using the actual H-N-C^α-H^α dihedral angles, with ¹H positions determined by measurement of residual dipolar couplings (RDCs), as input to the Karplus equation, were rmsd's well below 0.5 Hz obtained (Vogeli et al. 2007)(Maltsev et al. 2014). This result indicates that the earlier, higher rmsd values were dominated by deviations from idealized geometries, in particular the assumption of the amide hydrogen being located in the peptide plane.

Here we demonstrate that for small or intrinsically disordered proteins ³J_HNHα can be measured conveniently and at high accuracy from a 2D ¹H-¹⁵N TROSY-HSQC spectrum (Pervushin et al. 1997)(Pervushin et al. 1998)(Schulte-Herbruggen and Sorensen 2000). However, as discussed below, care must be taken in adjustment of the pulses that normally have a “water flip-back” function, such that they also invert the ¹H^α resonances. Appropriate choice of the flip back pulses will suppress ³J_HNHα-modulation during the last phase of the magnetization transfer from ¹⁵N to ¹H, preventing an antiphase contribution to the ¹H^N-{¹H^α} doublet line shape. When ¹H-¹⁵N TROSY-HSQC spectra are recorded on protonated proteins, unresolvable ²J_HαN, ³J_HαN, and ³J_HβN splittings can limit the attainable resolution in small or intrinsically disordered protein, and it then is useful to remove such splittings by insertion of a band-selective decoupling pulse at the mid-point of the ¹⁵N evolution period.

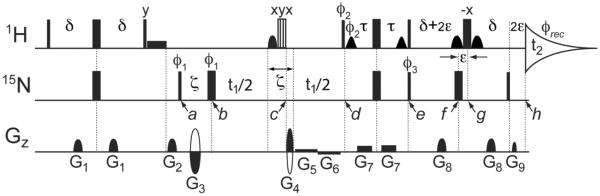
The pulse scheme of the water-flip-back ¹H-¹⁵N TROSY-HSQC experiment is shown in Figure 1 and it is essentially the same as the original ¹H-¹⁵N TROSY-HSQC experiment (Pervushin et al. 1998)(Schulte-Herbruggen and Sorensen 2000), except for the decoupling pulse applied to the aliphatic protons at time point c. Note that this decoupling pulse is implemented as a combination of an H^N-selective 180° pulse, using an IBURP2 shape (Geen and Freeman 1991), followed by a non-selective offset-compensated composite 180° pulse (Levitt and Freeman 1981). Together, this pulse pair inverts all ¹H except for ¹H^N, yielding a convenient and effective method for decoupling aliphatic protons during ¹⁵N evolution (Bruschweiler et al. 1988). In order to permit ¹⁵N coherence encoding without introducing the requirement of a large frequency-dependent phase correction in the ¹⁵N dimension, a short gradient encoding period (using gradients G₃ and G₄, separated by a ¹⁵N 180° pulse at time point b is inserted in the standard manner (Kay et al. 1992). To avoid the need for a frequency-dependent phase correction in the ¹H dimension, the last pair of ¹H/¹⁵N 180° pulses are slightly offset relative to one another: By applying the last non-selective ¹H 180° pulse (time point g) a short time, ε≈150 μs, after the ¹⁵N 180° pulse (time point f), full ¹H^N chemical shift refocusing after the last simultaneous pair of ¹H/¹⁵N 90° pulses (time point e) is delayed by 2ε, whereas ¹J_NH rephasing is active for the regular duration, 2δ = ¹/(2¹J_NH) ≈5.3 ms. This permits insertion of the last pulsed field gradient decoding pulse after the last ¹⁵N 90° pulse, before ¹H^N chemical shifts are refocused at time point h, which completes the ST2-PT polarization transfer (Pervushin et al. 1998). Water suppression is very effective with this pulse scheme, also on cryogenic probeheads, due to the combined effects of water-flip-back (Grzesiek and Bax 1993), the WATERGATE element (Piotto et al. 1992b), and coherence selection (Kay et al. 1992).

Fig. 1.

Pulse scheme of the water-flip-back ¹H-¹⁵N TROSY-HSQC experiment. The narrow and wide filled bars represent the hard 90° and 180° pulses, while the vertically hatched open bar is a 90_x210_y90_x composite 180° ¹H pulse. The filled rectangular box before the G₂ gradient pulse is a 1- ms rectangular water-flipback pulse that returns the solvent magnetization to +z after the INEPT transfer. The shaped pulse applied for the band selective decoupling in the middle of t₁ has an IBURP2 (Geen and Freeman) shape (1.1 ms duration at 800 MHz), is applied to H^N and centered 3.6 ppm downfield from the H₂O resonance. Two water-flipback pulses (center lobe of a sinc profile, 1.0 ms) are applied between time points d and e to ensure the water magnetization returns to +z at time point e. At time point g, two sine-bell shaped pulses (600 μs) flanking the non-selective 180° ¹H pulse are used to keep the water magnetization at +z, and to refocus ³J_HNHα evolution during the 2δ+4ε delay. All pulses are applied along x unless otherwise indicated. Durations of all shaped pulses are for a ¹H frequency of 800 MHz and should be scaled inversely relative to this frequency if applied at higher or lower magnetic fields. Delay durations: δ = 2.65 ms,; ε = 150 μs; ζ = 2081 μs; τ ≈ 2.1 ms (shorter than 1/(4¹J_NH) to minimize the ¹⁵N anti-TROSY component (Schulte-Herbruggen and Sorensen 2000)). Phase cycling: ϕ₁ = y, x, −y, −x; ϕ₂ = y; ϕ₃ = y; ϕ_rec = y, −x, −y, x. To obtain the second FID for the echo-antiecho quadrature detection, the following phase cycling is used together with inversion of the G₃ and G₄ gradient pulses: ϕ₁ = y, −x, −y, x; ϕ₂ = −y; ϕ₃ = −y. These phase parameters pertain to Bruker spectrometers; for Varian/Agilent spectrometers y and −y should be interchanged. Gradients are sine-bell or rectangular shaped, as marked in the figure, with durations: G_{1,2,3,4,5,6,7,8,9} = 0.977, 1.2, 1.1, 0.9, t₁/4, t₁/4, 1.086, 0.977, 0.202 ms, and strengths of 21.7, 28.7, −41.3, 41.3, 0.91, −0.91, 2.1, 25.9, 41.3 G/cm.

³J_HNHα dephasing during the initial INEPT magnetization transfer from ¹H^N to ¹⁵N (prior to time point a) and during the first half of the final ST2-PT element, between time points d and e, only results in very slight attenuation of the final signal intensity at time point h (by a factor of ca. cos[2π ³J_HNHα τ]{1+ cos[2π ³J_HNHα τ]}/2) and creation of multiple quantum ¹H^N-¹H^α coherences that will remain invisible during detection. This dephasing prior to time point e therefore may be safely ignored. However, ³J_HNHα dephasing between time points e and h will remain intact if only the non-selective ¹H 180° pulse were applied at time point g. Refocusing of the ³J_HNHα dephasing at time point h is achieved if only the ¹H^N is inverted by the 180° pulse at time point g. In practice, this can be accomplished by again using the combination of a non-selective 180° pulse, followed or preceded by a selective ¹H^α inversion pulse, which forms the basis for band-selective homonuclear (BASH) decoupling (Bruschweiler et al. 1988)(Ying et al. 2014). In Pervushin's ST2-PT implementation of the TROSY experiment, this last non-selective ¹H 180° pulse is already surrounded by two water-selective 90° flip-back pulses, ensuring that the water magnetization is minimally impacted by this combination of ¹H pulses, essentially constituting a WATERGATE element when surrounded by the standard pair of pulsed field gradients (Piotto et al. 1992a). ¹H^α spins that resonate close to the H₂O resonance therefore are also minimally affected by the soft/hard pulse combination, centered at time point g.

The width of the ¹H^α region not affected by the soft/hard pulse combination is remarkably wide, due to the offset-compensating effect of this symmetric 90°_x, 180°_−x, 90°_x composite pulse (Levitt and Freeman 1979; Shaka and Freeman 1983). For example, Figure 2 compares the inversion profile for the case where the non-selective 180°_−x pulse is applied just prior to two back-to-back sine-bell-shaped 600-μs 90°_x pulses with the profile obtained when the 180°_−x is applied in between these two pulses, as in the TROSY scheme of Figure 1. As can be seen, the non-inversion profile of the 90°_x, 180°_−x, 90°_x pulse combination has a favorable shape, leaving z magnetization above 85% (i.e., inverting less than ~7.5% of the H^α spins) for offsets up to ±640 Hz, and >90% inversion of z magnetization (i.e., inverting >95% of the ¹H spins) at offsets ≥2100 Hz. These bandwidths are inversely proportional to the duration of the shaped 90°_x pulses. Pulse shapes different from a sine bell, e.g. Gaussian shapes, can be used to fine tune the inversion profile. Even a single sine-bell shaped soft 180°_−x pulse, with a non-selective ¹H 180° pulse superimposed at its mid-point gives a desirable inversion profile (red line in Figure 2). In practice, we use the two sine-bell shaped 90°_x pulses separated by the non-selective 180° pulse as a compromise between an optimal inversion profile and a minimal total duration of this pulse combination. In principle, a REBURP 180° ¹H^N pulse (Geen and Freeman 1991) could be used instead of the 90°_x, 180°_−x, 90°_x pulse combination, but in practice we find the use of such a pulse less effective at optimizing suppression of the H₂O signal.

Fig. 2.

Inversion profile, M_z/M_o, as a function of resonance offset for different hard-soft pulse combinations, all using a 20 μs hard 180° pulse. Black line: 90°_x, 180°_−x, 90°_x, where the 90°_x pulses are sine-bell shaped with a duration of 1.5 ms each. Blue: 90°_x, 180°_−x, 90°_x, where the 90°_x pulses are sine-bell shaped with a duration of 0.6 ms each. Red; 90°_x, 180°_−x, 90°_x, where the first and second 90°_x pulse have the shape of the left half and of the right half of a sine-bell, respectively, and a duration of 0.6 ms each. For comparison, the green line corresponds to the inversion profile of a 90°_x, 90°_x, 180°_−x combination, with 0.6-ms sine-bell shaped 90°_x pulses.

In the absence of selective ¹H^α inversion, the phase of the two ¹H^N-{¹H^α} doublet components at time point h in Figure 1 is given by ±2π ³J_HNHα(δ+2ε). Although relatively small (ca ±k° for a ³J_HNHα coupling of k Hz and 2δ+4ε = 5.9 ms), such an antiphase dispersive contribution, which is not easily visible to the eye, will increase the apparent splitting, as measured from the maximum height position of each doublet component, by ca k×LW/90, where LW is the average line width of each doublet component (Fig. 3). So, the error introduced in the measured ³J_HNHα coupling when J-modulation is not suppressed is approximately proportional to both the size of the ³J_HNHα coupling and to the ¹H^N line width. For a typical ³J_HNHα coupling of 7.5 Hz and a digitally enhanced line width of 3 Hz, this therefore would result in an overestimate of the measured coupling by ca 0.25 Hz. However, as described above, this contribution is easily suppressed by adjusting the duration of the shaped 90°_x ¹H pulses such that the ¹H^α spins are not inverted. Note that the small error introduced by J modulation is distinct from the apparent decrease caused by the finite lifetime of the ¹H^α spin states, i.e., by the dependence on their selective inversion recovery rates (Harbison 1993). This latter effect can become quite significant in larger proteins, where zero frequency spectral density and therefore ¹H-¹H spin flip rates are high. It then needs to be accounted for either computationally (Vuister and Bax 1993)(Ball et al. 2013), or by altering the pulse scheme (Rexroth et al. 1995). For the smaller systems to which the TROSY-HSQC ³J_HNHα measurement is applicable, such as GB3, the effect tends to be minor, resulting in a small systematic difference of only ~0.12 Hz relative to the values measured previously (Vogeli et al. 2007) with a multi-quantum pulse scheme that was designed to suppress the effect.

Fig. 3.

Illustration of the effect of ³J_HH phase modulation prior to the start of ¹H data acquisition on the apparent splitting. Simulated data are shown for a doublet with ³J_HH = 6 Hz, marked by the dashed lines. The bottom doublet corresponds to the absence of phase modulation, with vertically displaced doublets having phase errors of ±10, ±20, and ±30°. The apparent splitting, as measured from the maxima of the two components, increases approximately linearly with the phase error. Note that the phase error introduced by the ca 5.5-ms ³J_HH modulation during the final half of the ST2-PT transfer for a 6 Hz ³J_HH coupling is only ±6°, but is responsible for the differences in apparent ³J_HH shown in Fig. 5b.

Figure 4 shows three small regions of the ¹H-¹⁵N TROSY-HSQC spectra of GB3, the Aβ^1-40 peptide, and α-synuclein. For the latter two, the ¹H^α spins all resonate upfield of the ¹H₂O water resonance and the ¹H carrier is shifted upfield by 0.3 ppm during application of the final 90°_x, 180°_−x, 90°_x pulse combination, such as to shift the band where ¹H^α spins are not inverted upfield relative to the H₂O resonance. For GB3 at 293 K, where H₂O resonates approximately at the center of the H^α region, no such frequency shift was used. As can be seen from the spectra, well resolved doublets are readily obtained for these proteins, whose ¹H^N line widths are significantly reduced by the TROSY effect (ca 1.5 to 2-fold at 800 MHz ¹H frequency) over regular HSQC spectra, i.e. by relaxation interference between the ¹H^N chemical shift anisotropy (CSA) and the ¹⁵N-¹H dipolar relaxation mechanisms.

Fig. 4.

Expanded small regions of the 800 MHz ¹H-¹⁵N TROSY-HSQC spectra recorded for samples of (a) 1.2 mM GB3 in 100 mM NaCl, 25 mM sodium phosphate, pH 6.4, 293 K and (b) 150 μM Aβ^1-40 in 20 mM sodium phosphate, pH 7.0, 277 K and (c) 300 μM α-synuclein in 25 mM sodium phosphate, pH 6.0, 288 K. Spectra were recorded with acquisition times of 284 ms (t₂) and 128 ms (t₁) for Aβ^1-40; 393 ms (t₂) and 74 ms (t₁) for GB3; and 393 ms (t₂) and 1016 ms (t₁) for α-synuclein, all using 0.6-ms sine-bell shaped pulses surrounding the last non-selective 180° pulse. For Aβ^1-40 and α-synuclein the carrier frequency was moved upfield by 0.3 ppm relative to the H₂O resonance position only during application of the last ¹H 90°_x, 180°_−x, 90°_x pulse combination, and for the remainder of the pulse sequences the ¹H carrier was positioned on the H₂O resonance. Spectra were resolution-enhanced in the ¹H dimension using a Lorentzian-to-Gaussian enhancement function, and processed and peak-picked with the NMRPipe software package (Delaglio et al. 1995).

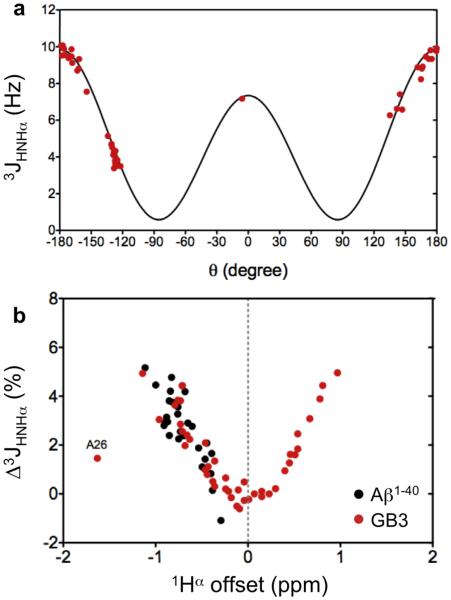
With an rmsd of only 0.37 Hz, ³J_HNHα couplings measured for GB3 from the TROSY-HSQC spectrum (Supplementary Table S1) agree very well with the previously parameterized Karplus equation (Vogeli et al. 2007) when using a recent RDC-refined structure of this protein (PDB entry 2N7J) to derive the dihedral angles, confirming the accuracy of our ³J_HNHα measurements (Fig. 5a).

Fig. 5.

Measurement of ³J_HNHα couplings from the HSQC-TROSY spectra of Figure 4. (a) Plot of the GB3 ³J_HNHα values (Table S1) as a function of the H-N-C^α-H^α dihedral angle, θ, derived from a RDC-refined structure (PDB entry 2N7J), using the Karplus equation parameterization ³J_HNHα = 7.97×cos²θ – 1.26×cosθ + 0.63 (Vogeli et al. 2007). Mobile residues L12 and D40 were not included in the fit. (b) Fractional difference Δ³J_HNHα = [³J_HNHα(1.5 ms) - ³J_HNHα(0.6 ms)]/³J_HNHα(0.6 ms), where ³J_HNHα(1.5 ms) and ³J_HNHα(0.6 ms) are the values measured using 1.5-ms and 0.6-ms duration 90° water-flip back pulses around the last ¹H 180° pulse. Δ³J_HNHα values are plotted as a function of the ¹H^α chemical shift offset relative to the frequency at which the radiofrequency carrier is positioned during the final 90°_x, 180°_−x, 90°_x pulse combination. Δ³J_HNHα values measured for Aβ^1-40 are in black, GB3 values in red. Note that for the far upfield shifted GB3 A26 resonance, neither measurement suppresses ³J_HNHα modulation, and both yield a slight over-estimate of the true coupling, and therefore a small Δ³J_HNHα.

As mentioned above, the error in the apparent ³J_HNHα splitting that exists when J modulation is not suppressed is proportional to the size of ³J_HNHα. Figure 5b shows the fractional difference (as a percentage of the actually measured ³J_HNHα coupling) between values measured from two ¹H-¹⁵N TROSY-HSQC spectra: one using 1.5 ms 90° shaped sine bell pulses and one using 0.6-ms pulses. The first measurement corresponds to 50% inversion of the ¹H^α spins at resonance offsets of ~±505 Hz relative to the carrier, and nearly complete suppression of J modulation over a ~±260 Hz bandwidth. For the measurement with 0.6-ms pulses, these bandwidths are 2.5 times larger. As can be seen in Figure 5b, when the J modulation is fully suppressed in both measurements, i.e., at small offsets, the fractional difference between the two sets is essentially zero. However, at ±810 Hz the fractional difference reaches a maximum, before again decreasing for large offsets (e.g. residue A26 at 3.19 ppm) where neither measurement was effective at suppressing J modulation.

Measurements of ³J_HNHα couplings are quite useful in the analysis of residual structure in IDPs, where they represent a particularly unambiguous reporter on the time- or ensemble-average of the ϕ angles.

We note that ¹H-¹⁵N TROSY-HSQC spectra that are free of ³J_HNHα phase modulation errors can also be generated with the powerful BEST-TROSY pulse scheme, which then additionally yields sensitivity enhancement over the scheme of Figure 1 (Favier and Brutscher 2011; Solyom et al. 2013). However, addition of aliphatic ¹H decoupling during ¹⁵N evolution (Fig. 1) is somewhat incompatible with the spirit of the BEST type experiments, which aim to avoid inversion of the aliphatic protons. Achieving the highest possible ¹⁵N resolution is often paramount, as illustrated for the most crowded region of the α-synuclein spectrum (Fig. 4c), and we therefore opted to modify the standard TROSY-HSQC pulse sequence instead. Note that, as applies for most experiments for ³J_HNHα measurement, hydrogen exchange with water causes line broadening in the ¹H^N dimension (and for TROSY type experiments such as the present one also in the ¹⁵N dimension) by an amount k_ex/π Hz, which can become a factor limiting the smallest couplings that can be measured.

A number of computational studies (Sgourakis et al. 2011)(Ball et al. 2011; Ball et al. 2013; Ball et al. 2014)(Rosenman et al. 2013) strongly rely on a set of relatively incomplete ³J_HNHα values measured for Aβ^1-40 and Aβ^1-42 by various groups (Hou et al. 2004)(Yan et al. 2008)(Sgourakis et al. 2007)(Waelti et al. 2015). Here, we have demonstrated that these couplings can be measured at very high precision and good accuracy in such systems, at a very high level of completeness. The only missing values are for the N-terminal residue and two His residues, which exhibit rapid exchange and concomitant broadening of their resonances, and the Gly residues, for which the ³J_HNHα2 and ³J_HNHα3 couplings give rise to triplet splitting patterns from which only the sum of their two ³J_HNHα couplings can be measured. Although, with a Pearson's correlation coefficient of R_P = 0.8, the values reported here for Aβ^1-40 (Supplementary Table S2) correlate well with random coil ³J_HNHα values (Maltsev et al. 2012) derived for IDP α-synuclein (Fig. 6), significant deviations are also seen. For example, values for V12 (6.78 Hz) and V24 (6.82 Hz) fall well below the 7.6-Hz random coil value of this β-branched residue, whereas V18 (8.30 Hz) and V39 (7.94 Hz) show significantly elevated values. Analysis of these couplings, in concert with other types of J couplings, chemical shifts, and NOEs, is currently on-going in our group in an effort to obtain quantitative, residue-specific ϕ/ψ distributions using the recently introduced MERA program (Mantsyzov et al. 2015).

Fig. 6.

Plot of ³J_HNHα values measured for Aβ^1-40 against “random coil” values, derived from the residue-specific averages observed for IDP α-synuclein (Maltsev et al. 2012). The Aβ^{1-40 3}J_HNHα couplings are reported in SI Table S2. The rmsd between observed and random coil ³J_HNHα couplings equals 0.45 Hz, and the Pearson's correlation coefficient, R_P is 0.8.