Abstract
In this study, quartz thickness-shear mode (TSM) resonator sensors were adopted to monitor the process of platelet activation. Resting platelets adhering to fibrinogen-coated electrodes were activated by different concentrations of thrombin (1, 10, and 100 U/mL), and the corresponding electrical admittance spectra of TSM resonators during this process were recorded. Based on a bilayer-loading transmission line model of TSM resonators, the complex shear modulus (G′ + jG″) and the average thickness (hPL) of the platelet monolayer at a series of time points were obtained. Decrease in thrombin concentration from 100 to 1 U/mL shifted all peaks and plateaus in G′, G″, and hPL to higher time points, which could be attributed to the partial activation of platelets by low concentrations of thrombin. The peak value of hPL was acquired when platelets presented their typical spherical shape as the first transformation in activation process. The G′ peak appeared 10 ∼ 20 min after hPL peak, when some filopods were observed along the periphery of platelets but without obvious cell spreading. As platelet spreading began and continued, G′, G″, and hPL decreased, leading to a steady rise of resonance frequency shift of TSM resonator sensors. The results show high reliability and stability of TSM resonator sensors in monitoring the process of platelet activation, revealing an effective method to measure platelet activities in real-time under multiple experimental conditions. The G′, G″, and hPL values could provide useful quantitative measures on platelet structure variations in activation process, indicating potential of TSM resonators in characterization of cells during their transformation.
Introduction
Platelets are blood components that play a critical role in a number of pathophysiological processes, including hemostasis, hemorrhage, inflammation, and cancer (1). During normal hemostasis, when the damaged vessel wall exposes collagen and basement membrane proteins, platelet adhesion to the substrate is initiated by platelet rolling. The adherent platelets aggregate gradually and are activated to release activation mediators, such as ADP and thromboxane A2. After activation, the platelets produce thrombin, catalyzing the initiation of coagulation cascade, which generates a meshlike fibrin deposit in the end (2).
After activation, platelets also release a variety of fundamental growth factors that are stored in their α-granules, such as PDGF, VEGF, TGF-β, and HGF (3, 4). Because these growth factors are essential for the tissue-repair process, patients with traumatic injuries are often treated with platelet-rich plasma (PRP), an autologous concentration of platelets in a small volume of plasma. PRP has been extensively applied in a series of clinical treatments including bone regeneration, skin rejuvenation, bleeding reduction, and other soft tissue healing (4, 5, 6). In orthopedic surgery and sports medicine, PRP is widely used by professional athletes to treat tendon and ligament injuries for a quick return to sports activities. Despite its prevalent use, efficacy of PRP treatment is still controversial due to conflicting outcomes from clinical trials, and a major contributor to these differential results is undesired variations of platelets during PRP preparation. In general, PRP is isolated simply by a low-speed centrifugation, where the stability of platelets is <2 h because PRP contains plasma proteins, in particular enzymes, which potentially activate these platelets (7). Therefore, it is important to analyze the states of platelets before use in clinical treatments to avoid inadvertent platelet activation by plasma proteins or other uncertainties.
As of this writing, most studies that evaluate platelets are based on optical microscopy observation of platelet morphologies, which is time-consuming and labor-intensive. Besides, some other measurement methods have been developed, including atomic force microscopy (AFM), thromboelastography (TEG), surface plasmon resonance, etc. (8, 9, 10, 11, 12). AFM is an invasive technique that applies an external force on individual cells. As the normal radius of AFM probe is usually <100 nm, it is difficult to statistically examine cell groups, although local measurement could be conducted on some specific parts of cells. TEG, on the other hand, is specifically used to measure platelet contribution during coagulation process. However, both AFM and TEG cannot be performed in situ. In comparison, surface plasmon resonance as a noninvasive technique is applied to monitor certain platelet activities, but it cannot analyze mechanical properties of platelets such as elasticity or viscosity (13). A quartz thickness-shear mode (TSM) resonator sensor is proposed in this study for a real-time analysis of platelets due to its high sensitivity, repeatability, and easy connection with electronic measurement systems (14, 15). A TSM resonator consists of a thin disk of AT-cut quartz with circular Au/Cr electrodes deposited on both sides, which can be electrically excited in a number of resonant thickness-shear modes. When its surface loading condition varies, for example with platelets adhering to the surface, corresponding changes occur in the electrically excited acoustic wave propagation through the entire quartz crystal. Compared with other methods, TSM resonator allows a simple, noninvasive, and quantitative method to extract the complex shear modulus of platelet groups.
Previous studies have presented some applications of TSM resonators in detecting platelet adhesion, activation, and aggregation (16, 17, 18, 19, 20, 21, 22). However, when characterizing platelets in PRP, platelets should not be activated on TSM resonators to avoid the formation of fibrin gel (16, 17, 18). Recent studies reported platelet activation and adhesion where suspended platelets were activated by agonists binding to the electrode surface of TSM resonators (19, 20, 21). In this case, TSM resonator’s response was recorded as a combination response of platelet activation and adhesion, posing a challenge to separate platelet activation signals from adhesion signals thus confounding interpretation of the results. Kunze et al. (22) compared the TSM resonator’s response to activation of adherent platelets with and without plasma proteins, but still lacking specific explanations to activation process. In addition, discussions from a perspective of mechanical properties are quite limited in these studies, and viscoelastic properties of platelets during activation process have not been precisely determined thus far. Changes in the viscoelasticity and the average thickness of platelets should be investigated as essential parameters, and results from such studies could contribute immensely to real-time detection and evaluation of platelet functions. In this study, TSM resonator was adopted to monitor activation process of platelets. Using fibrinogen-coated electrodes for platelet adhesion and thrombin for platelet activation, the electrical admittance spectra of TSM resonators during the entire process were recorded. The acquired electrical admittance was processed by a programmed analyzer based on a bilayer-loading model, and the corresponding storage modulus G′, loss modulus G″, as well as average thickness hPL of platelet monolayer at a series of time points, were obtained. Our findings show that G′, G″, and hPL could provide useful quantitative measures on platelet structure variations in activation process, indicating potential of TSM resonators in characterization of platelets.
Materials and Methods
Experimental materials
In this study, an isolation method by centrifugation and washing was adopted to obtain high-concentration platelet suspension in Tyrode’s buffer without damage and free from plasma proteins (7). Rat blood (freshly collected from 7- to 9-week-old rats) added with ACD (acid-citrate-dextrose; 1:6) was centrifuged at 2300 g for 1 min to obtain PRP in supernatant. PRP was centrifuged again at 2200 g for 5 min and the pellet containing platelets was collected by discarding the supernatant platelet-poor plasma. The platelets were washed twice in Tyrode’s albumin buffer (0.35% albumin) following the standard washing procedure, and then suspended in Tyrode’s albumin buffer (0.35% albumin) containing 0.02 U/mL apyrase to a final concentration of ∼1,000,000/μL.
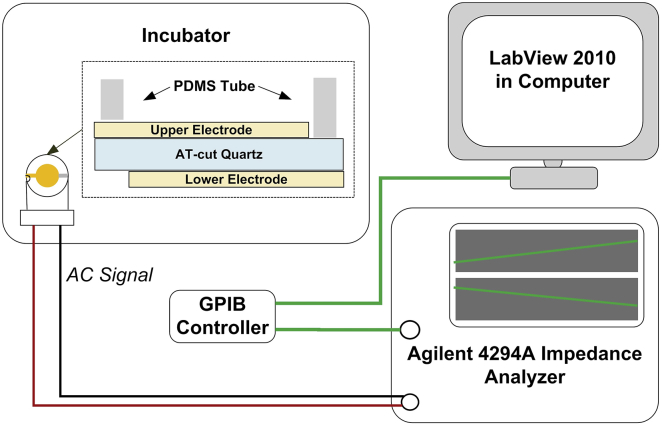
Fig. 1 schematically shows the measurement system of a 10 MHz TSM resonator (International Crystal Manufacturing, Oklahoma City, OK). The diameter of central circle electrodes was 5.10 mm. One tube (6.2/8.0 × 6 mm) made of poly(dimethylsiloxane) (PDMS; Dow Corning, Midland, MI) was located around the upper electrode, forming a well-like structure for platelet adhesion and activation. TSM resonators were placed in culture dishes, covered with lids, and then put into an incubator. The electrical admittance spectra of TSM resonators were obtained using a Cat. No. 4294A Precision Impedance Analyzer (Agilent Technologies, Palo Alto, CA). In sweep signaling, the frequency step was set as 20 Hz, and the driving voltage was 500 mV. For different TSM resonators in varied conditions, the sweep frequency range was adjusted within 9.96 ∼ 10.00 MHz. Before the measurements, the TSM resonators were sterilized overnight by exposure to UV light. After that, 100 μL of 100 μg/mL human fibrinogen (Cat. No. F3879; Sigma-Aldrich, St. Louis, MO) in phosphate-buffered saline (PBS; Mediatech, Manassas, VA) was added into wells and kept at 37°C with 5% CO2 for 2 h. Through this procedure, the entire electrode surface of TSM resonators was coated with fibrinogen, allowing resting platelets to adhere to the substrate and then form a dense monolayer (23, 24). Washing three times in PBS, these wells were refilled with 100 μL of a ∼1,000,000/μL platelet suspension, and incubated at 37°C with 5% CO2 for 2 h. During this period of time, suspended platelets were adhering to the fibrinogen-coated electrode surface gradually, and corresponding electrical admittance spectra of TSM resonators were recorded every 1 min. Subsequently, these wells were washed three times in PBS to remove excess, nonadherent platelets, followed by the addition of 100 μL Tyrode’s albumin buffer containing 0.02 U/mL apyrase. Adherent platelets were then activated by different concentrations of thrombin (1, 10, and 100 U/mL; Sigma-Aldrich, St. Louis, MO) and maintained in an incubator at 37°C with 5% CO2 for 2.5 h, and the corresponding admittance spectra during this process were recorded every 1 min. In addition, the initial admittance spectra of unloaded TSM resonators as well as that with Tyrode’s albumin buffer and fibrinogen coating were also recorded for the following extraction of platelet monolayer viscoelastic properties. All measurements were performed three times, and the platelets in three independent measurements for one thrombin concentration were from the same platelet isolation step. In parallel experiments, 100 μL of an ∼1,000,000/μL platelet suspension was added into fibrinogen-coated 96-well culture plate, and following the same procedure, adherent platelets were activated by 100 U/mL thrombin. Both unactivated and activated platelets were observed through optical microscopy (Eclipse TS100; Nikon, Tokyo, Japan).
Figure 1.
Schematic diagram of TSM resonator measurement system. To see this figure in color, go online.
To examine variations in platelet morphologies during the activation process, the platelet suspension as above was also added into fibrinogen-coated PDMS wells on Au/Si wafer and maintained in an incubator for 30 min. After washing in PBS to remove excess platelets and refilling 100 μL Tyrode’s albumin buffer containing 0.02 U/mL apyrase, adherent platelets of low density were located in the incubator for further 1.5 h. These platelets were then activated by 100 U/mL thrombin, fixed with 4% paraformaldehyde in PBS at a series of time points after the addition of thrombin, and sequentially washed with increasing concentrations of ethanol solution (10, 20, 30, 40, 50, 60, 70, 80, 90, and 100%). The platelet morphologies were examined by scanning electron microscopy (Helios NanoLab 600 SEM; FEI, Hillsboro, OR, accelerating voltage: 5 kV).
Theoretical model and analytical methods
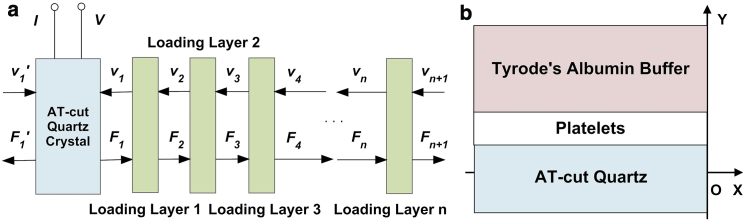
In general, two types of equivalent-circuit models are proposed to describe the TSM resonator: the lumped-element model (Butterworth-Van Dyke) and the distributed model (transmission line model, TLM), and the former could be derived from reduction of the latter in near-resonant circumstances (25). Because of zero error between its assumptions and actual electrical response of TSM resonator, TLM is chosen to provide a comprehensive description for TSM resonator with viscoelastic platelet monolayer in this study (25, 26). As shown in Fig. 2 a, TLM for TSM resonator has two acoustic ports and one electrical port, and via a transformer the acoustic variables, force F and linear velocity ν, are coupled to an electrical port (27, 28). Defining complex electrical admittance Y = G + jB = I/V, Y could be expressed as
| (1) |
where C∗0 is the total parallel capacitance measured at double fundamental-resonance frequency based on the limit relationship Y = jωC∗ 0 (29); Z1 and Z1′ are the surface mechanical impedance values on the two sides of TSM resonator, respectively, defined as Z1 = F1/ν1, Z1′ = F1′/ν1′, where F1, F1′, and ν1, ν1′ are the external force and linear velocity on surfaces; and ZC, αq, and C0 are, respectively, the mechanical impedance, phase, and static capacitance of the TSM resonator, when Zq and K2 are the characteristic mechanical impedance and piezoelectric stiffness factor variables of quartz, respectively. They could be obtained as follows, with relevant parameters shown in Table 1 (and see Salt (30)):
| (2) |
Figure 2.
Theoretical model. (a) TLM of TSM resonator. (b) Bilayer-loading model of TSM resonator with adherent platelets. To see this figure in color, go online.
Table 1.
Parameters of TSM Resonator (30)
| Density of quartz | ρq | 2.651 × 103 kg⋅m−3 |
|---|---|---|
| Shear stiffness of quartz | cq= c66 + e226/ε22 + jωηq | 2.970 × 1010 N⋅m−2 + jωηq |
| Piezoelectric constant of quartz | eq= e26 | 9.657 × 10−2 A⋅s⋅m−2 |
| Dielectric permittivity of quartz | εq= ε22 | 3.982 × 10−11 A2⋅s4⋅kg−1⋅m−3 |
| Surface area of TSM resonator | A | 2.047 × 10−5 m2 |
| Thickness of TSM resonator | hq (theoretical) | 165 μm |
In this study, with loading on upper electrode, Z1 is determined by the properties of all three mechanical impedance layers: the fibrinogen coating; the platelet monolayer; and the semiinfinite viscous liquid layer (buffer medium), when Z1′ is always zero. Because the fibrinogen coating is quite thin (under 20 nm), this multilayer-loading model could be simplified into an equivalent bilayer-loading model as described in Fig. 2 b by considering the fibrinogen coating as an intrinsic effect included into TSM resonator itself. In this case, Eq. 1 could be modified into Eq. 3, and thus an explicit relationship between the experimental observation (electrical response of TSM resonator) and relevant parameters is established:
| (3) |
| (4) |
Assuming the platelet monolayer as an isotropic, homogeneous, and uniform coating, the mechanical impedance and phase of first-loading layer Z1L, α1L could be calculated as
| (5) |
where ρPL, GPL, and hPL are the density, shear modulus, and average thickness of platelet monolayer, respectively. In the meantime, as the buffer medium is semiinfinite, surface mechanical impedance on the interface between first and second loading layers Z2 could be obtained as
| (6) |
where ρBuffer and ηBuffer are the density and viscosity of buffer medium, respectively.
Before extraction of platelet monolayer viscoelastic properties, effective parameters ηq, hq, C0, and Cp (external capacitance Cp = C∗0 – C0) for TSM resonators with fibrinogen coating were obtained firstly. Then, complex impedance of buffer medium was also calculated as
| (7) |
With modified parameters of TSM resonators and complex impedance of buffer medium, as well as the admittance spectra Y(ωi) = G(ωi) + jB(ωi) for TSM resonators with platelets, the specific solutions of complex shear modulus (G′ + jG″) and average thickness (hPL) of platelet monolayer could be determined through an algorithm based on the Regula-Falsi iteration method and error comparison (31). Fitting error is defined as Eq. 8, representing the cumulative error of experimental admittance spectrum deviating from the theoretical one,
| (8) |
where G(ωi)TLM and B(ωi)TLM values are developed from Eq. 3, and G(ωi)EXP and B(ωi)EXP values are from experimental admittance spectra. Detailed derivation and computation procedures were reported in our previous research (32).
Results and Discussion
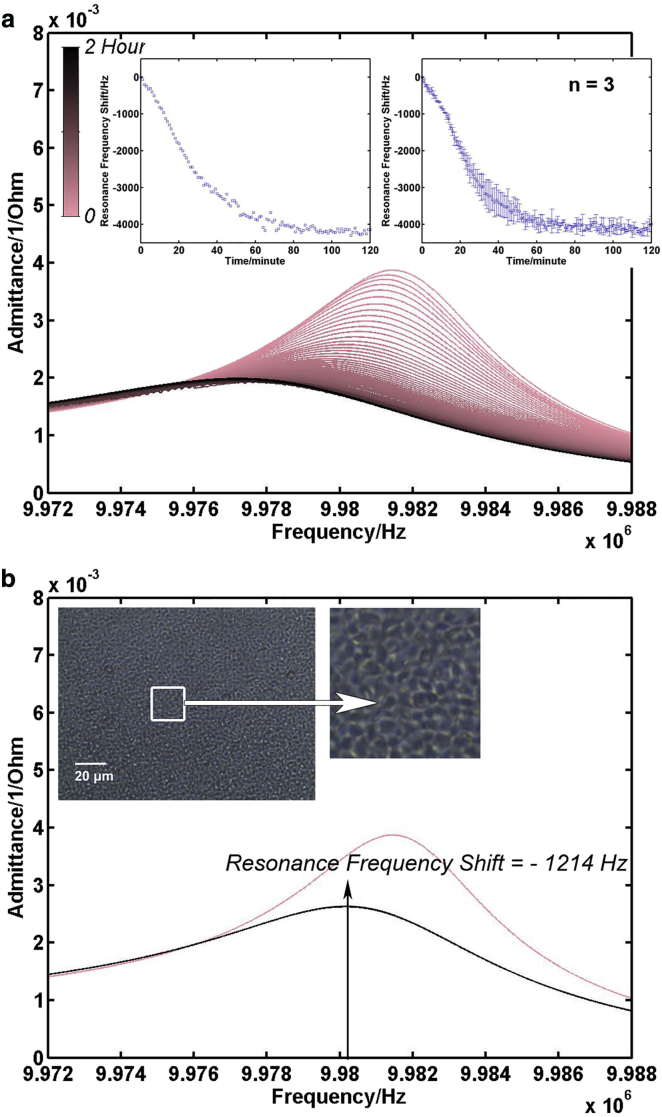
Fig. 3 a presents the typical electrical admittance spectra of TSM resonator sensor acquired during a 2 h platelet adhesion process. With an increase in incubation time, the color of admittance spectra shifts from pink to black gradually. As more and more platelets settled on electrodes, the intensity of resonance peaks decreased gradually, and the full width at half-maximum (FWHM) became larger. The inset on the left is the corresponding resonance frequency variation curve collected from these resonance peaks, and the one on the right is the mean resonance frequency shift curve for all three measurements. The extracted resonance frequencies decreased continuously in the first 1 h, and then plateaued as most platelets settled down. For all three independent measurements, the resonance frequency shift during the platelet adhesion process presented similar tendencies. Although the falling speed of platelets in suspensions varied, the overall frequency shift for TSM resonators kept relatively stable 2 h after seeding, and the mean frequency shift was −3991 ± 210 Hz. Fig. 3 b is the admittance spectrum of the TSM resonator after washing the well in PBS 2 h after seeding and adding the same amount of fresh Tyrode’s albumin buffer. Evidently, there was an increase in both resonance peak position and intensity compared with the spectra in black in Fig. 3 a, illustrating that not all platelets in suspension were adhered to fibrinogen-coated electrode surface. As they were not bonded to fibrinogen, those platelets on the bottom of wells were removed during washing procedure. Compared to TSM resonator with platelet suspension (spectrum in pink in Fig. 3 b), the resonance frequency shift with adherent platelets was −1214 Hz. For all three independent measurements, the increase in resonance frequency after washing was a characteristic, reproducible observation, and the mean frequency shift was −1206 ± 195 Hz. These results agree well with previous research that also used TSM resonator to monitor platelet adhesion process (17). In parallel experiments, an identical dose of platelet suspensions was added into a fibrinogen-coated 96-well culture plate and incubated for 2 h. Then these wells were washed three times in PBS, and a phase-contrast microscopy photo of adherent platelets was taken, as the inset of Fig. 3 b shows. The adherent platelets were uniformly sphere-shaped with average diameter of <2 μm. They formed a dense monolayer without any obvious overlap on the substrate, or any blank space that could allow more platelets to adhere to without affecting neighboring platelets, which leads to a reasonable assumption in the following calculation.
Figure 3.
Platelet adhesion. (a) Admittance spectrum set of TSM resonator during platelet adhesion process (adding platelet suspension at time (T) = 0). (Inset, left) Corresponding resonance frequency shift curve extracted from the admittance spectrum set; (inset, right) mean resonance frequency shift curve for all three measurements. (b) Admittance spectrum of TSM resonator with platelet suspension (pink) and with adherent platelet monolayer (black). (Inset) Phase-contrast photo of adherent platelets in 96-well plate taken after 2 h of platelet adhesion process. To see this figure in color, go online.
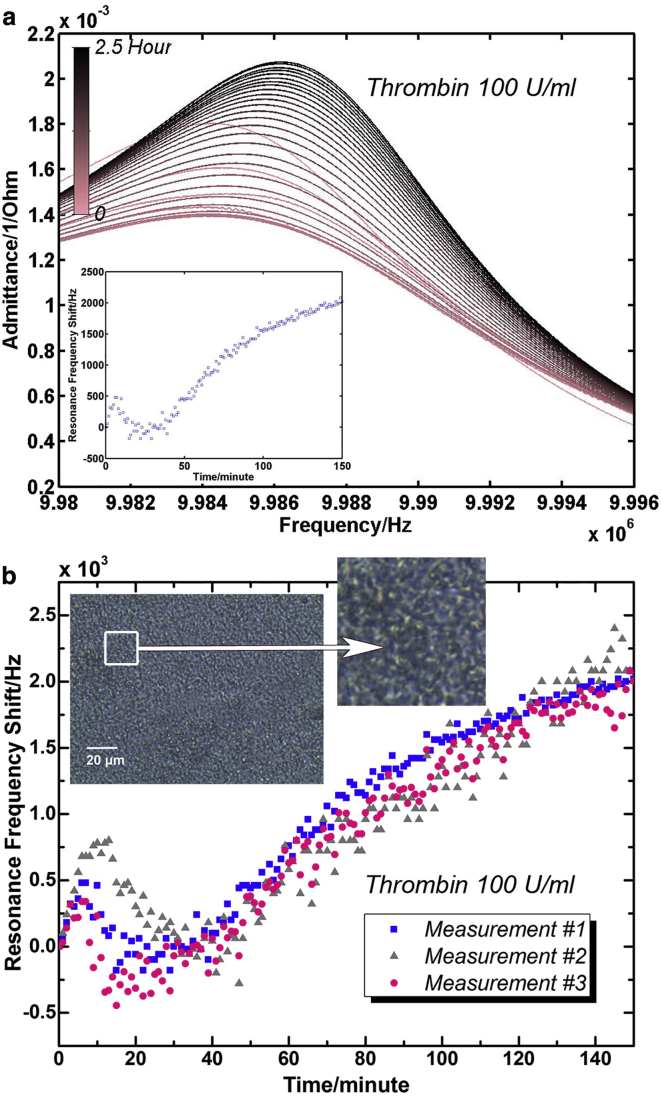
Fig. 4 shows the electrical admittance spectrum response of the TSM resonator sensors during the platelet activation process by thrombin (100 U/mL) for 2.5 h (TSM resonators used in Fig. 4 were not the same ones used in adhesion experiments, and TSM resonators used in Fig. 3 were applied to monitor platelet activation by 10 U/mL of thrombin). Fig. 4 a depicts the typical admittance spectra acquired in this process when the line color gradually changes from pink to black. During the first 30 min, the intensity of resonance peaks decreased along with a concomitant decrease in FWHM. As the platelet activation progressed, the intensity of resonance peaks began to increase, and the FWHM rose as well. The inset of Fig. 4 a is a corresponding resonance frequency variation curve extracted from this set of resonance peaks. All three resonance frequency variation curves from three independent measurements are presented in Fig. 4 b. The results indicated similar tendencies in resonance frequency variations during platelet activation. Three stages were evident in the entire process: Stage I) rapid increase; Stage II) decrease after a peak point; and Stage III) monotonic increase again. The initial peaks (Stages I and II) were completed within 20 ∼ 40 min for all three measurements. Following these peaks, a monotonic increase of frequency versus time curves (Stage III) showed an approximate slope of 20 Hz/min for all three sets of admittance spectra. Although variation magnitude and turning points are varied because of slight changes in platelet concentration and other related factors, these results exhibited consistent variation tendencies with previous research where TSM resonator was also applied to monitor platelet activation process (22). In parallel experiments, adherent platelets in a 96-well culture plate were activated by 100 U/mL thrombin, and a phase-contrast microscopy photo was taken after 2.5 h as the inset of Fig. 4 b shows. Compared with adherent platelets, activated platelets possessed highly fragmented morphologies. There was no regular, consistent disk shape for activated platelets, and a number of small pieces were observed over the entire substrate. Significant changes were demonstrated in the platelet architecture and the corresponding electrical response of TSM resonators during activation process. To further understand related changes on platelets, their morphologies and viscoelastic properties in the entire activation process were investigated.
Figure 4.
Platelet activation by thrombin (100 U/mL). (a) Admittance spectrum set of TSM resonator during platelet activation (adding thrombin directly after T = 0) and corresponding resonance frequency shift curve. For clarity, admittance spectra were plotted every 5 min. (b) Resonance frequency shift curves of TSM resonators during platelet activation and phase-contrast photo of activated platelets. (Inset) Phase-contrast photo of activated platelets in 96-well plate taken after 2.5 h of platelet activation process. To see this figure in color, go online.
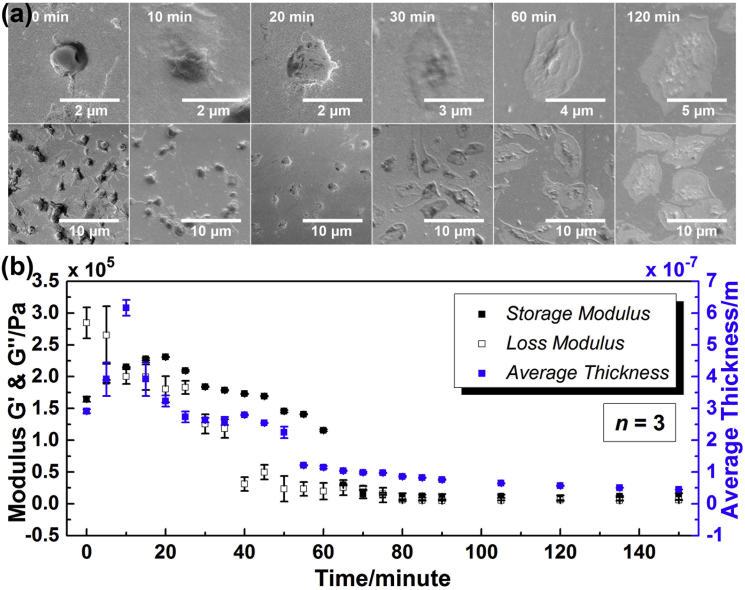
Fig. 5 a presents the mean ± SE photos of adherent platelets taken at a series of time points after thrombin (100 U/mL) was added into the PDMS wells on the Au/Si wafer. From left to right, these photos were taken after 0, 10, 20, 30 min, and 1 and 2 h in order, respectively. Photos in the first row are a partially enlarged view of corresponding ones in the second row, presenting the characteristic morphologies of platelets at different time points. During the entire activation process, although the overall shapes were varied between each other, adherent platelets still exhibited a relatively consistent, characteristic structure at each time point, indicating the platelet monolayer is an isotropic, homogeneous layer. It should be noted that with an increase in incubation time there were significant changes in platelet architecture. The first recognizable change was a transformation from a discoid to a more spherical shape during the first 10 min. Subsequently, some fingerlike projections, filopods (also called cellular antennae) were elaborated from the spheres surface as shown in 10- and 20 min photos. After filopodial growth, platelets began to spread onto the substrate at ∼20 min. By 30 min, large circumferential lamellae formed and platelets exhibited a fried-egg shape. Such spreading drastically increased the surface area of platelets. With continued incubation, some new filopods were also observed on the central dense aggregation part in 30-min photos. Growth of these filopods resulted in a shrunk, fragmented central part structure as shown in 60-min photos. Because of the continuous platelet spreading and the filopod extending, after 2 h, the platelets became quite thin, flat, and fragmented, and the appearance of fried-egg structure almost disappeared.
Figure 5.
Characterization of platelet monolayer at a series of time points during platelet activation by thrombin (100 U/mL) (adding thrombin directly after T = 0). (a) Mean ± SE photos of platelets (photos in the first row are a partially enlarged view of corresponding ones in the second row, presenting the characteristic morphologies of platelets at different time points). (b) Storage modulus G′, loss modulus G″, and average thickness hPL. To see this figure in color, go online.
Variations in platelet architecture from a discoid to an activated form primarily depend on the remolding of their internal actin cytoskeleton (1, 33). For a typical cell, the cytoskeleton as an intricate three-dimensional (3D) array of microfilaments, microtubules, and intermediate filaments, helps establish and maintain cell shape. With its support for cellular architecture, the lipid plasma membrane surrounding defines the cell’s boundary accordingly (34). In resting platelets, long actin filaments are distributed within the platelet cytoplasm to form a sparse fibrous network, supporting the initial disk structure together with a microtubule coil that runs along the perimeter of the disk. When platelets are activated by thrombin, these long actin filaments are fragmentized into a number of short actin filaments, and the microtubules forming the coil are disassembled as well, leading to a rounding up of platelets as the first recognizable change. Subsequently, accompanied by platelet spreading and filopod extending, a striking reorganization of actin cytoskeleton occurs in platelets. It is indicated that regions that correspond to circumferential lamellae are densely filled with a 3D network of short actin filaments, and these elaborated filopods are filled with long filaments with roots that are coalesced from filaments in the cytoskeletal center (1). Therefore, with continuous spreading, the rounding platelets could not only reorganize those short actin filaments that originated from the long ones, but also assemble new net filaments. The process of platelet cytoskeleton reorganization is carried out with the growth of abundant new actin filaments. For fully activated platelets, except drastically compressed central part, the entire platelets are occupied by a fully established dense 3D network of actin filaments.
In the meantime, based on the bilayer-loading model (see above), a programmed analyzer was built up for extraction of platelet monolayer viscoelastic properties. Assuming an isotropic, homogeneous platelet monolayer, its equivalent density was preset in the algorithm. In our previous work, a set of approximate values for the density of cell monolayer have been examined, and the theoretical model exhibited high consistency with experimental results in the case of 1.00 g/cm3 (32). Thus, in this study, 1.00 g/cm3 was adopted as the equivalent density of platelet monolayer. Sending the electrical admittance spectra acquired at a series of time points to the analyzer, the complex shear modulus of platelet monolayer G′, G″ as well as average thickness hPL were obtained. The error upper limit was set as 1%. Much smaller than this setting point, the fitting errors in extraction procedure were all stabilized <0.1%, indicating certainty and reliability of extracted parameters. Fig. 5 b gives G′, G″, and hPL at different time points during platelet activation. Significant variations of G′, G″, and hPL were observed in the initial stage of activation process. However, as activation continued beyond 1 h, both G′ and G″ presented similar stable tendencies. For storage modulus G′, there was an obvious increase in the beginning, followed by a decrease with continued incubation. The maximum value of G′ was 230,662 ± 452 Pa, achieved at 20 min. After 1 h, G′ tended to be stable, and the final value was ∼11,000 Pa. Loss modulus G″ decreased gradually from 284,520 ± 24,511 to 19,864 ± 13,084 Pa during the first 1 h, and then entered a plateau phase as well. Besides, the average thickness hPL increased sharply in the first 10 min with the peak value of 616 ± 25 nm acquired at 10 min, and then began to decrease with continued incubation. After 1 h, hPL already decreased to ∼100 nm. The rate of decrease reduced gradually, and the final value of hPL acquired after 2.5 h was <50 nm. During this period after 1 h incubation, continuous increase in resonance frequency shift shown in Fig. 4 was attributed to slight changes in G′, G″, and hPL, especially hPL. If using the average shear modulus obtained after 1 h G′ = 10,000 Pa and G″ = 5000 Pa, the relation between the resonance frequency shift and coating thickness keeps a good linearity as coating thickness goes into 0.04 ∼ 0.09 μm (this range is where average thickness of platelets obtained after 1 h). The change rate of the resonance frequency shift is ∼−16 Hz/nm. Thus, although Fig. 5 b presented relatively stable tendencies for G′, G″, and hPL after 1 h, the resonance frequency shift still changed continuously.
The changes in both viscoelasticity and average thickness of platelet monolayer could be associated with variations in platelet architecture based on remolding of their internal actin cytoskeleton. Fig. 5 illustrates that hPL could accurately describe the average thickness of platelet monolayer. When platelets transformed from a discoid to a more spherical structure, their effective height increased as shown in hPL’s increase during the first 10 min. Peak value of hPL was acquired when platelets showed their typical spherical shape. As platelets began spreading, their height decreased significantly, which was demonstrated by hPL’s continuous decrease after 10 min. G′ and G″ values also correlated well with the corresponding variations in platelet architecture. The peak position of G′ was at 20 min following the peak position of hPL, when some filopods were elaborated from the periphery of platelets but without obvious cell spreading. Although the shear stiffness of original long-fibrous network was reduced partially with filament fragmentation and cell rounding, the growth of filopods, which were filled with bundled long actin filaments, could increase the cytoskeletal stiffness to some extent. However, as platelets began spreading, a dense 3D network of short actin filaments was established gradually. Compared to the long-fibrous network of resting platelets, the short-flocculent structure occupying the interior space of activated platelets could reduce the overall shear stiffness due to good deformation capacity of short-actin-filament connections. Thus, as more and more net filaments assembled and large lamellae overlapped, G′ of platelet monolayer decreased until 1 h. In the meantime, both filopod extending and platelet spreading through short-actin-filament assembly could compress the cytoplasm regions extensively, thereby decreasing the effect of cytoplasm viscosity on G″. In this case, the G″ value of the platelet monolayer decreased continuously during the entire activation process. After 1 h of activation, when the interior of almost all the platelets was occupied by a dense 3D network of short actin filaments, and there were no further considerable changes in platelet cytoskeleton, both the G′ and G″ values tended to be stable, and only a slight decrease could be observed in hPL. The viscoelasticity and average thickness of platelet monolayer exhibited quite different tendencies with the resonance frequency shift of TSM resonators. In comparison, G′, G″, and hPL could provide quantitative, conclusive details on platelet structure variations in activation process.
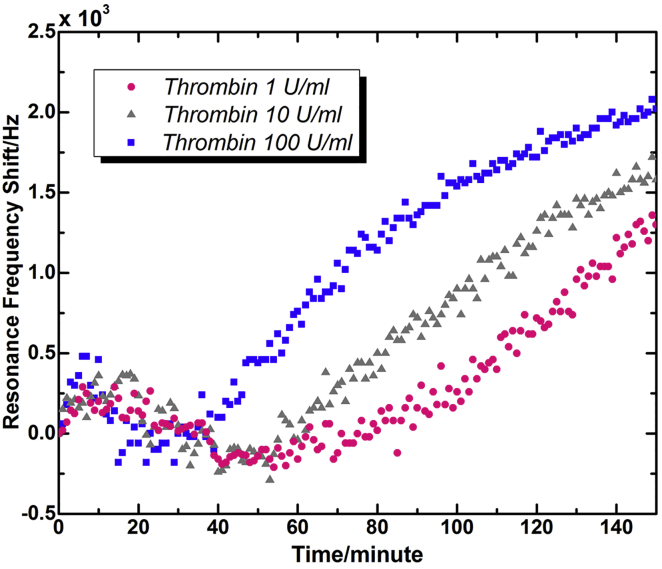
Fig. 6 shows the typical resonance frequency variation curves of TSM resonators during platelet activation by different concentrations of thrombin. Similar to that of thrombin of 100 U/mL in Fig. 4 b, three independent measurement results of both 10 and 1 U/mL presented consistent tendencies in resonance frequency variations during platelet activation. For clarity, typical resonance frequency shift curve was applied to represent characteristic variations of all three measurements. It is indicated that the resonance frequencies extracted from electrical admittance spectrum sets exhibited similar variation tendencies: 1) initial increase, 2) decrease after a peak point, and 3) monotonic increase again. The main differences between Figs. 4 and 6 were merely expressed in the time distributed to three stages, as well as the magnitude of frequency change. Compared with 100 U/mL, the peak positions for 1 and 10 U/mL were postponed to 10 ∼ 20 min. Accordingly, the elapsed time before monotonic increase (Stage 3) was also extended as the concentration of thrombin decreased. The second increase for 1 and 10 U/mL started at ∼70 and 50 min, respectively, when that of 100 U/mL started after only 20 min of activation. This phenomenon could be attributed to the mechanism of platelet activation. When high concentration of thrombin (100 U/mL) was added into PDMS wells, a large part of adherent platelets were activated simultaneously, and the performance of platelets exhibited group consistency as shown in those mean ± SE photos in Fig. 5. Thus, corresponding electrical response of TSM resonators presented explicit changes that related well with specific cellular architecture variations of a platelet group. Nevertheless, in response to low concentrations of thrombin (1 and 10 U/mL), a small part of the adherent platelets was activated at first, when others kept resting until new potent agonists were secreted by activated platelets (1, 2). In this case, there was no obvious group consistency for platelets at the beginning of activation process, and with continuous secretion of agonists, a large number of resting platelets were activated in succession. Only when the number of platelets activated at the same time was large enough, dominant activities of platelet group could be manifested in TSM resonator’s response to some extent, resulting in a flatter peak and a longer valley before the second increase. Besides, for all three thrombin concentrations the monotonic increase curves kept similar increase slopes. In Figs. 4 and 5, for 100 U/mL, the starting time point of monotonic increase was associated with the peak position of G′, as well as the initial spreading of platelets. Because of continuous spreading of platelets, the viscoelasticity, and average thickness of platelet monolayer kept decreasing, leading to a steady rise of resonance frequency shift of TSM resonators. Therefore, it could be deduced that for 1 and 10 U/mL, despite varied conditions of spreading, almost all the platelets had started to spread after ∼70 and 50 min, respectively.
Figure 6.
Typical resonance frequency shift curves of TSM resonators during platelet activation by different concentrations of thrombin (adding thrombin directly after T = 0). To see this figure in color, go online.
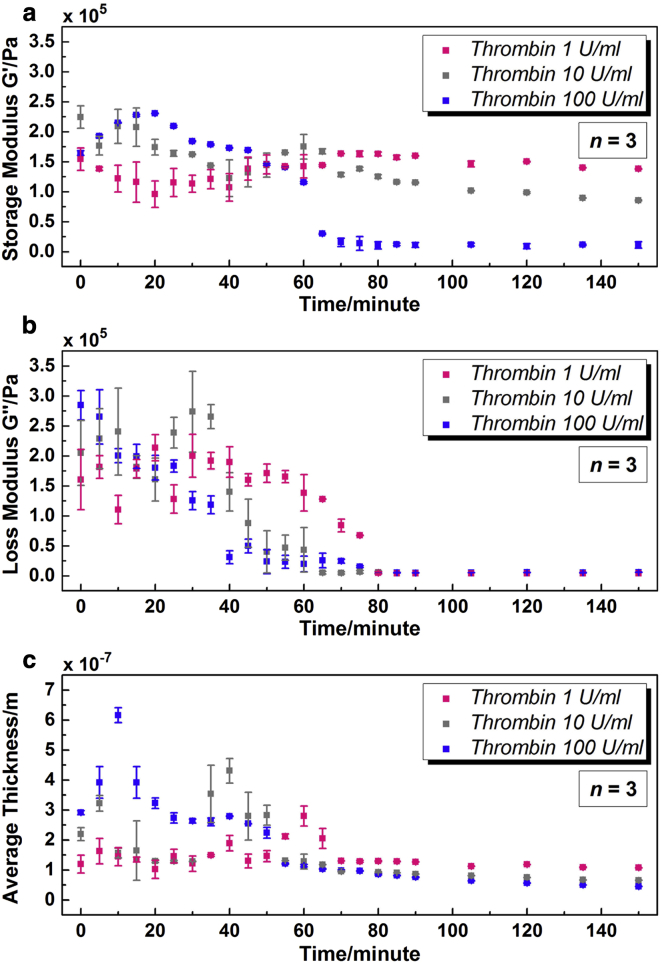
Fig. 7 gives the extracted G′, G″, and hPL at a series of time points of platelet activation by different concentrations of thrombin. The fitting errors for all three concentrations are stabilized <0.2%. Fig. 7 a shows that with varied concentrations of thrombin, the variation tendencies of storage modulus G′ were not exactly the same. For 100 U/mL, there was an increase at first, and then a decrease with continued incubation. However, for 1 and 10 U/mL, there was a slight decrease in the beginning, followed by an increase and a decrease again. As the concentration of thrombin decreased, peak value of G′ decreased gradually, and peak position shifted to a higher time point. G′ could achieve the maximum value of 230,662 ± 452 Pa at 20 min with 100 U/mL thrombin, when the peak values for 1 and 10 U/mL, were, respectively, 163,606 ± 382 Pa at 70 min and 174,973 ± 20,544 Pa at 60 min. After 1 h, as G′ for 100 U/mL tended to be stable, there was still an obvious decrease for low concentrations. In comparison, the variation tendencies of loss modulus G″ for different concentrations were quite similar as shown in Fig. 7 b. G″ went down continuously and then entered a plateau. Primary differences were focused on an extended duration of reduction as the concentration of thrombin decreased. With 100 U/mL thrombin, G″ became <40,000 Pa after only 40 min, when that turned to 80 and 60 min for 1 and 10 U/mL, respectively. In addition, as it is shown in Fig. 7 c, variations of average thickness hPL for three concentrations were also analogous to each other. The value hPL increased in the beginning, and then decreased gradually with continued incubation. For low concentrations, there was a relatively stable stage before hPL arrived at its peak point. The sharp peak observed in hPL of 100 U/mL disappeared in the case of low concentrations, replaced by a flat, backward-shifting peak. For 100 U/mL, the peak value of hPL acquired at 10 min was 616 ± 25 nm. For 1 and 10 U/mL, the peak values were achieved as 280 ± 33 nm at 60 min and 431 ± 41 nm at 40 min, respectively. The final value of hPL rose as the concentration of thrombin decreased. However, for all three concentrations, hPL values were <100 nm after 2.5 h.
Figure 7.
Characterization of platelet monolayer at a series of time points during platelet activation by different concentrations of thrombin (adding thrombin directly after T = 0). (a) Storage modulus G′; (b) loss modulus G″; (c) average thickness hPL. To see this figure in color, go online.
Variations in G′, G″, and hPL depending on thrombin concentrations could be associated with the activation mechanism discussed above. Despite some differences in details, with a decrease of thrombin concentration from 100 to 1 U/mL, all variation peaks and plateaus in G′, G″, and hPL were shifted to higher time points. Changes of low concentrations (1 and 10 U/mL) were not as sharp as that of 100 U/mL, especially the flat peak shapes and low peak values. With addition of thrombin in low concentrations, the activation processes of all adherent platelets were not simultaneous, and part of the resting platelets need to be activated by agonists secreted by activated platelets. When enough platelets had been activated, variations in G′, G″, and hPL started to show evident tendencies, revealing the dominant activities of platelets on TSM resonators. Peak value of hPL was acquired when platelets showed their typical spherical shape as the first transformation in activation process. For 1 and 10 U/mL, the peak values were obtained at 60 and 40 min, respectively, indicating the starting time point of shape transformation for a dominant part of platelets. The peak of G′ appeared 10 ∼ 20 min after the peak of hPL, when some filopods were elaborated from the periphery of platelets but without obvious cell spreading. For 1 and 10 U/mL, the spreading of a large part of platelets started at ∼70 and 60 min, respectively, reaching a good agreement with previous observations from Fig. 6. In fact, for all three concentrations, the overall viscoelasticity and average thickness kept decreasing with platelet spreading, leading to a steady rise of resonance frequency shift of TSM resonators. Thus, specific stages during activation process could be deducted from variations of G′, G″, and hPL. With comparable values of G′, G″, and hPL, it is indicated that the condition of platelets at 2.5 h with thrombin of 1 U/mL were analogous to that at 60 min with 100 U/mL as shown in Fig. 7.
In a series of transmission electron microscopy photos, the cross section of resting platelets is a Frisbee-like shape, and periphery thickness is smaller than the central thickness (central thickness is ∼0.5 μm). Once activated, the thickness of elaborated filopods and lamellipods are observed to be quite thin (<100 nm). In Fig. 5 b, the average thickness hPL of resting platelets was 291 ± 6 nm, and after 1 h of thrombin incubation was ∼100 nm, indicating the same order as that observed by transmission electron microscopy (1). Besides, viscoelasticity of activated platelets in this study is in a good agreement with that obtained by AFM, even though local measurement on individual platelets was conducted in AFM. According to viscoelasticity theory, complex shear modulus GPL = G′ + jG″ depends on oscillation frequency ω. Their relation is described in power-law structural damping model functionally as
| (9) |
where G0 is a modulus scale factor, f0 is a frequency scale factor, α is the power-law exponent usually assigned in 0.10–0.16, λ is structural damping coefficient related to α by λ = tan(πα/2), and μ is a Newtonian viscous damping coefficient (35, 36). With α of small values, the factor Г(1−α)cos(πα/2) is close to unity and so Eq. 9 could be simplified as
| (10) |
Thus, as G0 = constant, G′ ∞ f α. For different concentrations of thrombin, storage modulus G′ of activated platelets was 10 ∼ 130 kPa after 2.5 h. When α is assigned with 0.12, G′ of activated platelets at 20 Hz is calculated as 2 ∼ 27 kPa. When α = 0.14, G′ turns out to be 1 ∼ 21 kPa. The converted storage modulus G′ at low frequency is of the same order of magnitude with AFM results (1 ∼ 50 kPa, ∼20 Hz) (8). From this perspective, G′ as a statistical stiffness of platelet monolayer could reflect the characteristic shear elasticity of individual platelet in a group. In the meantime, due to the stable, average, statistical features of TSM resonators, variations of platelet viscoelasticity during the activation process could be amplified appropriately compared with other local-measurement techniques, implying a potential of TSM resonator sensors for mechanical-property mark. Through high-frequency TSM resonators, reliable and repeatable shear modules of platelet monolayer with varied cytoskeleton are provided in an economic, simple, noninvasive manner. Furthermore, the average thickness of platelet monolayer is obtained as well. According to variations in the shear modulus and the average thickness of cell monolayer, the internal cellular architecture could be deduced and the corresponding status in a variety of procedures (activation, aggregation, etc.) acquired.
Conclusions
In this study, quartz TSM resonator sensor was adopted to monitor the process of platelet activation. Resting platelets adhering to fibrinogen-coated electrodes were activated by different concentrations of thrombin (1, 10, and 100 U/mL), and the corresponding complex shear modulus (G′ + jG″) and the average thickness (hPL) of platelet monolayer at a series of time points were obtained. The extracted G′, G″, and hPL exhibited similar tendencies for varied concentrations of thrombin. Decrease of thrombin concentration brought an overall shift of peaks and plateaus to higher time points in G′, G″, and hPL, which could be associated with the partial activation of platelets by low concentrations of thrombin. Meanwhile, changes of low concentrations (1 and 10 U/mL) were not as sharp as that of 100 U/mL, especially the flat peak shapes and low peak values. Variations in G′, G″, and hPL during activation process could be attributed to the remolding of actin cytoskeleton in platelets, which also induced evident changes in cell morphologies. The peak value of hPL was acquired when platelets presented their typical spherical shape as the first transformation in activation process. The G′ peak appeared 10 ∼ 20 min after hPL peak, when some filopods were observed along the periphery of platelets but without obvious cell spreading. As platelet spreading began and continued, G′, G″, and hPL decreased, leading to a steady rise of resonance frequency shift of TSM resonators. These evaluations identify an economic, quantitative, noninvasive method to measure relevant properties of platelets in real-time, which could also contribute to current PRP treatment. Furthermore, viscoelasticity and thickness changes reflect internal cytoskeleton variations that are involved extensively in a variety of cell activities, such as contractility, proliferation, and differentiation. G′, G″, and hPL could provide useful quantitative measures on platelet structure variations in activation, indicating potential of TSM resonators in characterization of cells during some specific transformation processes. TSM resonators exhibit high reliability and stability in monitoring of platelet activation, revealing an advisable technique to investigate cell activities in general, and platelet activation in particular.
Author Contributions
Q.-M.W. and J.H.-C.W. designed the research; H.W. and G.Z. performed the experiments; H.W. and H.Z. analyzed the data; and H.W., Q.-M.W., and J.H.-C.W. wrote the article.
Acknowledgments
The authors thank Drs. Jianying Zhang and Dr. Yiqin Zhou for their helpful discussions during the course of this study.
This work was supported in part by grant Nos. AR060920, AR061395, and AR065949 (to J.H.-C.W.).
Editor: Douglas Robinson.
Contributor Information
James H.-C. Wang, Email: wanghc@pitt.edu.
Qing-Ming Wang, Email: qiw4@pitt.edu.
References
- 1.Michelson A.D. Elsevier; New York: 2002. Platelets. [Google Scholar]
- 2.Semple J.W., Italiano J.E., Jr., Freedman J. Platelets and the immune continuum. Nat. Rev. Immunol. 2011;11:264–274. doi: 10.1038/nri2956. [DOI] [PubMed] [Google Scholar]
- 3.Foster T.E., Puskas B.L., Rodeo S.A. Platelet-rich plasma: from basic science to clinical applications. Am. J. Sports Med. 2009;37:2259–2272. doi: 10.1177/0363546509349921. [DOI] [PubMed] [Google Scholar]
- 4.Everts P.A.M., Knape J.T.A., van Zundert A. Platelet-rich plasma and platelet gel: a review. J. Extra Corpor. Technol. 2006;38:174–187. [PMC free article] [PubMed] [Google Scholar]
- 5.Nikolidakis D., Jansen J.A. The biology of platelet-rich plasma and its application in oral surgery: literature review. Tissue Eng. Part B Rev. 2008;14:249–258. doi: 10.1089/ten.teb.2008.0062. [DOI] [PubMed] [Google Scholar]
- 6.Alsousou J., Thompson M., Willett K. The biology of platelet-rich plasma and its application in trauma and orthopaedic surgery: a review of the literature. J. Bone Joint Surg. Br. 2009;91:987–996. doi: 10.1302/0301-620X.91B8.22546. [DOI] [PubMed] [Google Scholar]
- 7.Cazenave J.-P., Ohlmann P., Gachet C. Preparation of washed platelet suspensions from human and rodent blood. Methods Mol. Biol. 2004;272:13–28. doi: 10.1385/1-59259-782-3:013. [DOI] [PubMed] [Google Scholar]
- 8.Radmacher M., Fritz M., Hansma P.K. Measuring the viscoelastic properties of human platelets with the atomic force microscope. Biophys. J. 1996;70:556–567. doi: 10.1016/S0006-3495(96)79602-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ploehn H.J., Liu C. Quantitative analysis of Montmorillonite platelet size by atomic force microscopy. Ind. Eng. Chem. Res. 2006;45:7025–7034. [Google Scholar]
- 10.Michelson A.D. Methods for the measurement of platelet function. Am. J. Cardiol. 2009;103(Suppl):20A–26A. doi: 10.1016/j.amjcard.2008.11.019. [DOI] [PubMed] [Google Scholar]
- 11.Hansson K.M., Vikinge T.P., Lindahl T.L. Surface plasmon resonance (SPR) analysis of coagulation in whole blood with application in prothrombin time assay. Biosens. Bioelectron. 1999;14:671–682. doi: 10.1016/s0956-5663(99)00050-0. [DOI] [PubMed] [Google Scholar]
- 12.Hansson K.M., Johansen K., Tengvall P. Surface plasmon resonance detection of blood coagulation and platelet adhesion under venous and arterial shear conditions. Biosens. Bioelectron. 2007;23:261–268. doi: 10.1016/j.bios.2007.04.009. [DOI] [PubMed] [Google Scholar]
- 13.Vikinge T.P., Hansson K.M., Höök F. Comparison of surface plasmon resonance and quartz crystal microbalance in the study of whole blood and plasma coagulation. Biosens. Bioelectron. 2000;15:605–613. doi: 10.1016/s0956-5663(00)00125-1. [DOI] [PubMed] [Google Scholar]
- 14.Bandey H.L., Martin S.J., Hillman A.R. Modeling the responses of thickness-shear mode resonators under various loading conditions. Anal. Chem. 1999;71:2205–2214. doi: 10.1021/ac981272b. [DOI] [PubMed] [Google Scholar]
- 15.Hossenlopp J., Jiang L., Josse F. Characterization of epoxy resin (SU-8) film using thickness-shear mode (TSM) resonator under various conditions. J. Polym. Sci., B, Polym. Phys. 2004;42:2373–2384. [Google Scholar]
- 16.Weber N., Wendel H.P., Kohn J. Formation of viscoelastic protein layers on polymeric surface relevant to platelet adhesion. J. Biomed. Mater. Res. 2005;72A:420–427. doi: 10.1002/jbm.a.30272. [DOI] [PubMed] [Google Scholar]
- 17.Sinn S., Müller L., Gehring F.K. Platelet aggregation monitoring with a newly developed quartz crystal microbalance system as an alternative to optical platelet aggregometry. Analyst (Lond.) 2010;135:2930–2938. doi: 10.1039/c0an00474j. [DOI] [PubMed] [Google Scholar]
- 18.Li R., Sun Y. Surface modification of poly (styrene-b-(ethylene-co-butylene)-b-styrene) elastomer and its plasma protein adsorption by QCM-D. Appl. Surf. Sci. 2014;301:300–306. [Google Scholar]
- 19.Fatisson J., Merhi Y., Tabrizian M. Quantifying blood platelet morphological changes by dissipation factor monitoring in multilayer shells. Langmuir. 2008;24:3294–3299. doi: 10.1021/la7023204. [DOI] [PubMed] [Google Scholar]
- 20.Fatisson J., Mansouri S., Tabrizian M. Determination of surface-induced platelet activation by applying time-dependency dissipation factor versus frequency using quartz crystal microbalance with dissipation. J. R. Soc. Interface. 2011;8:988–997. doi: 10.1098/rsif.2010.0617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lord M.S., Cheng B., Whitelock J.M. The modulation of platelet adhesion and activation by chitosan through plasma and extracellular matrix proteins. Biomaterials. 2011;32:6655–6662. doi: 10.1016/j.biomaterials.2011.05.062. [DOI] [PubMed] [Google Scholar]
- 22.Kunze A., Hesse C., Svedhem S. Real-time monitoring of surface-confined platelet activation on TiO2. Colloids Surf. B Biointerfaces. 2014;116:446–451. doi: 10.1016/j.colsurfb.2014.01.025. [DOI] [PubMed] [Google Scholar]
- 23.Savage B., Saldívar E., Ruggeri Z.M. Initiation of platelet adhesion by arrest onto fibrinogen or translocation on von Willebrand factor. Cell. 1996;84:289–297. doi: 10.1016/s0092-8674(00)80983-6. [DOI] [PubMed] [Google Scholar]
- 24.Osemene N.I. The pharmacist’s role in antiplatelet therapy. US Pharm. 2012;37:32–39. [Google Scholar]
- 25.Ballantine D.S., White R.M., Wohltjen H. Acoustic wave sensor: theory, design, and physico-chemical applications. In: Stern R., Levy M., editors. Applications of Modern Acoustics. Academic Press; Waltham, MA: 1997. [Google Scholar]
- 26.Jiménez Y., Fernández R., Arnau A. A contribution to solve the problem of coating properties extraction in quartz crystal microbalance applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2006;53:1057–1072. [PubMed] [Google Scholar]
- 27.Kino G.S. Prentice-Hall; Englewood Cliffs, NJ: 2000. Acoustic Waves: Devices, Imaging, and Analog Signal Processing; p. 625. [Google Scholar]
- 28.Lucklum R., Behling C., Martin S.J. Determination of complex shear modulus with thickness shear mode resonators. J. Phys. D Appl. Phys. 1997;30:346–356. [Google Scholar]
- 29.Cady W.G. Dover; Mineola, NY: 1964. Piezoelectricity: An Introduction to the Theory and Applications of Electromechanical Phenomena in Crystals; p. 822. [Google Scholar]
- 30.Salt D. Van Nostrand Reinhold, Wokingham; Buckinghamshire, UK: 1987. Hy-Q Handbook of Quartz Crystal Devices. [Google Scholar]
- 31.Qin L., Cheng H., Wang Q.-M. Characterization of polymer nanocomposite films using quartz thickness shear mode (TSM) acoustic wave sensor. Sens. Actuators A Phys. 2007;136:111–117. [Google Scholar]
- 32.Wu H., Zhao G., Wang Q.-M. Aging-related viscoelasticity variation of tendon stem cells (TSCs) characterized by quartz thickness shear mode (TSM) resonators. Sens. Actuators. 2015;210:369–380. doi: 10.1016/j.snb.2014.12.117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shattil S.J., Kashiwagi H., Pampori N. Integrin signaling: the platelet paradigm. Blood. 1998;91:2645–2657. [PubMed] [Google Scholar]
- 34.Hardin J., Bertoni G., Kleinsmith L.J. Pearson Education; Upper Saddle River, NJ: 2012. Becker’s World of the Cell. [Google Scholar]
- 35.Fabry B., Maksym G.N., Fredberg J.J. Scaling the microrheology of living cells. Phys. Rev. Lett. 2001;87:148101–148104. doi: 10.1103/PhysRevLett.87.148102. [DOI] [PubMed] [Google Scholar]
- 36.Smith B.A., Tolloczko B., Grütter P. Probing the viscoelastic behavior of cultured airway smooth muscle cells with atomic force microscopy: stiffening induced by contractile agonist. Biophys. J. 2005;88:2994–3007. doi: 10.1529/biophysj.104.046649. [DOI] [PMC free article] [PubMed] [Google Scholar]