Abstract
Bacteria that are subjected to ribosome-inhibiting antibiotic drugs show an interesting behavior: Although the drug slows down cell growth, it also paradoxically increases the cell’s concentration of ribosomes. We combine our earlier nonlinear model of the energy-biomass balance in undrugged Escherichia coli cells with Michaelis-Menten binding of drugs that inactivate ribosomes. Predictions are in good agreement with experiments on ribosomal concentrations and synthesis rates versus drug concentrations and growth rates. The model indicates that the added drug drives the cell to overproduce ribosomes, keeping roughly constant the level of ribosomes producing ribosomal proteins, an important quantity for cell growth. The model also predicts that ribosomal production rates should increase and then decrease with added drug. This model gives insights into the driving forces in cells and suggests new experiments.
Introduction
Drugs such as chloramphenicol act to reduce bacterial cell growth rates by inhibiting bacterial ribosomes and thereby reducing the cell’s production of proteins. What actions does the cell invoke to counter the effects of the drug? On the one hand, there is often a good understanding of how the drug binds at its ribosomal site (1, 2, 3), and it is sometimes known how that binding interferes with protein elongation (4, 5, 6, 7). It is also sometimes known how drugs sensitize local networks to evoke adaptive responses (8, 9, 10, 11). On the other hand, there is usually less understanding of what global stresses the drug triggers, how it shifts the balances of energy and biomass, or what homeostatic condition the cell might be trying to preserve.
There are various approaches to cell-level modeling. One approach models the dynamics of the cell’s networks of biochemical reactions (12, 13, 14). Even in an organism as simple as a bacterium, there are very many interconnected reactions, making it complicated to model. Another approach has been flux-balance analysis (15, 16), which gives solutions by linearizing the forces around some given homeostasis point. Here, however, we are interested in how those homeostasis points themselves are shifted by the drug. Homeostasis is a fundamentally nonlinear phenomenon, describing the cell’s return to a stable state after a perturbation. Like the Le Chatelier principle in physics (17), homeostasis describes a process resembling a marble rolling back to the bottom of a well after being pushed, with the stable state acting as the well bottom of an energy function. Here, we address the nonlinearities and feedback that are needed to explore how the homeostasis balance is tipped by the drug, but to do this in a way that can give simple insights, we use a reduced (minimalist) description of the bacterial cell (18). We use this model to study the response of Escherichia coli to chloramphenicol.
Our goal here is a quantitative description of the energy-limited cell in the absence and presence of varying amounts of drug, in terms of the physicochemical processes of the undrugged cell developed recently (18). (By energy-limited cells, we mean cells whose growth is limited by a sugar source, such as glucose, rather than by amino acids, for example). Our minimal model expresses the dynamical concentrations and fluxes of three internal cell components—ribosomal protein, nonribosomal protein, and internal energy (lumped into a single category we call ATP)—as a function of external sugar, such as glucose. We previously found that healthy E. coli under good growth conditions (speeds up to one duplication per hour) have achieved an evolutionary balance (18). On the one hand, the cell invests energy and biomass in increasing its ribosome concentration, because that increases the cell’s growth speed. On the other hand, too much energy and biomass devoted to producing ribosomes leads to starving the cell’s ability to take in food and convert it to ATP. In this article, we ask how drugging the cell affects its balance of energy and biomass.
Materials and Methods
A minimal model of E. coli in the presence of drugs
We model the energy-limited growth of E. coli using three rate equations to characterize energy (ATP concentration (A)), ribosomal (Ract) and nonribosomal protein concentrations (P) as functions of time, t (18), and a constraint:
| (1) |
| (2) |
| (3) |
| (4) |
where the fluxes are defined as
| (5) |
| (6) |
| (7) |
Here, Ja is the rate of glucose conversion for ATP generation, and Jp and Jr are the respective rates of synthesis of nonribosomal proteins and ribosomes. kr, kp, and ka(G) are the respective rate constants for ribosomal biogenesis, protein translation, and energy generation. The units of rates and rate constants are mM/h and per hour, respectively. ma is the moles of ATP per mole of glucose generated, and mr and mp are the respective moles of ATP consumed per unit mole of ribosome (≡ Mr g ribosomal proteins) and nonribosomal proteins (≡ Mp g) synthesized. Our work is not the first to model the biomass balance in bacteria (see previous studies (19, 20, 21, 22, 23, 24, 25)). What is new here, to our knowledge, is the coupling between the biomass and energy balance (also see Weisse et al. (26)).
The functional forms in Eqs. 5–7 reflect wild-type regulatory mechanisms that coordinate the syntheses of ribosomal and nonribosomal proteins, which are complex (27, 28) and depend on the cell’s energy status. To capture these dependencies, we adopt the undrugged cell functions (18):
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
See the Supporting Material for values of biophysical constants, capacities , , and , and parameters Dr, Dp, Dpp, Dg, and Da, which define the nonlinearities in the respective pathways. In addition, here we consider the effects of drug X as shown in Fig. 1. X is an antibiotic drug that targets ribosomes. There is a broad class of natural and synthetic bacteriostatic antibiotics of this type, such as chloramphenicol, that target protein synthesis. The model presented here is intended as a general description of that class of drugs (3). We assume that X permeates passively from the extracellular medium into the cytosol through the cell membrane. We assume that free drug concentrations outside and inside the cell are equal, a reasonable approximation for E. coli based on similar values of drug binding kinetics from in vivo and in vitro measurements (see Harvey and Koch (29) and Lewinson et al. (30).
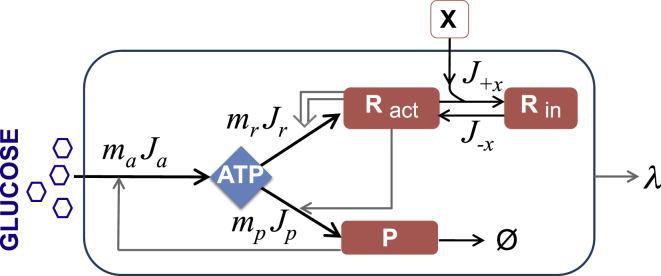
Figure 1.
Minimal kinetic model of E. coli. The model expresses the dynamical fluxes (arrows) and concentrations of active ribosomes (Ract), nonribosomal proteins (P), and a lumped internal energy (ATP). The double arrow shows a positive feedback mechanism for ribosomal autosynthesis, a key controller of growth behavior. Antibiotic inhibitor molecules are represented by X. X binds reversibly with active ribosomes. While in the bound form, Rin, the ribosomes are inactivated, and they do not translate proteins. P degrades with rate constant γ. The cell grows exponentially, with a specific growth rate of λ.
The binding of X to the ribosomes, which occurs with rate constant k+x, halts peptide-chain elongation, as represented by the dynamics
| (13) |
| (14) |
Here, J+x is the rate at which ribosomes become inactivated due to binding with the drug and J−x is the rate of unbinding. Rin is the concentration of ribosomes that have been inactivated by binding to the drug, and Ract, as noted above, is the intracellular concentration of active ribosomes. Thus, Ract + Rin is the total concentration of ribosomes in the cell. x is the extracellular concentration of drugs.
A key quantity in this model is the fraction of ribosomes that are active α(x) for a given drug concentration x. We assume a steady state, so we set dRin/dt = 0 in Eq. 13. We also assume that the rate constant for drug-ribosome unbinding is much faster than dilution, k−x ≫ λ. Thus, we get
| (15) |
| (16) |
For the equilibrium dissociation constant of chloramphenicol, we use (k−x/k+x) ≡ Kd ∼3 μM (29). α = 1 represents the situation of no drug. Increasing drug concentration decreases α toward zero.
The fraction of all proteins (by mass) that are active ribosomes is
| (17) |
and the fraction of all proteins that are all ribosomes (active plus inactive) is
| (18) |
The last equality in Eq. 18 expresses how the ribosomal content of the cell depends on its growth rate, λ, and other properties. Then, the fraction of active ribosomes devoted to translating ribosomal proteins is
| (19) |
Further, the rate of ribosome synthesis, Jfr ≡ MrJr/ρ, in units of grams of ribosomal protein per gram of total protein per hour can be computed as (see the Supporting Material)
| (20) |
Under growth conditions in the absence of drugs, α = 1 and , we use Eqs. 18 and 20 to obtain the rate of ribosome synthesis as
| (21) |
Results
The drugged cell overproduces total ribosomes to maintain sufficiently many active ribosomes
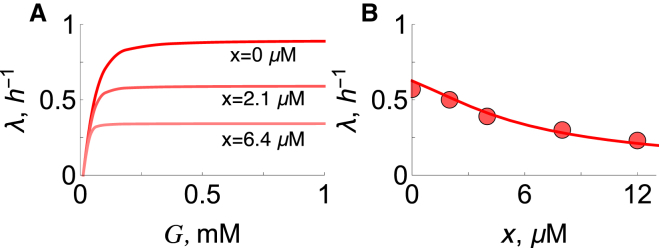
Here, we describe the model predictions. We solve ordinary differential equations (ODEs) 1–14 under steady-state conditions for different concentrations of glucose and antibiotic drug. Fig. 2 A shows that the model predicts Monod-like behavior (31) of growth rate versus glucose concentration under different drug concentrations. As expected, the model predicts that increasing the drug leads to diminishing maximum growth rates.
Figure 2.
E. coli physiological correlations. (A) Growth rate versus extracellular glucose concentration from a simulation for antibiotic (chloramphenicol) concentrations of 0, 2.1, and 6.4 μM. (B) Dependence of growth rate, λ, on antibiotic concentration, x. The line is the numerical solution of the ODE model, with G = 0.08 mM (red line). Red solid circles represent the experimental data (10) of E. coli grown on glucose + M63.
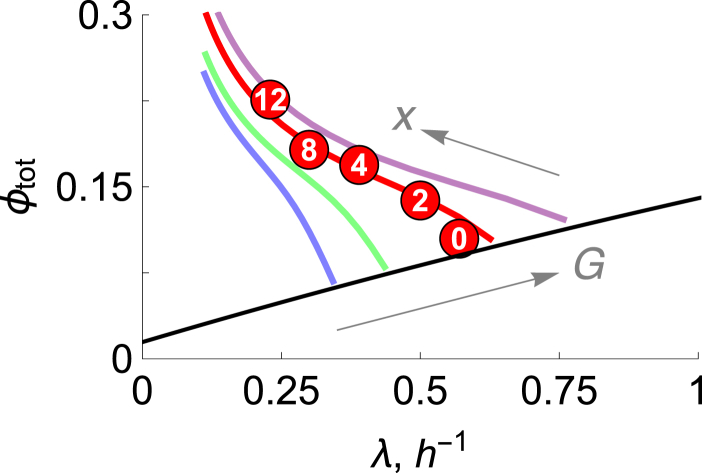
Fig. 3 shows that the model is consistent with experiments indicating how the added drug stimulates total ribosome production even as it reduces the cell’s growth rate (10, 32). The black line shows that for undrugged cells, ribosomes become upshifted relative to other protein biomass with increasing cellular growth rate. The red line and data points show that the added drug does two things: it increases the ribosomal fraction while simultaneously reducing the growth rate.
Figure 3.
E. coli ribosomal protein fraction versus growth rates. Numerical solutions of the ODE model, with increasing glucose concentrations (in mM) G = 0.04 (blue), 0.05 (green), 0.08 (red), and 0.125 (purple), and antibiotic concentrations x = 0 → 25 μM (arrows). Circles represent the experimental data (10) for E. coli grown on glucose + M63 at different dosages of chloramphenicol (in μM). To get ϕ, the rRNA/protein ratio from Scott et al. (10) is scaled by a factor of 0.46 (20). The black line represents the prediction from theory (Eq. 18), with , h−1, γ = 0.1 h−1, and α = 1 (absence of drugs).
Our result reduces to the linear model of Scott et al. (10) in the limit of zero degradation. To see this, note that (see Supporting Material)
| (22) |
where λa ≡ (maka)/mp is a measure of the specific rate of energy generation and εrp = (εp − εr)/εr. εr ≡ (Mr/mr) and εp = (Mp/mp) are constants denoting the respective gram weights of ribosomal and nonribosomal proteins synthesized per mole of ATP. Setting εrp ∼0 and γ ∼0 gives ϕtot ∼1 − λ/λa, which is just the linear relationship of Scott et al. (10).
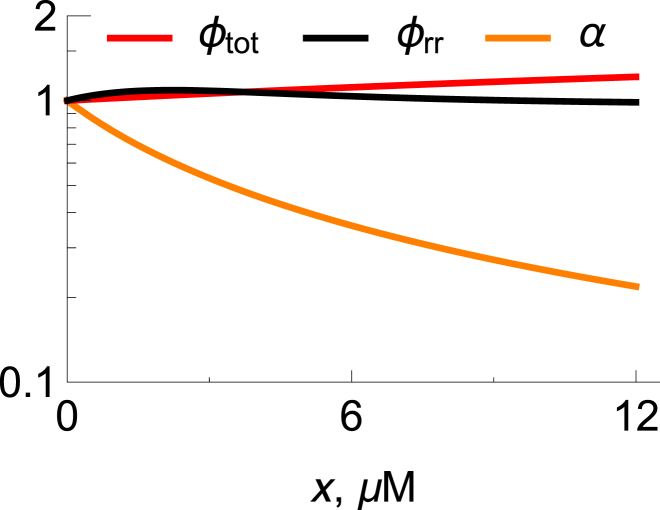
What is the cell trying to achieve under the burden of the drug? As noted above, the effect of the drug is to decrease substantially the fraction of useful ribosomes, as depicted by the quantity α in Fig. 4. However, Fig. 4 also shows that there is remarkable relative constancy in two other quantities, ϕtot and ϕrr, independent of the concentration of drug. Ribosomes make either ribosomal or nonribosomal proteins. ϕrr is the fraction of active ribosomes that are producing other ribosomes (see Fig. 1, double arrow; see also Figs. S2–S4), and ϕtot is the fraction of all proteins that are ribosomal. The constancy of these quantities suggests that the cell senses and regulates how many of its proteins are ribosomes, or how many are ribosomes producing other ribosomes. Such processes may be mediated by ppGpp, the molecule that provides stringent control of ribogenesis in the presence of antibiotic stress (27, 33). To our knowledge, ϕrr has not been measured experimentally.
Figure 4.
Effect of ribosomal inhibitors on cellular homeostasis. Lines are scaled numerical solutions of the ODE model, with G = 0.08 mM. The orange line represents the active ribosomes, [α(x)/α(x = 0)], as a function of drug concentration, x. The red line represents the total ribosomes, [ϕtot(x)/ϕtot(x = 0)]. The black line represents the fraction of active ribosomes that are producing ribosomal proteins, [ϕrr(x)/ϕrr(x = 0)] (Eq. 19). Also see Figs. S2–S4.
The drug shifts the production rate of ribosomes but has little effect on energy flow from glucose to ATP
In this section, we get further insights from looking at two additional properties of the model. First, in Fig. 5, we go beyond concentrations of ribosomes and consider the rate of production of ribosomes, Jfr = λ × ϕtot(λ) (Eq. 20), which we also call ribosomal flux. We find (see below) that although high drug concentrations increase the number of ribosomes, they also reduce the rate of ribosome production. Second, Fig. 6 shows that added drug reduces the growth rate by reducing the catabolic conversion of glucose to ATP. Here are the details.
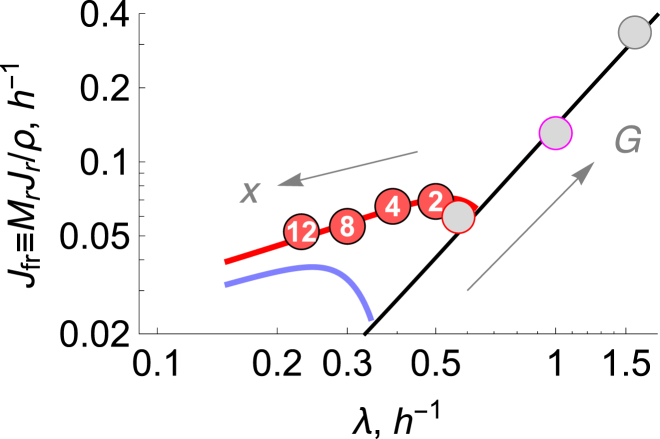
Figure 5.
Effect of ribosomal inhibitors on ribosomal activity. The symbols show the rate of ribosomal synthesis, Jfr = MrJr/ρ, versus specific growth rate of E. coli converted from the experimental ϕ − k data. Chloramphenicol concentrations (in μM) are indicated inside the circles. Nutrients were M63 + glucose (red) at T = 37 C (10). Gray solid circles represent experimental data (10) in the absence of drugs. To get ϕ, the rRNA/protein ratio from Scott et al. (10) is scaled by a factor of 0.46 (20). The blue line represents the ODE model prediction at constant G = 0.04 mM with chloromaphenicol varied according to x = 0 → 15 μM (arrow). The black line represents the theoretical prediction (Eq. 21) in the absence of drugs, with , h−1, and h−1. Also see Fig. S1.
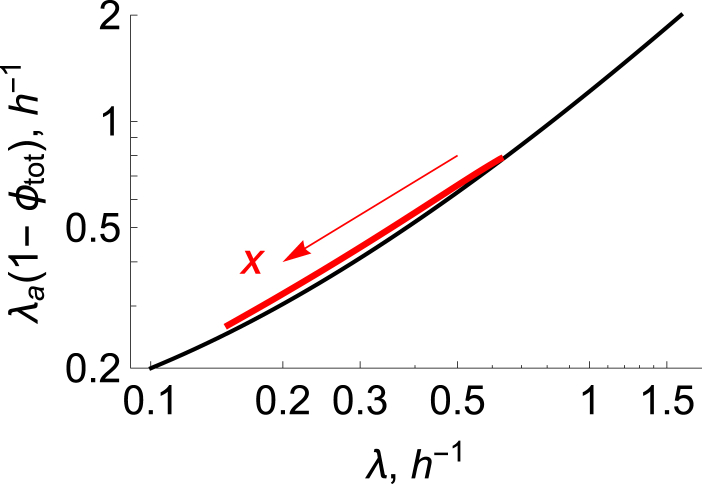
Figure 6.
Effect of ribosomal inhibitors on the rate of energy metabolism. Shown are predictions of the rate of energy metabolism versus growth rate, λ, from the ODE model with glucose varied, G = 0 − 1 mM, and no drugs (black line), and the prediction at G = 0.04 mM (red line), with the drug dosage varied according to x = 0 → 15 μM (arrow). An increase in drug concentration reduces both rates of growth and energy generation.
First, focus on the black line in Fig. 5. According to the model, under the no-drug condition, the ribosomal production rate should scale as the square of the growth rate, , since ϕtot ∝ λ. Fig. 5 shows a log-log plot. The black line shows the square-law prediction for undrugged cells. The data points shown in gray lie along this black line, indicating that the model predicts well the ribosomal production rates of undrugged cells growing at different speeds.
Next, focus on the red points in Fig. 5. The data points, containing circled numbers between 2 and 12 (μM), show the effects of increasing the amount of drug at fixed nutrients. Following the red line toward the left, which describes increasing drug concentrations, shows how the drug reduces the growth rate while also reducing the production rate of ribosomes. The experimental data points are from Scott et al. (10); also see the Supporting Material.
Finally, the blue line in Fig. 5 makes an interesting prediction, for which, to our knowledge, there is no experimental evidence. The blue line represents cell growth under low nutrients, 0 < λ ≲ 0.8 h−1, and it has curvature. This shows that although ribosomal flux is increased by small amounts of added drug, that flux is decreased by larger amounts of drug due to the reduction of cell growth at high drug concentrations.
We can draw another inference by comparing the blue and black lines on Fig. 5. Those two lines intersect around λ = 0.35 h−1, defining the point of no drug. From this point, there are two ways to increase the ribosomal flux, Jfr (the y axis). You can either give the cells more food (leading to the black line, increasing to the right) or give them drugs (leading to the blue line, increasing to the left). It suggests that there are (at least) two signals that increase cellular ribosome fluxes: a signal about energy availability and a signal about numbers of active ribosomes.
Related to that point, Fig. 6 shows the prediction of λa(1 − ϕ), which is a measure of the energy flux in the conversion of glucose to ATP, maka(G) × P. Fig. 6 shows that there is a single universal relationship between that energy flux and growth rate, irrespective of whether growth is controlled by drugs or food. This indicates the nature of feedback in the cell. It is not simply the energy inflow (input) that dictates the growth rate (output). The growth rate is also a controller of the energy influx. This is interesting in the context of drugs, which can more strongly affect the growth-rate dependence of the rate of ribosomal synthesis than energy influx. As far as we know, there are no experiments that bear out this prediction.
Discussion
This model makes some predictions that have not yet been tested experimentally. We hope experimentalists will make such tests, to give deeper insights into these nonlinear behaviors that will ultimately lead to improved models. Current experiments on drugged and undrugged bacteria are run on different food sources and in different media. Deeper tests of our model could come from studies in which the types of nutrient and the media are fixed and only the food concentration is varied. In addition, a key variable here is λa, the cell’s conversion efficiency of sugar to internal energy, such as ATP. It would be valuable to have measurements of glucose and oxygen uptake rates, ATP production rates (maJa), ATP concentrations, and ribosome production rates (Jr), as well as key glycolytic, tricarboxylic acid cycle, and fermentation enzyme concentrations, as a function of external glucose and antibiotic concentrations.
Somewhat different models are those of Elf et al. (34) and Deris et al. (35), who consider bistabilities of cells resulting either from membrane properties or drug resistance. Other models focus on mechanisms of microscopic control of ribosome synthesis, such as the stringent response, a negative feedback mechanism triggered when some of a cell’s excess usable energetic molecules are converted to unusable ppGpp in response to endogenous limitations of amino acids (21, 28, 36). Because of its simplicity, the treatment described here could be extended to explore other factors that are of interest, such as cellular geometry (surface-volume considerations), multidrug effects (37), or drug-dependent cellular multistabilities that lead to antibiotic resistance and persistence (34, 35).
Conclusions
Here, we model the balance of energy, ribosomes, and nonribosomal proteins in E. coli cells in the presence of chloramphenicol, an antibiotic drug. We suppose that chloramphenicol binds to ribosomes and inactivates them, in a Michaelis-Menten fashion. We combine this binding-induced inactivation of ribosomes with a three-component dynamical model of E. coli’s energy and ribosomal and nonribosomal protein biomass as a function of growth rates, which was previously validated against experiments on undrugged bacteria. This model gives quantitative predictions for how the cell’s growth rate decreases with added drug, and how the total ribosomal fraction of the protein increases with drug. Also, it predicts that adding drugs to slow-growing cells leads to an increase in the rate of ribosomal synthesis, followed by a decrease as the cell gets sicker. We show the model agreement with the data. However, more important are the insights the model gives about how the cell responds to the drug, what varies and what stays constant. We find that although drugging the cell reduces the concentration of active ribosomes, it also stimulates more total ribosome production, holding relatively constant the ribosomal production of ribosomes, a key quantity the cell uses to toggle between growth and self-protection.
Author Contributions
A.M. and K.A.D designed the research; A.M. performed the research; A.M. and K.A.D. analyzed the data; and A.M. and K.A.D. wrote the article.
Acknowledgments
We appreciate support from the Laufer Center at Stony Brook University.
Editor: Dennis Bray.
Footnotes
This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).
Supporting Materials and Methods, four figures, and three tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)04758-X.
Supporting Material
References
- 1.Poehlsgaard J., Douthwaite S. The bacterial ribosome as a target for antibiotics. Nat. Rev. Microbiol. 2005;3:870–881. doi: 10.1038/nrmicro1265. [DOI] [PubMed] [Google Scholar]
- 2.Tenson T., Mankin A. Antibiotics and the ribosome. Mol. Microbiol. 2006;59:1664–1677. doi: 10.1111/j.1365-2958.2006.05063.x. [DOI] [PubMed] [Google Scholar]
- 3.Wilson D.N. Ribosome-targeting antibiotics and mechanisms of bacterial resistance. Nature Rev. Microbiol. 2014;12:35–48. doi: 10.1038/nrmicro3155. [DOI] [PubMed] [Google Scholar]
- 4.Kurland C.G., Maaloe O. Regulation of ribosomal and transfer RNA synthesis. J. Mol. Biol. 1962;4:193–210. doi: 10.1016/s0022-2836(62)80051-5. [DOI] [PubMed] [Google Scholar]
- 5.Coffman R.L., Norris T.E., Koch A.L. Chain elongation rate of messenger and polypeptides in slowly growing Escherichia coli. J. Mol. Biol. 1971;60:1–19. doi: 10.1016/0022-2836(71)90442-6. [DOI] [PubMed] [Google Scholar]
- 6.Drainas D., Kalpaxis D.L., Coutsogeorgopoulos C. Inhibition of ribosomal peptidyltransferase by chloramphenicol. Kinetic studies. Eur. J. Biochem. 1987;164:53–58. doi: 10.1111/j.1432-1033.1987.tb10991.x. [DOI] [PubMed] [Google Scholar]
- 7.Siibak T., Peil L., Tenson T. Erythromycin- and chloramphenicol-induced ribosomal assembly defects are secondary effects of protein synthesis inhibition. Antimicrob. Agents Chemother. 2009;53:563–571. doi: 10.1128/AAC.00870-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tamae C., Liu A., Miller J.H. Determination of antibiotic hypersensitivity among 4,000 single-gene-knockout mutants of Escherichia coli. J. Bacteriol. 2008;190:5981–5988. doi: 10.1128/JB.01982-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kohanski M.A., Dwyer D.J., Collins J.J. How antibiotics kill bacteria: from targets to networks. Nat. Rev. Microbiol. 2010;8:423–435. doi: 10.1038/nrmicro2333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Scott M., Gunderson C.W., Hwa T. Interdependence of cell growth and gene expression: origins and consequences. Science. 2010;330:1099–1102. doi: 10.1126/science.1192588. [DOI] [PubMed] [Google Scholar]
- 11.Nonejuie P., Burkart M., Pogliano J. Bacterial cytological profiling rapidly identifies the cellular pathways targeted by antibacterial molecules. Proc. Natl. Acad. Sci. USA. 2013;110:16169–16174. doi: 10.1073/pnas.1311066110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kitano H. Computational cellular dynamics: A network-physics integral. Nat. Rev. Mol. Cell Biol. 2006;7:163. [Google Scholar]
- 13.Domach M.M., Leung S.K., Shuler M.L. Computer model for glucose-limited growth of a single cell of Escherichia coli B/r-A. Biotechnol. Bioeng. 1984;26:203–216. doi: 10.1002/bit.260260303. [DOI] [PubMed] [Google Scholar]
- 14.Chassagnole C., Noisommit-Rizzi N., Reuss M. Dynamic modeling of the central carbon metabolism of Escherichia coli. Biotechnol. Bioeng. 2002;79:53–73. doi: 10.1002/bit.10288. [DOI] [PubMed] [Google Scholar]
- 15.Orth J.D., Thiele I., Palsson B.O. What is flux balance analysis? Nat. Biotechnol. 2010;28:245–248. doi: 10.1038/nbt.1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Edwards J.S., Palsson B.O. The Escherichia coli MG1655 in silico metabolic genotype: its definition, characteristics, and capabilities. Proc. Natl. Acad. Sci. USA. 2000;97:5528–5533. doi: 10.1073/pnas.97.10.5528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dill K., Bromberg S. Garland Science; New York: 2003. Molecular Driving Forces: Statistical Thermodynamics in Chemistry and Biology. [Google Scholar]
- 18.Maitra A., Dill K.A. Bacterial growth laws reflect the evolutionary importance of energy efficiency. Proc. Natl. Acad. Sci. USA. 2015;112:406–411. doi: 10.1073/pnas.1421138111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hinshelwood C.N. On the chemical kinetics of autosynthetic systems. J. Chem. Soc. 1952:745–755. [Google Scholar]
- 20.Bremer H., Dennis P. Modulation of chemical composition and other parameters of the cell by growth rate. In: Neidhardt F.C., Ingraham J.L., Magasanik B., Low K.B., Schaechter M., Umbarger H.E., editors. Escherichia coli and Salmonella: Cellular and Molecular Biology. ASM Press; Washington, DC: 1996. pp. 1553–1569. [Google Scholar]
- 21.Scott M., Klumpp S., Hwa T. Emergence of robust growth laws from optimal regulation of ribosome synthesis. Mol. Syst. Biol. 2014;10:747. doi: 10.15252/msb.20145379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Marr A.G. Growth rate of Escherichia coli. Microbiol. Rev. 1991;55:316–333. doi: 10.1128/mr.55.2.316-333.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Molenaar D., van Berlo R., Teusink B. Shifts in growth strategies reflect tradeoffs in cellular economics. Mol. Syst. Biol. 2009;5:323. doi: 10.1038/msb.2009.82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zaslaver A., Kaplan S., Itzkovitz S. Invariant distribution of promoter activities in Escherichia coli. PLOS Comput. Biol. 2009;5:e1000545. doi: 10.1371/journal.pcbi.1000545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bosdriesz E., Molenaar D., Bruggeman F.J. How fast-growing bacteria robustly tune their ribosome concentration to approximate growth-rate maximization. FEBS J. 2015;282:2029–2044. doi: 10.1111/febs.13258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Weisse A.Y., Oyarzún D.A., Swain P.S. A mechanistic link between cellular trade-offs, gene expression and cellular growth. Proc. Natl. Acad. Sci. USA. 2015;112:E1038. doi: 10.1073/pnas.1416533112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nomura M., Gourse R., Baughman G. Regulation of the synthesis of ribosomes and ribosomal components. Annu. Rev. Biochem. 1984;53:75–117. doi: 10.1146/annurev.bi.53.070184.000451. [DOI] [PubMed] [Google Scholar]
- 28.Lemke J.J., Sanchez-Vazquez P., Gourse R.L. Direct regulation of Escherichia coli ribosomal protein promoters by the transcription factors ppGpp and DksA. Proc. Natl. Acad. Sci. USA. 2011;108:5712–5717. doi: 10.1073/pnas.1019383108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Harvey R.J., Koch A.L. How partially inhibitory concentrations of chloramphenicol affect the growth of Escherichia coli. Antimicrob. Agents Chemother. 1980;18:323–337. doi: 10.1128/aac.18.2.323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lewinson O., Adler J., Bibi E. The Escherichia coli multidrug transporter MdfA catalyzes both electrogenic and electroneutral transport reactions. Proc. Natl. Acad. Sci. USA. 2003;100:1667–1672. doi: 10.1073/pnas.0435544100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Koch A.L. Multistep kinetics: choice of models for the growth of bacteria. J. Theor. Biol. 1982;98:401–417. doi: 10.1016/0022-5193(82)90127-8. [DOI] [PubMed] [Google Scholar]
- 32.Dennis P.P. Effects of chloramphenicol on the transcriptional activities of ribosomal RNA and ribosomal protein genes in Escherichia coli. J. Mol. Biol. 1976;108:535–546. doi: 10.1016/s0022-2836(76)80135-0. [DOI] [PubMed] [Google Scholar]
- 33.Potrykus K., Murphy H., Cashel M. ppGpp is the major source of growth rate control in E. coli. Environ. Microbiol. 2011;13:563–575. doi: 10.1111/j.1462-2920.2010.02357.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Elf J., Nilsson K., Ehrenberg M. Bistable bacterial growth rate in response to antibiotics with low membrane permeability. Phys. Rev. Lett. 2006;97:258104. doi: 10.1103/PhysRevLett.97.258104. [DOI] [PubMed] [Google Scholar]
- 35.Deris J.B., Kim M., Hwa T. The innate growth bistability and fitness landscapes of antibiotic-resistant bacteria. Science. 2013;342:1237435. doi: 10.1126/science.1237435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.English B.P., Hauryliuk V., Elf J. Single-molecule investigations of the stringent response machinery in living bacterial cells. Proc. Natl. Acad. Sci. USA. 2011;108:E365. doi: 10.1073/pnas.1102255108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bollenbach T., Quan S., Kishony R. Nonoptimal microbial response to antibiotics underlies suppressive drug interactions. Cell. 2009;139:707–718. doi: 10.1016/j.cell.2009.10.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.