Abstract
During development, interactions between transcription factors control the specification of different cell fates. The regulatory networks of genetic interactions often exhibit multiple stable steady states; such multistability provides a common dynamical basis for differentiation. During early murine embryogenesis, cells from the inner cell mass (ICM) can be specified in epiblast (Epi) or primitive endoderm (PrE). Besides the intracellular gene regulatory network, specification is also controlled by intercellular interactions involving Erk signaling through extracellular Fgf4. We previously proposed a model that describes the gene regulatory network and its interaction with Erk signaling in ICM cells. The model displays tristability in a range of Fgf4 concentrations and accounts for the self-organized specification process observed in vivo. Here, we further investigate the origin of tristability in the model and analyze in more detail the specification process by resorting to a simplified two-cell model. We also carry out simulations of a population of 25 cells under various experimental conditions to compare their outcome with that of mutant embryos or of embryos submitted to exogenous treatments that interfere with Fgf signaling. The results are analyzed by means of bifurcation diagrams. Finally, the model predicts that heterogeneities in extracellular Fgf4 concentration play a primary role in the spatial arrangement of the Epi/PrE cells in a salt-and-pepper pattern. If, instead of heterogeneities in extracellular Fgf4 concentration, internal fluctuations in the levels of expression of the transcription factors are considered as a source of randomness, simulations predict the occurrence of unrealistic switches between the Epi and the PrE cell fates, as well as the evolution of some cells toward one of these states without passing through the previous ICM state, in contrast to what is observed in vivo.
Introduction
During early murine embryogenesis, two differentiation processes take place before the implantation of the egg in the uterus. The first one gives rise to the inner cell mass (ICM) and the trophectoderm (TE), which express Oct4 and Cdx2, respectively. The second differentiation process corresponds to the specification of ICM cells into primitive endoderm (PrE) and epiblast (Epi) cells. Whereas PrE and TE cells contribute to the formation of extraembryonic tissues, such as the placenta, Epi cells mainly give rise to the embryo itself. The epiblast is also the cellular compartment from which embryonic stem (ES) cells can be derived. ES cells are invaluable tools in a wide range of medical applications. For these reasons, understanding the molecular mechanisms leading to the formation of Epi cells constitutes an important goal in developmental biology.
The differentiation of ICM cells into Epi and PrE is controlled by two antagonistic transcription factors, Nanog and Gata6. Nanog is necessary to produce Epi cells (1, 2, 3, 4), whereas Gata6 is required for the specification of PrE cells both in vitro and in vivo (5, 6). These genes start to be zygotically expressed around the two/four-cell stage (corresponding to embryonic day E1.5–E2), and both proteins can be detected in most ICM cells by the eight-cell stage (E2.5). Between the 8- and 32-cell stages, Nanog and Gata6 proteins are coexpressed at increasing levels in almost all ICM cells (7, 8, 9, 10). Then, from E3.0–E3.25, their expression patterns start to become mutually exclusive. As a consequence, at E3.75, two distinct cell types—distributed in a salt-and-pepper pattern—constitute the ICM: Gata6-expressing PrE progenitors and Nanog-expressing Epi progenitors (8, 9, 11, 12, 13). Later on, these two populations are sorted out so that PrE cells form an epithelium that separates the Epi cells from the blastocoel (8, 14, 15, 16).
The Fgf/Erk signaling pathway has been shown to bias the Epi/PrE fate choice during embryonic development. Indeed, the proper specification of PrE requires the expression of the Fgf receptor Fgfr2, the Fgf ligand Fgf4, and the Erk adaptor Grb2 (12, 17, 18, 19, 20, 21, 22). Moreover, between E3.0–E3.25 and E4.0, ICM cells can be forced to differentiate into a specific fate (Epi or PrE) in response to exogenously induced, nonphysiological variations in Fgf/Erk signaling. Indeed, culturing wild-type (WT) embryos with inhibitors of the Fgf/Erk signaling pathway leads to the absence of PrE cells, whereas culturing them with recombinant Fgf4 induces a severe reduction in the number of Epi cells (23, 24).
To back up the experimental investigation of the intricate roles of Nanog, Gata6, and Fgf signaling in determining the Epi or PrE cell fates, we previously built a computational model describing the gene regulatory network (GRN) controlling ICM specification (6). We found that in appropriate conditions, this model exhibits three stable steady states (tristability), which correspond to ICM, Epi, and PrE cells, respectively. Computational simulations replicated or predicted a variety of cell behaviors observed in different experimental conditions, namely, 1) the self-organized evolution of a population of 25 cells toward the ICM-like state first, followed by a specification into Epi or PrE cells (reaching similar amounts and displaying a salt-and-pepper pattern); 2) forced differentiation into a specific fate (Epi or PrE) in response to the exogenously induced variations in Fgf/Erk signaling described in the previous paragraph; 3) specification into the Epi phenotype for all cells in the Gata6−/− mutant, as well as a partial deficit in the specification of PrE cells in Gata6+/− embryos; and 4) faster specification into Epi cells in Gata6 mutants and heterozygotes compared to wild-type embryos.
In this work, we further develop our analysis of the transition between ICM and PrE or Epi cells corresponding to switches between the three possible steady states of the Fgf-modulated GRN. We first address the origin of tristability, in particular as compared to the conceptual mechanism initially proposed by Huang et al. (25). Second, we elaborate on the specification mechanism based on self-organized transitions between the three steady states; to this end, we consider a simplified model describing the interplay between two ICM cells through Fgf/Erk signaling. Going back to the full model for a population of cells, we then demonstrate that it also accounts for the developmental behavior of Nanog−/− mutant embryos previously described (4). Finally, we compare the potential roles of molecular fluctuations in gene expression and of inhomogeneity in extracellular Fgf4 concentration in the process of cell-fate specification and in the establishment of the salt-and-pepper pattern.
Materials and Methods
Model
The model and the default values of the parameters are the same as in our previous work (6). Evolution equations describe the GRN and its interactions with Fgf4/Erk signaling. To model the GRN in a single cell, we used four evolution equations that govern the evolution of the key factors, G (Gata6 concentration), N (Nanog concentration), FR (Fgf receptor 2 (FGFR2) concentration), and ERK (normalized level of Fgf/Erk activity):
| (1) |
| (2) |
| (3) |
| (4) |
Fp is a parameter that represents the extracellular concentration of Fgf4. The explanation of the terms and the definitions of the parameters are given in the Supporting Material and in our previous work (6).
Results
Tristability in the GRN controlling Epi versus PrE specification
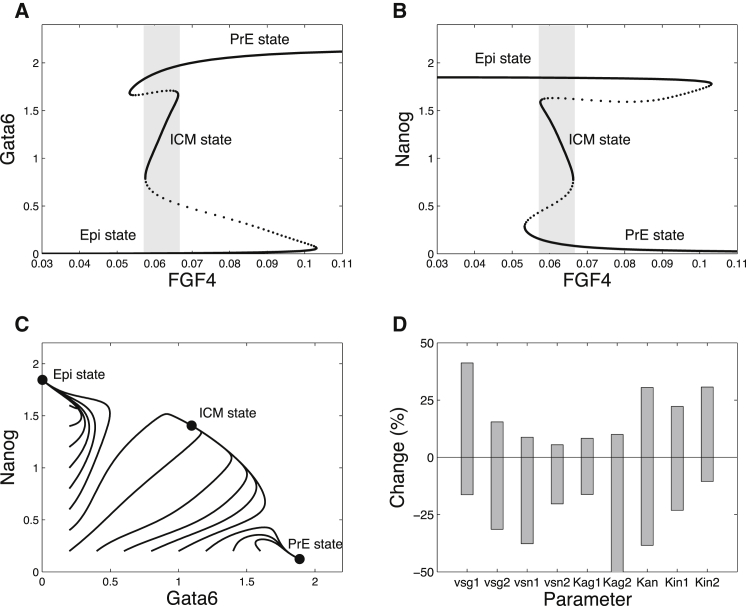
We first analyzed the system describing the interactions between the transcription factors Nanog and Gata6, as well as the interplay of these factors with the Fgf/Erk signaling pathway within one cell (Fig. 1 and Eqs. 1–4). In this simplest version of the model, Fp, which represents the extracellular concentration of Fgf4, is a control parameter. As shown in our previous work (6), there are three distinct branches of stable steady states in the bifurcation diagram showing the steady states of the system as a function of the extracellular Fgf4 concentration (Fig. 2, A and B). Each of these three branches corresponds to a distinct differentiation status of ICM cells: PrE (low Nanog, high Gata6, FGFR2, and Fgf/Erk), Epi (high Nanog, low Gata6, FGFR2, and Fgf/Erk), and undifferentiated ICM (intermediate levels of Nanog, Gata6, FGFR2, and Fgf/Erk). For intermediate concentrations of Fgf4 (0.053 < Fp < 0.103 for the set of parameter values given in Table S1), the system presents more than one stable steady state. In particular, for 0.057 < Fp < 0.066, the EPI-like, PrE-like, and ICM-like states are stable and the system thus exhibits tristability (Fig. 2, A and B, gray area). The basin of attraction of the ICM-like state surrounds the bisectrix in the (Gata6, Nanog) plane, which means that the ICM state is reached from G and N values that are initially close. If initially N ≫ G, the system will evolve toward the Epi state. Conversely, it will evolve toward the PrE state if initially G ≫ N (Fig. 2 C).
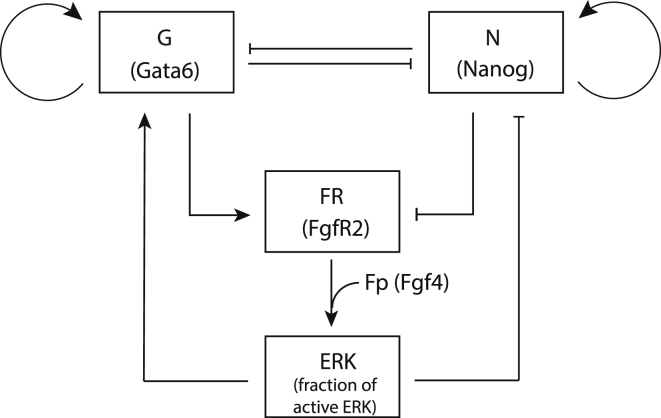
Figure 1.
Intracellular GRN controlling the differentiation of the ICM into Epi and PrE. Gata6 and Nanog inhibit each other and self-activate. Fgf/Erk signaling, which is activated through the binding of Fgf4 to the receptor FGFR2, activates Gata6 and inhibits Nanog. The synthesis of the receptor FGFR2 is activated by Gata6 and inhibited by Nanog. The extracellular concentration of Fgf4 perceived by the cell (Fp) is considered as a control parameter (redrawn from our previous work (6)).
Figure 2.
Tristability in the intracellular GRN controlling the differentiation of ICM cells into Epi and PrE. (A and B) Bifurcation diagrams of the model defined by Eqs. 1–4 as a function of parameter Fp, which represents the extracellular concentration of Fgf4. Three stable steady states coexist in the (0.0575,0.0663) interval. (C) Time evolutions in the (Gata6, Nanog) phase space from different initial conditions, showing the basins of attraction of the three stable steady states. Simulations correspond to Fp = 0.06, which value belongs to the domain of tristability. Parameter values are given in Table S1. (D) Sensitivity analysis of tristability. For each parameter listed, the bar indicates the range of relative variation—expressed as a change in percentage in the parameter value with respect to its default value—in which tristability is maintained. Default parameter values are listed in Table S1. Bifurcation diagrams were generated with AUTO (45).
To assess the robustness of the situation depicted in the bifurcation diagrams shown in Fig. 2, A and B, we performed a sensitivity analysis (Fig. 2 D). Because we are only interested in the coexistence of three stable steady states corresponding to physiologically relevant states, we only focused on the coexistence between the states where G ≫ N, N ≫ G, and N ∼ G ≠ 0. For each parameter shown in Fig. 2 D, we determined the extent of the tristability domain by constructing bifurcation diagrams. For example, the default value of vsg1 is 1.202 (Table S1). Bifurcation analysis with vsg1 as a bifurcation parameter indicates that tristability occurs for vsg1 ∈ (1.006, 1.501). In other words, tristability still occurs if vsg1 is reduced by a maximum of 16.3% or increased by a maximum of 41.2%, with respect to the default value listed in Table S1. Overall, Fig. 2 D indicates that the coexistence between the ICM, Epi, and PrE states is a rather robust phenomenon.
The GRN modeled by Eqs. 1–4 can exhibit tristability for other sets of parameter values than those presented in Table S1 and used for Fig. 2. As an example, another parameter set exhibiting tristability is given in Table S2. That tristability represents a relatively robust mode of behavior in the model is also shown in Fig. S4 (see Supporting Material), where the domain of tristability is determined, along with the domains of monostability and bistability, in a two-parameter space.
How is tristability related to the precise structure of the regulatory network considered in Fig. 1? A simple network of two cross-inhibiting compounds is well known to allow for bistability in an appropriate range of parameter values; such a regulatory system is referred to as a toggle switch (26). Later studies demonstrated that a system of two cross-inhibiting proteins can also generate tristability if these proteins activate their own expression (25, 27); such a network of interactions is also known as a self-activating toggle switch (28). From a mathematical point of view, Huang et al. (25) used two distinct, additive terms for autoactivation and cross-inhibition in the evolution equations for the two antagonistic transcription factors. This implies that the synthesis of each of these transcription factors can occur either because its own level is high or because the level of the other one is low. To describe these interactions in our model, we used, instead, multiplicative terms for these regulations; thus, in the absence of Fgf/Erk signaling, significant synthesis of one transcription factor can occur only if its own level is sufficiently high and the level of the other one is not too elevated. The resulting two-variable system (defined by Eqs. 1 and 2 with vsg1 = vsn1 = 0, since we did not consider the Fgf/Erk pathway at this stage) never exhibited three stable steady states for the values of the parameters that we tested (the trivial (0,0) state not being considered). The states with intermediary values for N and G were indeed always unstable. Upon addition of terms representing the Fgf/Erk pathway, which allows synthesis of each of the transcription factors when the level of the other is very small, we recovered tristability. The occurrence of tristability (Fig. 2, A and B) in the full model shown in Fig. 1 and defined by Eqs. 1–4 thus originates from the interplay between Nanog and Gata6 autoactivation and cross-inhibition on one hand, and the Fgf/Erk pathway on the other hand. Tristability only occurs for intermediate levels of Erk signaling that allow for a balance between autoactivation and cross-inhibition (see Fig. S4).
The precise arrangement of terms for autoactivation, cross-inhibition, and Erk signaling not only determines the possible existence of tristability but also governs the dynamical behavior of the model. To select the most appropriate mathematical description, we compared each possible arrangement of the regulatory terms with key experimental observations about Epi and PrE cell specification. The results of this investigation are summarized in Table 1, where successive rows depict possible logical architectures and their adequacy with experimental observations. A detailed description of the results shown in Table 1 is provided in the Supporting Material. The results of this comparative study indicate that Eqs. 1 and 2 represent the only combination of terms representing autoactivation, cross-inhibition, and regulation by Fgf/Erk signaling that accounts for both the existence of tristability and key experimental observations on the mechanism of specification of ICM cells into either Epi or PrE cells.
Table 1.
Impact of the Logical Architecture of the Regulatory Network Describing Specification of ICM Cells into Epi or PrE Cells on the Behavior of the Model
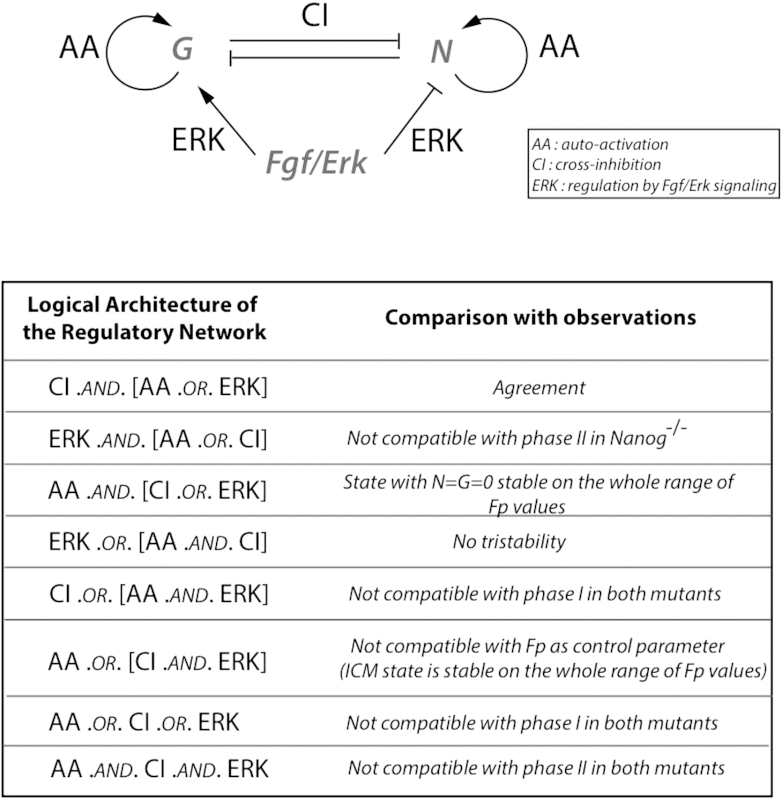 |
Only the structure of the equations describing the interactions between Gata6 (G) and Nanog (N) are considered (Eqs. 1 and 2). These interactions are either direct through cross-inhibition (CI) or autoactivation (AA), or indirect through the Fgf/Erk signaling pathway (ERK) that stimulates Gata6 expression and inhibits Nanog expression. The eight possible logical structures for this network are considered. Phases I and II refer to different responses of cells of mutant embryos to exogenous treatments with Fgf4 or Fgf/Erk inhibitors. For example, in Nanog−/− mutants, early treatment with inhibitors prevents any increase in Gata6, whereas later treatment with the same inhibitors does not prevent Gata6 increase. In Gata6−/− mutants, the same phenomenon occurs if cells are treated with Fgf4. The periods of sensitivity and insensitivity are referred to as phases I and II, respectively (6).
Mechanism of specification arising from the cross talk between two cells through Fgf signaling
Experimental data have shown that during the early stages of murine embryogenesis, the synthesis of Fgf4 by ICM cells varies with time. In particular, Nanog promotes the transcription of Fgf4, which is thus produced at a higher rate by Epi progenitors than by PrE cells (4, 9). Since this Fgf ligand plays an essential role in the Epi/PrE specification process, we analyzed a model in which the extracellular concentration of Fgf4 is no longer a control parameter (Fp in Eq. 4), but instead becomes a variable (Fsi) whose value depends on the rate of Fgf4 synthesis by the cell:
| (5) |
This equation describes the Nanog-stimulated Fgf4 secretion and the degradation of this compound in the extracellular medium. The last term, vex, represents the possible addition of external Fgf4, which allows us to simulate the administration of drugs interfering with the Fgf/Erk signaling pathway (see below).
As the simplest possible situation accounting for cell coupling through Fgf4, we analyzed a two-cell model. Each cell possesses the same GRN, described by Eqs. 1–4, and the same evolution for secreted Fgf4 (Eq. 5). The two cells are coupled through the extracellular Fgf4 concentration, which is computed at each time step as the average (F) between the amounts of Fgf4 secreted by the two cells. However, the Fgf4 concentration perceived by these cells slightly differs, because the high level of cellular compaction in the developing embryo hinders perfect homogenization of Fgf4. Thus, the concentrations of Fgf4 perceived by each cell differ from the average concentration, F, by a small percentage, γ:
| (6) |
| (7) |
This source of external noise, introduced in the model as the local variability in Fgf4 concentration or availability, is required for the emergence of both epiblastic and PrE progenitors within the ICM (21, 22).
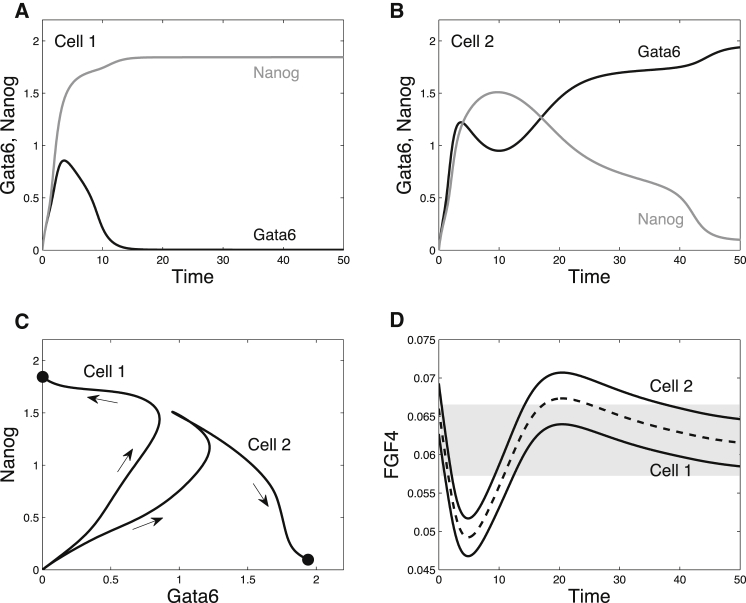
The two-cell system provides a useful framework to understand how tristability between the ICM, Epi, and PrE states can account for the specification process observed experimentally (Fig. 3). Before Nanog and Gata6 levels start to increase in ICM cells, the level of extracellular Fgf4 is relatively high (9). We incorporate this condition into the model by considering an initial value for the concentration of extracellular Fgf4 (Fs) such that Fp1 and Fp2 both belong to a region of tristability. Thus, starting from N = G = 0 (as time 0 arbitrarily corresponds to the time at which Nanog and Gata6 start to be expressed), the levels of both proteins will first increase together toward the ICM state (Fig. 3, A–C). At the same time, the concentration of extracellular Fgf4 decreases (Fig. 3 D) due to its degradation—according to observations at the level of Fgf4 mRNAs (9)—and because the level of Nanog is not yet high enough to promote Fgf4 expression. As a result, the cell that perceives the smallest amount of Fgf4 (cell 1 in Fig. 3) will evolve toward the Epi state (Fig. 3, A and C), because the ICM is not a steady state of the system anymore at this concentration of Fgf4, which is <0.057. This evolution corresponds to an increase in Nanog concentration, accompanied by an increased rate of Fgf4 secretion (Fig. 3 D). Due to this increase, Gata6 synthesis is amplified in the other cell (cell 2 in Fig. 3), which still expresses a sufficient amount of Fgf receptors, as it is in the ICM state. Cell 2 then finally reaches the PrE state. As the Epi state is stable over an extended range of Fgf4 concentrations (Fig. 2, A and B), cell 1 remains in the Epi state.
Figure 3.
Cell fate specification mechanism in the two-cell system. (A and B) Time evolution for Nanog and Gata6 in cells 1 and 2. Cell 1 and cell 2 direct themselves toward the ICM-like state, before cell 1 is finally attracted by the Epi-like state (and thus increases its rate of Fgf4 secretion). In consequence, cell 2 goes to the PrE-like state (and stops producing Fgf4). (C) Trajectories in the phase space. (D) Corresponding evolution of Fgf4 (variables Fp1 and Fp2). The dashed line shows the average concentration of Fgf4 in the extracellular medium (F), whereas the plain lines represent the concentrations of Fgf4 perceived by both cells (Fp1 and Fp2), i.e., F − γ and F + γ, respectively. The gray-shaded region corresponds to the domain of tristability. Variability is set to γ = 3%. Parameter values are listed in Table S1. Initial conditions are: G1/2 = N1/2 = 0, FR1/2 = 2.8, ERK1/2 = 0.25, and F = 0.066.
The proposed scenario for specification requires the domain of tristability to be smaller than that of bistability, so that the ICM state reached initially will lose its stability for the Epi and PrE states upon slight changes in extracellular Fgf4. This is why the cross-inhibition factor must be multiplied by both the autoactivation and the ERK terms in Eqs. 1 and 2 (see the comparison in Table 1 between the situations CI.AND.[AA.OR.ERK] and AA.OR.[CI.AND.ERK] in the previous section and the section titled Logical architecture of the regulatory network in the Supporting Material).
In the specification mechanism just described, parameter γ, which allows both cells to perceive slightly different concentrations of Fgf4, plays a predominant role. If γ is too small, both cells remain on the ICM-like state. In contrast, if γ is too large, both cells will directly evolve toward the differentiated states without passing through the ICM-like state, as suggested by the phase portrait shown in Fig. 2 C.
In conclusion, a simplified two-cell model that takes into account the intercellular cross talk via Fgf4 signaling can reproduce the self-organized transition from two ICM cells into one Epi and one PrE cell if slight inhomogeneities in the concentration of extracellular Fgf4 are considered. The two-cell model thus shows how tristability allows for the specification mechanism into the Epi or PrE cell types. However, it does not allow investigation into the mechanism of emergence of the salt-and-pepper pattern of Epi and PrE cells observed in the embryo, for which we must consider the dynamics of cell-fate specification in a cell population.
ICM differentiation in wild-type embryos
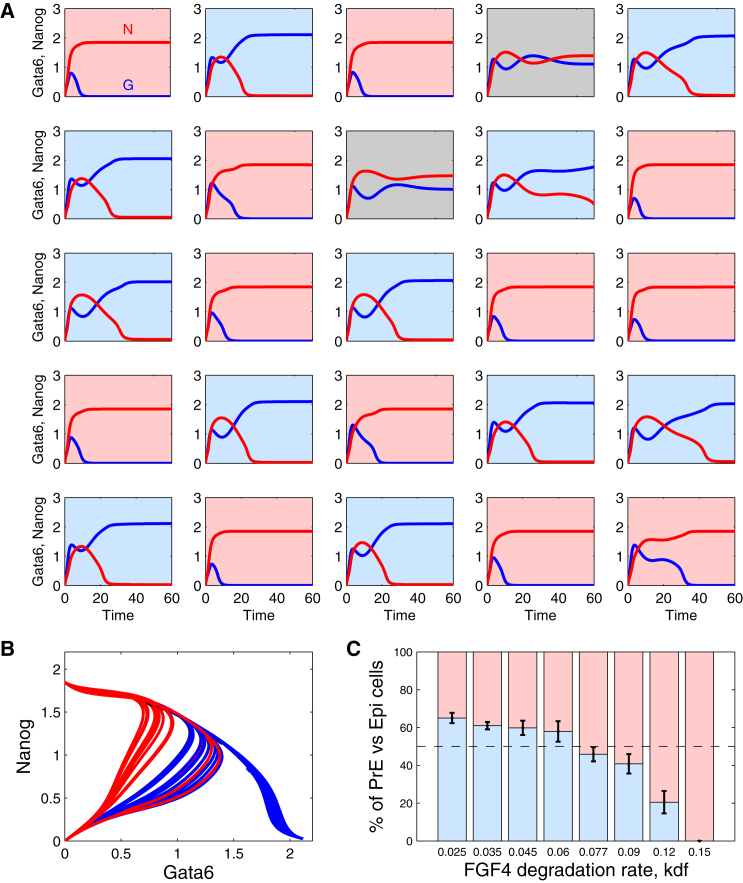
In a multicellular system, cells perceive the local concentration of extracellular Fgf4. In the model for 25 cells (see Supporting Material for the complete description of the population model), this concentration corresponds to the average level of Fgf4 produced by the cell itself and by its four closest neighbors. For each cell, this average value is perceived with some noise (γi), different for each cell (see Eq. S9). As shown in Fig. 4 A, in such conditions, a typical salt-and-pepper distribution of PrE and Epi cells spontaneously arises in the simulations. As is clearly visible in Fig. 4 B, different cells in the populations follow different trajectories. This is initially due to the differences in the individual values of γi, which determine the amount of Fgf4 perceived by the cells and, thereby, the rate of change in Erk activity that in turn determines the levels of Nanog and Gata6. Differences in Fgf4 concentrations, and subsequently in the levels of expression of the transcription factors, are then amplified through the Nanog-dependent secretion of Fgf4. This behavior of the model compares well with the highly heterogeneous levels of Nanog (6) and Fgf4 (29) expression observed in early blastocysts. In the simulations, heterogeneity in extracellular Fgf4 concentration represents a very robust mechanism to induce the salt-and-pepper pattern. Indeed, if one considers that only one cell in the population has a γi different from 0, a mosaic pattern of Epi and PrE cells will arise. In the example shown in Fig. S3, γi = −0.1 for the central cell and 0 for all the other cells of the population. Because it perceives less Fgf4, the central cell evolves toward an Epi fate. Thus, it will secrete more Fgf4, inducing its neighbors to evolve toward the PrE fate. Because these cells secrete less Fgf4, their neighbors will in turn tend toward the Epi fate, etc.
Figure 4.
Spontaneous evolution of ICM cells to a salt-and-pepper pattern of Epi and PrE cells and effect of the rate of degradation of extracellular Fgf4. (A) A population of 25 cells defined by the same GRN and interacting through Fgf4 is simulated on a 5 × 5 grid. Frames are colored depending on the fate of the cell at the end of the simulation (100 arbitrary time units): light gray (red) for Epi, dark gray (blue) for PrE, and white (gray) for ICM. (B) Trajectories of all individual cells shown in (A) in the (Gata6, Nanog) phase plane. (C) Influence of the rate of degradation of Fgf4, kdf, on the proportion of PrE cells in the final population. Statistics were performed on 10 simulations. Parameter values are listed in Table S1. All γi values are randomly chosen in the (−10%,+10%) interval. Initial conditions are identical for each cell and, as in Fig. 3, Gi = Ni = 0, FRi = 2.8, ERKi = 0.25, and Fsi = 0.066 (i = 1,…25). To see this figure in color, go online.
In Fig. 4 A, at steady state, 12 cells (48%) are in an Epi state, 11 cells (44%) are in a PrE state, and two cells (8%) are still in an ICM state. On average, Epi cells specify earlier than PrE cells, as shown in our previous study (6). Undecided cells could correspond to those that will disappear by apoptosis during the sorting process that occurs after E3.75 (4, 8, 15, 30). The proportions of PrE and Epi cells obtained with the model agree with some experimental observations (31). The difference between these results and those shown in our previous work (6), where we got 42%, 46%, and 12% of Epi-, PreE-, and ICM-state cells, respectively, is due to the different value taken for the rate of degradation of extracellular Fgf4, kdf. The model predicts that this parameter has a key influence on the respective proportions of the two cell types (Fig. 4 C). Higher degradation rates tend to favor the appearance of Epi cells. This is in agreement with the experimentally observed differences in Epi/PrE ratios obtained between mouse strains, which probably reflect variabilities in Fgf signaling (31). In the model, if the degradation rate of Fgf4 (kdf) is too small, cells either stay undifferentiated or evolve toward the PrE state. If degradation is too fast, all cells reach the Epi state; indeed, in these conditions, the secretion of Fgf4 by the Epi cells can never be high enough to compensate its degradation, and this prevents the possible specification of other cells into the PrE state.
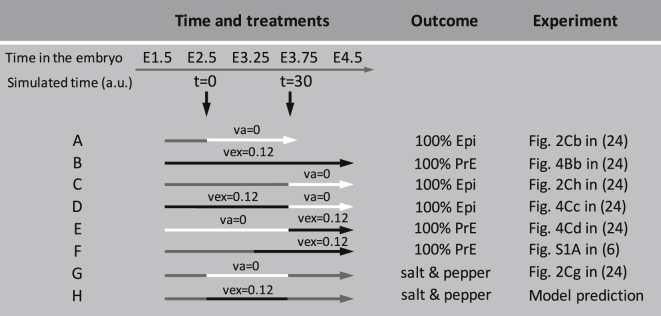
The primary role played by the Fgf/Erk signaling pathway in the differentiation mechanism of ICM cells into epiblast and primitive endoderm was uncovered by several experiments in which compounds altering this pathway were introduced (4, 23, 24). In the model, to simulate the administration of FGFR and Fgf/Erk inhibitors, we attribute a null value to the rate of Erk activation (va (Eq. 4)). A treatment by exogenous Fgf4 is reproduced by setting the rate of Nanog-independent Fgf4 synthesis (vex, Eq. 5) to a nonzero value. The different experimental protocols and their outcomes are summarized in Fig. 5.
Figure 5.
Effect of exogenous compounds interfering with the Fgf/Erk signaling pathway on cell-fate specification. White arrows indicate the times during which Fgf/Erk inhibitors are administered (the rate of Erk activation, va, is set equal to zero), whereas black arrows indicate the times during which exogenous Fgf4 has been added (the rate of addition of exogenous Fgf4, vex, is set equal to 0.12). Gray corresponds to the control medium. Column 3 indicates the outcomes of the simulations, performed as in Fig. 4A. The last column indicates the corresponding experiment in the literature. The last protocol is a theoretical prediction.
When development occurs in the absence of Fgf4 signaling or in the presence of a constant high level of exogenous Fgf4 (23, 24), all cells evolve toward the Epi or PrE state, respectively (see Fig. 5, rows A and B). In both cases, indeed, the system directly evolves toward the unique steady state that corresponds to either low or high Fgf4 concentration. The bifurcation diagrams shown in Fig. 2, A and B, indicate that, once specified, the fate of the cells can be changed from Epi to PrE and vice versa by manipulating the Fgf/Erk signaling pathway. This suggests that in vivo, cells remain plastic after specification as long as the maturation processes, which likely involve other transcription factors not taken into account in the model, have not been switched on. Plasticity corresponds to rows C–F in Fig. 5. Indeed, whatever the state of the cells at E3.25 or E3.75, the final treatment by Fgf/Erk inhibitors or by exogenous Fgf4 determines the fate of the whole population.
Yamanaka et al. (24) investigated whether ICM cells submitted to an early treatment with Fgf/Erk inhibitors (from E2.5 to E3.75) could be induced to change fate upon sole removal of the inhibitors. Thus, they administered Fgf/Erk inhibitors from E2.5 to E3.75 and then transferred the embryos into a control culture medium (Fig. 5, row G). Upon removal of the inhibitors, the embryos re-established a normal ICM, with Epi and PrE progenitors in normal proportions. The outcome of the simulations of this experimental protocol is more difficult to predict intuitively, as the final situation corresponds to the region of multistability that arises at intermediate Fgf4 concentrations. In silico, as in the experiments, Epi and PrE progenitors are arranged in a salt-and-pepper pattern at the end of the process. Thus, even if Fgf/Erk signaling starts to be activated when most cells are already specified into an Epi state, the slightly different timings due to the variations in the local Fgf4 concentrations allow for dynamical intercellular cross-talk leading to the establishment of the salt-and-pepper pattern. In a symmetrical manner, the model predicts that ICM cells submitted to an early treatment with exogenous Fgf4 (from E2.5 to E3.75) can be induced to change fate upon sole removal of Fgf4 (Fig. 5, row H), thus allowing the establishment of the salt-and-pepper pattern.
Nanog mutants
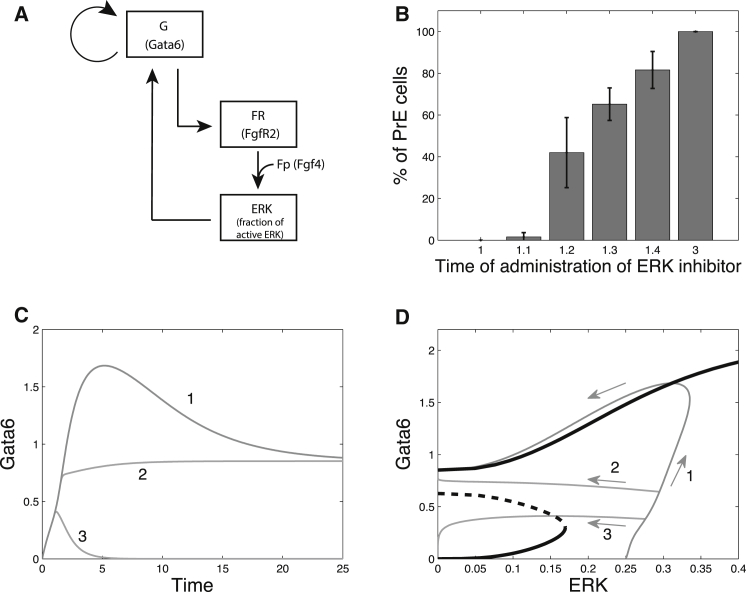
In Nanog−/− embryos, all cells within the ICM express Gata6 (4). In the model, the mutation of Nanog is implemented by attributing a null value to the rate of Nanog synthesis (vsn1 = vsn2 = 0 in Eq. 2). In these conditions, Gata6 is high and Nanog is absent in all cells. Nanog−/− embryos are obviously not affected by the administration of exogenous Fgf4 (4), which is reproduced by the model, too. In contrast, the administration of Fgf/Erk inhibitors can impact the expression of Gata6 in Nanog−/− embryos. When these inhibitors are administered as early as E2.5, Gata6 (protein) is not accumulating. Conversely, if they are administered at E3.25, the majority of cells (67%) maintain Gata6 expression (4). In the model, once Gata6 is high enough, it remains high despite the administration of the inhibitors due to both the self-amplification loop and the indirect positive feedback of Gata6 on itself (Gata6 → FGFR2 → Erk → Gata6 (Fig. 6 A)). In the simulations, the proportion of inhibitor-insensitive cells increases with the time of administration (Fig. 6 B); the experimentally observed proportions correspond to the case where the addition of the inhibitor is assumed to occur at 1.3 simulated time. Again, one can understand this behavior by resorting to bifurcation diagrams. In the absence of Nanog, there are only two possible steady states, as shown in Fig. 6 D, one corresponding to the PrE and one for which G ∼ N ∼ 0. In the absence of inhibitor (Fig. 6, C and D, curve 1), the system evolves toward the PrE state as the initially high level of Fgf4 triggers the self-amplification loop. Upon administration of Fgf/Erk inhibitors, the trajectory of the curve is deviated to the left. If this occurs after the system has passed the separatrix defined by the unstable branch, the PrE state will be reached (Fig. 6, C and D, curve 2). In contrast, if inhibitors are added earlier, the system will end up in the (0,0) state (Fig. 6, C and D, curve 3). These results agree with the experimental data: in Nanog−/− embryos treated with Fgf/Erk inhibitors at E2.75, only 27% of the cells continue to express Gata6 (4). Thus, in vivo and in the model, Fgf signaling becomes dispensable for the synthesis of Gata6 in Nanog−/− embryos only when a sufficient amount of Gata6 is already expressed in the cell.
Figure 6.
Influence of the time of administration of Fgf/Erk inhibitors on cell fate in Nanog−/− embryos. (A) Scheme of the GRN corresponding to the Nanog−/− mutant. (B) Proportions of cells maintaining Gata6 expression as a function of the time at which Fgf/Erk inhibitors are administered, simulated by setting va = 0 for all cells of the population. The histogram shows the average values for 10 simulations of the 25-cell model. γi is randomly chosen for each cell in the (−10%,+10%) interval. Parameter values and initial conditions are the same as in Fig. 4, with vsn1 = vsn2 = 0. (C) Time evolution of Gata6 simulated for the single-cell model. Cell 1, no inhibitor; cell 2, Fgf/Erk inhibitors administered at t = 1.5; cell 3, Fgf/Erk inhibitors administered at t = 1. (D) Bifurcation diagram of Gata6 as a function of ERK (taken as a control parameter) in the single-cell model (black curves), with the trajectories of the three cells shown in (C) (gray curves).
Internal versus external noise in cell-fate specification
The emergence of a random salt-and-pepper pattern during early blastocyst development suggests a primary role for stochasticity in the dynamical processes underlying the specification of Epi and PrE progenitors. In the model, the source of randomness was so far introduced through the variability in the concentration of extracellular Fgf4 perceived by each cell. This variability, which we refer to as external noise, is measured by parameter γi, which is fixed randomly in a well-defined range for each cell at the beginning of the simulation. It allows the various cells of the population to follow different trajectories, ending up in different states, which leads to the emergence of the salt-and-pepper pattern. This hypothesis about the heterogeneity in the level of Fgf4 perceived by each cell in the blastocyst agrees with the observation that Fgf ligands are heterogeneously expressed within the ICM at the 32-cell stage (9), but it remains to be demonstrated for earlier stages of development.
Several studies performed on ES cells have reported random fluctuations in Nanog levels (32, 33, 34). Given the close similarities between Epi and ES cells, these observations led us to investigate whether randomness in Epi versus PrE specification could instead rely on fluctuations in the concentrations of all the variables of the model, i.e., Nanog, Gata6, FGFR, Erk signaling, and secreted Fgf4; because it arises from stochastic fluctuations inside the cell, we call this noise internal. To test the effect of internal noise, we developed a stochastic version of the model using Gillespie’s algorithm (35). This method associates a probability with each kinetic transition considered in the GRN. At each time step of the simulation, the algorithm stochastically determines the reaction that takes place according to its relative propensity, which depends on the number of molecules involved in the reaction, on the rate constants, and on the time interval to the next reaction step. The transitions considered are summarized in Table S3 (see Supporting Material). The level of molecular noise, which determines the amplitude of the fluctuations around the corresponding deterministic evolution, is scaled by parameter Ω. The higher the value of Ω, the larger the number of molecules considered in the simulations and the lower the amplitude of the fluctuations.
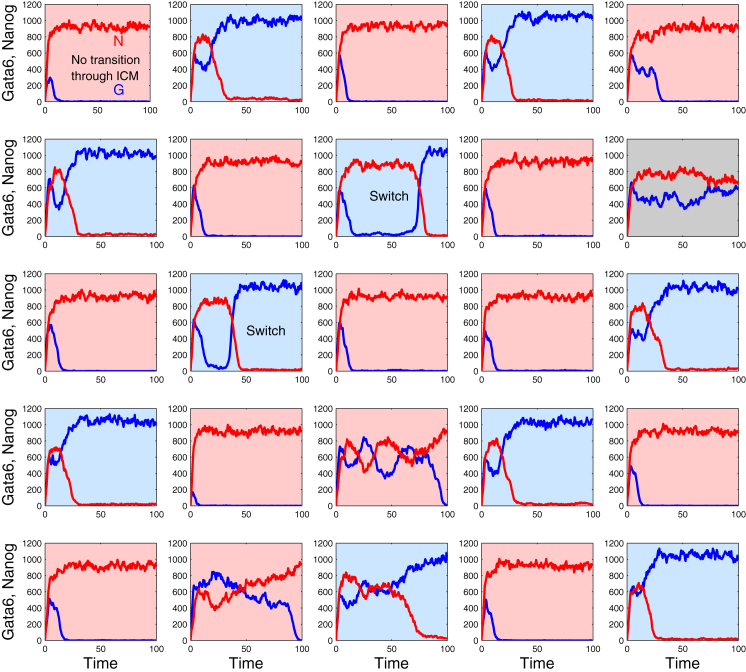
We used this algorithm to investigate whether the model still exhibits a behavior that matches experimental observations when external noise is replaced by internal noise. For large values of Ω, stochastic simulations of a population of cells for all of which γi = 0 reproduce a specification pattern very similar to the deterministic case (Fig. 7), with small-amplitude fluctuations in the amounts of Nanog and Gata6 due to molecular noise. However, two atypical behaviors were observed in the stochastic simulations. First, one observes two cells switching from the Epi to the PrE state (see patterns labeled Switch in Fig. 7). In the bifurcation diagram (Fig. 2 A), this corresponds to a cell on the Epi branch, in the bistability domain, which undergoes a fluctuation that is large enough to drive it above the unstable branch, so that this cell is finally attracted by the PrE state. Another intriguing behavior is that of the cell that goes directly toward the Epi state, without passing first through the ICM state characterized by the coexpression of Nanog and Gata6 (see Fig. 7, upper left pattern). This evolution is readily understood in the phase plane (Fig. 2 C); it corresponds to an early fluctuation that drives the cell from a state close to (0,0) to a state outside the basin of attraction of the ICM state.
Figure 7.
Salt-and-pepper pattern of Epi and PrE cells driven by internal noise. Shown is the spontaneous evolution of a population of ICM cells in the same conditions as in Fig. 4, except that internal fluctuations in the number of molecules are taken into account and external noise is absent. Reactions are listed in Table S3 and parameter values are given in Table 1. Ω = 500 and γi = 0 for all cells. The color code is the same as in Fig. 4. Stochastic simulations are performed by means of the algorithm of Gillespie (35). As discussed in the text, two cells of the simulated population switch from the Epi to the PrE state and one cell does not pass through an ICM-like state before becoming an Epi cell. To see this figure in color, go online.
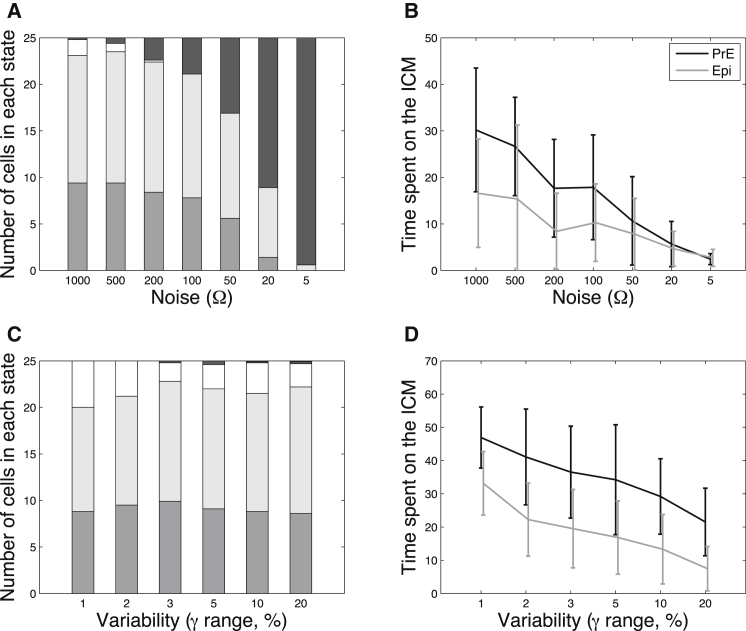
These atypical behaviors were quantified for different values of Ω. Fig. 8 A shows the statistics of the number of cells ending in the Epi, PrE, or ICM states, as well as the number of cells displaying switches between the PrE and the Epi states in the time window of the simulation (100 arbitrary time units). As expected intuitively, the number of switching cells markedly increases with the extent of noise (decreasing Ω values). In contrast, when the source of noise is external (Fig. 8 C), the number of cells displaying such switches is very low and practically insensitive to the level of noise. The average time spent in the ICM state rapidly decreases when the molecular noise increases (Fig. 8 B), although this diminution is slower with the external noise (Fig. 8 D). Another physiologically relevant outcome of the simulations is the variability in the time spent on the ICM. This variability reflects the level of synchrony in the cell population. For example, if the variance is of the order of the time needed to reach the ICM, some cells of the embryo would start expressing Nanog and Gata6, whereas others are already specified. As can be seen in Fig. 8, B and D, the variability in the time spent on the ICM is smaller in the case of the external noise, at least for sufficiently large times spent on the ICM.
Figure 8.
Behavior of the model with internal noise compared to that with external noise. (A) Statistics of the final outcomes of the stochastic simulations with Gillespie’s algorithm in the absence of variability on Fgf4 (γi = 0 for all cells), where medium gray indicates the average number of cells in the PrE state, light gray the average number of cells in the Epi state, white the average number of cells in the ICM state, and dark gray the average number of cells that switch at least once from Epi to PrE or vice versa during the simulation (100 arbitrary time units). (B) Statistics of the time spent in the ICM state in the same conditions as in (A). The cells are considered to be in the ICM state as long as |Gi − Ni| < 1.2. (C) Statistics of the final outcomes of deterministic simulations including variability on Fgf4 (γi randomly chosen in the (−γ, + γ%) interval for each cell of the population). The color code is the same as in (A). (D) Statistics of the time spent in the ICM state in the same conditions as in (C). For all graphs, parameter values are given in Table S1 and initial conditions are as in Fig. 4.
In conclusion, the model suggests that external noise in the form of Fgf4 heterogeneity could in principle be replaced by internal fluctuations in the levels of expression of the transcription factors, as it also leads to the salt-and-pepper pattern and to asynchronous fate specification throughout the population of cells. However, internal noise greatly increases the number of unrealistic switching between states, reduces the time spent by the cells in the ICM state before specification into Epi or PrE, and increases the developmental asynchrony between the different ICM cells of the embryo. The results obtained in silico in the case of internal noise do not fit well with in vivo observations (see Discussion); therefore, the model tends to favor a scenario in which noise affecting the cell specification mechanism primarily originates from fluctuations in extracellular Fgf4.
Discussion
Theoretical models are widely used to gain a deeper understanding of the molecular mechanisms underlying cell-fate choice during development (see, for example, Rouault and Hakim (36)). Here, we analyzed in further detail a model that we previously proposed to account for the specification of ICM cells into Epi or PrE cells in the early mouse blastocyst. Upon increase in Nanog and Gata6, simulated cells first evolve toward the ICM-like state; cell-autonomous changes in Erk signaling then spontaneously drive the cells toward the Epi or PrE fates, depending on the status of the surrounding cells. This scenario holds qualitatively with experimental observations.
The mechanism for cell-fate specification analyzed in this study bears similarities to the mechanisms proposed by Huang et al. (25) for the choice between erythroid and myelomonocytic fates governed by the transcription factors GATA1 and PU.1, and by Lu et al. (28) for the microRNA-regulated epithelial-hybrid-mesenchymal fate determination. The latter scenarios are also based on tristability relying on autoactivation and cross-inhibition between two transcription factors. A main difference, however, is that in our model, interplay with Fgf/Erk signaling is required for the occurrence of tristability. This is due to the fact that we used multiplicative terms, instead of additive terms, for autoactivation and cross-inhibition. From a physiological point of view, this means we assumed that cross-inhibition between Nanog and Gata6 causes them to hinder, or even suppress—and not simply decrease—each other’s expression. How the underlying mechanistic details affect the existence and range of multistability in models for autoregulatory networks has been investigated in detail in previous studies (27, 37, 38, 39).
The effect of noise was analyzed in a minimal model for the distinct GRN controlling pluripotency, which involves interactions between Nanog and the heterodimer Oct4/Sox2 (33). The authors characterized the dynamics of noise-induced transitions between a stable, high-Nanog state, which is excitable, and an unstable, low-Nanog state in which the cells are more prone to differentiate. This model accounts for the bimodal distribution of Nanog expression observed in ES cell populations. Glauche et al. (40) showed that this bimodal distribution could also be obtained, in a similar model, through oscillatory behavior or noise-driven transitions between two coexisting stable steady states. On the other hand, Chickarmane et al. (41, 42) developed bistable models for the specification of ES cells into PrE progenitors in vitro. However, these models cannot be used to describe the emergence of PrE progenitors in vivo. First, Oct4, which plays a key role in these models, is not involved in the core regulatory network, as at E3.75, Oct4−/− embryos contain both Epi and PrE progenitors arranged in a salt-and-pepper distribution (43, 44). Moreover, the model of Chickarmane et al. (41, 42) assumes that Nanog cannot be upregulated in the absence of Oct4, which also contradicts the experimental data in vivo (43, 44). Second, these models do not focus on the emergence of common ICM progenitors coexpressing Nanog and Gata6 and thus do not account for the self-organized specification of these progenitors into a mixed population of Epi and PrE cells.
We have shown that the model based on the regulatory scheme of Fig. 1 can simulate experiments where embryos were manipulated with treatments affecting the Fgf/Erk signaling pathway. The outcome of most of the treatments by Fgf4 or Fgf/Erk is readily accounted for by the structure of the bifurcation diagram of the model as a function of extracellular Fgf4 (Fig. 2). The model also shows, in agreement with the observations of Yamanaka et al. (24), that the salt-and-pepper pattern emerges even if Fgf signaling starts to be activated when most of the cells are already specified into the Epi state, due to the presence of Fgf/Erk inhibitors up to E3.75. Similarly, the final state of the population is not altered if the cells are treated with external Fgf4 until E3.75 and are thus specified into the PrE state. This prediction of the model remains to be verified experimentally.
The model can be extended in several ways. So far, we have considered only the levels of proteins and not the levels of their corresponding mRNAs. The absolute protein levels cannot be directly related to experimental measurements, which so far mainly pertain only to mRNAs. Also, time units are arbitrary and not realistically related to embryonic days. Finally, at this stage, the model only describes a population made of a fixed number of cells, whereas the developmental process we are looking at ranges from two to four cells to ∼25 cells. Future work will take cell division into account to study how it affects the dynamics of specification of ICM cells into Epi or PrE cells.
We previously showed that the model reproduces the behavior of Gata6−/− mutants and correctly predicts that the epiblastic specification is faster in Gata6+/− than in wild-type embryos (6). Here, we focused on Nanog−/− mutants. In this case, there are only two possible steady states (G high, N = 0 or G ∼ N = 0) (Fig. 6). The G ∼ N = 0 state is reached from states characterized by low levels of Gata6 and Erk activity. In contrast, if Erk is elevated, the only possible steady state corresponds to PrE. Due to hysteresis, cells will remain on this state even if the activity of the Erk pathway later diminishes. This is in agreement with the observation that the proportion of Gata6-expressing cells increases with the time at which Fgf/Erk inhibitors are administered in Nanog−/− embryos (4).
Finally, we addressed the question of the nature of the source of randomness that is responsible for the asynchronous switching from the ICM to the Epi or PrE state and establishment of the salt-and-pepper pattern. To this end, we compared the behavior of models described by the same regulatory network but differing in their sources of randomness. In the initial version of the model (6), noise is external, as we considered some stochastic deviations (γi values) in the levels of Fgf4 perceived by each cell around the average of the amounts secreted by its neighbors. Here, we also considered another version of the model in which such deviations do not occur (γi = 0 for all cells) but random fluctuations arising from molecular noise are taken into account. We found that such internal noise is also able to lead to the asynchronous switching of the cells and to the salt-and-pepper pattern.
With internal noise, some characteristics of the specification scenario do not fit well with experimental observations. First, simulations predict a high probability of fate reversal, with most such switches occurring from the Epi to the PrE cell fate. Experimentally, only rare reversals from PrE to Epi in the mouse blastocyst have been reported; no Epi-to-PrE transitions have been observed. However, the PrE identity was not fully established in these experiments (30). The asymmetry in the probability of stochastic fate switching observed in the model is due to the asymmetry in the bifurcation diagram (Fig. 2). We thus conclude that the specification mechanism proposed in this study and schematized in Fig. 1 is not compatible with the high level of internal noise that would be necessary to allow for specification into a salt-and-pepper pattern in the absence of external noise. However, in the presence of an external source of randomness (γi ≠0), the model is robust against the moderate level of internal noise that is inherent to all biological systems.
From an experimental point of view, the fact that only PrE-to-Epi transitions have been observed (30) contrasts with the situation in ES cells where fluctuations between high and low Nanog states are observed (34). The difference between the two situations can be ascribed to the much longer observation times in ES cells and tends to favor the mechanism based on external noise, because in this case, there is a very low, but not zero, probability of fate reversal, in contrast to the prediction of the model where stochasticity originates from internal noise due to intracellular fluctuations.
Additionally, the time spent in the ICM-like state is shorter if the source of noise is internal. As it is delicate to draw conclusions about durations in this qualitative model, we defined this duration as the time during which Nanog and Gata6 have approximately the same value. Thus, if this time is very short, it means that the cell goes directly to the Epi or the PrE state, without passing through the ICM state. As this situation has not been encountered in experiments, we associated short times spent in the ICM state with physiologically unrealistic situations. In this context, it also appears that a mechanism based on external noise is more plausible, to avoid both a direct specification into Epi or PrE states and an improbable dispersion of the timing of cell-fate specification.
Author Contributions
All authors conceived and designed the simulations. L.D.M. and D.G. performed the simulations. All authors analyzed the data. All authors wrote the manuscript.
Acknowledgments
We thank Benjamin Rishirumuhirwa and Alen Tosenberger for fruitful discussions.
G.D. is Research Director at the Fonds National de la Recherche Scientifique (FRS-FNRS) and acknowledges support from the Fonds David et Alice Van Buuren. C.C. was funded by ARC (PJA 20131200380), ANR EpiNodal, and PrEpiSpec. S.B. was supported by the Région Auvergne and the FEDER.
Editor: Reka Albert.
Footnotes
Supporting Materials and methods, four figures, and three tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)04763-3.
Supporting Citations
References (46, 47, 48, 49, 50, 51, 52, 53, 54, 55) appear in the Supporting Material.
Supporting Material
References
- 1.Mitsui K., Tokuzawa Y., Yamanaka S. The homeoprotein Nanog is required for maintenance of pluripotency in mouse epiblast and ES cells. Cell. 2003;113:631–642. doi: 10.1016/s0092-8674(03)00393-3. [DOI] [PubMed] [Google Scholar]
- 2.Silva J., Nichols J., Smith A. Nanog is the gateway to the pluripotent ground state. Cell. 2009;138:722–737. doi: 10.1016/j.cell.2009.07.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Messerschmidt D.M., Kemler R. Nanog is required for primitive endoderm formation through a non-cell autonomous mechanism. Dev. Biol. 2010;344:129–137. doi: 10.1016/j.ydbio.2010.04.020. [DOI] [PubMed] [Google Scholar]
- 4.Frankenberg S., Gerbe F., Chazaud C. Primitive endoderm differentiates via a three-step mechanism involving Nanog and RTK signaling. Dev. Cell. 2011;21:1005–1013. doi: 10.1016/j.devcel.2011.10.019. [DOI] [PubMed] [Google Scholar]
- 5.Schrode N., Saiz N., Hadjantonakis A.K. GATA6 levels modulate primitive endoderm cell fate choice and timing in the mouse blastocyst. Dev. Cell. 2014;29:454–467. doi: 10.1016/j.devcel.2014.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bessonnard S., De Mot L., Chazaud C. Gata6, Nanog and Erk signaling control cell fate in the inner cell mass through a tristable regulatory network. Development. 2014;141:3637–3648. doi: 10.1242/dev.109678. [DOI] [PubMed] [Google Scholar]
- 7.Dietrich J.E., Hiiragi T. Stochastic patterning in the mouse pre-implantation embryo. Development. 2007;134:4219–4231. doi: 10.1242/dev.003798. [DOI] [PubMed] [Google Scholar]
- 8.Plusa B., Piliszek A., Hadjantonakis A.K. Distinct sequential cell behaviours direct primitive endoderm formation in the mouse blastocyst. Development. 2008;135:3081–3091. doi: 10.1242/dev.021519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Guo G., Huss M., Robson P. Resolution of cell fate decisions revealed by single-cell gene expression analysis from zygote to blastocyst. Dev. Cell. 2010;18:675–685. doi: 10.1016/j.devcel.2010.02.012. [DOI] [PubMed] [Google Scholar]
- 10.Miyanari Y., Torres-Padilla M.E. Control of ground-state pluripotency by allelic regulation of Nanog. Nature. 2012;483:470–473. doi: 10.1038/nature10807. [DOI] [PubMed] [Google Scholar]
- 11.Rossant J., Chazaud C., Yamanaka Y. Lineage allocation and asymmetries in the early mouse embryo. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2003;358:1341–1348. doi: 10.1098/rstb.2003.1329. discussion 1349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chazaud C., Yamanaka Y., Rossant J. Early lineage segregation between epiblast and primitive endoderm in mouse blastocysts through the Grb2-MAPK pathway. Dev. Cell. 2006;10:615–624. doi: 10.1016/j.devcel.2006.02.020. [DOI] [PubMed] [Google Scholar]
- 13.Kurimoto K., Yabuta Y., Saitou M. An improved single-cell cDNA amplification method for efficient high-density oligonucleotide microarray analysis. Nucleic Acids Res. 2006;34:e42. doi: 10.1093/nar/gkl050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rula M.E., Cai K.Q., Xu X.X. Cell autonomous sorting and surface positioning in the formation of primitive endoderm in embryoid bodies. Genesis. 2007;45:327–338. doi: 10.1002/dvg.20298. [DOI] [PubMed] [Google Scholar]
- 15.Meilhac S.M., Adams R.J., Zernicka-Goetz M. Active cell movements coupled to positional induction are involved in lineage segregation in the mouse blastocyst. Dev. Biol. 2009;331:210–221. doi: 10.1016/j.ydbio.2009.04.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Artus J., Chazaud C. A close look at the mammalian blastocyst: epiblast and primitive endoderm formation. Cell. Mol. Life Sci. 2014;71:3327–3338. doi: 10.1007/s00018-014-1630-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Feldman B., Poueymirou W., Goldfarb M. Requirement of FGF-4 for postimplantation mouse development. Science. 1995;267:246–249. doi: 10.1126/science.7809630. [DOI] [PubMed] [Google Scholar]
- 18.Wilder P.J., Kelly D., Rizzino A. Inactivation of the FGF-4 gene in embryonic stem cells alters the growth and/or the survival of their early differentiated progeny. Dev. Biol. 1997;192:614–629. doi: 10.1006/dbio.1997.8777. [DOI] [PubMed] [Google Scholar]
- 19.Arman E., Haffner-Krausz R., Lonai P. Targeted disruption of fibroblast growth factor (FGF) receptor 2 suggests a role for FGF signaling in pregastrulation mammalian development. Proc. Natl. Acad. Sci. USA. 1998;95:5082–5087. doi: 10.1073/pnas.95.9.5082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Goldin S.N., Papaioannou V.E. Paracrine action of FGF4 during periimplantation development maintains trophectoderm and primitive endoderm. Genesis. 2003;36:40–47. doi: 10.1002/gene.10192. [DOI] [PubMed] [Google Scholar]
- 21.Kang M., Piliszek A., Hadjantonakis A.K. FGF4 is required for lineage restriction and salt-and-pepper distribution of primitive endoderm factors but not their initial expression in the mouse. Development. 2013;140:267–279. doi: 10.1242/dev.084996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Krawchuk D., Honma-Yamanaka N., Yamanaka Y. FGF4 is a limiting factor controlling the proportions of primitive endoderm and epiblast in the ICM of the mouse blastocyst. Dev. Biol. 2013;384:65–71. doi: 10.1016/j.ydbio.2013.09.023. [DOI] [PubMed] [Google Scholar]
- 23.Nichols J., Silva J., Smith A. Suppression of Erk signalling promotes ground state pluripotency in the mouse embryo. Development. 2009;136:3215–3222. doi: 10.1242/dev.038893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yamanaka Y., Lanner F., Rossant J. FGF signal-dependent segregation of primitive endoderm and epiblast in the mouse blastocyst. Development. 2010;137:715–724. doi: 10.1242/dev.043471. [DOI] [PubMed] [Google Scholar]
- 25.Huang S., Guo Y.P., Enver T. Bifurcation dynamics in lineage-commitment in bipotent progenitor cells. Dev. Biol. 2007;305:695–713. doi: 10.1016/j.ydbio.2007.02.036. [DOI] [PubMed] [Google Scholar]
- 26.Gardner T.S., Cantor C.R., Collins J.J. Construction of a genetic toggle switch in Escherichia coli. Nature. 2000;403:339–342. doi: 10.1038/35002131. [DOI] [PubMed] [Google Scholar]
- 27.Lu M., Jolly M.K., Ben-Jacob E. MicroRNA-based regulation of epithelial-hybrid-mesenchymal fate determination. Proc. Natl. Acad. Sci. USA. 2013;110:18144–18149. doi: 10.1073/pnas.1318192110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lu M., Jolly M.K., Ben-Jacob E. Tristability in cancer-associated microRNA-TF chimera toggle switch. J. Phys. Chem. B. 2013;117:13164–13174. doi: 10.1021/jp403156m. [DOI] [PubMed] [Google Scholar]
- 29.Ohnishi Y., Huber W., Hiiragi T. Cell-to-cell expression variability followed by signal reinforcement progressively segregates early mouse lineages. Nat. Cell Biol. 2014;16:27–37. doi: 10.1038/ncb2881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Xenopoulos P., Kang M., Hadjantonakis A.-K. Heterogeneities in Nanog expression drive stable commitment to pluripotency in the mouse blastocyst. Cell Reports. 2015;10:1508–1520. doi: 10.1016/j.celrep.2015.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Batlle-Morera L., Smith A., Nichols J. Parameters influencing derivation of embryonic stem cells from murine embryos. Genesis. 2008;46:758–767. doi: 10.1002/dvg.20442. [DOI] [PubMed] [Google Scholar]
- 32.Chambers I., Silva J., Smith A. Nanog safeguards pluripotency and mediates germline development. Nature. 2007;450:1230–1234. doi: 10.1038/nature06403. [DOI] [PubMed] [Google Scholar]
- 33.Kalmar T., Lim C., Martinez Arias A. Regulated fluctuations in nanog expression mediate cell fate decisions in embryonic stem cells. PLoS Biol. 2009;7:e1000149. doi: 10.1371/journal.pbio.1000149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Abranches E., Guedes A.M., Henrique D. Stochastic NANOG fluctuations allow mouse embryonic stem cells to explore pluripotency. Development. 2014;141:2770–2779. doi: 10.1242/dev.108910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gillespie D. A general method for numerically simulating the stochastic time evolution of coupled chemical reaction. J. Comput. Phys. 1976;22:403–434. [Google Scholar]
- 36.Rouault H., Hakim V. Different cell fates from cell-cell interactions: core architectures of two-cell bistable networks. Biophys. J. 2012;102:417–426. doi: 10.1016/j.bpj.2011.11.4022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Guantes R., Poyatos J.F. Multistable decision switches for flexible control of epigenetic differentiation. PLOS Comput. Biol. 2008;4:e1000235. doi: 10.1371/journal.pcbi.1000235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Macía J., Widder S., Solé R. Why are cellular switches Boolean? General conditions for multistable genetic circuits. J. Theor. Biol. 2009;261:126–135. doi: 10.1016/j.jtbi.2009.07.019. [DOI] [PubMed] [Google Scholar]
- 39.Tiwari A., Igoshin O.A. Coupling between feedback loops in autoregulatory networks affects bistability range, open-loop gain and switching times. Phys. Biol. 2012;9:055003. doi: 10.1088/1478-3975/9/5/055003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Glauche I., Herberg M., Roeder I. Nanog variability and pluripotency regulation of embryonic stem cells—insights from a mathematical model analysis. PLoS One. 2010;5:e11238. doi: 10.1371/journal.pone.0011238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Chickarmane V., Peterson C. A computational model for understanding stem cell, trophectoderm and endoderm lineage determination. PLoS One. 2008;3:e3478. doi: 10.1371/journal.pone.0003478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Chickarmane V., Olariu V., Peterson C. Probing the role of stochasticity in a model of the embryonic stem cell: heterogeneous gene expression and reprogramming efficiency. BMC Syst. Biol. 2012;6:98. doi: 10.1186/1752-0509-6-98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Frum T., Halbisen M.A., Ralston A. Oct4 cell-autonomously promotes primitive endoderm development in the mouse blastocyst. Dev. Cell. 2013;25:610–622. doi: 10.1016/j.devcel.2013.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Le Bin G.C., Muñoz-Descalzo S., Nichols J. Oct4 is required for lineage priming in the developing inner cell mass of the mouse blastocyst. Development. 2014;141:1001–1010. doi: 10.1242/dev.096875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Doedel E. AUTO, a program for the automatic bifurcation analysis of autonomous systems. Congr. Numer. 1981;30:265–384. [Google Scholar]
- 46.Molkentin J.D., Antos C., Olson E.N. Direct activation of a GATA6 cardiac enhancer by Nkx2.5: evidence for a reinforcing regulatory network of Nkx2.5 and GATA transcription factors in the developing heart. Dev. Biol. 2000;217:301–309. doi: 10.1006/dbio.1999.9544. [DOI] [PubMed] [Google Scholar]
- 47.Fujikura J., Yamato E., Niwa H. Differentiation of embryonic stem cells is induced by GATA factors. Genes Dev. 2002;16:784–789. doi: 10.1101/gad.968802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Boyer L.A., Lee T.I., Young R.A. Core transcriptional regulatory circuitry in human embryonic stem cells. Cell. 2005;122:947–956. doi: 10.1016/j.cell.2005.08.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Shimosato D., Shiki M., Niwa H. Extra-embryonic endoderm cells derived from ES cells induced by GATA factors acquire the character of XEN cells. BMC Dev. Biol. 2007;7:80. doi: 10.1186/1471-213X-7-80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Singh A.M., Hamazaki T., Terada N. A heterogeneous expression pattern for Nanog in embryonic stem cells. Stem Cells. 2007;25:2534–2542. doi: 10.1634/stemcells.2007-0126. [DOI] [PubMed] [Google Scholar]
- 51.Kim J., Chu J., Orkin S.H. An extended transcriptional network for pluripotency of embryonic stem cells. Cell. 2008;132:1049–1061. doi: 10.1016/j.cell.2008.02.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Fidalgo M., Faiola F., Wang J. Zfp281 mediates Nanog autorepression through recruitment of the NuRD complex and inhibits somatic cell reprogramming. Proc. Natl. Acad. Sci. USA. 2012;109:16202–16207. doi: 10.1073/pnas.1208533109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Hamazaki T., Kehoe S.M., Terada N. The Grb2/Mek pathway represses Nanog in murine embryonic stem cells. Mol. Cell. Biol. 2006;26:7539–7549. doi: 10.1128/MCB.00508-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Niakan K.K., Ji H., Eggan K. Sox17 promotes differentiation in mouse embryonic stem cells by directly regulating extraembryonic gene expression and indirectly antagonizing self-renewal. Genes Dev. 2010;24:312–326. doi: 10.1101/gad.1833510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Ma Z., Swigut T., Wysocka J. Sequence-specific regulator Prdm14 safeguards mouse ESCs from entering extraembryonic endoderm fates. Nat. Struct. Mol. Biol. 2011;18:120–127. doi: 10.1038/nsmb.2000. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.