Phase Analysis of Metabolic Oscillations and Membrane Potential in Pancreatic Islet β-Cells

Abstract

Metabolism in islet β-cells displays oscillations that can trigger pulses of electrical activity and insulin secretion. There has been a decades-long debate among islet biologists about whether metabolic oscillations are intrinsic or occur in response to oscillations in intracellular Ca²⁺ that result from bursting electrical activity. In this article, the dynamics of oscillatory metabolism were investigated using five different optical reporters. Reporter activity was measured simultaneously with membrane potential bursting to determine the phase relationships between the metabolic oscillations and electrical activity. Our experimental findings suggest that Ca²⁺ entry into β-cells stimulates the rate of mitochondrial metabolism, accounting for the depletion of glycolytic intermediates during each oscillatory burst. We also performed Ca²⁺ clamp tests in which we clamped membrane potential with the K_ATP channel-opener diazoxide and KCl to fix Ca²⁺ at an elevated level. These tests confirm that metabolic oscillations do not require Ca²⁺ oscillations, but show that Ca²⁺ plays a larger role in shaping metabolic oscillations than previously suspected. A dynamical picture of the mechanisms of oscillations emerged that requires the restructuring of contemporary mathematical β-cell models, including our own dual oscillator model. In the companion article, we modified our model to account for these new data.

Introduction

In the consensus model of the β-cell triggering pathway, elevation of glucose metabolism triggers an increase in the ATP/ADP ratio, which initiates plasma membrane depolarization by inhibiting ATP-dependent K⁺ channels (K_ATP channels). This in turn stimulates voltage-dependent Ca²⁺ influx and insulin release. Importantly, measurements of insulin in the circulation indicate that secretion is pulsatile (1, 2, 3, 4) and this pulsatility facilitates insulin action at the liver (5, 6). The mechanisms underlying pulsatile insulin secretion have been debated for many years, and although there is consensus that metabolic oscillations are involved, there is debate as to whether they are intrinsic or result from islet Ca²⁺ oscillations (7). The most likely candidate for intrinsic metabolic oscillations is positive feedback mediated by the allosteric glycolytic enzyme phosphofructokinase-1 (PFK1). It has been shown that the muscle isoform of this enzyme can mediate glycolytic oscillations (8, 9, 10), and that PFK1 is expressed and active in β-cells (11). We recently developed a Fourier resonance energy transfer (FRET) biosensor (pyruvate kinase activity reporter, PKAR) that is sensitive to the fructose 1,6-bisphosphate (FBP) produced by PFK1 and thus serves as a marker for glycolytic activity (12). We showed that the PKAR signal oscillated with a 2–10 min period in glucose-stimulated islets. While this clearly demonstrated that glycolysis oscillates, we did not determine the relationship between the glycolytic oscillations and electrical or Ca²⁺ oscillations.

The relationships between oscillating variables in the β-cell are predicted by a mathematical model, the dual oscillator model (DOM), which couples PFK1-generated oscillations to electrical oscillations at the plasma membrane (7, 13, 14, 15, 16). These two oscillators are linked by Ca²⁺ feedback, which affects metabolism in several important ways that are reflected in the model. First, by entering mitochondria through transporters in the inner membrane (17), Ca²⁺ depolarizes mitochondrial membrane potential (ΔΨm), reducing the electrochemical driving force for H⁺ transport through Complex V, in turn reducing the efficiency of ATP production (18, 19, 20). Ca²⁺ entry also stimulates mitochondrial dehydrogenases (pyruvate dehydrogenase, isocitrate dehydrogenase, and α-ketoglutarate dehydrogenase (21)), increasing flux through the TCA cycle and producing mitochondrial reducing equivalents (NADH and FADH₂) for consumption by the electron transport chain (22). Finally, ATP is consumed in the cytosol by Ca²⁺-ATPases on the ER (SERCA) and plasma membrane (PMCA). Each of these feedback pathways has been invoked in distinct computational models as the mechanism that induces metabolic oscillations (18, 19, 23, 24, 25, 26), while the DOM, uniquely, proposes that glycolytic oscillations are intrinsic (7).

Given that Ca²⁺ can simultaneously augment and repress ATP levels, which of these processes is dominant during the course of oscillations? Furthermore, are glycolytic oscillations intrinsic or dependent upon Ca²⁺ oscillations? Here we used the patch-FRET technique to determine the relationship between glycolytic, mitochondrial, and Ca²⁺ oscillations in the free running islet, and to ascertain the dominant mode of Ca²⁺ feedback onto metabolism during the pulses. While we confirmed that glycolytic oscillations are intrinsic, the phase relationships we observed between the metabolic oscillations and membrane potential were at odds with the DOM, motivating us to reassess the role of Ca²⁺ feedback in the β-cell. In the companion article (39), we demonstrate that these data are consistent with a large role for Ca²⁺ in the activation of dehydrogenases and as an inducer of ATP hydrolysis by Ca²⁺ ATPase pumps.

Materials and Methods

Molecular biology

Adenoviruses were used to express PKAR FRET biosensors in pancreatic islet β-cells under control of the rat insulin promoter as in Merrins et al. (12). Perceval-HR ATP/ADP sensor (Addgene 49082 (27)) was then cloned in place of PKAR, and high titer adenovirus was prepared by the University of Michigan Viral Vector Core.

Pancreatic islet isolation and introduction of biosensors

Mice were sacrificed by cervical dislocation according to the regulations of the University of Wisconsin-Madison, William S. Middleton Memorial Veterans Hospital, and the University of Michigan Committee Institutional Animal Care and Use Committees. Islets were isolated from the pancreas and infected with adenovirus as in Merrins et al. (12), and maintained in culture for up to 3 days in RPMI1640 supplemented with 10% (v/v) fetal bovine serum, 100 units/mL penicillin and 100 μg/mL streptomycin (Invitrogen, Carlsbad, CA). For dye measurements of Ca²⁺, islets were preincubated in 2.5 μM Fura2 or FuraRed (Molecular Probes, Eugene, OR) for 30–45 min at 37°C. For dye measurements of mitochondrial membrane potential (ΔΨm), islets were preincubated in 0.83 μM Rhodamine-1,2,3 (Molecular Probes) for 5 min at 37°C, following by 30 s washing in fresh media without dye.

Imaging

Islets were placed in a glass-bottomed chamber (54 μLvolume) (Warner Instruments, Hamden, CT) on a model No. IX71 inverted microscope (Olympus, Melville, NY) equipped with a 20×/0.75 NA objective (Nikon Instruments, Melville, NY). The chamber was perfused at 0.3 mL/min and temperature was maintained at 33°C using inline solution and chamber heaters (Warner Instruments). Excitation was provided by a TILL Polychrome V monochromator as in our previous study (16) or by a SOLA SE II 365 (Lumencor, Beaverton, OR); each light source was set to 10% output. Excitation (x) or emission (m) filters (ET type; Chroma Technology, Bellows Falls, VT) were used in combination with an FF444/521/608-Di01 dichroic (Semrock, Lake Forest, IL) as follows: Flavin⁻¹, 430/24x, 470/24m and 535/30m (430x – R470m/535m) (12); Fura2, 340/10x and 380/10x, 535/30m (R340x/380x – 535m); FuraRed, 430/24x and 500/20x, 630/60m (R430x/500x – 630m); NAD(P)H, 365/20x, 470/24m (365x – 470m); Perceval-HR, 430/24x and 500/20x, 535/30m (R500x/430x – 535m) (27); PKAR, 430/24x, 470/24m and 535/30m (430x – R535m/470m) (12); Rhodamine-1,2,3, 500/20x, 535/30m (500x – 535m). Fluorescence emission was collected with a QuantEM:512SC camera (PhotoMetrics, Tucson, AZ) or an ORCA-Flash4.0 V2 Digital CMOS camera (Hamamatsu, Skokie, IL) at 0.125–0.2 Hz. A single region of interest was used to quantify the average response of each islet using MetaMorph (Molecular Devices) or Elements (Nikon Instruments) software.

Electrophysiology and solutions

A model No. MP-225 micromanipulator (Sutter Instrument, Novato, CA) was used together with a HEKA EPC10 patch-clamp amplifier (Heka Instruments, Bellmore, NY) in the perforated patch-clamp configuration to record β-cell membrane potential (Vm) using a sampling interval of 40 μs. Intact islets were perfused with a standard external solution containing (135 mM NaCl, 4.8 mM KCl, 5 mM CaCl₂, 1.2 mM MgCl₂, 20 mM HEPES, 10 mM glucose; pH 7.35), or higher [KCl] solutions using equimolar replacement of NaCl. Pipette tips were filled with an internal solution (28.4 mM K₂SO₄, 63.7 mM KCl, 11.8 mM NaCl, 1 mM MgCl₂, 20.8 mM HEPES, 0.5 mM EGTA; 40 mM sucrose; pH 7.2) containing 0.36 mg/mL amphotericin B. Islet β-cells were identified by the presence of slow oscillations in 10 mM glucose.

Data analysis

For analysis of slow oscillations, current-clamp (Vm) data were imported into Igor Pro software (WaveMetrics, Portland, OR). The onset and termination of each active phase (AP) were defined by a 10 mV elevation relative to the average Vm of the adjacent silent phase (SP). The period of each slow oscillation was measured from the start of each AP to the start of the following AP, to determine an average oscillation period for each islet. For analysis of phase, the AP onset (defined as phase = 0) was expressed as a fraction of the AP termination (defined as phase = 1), a method that leaves the phase of the subsequent AP ambiguous (i.e., the phase of the subsequent AP ≠ 2), but allows quantification of oscillations at different frequencies. Peaks and nadirs within the superimposed imaging data were then quantitatively assigned a phase as described in the Results. In some instances the slower sampling interval of the imaging data (5–8 s) relative to the current-clamp data (40 μs) gave the appearance of a peak that slightly preceded phase = 0; these data were manually corrected to phase = 0 in our analyses.

Results

Phase analysis of glycolytic oscillations

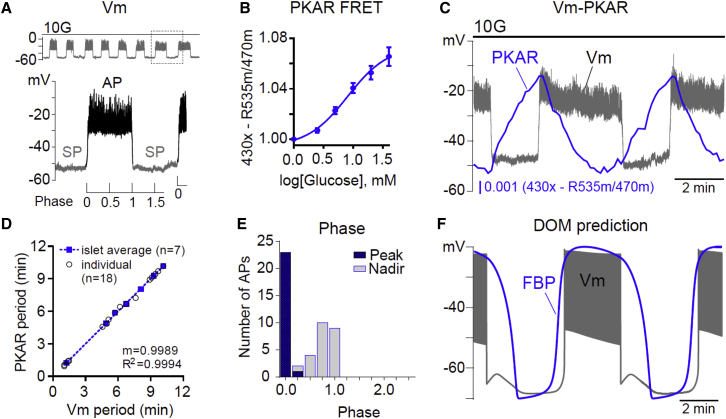
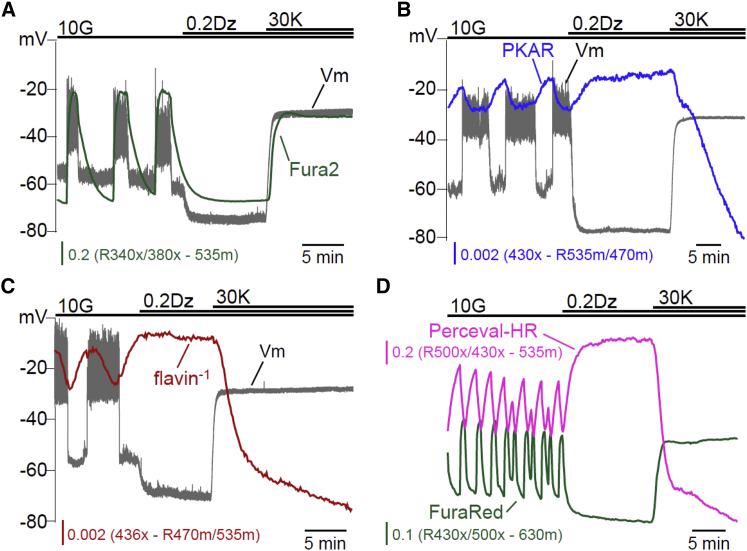
A variety of optical reporters were utilized in islets to map the relationships between the β-cell oscillatory signals induced by glucose stimulation. As a reference, slow oscillations in membrane potential (Vm) were measured from a surface β-cell on the same islet. Vm was chosen because the SP and AP of each oscillation are sharply delineated (Fig. 1 A), with the latter occurring in concert with insulin secretion. To assess glycolytic activity, we expressed a FRET reporter sensitive to FBP levels, PKAR (12).

Figure 1.

Phase analysis of β-cell glycolytic oscillations. (A) Oscillations in β-cell membrane potential (Vm) stimulated by 10 mM glucose (10G) were used to define the silent phase (SP) and active phase (AP). As depicted, phase was defined as a fraction of the AP. (B) Response of FBP-sensitive PKAR FRET to glucose (0–40 mM, n = 18). (C) Example recording of Vm-FBP oscillations (n = 7). (D) The relationship between the period of Vm and FBP is plotted for individual oscillations (open circles) and islet averages (solid boxes), which were fit by linear regression. (E) The phase of each FBP peak and nadir was calculated relative to Vm as in (A) and plotted as a histogram. The charts reflect 24 APs from seven simultaneous Vm-PKAR recordings. (F) The DOM clearly predicts a different phase relationship than we observed, with the FBP and Vm being largely in phase. Equations for the model are described in the companion article (39). To see this figure in color, go online.

When expressed in β-cells, PKAR responded to glucose in a dose-dependent manner, exhibiting a near-linear response between 2.5 and 20 mM glucose (Fig. 1 B). During the course of simultaneously monitored Vm oscillations (Fig. 1 C), FBP rose during the SP and fell during the AP based on observed changes in PKAR activity. The Vm and FBP oscillations had identical periods (5.3 ± 0.8 min on average, n = 7). These periods are plotted in Fig. 1 D, where the tight clustering around the dashed regression line (m = 0.9989) confirms that the periods of PKAR and Vm were highly correlated within each islet (R² = 0.9994).

Next, the phase of each oscillation’s peak and nadir was calculated, using the Vm waveform as a reference. In our analyses the phase was defined as 0 at the AP onset and 1 at the AP termination (Fig. 1 A), a method that is frequency-independent. The peak of FBP (phase = 0.011 ± 0.004, n = 47) almost invariably occurred at the onset of the AP, while the nadir of FBP (phase = 0.79 ± 0.03) occurred at or before the end of the AP (Fig. 1 E). As shown in Fig. 1 F, the phase of the FBP oscillations we observed in mouse islets differed from the prediction of the DOM, in which glycolytic FBP remains elevated throughout much of the active phase. This prompted us to investigate the cause of the deviation.

Phase analysis of mitochondrial oscillations

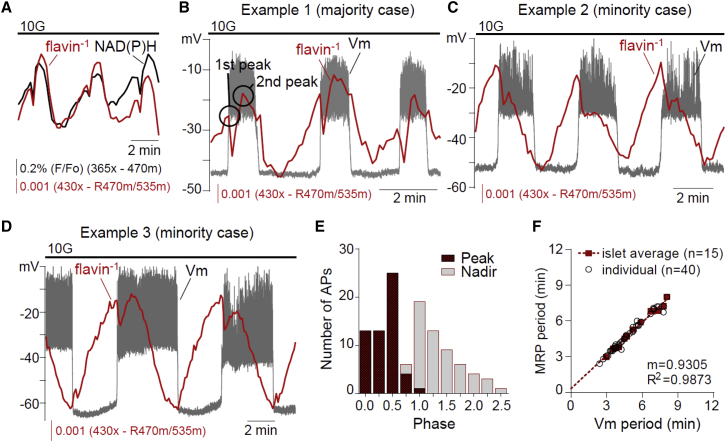
To assess mitochondrial activity, we measured endogenous islet flavin fluorescence (expressed as flavin⁻¹). This yielded data that were comparable to the changes we observed in NAD(P)H fluorescence (Fig. 2 A). Both measurements reflect the reducing equivalents available to fuel the electron transport chain (12, 28, 29) and were previously confirmed to be functional mitochondrial variables as their glucose-dependent fluorescence was eliminated by addition of the mitochondrial uncoupler FCCP (12).

Figure 2.

Phase analysis of β-cell mitochondrial flavin⁻¹ oscillations. (A) Simultaneous recording of islet NAD(P)H and flavin⁻¹ oscillations (n = 20). (B–D) Example recordings of Vm-flavin⁻¹ oscillations in 10 mM glucose (n = 15). (E) The phase of each flavin⁻¹ nadir and largest peak was calculated relative to Vm as shown in Fig. 1A and plotted as a histogram. The chart reflects 40 APs from 15 simultaneous Vm-flavin⁻¹ recordings. (F) The relationship between Vm period and flavin⁻¹ period is plotted for individual oscillations (open circles) and islet averages (solid boxes). Islet averages were then fit by linear regression. To see this figure in color, go online.

Fig. 2, B–D, shows three examples of Vm-flavin⁻¹ recorded simultaneously. In all cases, flavin⁻¹ rose during the silent phase but was delayed relative to FBP (compare to Fig. 1 C), as expected if glycolytic output drives mitochondrial NADH and FADH₂ production in the TCA cycle. At the AP onset, flavin⁻¹ declined sharply, much like FBP, so that a flavin⁻¹ peak occurred at the beginning of the AP (phase = 0.018 ± 0.007, n = 6). However, in 44 of 56 cases (79%) flavin⁻¹ rose sharply after a 14 ± 1 s delay, producing a larger second peak (Fig. 2 B) that in 12 of 56 cases (21%) resembled more of a shoulder (Fig. 2 C); the phase of this second peak was 0.47 ± 0.03. Occasionally, as in Fig. 2 D, the relative peak sizes changed from burst-to-burst. Consequently, the occurrence of the larger of the two flavin⁻¹ peaks exhibited much more variability than the FBP peak in Fig. 1, ranging from phase 0–0.95 with an average of 0.36 ± 0.03 (n = 56) (Fig. 2 E). The placement of the second peak was not correlated with AP duration (R² = 0.0792) or Vm plateau fraction (the fraction of time spent in the AP during one cycle; R² = 0.1657), even though the periods of the Vm and flavin⁻¹ oscillations were tightly correlated (R² = 0.9873; Fig. 2 F).

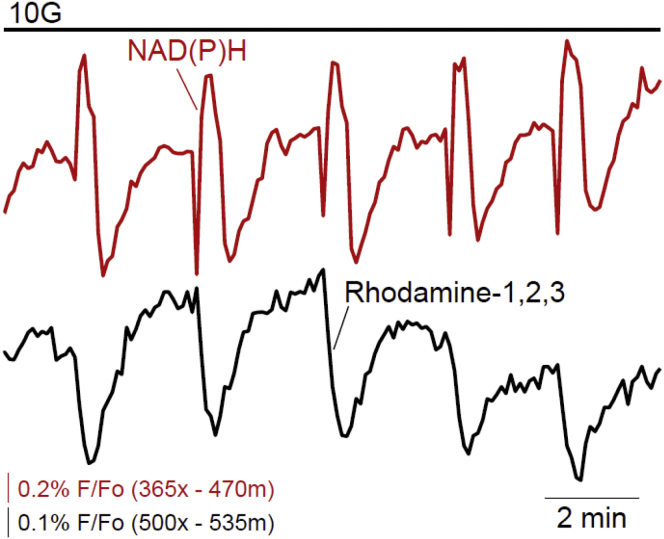
One possible explanation for the second flavin⁻¹ peak is decreased NADH consumption by the electron transport chain due to Ca²⁺-dependent mitochondrial depolarization, which has been proposed to be a consequence of Ca²⁺ entry during the AP (18, 19). To investigate this hypothesis, we simultaneously recorded NAD(P)H with mitochondrial membrane potential (ΔΨm) using Rhodamine-1,2,3 fluorescence (Fig. 3). Using the sharp drop in NAD(P)H as a marker of the AP onset (compare to Fig. 2), we found that ΔΨm decreased (hyperpolarized) with a displacement of several seconds (8.2 ± 0.2 s, n = 30) relative to Vm depolarization, but coincident with the resurgence in NAD(P)H during the AP. The timing of mitochondrial hyperpolarization is therefore inconsistent with the hypothesis that Ca²⁺ depolarization of ΔΨm (18, 19, 20, 30), and a slowing of the mitochondrial electron transport chain, can explain the dynamics of the NAD(P)H rise we observed.

Figure 3.

Relationship between islet NAD(P)H and mitochondrial membrane potential (ΔΨm). Mitochondrial membrane potential is plotted as Rhodamine-1,2,3 fluorescence (n = 30 islets from three animals). Note that a decrease in fluorescence corresponds to ΔΨm hyperpolarization and increased driving force for ATP production. To see this figure in color, go online.

Antagonism between ATP/ADP and Ca²⁺ oscillations

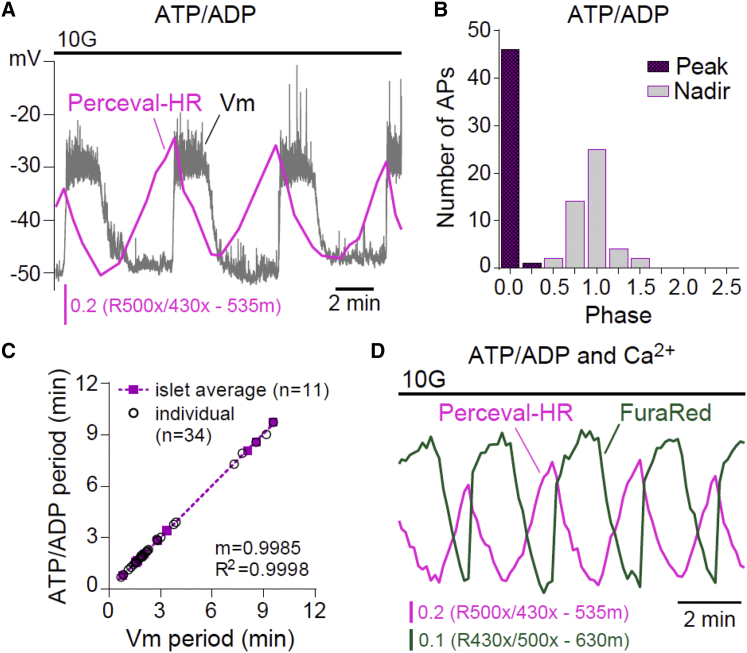
Having ruled out Ca²⁺-dependent mitochondrial depolarization, a second hypothesis for the rise in NAD(P)H during the AP is that a rise in cytosolic ATP-inhibited ATP synthesis, which in turn reduced NADH consumption by the electron transport chain. To test this possibility, we examined the relationship between ATP/ADP and Vm, taking advantage of a second-generation ATP/ADP sensor, Perceval-HR (27). We expressed Perceval-HR in islet β-cells and measured it together with Vm. As ATP/ADP increased during the SP and fell during the AP, the second hypothesis could not account for the changes in NAD(P)H we observed.

A third possibility for the rise in flavin⁻¹ we observed during the AP is increased NADH and FADH₂ production during the TCA cycle, stimulated by Ca²⁺-dependent dehydrogenase activation (21, 22, 31, 32, 33). Indeed, if our model is modified to include such activation, it can then reproduce the sawtooth PKAR pattern that we observe in our data (Fig. 1). This is illustrated and explained in the companion article (39), and lends support to this third postulated mechanism for the second peak in the flavin⁻¹ time course.

It is interesting that the ATP/ADP time course, as measured with Perceval-HR (Fig. 4 A), looks much like the PKAR time course, exhibiting a sawtooth pattern with peak near the beginning (phase 0) and nadir near the end (phase 1) of the AP (Fig. 4 C). The close similarity between the FBP and ATP/ADP time courses—and to an extent ΔΨm hyperpolarization—suggests that common factors might control each of these metabolic variables. One likely controlling factor is Ca²⁺. In the vicinity of the plasma membrane, increased Ca²⁺ has been shown to correlate with reduced ATP levels (34, 35), suggesting that ATP consumption by plasma membrane as well as ER Ca²⁺-ATPases likely play a large role in determining β-cell ATP levels. Indeed, we observed that Ca²⁺ and ATP/ADP oscillations were out of phase (Fig. 4 D), further confirming the antagonistic relationship between ATP/ADP and intracellular Ca²⁺. The ATP/ADP ratio fell even though mitochondrial NADH remained elevated (Fig. 2 B) and the mitochondria were still hyperpolarized, indicating that the rate of consumption of ATP increases during the AP when the Ca²⁺ level is elevated.

Figure 4.

Phase analysis of β-cell ATP/ADP oscillations. (A) Example recording of Vm-ATP/ADP oscillations in 10 mM glucose (n = 13). (B) The phase of each ATP/ADP peak and nadir was calculated relative to Vm as shown in Fig. 1 A and plotted as a histogram. The charts reflect 40 APs from 10 simultaneous Vm-ATP/ADP recordings. (C) The relationships between Vm period and ATP/ADP period are plotted for individual oscillations (open circles) and islet averages (solid boxes). Islet averages were then fit by linear regression. (D) Example recording of ATP/ADP and cytosolic Ca²⁺ oscillations in 10 mM glucose (n = 10). To see this figure in color, go online.

Ca²⁺ feedback on β-cell metabolism

To investigate the feedback of Ca²⁺ on FBP, flavin⁻¹, and ATP/ADP in more detail, cytosolic Ca²⁺ was reduced by adding 200 μM diazoxide (Dz) to open K_ATP channels and then augmented by depolarizing the plasma membrane with 30 mM KCl (Dz/KCl) (Fig. 5 A). Importantly, the use of Dz simplified the system by preventing oscillations—Ca²⁺ remained at a steady nonoscillatory level when Dz was present. Lowering Ca²⁺ with Dz increased FBP (Fig. 5 B), flavin⁻¹ (Fig. 5 C), and ATP/ADP (Fig. 5 D), as expected from the increases in each response during the burst SP (Figs. 1, 2, and 4). Consistently, increasing Ca²⁺ with Dz/KCl reduced FBP (Fig. 5 B), flavin⁻¹ (Fig. 5 C), and ATP/ADP (Fig. 5 D).

Figure 5.

Effects of steady-state Ca²⁺ on the β-cell triggering pathway. The effects of lowering islet Ca²⁺ with diazoxide (Dz, 200 μM) and raising Ca²⁺ with Dz/KCl ([K⁺]_o = 30 mM) were assessed by simultaneous measurements of Vm and intracellular Ca²⁺ (n = 4) (A), FBP (n = 4) (B), flavin⁻¹ (n = 5) (C), or cytosolic Ca²⁺ and ATP/ADP (n = 45) (D). To see this figure in color, go online.

Glycolytic oscillations can persist without Ca²⁺ oscillations

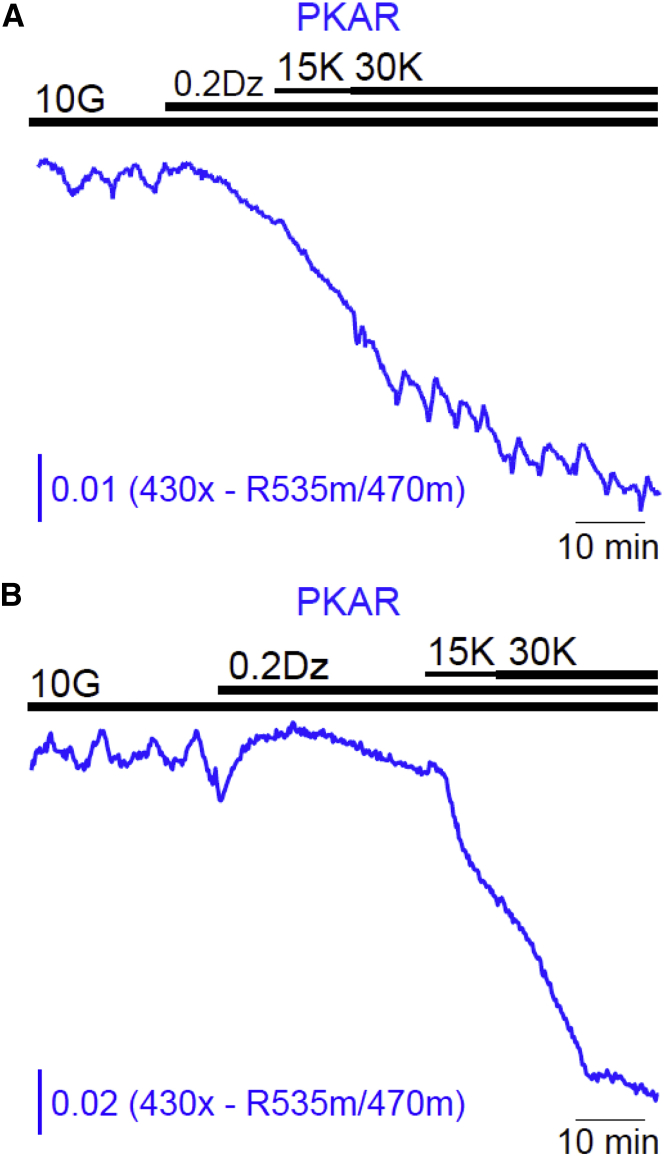
The data above all point to effects of Ca²⁺ on metabolism, as we illustrate in greater detail in the companion article (39). But are Ca²⁺ oscillations required for the production of metabolic oscillations in islets, as some have previously proposed (18, 19, 23, 24, 25, 26)? This view is supported by reports that NAD(P)H oscillations are terminated by diazoxide (15, 36), which fixes cytosolic Ca²⁺ at a low and nonoscillatory level. We confirmed this and found that Dz addition terminated FBP, flavin⁻¹, and ATP/ADP oscillations as well (Fig. 5). An alternative explanation, as given by the DOM, is that membrane hyperpolarization reduced β-cell Ca²⁺ and in turn reduced ATP-dependent Ca²⁺ pumping, increasing cytosolic ATP, as shown directly by Fig. 5 D. Increased ATP inhibits PFK1 (37). Thus, lowering the Ca²⁺ level with Dz terminates metabolic oscillations not because the Ca²⁺ oscillations are terminated per se, but because Dz indirectly inhibits glycolytic oscillations due to ATP-dependent inhibition of PFK1. However, if Ca²⁺ is raised by subsequently depolarizing the cell with KCl, then ATP levels fall as ATP is hydrolyzed by Ca²⁺ pumps. If the right amount of KCl is applied, neither too much nor too little, then the model predicts that PFK1 will be sufficiently disinhibited to rescue glycolytic oscillations (15). We previously tested this prediction by measuring NAD(P)H, and found that in a fraction of islets it was indeed possible to rescue metabolic oscillations via membrane depolarization (15).

However, as NAD(P)H is only an indirect monitor of glycolysis, we retested this prediction using PKAR to directly measure glycolytic FBP. As predicted, stepwise elevation of Ca²⁺ restored glycolytic oscillations in a small fraction (8%) of islets tested (n = 25) (Fig. 6). Relative to the oscillations recorded in 10 mM glucose alone, the frequency of the oscillations in Dz/KCl increased ∼33%. After the removal of Dz/KCl, the resumption of strong islet glycolytic and Ca²⁺ oscillations demonstrated that the islets retained normal physiological function even after a period of elevated Ca²⁺ (not shown). These results are in good qualitative agreement with our previous experiments measuring NAD(P)H oscillations (15), and confirm a central prediction of the DOM, that glycolytic oscillations are intrinsic to the β-cell. The fact that glycolytic oscillations were rescued in only a small fraction of islets is consistent with the model prediction that the Ca²⁺ level must be within an intermediate range, neither too high nor too low, for the rescue to succeed (15).

Figure 6.

Glycolytic oscillations can occur without Ca²⁺ oscillations. After suppression of FBP oscillations with Dz, stepwise elevation of [K⁺]_o from 15 to 30 mM restored oscillations in two of 25 islets (8%) in five experiments (A). In the majority of islets, oscillations were not restored (B). To see this figure in color, go online.

Discussion

Using the patch-FRET technique, we have determined the oscillatory time course of glycolysis in islets (measured with the PKAR sensor) simultaneous with the electrical bursting time course of a β-cell within an intact islet (measured by patch-clamp). This revealed a sawtooth pattern of the FBP level, in which FBP declines during a burst active phase and rises during a silent phase. This unexpected pattern, which is not in agreement with the DOM (Fig. 1), suggests that the elevation in the intracellular Ca²⁺ level that occurs during an active phase is responsible for the decline in FBP, and the low Ca²⁺ concentration of a silent phase allows FBP to rise. This correlational finding was further examined by manipulating the Ca²⁺ concentration pharmacologically, first decreasing it (and terminating oscillations) with diazoxide and then increasing it (without restoring Ca²⁺ oscillations) using KCl (Fig. 5). This experiment again supported the view that elevated Ca²⁺ causes a decrease in FBP, the product of the enzyme PFK1. How can this be explained? One speculation is that Ca²⁺ inactivates PFK1, causing a reduction in FBP production. However, we are not aware of any biochemical evidence supporting this. Perhaps the decline in FBP concentration is due to an increase in consumption rather than a decrease in production. This could occur if Ca²⁺ stimulates some metabolic reaction downstream of PFK1. In fact, there is considerable evidence for this, because it has been shown that several dehydrogenases are stimulated by Ca²⁺ (21, 22, 31, 32, 33) including pyruvate dehydrogenase, which follows the glycolytic pathway (33). In the companion article (39), we use mathematical modeling to show that if a Ca²⁺ dependence is added to the expression for the metabolic flux through pyruvate dehydrogenase, then we obtain the sawtooth FBP pattern shown here. Furthermore, this Ca²⁺-dependent increase in glycolytic flux is consistent with the upward spike of flavin⁻¹ we showed in Fig. 2, as well as the hyperpolarization of mitochondrial membrane potential during a burst active phase that we showed in Fig. 3. Thus, this explanation, which is supported by biochemical studies of dehydrogenases, explains many features of our data.

We also measured the ATP/ADP ratio using Perceval-HR, during glucose-induced bursting and during pharmacological manipulations of the Ca²⁺ level. Again, we found a sawtooth pattern in which ATP/ADP declines during the active phase and rises during the silent phase of a burst (Fig. 4). This correlation was seen again when the Ca²⁺ concentration was lowered by membrane hyperpolarization with diazoxide and subsequently raised with KCl (Fig. 5). That is, the Perceval-HR signal increased when the Ca²⁺ concentration was reduced and decreased when the Ca²⁺ concentration was elevated. Can the relationship between Ca²⁺ and the Perceval-HR time course be explained the same way as the PKAR time course, or is it due to a different mechanism? The decline in ATP/ADP during a burst active phase could be due to a reduced production of ATP, but this is inconsistent with our hypothesis above that flux through glycolysis is increased during the active phase. An alternate explanation is that ATP consumption is increased during an active phase. This is actually quite reasonable, because the elevation of cytosolic Ca²⁺ that occurs during an active phase (or after application of KCl) will induce hydrolysis of ATP to power the Ca²⁺ ATPases that pump Ca²⁺ out of the cell or into the endoplasmic reticulum (34, 35, 38). In the companion article (39), we demonstrate that the DOM, which includes terms for this Ca²⁺-dependent hydrolysis, produces the sawtooth Perceval-HR pattern that we see in our data. Furthermore, the model reproduces our finding that PKAR and Perceval-HR peaks occur almost always at the start of a burst active phase, but the timing of the nadirs is much more variable near the end of the active phase (Figs. 2 and 4).

Others have measured the mitochondrial membrane potential (ΔΨm) under various conditions. Notably, Krippeit-Drews et al. (30) used Rhodamine-1,2,3 fluorescence to show that, during bursting, ΔΨm depolarized during each Ca²⁺ increase. We found the opposite, that ΔΨm hyperpolarized during each burst active phase. Why the difference? The oscillations characterized by Drews et al. (20) were fast, with a period of less than a minute, suggesting that they were not driven by glycolytic oscillations, but instead were driven by Ca²⁺ feedback onto K(Ca) ion channels. In contrast, in our experiments the oscillations were slow, reflecting glycolytic oscillations. Thus, in our case there were two competing effects on mitochondrial membrane potential: 1) a rise in Ca²⁺, which would depolarize mitochondrial membrane potential, and 2) an increase in metabolic flux that occurs simultaneously with the rhythmical Ca²⁺ elevations, and which in turn hyperpolarizes mitochondrial membrane potential. We believe that the hyperpolarization we observed during Ca²⁺ elevations occurred because the glycolytic effect in our hands was greater than the direct effect of Ca²⁺.

An important prediction of the DOM is that metabolic oscillations that are terminated by membrane hyperpolarization (using diazoxide, for example) can sometimes be restored if Ca²⁺ is subsequently elevated (using KCl, for example). We previously tested this prediction, measuring NAD(P)H as a readout for metabolism (15), and found that indeed it was sometimes possible to rescue metabolic oscillations even though Ca²⁺ was not oscillating. However, it was still possible that some other mechanism, downstream of glycolysis, could be responsible for the rescued metabolic oscillations. In this article we redid the experiment, but this time with PKAR, a direct glycolytic readout. As shown in Fig. 6, it was indeed possible to rescue metabolic oscillations in the absence of Ca²⁺ oscillations, but now we have established that the oscillations occur in the glycolytic pathway. This rescue was rare (8% of islets tested), but this is not unexpected. The model predicts that Ca²⁺ must be held at some intermediate level to reactivate the glycolytic oscillator. If the Ca²⁺ concentration is too low then there will be insufficient ATP hydrolysis by Ca²⁺ ATPases to lower the ATP level sufficiently and thus the PFK1 will remain largely inhibited. If the Ca²⁺ concentration is too high then the ATP hydrolysis will be so large that too much inhibition will be removed from PFK1, putting it into an overstimulated state. The lower and upper Ca²⁺ thresholds depend on properties of PFK1 as well as the expression levels of the Ca²⁺ ATPases, and these (particularly the latter) are expected to vary from islet to islet. Thus, adjusting the KCl level so that the Ca²⁺ level lies between the thresholds, when we do not know the value of the thresholds, makes the chance of successful rescue very low. However, we stress that even rescuing a minority of the glycolytic oscillations is proof of the concept that the oscillations are not simply the byproduct of Ca²⁺ oscillations; glycolytic oscillations therefore can be produced even when Ca²⁺ is not oscillating.

The experimental results taken together support a central and unique tenet of the DOM: metabolic oscillations in β-cells centrally involve glycolytic oscillations. They also support a modification of the model (presented in McKenna et al. (39)) in which the influx of free Ca²⁺ during the active phase stimulates the rate of mitochondrial metabolism and hastens the depletion of glycolytic intermediates during the slow bursts of electrical activity and Ca²⁺ influx. It remains to be seen whether metabolic defects in the β-cells of humans may account for the defects in pulsatile secretion seen in Type 2 diabetes.

Author Contributions

M.J.M. and L.S.S. designed experiments; M.J.M. and C.P. performed experiments; and M.J.M., C.P., J.P.M., A.S., R.B., J.H., and L.S.S. analyzed data and wrote the article.

Editor: David Piston.