Ca²⁺ Effects on ATP Production and Consumption Have Regulatory Roles on Oscillatory Islet Activity

Abstract

Pancreatic islets respond to elevated blood glucose by secreting pulses of insulin that parallel oscillations in β-cell metabolism, intracellular Ca²⁺ concentration, and bursting electrical activity. The mechanisms that maintain an oscillatory response are not fully understood, yet several models have been proposed. Only some can account for experiments supporting that metabolism is intrinsically oscillatory in β-cells. The dual oscillator model (DOM) implicates glycolysis as the source of oscillatory metabolism. In the companion article, we use recently developed biosensors to confirm that glycolysis is oscillatory and further elucidate the coordination of metabolic and electrical signals in the insulin secretory pathway. In this report, we modify the DOM by incorporating an established link between metabolism and intracellular Ca²⁺ to reconcile model predictions with experimental observations from the companion article. With modification, we maintain the distinguishing feature of the DOM, oscillatory glycolysis, but introduce the ability of Ca²⁺ influx to reshape glycolytic oscillations by promoting glycolytic efflux. We use the modified model to explain measurements from the companion article and from previously published experiments with islets.

Introduction

Pancreatic islets respond to elevated blood glucose by secreting pulses of insulin (1) that parallel oscillations in β-cell metabolism, intracellular Ca²⁺ concentration, and bursting electrical activity (2). Pulsatile release facilitates glucose homeostasis (3, 4, 5) and is lost or irregular in patients with type 2 diabetes (6, 7, 8). How cellular signals coordinate to maintain an oscillatory response is not fully understood, but several mathematical models have been formulated. Models that include metabolic pathways may be classified according to whether they propose that metabolism is intrinsically oscillatory (2, 9, 10, 11) or that oscillatory metabolism results only from oscillations in intracellular Ca²⁺ concentration (12, 13, 14, 15).

Bertram et al. (16) formulated the dual oscillator model (DOM), which proposed that endogenous glycolytic oscillations modulate a Ca²⁺-dependent oscillatory mechanism. Inclusion of oscillatory glycolysis in the model was motivated partly by experiments demonstrating that the dominant isoform of the glycolytic enzyme phosphofructokinase (PFK) expressed in β-cells produces oscillations, where it is also expressed in muscle extracts (17). The DOM has received considerable experimental support since it was proposed. It can simulate a variety of observed responses to stimulatory glucose including slow (>2 min), fast (<2 min), and compound (fast superimposed on slow) oscillations (16, 18). It accounts for the persistence of metabolic oscillations when Ca²⁺ oscillations are prevented in stimulatory glucose (19). It agrees with the pattern of membrane conductance changes of voltage-clamped β-cells measured in islets (20) and with the effects of modulating allosteric activation of PFK (21). However, these experiments offer only indirect support for the existence of oscillatory glycolysis in β-cells.

Merrins et al. (22) provided direct evidence of oscillatory glycolysis in β-cells using a FRET sensor, pyruvate kinase activity reporter (PKAR) that dynamically reports activity of the glycolytic enzyme pyruvate (PYR) kinase in β-cells. In the companion article, we use PKAR and another sensor, Perceval-HR, which reports the [ATP]/[ADP] ratio, to measure metabolic oscillations simultaneously with membrane potential. In this report, we show that the DOM can account for these PKAR and Perceval-HR recordings by adding an established Ca²⁺ dependence to an expression for a mitochondrial dehydrogenase in the model. With this modification, we replicate PKAR and Perceval-HR recordings and explain the coordination of metabolic and Ca²⁺ oscillations in various experimental protocols. We then use the modified DOM to address two prior experiments with islets in which slow oscillations were triggered by stimulatory glucose in PFK-M knockout mice (23) or by fuels entering metabolism downstream of glycolysis in the absence of stimulatory glucose (24). Both of these present major challenges to the DOM, and can now be accounted for by the modified model.

Materials and Methods

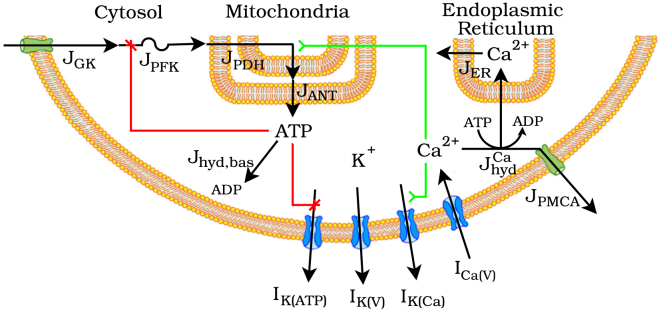
We start with the dual oscillator model (DOM), recently described in Watts et al. (25), which has components for glycolysis, ATP production and hydrolysis, and ionic currents. For an appropriate balance of glycolytic influx to efflux, the phosphofructokinase (PFK) reaction introduces, through autocatalysis, oscillations in the concentrations of glycolytic metabolites with a period of several minutes. Depolarization of the membrane above threshold initiates bursting oscillations in membrane potential accompanied by oscillations in free cytosolic Ca²⁺, $C{a}_c$, with a period of several seconds to minutes (2). These glycolytic and electrical oscillators are self-regulated through ATP and Ca²⁺ in that ATP allosterically inhibits PFK and hence glycolytic flux, and that intracellular Ca²⁺ induces current through Ca²⁺-activated K⁺ (K(Ca)) channels to repolarize the membrane. They are also coupled through ATP and Ca²⁺ in that phosphorylation of ADP by glycolysis deactivates ATP-sensitive K⁺ (K(ATP)) channels to depolarize the membrane, and Ca²⁺ conducted into the cell promotes ATP hydrolysis to both disinhibit PFK and reactivate K(ATP) channels. A schematic of the model is depicted in Fig. 1.

Figure 1.

Schematic of the DOM. I, current; J, flux; GK, glucokinase; PFK, phosphofructokinase; PDH, pyruvate dehydrogenase; ANT, adenine nucleotide translocator; ER, endoplasmic reticulum; hyd, hydrolysis; PMCA, plasma membrane Ca²⁺ ATPase. The modification to the model considered in this report is symbolized by the activating arrow from Ca²⁺ to $J_{\text{PDH}}.$ To see this figure in color, go online.

The glycolytic component of the DOM, adapted from Smolen (26) and qualitatively similar to Westermark and Lansner (10), models the kinetics of the reaction catalyzed by PFK. Influx to the component is through glucokinase, which phosphorylates glucose to glucose 6-phosphate. Efflux is through the mitochondrial pyruvate dehydrogenase (PDH) complex, which decarboxylates the final glycolytic product pyruvate to supply acetyl CoA to the citric acid cycle. It is a system of two differential equations for the rates of concentration change of the PFK reaction substrate, fructose 6-phosphate (F6P), and product, fructose 1,6-bisphosphate (FBP):

$$\begin{array}{c}\frac{d\left[\text{F}6\text{P}\right]}{dt}=\frac{1}{1+k_{\text{GPI}}}\left(J_{\text{GK}}-J_{\text{PFK}}\right)\\ \frac{d\left[\text{FBP}\right]}{dt}=\frac{1}{1+\frac{1}{2}\sum k_P}\left(J_{\text{PFK}}-\frac{1}{2}{J}_{\text{PDH}}\right)\end{array}$$ (1)

derived by assuming the glucose 6-phosphate isomerase reaction upstream to PFK and the series of reactions downstream to PFK are at equilibrium (27, 28) with proportionality constants $k_{\text{GPI}}=\left[\text{G}6\text{P}\right]/\left[\text{F}6\text{P}\right]$ and $k_P=\left[\text{P}\right]/\left[\text{FBP}\right]$ for each glycolytic product P, glyceraldehyde 3-phosphate through pyruvate, downstream to FBP (see the Supporting Material for complete derivation). $J_{\text{GK}}$ is an increasing function of glucose concentration and is held constant to simulate perfusion of islets in constant glucose. $J_{\text{PFK}}$ depends on the concentrations of PFK substrate, F6P, product, FBP, and allosteric effectors, FBP, ATP, and AMP, and its form has previously been described in Smolen (26). PDH and several other dehydrogenases involved in the citric acid cycle are regulated by changes in mitochondrial Ca²⁺, $C{a}_m$ (29). We incorporate the stimulatory effect of Ca²⁺ on PDH:

$$J_{\text{PDH}}=k_{\text{PDH}}{\left[\text{PYR}\right]}^{1/2}\frac{\left[C{a}_m\right]}{\left[C{a}_m\right]+k_{\text{PDH}}^{Ca}}$$ (2)

with the choice of $k_{\text{PDH}}^{Ca}$ guided by Denton (29) and the assumption that $\left[C{a}_m\right]$ is proportional to cytosolic Ca²⁺ concentration, $\left[C{a}_m\right]$, as $\left[C{a}_m\right]=k_{Ca}\left[C{a}_c\right]$ guided by Ca²⁺ imaging studies (30,31).

The cytosolic ATP, ATP_c, concentration is given by a differential equation reflecting ATP production and hydrolysis. The concentration increases as adenine nucleotide translocators export ATP from the mitochondrial matrix to the cytosol and decreases with hydrolysis (hyd):

$$\frac{d\left[{\text{ATP}}_c\right]}{dt}=J_{\text{ANT}}-J_{\text{hyd}}.$$

$J_{\text{ANT}}$ is a sigmoidally increasing function of $\left[{\text{ATP}}_m\right]/\left[{\text{ADP}}_m\right]$ (Eq. 2.5 in Watts et al. (25)), where $\left[{\text{ATP}}_m\right]$ is an increasing function of glycolytic input $J_{\text{PDH}}$:

$$\left[{\text{ATP}}_m\right]=A_{m,\text{tot}}-q_1\left[C{a}_c\right]-q_2\text{exp}\left(-J_{\text{PDH}}/q_3\right)$$ (3)

and mitochondrial adenine nucleotides are conserved as $A_{m,\text{tot}}=\left[{\text{ADP}}_m\right]+\left[{\text{ATP}}_m\right]$. $J_{\text{hyd}}$ is the sum of basal and Ca²⁺-dependent ATP_c hydrolysis

$$J_{\text{hyd}}=J_{\text{hyd},\text{bas}}+J_{\text{hyd}}^{Ca},$$

where $J_{\text{hyd},\text{bas}}$ is proportional to the concentration of ATP_c and $J_{\text{hyd}}^{Ca}$ is proportional to the concentrations of both ${\text{ATP}}_c$ and $C{a}_c$:

$$J_{\text{hyd},\text{bas}}=k_{\text{hyd},\text{bas}}\left[{\text{ATP}}_c\right]$$

$$J_{\text{hyd}}^{Ca}=k_{\text{hyd}}^{Ca}\left[{\text{ATP}}_c\right]\left[C{a}_c\right].$$

Ca²⁺-dependent hydrolysis powers the actions of Ca²⁺ pumps in the ER and plasma membranes.

The ionic current component, described in Bertram et al. (16), is a conductance-based model of transmembrane currents coupled to a model of intracellular Ca²⁺ transport. The model of transmembrane currents includes voltage-activated Ca²⁺ (Ca(V)) and K⁺ (K(V)) currents, Ca²⁺-activated K⁺ (K(Ca)) current, and ATP-sensitive K⁺ (K(ATP)) current. The model of intracellular Ca²⁺ transport includes three compartments: the cytosol, ER, and mitochondria.

In the final step of glycolysis in β-cells, the M2 isoform of pyruvate kinase (PK) dephosphorylates phosphoenolpyruvate to pyruvate. Catalytic activity of the PK-M2 isoform is substantially greater in its tetramer than its dimer or monomer forms, and multimerization is accomplished via feedforward activation by FBP (32, 33). In the companion article, PK-M2 activity is measured by the FRET sensor PKAR, which we model as

$$\text{PKAR}=\frac{\left[\text{FBP}\right]}{\left[\text{FBP}\right]+k_{\text{PK}}^{\text{FBP}}},$$ (4)

with the choice of $k_{\text{PK}}^{\text{FBP}}$ guided by Dombrauckas et al. (34). In β-cells, ATP acts a signaling molecule by modulating electrical and metabolic activity. In the companion article, the [ATP]/[ADP] ratio is measured with Perceval-HR, a genetically encoded fluorescent sensor on which ATP and ADP competitively bind to a single high-affinity site (35, 36). Perceval-HR is a second-generation sensor that, herein, we refer to as “Perceval” and model as

$$\text{Perceval}=\frac{\left[{\text{ATP}}_c\right]/\left[{\text{ADP}}_c\right]}{\left[{\text{ATP}}_c\right]/\left[{\text{ADP}}_c\right]+k_{\text{Perceval}}^{A_c}},$$

with the choice of $k_{\text{Perceval}}^{A_c}$ guided by Berg et al. (35). Model equations were integrated using the backward differentiation formulas implemented by the CVODE and XPP software packages. All equations and parameter values are in Table S1 in the Supporting Material and can be downloaded as freeware from http://www.math.fsu.edu/∼bertram/software/islet.

Results

Ca²⁺ regulation of pyruvate dehydrogenase shapes PKAR and Perceval signals

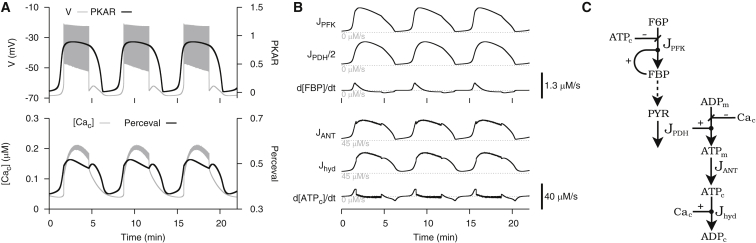
In the companion article, we observed in glucose-stimulated β-cells that PKAR and Perceval signals rose preceding the active phase, abruptly started to fall at the beginning of the active phase, and recovered by the next silent phase. In contrast, simulations with the DOM predicted that PKAR and Perceval would exhibit a rise sustained throughout the active phase (Fig. 2 A). Our first goal was to understand how these time courses are produced by the DOM, whose metabolic pathway is depicted in Fig. 2 C. Whether the model PKAR signal is rising or falling is determined by the sign of $d\left[\text{FBP}\right]/dt$, which, in turn, is determined by the difference in magnitude between the flux through PFK, $J_{\text{PFK}}$, and glycolytic efflux, $J_{\text{PDH}}/2$. Similarly, whether the model Perceval signal is rising or falling is determined by the sign of $d\left[{\text{ATP}}_c\right]/dt$, which, in turn, is determined by the difference in magnitude between ATP_c production flux, $J_{\text{ANT}}$, and hydrolysis flux, $J_{\text{hyd}}$.

Figure 2.

Simulation of a glucose-stimulated β-cell using the DOM in its original form (i.e., with $k_{\text{PDH}}^{Ca}=0$ in Eq. 2). All parameter values are as previously published corresponding to Fig. 1A in Watts et al. (25) with the exception of $g_{K\left(Ca\right)}$ = 200 pS. (A) In contrast with experimental observation, PKAR and Perceval exhibit a sustained rise throughout the active phase. (B) Metabolic fluxes and time derivatives; $d\left[\text{FBP}\right]/dt$ has the same sign as $J_{\text{PFK}}-J_{\text{PDH}}/2$ and $d\left[\text{ATP}\right]/dt$ has the same sign as $J_{\text{ANT}}-J_{\text{hyd}}.$ (C) Model schematic of metabolic fluxes.

$J_{\text{PFK}}$ (Fig. 2 B) oscillates because of autocatalytic activation of PFK by its product, FBP. Assuming glucose concentration is constant and the glycolytic reactions upstream to PFK are at equilibrium, F6P is supplied at a constant rate as substrate to PFK. The rate at which it is consumed by PFK, however, varies with the concentration of FBP. When $\left[\text{FBP}\right]$ is low, PFK, mostly in its inactive form, only slowly converts F6P to FBP. As FBP accumulates, it allosterically converts PFK to its active form, which speeds up F6P conversion to FBP. Eventually, as F6P is consumed by PFK and FBP is consumed by the next glycolytic reaction, PFK deactivates to begin another cycle of the oscillation. Assuming glycolytic reactions downstream to PFK are at equilibrium, oscillations introduced by PFK propagate down the glycolytic stream and serve as input to the mitochondria. Hence, $J_{\text{PDH}}$ (Fig. 2 B) relays glycolytic oscillations to the citric acid cycle by oscillating in response to $J_{\text{PFK}}$. Because $J_{\text{PDH}}/2$ is delayed but has nearly the same range of magnitudes and qualitative shape relative to $J_{\text{PFK}}$, the two fluxes cross twice in each cycle: when an accumulation of FBP causes $J_{\text{PFK}}$ to surge upwards preceding the active phase, and when depletion of F6P and FBP cause $J_{\text{PFK}}$ to decline in the middle of the active phase. These crossings coincide with a switch to rising or falling PKAR signals, respectively. The difference between $J_{\text{PFK}}$ and $J_{\text{PDH}}/2$ results in an [FBP] time derivative that peaks at the onset of a burst, and is then mostly flat (Fig. 2 B), producing the square-wave-like PKAR time course shown in Fig. 2 A.

Glycolysis increases mitochondrial ATP production, which subsequently increases ATP transport from the mitochondria, hence $J_{\text{ANT}}$ (Fig. 2 B) relays glycolytic oscillations further by oscillating in response to $J_{\text{PDH}}$. Additionally, $J_{\text{ANT}}$ exhibits fast, small-amplitude oscillations during the active phase that reflect the inhibitory effect of Ca²⁺ on the mitochondrial electrochemical force (15). The rate of basal ATP_c hydrolysis is proportional to [ATP_c], so $J_{\text{hyd}}$ (Fig. 2 B) oscillates in response to $J_{\text{ANT}}$. The fast, small-amplitude oscillations of $J_{\text{hyd}}$ during the active phase reflect ATP_c hydrolysis by Ca²⁺ ATPase pumps in the plasma and ER membranes. The difference between $J_{\text{ANT}}$ and $J_{\text{hyd}}$ results in an (ATP_c) time derivative that peaks at the onset of a burst and is then mostly flat (Fig. 2 B), producing the square wave-like Perceval time course in Fig. 2 A.

In Fig. 2, bursting is driven by endogenous glycolytic oscillations, which are shaped by enzyme kinetics and are only indirectly affected by ionic currents. Experimental recordings from our companion article in this issue of Biophysical Journal (37) and Li et al. (38), however, reveal an abrupt decline in PKAR and Perceval signals at the beginning of the active phase. This discrepancy suggests an interaction between electrical activity and metabolism is missing from the model. We considered one such interaction, activation of PDH by Ca²⁺ (29, 31, 39), by making $J_{\text{PDH}}$ a sigmoidally increasing function of $\left[C{a}_m\right]$ (Eq. 2). With this modification, model PKAR and Perceval signals agree with our experimental observations (Fig. 3). Our next goal was to understand how these time courses are produced by the modified DOM, whose metabolic pathway is depicted in Fig. 3 C.

Figure 3.

Simulation of a glucose-stimulated β-cell using the modified DOM. Modifying the effects of Ca²⁺ provides agreement with experimental data. Parameter values for this and the following figures, unless otherwise specified, are listed in Table S1 in the Supporting Material. (A) PKAR and Perceval have a peak at the beginning of the active phase and a nadir near the end of the active phase. (B) Metabolic fluxes and time derivatives; $d\left[\text{FBP}\right]/dt$ has the same sign as $J_{\text{PFK}}-J_{\text{PDH}}/2$ and $d\left[\text{ATP}\right]/dt$ has the same sign as $J_{\text{ANT}}-J_{\text{hyd}}.$ (C) Model schematic of metabolic fluxes. In contrast to Fig. 2, Ca²⁺-activation of PDH is incorporated and Ca²⁺ inhibition of mitochondrial ATP production is neglected.

In the modified model, Ca²⁺ influx promotes glycolytic efflux, $J_{\text{PDH}}$, which depletes FBP and deactivates PFK during the active phase. This effect results in the abrupt decline in $J_{\text{PFK}}$ (Fig. 3 A) at the beginning of the active phase. That is, flux through PFK increases preceding the active phase due to autocatalytic feedback as in the original model, but begins to decline at the onset of a burst due to Ca²⁺ influx. As in the original model, $J_{\text{PDH}}$ (Fig. 3 B) relays glycolytic oscillations to mitochondria by oscillating in response to $J_{\text{PFK}}$. The abrupt rise in $J_{\text{PDH}}$ at the start of the active phase reflects the onset of Ca²⁺-activation of PDH and marks a crossing of $J_{\text{PFK}}$ and $J_{\text{PDH}}/2$ that coincides with a switch to a falling PKAR signal. The difference between $J_{\text{PFK}}$ and $J_{\text{PDH}}/2$ results in a square wave-like $\left[\text{FBP}\right]$ time derivative that switches from positive during the silent phase to negative during the active phase (Fig. 3 B), producing the sawtooth PKAR time course in Fig. 3 A.

As in the original model, $J_{\text{ANT}}$ (Fig. 3 B) oscillates in response to glycolytic input to mitochondria, $J_{\text{PDH}}$. The abrupt rise in $J_{\text{ANT}}$ at the start of the active phase reflects Ca²⁺ promotion of mitochondrial ATP production. As in the original model, $J_{\text{hyd}}$ (Fig. 3 B) oscillates in response to $J_{\text{ANT}}$. The rapid increase and decrease of $J_{\text{hyd}}$ delimit the active phase as well as the small-amplitude oscillations during the active phase reflect Ca²⁺ promotion of ATP_c hydrolysis. The difference between $J_{\text{ANT}}$ and $J_{\text{hyd}}$ results in a square wave-like [ATP_c] time derivative that switches from positive during the silent phase to negative during the active phase (Fig. 3 B), producing the sawtooth Perceval time course in Fig. 3 A.

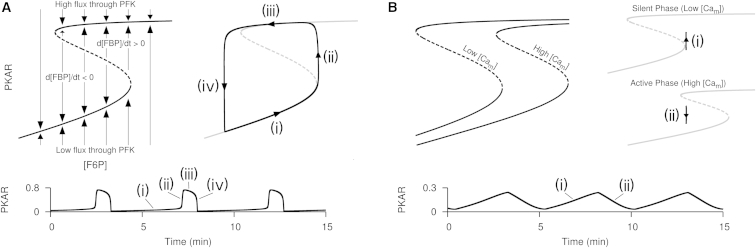
Next, we elaborated as to how incorporating Ca²⁺-activation of PDH allows Ca²⁺ oscillations to reshape endogenous glycolytic oscillations. In simulations with the glycolytic component (Eq. 1), FBP approaches the equilibrium state defined by $d\left[\text{FBP}\right]/dt=0$, which is equivalent to the equilibrium state $d\text{PKAR}/dt=0$ by the algebraic relation Eq. 4. Viewed in the (F6P) versus PKAR phase plane, the curve defined by $d\text{PKAR}/dt=0$, called a nullcline, has an S-shape composed of lower and upper branches, corresponding to low and high flux through PFK, connected through two turning points by a middle branch (Fig. 4 A, left). Each point in the phase plane corresponds to a possible state of the glycolytic component, and the nullcline partitions the space of possible states so that PKAR falls to its left and rises to its right. Glycolytic oscillations are produced as the phase point alternates between the lower and upper branches as F6P slowly changes (Fig. 4 A, right). On the lower branch, F6P accumulates because flux through PFK is low, hence the phase point passes to the right of the lower turning point to approach the upper branch. On the upper branch, F6P is depleted by high flux through PFK, hence the phase point passes to the left of the upper turning point to approach the lower branch.

Figure 4.

Phase plane and time series analysis of the glycolytic component in isolation (A) and in the full modified model (B). (A) Autocatalytic feedback onto PFK by its product FBP produces relaxation oscillations with F6P and PKAR as the slow and fast variables, respectively. (B) Ca²⁺ oscillations reshape endogenous glycolytic oscillations to produce a sawtooth like PKAR time course.

In simulations with the full modified model, glycolytic oscillations are reshaped by Ca²⁺-induced motion of the nullcline (Fig. 4 B). PFK is activated by its product FBP, yet FBP and downstream glycolytic metabolites are depleted by efflux through PDH. When PDH is activated by elevated $\left[C{a}_m\right]$, relatively high glycolytic influx (via substrate F6P) is required to switch from a state of low to high flux through PFK or to maintain a state of high flux through PFK. Therefore, the nullcline in high $\left[C{a}_m\right]$ is shifted rightward relative to the nullcline in low $\left[C{a}_m\right]$ (Fig. 4 B, left). When flux through PFK is low, F6P accumulates, hence the phase point approaches the upper branch (Fig. 4 B, top right). As flux through PFK increases, the active phase begins and Ca²⁺ influx moves the nullcline rightward past the phase point, causing the phase point to approach the lower branch (Fig. 4 B, bottom right). As flux through PFK decreases, the active phase ends and a decrease in mitochondrial Ca²⁺ moves the nullcline leftward past the phase point to begin another cycle of the oscillation. This results in a peak in PKAR at the beginning of the active phase when an increase in mitochondrial Ca²⁺ moves the nullcline rightward and a nadir in PKAR near the end of the active phase, when a decrease in mitochondrial Ca²⁺ moves the nullcline leftward. Because glycolytic oscillations lead downstream to $\left[{\text{ATP}}_c\right]/\left[{\text{ADP}}_c\right]$ oscillations as described above, this also results in a Perceval peak at the beginning of the active phase and nadir near the end of the active phase.

Timing of PKAR and Perceval peaks and nadirs depends on coupling between glycolysis and mitochondrial ATP production

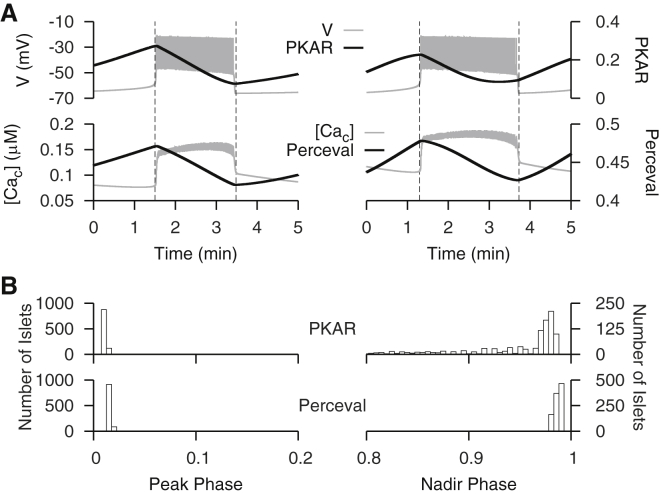
In our companion article (37), we observed that the peaks of PKAR and Perceval signals are tightly correlated with the beginning of the active phase (phase 0), whereas the nadirs occur with considerable variation near the end of the active phase (phase 1). Are the same features produced by the modified DOM? To test this, we vary a key parameter that determines the strength of coupling between glycolysis and mitochondrial ATP production ($q_3$ in Eq. 3). Physiologically, variation in the value of $q_3$ can be interpreted as variation in the catalytic activity of enzymes in the citric acid cycle, which links glycolysis to mitochondrial ATP production.

Fig. 5 A depicts two extreme examples of bursts for which the PKAR nadir occurs late (left) or early (right) in the burst. When mitochondrial ATP production is strongly coupled to glycolysis (low q₃), a relatively small increase in glycolytic flux is needed to act downstream on K(ATP) channels and begin the active phase. During the active phase, Ca²⁺-activation of pyruvate dehydrogenase promotes glycolytic efflux, which counteracts this relatively small increase before the end of the active phase and produces a nadir before phase 1. When mitochondrial ATP production is weakly coupled to glycolysis (high $q_3$), a relatively large increase in glycolytic flux is needed to begin the active phase. During the active phase, Ca²⁺-activation of pyruvate dehydrogenase cannot promote glycolytic efflux enough to completely counteract this relatively large increase before the end of the active phase; instead, a nadir occurs when Ca²⁺ influx is terminated at phase 1. Fig. 5 B depicts histograms of model PKAR and Perceval phases from a uniform sampling of 1000 $q_3$ values between 3.4 and 6 μM/s. As with the experimental data in the companion article (37), the peaks are clustered near phase 0, while the nadirs show a greater variation near phase 1.

Figure 5.

Analysis of PKAR and Perceval peak and nadir phases. (A) Examples of bursts with late phase ≈1 (left) and early phase <1 (right) PKAR and Perceval nadirs. In both examples, the peak occurs at phase ≈0. (B) Distribution of PKAR and Perceval peak and nadir phases from 1000 trials with the modified DOM while varying parameter $q_3$ between 3.4 and 6 μM/s.

Oscillatory Ca²⁺ is not required for oscillatory glycolysis

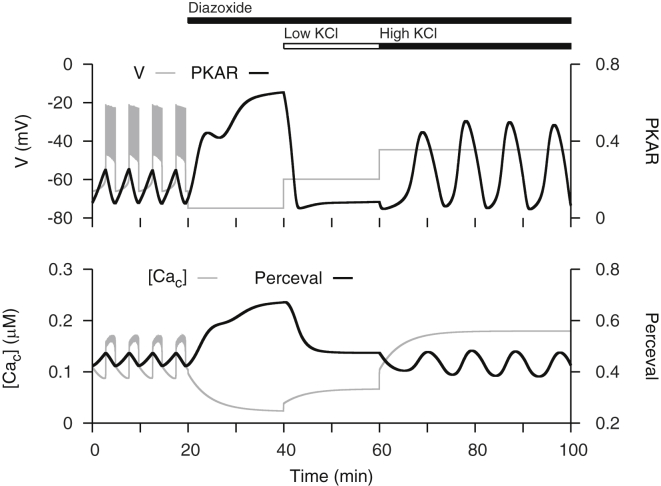
Although we introduced a Ca²⁺-dependence into the glycolytic component of the model, glycolysis still oscillates endogenously. We demonstrate this by simulating an experiment performed in the companion article (37) in which islets are manipulated in stimulatory glucose with the K(ATP) channel opener diazoxide and the membrane depolarizer KCl (Fig. 6). The experiment demonstrates that when glycolytic oscillations are abolished by preventing Ca²⁺ oscillations, they may be restarted by subsequently increasing intracellular Ca²⁺ concentration.

Figure 6.

Ca²⁺ clamp simulations, as performed in the companion article (37). Glycolytic oscillations abolished by preventing Ca²⁺ oscillations in stimulatory glucose can be restarted by raising intracellular Ca²⁺. To simulate addition of Dz, K(ATP) channel conductance $\left(g_{K\left(\text{ATP}\right)}\right)$ is set to its maximal value and to simulate addition of low and high KCl, K⁺ reversal potential (V_K) is set to −60 and −45 mV, respectively.

Adding diazoxide in stimulatory glucose activates K(ATP) channels to repolarize the membrane and prevent Ca²⁺ influx (Fig. 6, 20 < t < 40 min). The resulting decrease in $\left[C{a}_c\right]$ deactivates PDH, which allows FBP to accumulate and increase the PKAR signal. It also reduces activity of Ca²⁺ ATPases, which allows ATP_c to accumulate and increase the Perceval signal. The increase in [ATP_c] abolishes glycolytic oscillations by allosterically inhibiting PFK. Subsequently adding KCl in the presence of glucose and diazoxide depolarizes the membrane and thereby increases Ca²⁺ influx (Fig. 6, t > 40 min). With a low concentration of KCl, a minor increase in $\left[C{a}_c\right]$ activates PDH, which promotes glycolytic efflux to lower the PKAR signal. It also increases the activity of Ca²⁺ ATPases to reduce the cytosolic ATP concentration and therefore decreases the Perceval signal (Fig. 6, 40 < t < 60 min). With a high concentration of KCl, the activity of Ca²⁺ ATPases is increased enough to remove ATP inhibition of PFK and restart glycolytic oscillations that are reflected in both PKAR and Perceval signals (Fig. 6, t > 60 min). Thus, this manipulation of the membrane voltage allows one to observe the underlying glycolytic oscillations without interference from Ca²⁺ oscillations.

Oscillatory glycolysis is not always mandatory for oscillatory Ca²⁺

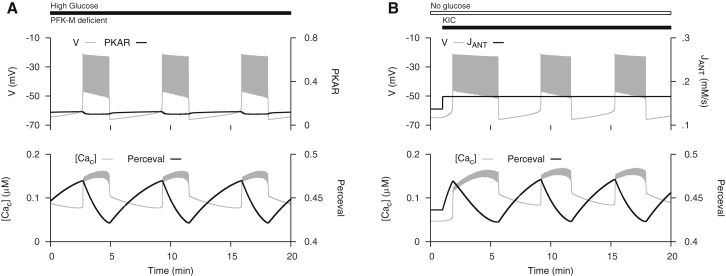
PFK exists as a tetramer of three different subunit isoforms, of which only the muscle (M) type is capable of producing glycolytic oscillations through autocatalytic activation by the product FBP (40). The other isoforms are saturated by basal levels of FBP. While we have provided evidence for the importance of slow glycolytic oscillations for slow Ca²⁺ oscillations in islets, our simulations involving increased emphasis on Ca²⁺ pumping and ATP utilization suggested that an additional mode of slow oscillations could occur without glycolytic oscillations if conditions are right. We have thus found that metabolic oscillations may persist even though PFK-M activity is greatly reduced. Richard et al. (23) found in experiments that when expression of PFK-M in mice was reduced >95% by genetic knockout, glucose could still induce slow Ca²⁺ oscillations, suggesting that glycolytic oscillations may not be necessary for slow Ca²⁺ oscillations. We simulate this experiment in Fig. 7 A using the modified DOM with 98% of the PFK-M isoform replaced by the PFK-C isoform. Replacement of 98% of PFK-M isoform by PFK-C was simulated by replacing J_PFK with $0.02J_{\text{PFK}}+0.98J_{\text{PFK}-C}$, where $J_{\text{PFK}-C}$ is parameterized to account for saturation by basal levels of FBP. The slow Ca²⁺ oscillations and electrical bursting produced here appear similar to those produced by the DOM with glycolytic oscillations. However, in this case, there are clear oscillations in Perceval, but only tiny PKAR oscillations that would not be resolved experimentally. Hence, the mechanism of slow bursting can be identified by the PKAR reporter. These findings suggest that slow oscillations may have multiple origins under different conditions in islets, emphasizing their likely selective advantage for islet function and ultimately survival.

Figure 7.

Slow oscillations without glycolytic oscillations. (A) Slow Ca²⁺ oscillations are triggered by glucose in mice deficient in the muscle type isoform of PFK subunit. Replacement of 98% of PFK-M isoform by PFK-C was simulated by replacing $J_{\text{PFK}}$ with $0.02J_{\text{PFK}}+0.98J_{\text{PFK}-C}$, where $J_{\text{PFK}-C}$ has the same form as $J_{\text{PFK}}$ but with a parameter adjusted to account for saturation by basal levels of FBP. Parameters are listed in the Supporting Material. (B) Slow Ca²⁺ oscillations are triggered by mitochondrial fuel α-ketoisocaproate (KIC). Addition of KIC was simulated by increasing $J_{\text{ANT}}$.

In separate studies, it was found that the mitochondrial fuel α-ketoisocaproate (KIC), which enters metabolism downstream of glycolysis, can trigger slow Ca²⁺ oscillations in the absence of stimulatory glucose (24, 41), again suggesting that glycolytic oscillations are not necessary for slow Ca²⁺ oscillations. We simulate this experiment with the modified model in Fig. 7 B. This simulation shows that an increase in mitochondrial ATP production in the absence of glycolytic flux can produce slow Ca²⁺ oscillations.

In both simulations, bursting and Ca²⁺ oscillations are maintained by a nonglycolytic mechanism mediated by Ca²⁺-dependent ATP hydrolysis. During the silent phase, mitochondrial ATP production deactivates K(ATP) channels to initiate the active phase. During the active phase, intracellular transport of Ca²⁺ by pumps in the ER and plasma membranes hydrolyzes ATP to reactivate K(ATP) channels and recover the silent phase. This results in the sawtooth-like Perceval time course that increases during the silent phase and decreases during the active phase (Fig. 7). These predictions could be tested by measuring Perceval in islets from PFK-M deficient mice or from wild-type islets stimulated by KIC in the absence of glucose.

Discussion

The central aim of this report was to interpret data on islet calcium and metabolic oscillations using the DOM. Our first result was the finding that the sawtooth time courses of the sensors PKAR and Perceval can both be replicated by the DOM when Ca²⁺-activation of pyruvate dehydrogenase is included in the model (Fig. 3). Without this feedback, neither the model PKAR nor Perceval time courses agree with the experimental data. This highlights an important role for Ca²⁺-activation of mitochondrial dehydrogenases in shaping the dynamics of ATP, which in turn shapes the cell’s electrical activity through ATP deactivation of K(ATP) channels.

We have considered two other possible explanations for the data in the companion article (37). One possibility is that Ca²⁺ feeds back onto PFK and inhibits it. Although there is no direct experimental support for this, we explored the ramifications of such a negative feedback by adding it to the model. The result was a disruption of the oscillation if the feedback strength was strong, and in no case were phase relations obtained that were similar to the experimental data. A second possibility is that one of the sensors is Ca²⁺-dependent. Again, there is no direct experimental support for this, and even if it were the case, it would not explain the data obtained from the other sensors used in the companion article (37). The explanation suggested herein, that Ca²⁺-activation of pyruvate dehydrogenase is responsible for the phase relations observed in the companion article, is preferable to these alternate explanations.

The next result was an explanation for data from the companion article showing that the peak of the PKAR and Perceval signals always occurs at the start of a burst active phase, while the timing of the nadir is more variable. In the model, the PKAR sensor level declines immediately at the start of the active phase due to Ca²⁺-activation of pyruvate dehydrogenase, which increases efflux from glycolysis (and decreases the FBP level to deactivate PFK) when the Ca²⁺ concentration increases. The decline in Perceval at the start of the active phase reflects the combination of decreased glycolytic flux and a different mechanism; the elevation of Ca²⁺ that occurs during the active phase increases ATP hydrolysis by Ca²⁺ pumps in the plasma and ER membranes, lowering the cytosolic ATP concentration and increasing the ADP concentration. Perceval measures the ratio of these two. In contrast to the precision of the peak timing, the more variable timing of the PKAR and Perceval nadirs reflects the relative strength of glycolytic flux and Ca²⁺-induced hydrolysis of ATP in setting the level of mitochondrial nucleotides. Cell-to-cell variation in this relative strength has no impact on the timing of the peak, but shifts the timing of the nadir (Fig. 5).

One of the difficulties in interpreting metabolic time courses from β-cells is the multiple ways that Ca²⁺ affects metabolism in these cells. Both experimental and theoretical studies suggest that Ca²⁺ flux across the mitochondrial inner membrane decreases the electrical driving force that powers ATP synthases (15, 42, 43, 44). Mitochondrial dehydrogenases are stimulated by Ca²⁺ (29). Finally, elevations in the cytosolic Ca²⁺ concentration induce increased ATP hydrolysis to power Ca²⁺ pumps. When the Ca²⁺ concentration varies over time, as it does in glucose-stimulated islets, this makes interpretation of metabolic signals particularly challenging. This complexity has motivated us to use a Ca²⁺-clamp protocol in which Ca²⁺ oscillations are terminated by application of diazoxide and the constant Ca²⁺ level is manipulated by application of KCl. This approach was used in the companion article (37), and simulated here (Fig. 6). The decrease in Ca²⁺ concentration that is produced by diazoxide reduces flux through glycolysis via deactivation of pyruvate dehydrogenase, allowing the FBP level to build up. This causes an increase in the PKAR signal. Depolarizing the membrane with KCl increases the Ca²⁺ level, which increases flux through glycolysis and thus decreases the FBP level. This results in a decrease in the PKAR signal. At the right level of depolarization it is possible to activate the glycolytic oscillator (as in Merrins et al. (19)), producing oscillations in FBP and the sensor PKAR. These rescued oscillations are larger than the original oscillations, because they are produced solely by the glycolytic oscillator, without feedback from oscillatory Ca²⁺. The rescue of PKAR oscillations is also seen in companion experiments (Merrins et al. (37); Fig. 6 C), but in contrast to the model prediction, the rescued PKAR oscillations are not larger than the original ones. The reason for this discrepancy is unclear.

In addition to its use as a tool for interpreting the data from the companion article, the recalibration of the model required to reproduce the ATP and FBP time courses led to some unexpected findings (Fig. 7). First, we found that the recalibrated DOM could reproduce data showing that slow Ca²⁺ oscillations can be observed in islets in which the M-type isoform of PFK has been knocked out in islets (23). In the model, it is assumed that activity of the nonoscillatory C-type of PFK is upregulated in response to downregulation of the M-type isoform. The C-type isoform provides the necessary flux through glycolysis to generate ATP for K(ATP) channel deactivation, but it itself does not contribute to the Ca²⁺ oscillations. The Ca²⁺ oscillations are then driven by Ca²⁺-dependent hydrolysis. When the cell is bursting, Ca²⁺ is elevated due to increased influx, and the ATP level declines due to ATP utilization by Ca²⁺ pumps. As ATP declines, the K(ATP) conductance rises, eventually turning off the spiking activity. When Ca²⁺ influx ends, Ca²⁺ concentration falls and the rate of hydrolysis declines, leading to an increase in the ATP level and inhibition of K(ATP) channels. This restarts the burst cycle. The model predicts that the Perceval signal in these islets should be oscillatory, just as in the wild-type islets. However, the PKAR signal should exhibit at most very small oscillations, due to the residual PFK-M activity that would likely be too small to detect. This prediction remains to be tested.

Another unexpected finding obtained with the recalibrated model, which has an emphasized reliance on Ca²⁺ pumping-induced ATP utilization, is that it is possible for a fuel entering the metabolic pathway downstream of glycolysis to initiate slow Ca²⁺ oscillations. The mechanism for this is again Ca²⁺-dependent hydrolysis, and once again the prediction is that Perceval will exhibit slow oscillations while the PKAR signal will be nonoscillatory (and very low). Several labs have applied the fuel KIC to mouse islets in 0 mM glucose, but the results have been mixed. Some have found Ca²⁺ oscillations with periods similar to those induced by glucose (24, 41), while others have failed to see them (45, 46). The fact that some see KIC-induced slow oscillations in the absence of glucose while others do not is consistent with the DOM. We find that this behavior is sensitive to system parameters, so we would expect to see islet-to-islet variation in the response to KIC. For many parameter sets we fail to observe slow oscillations for any level of simulated KIC application. For example, we simulated KIC application as in Fig. 7 by varying $J_{\text{ANT}}$. If $J_{\text{ANT}}$ was too low or high, it did not induce slow oscillations. This issue will require additional investigation, but having the modified model will facilitate progress.

In conclusion, our model suggests that slow islet oscillations are due to the interactions of glycolytic oscillations with Ca²⁺ feedback from at least two entry points: Ca²⁺ activation of pyruvate dehydrogenase (and probably other dehydrogenases) and Ca²⁺-dependent ATP hydrolysis. In free-running islets, glycolytic oscillations and Ca²⁺ feedback are both utilized, and together shape the time course of ATP that drives electrical and Ca²⁺ oscillations. Evidence for either oscillatory mechanism can be found by removing the other; glycolytic oscillations are revealed using the Ca²⁺-clamp protocol, while oscillations driven by Ca²⁺ feedback are revealed by knocking out M-type PFK or adding fuels downstream of glycolysis. These manipulations are very useful for isolating feedback pathways, but do not capture the full complexity of the free-running islet. The data presented in the companion article (37), along with the model simulations shown here, paint a more textured picture in which both glycolytic oscillations and Ca²⁺ feedback are partners in controlling metabolic oscillations, Ca²⁺ oscillations, electrical bursting, and ultimately pulsatile insulin secretion.

Author Contributions

All authors designed the research and wrote the article. J.P.M., J.H., A.S., and R.B. performed the research.

Editor: James Sneyd.