DNA Shape versus Sequence Variations in the Protein Binding Process

Abstract

The binding process of a protein with a DNA involves three stages: approach, encounter, and association. It has been known that the complexation of protein and DNA involves mutual conformational changes, especially for a specific sequence association. However, it is still unclear how the conformation and the information in the DNA sequences affects the binding process. What is the extent to which the DNA structure adopted in the complex is induced by protein binding, or is instead intrinsic to the DNA sequence? In this study, we used the multiscale simulation method to explore the binding process of a protein with DNA in terms of DNA sequence, conformation, and interactions. We found that in the approach stage the protein can bind both the major and minor groove of the DNA, but uses different features to locate the binding site. The intrinsic conformational properties of the DNA play a significant role in this binding stage. By comparing the specific DNA with the nonspecific in unbound, intermediate, and associated states, we found that for a specific DNA sequence, ∼40% of the bending in the association forms is intrinsic and that ∼60% is induced by the protein. The protein does not induce appreciable bending of nonspecific DNA. In addition, we proposed that the DNA shape variations induced by protein binding are required in the early stage of the binding process, so that the protein is able to approach, encounter, and form an intermediate at the correct site on DNA.

Introduction

Protein-DNA interactions are diverse and use a wide variety of recognition mechanisms, which depend on an individual protein and its function at particular specific or various nonspecific binding sites. The binding process of a protein with DNA is proposed to involve three stages: approach, encounter, and association (1). The conformational switch mechanism (2, 3, 4, 5) has been proposed in which the proteins take an inactive conformation interacting with DNA nonspecifically in the searching (S) mode, while, in the recognition (R) mode, the inactive conformation switches to an active conformation that can be recognized specifically by DNA. Rapid conformational transitions between the S and R mode speed up the protein-DNA binding rate. However, we wish to understand how the DNA responds to the protein’s conformational switch and how the conformation and the information in the DNA sequences affect the binding process. It is unclear in particular cases the extent to which the DNA structure adopted in the complex is induced by protein binding, or is instead intrinsic to the DNA sequence (3).

Consideration of the problems above requires comparison of the structures and thermodynamics of the uncomplexed DNA and protein with their complexed forms. Unfortunately, experimental data on free-DNA structures are limited and lack diversity in sequences. Computational approaches, particularly molecular dynamics (MD) simulations, provide more detailed model information at an atomic level and in solvent environment. Dixit et al. (6) performed 5-ns MD simulations on the CAP-DNA systems and showed that with respect to canonical B-form DNA, the extreme bending of the DNA in the complex with CAP is 60% protein-induced and 40% intrinsic to the sequence-dependent structure of the free oligomer. Hancock et al. (7) compared the x-ray structures and 50-ns MD simulations of Fis binding on different sequences and provided evidence that high-affinity Fis-binding sites containing A/T-rich centers have intrinsic minor groove shapes that resemble the bound conformation. The authors also proposed that the DNA could transiently have narrow minor groove segments, which can be selected by Fis. Bouvier et al. (8) studied dissociation of SRY protein from the DNA and proposed that a sequence-specific DNA conformational switch (rather than a protein switch) controls a passage through an energy barrier from nonspecific to specific binding.

Here we use a multiscale simulation approach to consider the binding process of a regulatory protein with DNA in terms of DNA sequence, conformation, and interactions to elucidate how induced fit and the intrinsic conformational properties of unbound DNAs contribute to the overall binding process. We focus on myocyte enhancer factor 2 (MEF2) (9, 10), which binds specifically to a conserved A/T-rich DNA sequence in the control regions of the majority of muscle-specific genes in vertebrates. MEF2 plays important roles in regulating transcription programs involved in muscle metabolism, cardiac growth, bone development, and neuronal differentiation and survival. There are four members of mammalian MEF2, designated MEF2a-d, which share a highly conserved N-terminal region (residue 1-93), followed by a more divergent C-terminal region. The N-terminal region contains the MADS-box domain (residue 1-58), which is the DNA-binding domain, and the MEF2-specific domain (residue 59-93), which interacts with other signaling proteins and transcriptional cofactors. In a dimer state, the consensus sequence is YTA(A/T)₄TAR (Y, pyrimidine; R, purine).

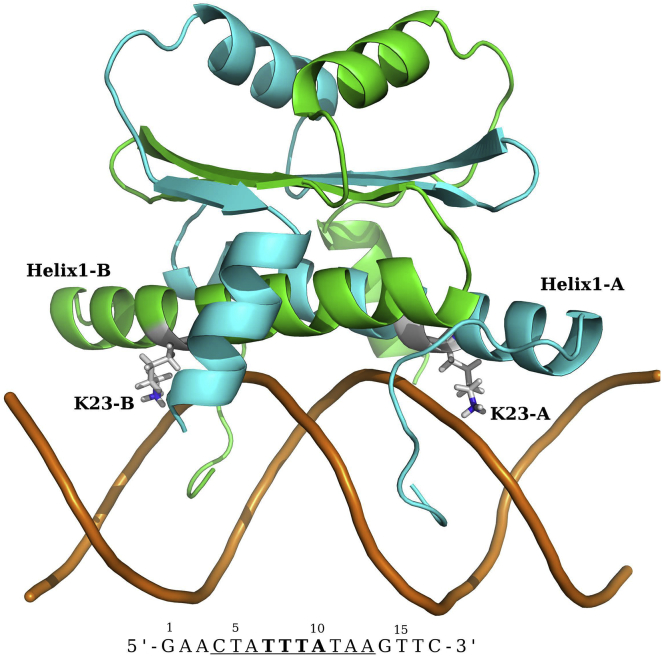
The structure of the complex of MEF2a with its cognate DNA sequence has been solved by x-ray crystallography (11, 12) and NMR spectroscopy (13). Structural analyses showed that MEF2a binds DNA through the N-terminal tail (residue 1-13) and Helix1 (Fig. 1), which forms a clamp that grips the DNA in the minor groove. The residues in the N-tail deeply insert into the minor groove, and residues in Helix1 form extensive contacts with the backbone of DNA bordering the minor groove at the center of the binding site. The base-specific recognition in the major groove is mediated by Lys²³. The narrowed minor groove is a predominant feature of DNA binding by MEF2a. A narrowed minor groove, commonly observed in A/T-rich segments in bound DNA crystal structures, exhibits an enhanced negative electrostatic potential by Poisson-Boltzmann calculations (14) and more counterion binding by MD (15).

Figure 1.

The structure of homodimeric MEF2a in complex with a 17-bp DNA sequence. The specific sequence is underlined.

In this study, Brownian dynamics (BD) and MD were used to span the spatial and temporal scales required. First, BD simulations were performed on MEF2a approaching and encountering three DNA sequences: a specific sequence GAACTATTTATAAGTTC extracted from the crystal structure, the same specific sequence built in the canonical B-form, and a nonspecific sequence GAACTACCCGTAAGTTC built in the B-form as well. The sequence of the proposed binding site is underlined and the flanking sequences were held constant. The binding site on the DNA from the crystal structure has a narrowed minor groove. Comparison of the binding pathways of these three DNAs with MEF2a helps us understand the influence of conformation and sequence of DNA on the protein approaching and encountering its target site. Next, for structures starting near molecular contact distances we performed all-atom MD simulations in explicit water and ions on unbound DNA with specific and nonspecific sequences as well as their corresponding transient complexes predicted from BD simulations. The resulting structures and free energies were then analyzed. The coupled BD and MD simulations provide extensive configurational sampling to study how a protein recognizes its specific target site on a DNA.

Materials and Methods

BD simulations

We perform BD simulations on three MEF2a-DNA complex systems, x-S, c-S, and c-NS, defined below, using the software program Simulation of Diffusional Association of proteins (16), which was modified to suit protein-DNA association (1). The structure of x-S was taken from the cocrystal structure (PDB: 3KOV), in which the homodimeric MEF2a consists of 180 amino acids and the 13-mer DNA duplex comprises the sequence 5′d-(AACTATTTATAAG) with the 10 bp consensus sequence (underlined) in the middle. To make sure there are enough basepairs flanking the cognate binding site, we extend the DNA sequence to 17 basepairs (GAACTATTTATAAGTTC) using the x3DNA software (17). Crystallographic water molecules were removed before energy minimization.

The structure of c-S has the same DNA sequence as x-S, but was built in the standard B-form conformation, so it differs from x-S only in the DNA conformation. The structure of c-NS has the DNA in the standard B-form conformation as well, but the sequence was mutated to GAACTACCCGTAAGTTC. It differs from the model-built c-S only in the DNA sequence. For all three systems, hydrogen atoms were added, and their starting positions were optimized by energy minimization with the in-house ESP program (18). Partial atomic charges and atomic radii were assigned from the CHARMM27 parameter set (19, 20). The protonation states of titratable residues were assigned according to their standard protonation states at pH 7.0.

Details of the BD simulation method for protein-DNA association were as described in Chen and Pettitt (1). The relative translational and rotational diffusion constant were estimated to be 0.0235 Å²/ps and 1.455 × 10⁻⁵ radian²/ps, respectively. The binding free energy ΔG_BD from the BD simulations may be approximated as (1, 21)

$$\Delta G_{\text{BD}}=\Delta G_{\text{ele,BD}}-T\Delta S_{\text{BD}},$$ (1)

where ΔG_ele,BD is the total effective interaction energy consisting of the electrostatic potential energy component and the desolvation energy component. ΔS_BD is the total configurational entropy loss of protein-DNA complex. T is the absolute temperature. At T = 300 K, the solvent dielectric constant is taken as 78.0, and the solute interior dielectric constant is 4.0.

MD simulations

MD simulations were performed on the specific and nonspecific DNA sequences in both the unbound state and the bound state using the in-house software program ESP (18). The initial structure of the unbound specific DNA was extracted from the model x-S, and the unbound nonspecific DNA from the model c-NS. They are denoted as dna-x-S and dna-c-NS, respectively. For the initial structures of the complexes, we categorize the complexes into two groups: the associated and intermediate forms. In the associated form, the complexes have the binding interface as in the crystal structure, for each of x-S, c-S, and c-NS. The intermediate form includes the encounter states that resulted from the BD simulations.

Each initial model structure was put into a preequilibrated box of TIP3P water using standard procedures. Na⁺ and Cl⁻ were randomly added to ensure a neutralized system and set the salt concentration to 0.15 M. Each box contains ∼53,000 total numbers of the atoms. The simulations were run using the all-atom CHARMM 27 parameter set (19, 20). Equations of motion were integrated with a 2-fs time step in the microcanonical ensemble (NVE) with periodic boundary conditions. Electrostatic interactions were treated with an Ewald sum using a fast linked-cell algorithm (22). After several steepest descent energy minimization steps, each system was equilibrated at 300 K for several nanoseconds and then continued to 100∼200 ns. The coordinates were saved for analysis at an interval of 0.1 ps.

An approximate binding free energy was estimated using molecular mechanics/Poisson-Boltzmann surface area methodology (23), which has been employed in a variety of similar applications (24). The Poisson-Boltzmann surface area binding free energy was estimated from the total electrostatic binding energy ΔG_ele,MD, the nonpolar desolvation binding free energy ΔG_np,MD, van der Waals (vdW) binding energy ΔE_vdW,MD, and the vibrational, rotational, and translational entropies S_MD,

$$\Delta G_{\text{tot,MD}}=\Delta G_{\text{ele,MD}}+\Delta G_{\text{np,MD}}+\Delta E_{\text{vdW,MD}}-T\Delta S_{\text{MD}}.$$ (2)

The intramolecular energies effectively cancel out when single-trajectory analysis is applied (25). ΔG_ele,MD was computed from the finite difference Poisson-Boltzmann method in the APBS package (26) on the MD structures, and ΔG_np,MD = gΔSASA + b, where g = 0.022 kJ/mol/Ų, b = 3.85 kJ/mol, and ΔSASA is the buried solvent-accessible surface area. The configurational entropy ΔS_MD can be approximated using Schlitter’s formula (27) or quasi-harmonic (QH) analysis (28). The QH method provides a tighter upper bound to the conformational entropy. The calculation of the entropy from the Schlitter/QH methods is sensitive to the length of the simulation and the position of the sampling window. When a system has a rough energy landscape containing multiple minima, the entropy will change as different regions are explored. The absolute entropy of a flexible peptide from the Schlitter and QH methods becomes similar, when the simulation approaches 1.0–2.0 μs (29). In the study of the binding free energy of a protein-DNA complex, the difference of ΔS between the Schlliter and QH method is ∼0.1 kJ/mol/K when a stable 30-ns interval is used (data not shown here). Here we used the Schlitter formula. Although the convergence of ΔS requires longer simulation time, we used the consistent approach to make the difference results comparable. To reduce convergence problems to some extent, the binding free energy calculations in this study were averaged over a stable 40-ns trajectory period.

Results and Discussion

BD simulations

We perform the BD simulations on the system x-S, c-S, and c-NS, in 0.15 M salt solution. For each system, a total of 40,000 trajectories are generated and analyzed to obtain the probabilistic paths to the encounter states. The average length of a single trajectory is ∼1.9 μs or a total of 76 ms for each system.

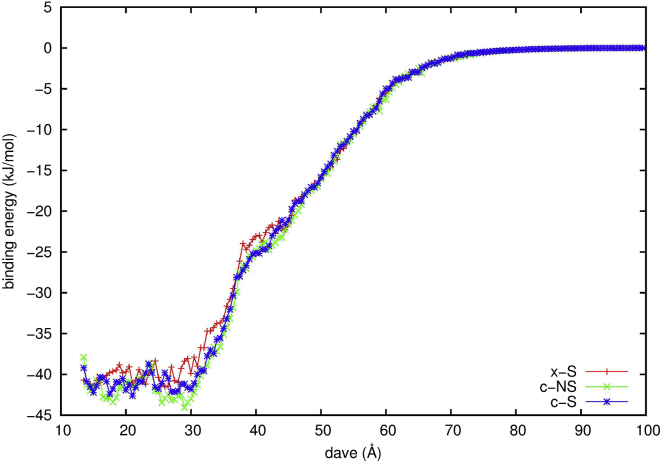
Following the same procedures as described previously, we assign the spatial and orientational coordinates (r, z, φ, r_p, θ_p, φ_p) of the protein to a six-dimensional grid at each time step of the simulated trajectories. The set (r, z, φ) defines the position of the protein with respect to the DNA. Here, r is the distance of the center of the protein from the helical axis of the DNA. Relative to the crystal structure, z is the displacement of the protein translating along the DNA, and φ (in degree) is the azimuthal angle displacement of the protein. The set (r_p, θ_p, φ_p) defines the orientation of the protein in a spherical coordinate system, in which r_p is the distance between the center of the protein and the center of Helix1from both monomers, θ_p is the polar angle, and φ_p is the displacement of the azimuthal angle of the orthogonal projection of r_p relative to the reference crystal structure. At each grid point, we store the minimum total binding energy, the spatial and orientational occupancy of the protein, and entropy loss, and then obtain the binding profiles for all three systems (Fig. 2). The average distance of all contact pairs along the local minimum of the binding free energy is d_ave, which we find is a reasonable choice to better describe not only the location of the protein but also the influence of orientation of the protein. In all three systems, the interactions between the protein and DNA become more negative when the protein approaches to the DNA, which is expected from the overall charges of the protein and DNA. Along the binding profile within d_ave = 30 Å, several energy minima are observed. This suggests that MEF2a is able to encounter the DNA at many energetically favorable sites. At those sites, MEF2a orients itself to make the N-tails and Helix1face the DNA in the approach stage.

Figure 2.

The binding profiles of MEF2a with DNA in the BD simulations. x-S, the DNA has the specific sequence and narrowed minor groove; c-NS, the canonic B-DNA has the nonspecific sequence; and c-S, the canonical B-DNA has the specific sequence. To see this figure in color, go online.

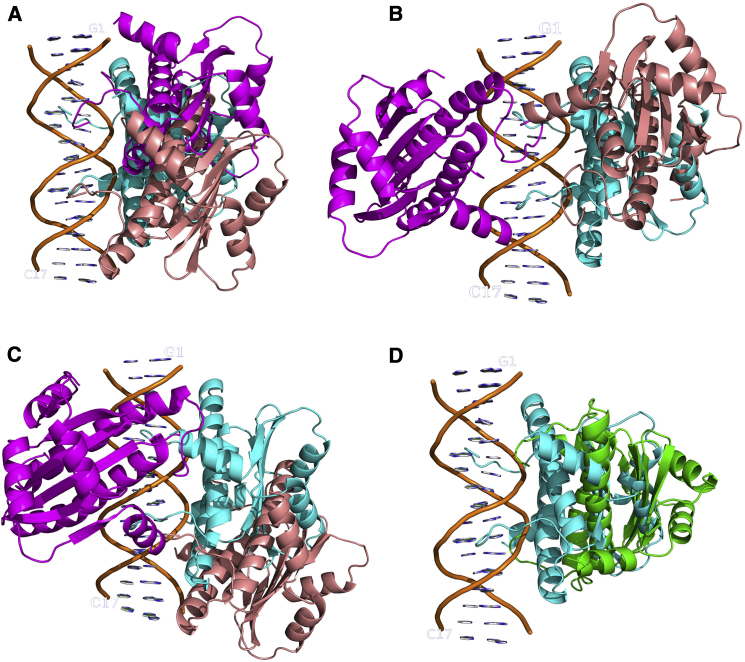
We further examine the binding occurrence during the formation of the complex along the reaction or binding profile within d_ave = 30 Å. For each system, 34 complex states are collected, and their structures are analyzed. MEF2a is found mostly to have two types of binding interface with the DNA (Fig. 3). In one type (salmon color), each monomer places its N-tail and Helix1 close to the minor groove of the DNA, while in the other (magenta), both the N-tails and Helix1 are close to the major groove. The minor-groove-binding interface is the one identified in the experiments. In the lower half of the energy range from the minimum to the maximum, for each case in turn the probability of the minor-groove-binding interface, P_min, is 60% in x-S, 80% in c-S, and 35% in c-NS, while the probability of the major-groove-binding interface, P_maj, is 15% in x-S, 20% in c-S, and 65% in c-NS. In addition to the minor- and major-groove-binding interfaces, particularly in the x-S system, another binding interface with 25% probability is also found. In this binding interface (denoted as cross-binding), the N-tails of the protein grip the major groove and Helix1 is close to the minor groove of the DNA (green in Fig. 3 D).

Figure 3.

Encounter complexes with different interfacial binding types predicted from the BD simulations on three systems: (A) x-S; (B) c-S; and (C) c-NS. The starting structures in x-S, c-S, and c-NS are in cyan. The examples of the minor-groove-binding type, e.g., EC1-min, EC2-min, and EC3-min are in salmon, and the major-groove-binding type, e.g., EC1-maj, EC2-maj, and EC3-maj are in magenta. (D) The crossing-binding type EC1-cro (green).

Considering the DNA groove preference, analysis of the binding interface occurrence for our models indicates that in the approach and encounter processes MEF2a can complex with the DNA at either the minor groove or major groove. This is consistent with our previous work on the NColE7-DNA system (1). MEF2a prefers, in an equilibrium sense, encountering the minor groove of specific DNA and the major groove of a nonspecific one. The different probabilities of the binding interfaces among three systems suggest that the DNA sequence and conformation influence the formation of the complex even in the early stage of protein binding.

Sequence and conformation of DNA are not independent of each other (30). However, their individual effect on the specific recognition can be conceptually separated. Duzdevich et al. (31) have suggested a protein-DNA binding continuum, in which a pure sequence recognition and a pure structure recognition are the extremes, and any particular system could be placed somewhere in between. In this work we are able to examine how sequence and conformation influence the binding probabilities at each end of that binding continuum.

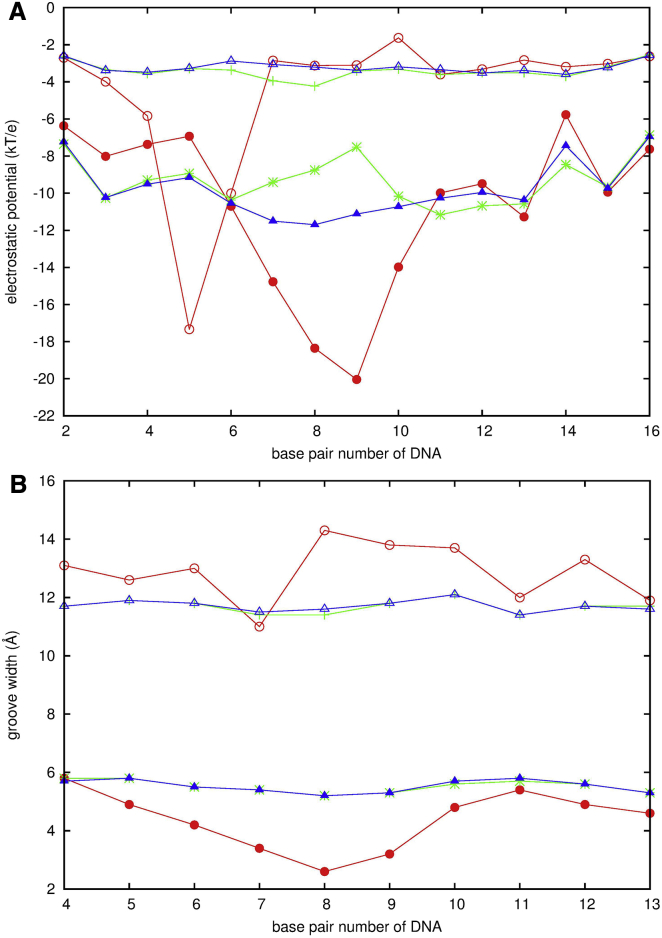
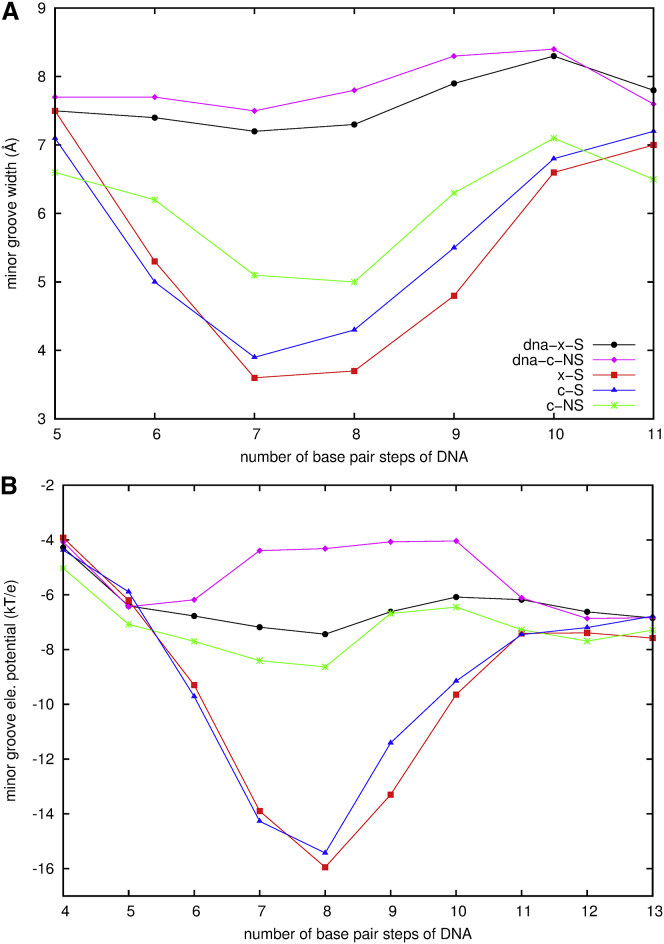
The DNAs of c-S and c-NS possess the same conformation, so comparison of c-S with c-NS presents a case of pure sequence recognition. The minor-groove-binding mode in c-S is ∼2.3 times higher than in c-NS. This indicates that the specific sequence enhances the probabilities of MEF2a encountering the correct site in the correct orientation. Estimate of the electrostatic potentials (Fig. 4 A) at the minor and major groove of the DNAs shows that the electrostatic potentials at sequence position 7-10 for the minor groove are more negative in c-S than in c-NS; the more negative electrostatic potentials will be more favorable for the protein to approach to this site.

Figure 4.

The electrostatic potentials (A) and widths (B) of the minor (solid symbol) and major (open symbol) groove of the DNA in three systems: x-S (red), c-S (blue), and c-NS (green) in the BD simulations. To see this figure in color, go online.

The DNAs in x-S and c-S differ in the conformation, not sequence, so comparison between them represents a purely conformational effect on recognition. The minor groove binding mode in x-S is ∼1.5 times lower that in c-S, which indicates that conformation limits the chance for MEF2a to encounter the correct site. The electrostatic potentials at position 7-10 of the minor groove are 19∼50% more negative in x-S than in c-S, as shown in Fig. 4 A. Although chemistry of the sequence favors the encounter at this location, the conformation plays the critical role for a given sequence. We should keep in mind that the DNA in x-S possesses a preformed shape from the final functional complex. It has the narrowed minor groove (Fig. 4 B), induced by the protein binding. Before an encounter forms, if the DNA takes the final form, the narrowed minor groove will prevent the protein from inserting the N-tails into the minor groove to some extent. To reduce this limitation, the DNA should have conformation between a straight B-form and a final form. This can happen because DNA is dynamic and also flexible in solution; it has a probability to transiently narrow its minor groove to enhance the binding occurrence for the protein.

Along the binding profile in each system, we identify several encounters that have the minimum binding free energies for both the minor-groove-binding type and the major-groove-binding type (Fig. 3). They are denoted, respectively, as EC1-min and EC1-maj predicted from the system x-S; EC2-min and EC2-maj from c-NS; and EC3-min and EC3-maj from c-S. The relative positions of MEF2a with respect to the DNA constructs are listed in Table 1. Compared to the reference structure x-S, MEF2a in these encounter states is ∼5∼8 Å farther from the DNA helical axis and is positioned at the different sites along the DNA. These encounter complexes will be considered as the initial structures in MD simulations.

Table 1.

The Relative Position of the Protein with Respect to DNA, Compared to the Initial Structure of x-S

	R (Å)	Initial Δφ (°)	Δz (Å)	R (Å)	Average Δφ (°)	Δz (Å)
x-S	19.477	0	0	18.469	4.485	−2.302
c-NS	19.430	−0.145	−0.010	19.701	8.255	−0.771
c-S	19.480	0.033	−0.032	19.021	9.291	−0.443
EC1-min	27.999	44.142	9.195	21.649	43.317	12.536
EC1-maj	24.975	27.872	−10.825	20.280	51.622	−3.337
EC2-min	25.991	3.020	16.147	23.486	61.034	7.484
EC3-min	25.844	32.020	−8.009	22.356	−4.597	1.245
EC3-maj	25.034	143.897	−0.237	19.518	177.213	−0.423

MD simulations

We perform MD simulations on specific and nonspecific DNA sequence in their unbound and bound states. For the unbound state and the association state, the simulations extend to 200 ns to ensure the sampling is sufficient for determining statistical errors and for comparison. For each encounter complex, except EC2-maj, a stable intermediate state is obtained when the simulation reaches ∼100 ns. However, for EC2-maj, a 150 ns simulation is still not long enough to produce a stable state, so data will not be compared for that case.

Dna-x-S versus dna-c-NS

DNA is dynamic in solution. With our model simulations we can ask whether a transient state similar to the bound state can be observed for the specific DNA sequence. In addition, we wish to understand what differences can be observed between the specific and nonspecific DNA. The flexibility of DNA in solution can be approached by probing its conformational properties such as backbone geometry, distribution of its helical parameters, deformability of basepair step and groove dimension, etc. We compare dna-x-S to dna-c-NS in their canonical structures, deformability of basepair step, and groove width. The MD simulation on dna-x-S shows that the backbone root mean-square deviation from the averaged structure of dna-c-NS is only 0.54 Å, which indicates that the deformed DNA relaxes into a form similar to dna-c-NS. In addition, the minor and major groove widths averaged over all basepair steps are 7.6 Å and 11.4 Å, respectively, in dna-x-S, comparable to 7.9 and 11.0 Å in dna-c-NS within the statistical error (Table 2). These reflect the considerable similarity of the global structural properties of dna-x-S and dna-c-NS in solution. However, the fluctuations of the groove width are ∼1.0∼1.5 Å and so we consider whether the sequence-dependent fluctuations contribute equally.

Table 2.

The Averaged Widths and Electrostatic Potentials of the Major and Minor Grooves of the Unbound DNA in Solution

	Minor Groove			Major Groove
dna-x-S	dna-c-NS	t	dna-x-S	dna-c-NS	t
Width (Å)
5 TA/TA	7.5 (1.0)	7.7 (1.0)	1.5	11.5 (1.4)	11.2 (1.4)	2.3
6 AT/AT (AC/GT)	7.4 (1.0)	7.7 (1.0)	2.6	10.8 (1.4)	11.0 (1.5)	0.1
7 TT/AA (CC/GG)	7.2 (1.0)	7.5 (1.0)	3.8	10.3 (1.5)	10.6 (1.6)	0.4
8 TT/AA (CC/GG)	7.3 (1.1)	7.8 (0.9)	4.5	11.7 (1.6)	11.7 (1.7)	0.0
9 TA/TA (CG/CG)	7.9 (1.1)	8.3 (1.0)	3.9	11.7 (1.4)	10.5 (1.6)	5.3
10 AT/AT (GT/AC)	8.3 (1.1)	8.4 (1.1)	0.7	12.1 (1.4)	10.9 (1.4)	5.2
11 TA/TA	7.8 (1.1)	7.6 (1.0)	2.7	11.6 (1.4)	11.0 (1.4)	3.2
elepot (kBT/e)
5 TA/TA	−6.4 (1.0)	−6.4 (1.1)	0.3	−3.0 (1.1)	−3.3 (1.0)	0.4
6 AT/AT (AC/GT)	−6.8 (1.3)	−6.2 (1.0)	3.6	−3.7 (1.3)	−4.7 (0.9)	6.1
7 TT/AA (CC/GG)	−7.2 (1.4)	−4.4 (2.3)	10.8	−3.2 (0.8)	−4.6 (1.3)	8.2
8 TT/AA (CC/GG)	−7.4 (1.6)	−4.3 (2.6)	9.2	−3.9 (1.3)	−3.4 (0.9)	3.8
9 TA/TA (CG/CG)	−6.6 (1.2)	−4.1 (2.4)	9.2	−4.0 (1.3)	−2.2 (0.8)	12.4
10 AT/AT (GT/AC)	−6.1 (0.9)	−4.0 (2.2)	7.3	−4.2 (2.4)	−3.0 (1.4)	6.5
11 TA/TA	−6.2 (0.9)	−6.1 (0.9)	0.5	−4.2 (2.1)	−4.4 (1.2)	1.4

Student’s t-test: t_c (α = 0.01, df = 200) = 2.6. The basepair step in parentheses is for dna-c-NS. Data in parentheses are the standard deviations. t-values larger than t_c are in bold.

We apply the Student’s t-test to test the statistical hypothesis that the mean values of the distributions of a DNA basepair step parameter from two different simulations are equal. At the confidence level 99%, 200 degrees of freedom, the mean values can be considered significantly different at 99% confidence level if the absolute value of the t-score is >2.6. According to Table 2, the t-score at position 7–9 at the minor groove is larger than the critical t_c = 2.6, which means the differences in the minor groove width between the specific and nonspecific DNA are statistically significant for our confidence level.

It has been established that the electrostatic potential and the minor groove width are well connected (32), so we further estimate the electrostatic potentials at each groove (Table 2). Similar to the groove width, the electrostatic potentials at position 6-10 at the specific minor groove are significantly different from those at the nonspecific minor groove. Locally, the electrostatic potentials at the minor groove of the binding site are more negative in dna-x-S than in dna-c-NS. This offers a general mechanism for sequence-specific recognition of DNA shape, particularly in the approaching stage.

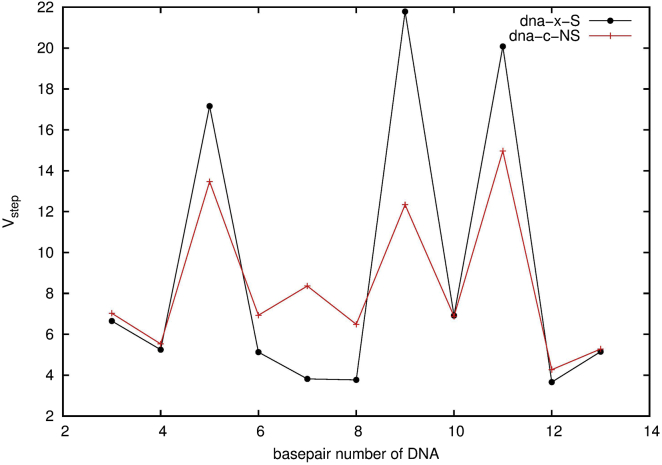
In addition to the groove properties, we compare the sequence-dependent deformability of each basepair step in both DNA systems. Following the work of Yonetani and Kono (33), to quantify the deformability of basepair steps, we evaluate the fluctuations, V_step (ųdeg³), in the six variables θ_i (i = 1, 2,…, 6 for shift, slide, rise, tilt, roll, and twist). $V_{\text{step}}=\prod _{i=1}^6\sqrt{{\lambda }_i}$, in which λ_i is the eigenvalue for the covariance matrix M having the components $m_{ij}=\langle \left({\theta }_i-\langle {\theta }_i\rangle \right)\left({\theta }_j-\langle {\theta }_j\rangle \right)\rangle$. The brackets 〈〉 means we averaged over the whole trajectory. M can be diagonalized using an orthonormal transformation matrix R for M, R^tMR = diag(λ₁, λ₂,…, λ₆). The V_step values obtained here are comparable to and have a similar trend to the results estimated from Yonetani and Kono’s work (33). As shown in Fig. 5, the specific sequence has three high peaks at all TA steps, 5, 9, and 11. This indicates these steps are highly deformable. The nonspecific sequence also has three peaks, but the peak values are lower and the V_step difference between the peaks and the other steps is not as conspicuous as in the specific one.

Figure 5.

The deformability (in ųdeg³) of the basepair step of the DNA in unbound DNAs from the MD simulations. To see this figure in color, go online.

All the analysis of the flexibility of DNA in solution together suggest that although the overall structures of dna-x-S and dna-c-NS resemble each other as B-form, the local specific shapes and deformability differ significantly because of the sequence. The differences seem subtle but substantial enough for MEF2a to distinguish during its search and recognition.

Sequence versus conformation in association forms

Comparison of the available data of the unbound DNAs to the bound ones enables us to understand if the binding of MEF2a induces the conformational change of the DNA, and to what extent. Complexes c-S and c-NS were built based on information from x-S, so the proteins in their initial structures have similar positions and orientations with respect to DNA (Table 1). c-S and c-NS represent one type of extreme situation of association, in which a protein associates with a straight segment of DNA and forms a complex at an optimal minimum energy. Because the DNA in c-S has the same sequence as in x-S, it is expected that the interactions of the protein with DNA will deform the DNA to some extent. The groove properties of the DNAs in x-S, c-S, and c-NS are summarized in Table S1 in the Supporting Material. Fig. 6, A and B, displays the widths and electrostatic potentials at the minor grooves for x-S, c-S, c-NS, dna-x-S, and dna-c-NS, respectively. Compared to the corresponding unbound DNA, the binding of the protein induces the minor groove to become narrowed by 20∼50% in x-S, 18∼46% in c-S, and 15∼36% in c-NS, respectively. The electrostatic potentials turn more negative by 37∼115% in x-S, 43∼108% in c-S, and 24∼100% in c-NS, respectively. The negative potentials are largely enhanced for all three association forms, but more so for the specific sequences. A deep and broad valley around sequence position 6-10 for the specific sequence is formed in the plot of the electrostatic potential as a function of DNA basepair number, while only a flat curve exists for the nonspecific sequence.

Figure 6.

Comparison of the minor groove properties of the DNAs in the free state to the DNAs in the association forms from the MD simulations. (A) The groove widths; (B) the electrostatic potentials. The standard deviations are listed in Table S1 and Table S2. To see this figure in color, go online.

Narrow minor grooves are often associated with A/T-rich sequences, and control the magnitude of the local electrostatic potentials. In particular, isolated A-tracts embedded in small DNA oligomers are observed to be intrinsically curved. A₆- and A₄-track DNAs in solution bend by 19° and 9°, respectively, as observed by NMR (34). MC simulations on papilloma virus E2 DNA (d-ACCGAATTCGGT) (35) gave the global bending angle of 10°, somewhat different from the value of 16° provided from a 15-ns MD simulation, which indicates a measure of force field reliability (36). All these studies reflect the intrinsic sequence-dependent bending properties of DNA free in solution. The specific binding site for MEF2a contains a short A-track region, ATTT. We expect this region to show a similar bending tendency. The calculated bending angle of the center of the specific binding site is ∼30° ± 8° in x-S and c-S, compared to 17° ± 9° in dna-x-S. This indicates that ∼40% of the bending is intrinsic and that ∼60% is induced by the protein based on our model simulations. However, it is surprising to find that the bending angle of the free nonspecific DNA is 16° ± 8°, the same as the specific one alone, in solution. The protein does not induce bending on the nonspecific DNA.

Comparison of the calculated approximate binding free energies among x-S, c-S, and c-NS (Table 3) reveals that x-S has the lowest binding energy of the three. For the differential change c-NS → c-S, ΔΔG_ele,MD is −55 kJ/mol, much more negative than −34 kJ/mol of ΔΔG_vdw,MD and entropically we find −15 kJ/mol of −TΔΔS_MD. This indicates that the sequence is the primary contributor for MEF2a to favor the association with a straight B-form DNA. c-S is more disordered than c-NS, which indicates that the conformation changes more in c-S than in c-NS. The minor groove widths at position 6-9 in c-S are ∼1 Å narrower than in c-NS, and the DNA is ∼15° more bent. Although the binding entropies in the process of complexation are all negative, the extent of the entropy loss is more on association with a nonspecific sequence than with a specific one.

Table 3.

Binding Free Energies Relative to x-S

	c-NS	c-S	EC1-Min	EC1-Maj	EC1-Cro	EC2-Min	EC3-Min	EC3-Maj
ΔΔGele,MD	87	32	32	43	60	21	12	37
ΔΔGnp,MD	9	8	25	23	30	34	35	24
ΔΔEvdw,MD	98	64	172	212	282	267	299	217
−TΔΔSMD	52	37	29	65	41	31	14	56
ΔΔGtot,MD	246	141	258	343	413	353	360	334

Free energies are in kJ/mol.

Sequence versus conformation in intermediate forms

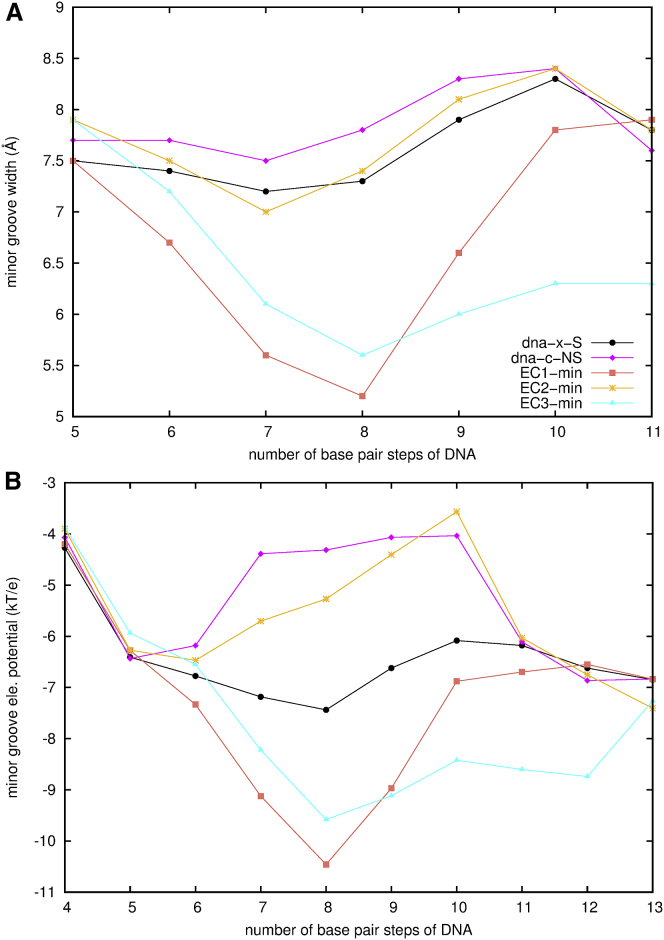
Before the formation of an association, a protein will form an intermediate state with DNA via the encounter process. Utilizing the coupled BD and MD simulations, we are able to observe the roles played by sequence and conformation in several intermediate forms. One-hundred-nanosecond MD simulations on several encounter complexes show that the intermediate states have a binding interface (∼2300–2800 Å²) that is not as tight as the association form (∼3500–3900 Å²), but the protein binding influences the shapes of the DNA to some extent.

EC2-min and EC3-min both have the protein binding at the minor groove of the DNA, but differ in the sequence. Structural comparison shows that the position of the protein in EC3-min is most similar to that in the association form x-S, as shown in Table 1. In EC2-min the relative position of the protein with respect to the DNA is (23.5 Å, 7.5 Å, 61.0°), or ∼2-bp more upstream than that in EC3-min. In addition, the protein binding in EC2-min does not influence the minor groove width, but enhances the electrostatic potentials of the minor groove just at position 7-8 by ∼30%. While in EC3-min, the region affected by the protein binding is expanded to position 7-12, as shown in Fig. 7 and Table S2. Particularly, the minor groove widths at position 7-10 are narrowed by 15∼24%, and the electrostatic potentials are enhanced by 14–38%. The DNA is induced to bend by ∼25°. The energy difference of EC2-min → EC3-min is −9 kJ/mol in ΔΔG_ele,MD, +1 kJ/mol in ΔΔG_np,MD, +32 kJ/mol in ΔΔG_vdw,MD, and −17 kJ/mol in −TΔΔS_MD, respectively. The entropy and enthalpy compensate each other to make the total energy change comparable within the statistical errors. Although the protein binding influences the DNA differently in EC2-min and EC3-min, the binding energies are similar.

Figure 7.

Comparison of the minor groove properties of the DNAs in the free state to the DNAs in the intermediate forms from the MD simulations. (A) The groove widths; (B) the electrostatic potentials. The standard deviations are listed in Table S1 and Table S2. To see this figure in color, go online.

EC1-min and EC3-min both have minor groove-binding at the same specific sequence on DNA, but differ in conformation of the DNA. In EC1-min, the binding site is ∼3-bp more upstream than in EC3-min. The electrostatic potentials at position 6-10 at the minor groove are enhanced by 7∼42%. The energy difference ΔΔG_ele,MD (EC1-min → EC3-min) is −20 kJ/mol, ΔΔG_np,MD is +10 kJ/mol, ΔΔG_vdw is +127 kJ/mol, and −TΔΔS_MD is −15 kJ/mol, respectively. Generally complexation of the protein with the DNA favors EC1-min, which largely is due to ΔG_vdw,MD. EC3-min has a positive entropy change, which could be caused by the bending of the DNA with a bending angle of 25° ± 10° and the smaller binding interface (2291 ± 219 Å²) between the protein and DNA. However, the entropy gain is not large enough to counterbalance the enthalpy change. The minor groove in the DNA of EC1-min is initially narrowed, which is an advantage by the protein to have larger interfacial binding area (2754 ± 137 Å²) and more contacts to make the whole binding more favorable (2, 4).

Comparing the binding energies among all the intermediate states shows that the order for ΔG_tot,MD is EC1-min < EC3-maj ≤ EC1-maj ≤ EC2-min ≈ EC3-min. EC1-min is the most favorable intermediate state, in which MEF2a binds at the preformed narrowed minor groove of the specific DNA sequence. The other intermediate states in terms of the total binding energy are all comparable, regardless of whether the DNA is straight or curved, specific or nonspecific, or the binding is a major groove-binding or minor groove-binding type. This makes the dissociation-reassociation process in sequence searching feasible for the protein (2, 4).

EC3-min is the least favorable intermediate state. We consider why MEF2a in the approaching process has the largest probability of encounter at the minor groove of a straight specific DNA sequence, but has the least favorable intermediate state. It is noteworthy that the binding in the approach and encounter stages are dominated by the electrostatic interactions. Once the protein and DNA encounter, vdW interactions take control in forming an intermediate state. The binding interface between the protein and a straight DNA is not large enough to provide more contacts for a stronger binding. The interfacial area in EC3-min is 2291 Å², smaller than ∼2800 Å² in the other intermediate states.

Binding to a specific sequence from several intermediate states to the final association state, for example, EC3-min → EC1-min → x-S, requires the conformational change of both the partners to obtain more interfacial area, more contact numbers, and less entropy loss. That DNA and the protein become equal partners is not unexpected (37). In contrast to EC3-min, it is less favorable for the protein to encounter the correct EC1-min binding site, but more favorable to form an intermediate state in terms of the binding energy. To enable the protein to encounter and form an intermediate at the correct site, the DNA could have a transient state that is similar to the bound state and can be selected by the protein. Alternatively, in the early stage of the binding process, e.g., encounter process, the process induces some shape variations of the DNA, then the protein proceeds with dissociation-reassociation (hopping) until it targets its specific site to form a final functional state. In support of the first possibility, the studies of Fis binding with different sequences (7) supports that idea that the DNA could transiently have narrow minor groove segments, which can be selected by Fis. In the study of the Jun-Fos model (38), the authors find that unrestrained simulations with the major force fields do not reproduce the NMR observables, but under NMR internucleotide restraints the simulations produce the dynamics of the free DNA in solution reliable enough to characterize the transient state that is similar to the bound DNA. In our study unrestrained simulations were applied. The transient states are not identified by comparison of the free DNA of the specific sequence with the nonspecific one. Nevertheless we find that the local shapes and surfaces differ significantly because of the sequence, which can be distinguished by MEF2a during its search and recognition. Our study supports the proposal that shape changes in the DNA induced by the protein binding (which incurs some changes as well) in the early stage of the process is required for a specific complex.

Conclusions

The protein search and the recognition of the target site on DNA has been a subject of much investigation in the past few years (2, 4, 39). According to the cocrystal structures, the complexation of protein and DNA involves mutual conformational changes, especially for a specific sequence association. Proteins can experience a disordered-to-ordered transition upon the binding, while DNA could change shape (bend or kink) induced by the binding. However, it has been less clear to what extent the DNA structure adopted in the complex was induced by protein binding or was instead intrinsic to the DNA sequence, and how these two factors contribute to the specific target search of the protein.

In this study, we used a multiscale simulation approach to study the binding process of the protein with DNA in terms of DNA sequence, conformation, and interactions. We considered two extreme cases in the protein approach and encounter process. One was the case of pure sequence recognition and the other, pure structure recognition. MEF2a was found to bind at both the major and minor groove on approach to DNA, but it has binding preference, depending on the sequence and conformation of DNA. A straight specific sequence provides more chances for a protein to reach near the correct location with the correct orientation. A specific sequence with a preformed shape, however, reduces the chances of encountering the correct site by ∼1.5 times. A straight nonspecific sequence is the least favorable for the protein to encounter at the assumed-to-be binding site. The intrinsic property of the DNA plays significant roles in the protein recognition of the specific sequence in the early stage of the binding process.

After the encounter process, an intermediate state is formed, which has a higher binding energy and a smaller binding interfacial area than an association form. Binding has little effect on the shape of a nonspecific DNA sequence, but it significantly narrows the minor groove of the binding site at a specific sequence, which enhances the electrostatic potentials as well. Contrary to the protein binding in the approach stage, forming an intermediate with a straight specific DNA is much less favorable than with a preformed one. We also find that the unbound states of a specific sequence and a nonspecific one resemble each other in their general structures, but differ significantly in their local shapes. However, a transient state that is proposed to resemble the bound state was not identified here. We propose that if the protein approaches, encounters, and forms an intermediate at the correct site, the binding should induce the DNA shape change in the early stage of the binding process. The protein would proceed with dissociation-reassociation hopping until it targets its specific site to form a final functional state.

Author Contributions

C.Y.C. performed all the calculations. B.M.P. and C.Y.C. designed aspects of the study, analyzed results, and wrote the article.

Editor: Michael Feig.