Computational Studies of Molecular Permeation through Connexin26 Channels

Abstract

A signal property of connexin channels is the ability to mediate selective diffusive movement of molecules through plasma membrane(s), but the energetics and determinants of molecular movement through these channels have yet to be understood. Different connexin channels have distinct molecular selectivities that cannot be explained simply on the basis of size or charge of the permeants. To gain insight into the forces and interactions that underlie selective molecular permeation, we investigated the energetics of two uncharged derivatized sugars, one permeable and one impermeable, through a validated connexin26 (Cx26) channel structural model, using molecular dynamics and associated analytic tools. The system is a Cx26 channel equilibrated in explicit membrane/solvent, shown by Brownian dynamics to reproduce key conductance characteristics of the native channel. The results are consistent with the known difference in permeability to each molecule. The energetic barriers extend through most of the pore length, rather than being highly localized as in ion-specific channels. There is little evidence for binding within the pore. Force decomposition reveals how, for each tested molecule, interactions with water and the Cx26 protein vary over the length of the pore and reveals a significant contribution from hydrogen bonding and interaction with K⁺. The flexibility of the pore width varies along its length, and the tested molecules have differential effects on pore width as they pass through. Potential sites of interaction within the pore are defined for each molecule. The results suggest that for the tested molecules, differences in hydrogen bonding and entropic factors arising from permeant flexibility substantially contribute to the energetics of permeation. This work highlights factors involved in selective molecular permeation that differ from those that define selectivity among atomic ions.

Introduction

Connexin proteins form channels in plasma membrane and between cells that are permeable to atomic ions and small molecules, mediating electrical and molecular signaling. The connexin channels between cells (gap junction channels) are formed by extracellular docking of two hexameric hemichannels. Gap junction channels allow intercellular propagation of electrical and molecular signals (1, 2, 3). Unpaired hemichannels play an autocrine/paracrine role by releasing transmitters such as glutamate and ATP into the extracellular environment (4, 5). The molecular signaling mediated by connexin channels, whether intercellular or paracellular, is of critical biomedical importance. Throughout the body, connexin channels are intimately involved in development, normal physiology, and response to trauma and disease. Defects in connexin channels (e.g., in the molecular signaling they mediate) cause a variety of human pathologies (3, 6). Although connexin channels as a class are permeable to a wide variety of molecules, channels formed by each of the 21 human connexin isoforms have strikingly different ionic and molecular selectivities, particularly among biological molecules (2, 7, 8, 9, 10, 11, 12, 13, 14). The channels formed by different connexin isoforms show little correlation between unitary conductance, limiting pore diameter and/or charge selectivity (7, 15, 16). The molecular permselectivity is not a simple function of pore width (8) but depends on as yet uncharacterized interactions between specific permeants and the pore lumen formed by each connexin isoform. These interactions determine whether and how well a specific molecule can pass through the pore.

To help elucidate the mechanisms and factors that affect and define selective permeation, molecular dynamics (MD) simulations were applied to permeation of molecules through the human connexin26 (Cx26) hemichannel. An equilibrium method (umbrella sampling (US) Hamiltonian replica exchange MD (US/H-REMD) was used to explore the free energy profiles of two aminopyridyl(PA)-labeled maltosaccharides in the Cx26 pore, one that is permeant (PA-maltose, a derivatized disaccharide) and one that is impermeant (PA-maltotriose, a derivatized trisaccharide) (17, 18). By comparing the results for a known permeant with a known impermeant we hoped to gain insight regarding the energetic and structural interactions between the molecules and the connexin pore that influence permeation. In addition, by using molecules that are in the size range of biological permeants of connexin channels, and that have conformational flexibility, we hoped to identify factors that come into play in selective molecular permeation of wide pores, which may be different from those that dominate permeation of atomic ions through ion-selective pores.

A key feature of our work is that the model of the Cx26 channel has been validated in that it reproduces the ionic selectivity properties of the native channel. The simulation system is an MD-equilibrated Cx26 channel, in explicit membrane/solvent that incorporated a key N-terminal acetylation identified by tandem mass spectrometry (MS/MS). Elimination of the positive charge of the terminal amine effected by this modification was required to reproduce the electrical conductance characteristics of the native channel by grand canonical Monte Carlo Brownian dynamics (GCMC/BD) (19). In addition to calculation of the potential of mean force (PMF), the reversible work required to move the molecule through the pore, we explored various energetic and structural interactions of the molecules that could contribute to the PMF, as well as changes in permeant shape and dynamics, effects on effective pore radius, and interactions with water and ions. The results are informative regarding the basis of the different permeability properties of the selected molecules, and highlight a variety of issues and factors that come into play specifically when considering molecular permeation of wide pores.

Materials and Methods

Computational model

The simulation system was based on that of Kwon et al. (19), which included the equilibrated structure of the Cx26 in explicit membrane and solvent. This system was transformed to a simulation cell with hexagonal symmetry, and the N-terminal methionine residues were acetylated at the α-amines (as shown by MS/MS (20)). The system was initially neutralized with Cl⁻, followed by the addition of K⁺ and Cl⁻ to yield a concentration of 0.1 M KCl (118 K⁺ and 166 Cl⁻ in total). The Cx26 hexamer was solvated in a fully hydrated 1-palmitoyl-2-oleoylphosphatidylcholine (POPC) bilayer (535 POPC molecules) with a 25 Å layer of explicit water (49,866 water molecules) above and below the 63-Å-thick bilayer. The total number of atoms was 243,940. The final prepared system is shown in Fig. 1 A. In the simulations, the channel is aligned along the z axis/membrane normal from −47 to 47 Å (cytoplasmic to extracellular end of the pore). The region of the pore in which the test molecules were studied spanned the portion of the pore with radius <16 Å, which is approximately from −26 to 45 Å (Fig. 1 A, right). Position z = 0 corresponds to the position of the Cα carbon of MET1. The resulting Cx26-POPC-H₂O-KCl system, with and without the test molecules, was then reequilibrated as described below.

Figure 1.

Simulation system and tested molecules. (A) (Left) Side view of the simulation cell showing the Cx26 transmembrane channel and lipid bilayer. The K⁺, Cl⁻, and the water layers above and below the membrane are not shown. (Right) Cut-away view of vdW surface of the channel showing z coordinate values used in the simulations. The side chains of ASP2, GLU42, ASP46, LYS61, and LEU56 are shown. One of the test molecules (disaccharide) is shown with its center-of-mass at z = 0. The channel is oriented with the cytoplasmic end at the top. (B) Molecules used in the permeability simulations. (Upper) PA-disaccharide (permeable). (Lower) PA-trisaccharide (impermeable). Solution-equilibrated structures are to the right.

The molecules whose energetics within the connexin pore are assessed are maltose (a disaccharide) and maltotriose (a trisaccharide) derivatized with an aminopyridyl (PA) group, as described in Bevans et al. (17) and shown in Fig. 1 B. The α1→4 linkages between the saccharide units impart a chiral structure, such that the minimal cross-sectional dimensions increase with the number of saccharide units. The PA-disaccharide was shown to be permeable, and the PA-trisaccharide was shown to be not detectibly permeable, through Cx26 channels. In this article, for simplicity we refer to the PA-derivatized molecules as “disaccharide” and “trisaccharide” (and in the figures as “disa” and “trisa”), and to both of them as “test molecules”. The input files for the test molecules including topology, parameter, and initial coordinate files were obtained using CHARMM-GUI (21).

Computational details

CHARMM parameter sets were used throughout, including the CHARMM22/CMAP parameters (22, 23) for the protein and ions, the additive C36 all-atom parameters for lipids (24), CHARMM general force fields (CGenFF) (25) for the test molecules and TIP3P for water (26). All systems were simulated with a 1 fs time step using the particle mesh Ewald (PME) method (27) for electrostatics and a Lennard-Jones (LJ) switching function for the van der Waals (vdW) interactions (28). The PME real space and LJ cutoff was 12 Å, the corresponding default value for the parameter sets. Hexagonal periodic boundary conditions were used for all simulations in the isobaric-isothermal (NPT) ensemble using Langevin thermostat and Andersen-Hoover barostat. The pressure and temperature were maintained at 1 atm and 300°K, respectively (29). Both CHARMM version c36b1 (30, 31) and NAMD version 2.9 (32) were used in the simulations. CHARMM was used to construct the Cx26 system, including the membrane and solvation, to place the test molecule at an initial position at the entrance of the pore at the cytosolic end (z = −30 Å), and to perform short equilibrations. Longer simulations and all steered molecular dynamics (SMD) simulations were performed with NAMD. A 50 ns equilibration was performed on the solvated Cx26 membrane system using NAMD, which incorporated a restraint with a force constant of 5 kcal/mol/Ų on the z axis of the center of mass of the Cx26 channel to maintain the channel at the center of the simulation cell. The MD simulations allow radial asymmetry of the cross section of the pore lumen at all z positions because of fluctuations of backbone carbons and side chains of each subunit (e.g., sixfold axial symmetry is not imposed). Pore radius, including contributions from amino acid side chains, was calculated from a CHARMM script that allows for a noncircular lumen cross section.

Root mean-squared deviation and fluctuation

The root mean-squared deviation (RMSD) of the protein backbone was used to monitor equilibration of the system. The RMSD of the Cx26 heavy atoms was calculated relative to the starting structure. As the system equilibrates, the RMSD reaches a stable plateau value, as shown in Fig. S1 in the Supporting Material. The amino-terminal (NT) and cytosolic carboxyl-terminal (CT) domains (residues 1−10 and 206−226, respectively) were excluded from the RMSD calculation because of their high inherent flexibility. Values of the spatial separation between the coordinates of the overlaid conformations were used to calculate the root mean squared fluctuation (RMSF). The RMSF provides information about the fluctuations of each atomic position during a simulation and is related to the crystallographic B-factor parameter. Fig. S2 shows the RMSF for the backbone atoms of the six connexin monomers, after equilibration, during a time period of 50 ns. The RMSF values are averaged for all atoms within each residue and plotted against residue number.

Steered molecular dynamics (SMD)

The initial coordinates for each replica in the umbrella sampling (US) simulations described below were taken from the snapshots of an SMD trajectory. Each test molecule was introduced into the lumen of the Cx26 channel in the equilibrated hydrated bilayer system at z = −30 Å, which is inside the cytoplasmic end of the pore. A short minimization and 4 ns equilibration were performed in which the test molecule center-of-mass (COM) was constrained to remain at z = −30 Å and x, y = 0, 0 Å. The COM of the test molecule was then subjected to a harmonic spring, and the free end of the spring was moved along the Cx26 channel z axis with a constant velocity. The potential energy of the test molecules as it is pulled along the z axis is given by $U\left(z\left(t\right)\right)=\frac{k}{2}{\left(v\times t-\left[z\left(t\right)-z\left(0\right)\right]\right)}^2,$ (Eq. 1) where k is the force constant, v is the pulling velocity, t is time, z(t) is the z coordinate of the test molecule COM at time t, and z(0) is the reference COM z coordinate for the test molecule. The derivative of the above equation with respect to z yields the force on the test molecule in the pulling direction, $f\left(z\left(t\right)\right)=-\frac{dU\left(z\right)}{dz}=-k\left(v\times t-\left[z\left(t\right)-z\left(0\right)\right]\right),$ (Eq. 2). The force vector on the COM of the test molecule was directed along the z axis to pull the test molecule from z = −30 Å (intracellular end of the channel) to z = 50 Å (extracellular end of the channel). A pulling speed of 20 Å/ns and a force constant of 347 pN was employed in Eqs. 1 and 2. This pulling speed was selected on the basis of empirical trials, starting at lower speeds, as the lowest speed that reduced to acceptable levels the variation in test molecule z distance from one trajectory to another. It is at or below pulling speeds typically used in such studies (33, 34, 35). A center of mass restraint was placed on the protein to prevent it from drifting within the simulation cell. PMFs were also derived from the SMD simulations (36) but were found to be less informative than the US/H-REMD results. The SMD simulations are discussed in Supporting Results.

Hamiltonian replica exchange MD umbrella sampling: US/H-REMD

Conventional US is a widely used equilibrium approach for determining free energy changes as a function of given reaction coordinates. The US method relies on a series of harmonically restrained closely spaced windows along the chosen reaction coordinate(s), the z axis along the Cx26 channel lumen in our study. The PMF was recovered from the biased distributions in each window using the histogram analysis method WHAM (37, 38). As robust as the US method is, its limitation lies primarily in the inability to sample complex systems that have hidden slow degrees of freedom orthogonal to the chosen reaction coordinates. It has been shown that combining US with Hamiltonian replica exchange (H-REMD) can alleviate this limitation (39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52). This enhancement is achieved by allowing energy barrier crossing along the orthogonal degrees of freedom by permitting frequent configurational exchange between adjacent windows while preserving the Boltzmann distribution, according to a Metropolis criterion (53). For calculating the PMF of aminopyridyl-labeled maltosaccharides passing through the Cx26 channel, we found that the complexity and flexibility of the test molecules made US/H-REMD the most viable approach (54).

All the US/H-REMD simulations were carried out using NAMD 2.9 (32). The one-dimensional PMF, W(z), was calculated using a set of equally spaced simulations biased by the harmonic potential W(z) = 1/2k(z − z_i)² to restrain the test molecule near specific positions z_i along the z axis. The distributions of positions z_i and the force constant of the harmonic potential were adjusted to obtain an acceptable acceptance ratio during the short US/H-REMD test runs. For both disaccharide and trisaccharide, 64 z_i positions were set up for 64 replicas (i.e., umbrella windows), separated by ∼1.1 Å increments from −25 to 45 Å in the z direction. The initial coordinates for each replica taken from the snapshots of an SMD trajectory were further equilibrated 500 ps/replica for umbrella sampling. A force constant of 5.0 kcal/mol/Ų was used for the harmonic potential. The average acceptance ratio is ∼12% with an attempt exchange frequency of 0.1/ps. All US/H-REMD simulations were carried out under the same conditions described in the Computational Details section above. The results were unbiased using the WHAM method with a bin size of 0.2 Å and a stringent tolerance of 0.00001 kcal/mol on every point in the PMF. The standard deviations of the PMFs were calculated using bootstrapping implemented in g_wham (55). Two bootstrap methods were used: bootstrapping new trajectories based on the umbrella histograms and autocorrelation time for each umbrella window, and Bayesian bootstrapping via the assignment of random weights to the histograms. The PMF is not symmetric, as the comparison between two test molecules is based on the shape and energy barrier of the PMFs within the interior narrow region of the channel only and does not extend to bulk water on either side.

To assess progress toward convergence, the time evolution of the PMFs was monitored. The US/H-REMD simulation for the disaccharide was performed for 6 ns per replica, giving 384 ns in total. As illustrated in Fig. S3, there is no significant change in the PMF profile during the last 3 ns. However, for the trisaccharide, even after 12 ns per replica (a total of 768 ns of US/H-REMD simulation), the time evolution of the PMFs showed significant shape change and lack of convergence. We speculate that one-dimensional US/H-REMD is not sufficient to sample the additional hidden degrees of freedom or orthogonal energy barriers introduced into the system by the trisaccharide. One way to potentially overcome this problem is to use higher-dimensional US/H-REMD, assuming that orthogonal slow degrees of freedom that hinder the convergence will be captured as 2nd or 3rd reaction coordinates. However, the derivatized trisaccharide backbone has 10 dihedral angles and our trajectory analysis shows that none of them have a dominant effect on the shape of the molecule. The dipole moment of the trisaccharide is not strictly correlated with tumbling of the molecule as it varies through overall conformational changes and reorientation of up to nine hydroxyl groups. Considering that a goal of this study is to distinguish the energetics and interactions of a permeant and a nonpermeant molecule with the Cx26 pore, a less computationally expensive approach was applied to estimate the energy barrier of the trisaccharide by adding a restraint on the radial x-y deviation of the center of mass (COM_xy) to keep it close to the center of the pore lumen, thus reducing the configurational space. The radial restraint on the trisaccharide center of mass was implemented using a harmonic potential and the colvar distanceXY module in NAMD. A force constant of 2 kcal/mol/Ų was sufficient to keep the deviation from the center of the pore within 0.5 Å. To assess the effect of the COM_xy restraint on the US/H-REMD PMF, it was first applied to the disaccharide simulations. The disaccharide PMFs with and without the COM_xy restraint are compared in Fig. S4, and show that the disaccharide PMF with the COM_xy restraint has a similar energy barrier at the same position (z ≈ 20 Å) as the PMF without the restraint, and that the essential energetic features are preserved. The trisaccharide US/H-REMD with the COM_xy restraint was started from the last snapshots of the previous US/H-REMD run (without the COM_xy restraint), using the same parameters described above except now restraining the COM of the trisaccharide to be near the center of the lumen (x, y, z = 0, 0, z_i) (Fig. S5). The total umbrella sampling for the trisaccharide was 1024 ns (64 replicas of 16 ns each). The PMF was calculated from the last 6 ns of each replica with COM_xy restraint. Although one cannot eliminate the effect of the COM_xy restraint on the trisaccharide PMF, the PMFs clearly distinguish the permeant from the nonpermeant molecule, and demonstrate that applying the COM_xy restraint allows a semi-quantitative depiction of the PMF.

Force decomposition and polar interactions

The total force contributed to the PMFs can be decomposed into individual contributions from the test molecule’s interactions with each component of the system: the channel, water molecules, ions, and membrane. Pair interactions including the vdW force and electrostatic force along the z direction between two groups of atoms are calculated using the PairInteraction option in NAMD for the last 1 ns trajectories generated from US/H-REMD. Mean forces are calculated using 0.1 Å bins and smoothed by a 10-point running average. The polar interaction energies between the test molecules and the protein were calculated using Coulomb’s law and a dielectric constant (relative permittivity; ε) of 20. Because the magnitude of the interaction energy is a linear function of ε, the arbitrary value 20 is chosen for the purpose of identifying regions of the pore at which there is a possibility for significant polar interactions, and differences in such interactions between the two test molecules.

Results

Potentials of mean force

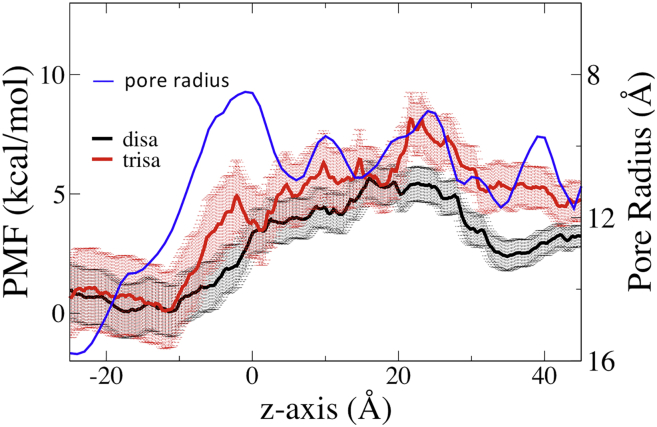
The PMFs for the two tested molecules (a derivatized disaccharide that permeates Cx26 channels and a derivatized trisaccharide that does not, both of which are referred to herein as “test molecules”) in the Cx26 pore were obtained by US/H-REMD as described in Materials and Methods. Note that all positions along the pore (“z positions”) will refer to the position of the center-of-mass of the test molecule, except for those that designate the positions of specific Cx26 residues, pore radius, or ion distribution. The US/H-REMD PMFs for both test molecules show a gradual and broad increase that extends most of the way through the pore (Fig. 2). The disaccharide PMF has a broad peak between 16 and 23 Å, with a maximum at 16 Å. The trisaccharide PMF increases more steeply than that of the disaccharide to reach a broad peak at 22 ∼ 23 Å. Beyond this region, toward the extracellular end of the pore, both PMFs decrease (the PMFs do not return to the initial values because the simulation does not fully extend to bulk water). The rising phase of the disaccharide PMF is relatively featureless, whereas that of the trisaccharide has several minor peaks, the most notable at −2 Å. Detailed comparison of the PMFs reveals that key regions of the pore that discriminate against the trisaccharide relative to the disaccharide are the regions −10 to −2 Å, 1 to 3 Å, and 19 to 23 Å. Fig. 2 also shows how the PMFs compare with changes in the pore radius. The peaks of the trisaccharide PMF tend to correlate with regions of pore narrowing, whereas the disaccharide PMF is relatively unaffected by these narrowings. The difference between the two PMFs is compared with pore width in Fig. S6. This figure shows that the pore narrowings that affect the differences in the PMFs most significantly are those centered at z ≈−2 Å and 24 Å, with a secondary contribution of the narrowing at 10 Å. The differences in the PMFs at pore narrowings may be because of steric influences directly and/or to interactions facilitated by steric constraint. The pore narrowings at z = −2, 10, and 24 Å, respectively, correspond approximately to the positions of the highly flexible amino-terminal end of the protein (residues 1–5) that folds inside the pore, the side chain of LYS41 and the less flexible backbone of ASP46, respectively. Identification of z positions of amino acid residues are only approximate; there can be substantial deviation along the z axis because of backbone and side-chain fluctuation, and asymmetry among the six subunits.

Figure 2.

PMFs for disaccharide and trisaccharide from US/H-REMD. The blue line is the unoccupied pore radius obtained from CHARMM, plotted with decreasing width toward the top. The error bars are standard deviations calculated from 100 bootstrapped PMFs. In this and all subsequent figures, the disaccharide and trisaccharide are denoted by “disa” and “trisa,” respectively.

These PMFs convey that within the pore the barriers to permeation are quite broad, lacking obvious binding sites. These features contrast with the permeation of atomic ions through most ion-selective channels, in which “selectivity” occurs in a highly localized region and includes clear binding sites. The peak of the trisaccharide PMF is ∼2.9 kcal/mol greater than that of the disaccharide. If relative permeability of the two molecules is determined solely by the difference in the peak values of the PMFs, from the Boltzmann factor exp(ΔG/k_BT) the trisaccharide is ∼125 times less permeable than the disaccharide at room temperature. Alternatively, transition state theory (TST) may be applied to estimate the relative transition rate of two test molecules passing through the narrowest region of the pore. The microscopic transition rate constant can be calculated from the following equation (56, 57), which has been used to characterize the transition rate of ions through ion-specific channels (40, 58, 59):

$$k=\kappa k_{TST}=\kappa \sqrt{\frac{k_{B}T}{2\pi m}}\times \frac{e^{\left[w\left(z_{\text{min}}\right)-w\left(z_{max}\right)\right]/k_{B}T}}{{\int }_{z_1}^{z_{max}}{e}^{-\left[w\left(z^{\prime }\right)-w(z_{min})\right]/k_{B}T}d{z}^{\prime }},$$ (3)

where the quantity $\kappa$ is the transmission coefficient between 0 and 1, which reflects the deviation of the transition rate from the classical transition-state theory rate $k_{TST}$ because of dissipative and collisional recrossing effects during the transition (to simplify the comparison, we assume $\kappa$ to be similar for the disaccharide and the trisaccharide); m is the mass of the test molecule; and w(z) is the PMF along the z coordinate. Therefore $\left[w\left(z_{\max }\right)-w\left(z_{\text{min}}\right)\right]$ corresponds to the activation free energy, and the integral is from z = −11 Å to the highest energy barrier. The activation energy is 5.3 kcal/mol for disaccharide and 8.2 kcal/mol for trisaccharide. The estimated $k_{TST}$ from the PMF is 1984.5 s⁻¹ for the disaccharide and 19.7 s⁻¹ for the trisaccharide. By this analysis, the disaccharide is 100 times more likely to pass through the restricted region of the channel than is the trisaccharide. Each of the treatments above simplifies the system in different ways, but they are consistent with each other and with the experimental finding that the trisaccharide is not detectibly permeable through this channel, relative to the disaccharide (i.e., its permeation through a membrane is unaffected by the presence of functional Cx26 channels).

Force decomposition and role of K⁺ ions

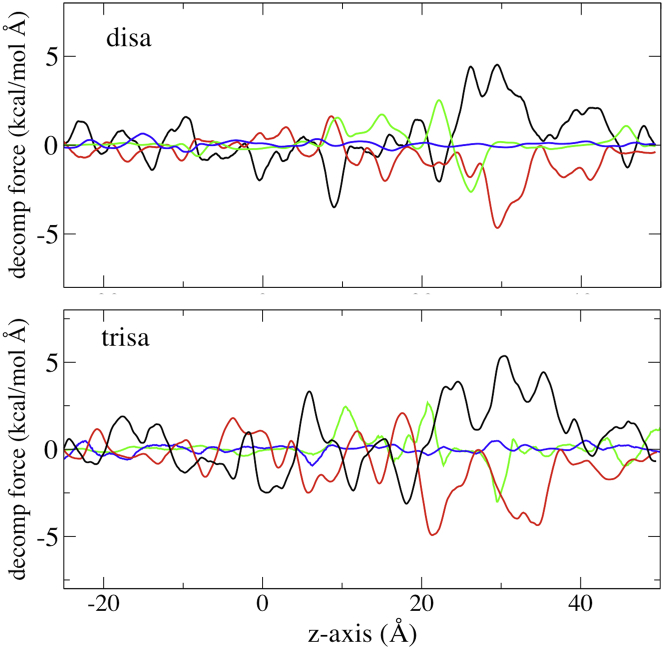
To reveal the interplay of forces that contribute to the PMF, the pairwise forces between the test molecules and the components of the system (water, Cx26, K⁺, Cl⁻, membrane) were calculated from the last 1 ns trajectory in each US window (60, 61). For the disaccharide (Fig. 3, upper), overall there are opposite but not entirely overlapping contributions from water and from the Cx26 protein, with the most-prominent reciprocal forces in a broad region between z = 25 to 30 Å. The component forces for the trisaccharide (Fig. 3, lower) show many of the same features, but differ most prominently between z = 20 to 25 Å where there is a force between the trisaccharide and the protein opposing permeation (at the peak of the PMF) that does not occur for the disaccharide, and a partial compensatory contribution from water.

Figure 3.

Decomposition of the forces on the test molecules that contribute to the US/H-REMD PMF: water, black; Cx26, red; K⁺, green; Cl⁻, blue. Mean forces are calculated using 0.1 Å bins and smoothed by a 10-point running average. (Upper) Disaccharide. (Lower) Trisaccharide.

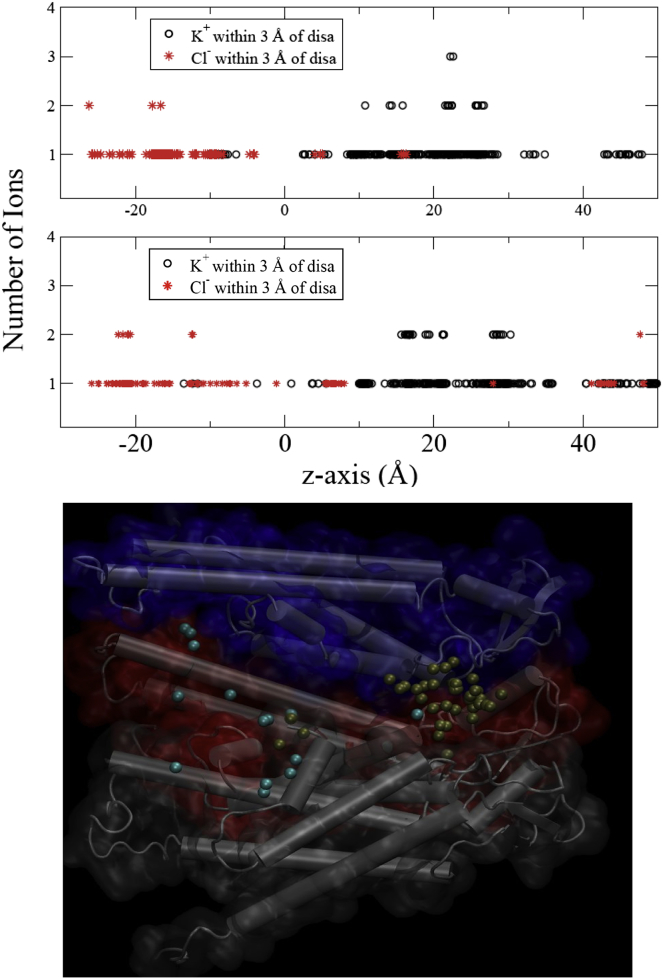
The force decomposition indicates that interactions with K⁺ contribute substantially to both PMFs at specific z positions greater than 7 Å, at some places opposing interaction with water and elsewhere opposing interaction with the protein. Interactions with Cl⁻ ions were negligible, as were those with membrane (not shown). The degree of test molecule interaction with K⁺ was somewhat unexpected; the force decomposition shows that its contribution can approach the same order of magnitude as interaction with protein or with water. To further explore the interaction of the test molecules with K⁺ and Cl⁻, the accumulated number of each ion within 3 Å of the test molecules was calculated from a total of 3000 snapshots along the z axis (Fig. 4, upper). The distributions of K⁺ and Cl⁻ closely associated with the test molecules were essentially nonoverlapping, with Cl⁻ associated at negative z values, and K⁺ at positive z values. Fig. S7 shows that the distributions of the ions along the z axis remain consistent along the simulation. This is likely a function of a slight negative surface potential in the extracellular half of the pore. The number of ions closely associated with the test molecules is low. However, the probability of a K⁺ being close to a test molecule is significantly higher than for a Cl⁻. The number of associated K⁺ is maximal between z = 22 and 29 Å for the disaccharide, and between 17 and 31 Å for the trisaccharide. The largest interactions with K⁺ in the force decomposition (Fig. 3) lie within these regions. Comparison with the force decomposition results show that even though Cl⁻ is associated with the test molecules at negative z positions, there is essentially no energetic interaction with Cl⁻. The greater energetics of interaction with K⁺ may arise from the fact that K⁺ is located in the relatively narrow and rigid part of the pore and its accessibility to hydroxyl groups of the test molecules whose dipolar orientation would favor interaction with cations. To illustrate the distribution of K⁺ and Cl⁻ in the pore during permeation, the coordinates of the ions within 3 Å of the disaccharide through the pore are overlapped (300 snapshots) in Fig. 4, lower. The results show a diffuse cloud of Cl⁻ ions in the cytoplasmic half of the pore, and a compact cloud of K⁺ ions in the extracellular end of the pore, consistent with the force decomposition data and greater force interaction with K⁺.

Figure 4.

Distribution of K⁺ and Cl⁻ in the pore within 3 Å of the test molecules. (Upper) Number of K⁺ and Cl⁻ ions within 3 Å of each test molecule. Upper: disaccharide; lower, trisaccharide. (Lower) K⁺ (yellow) and Cl⁻ (blue) within 3 Å of the disaccharide from 300 overlapped snapshots from US/H-REMD simulations.

The vdW and polar character of the interactions of the test molecules within the pore were explored (see Supporting Results and Figs. S8 and S9). The results indicate that protein and water molecules compete in forming favorable vdW contacts with the test molecules throughout the permeation process. They also reveal that the region centered at z = 10 Å has significant potential for favorable polar interactions. The association of water with the test molecules was investigated (Supporting Results), revealing that although the number of closely associated water molecules varies somewhat through the pore, there is no significant dehydration of the test molecules.

Pore width and dynamics

The unoccupied pore radius profile and its standard deviations are shown in Fig. 5 (upper, black line). The data suggest that in some regions the pore width is more intrinsically variable than in others, with the greatest variation between z = −10 and −3 Å, which corresponds to where the highly flexible and unstable NT domain of the protein folds into the pore. There is a secondary peak in width variation between z = 22 and 28 Å (Fig. S10 shows the variation as a function of z position). The pore width is least variable at z = −25 Å; but this is a wide region of the pore, so it is unlikely to affect permeation. Other minima in variability are at z ≈ −18 (another wide region), −1, and 20 Å.

Figure 5.

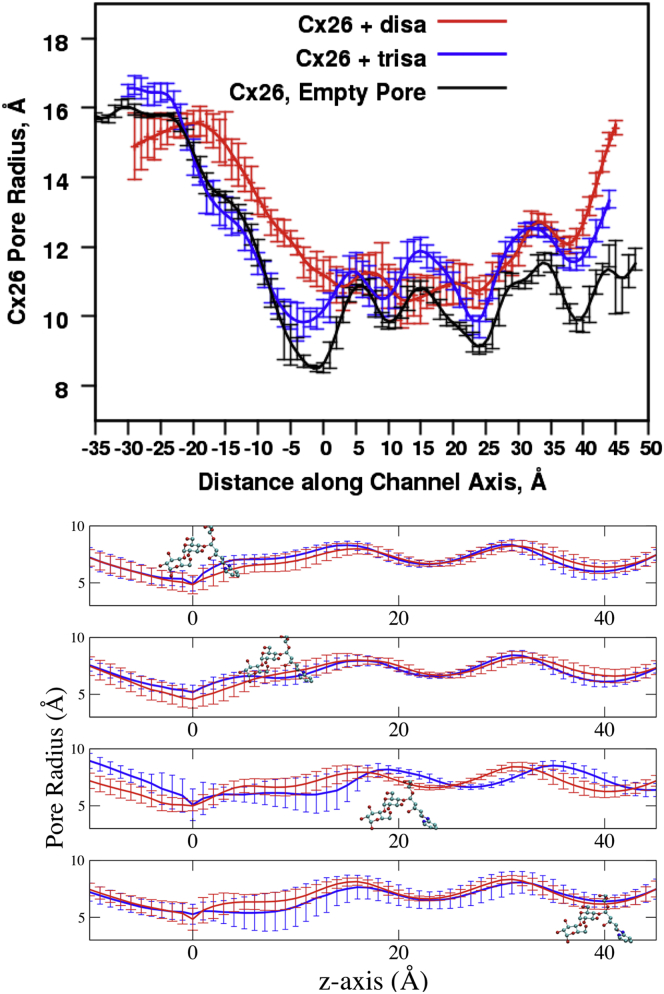
Pore radius and variations. (Upper) Radius of the pore at the position of the test molecules. The average radius of the pore at the position of the test molecule at each position with a COM_xy restraint. For comparison, the Cx26 pore radius without the test molecules is shown. The error bars are standard errors of the mean. (Lower) Variation in pore radius with molecular permeation. Means and standard deviations of pore radius for US/H-REMD simulations with the test molecules at the positions indicated. Red, disaccharide; blue, trisaccharide. Pore radius was determined from 100 snapshots (20 ps apart) with test molecule COM at the indicated z position.

The variations in the width of the unoccupied pore during the simulations suggest that the presence of a test molecule within the pore may affect pore width and dynamics. To examine this possibility, the pore radius at the position of each test molecule along the z axis was determined from the SMD trajectories (Fig. 5, upper, red and blue lines). In most of the narrow region of the pore with radius <12 Å (z positions more positive than −10 Å), the average pore width with test molecule present is greater than that of the unoccupied pore, suggesting that the test molecules tend to “widen” the lumen as they pass through. This effect is consistent with the overall interaction between the test molecules and the protein being repulsive and indicates that the test molecules may do work on the pore. A plot of the degree of pore widening, relative to the unoccupied pore, effected by each test molecule is shown in Fig. S11. Two features present in Fig. 5, upper, are more evident in this figure: overall, the disaccharide widens the pore more than does the trisaccharide, and the region of greatest variation in unoccupied pore width (z = −10 to −3 Å, the region of the NT) correlates with a peak in the effect of the test molecules on pore width, particularly noticeable for the disaccharide.

To further explore the effect of the test molecules on pore dynamics, the pore radius, and its variation during US/H-REMD simulations of each test molecule through the segment of the pore with radius less than 10 Å are depicted in Fig. 5, lower. The results indicate that variation in pore width is affected by the position of the test molecule, and, notably, that these effects are not limited to the location of the test molecule itself. The most rigid part of the pore assessed in this manner is z ≈ 25 to 30 Å (corresponding to part of the parahelix region, residues 46 to 50 (62)). There is a surprising degree of test molecule-dependent variability in the region surrounding z = 10 Å, especially for the trisaccharide.

Hydrogen bonds

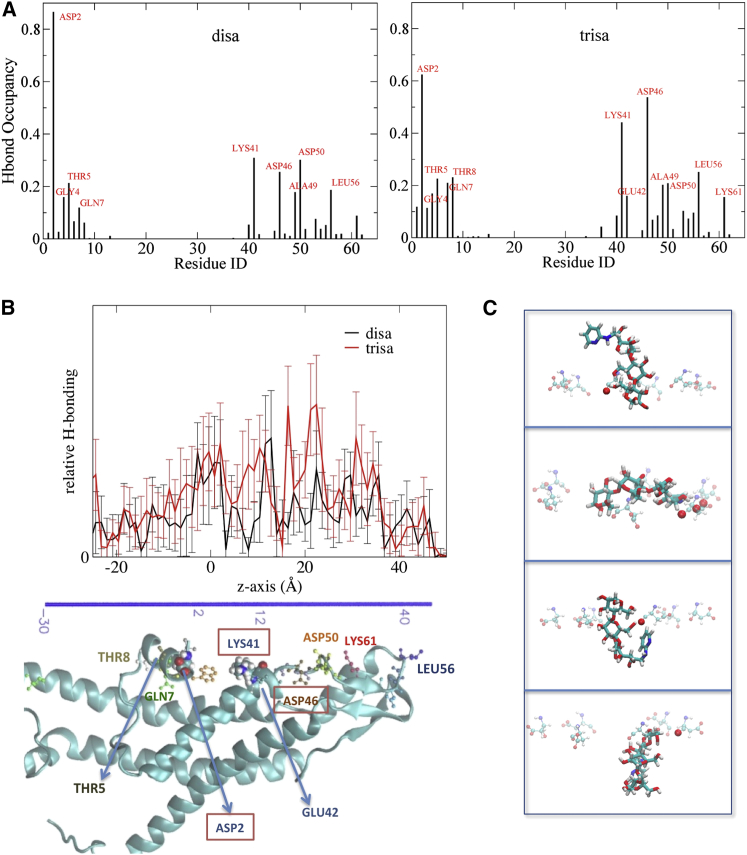
To identify the specific amino acid residues of Cx26 that interact with the test molecules via hydrogen bonds, the US/H-REMD trajectories were inspected for hydrogen bonds between the test molecules and the Cx26, either directly or through an intervening water molecule. The snapshots were extracted every 10 ps, which is about the maximum lifetime of the hydrogen bonding with disaccharide (a histogram of the lifetimes of hydrogen bonds between disaccharide and water molecules is shown in Fig. S13). The fraction of the snapshots in which each interaction occurred reflects the relative occurrence (“occupancy”) of that interaction. In this way, it was possible to identify the amino acid residues that interacted most with the permeating molecules (Fig. 6 A). Table S1 tabulates the data by residue and by z position of the Cx26 atom involved in the interaction, and indicates the proportion of each interaction that was with residue backbone or with the side chain. This analysis indicates that the key differences in the hydrogen bond interactions between the test molecules and the Cx26 are significantly greater interactions of the trisaccharide with GLN7 and THR8 in the NT helix, with LYS41, GLU42, and ASP46 in the parahelix and with LYS61. The increased interaction of the trisaccharide with GLN7, THR8, and LYS61 correlated with increased interaction with side chains. Among the strongest interactions for both test molecules were interactions with the charged residues ASP2, LYS41, and ASP46 (highlighted in boxes in Fig. 6 B). In addition, the disaccharide had significant interaction with ASP50, primarily with the side chain, which was less significant for the trisaccharide.

Figure 6.

Hydrogen bonds between test molecules and specific Cx26 residues (directly and via intervening water). For each Cx26 residue, the number of hydrogen bonds present in all snapshots in all windows during the US/H-REMD simulations, divided by the number of snapshots (3200 snapshots), gives the fractional amount of the total time (occupancy) a hydrogen bond was present. (A) Hydrogen bonds to identified Cx26 residues. (B) Graph of hydrogen bonds between test molecule and protein as a function of test molecule position. The channel graphic below indicates the positions of the key residues involved in hydrogen bonding to the test molecules aligned with the z axis scale of the graph. (C) Trisaccharide passing through the ring of ASP46 at the peak of the PMF. Representative snapshots were taken from the US/H-REMD simulation showing hydrogen bonding between trisaccharide and ASP46 residues, which are located at z = 22 to 25 Å (time sequence: upper to lower). The red balls depict the carboxylic oxygen atoms of the Asp residues (transparent) that are within hydrogen-bond distance (3 Å) of the hydroxyl groups of the trisaccharide. The trisaccharide undergoes dramatic conformational changes and the making and breaking of hydrogen bonds as it moves past the ASP46 ring. See Movie S1 for more snapshots from US/H-REMD simulation.

Fig. 6 B depicts the relative occurrence of the direct and water-mediated Cx26-test molecule hydrogen bond interactions as a function of the z position of test molecules. Each test molecule has a broad peak between z = −5 and 2 Å, indicating close interactions with the flexible NT helix. The trisaccharide has a much broader peak from z = 8 to 13 Å than does the disaccharide, indicating more interaction with residues in this region (ALA40, LYS41, GLU42), which is consistent with Fig. 6 A and Table S1. The two highest peaks for the trisaccharide are at z = 16.5 and 22.5 Å. This region shows significant water-mediated hydrogen bonding for the trisaccharide, but not for the disaccharide (Table S1). The greater peak at z = 31 Å for the trisaccharide reflects the hydrogen bonding with LYS61, which is absent for the disaccharide. Overall, the number of hydrogen bonds that involve the trisaccharide and the protein show a series of peaks at nearly the same positions as for the disaccharide, but which are greater in magnitude. The significant difference is mostly contributed by the extensive water-mediated trisaccharide-Cx26 hydrogen bonding, particularly with side-chain atoms. The distributed and overlapping regions of hydrogen bond interactions reinforce the idea that the interactions that influence permeation of these molecules are also distributed and overlapping.

To help understand the interplay between hydrogen bond formation and test molecule configuration in this region, Fig. 6 C and Movie S1 show a series of snapshots from US/H-REMD trajectories as the trisaccharide passes ASP46 (at the peak of its PMF). The trisaccharide undergoes dramatic changes in configuration and orientation, accompanied by making and breaking several hydrogen bonds with the backbone and side chain of ASP46 at each interval. This conveys a complex and reciprocal interaction between enthalpic and entropic energy components at this critical region of the pore. Note that in this process, the configuration of the ASP46 side chain is nearly invariant. This can be attributed to salt bridge interactions of the ASP46 side chain with ARG184 and LYS188 within the connexin monomer (63). Interestingly, ASP46 is highly conserved among human connexin channels. The ability of a potential molecular permeant to be energetically stabilized by interaction with a residue side chain may be enhanced if the side chain is relatively flexible (e.g., has a large RMSF, unlike that of ASP46). That is, side-chain fluctuation may be important in terms of the ability to interact electrostatically with permeants. The RMSF of side-chain atoms only is depicted in Fig. S14. It shows that from the cytoplasmic entrance of the pore up to z = ∼10 Å (at the side chain of LYS41) the pore is lined by residues with relatively large RMSF, unlike beyond that point in the channel, which includes ASP46, whose side chain is relatively rigid. Thus, a bulky and rigid side chain with strong potential for electrostatic interactions is located at the peak of the trisaccharide PMF and the point of greatest difference between the trisaccharide and disaccharide PMFs. This combination of factors exists nowhere else in the pore.

Behavior of the test molecules

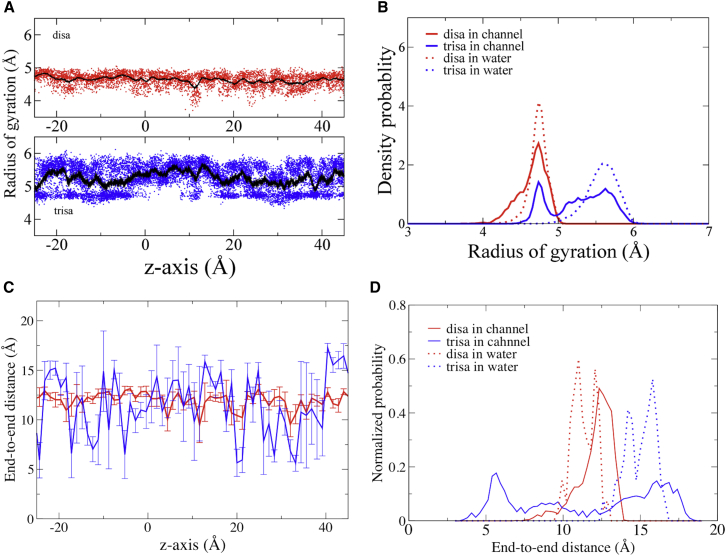
A view of the path taken by the trisaccharide through the pore in a US/H-REMD simulation is shown in Fig. S15. It conveys that these molecules tumble wildly through the pore and experience wide variations in degrees of configurational and orientational freedom. Changes in rotational, translational, and configurational degrees of freedom of a molecule are accompanied by changes in its entropy. The radius of gyration (r_gyr) and end-to-end distance of each test molecule were calculated along the channel z axis. Fig. 7 A shows the r_gyr of the test molecules as a function of position in the pore. Both test molecules have a notable drop in r_gyr at z ≈ 10 Å (which corresponds to the side chain of LYS41). Aside from this, the disaccharide has a fairly constant r_gyr distribution throughout the pore. The trisaccharide accesses two distributions of r_gyr over most of the pore length, one that is larger than that of the disaccharide, and one that is approximately the same as the disaccharide, reflecting a more compact configuration. At only two segments (0 to 8 Å and 12 to 13 Å, corresponding to two wide regions of the pore, does it occupy only the larger r_gyr.

Figure 7.

Radius of gyration and end-to-end distances of test molecules in US/H-REMD simulations. (A) Radius of gyration of the test molecules as a function of position. (Upper) Disaccharide. (Lower) Trisaccharide. All points are plotted as small circles, with the mean a black line. (B) Probability density functions of test molecule radius of gyration within the pore and in bulk water. Figs. S16 and S17 show that the time constants of the autocorrelation functions of the radius of gyration and of rotation around each axis are well below the durations of the computation times at each position within the pore (US/H-REMD simulation times were 6 and 16 ns per replica for disaccharide and trisaccharide, respectively), and therefore sufficient to capture the equilibrium distributions of these parameters of test molecule configuration. (C) End-to-end distance of each test molecule as a function of z position: disaccharide, black; trisaccharide, red. (D) Probability density functions of test molecule end-to-end distance within the pore and in bulk water.

The distribution probabilities of the r_gyr of the test molecules in the pore and in bulk water are compared in Fig. 7 B. The r_gyr of the test molecules in bulk water were calculated from 100 ns simulations in bulk. These confirm that within the pore the trisaccharide populates two configurations with different r_gyr, and show that its larger r_gyr in the pore is essentially that in bulk water; the smaller r_gyr is induced by its presence in the pore. In contrast, within the pore the disaccharide has a single dominant r_gyr corresponding to that in bulk water, but it does occupy a smaller r_gyr for a small percentage of the time, indicated by the shoulder on the left side of the main peak. This smaller r_gyr likely reflects the configurations near z = 10 Å and 23 Å (suggested in Fig. 7 A). These results suggest that the configurational distribution of the trisaccharide is substantially different from that in bulk water at nearly every position within the pore, but for the disaccharide this occurs only at two discrete regions of pore narrowing. This suggests a larger configurational entropic cost for trisaccharide to permeate than the disaccharide.

The difference between the average r_gyr of disaccharide and trisaccharide is less than 1 Å. For highly flexible molecules, a single value of r_gyr may represent a large ensemble of configurations. Although there is clear difference in the distribution of r_gyr between disaccharide and trisaccharide, r_gyr may not be sensitive enough to capture the changes in the conformation of the test molecules along channel axis. A more direct way to compare the conformational changes between disaccharide and trisaccharide is the end-to-end distance. Fig. 7 C shows that the fluctuation of the end-to-end distance of the disaccharide is much smaller than for the trisaccharide. The trisaccharide average end-to-end distance at each z position fluctuates between 5.6 and 17.1 Å, and the disaccharide end-to-end distance fluctuates between 9.6 and 13.1 Å. By this measure, the most significant configurationally confined regions of the pore for the trisaccharide are at ∼−12, 20, and from 23 to 33 Å. In contrast, the disaccharide show only minor conformational restriction at ∼20 Å. Notably, in the pore the mean end-to-end distance of the trisaccharide is indistinguishable (though more variable) from that of the disaccharide, despite its larger size (12.0 ± 1.1 Å and 11.4 ± 3.8 Å for the disaccharide and trisaccharide, respectively). The distribution probability of the end-to-end distance in the pore and in bulk (Fig. 7 D) shows the same trend of molecular behavior as the distribution of r_gyr (Fig. 7 B), further confirming that the configurational distribution of the trisaccharide is substantially altered toward the smaller end-to-end distance by the pore compared with that in bulk water. In addition to the overall trend, the end-to-end distance distributions also indicate that for both test molecules, a small but significant fraction of the molecular configurations sample the larger end-to-end distances seen in bulk water, especially for the disaccharide.

Discussion

A signal property of connexin channels is the ability to mediate selective diffusion of molecules across plasma membrane(s), but this process has yet to be well-characterized in mechanistic or energetic terms. The structural and energetic factors that affect the ability of a molecule to permeate a protein pore may differ from those that are dominant in the permeation of atomic ions such as K⁺ and Na⁺ through ion-selective pores. This study was undertaken to identify and explore these factors, and to validate a system and technique to do so for connexin channels. Computational studies were performed using an experimentally validated model of the connexin channel. A key finding is that the PMFs obtained for the two tested molecules are consistent with their experimentally determined permeability/impermeability. This provides a qualitative validation of this system for exploration of molecular permeation of this connexin channel and perhaps others. Information was obtained regarding the pore lumen, the behavior of the tested molecules (one permeant and one impermeant), and the interactions and forces involving the molecules at different positions in the pore. Most of the observations of interest arise from considerations of the flexibility of the test permeants in the context of relatively weak interaction energies (i.e., larger relative contributions from entropic factors).

For this work, it was essential to have confidence that the model of the channel being used approximated the native channel. The initial channel model used in the simulations is essentially that developed by Kwon et al. (19) Using grand canonical Monte Carlo Brownian dynamics (GCMC/BD), they found that the crystal structure of the channel (once the residues and domains unresolved in the x-ray structure were added) was essentially impermeant even to atomic ions. Equilibration by MD was required to relax the structure sufficiently to permit ion permeation. Crucially, the native current-voltage relations and ionic selectivity could not be reproduced without incorporating the loss of charge at the terminal amine of the N-terminal methionine, because of its acetylation in the native protein shown by MS/MS (20) and consistent with known sequence determinants for this cotranslational modification. In our work, MET1 was explicitly acetylated.

The pore width variations

In the simulations carried out in the absence of the test molecules, the profile of pore width corresponds well to that of Kwon et al. (19) The pore showed regions of greater and lesser flexibility, inferred from variations in pore width across different trajectories. The most variable region in the relevant portion of the pore (radius <12 Å) corresponds roughly to pore-lining residues MET1 to ILE9 (part of the NT domain) and the most rigid region to the position of ASP46. The rigid region around ASP46 corresponds to the “parahelix” region thought to be involved in channel gating (62) and which was shown in previous dynamics studies to be the most stable region of the open channel pore (19).

The test molecules and their waters

One important factor when considering molecular as opposed to atomic permeation, in addition to size, is that potential molecular permeants are rarely spherical or rigid; they can have complex physical and electrostatic structures, as well as conformational and rotational flexibility. Indeed, the test molecules used in this study have complex conformational flexibility because of multiple dihedral angles. We found that the r_gyr and end-to-end distance, reflecting “compactness” of each test molecule, was affected by its presence in the pore, and was affected differently in different regions of the pore. Within the pore, the r_gyr of the disaccharide is the same as that in bulk water, except for two discrete locations of pore narrowing. In contrast, throughout the pore the trisaccharide r_gyr fluctuated between that in bulk water and a smaller value (approximately that of the disaccharide in bulk water) except in two regions that roughly correspond to maxima in pore width. One may infer that through much of the pore there was an entropic penalty as reflected in substantial occupancy of a more compact structure. This is supported by end-to-end distance data showing that there was strong configurational constraint of the trisaccharide at the z position corresponding to the peak of the PMF, whereas the disaccharide data showed little indication of such a constraint.

Dehydration plays a crucial role in the permeation of atomic ions through ion-specific channels. Although the number of water molecules closely associated with the test molecules (within 5 Å) varied significantly with z position, and the changes with position were different for the two molecules (Fig. S12), both remained substantially surrounded by water, with no particular correlation with the overall PMF. The PMF decomposition shows that there are positions in the pore at which forces arising from interaction with water favor or disfavor permeation (usually inversely correlated with the forces arising from interaction with the protein). Although these energies are of the same order of magnitude as interaction with the protein, and contribute substantially to the overall PMF, the total energies involved are much smaller than those generated by actual dehydration. The findings suggest that dehydration was not a major factor in the energetics of permeation of these molecules, even at the narrowest locations in the pore.

Permeation: effects of test molecules on pore width and pore width variation

Analyses of pore width during molecular permeation revealed two effects of the test molecules. At essentially every position of the disaccharide, the pore is wider than when it is unoccupied. The same is true for the trisaccharide at z positions more positive than −5 Å. Pore widening at the position of the test molecules indicates that they exert repulsive force on pore-lining moieties. It is intriguing that the effect on pore width is greater for the disaccharide than for the trisaccharide. This counterintuitive effect may be explained by increased formation of attractive hydrogen-bond interactions with the Cx26, as indicated in Fig. 6, by the trisaccharide relative to the disaccharide, because of the closer approach to the walls of the pore.

The unoccupied pore showed differences in the variability of pore width along its length. Comparison of this variation with the degree of pore width expansion effected by the test molecules shows that although in general they widened the pore to a degree correlated with the variability of the unoccupied pore, there were significant exceptions. One notable exception was the region between z = −5 and 0 Å, at which both test molecules expanded the pore width in excess of that expected based on unoccupied pore variability. This is where the flexible and structurally unstable NT helix is located. The different effects of the test molecules on pore width suggest that the molecules can have effects on the pore width that are not entirely predictable from simple considerations of size and pore flexibility, and that depend on other factors specific to the residues involved. The other notable effect of the test molecules on the pore is that they affect the variation in pore width at positions other than where they are located (Fig. 5, lower). That is, a molecule within the pore can have nonlocal effects on the dynamics of the pore lumen.

Permeation: wide barriers but no binding

The PMFs show little indication of “binding” of these molecules within the pore; there are no significant wells in the energy profiles. This distinguishes the energy landscape experienced by these molecules from that experienced by ions in ion-selective channels and from that described for some molecular permeants of wide pore, in which residency at binding sites plays a major role in permeation and selectivity. A similar absence of energy wells is seen in the PMF of permeation of glycerol through the glycerol uptake facilitator (GlpF) of Escherichia coli (64, 65) and permeation of nucleotides through the α-hemolysin pore (66).

A distinguishing feature of the PMFs is that the energy barriers extend through most of the length of the pore, rather than being highly localized to a narrow “selectivity-filter” region, as is common in ion-selective channels. Viewed simplistically, given the near absence of energetically stabilizing positions in the pore, this could imply that overcoming such barriers is not a matter of a molecule transiently achieving the energy required to pass a peak barrier, but rather the energy being maintained for a duration that allows diffusion along the physical width of the barrier. For example, the PMF for the trisaccharide is nearly flat between z ≈ 13 and 19 Å but transit of that physical distance may not be instantaneous. At a minimum, the intrapore diffusion constant of a potential permeant will have an effect on the rate of the diffusion and the magnitude of this effect will be a function of the width of the barrier. The TST analysis takes into account the width of the barriers in thermodynamic terms, but not the effects of intrapore diffusion constants and differences among them.

Permeation: forces contributing to PMF differences

The force decomposition of the PMF provides insight regarding the interplay of forces experienced by each molecule as it transits the pore. The forces between the molecules and water and with the Cx26 protein vary over the length of the pore, often, but not always, in inverse fashion. An unexpected feature was the substantial contribution of interaction with K⁺, which usually interacted with the test molecule with energy opposite to the interactions with water, more commonly for the disaccharide than the trisaccharide. The contribution of K⁺ indicates a charge-dipole interaction between the ion and the test molecule, perhaps displacing dipole-dipole interactions with water. This type of interaction is unlikely to play a significant role in narrow, ion-selective channels, but may be a significant contributor to the energetics of permeation of wide channels.

Determinants of selectivity

The results suggest that pore width influences the PMFs of these molecules but affects them differently. The narrowest regions of the pore, in order of decreasing constriction, are at z ≈ −2, 24, and 10 Å, which correspond to the regions of substantial difference in the PMFs of the test molecules. At each point of narrowing, the properties of the pores differ, leading to the following different effects on the PMFs:

• •The narrowest part of the pore (z ≈ −2 Å), contributed by the end of the NT domain, is also the most flexible in the absence of the test molecules. It is also the region whose dimensions are most affected by the presence of the test molecules (Figs. 5, upper, S10, and S11). The high degree of flexibility at this region may explain why both test molecules have substantial but roughly equivalent hydrogen bond interactions with the protein (Fig. 6).
• •The lesser pore constriction at z ≈ 10 Å corresponds approximately to a secondary peak in the difference between the PMFs of the test molecules (Figs. 2 and S6). It correlates with the position of the bulky side chain of LYS41, which is likely responsible for the increased opportunity for polar interaction between the molecules and the protein (Fig. S9). Consistent with this, at this position hydrogen bond interactions between the protein and the trisaccharide are greater than for the disaccharide (Fig. 6).
• •The pore narrowing centered at z = 24 Å corresponds to the peak of the trisaccharide PMF but is not reflected in the disaccharide PMF. In this region, the unoccupied pore width varies little, and there is a substantially greater unfavorable interaction with the protein for the trisaccharide than for the disaccharide (Fig. 3). This is the region of interaction with ASP46, whose side chain, unlike that of LYS41, is quite rigid (Fig. S14), being stabilized by intersubunit salt bridges. It is tempting to infer that this region is the most important regarding the selective permeability of these molecules.

Configurational entropy can be a substantial contributor to the free energy of permeation for flexible molecules, unlike for atomic ions. For example, during Na⁺ or K⁺ permeation of ion channels, electrostatic interaction and hydration (e.g., replacement of water by charged groups) plays a major role in defining the PMF. By comparison, interactions that conformationally restrict a flexible molecule may incur a substantial entropic cost. Such considerations have been noted for interactions of glycerol in the narrow selectivity filter region of GlpF (64). To pass the selectivity region, glycerol must adopt a specific conformation and a specific orientation, which are defined and constrained by enthalpic and entropic effects arising from hydrogen bond interactions with the protein in the process. Accordingly, the energetic barrier to glycerol permeation spatially corresponds to increased hydrogen bond interactions, a somewhat counterintuitive finding, because one might expect that increased hydrogen bond interactions would tend to lower rather than raise the free energy (i.e., generate a well rather than a peak in the PMF). However, for flexible molecules and relatively small interaction energies, the balance between entropic cost and enthalpic benefit may be much closer than in ion-specific selectivity. We see a similar situation for the pore narrowing in the connexin channel that dominates the selectivity between the test molecules (z ≈ 24 Å); this region is also one of increased hydrogen bond interactions between the trisaccharide and the protein (Fig. 6). Also, the trisaccharide is much more flexible than glycerol, therefore the contribution of such an entropic penalty may be greater. These considerations may be fundamental to understanding the energetics of molecular as opposed to ionic selectivity; the consequences of the configurational flexibility of the molecules, particularly in situations where the enthalpic interactions are relatively weak. If the entropic cost in adopting the configuration/orientation that permits permeation at a “selectivity region” is too high, relative to the compensating enthalpic stabilization, it cannot proceed. In this view, hydrogen bonds between a prospective permeant and protein provide both energetic benefit and energetic cost as the molecule “works” at getting past a constriction; there is an enthalpic benefit in the hydrogen bonds transiently stabilizing a configuration (with an entropic cost), and an enthalpic cost as the hydrogen bonds are broken (with an entropic benefit) as a new configuration is sampled. The snapshots shown in Fig. 6 C and Movie S1 are consistent with such a process.

In addition to the conformational and orientational fluctuations of a permeant, side-chain fluctuations within the pore play a key role in molecular selectivity in this channel. The ASP46 side chain is rigid (has a low RMSF), unlike other pore-lining residues at narrow regions of the pore. Therefore, it cannot structurally adjust to the presence of a potential permeant, requiring that the molecule conform to a specific conformation/orientation (pay an entropic cost) to take advantage of the hydrogen-bonding opportunities the ASP side chain presents. Therefore, the structural fluctuations and associated entropic costs of both permeant and residue side chain play key roles in molecular permeation through this channel.

The above discussion points out that each region of pore constriction can have different effects on the magnitude and character of the interactions between each potential permeant and the pore. This provides a basis for the inferences from experiments that limiting pore width per se is not the key determinant of selective molecular permeation through connexin channels (12, 17). Instead, it appears that the nature of the specific interactions between the protein and the potential permeant, enabled or imposed by the narrowings, and modulated by the potential molecular permeant and the side-chain flexibility are what matter most. For flexible molecules in wide pores, hydrogen bond formation can impose a relatively large entropic effect/cost because of effects on configurational/rotational flexibility of the potential permeant. Thus, our simulations indicate that forces influencing permeation can be quite different for flexible organic versus atomic ion permeants.

Relation to previous MD work on connexins

Although a few studies have applied MD to investigate the electrical conductance and charge selectivity among atomic ions such as K⁺ and Cl⁻ in connexin channels (67, 68), only one has done so for a molecular permeant (69). MD studies by Zonta et al. examined permeation of the highly anionic molecule calcein through the Cx26 pore (69). The starting model of the channel differed in several aspects from that in our study, but the overall structure, character, and dynamics were similar. The main difference of significance was the status of the N-terminal methionine, which in our system was acetylated in accordance with MS/MS findings, eliminating the positive charge of the terminal amine. The PMF of calcein in the pore, like those in our study, showed a very broad peak, with no evidence of sites of stabilization (energy wells). However, the calcein PMF had a barrier of ∼45kT (∼27 kcal/mol), which would preclude permeation, whereas experimental measurements showed calcein to be somewhat permeable. It was suggested that the multiple anionic sites of calcein formed extensive salt bridges with several cationic residues within the pore, including the (unacetylated) terminal amine of MET1 and the LYS41 side chain. Elimination of the capacity of calcein to form salt bridges, by eliminating its charges in the model, reduced the calculated barrier to ∼20kT (∼12 kcal/mol). It was suggested that in the native connexin channel these charge interactions are dramatically reduced, perhaps because of charge-changing posttranslational modifications suggested by MS (including the acetylation of MET1 (20)) and/or other factors that affect the protonation state of the residues involved. In our study, LYS41 corresponds to the site of the most prominent position of potential polar interactions for the larger of the two molecules we tested (Fig. S9).

Implications for selectivity among biological permeants

How do these findings relate to the permeation of molecules through connexin channels in vivo? The test molecules assessed in this study are uncharged, maltosaccharide derivatives. Although the maltose structure occurs in nature, it is not found in the cytosol of animal cells so is not a “natural” connexin permeant; the molecules used in our study were employed to confirm a first-order, qualitative correspondence between experimental data and the computational system. Connexin channels are often regarded as nonselective pores with a simple size cutoff. If the difference in the permeability characteristics of the two tested molecules was strictly because of their difference in size, independent of any other factors, their interactions with the connexin protein would be a straightforward function of vdW interactions and size-dependent entropic cost. However, because they are flexible and capable of electrostatic interactions, the difference in their size (e.g., minimal diameter presented to the pore lumen) can lead to interactions of different character and magnitude because of differences in degree of approach to pore walls. Also, the additional saccharide unit of the trisaccharide provides greater opportunities for interaction, compared with the disaccharide. Put another way, a simple size cutoff would pertain only to potential permeants that are isotropic in structure and chemistry (i.e., spherical molecules with homogeneous solvent-exposed moieties). For other potential permeants, there will be selectivity that is not a function of size alone, but is a function of the molecular structure, flexibility, and chemistry and the associated entropic costs. In our study, for the tested molecules, this is illustrated by the differences in the force decomposition results, in the potential for polar interactions, in the different ways that the width of the pore lumen is affected, and the differences in hydrogen bond interactions.

The potential cellular vocabulary of connexin-permeant molecules is large, consisting of all cytosolic molecules that can present a minimal cross-sectional diameter less than the limiting pore width of a given connexin channel (taking into account the ability of a molecule to widen the pore, as demonstrated here). Few, if any, such molecules, are spherical. Some are uncharged (e.g., sugars, uncharged forms of cytosolic pH buffers), but most are either zwitterionic or have net charge. We demonstrate in this study the differences that can occur between two highly homologous uncharged polar molecules of slightly different minimal cross-sectional size and different degrees of flexibility. We show that even for these “uncharged” test molecules, there is a region at which polar interactions can be significant. The presence of charged moieties would greatly enhance the potential for selectivity.

Conclusions

This study provides qualitative validation of the Cx26 model and the MD approach to the study of molecular permeation though a connexin channel. Our work shows that application of US/H-REMD reproduces the permeant/nonpermeant properties of two molecules. The results highlight factors uniquely involved in permeation by molecules, as opposed to atomic ions. These include factors that arose from 1) mechanisms of selectivity involving lower-energy interactions, 2) “permeant” and side-chain flexibility, orientation, and anisotropy, and 3) a wider pore. The computed energetic barriers extend through most of the pore, as opposed to a narrow “selectivity filter” region. There is no significant binding (energy wells) of either the permeant or impermeant tested molecule. Pore width influences the PMFs of these molecules and differences between them, but other factors are strongly involved. For the tested molecules, the largest difference in the PMFs correlated with 1) differences in hydrogen-bonding between each molecule and the protein, direct or via intervening water, and 2) differences in the balance of forces between the molecules and water, protein and K⁺. It also correlated with the most rigid part of the pore lumen. A key factor in the energetic landscape is the consideration of entropic costs when dealing with molecules that can occupy many configurations and orientations. The results suggest that this system can be used to explore the molecular basis by which connexin channels select among (potential) permeating molecules, and how mutations alter the permeation process.

Author Contributions

Y.L., A.R., and A.H. designed research. Y.L. and A.R. performed simulations, analyzed data, and produced the figures and table. A.H., A.R., and Y.L. wrote the article.

Editor: Carmen Domene

Supporting Citations

References (70, 71, 72, 73) appear in the Supporting Material.