CUSUM-Logistic Regression Analysis for the Rapid Detection of Errors in Clinical Laboratory Test Results

Abstract

Objective

The main drawback of the periodic analysis of quality control (QC) material is that test performance is not monitored in time periods between QC analyses, potentially leading to the reporting of faulty test results. The objective of this study was to develop a patient based QC procedure for the more timely detection of test errors.

Method

Results from a Chem-14 panel measured on the Beckman LX20 analyzer were used to develop the model. Each test result was predicted from the other 13 members of the panel by multiple regression, which resulted in correlation coefficients between the predicted and measured result of >0.7 for 8 of the 14 tests. A logistic regression model, which utilized the measured test result, the predicted test result, the day of the week and time of day, was then developed for predicting test errors. The output of the logistic regression was tallied by a daily CUSUM approach and used to predict test errors, with a fixed specificity of 90%.

Results

The mean average run length (ARL) before error detection by CUSUM-Logistic regression (CSLR) was 20 with a mean sensitivity of 97%, which was considerably shorter than the mean ARL of 53 (sensitivity 87.5%) for a simple prediction model that only used the measured result for error detection.

Conclusion

A CUSUM-Logistic Regression analysis of patient laboratory data can be an effective approach for the rapid and sensitive detection of clinical laboratory errors.

1.0 Introduction

The periodic measurement of quality control (QC) material is the main practice used for monitoring the analytical performance of diagnostic tests [1]. A major drawback of this approach is that test performance is not monitored in the time periods between analysis of QC material. This can potentially result in the reporting of a large number of inaccurate test results until the problem is discovered, because QC material is often analyzed only once a day. The advent of advanced automation of chemistry analysers and their subsequent increase in sample throughput has further aggravated this problem and increased the need for the more timely monitoring of clinical laboratory tests.

Another common problem encountered in our current QC practices is that it typically depends on the use of non-commutable QC material. It is not uncommon to observe apparent shifts in test values of QC material but not in real specimens or, shifts in real specimens that are not reflected in QC material because of their different sample matrices [2,3]. Another limitation is that the use of standard QC material does not assess all the steps in the analysis of a specimen [4]. For example, it does not detect pre-analytical problems related to specimen collection or processing or postanalytical problems related to the calculation and reporting of test results.

The use of patient sample based QC procedures is an alternative approach for detecting test errors [5]. In 1965, Hoffman et al described the Average of Normals method in which the test results of a large number of patients falling within normal reference intervals are averaged and used to monitor potential changes in the testing process [6]. Later, Cembrowski et al [7] used computer simulation to demonstrate the primary factors affecting error detection by this method. Besides the number of patient values used to calculate the mean, the ratio of the standard deviation of the truncated patient population to the precision of an analytical method was a major factor in the sensitivity of error prediction. They also showed that the truncation limits should be chosen so that they exclude outliers but still include the majority of the patient test results within the central test distribution [7]. Other improvements to the Average of Normals approach include the exponentially weighted moving average and other computational methods for establishing a mean of a moving window of patient test results [5,8]. Although patient sample based QC procedures in theory provide a way to monitor analytical performance between QC runs, they are not widely used. This is largely due to the fact that for many less frequently ordered tests, the number of patient results that are needed to detect a clinically significant error is often greater than the number of patient samples that would typically be analyzed between QC runs for many clinical laboratories. This is also true for those tests with a wide reference range, which greatly limits the sensitivity of error detection by this method [5].

In this study, we describe a novel patient sample based QC procedure involving the use of CUSUM scoring and logistic regression, which we refer to as CUSUM-Logistic Regression (CSLR). In addition to monitoring the value of patient test results, it depends upon the inter-relationship between test results, as well as the time of day and day of the week that a test is performed. Using data from a standard clinical chemistry metabolic panel, we show that the CSLR approach is a relatively simple and sensitive method for using patient sample test results to monitor the performance of clinical laboratory tests between QC runs.

2 0 Materials and Methods

2.1 Clinical Laboratory Analysis

Laboratory test results from a commonly used Chem-14 metabolic chemistry panel (sodium (Na), potassium (K), chloride (Cl), urea (BUN), creatinine (Creat), bicarbonate (HCO3), alkaline phosphatase (ALP), alanine transaminase (ALT), aspartate transaminase (AST), glucose (Glu), albumin (Alb), calcium (Ca), total protein (TP), total bilirubin (TB)) were collected over a four year period. Samples were analyzed on the Synchron LX20 analyzer (Beckman Coulter, Atlanta GA 30326) at the Department of Laboratory Medicine, National Institutes of Health, Bethesda.

2.2 Modeling, Calculations and Statistical Analysis

Non-normally distributed data (ALP, ALT, AST, Glu, TB, Creat and BUN were log transformed before analysis. Using three years of reported test results (n=179,280), we established multiple regression models for predicting the value of one analyte based on the measured value of the 13 other members of the Chem-14 panel. This was done using stepwise forward multiple regression and included all covariates and interaction terms that had a T-ratio >10. The difference between the measured analyte and the predicted analyte from this calculation is referred to as the delta test result.

A full CUSUM-logistic regression (CSLR) model for error prediction was developed by using the measured test result, the delta test result, time of day, and day of week. A simple CSLR model that only included the measured test result was used to compare with the full CSLR model. To train the logistic regression models, a second set of reported laboratory test results from one year (n=53,607) were randomized so that half were mathematically transformed to simulate “bad” laboratory data containing test errors and the other half remained as untransformed “good” data. Either a fixed concentration value was added or subtracted from the measured test result or the measured test result was multiplied or divided by a fixed percentage to mathematically simulate test errors (Table 1) based on the current CLIA recommendations for the detection of total allowable errors [9].

Table 1.

Performance of the Full versus Simple CSLR Model in Error Prediction. The Average Run Length (ARL) needed to detect test results with either a low or high bias for the full and simple CSLR models. The sensitivity of error detection for each test is shown in parenthesis. Specificity was fixed at 90%. All differences in ARL between the full and simple model were hightly statistically significant (P<0.0001).

		Low Bias		High Bias
		Simple Model	Full Model	Simple Model	Full Model
Test	Error	ARL (Sens)	ARL (Sens)	ARL (Sens)	ARL (Sens)
Na	± 4 mmol/L	27 (100)	13 (100)	42 (94)	10 (100)
K	± 0.5 mmol/L	23 (100)	13 (100)	46 (92)	15 (100)
Cl	± 5%	28 (100)	4 (100)	28 (100)	8 (100)
HCO3*	± 10%	41 (99)	14 (100)	64 (73)	21 (99)
Ca	± 0.25 mmol/L	26 (100)	5 (100)	55 (78)	4 (100)
Alb	± 10%	60 (90)	27 (99)	129 (61)	25 (98)
TP	± 10%	42 (99)	15 (100)	110 (67)	18 (100)
ALP	± 30%	58 (80)	16 (100)	47 (94)	26 (91)
ALT	± 20%	86 (69)	27 (96)	76 (81)	33 (88)
AST	± 20%	66 (77)	19 (100)	62 (89)	25 (96)
TB	± 0.4 mg/dL	36 (98)	19 (100)	31 (100)	20 (100)
Creat	± 0.3 mg/dL	20 (100)	13 (100)	34 (99)	21 (100)
Glu	± 10%	87 (68)	31 (94)	55 (96)	40 (83)
BUN	± 2 mg/dL	49 (87)	37 (86)	63 (72)	40 (84)
Mean		46 (90)	18 (98)	60 (85)	22 (96)

^*No available CLIA error recommendation.

The output of the models varied from 0 to 1, which represents the probability of a test result containing an error. These probabilities were tallied, using a daily CUSUM approach [10]. This is simply calculated by subtracting the mean prediction score of “good” laboratory data from the prediction score for each new test and summing this with all the previous prediction scores to produce a cumulative or CUSUM score. The CUSUM score was reset to 0 each day at midnight. A straight line fitting the upper outer contour of the daily CUSUM plot for each analyte was used to establish a cut-point for error detection. This line was chosen so that the daily specificity of error detection would be 90%, meaning that a false positive would occur on average only once every 10 days. The mean average-run-length (ARL) before error detection was the main metric for comparison of the two models. The percent of daily runs with a simulated error that was correctly identified was used as a measure of the sensitivity of error detection. All data and statistical analyses were performed, using JMP software (SAS,Cary, NC 27513).

3.0 Results

3.1 Multiple Regression Model for Predicting Test Results

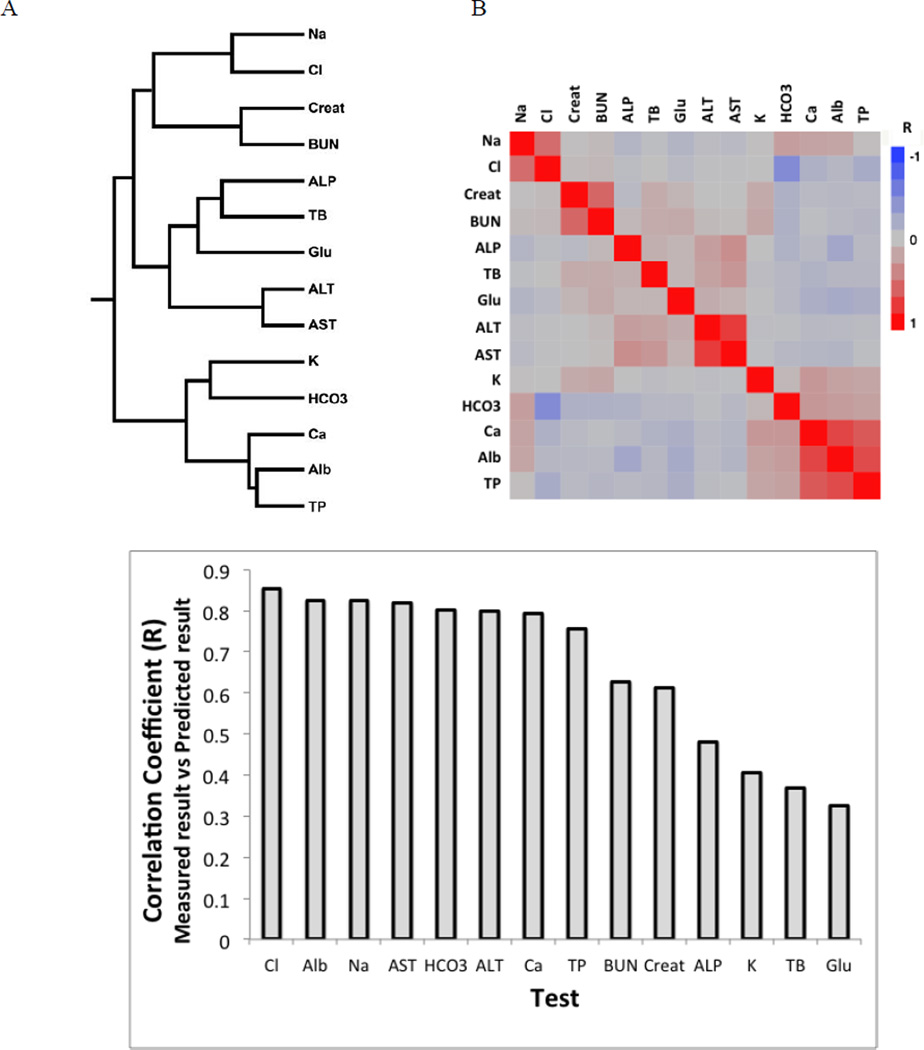
Because of the homeostatic and pathophysiologic relationships between test analytes there is often a close correlation between many different laboratory test results. Using hierarchical based clustering, this test inter-relationship for the Chem-14 test panel can be observed by their cluster pattern (Fig. 1A). Similar relationships were observed in the correlation coefficients between test pairs (Fig 1B). For example, Ca, Alb and TP formed a tight cluster, with all these tests positively correlated to each other. Based on these inter-relationships, we developed multiple regression models for predicting the value of each analyte based on the measured value of the 13 other members of the Chem-14 panel. As shown in Figure 1C, for more than half of the tests in the panel, the R-value for the correlation between the predicted and measured test result was greater than 0.7. The delta test result is calculated by subtracting the predicted test result from the measured test result. It can be viewed as a metric for the plausability of the measured test value given the other measured values in the test panel.

Figure 1. Inter-relationships between test results in Chem-14 panel.

(A)Heirarchial based clustering of Chem-14 panel test results. (B)Heat map showing relationship between test results panel based on linear correlation coefficients (R) between individual test pairs. (n=53,607). (C)Stepwise forward multiple regression was used to predict test result from the 13 other tests in the Chem-14 panel. The correlation coefficient (R) for the predicted result based on the multiple regression model versus the measured test result is shown on the Y-axis. (n=179,280).

3.2 Effect of Time on Test Result Distribution

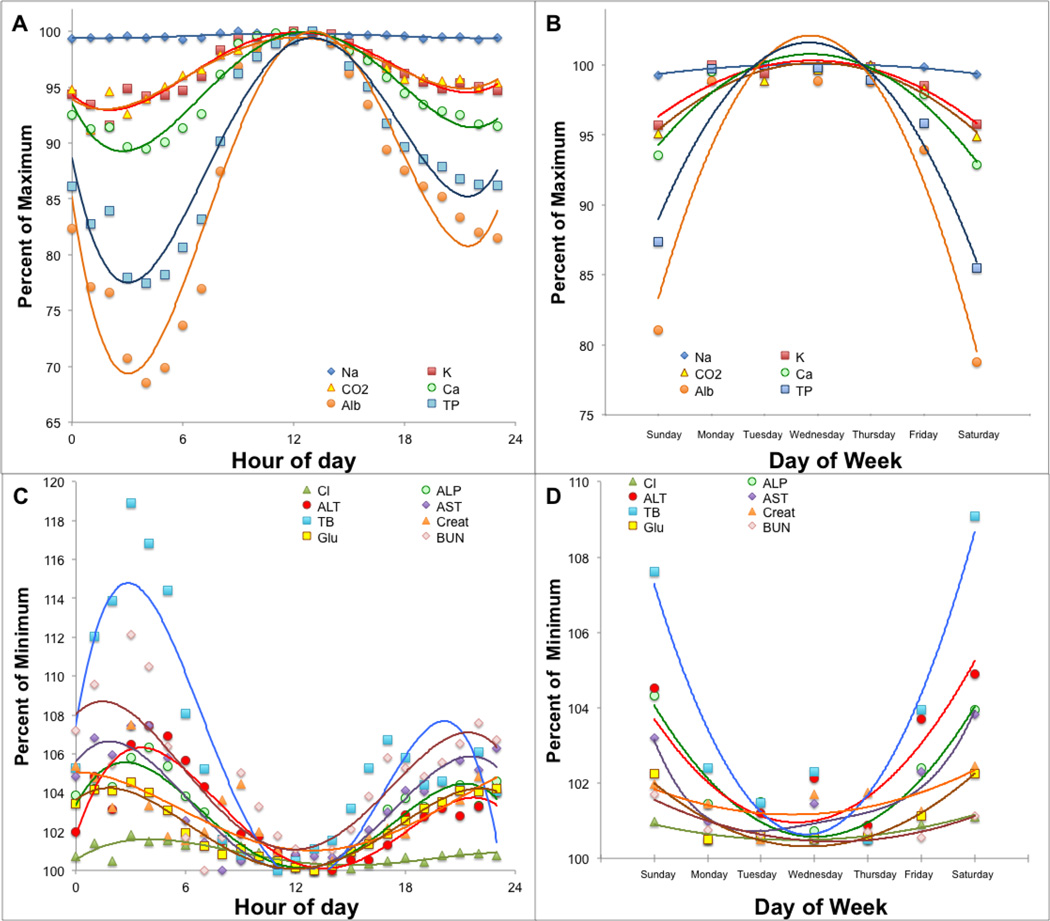
In Fig. 2, we plotted the hourly mean of the various tests. None of these analytes are thought to have significant diurnal variations; nevertheless, we observed a striking sigmoidal-like change in their hourly mean. One set of tests peaked at approximately noon (Fig. 2A) and had a nadir around 4AM, whereas the other set had a nadir at noon and peaked at about 4AM (Fig. 2C). We also noted that the majority of the test results at noon tended to fall in the middle of the reference range, whereas the test results in the evening and early morning hours were more likely to be outside of the reference range. These time dependent changes most likely reflect differences in the type of patient samples that are analyzed throughout the day. Our outpatient samples are mostly from relatively healthy individuals and are collected and processed during the late morning and early afternoon, whereas samples in the evening and midnight shifts are more often from hospitalized inpatients, who are more likely to be acutely ill and have abnormal test results.

Figure 2. Effect of time of day and day of the week on mean test results.

The hourly mean (Panel A and C) or daily mean (Panel B and D) of each test in the Chem-14 panel was calculated and plotted against time. Tests were grouped into 2 categories based on the differential effect of time on test result distributions (n=179,280)

Similarly, the effect of the day of the week on test result distribution was analyzed by plotting the daily mean throughout the week. The tests that peaked at noon were higher during the week but decreased on weekends (Fig. 2B). In contrast, those tests that showed a peak in the early morning were also the highest during the weekend and the lowest during the week (Fig. 2D). Again, this is likely due to changes in the distribution of patient samples analyzed during the week, with a greater number of healthy outpatients during the week and more from sicker inpatients on weekends.

3.3 Error Prediction by Logistic Regression Model

In order to improve upon the Average of Normal method for error prediction [5], we included additional information besides the measured test result in our analysis, namely the delta test result (difference between the measured and predicted test result), the time of day, and day of week. Because the 4 input variables for the full CSLR model contained both continuous and categorical data, logistic regression was used.

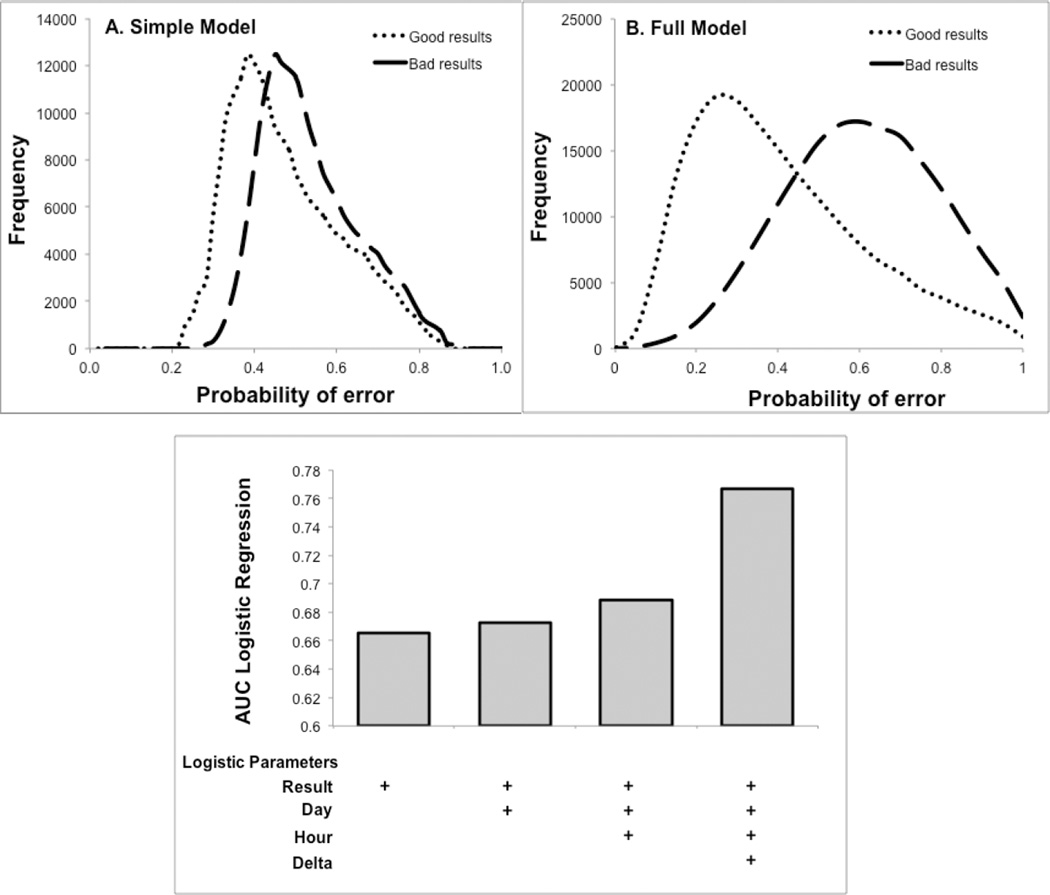
An example of logistic regression output for predicting a 10% proportional low bias in Alb is shown in Fig. 3. The bias results were generated by mathematically transforming the good Alb test results but not changing any of the other test values in the panel. The output for the logistic regression ranges from 0 (low probability of erorr) to 1 (high probability of error). Considerably less overlap was observed in the full CSLR model (Fig. 3B) than the simple CSLR model (Fig. 3A) in distinguishing between the good and mathematically transformed bad Alb test results, indicating superior error prediction. The contribution of each input variable for the full CSLR model was determined by calculating the area under the curve (AUC) by ROC analysis (Fig. 3C.). Based on the incremental improvement of the AUC values, the delta test value contributed the most to error prediction.

Figure 3. Difference in error prediction between full and simple CSLR models.

A 10% proportional low bias was introduced into reported “good” test results (n=53,607) to simulate “bad” test results and were analysed by the simple (Panel A) and the full (Panel B) CSLR model. The AUC of a ROC plot was calculated for distinguishing good versus bad Alb test results for the full CSLR model. This was done after stepwise inclusion of the four different input variables shown. (n=179,280) (Panel C).

3.4 CUSUM Scoring of Logistic Regression Model Output

Despite its superior error prediction, there was still sufficient overlap in the logistic regression output of the full CLSR model (Fig. 3B) to make error prediction based on a single test result not practically useful because of relatively low sensitivity and specificity. To address this problem, a running tally of the output of the logistic regression output was instead monitored for predicting errors. This was done by daily CUSUM scoring [9], which was reset to 0 each day at midnight. The CUSUM score is calculated by subtracting the mean logistic prediction score of “good” laboratory data from the logistic prediction score for each new test result and summing this with all the previous scores on that day to produce a daily cumulative or CUSUM score.

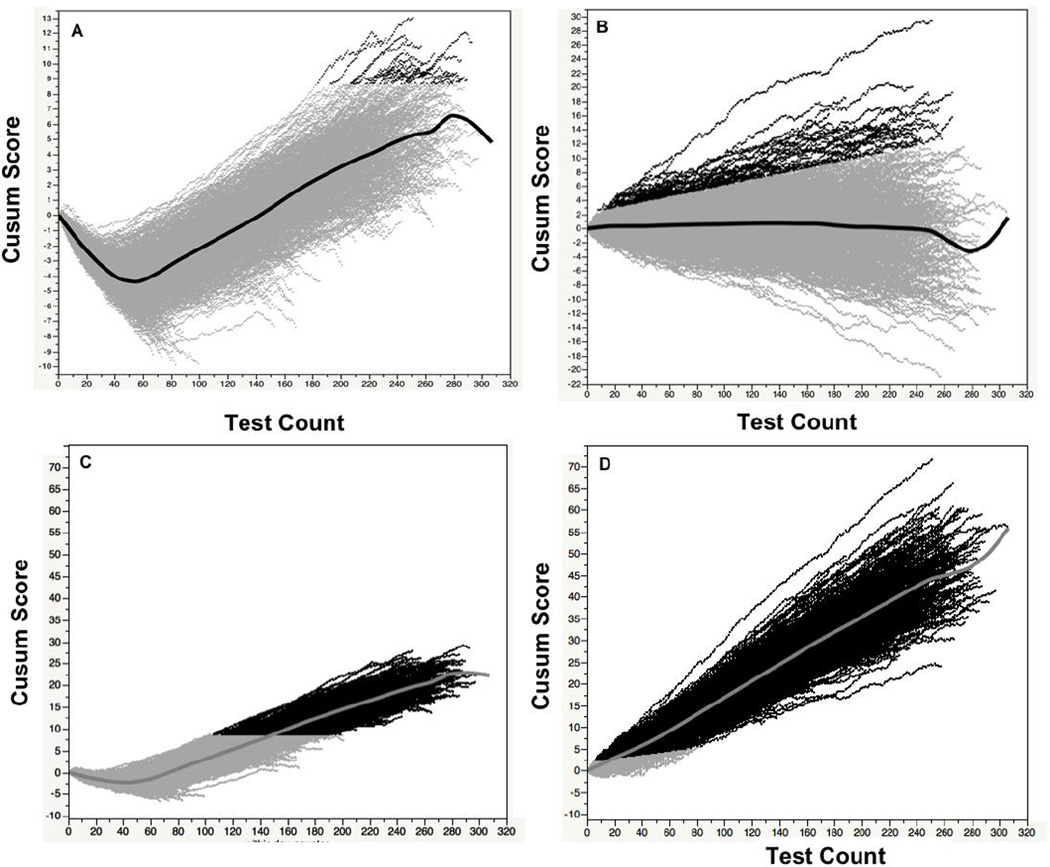
Fig. 4 shows a plot of the daily CUSUM score over a 3-year period for the full and simple CSLR models for good and bad Alb test results, with a 10% proportional high bias. Initially, the CUSUM score for good Alb test data with the simple model decreases and then later increases, corresponding to the drop in mean Alb values seen at night and the later increase in Alb seen during the day (Fig. 4A). Because of this time dependent change, it makes it difficult to establish a single sensitive cut-point for error detection with the simple CSLR model. Using a horizontal time-independent line, a cutpoint was chosen for the simple model of good Alb test results to yield a specificity of 90%, so that one false positive event would occur on average once every 10 days. In contrast, for the full CSLR model (Fig. 4B), which is adjusted for both time of day and day of week, the CUSUM scores for albumin do not show a time dependence and deviates around 0 throughout the day for the good Alb test results. A time dependent linear line was empirically fitted to the outer contour of this plot to achieve a specificity of 90%. The different cut-offs were then applied to bad Alb test results for both the simple (Fig. 4C) and the full CSLR model (Fig. 4D). For the full CSLR model, an error was correctly predicted in nearly all (98%) of the daily runs containing bad Alb test data. The majority of the daily runs with an error that were not detected occured on the weekends when only a small number of samples were analyzed. The number of bad test results needed for error detection varied from as few as 7 to as many as 80. In contrast, for the simple model an error was detected in only 61% of the daily runs of bad Alb test results and typically required much longer run lengths between 87 to 172 samples

Figure 4. Daily CUSUM scores for albumin.

The daily CUSUM score for Alb was calculated for either good Alb (Panel A and B) or bad (10% high bias) Alb test results (Panel C and D) for the simple (Panel A and C) and full CSLR model (Panel B and D). Dark points show CUSUM scores that exceed the cutpoint for error detection. Central line shows mean Cusum score versus test count. (n=1093 days)

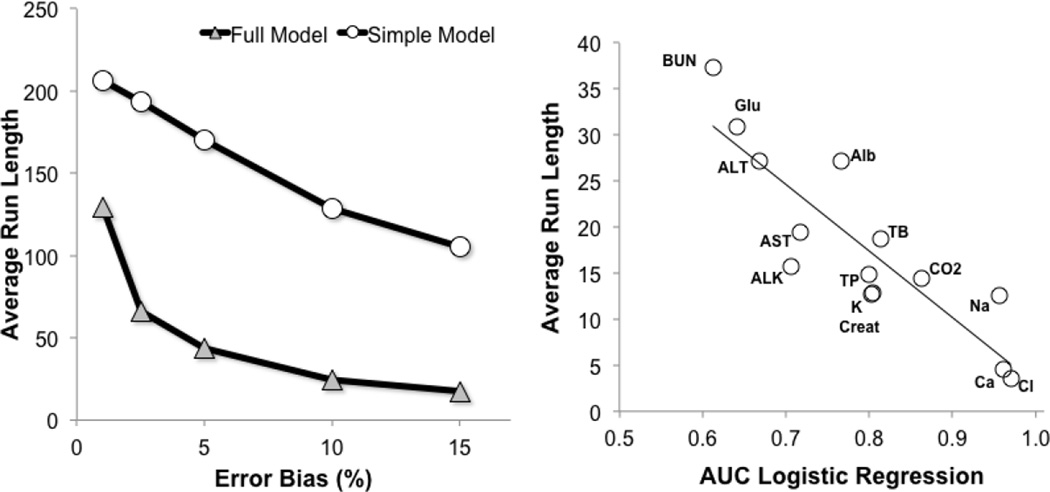
In Fig.5A, we varied the amount of the proportional error in the Alb test results to determine the effect of error magnitude on the sensitivity of detection. As before, a cutpoint with a fixed specificity of 90% was chosen. As would be expected, the average-run-length (ARL), in other words the mean number of samples needed before error detection, decreased with increasing error magnitude for both the full and simple CSLR models. Regardless of the degree of error, the ARL was substantially less for the full CSLR model than the simple model. For example, at a 10% high bias, the ARL for the full CSLR model was 25, but was 129 for the simple CSLR model. The relatively small sample size of 25 needed to detect an error in Alb for the full CSLR model means that the error should be rapidly detected within a few hours or less, depending on the test volume.

Figure 5. Relationship between magnitude of test error and ARL.

Good Alb test results were mathematically transformed to simulate various amounts of high bias as shown on the X-axis. The ARL for error detection was calculated for the simple (circle) and full (triangle) models. (Panel A, n=179,280). For each of the indicated tests, the AUC for error prediction was plotted against the ARL for error prediction for high biased tests containing errors shown in Table 1. (Panel B, n=179,280).

At a fixed specificity of 90%, the ARLs for each analyte in the Chem-14 panel for detecting the total error goals recommend by CLIA are shown in Table 1. The two error prediction models were tested for results with either a high or a low bias. In every instance, the ARL for the full CSLR model was significantly smaller than the simple model. On average the the ARL was approximatley 60% less for the full than the simple model but varied depending on the test. Most of the tests for the full CSLR model had an ARL of approximately 30 or less, which should allow for timely error detection. In contrast, the ARLs for the simple model were often much longer and for some tests were over 100. As expected, we observed a close relationship between the AUC for error prediction and the ARL (Fig. 5B). The deviation about the regression line between AUC and ARL in Fig. 5B is most likely due to differences in the magnitude of the error detection selected for each test.

In addition to having a smaller ARL, the full CSLR model had overall superior sensitivity in error prediction than the simple model (Table 1). This was calculated as the percent of daily runs containing laboratory errors that were correctly identified. The full model identified nearly all the daily runs with bad results with sensitivities that were close to 90% or better. The majority of the false negatives predictions for the full CSLR model occurred on weekends when the total test counts were sometimes less than the ARL. Thus, with the same specificity of 90%, the full CSLR model was both more timely (lower ARL’s), and more sensitive than the simple model in test error prediction.

4.0 Discussion

QC procedures for monitoring the production of most manufactured goods is conceptally more straight forward. The desired specifications of any given product can be defined a priori and then be monitored in real time to determine if they are being met during the manufacturing process. This approach is obviously not appplicable for clinical laboratory testing and we instead usually monitor QC material and not patient samples. To control costs and improve sample throughput, QC material is only analyzed periodically, thus creating a problem when a systematic analytical error occurs between QC runs. Until an error is detected, inaccurate test results may be reported, leading to medical errors in patient care. Except for monitoring alert values and the visual inspection of test results, which have limited scope and value, most clinical laboratories do not have a systematic way for detecting test errors between QC runs. Once an analytical problem is detected by QC material, it is common practice to reanalyze all the preceding patient samples, since the last good QC run. This, however, may not occur until after several hours or even days of reporting erroneous test results. Therefore, the monitoring of patient test results for errors is an attractive approach for addressing this problem. This strategy also has the advantages over the use of conventional QC material of not having matrix commutability problems [2,3], and it also assesses both pre and post-analytical phases of clinical laboratory testing. Despite the many advantages of patient sample based QC monitoring, it is not widely used because it is relatively insensitive and for many analytes will often require a larger number of samples than what is typically analyzed between QC runs [5].

In this study, we improved upon the conventional approach of patient sample based QC monitoring by incorporating additional information, which makes our test error predictions more sensitive and thus more timely. Most patient sample based QC approaches only monitor a moving mean of patient test results [5]. In addition, to this parameter, we added the delta test result between a predicted and the measured test result, the time of day, and the day of the week to our error prediction model. By using this additional information, error prediction by CUSUM scoring of a logistic regression model was more sensitive and had lower ARLs (Table 1). Depending on the test, ARL’s between 4–40 were sufficient for detecting medically relevant errors with the full CSLR model (Table 1), which should allow for the rapid and timely detection of test errors.

Based on ROC analysis (Fig. 3C), the difference between the predicted and measured result, the delta test value, added more predictive value for error detection than did the time of day or day of week. Error prediction, however, could be further improved by adding other tests and information besides those examined in this study. We only examined the Chem-14 panel because it is widely used, but other sets of tests both smaller and larger could potentially be used for this type of analysis. For example, TB, which had a relatively high ARL in our study, would likely be considerably improved if unconjugated bilirubin was added to the prediction model, because these two tests are well known to be highly correlated. Other areas besides general chemistry, such as thyroid function tests and other endocrine tests, which are also often highly correlated, could also benefit from this approach. It is possible, however, when large panels are used that multiple errors could simultaneously exist and the different errors could potentially compensate for each other and detoriate error detection.

Although the time of day and day of week parameters did not appear to improve the AUC for predicting errors as much as the delta test result (Fig. 3C), this is somewhat misleading, because without these time dependent variables the CUSUM scoring would not have been as sensitive or specific (Fig. 4). Because CUSUM is a cumulative score, it is highly sensitive but is prone to many false positives [9]. This is the reason that most patient sample based approaches for monitoring errors have used a moving mean of results for detecting errors. Adjusting the output of the logistic regression model with the two time parameters (time-of-day and day-of-week) smoothed out the daily CUSUM score, which was not possible in the simple model that had an output that varied with time (Fig 4). Because time in our model is mostly just a surrogate for the type of patient samples being analyzed, one could perhaps further improve error detection by also including other patient based information, such as the hospital unit and ordering physician into the prediction model. There are also many other factors related to the patient that are readily available in most hospital and or clinical laboratory information systems that could also improve error prediction, such as age, sex and the diagnosis of the patient.

Because many clinical laboratories have multiple instruments for critical tests, the CSLR approach could be used to compare instruments. If the CUSUM score of a particular instrument starts to deviate relative to other identical instruments analyzing the same type of samples, a potential analytical problem may have occured. Based on current regulatory requirements, most clinical laboratories only compare the test output of multiple instruments on patient samples a few times a year. Thus, the daily monitoring of the CUSUM score could facilitate the more timely identification of an instrument with a test output that starts to deviate relative to another instrument.

It is critical that any algorithm for predicting laboratory errors have a low false positive rate. This is because analytical problems leading to major shifts in patient results are relatively rare [4,11]. We arbitrarily chose a detection limit with a specificity of 90% so that a false positive would occur only once every 10 days. When a possible error is detected by this approach, the analysis of patient samples should be paused and standard QC material analyzed. If a test appears out of control based on QC material, measures should be taken to correct the problem and past patient samples should be re-analyzed based on when the CSLR model first predicted an error. If there does not appear to be a problem with the QC material, the output from the CSLR model should be considered a false positive, and patient sample testing can be resumed. For some tests that are perhaps less robust or for which the consequences of a laboratory error have greater negative medical consequences, it may be preferable to have a higher false positive rate. If a higher false positive rate is used, this would lead to even lower ARLs and likely greater sensitivities and even faster error detection. Another consideration would be to set the false positive rate so that it would occur on average at least once a day. CSLR analysis could then be used to determine when to analyze standard QC material rather than analyzing it a fixed time intervals, which should further lower the ARL and improve the sensitivity of error detection.

In terms of implementing CSLR analysis, a major hurdle will likely be software. The ongoing improvement in computer processing speed and the ability to customize software, however, should facilitate this process. Middleware, which acts as a real-time conduit of information between the laboratory information system and chemistry analyzers, would be a natural site to install the needed software. Many chemistry analyzers, in fact, now already contain middleware with user definable rules for monitoring a daily mean of test results, which could be modified to implement this approach.

In summary, we describe a novel procedure for monitoring patient laboratory data for test error detection. It is based on a combined CUSUM-Logistic Regression approach, and the number of patient samples needed to detect errors from patient test samples are considerably less than other competing methods. The use of CSLR analysis could significantly improve the accuracy of clinical laboratory testing and reduce the frequency of test errors, without adding considerable costs or significant time delays.

Highlights.

• Laboratory test errors between QC runs can remain undetected for long periods.

• A lengthy delay in detecting errors may lead to medical errors.

• Traditional moving mean methods of using patient samples for QC are not timely.

• We describe a rapid method of using patient samples for test error detection.

Abbreviations

QC

Quality Control

CUSUM

Cumulative sum of means

Na

sodium

K

potassium

Cl

chloride

BUN

urea

Creat

creatinine

HCO₃

bicarbonate

ALP

alkaline phosphatase

ALT

alanine transaminase

AST

aspartate transaminae

Glu

glucose

Alb

albumin

Ca

calcium

TP

total protein

TB

total bilirubin