Improved prediction of drug-target interactions using regularized least squares integrating with kernel fusion technique

Abstract

Identification of drug-target interactions (DTI) is a central task in drug discovery processes. In this work, a simple but effective regularized least squares integrating with nonlinear kernel fusion (RLS-KF) algorithm is proposed to perform DTI predictions. Using benchmark DTI datasets, our proposed algorithm achieves the state-of-the-art results with area under precision-recall curve (AUPR) of 0.915, 0.925, 0.853 and 0.909 for enzymes, ion channels (IC), G protein-coupled receptors (GPCR) and nuclear receptors (NR) based on 10 fold cross-validation. The performance can further be improved by using a recalculated kernel matrix, especially for the small set of nuclear receptors with AUPR of 0.945. Importantly, most of the top ranked interaction predictions can be validated by experimental data reported in the literature, bioassay results in the PubChem BioAssay database, as well as other previous studies. Our analysis suggests that the proposed RLS-KF is helpful for studying DTI, drug repositioning as well as polypharmacology, and may help to accelerate drug discovery by identifying novel drug targets.

Graphical Abstract

Flowchart of the proposed RLS-KF algorithm for drug-target interaction predictions.

1. Introduction

Identifying interactions between chemical compounds and target proteins plays a fundamental role in drug discovery processes. Pharmaceutical companies, on the one hand, would like, as soon as possible, to detect hidden adverse events (such as adverse drug reactions), which has been a major global health concern, causing side effects, hospitalizations, even deaths [1]. On the other hand, they also would like to explore adverse events to find new applications [2] (drug repositioning or drug repurposing). Both of the purposes can be attributed to accurately identify the potential drug-target interactions (DTI). It is well known that experimental validation of interactions is costly and laborious. Therefore, application of in silico methods for this challenge is needed.

Several traditional methods [3, 4], such as ligand-based QSAR (quantitative structure-activity relationship) and receptor-based docking, are often used to predict DTI. However, they often have limitations. For QSAR, its performance might be decreased when the training samples are not enough. For docking, it largely depends on the 3D crystal structures of protein targets. Therefore, it is difficult to study DTI for membrane proteins due to the limited number of known 3D structures. In addition, docking-based methods are not computationally efficient and previous studies mostly focused on one single target. With the advent of chemogenomics research accelerated by high-throughput screening (HTS) campaigns of large-scale chemical libraries and the completion of human genome project, more chemical and genomic data are now publicly available, which enables researchers to study DTI at a large scale, such as studying interactions among multiple drugs and multiple targets using computational approaches.

In 2008, Yamanishi and colleagues [5] proposed a bipartite network method for the integration of chemical and genomic spaces to predict DTI of four classes of protein targets, i.e., enzymes, ion channels (IC), G protein-coupled receptors (GPCR) and nuclear receptors (NR). Their models suggested many potential interaction pairs between drugs and targets. As a following study, Bleakley et al. [6] proposed a novel supervised inference method to predict unknown drug-target interactions from the same datasets used by Yamanishi and co-workers. Their kernel-based models using support vector machine (SVM) transformed the edge-prediction problem into the binary classification problem of points with label. Results from their models gave high performance in terms of AUC (area under receiver operating characteristic curve) and AUPR (area under precision-recall curve).

van Laarhoven et al. [7] used a simple machine learning method called (kernel) regularized least squares (RLS) to predict DTI by using only the topological information from the adjacency matrix of drug-target network. Then they defined a kernel on the topology profiles, called Gaussian interaction profile (GIP) kernel. Using the only defined kernel, results from their models exhibited a significant improvement for AUPR over results of the state-of-the-art methods at that time. Furthermore, they found that by combining the topological information with others (such as chemical and genomic information), the performance could further be improved. However, their method was focusing on the setting where both drugs and targets are known, which means that they used known interactions for predicting novel ones. Thus, for the situation where both drugs and targets are new (meaning that there are not interactions between them), these models are not feasible. In order to overcome such limitation, Mei and co-workers [8] introduced a neighbor-based interaction-profile inferring (NII) method and integrated it into the existing bipartite local model (called BLM-NII). By incorporating NII algorithm, the performance of DTI predictions for the four benchmark datasets presented a significant improvement, which turned out to be the best results.

Apart from the aforementioned popular methods for predicting DTI, various novel statistical methods were also proposed, such as restricted Boltzmann machines [9], Bayesian matrix factorization [10], even ranking-based method [11]. All these methods exhibited good performance but those kernel-based methods have been the most popular ones.

It is noted that the previous kernel-based methods [7, 8] for DTI predictions used only a simple linear combination of different kernels as input to form final kernel matrix. However, that approach may not be appropriate when linear relationship is not evident among kernels. Thus, in this work, we explored a nonlinear kernel fusion (KF) technique, which was originally applied successfully in patient similarity network by Wang et al. [12], to combine different kernels for predicting DTI. The kernel fusion algorithm can derive both shared and complementary information from various kernel matrices, even those from a small number of samples. In order to validate the effectiveness of our proposed algorithm, we integrated a simple but effective regularized least squares (incorporating NII) with novel nonlinear kernel fusing (RLS-KF) technique, and compared the results of DTI predictions for the four benchmark DTI datasets [5] with those from previously reported methods. Moreover, we recalculated the kernel matrices of drug compounds and target proteins, and results based on this exhibited a further improvement especially for the small NR dataset. Importantly, most of the top predicted interaction pairs have been successfully validated by either experimental data reported in the literature, confirmatory assay results in the PubChem BioAssay database, as well as by results in other previous studies.

2. Material and experimental methods

2.1. Dataset

Four drug-target interaction networks, including enzymes, ion channels, G protein-coupled receptors and nuclear receptors in human, originally studied by Yamanishi et al. [5], were used as the benchmark datasets in the current work. These interaction information was retrieved from KEGG BRITE [12], BRENDA [13], SuperTarget [14] and DrugBank [15] databases. Protein sequences of the target proteins were obtained from the KEGG GENES database [12]. Target sequence similarity matrices (denoted by S^t, which is an M by M square matrix, where M denotes the number of targets) between proteins were computed using a normalized version of Smith-Waterman score [16]. Chemical compounds were derived from the KEGG DRUG and COMPOUND databases [12]. Chemical structure similarity matrices (denoted by S^d, which is an N by N square matrix, where N denotes the number of drugs) between compounds were computed using the SIMCOMP tool [17]. The M by N adjacency matrix, Y, where Y_ij = 1 if drug i interacts with target j, and Y_ij = 0 otherwise, was the same to that used in the previous study [5]. Table 1 lists the summary of all four datasets.

Table 1.

Summary of the four benchmark datasets.

Data	Enzymes	IC	GPCR	NR
Number of targets	664	204	95	26
Number of drugs	445	210	223	54
Number of interactions	2926	1476	635	90

2.2. Problem formalization

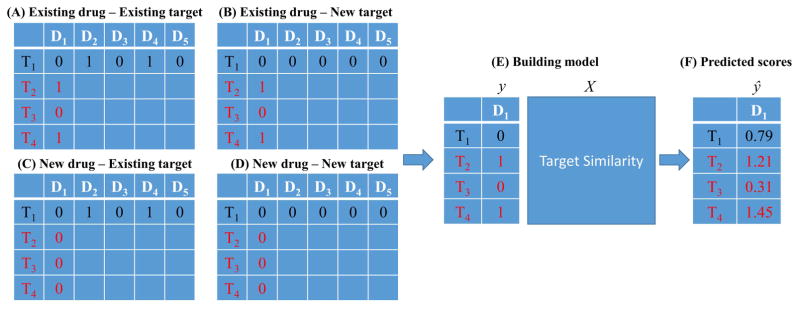
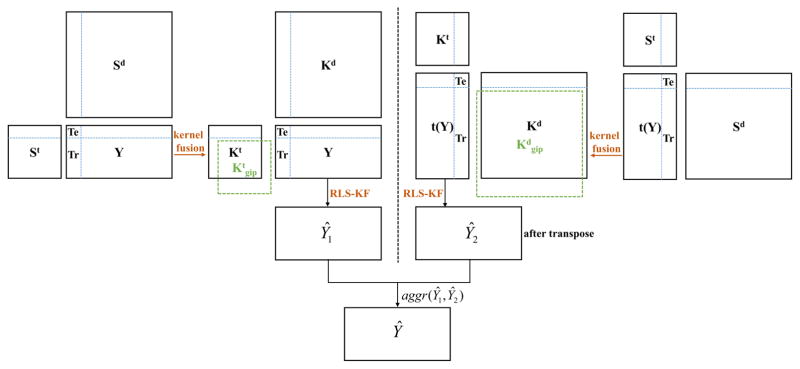
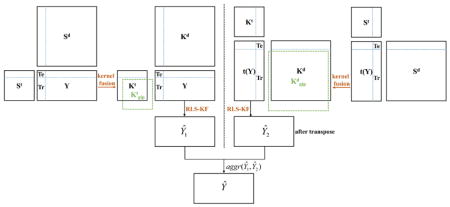
Given three matrices, S^t, S^d and Y, the task is how to make use of them to predict interactions between drug compounds and target proteins, which includes four scenarios of interactions between existing/new drugs and targets as described in the literature [8]. A brief diagram (Fig. 1) is given to explain the notation of existing/new drugs and targets, which assumes there are 4 targets (T₁ through T₄) and 5 drugs (D₁ through D₅) in total. Taking the first drug, D₁, as a query drug, the purpose of current work is to predict if D₁ interacts with T₁ (in the test set) by using the related information from the training set (labelled in red). If there is at least one interaction known between D₁ and any target from T₂ through T₄, then the current query drug is denoted as an existing drug (Figs. 1A and 1B), or a new drug otherwise (Figs. 1C and 1D). Similarly for the definition of existing targets and new targets, if there is at least one interaction between T₁ (in the test set) and any drug from D₁ through D₅, the current target is denoted as an existing target (Figs. 1A and 1C), or a new target otherwise (Figs. 1B and 1D). Thus, four scenarios are (A) existing drug – existing target, (B) existing drug – new target, (C) new drug – existing target and (D) new drug – new target. After determining one of these four scenarios, the prediction model is built (Fig. 1E) using the proposed RLS-KF algorithm, and finally the algorithm assigns a score to a drug-target pair (Fig. 1F) estimating the likelihood of an interaction between them, whereas the higher score is, the more likely the drug and target interact with each other. For other query drugs, they follow the same process. The complete flowchart of the proposed RLS-KF algorithm for DTI predictions is shown in Fig. 2.

Fig. 1.

Brief diagram of four scenarios for DTI predictions.

Fig. 2.

Flowchart of the proposed RLS-KF algorithm for DTI predictions.

2.3. Gaussian kernel of adjacency matrix Y

Given the adjacency matrix Y indicating the interaction profiles between drugs and targets, the Gaussian kernel between targets was calculated using the following equation:

$$K_{\mathit{gip}}(t_i,t_j)=exp(-\frac{{\Vert Y_{ti}-Y_{tj}\Vert }^2}{\sigma })$$ (1)

Where Y_ti (or Y_tj) is the interaction profile for the current target i (or j) with drugs, ||·|| denotes the Euclidean distance between Y_ti and Y_tj, and σ is the kernel bandwidth. Generally, the kernel bandwidth can be determined by cross-validation, here in this work we just set it as the average interaction number for each target as described in the previous work [7]. Finally, the Gaussian interaction kernel for targets, denoted by K^t_gip (see Fig. 2, left panel), is an M by M symmetric matrix where M is the total number of targets. It should be noted that K^t_gip had to be recalculated since the adjacency Y matrix changed when performing cross-validation prediction. Likewise, the Gaussian interaction kernel matrix for drugs, denoted by K^d_gip (an N by N symmetric matrix where N is the total number of drugs), was obtained in the same way (see Fig. 2, right panel). The details for calculating the Gaussian kernel can be referred to this literature [7].

2.4. Fusion of kernel matrices

The similarity matrices for targets and drugs, S^t and S^d, were first converted into kernel matrices by two simple steps: (1) making them symmetric using the following formula, S_sym = (S + S^T) / 2, where S^T denotes the transpose of S; (2) making them positive semi-definite by adding a small multiple of identity matrix as described in the work by van Laarhoven et al. [7]. The original S^t and S^d were subsequently converted into K^t and K^d (see Fig. 2). Different from the work by Mei et al. [8], which combined the Gaussian kernel matrix with chemical and genomic kernel matrices using a simple linear combination method by setting a weight parameter α (usually 0.5), in the work, the nonlinear kernel fusion technology was adopted. Given four kernel matrices, K^t, K^d, K^t_gip and K^d_gip, two kinds of fused matrices were obtained, respectively: (1) between K^t and K^t_gip, denoted by K^t_kf and (2) between K^d and K^d_gip, denoted by K^d_kf (see Fig. 2). The basic fusion process is described as what follows below (here, taking the fusion steps between K^t and K^t_gip as an example, whereas fusion between K^d and K^d_gip follows the similar process). First, these kernel matrices were normalized by dividing by the sum of the rows, such that each row of normalized matrix sums to one and then the normalized matrices were symmetrized as described above. The resulting matrices were denoted by P⁽¹⁾, and P⁽²⁾, respectively for K^t and K^t_gip. Secondly, local similarity matrix for each P matrix was calculated by the following equation:

$$L(i,j)=\{\begin{array}{r}\hfill \frac{P(i,j)}{{\sum }_{k\in N_i}P(i,k)},j\in N_i\\ \hfill 0,\mathit{others}\end{array}$$ (2)

Where N_i denotes the nearest neighbors of the current target i, and the number of nearest neighbors (k) should be set by user (in this work k = 4). It can be noted that this operation made the similarities among non-nearest neighbors to zero. The generated matrices were denoted by L⁽¹⁾ and L⁽²⁾, respectively, for P⁽¹⁾ and P⁽²⁾. Thirdly, the key step of fusion operation was an iteration process and it was performed as follows:

$$P_{t+1}^{(1)}=L^{(1)}{P}_t^{(2)}{(L^{(1)})}^T$$ (3)

$$P_{t+1}^{(2)}=L^{(2)}{P}_t^{(1)}{(L^{(2)})}^T$$ (4)

Where P⁽¹⁾_t+1 is the status matrix of target kernel (K^t) after t iterations, while P⁽²⁾_t+1 is the status matrix of the Gaussian-based kernel (K^t_gip). It should be noted that in the each iteration, the status matrices, P⁽¹⁾_t and P⁽²⁾ _t, were further changed as follows: P⁽¹⁾_t = P⁽¹⁾_t+1+ I and P⁽²⁾_t = P⁽²⁾_t+1+ I, where I denotes identity matrix. After that, both P⁽¹⁾_t and P⁽²⁾_t were further symmetrized as described before, respectively. The resulting status matrices were used in the next iteration. Here, the iteration step t should be set by user (in this work t = 2). After t steps, the two final status matrices (P⁽¹⁾_t and P⁽²⁾_t) were averaged (i.e., K^t_kf = (P⁽¹⁾_t + P⁽²⁾_t) / 2) and then K^t_kf was normalized as before. At last, K^t_kf was further transformed as follows: K^t_kf = (K^t_kf + (K^t_kf)^T + I) / 2), where (K^t_kf)^T denotes the transpose of K^t_kf and I is identity matrix. For drugs, after applying the same steps, we can also obtain the final kernel matrix, K^d_kf. More detailed description of the fusion process was described in the work by Wang and co-workers [18].

2.5. Regularized least squares integrating with kernel fusion matrix

A simple but effective machine learning method, regularized least squares, was used to train the models. As described in the literature [19], the algorithm can be formulated by optimizing the choice coefficient c, which has a closed-form solution as follows:

$$c^{\ast }={(K_{Tr}+\lambda I)}^{-1}{y}_{Tr}$$ (5)

Where K_Tr is the (N_Tr by N_Tr, where N_Tr denotes the number of samples in the training set) kernel matrix of the training set, and λ is a tuning parameter (set to 1 in this work). After solving the choice coefficient, the prediction in the test set can be easily obtained using the following equation:

$${\widehat{y}}_{Te}=K_{Te}{c}^{\ast }$$ (6)

Where K_Te is the (N_Te by N_Tr, where N_Te denotes the number of samples in the test set) matrix of the test set (see Fig. 2).

The flowchart for current DTI predictions is described in Fig. 2, where the left panel shows the prediction based on targets, and the right panel shows the prediction based on drugs. Thus, two predicted matrices, Ŷ₁ and Ŷ₂, can be obtained. Then an aggregation function, aggr(Ŷ₁, Ŷ₂), was used to derive the final prediction Ŷ. Herein, the average and maximum aggregation functions were used similarly to the previous studies [7, 8].

The current algorithm absorbed the NII idea [8] in order to predict interactions from new drugs (or new targets). The key idea of NII is summarized as follows. When the current output profile values (one of columns of Y), y_Tr, are all zeros (e.g., see Fig. 1C and Fig. 1D), which means that the current query drug does not interact with any target at all, the choice coefficient cannot be appropriately obtained using equation 5. To resolve this need, a putative interaction profile can be obtained by NII described as the following (taking target-based prediction (shown on the left panel in Fig. 2) as an example):

$$I^{di}=\sum _{k=1}^N{Y}_{.,k}{K}_{ki}^d$$ (7)

Where K^d_ki denotes the chemical structure similarity score for the current drug i and drug k, and I^di is the putative interaction profile for current drug i. After that, I^di was further scaled to [0, 1] using the following equation.

$$I^{di}=\frac{I^{di}-min(I^{di})}{max(I^{di})-min(I^{di})}$$ (8)

Thus, the putative interaction profile I^di can be used as y_Tr in equation 5 to derive the choice coefficient. It should also be noted that when the protein target was new (e.g., see Figs. 1B and 1D), which means there was no interaction between this protein and any drugs, the prediction in the test set was obtained using K^t itself in order to reduce noise (that is ŷ_Te = K^tc^* for the test set, see equation 6), rather than K^t_kf (taking target-based prediction as an example, which is shown in the left panel of Fig. 2). The proposed RLS-KF algorithm implemented in R language [20], can be downloaded in the github (https://github.com/minghao2016/RLS-KF)

3. Results and discussion

3.1. Kernel matrices of four DTI datasets

Recently, kernel-based methods have been popular in various fields due to its high performance. It is well known that the choice of an effective kernel plays a key role in kernel methods. In this work, we first check kernel properties (positive semi-definite for the KF operation) of four similarity matrices in the benchmark datasets (enzymes, IC, GPCR and NR) to satisfy our proposed algorithm. As a result, all four similarity matrices for drug target sequences are already positive semi-definite, thus they are taken directly as the kernel matrices without any change. However, for the similarity matrices for drug compounds this is not the case. For the NR dataset, once we make the matrices symmetric, it is already positive semi-definite, while for GPCR, IC and enzymes, we need to perform two steps as described in the method to obtain appropriate kernel matrices. For the adjacency matrix, we calculate the Gaussian kernel matrix between objects based on the interaction profiles, since it has been reported this kernel can improve prediction performance when comparing with other kernels such as those based on correlation or inner products [7].

3.2. Parameter

In our work, the proposed kernel fusion technique requires two hyper-parameters. The first one is the number of nearest neighbor (denoted by k, in this work we simply set k = 4 for all tests) when constructing local similarity matrix in equation 2. It should be pointed out when there are multiple nearest neighbors with equal values at top k, we keep them all (considering all of them to be equally important), which is different from the work from Wang et al. [18], where they adopted only one of these equal nearest neighbor values. As a result when we set k to 4, the non-zero neighbors may be more than 4 in a row of the local matrix if multiple equal nearest neighbors co-exist. The second hyper-parameter of KF is the number of iteration (denoted by t, in this work we simply set t = 2 for all tests). It is noteworthy that the k and t values in this work are relatively small indicating that the KF process is computationally efficient. The other two hyper-parameters, σ and λ, used in equations 1 and 5 respectively, were set empirically in this work as described above.

3.3. Evaluation of the proposed RLS-KF algorithm

To assess the effectiveness of our proposed RLS-KF algorithm for predicting drug-target interactions, we apply it to the four benchmark datasets. In the current work, we choose to use the 10-fold cross-validation method (specifically, it is per-column 10-fold cross-validation, and this is repeated for each column) and repeat it 10 times, since it has been reported that this method provides a more robust evaluation for machine learning algorithms compared to the leave-one-out (LOO) cross-validation method [21]. Suitable statistical metrics are also important to provide an adequate evaluation for the proposed algorithm. Here, we utilize AUC and AUPR as the evaluation metrics in the current work. Table 2 shows the results of our proposed RLS-KF algorithm for predicting drug-target interactions for the four benchmark datasets. It is encouraging that the AUC values for all the benchmark datasets are highly satisfactory. On the other hand, we also note that all of the four benchmark datasets possess the imbalanced property, e.g. the number of drug-target pairs with known interactions is far less than the number of pairs with no interaction evidence. Therefore, the AUPR metric, which is more sensitive for unbalanced datasets, is also used for assessing prediction results. When evaluated by AUPR, all of the predictive results are still encouraging, and AUPR values for the most of the predictions are higher than 90% except that for the GPCR dataset. We also note that the aggregation methods, e.g. average-based vs max-based, have an effect on the results. In most cases, the average aggregation method outperforms the max-based aggregation method. The exception is however, for the NR dataset, for which predictive results from both methods are good and comparable.

Table 2.

Results of RLS-KF based on 10 trails of 10-fold cross-validation for predicting the four benchmark datasets.

Datasets	Aggregation function	AUPR	AUC
Enzymes	Max	0.892 ± 0.011	0.990 ± 0.001
	Average	0.915 ± 0.007	0.990 ± 0.001
IC	Max	0.901 ± 0.006	0.987 ± 0.001
	average	0.925 ± 0.005	0.989 ± 0.001
GPCR	Max	0.806 ± 0.010	0.981 ± 0.001
	average	0.853 ± 0.006	0.984 ± 0.001
NR	Max	0.911 ± 0.011	0.987 ± 0.002
	average	0.909 ± 0.013	0.987 ± 0.002

3.4. Comparison with the state-of-the-art method

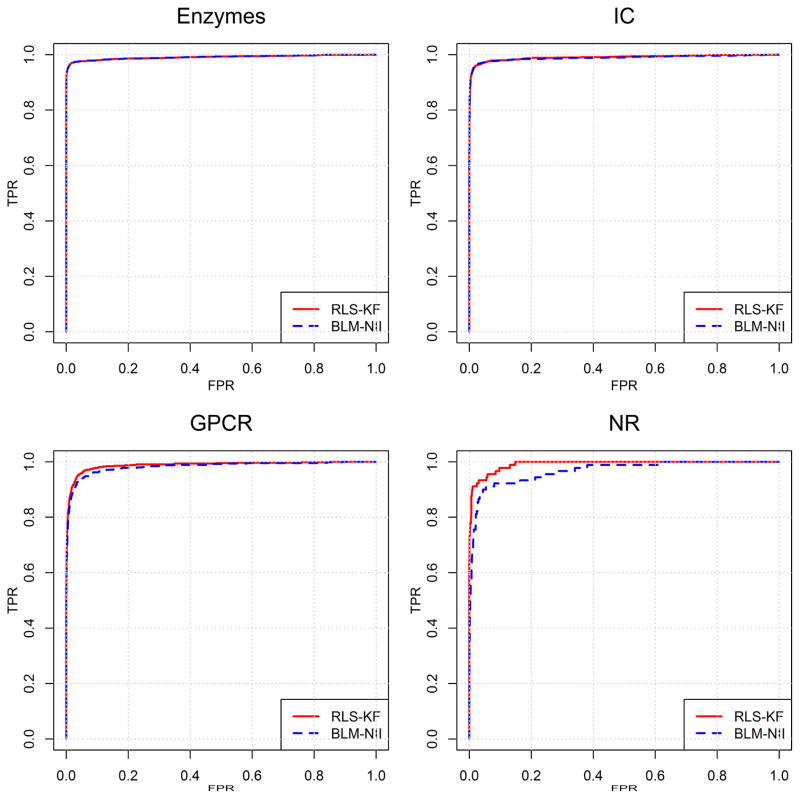
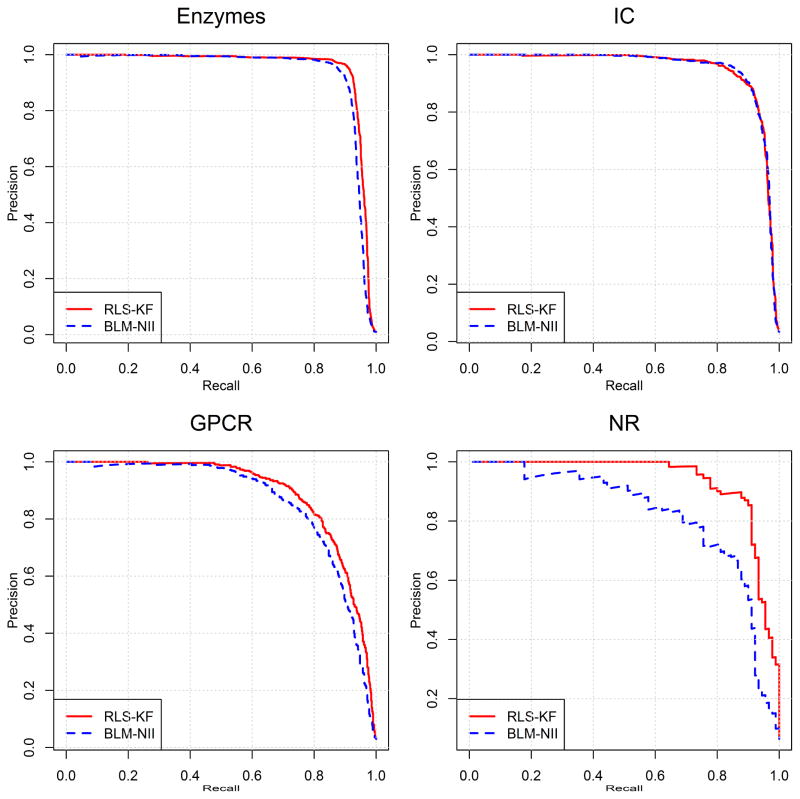
The proposed RLS-KF method is also evaluated by comparing it with BLM-NII from Mei and co-workers [8], which ranked as the top ones among several similar work for DTI predictions [5–7], and hence was considered as the state-of-the-art method. In addition there are two other reasons to select BLM-NII for this comparison. (1) Both RLS-KF and BLM-NII are formulated in a similar way for predicting DTI. The difference between the two is, however, that the former uses the kernel fusion technique to combine multiple similarity matrices, while the latter uses the simple linear combination technique; (2) Both algorithms are applicable to DTI predictions for new drugs (or new targets). Results from the comparison between RLS-KF and BLM-NII are listed in Table 3. It should be noted that these results are obtained from 10 trials of 10-fold cross-validation obtained using the average aggregation function. It should also be pointed out that the current results of BLM-NII are derived from our implementation (by setting hyper-parameter α = 0.5 in BLM-NII) which are slightly different from the original results reported by Mei et al. [8]. As shown in Table 3, when evaluated by AUC, it can be seen that there is no significant difference between results from the two algorithms with RLS-KF performing slightly better than BLM-NII for all of four datasets. The performance differences become apparent when evaluated by AUPR, however. Based on AUPR, BLM-NII outperforms RLS-KF for the IC dataset, though only marginally. For the other three datasets including Enzymes, GPCR and NR, our proposed RLS-KF consistently performs better than BLM-NII. It is interesting to note that for the NR dataset, which has the smallest size among the four benchmark datasets, results from RLS-KF are very encouraging. For this dataset, AUPR from RLS-KF is 0.909, which significantly outperforms the result from BLM-NII (0.783). In fact, the previous studies [5–7] have suggested that prediction for the NR dataset is the most difficult task since the number of samples is relatively less sufficient. However, the proposed kernel fusion technique proves to be efficient for DTI predictions for this small dataset. Fig. 3 and Fig. 4 show the corresponding AUC and AUPR curves, respectively. In summary, this comparison analysis suggests that the proposed regularized least squares algorithm integrating with the novel nonlinear kernel fusion technique, RLS-KF, can make stronger DTI predictions, and the kernel fusion technique to combine multiple similarity matrices plays a critical role in its success.

Table 3.

Performance comparison of RLS-KF with BLM-NII based on 10 trails of 10-fold cross-validation.

Data	Method	AUPR	AUC
Enzymes	BLM-NII	0.893 ± 0.005	0.984 ± 0.0004
	RLS-KF	0.915 ± 0.007	0.990 ± 0.001
IC	BLM-NII	0.931 ± 0.004	0.988 ± 0.001
	RLS-KF	0.925 ± 0.005	0.989 ± 0.001
GPCR	BLM-NII	0.827 ± 0.004	0.979 ± 0.001
	RLS-KF	0.853 ± 0.006	0.984 ± 0.001
NR	BLM-NII	0.783 ± 0.021	0.962 ± 0.003
	RLS-KF	0.909 ± 0.013	0.987 ± 0.002

Fig. 3.

AUC curves of RLS-KS and BLM-NII for DTI predictions of the four benchmark datasets.

Fig. 4.

AUPR curves of RLS-KS and BLM-NII for DTI predictions of the four benchmark datasets.

3.5. Effect of similarity measures on the performance of RLS-KF

The comparisons on AUPR and AUC described above for our proposed RLS-KF algorithm and the start-of-the-art method was done using the benchmark similarity matrices. It would be interesting naturally to investigate how similarity measures can affect the performance of the algorithm. Thus, in this work, we also calculated additional similarity matrices both for the drugs and targets. The new similarity matrices for the protein targets are calculated based on two methods. The first one is obtained by using the spectrum kernel (denoted by SK, the hyper-parameter kmers is set to 3 in this work) [22], and the other one is obtained by using Clustal Omega (denoted by CO) [23], for which Clustal Omega gives the distant matrix (denoted by distM), and (1 – distM) is calculated to obtain the similarity matrix. For the drug compounds, the similarity matrix is obtained by using the PubChem fingerprint (denoted by PCFP, ftp://ftp.ncbi.nlm.nih.gov/pubchem/specifications/pubchem_fingerprints.txt), which has been successfully applied in other research [24, 25]. As a result, we obtained two sets of combined matrices: SK-PCFP and CO-PCFP. Table 4 shows the results of RLS-KF based on 10 trials of 10-fold cross-validation using the new constructed similarity matrices. The results are based on the average aggregation function. It can be noted that the results based on the new constructed similarity matrices do not show significant differences on AUC compared to those used in the earlier comparison analysis (Tables 3 and 4). When looking at AUPR, the performance of the benchmark matrices for the three larger benchmark datasets is only marginally better. However, for the smallest NR dataset, the performance (AUPR of 0.945 in SK-PCFP) exhibits further improvement compared to those obtained earlier from the benchmark similarity matrices (AUPR of 0.909 obtained by RLS-KF, shown in Table 3). Further analysis of this result shows that, by using our proposed RLS-KF algorithm based on the combination of SK-PCFP, all the 90 known interactions for the NR dataset (see Table 1) can be retrieved from about the top 204 predictions (sorting by descending order of prediction scores) out of the total 1404 possible combination of the drug-target pairs. These results are very encouraging which indicate the effectiveness of both the proposed RLS-KF algorithm and the new constructed similarity matrices (SK-PCFP), and suggest that the new similarity measures indeed have a positive effect on the performance of RLS-KF, especially for a dataset of smaller size. It should also be pointed out that in the current work, only drug-target network information, coupled with chemical structure information for the drugs and sequence information for protein targets, was used. It would be interesting to see whether prediction performance can be further improved by combining additional information, such as those from side effects [26], protein-protein interactions, drug-drug interactions [27].

Table 4.

Results of RLS-KF based on 10 trials of 10-fold cross-validation using the new constructed similarity matrices.

Data	Combination	AUPR	AUC
Enzymes	SK-PCFP	0.907 ± 0.011	0.990 ± 0.001
	CO-PCFP	0.911 ± 0.007	0.989 ± 0.001
IC	SK-PCFP	0.912 ± 0.005	0.987 ± 0.001
	CO-PCFP	0.922 ± 0.005	0.988 ± 0.001
GPCR	SK-PCFP	0.835 ± 0.009	0.979 ± 0.001
	CO-PCFP	0.842 ± 0.009	0.982 ± 0.002
NR	SK-PCFP	0.945 ± 0.004	0.993 ± 0.001
	CO-PCFP	0.942 ± 0.007	0.992 ± 0.001

3.6. Predicted interactions and validation

As shown in Table 4, it can be seen that our proposed RLS-KF algorithm combined with SK-PCFP gives the best results for the NR dataset, which is the most challenging dataset for DTI predictions as shown in the previous studies [5, 7, 8]. Therefore, we took the NR dataset as an example to further analyze the results of our proposed algorithm in greater details by looking into the novel predictions. Table 5 lists the top 10 predicted interactions (e.g. interactions not indicated by the benchmark dataset, sorted based on descending order of predicted scores) for NR based on the RLS-KF/SK-PCFP combination.

Table 5.

Top 10 predicted interactions for the NR dataset using RLS-KF based on the SK-PCFP combination.

Order	KEGG drug ID	Drug name	KEGG target ID	Target name
1	D00316	Etretinate	hsa6096	RAR-related orphan receptor β
2	D00182	Norethisterone	hsa2099	Estrogen receptor 1
3	D00443	Spironolactone	hsa5241	Progesterone receptor
4	D00327	Fluoxymesterone	hsa5241	Progesterone receptor
5	D00075	Testosterone	hsa5241	Progesterone receptor
6	D00075	Testosterone	hsa2099	Estrogen receptor 1
7	D01115	Eplerenone	hsa2908	Glucocorticoid receptor
8	D01217	Dydrogesterone	hsa2099	Estrogen receptor 1
9	D00951	Medroxyprogeste rone acetate	hsa2099	Estrogen receptor 1
10	D00094	Tretinoin	hsa3174	Hepatocyte nuclear factor 4 gamma

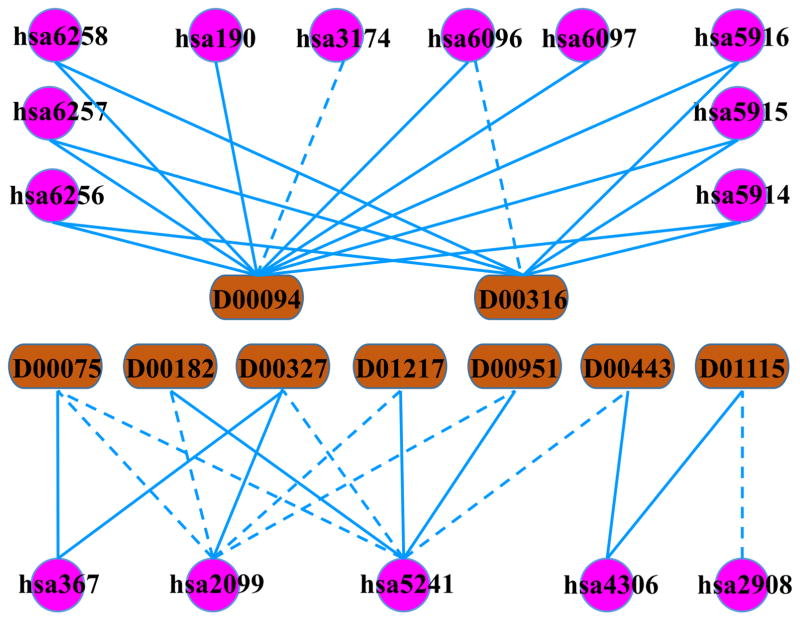
The top one predicted interaction occurs between D00316 (Etretinate) and hsa6096 (RAR-related orphan receptor β). Etretinate is a medication which originally was used to treat severe psoriasis but withdrawn due to the high risk of birth defects. Now it is used to treat T-cell lymphomas [28]. As it can be seen in Fig. 5, D00316 interacts with hsa5914, hsa5915, hsa5916, hsa6256, hsa6257 and hsa6258 in the benchmark NR dataset (blue solid line). Here, our RLS-KF algorithm predicts that it may also interact with RAR-related orphan receptor β (RORβ, hsa6096), which is consistent with the prediction by another previous study [21]. In addition, results from the study by Stehlin-Gaon et al. [29] indicate that several retinoids bind to RORβ. As Etretinate is an aromatic retinoid, a second-generation retinoid, there is a strong possibility of an interaction between Etretinate and RORβ. D00182 (Norethindrone), the drug at the second position in Table 5, is an approved small molecular drug, which is known as an agonist for the progesterone receptor (hsa5241 in Fig. 5). In this work, it is predicted to interact with hsa2099 (Estrogen receptor 1). To validate this prediction, we searched the bioactivity data of D00182 in the PubChem BioAssay database [30], which has been successfully used by many studies [31–34]. It is interesting that both the confirmatory assays deposited by Tox21 (PubChem BioAssay ID: AID 743075 and AID 743079) and the binding assay from ChEMBL [35] (AID 625258) support our prediction. For the third drug D00443 (Spironolactone) shown in Table 5, the predicted D00443-hsa5241 interaction pair by our algorithm gets confirmed by resorting to the latest version of DrugBank, where Spironolactone is listed to act as an agonist for the progesterone receptor. The fourth drug, D00327 (Fluoxymesterone) is used in the treatment of breast neoplasms in women, which interacts with hsa367 and hsa2099 as reported in the benchmark dataset (Fig. 5). Here, an D00327-hsa5241 interaction is predicted which is in line with the prediction in ChemSpider based on the SimBioSys LASSO score [36] (CSID 6205). D00075 (Testosterone) is a steroid sex hormone which plays an important role in sustaining human health. It has been reported to target the Androgen receptor as an agonist (hsa367, Fig. 5). RLS-KF algorithm suggested two additional interactions with hsa5241 and hsa2099 respectively. The former interaction was actually reported by the work from Duda et al. [37], while the predicted Testosterone-hsa2099 interaction is also suggested by multiple confirmatory bioassay data in PubChem (PubChem BioAssay ID: AID 588514 from NCGC, AID 743079 and AID 743075 from Tox21, as well as AID 402360 from ChEMBL). D01115 (Eplerenone), acts as an antagonist against the Mineralocorticoid receptor (hsa4306). Our study predicts it interacts with hsa2908, a Glucocorticoid receptor. An antagonist activity assay confirms our prediction (PubChem BioAssay ID: AID 761383 from ChEMBL). Our prediction on the D01217 (Dydrogesterone)-hsa2099 interaction is cross-validated by the prediction obtained from ChemSpider based on LASSO score (CSID 8699). As for the predicted interaction between D00951 (Medroxyprogesterone acetate) and hsa2099, the latest DrugBank version supports our result. As shown in Fig. 5, D00094 (Tretinoin) is the most promiscuous drug which interacts with nine targets as reported in the original NR dataset. Our algorithm predicts it may interact with one more target, hsa3174. However, this prediction is inconsistent with the result deposited in a profiling assay for RORA modulators in PubChem BioAssay (AID 2277) which reports small molecule bioactivity data for a panel of targets and flags Tretinoin as inactive against hsa3174. But, it should be noted that the primary screening data presented in AID 2277 may be prone to include false positives as well as false negatives. Therefore, further experiments are needed to validate this interaction proposed by our work.

Fig. 5.

Network of the top 10 predicted interactions for NR by RLS-KF algorithm, where the blue solid line denotes the known interactions reported in the benchmark NR dataset, while the blue dashed line denotes the predicted interactions.

In summary, by using the proposed RLS-KF algorithm, 6 out of the top 10 predicted interactions for the NR dataset can be validated by experimental data and the other three predictions are consistent with predictions from other studies.

3.7. External validation

Although our model exhibits encouraging results than the previous counterparts based on the benchmark datasets, it is also interesting to find out if the proposed algorithm can handle new dataset that was not covered by the benchmark datasets. Thus, taking the NR dataset as an example, we collected additional NR targets and corresponding drugs which are reported only in the latest DrugBank database. By a careful search in the DrugBank database, we retrieved 7 new NR targets and 26 corresponding drugs with a total of 31 newly indicated interactions between them. Then, we extended the benchmark NR dataset to 33 targets with 80 drugs from the original 26 targets with 54 drugs. Following the same procedure, we used Gaussian kernel for drug molecules and spectrum kernel (kmers = 3) for protein targets. The parameters in the fusing process are kept as the same to those used before for the benchmark NR dataset (k = 4, and t = 2). When building models, we also performed 10 trails of 10-fold cross-validation with predicted scores ranked by descending order. As a result, about 90% out of the 31 interactions in the external set ranked at the top 100 positions or above out of the total 2640 potential drug-target pairs, and all the 31 known interactions can be retrieved (see supporting information) at about top 300 positions, indicating our proposed RLS-KF algorithm can handle the external dataset effectively.

4. Conclusion

In the work, we propose an effective similarity fusion method (RLS-KF) for drug-target interaction predictions. By comparing our method with other state-of-the-art methods, it is shown that RLS-KF produces higher AUC and AUPR in general demonstrating its enhanced power in DTI predictions. The results from our method are particularly encouraging for the NR dataset, which has shown as the most challenging dataset for the previous studies. Furthermore, when incorporating additional similarity measurement calculated for both drug compounds and target proteins, the prediction performance was further improved. Importantly, most of the top ranked DTI predictions can be validated by experimental results reported in the literature (which were reviewed retrospectively) and bioassay data deposited in PubChem, or otherwise supported by various in-silico studies. Such encouraging results indicate that RLS-KF is effective for studying DTI and novel target identification. Our analysis suggests that the proposed method can be helpful in constructing drug polypharmacological profiles, hence providing new perspectives for network pharmacology and facilitating drug repositioning.

1. A nonlinear kernel fusion algorithm is proposed to perform drug-target interaction predictions.

2. Performance can further be improved by using the recalculated kernel.

3. Top predictions can be validated by experimental data.