Quantifying renewable groundwater stress with GRACE

Abstract

Groundwater is an increasingly important water supply source globally. Understanding the amount of groundwater used versus the volume available is crucial to evaluate future water availability. We present a groundwater stress assessment to quantify the relationship between groundwater use and availability in the world's 37 largest aquifer systems. We quantify stress according to a ratio of groundwater use to availability, which we call the Renewable Groundwater Stress ratio. The impact of quantifying groundwater use based on nationally reported groundwater withdrawal statistics is compared to a novel approach to quantify use based on remote sensing observations from the Gravity Recovery and Climate Experiment (GRACE) satellite mission. Four characteristic stress regimes are defined: Overstressed, Variable Stress, Human‐dominated Stress, and Unstressed. The regimes are a function of the sign of use (positive or negative) and the sign of groundwater availability, defined as mean annual recharge. The ability to mitigate and adapt to stressed conditions, where use exceeds sustainable water availability, is a function of economic capacity and land use patterns. Therefore, we qualitatively explore the relationship between stress and anthropogenic biomes. We find that estimates of groundwater stress based on withdrawal statistics are unable to capture the range of characteristic stress regimes, especially in regions dominated by sparsely populated biome types with limited cropland. GRACE‐based estimates of use and stress can holistically quantify the impact of groundwater use on stress, resulting in both greater magnitudes of stress and more variability of stress between regions.

Key Points:

• Renewable groundwater stress is quantified in the world's largest aquifers

• Characteristic stress regimes are defined to determine the severity of stress

• Overstressed aquifers are mainly in rangeland biomes with some croplands

1. Introduction

Freshwater is a fundamental resource for natural ecosystems and human livelihoods, and access to it is considered a universal human right [United Nations Committee on Economic, Social and Cultural Rights, 2003]. Water resources are under pressure to meet future demands due to population growth and climate change, both of which may alter the spatial and temporal distribution of freshwater availability globally [Döll, 2009; Kundzewicz et al., 2008; Kundzewicz and Döll, 2009; Famiglietti, 2014]. As the distribution of freshwater changes, the global population without access to potable water will likely increase [Alcamo et al., 2007; Kundzewicz et al., 2008]. It is critical to understand how human and natural dynamics are impacting available water resources to determine levels of sustainable use and to ensure adequate access to freshwater.

Surface water is the principal freshwater supply appropriated to meet human water demand globally, but the importance of groundwater is increasing as surface supplies become less reliable and predictable [Kundzewicz and Döll, 2009] and groundwater is increasingly relied upon during times of drought as a resilient water supply source [Famiglietti, 2014]. Groundwater is currently the primary source of freshwater for approximately two billion people [Alley, 2006; Kundzewicz and Döll, 2009]. Despite its importance, knowledge on the state of large groundwater systems is limited as compared to surface water [Foster and Chilton, 2003; Famiglietti, 2014], largely because the cost and complexity of monitoring large aquifer systems is often prohibitive.

The United States government has identified water stress as a potential driver of regional insecurity that can contribute to regional unrest [Intelligence Community Assessment (ICA), 2012]. Water stress analyses provide a framework to understand the dynamics between human and natural systems by directly comparing water availability to human water use. There are three main approaches to quantify physical water stress [Rijsberman, 2006]: (1) a per‐capita water availability ratio [Falkenmark, 1989], (2) a comparison between use and availability either as the difference between the two [Wada et al., 2010, 2011; van Beek et al., 2011] or as the ratio [Alcamo et al., 1997; Vörösmarty et al., 2000; Oki and Kanae, 2006; Döll, 2009], and (3) the evaluation of the socio‐economic and physical factors that impact stress [Sullivan et al., 2003]. This study defines renewable groundwater stress (RGS) following the second approach as the ratio of groundwater use to groundwater availability in equation (1) [Alcamo et al., 1997].

$$\mathit{RGS}=\frac{\mathit{use}}{\mathit{availability}}$$ (1)

The simplicity of equation (1) provides a proverbial “two edge sword.” On one hand, renewable groundwater stress can be calculated with estimates of two variables. On the other, inconsistent assumptions and differing estimates and definitions of use and availability result in variable calculations of renewable stress. Previous studies defined water use as water withdrawals and quantified use with national withdrawal statistics in which a single value represents per‐capita water use for an entire country [e.g., Vörösmarty et al., 2000], thus assuming water is used homogenously within a country. The statistics represent groundwater withdrawals but do not account for the impact of withdrawals on the state of the system. Additionally, the definition of availability has focused on the renewable fluxes of the dynamic water cycle [UN World Water Assessment Program (WWAP), 2003], including river runoff and groundwater recharge [Lvovich, 1979; Falkenmark et al., 1989; Postel et al., 1996; Shiklomanov, 2000; WWAP, 2003; Zekster and Everett, 2004]. Only recently have stress studies evolved from implicitly including groundwater as base flow in modeled runoff [Alcamo et al., 1997; Vörösmarty et al., 2000; Oki and Kanae, 2006], to explicitly quantifying stress with groundwater withdrawal statistics, modeled recharge [Döll, 2009; Wada et al., 2010], and nonrenewable groundwater use from compiled withdrawal statistics [Wada et al., 2011; van Beek et al., 2011].

These recent advances in groundwater stress analysis have improved our global understanding of groundwater availability to meet current water demands. However, groundwater withdrawal statistics are often outdated and measured by inconsistent methods between geopolitical boundaries [Shiklomanov and Penkova, 2003; Alley, 2006]. Thus, the acquisition of accurate water use data represents a major challenge and an impediment to accurate estimates of water stress and associated security threats. Remote sensing has been shown to greatly improve estimates of groundwater depletion [Colesanti et al., 2003; Schmidt and Bürgmann, 2003; Lanari et al., 2004; Rodell et al., 2009; Famiglietti et al., 2011; Voss et al., 2013; Castle et al., 2014], specifically, with the Gravity Recovery and Climate Experiment (GRACE) satellite mission from the National Aeronautics Space Administration (NASA) [Tapley et al., 2004].

This study estimates groundwater stress from equation (1) and assesses the variability in stress that results from different definitions of groundwater use. In this study, groundwater availability is defined as groundwater recharge. We assess groundwater use with groundwater withdrawal statistics, Q in equation (2), and then redefine use as the trend in subsurface storage anomalies using remote sensing approaches, dGW/dt in equation (2). Equation (2) represents the water balance in a system with groundwater withdrawals, Q, as introduced by Bredehoeft and Young [1970]. The equation shows that when pumping occurs, there is an increase in recharge (ΔR₀) from its natural state (R₀) and/or a decrease in discharge (ΔD₀) from its natural state (D₀) [Theis, 1940]. Lohman [1972] defined (ΔR₀ ‐ ΔD₀) as capture. If equilibrium has been reached such that capture balances Q then dGW/dt, the change in groundwater storage, is zero. However, storage loss will occur while Q exceeds capture and an increase in storage will occur where capture exceeds Q. The time scales required to reach equilibrium, especially for large aquifer systems, can be up to hundreds of years [Bredehoeft and Young, 1970] and well beyond our study period of January 2003 to December 2013.

$$\left({\mathit{R}}_0+\Delta {\mathit{R}}_0\right)-\left({\mathit{D}}_0+\Delta {\mathit{D}}_0\right)-\mathit{Q}=\frac{\mathit{dGW}}{\mathit{dt}}$$ (2)

Groundwater sustainability, defined as the continued development of groundwater resources such that negative environmental, societal, or economic impacts do not occur, requires a balance of withdrawals and replenishment over time [Alley et al., 1999]. Therefore, a stress study is inherently a sustainability study to understand the balance between supply and demand. Simply defining Q as a measure of use independent from the remaining components of equation (2) cannot fully characterize the impact of Q on the state of the system and therefore, its sustainability. Instead, we use the trend in subsurface storage anomalies over our study period to quantify dGW/dt in equation (2) to holistically account for withdrawals, capture, and changes in R₀ and D₀ due to natural factors such as drought. For example, a negative trend in dGW/dt indicates the rate of withdrawals, represented as a negative value of Q, is greater than the rate of capture, (ΔR₀ ‐ ΔD₀). A negative trend in dGW/dt can also indicate that D₀ exceeds R₀ during the study period due to natural variability (i.e., drought).

By categorizing characteristic stress regimes (Section 2.1) we can holistically assess the impact of groundwater use on the state of an aquifer system. Understanding the impact of depletion on groundwater storage is crucial for quantifying groundwater stress in a way that accounts for an aquifer's response to withdrawals and natural climate variability. Our results illustrate that stress will not occur in every region where withdrawals exceed recharge, as is implied when groundwater withdrawal statistics are used to define use. Instead, we find that stress occurs in the systems where withdrawals exceed capture such that storage loss occurs.

2. Data and Methods

Renewable groundwater stress (RGS) is computed for the 37 largest global aquifer systems in the Worldwide Hydrogeological Mapping and Assessment Program (WHYMAP) [WHYMAP and Margat, 2008] (Figure 1 and Table 1) for a study period of January 2003 to December 2013. WHYMAP was created in 2000 as a joint project between the United Nations Educational, Scientific, and Cultural Organization (UNESCO), the Commission for the Geological Map of the World (CGMW), the International Association of Hydro‐geologists (IAH), the International Atomic Energy Agency (IAEA) and the German Federal Institute for Geosciences and Natural Resources (BGR). The WHYMAP network serves as a central repository and hub for global groundwater data, information, and mapping with a goal of assisting regional, national, and international efforts toward sustainable groundwater management. As such, the WHYMAP network contains the best available global aquifer information. We define our study area as the 37 “Large Aquifer Systems of the World” [WHYMAP and Margat, 2008]. These systems represent the international consensus on the boundaries of the world's most productive groundwater systems that contain the majority of the world's accessible groundwater supply [Margat, 2007; Margat and van der Gun, 2013]. Additionally, the area of each of these aquifer systems is consistent with the spatial resolution required by GRACE observations (Section 2.2.2).

Figure 1.

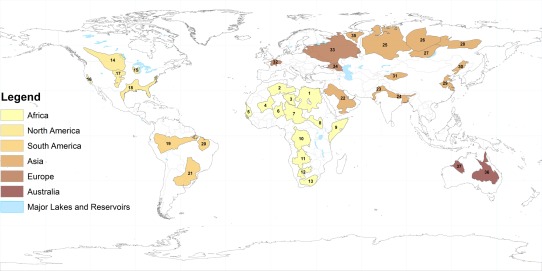
Study aquifers by continent based on the WHYMAP delineations of the world's Large Aquifer Systems [WHYMAP and Margat, 2008]. The number represents the aquifer identification number for each aquifer system. The world's largest lakes and reservoirs are based on the Global Lake and Wetland Database Level‐1 lakes and reservoirs [Lehner and Döll, 2004].

Table 1.

Study Aquifers With the Aquifer Identification Number

Aquifer ID	Aquifer Name
1	Nubian Aquifer System (NAS)
2	Northwestern Sahara Aquifer System (NWSAS)
3	Murzuk‐Djado Basin
4	Taoudeni‐Tanezrouft Basin
5	Senegalo‐Mauritanian Basin
6	Iullemeden‐Irhazer Aquifer System
7	Lake Chad Basin
8	Sudd Basin (Umm Ruwaba Aquifer)
9	Ogaden‐Juba Basin
10	Congo Basin
11	Upper Kalahari‐Cuvelai‐Upper Zambezi Basin
12	Lower Kalahari‐Stampriet Basin
13	Karoo Basin
14	Northern Great Plains Aquifer
15	Cambro‐Ordovician Aquifer System
16	Californian Central Valley Aquifer System
17	Ogallala Aquifer (High Plains)
18	Atlantic and Gulf Coastal Plains Aquifer
19	Amazon Basin
20	Maranhao Basin
21	Guarani Aquifer System
22	Arabian Aquifer System
23	Indus Basin
24	Ganges‐Brahmaputra Basin
25	West Siberian Basin
26	Tunguss Basin
27	Angara‐Lena Basin
28	Yakut Basin
29	North China Aquifer System
30	Song‐Liao Basin
31	Tarim Basin
32	Paris Basin
33	Russian Platform Basins
34	North Caucasus Basin
35	Pechora Basin
36	Great Artesian Basin
37	Canning Basin

First, we introduce characteristic stress regimes that define four types of stress that can occur based on the sign of water use and availability (Section 2.1). Two methods to quantify use, the numerator presented in equation (1), are introduced based on spatially distributed withdrawal statistics (Section 2.2.1) and the trend in GRACE‐based subsurface storage anomalies (Section 2.2.2). Modeled groundwater recharge is introduced as the definition of groundwater availability (Section 2.3), the denominator in equation (1). The RGS ratio is computed based on equation (1) (Section 2.4). Finally, anthropogenic biomes are introduced (Section 2.5) to analyze the land‐use patterns that influence different stress regimes and severity levels. Simplifications and assumptions are made in our approach that allow for a consistent method of assessment across 37 diverse aquifer systems. We utilize remote sensing observations, described in Section 2.2.2, and model output since the quantity and quality of available in situ observations in the study aquifers is highly variable.

2.1. Characteristic Stress Regimes

The Renewable Groundwater Stress (RGS) ratio of groundwater use to groundwater availability is used to define groundwater stress, according to equation (1) [Alcamo et al., 1997]. Water stress indicators following the U.N. water stress scale (Table 2) [UN/WMO/SEI, 1997] are based on traditional approaches where use in equation (1) is negative and availability estimates as annual recharge in equation (1) are positive. Stress regimes, however, can theoretically exhibit four end‐member behaviors similar to those of Weiskel et al. [2007] (Figure 2): Unstressed, Variable Stress, Human‐dominated Variable Stress and Overstressed. These end members encompass the spectrum of outcomes given positive (gaining) or negative (depleting) estimates of use and positive (recharging) or negative (discharging) estimates of annual recharge. Thus, quite simply, the ratio in equation (1) represents the percent of recharge that is used to meet water demands.

Table 2.

United Nations Renewable Stress Scale^a

Stress Ratio	Stress Level
0–0.1	Low
0.1–0.2	Moderate
0.2–0.4	High
> 0.4	Extreme

^aThe stress ratio represents the dimensionless Renewable Groundwater Stress Ratio used in this study.

Figure 2.

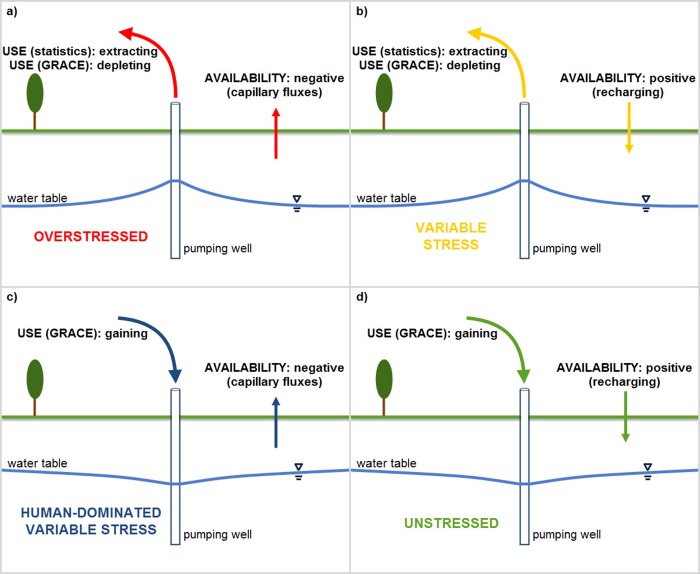
Characteristic stress regimes that encompass the possible behavior of stress given positive (gaining) or negative (extracting/depleting) use behavior and positive (recharging) or negative (capillary fluxes) groundwater availability. The schematics represent integrated behavior across an aquifer system.

In the Overstressed case, the RGS ratio is positive since both recharge and use are negative. This case, resulting from a combination of large withdrawals and negative recharge, implies groundwater mining or active depletion. In shallow aquifers, negative or negligible recharge is largely driven by groundwater supported evapotranspiration, especially in summer months and during dry periods [Yeh and Eltahir, 2005a, 2005b; Yeh and Famiglietti, 2009; Szilagyi et al., 2013; Koirala et al., 2014]. Scanlon et al. [2003] found that in semiarid to arid regions, the vadose zone is only influenced by surface climate forcings to a depth of about 3 m. Capillary rise, which we term negative recharge, beneath this depth is the dominant subsurface moisture flux [Coudrain‐Ribstein et al., 1998; Walvoord et al., 2002; De Vries and Simmers, 2002; Scanlon et al., 2003; Walvoord and Scanlon, 2004]. Aquifer systems undergoing Overstressed conditions may trigger or exacerbate land subsidence [Galloway and Riley, 1999; Bawden et al., 2001; Konikow and Kendy, 2005], ecosystem habitat destruction [Stromberg et al., 1996; Gleeson et al., 2012] and aquifer compaction [Galloway et al., 1998; Konikow and Kendy, 2005] that limit future aquifer productivity and recharge potential.

The Variable Stress case follows the criticality ratio of previous stress studies [Alcamo et al., 1997; Vörösmarty et al., 2000], where use is negative (withdrawals) and recharge is entering the system, resulting in a negative RGS ratio. There are four levels of Variable Stress according to the United Nations (Table 2). Consider a ratio less than one. The rate of use is less than the natural recharge rate; however, small perturbations to the system can result in negative environmental impacts, for example, by decreasing base flow and ultimately drying streams, marshes, and springs [Sophocleous, 1997; Bredehoeft, 1997; Faunt, 2009]. A ratio with an absolute value greater than one represents use rates that exceed natural recharge rates and increases the rate of capture. This condition can create the potential for water quality impacts if recharge is induced from contaminated sources [Theis, 1940].

Both the statistics‐based method and the GRACE‐based method to estimate use can result in the Overstressed and Variable Stress cases. Only the GRACE‐based estimate can quantify the remaining Human‐dominated Variable Stress and Unstressed cases. In these cases, the study aquifers have positive trends in subsurface storage anomalies and are therefore “gaining.” We consider the Human‐Dominated case to be the result of a positive trend from GRACE and negative recharge. Natural behavior of these systems would be a loss of groundwater through capillary flux to the root zone [Coudrain‐Ribstein et al., 1998; Walvoord et al., 2002; De Vries and Simmers, 2002; Scanlon et al., 2003; Walvoord and Scanlon, 2004; Lo et al., 2008] or by direct evapotranspiration [Yeh and Eltahir, 2005a, 2005b; Yeh and Famiglietti, 2009; Szilagyi et al., 2013; Koirala et al., 2014]. A combination of induced capture and human practices may be contributing to the gaining trend in groundwater storage, for example, from artificial recharge using surface water diversions in irrigated areas. The Unstressed case has a positive trend in groundwater storage anomalies and positive recharge. This case is only considered unstressed from a water quantity perspective. Induced capture may draw additional recharge from sources that could negatively impact water quality.

2.2. Water Use

2.2.1. Compiled Withdrawal Statistics

We follow methods similar to Vörösmarty et al. [2000] and Wada et al. [2010] to spatially distribute available groundwater withdrawal statistics into the study aquifers, representing Q (equation (2)). First, we compile national groundwater withdrawal statistics from multiple sources in cubic kilometers per year [FAO, 2003; IGRAC, 2004; Margat and van der Gun, 2013]. The statistics represent groundwater withdrawals across all sectors of water use (agriculture, domestic, industrial) and provide percentages of groundwater use for each sector. We use these percentages to determine the rate of agricultural, domestic, and industrial withdrawals as a function of the national withdrawal rate. The majority of these percentages are based solely on sectoral withdrawals as a function of total groundwater withdrawals, although percentages based on total withdrawals are used when groundwater percentages are unavailable.

National level agricultural statistics are distributed spatially based on the 0.5° × 0.5° gridded “Water Withdrawals for Irrigation” data set [GWSP Digital Water Atlas, 2008a], which provides the theoretical water demand for irrigated crops as a function of climate. The single national agricultural statistic is distributed based on the percent of national irrigation demand in each grid cell by assuming groundwater withdrawals occurs in close proximity to where it is needed to meet demand [Wada et al., 2010]. Similarly, the sum of national domestic and industrial withdrawal statistics is distributed by gridded population density, following Vörösmarty et al. [2000], based on the 0.5° x 0.5° gridded “Population (Total)” [GWSP Digital Water Atlas, 2008b] data set. The resulting spatially distributed agricultural, domestic, and industrial withdrawal rates are summed within each grid cell and scaled up to 1° x 1° spatial resolution, to match the resolution of the remote sensing observations. Basin‐averaged groundwater withdrawals are computed for the 37 study aquifers as the statistics‐based estimate of use.

2.2.2. GRACE Observations

Remote sensing observations from the Gravity Recovery and Climate Experiment (GRACE) satellite mission [Tapley et al., 2004] are used to quantify a novel estimate of groundwater use, dGW/dt in equation (2). The GRACE satellites, a joint mission between the National Aeronautics and Space Administration (NASA) in the United States and the Deutsche Forschungsanstalt für Luft und Raumfahrt (DLR) in Germany, measure monthly changes in total terrestrial water storage by converting observed gravity anomalies into changes of equivalent water height [Rodell and Famiglietti, 1999; Syed et al., 2008; Ramillien et al., 2008].

The Center for Space Research at the University of Texas at Austin provided the 132 months of GRACE gravity coefficients from Release‐05 data used in this study. Gravity anomalies for this time period (January 2003 to December 2013) underwent processing to obtain an estimate of the average terrestrial water storage anomalies for each of the 37 study aquifers [Swenson and Wahr, 2002; Wahr et al., 2006; Swenson and Wahr, 2006]. Aquifer‐specific scaling factors were used to account for the lost signal power from truncating the gravity coefficients (at degree and order 60) and filtering for unbiased estimates of mass change in each aquifer system [Velicogna and Wahr, 2006].

$$\Delta {\mathit{S}}_{\mathit{N}+\mathit{A}}=\Delta {(\mathit{SW}+\mathit{SWE}+\mathit{SM}+\mathit{GW})}_{\mathit{N}+\mathit{A}}$$ (3)

$$\Delta \mathit{SU}{\mathit{B}}_{\mathit{N}+\mathit{A}}=\Delta {\mathit{S}}_{\mathit{N}+\mathit{A}}-\Delta {(\mathit{SW}+\mathit{SWE})}_{\mathit{N}}$$ (4)

The total water storage changes can be partitioned into components resulting from natural change (N) or anthropogenic change (A) according to equation (3) where S is the total terrestrial water storage anomalies from GRACE, SW is surface water, SWE is snow water equivalent, SM is soil moisture, and GW is groundwater. Individual storage components can be isolated from the total GRACE signal with supplemental data sets to represent the remaining storage terms [Rodell and Famiglietti, 2002; Swenson et al., 2006; Yeh et al., 2006; Strassberg et al., 2007, 2009; Rodell et al., 2004b, 2007, 2009; Swenson et al., 2008; Famiglietti et al., 2011; Scanlon et al., 2012; Castle et al., 2014]. We isolate subsurface anomalies (SUB) as combined anomalies in soil moisture (SM) and groundwater (GW) in equation (4).

Model output or in situ observations are required to isolate changes in a storage component from the total GRACE terrestrial water storage anomalies. We use monthly output from three models within the NASA Global Land Data Assimilation System (GLDAS) modeling system including Noah [Chen et al., 1996; Koren et al., 1999], Variable Infiltration Capacity (VIC) [Liang et al., 1994], and Community Land Model 2.0 (CLM 2.0) [Dai et al., 2003] to compute monthly mean gridded output at 1° x 1° spatial resolution for canopy surface water (CAN) and SWE. Surface water storage in lakes, reservoirs, and river channels is not included in the GLDAS modeling system [Rodell et al., 2004a]. We estimate SW as the sum of CAN from the three‐model GLDAS ensemble and routed surface water discharges (RIV) from offline output from CLM 4.0 [Oleson et al., 2010]. The CLM 4.0 model run is described in Section 2.3. The model‐based storage anomalies of SWE and SW are subtracted from the GRACE storage anomalies to estimate monthly GRACE‐derived subsurface anomalies for each aquifer.

Error in the subsurface anomalies is computed according to equation (5) for each month (i), assuming independence between component errors. Aquifer specific satellite measurement and leakage error from processing the gravity anomalies is computed following Wahr et al. [2006] to estimate error in the total GRACE signal. Variance of SWE and CAN was determined using the three‐model ensemble, which we assume represents the uncertainty induced by the estimate error and model structural error. The U.S. Geological Survey errors for hydrologic measurements range from excellent (5% error) to fair (15% error) [U.S. Geological Geological Survey (USGS), 2014]; therefore, for our evaluation, we assume measurement error of 50% in routed discharge to represent a conservative uncertainty in GRACE subsurface variability. It is the assumed the errors in equation (5) are independent. Area‐weighted basin averages of SWE and SW are computed for each of the study aquifers to account for latitudinal differences in gridded area. The temporal mean is removed from the basin averages to compute anomalies in SWE and SW.

$${\mathit{\sigma }}_{\Delta \mathit{SUB},\mathit{i}}=\sqrt{{\mathit{\sigma }}_{\mathit{S},\mathit{i}}^2+{\mathit{\sigma }}_{\mathit{SWE},\mathit{i}}^2+{\mathit{\sigma }}_{\mathit{CAN},\mathit{i}}^2+{\mathit{\sigma }}_{\mathit{RIV},\mathit{i}}^2}$$ (5)

We argue that the anthropogenic impacts on total water storage anomalies in the study aquifers are dominated by subsurface variations, particularly from groundwater, as these aquifers contain the majority of productive and available supply for groundwater use [Margat and van der Gun, 2013]. Therefore, anthropogenic changes in surface water and snow water are negligible at the study's spatial scale. Natural water stocks or built infrastructure are necessary to capture water supplies for human use [Vörösmarty et al., 2000], for example, lakes or reservoirs, particularly for surface water and snow meltwater. However, only 0.5% of the study aquifers' land area is overlain with lakes and reservoirs larger than 50 km² [Richey and Famiglietti, 2012], which is significantly smaller than the 1° spatial resolution of this study. We therefore assume negligible anthropogenic influences of surface water and snow in the study aquifers as compared to groundwater.

$${\mathit{Y}}_{\mathit{i}}={\mathit{\beta }}_0+{\mathit{\beta }}_1{\mathit{w}}_{\mathit{i}}{\mathit{x}}_{\mathit{i}}+{\mathit{\varepsilon }}_{\mathit{i}} \mathrm{where} {\mathit{w}}_{\mathit{i}}=\frac{1}{{\mathit{\sigma }}_{\mathbf{\Delta }\mathit{SUB},\mathit{i}}^2}$$ (6)

The majority of soil water storage trends are not significant globally [Sheffield and Wood, 2008; Dorigo et al., 2012]. Therefore, we use a conservative estimate of groundwater trends by attributing observed subsurface trends solely to groundwater storage. We consider the groundwater trend to be representative of the net flux of water storage resulting from groundwater use (ΔGW_N+A), including the aquifer response to pumping as predicted by Theis [1940], and natural climatic variability. Annual trend magnitudes, ΔGW_trend, were estimated using the weighted regression in equation (6) to quantify the change in groundwater storage from equation (2). The weights, w_i, are a function of the variance in the monthly estimates of subsurface storage anomalies. Aquifers with a negative coefficient were considered to be depleting in aquifer storage while positive coefficients were considered to be recharging systems. Here we evaluate only the magnitude of trends without regard to trend significance.

2.3. Water Availability: Groundwater Recharge

Renewable groundwater availability is defined as mean annual groundwater recharge, following Döll [2009] and Wada et al. [2010]. The majority of land surface parameterizations do not have an explicit representation of groundwater and are therefore unable to capture both positive and negative recharge fluxes [Yeh and Famiglietti, 2009]. Instead, groundwater recharge is frequently estimated as model drainage from the bottom of a soil column [e.g., Rodell et al., 2004a] or as the residual of precipitation and evapotranspiration [e.g., Weiskel et al., 2007]. These approaches assume the flux is always positive (downward) and that average recharge is approximately equal to base flow. These assumptions are not always true, particularly in semiarid and arid regions where capillary fluxes can be the dominant subsurface flux as opposed to downward recharge [De Vries and Simmers, 2002]. Assuming recharge is always positive may falsely represent the level of stress in a region.

Direct model output from the Community Land Model version 4.0 [Oleson et al., 2010] is used to estimate natural recharge, R₀, in equation (2). CLM 4.0 is the land surface model used within the Community Earth System Model (CESM) [Oleson et al., 2010]. CLM 4.0 is one of the few land surface models that includes an unconfined aquifer layer coupled to the bottom soil layer and is therefore able to capture both positive and negative recharge. Recharge is computed as the vertical flux between the aquifer and bottom soil layer, such that positive recharge flows downward as gravity drainage and negative recharge flows upward by capillary fluxes [Oleson et al., 2008; Lo et al., 2008].

CLM 4.0 was run in an offline simulation driven by atmospheric forcing data including precipitation, near surface air temperature, solar radiation, specific humidity, wind speed, and air pressure. Three hourly forcing data from GLDAS Version‐1 [Rodell et al., 2004a] were used to drive the model at a 1 h time step, which is then interpolated to monthly model output. The model was run at 0.9° x 1.25° spatial resolution and linearly interpolated to 1° x 1°. Basin averaged recharge is computed for each study aquifer as an area‐weighted average across all grid cells. The mean annual recharge is computed from the monthly values for each study aquifer for our study period of January 2003 to December 2013. The spatial distribution of modeled CLM 4.0 recharge results are comparable to previous modeled recharge estimates using the PCR‐GLOBWB global hydrological model [Döll, 2009; Wada et al., 2010].

2.4. Groundwater Stress

2.4.1. Renewable Stress: Criticality Ratio

Following the traditional water stress approach [Alcamo et al., 1997; UN/WMO/SEI, 1997; Vörösmarty et al., 2000; Oki and Kanae, 2006; Döll, 2009], we define Renewable Groundwater Stress (RGS) as the ratio of groundwater use to renewable groundwater availability in equation (1). This dimensionless ratio represents the percent of renewable water being used to meet human water demand.

Mean annual recharge, R₀, from Section 2.3 is used to calculate renewable groundwater availability. It has been repeatedly cited that recharge cannot be used to define renewable available groundwater and that only a percent of recharge (less than or equal to the rate of capture) can be considered available for sustainable use [Bredehoeft, 1997; Sophocleous, 1997; Bredehoeft, 2002; Zhou, 2009]. Thus, this study uses simulated recharge to represent the maximum available natural renewable groundwater and is therefore the most optimistic estimate of available supplies and resulting stress. Additionally, systems with negative modeled mean annual recharge are considered to lack renewable supplies. In this case, there is no recharge available to replenish the system and the level of stress is determined by the magnitude of use alone.

Groundwater use is quantified by groundwater withdrawal statistics, Q_stat, in equation (7), as described in Section 2.2.1 and the trend in GRACE‐derived subsurface anomalies in equation (8), ΔGW_trend, as described in Section 2.2.2, to assess the difference in stress between the estimation schemes.

$$\mathit{RG}{\mathit{S}}_{\mathit{stat}}=\frac{{\mathit{Q}}_{\mathit{stat}}}{{\mathit{R}}_0}$$ (7)

$$\mathit{RG}{\mathit{S}}_{\mathit{GRACE}}=\frac{\Delta \mathit{G}{\mathit{W}}_{\mathit{trend}}}{{\mathit{R}}_0}$$ (8)

2.5. Approximating Anthropogenic Influences

We introduce an additional data set to better understand the driving factors behind differing levels of use and stress. The world map of anthropogenic biomes [Ellis and Ramankutty, 2008], is used to determine the dominant land use type by accounting for both land use/land cover types and the degree to which a region is inhabited. There are six broad characteristic biome types including Dense Settlements, Villages, Croplands, Rangeland, Forested, and Wildlands, with a total of 21 subcategories within these types. The subcategories break down the anthropogenic biome types into different levels of remote and populated areas that are dominated by rain or irrigated area (Figure 3). The six most dominant anthropogenic biome types are assigned for each study aquifer based on the percent of aquifer area covered by each biome type (Table A1 in Appendix A).

Figure 3.

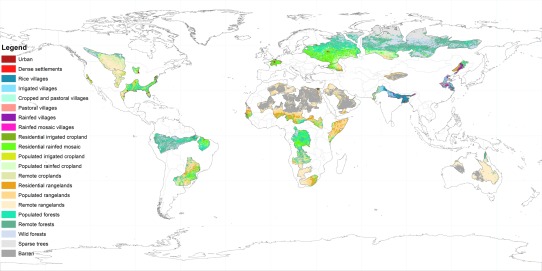
Anthropogenic biome types within the study aquifers. Biome types are gridded at 0.0833° spatial resolution from Ellis and Ramankutty [2008].

3. Results

3.1. Groundwater Use: Statistics and GRACE

A comparison between GRACE‐depletion methods (Figure 4) and statistics‐based methods (Figure 5) show how the GRACE‐based approach incorporates temporal variations in use over the study period whereas the statistics approach quantifies use as a static value in time. Figure 4 illustrates the GRACE‐depletion method that uses model output to isolate groundwater storage changes from the GRACE observations of total terrestrial water storage anomalies. The figure presents the time series components of the water budget for the Ganges‐Brahmaputra Basin (Aquifer #24, “Ganges”). By comparing the modeled storage anomalies to the GRACE‐derived groundwater anomalies, it is clear that changes in groundwater storage are dominating the GRACE observations of declining terrestrial water storage. Figure 5 presents the statistics‐based method to estimate use as groundwater withdrawal statistics that are spatially distributed by population density and theoretical water withdrawals for irrigation. The influence of geopolitical boundaries on the method is clear as national level groundwater withdrawals can differ between neighboring countries. In the United States, the national withdrawal rate is 111.7 cubic kilometers per year (km³/yr) versus Canada's withdrawal rate of 1.87 km³/yr [Margat and van der Gun, 2013]. Table 3 summarizes the rates of use based on GRACE and the statistics.

Figure 4.

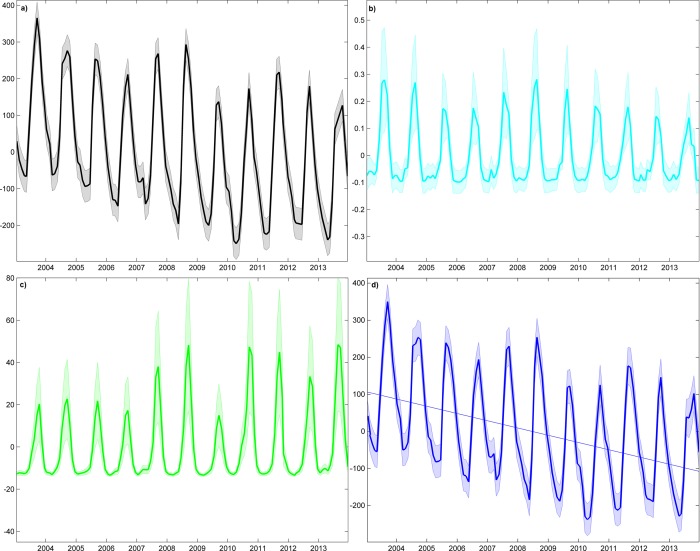
Water storage components in the Ganges‐Brahmaputra Basin in millimeters per year. (a) Total GRACE‐derived terrestrial water storage anomalies, (b) the sum of model output from the Global Land Data Assimilation System (GLDAS) of snow water equivalent (SWE) and canopy water storage (CAN) anomalies, (c) routed river storage anomalies from the Community Land Model (CLM) 4.0, (d) subsurface storage anomalies as the difference between total storage anomalies and the sum of SWE, CAN, and river storage.

Figure 5.

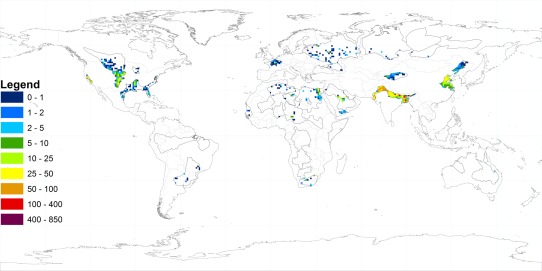
Spatially distributed groundwater withdrawal statistics in the study aquifers in millimeters per year. The statistics represent the sum of withdrawals for agricultural, domestic, and industrial end uses.

Table 3.

Study Aquifers With Basin Averaged Groundwater Withdrawal Statistics (Q_stat) (mm/yr), GRACE‐Derived Subsurface Depletion (ΔSUB_N+A) (mm/yr) and the ΔSUB_N+A Error (ΔSUB_error) (mm/yr), Mean Annual Recharge (R) (mm/yr), the Dimensionless Statistics‐Based Renewable Groundwater Stress Ratio (RGS_stat), and the Dimensionless GRACE‐Based Renewable Groundwater Stress Ratio (RGS_GRACE)

Aquifer ID	Qstat	ΔSUBN+A	ΔSUBerror	R	RGSstat	RGSGRACE
1	−0.46	−2.91	0.88	−0.27	1.69	10.59
2	−0.34	−2.81	0.79	−0.26	1.33	10.80
3	−0.46	−4.28	1.02	−0.23	2.04	18.92
4	−0.01	−0.50	0.65	1.04	−0.01	−0.48
5	−0.38	4.65	1.68	34.38	−0.01	0.14
6	−0.15	2.41	1.07	11.18	−0.01	0.22
7	−0.23	−1.04	0.85	5.99	−0.04	−0.17
8	−0.01	−2.86	1.09	−18.43	0.00	0.16
9	−0.06	−0.34	1.06	−5.89	0.01	0.06
10	−0.05	−4.85	0.95	18.99	0.00	−0.26
11	−0.04	24.28	1.03	101.11	0.00	0.24
12	−0.20	3.20	1.03	−12.30	0.02	−0.26
13	−0.23	5.59	1.24	−11.80	0.02	−0.47
14	−0.71	4.95	0.84	8.42	−0.08	0.59
15	−3.35	2.45	1.56	151.81	−0.02	0.02
16	−26.50	−8.89	1.91	24.10	−1.10	−0.37
17	−10.06	0.31	1.00	−3.67	2.74	−0.08
18	−1.93	−5.93	1.01	168.35	−0.01	−0.04
19	−0.04	7.13	1.03	546.56	0.00	0.01
20	−0.15	6.71	1.33	323.00	0.00	0.02
21	−0.33	−0.58	0.94	225.66	0.00	0.00
22	−1.37	−9.13	0.90	−2.58	0.53	3.54
23	−51.55	−4.26	0.87	−4.62	11.16	0.92
24	−63.05	−19.56	1.22	214.40	−0.29	−0.09
25	−0.13	−1.98	0.99	39.37	0.00	−0.05
26	−0.03	1.66	1.24	36.22	0.00	0.05
27	−0.14	3.99	1.26	36.44	0.00	0.11
28	−0.05	2.89	1.20	16.51	0.00	0.18
29	−12.49	−7.50	1.30	96.56	−0.13	−0.08
30	−3.29	2.40	1.54	20.16	−0.16	0.12
31	−1.39	−0.23	0.30	−0.74	1.89	0.32
32	−2.30	−4.12	1.45	133.56	−0.02	−0.03
33	−0.58	−4.01	1.06	98.55	−0.01	−0.04
34	−0.34	−16.10	1.41	28.77	−0.01	−0.56
35	−0.06	3.04	1.65	161.30	0.00	0.02
36	−0.05	10.60	0.98	13.67	0.00	0.78
37	0.00	−9.41	1.34	6.05	0.00	−1.56

Figure 6 illustrates the basin‐averages of groundwater use as determined by the groundwater withdrawal statistics (Figure 6a) and the GRACE‐derived trend in groundwater storage anomalies (Figure 6b) within each study aquifer. The differences between Figure 6a and Figure 6b result solely from the definition of use in equation (1). In Figure 6a, use statistics are consistently negative and thus do not represent the full variability in stress regimes as illustrated in Figure 2. The GRACE‐derived trend captures the dynamics of groundwater use by integrating the human and natural impacts of use on groundwater storage, including changes in recharge and discharge regimes and water management practices. As a result of the integrated storage changes, aquifers can have either a positive or negative trend in groundwater storage anomalies as observed from GRACE. There are 16 study aquifers that have positive subsurface trends from GRACE‐derived use and 21 that are negative.

Figure 6.

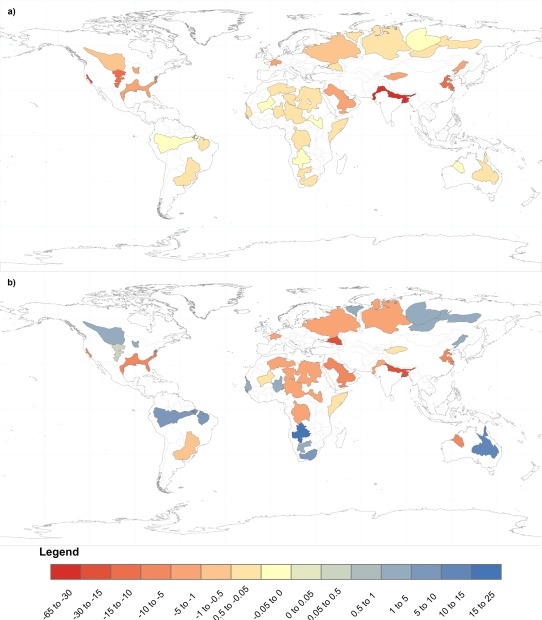
Basin‐averaged groundwater use quantified by (a) groundwater withdrawal statistics and (b) GRACE‐derived depletion in millimeters per year. The GRACE‐derived estimates have both positive and negative estimates, while the withdrawal statistics are limited to negative estimates alone.

There are five aquifers with negative rates of use where the statistics‐based withdrawal rate exceeds the GRACE‐based estimates. These include the Ganges, the Indus Basin (Aquifer #23, “Indus”), the Californian Central Valley Aquifer System (Aquifer #16, “Central Valley”), the North China Aquifer System (Aquifer #29, "North China), and the Tarim Basin (Aquifer #31, “Tarim”). The assumption used to spatially distribute the statistics based on irrigation demand and population density (Figure 5) influences the magnitude of use from the statistics exceeding GRACE depletion, by multiple factors in some cases. Four of these five aquifers also have the four highest levels of irrigation demand and among the highest levels of population density. For example, the Ganges has the highest rate of use from both GRACE and the statistics. However, the high population and irrigation demand results in a rate of use from the statistics of −63.1 millimeters per year (mm/yr) as compared to the estimate by GRACE of −19.6 ± 1.2 mm/yr.

The aquifers with the highest rates of depletion from GRACE cover a wide range of dominant biome types globally, including villages, cropland, wildland, forests, and rangeland. The high rate of depletion in the Ganges is largely driven by population and irrigation demand across populated biomes. Conversely, the Arabian Aquifer System (Aquifer #22, “Arabian”) has a depletion rate of −9.13 ± 0.9 mm/yr with 67% of the system covered by rangeland (Table A1). Irrigation for agriculture is a common groundwater use practice in the Arabian [Siebert et al., 2010], and is likely a main contributor to the GRACE‐derived estimate of use. The Canning Basin (Aquifer #37, “Canning”) is a unique case, where less than 1% of the aquifer is covered by residential area, but the third highest rate of GRACE‐derived depletion occurs in this system (−9.40 ± 1.34 mm/yr). Mining activities in the rural Canning Basin are likely influencing the GRACE signal which is lost in the statistics‐based use rate of −0.002 mm/yr.

3.2. Distribution and Severity of Renewable Groundwater Stress

The differences between GRACE‐derived groundwater depletion and water withdrawal statistics discussed in Section 3.1 further influence the distribution and severity of Renewable Groundwater Stress (RGS) in the study aquifers (Table 3). Our estimates of mean annual recharge (Figure 7) counteract or enhance the influence of the use estimates on stress. Groundwater use as quantified by the withdrawal statistics results in only two of the characteristic stress regimes (Figure 2), Overstressed and Variable Stress, because water use is always negative with this approach. RGS calculated with GRACE‐derived use exhibits characteristics of all regimes illustrated in Figure 2. Figure 8 shows the RGS ratio based on equation (7) and Figure 9 shows the RGS ratio based on equation (8).

Figure 7.

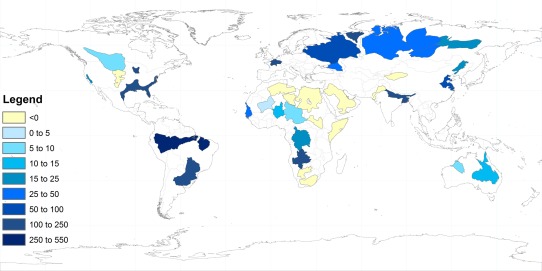
Basin‐averaged mean annual recharge from CLM 4.0 model output in millimeters per year. Negative recharge represents capillary fluxes as a flow out of the groundwater system. Positive recharge represents vertical flow into the system.

Figure 8.

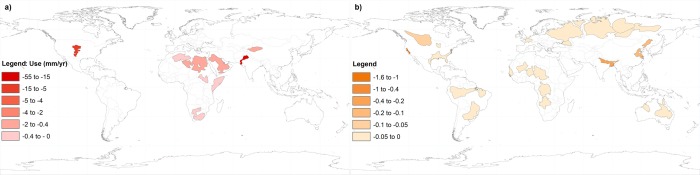
Renewable groundwater stress ratio derived from groundwater withdrawal statistics. (a) Overstressed conditions are shown as the rate of withdrawals assuming no available recharge (mm/yr). (b) Variable stressed conditions are dimensionless with a positive value of recharge and a negative value of use.

Figure 9.

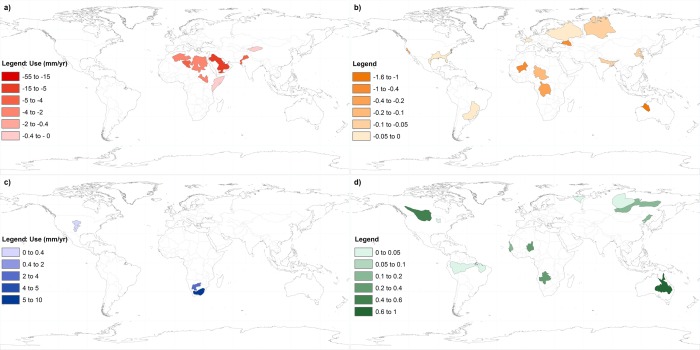
Renewable Groundwater Stress ratio derived from GRACE‐based groundwater depletion. (a) Overstressed conditions and (c) human‐dominated stress are shown as the rate of GRACE‐based use assuming no available recharge (mm/yr). (b) Variable stressed conditions have a positive value of recharge and a negative value of use. (d) Unstressed systems have positive estimates of use and availability. The values are dimensionless in Figures 9b and 9d.

Groundwater recharge is negative in 11 study aquifers, predominantly in semiarid and arid regions, thus capillary fluxes are the dominant subsurface flux and recharge does not occur. This corresponds with previous findings that in thick desert vadose zone regions there is a long‐term transient drying state dominated by upward moisture fluxes, and drainage beneath the root zone is not representative of recharge to the underlying aquifer [Walvoord et al., 2002; Scanlon et al., 2003; Walvoord and Scanlon, 2004]. The magnitude of the negative recharge could be influenced by the model structure whereby water is withdrawn from the aquifer, as a capillary flux, to maintain the minimum water content in the soil layers as prescribed by the model [Oleson et al., 2010]. The temporal and spatial scale of our study approach does not account for localized recharge zones, such as through cracks or fissures in the subsurface, or intense precipitation events that provide recharge in semiarid and arid regions [De Vries and Simmers, 2002] and could increase recharge in the study aquifers.

3.2.1. Overstressed RGS Regime

There are eight Overstressed aquifers based on RGS_GRACE in equation (8) and 11 Overstressed aquifers quantified by RGS_stat in equation (7). Estimates of both use and availability are negative in the Overstressed regime. Negative recharge predominantly occurs in semiarid to arid regions (Figure 7), as described above. The most Overstressed aquifer systems based on RGS_GRACE are the Arabian and the Murzuk‐Djado Basin (Aquifer #3, “Murzuk”), where the depletion rates are the highest with no available recharge. The most Overstressed aquifer from RGS_stat is the Indus. All of the aquifers that are Overstressed as determined using RGS_GRACE are dominated by a mixture of rangeland and cropland, although rangeland is the main biome in six of the eight overstressed aquifers. The majority of these systems are more Overstressed from GRACE than from the statistics that are unable to capture use in regions dominated by less densely populated rangeland. The Indus is the only exception where high population and irrigation demand result in the second highest rate of use from the statistics.

3.2.2. Human‐Dominated RGS Regime

The eight Overstressed aquifers as determined by RGS_GRACE in equation (8) (Figure 9a) are also Overstressed from the withdrawal statistics (Figure 8a). There are three aquifers that are Overstressed based on the statistics, but are estimated to be in the Human‐dominated Variable stress category based on GRACE due to gaining trends in groundwater storage anomalies. In this case, capillary fluxes are believed to be dominant in removing groundwater from storage through natural processes. However, human practices are likely artificially increasing the amount of recharge entering the system such that groundwater storage changes from GRACE are increasing. The positive GRACE trend could also be influenced by a wet period toward the end of the study period that has not manifested in recharge yet due a lag in between surface wet periods and recharge. Therefore, RGS_GRACE is negative due to a positive trend in groundwater storage anomalies but a negative rate of mean annual recharge. In the Ogallala Aquifer (Aquifer #17, “Ogallala”), irrigation for agriculture is likely increasing the amount of water available for recharge through return flow [Sophocleous, 2005]. Since the water withdrawal statistics only capture static withdrawals from the system, equation (7) is unable to capture this characteristic stress regime that is dominated by influxes into the system.

3.2.3. Variable RGS Regime

The majority of the study aquifers follow the Variable Stress regime based on equation (7), where there is potential for recharge to offset use. The aquifers in the Variable Stress category are predominately cropland with some villages and dense settlements. There are 26 aquifers in the Variable Stress regime from RGS_stat in equation (7), 22 of which are characterized by low stress according to the UN stress scale (Table 2). In these systems, 10% or less of renewable available groundwater is used to meet human demand. The Central Valley is the only extremely stressed aquifer from equation (7) with a ratio of −1.1, indicating more water is being extracted than is recharging the system. The Central Valley is dominated by populated irrigated cropland, which drives the third highest rate of use from the statistics.

Only 13 of the study aquifers are variably stressed based on RGS_GRACE. Seven of these systems are in the low stress category, including the Ganges, where a high rate of mean annual recharge (214 mm/yr) balances the highest rates of use based on both the statistics and GRACE. The magnitude of use in the Ganges, discussed in Section 3.1, influences the categorization of the aquifer as either low stress by RGS_stat or high stress by RGS_GRACE. The seven low‐stress systems are mainly dominated by rainfed and forested regions with only minor irrigated area.

Two aquifers are highly stressed based on RGS_GRACE including the Central Valley, which was extremely stressed from RGS_stat. The Congo Basin (Aquifer #10, “Congo”) is characterized as low stress from RGS_stat, where the diversity of biome types could not be represented by the distributed statistics. Three aquifers are considered extremely stressed from RGS_GRACE, two of which are dominated by unpopulated rangeland and wildland. For example, the stress ratio in the Canning is −1.6, implying that about 150% more water is being depleted than is naturally available and water in storage is used to supplement available supplies [Taylor, 2009]. In reality, storage loss and environmental degradation can occur when the RGS ratio is less than one [Bredehoeft, 1997; Sophocleous, 2000; Sophocleous, 2005]. Although the Taoudeni has one of the smallest depletion rates from GRACE, it has the smallest mean annual recharge rate that dominates the extreme stress estimate.

3.2.4. Unstressed RGS Regime

Unstressed aquifers have positive estimates of both groundwater use and availability, and can therefore only be quantified by equation (8). There are 13 unstressed aquifers in this category. Overall, the unstressed aquifer systems are mainly in remote forested areas and rainfed regions. The unstressed systems have very limited irrigated area.

An unstressed ratio close to one implies that the trend in increasing groundwater storage anomalies approaches the mean annual recharge rate, thus the system is more influenced by natural recharge than external perturbations. The Great Artesian Basin (Aquifer #36 “Great Artesian”) and the Northern Great Plains Aquifer (Aquifer #14, “Great Plains”) have the unstressed ratio closest to one at 0.78 and 0.59, respectively. Both of these systems are predominantly remote cropland, rangeland, and forested area. The Great Plains is also dominated by populated rainfed cropland; therefore groundwater is not the dominant water supply source for agriculture.

The Amazon Basin (Aquifer #19) has the highest mean annual recharge rate, but a ratio of 0.01, implying that the large recharge is not dominating the trend in groundwater storage anomalies from GRACE. Given the dominance of the Amazon River in this heavily forested region, it could be inferred that high recharge rates are balanced by high base flow rates [Pokhrel et al., 2013]. Thus, the trend in groundwater storage anomalies is not as controlled by recharge alone.

4. Discussion

As the dependence on groundwater increases into the future [Kundzewicz and Döll, 2009; Famiglietti, 2014], it is increasingly critical to understand where and why groundwater stress occurs to evaluate future stress conditions. We have shown in this study that the definition of “groundwater use” in the Renewable Groundwater Stress (RGS) ratio can lead to large differences in how stressed a specific region may appear to be. We find that the GRACE‐based approach to quantify RGS (equation (8)) captures the variability of stress that is expected in a natural system (Figure 2). The traditional approach to define groundwater use based on distributed withdrawal statistics can only capture two characteristic stress regimes. This statistics‐based approach to quantify RGS (equation (7)) is controlled by the assumptions that groundwater use is correlated to population and irrigation demand [Vörösmarty et al., 2000; Wada et al., 2010]. These assumptions do not allow for heterogeneous use of groundwater within a country in space or time.

Understanding the dominant biomes in the study aquifers is a key to assessing how groundwater stress may change into the future and where conflicts may arise based on external pressures including population growth, food demand, and climate variability. GRACE‐derived stresses capture the variability of possible stress regimes. The end‐member regimes are predominately grouped by anthropogenic biome type. We find that the majority of the overstressed aquifers from GRACE are in rangeland biomes with remote regions where the withdrawal statistics are unable to capture use. Conversely, the unstressed aquifers are predominately in forested, rainfed, and remote areas. The Central Valley and the Congo exemplify the importance of incorporating biomes to understand the difference between the stress estimates based on equations (7) and (8).

The dominant biome type in the Central Valley is irrigated cropland with minor (1 – 10 persons per km²) to substantial (10–100 persons per km²) human populations (Figure 3). The distribution of use in aquifers dominated by similar biomes as the Central Valley can be captured by the statistics since water use in such regions is related to population density and irrigation demand. In the Central Valley, the estimate of use by the statistics is −26.5 mm/yr compared to −8.91 ± 1.91 mm/yr from GRACE.

The Congo represents the opposite case, whereby the dominant biome types limit the characterization of use from the distributed statistics. The Congo is dominated by a mix of populated and remote regions with a combination of forested area and rainfed cropland. Population dominates the distribution of statistics in this case given low irrigation demand, but groundwater only provides about a quarter of urban supply [Groundwater Consultants Bee Pee Ltd., and SRK Consulting Ltd., 2002]. Boreholes are spread throughout the region and are not solely used for irrigation [Groundwater Consultants Bee Pee Ltd., and SRK Consulting Ltd., 2002]. The Congo is experiencing a combination of a drying trend [Zhou et al., 2014] and deforestation in the region [Zhang et al., 2005, Duveiller et al., 2008; Hansen et al., 2008] that may be increasing temperatures and decreasing precipitation in the basin [Nogherotto et al., 2013]. The combination of these factors can increase pressure on groundwater resources that can't be captured by statistics, but may be influencing the GRACE trend. The estimate of use by the statistics is −0.05 millimeters per year (mm/yr) compared to −4.27 ± 0.91 mm/yr from GRACE in the Congo.

5. Conclusion

It is important to understand where existing socio‐economic tensions may collide with water stress to produce stress‐driven conflicts [ICA, 2012; U.S. Department of State, 2013]. However, the definitions of water stress by both the U.S. Department of State and the United States Agency for International Development (USAID) depend on either the Falkenmark Indicator or a high ratio of withdrawal statistics to availability [ICA, 2012; U.S. Department of State, 2013]. The Falkenmark Indicator does not account for groundwater as a water supply source or water use that is not driven by population density, such as irrigated agriculture. We have shown that simply quantifying water use based on withdrawal statistics cannot fully capture the range of impacts that groundwater use has on groundwater systems.

This study has shown how quantifying groundwater use with trends in groundwater storage anomalies from GRACE holistically represents the distribution of renewable groundwater stress. GRACE incorporates the influence of withdrawals, the aquifer's response to withdrawals through capture, and natural variability. Additionally, the GRACE‐based estimates of use can encompass natural and anthropogenic variations on groundwater systems across a range of biome types. Although natural variability is integrated into the statistics‐based estimate of stress through variability in recharge, the statistics‐based approach to quantify use is based on withdrawals alone. As a result, the withdrawal statistics provide an incomplete representation of characteristic stress regimes by not accounting for dynamic aquifer responses to pumping and natural variability. The statistics‐based estimates of use are limited to biomes dominated by populated and cropland regions.

The study implications extend to an improved ability to distribute aid to regions currently identified as experiencing varying levels of water stress with a greater understanding of the driving land cover factors behind such stress. The results highlight regions that may be vulnerable to tipping points toward higher levels of stress driven by a range of factors including land cover, for example, through conversion to intensified agriculture, or population pressures that increase demand. We conclude that the estimate of groundwater stress using GRACE‐derived estimates of use can provide additional information in assessing RGS within the world's largest aquifer systems.

Appendix A.

The dominant anthropogenic biome types by Ellis and Ramankutty [2008] are determined for each study aquifer. The percentage of aquifer area covered by the six most common biome types are listed. The dominant biome types were used to determine land use drivers behind different levels of stress.

Table A1.

The Six Most Common Anthropogenic Biome Types in Each Study Aquifer^a

Aquifer ID	Dominant Anthropogenic Biome Types
1	Remote rangelands	Populated rangelands	Barren	Residential rangelands	Remote croplands	Sparse trees
	57%	17%	12%	10%	1%	1%
2	Remote rangelands	Populated rangelands	Barren	Residential rangelands	Residential irrigated cropland	Cropped and pastoral villages
	36%	26%	16%	14%	3%	2%
3	Remote rangelands	Barren	Populated rangelands	Residential rangelands	Cropped and pastoral villages	Populated irrigated cropland
	61%	15%	12%	7%	2%	2%
4	Remote rangelands	Barren	Populated rangelands	Residential rangelands	Populated rainfed cropland	Urban
	52%	25%	18%	4%	2%	0%
5	Populated rainfed cropland	Residential rangelands	Populated rangelands	Residential rainfed mosaic	Remote rangelands	Populated forests
	19%	15%	14%	12%	7%	6%
6	Remote rangelands	Residential rainfed mosaic	Residential irrigated cropland	Cropped and pastoral villages	Populated rangelands	Barren
	19%	15%	14%	12%	12%	10%
7	Populated rainfed cropland	Populated rangelands	Residential rangelands	Residential rainfed mosaic	Remote rangelands	Populated forests
	18%	17%	16%	15%	12%	6%
8	Populated rainfed cropland	Populated rangelands	Residential rangelands	Residential rainfed mosaic	Populated forests	Remote rangelands
	29%	19%	19%	14%	12%	2%
9	Residential rangelands	Populated rainfed cropland	Populated rangelands	Residential rainfed mosaic	Remote rangelands	Populated forests
	26%	22%	16%	10%	9%	9%
10	Populated forests	Residential rainfed mosaic	Remote forests	Populated rainfed cropland	Populated rangelands	Rainfed mosaic villages
	27%	21%	20%	15%	5%	4%
11	Populated forests	Populated rangelands	Remote forests	Remote rangelands	Populated rainfed cropland	Residential rainfed mosaic
	23%	22%	15%	13%	13%	9%
12	Populated rangelands	Barren	Remote forests	Remote rangelands	Sparse trees	Residential rangelands
	33%	13%	11%	11%	9%	9%
13	Populated rangelands	Residential rangelands	Residential rainfed mosaic	Populated rainfed cropland	Remote rangelands	Pastoral villages
	21%	20%	16%	11%	10%	7%
14	Populated rainfed cropland	Remote croplands	Remote rangelands	Populated rangelands	Residential rainfed mosaic	Remote forests
	24%	15%	14%	11%	9%	8%
15	Residential rainfed mosaic	Populated rainfed cropland	Residential irrigated cropland	Populated forests	Dense settlements	Urban
	32%	20%	19%	11%	7%	3%
16	Populated irrigated cropland	Residential irrigated cropland	Populated rangelands	Remote rangelands	Remote croplands	Populated rainfed cropland
	14%	14%	11%	9%	8%	7%
17	Populated irrigated cropland	Populated rangelands	Remote croplands	Populated rainfed cropland	Residential irrigated cropland	Remote rangelands
	18%	16%	15%	15%	14%	9%
18	Residential rainfed mosaic	Populated rainfed cropland	Populated forests	Residential irrigated cropland	Remote forests	Rainfed mosaic villages
	19%	19%	13%	9%	9%	6%
19	Wild forests	Populated forests	Remote forests	Residential rainfed mosaic	Populated rainfed cropland	Remote rangelands
	31%	27%	22%	10%	6%	1%
20	Populated rainfed cropland	Populated forests	Residential rainfed mosaic	Remote forests	Residential rangelands	Populated rangelands
	45%	19%	14%	6%	4%	3%
21	Populated rainfed cropland	Residential rainfed mosaic	Populated forests	Populated rangelands	Residential rangelands	Remote forests
	20%	14%	12%	12%	10%	9%
22	Remote rangelands	Populated rangelands	Residential rangelands	Barren	Populated irrigated cropland	Remote croplands
	31%	22%	14%	13%	5%	5%
23	Residential irrigated cropland	Cropped and pastoral villages	Residential rangelands	Urban	Populated rangelands	Rainfed villages
	24%	17%	14%	8%	7%	6%
24	Rainfed villages	Urban	Dense settlements	Residential irrigated cropland	Rainfed mosaic villages	Rice villages
	20%	18%	12%	10%	10%	9%
25	Remote forests	Populated forests	Wild forests	Sparse trees	Residential rainfed mosaic	Populated rainfed cropland
	20%	19%	18%	12%	10%	7%
26	Remote forests	Wild forests	Sparse trees	Populated forests	Remote rangelands	Barren
	37%	24%	17%	12%	5%	2%
27	Remote forests	Populated forests	Wild forests	Residential rainfed mosaic	Populated rainfed cropland	Remote rangelands
	31%	23%	17%	10%	6%	5%
28	Wild forests	Remote forests	Populated forests	Sparse trees	Remote rangelands	Residential rainfed mosaic
	37%	26%	20%	10%	3%	2%
29	Dense settlements	Rainfed villages	Irrigated villages	Urban	Rice villages	Residential irrigated cropland
	25%	22%	10%	9%	7%	6%
30	Residential rainfed mosaic	Pastoral villages	Residential irrigated cropland	Populated forests	Populated rainfed cropland	Dense settlements
	21%	14%	11%	8%	7%	6%
31	Remote rangelands	Populated rangelands	Residential rangelands	Barren	Cropped and pastoral villages	Residential irrigated cropland
	32%	20%	16%	7%	7%	7%
32	Rainfed villages	Rainfed mosaic villages	Residential irrigated cropland	Dense settlements	Urban	Residential rainfed mosaic
	27%	20%	14%	14%	5%	4%
33	Populated rainfed cropland	Populated forests	Residential rainfed mosaic	Remote forests	Wild forests	Rainfed mosaic villages
	27%	18%	18%	17%	5%	3%
34	Populated rainfed cropland	Residential rainfed mosaic	Rainfed villages	Residential rangelands	Populated rangelands	Residential irrigated cropland
	21%	15%	12%	8%	7%	6%
35	Remote forests	Populated forests	Wild forests	Sparse trees	Remote rangelands	Residential rainfed mosaic
	44%	21%	16%	11%	3%	3%
36	Remote forests	Remote rangelands	Sparse trees	Remote croplands	Barren	Populated rangelands
	22%	19%	16%	11%	11%	9%
37	Sparse trees	Remote rangelands	Remote forests	Barren	Populated rangelands	Populated forests
	59%	12%	12%	11%	3%	2%

^aThe percentages list the percent of the aquifer area that is dominated by the corresponding biome type.

Richey, A. S. , Thomas B. F., Lo M.‐H., Reager J. T., Famiglietti J. S., Voss K., Swenson S., and Rodell M. (2015), Quantifying renewable groundwater stress with GRACE , Water Resour. Res., 51, 5217–5238, doi:10.1002/2015WR017349.