The emergence of hydrogeophysics for improved understanding of subsurface processes over multiple scales

Abstract

Geophysics provides a multidimensional suite of investigative methods that are transforming our ability to see into the very fabric of the subsurface environment, and monitor the dynamics of its fluids and the biogeochemical reactions that occur within it. Here we document how geophysical methods have emerged as valuable tools for investigating shallow subsurface processes over the past two decades and offer a vision for future developments relevant to hydrology and also ecosystem science. The field of “hydrogeophysics” arose in the late 1990s, prompted, in part, by the wealth of studies on stochastic subsurface hydrology that argued for better field‐based investigative techniques. These new hydrogeophysical approaches benefited from the emergence of practical and robust data inversion techniques, in many cases with a view to quantify shallow subsurface heterogeneity and the associated dynamics of subsurface fluids. Furthermore, the need for quantitative characterization stimulated a wealth of new investigations into petrophysical relationships that link hydrologically relevant properties to measurable geophysical parameters. Development of time‐lapse approaches provided a new suite of tools for hydrological investigation, enhanced further with the realization that some geophysical properties may be sensitive to biogeochemical transformations in the subsurface environment, thus opening up the new field of “biogeophysics.” Early hydrogeophysical studies often concentrated on relatively small “plot‐scale” experiments. More recently, however, the translation to larger‐scale characterization has been the focus of a number of studies. Geophysical technologies continue to develop, driven, in part, by the increasing need to understand and quantify key processes controlling sustainable water resources and ecosystem services.

Key Points:

• A review of the emergence and development of hydrogeophysics

• Outline of emerging techniques in hydrogeophysics

• Presentation of future opportunities in hydrogeophysics

1. Introduction

The ability to observe the fabric of the subsurface environment and processes that occur within it remains a challenge in many branches of science and engineering. This is particularly the case for hydrology, where the transport and transformation of fluids in the shallow subsurface (commonly <100 m deep) are governed by interactions between physical, biological, and geochemical processes occurring in highly heterogeneous and often variably saturated soils, sediments, and bedrock compartments (Figure 1). These complex and multiscale interactions are difficult to observe and thus hinder our ability to understand, predict, and ultimately manage shallow systems in a sustainable manner. The need to improve our understanding of processes within the subsurface environment exists due to several drivers, including demands on provision of suitable quantities of groundwater at appropriate quality; determining the legacy of industrial, agricultural, and military sources of groundwater contamination; quantifying terrestrial carbon cycling feedbacks to climate; ensuring food security; and understanding water resource impacts on ecosystem function. Hydrogeophysics provides a suite of tools that may assist in addressing such drivers through the quantification of the structure and function of the shallow subsurface (Figure 1).

Figure 1.

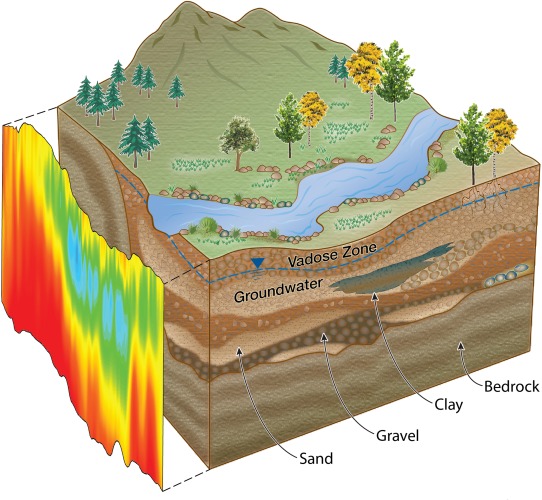
Cartoon of a terrestrial environment, illustrating hydrogeological heterogeneity and how geophysical methods are often used to characterize the “hidden” subsurface. Geophysical data sets provide information about geophysical properties, such as electrical conductivity (shown here), which can potentially be related to hydrogeological properties as shown in Table 1.

Traditional in situ “point‐scale” sampling of the subsurface for system properties (e.g., permeability) and states (e.g., water content, ion concentrations, and redox potential) has been widely based on invasive drilling approaches, through the recovery of samples (e.g., cores) and installation of fluid sampling apparatus. While such approaches may be relatively easy in the very near surface (<1 m), their financial (and labor) costs often constrain such investigations at greater depths, enforcing an interpretation based on few observations and at shallow depths. These measurements are also limited by the scale of measurement they offer, as it is widely accepted that the subsurface process or property under investigation (e.g., permeability) can be scale dependent [e.g., Schulze‐Makuch et al., 1999], particularly in fractured media. Furthermore, in some instances, invasive sampling of the subsurface is severely restricted, for example, due to inaccessibility caused by features on the ground surface (e.g., built infrastructure), environmental protection constraints, the hazardous nature of a site, or the threat of disturbing and transforming contaminant pathways through an invasive activity. For these reasons, geophysical methods, many of which were originally developed for oil and mineral exploration, have emerged as valuable tools for supporting investigation of the shallow subsurface and for monitoring the dynamics of hydrological and biogeochemical processes that occur within it.

Several geophysical methods have been used in hydrological investigations for decades. Geophysical well logging, for example, is well established and routinely used to assist drilling operations through the recording of lithological geophysical descriptors, thus helping the development of hydrogeological conceptualizations at a site. However, over the past two or three decades, new geophysical methods have emerged (or have developed significantly), several of which have proved to be extremely effective in providing valuable information about the subsurface environment beyond the borehole wall. New approaches have been developed to exploit the information attainable from these techniques, supported by new insights into relationships between properties of interest and observable geophysical properties. During the 1990s, “hydrogeophysics” arose as an interdisciplinary field that focuses on the improved understanding of hydrological processes through geophysical observations. While initially focused on aiding in the development of conceptual subsurface models, applications of hydrogeophysics have developed to provide new insight into subsurface mechanisms, to aid in the parameterization of subsurface flow and transport models, and to advance new tools for monitoring the hydrological and biogeochemical status of the subsurface environment.

Several key challenges exist in translating geophysical measurements into information that is useful for improving our understanding and management of shallow subsurface systems. First and foremost, geophysical measurements do not generally provide direct information about hydrogeological properties or states and as such, their effective use is governed by the strength of the relationships between estimated geophysical properties and the properties of interest. In addition, they can suffer from limitations of measurement scale and resolution in that the target to be characterized may be much smaller than the footprint of the geophysical measurement. Profound understanding of these factors is essential for successful application, and motivates the existence and continued evolution of hydrogeophysics as a research field.

Many of the key advances in hydrogeophysics have been documented in Water Resources Research; Figure 2 illustrates the growth of hydrogeophysics activity in the journal since 1990. The number of hydrogeophysics‐related papers has continued to grow at an almost constant rate (Figure 2a) and now accounts for typically 5–6% of the journal content (Figure 2b). We use this celebratory issue to reflect on the emergence of the field through publications in the journal and the wider literature.

Figure 2.

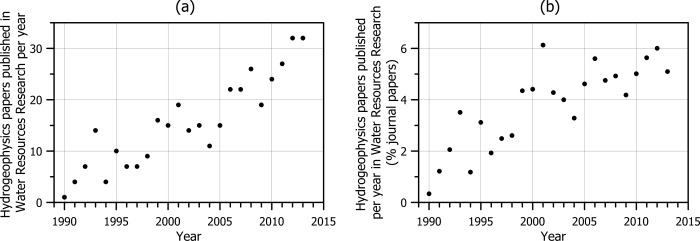
(a) Number of hydrogeophysics‐related papers published per year in Water Resources Research since 1990. (b) Number of hydrogeophysics‐related papers expressed as a percentage of total published papers per year in Water Resources Research (source: ISI Web of Science).

In this review, we first introduce the commonly used geophysical methods for hydrological investigations and outline the principles of geophysical data inversion and measurement scale. We then discuss developments in hydrogeophysical relationships, which underpin successful application of hydrogeophysics. Early approaches of geophysical methods to hydrology based on characterizing structure are reviewed, followed by subsequent developments addressing temporal dynamics, biogeochemical processes, and applications to ecosystem science. We then offer a vision for the future direction of hydrogeophysics.

2. Geophysical Methods

A range of geophysical methods have been used effectively in hydrological investigations. Details of such methods can be found in many texts [e.g., Rubin and Hubbard, 2005; Vereecken et al., 2006; Robinson et al., 2008a]; we restrict this review to the general concepts. Within most methods a geophysical property (or properties) of the subsurface is evaluated using sensors deployed on the boundary of the area of study in response to a natural or activated source. A link between such a property and a hydrological property or state is clearly essential to using these data for hydrologic inference, as discussed later. Assuming such a link exists, the success of the method then relies on the ability to infer variations in the property (or state) of interest from the accuracy and resolution‐limited geophysical parameter(s). The most commonly used methods for hydrological applications (in no particular order) are direct current (DC) resistivity, induced polarization (IP), self‐potential (SP), ground penetrating radar (GPR), electromagnetic induction (EMI), seismic refraction, nuclear magnetic resonance (NMR), and microgravity. (Note that we use the term induced polarization here to capture a broad range of polarization measurement methods; IP is often used to define a time domain measurement and complex resistivity is commonly used as a reference to measurements in the frequency domain, while spectral induced polarization (SIP) refers to the measurement of the frequency spectrum of complex resistivity.) Table 1 lists the geophysical properties that these methods provide and the hydrological properties that have commonly been derived from these geophysical properties. Note that we have not included temperature sensing as a geophysical approach here, although we recognize the immense success in developments of such approaches for hydrological investigations [e.g., Hatch et al., 2006; Selker et al., 2006; Keery et al., 2007; Tyler et al., 2009].

Table 1.

List of Commonly Used Geophysical Methods in Hydrology and the Geophysical Properties They Sense

Geophysical Method	Geophysical Properties	Examples of Derived Properties and States
DC resistivity	Electrical conductivity	Water content, clay content, pore water conductivity
Induced polarization	Electrical conductivity, chargeability	Water content, clay content, pore water conductivity, surface area, permeability
Spectral induced polarization	As above but with frequency dependence	Water content, clay content, pore water conductivity, surface area, permeability, geochemical transformations
Self‐potential	Electrical sources, electrical conductivity	Water flux, permeability
Electromagnetic induction	Electrical conductivity	Water content, clay content, salinity
Ground penetrating radar	Permittivity, electrical conductivity	Water content, porosity, stratigraphy
Seismic	Elastic moduli and bulk density	Lithology, ice content, cementation state, pore fluid substitution
Seismoelectrics	Electrical current density	Water content, permeability
Nuclear magnetic resonance	Proton density	Water content, permeability
Gravity	Bulk density	Water content, porosity

Several methods can be deployed in various configurations, allowing the user to tailor the survey to optimize the sensitivity. Electrical methods (DC resistivity, IP, SIP, and SP), which involve making measurements using electrodes with galvanic or capacitive contact with the subsurface, allow significant flexibility in terms of acquisition configuration for plot‐scale (<10 m deep) investigations. Most early applications of electrical methods in hydrology were based on surface‐based configurations originally developed for resource exploration. However, the inherent adaptability of the basic configuration to target the problem of interest led to deployment in alternative configurations, e.g., in boreholes [e.g., Daily et al., 1992; Singha and Gorelick, 2005], or surrounding a column or object under examination, as in laboratory or lysimeter‐based studies [e.g., Binley et al., 1996; Koestel et al., 2008]. In some cases, deployment in contact with the water surface above the area of investigation (i.e., waterborne) has proved to be effective [e.g., Slater et al., 2010].

Geophysical methods based on electromagnetic induction (EMI) offer greater range of both application and scale of investigation than electrical methods. These methods may be deployed on the ground surface (manually or using towed platforms), in boreholes, and also in an airborne manner. Depth of investigation is controlled by varying the excitation frequency or separation of electromagnetic coils. Alternatively, depth information may also be obtained from the analysis of time dependency in a measured transient signal response [Keller and Frischknecht, 1966].

GPR methods are based on the recording of high‐frequency electromagnetic signals transmitted into the ground. Ground‐based surveys are used to sense signals that are either directly transmitted between antennas at shallow depths or reflected from greater depths to return to the ground surface; cross‐borehole surveys, in contrast, measure transmitted energy between boreholes [Huisman et al., 2003]. Reflection mode GPR can also be applied in single boreholes, as demonstrated, for example, by Dorn et al. [2011]. The popularity of GPR in hydrogeophysics can be attributed to the relatively high spatial resolution and the direct connectivity between radar velocity and moisture content [Topp et al., 1980]. However, in most environments the depth of investigation of ground‐based GPR is limited to a few meters because of the high attenuation of electromagnetic energy in electrically conductive porous media. GPR methods can also be used to determine information about the electrical conductivity of the subsurface, given the measurement of signal attenuation at the receiver.

Seismic methods measure the velocity and attenuation of seismic waves in order to infer information about mechanical properties of the subsurface. Like GPR, seismic methods are based on the transmission of an energy source (originating, for example, from a sledgehammer at the surface) and the measurement of a signal at a receiver (geophone). Again, like GPR, seismic methods may be used in a ground‐based or cross‐borehole configuration. New techniques have been developed to exploit the link between seismic and electromagnetic energy [Revil et al., 2014a; Sava et al., 2014].

The SP method is a passive method (i.e., there is no applied source of signal) that probes directly nonequilibrium thermodynamic processes in the subsurface. A major application of SP measurements in hydrology is sensing the flow of the groundwater, which drags the excess of ionic charges located in the vicinity of a charged mineral surface and therefore produces a (streaming) electrical current [Abaza and Clyde, 1969; Revil et al., 2003]. This approach has proven useful for estimating hydraulic properties during pumping tests [e.g., Darnet et al., 2003] and hydraulic tomography [Ahmed et al., 2014] or for mapping preferential flow paths [Ikard et al., 2012].

A relatively new geophysical technique that has shown potential for hydrological applications is nuclear magnetic resonance (NMR). Measurements can be made using downhole sondes, although the surface‐based sounding (called magnetic resonance sounding (MRS), or surface NMR (SNMR)) can provide 1‐D and 2‐D models of hydraulic properties to depths of several tens of meters [e.g., Herckenrath et al., 2012; Vilhelmsen et al., 2014].

In contrast to NMR, gravimetry is a well‐established geophysical technique. The method was originally developed for exploration and geodesy purposes. Gravimeters can sense differences in gravity caused by local variations in density. The temporal variability in gravimetry measurements offers the greatest value of this technique in hydrogeophysical studies. Such variation due to groundwater level changes has been studied in detail since, for nonhydrological applications, this contributes a significant noise component. Such “noise” can thus represent “signal” for monitoring groundwater storage changes [e.g., Gehman et al., 2009] and constraining hydraulic parameter estimates [e.g., Blainey et al., 2007]. We also note the immense impact of the Gravity Recovery and Climate Experiment (GRACE) satellite‐based gravimetry measurements on large‐scale observations of water storage and groundwater depletion in aquifers [e.g., Yeh et al., 2006; Feng et al., 2013], although we limit this review to land‐based and airborne approaches.

A wide range of geophysical methods therefore exists, allowing us to investigate the subsurface at a range of spatial scales in a variety of survey configurations. As discussed later, some of these methods offer direct insight into the hydrological characteristics of the subsurface; furthermore, a number of methods are well suited to studying the temporal variability of subsurface processes.

2.1. Data Inversion

Typically, geophysical surveys are conducted to assess the spatial variability of a property (or changes in a property) within the study region. The translation of raw geophysical measurements to spatial patterns of geophysical parameters is usually achieved through an inversion process (Figure 3). In the 1980s, rapid growth in available computer resources needed for such inversion prompted numerous developments in inversion algorithms, leading to widely available tools that are now robust, and in many cases, capable of rapid production of 2‐D and 3‐D images of the subsurface.

Figure 3.

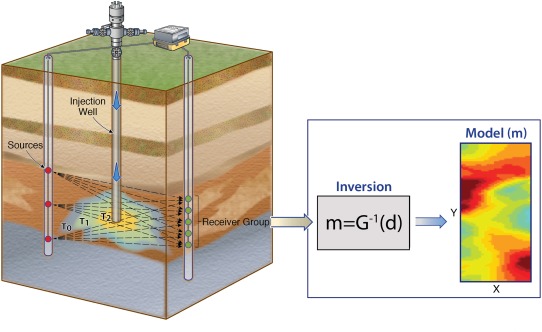
Schematic representation of geophysical data inversion. The region of interest is investigated through the measurement of responses to signal sources recorded on a number of receiver sensors. The region is discretized into a series of geophysical model parameters (m) that are consistent with the data (d) through some inverse function (G⁻¹). (left) Changes in subsurface states at different times (T₀, T₁, and T₂), which may represent evolution of a remediation process or contaminant plume. (right) The geophysical image represents a snapshot of the distribution of a geophysical property at a particular time.

Often the inversion of geophysical data is challenging because of ill‐posedness and nonuniqueness, and typically some stabilizing mechanism is needed. Originating from exploration and deep Earth studies, the introduction of regularization functions to address problems of ill‐posed, nonunique solutions by minimizing the roughness of an image [e.g., Tikhonov and Arsenin, 1977; Constable et al., 1987; Tarantola, 2005] transformed the robustness of geophysical inverse codes and opened up some of the geophysical methods (in particular electrical methods) to a broader user base. Such approaches often naturally lead to smoothed images of some geophysical property, which can be argued as introducing a priori information about the subsurface as we may expect there to be some autocorrelation of properties over length scales. However, such approaches do not typically account for our quantitative knowledge of spatial variability of properties: they recognize that it exists but in many approaches the level of smoothing does not necessarily honor explicitly the geostatistical information that may be known about the subsurface. More sophisticated inverse methods that do consider such prior information on subsurface heterogeneity have been developed in hydrogeophysics [Hyndman et al., 1994; Eppstein and Dougherty, 1998; Yeh et al., 2002; Linde et al., 2006; Hermans et al., 2012]. Introducing such additional knowledge (or assumed knowledge) of the subsurface in the inversion can have a dramatic effect on the resultant images: the spatial structure can be significantly enhanced. However, such approaches have to date been limited to synthetic studies or extremely well‐characterized research sites as applied to hydrologic systems.

Large‐scale (e.g., airborne) investigations introduce further challenges for the inversion process due to the size of data sets. Traditionally, in airborne EMI surveys, maps of apparent electrical conductivity data would be constructed or individual soundings analyzed as 1‐D (conductivity‐depth) models. However, developments in laterally constrained inversion methods [e.g., Auken and Christiansen, 2004] permit large‐scale quantitative modeling of the subsurface using airborne acquired data [e.g., Siemon et al., 2009]. The computational constraints of solving large‐scale inverse problems for a wide range of geophysical problems has prompted developments in the use of wavelet transformations to reduce the density of the sensitivity matrix [e.g., Li and Oldenburg, 2003], seek adaptive mesh parameterization [e.g., Davis and Li, 2011] and exploit highly parallel computation [e.g., Cuma and Zhdanov, 2014]. There has also been a migration toward unstructured meshes that permit better adaptation to geological structures and topography, prompting the development of new regularization strategies [e.g., Lelièvre and Farquharson, 2013] that can exploit such flexible discretization of the subsurface.

Most inversion applications in hydrogeophysics have focused on the analysis of a single geophysical modality (e.g., DC resistivity); however, joint inversion of data from multiple geophysical data types may generate greater information about the subsurface. In its simplest form, joint inversion may focus on a simultaneous inversion of geophysical data sensitive to a common property (e.g., electrical conductivity). Monteiro Santos et al. [2007] illustrated such an approach for 2‐D imaging of resistivity using DC resistivity and audio‐magnetotelluric data. In a petrophysical approach, geophysical parameters are linked through rock properties (such as porosity or water content) to constrain the inversion. In this approach, the problem is often solved with a priori knowledge of some physical relationships between the parameters controlling the geophysical data [e.g., Hoversten et al., 2006]. The drawback of this approach is that the final model is a function of the a priori relationship, which may be poorly known and not necessarily constant within the area of investigation. In a structural approach, it is assumed that spatial changes in geophysical parameters are related, irrespective of any common petrophysical relationship, i.e., changes in one parameter should coincide with changes in another parameter. The simple concept of cross‐gradient constraints introduced by Gallardo and Meju [2003] has provided a flexible approach for addressing structural inversion of geophysical data (see also review by Gallardo and Meju [2011]). Linde et al. [2006] illustrated the use of this approach in hydrogeophysics, using cross‐borehole DC resistivity and GPR data. The resulting jointly inverted images (Figure 4) were then analyzed to determine bivariate trends in electrical conductivity and permittivity, revealing different lithological units at the study site.

Figure 4.

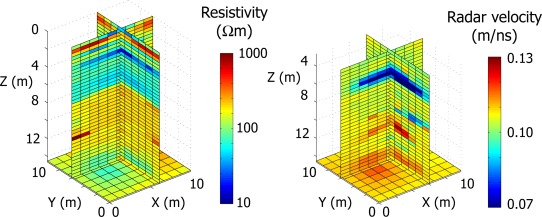
Example joint inversion of cross‐well ERT and GPR data in the unsaturated zone of a sandstone aquifer (modified after Linde et al. [2006]). The 3‐D volume contains regions where electrical conductivity (from cross‐well ERT) and relative permittivity (from cross‐well GPR) follow different joint relationships, which Linde et al. [2006] quantified to propose four lithological units.

As discussed later, studying the temporal dynamics of geophysical signals can provide improved knowledge of the system's behavior. Data inversion techniques have developed to exploit such approaches. Early methods relied on relatively simple comparisons of two data sets [e.g., Daily and Owen, 1991; LaBrecque and Yang, 2001]. More recently, approaches have been developed to invert multiple time‐lapse data sets simultaneously [e.g., Kim et al., 2009; Karaoulis et al., 2011].

One may consider a geophysical image as a proxy for the spatial distribution of a property of interest (e.g., permeability) and traditionally geophysical data were used in this way, i.e., the flow of information is one way: from geophysics to hydrology. However, provided adequate knowledge of the relationship between geophysical and hydrological properties (or states) is known (through petrophysical transforms) then the inversion can be cast in a coupled manner, whereby a hydrological model generates proposals (e.g., the distribution of soil water content) and the consistency with observed geophysical measurements is evaluated (often in combination with other data). Thus, the hydrological model constrains the inversion and the final result is guaranteed to be consistent with the hydrological conceptualization. Such an approach may be considered to be a truly coupled hydrogeophysical inversion as feedback between geophysics and hydrology is explicitly defined. Furthermore, artifacts resulting from traditional (potentially unphysical) regularized geophysical inversion are eliminated. Kowalsky et al. [2005] documented one of the first attempts at following such a coupled approach, using cross‐well GPR data to estimate soil water content in the vadose zone. Other examples following similar concepts include those of Looms et al. [2008], Hinnell et al. [2010], Huisman et al. [2010], Irving and Singha [2010], Scholer et al. [2011], Pollock and Cirpka [2012], Jardani et al. [2013], and Vilhelmsen et al. [2014]. A further advantage of these methods is the natural ability to incorporate other data sources within the inversion; thus, the geophysical data merely represent one of several possible data sources. The disadvantages of such coupled inversion approaches are (1) greater computational burden and (2) the reliance on uncertain petrophysical relationships linking geophysical and hydrological quantities. Moreover, adopting such an approach enforces the prior hydrological conceptualization and thus relies on adequate confidence in the hydrological conceptual model. In some cases one may wish to explore the geophysical data independent of prior hydrological conceptualizations to reveal new insight rather than simply affirm prior assumptions of a system.

Oware et al. [2013] offer an interesting alternative to the coupled approach by training images generated from a hydrogeological model within a framework that solves for sets of geophysical parameters with overall reduced dimensionality. They demonstrate that, under conditions of high uncertainty in the underlying hydrogeological model, their approach is superior to conventional smoothed or coupled inversions. Others have solved directly for hydrologic parameters of interest, such as plume moments or geometry [Day‐Lewis et al., 2007; Miled and Miller, 2007; Pidlisecky et al., 2011], effective velocity and dispersivity [Koestel et al., 2008]. As in many areas of natural science, data may be used to support or to illuminate: the choice of inversion scheme will depend on the focus of the investigation and the level of a priori knowledge of the system.

2.2. Measurement Scale

As noted earlier, a significant advantage of geophysical measurements over many traditional subsurface observational approaches is the greater measurement support volume that they offer. Western et al. [2002] already highlighted that the limited support volume of conventional sensors can constrain the value of hydrological process data.

We consider two aspects of measurement scale here. First, by conducting geophysical surveys over transects along the surface, or, for example, between boreholes, we can assess variability over some survey scale. Second, each individual geophysical measurement is an integrated measure, with its own support scale. The latter will constrain the spatial resolution achievable from the method, but has the advantage of characterizing properties over scales that may be more representative of the hydrological property or process under investigation. For example, the measurement of the time of flight of a radar signal between two boreholes is sensitive to the total water content along the pathway from transmitter to receiver. Thus, such a measurement can provide an integrated water content measure over several meters [e.g., Parkin et al., 2000; Binley et al., 2001; Strobach et al., 2014]. Similarly, developments in surface‐based GPR based on measurement of direct waves travelling close to the ground surface [e.g., Huisman et al., 2001; Grote et al., 2003] or using aboveground sensors [e.g., Lambot et al., 2006], offer the capability of providing mobile soil moisture sensors that sample larger volumes than normally achievable with standard point sensors. This enhanced measurement support volume is often overlooked, although it does present challenges as we strive to assess these new techniques but are constrained by verification from “acceptable” measurement approaches based on a much smaller spatial scale [e.g., Huisman et al., 2002].

The survey scale for geophysical techniques varies considerably. Some methods (e.g., surface deployed GPR, frequency domain EMI) are fully mobile and can often provide information without the need for data inversion over extensive areas. Frequency domain EM tools are particularly well suited to vehicle‐towed platforms [e.g., Sudduth et al., 2001; André et al., 2012]. Others, for example, electrical and seismic methods use grounded multisensors on cable arrays that limit the mobility of measurement arrays, as does the survey time required for an individual measurement. Time domain EMI and NMR can require extensive setup periods for ground‐based surveys, again limiting mobility. Attempts have been made to develop mobile land‐based platforms, particularly for electrical methods. Panissod et al. [1998] and Christensen and Sørensen [2001], for example, illustrated different approaches using vehicle‐towed electrical arrays, which have proved effective, particularly for relatively shallow investigations. Allred et al. [2008] discuss other vehicle‐mounted electrical measurement systems. Waterborne surveys can also be effective for greater scale of investigation. Rucker et al. [2011], for example, completed over 660 line kilometers along the Panama Canal, using a 170 m long floating electrode array.

As noted earlier, EMI methods can be used on airborne platforms. As in many other geophysical methods, airborne electromagnetic methods were originally developed for mineral resource exploration, however, the value of these techniques for large‐scale hydrogeological studies is now well established. Cook and Kilty [1992] illustrated the use of helicopter‐borne frequency domain EMI (FDEM) surveys for mapping recharge rates over an area of 32 km² in south east Australia. They established an inverse relationship between subsurface electrical conductivity and recharge rate (due to leached salts and low water content in highly recharged areas) and thus were able to utilize maps of the variation in electrical conductivity in the top few tens of meters of the subsurface to obtain immensely valuable hydrogeological information. Paine [2003] illustrated the effectiveness of FDEM surveys for mapping groundwater salinization over a 35 km² area. Kirkegaard et al. [2011] utilized helicopter‐borne time domain electromagnetic (TDEM) surveys to identify zones of low‐salinity groundwater discharging into a coastal lagoon in Denmark. Such examples demonstrate the immense power of airborne methods for surveying at regional scales.

Geophysical methods are often compared based on a measure of achievable horizontal survey scale; however, one also needs to consider the vertical (depth) scale of sensitivity that can be practically achieved. To illustrate this, Figure 5 shows a typical horizontal and vertical scale achievable in 1 day for three different methods (ERT, FDEM, and TDEM) of sensing the spatial variation in electrical conductivity. For this comparison we assume (i) a two person field crew; (ii) land‐based application, not vehicle mounted; (iii) easily accessible terrain; and (iv) a single transect survey. The comparison of horizontal and vertical scales shown in Figure 5 demonstrates the range achievable from different geophysical methods, which is important to consider in selecting an appropriate method for a given problem. FDEM methods may offer significant horizontal coverage but can lack depth of investigation, in contrast ground‐based TDEM provides superior depth of investigation but mobility is more restricted than FDEM and thus horizontal coverage is limited. ERT offers greater flexibility in horizontal and vertical coverage by adjusting electrode spacing. The examples in Figure 5 show spatial coverage for 1 and 5 m electrode‐spaced ERT arrays: greater depth of investigation is achievable for larger spacing of electrodes, although both horizontal and vertical resolution deteriorates.

Figure 5.

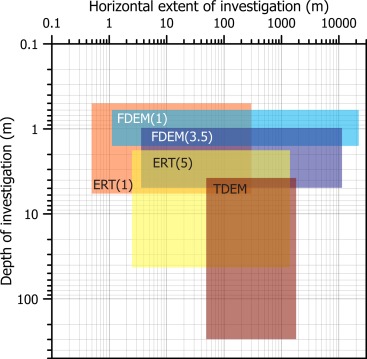
Comparison of horizontal and vertical survey scales typically achievable in 1 day by a two person field crew for ERT, FDEM, and TDEM. ERT(1) and ERT(5) refer to 1 and 5 m spaced electrode arrays, respectively. FDEM(1) and FDEM(3.5) refer to 1 m coil and 3.5 m coil instruments, respectively. For TDEM, we assume a 50 m loop sounding at multiple stations along a transect.

3. Hydrogeophysical Relationships

Constitutive relationships that link measured geophysical parameters to hydrological properties (or states) are essential for reliable hydrological interpretation of geophysical data (Figure 6). A number of relationships have long been established [e.g., Archie, 1942]; however, over the past two decades we have seen significant exploration into new theoretical or empirical models connecting hydrogeological properties and processes to geophysical observables. Some of this work has been driven by new insight into microscale mechanisms, new ways of simulating the effective properties of porous media, and also the arrival of new measurement techniques.

Figure 6.

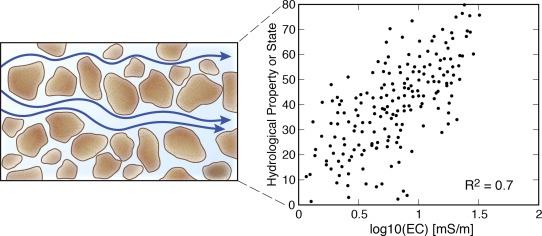
Illustration of hydrogeophysical relationships in porous media. The blue arrows represent electrical pathways at the pore scale. At some representative volume, the macroscopic measurement of electrical conductivity (EC) is linked to some property (e.g., porosity) or state (e.g., fluid saturation).

The work of Topp et al. [1980] (the second most cited paper in Water Resources Research) provided empirical polynomial relationships for mineral and organic soil that link soil moisture to dielectric properties or permittivity. The models underpin the now routinely used time domain reflectometry (TDR) method for soil water content measurement [Robinson et al., 2003] but also provide a valuable relationship for linking GPR‐derived radar velocities to soil moisture content, since the radar velocity is inversely proportional to permittivity. Further studies of soil permittivity [Saarenketo, 1998] and rock permittivity [Chelidze and Gueguen, 1999] have explored frequency dependence (for example in the experimental studies of West et al. [2003], the effective medium modeling work of Chen and Or [2006], or the volume averaging approach of Revil [2013]), which is important to develop appropriate relationships for typical GPR frequencies (often lower than those used for TDR). Investigations of, and insight into, links between soil water content and electrical conductivity of porous media have also continued [e.g., Mualem and Friedman, 1991; Roberts and Lin, 1997; Brovelli et al., 2005; Revil, 2013]. An improved understanding of the role of textural properties on bulk permittivity and conductivity behavior has also been achieved [Friedman and Robinson, 2002; Brovelli and Cassiani, 2011]. While most investigations exploring rock physics relations for GPR have focused on classical porous media, Comas and Slater [2007] and Parsekian et al. [2012] examined the unique characteristics of peat in order to derive ways of estimating biogenic gas content in peat bogs using permittivity measurements derived from GPR.

Most constitutive relationships for GPR have been developed at the scale of a representative homogenous medium; however, several researchers have identified potential bias in assuming these relations hold in layered [e.g., Chan and Knight, 1999; Robinson et al., 2005] or heterogeneous [e.g., Moysey and Knight, 2004] media, with clear implications for interpretation of field data.

Models that link permeability to measurable geophysical properties have been the quest of many researchers over the past few decades, and continue to drive many hydrogeophysics studies. As illustrated by Worthington [1977], Urish [1981], and Purvance and Andricevic [2000], electrical conductivity and permeability relationships do not universally hold because of the surface conduction mechanisms in finer grained media. Recognizing this, Revil and Cathles [1999] provided a mechanistic framework for linking electrical conductivity and permeability in both clean and shaly sands; Doussan and Ruy [2009] later proposed the incorporation of a measurement of clay content to account for such surface conduction (although we note here that the clay mineralogy, not only the content, is important in accounting for surface conduction). Even totally clean (clay‐free) rock formations exhibit an appreciable amount of surface conductivity for freshwater aquifers [see Revil et al., 2014b], a point often neglected in hydrogeophysics. The challenges associated with electrical conductivity‐permeability models have driven recent research into utilizing measures of the ability of the porous medium to polarize electrically to infer permeability.

Induced polarization (IP) is a well‐established technique, originally developed for mineral exploration, which provides a measure of how well a material polarizes due to an applied electrical field. If we assume that the polarization occurs along the (charged) grain boundary, or at pore throat constrictions, then the extent of polarization is related to geometrical characteristics of the pore space that also influence permeability. Thus, while electrical conductivity is principally sensitive to the pore volume and its connectivity, IP offers an additional measure of a grain/pore throat size effect. Slater and Lesmes [2002] illustrated the link, in an empirical sense, between a measure of polarization and permeability in unconsolidated sediments. Slater et al. [2014] extended this further for highly permeable sands and gravel mixtures in a cobble framework. This recent study highlights some of the limitations of using IP: while it may be possible to differentiate low‐permeability and high‐permeability units, to accurately resolve permeability in a coarse‐grained matrix is extremely challenging in a field setting given the weak polarization characteristic of such media relative to the resolving power of current field instrumentation.

Extending IP measurements into the frequency domain permits an assessment of the time (or distribution of times) taken for the electrical polarization to return to equilibrium (i.e., relaxation times). Binley et al. [2005] explored such measurements in their study of sandstone permeability and illustrated, for the first time, a clear positive relationship between a measure of an effective electrical relaxation time and permeability. Revil et al. [2012a] developed an approach connecting the relaxation times of IP and the intrinsic formation factor to permeability. The relationships developed were, however, empirical and their universality is questionable. Developments of mechanistic models, however, have started to provide some insight into the potential link between IP measurements and permeability [e.g., Revil, 2012, 2013] (Figure 7).

Figure 7.

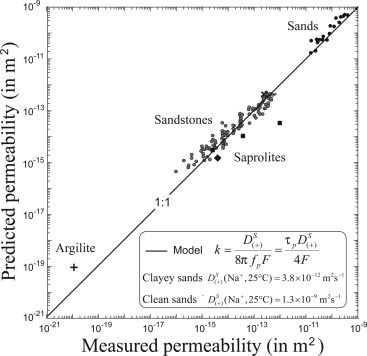
Comparison of permeability (k) modeled from SIP measurements of an electrical time constant ( ${\tau }_p$) or relaxation frequency (f_p) and measured permeability (modified from Revil [2013]). Here $D_{(+)}^S$ is the diffusion coefficient of cations in the Stern layer of the electrical double layer, and F is the formation factor.

More mechanistic models are also being developed in order to fully exploit the possible value of using measurements of patterns of the natural voltage (SP) in the subsurface to infer hydrological states, for example, water table elevations [Revil et al., 2003] and pore water velocity [Ikard et al., 2012]. Revil and Mahardika [2013] took such approaches further by also considering seismoelectric sources in their unified, coupled model of hydromechanical and electromagnetic disturbances in porous media. They provided a general framework that might be used with harmonic pumping tests to jointly invert hydraulic heads, ground deformation, and SP signals in order to image permeability and the specific storage around wells in confined and unconfined aquifers.

Geophysical use of NMR was originally developed in the oil industry. These measurements directly sense the water component, as, when hydrogen atoms located in a static magnetic field are stimulated by a secondary alternating electromagnetic field, they produce a magnetic field. Studies into the links between NMR signals and pore size distributions [e.g., Hinedi et al., 1993, 1997; Stingaciu et al., 2010; Mohnke and Hughes, 2014] and extensions to water retention models [Costabel and Yaramanci, 2013] have been explored. It is perhaps the potential of using these measurements to infer permeability [e.g., Ioannidis et al., 2006; Gladkikh et al., 2007; Dlubac et al., 2013] that offers the greatest possible impact. As in the case of electrically based models, NMR‐permeability relationships still remain empirically based and are likely to be site specific.

Recognizing the potential sensitivity of geophysical properties to subsurface contamination, a number of studies have explored the geophysical response to changes in groundwater quality, particularly for nonaqueous phase liquids. Hedberg et al. [1993] demonstrated the sensitivity of NMR measurements to the different fluid phases of gasoline‐saturated sandstone, while Li et al. [2001] illustrated how the bulk dielectric behavior of soils is affected by the sorption of oil onto the grain surface. In their experimental study, Shefer et al. [2013] revealed the effect of decane (as a nonaqueous phase) on the electrical polarization of soils, showing an apparent change in the dominant relaxation time of the sample as the concentration of decane changed. The SP method has also been used with success to determine the redox potential of some organic‐rich contaminant plumes [Revil et al., 2010]. Minsley et al. [2007] showed, through a field‐based investigation, how SP measurements are sensitive to tetrachloroethylene (PCE) and trichloroethylene (TCE) contamination at the Savannah River field site, although they acknowledge that more insight into the mechanisms influencing measurable natural voltages in the subsurface is needed. In fact, most studies to date on contaminant‐geophysical behavior have been purely empirical and an overarching physicochemical model that explains observed geophysical signals is currently lacking. Given the complexity of physicochemical processes within contaminated porous media, the search for universal models that link geophysical signals to contaminant characteristics is likely to be futile.

4. Characterizing Hydrogeological Heterogeneity With Static Geophysical Data

During the late 1970s/early 1980s, the role of aquifer heterogeneity on solute transport in groundwater was realized, along with the inadequacy of traditional lumped representations of aquifer properties for predicting the fate of subsurface contaminants [e.g., Gelhar, 1986]. A large number of studies explored these issues in the new field of “stochastic groundwater hydrology,” mainly focusing on the impact of spatial variability in hydraulic conductivity on solute transport and the possible representation of such heterogeneity through effective parameters [e.g., Pickens and Grisak, 1981; Gelhar and Axness, 1983; Gomez‐Hernandez and Gorelick, 1989; Dagan, 1990], leading to a greater appreciation of the effect of spatial‐scale effects on solute transport behavior [e.g., Gelhar et al., 1992; Neuman, 1990]. Driven by some of these studies, the influence of soil heterogeneity on hillslope rainfall‐runoff responses was also explored [e.g., Binley et al., 1989; Merz and Plate, 1997].

A number of large‐scale tracer experiments, for example at the Cape Cod site [LeBlanc et al., 1991] and the Borden site [Woodbury and Sudicky, 1991], provided new experimental insight into solute transport processes; however, the need for better tools to characterize heterogeneity at the field scale was evident. This was already recognized in the review of stochastic hydrology by Gelhar [1986], who commented: “Future research should be directed to finding better methods of estimating input covariance parameters including improvements in statistical methodology as well as on indirect methods based on geophysical and geologic information or bulk hydraulic properties.” Following this recognition, the use of geophysics to aid characterization was indeed explored in some large‐scale tracer transport studies. For the Canadian Twin Lake tracer tests [Moltyaner and Wills, 1991], over 5 km of GPR survey data were collected and used to support interpretation of borehole core logs to develop hydrostratigraphic profiles [Killey and Moltyaner, 1988]. Perhaps more significant, however, is the geophysical work conducted at the Macrodispersion Experiment (MADE) site in Columbus, Mississippi in the late 1980s. DC resistivity, EMI, and SP surveys were conducted over the site with a view to determining geostatistical models that could relate to hydraulic conductivity variability through relatively simple, assumed, hydrogeophysical relationships. Although the EMI data proved ineffective, Rehfeldt et al. [1992] reported computed correlation lengths from the DC resistivity and SP data and compared these against those computed from more direct measures of hydraulic conductivity. This was the first study where geophysical data were used to infer statistical properties of the spatial structure of hydraulic properties, and this work no doubt helped to trigger greater interest in the use of geophysical data for quantitative subsurface characterization.

By the early 1990s, several stochastic hydrology methods had been developed that helped provide information about the spatial structure of aquifer permeability given localized measurements of permeability (e.g., from core samples) and piezometric head data; however, most of these approaches were limited in a practical sense from the lack of data with a high spatial sampling density. Rubin et al. [1992] recognized the value of geophysical data to support such approaches and proposed a new Bayesian approach that used seismic data alongside traditional hydrology data to improve spatial models of permeability. Developments to their initial concepts using seismic data followed [Copty et al., 1993; Copty and Rubin, 1995], while Hubbard et al. [1997] explored the value of surface GPR surveys in recovering bimodal permeability structures in the vadose zone, assuming a link between permittivity and hydraulic conductivity. Also recognizing the potential of high‐resolution GPR data for near‐surface investigations, Rea and Knight [1998] explored the characteristics of GPR data in an attempt to determine geostatistical properties of sedimentary structures, from which some relation to patterns in permeability was assumed. Irving et al. [2009] later continued this work in their study of the correlation structure of soil water content using high‐resolution GPR data. In the work of Hubbard et al. [1999] an explicit framework for the computation of correlation structure information using geophysical data was developed, exploiting the availability of new (cross‐borehole) tomographic techniques. Building on the Bayesian approach originally proposed by Rubin et al. [1992], Hubbard et al. [2001] demonstrated the value of GPR and seismic data for the estimation of hydraulic conductivity distributions at the South Oyster Bacterial Transport Site, using tracer test data for verification of estimated models. This study took advantage of site‐specific relationships between geophysical attributes and hydraulic conductivity developed using colocated field measurements. In a study performed to quantify the value of different types of data for constraining numerical flow and transport models based on different data sets collected at the South Oyster study site, Scheibe and Chien [2003] found that conditioning to geophysical interpretations with larger spatial support significantly improved the accuracy and precision of subsurface model predictions, while conditioning to a large number of small‐scale (borehole‐based) measurements did not significantly improve model predictions, and in some cases led to biased or overly confident predictions.

Again with the goal of developing a model of the spatial variability of permeability, McKenna and Poeter [1995] demonstrated how cross‐well seismic tomography data can be used to identify hydrofacies, which can help constrain a permeability inverse model based on hydraulic head data. The work of Hyndman et al. [1994] and Hyndman and Gorelick [1996] followed a similar approach in that cross‐borehole seismic tomography data (Figure 8) were used to assign hydrofacies, but in these two studies the permeability of each hydrofacies was inversely estimated from solute concentration measurements from a tracer test. More recent examples demonstrating the use of geophysical data to develop hydrofacies include Parra et al. [2006] and He et al. [2014].

Figure 8.

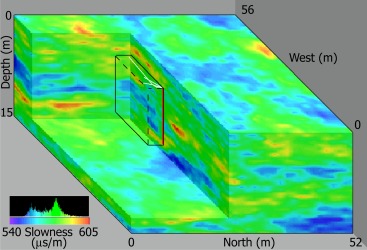
Distribution of seismic slowness at the Kesterton site (modified after Hyndman and Gorelick [1996]). The 3‐D distribution represents a realization of slowness generated using sequential Gaussian simulation, preserving the correlation lengths and probability distributions from cross‐well seismic tomograms obtained within the boxed region in the image. Hyndman and Gorelick [1996] used this information along with observations from tracer tests to compute 3‐D images of the zonation of hydraulic conductivity at the site.

Significant advances in characterizing hydrogeological heterogeneity using geophysical methods have clearly been made. The field of hydrogeophysics has progressed from using geophysics in isolation to approaches that attempt to honor multiple data types. In real problems, various data sources are likely to exist and methodologies that can incorporate the breadth of data (with variable quality) are likely to have practical value. Some approaches have focused on detailed mapping of hydraulic conductivity and although such methods are likely to have value for problems at the site scale (e.g., in groundwater cleanup operations), the approaches that extend to larger scales offer exciting potential. He et al. [2014], for example, tackle structural characterization at the scale of multiple km² by using 3‐D maps of electrical conductivity derived from airborne EM surveys along with borehole geological logs to develop hydrofacies through a transitional probably framework (see Figure 9). Such methods account for uncertainty within the hydrogeological model and are underpinned by geological reasoning, and may lead to a new era of hydrogeological structural characterization at the large scale using geophysics.

Figure 9.

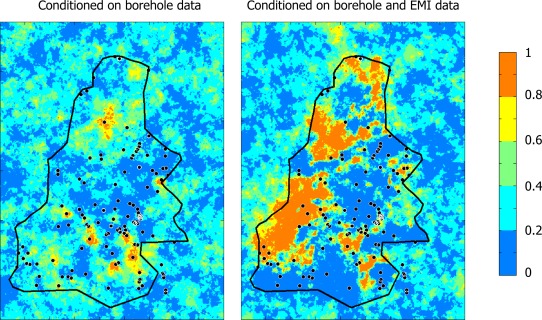
Simulated probabilities of sand fraction at a specific depth based on transitional probabilities conditioned on different data (modified after He et al. [2014]). (left) Probabilities conditioned on borehole data (locations shown as dots in the image). (right) Probabilities conditioned on borehole data and electrical conductivity obtained using airborne EMI. The black line shows the boundary of the geophysical survey. Each rectangular image represents an area of 108 km². He et al. [2014] demonstrate the value of adding the geophysical data to this structural characterization problem.

5. Time—A New Dimension for Geophysical Observations

Many of the early applications of geophysics to subsurface hydrology focused on structural characterization using static geophysical data (as, for example, shown schematically in Figure 1). Limited by the nonuniqueness of some geophysical—hydrological property relationships, many of these investigations utilized geophysical measurements as “soft” data, aiding in the identification of hydrostratigraphy. However, it was soon realized that a number of geophysical properties are sensitive to groundwater and soil states (moisture content, salinity, etc.) and thus a new avenue of research developed, utilizing geophysical methods to explore temporal changes in states (see, for example, the schematic in Figure 3). Those based on electrical conductivity or permittivity were initially explored as some of the methodologies were reaching a level of maturity and the links between electrical conductivity/permittivity and pore water composition and content were reasonably well understood.

Daily and Ramirez [1989] is one of the pioneering studies of time‐lapse geophysical imaging. They demonstrated the use of “electromagnetic geotomography” for monitoring changes in water content due to heating of rock mass (used as a preliminary experiment for examining the changes in water content in a nuclear repository setting). Their method is effectively cross‐borehole low frequency GPR, which senses variation in permittivity. The study of Daily et al. [1992] brought a major breakthrough in hydrogeophysical investigation through their demonstration of a new technology, electrical resistivity tomography (ERT), in cross‐borehole mode to examine the movement of a water tracer through the vadose zone. They ran two field experiments (one lasting one day, the other lasting 72 days) and demonstrated the capability of ERT for tracking the tracer movement (see Figure 10). Ramirez et al. [1993] took this technology further by demonstrating its effectiveness in monitoring subsurface flow pathways during steam injection for the remediation of hydrocarbon‐contaminated groundwater, using changes in electrical conductivity as a proxy for changes in temperature.

Figure 10.

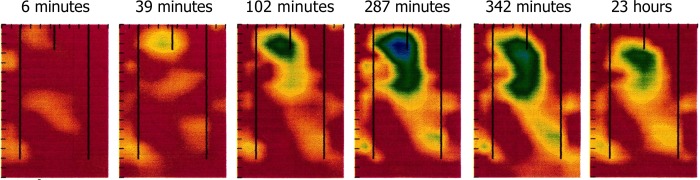
Tracking the migration of a water tracer injected in the vadose zone using cross‐well ERT (modified after Daily et al. [1992]). The images show change in resistivity at different times after injection of the tracer. The two long vertical lines indicate the 17.3 m deep boreholes (positioned 7.4 m apart). The tracer was injected in the central 4 m deep borehole (also shown). Cooler colors represent a decrease in resistivity (associated with an increase in water content). The tracer injection stopped after 150 min.

Other early time‐lapse geophysical studies include that of Binley et al. [1996], who studied the spatiotemporal changes in electrical conductivity (with ERT) in a large soil core during a tracer experiment. Their results revealed a three‐dimensional distribution of breakthrough curves, illustrating preferential flow pathways. To illustrate the high spatiotemporal sampling of transport behavior they coined the term “pixel breakthrough curves,” which was subsequently used in a number of time‐lapse hydrogeophysical studies. Zhou et al. [2001] also demonstrated the use of ERT for mapping preferential flow, in this case in a small field plot. Eppstein and Dougherty [1998], Parkin et al. [2000], Binley et al. [2001], Tsoflias et al. [2001], Alumbaugh et al. [2002], and Day‐Lewis et al. [2003] are early examples of the use of GPR for monitoring stimulated changes to the subsurface (e.g., tracer injection or well pumping).

ERT and GPR techniques deal mostly with the production of 2‐D slices of the subsurface, or limited size 3‐D volumes. In comparison, EMI has proved useful in providing time‐lapse images over relatively large spatial areas. Although capable of providing semiquantitative moisture maps [Huth and Poulton, 2007; Robinson et al., 2012], especially when combined with point sensor data, the real strength in EMI is in collecting qualitative data that identifies subsurface patterns of soil wetting and drying [Sherlock and McDonnell, 2003; Robinson et al., 2009].

Most of these early examples served as demonstrations of techniques and provided only qualitative interpretation of time‐lapse geophysical signals. Binley et al. [2002] is one of the first attempts to use time‐lapse geophysical data from the field (in this case, cross‐borehole ERT and GPR) to calibrate a hydrological model in a study of flow in an unsaturated sandstone. Kemna et al. [2002] and Vanderborght et al. [2005] also showed how time‐lapse geophysical data (ERT) could be used to help quantify hydraulic properties. Kowalsky et al. [2005] also demonstrated the value of time‐lapse geophysical data for hydraulic parameter estimation. Several other studies have followed [e.g., Farmani et al., 2008; Pollock and Cirpka, 2012; Camporese et al., 2012; Busch et al., 2013; Anh Phuong et al., 2014]. From this wide range of investigations, numerous approaches are now available for hydraulic parameter estimation using geophysics as a primary or secondary source of data.

Time‐lapse geophysical imaging has also been effective in revealing new insight into subsurface flow and transport mechanisms. Singha et al. [2007], for example, showed how time‐lapse electrical resistivity measurements can be used to characterize mass transfer in dual‐porosity systems [see also Swanson et al., 2012; Briggs et al., 2013]. Slater et al. [2007] demonstrated the use of electrical conductivity monitoring for revealing biogenic gas development in peat, thus offering the potential to explore, at the field scale, the mechanisms of carbon‐gas generation in peatland environments. Hayley et al. [2009], Strobach et al. [2014], and Van Dam et al. [2014], among others, have utilized time‐lapse geophysical methods to reveal complex infiltration and shallow recharge processes, contributing to our understanding of field‐scale processes.

The need to better understand the interaction of groundwater and surface water and the appreciation of the potential significance of biogeochemical processes that occur at the interface of groundwater and surface water (e.g., within the hyporheic zone) has encouraged the search for new ways of investigating this zone of interaction. Geophysical methods have provided some insight into the complexity of the architecture of the subsurface at this interface [e.g., Crook et al., 2008; Slater et al., 2010; Chambers et al., 2014]; however, time‐lapse geophysical imaging has proved to be highly effective in mapping the dynamics of vertical and lateral exchange of flows under natural conditions [Christiansen et al., 2011; Ward et al., 2012; Meyerhoff et al., 2014] and due to anthropogenic induced events [Johnson et al., 2012; Wallin et al., 2013].

One issue with time‐lapse data is the volume of data generated, and how to explore signals in those data effectively. One successful example of manipulating and parsing multiple large time‐lapse data sets is that of Johnson et al. [2012], who focused on ways to extract relevant hydrological information using time series analysis techniques applied to large data sets obtained from autonomous data collection systems. They utilized time‐frequency analysis to identify relations between river stage and bulk electrical conductivity to understand the potential impacts of uranium transport in an aquifer connecting to the Columbia River (see Figure 11).

Figure 11.

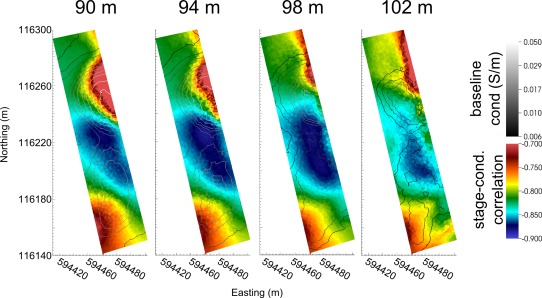
Time series analysis of ERT data (modified after Johnson et al. [2012]). The images show the correlation between the temporal variation in river stage and observed changes in subsurface electrical conductivity. The river is on the eastern edge of the imaged region. Each image is a horizontal slice at different elevations through the 3‐D volume. The horizontal slice at 98 m highlights the localized area of temporal changes in electrical conductivity that appear strongly linked to river stage change.

Such time series analysis approaches offer one way of handling such large volumes of data; another is joint inversion of hydrologic and geophysical data (see earlier discussion on data inversion). Numerous techniques have evolved in recent years, including methods that focus on using tomograms themselves, which include the errors from inversion, to those based on hydrologic and geophysical data directly [e.g., Hyndman and Gorelick, 1996; Kowalsky et al., 2005; Looms et al., 2008]. Markov chain Monte Carlo methods are growing in popularity for jointly inverting hydrologic and geophysical data [Hinnell et al., 2010; Huisman et al., 2010; Irving and Singha, 2010; Laloy et al., 2012]. Such schemes offer future potential for parsing these large, complex hydrogeophysical data sets.

6. Biogeophysics: Adding a Biogeochemical Dimension

As outlined above, early hydrogeophysical studies focused on characterizing the hydrogeological structure of the subsurface, in many cases motivated by the need to predict the fate of subsurface contaminants. Driven by the legacy of former industrial and military operations, some studies began to focus attention on using hydrogeophysical methods to assist in designing, and monitoring the effectiveness of, remediation techniques. Initially, these studies attempted to address the need for better understanding of subsurface heterogeneity in order to provide a hydrological structure in which the biogeochemical mechanisms could be assessed. The study by Hubbard et al. [2001] at the South Oyster Bacterial Transport Site is a key example of such work. Here multiple geophysical techniques were used to develop a permeability model, with which the transport of bacteria injected into the site (for bioremediation) could be assessed.

It was soon realized that some geophysical measurements may offer additional value beyond describing the physical heterogeneity of the subsurface. Although both sediment physical and mineralogical properties play a critical role in controlling the geochemical and biogeochemical processes occurring in the subsurface, field studies typically acquire little or no mineralogical data. Because several geophysical attributes are influenced by sediment texture, and because mineralogy often covaries with texture, geophysical methods can potentially be used to characterize mineralogy. As a first illustration of this concept, Chen et al. [2004] used a stochastic approach and GPR data to estimate subsurface ferric and ferrous iron distributions, estimates that were in turn used to improve reactive transport simulations of redox‐sensitive process at the South Oyster site [Scheibe et al., 2006]. The recent work of Sassen et al. [2012] and Wainwright et al. [2014] developed and field tested a “reactive facies” concept focused on using geophysical methods to characterize subsurface units having distinct and linked physicochemical properties—a reactive transport equivalent (conceptually at least) to the much earlier hydrofacies mapping of Hyndman et al. [1994], McKenna and Poeter [1995] and others (see Figure 12).

Figure 12.

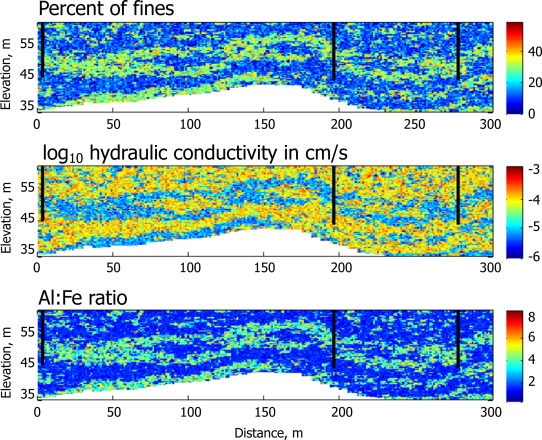
Reactive facies‐based transport properties along the centerline of the uranium‐contaminated Savanah River Site F‐Area plume (modified after Wainwright et al. [2014]). Stochastic approaches were used to integrate multiscale, multitype measurements (including surface seismic data), providing estimates of hydrological and mineralogical properties important for controlling plume behavior to a reactive transport model—in high resolution and over plume‐relevant spatial extents. (top) Estimated percent fines, (middle) hydraulic conductivity (log₁₀ cm/s), and (bottom) Al‐Fe ratios.

Geophysical surveys have also assisted in developing biogeochemical conceptual models at contaminated sites, using, for example, electrical conductivity as a proxy for oxidation‐reduction processes [e.g., Lendvay et al., 1998]. The challenge is to use geophysical properties as indicators of complex biogeochemical interactions at the field scale. Controlled laboratory experiments (e.g., as reported in Williams et al. [2005], Chen et al. [2009], Regberg et al. [2011], and Revil et al. [2012b]) are necessary to assess the value of geophysical measurements for quantifying biogeochemical processes and products. Whereas electrical conductivity may remain an ambiguous measure for such purposes (since it is controlled by physical and chemical states of the porous medium and its fluids), measures of the electrical polarization of porous media have shown greater potential in the context of biogeochemical characterization, given that these measures are more directly sensitive to grain/mineral surface processes. For example, Williams et al. [2009] used time‐lapse field IP data to infer spatiotemporal variations in groundwater geochemistry due to microbial iron and sulfate reduction induced through bioremediation and Vaudelet et al. [2011] illustrated the different electrical polarization responses of silica sand with sorbed copper and sodium ions.

Despite the progress made, a reality check is prudent here to insure against unrealistic expectations of geophysical measurements with respect to extractable information on biogeochemical processes. Many biogeochemical processes involve a multitude of physical, chemical, and/or biological transformations, some of which may generate geophysical signatures [Atekwana and Atekwana, 2010]. Whereas it may be possible to use time series of geophysical data to ascertain when, where, and even how quickly biogeochemical transformations are occurring, the complexity of these transformations limits the use of geophysical measurements alone to quantify geochemical reactions involved or to quantify reliable reaction rates at the field scale. However, recent developments have indicated how the integration of time‐lapse geophysical and aqueous geochemical data sets can be used to estimate the onset and spatiotemporal distribution of biogeochemical transformations, including critical redox transitions [Chen et al., 2009, 2013]. Similarly, although geophysical data sets may increasingly be used to highlight hot spots of biogeochemical activity, for example associated with biodegraded contaminant plumes, quantifying concentrations of microbes or aqueous/solid phase by‐products of microbial activity from geophysical observations is currently unlikely. However, laboratory electrical geophysical measurements have been shown to produce time‐lapse data that mimic the shape of classical bacterial growth curves [Slater et al., 2009; Revil et al., 2012b], suggesting that characteristics of electrical data sets could be used to infer some information on microbial growth rates (see Figure 13).

Figure 13.

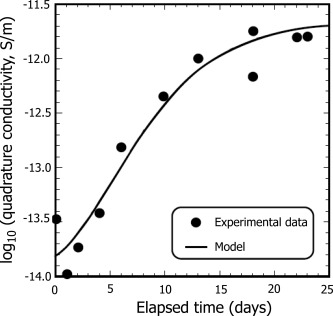
Modeled and measured change in quadrature electrical conductivity (from IP) during bacterial growth (modified after Revil et al. [2012b]).

6. Applications to Ecosystem Science

Recognizing the two‐way interaction between hydrological and ecological systems, many hydrological investigations are nowadays linked to some ecosystem response; geophysics is suited to addressing such issues and wider ecosystem questions [Jayawickreme et al., 2014]. For example, as nitrate concentrations in an aquifer rise, recharge to a river or lake can have significant impact on the ecosystems that depend on the surface water body. Similarly, as we strive to address the agricultural demands of the planet, we must appreciate the subsurface water environment that crops (and hence livestock) depend on [Sudduth et al., 2001]. Hydrogeophysical methods have evolved relatively recently to address such ecohydrological problems.

Some key questions in ecohydrology include: What controls the spatial patterns of vegetation? How do these spatial patterns influence local hydrology? How will hydrological and vegetation interactions evolve with global change? How do these interactions influence the transfer of macronutrients to and from the terrestrial environment? At the field and small catchment scale, addressing these questions often presents a challenge because soil survey data often only provide qualitative information.

The work of Holden [2005] is an excellent early illustration of the value of hydrogeophysics for exploring the link between surface vegetation species and piping in peatland catchments. He investigated the occurrence of soil pipes in 160 UK peat catchments using a total of 115 km of GPR data. By simultaneously mapping vegetation species in each plot, a link between Calluna species and soil pipe occurrence was established that suggested that Calluna root development enhanced preferential flow in these northern peatland environments.

EMI and electrical methods have also proved useful in addressing ecohydrological issues. EMI has been used to investigate links between soil and vegetation spatial patterns in dryland ecosystems [Robinson et al., 2008b, 2010; Cassiani et al., 2012] and in the tropics [Bréchet et al., 2012]. Recently, Franz et al. [2011] used EMI surveys of electrical conductivity to reveal how soil water patterns are influenced by, and influence, vegetation in a Kenyan dryland environment (see Figure 14). Frequency domain, ground‐based EMI methods were once considered primarily as reconnaissance tools for qualitative mapping, however, there has been renewed interest given recent developments in multicoil instrumentation, which now offer the potential for rapid surveying of electrical conductivity at multiple depths [e.g., Dafflon et al., 2013; Doolittle and Brevik, 2014; von Hebel et al., 2014].

Figure 14.

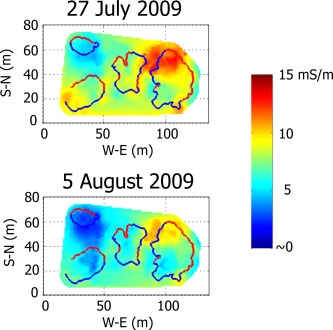
Electrical conductivity maps obtained from EMI surveys at a Kenyan dryland site (modified after Franz et al. [2011]), showing electrical conductivity variations over time, reflecting moisture content changes in patches of Sansevieria volkensii following a 6 mm rainfall even on 24/25 July 2009. The blue boundaries indicate surface run‐on zones; red boundaries show surface runoff zones. More noticeable changes in electrical conductivity, and hence soil moisture, occur inside the S. volkensii patches than in the interpatch areas. Franz et al. [2011] hypothesized this to be due to low infiltration within the interpatches, coupled with capture of run‐on and increased infiltration in the S. volkensii patches.

DC resistivity has proved valuable for understanding soil moisture wetting patterns, redistribution, and vegetation uptake. Jayawickreme et al. [2008] used it to monitor the influence of climate and vegetation on root‐zone soil moisture, bridging the intermediate‐scale gap between remotely sensed and in situ point measurements. They went on to infer the hydrological consequences of land‐cover change [Jayawickreme et al., 2010]. The ability to penetrate to substantial depth allows for monitoring of deep rooted trees which is infeasible using other methods. For example, Davidson et al. [2009] used DC resistivity to study deep (>11 m) rooting soil‐water uptake in Amazonian woodlands during drought. Moreover, the sensitivity to salinity allowed Jackson et al. [2005] to use it to show that the planting of eucalyptus in shallow groundwater areas of Argentina had resulted in groundwater salinization. Other recent examples illustrating how electrical methods can help with understanding ecohydrological linkages include that of Comte et al. [2010], who showed, through electrical imaging of the subsurface, how vegetation can influence the development of freshwater lenses in a small coral island. Befus et al. [2013], in contrast, used electrical imaging to examine thermal buffering of intertidal zones by coastal groundwater systems, and highlight the ecological significance of such processes for maintaining the habitat of marine ecosystems.

Geophysical methods have also been used to study hydrological processes associated with managed ecosystems, such as agricultural sites [Allred et al., 2008]. Examples include the use of soil moisture to map vineyard water content and its influence on grapevine vigor [Lunt et al., 2005] and the joint use of EMI and gamma‐radiometric approaches to estimate cation‐exchange capacity and clay content in cereal and sugarcane farms [Rodrigues et al., 2015]. Time‐lapse geophysical monitoring has also been useful for understanding the effectiveness of irrigation. For example, Michot et al. [2003] applied resistivity imaging to monitor wetting patterns under irrigated corn (Figure 15); more recently, Garré et al. [2011] illustrated the value of 3‐D resistivity imaging for improved understanding of root water uptake processes. Geophysical techniques are also beginning to provide data to assist plant scientists in plant breeding programs. Macleod et al. [2013] showed how ERT can support more conventional data types in identifying grass hybrids that enhance soil structure and potentially alleviate flooding potential. More recently, Shanahan et al. [2015] illustrated how EMI can help phenotype root function in wheat at the field scale.

Figure 15.

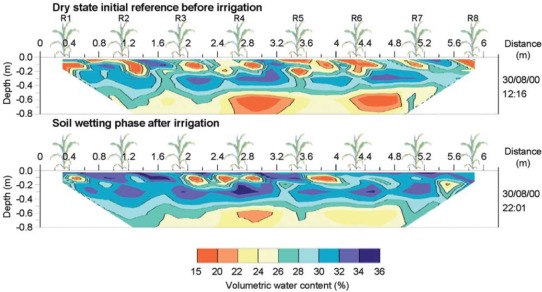
Changes in soil water content derived from ERT images, during irrigation of a corn crop (modified after Michot et al. [2003]). Thirty‐two electrodes were placed at 0.2 m spacing along the ground surface. The images show changes in soil water content inferred from changes in resistivity.

Complementing the ecohydrological studies described above, several studies have recently illustrated the use of geophysical data to investigate hydrological and other controls on subsurface production of greenhouse gasses, particularly in northern peatland and permafrost regions. Such improved understanding of interactions between hydrological and biogeochemical processes occurring within terrestrial ecosystems is required to reduce the uncertainty associated with global climate predictions [Friedlingstein et al., 2014]. Terrestrial ecosystem feedbacks to climate can occur through a variety of mechanisms, including through altering the energy balance, through vegetation dynamics, and through microbial decomposition of soil organic carbon, which can release a large amount of carbon back into the atmosphere as CO₂ and CH₄. Quantifying controls on greenhouse gas fluxes in terrestrial ecosystems is challenging due to the wide range of interactions that occur in and across different compartments of the ecosystem, including vegetation, land surface, and the subsurface.

A review of several studies given by Comas and Slater [2009] describes the use of GPR to characterize the stratigraphy of peat systems and examine controls on CH₄ production dynamics in these systems, including peat structure [Comas et al., 2014] and atmospheric pressure [Comas et al., 2011]. Permafrost systems, which are vulnerable to climate change because large volumes of organic carbon are locked up in the currently frozen but gradually warming permafrost, have also been a focus of recent hydrogeophysical studies. In particular, geophysical methods have been used to characterize the nature and distribution of properties within all compartments of these systems, including the permanently frozen zone [e.g., Dou and Ajo‐Franklin, 2014; Hauck et al., 2010] and the active layer [e.g., Brosten et al., 2009]. A few new directions have emerged from these early studies that appear to be useful for developing insights about how these complex systems function and for tractably providing information over scales relevant for predicting ecosystem feedbacks. One is the use of airborne data sets to characterize the spatial variability of specific compartments of the system over large spatial extents, including permafrost using EMI [Minsley et al., 2012] and the active layer using LiDAR [Gangodagamage et al., 2014]. The other is the coincident use of multiple above and belowground geophysical data sets to characterize the covariation of permafrost, active layer, and land‐surface properties, and to use that information to delineate functional zones in the landscape that have unique distributions of properties that influence greenhouse gas fluxes [Hubbard et al., 2013].

The consideration of hydrogeophysical methods in ecosystem studies will no doubt continue to grow because of the unique ability of hydrogeophysical measurements to provide spatially continuous information on the shallow subsurface at the same landscape scale that is fundamental to understanding many ecosystem processes. As already advocated by Robinson et al. [2008a], a top‐down multiscale approach to ecosystem characterization seems ideal to make progress here. In such an approach, joint semiquantitative interpretation of multiple geophysical data can provide meaningful delineations of landscape units that can be used to guide more detailed and quantitative site investigations. Ideally, such an approach simultaneously provides the much needed spatial context to local‐scale investigations, and ensures that local‐scale investigations are performed at representative sites that capture landscape heterogeneity.

7. Future Directions

Despite the significant developments in both theoretical and experimental aspects of hydrogeophysics, as illustrated above, many challenges remain as we seek to better understand the subsurface hydrological and biogeochemical processes, and their interaction with ecosystems. We highlight here a number of areas worthy of future research within hydrogeophysics.

8.1. Watershed Systems: Key Controls and Characteristics

One of the key drivers for hydrogeophysics is the potential for mapping subsurface patterns over large areas. Much of the development to date, however, has been directed at plot‐scale (i.e., tens of meters) experiments. Just as environmental regulators have established procedures for dealing with point source groundwater pollution but still struggle to manage diffuse source contamination, we have seen immense development of local‐scale characterization in hydrogeophysics, but very little addressing problems at larger scales or beyond. For example, while cross‐borehole methods may provide high‐resolution information about geophysical properties, which may help quantify hydrological and biogeochemical parameters, they still have limited spatial extent. A few exemplars of large‐scale mapping do exist, however, such as the aquifer mapping of Denmark, where successful attempts have been made to utilize ground‐based and airborne geophysical surveys to aid the production of high‐resolution maps of aquifer bodies in order to develop reliable groundwater protection strategies [Thomsen et al., 2004]. We see an increasing trend in geophysical methodologies to characterize and monitor systems over watershed and landscape scales, or scales that are relevant to the management of systems for environmental remediation, water resources, agriculture, and carbon cycling challenges. We also anticipate an increasing trend in the strategic deployment of plot‐scale experiments to reveal dominant mechanisms that have an impact at the larger scale, and to quantify hot spots (locations in space that exert an inordinate control on larger system behavior) and hot moments (sporadic periods in time associated with high levels of activity). In attempting to understand the transfer of macronutrients from terrestrial to freshwater environments, for example, it may be valid to focus attention along the zone of exchange (i.e., “hot spots”), rather than in the entire watershed [e.g., Binley et al., 2013]. Furthermore, using geophysical techniques to help with the understanding of biogeochemical processing at the interface of groundwaters and surface waters (e.g., within the hyporheic zone) could be extremely beneficial to tackle the problems faced with managing diffuse pollution, particularly if such techniques can be applied over large scales.

7.1. Ubiquitous and Autonomous Environmental Sensing

The need to characterize over larger scales and monitor key dynamics with sufficient temporal resolution has been driving the development of new sensing approaches and platforms. For example, autonomous electrical resistivity tomographic methods are becoming commonly used for monitoring moisture content dynamics with high temporal and spatial resolution. Fiber‐optic based distributed temperature sensing methods [e.g., Selker et al., 2006] have recently enabled catchment hydrological monitoring over greater scales of investigation and with significantly increased temporal and spatial resolution relative to conventional approaches. Technological developments in Distributed Acoustic Sensing (DAS) technologies emerging from the oil exploration industry [e.g., Mateeva et al., 2014], may similarly enable improved characterization of subsurface systems, including permafrost dynamics. At much larger scales, the opportunities presented by airborne methods become interesting. The study of He et al. [2014] illustrated how electrical conductivity data obtained from an airborne platform can be integrated into a stochastic geological modeling environment, covering an area of over 100 km² (see Figure 9). Resolution of shallow (<10 m) structures is still relatively poor with such surveys, but the technology is developing and improvements tailored to shallow mapping are emerging. Natural gamma surveys are proving particularly useful for mapping mineral soils [Cook et al., 1996] and even soil organic carbon (SOC). Rawlins et al. [2009] showed that the precision of regional predictions of SOC across Northern Ireland was substantially improved by using auxiliary information on radiometric potassium from airborne surveys. The challenges associated with both scale and cost of traditional airborne sensing approaches are likely to be mitigated by the rapid development of unmanned land and aerial vehicles. In particular, technological innovations associated with unmanned aerial vehicles (UAVs) (which are allowing longer flight times, multiple sensor payloads, and cheaper cost) are expected to greatly accelerate the ability to monitor natural environments.

7.2. Data Fusion and Assimilation

The majority of hydrogeophysical applications to date have focused on single modality data sets (i.e., one geophysical measurement approach). Combining multiple single modality surveys is relatively straightforward and thus “stitching” data sets to form composite data sets covering a large area is achievable. However, in many cases we may be armed with data from multiple modalities, measuring different properties, in different configurations, with different depths of investigation and measurement support volume (e.g., Figure 5). Rather than treating each data set independently, we should endeavor to formulate a single coherent image (model) of the subsurface. Coupled hydrogeophysical inversion approaches, as discussed earlier, go some way toward achieving this goal, but no generalized approach currently exists and more work is needed to provide practical solutions that do not depend on substantial a priori knowledge of the subsurface.

7.3. Uncertainty and Information

Uncertainty in hydrological models is now well established and yet most hydrogeophysical studies fail to recognize uncertainty in geophysical models and the transfer of these to hydrology. The treatment of measurement and model uncertainty in geophysics is not new, and yet it is routinely ignored. Such failure to account for uncertainty can incorrectly portray accuracy and resolution and can lead to misleading interpretation. The computational burden of computing some form of uncertainty estimate in an inversion is probably the main cause of such failure, however, for many plot‐scale 2‐D studies computational demands should not preclude some assessment of model uncertainty. Uncertainty in model interpretation also propagates through from any constitutive relationships linking geophysical and hydrological properties, and yet these relationships are frequently assumed to be precise and error free. Greater recognition of all the contributing sources of uncertainty is needed in future studies. It may be that in some cases, geophysical data can provide little improvement over a priori estimates of some hydrological (or biogeochemical) quantity. Declaration of this limitation will not undermine hydrogeophysics.

Related to uncertainty estimation, there has also been a distinct lack of analysis of information content (or data worth) in the majority of hydrogeophysical studies. As we invest more resources for subsurface investigation it may be appropriate, in some studies, to question the worth of data during the survey design stage. JafarGandomi and Binley [2013] recently examined the information content of different geophysical data modalities using a simple Shannon Entropy measure in a Bayesian data fusion framework. One can envisage using cost functions in such an approach to deliver a realistic cost‐benefit analysis of different geophysical data types.

7.4. N = 1 Experimentation

As in other areas of field‐based experimental hydrology, we are often challenged with a sample size of one (a single hillslope, watershed, etc.). Consequently, in comparison to other science disciplines, our observations may be perceived to be anecdotal. For example, revealing preferential flow through soils in one small field plot does not necessarily demonstrate that such a phenomenon is prevalent across an entire watershed. However, there are opportunities, in some cases, for more robust experimental design that can help strengthen the value of hydrogeophysics. Where possible, comparisons against controls are needed along with more replicate studies. In a recent study, for example, Shanahan et al. [2015] used time‐lapse EMI measurements on plots each sown with one of 23 breeds of wheat, each with four replicates in a random block experimental design, to demonstrate that different breeds extract water from different depths of soil. Such experimental design may not be appropriate for many hydrogeophysical applications, but where applicable they can help steer hypothesis‐driven research. The failure to use replicates in laboratory experiments is a clear weakness of many studies of the relationships between geophysical and hydrological properties.

7.5. Emerging Application Areas

We have illustrated throughout this paper the progression of hydrogeophysics from tools for structural characterization to a means of studying the dynamics of subsurface hydrological and biogeochemical processes, and branching out to ecosystem science. We anticipate greater exploitation of geophysics for studying both natural and managed ecosystems. For example, as the need to produce more food with less resources (fertile land, fertilizer, water) increases, there is a significant opportunity to use geophysical approaches to advance precision farming and plant breeding programs. The plant sciences literature is beginning to show recognition of the potential value of geophysical methods in a wide range of areas, such as ERT and SP for monitoring root function and biomass [Amato et al., 2009; Li et al., 2015], and mapping root architecture with GPR [Hirano et al., 2012]. In his discussion on ecohydrology, van Dijk [2004] argued that: “to date, no consistent physical theory has been developed to describe the relationships between topography, ecosystem maintenance and modification of soil structure, and the alteration of soil hydraulic properties all of which contribute to the expression of plant community structure, and are fundamental to understanding the long‐term impacts of climate and land‐use change.” As previously described, geophysical approaches are now being developed to study the interactions and feedbacks between different compartments of terrestrial environments, with recent examples in peatland and permafrost ecosystems that are particularly vulnerable to climate change. New trends, such as the use of above‐and‐belowground sensing approaches and the identification of ecosystem functional zones [Hubbard et al., 2013] are expected to provide insights about how terrestrial environments are responding to climate and land use associated stresses, and the associated implications for ecosystem services, including food production, clean water availability, and carbon sequestration.

8. Closing Remarks

As illustrated with the examples reported here, the past 25 years have seen an immense growth in the development of new geophysical measurement approaches (and customization of existing methods) for investigating the subsurface environment. We have now developed greater insight into the sensitivity of geophysical parameters to processes that control the hydrological, biogeochemical and ecological functioning of the subsurface and interactions with nonterrestrial environments. The numerous works published in Water Resources Research and many other journals and texts illustrate how hydrogeophysics has emerged as an established subdiscipline of hydrology, with strong connections to many other fields, such as biogeochemistry, ecology, and near‐surface geophysics. The field is growing rapidly as emerging technologies (instruments, models) and new insights into hydrogeophysical relationships open up new areas for research and potential solutions to significant and challenging environmental problems.

Binley, A. , Hubbard S. S., Huisman J. A., Revil A., Robinson D. A., Singha K., and Slater L. D. (2015), The emergence of hydrogeophysics for improved understanding of subsurface processes over multiple scales, Water Resour. Res., 51, 3837–3866, doi:10.1002/2015WR017016.