Cell-Size Control

Abstract

Cells of a given type maintain a characteristic cell size to function efficiently in their ecological or organismal context. They achieve this through the regulation of growth rates or by actively sensing size and coupling this signal to cell division. We focus this review on potential size-sensing mechanisms, including geometric, external cue, and titration mechanisms. Mechanisms that titrate proteins against DNA are of particular interest because they are consistent with the robust correlation of DNA content and cell size. We review the literature, which suggests that titration mechanisms may underlie cell-size sensing in Xenopus embryos, budding yeast, and Escherichia coli, whereas alternative mechanisms may function in fission yeast.

Some cells (e.g., fission yeast) may regulate size geometrically, whereas others (e.g., Xenopus embryos) may regulate size by titrating a constant concentration regulator against a fixed “yardstick” (e.g., DNA content).

INTRODUCTION: CELLS MAINTAIN A CHARACTERISTIC CELL SIZE

Cells size varies greatly depending on cell type and species. Among eukaryotic cells, ∼1-mm frog oocytes (Wallace et al. 1981) are 1000 times larger in diameter than ∼1-μm phytoplankton, a billion-fold difference in volume (Palenik et al. 2007). Many soil bacteria are ~250 nm in diameter (Luef et al. 2015), whereas the largest prokaryote, Thiomargarita namibiensis, can be larger than >100 μm (Schulz et al. 1999). Even within an organism, cells of different types may be of very different sizes: human blood cells are tiny (<10 μm) compared with >1-m-long neurons.

For each type of cell, efficient function depends on appropriate size. Unicellular organisms need to proliferate in a variety of environmental contexts that exert selective pressures on cell size. Indeed, it has recently been shown that cell size correlates precisely with fitness for bacteria growing in a fluctuating environment (Monds et al. 2014). For the larger unicellular organisms, surface transport may be limiting for cell growth. Maximum transport rates of nutrients across the cell surface are expected to scale with surface area, whereas the metabolic requirements likely scale with volume. Thus, in the case of nutrient limitation, the surface-to-volume ratio may exert a selective pressure for smaller size. Consistent with this idea, the availability of atmospheric oxygen, which varies more than twofold on geological time scales, appears to be a major constraint on the cell size of ∼1-mm-diameter unicellular, marine protist, foraminifera (Payne et al. 2012, 2013). In addition, there may be constraints on the ratio of parent and offspring size in foraminifera, suggesting that there may be a limited range of cell sizes that can be controlled by a specific genome (Caval-Holme et al. 2013).

In contrast to unicellular organisms, cells within multicellular organisms experience much more constant environments, wherein nutrients are unlikely to be limiting. However, the function of these cells still strongly depends on their size. For example, blood cells must maintain a sufficiently small size to allow them to pass through capillaries, and neurons must span great distances to transduce signals down the lengths of limbs. Furthermore, defects in cell size are associated with diseases, such as Lhermitte–Duclos disease, in which increased cerebellar granule cell size leads to seizures and eventual death (Kwon et al. 2001).

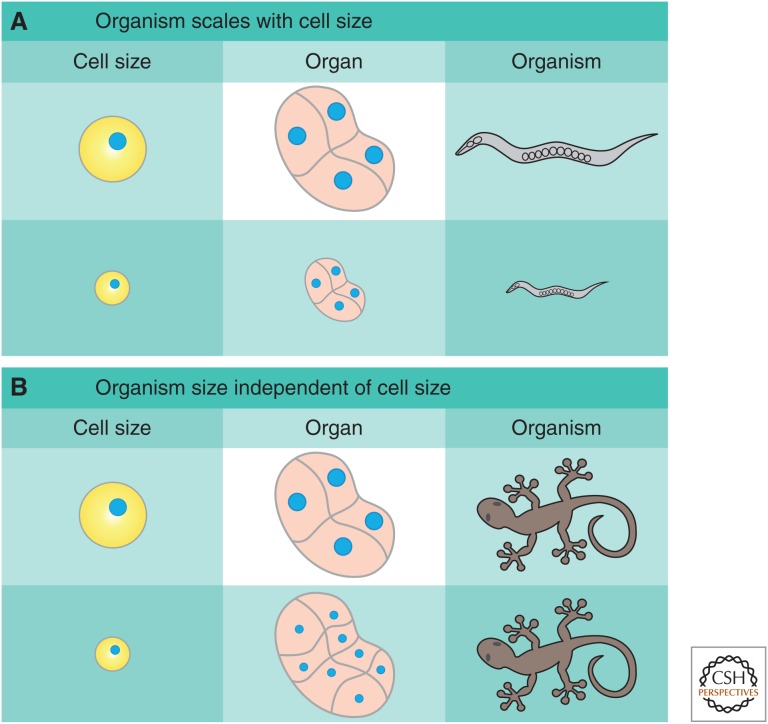
In some multicellular organisms, cell size can influence organ and organism size. This scaling is absolute in Caenorhabditis elegans, in which the cell number is fixed and perturbations to cell size result in proportional changes in organ and organism size (Irle and Schierenberg 2002; Cook and Tyers 2007; Watanabe et al. 2007). However, in a large number of species, such as the tiger salamander, alterations to cell size can be compensated for by changes in cell number to preserve organ size (Fig. 1) (Fankhauser 1945). In addition, forcing proliferation in fly wing imaginal discs alters cell size, but triggers sufficient apoptosis to maintain organ size (Neufeld et al. 1998). We refer the reader to Roth and Walkowiak (2015) and Penzo-Méndez and Stanger (2015) for further discussion of organ size regulation.

Figure 1.

Influence of cell size on organ and organism size. In multicellular organisms, cell size can interface with organ and organism size in one of two ways. (A) If the number of cells is fixed, changes in cell size will lead to changes in organ and, subsequently, organism size, as in C. elegans. (B) If organ size is regulated independently of cell size, changes in cell size will be compensated for by changes in cell number, resulting in a constant organ and organism size, as happens in salamanders. A mix of both mechanisms is also possible in which cell size affects organ size, but is partially compensated for by changes in cell number.

Because of functional constraints, cells are under pressure to maintain a characteristic size for their given type. To accomplish this size homeostasis, growth and division must be coupled. For example, yeast grown in nutrient-poor conditions adjust their cell-cycle duration to accommodate for slower growth, so that cells divide at roughly similar sizes as in nutrient-rich environments (Jorgensen et al. 2002; Di Talia et al. 2007, 2009; Brauer et al. 2008). This size-dependent cell-cycle progression implies that cells have a way of sensing their own size. Yet, how size homeostasis is maintained has remained elusive. Certainly, it is not necessary that cells measure their volume per se and we interpret the word “size” more liberally to encompass a range of correlated properties, such as total protein, ribosome content, or biosynthetic capacity (Carlson et al. 1999). The specific property measured may well be distinct in different organisms and cell types, which will have implications for the specific molecular mechanism used. Here, we review recent advances and discuss a conceptual framework that potentially links a large class of cell-size questions.

THE RELATIONSHIP BETWEEN GROWTH AND SIZE CONTROL

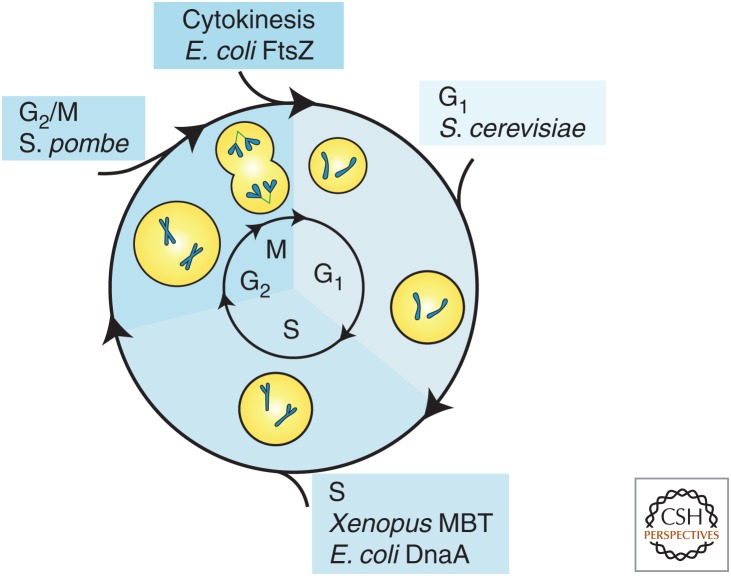
At its most fundamental, cell-size control within a specified time interval ensures that larger cells grow proportionally less than smaller cells. This means that growth and the cell-division cycle must be coordinated. In theory, this regulation could take place at any point in the cell cycle, which is conventionally divided into four distinct phases. The first is a growth period immediately following the previous division called G₁. The second is the phase in which the DNA is synthesized, known as S phase. The third is another post–S phase growth period called G₂, and the fourth is mitosis or M phase, in which the DNA is packaged and separated into two daughter cells (Fig. 2). Importantly, size control does not have to completely compensate for initial cell-size differences. Rather, size control is a quantitative feature whose strength in an interval can be measured (Wheals 1982; Tyson and Diekmann 1986; Sveiczer et al. 1996; Di Talia et al. 2007, 2009). For example, weak size control might require multiple cell-division cycles to return an initially aberrantly large or small cell to the characteristic size, whereas strong size control could do this in one cycle.

Figure 2.

The cell cycle and cell size. The cell cycle is divided into four phases. G₁ is a growth phase immediately following the previous division. S phase is when the DNA is replicated. G₂ is a second growth period followed by mitosis or M phase when the DNA is condensed and partitioned into the daughter cells. The relevant phases for cell-size control in different systems discussed in the text are as marked. MBT, midblastula transition.

For some cell-growth dynamics, cell-size homeostasis can be maintained without a cell-size sensor. All that is required for size homeostasis is that smaller cells grow proportionally more than larger cells in a cell cycle so that size variation is reduced in the next generation. For example, in the case of a constant rate of linear growth, the cell size, V, will increase at a constant rate so that dV/dt = C. In this case, specifying the duration of the cell cycle determines the amount of growth so that, in proportion, smaller cells grow more than larger cells and the population approaches a mean size without any specific size-sensing mechanism (Conlon and Raff 2003). Thus, some cell-growth dynamics do not require a cell-size measurement to maintain size homeostasis.

Other growth dynamics do necessitate a size measurement. One such example is exponential growth, in which the rate of growth is proportional to cell size: dV/dt = αV. Here, a timer mechanism will not maintain size homeostasis because cells born larger would grow proportionally more during a specified period. Fluctuations in division times will then result in a progressively wider size distribution unless the cells use a size-sensing mechanism to limit cell-cycle duration in larger cells (Tyson and Hannsgen 1985).

The importance of the dynamics of cell growth for size control has motivated many studies (Mitchison 2003; Ginzberg et al. 2015). In the case of budding yeast, Escherichia coli and Caulobacter crescentus, cell growth in an unperturbed cell cycle is likely close to exponential, as supported by both single-cell analyses using fluorescence time-lapse microscopy and microchannel resonators, as well as classical bulk experiments using radioactive labeling (Elliott and McLaughlin 1978; Di Talia et al. 2009; Godin et al. 2010; Campos et al. 2014; Osella et al. 2014). However, other groups have argued that the budding yeast G₁ growth is closer to linear based on estimates of cell volume using time-lapse phase contrast microscopy (Ferrezuelo et al. 2012), and that growth rates are altered by cell-cycle phase (Goranov et al. 2009). For a more complete discussion of yeast size control and growth, see Turner et al. (2012). Fission yeast growth is certainly less likely to be exponential as reviewed in Mitchison (2003), and growth in metazoan cells is almost certainly not (Son et al. 2012; Kafri et al. 2013; Sung et al. 2013). The clear deviation from exponential growth in mammalian and other cells does not imply that these cells do not use a size sensor. In cases in which size sensors are not strictly necessary, they may still be desirable to enhance size control to keep the cell closer to the optimal range of sizes for proliferation and function. Thus, the only way to determine if cell-size sensors are operating in a given cell type is to identify the molecular mechanisms regulating size.

MANY POTENTIAL SIZE-SENSING MECHANISMS

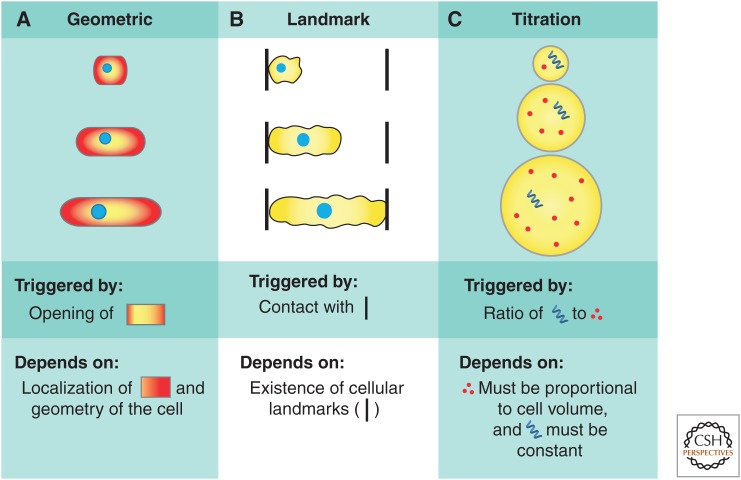
Active regulation of cell-cycle progression in response to cell size requires that cells have a method to accurately measure their size. Cells might accomplish size measurement through a geometric mechanism if there is little cell-to-cell variation in their geometry. A geometric mechanism seems unlikely in amoeboid cells or in the microvilli-containing cells of the small intestine, but is much more plausible in rod-shaped bacteria and fission yeast, which grow in a well-specified geometry along a single dimension. One means of determining size geometrically would be to measure the ratio of surface area to volume because, for many geometries, surface area increases less rapidly than volume. A related possibility is that cells might sense cell length via intracellular gradients of cell-cycle regulators (Martin and Berthelot-Grosjean 2009; Moseley et al. 2009). In this case, segregation of critical components to designated subcellular locations would allow the cell to assess the distance between these compartments as a proxy for cell size (Fig. 3A).

Figure 3.

Cell-size measurement mechanisms. Cells can potentially sense their size via a number of different mechanisms, including (A) aspects of their cell geometry, such as surface area to volume or cell length, via intracellular gradients, (B) extracellular landmarks, and (C) titration of a constant concentration regulator, whose amount scales with cell size against a fixed “yardstick” to measure cell size.

In multicellular organisms, external landmarks, such as tissue edges or junctions with target cells, could be used to constrain cell growth. For example, some neurons grow until they make contact with their target (Fig. 3B) (Guthrie 2007). However, this mechanism requires that an external pattern is already in place and cannot generate size control de novo, so we do not focus our attention on this mechanism in this review.

Finally, cells could measure their volume directly by titration of a constant-concentration sensor molecule against a fixed internal “yardstick.” This mechanism requires that the production of the volume sensor be proportional to cell growth and that there be a fixed yardstick to measure, that is, titrate against (Fig. 3C). Here, we explore the relevance of titration mechanisms in several biological contexts.

CELL SIZE CORRELATES WITH DNA CONTENT

One of the earliest and most consistent observations about cell size is its relationship to ploidy. In the early 1900s, Theordor Boveri produced sea urchin embryos in a range of ploidies by manipulating the conditions of fertilization. Haploid embryos divided more than diploid embryos and, thereby, maintained a consistent final ratio of DNA to cytoplasm. In further experiments, he created triploid and tetraploid embryos through multiple fertilizations. In these embryos, spindle abnormalities caused an uneven distribution of chromosomes so that not all cells received integer multiples of the genome. In all cases, Boveri observed that the number of divisions within a given sector of the embryo was affected by the DNA content that sector received in the first cleavage. By the pluteus larval stage, urchin cells that had received more DNA were proportionally larger than those that had received less, which indicated that the relationship extended beyond a simple size scaling with ploidy (Wilson 1926).

The relationship between cell size and ploidy holds well beyond the embryo. Viable adult salamanders can be created from haploid to pentaploid. In all cases, the size of the cells within their tissues increases or decreases correspondingly, although compensatory variations in cell number maintain a relatively invariant total organism size (Fankhauser 1945). This relationship is true in unicellular eukaryotes as well. For example, the cell size of budding yeast correlates with ploidy from haploid to hexaploid (Mortimer 1958; Mayer et al. 1992).

Developmentally regulated changes in ploidy correlate with cell size in numerous large cell types. Often, as in the case of fly salivary gland and the mammalian trophoblast, cells increase their ploidy by undergoing rounds of endoreduplication. In many cases, such as the wing scale cells in the moth, Ephestia, the degree of endoreduplication correlates with cell size within a tissue (Fig. 4B) (Edgar and Orr-Weaver 2001). Similarly, as the land-slug Limax grows over its lifetime, it increases the size of the neurons within its brain through endoreduplication (Yamagishi et al. 2011). A very tight relationship has been shown between DNA content and cell size in the green algae, Eudorina (Tautvydas 1976). The filamentous yeast, Ashbya, also contains many copies of its genome within a single cytoplasm. In this case, individual nuclei appear to be carefully spaced within the growing cells to retain a relatively constant local and global ratio of DNA to cytoplasm (Nair et al. 2010; Anderson et al. 2013).

Figure 4.

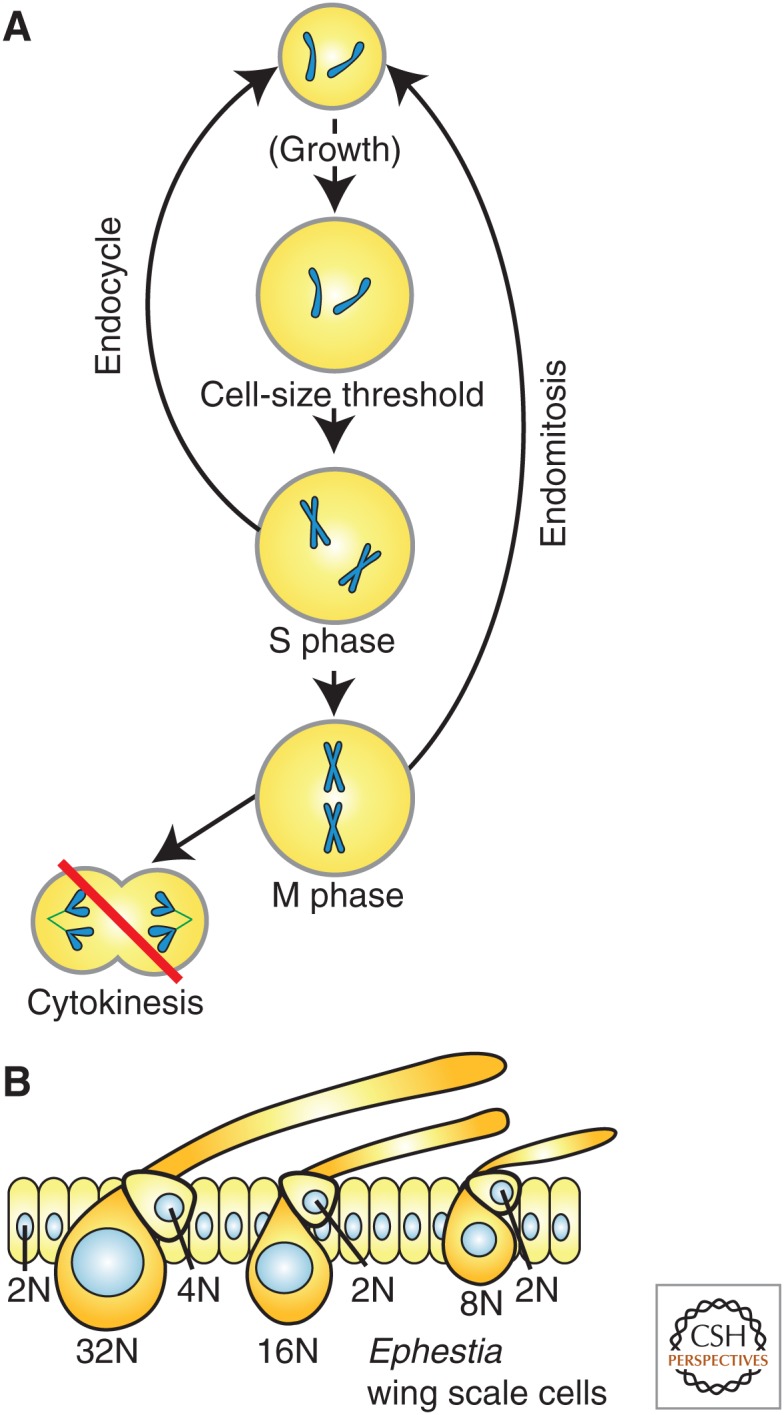
Endoreduplication increases cell size. DNA content correlates with cell size in a variety of organisms and contexts. (A) Endoreplicative cell cycles are similar to mitotic cycles without cytokinesis. Endocycling cells proceed directly from an S/G₂-like state to another G₁, whereas endomitotic cells undergo a partial mitosis but abort before cytokinesis. (B) The wing scale cells of the moth, Ephestia, vary in ploidy from 8N to 32N with higher ploidy cells being larger than lower ploidy cells (modified from data in Edgar and Orr-Weaver 2001).

Endoreduplicative cell cycles increase ploidy by entering a relatively normal S phase, but then skip cytokinesis, resulting in a doubling of the DNA content with each iteration. This process can be repeated a large number of times resulting in very high ploidies (up to 24,000C in the case of some plant endosperms) (Traas et al. 1998). Endoreduplicating cell cycles are not simply unregulated or prolonged S phases. Instead, these cells go through a normal G₁ and S phase in which the DNA is only replicated once. They then either proceed directly from G₂ into another G₁-like state (called an endocycle), or they enter into mitosis, but abort before cytokinesis is completed and return to the G₁-like state (called an endomitosis) (Fig. 4A) (Zielke et al. 2013). In both cases, the activity of conventional M-phase regulators is absent or prematurely lost. However, G₁/S regulation in endoreplicating cells appears to be broadly similar to what is found in conventional mitotic cell cycles (Edgar and Orr-Weaver 2001). This implies that, if a mechanism to measure cell size relative to DNA content were operable at the G₁/S transition, it might also explain the ploidy–size relationship observed for endoreduplicated cell types.

We note that the relationship between DNA content and cell size is not only true within single species, but seems to be constant across most eukaryotes, which encompasses more than six orders of magnitude in cell size. A similar correlation between cell size and DNA content has also been observed in prokaryotes, although the DNA content increases much more slowly with cell size than in eukaryotes (Gregory 2000; Cavalier-Smith 2001). Note that this does not imply that the mechanism of size measurement is identical in all clades, but rather that there exist selective pressures that maintain a roughly linear relationship between DNA content and cell size across eukaryotes.

A TITRATION SENSOR REGULATES THE MIDBLASTULA TRANSITION IN Xenopus

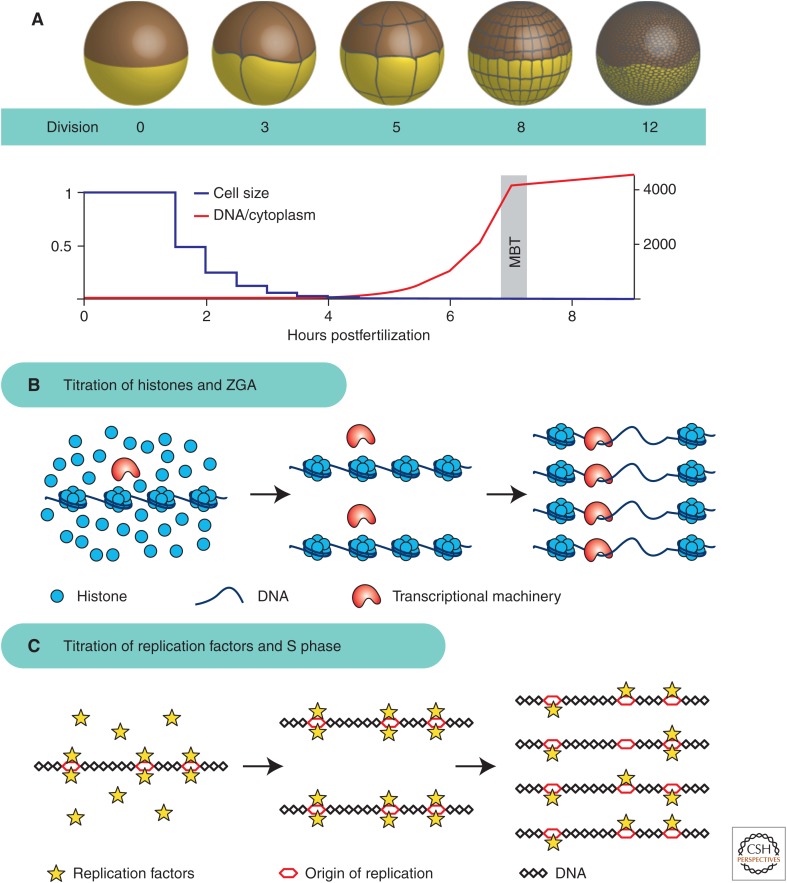
As noted by Boveri (discussed above), DNA content strongly affects cell size during early development. In many fast-developing species, cell division is uncoupled from cell growth during the early cleavage divisions. These embryos typically start out with very large cells that undergo rapid divisions without growth phases. Because of the lack of growth phases, the total cytoplasmic volume remains constant, whereas the cell size decreases exponentially. These divisions are also unusual in that they lack cell-cycle checkpoints and are transcriptionally inactive. These rapid cell cycles continue for a set number of divisions until the onset of a developmental transition called the midblastula transition (MBT). At the MBT, the cell cycle lengthens with the addition of growth phases, checkpoints become active, and the zygotic genome initiates large-scale transcription (Fig. 5A) (Masui and Wang 1998).

Figure 5.

Midblastula transition (MBT) controlled by titration of regulators against DNA. (A) During the early cleavage cycles, Xenopus embryos divide without growth, resulting in an exponentially decreasing cell size and an exponentially increasing ratio of DNA to cytoplasm. (B) Titration of constant-concentration histones against the exponentially increasing quantity of DNA sets the timing of zygotic genome activation (ZGA) by inhibiting transcription below the threshold DNA concentration. When DNA concentration reaches a critical threshold, inhibition is relieved and transcription becomes activated (Amodeo et al. 2015). (C) Titration of key replication factors against DNA sets the timing of S-phase lengthening. When DNA concentration becomes sufficiently high, the available replication factors are no longer able to efficiently trigger S phase, resulting in a longer cell cycle (Collart et al. 2013).

Early experiments on the MBT in frogs identified the DNA-to-cytoplasmic ratio as critical for its regulation. A large body of experimental evidence shows that alteration of this ratio results in corresponding changes to the number of rapid cell cycles before the MBT. Haploid embryos undergo the MBT one cell cycle later (Masui and Wang 1998). Polyspermic embryos and embryos injected with plasmid DNA undergo premature cell-cycle lengthening and transcriptional activation, respectively (Newport and Kirschner 1982a,b). Perhaps most convincingly, embryos that are tied in half with an unequal distribution of DNA show premature cell-cycle lengthening on the half of the embryo with increased DNA and delayed cell-cycle lengthening in the half with reduced DNA (Newport and Kirschner 1982b). This experiment is especially compelling because the two halves of the embryo were fertilized at the same time and the nuclei have undergone the same number of divisions. The only difference between the two sides is their DNA-to-cytoplasm ratio. These findings lead to the hypothesis that the embryo begins development with a relatively constant store of maternally deposited inhibitor, which is titrated against the exponentially increasing amount of DNA (Newport and Kirschner 1982b). Once a critical threshold is met, the embryo initiates transcription and the MBT. Therefore, sensing the ratio of cytoplasm per genome is one way of sensing cell size, the MBT can be viewed as a size-sensing problem. Here, the amount of regulator is proportional to cell size, which is measured by titration against the amount of DNA in a cell. This mechanism is an elegant way to measure cell size independent of cell geometry or external cues.

Recent work has sought to identify factor(s) that are titrated against DNA to set the threshold for the MBT in frogs and thereby support the titration model. Three different groups of factors have been proposed. The first is the phosphatase PP2A, which appears to be limiting for S-phase progression in vitro at DNA concentrations close to those found at the MBT. For increasing DNA-to-cytoplasm ratios, S phase slows without addition of exogenous PP2A (Murphy and Michael 2013). Similarly, addition of a cocktail of four DNA replication factors, Cut5, RecQ4, Treslin, and Drf1, which become unstable at the MBT, can lead to additional rapid cell cycles in vitro and in embryos (Fig. 5C) (Collart et al. 2013). Our work suggests that core histones H3 and H4 are directly titrated against DNA to activate transcription in vitro and in vivo (Fig. 5B) (Amodeo et al. 2015). Alteration of histone concentration in vitro shifts the amount of DNA required for transcriptional activation. Moreover, an ∼50% reduction of H3 in vivo results in the MBT occurring precisely one cell cycle earlier, consistent with histone-DNA titration being responsible for triggering the MBT. In addition to these proposed titrated components, nuclear import factors and resulting nuclear size has recently been suggested to regulate MBT timing (Jevtic and Levy 2015). This observation suggests that nuclear concentration of inhibitory factors may be critical for cell-size sensing in the early embryo. Overall, these potentially overlapping mechanisms provide good evidence that the MBT is controlled by a cytoplasm-to-DNA ratio mechanism resulting from the titration of some constant concentration regulator(s) against the DNA.

TITRATION OF CYCLINS IN BUDDING YEAST

Cell-size control can be most directly studied in unicellular rather than multicellular organisms because cell size is more easily measured and the number of cell types more limited. For this reason, the yeasts Saccharomyces cerevisiae and Schizosaccharomyces pombe have been favorite models for the study of cell-size regulation.

Budding yeast divide asymmetrically, and size control occurs in the smaller daughter cells primarily in G₁ (Di Talia et al. 2009). Smaller cells spend more time in G₁, but this size control is imperfect because variations in size are not eliminated in a single cell cycle (Johnston 1977; Di Talia et al. 2007). Progression through G₁ is initiated by the cyclin Cln3. Cyclins are canonical cell-cycle regulators whose levels often oscillate during the cell cycle to coordinate the activity of their partner kinases, the cyclin-dependent kinases or CDKs and thereby promote cell-cycle progression. Cln3 binds and activates CDK1 to partially inactivate the transcriptional inhibitor Whi5 (Bertoli et al. 2013). Inactivation of Whi5 relieves inhibition of the transcription factor SBF, whose target genes include the additional cyclins, Cln1 and Cln2. These two cyclins complete inactivation of Whi5 via a positive feedback loop, which drives further cell-cycle progression (Eser et al. 2011). Activation of this feedback loop ensures irreversible commitment to cell-cycle progression (Skotheim et al. 2008; Charvin et al. 2010; Doncic and Skotheim 2013). Interestingly, the levels of the upstream rate-limiting cyclin Cln3 oscillate weakly through the cell cycle compared with other cyclins and may be at a constant concentration during mid G₁ (Tyers et al. 1993). Therefore, Cln3 might be used to sense cell size via a titration mechanism.

Cln3 may be titrated against genomic DNA itself, or against specific binding sites. Consistent with the latter possibility, cell size was shifted by a high-copy plasmid containing multiple SBF-binding sites in a Cln3-Whi5-dependent manner (Wang et al. 2004). In either case, Cln3-Cdk complexes, whose number is likely proportional to cell size, would be titrated against a constant DNA yardstick. Consistent with this model, a recent study constitutively expressing Cln3 at different levels showed that the concentration of Cln3 inversely correlated with G₁ length (Liu et al. 2015). However, the implications of these Cln3-titration conjectures remain largely untested.

Although the proposal of titrating Cln3 against the genome is attractive because of the fixed genome size during G₁, this is not the only possibility. Cln3 could potentially be titrated against another protein whose abundance did not scale with cell size to produce a cell-size measurement (Fantes et al. 1975). The majority of yeast proteins are found at relatively constant concentrations and, thus, their total amounts scale linearly with volume (Newman et al. 2006). However, transcription of several genes, including many cell-surface-related proteins, is not proportional to cell size so that larger cells have lower messenger RNA (mRNA) concentrations for these specific targets (Wu et al. 2010). Thus, the proteins encoded by this set of genes are expected to be at lower concentrations in larger cells. One of these nonscaling genes could therefore serve as a titrated counterpart to Cln3 to affect G₁ size control. Indeed, it was recently shown that the synthesis of the cell-cycle inhibitor Whi5 does not scale with size (Schmoller et al. 2015). This results in smaller-born daughter cells beginning the cell cycle with higher concentrations of Whi5. Because the synthesis of Whi5 is restricted to the S/G₂/M phase of the cell-division cycle, cell growth dilutes Whi5 in G₁ to trigger progression into the cell cycle.

An alternate model for cell-size control in budding yeast posits a mechanism that prevents Cln3 nuclear entry below a threshold cell-size or size-dependent growth rate (Ferrezuelo et al. 2012). In this model, switch-like translocation of Cln3 results from a positive feedback loop based on the mutual inhibition of Cln3 and Whi7, a Whi5 paralog localized to the endoplasmic reticulum (Yahya et al. 2014). The chaperone protein, Ydj1, and the posttranscriptional regulator, Whi3, may also be involved in Cln3 retention outside the nucleus (Gari et al. 2001; Wang et al. 2004; Verges et al. 2007). However, the size-dependent retention of Cln3 is still under debate. Other groups have failed to observe Cln3 outside the nucleus, although this might be caused by the low number of Cln3 molecules (Miller and Cross 2000; Edgington and Futcher 2001; Cai and Futcher 2013). Finally, even if the Cln3-import model is correct, it does not yet easily explain how cell size or growth rate is sensed to trigger Cln3 translocation.

Although G₁ appears to contain the major size checkpoint in budding yeast, evidence also exists for S/G₂/M size regulation. Cells that are experimentally forced through G₁ by overexpression of G₁ cyclins maintain size homeostasis. In this case, cells that are smaller when entering S phase spend slightly more time in S/G₂/M and, thereby, partially compensate for reduced G₁ growth (S Di Talia, pers. comm.). This suggests the possibility that the network regulating entry to mitosis might also contribute to size homeostasis, in addition to its more defined role in the morphogenesis checkpoint (Harvey and Kellogg 2003; McNulty and Lew 2005; Howell and Lew 2012; Zapata et al. 2014).

TITRATION OF DnaA IN E. Coli

Titration of regulatory molecules against a cellular component whose size is invariant with growth has been proposed to regulate specific points of the bacterial cell cycle (Chien et al. 2012). Whereas any point in the cell cycle can potentially be regulated via a size checkpoint, two specific points of control have been identified through studies of E. coli and Bacillus subtilis. Bacterial size control has been reported to impact the onset of DNA replication and cell division. In both cases, a titration mechanism has been suggested as the basis of size-dependent, cell-cycle-progression signals (Donachie 1968; Teather et al. 1974; Chien et al. 2012).

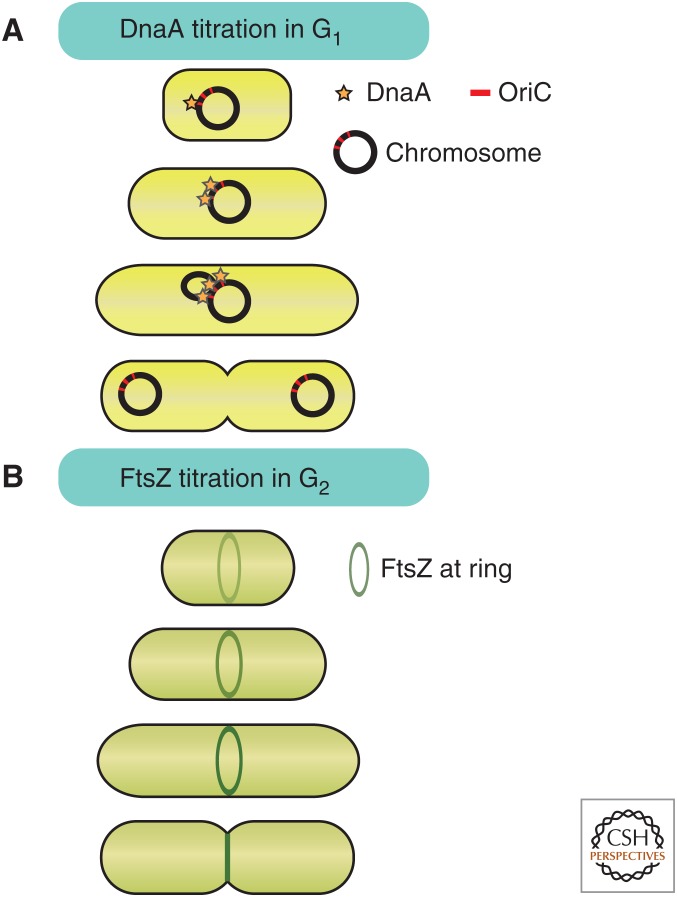
To control replication, Donachie (1968) proposed that a constant concentration activator would accumulate at the origins of replication. In this model, a regulator whose number increases with cell size would titrate against the fixed number of origins to yield a size-dependent activating signal. Consistent with this model, cell size at the onset of replication in E. coli was similar regardless of birth size and growth rate. Even in the case of the fastest growing E. coli, in which mass doubling outpaces the duration of replication so that large cells contain multiple copies of partial genomes, replication is triggered at a constant size-to-origin ratio (Donachie 1968).

The most likely candidate for Donachie’s titrated replication activator is DnaA, which binds cooperatively to origins to promote loading of the replication machinery (Kaguni 2006). Consistent with the DnaA-titration model, the size-to-origin ratio at replication initiation is sensitive to DnaA expression levels (Lobner-Olesen et al. 1989). Furthermore, mutations affecting cell size at division, but not cell-growth rate, do not change DnaA concentration or the size at which cells initiate replication. Mutations making cells twice as large lead to cells containing twice the amount of DNA (Hill et al. 2012). Taken together, this evidence suggests molecular titration as the most plausible mechanism for coupling cell size to the onset of DNA replication in E. coli (Fig. 6A).

Figure 6.

Proposed titration mechanisms for cell-size measurement in bacteria. (A) ATPase DnaA accumulates on origins of replication in a size-dependent manner until a critical threshold triggers replication. (B) FtsZ accumulates at the site of cytokinesis as the cell grows until reaching a threshold that triggers cytokinesis.

In addition to coordinating S phase with cell size, E. coli may also coordinate cell division with cell size (Chien et al. 2012). The accumulation of the constant concentration regulator FtsZ at the cytokinetic ring could function as a titration-based cell-size sensor (Teather et al. 1974; Chien et al. 2012). Because cell growth of rod-shaped bacteria maintains a constant width, the circumference at the midcell is constant. Thus, titration of FtsZ against the midcell perimeter could yield a size-dependent signal to initiate cytokinesis (Fig. 6B). Although titration models have an inherent appeal for the size-dependent control of replication and division in bacteria, they have been insufficiently tested and we refer the reader to Levin and Angert (2015) for caveats to these models.

Recently, it has been shown that C. crescentus, B. subtilis, and E. coli cells are not subject to strict cell-size regulation (Amir 2014; Campos et al. 2014; Jun and Taheri-Araghi 2015; Taheri-Araghi et al. 2015). Rather, for a particular bacterial species growing in a particular environment, all cells grow about the same amount during a division cycle independent of their size at birth. Thus, cell-size fluctuations are not compensated for in a single-cell cycle, but dampened over several division cycles. That several groups independently arrived at a phenomenological model based on a constant size increase per division cycle requires, at the very least, a reformulation of the existing bacterial DNA–based or cytokinetic ring–based titration models.

GEOMETRIC SIZE SENSING IN FISSION YEAST

Similar to E. coli, fission yeasts are rod shaped and grow by lengthening at a constant width so that volume is proportional to length (Mitchison 2003). It has been proposed that fission yeast use a spatial gradient of the mitotic inhibitor Pom1 emanating from its poles to measure cell size geometrically via length (Martin and Berthelot-Grosjean 2009; Moseley et al. 2009). In this model, division ensues when the concentration of Pom1 dips below a critical concentration at the midcell, which occurs at a specific cell length.

Pom1 regulates the mitotic trigger network centered on the competing kinase and phosphatase pair, Wee1 and Cdc25, which regulates Cdk activity. Pom1 inhibits the Wee1-inhibitory kinases, Cdr1 and Cdr2, which localize to specific nodes at the midcell (Deng and Moseley 2013). As a cell grows, the gradient in Pom1 from the poles ensures that its concentration at the midcell decreases, which could allow Cdr1 and Cdr2 to inactivate Wee1 and thereby promote mitotic entry. Perturbations of the Pom1 gradient result in both changes to the Cdr2 distribution and cell size (Martin and Berthelot-Grosjean 2009; Moseley et al. 2009; Hachet et al. 2011; Bhatia et al. 2013).

However, several recent results have begun to cast doubt on the gradient model. First, the length scale of the exponential Pom1 gradient (∼1.5 µm) appears to be too short to accurately measure the length of a >10-µm cell (Saunders et al. 2012). Second, the gradient has a difficult time explaining why the DNA-to-cytoplasm ratio is maintained in fission yeast cells of different ploidy and in temperature-sensitive cytokinesis mutants (Neumann and Nurse 2007). Third, in fission yeast mutants of different widths, volume at mitosis was more variable than area, suggesting a surface-area-based model (Pan et al. 2014). Finally, cell-size control occurs, albeit less effectively, in cells lacking regulation of Cdk1 by Wee1 and Cdc25, indicating that the Pom1 pathway is certainly not the only size-control mechanism (Coudreuse and Nurse 2010; Wood and Nurse 2013).

TITRATION-BASED CELL-SIZE SWITCHES

To link growth and proliferation, size-sensing mechanisms regulate cell-cycle transitions, which are typically switch-like and associated with threshold-ultrasensitive responses. Switch- like transitions are used to ensure coordination of downstream responses. For example, switch-like increases in Cdk activity ensure the coherent transcription of G₁/S phase regulators, the all-or-none replication of the genome during S phase, and the robust phosphorylation of mitotic targets (Georgi et al. 2002; Skotheim et al. 2008; Ferrell et al. 2009; Koivomagi et al. 2011; Yang et al. 2013).

Under some conditions, titration mechanisms can directly generate ultrasensitive responses (Buchler and Louis 2008). For example, titration with a high-affinity stoichiometric inhibitor can generate an ultrasensitive response curve. Consider two proteins A and B that bind to form an inactive complex AB. The response can be characterized as the amount of active A as a function of the total amount of A given a fixed amount of B. For high-affinity interactions with B, low amounts of A will be fully inactivated by B. However, for increasing amounts of A, the inhibitor B is eventually titrated out so that, above a threshold, the amount of active A increases rapidly. In the case of DNA-binding proteins, such as DnaA, high-affinity decoy sites could serve the purpose of stoichiometric inhibitors because these sites will be occupied before the relevant target site and, therefore, titrate out the regulator to create an ultrasensitive response (Kitagawa et al. 1996).

Although titration mechanisms can produce ultrasensitivity, they need not generate the switch themselves. Graded upstream signals can be converted downstream to produce a switch-like response. For example, positive feedback loops at the G₁/S and G₂/M transitions convert small changes in the upstream kinase input signal to dramatic increases in downstream kinase activity associated with the next cell-cycle phase (Pomerening et al. 2003; Skotheim et al. 2008). In the case of budding yeast, a graded Cln3 signal may be coupled via Whi5 to a Cln1/2 positive feedback to generate a sharp increase in Cdk activity. Thus, downstream switches can generate threshold responses, thereby alleviating any such requirement on the upstream size-dependent signal.

Additional pathways may tune size thresholds in response to different conditions (Baroni et al. 1994; Tokiwa et al. 1994; Jorgensen and Tyers 2004). A size threshold can be modulated by regulation of either the upstream size-dependent signal or by modification of feedback loop components that affect sensitivity to the upstream signal. This is consistent with observations of core signaling components producing a positive feedback-driven switch and more peripheral signaling pathways modifying the threshold to achieve condition-dependent responses (Sha et al. 2003; Justman et al. 2009; Doncic and Skotheim 2013).

Whether ultrasensitive or not, titration-based size sensors are relatively easy to generate. All they require is one component that is produced proportionally to cell size and another that is constant. Many proteins fit the profile for the titrated molecule because the majority of proteins and RNAs are found at roughly constant concentration during the cell-division cycle. This is supported by the fact that <20% of yeast and mammalian transcripts cycle (Spellman et al. 1998; Whitfield et al. 2002; Oliva et al. 2005). Furthermore, a genome-wide analysis of green fluorescent protein (GFP)-tagged open reading frames (ORFs) in budding yeast concluded that most of the variability in protein abundance arose from variations in cell size (Newman et al. 2006). This is a natural consequence of larger cells having more protein and that the proportions of most protein species remain relatively constant during cell growth. Any one of these “cell-cycle-independent” proteins could potentially be titrated against a constant yardstick to yield a size sensor.

Constant yardsticks are much less common within growing cells because, much like proteins, the majority of organelles scale with cell size (see Marshall 2015; Reber and Goehring 2015). For example, nuclear size relative to that of the cell shows little variation. The nuclear size in yeast is ∼8%–10% of cell size in a variety of mutants (Neumann and Nurse 2007; Zhao et al. 2008). In contrast to organelles scaling with cell size, DNA is a more promising yardstick candidate because its amount is fixed for all segments of the cell cycle except S phase. Moreover, size scales with DNA content in many experimental and endogenous contexts as discussed above. Thus, most DNA-binding proteins could potentially be used as a size sensor. Although DNA may be the most likely yardstick, it is not the only possibility as the synthesis of some protein species is also not proportional to cell size (Wu et al. 2010). Indeed, recent work in budding yeast showed that the cell-cycle inhibitor Whi5 is present in similar numbers in large and small cells (Schmoller et al. 2015). The titration of Whi5 against the cell-cycle activator Cln3, whose synthesis scales with cell size, then results in size-dependent progression through G₁.

Cell size is one of the most basic and defining features of a given cell type, yet the molecular mechanisms underlying its control have remained elusive. We are excited by recent work revisiting this long-standing problem. Here, we reviewed the current understanding of size-sensing mechanisms and highlighted the potential of titration-based mechanisms. However, because of the ease with which size-dependent signals might be generated by any constant concentration DNA-binding protein, we do not expect conservation of the specific regulatory molecules.