Summary
A robust test of ecological theory is to gauge the predictive accuracy of general relationships parameterized from multiple systems but applied to a new area. To address this goal, we used an ecosystem‐level experiment to test predator–prey theory by manipulating prey abundance to determine whether predation was density dependent, density independent, compensatory or depensatory (inversely density dependent) on prey populations.
Understanding the nature of predation is of primary importance in community ecology because it establishes whether predation has little effect on prey abundance (compensatory), whether it promotes coexistence (density dependent) and reduces the equilibrium of prey (density independent) or whether it can be destabilizing (depensatory).
We used theoretical predictions consisting of functional and numerical equations parameterized independently from meta‐analyses on wolves (Canis lupus) and moose (Alces alces), but applied to our specific wolf–moose system. Predictions were tested by experimentally reducing moose abundance across 6500 km2 as a novel way of evaluating the nature of predation.
Depensatory predation of wolves on moose was the best explanation of the population dynamic – a mechanism that has been hypothesized to occur but has rarely been evaluated. Adding locally obtained kill rates and numerical estimates to the independent data provided no benefit to model predictions, suggesting that the theory was robust to local variation.
These findings have critical implications for any organism that is preyed upon but that also has, or will be, subject to increased human exploitation or perturbations from environmental change. If depensatory predation is not accounted for in harvest models, predicted yields will be excessive and lead to further population decline.
Keywords: adaptive management, Allee, caribou, conservation, depensatory, limitation, moose, predation, regulation, wolves
Introduction
A primary goal in ecology is to identify principles that are general enough to transcend ecosystems, but useful enough to make predictions within specific study areas (Levins 1966; Krebs 2009). This undertaking is particularly challenging in field ecology because complex and often unpredictable relationships can obscure our basic understanding of how natural systems operate (Strong 1986; Doak et al. 2008). Yet, if ecological relationships can be applied across systems, even when parameterized with independent data, then this approach constitutes one of the strongest means of validating whether the theory is an accurate portrayal of the observed patterns.
Predator–prey theory has received considerable attention in the biological literature because it is a fundamental evolutionary and ecological process (Holling 1959a,b; Abrams 2000; Abrams & Ginzburg 2000). Nonetheless, the effects of predation on prey populations are continually debated (Schmitz, Hamback & Beckerman 2000; Shurin et al. 2002), even within a specific study system (Post & Stenseth 1998). The impacts of predation have reportedly ranged from compensatory (Errington 1946; Vucetich, Smith & Stahler 2005), to limiting (Gasaway et al. 1983), to regulating prey populations (dependent on prey densities; Messier 1994). These distinctions have important implications for the structure of ecological communities. If predation is completely compensatory, then it does not have an effect on the equilibrium abundance of prey, whereas equilibrium prey density is reduced if predation is limiting (Sinclair 1989). If predation is regulating however, it is possible that multiple equilibria can be established (Messier 1994), and predation becomes a key mechanism promoting the coexistence of predators and prey due to the feedback between the two trophic levels.
For vagile and large‐bodied animals, the most relevant scale to investigate factors limiting population growth is at the ecosystem level, and in recent decades, ecologists have been urged to use management experiments to achieve this goal (Walters & Holling 1990; Doak et al. 2008). Several ambitious management experiments have been attempted to quantify the effect of predation on large mammal communities (Hayes et al. 2003; Hurley et al. 2011). Although there are notable exceptions (Hurley et al. 2011), predator removal experiments often result in increased recruitment or abundance of prey, particularly when predation is a substantial component of prey mortality (Bergerud & Elliot 1986; Hayes et al. 2003; Krebs 2011; Hervieux et al. 2014). However, although predator removal experiments reveal the degree that predation is compensatory or additive, they do not address whether it is regulating (Boutin 1992). An alternative experiment that is only recently receiving attention involves manipulating prey numbers to evaluate the role of predation. This experiment is important for two reasons: (i) by varying the abundance of prey, the predation rate (PR) can be estimated across a range of prey densities. This approach will help resolve whether predation is density independent, dependent, depensatory (i.e. inversely density dependent) or compensatory; (ii) a number of species are endangered because of predator‐mediated apparent competition between prey (DeCesare et al. 2010), and it remains unknown whether reducing the overabundant prey will reduce predation on the rare and declining prey (Serrouya et al. 2011; Steenweg 2011; Wittmer et al. 2013).
In our system, we made use of a broad‐scale experiment to evaluate the impact of wolf (Canis lupus) predation on moose (Alces alces) by reducing moose density using sport hunting across a 6500‐km2 area. The treatment was to increase the number of moose hunted by a factor of 10 for 3 years, with an associated reference area where moose harvests were comparatively stable. Because the moose population continued to decline substantially after the hunting treatment was reduced, it became clear that factors other than hunting were influencing moose population dynamics. What was unclear was the relative importance of these factors. Therefore, our objective was to contrast a set of hypotheses, expressed as mathematical models, to explain the continued decline in moose following the cessation of high human harvest. We tested four hypotheses as to the role of wolf predation in the system: it was completely compensatory, density dependent, density independent or depensatory (i.e. the PR increased as moose densities declined; Fig. 1). The last hypothesis is of particular interest because its prediction was modelled by Messier (1994) as a unimodal PR, but has received little field validation (but see Hossie & Murray 2010). For each of these models, we took a reductionist approach by decomposing the PR into functional (FR) and numerical responses (NR), because it was these fundamental relationships that were used to generate the PR curves (see Fig. 1). Our fifth hypothesis was that hunting was not a factor in the decline, but the decline was driven solely by predation, so we treated hunting as compensatory by removing its effect from the model.
Figure 1.
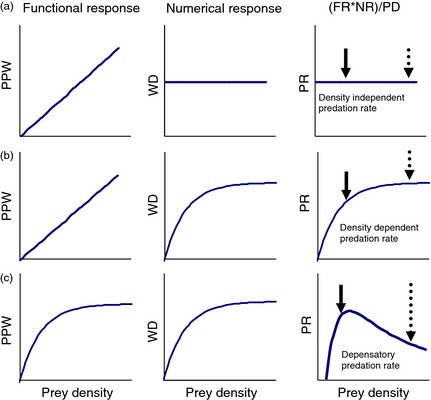
Predation‐related hypotheses of the moose decline based on different predation rates (PR), generated from varying the form of the functional (FR) and numerical response (NR). PPW is prey consumed per wolf, and WD is wolf density (see text for details). (a) a Type I FR and Type 0 NR yields a density‐independent PR; (b) a Type I FR and Type II NR yields a density‐dependent PR; and (c) a Type II FR and Type II NR can transition from a depensatory PR to a density‐dependent PR. Scenario (b) can also be achieved by reversing the forms of the FR and NR (i.e. a Type II FR and Type I NR). Dotted and solid arrows, respectively, indicate the hypothetical moose population at the beginning and latter part of the moose reduction. Modified from Holling (1959b).
The strength of our approach was that we compared alternative hypotheses using FR and NR models that were parameterized with independent empirical data (i.e. data collected outside the study system) from meta‐analyses with spatial replication (Messier 1994; Fuller, Mech & Cochrane 2003). If these independent equations could reliably predict moose population dynamics in this experimental system, then not only would their generality be supported, but so would the theoretical relationships that are used to predict the magnitude of predation. This type of independent validation rarely occurs in field ecology (Vucetich et al. 2011), particularly for large mammal systems.
In addition to the basic relationships presented above, many other factors can affect predator–prey dynamics including time‐lags of the predator's NR (Gasaway et al. 1983), alternative FR relationships (e.g. ratio dependent; Abrams & Ginzburg 2000; Jost et al. 2005; Hebblewhite 2013), body condition mediated by winter severity (Hurley et al. 2011) or summer nutrition (Brown 2011). Including all these possible combinations would result in many candidate models to apply to a single study system (Burnham & Anderson 2002). Therefore, we restricted the initial analyses to the five hypotheses presented above, but then conducted post hoc, heuristic analyses to incorporate time‐lags and alternative FR. We also include wolf FR and NR data from our study system to determine if local information improved the outcomes predicted by the independent data of Messier (1994) and Fuller, Mech & Cochrane (2003). Finally, we discuss results in the context of other systems that have been subjected to increased human exploitation, but where there was little consideration of how changes to the PR may have contributed to population decline.
Materials and methods
Study area
The study occurred in a 9400‐km2 area along three parallel mountain ranges oriented N–S in the interior of British Columbia, Canada: the Selkirk, Monashee and Cariboo mountains. The treatment area was 6500 km2 and was bounded by the Selkirk and Monashee mountains (51°34′ N, 118°30′ W). The reference area was 2900 km2, was between the Monashee and Cariboo mountains (52°18′ N, 119°30′ W) and had similar ecosystem characteristics (precipitation, temperature, forest composition; Meidinger & Pojar 1991; Fig. 2). These areas range from 500 m a.s.l. in valley bottoms to mountain peaks reaching 3500 m, providing closure between the treatment and reference areas (Serrouya et al. 2011). The climate is wet, with >200 cm of annual precipitation, most of which falls as snow. Forests are highly productive and consist primarily of western red cedar (Thuja plicata) and western hemlock (Tsuga heterophylla) trees at low elevations, and subalpine fir (Abies lasiocarpa) and Engelmann spruce (Picea engelmannii) at higher elevations (>1300–1500 m a.s.l.). Regenerating cut blocks include willow (Salix spp.), cottonwood (Populus balsamifera), red‐osier dogwood (Cornus stolonifera), huckleberry (Vaccinium membranaceum), falsebox (Paxistima myrsinities), thimbleberry (Rubus parviflorus) and Indian hellebore (Veratrum viride).
Figure 2.
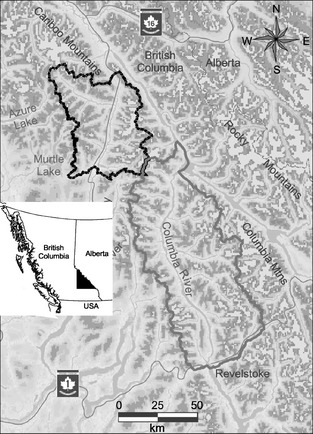
Study area in Southern British Columbia, Canada, with the moose reduction treatment area outlined in grey and the reference area in black. Mountain peaks are darker, with glaciers shown as the lightest shade.
Large mammals consist of wolves, black and grizzly bears (Ursus americanus and U. arctos), and moose. Cougars (Felis concolor), mule and white‐tailed deer (Odocoileus hemionus and O. virginianus), mountain goats (Oreamnos americanus) and woodland caribou (Rangifer tarandus) also occur but are uncommon. Moose densities in 2003 were 1·58 km−2 in the treatment area. In 2007, moose were surveyed in both the treatment and reference area and density estimates were the same, at 0·96 km−2 (Serrouya & Poole 2007). These values are winter densities corresponding to when moose are counted from the air on winter ranges. Winter ranges are considerably smaller than the overall study area, at c. 1100 km2 in the treatment area and 350 km2 in the reference area.
Moose reduction and hypothesis testing
The moose reduction began in the treatment area with a 10‐fold increase in hunter harvest of both male and female moose from 2003 to 2005, followed by a much reduced harvest level (Table 1). During the decade preceding the increased harvest, the moose population doubled (Serrouya et al. 2011), and harvest was light (<4%). All harvest was tightly controlled using a lottery system, so permits and kills could be tracked (Table 1). No major change to moose‐hunting allocations occurred in the reference area (Table 1), and wolf harvest was not manipulated in either area during the study. Due to thick cover and heavy snowfall, wolf hunting and trapping was light (0·11 and 0·16 annual rates in treatment and reference areas, respectively; Serrouya 2013) compared to other public lands (Webb, Allen & Merrill 2011). Moose abundance was estimated in the treatment area based on four aerial censuses over 10 years, using a stratified random block design (Gasaway 1986), with annual transects where pellets were counted and cleared each spring in 100‐m2 plots (details in Serrouya et al. 2011). The relative change in pellet densities mirrored the relative change in abundance, so the pellets could be used as an annual index of population change (Serrouya et al. 2011; updated with data in Appendix S1). In the reference area, only one moose population estimate was done (Serrouya & Poole 2007), so we relied on catch per unit effort (CPUE) data to compare population change between reference and treatment areas. CPUE is fraught with biases (Walters 2003; Peacock & Garshelis 2006) that are rarely evaluated, but we had the ability to independently assess the reliability of the CPUE. This evaluation was done by comparing moose population estimates in the treatment area with CPUE data for that same area, and the correlation was r = 0·91 (Appendix S2). CPUE data were only used to broadly compare moose population trends in the treatment vs. the reference area, not to quantitatively evaluate the five hypotheses. The comparison of moose trend between the treatment and reference areas served to determine whether the moose decline in the treatment area was initiated by hunting, or broad‐scale climatic factors that are known to affect large mammal predator–prey systems (Post & Stenseth 1998; Vucetich, Smith & Stahler 2005; Murray et al. 2006; Brown 2011).
Table 1.
Number of moose harvested in the treatment and reference areas. The moose reduction treatment began in 2003. Per cent of the harvest estimated to be adult male moose is shown in brackets
| Year | Treatment | Reference |
|---|---|---|
| 2000 | 18 (95) | 9 (100) |
| 2001 | 19 (50) | 8 (100) |
| 2002 | 13 (43) | 10 (100) |
| 2003 | 164 (55) | 11 (100) |
| 2004 | 250 (48) | 19 (100) |
| 2005 | 128 (51) | 17 (100) |
| 2006 | 46 (92) | 16 (100) |
| 2007 | 29 (86) | 8 (100) |
| 2008 | 27 (100) | 10 (100) |
| 2009 | 49 (70) | 13 (82) |
| 2010 | 27 (100) | 11 (100) |
| 2011 | 40 (48) | 12 (76) |
Our approach was to use difference equations to represent competing hypotheses to explain the magnitude and causes of the moose population decline (Table 2). The equations included variables with both known (i.e. estimated) and unknown values. Estimates included the annual moose population size, ratios of adult females, calves and adult males, hunting mortality and natural, but non‐predation mortality (i.e. accidents or poor condition; Table 2). Condition‐related mortality included malnutrition, potential disease or old age. The difference equations were programmed in r (code and data are included in Appendix S3) and can be used to potentially predict short‐term moose population dynamics with certain key inputs obtained from the field, including recent harvest estimates and ratios of calves to adult females.
Table 2.
Model structure for each hypothesis used to explain the decline of moose
| Hypothesis | Births | Calf deaths | Condition deaths | Hunting deaths | Wolf predation deathsa | ||
|---|---|---|---|---|---|---|---|
| Hunting caused the decline, no predation | N t+1= | N t | +N b | −N dn | −N dc | −N dh | |
| Hunting, and predation is DI (Fig. 1a) | N t+1= | N t | +N b | −N dn | −N dc | −N dh | −aNC 0 |
| Hunting, and predation is DD (Fig. 1b) | N t+1= | N t | +N b | −N dn | −N dc | −N dh | −aNC 2 |
| Hunting, and predation is DD and DEP (Fig. 1c) | N t+1= | N t | +N b | −N dn | −N dc | −N dh | −aNC 2/(1 + aNT h) |
| Predation is DD and DEP, but no hunting | N t+1= | N t | +N b | −N dn | −N dc | −aNC 2/(1 + aNT h) | |
DD, density dependent, DI, density independent, DEP, depensatory.
a is the attack rate for the Type I or II functional response (FR), T h is the handling time from the Type II FR, N is moose abundance, C 0 is wolf abundance that does not change with moose abundance, and C 2 is wolf abundance that changes asymptotically with moose abundance (equation from Messier 1994).
Recruitment and sex/age composition were estimated from five aerial composition surveys, and births were estimated by multiplying the pregnancy rate (0·897) by the number of adult females. Pregnancy was determined at the University of Saskatchewan's Endocrine Laboratory based on plasma progesterone. The number of adult females ranged from 48% to 57% of the population. Sex composition of the harvested moose was not specified in the difference equations because the post‐harvest sex ratio of the population was estimated through the five aerial classifications and thus accounted for changes in sex ratio, and would be a more appropriate reflection of pregnant females and thus calves produced each spring. Aerial surveys included sightability correction factors accounting for the age and sex classes of missed animals based on radio‐marked moose in British Columbia (Quayle, MacHutchon & Jury 2001). Calf recruitment (CR, ratio of 8‐month‐old calves to adult females) was found to be density dependent based on data from Serrouya et al. (2011) and was represented by CR = −0·13 × ln(N) + 1·25, where N is moose abundance. We calculated the number of calf deaths by subtracting the number of 8‐month‐old recruits (based on the CR equation above) from the number of births (Table 2). These calf deaths were likely caused by a variety of factors (bears, wolves, nutrition) that were not estimated separately, but were simply treated as calf deaths.
Condition‐related mortality was estimated based on radiocollar‐assisted mortality investigations and analysed using the Heisey–Fuller approach (Heisey & Fuller 1985). Condition‐related deaths may have been caused by poor nutrition, disease or old age but were grouped to estimate natural (but non‐predation) mortality. To help reduce possible biases associated with differential mortality risk throughout the year, we chose 12 risk periods corresponding to each calendar month, which converges to the Heisey–Patterson approach (Heisey & Patterson 2006). Annual survival rates were calculated from the product of the 12 monthly rates. Monthly survival rates were calculated by exponentiating the daily survival partitioned within each month, by the number of days within that month. Daily survival was calculated as 1 − (no. deaths)/(Σ monitoring days in the corresponding month). Annual survival rates were used to determine whether survival and recruitment values could corroborate the observed population decline, but annual survival was not required in the difference equations (Table 2). Uncertainty was calculated using 1000 bootstrap replicates using Pop Tools (Hood 2010) in Excel using the individual animal as the sample unit.
The unknown value in the difference equations was predation deaths due to wolves, and the magnitude of predation was treated as competing hypotheses based on the forms in Fig. 1, with the equations detailed in Table 2. We used an approach based on first principles by varying the type of the FR and NR to obtain PRs, using existing equations from the literature. The PR was calculated as PR = (FR × NR)/Prey density (Holling 1959b; Messier 1994). Predation was density independent if there was a Type I FR and a Type 0 NR (Fig. 1a, Table 2). The wolf abundance was set at 33·2 for the Type 0 NR, based on 1650 moose and the equation from Fuller, Mech & Cochrane (2003). Predation was density dependent if there was a Type I NR with a Type II FR, or if there was a Type II FR with a Type I NR (Fig. 1b). Predation was depensatory if both the FR and NR were Type II, but transitioned to density dependent at lower prey densities (Fig. 1c; Messier 1994). Parameters for the Type I and II NRs were obtained from Fuller, Mech & Cochrane (2003) and Messier (1994), respectively. Parameters for a and T h (the attack rate and handling time, respectively; Holling 1959a) for the FR were estimated based on Messier (1994) (see Appendix S4 for details).
We also tested the hypothesis that predation was compensatory by completely removing wolf predation from the model. Because wolf diets in the treatment area consist mainly of moose (Stotyn 2008), removing this source of mortality from the model implies that wolf predation was compensatory. Similarly, we removed hunting from the model to test whether this factor was compensatory. Yet, to be conservative, in this case we specified the most severe form of predation (i.e. depensatory; Table 2). This approach allowed us to compare the relative influence of predation vs. hunting to explain the magnitude of the moose population decline. In summary, five alternative hypotheses with associated predictions were compared, four involving predation of various forms and the fifth included only hunting (Table 2).
Heuristic models
In addition to the primary hypotheses outlined above, we considered the following modifications: time‐lags of the wolf NR, a ratio‐dependent FR, a function accounting for compensatory predation that was density dependent (i.e. stronger at higher moose abundance, rather than dichotomously compensatory or not, Appendix S5) and derivation of parameters from our study system as opposed to the literature (i.e. Messier 1994; Fuller, Mech & Cochrane, 2003; Appendix S4). We included a 1‐year time‐lag of the wolf NR by setting the wolf population as a function of the previous years' moose abundance and predicted that this would increase the PR because moose were declining. The ratio‐dependent FR was calculated as kill rate = (a N)/(C + a N T h), where C is predator abundance (Abrams & Ginzburg 2000).
To determine if local data improved the general predictions from the broader research (Messier 1994; Fuller, Mech & Cochrane 2003), we included FR and NR response data from the treatment area. We obtained a new FR curve by estimating parameters for a and T h, using Messier's data but supplemented with 10 winter kill rate estimates from five wolf packs during the moose decline in the treatment area (see Appendix S4 for parameter estimation). We also estimated a and T h using the local data only, though fitting a disc‐equation curve to 10 data points may be suspected. In any case, we assessed the influence of including local data in two different ways, by adding them to the Messier data and by treating the local data on their own. We also used empirical wolf abundance estimates from our system that were available from 2007 to 2012 instead of the independent predictions from Messier's (1994) Type II NR and Fuller, Mech & Cochrane (2003) Type I NR, again to determine if local data improved predictions. We assessed each hypothesis using predicted vs. observed plots of population trajectory, using three criteria: slope and intercept closest to 1 and 0, respectively (i.e. perfect fit or accuracy), and by comparing the residual sums of squares (RSS) among models. These three metrics were based on median values from 10 000 bootstrap iterations. We also used Akaike information criteria (AICc) to address model parsimony, though AIC (Akaike 1973) is not consistently used for model validation because it is less revealing about model accuracy (i.e. slope and intercept of predicted vs. observed data; Haefner 2005).
Results
Based on the CPUE data, moose declined in the treatment area 4·6 times more than in the reference area (Fig. 3), and the decline was highly significant in the treatment area but non‐significant in the reference area [slopes were −6·27 (−8·10 to −4·60) compared to −1·35 (−3·58 to 1·11), for the treatment and reference areas, respectively]. In the treatment area, radiocollar data indicated that annual adult moose survival was 0·815 (0·723–0·886, 95% CI). This estimate was based on 89·6 moose‐years of monitoring 54 moose (39 F, 15 M). For just adult females, the survival rate was 0·828 (0·713–0·925). For larger cervids, this survival rate, coupled with observed calf : cow ratios that ranged between 22% and 35% (Serrouya et al. 2011), is suggestive of a declining population (DeCesare et al. 2012) and corroborates the trend observed in the treatment area. Seventeen moose deaths were recorded (11 F, 6 M), with six (35·3%; 3 F, 3 M) caused by hunting, five from predation (29·4%; 4 F, 1 M), four were from unknown causes (23·5% 3 F, 1 M), one from a vehicle collision (5·9%; 1 M) and one from poor body condition (5·8%; 1 F). Unknown deaths were not caused by vehicle collisions or hunting, but were likely caused by either predation, poor nutrition or natural accidents. To be conservative and not overemphasize the top‐down effects of predation or hunting, we assigned one unknown cause, which appeared to be accidental, as a natural (non‐predation) death. Thus, the annual death rate from condition/accidents was 0·024 (0–0·066) and was treated as a density‐independent rate in the difference equations (Table 2). Of the 54 moose radiocollared during this study (plus 18 moose collared since this study ended in 2012), two moose left the treatment area but one returned, leaving only one case of dispersal. Movement out of the treatment area was minimal, with >99·9% of 35 529 GPS telemetry locations from moose caught in the treatment area remaining there.
Figure 3.
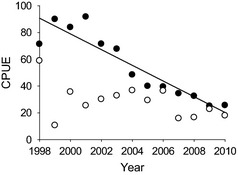
Catch per unit effort (CPUE; % hunter success) of moose harvest in the treatment (solid circles) and reference (open circles) area. The slope of the treatment area is −6·27 (−8·10 to −4·60), but non‐significant for the reference (−1·35, −3·58 to 1·11). CIs were obtained from bootstrapping years (n = 1000). CPUE data were validated with empirical abundance data from the treatment area (Appendix S2).
Hypotheses explaining the moose decline
Models that excluded either hunting or predation failed to predict the magnitude of the observed moose decline. However, models that included predation (without hunting) produced a much more realistic population decline compared to the effect of hunting without predation (Fig. 4). Including hunting, without any effect of predation (i.e. compensatory predation), produced the least plausible explanation because it predicted an increasing moose population (Fig. 4). Of the models that included predation, those using a Type II NR and Type II FR provided the best explanation of the decline, indicating that the PR was depensatory (Fig. 1c) for the initial phase of the decline. Evidence supporting the depensatory hypothesis was strongest because its goodness‐of‐fit plot included a slope closest to 1, intercept closest to 0 and lowest deviation from predicted values (lowest RSS), and was most parsimonious (Fig. 5a). By dividing the predicted number of predation deaths by the predicted population size, the PR from the depensatory hypothesis is estimated at 15·5% in 2003 and increased to a peak of 18·2% in 2008 (data output shown in r code from Appendix S3).
Figure 4.
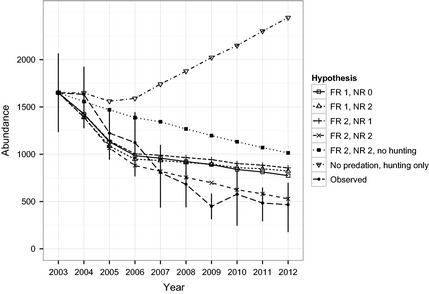
Comparison of model predictions to observed moose abundance. Hypotheses are as follows: hunting caused the decline (thus predation was compensatory), predation caused the decline (FR2 NR2) and no effect of hunting, or hunting and predation, but predation was (1) depensatory (FR 2, NR 2); or (2) density independent (FR1 NR0); or (3) density dependent (FR 1 NR 2 or FR2 NR 1). Error bars are 90% CIs for the observed moose abundance.
Figure 5.
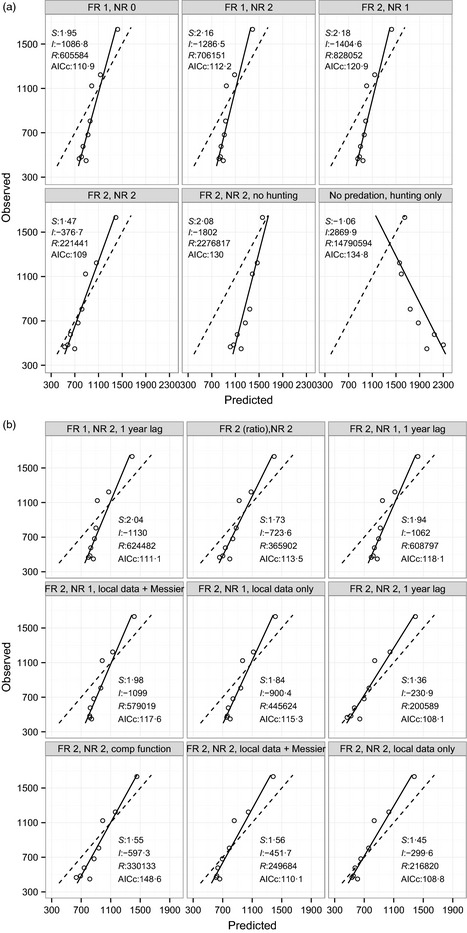
Observed vs. predicted validation plots for competing hypotheses used to explain the moose population decline in the treatment area. Panel (a) shows the initial hypotheses, with FR and NR parameters from outside the study system (i.e. Messier 1994; Fuller, Mech & Cochrane 2003). Panel (b) shows the heuristic models: Comp function = compensatory predation function, ratio = a ratio‐dependent functional response, 1 year lag = a 1‐year lag of the predator's NR to moose abundance. FR = function response and NR = numerical response, with numbers indicating the type. S, I and R represent the slope, intercept and residual sums of squares (RSS), respectively, of the goodness‐of‐fit (GOF). Models are more accurate with a slope closer to 1 and 0 intercept, and more precise with a lower RSS. AICc is the Akaike information criteria. Solid line is the GOF plot, and dashed line is the idealized 1 : 1 plot.
Models that included predation, but without a depensatory component, did not predict the same magnitude of the moose decline (Figs 4 and 5a). These models overestimated the moose population by at least 65%, based on abundance values in 2012 (Fig. 4). Even though some models without depensatory predation were within two AICc of the top model (Fig. 5; e.g. FR1 NR0), they overestimated the moose population size by more than 300 animals (Fig. 4). The heuristic models including variations such as predator time‐lags, a ratio‐dependent FR or local data produced one improvement over the basic models (Fig. 5a vs. 5b). The model with depensatory predation that was supplemented with a 1‐yr time‐lag of the wolf decline produced the most accurate prediction of the moose decline. Relative to all other models, this model had the lowest RSS, a slope closest to 1 (Fig. 5a,b), and predicted 468 moose in 2012 (observed value was 466). The models that included local FR and NR data to supplement Messier's equations (Fig. 5b) did not produce a substantial improvement over the models with only Messier's data (Fig. 5a). Considering all 15 models, those that had a depensatory predation component (i.e. Type II NR and Type II FR) consistently had slopes closer to 1 and a lower RSS. Models with compensatory predation or the ratio‐dependent FR were not well supported (Fig. 5a,b).
Discussion
Our approach was to use predator–prey theory, parameterized with FR and NR data from elsewhere, to determine which hypotheses could be used to predict population dynamics at a local scale (Hilborn & Mangel 1997). Although no equation was perfect, it was notable how well some independent relationships predicted population dynamics within the study system. Furthermore, the spatial reference area allowed us to establish that the moose decline observed in the treatment area was not caused by broad‐scale climatic processes, but was initiated by the hunting treatment.
Models that included a depensatory PR were best able to predict the decline of moose in the treatment area. This finding is consistent with the hypothesis proposed by Messier (1994) who suggested that the combination of Type II FR and NR would produce a unimodal PR (Holling 1959b) with a depensatory phase (Fig. 1c). Although Messier's FR and NR were parameterized from meta‐analyses, the resulting unimodal PR has been suggested as a primary mechanism of moose–wolf dynamics by researchers in both Europe (Jedrzejewski et al. 2002) and North America (Gasaway et al. 1992). A unimodal PR also sets the stage for a 2‐state system because two stable intersections with another vital rate (i.e. recruitment) can occur (Messier 1994), though our experiment was not designed to evaluate this condition (Beisner, Haydon & Cuddington 2003).
Following the recolonization of wolves in Banff National Park, Hebblewhite (2013) found stronger support for a ratio‐dependent Type II FR, yet the end result was similar, depensatory predation on elk (Cervus elaphus). Whether the Type II FR is ratio‐ or prey dependent, when combined with a Type II NR, the PR will be depensatory. The underlying mechanism for a depensatory PR is that at high prey density, predators are satiated by the limitation imposed by handling time. Also at high prey density, predator numbers are constrained (Cariappa et al. 2011), likely due to social factors associated with territoriality or strife among family units (Cubaynes et al. 2014). Then, as prey are reduced, a similar number of predators consume a similar number of prey (on a per predator basis), but out of a smaller prey population, thereby increasing the PR. This pattern holds until the inflection point on either the Type II FR or NR is achieved, at which point the PR is relaxed.
An unexpected outcome of this work was that supplementing independent predictions with local data (FR and NR of wolves) did not substantially improve model predictions, despite enormous cost and effort to collect these data. Adding the local data suggested slightly less model parsimony (1·1 AICc units higher), and less accuracy (a lower intercept and higher slope), but was still a plausible explanation of observed pattern. The 2012 population estimate was 466 moose, the independent parameters from Messier (1994) predicted 527, whereas the prediction was 611 moose when parameters were updated with the local FR and NR data. These results may be viewed as a failing but in fact suggest that the theory was robust to local variation. From an applied perspective, if approximate and short‐term predictions are all that are required, then the task of managers is greatly simplified. Using basic parameters that are often collected by management agencies (age and sex ratios and harvest statistics of prey), short‐term moose dynamics can be predicted in the absence of local wolf behavioural and numeric data, which are far more difficult to collect. If environmental changes occur that facilitate disease or condition‐related mortalities (Murray et al. 2006), then the models' predictions would not hold. Periodic radiocollaring of prey species to estimate mortality causes can help safeguard against this risk.
Our results are not in agreement with some other large mammal predator–prey systems. Following the reintroduction of wolves in the Yellowstone ecosystem, wolf predation was found to be primarily compensatory (Vucetich, Smith & Stahler 2005) when the magnitude of an elk decline was similar to our moose decline. Vucetich outlines several plausible reasons for why predation may have been additive vs. compensatory, yet we suggest an additional explanation that in Yellowstone, wolf predation was a relatively minor component of elk mortality (<9% but most often <5%, as an annual PR; Vucetich et al. 2011), whereas in our system, wolves may be a greater source of adult moose mortality (predicted to be up to 18% based on the most supported model). These differences highlight the need to focus on major limiting factors when attempting to generalize predator–prey dynamics among ecosystems (Sinclair 1989; Krebs 2009).
The models may be criticized for not explicitly incorporating nutritional and climate‐related factors that are known to influence population dynamics of large herbivores (Post & Stenseth 1998; Vucetich, Smith & Stahler 2005; Murray et al. 2006; Brown 2011). Yet, several lines of evidence suggest that nutrition and climate were not primary factors of the moose decline. There were few mortalities caused by body condition, the adjacent reference area did not show a population decline in the absence of an increased harvest, and the treatment population was initially more abundant but reduced with hunter harvest. If bottom‐up factors were causing the decline, deaths of collared moose would have been dominated by animals that were nutritionally stressed, as was observed in other systems (e.g. Murray et al. 2006).
The results from this study have important implications for any organism that is preyed upon but that also has, or will be, subject to increased human exploitation. If sustained harvest models fail to account or at least assess the potential for depensatory predation, then yields may be excessive. The outcome would be a negative feedback loop of increased predation and harvest that would be difficult to reverse even with a substantial reduction in harvest. North Atlantic cod (Gadus morhua) stocks were driven to historic lows because of overharvest, but predation by seals continued, which did not decline proportionately in abundance during or after the cod collapse. This would theoretically result in a depensatory PR that would accelerate the decline and even inhibit recovery, particularly if a 2‐state system is realized (Fu, Mohn & Fanning 2001; Frank et al. 2005; Trzcinski, Mohn & Bowen 2006). To our knowledge, harvesting models do not explicitly account for increasing PRs and we suggest this would be an important avenue for future work, particularly for systems that are subject to increased harvest by humans or perturbations from other factors.
In the last decade, there have been several attempts, across taxonomic groups, to reduce overabundant prey where rare prey are being driven to extinction by predator‐mediated apparent competition (Courchamp, Woodroffe & Roemer 2003; Serrouya et al. 2011; Steenweg 2011; Wittmer et al. 2013). Yet, if depensatory predation is not accounted for while reducing the overabundant prey, these populations may decline faster than anticipated and exacerbate switching of predators to the rare prey (Serrouya et al. 2015). The outcome may be to unintentionally increase extinction risk to the rare prey. Given these risks, the most prudent action may be to concurrently reduce overabundant prey and predators, and keep prey at low numbers to reduce the need for long‐term predator management.
Data accessibility
r scripts for model predictions, and observed data, are included as online Appendix S3.
Supporting information
Appendix S1. Details of aerial survey and pellet counts to monitor moose abundance.
Appendix S2. Linking moose abundance to catch per unit effort data.
Appendix S3. R script for difference equations of model predictions contrasted with observed moose population data.
Appendix S4. Estimate of the rate of foraging efficiency (a) and handling time (T h) from Holling's disc equation.
Appendix S5. Density dependent compensatory predation function.
Acknowledgements
K. Artelle was a partner for a class project on this work with R. Serrouya, and we thank him for his feedback. Moose collars were purchased by the Selkirk College Geospatial Research Centre, and fieldwork was funded by the British Columbia Ministry of Forests. R. Serrouya was supported by a scholarship from the Natural Sciences and Engineering Research Council of Canada and from Alberta Ingenuity. Thanks to the many field technicians who helped collect moose data, to K. Poole for helping with aerial censuses and to T. Szkorupa and P. Stent for assistance compiling the moose harvest data. We sincerely thank I. Hatter, M. Lewis, M. Hebblewhite, J. Fryxell and an anonymous reviewer for comments that improved this manuscript. The authors declare no conflict of interest with this research.
References
- Abrams, P.A. (2000) The evolution of predator‐prey interactions: theory and evidence. Annual Review of Ecology and Systematics, 31, 79–105. [Google Scholar]
- Abrams, P.A. & Ginzburg, L.R. (2000) The nature of predation: prey dependent, ratio dependent or neither? Trends in Ecology & Evolution, 15, 337–341. [DOI] [PubMed] [Google Scholar]
- Akaike, H. (1973) Information theory as an extension of the maximum likelihood principle Second International Symposium on Information Theory (eds Petrov B.N. & Csaki F.), pp. 267–281. Akademiai Kiado, Budapest. [Google Scholar]
- Beisner, B.E. , Haydon, D.T. & Cuddington, K. (2003) Alternative stable states in ecology. Frontiers in Ecology and the Environment, 1, 376–382. [Google Scholar]
- Bergerud, A.T. & Elliot, J.P. (1986) Dynamics of caribou and wolves in northern British Columbia. Canadian Journal of Zoology, 64, 1515–1529. [Google Scholar]
- Boutin, S. (1992) Predation and moose population dynamics – a critique. Journal of Wildlife Management, 56, 116–127. [Google Scholar]
- Brown, G.S. (2011) Patterns and causes of demographic variation in a harvested moose population: evidence for the effects of climate and density‐dependent drivers. Journal of Animal Ecology, 80, 1288–1298. [DOI] [PubMed] [Google Scholar]
- Burnham, K.P. & Anderson, D.R. (2002) Model Selection and Multimodel Inference: A Practical Information‐Theoretic Approach, 2nd edn Springer, New York, New York, USA. [Google Scholar]
- Cariappa, C. , Oakleaf, J.K. , Ballard, W.B. & Breck, S.W. (2011) A reappraisal of the evidence for regulation of wolf populations. The Journal of Wildlife Management, 75, 726–730. [Google Scholar]
- Courchamp, F. , Woodroffe, R. & Roemer, G. (2003) Removing protected populations to save endangered species. Science, 302, 1532. [DOI] [PubMed] [Google Scholar]
- Cubaynes, S. , MacNulty, D.R. , Stahler, D.R. , Quimby, K.A. , Smith, D.W. & Coulson, T. (2014) Density‐dependent intraspecific aggression regulates survival in northern Yellowstone wolves (Canis lupus). Journal of Animal Ecology, 83, 1344–1356. [DOI] [PubMed] [Google Scholar]
- DeCesare, N.J. , Hebblewhite, M. , Robinson, H.S. & Musiani, M. (2010) Endangered, apparently: the role of apparent competition in endangered species conservation. Animal Conservation, 13, 353–362. [Google Scholar]
- DeCesare, N.J. , Hebblewhite, M. , Bradley, M. , Smith, K.G. , Hervieux, D. & Neufeld, L. (2012) Estimating ungulate recruitment and growth rates using age ratios. Journal of Wildlife Management, 76, 144–153. [Google Scholar]
- Doak, D.F. , Estes, J.A. , Halpern, B.S. , Jacob, U. , Lindberg, D.R. , Lovvorn, J. et al (2008) Understanding and predicting ecological dynamics: are major surprises inevitable? Ecology, 89, 952–961. [DOI] [PubMed] [Google Scholar]
- Errington, P.L. (1946) Predation and vertebrate populations. Quarterly Review of Biology, 21, 144–177. [Google Scholar]
- Frank, K.T. , Petrie, B. , Choi, J.S. & Leggett, W.C. (2005) Trophic cascades in a formerly cod‐dominated ecosystem. Science, 308, 1621–1623. [DOI] [PubMed] [Google Scholar]
- Fu, C.H. , Mohn, R. & Fanning, L.P. (2001) Why the Atlantic cod (Gadus morhua) stock off eastern Nova Scotia has not recovered. Canadian Journal of Fisheries and Aquatic Sciences, 58, 1613–1623. [Google Scholar]
- Fuller, T.K. , Mech, L.D. & Cochrane, J.F. (2003) Wolf population dynamics Wolves: Behavior, Ecology, and Conservation (eds Mech D.L. & Boitani L.), pp. 161–191. University of Chicago Press, Chicago, Illinois, USA. [Google Scholar]
- Gasaway, W.C. (1986) Estimating Moose Population Parameters from Aerial Surveys. Institute of Arctic Biology, Fairbanks, Alaska, USA. [Google Scholar]
- Gasaway, W.C. , Stephenson, R.O. , Davis, J.L. , Shepherd, P.E.K. & Burris, O.E. (1983) Interrelationships of wolves, prey, and man in interior Alaska. Wildlife Monographs, 84, 1–50. [Google Scholar]
- Gasaway, W.C. , Boertje, R.D. , Grangaard, D.V. , Kelleyhouse, D.G. , Stephenson, R.O. & Larsen, D.G. (1992) The role of predation in limiting moose at low‐densities in Alaska and Yukon and implications for conservation. Wildlife Monographs, 120, 1–59. [Google Scholar]
- Haefner, J.W. (2005) Modeling Biological Systems: Principles and Applications, 2nd edn Springer, New York, New York, USA. [Google Scholar]
- Hayes, R.D. , Farnell, R. , Ward, R.M.P. , Carey, J. , Dehn, M. , Kuzyk, G.W. et al (2003) Experimental reduction of wolves in the Yukon: ungulate responses and management implications. Wildlife Monographs, 152, 1–35. [Google Scholar]
- Hebblewhite, M. (2013) Consequences of ratio‐dependent predation by wolves for elk population dynamics. Population Ecology, 55, 511–522. [Google Scholar]
- Heisey, D.M. & Fuller, T.K. (1985) Evaluation of survival and cause‐specific mortality rates using telemetry data. Journal of Wildlife Management, 49, 668–674. [Google Scholar]
- Heisey, D.M. & Patterson, B.R. (2006) A review of methods to estimate cause‐specific mortality in presence of competing risks. Journal of Wildlife Management, 70, 1544–1555. [Google Scholar]
- Hervieux, D. , Hebblewhite, M. , Stepnisky, D. , Bacon, M. & Boutin, S. (2014) Managing wolves (Canis lupus) to recover threatened woodland caribou (Rangifer tarandus caribou) in Alberta. Canadian Journal of Zoology, 92, 1029–1037. [Google Scholar]
- Hilborn, R. & Mangel, M. (1997) The Ecological Detective: Confronting Models with Data. Princeton University Press, Princeton, New Jersey, USA. [Google Scholar]
- Holling, C.S. (1959a) Some characteristics of simple types of predation and parasitism. Canadian Entomologist, 91, 385–398. [Google Scholar]
- Holling, C.S. (1959b) The components of predation as revealed by a study of small‐mammal predation of the European pine sawfly. Canadian Entomologist, 91, 293–320. [Google Scholar]
- Hood, G.M. (2010) PopTools version 3.2.5. http://www.poptools.org
- Hossie, T.J. & Murray, D.L. (2010) You can't run but you can hide: refuge use in frog tadpoles elicits density‐dependent predation by dragonfly larvae. Oecologia, 163, 395–404. [DOI] [PubMed] [Google Scholar]
- Hurley, M.A. , Unsworth, J.W. , Zager, P. , Hebblewhite, M. , Garton, E.O. , Montgomery, D.M. et al (2011) Demographic response of mule deer to experimental reduction of coyotes and mountain lions in southeastern Idaho. Wildlife Monographs, 178, 1–33. [Google Scholar]
- Jedrzejewski, W. , Schmidt, K. , Theuerkauf, J. , Jedrzejewska, B. , Selva, N. , Zub, K. et al (2002) Kill rates and predation by wolves on ungulate populations in Bialowieza Primeval Forest (Poland). Ecology, 83, 1341–1356. [Google Scholar]
- Jost, C. , Devulder, G. , Vucetich, J.A. , Peterson, R.O. & Arditi, R. (2005) The wolves of Isle Royale display scale‐invariant satiation and ratio‐dependent predation on moose. Journal of Animal Ecology, 74, 809–816. [Google Scholar]
- Krebs, C.J. (2009) Ecology: The Experimental Analysis of Distribution and Abundance, 6th edn Benjamin Cummings, San Francisco, California; London. [Google Scholar]
- Krebs, C.J. (2011) Of lemmings and snowshoe hares: the ecology of northern Canada. Proceedings of the Royal Society B‐Biological Sciences, 278, 481–489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levins, R. (1966) The strategy of model building in population biology. American Scientist, 54, 421–431. [Google Scholar]
- Meidinger, D.V. & Pojar, J. (1991) Ecosystems of British Columbia. Special Report Series 4 British Columbia Ministry of Forests, Victoria, British Columbia, Canada. [Google Scholar]
- Messier, F. (1994) Ungulate population models with predation: a case study with the North American Moose. Ecology, 75, 478–488. [Google Scholar]
- Murray, D.L. , Cox, E.W. , Ballard, W.B. , Whitlaw, H.A. , Lenarz, M.S. , Custer, T.W. et al (2006) Pathogens, nutritional deficiency, and climate influences on a declining moose population. Wildlife Monographs, 166, 1–29. [Google Scholar]
- Peacock, E. & Garshelis, D.L. (2006) Comment on “On the regulation of populations of mammals, birds, fish, and insects'' IV. Science, 313, 45. [DOI] [PubMed] [Google Scholar]
- Post, E. & Stenseth, N.C. (1998) Large‐scale climatic fluctuation and population dynamics of moose and white‐tailed deer. Journal of Animal Ecology, 67, 537–543. [Google Scholar]
- Quayle, J.F. , MacHutchon, A.G. & Jury, D.N. (2001) Modeling moose sightability in south‐central British Columbia. Alces, 37, 43–54. [Google Scholar]
- Schmitz, O.J. , Hamback, P.A. & Beckerman, A.P. (2000) Trophic cascades in terrestrial systems: a review of the effects of carnivore removals on plants. American Naturalist, 155, 141–153. [DOI] [PubMed] [Google Scholar]
- Serrouya, R. (2013) An adaptive approach to endangered species recovery based on a management experiment: reducing moose to reduce apparent competition with woodland caribou. PhD thesis, University of Alberta, Edmonton, Alberta, Canada. [Google Scholar]
- Serrouya, R. & Poole, K. (2007) Moose Population Monitoring in the Lake Revelstoke (Management Units 4–38 and 4–39) and North Thompson (MUs 3–43 and 3–44) Valleys, January 2006 and 2007. Unpublished report for the BC Fish and Wildlife Compensation Program, Columbia Basin. [Google Scholar]
- Serrouya, R. , McLellan, B.N. , Boutin, S. , Seip, D.R. & Nielsen, S.E. (2011) Developing a population target for an overabundant ungulate for ecosystem restoration. Journal of Applied Ecology, 48, 935–942. [Google Scholar]
- Serrouya, R. , Wittmann, M.J. , McLellan, B.N. , Wittmer, H.U. & Boutin, S. (2015) Using predator‐prey theory to predict outcomes of broadscale experiments to reduce apparent competition. The American Naturalist, 185, 665–679. [DOI] [PubMed] [Google Scholar]
- Shurin, J.B. , Borer, E.T. , Seabloom, E.W. , Anderson, K. , Blanchette, C.A. , Broitman, B. et al (2002) A cross‐ecosystem comparison of the strength of trophic cascades. Ecology Letters, 5, 785–791. [Google Scholar]
- Sinclair, A.R.E. (1989) Population regulation in animals Ecological Concepts (ed. Cherrett J.M.), pp. 197–241. Blackwell, Oxford. [Google Scholar]
- Steenweg, R. (2011) Interactions of wolves, mountain caribou, and an increased moose‐hunting quota – primary‐prey management as an approach to caribou recovery. MSc thesis, University of Northern British Columbia, Prince George, British Columbia, Canada. [Google Scholar]
- Stotyn, S. (2008) Ecological interactions of mountain caribou, wolves and moose in the north Columbia Mountains, British Columbia. MSc thesis, University of Alberta, Edmonton, Alberta, Canada. [Google Scholar]
- Strong, D.R. (1986) Density‐vague population change. Trends in Ecology & Evolution, 1, 39–42. [DOI] [PubMed] [Google Scholar]
- Trzcinski, M.K. , Mohn, R. & Bowen, W.D. (2006) Continued decline of an Atlantic cod population: how important is gray seal predation? Ecological Applications, 16, 2276–2292. [DOI] [PubMed] [Google Scholar]
- Vucetich, J.A. , Smith, D.W. & Stahler, D.R. (2005) Influence of harvest, climate and wolf predation on Yellowstone elk, 1961–2004. Oikos, 111, 259–270. [Google Scholar]
- Vucetich, J.A. , Hebblewhite, M. , Smith, D.W. & Peterson, R.O. (2011) Predicting prey population dynamics from kill rate, predation rate and predator‐prey ratios in three wolf‐ungulate systems. Journal of Animal Ecology, 80, 1236–1245. [DOI] [PubMed] [Google Scholar]
- Walters, C. (2003) Folly and fantasy in the analysis of spatial catch rate data. Canadian Journal of Fisheries and Aquatic Sciences, 60, 1433–1436. [Google Scholar]
- Walters, C.J. & Holling, C.S. (1990) Large‐scale management experiments and learning by doing. Ecology, 71, 2060–2068. [Google Scholar]
- Webb, N.F. , Allen, J.R. & Merrill, E.H. (2011) Demography of a harvested population of wolves (Canis lupus) in west‐central Alberta, Canada. Canadian Journal of Zoology, 89, 744–752. [Google Scholar]
- Wittmer, H.U. , Serrouya, R. , Elbroch, M. & Marshall, A.J. (2013) Conservation strategies for species affected by apparent competition. Conservation Biology, 27, 254–260. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1. Details of aerial survey and pellet counts to monitor moose abundance.
Appendix S2. Linking moose abundance to catch per unit effort data.
Appendix S3. R script for difference equations of model predictions contrasted with observed moose population data.
Appendix S4. Estimate of the rate of foraging efficiency (a) and handling time (T h) from Holling's disc equation.
Appendix S5. Density dependent compensatory predation function.
Data Availability Statement
r scripts for model predictions, and observed data, are included as online Appendix S3.


