Harmonic Ratios: A quantification of step to step symmetry

Abstract

The harmonic ratio (HR), derived from Fourier analysis of trunk accelerations, has been described in various ways as a measure of walking smoothness, walking rhythmicity, or dynamic stability. There is increasing interest in applying the HR technique to investigate the impact of various pathologies on locomotion; however, explanation of the method has been limited. The aim hereis to present a clear description of the mathematical basis of HRs and an understanding of their interpretation. We present harmonic theory, the interpretation of the HR using sinusoidal signals, and an exampleusing actual trunk accelerations and harmonic analyses during limb-loading conditions. We suggest that the HR method may be better defined, not as a measure of rhythmicity or stability, but as a measure of step-to-step symmetry within a stride.

1. Introduction

The Harmonic Ratio (HR) is a measure used to quantify smoothness of walking (Gage, 1964; Menz et al, 2003b; Smidt et al., 1971; Yack & Berger, 1993). In gait research, the HR is most commonly extracted from trunk accelerations in the anteroposterior (AP), vertical (VT) and mediolateral (ML) directions. The VT and AP accelerations are biphasic within a stride due to the right and left steps, while the ML accelerations are monophasic (Figure 1). The HR quantifies the harmonic composition of these accelerations for a given stride, where a high HR is interpreted as greater walking smoothness. The HR calculated from trunk accelerations, unlike typical spatiotemporal parameters, is a summary measure of whole body movement. HRs have discriminated between the gait of young and older adults (Brach et al, 2011; Kavanagh et al, 2005a; Yack & Berger, 1993), older adults who have and have not fallen (Menz et al, 2003a), and the gait of healthy older adults and individuals with neurologic disorders (Latt et al., 2009; Lowry et al, 2009; Menz et al, 2004). Recently there is increasing interest in applying the HR technique to discriminate between individuals with different pathologies and to monitor the impact of rehabilitation protocols.

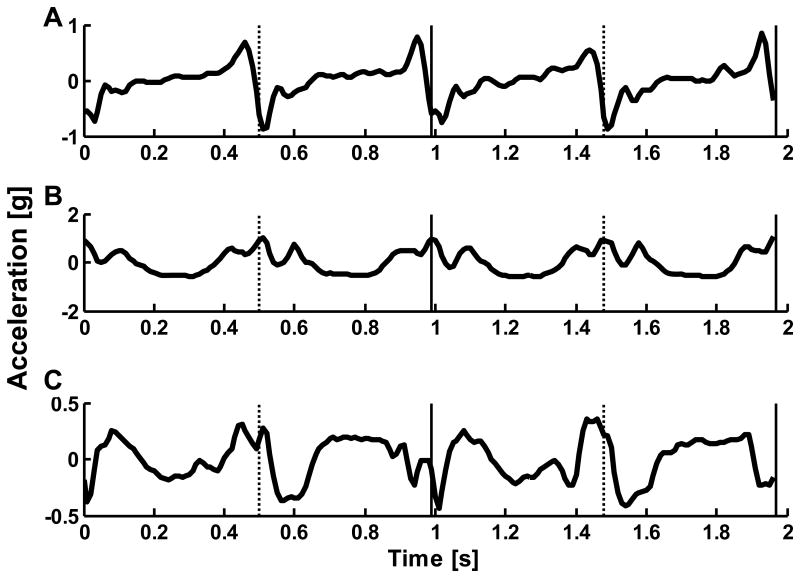
Figure 1.

Example L3/L4 acceleration signal for (A) anterioposter, (B) vertical, and (C) mediolateral directions with right (vertical solid) and left (vertical dotted) heel contacts. Note: the gravitational component has been removed.

While showing potential as a gait analysis tool, the terminology used to define and explain HRs has generated some confusion across disciplines. An early study described HRs as “reflecting the frequency of force changes experienced by the body during the walking cycle, providing an index for the smoothness of walking” (Smidt et al, 1977). However, researchers have also used the terms rhythmicity (Latt et al., 2008; Menz, et al, 2003b), dynamic stability (Yack & Berger, 1993), and walking balance (Menz et al, 2003c) interchangeably with smoothness of walking. These terms do not share the same meaning. Rhythmicity can refer to any rhythm, whereas HRs specifically quantifies the biphasic and monophasic nature of the signals. Also, dynamic stability has been recently been defined by researchers as “the sensitivity of a system to infinitesimally small perturbations” and been quantified by Lyapunov exponents ((Dingwell & Marin, 2006). Our goal is to provide a clear description of the mathematical basis of HRs and an understanding of their physiological interpretation.

2. Methods

2.1 Harmonic theory

The HR method is based upon harmonic theory to examine the symmetry within a stride by exploiting the periodicity of the signal (Gage, 1964; Smidt et al, 1971). The measured accelerations for each stride are analyzed in the frequency domain through a well-established technique of Fourier analysis based on the stride frequency (Oppenheim, 1997). Since the DFT is performed on each stride separately, the measure allows for variance of the stride frequency within a trial. However, given the basis in single stride analysis, the measure sensitive to errors in stride frequency; thus, consistency of stride segmentation location (i.e. identification of heel contact) is very important. The HR is then defined from the DFT as the ratio of the sum of the amplitudes of the even harmonics (n=2,4,6,…) to the sum of the amplitudes of the odd harmonics (n=1,3,5,…). However, because of the differing biphasic and monophasic natures of the AP and VT versus ML components, the ratios of the odd to even harmonics are calculated inversely.

Traditionally, the first twenty harmonic coefficients are used to calculate the HRs (Smidt, et al, 1971). This is justified for normal cadences, because the majority of the power occurs below 10Hz (Kavanagh et al, 2005b), and the normal stride frequency generally ranges from 0.8Hz for older adults walking slowly to 1.1Hz for young adults walking quickly (100 to 135 steps/min respectively) (Hollman et al, 2011; Sekiya & Nagasaki, 1998). Cadences of 60 steps/min or slower (0.5Hz stride frequency) may be problematic, since the first 20 harmonics only encompasses frequencies up to 10Hz. When using HRs, the power spectrum should be inspected to ensure enough coefficients are incorporated into the ratio, and the number of coefficients can be increased by twos if needed.

2.2. Sinusoid example

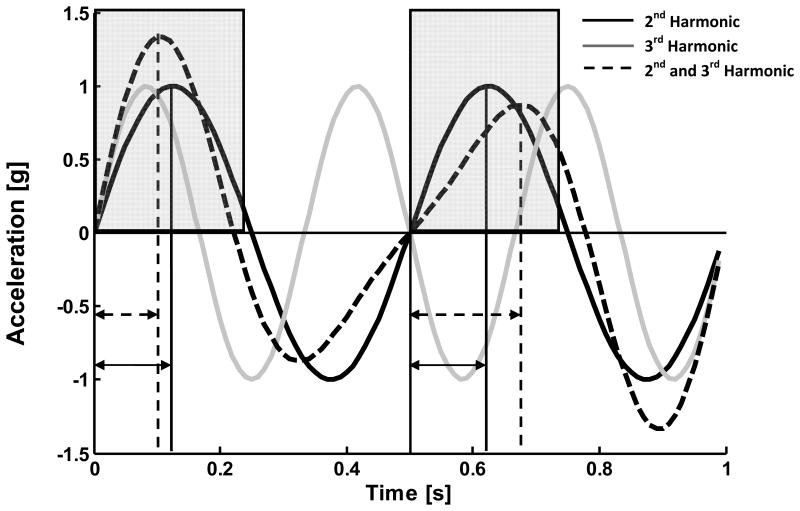
To demonstrate the differing effects of even and odd harmonic components, we present a simple example implementing the HR technique on sinusoids for the biphasic case. Two harmonics of a 1 Hz sinusoid (2^nd and 3^rd harmonics) are used. The 1Hz sinusoid can be thought of as the “stride frequency,” and the “steps” are half of the sinusoid, bisected at 0.5s. In Figure 2 we depict the even 2^nd harmonic, the odd 3^rd harmonic, and a summation of scaled 2^nd and 3^rd harmonics. As odd harmonics cannot be divided evenly within each step, adding them to the even harmonics results in differing constructive and destructive interference in the first and second halves of the cycle (i.e. each step). Thus, interference between the amplitudes of the odd and even harmonics results in changes in magnitude and timing between steps; this effect is entirely based on the magnitude of the harmonic frequencies and not the phase. This effect is reflected in the HR, as in this sinusoidal example the HR for the 2^nd harmonic alone would be infinity and the summation of the 2^nd and 3^rd harmonic would be reduced to 2.5.

Figure 2.

Effect of odd harmonic components on sinusoidal summations. When compared to the regular patterns of the 2^nd (black solid line; sin(2·2π)) and the 3^rd harmonics (gray solid line; sin(3·2π)), the summation of the 2^nd and 3^rd (dashed line; sin(2·2π) + 0.4sin(3·2π)) demonstrates changes in both timing and magnitude between steps. The 3^rd harmonic constructively combines with the positive peak of the 2^nd harmonic in the first step and destructively in the second, generating the magnitude differences in the summation highlighted by the gray regions. The constructive/destructive summation also induces a timing shift in the peaks as indicated by the timing of dashed vertical lines from the start of each step and as compared to the consistent solid vertical lines of the 2^nd harmonic.

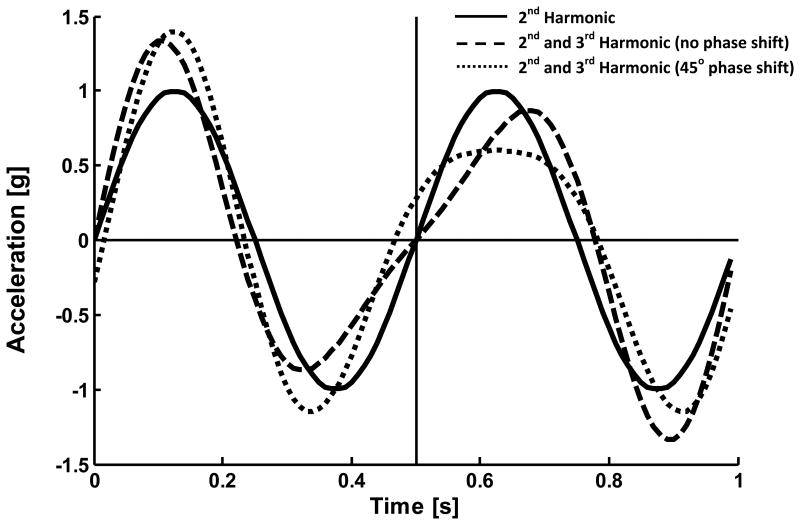
The phases of the even and odd harmonics within a stride are not used within the calculation of the HR. The unaccounted-for phase of each harmonic affects where in the stride the magnitude and timing changes occur, but not the amount. Thus, an infinite number of phase combinations can produce the same HR. Figure 3 displays an example of the effect of phase shift, where one of the summations of 2^nd and 3^rd harmonics has a 45 degree phase shift added to the 3^rd harmonic. The phase shift modulates the shape of the signal but not the amount of magnitude and timing changes and both summations have the same HR.

Figure 3.

The effect of phase shift on sinusoidal summations. The summation of the 2^nd and 3^rd harmonic with zero phase (dashed line; sin(2·2π) + 0.4sin(3·2π)) and the summation of the 2^nd and 3^rd harmonics with 45 degrees of phase shift added to the 3^rd harmonic (dotted line; sin(2·27π) + 0.4sin(3·2π+π/4)) are shaped differently. However, the timing and magnitude changes between steps caused by the 3^rd harmonic can still be seen when comparing to the 2^nd harmonic alone (solid line; sin(2·2π)). The phase shift only changes the location of these changes, hence the harmonic ratio of these signals remain the same (2.5 summations; ∞ 2^nd harmonic only).

2.3 Example Using Unilateral Limb Loading Data

To demonstrate the ability of HR analysis to identify asymmetry between steps, we used a unilateral limb loading paradigm. Adding weight to one leg has been shown to induce asymmetry in both kinetics and kinematics (Haddad et al, 2006; Kodesh et al, 2012; Smith & Martin, 2007). Thus, the HR should change as the asymmetry increases with increased loading.

The subject walked 9 meters along a straight path. AP, VT, and ML accelerations were collected from an accelerometer attached posteriorly at L3/L4. Data collected during the middle 7.5m were used. The subject walked to the beat of a metronome to maintain consistent cadence and was instructed to take the same number of steps to maintain gait speed. A unilateral load was applied via cuff weights secured around the right ankle (masses of 0, 0.45, 1.36, and 2.27kg) (Kodesh, et al, 2012). Identification of heel contact for stride segmentation was determined using footswitches. HRs were calculated for each stride and averaged across two trials (Brach, et al, 2011).

3. Results of Unilateral limb loading

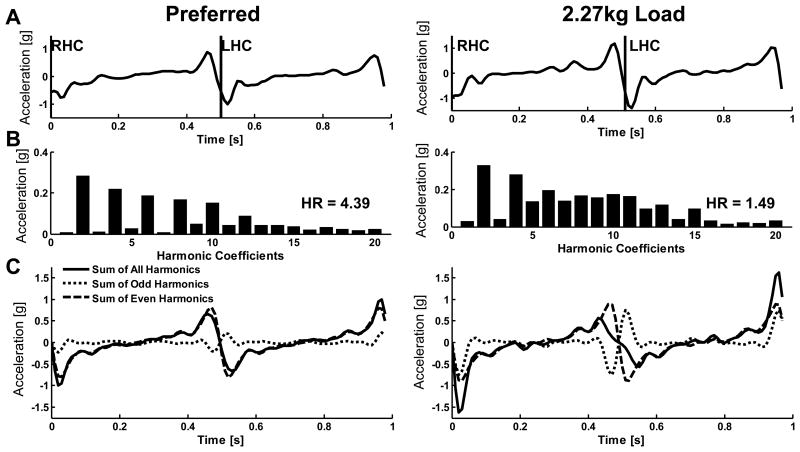
Step time was held relatively constant (0.50±0.01s 0kg; 0.50±0.01s 0.45kg; 0.50±0.02s 1.36kg; 0.49±0.02s 2.27kg) inducing modulation of within-step limb accelerations. The HRs generally decreased with the progressive limb loading (Table 1). The underlying cause of the change in HR with induced asymmetry can be seen in the distribution of the coefficients in the harmonic breakdown. Figure 4 demonstrates differences in the coefficients when comparing unloaded and limb-loaded walking. Both conditions exhibit a dominant second harmonic consistent with the biphasic nature of the AP signal; however, the asymmetries in the accelerations caused by the loaded condition result from a greater contribution of odd harmonics, which interfere with the even harmonics to produce a lower HR(1.59) compared to the preferred HR (4.39).

Table 1.

Harmonic ratios for the limb loading conditions.

Condition		Harmonic Ratio
	AP	VT	ML
0 kg	3.55	5.16	2.67
0.45 kg	3.68	4.18	2.21
1.36 kg	2.11	2.46	1.82
2.27 kg	1.69	1.88	1.49

Figure 4.

(A) Typical AP L3-L4 acceleration over one stride during preferred walking (left) and during 2.27kg unilateral limb loading (right) for the same subject (RHC – right heel contact; LHC – left heel contact). (B) Harmonic magnitude coefficients of the strides in (A). (C) Magnitude reconstruction of the original signal (solid) broken down into odd components (dotted) and even components (dashed).

4. Discussion

The HR method can be used to investigate changes in gait patterns; specifically, step-to-step asymmetry within a stride. In the AP and VT directions, the even harmonics represent the biphasic symmetry of the acceleration signal, while the odd harmonics represent the deviation from symmetry. However, the magnitude differences between odd and even harmonics do not tell the whole story. Actual gait acceleration is a complex combination of phase and amplitude of the harmonic components (i.e. DFT phase-amplitude notation). HRs are a global measure that do not account for phase; that is, they do not explain where the deviations from symmetry occur. Thus, different pathologies may impact phase differently, yet result in the same HRs. Additional spatial and temporal analyses or instrumentation, such as 3-D kinematics and kinetics, may allow the separation of these two aspects.

HRs are useful in the characterization of gait beyond obvious lower limb asymmetry. While reduced HRs have been found in persons with unilateral lower limb involvement, e.g. in degenerative and rheumatoid arthritis and in healthy individuals wearing AFOs (Smidt, et al, 1971; Smidt, et al, 1977), they have also been observed in persons where lower extremity involvement is not evident. Lower HRs were found in healthy older adults whose spatiotemporal parameters were similar to young adults (Brach, et al, 2011; Lowry et al, 2012) and in individuals in the early stages of Parkinson's disease whose speed and stride length was similar to healthy controls (Lowry, et al., 2009). Thus, HRs are able to characterize subtle alterations in locomotor mechanisms not recognized in typical spatiotemporal gait characteristics used to describe mobility.

While research has shown that there are differences in HRs between groups walking at their preferred speeds, HRs also change nonlinearly with respect to gait speed for an individual walking from very slow to very fast speeds (Kavanagh et al, 2006; Latt, et al, 2008; Lowry, et al, 2012; Mazza et al., 2008). There is consensus that HRs decrease when walking at speeds slower than preferred, thus care should be taken when using HRs with repeated measures designs if conditions are expected to alter gait speed. To avoid confounding the results in the limb loading example, we held gait speed constant. Therefore the changes in HRs were due to the changes in control to compensate for the added mass.

In conclusion, HRs offer a unique global measure that highlights changes in symmetry between steps. We suggest that when describing or explaining HRs in methodology that instead of using the terms rhythmicity, dynamic stability, or walking balance, the term “symmetry” is emphasized as the defining characteristic.