A Million-Plus Neuron Model of the Hippocampal Dentate Gyrus: Critical Role for Topography in Determining Spatio-Temporal Network Dynamics

Abstract

Goal

This manuscript describes a million-plus granule cell compartmental model of the rat hippocampal dentate gyrus, including excitatory, perforant path input from the entorhinal cortex, and feedforward and feedback inhibitory input from dentate interneurons.

Methods

The model includes experimentally determined morphological and biophysical properties of granule cells, together with glutamatergic AMPA-like EPSP and GABAergic GABA_A-like IPSP synaptic excitatory and inhibitory inputs, respectively. Each granule cell was composed of approximately 200 compartments having passive and active conductances distributed throughout the somatic and dendritic regions. Modeling excitatory input from the entorhinal cortex was guided by axonal transport studies documenting the topographical organization of projections from subregions of the medial and lateral entorhinal cortex, plus other important details of the distribution of glutamatergic inputs to the dentate gyrus. Information contained within previously published maps of this major hippocampal afferent were systematically converted to scales that allowed the topographical distribution and relative synaptic densities of perforant path inputs to be quantitatively estimated for inclusion in the current model.

Results

Results showed that when medial and lateral entorhinal cortical neurons maintained Poisson random firing, dentate granule cells expressed, throughout the million-cell network, a robust, non-random pattern of spiking best described as spatio-temporal “clustering”. To identify the network property or properties responsible for generating such firing “clusters”, we progressively eliminated from the model key mechanisms such as feedforward and feedback inhibition, intrinsic membrane properties underlying rhythmic burst firing, and/or topographical organization of entorhinal afferents.

Conclusion

Findings conclusively identified topographical organization of inputs as the key element responsible for generating a spatio-temporal distribution of clustered firing. These results uncover a functional organization of perforant path afferents to the dentate gyrus not previously recognized: topography-dependent clusters of granule cell activity as “functional units” or “channels” that organize the processing of entorhinal signals. This modeling study also reveals for the first time how a global signal processing feature of a neural network can evolve from one of its underlying structural characteristics.

I. Introduction

Developing large-scale, quantitatively based models of neural systems has become a realizable goal in recent years [1]–[3], largely because of three major developments: (i) data collection over the course of the past several decades has led to substantial databases of anatomical and physiological properties for many neural systems [4]–[11]; (ii) the development of sophisticated and parallelizable software systems for representing these anatomical and physiological characteristics [12]–[15]; (iii) the continued growth of high performance computing systems capable of sustaining the numerical burden of such large-scale models [16], [17].

One of the most extensively studied regions of the brain is the hippocampal formation. Numerous anatomical analyses over the course of the last century have documented the classes, numbers, and organization of principal neurons [18]–[22] and interneurons [23], [24] in this limbic region. Extensive studies at the electron microscopic level have provided knowledge of the numbers, densities, membrane locations, and neurotransmitter properties of synapse populations [25]–[29]. Despite this wealth of knowledge, there have been few detailed, quantitative models of the hippocampal system. Those that have been developed have been limited to subregions of the hippocampus, understandably given the complexity of the system. These initial models have been successful in providing insights into functional properties of the hippocampus at a subsystems level [30]–[33].

Here we describe the first step in an implementation of a full-scale model of the hippocampal formation. We have dealt with the first stage in what has been termed the intrinsic “tri-synaptic pathway” of the hippocampus, i.e., the “perforant path” excitatory projections from the entorhinal cortex (EC) to granule cells of the dentate gyrus (DG), including inhibitory feedback from DG interneurons. Our model is based on the hippocampal formation of the rat, as the majority of quantitative anatomical information available is for the rat species. We have taken into consideration a number of factors concerning the EC-DG projection in an attempt to attain a model that is as biologically realistic as is achievable given current knowledge. In general, these factors include: the number and ratio of layer II EC neurons and dentate granule cells; the ratio of inhibitory interneurons and dentate granule cells; the dendritic morphological structure and morphological variability of granule cells; the terminal field distributions of EC layer II cells; the synaptic density of EC layer II cells onto dentate granule cells; the passive membrane properties of granule cells; both somatic and dendritic active conductances responsible for the action potential and for other voltage-dependent properties.

One other anatomical feature that also is the focus of the present study concerns the topographical organization of ECDG projections. Topography of anatomical connections, i.e., the point-to-point relation of typically non-uniform synaptic connectivity between any two brain regions, is a property of nearly all mammalian brain systems, and is distinctly different for each. The topography of EC-DG projections in the rat has been studied elegantly and reported previously [34]–[38]. The question being asked in the present study is the functional consequence of that topography. To our knowledge, the issue of the functional significance of the topographical organization of a projection system has yet to be addressed quantitatively for any brain system, and is an issue particularly well-suited for a large-scale, structural-functional model. We show here that the topographical characteristics of EC projections to the DG impose quantifiable boundaries on the spatio-temporal properties of granule cell network activity. Findings conclusively identified topographical organization of inputs as the key element responsible for generating a spatio-temporal distribution of clustered firing. As such, these results uncover a functional organization of perforant path afferents to the DG not previously recognized: topography-dependent clusters of granule cell activity as “functional units” or “channels” that organize the processing of EC signals.

II. Methods

A. Model Scale and Features

Models of the EC-DG system were completed according to two scales – one with 1,000,000 granule cells, i.e., equivalent to the number of cells in one hemisphere of the rat hippocampus [7], [39], and one with 100,000 granule cells, i.e., equivalent to 1:10 scale to accelerate simulation time. All results reported here were observed at both scales. All networks studies were composed of dentate granule cells and inhibitory interneurons, with excitatory input to granule cells modeled after the organization of layer II EC afferents. In general terms, the models featured complex and variable morphologies for granule cells, multiple active conductances distributed non-uniformly throughout granule cell membranes, interneurons configured (as cell bodies only) to provide both feed-forward and feedback inhibition, and either randomly or topographically organized excitatory input to network neurons. Specifics are provided below.

B. Granule Cell Morphology

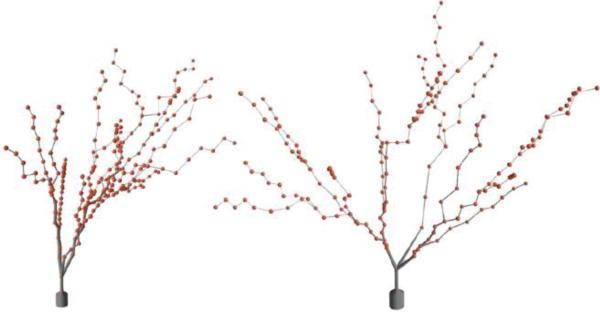
The morphological characteristics of hippocampal dentate granule cells have been studied in depth and with quantitative detail [40]–[42]. Example three-dimensional dendritic structure was obtained from sample reconstructed neurons labeled using a variety of methodologies and available through neuromorpho.org [5]. To incorporate morphological diversity in the granule cell population, however, the L-NEURON tool [43] was used. L-NEURON allows for the generation of unique dendritic and axonal trees based on sampling from a set of statistical distributions that describe their fundamental structural parameters [43], [44]. Table I shows the distributions used for each of the granule cell parameters, while Fig. 1 shows a sample of L-NEURON generated granule cell somata and dendritic trees. Only the somata of basket cells were modeled as part of the present study, so no basket cell dendritic structures were included; no cells were given an explicit axon.

TABLE I.

Morphological Parameters for Dentate Granule Cells

Variable	Distribution	Mean/Min	Std. Dev./Max
Soma Diameter	Gaussian	9.00	2.00
Number of Stems	uniform	2.00	4.00
stem initial diameter	Gaussian	1.51	0.79
Branching diameter	Gaussian	0.49	0.28
IBF branch length	Gaussian	10.70	8.40
Term. branch length	Gaussian	10.70	8.40
Daughter ratio	uniform	1.00	2.00
Taper ratio	Gaussian	0.10	0.08
Rall power	Constant	1.50	---
Bifurcation amp.	Gaussian	42.00	13.00
Tree elev. (narrow)	Gaussian	10.00	2.00
Tree elev. (medium)	Gaussian	42.00	2.00
Tree elev. (wide)	Gaussian	75.00	2.00

Fig. 1.

Two sample dentate granule cell morphologies generated using L-NEURON with the parameter distributions shown in Table I.

C. Granule Cell Bioelectric Properties

Biophysical properties for each of the cell types in the model were taken from previously published experimental data and from previously published mathematical models of the DG [4], [45]–[52]. Table II shows the channel distribution for granule cells, while Table II and Fig. 2 show key passive and active properties for one instance of a granule cell.

TABLE II.

Passive & Active Properties for Dentate Granule Cells

Passive Property	Value	Mechanism	Soma	GCL	Inner 1/3	Middle 1/3	Outer 1/3
Soma S.A. (cm2)	4.97E-4	Cm (uF/cm2)	9.8	9.8	15.68	15.68	15.68
Soma Volume (cm3)	1.11E-6	Ra (ohm-cm)	210	210	210	210	210
R.M.P. (mV)	−75.01	Leak (S/cm2)	2.9E-4	2.9E-4	4.6E-4	4.6E-4	4.6E-4
Rin (M-Ohms)	185.86	sodium (S/cm2)	0.84	0.126	0.091	0.056	---
Membrane time const. (ms)	31.0	Delayed Rectifier K (slow) (S/cm2)	6.0E-3	6.0E-3	6.0E-3	6.0E-3	8.0E-3
Latency to first AP (ms)	100.0	Delayed Rectifier K (fast) (S/cm2)	0.036	9.0E-3	9.0E-3	2.25E-3	2.25E-3
		A-type K (S/cm2)	0.108	---	---	---	---
		L-type Ca (S/cm2)	2.5E-3	3.8E-3	3.8E-3	2.5	---
		N-type Ca (S/cm2)	1.5E-3	7.4E-4	7.4E-4	7.4E-4	7.4E-4
		T-type Ca (S/cm2)	7.4E-5	1.5E-4	5.0E-4	1.0E-3	2.0E-3
		Ca-dependent K (S/cm2)	1.0E-3	4.0E-4	2.0E-4	---	---
		Ca- and V- dependent K (S/cm2)	1.2E-4	1.2E-4	2.0E-4	4.8E-4	4.8E-4
		Tau for decay of intracell. Ca (ms)	10.0	10.0	10.0	10.0	10.0
		Steady-state intracell. Ca (mol)	5.0E-6	5.0E-6	5.0E-6	5.0E-6	5.0E-6

Fig. 2.

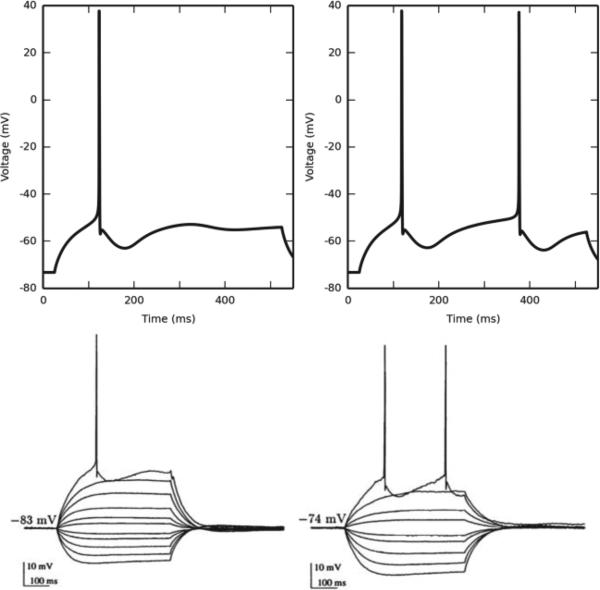
Granule cell active properties. Top left: When subjected to a current clamp stimulus at the soma, the granule cell responds by firing an action potential with a latency of approximately 100 ms. Top right: When the current clamp amplitude is just over the threshold required to elicit a second AP, its latency is approximately 350 ms. This matches experimental data (bottom, reproduced from [50]).

The modeled network used AMPA and GABAergic synapses for connectivity. We modeled the postsynaptic conductance as a sum of two exponentials, with the rise time, fall time and maximum conductance, optimized to match experimentally recorded EPSPs and IPSPs in both granule and basket cells [53]–[58], to the extent such data was available. At certain levels of basket cell inhibition, whether feedforward or feedback, there was pronounced synchrony in network activity (see Fig. 5). Because highly synchronous firing was not the focus of the present study, and without complete knowledge of IPSP size for granule cells, we scaled the basket cell inhibition until the persistent synchrony disappeared. Because axons were only implicitly modeled, a delay to postsynaptic activation was added to account for axonal conduction of action potentials. In the million-granule-cell model, the number of synapses in the network corresponded to the number of reported spines on granule cells [27], [42], [59]. In the 1:10 scale model, we scaled the number of synapses down by a factor of 10, while simultaneously increasing peak synaptic conductance by a factor of 10. Table III shows the relevant synaptic parameters for the network.

TABLE III.

Synaptic Parameters for a 1/10-Scale Network

Synapse Counts:
GC # spines - inner 1/3:	115 - 135	GC to BC	50 - 140
GC # spines - middle 1/3:	105 - 120	MEC to BC	10 - 20
GC # spines - outer 1/3:	110 - 130	LEC to BC	10 - 20
BC to GC:	4 - 8
Synaptic Weights (S/cm2):
MEC to GC:	1.17E-4	GC to BC:	1.13E-3
LEC to GC:	1.5E-4	MEC to BC:	4.21E-5
BC to GC:	5.45E-5	LEC to BC:	4.21E-5
EPSP/IPSP Rise Time (ms):
MEC to GC:	1.05	GC to BC:	0.1
LEC to GC:	1.05	EC to BC:	1.05
BC to GC:	1.05
EPSP/IPSP Decay Time (ms):
MEC to GC:	5.75	GC to BC:	0.59
LEC to GC:	5.75	EC to BC:	18
BC to GC:	5.75
Reversal Potentials (mV):
MEC to GC:	0	GC to BC:	−75
LEC to GC:	0	EC to BC:	0
BC to GC:	0

D. Topography

The EC is divided into two areas termed the lateral entorhinal cortex (LEC) and the medial entorhinal cortex (MEC). Anatomically, the LEC lies rostral and lateral to the MEC. Both areas contribute to the perforant path that projects onto the DG in a laminar manner. The LEC primarily targets the outer third of the molecular layer of the DG, and the MEC primarily targets the middle third [60], [61]. This laminar organization is present in our model.

Two additional features of the EC-DG projection were used to define its topography. First, there was the relationship between the position of the presynaptic inputs (cell bodies) and the position of their projections (axons) onto the postsynaptic population. Second, there was the geometry of the axon terminal field. The combination of the two features constrained the subset of the DG population with which a given presynaptic neuron can synapse.

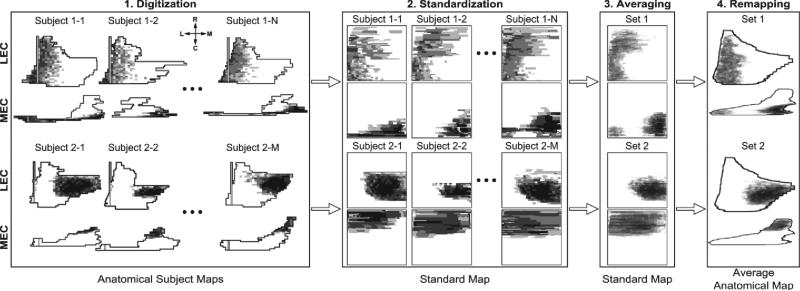
Experimental analyses have revealed that EC input to the DG is distributed with a non-random topography. In general, the lateral regions of the LEC and the lateral/caudal regions of the MEC project to the septal portion of the DG, and the medial regions of the LEC and the medial/rostral regions of the MEC project to the temporal portion of the DG (Fig. 3). Dolorfo and Amaral characterized this topography in rats, and their work is the basis of the specific topographical relationships implemented here, though we verified the generality of the Dolorfo and Amaral findings with those of other researchers [34]–[38]. Dolorfo and Amaral found that any injection within a particular septo-temporal quartile of the DG resulted in the same characteristic labeling of EC. Therefore, the data were divided into sets based on the quartiles in which the injection sites were located in order to calculate the mean EC area that projected to a given quartile. However, because each injection was performed on a different rat, each brain map had a different size and shape. In order to quantify this work, an image processing pipeline was designed that digitized the brain maps, projected the individual anatomical brain maps onto a common standard coordinate system, calculated the mean of the data, and projected the resulting data back onto an average anatomical map (Fig. 3). An average anatomical map was calculated by computing the mean of all of the dimensions of the individual anatomical subject maps.

Fig. 3.

Summary of the image processing pipeline used to quantify the EC-DG topography from data obtained from [38]. Not all data is shown. 1) The data in their anatomical subject maps are digitized and grouped according to injection location. 2) The maps are projected onto a standard coordinate space. 3) The sets are averaged. 4) The averaged group data are projected onto an average anatomical map. The compass represents the rostro-caudal and medio-lateral axes.

To determine the axon distribution, the maps were converted into probabilities where the intensity, or darkness, of the pixel corresponded to the probability that an EC neuron located within would send its axon to a particular quartile of the DG. The specific point within the quartile to which the axon is sent is referred to as the “perforation point.”

Upon reaching the perforation point, the axon branches out into the terminal field. The terminal field was limited to between 1.0 and 1.5 mm in the septo-temporal direction and encompassed the entire transverse width of the DG within this extent. The constraints were based on morphological and anatomical studies that characterized individual axon morphologies and the overall patterns of projection [61], [62].

E. Computational Platform

All simulations were run on a high-performance compute cluster consisting of 394 dual quad-core Intel-based nodes and 74 dual hexa-core Intel-based nodes, for a total of 4,040 processor cores. The system has 8.1 TeraB of distributed RAM, 73.1 TeraB of distributed disk space, and a maximum theoretical performance of 38.82 teraflops. All nodes are connected to a high-speed, low-latency 10G Myrinet networking backbone. These nodes are housed, maintained and monitored in facilities operated by the University of Southern California Center for High-Performance Computing and Communications. We used version 7.3 of the NEURON simulation engine [12], [63] to run all simulations, and used Python 2.7 for model specification, data visualization, and analysis [64], [65].

III. Results

A. Granule Cell Response to Random Entorhinal Input: Firing in Spatio-Temporal ”Clusters”

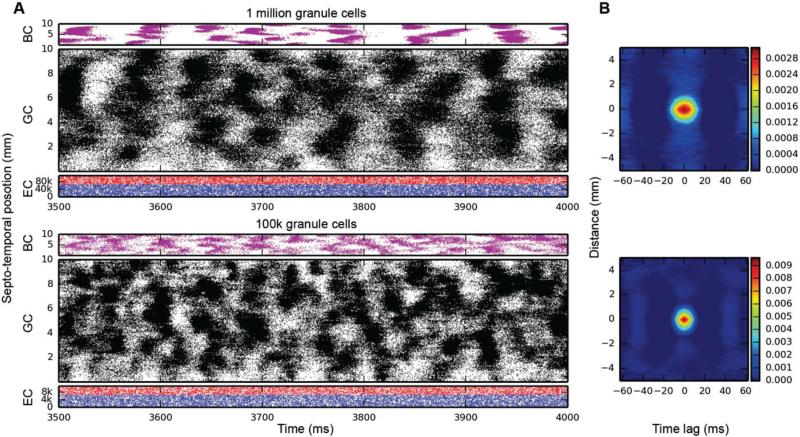
Initial simulations of granule cell network dynamics to EC input involved both medial and lateral entorhinal (MEC & LEC) neurons firing at a mean frequency of 3.0 Hz, accelerated (by design) over the course of approximately the first 1000 ms of the simulation. Four (4.0) seconds of time were simulated in all results presented here. Entorhinal inputs were topographically organized according to the relations described in the Methods. Basket cells were configured to provide both feedforward and feedback inhibition. All active granule cell membrane properties included those described in Table II. Simulation results with a one million granule cell population revealed that despite continued Poisson EC input, granule cells discharged in a decidedly non-random, nonuniform manner. As shown in Fig. 4 (top), granule cells throughout the entire septo-temporal extent of the DG fired in what we call here spatio-temporal “clusters,” i.e., irregular periods of spiking and non-spiking lasting approximately 50-100 ms “on” and 50-75 ms “off”. The granule cells engaged in firing changed spatial location along the septo-temporal axis, as evidenced by the apparent “drift” in patterned firing in Fig. 4A and other similar figures. The appearance of clustered spiking in response to Poisson EC input was not specific to million-granule cell populations, but was equally apparent for simulations involving 100k granule cells as well (Fig. 4, bottom).

Fig. 4.

Simulation results for topographically constrained EC-DG networks with feedforward and feedback inhibition, run at two different scales: 1M granule cells (top), and 100k granule cells (bottom). At both scales, spatio-temporal clusters appear in the granule cell activity, despite the random nature of the EC input. In the million-cell case, only a subset of the full dataset is plotted to keep it from appearing solid black. Column B: 2D autocorrelations confirm the presence of these clusters.

In some cases, the appearance of spatial-temporal clusters did not appear immediately with the onset of EC input, but instead only appeared after a period of highly rhythmic granule cell activity. In those cases, granule cell spiking started after approximately 200 ms, reaching a maximum at approximately 300 ms. At this time point granule cell output was highly synchronous, with granule cells along the entire extent of the septo-temporal axis firing at a high rate for a duration of approximately 100 ms. Approximately midpoint in this initial 100 ms of extended firing, basket cells fired synchronously as well, leading to a termination of extended granule cell firing. After a few more periods of synchronous granule cell discharge alternating with periods of heightened basket cell output the system appears to reach an equilibrium (after 800-900 ms into the simulation). It is at this point that a steady-state of “clustered” spike discharges emerges and continues.

Quantitative analyses verified the existence of clusters of spike firing. 2D autocorrelation allows an analysis of the data in both spatial and temporal dimensions, and was used to analyze most of the results presented here. It was constructed by computing every pairwise cross-correlation of discretized spike trains in a random sample of 10,000 neurons. The spike trains were discretized by counting the number of spikes elicited by a particular neuron within a bin size of 5 ms. The resulting cross-correlations were sorted by the distance between the neuron pairs and were further binned using a resolution of 0.05 mm. The mean cross-correlation within each bin was computed.

The right-hand column of Fig. 4 shows the 2D autocorrelations for the million-cell and 100k-cell simulations. What emerges from the analysis is something that looks like a typical cluster for each of the datasets: in the million-cell case, clusters are roughly elliptical, with a temporal width of approximately 40-50 ms and a spatial height of 1-2 mm. The analysis looks very similar for the 100k-cell simulation, which verifies that clusters exist and are similar at both simulation scales.

Further analysis was performed on the 100k-cell dataset using DENCLUE 2.0, a density-based cluster identification algorithm [66]. For this application, a Gaussian density kernel was used. Analyses show that a) clusters exist, and b) they appear in a wide variety of sizes, though their basic shape remains similar. Statistical analysis of the identified clusters shows that inter-centroid cluster time is 11±12 ms, and that the density of spikes within a cluster is approximately 12±9 spikes/ms-mm.

B. Mechanisms Responsible for Spatio-Temporal Clustered Spiking: Inhibition

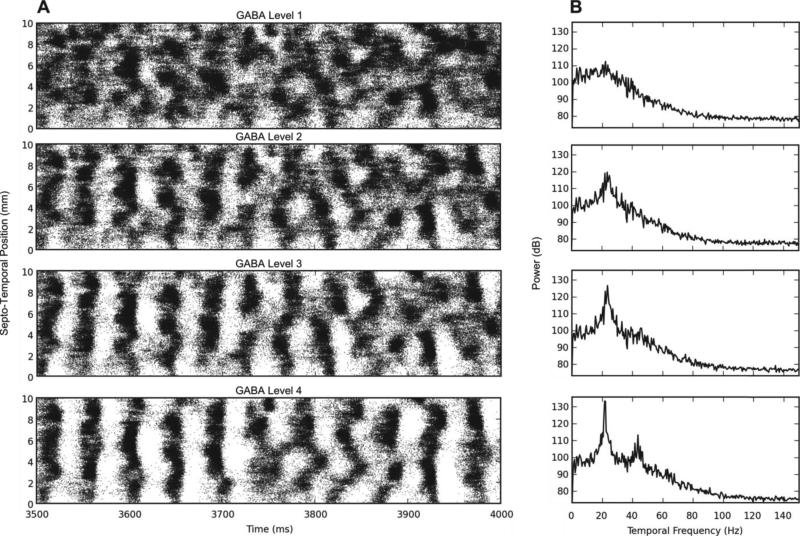
Following this initial characterization, we conducted experiments designed to identify the mechanisms underlying granule cell clustered spiking: what was responsible for transforming continuous random spike firing into non-continuous, non-periodic, clusters of spikes? A first hypothesis concerned a possible role for GABAergic inhibition, given the strong effect of interneuron activity in synchronizing granule cell activity in the early stages of the simulation. Indeed, when feedback inhibition was increased by 4-10 times that used in initial simulations, longer periods of synchronous activity, marked by multiple bands of high activity followed by bands of almost zero activity in the DG followed (Fig. 5A). This pattern of bands eventually becomes asynchronous, though, giving rise to spatio-temporal clusters similar to the ones we see with less inhibition. When we increase inhibition to a level 20 times greater than normal, however, the synchrony persists for the entire duration of the simulation.

Fig. 5.

Results of increasing the feedback GABA inhibition. A) The raster plot of the granule cell output for increasing levels of inhibition. GABA level 1 uses the original BC-GC conductance values while levels 2-4 use 4, 10, and 20 times larger conductance values, respectively. B) The 1D DFT plot of the data. As the inhibition increases, the granule cells develop synchronous firing at 22 Hz.

One-dimensional discrete Fourier transforms (DFTs) were used to analyze the temporal frequency spectrum of the spike data. They were computed using a spike density matrix. The matrix was constructed by counting the total number of spikes elicited within a spatio-temporal bin with a resolution of 0.05 mm and 2 ms. The 1D DFT was computed for each row of the matrix resulting in the temporal frequency spectrum at a particular septo-temporal location on the DG. The mean of all of the resulting DFTs was then computed.

As Fig. 5B shows, as the amount of GABAergic inhibition increases in the network, a small peak at approximately 22 Hz turns into a sharp one, followed by another sharp peak at about 45 Hz with even more inhibition. This points to oscillations occurring in the low to medium range of the gamma band. This GABA-dependent rhythmicity has been described previously [67], [68].

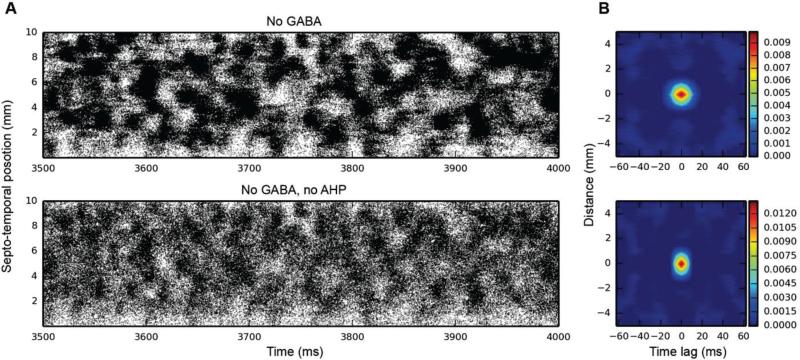
Given the synchrony introduced into granule cell spiking as a result of feedback inhibition, we decided to remove sources of inhibition to see whether the cluster activity would also disappear. There are two sources of inhibition in dentate granule cells: external inhibition, from the basket cell population, and internal inhibition, due to the afterhyperpolarization (AHP) that granule cells experience after one or more action potentials (APs). As Fig. 6 illustrates, spatio-temporal clusters persist with one or both of these sources of inhibition absent from the network.

Fig. 6.

Granule cell activity when removing internal and external sources of inhibition. Top: GABAergic inhibition removed; bottom: both AHP and GABA removed. Spatio-temporal clusters persist in both cases, as evidenced by both the raster plots and 2D autocorrelations (B).

C. Mechanisms Responsible for Spatio-Temporal Clustered Spiking: Topographic Organization of Entorhinal Afferents

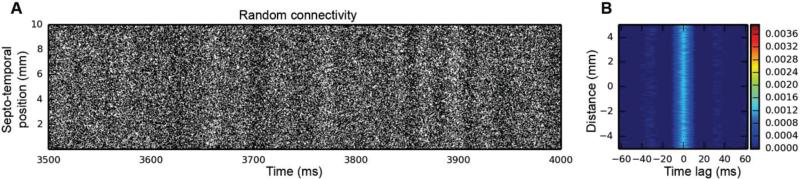
We next turn to topography as the potential source of clustering. As Fig. 7 shows, when the constraints placed on EC-to-DG connectivity are removed, thus allowing a randomly connected network where any EC neuron can synapse onto any dentate granule cell, the clusters that have always been present in the output disappear, and bands of activity appear in their place. The 2D autocorrelation corroborates this: while there's still a small amount of temporal structure in the network activity, it's 8×-10× weaker than in any of the topographically constrained cases, and the spatial component has completely disappeared – what once looked like an elliptical cluster in the 2D autocorrelation has become a band that occupies the full septo-temporal extent of DG. Thus, it is the topography of the EC-DG projection that's responsible for the emergence of spatio-temporal clusters, even when the input to the network is random.

Fig. 7.

Simulation results for a randomly connected EC-DG network. In this simulation, the granule cell AHP was removed, as was GABAergic inhibition. Spatio-temporal clusters are no longer present, having been replaced with bands of activity with a high level of background activity. In the 2D autocorrelation, what looked like a typical cluster is now a vertical band. Thus, while there's still a temporal variation in granule cell activity, the spatial component is gone.

D. Mechanisms Responsible for Spatio-Temporal Clustered Spiking: Axon Terminal Field Geometry

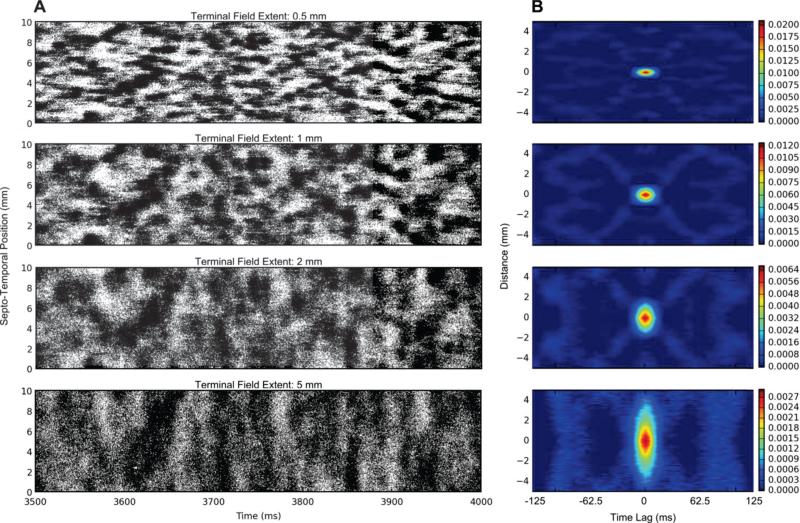
The previous results establish that the emergence of clusters in the spatio-temporal pattern of the granule cell output is caused by topography. An immediate question that came to mind, given these results, is how the parameters of the topography might influence the size and shape of the clusters. The following set of simulations varied the axons’ terminal field extents in the septo-temporal axis to investigate the contributions of the terminal field geometry to the emergence of spatio-temporal clusters. These simulations did not include basket cells.

The results clearly show a dependence between the terminal field size and the cluster size (Fig. 8). As the size of the terminal field increases, the cluster size increases. Furthermore, the density of the cluster decreases as the cluster size increases. This is verified given that each simulation resulted in approximately the same number of spikes (1,580,000±30,000 spikes with a range of 1,560,000 – 1,650,000 spikes). An increase in cluster size for the same number of spikes per time signifies a decrease in cluster density.

Fig. 8.

Effects of increasing the terminal field extent in the septo-temporal direction. A) Raster plot of the granule cell output. B) The 2D autocorrelation of the data. As the terminal field extent increases, the cluster size increases, and this is reflected by the increase in the spatial extent of the 2D autocorrelation.

The 2D autocorrelation demonstrates the relationship between spatio-temporal correlation and the terminal field extent. The analysis shows that the extent of the spatial correlation between one neuron and any other neuron increases as the terminal field increases. Also, the terminal field does not appear to affect the extent of the temporal correlation. However, the maximum of the 2D autocorrelation decreases as the terminal field extent increases. An approximately 10-fold decrease in the peak correlation is seen between a terminal field extent of 0.5 mm and 5 mm.

IV. Discussion

The study described here is based on the creation of a large-scale, compartmental neuron model of the EC-DG projection system of the hippocampal formation. We have intended for the model to be large-scale in the sense of including a total number of dentate granule cells, GABAergic interneurons, and EC axons that are equivalent to those found in one hemisphere of the rat brain. We have intended the model to be biologically realistic with respect to the numbers and ratios of different classes of neurons, granule cell dendritic morphologies, classes and distributions of somatic and dendritic conductances, and the presence of feedforward and feedback GABAergic interneurons. In this its first generation of development and use, the model has uncovered a functional organization of perforant path afferents to the DG not previously recognized: a spatio-temporal clustering of granule cell spiking on the order of 11 ms between clusters and 12 spikes/ms-mm within clusters. These findings are important in several respects. First, these spatio-temporal clusters of active granule cells represent “functional units” or “channels” that organize the processing of EC signals. Second, results of the present study clearly demonstrate that the spatio-temporal clustering property of the EC-DG pathway depends primarily on the topographic organization of perforant path afferents. This is the first time that a functional characteristic of a cortical projection has been linked specifically to topographic features of that projection. Third, this organizational property of the EC-DG pathway is apparent only when structural-functional relations are examined at large-scales. Smaller scale models would not have revealed the clustering phenomenon, and thus, these results point to the importance of large-scale modeling of cortical systems.

The model described in this report is not complete in the sense that there are several features of the biological dentate gyrus not included in the present model, and that ultimately may modify and extend the results reported here. One of these features includes other classes of interneurons within the dentate hilus that are activated by granule cells and/or perforant path axons, and that provide feedback to granule cells. Most prominent among these are mossy cells [69] which are the source of the dentate commissural-associational system [70] and that terminate throughout the inner one-third of the molecular layer [71]. This cell population lies beneath the granule cell layer, and is excitatory to both dentate granule cells and inhibitory interneurons [72], [73]. Additional types of hilar cells are not included in the present model, e.g., hilar perforant path-associated (HIPP) interneurons that provide inhibitory input to granule cells in the inner and outer thirds of the molecular layer, respectively [29], [74]. The precise role that these and other types of interneurons [23] play, if any, in modulating the spatio-temporal “cluster” firing of granule cells has yet to be determined.

Another difference between the present model and one that is completely biologically faithful concerns NMDA receptor-channels on the dendrites of granule cells. The current model has only AMPA receptor-channels mediating EC-DG glutamatergic synaptic transmission. The NMDA receptor subtype is activated preferentially by higher frequencies of afferent input [75], [76], so the shape and/or size of clusters may change with the inclusion of NMDA receptor subtypes. Future experiments will determine this, and may be conducted with higher mean frequencies of EC input.

These additional anatomical and biophysical properties of the DG will be included in future models, and ultimately will be examined for their influence on the topography-dependent clustered firing of granule cells.

Electrophysiological recordings from neurons within the hippocampal formation in the behaving animal have identified a number of correlates affiliated with animals’ learned behavior [77]–[79], spatial location [80], or spatio-temporal properties of the animal learned behavior [81]–[83]. Other studies have explored the anatomical distribution of spatial firing patterns of neurons in the hippocampus [84], [85]. Many of these observations have been extended to EC, parahippocampal and perirhinal cortices [86]–[88]. Differences between the EC and hippocampal cortical correlates must be attributable to neural processing performed by connections between the two structures, with the DG playing a major role [89]. Although speculative, it may be neural processing micro-structures like the EC-DG cluster firing channels described here that are in part responsible for the EC-to-hippocampal pyramidal cell transformations observed to date.