Abstract

Because of their unique electronic properties, cyclic molecular structures ranging from benzene to natural light-harvesting complexes have received much attention. Rigid π-conjugated templated porphyrin nanorings serve as excellent model systems here because they possess well-defined structures that can readily be controlled and because they support highly delocalized excitations. In this study, we have deliberately modified a series of six-porphyrin nanorings to examine the impact of lowering the rotational symmetry on their photophysical properties. We reveal that as symmetry distortions increase in severity along the series of structures, spectral changes and an enhancement of radiative emission strength occur, which derive from a transfer of oscillator strength into the lowest (k = 0) state. We find that concomitantly, the degeneracy of the dipole-allowed first excited (k = ±1) state is lifted, leading to an ultrafast polarization switching effect in the emission from strongly symmetry-broken nanorings.
Cyclic molecules can exhibit fundamentally different electronic dynamics compared with their linear counterparts due to the lack of chain end effects, high rotational symmetry, and the presence of ring strain.1,2 The photophysical properties of cyclic molecules have been extensively investigated for a large number of systems ranging from small aromatic rings3,4 to large molecular complexes.5 A recurrent key concept is exciton delocalization, which is known to lead to strong fluorescence suppression in cyclic molecular structures such as benzene.6,7 The high symmetry results in a dipole-forbidden lowest exciton (k = 0) state; however, emission is weakly enabled by Herzberg–Teller intensity borrowing from allowed higher energy transitions through the involvement of vibrations with suitable symmetry.8 Electronic delocalization also plays a major role in the efficient energy transfer between adjacent antennae in natural light-harvesting complex 2 (LH2) based on chlorophyll units,9,10 where the pigments are held loosely by protein scaffolds in circular structures.11 Such designs of nature have inspired many attempts to create synthetic nanoring analogues, for instance, cycloparaphenylenes,12,13 cyclic oligothiophenes,14 nanorings synthesized from phenylcarbazole units linked with phenylene-ethynylene-butadiynylene groups,15 and an extensive range of porphyrin arrays.16−19
While investigating electronic properties on structures with such high symmetry, an interesting question inevitably arises, namely, how symmetry distortions influence the photophysical properties. When defects are introduced into cyclic molecular structures, the lowest dipole-forbidden exciton state may be mixed with higher lying states and some absorption into the lowest state becomes possible.20,21 As the distortion becomes more and more prominent, deviations from high rotational symmetry dominate and the fluorescence is no longer suppressed.20 Symmetry breaking also plays an important role in structures found in natural systems, such as LH1 complexes containing a reaction center (RC) at their center, which can be divided into at least two distinct classes.9 The first class is monomeric, consisting of only one RC surrounded by one cyclic LH1 complex, as found in Rhodospirillum rubrum and Rhodospirillum palustris.9 However, while LH1 in Rsp. rubrum is believed to exhibit a highly symmetric ring-like structure,22 LH1 in Rsp. palustris displays a gap, providing a portal through which ubiquinone can transfer electrons across the boundaries of LH1, which is vital for photosynthetic processes.23,24 The second class of systems is dimeric, consisting of two circular RC-LH1 complexes as found in Rhodobacter sphaeroides.25,26 Such examples illustrate the urgent need for an understanding of how symmetry lowering in ring-like chromophore assemblies affects the electronic dipole transitions that control the absorption of light.
Previous studies have examined both experimentally and theoretically the effects of conformational and dynamic disorder on cyclic systems;2,27−31 however, investigations into the process of symmetry breaking based on ring-like compounds with geometrical defects require an excellent control over their structures. Fully π-conjugated porphyrin nanorings bound to wheel-like templates32,33 provide an ideal model system here: These nanorings have acquired a high level of rigidity through the butadiyne bridges and the template inside the rings, their initial excited states are fully delocalized over the entire ring,1 and symmetry defects of varying extent can be introduced through modifications in synthesis.
In this study we examine five synthetic porphyrin nanorings with structures mimicking those of the natural RC-LH1 complexes previously described. We investigate fully conjugated nanorings with and without defects, a nanoring featuring a gap due to broken conjugation, and systems consisting of two fused nanorings (see Figure 1). We reveal the effect of symmetry distortions on the electronic transitions in these systems, showing that as deviations from rotational symmetry increase, oscillator strength is transferred to the lowest (k = 0) state. Concomitantly, the degeneracy of the dipole-allowed first excited (k = ±1) state is shown to be lifted, leading to an ultrafast polarization switching effect in the emission from strongly symmetry-broken nanorings.
Figure 1.
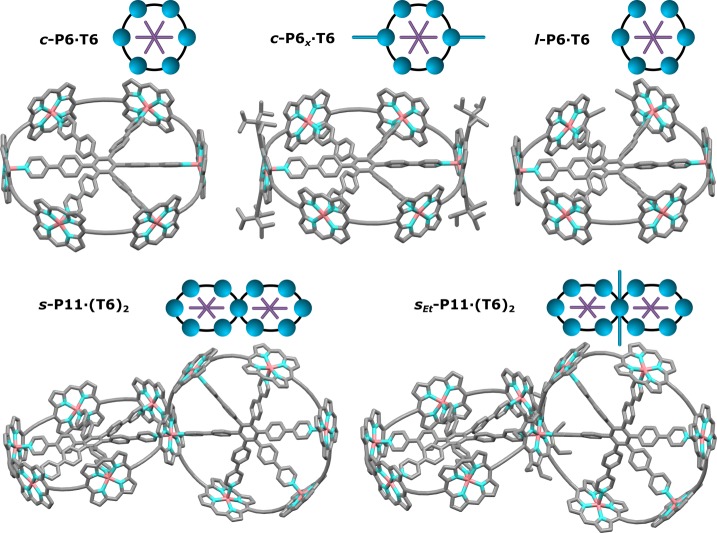
Chemical structures of the butadiyne-linked zinc porphyrin nanoring complexes investigated in this study. Carbon is indicated in gray, nitrogen in blue, and zinc in red. The structures are generated using HyperChem with side chains omitted for clarity. Icons corresponding to each compound are shown on top of each structure.
The synthesis and characterization of the nanoring complexes is described in detail in the Supporting Information and in previous literature reports.33−36Figure 1 shows the structures and simplified graphical representations of the five investigated nanorings consisting of zinc porphyrin units joined by butadiyne bridges. The six-legged (T6) templates inside all complexes bind to the porphyrin units, thus maintaining a rigid ring-like shape for the nanorings, which is vital because it suppresses competing symmetry weakening from ring distortions.
The most highly symmetric compound, c-P6·T6 has a closed ring structure with six porphyrin units,37 comparable to the D6h symmetry of benzene. For ring-like systems with 6-fold symmetry, such as benzene, the energy-level structure can easily be visualized through the simple Hückel molecular orbital method for π-conjugated molecules. This approach postulates two nondegenerate (k = 0, k = 3) and two pairwise degenerate (k = ±1, k = ±2) exciton states; however, simple analysis of the transition dipole moments to these states reveals that only the two degenerate k = ±1 states of orthogonal polarization can carry significant oscillator strength. In particular, the transitions to the lowest (k = 0) state can be visualized by the simple Kasha model38 as dipole contributions summing to zero in a hexagonal arrangement. Therefore, once the molecule has relaxed into its lowest state, emission is expected to be strongly suppressed, as we have shown to be the case for c-P6·T6.2,37
Figure 1 also displays four other compounds whose symmetry has been reduced with respect to c-P6·T6. Here c-P6x·T6 has a very similar structure, but with the minor modification that two opposite porphyrins have additional alkyne bridges with TIPS (triisopropylsilyl) end groups attached (see SI), leading to reduced symmetry. Stronger deviations are introduced by l-P6·T6, which comprises a linear six-porphyrin chain bound to the T6 template and therefore features a “gap” in the π-conjugated backbone. The two spiro fused ring structures s-P11·(T6)2 and sEt-P11·(T6)2 comprise 11 porphyrin units each and consist of two interlinked six-porphyrin nanorings with perpendicular template planes, as shown in Figure 1, with the only difference being the ethyl side chains attached to the shared porphyrin unit in the center of sEt-P11·(T6)2 (see SI).36 For all measurements reported, l-P6·T6 was dissolved in toluene, while all other samples were prepared in toluene/1% pyridine solutions to avoid aggregation.
We proceed to investigate the impact of symmetry on the electronic properties of ring-like molecules by investigating the changes in absorption and emission of these five porphyrin nanoring systems, ranging from almost perfect 6-fold symmetry, through modifications in structure, to ring structures with broken π-conjugation. As a first comprehensive insight into the energy level structure in these ring systems, Figure 2 shows the extinction coefficient spectra of the five compounds in the region of the Qx-band. Extinction coefficient spectra over a wider range of photon energies and emission spectra can be found in the SI. In contrast with zinc porphyrin monomers that display degenerate S0-S1 transitions at ∼550 nm (Q-band),39 the Q-band of the ring structures is split into Qx and Qy bands with polarizations parallel and perpendicular to the molecular backbone, respectively, and the Qx band is significantly red-shifted to ∼800 nm because of the increased conjugation length.28
Figure 2.

Extinction coefficient spectrum in the region of the Qx-band for (a) c-P6·T6, (b) c-P6x·T6, (c) sEt-P11·(T6)2, (d) s-P11·(T6)2 in toluene/1% pyridine, and (e) l-P6·T6 in toluene. Arrows indicate the trend in peak intensity ratios for each compound in comparison with c-P6·T6.
For the most highly symmetric molecule, c-P6·T6, the extinction coefficient spectrum shows three distinctive strong peaks with approximately equal energy difference. We have previously shown that excitations in this system are fully delocalized over the entire ring.2,37 Therefore, the simple Hückel model should hold as previously described, and only the lowest allowed k = ±1 exciton state carries significant oscillator strength. As we have previously discussed,37 the multiple peaks most likely arise from vibrational contributions, with the approximate 75 meV energy spacing between the three main peaks tentatively supporting an interpretation in terms of Franck–Condon vibronic progression within an adiabatic Born–Oppenheimer framework. As the symmetry is lowered for the other nanorings systems, two effects can be clearly observed in the extinction coefficient spectra. First, new features appear at the low-energy end (1.2 to 1.4 eV) of the spectra, which grow in intensity (red arrows in Figure 2) as symmetry distortions become more severe. We propose that such deviations from 6-fold symmetry may lead to oscillator strength being transferred to the lowest ( k = 0) exciton state. For the ring with broken π-conjugation (l-P6·T6) this low-energy peak rises to considerable strength (Figure 2e), suggesting a strongly allowed transition to the k = 0 state becomes possible. This phenomenon has analogies to observations in the natural RC-LH1 complexes from Rps. palustris, which features a gap in the LH1 ring24 that enhances absorption contributions for the k = 0 state. Concomitant with these changes, the distortions from 6-fold symmetry appear to also affect the peak intensity ratio of the three strong peaks visible in all extinction spectra. Compared with c-P6·T6, the first peak in the series, as indicated with green arrows in Figure 2, gradually rises with respect to the second peak as symmetry constraints are lifted. This effect may derive from higher energy vibronic progressions of the emerging k = 0 state overlapping with the k = 1 features and is therefore most likely of similar origin.
To ascertain whether a particular lowering of the nanoring symmetry indeed leads to the emergence of a dipole-allowed lowest (k = 0) state, we further probed the emissive properties of these molecules, following excitation into the Qx-band. While for a rotationally symmetric molecule, transitions from the k = 0 exciton state are dipole forbidden within the Franck–Condon approximation, weak emission is possible via Herzberg–Teller intensity borrowing through joint electronic-vibrational transitions that match the symmetry of the higher-lying allowed (k = 1) transition.37 A weakening of symmetry constraints, however, is expected to relieve the strict selection rules on the k = 0 state, leading to additional Franck–Condon emission.
To investigate such effects, we therefore measured the radiative emission rate of all molecules, which reflects the oscillator strength in the k = 0 state into which the system rapidly relaxes following excitation. For this purpose, the fluorescence lifetime was measured using time-correlated single-photon counting (TCSPC) and the quantum yield was obtained by comparing the fluorescence spectrum integral against that of a reference standard (full details of measurement are provided in SI). From these independent measurements, the radiative (Γr) and nonradiative (Γnr) rate contributions were evaluated, as listed in Table 1. It can be seen that the increasingly severe deviations from ring-like symmetry introduced along the group of molecules lead to a gradual increase in their radiative emission rates. The strongest enhancements are seen for l-P6·T6, for which Γr increases more than 6-fold with respect to c-P6·T6 as the π-conjugation is broken, resulting in efficient emission that suggests strong Franck–Condon allowed transitions. The spiro-fused rings show weaker increases, with the radiative rate more than doubling in comparison with the 6-fold symmetric c-P6·T6. The weakest effects are seen for c-P6x·T6, which may be partly because a C2-type symmetry reduction alone is not expected to lead to oscillator strength being transferred to the k = 0 state.24,40
Table 1. Photoluminescence Lifetime, τ, Quantum Yield, QY, Radiative Rate, Γr, and Non-Radiative Rate, Γnr, for the Five Compoundsa.
| molecule | τ (ps) | QY | Γr (ns–1) | Γnr (ns–1) |
|---|---|---|---|---|
| c-P6·T6 | 627 | 0.7% | 0.010 | 1.60 |
| c-P6x·T6 | 682 | 1.3% | 0.019 | 1.45 |
| sEt-P11·(T6)2 | 271 | 0.5% | 0.020 | 3.73 |
| s-P11·(T6)2 | 343 | 0.8% | 0.024 | 2.90 |
| l-P6·T6 | 364 | 2.3% | 0.064 | 2.69 |
Details of measurements are given in the Supporting Information.
In contrast and as expected, no correlation between nonradiative decay rates and molecular symmetry is observed. The fluorescence lifetime of sEt-P11·(T6)2 is particularly short, which is caused by stronger nonradiative decay channels (Γnr, Table 1) possibly introduced by the presence of the ethyl side chains attached to the shared porphyrin unit.
We proceed by establishing a quantitative correlation between such reduced-symmetry enhancements in radiative rates and the changes in the absorption features previously discussed. Figure 3 shows the correlation between (a) the absorption intensity of the k = 0 state and (b) the intensity ratio of the first two main peaks, plotted against the radiative emission rate for each of the five compounds. To capture the contributions to the absorption into the emerging k = 0 state (indicated by red arrows in Figure 2), we integrated the extinction coefficient spectrum over the low-energy wing up to a full width at half-maximum below the first main peak associated with the k = ±1 state (marked with yellow arrows). This integration limit ensures that the contribution from the allowed k = ±1 state is largely excluded from the integration result. To facilitate accurate comparison between the five compounds, we expressed the above calculated integral as a fraction of the extinction coefficient spectrum integral over the entire Qx-band. Figure 3a shows excellent correlation between the emergence of a partially allowed k = 0 feature in absorption and an enhancement of the radiative emission rate. In particular, the lowest state is most strongly suppressed in the most highly symmetric c-P6·T6 and most strongly enhanced in the ring with broken π-conjugation, with the other three compounds falling in between, as would be expected. We note, however, that even the highly symmetric c-P6·T6 appears to feature some small transition moment to the k = 0 state. This could be partly because Herzberg–Teller intensity borrowing can augment the absorption of Franck–Condon forbidden states (as in benzene7) but also partly because some disorder may exist through interaction with the solvent environment. In addition, Figure 3b demonstrates clear correlation between the intensity ratio of the strongest two peaks in absorption (green and yellow arrows in Figure 2) and the radiative rate of the molecules. As previously discussed, these intensity ratios are therefore most likely caused by underlying higher-energy replica of the k = 0 state overlapping with the k = ±1 peaks and therefore derive from similar origins and are subject to similar changes as the symmetry of the ring-like molecules is lowered.
Figure 3.
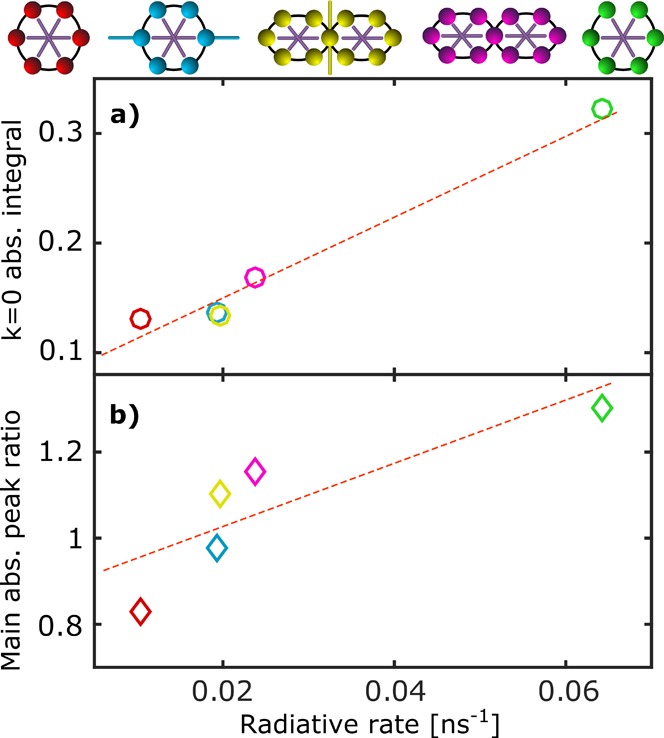
Analysis of the extinction coefficient spectra for the nanoring complexes c-P6·T6 (red), c-P6x·T6 (blue), sEt-P11·(T6)2 (yellow), s-P11·(T6)2 (magenta), and l-P6·T6 (green) in relation to their radiative emission rates. (a) Spectrally integrated extinction coefficient of the emerging low-energy (k = 0) peak, determined by integration of the spectra shown in Figure 2 up to a full width at half-maximum below the first main peak and given in relation to the integral over the full spectrum of the Qx band. (b) Intensity ratio of the first two peaks in the main (k = ±1) peak series of the extinction coefficient spectrum. Each data point corresponds to a ring complex with the colors depicted matching that of the icons above the graphs representing the structure. Dashed lines are guides to the eye, highlighting the strong correlation between the parameters, but do not imply a particular functional dependence.
Apart from a transfer of oscillator strength to the lowest (k = 0) excitonic state, a lowering of the ring symmetry can also lead to a lifting of the degeneracy of the allowed k = ±1 states.20,40 Because the two k = ±1 states carry orthogonal polarizations, such effects may conceivably be detected in polarization anisotropy spectroscopy. We have therefore measured the ultrafast photoluminescence anisotropy dynamics for these systems, which reflect the polarization memory loss of the compounds following excitation with a polarized light pulse41 (full experimental details are provided in the SI). The samples were excited using a range of wavelengths between 740 (1.68 eV) and 830 nm (1.49 eV) through the Qx-band in the region of the three main peaks in the absorption spectrum to allow clear separation from the detected emission. The PL anisotropy γ was evaluated from the PL intensity components polarized parallel (I∥) and perpendicular (I⊥) to the excitation polarization,42 according to γ = (I|| – I⊥)/(I|| + 2I⊥). As reported in previous studies,1,2 the PL anisotropy assumes a particular value within the time resolution (270 fs) of the system, indicating ultrafast exciton delocalization and rapid relaxation in these systems (see Figure S7 in Supporting Information). This initial PL anisotropy value remains constant over the next tens of picoseconds as this time scale is too short for molecular reorientation in solution that can cause additional polarization memory loss.28Figure 4a shows the value of this initial polarization anisotropy γ as a function of the excitation wavelength for c-P6·T6, c-P6x·T6, and l-P6·T6. Corresponding studies for the fused rings were not conducted because γ is very close to zero for these systems because of exciton delocalization across the orthogonal ring planes, as previously reported;36 therefore, any additional depolarization effects would be hard to discern. Figure 4a reveals that the initial PL anisotropy values for c-P6·T6 and c-P6x·T6 are unaffected by the choice of excitation wavelengths and assume values close to 0.1. Such dynamics are expected for complete polarization memory loss in the 2D ring plane,43 which can be induced by absorption into the two degenerate (or near-degenerate) k = ±1 states with orthogonal polarization in the ring plane, which will be followed by exciton relaxation into the k = 0 state.1,44 For l-P6·T6, on the contrary, a strikingly different dependence of γ on excitation wavelength is observed (Figure 4a). For excitation at 740 nm, the anisotropy is 0.1, similar to the value displayed by the two more symmetric nanoring compounds; however, as the excitation wavelength increases, γ decreases and reaches −0.1 at 830 nm. A negative anisotropy value suggests that a significant fraction of the emitting dipole moments are perpendicularly polarized to the absorbing transitions.41,45,46 We can rule out unintentional excitation of the Qy state of the porphyrin monomers (polarized perpendicular to the ring plane) as a cause because the excitation energies employed here are substantially lower than the transition energy of the Qy state visible in absorption (2.1 eV).
Figure 4.

(a) Initial value of the PL anisotropy following excitation with a short (100 fs) light pulse for c-P6·T6 (red), c-P6x·T6 (blue), and l-P6·T6 (green). Dashed lines serve as a guide to the eye. Anisotropy values have been calculated using the PL intensity polarized parallel and orthogonal to the excitation pulse, averaged over the first 5 ps following excitation, during which these intensities do not vary (see Supporting Information). (b) Schematic diagram illustrating the splitting of the k = ±1 level leading to the observed trend in PL anisotropy for l-P6·T6. For the highly symmetric c-P6·T6, Herzberg–Teller effects activate transitions from the k = 0 state to the ground state via vibrational levels (not shown), while for l-P6·T6 with broken π-conjugation such transition may become directly Franck–Condon allowed.
We propose that the polarization switching observed in l-P6·T6 is caused by the lifting of the degeneracy of the k = ±1 levels in this system, for which the symmetry is substantially lowered as a result of the clear break in conjugation. Figure 4b illustrates the mechanism that explains our experimental observations. Highly rotationally symmetric systems such as c-P6·T6 absorb light through the degenerate k = ±1 states that are orthogonally polarized. Following an ultrafast relaxation to the k = 0 state, Franck–Condon forbidden emission from this state takes place via weak Herzberg–Teller coupling. Because there is no preferred excitation polarization direction nor a net emission dipole moment in the nanoring plane, the polarization memory is completely lost in this 2D plane, resulting in γ = 0.1; however, for l-P6·T6 the lowered symmetry lifts the degeneracy of the k = ±1 states and results in the creation of new higher-lying states (labeled as k = 1, 2... in Figure 4b) with transition dipoles of well-defined orientation with respect to the symmetry plane. These changes are accompanied by a strong recovery of Franck–Condon allowed transitions from the lowest excited state, as previously discussed and examined in natural light-harvesting complexes.20,21,40 As indicated in Figure 4b, this scenario creates a well-defined relation between the orientation of the dipole moment associated with the lowest (k = 0) state and those of the nondegenerate higher-lying states, with some combinations being parallel and others orthogonal. In particular, the conjugation break in l-P6·T6 causes the lowest (k = 0) state wave function to have a lobe (probability density maximum) at the ring side opposite to the break, leading to a net dipole moment in the x direction (here we take the y direction to lie within the mirror-symmetry plane). Such deviation from a fully delocalized (i.e., no nodes) wave function in the k = 0 state of the highly symmetric c-P6·T6 thus transfers oscillator strength to the ground state of l-P6·T6, in accordance with the observed recovery in radiative rate. The higher lying k = 1 state of l-P6·T6 has some analogy to the degenerate k = 1 state of the symmetric c-P6·T6 as its nodes fall onto the symmetry plane and it is hence less perturbed by the conjugation gap than the orthogonal k = −1 state. Therefore, the observed polarization switch in l-P6·T6 can be understood in terms of an initial excitation into nondegenerate higher-lying states, such as the k = 1 state with polarization along the y direction, followed by relaxation into the k = 0 state that is associated with a dipole moment in the orthogonal x direction. Strictly speaking, orthogonal absorbing and emitting transition dipole moments should yield γ = −0.2, whereas collinear dipole moments result in γ = 0.4 for randomly oriented molecules in solution;41 however, contributions from higher lying (k ≥ 1) states and their vibrational progressions are broadly overlapping (clearly separate features are not discernible in the absorption of l-P6·T6; see Figure 2). Hence, in reality, anisotropy values between –0.1 and 0.1 are observed for the range over which the excitation wavelength is varied (Figure 4a); however, the strong observed variation of polarization anisotropy from negative to positive values as the excitation energy is tuned through the higher-lying excitation band provides clear evidence that severe symmetry lowering in such systems leads to a lifting of the degeneracy of the ring-like k = ±1 states, creating a series of states with well-defined transition dipole moments.
In conclusion, π-conjugated six-porphyrin nanorings with various distortions to the cyclic structures have been investigated to explore the influence of symmetry lowering on their photophysical properties. We have demonstrated that as symmetry distortions increase in severity along the series of structures, oscillator strength is transferred to the transition into the lowest (k = 0) state, which is Franck–Condon forbidden in the fully 6-fold rotationally symmetric rings. The associated increases in oscillator strength were shown to correlate with gradually emerging k = 0 absorption features at the lower energy end of the absorption spectra and changes in intensity ratio of higher-lying overlapping absorption peaks. Thus, symmetry plays a vital role in influencing and correlating absorptive and emissive properties of ring-like molecules, which we have been able to capture quantitatively. Furthermore, we have revealed through time-resolved photoluminescence anisotropy probes that strong symmetry breaking, induced, for example, through full breaks in conjugation, lifts the degeneracy of the k = ±1 states found in highly symmetric ring assemblies, instead creating a series of states with well-defined transition dipole moments. We note that these findings have direct relevance to ring-like complexes found in natural light-harvesting systems, which have a rich diversity of geometrical structures. Here chromophores can be arranged in circular, elliptically deformed or array arrangements, exhibit a gap, or form dimeric structures; however, comparable investigations of the impact of structural symmetries on photophysical properties are challenging in such biological systems, as the chromophores are held loosely together and interact significantly with their environment. Our study therefore highlights the outstanding potential of using synthetic biomimetic porphyrin nanorings as model systems to investigate the effect of symmetry and geometric arrangement on the fundamental nature of the light-harvesting states.
Acknowledgments
Support from European Research Council (COSUN) and the Engineering and Physical Sciences Research Council (EPSRC) is gratefully acknowledged. We thank the EPSRC National Mas Spectrometry Service at the University of Swansea for mass spectra.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.5b02617.
Synthetic procedures and characterization of all compounds. Full extinction coefficient and emission spectra of all compounds. Experimental details of up-conversion technique, TCSPC, and quantum yield measurement. PL transients and anisotropy dynamics. (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Parkinson P.; Kondratuk D. V.; Menelaou C.; Gong J. Q.; Anderson H. L.; Herz L. M. Chromophores in Molecular Nanorings: When Is a Ring a Ring?. J. Phys. Chem. Lett. 2014, 5, 4356–4361. 10.1021/jz5022153. [DOI] [PubMed] [Google Scholar]
- Yong C.-K.; Parkinson P.; Kondratuk D. V.; Chen W.-H.; Stannard A.; Summerfield A.; Sprafke J. K.; O’Sullivan M. C.; Beton P. H.; Anderson H. L.; et al. Ultrafast Delocalization of Excitation in Synthetic Light-Harvesting Nanorings. Chem. Sci. 2015, 6, 181–189. 10.1039/C4SC02424A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perrin M. H. Vibronic Coupling. VI. Vibronic Borrowing in Cyclic Polyenes and Porphyrin. J. Chem. Phys. 1969, 50, 4137–4150. 10.1063/1.1670879. [DOI] [Google Scholar]
- Bednarz M.; Reineker P.; Mena-Osteritz E.; Bäuerle P. Optical Absorption Spectra of Linear and Cyclic Thiophenes-Selection Rules Manifestation. J. Lumin. 2004, 110, 225–231. 10.1016/j.jlumin.2004.08.013. [DOI] [Google Scholar]
- van Oijen A. M.; Ketelaars M.; Köhler J.; Aartsma T. J.; Schmidt J. Unraveling the Electronic Structure of Individual Photosynthetic Pigment-Protein Complexes. Science 1999, 285, 400–402. 10.1126/science.285.5426.400. [DOI] [PubMed] [Google Scholar]
- Sponer H.; Nordheim G.; Sklar A. L.; Teller E. Analysis of the Near Ultraviolet Electronic Transition of Benzene. J. Chem. Phys. 1939, 7, 207–220. 10.1063/1.1750419. [DOI] [Google Scholar]
- Harris D. C.; Bertolucci M. D.. Symmetry and Spectroscopy; an Introduction to Vibrational and Electronic Spectroscopy; Oxford University Press, 1978. [Google Scholar]
- Hollas J. M.High Resolution Spectroscopy, 2nd ed.; Wiley, 1990. [Google Scholar]
- Cogdell R. J.; Gall A.; Köhler J. The Architecture and Function of the Light-Harvesting Apparatus of Purple Bacteria: from Single Molecules to in Vivo Membranes. Q. Rev. Biophys. 2006, 39, 227–324. 10.1017/S0033583506004434. [DOI] [PubMed] [Google Scholar]
- Hildner R.; Brinks D.; Nieder J. B.; Cogdell R. J.; van Hulst N. F. Quantum Coherent Energy Transfer over Varying Pathways in Single Light-Harvesting Complexes. Science 2013, 340, 1448–1451. 10.1126/science.1235820. [DOI] [PubMed] [Google Scholar]
- McDermott G.; Prince S. M.; Freer A. A.; Hawthornthwaite-Lawless A. M.; Papiz M. Z.; Cogdell R. J.; Isaacs N. W. Crystal Structure of an Integral Membrane Light-Harvesting Complex from Photosynthetic Bacteria. Nature 1995, 374, 517–521. 10.1038/374517a0. [DOI] [Google Scholar]
- Jasti R.; Bhattacharjee J.; Neaton J. B.; Bertozzi C. R. Synthesis, Characterization, and Theory of [9]-, [12]-, and [18]Cycloparaphenylene: Carbon Nanohoop Structures. J. Am. Chem. Soc. 2008, 130, 17646–17647. 10.1021/ja807126u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adamska L.; Nayyar I.; Chen H.; Swan A. K.; Oldani N.; Fernandez-Alberti S.; Golder M. R.; Jasti R.; Doorn S. K.; Tretiak S. Self-Trapping of Excitons, Violation of Condon Approximation, and Efficient Fluorescence in Conjugated Cycloparaphenylenes. Nano Lett. 2014, 14, 6539–6346. 10.1021/nl503133e. [DOI] [PubMed] [Google Scholar]
- Kromer J.; Rios-Carreras I.; Fuhrmann G.; Musch C.; Wunderlin M.; Debaerdemaeker T.; Mena-Osteritz E.; Bauerle P. Synthesis of the First Fully Alpha-Conjugated Macrocyclic Oligothiophenes: Cyclo[n]thiophenes with Tunable Cavities in the Nanometer Regime. Angew. Chem., Int. Ed. 2000, 39, 3481–3486. . [DOI] [PubMed] [Google Scholar]
- Aggarwal A. V.; Thiessen A.; Idelson A.; Kalle D.; Würsch D.; Stangl T.; Steiner F.; Jester S.-S.; Vogelsang J.; Höger S.; et al. Fluctuating Exciton Localization in Giant π-Conjugated Spoked-Wheel Macrocycles. Nat. Chem. 2013, 5, 964–970. 10.1038/nchem.1758. [DOI] [PubMed] [Google Scholar]
- Hori T.; Aratani N.; Takagi A.; Matsumoto T.; Kawai T.; Yoon M.-C.; Yoon Z. S.; Cho S.; Kim D.; Osuka A. Giant Porphyrin Wheels with Large Electronic Coupling as Models of Light-Harvesting Photosynthetic Antenna. Chem. - Eur. J. 2006, 12, 1319–1327. 10.1002/chem.200501373. [DOI] [PubMed] [Google Scholar]
- Nakamura Y.; Aratani N.; Osuka A. Cyclic Porphyrin Arrays as Artificial Photosynthetic Antenna: Synthesis and Excitation Energy Transfer. Chem. Soc. Rev. 2007, 36, 831–845. 10.1039/b618854k. [DOI] [PubMed] [Google Scholar]
- Terazono Y.; Kodis G.; Chachisvilis M.; Cherry B. R.; Fournier M.; Moore A.; Moore T. A.; Gust D. Multiporphyrin Arrays with π-πInterchromophore Interactions. J. Am. Chem. Soc. 2015, 137, 245–258. 10.1021/ja510267c. [DOI] [PubMed] [Google Scholar]
- Parkinson P.; Knappke C. E. I.; Kamonsutthipaijit N.; Sirithip K.; Matichak J. D.; Anderson H. L.; Herz L. M. Ultrafast Energy Transfer in Biomimetic Multistrand Nanorings. J. Am. Chem. Soc. 2014, 136, 8217–8220. 10.1021/ja504730j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsushita M.; Ketelaars M.; van Oijen A. M.; Köhler J.; Aartsma T. J.; Schmidt J.; Kohler J.; Aartsma T. J.; Schmidt J. Spectroscopy on the B850 Band of Individual Light-Harvesting 2 Complexes of Rhodopseudomonas Acidophila II. Exciton States of an Elliptically Deformed Ring Aggregate. Biophys. J. 2001, 80, 1604–1614. 10.1016/S0006-3495(01)76133-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mostovoy M. V.; Knoester J. Statistics of Optical Spectra from Single-Ring Aggregates and its Application to LH2. J. Phys. Chem. B 2000, 104, 12355–12364. 10.1021/jp001519k. [DOI] [Google Scholar]
- Gerken U.; Lupo D.; Tietz C.; Wrachtrup J.; Ghosh R. Circular Symmetry of the Light-Harvesting 1 Complex from Rhodospirillum Rubrum is not Perturbed by Interaction with the Reaction Center. Biochemistry 2003, 42, 10354–10360. 10.1021/bi034969m. [DOI] [PubMed] [Google Scholar]
- Roszak A. W.; Howard T. D.; Southall J.; Gardiner A. T.; Law C. J.; Isaacs N. W.; Cogdell R. J. Crystal Structure of the RC-LH1 Core Complex from Rhodopseudomonas Palustris. Science 2003, 302, 1969–1972. 10.1126/science.1088892. [DOI] [PubMed] [Google Scholar]
- Richter M. F.; Baier J.; Prem T.; Oellerich S.; Francia F.; Venturoli G.; Oesterhelt D.; Southall J.; Cogdell R. J.; Köhler J. Symmetry Matters for the Electronic Structure of Core Complexes from Rhodopseudomonas Palustris and Rhodobacter Sphaeroides PufX–. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 6661–6665. 10.1073/pnas.0611115104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siebert C. A.; Qian P.; Fotiadis D.; Engel A.; Hunter C. N.; Bullough P. A. Molecular Architecture of Photosynthetic Membranes in Rhodobacter Sphaeroides: the Role of PufX. EMBO J. 2004, 23, 690–700. 10.1038/sj.emboj.7600092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian P.; Bullough P. A.; Hunter C. N. Three-Dimensional Reconstruction of a Membrane-Bending Complex: the RC-LH1-PufX Core Dimer of Phodobacter Sphaeroides. J. Biol. Chem. 2008, 283, 14002–14011. 10.1074/jbc.M800625200. [DOI] [PubMed] [Google Scholar]
- Nieman G. C. Molecular Distortions and the Phosphorescence of Benzene. J. Chem. Phys. 1969, 50, 1674–1683. 10.1063/1.1671257. [DOI] [Google Scholar]
- Chang M.-H.; Hoffmann M.; Anderson H. L.; Herz L. M. Dynamics of Excited-State Conformational Relaxation and Electronic Delocalization in Conjugated Porphyrin Oligomers. J. Am. Chem. Soc. 2008, 130, 10171–10178. 10.1021/ja711222c. [DOI] [PubMed] [Google Scholar]
- Hestand N. J.; Spano F. C. The Effect of Chain Bending on the Photophysical Properties of Conjugated Polymers. J. Phys. Chem. B 2014, 118, 8352–8363. 10.1021/jp501857n. [DOI] [PubMed] [Google Scholar]
- Sener M. K.; Schulten K. General Random Matrix Approach to Account for the Effect of Static Disorder on the Spectral Properties of Light Harvesting Systems. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 2002, 65, 031916. 10.1103/PhysRevE.65.031916. [DOI] [PubMed] [Google Scholar]
- Kim P.; Park K. H.; Kim W.; Tamachi T.; Iyoda M.; Kim D. Relationship between Dynamic Planarization Processes and Exciton Delocalization in Cyclic Oligothiophenes. J. Phys. Chem. Lett. 2015, 6, 451–456. 10.1021/jz502395z. [DOI] [PubMed] [Google Scholar]
- Hoffmann M.; Wilson C. J.; Odell B.; Anderson H. L. Template-Directed Synthesis of a pi-Conjugated Porphyrin Nanoring. Angew. Chem., Int. Ed. 2007, 46, 3122–3125. 10.1002/anie.200604601. [DOI] [PubMed] [Google Scholar]
- Hoffmann M.; Kärnbratt J.; Chang M. H.; Herz L. M.; Albinsson B.; Anderson H. L. Enhanced pi conjugation around a porphyrin[6] nanoring. Angew. Chem., Int. Ed. 2008, 47, 4993–4996. 10.1002/anie.200801188. [DOI] [PubMed] [Google Scholar]
- Screen T. E. O.; Lawton K. B.; Wilson G. S.; Dolney N.; Ispasoiu R.; Goodson T. III; Martin S. J.; Bradley D. D. C.; Anderson H. L. Synthesis and Third Order Nonlinear Optics of a New Soluble Conjugated Porphyrin Polymer. J. Mater. Chem. 2001, 11, 312–320. 10.1039/b007250h. [DOI] [Google Scholar]
- Tait C. E.; Neuhaus P.; Anderson H. L.; Timmel C. R. Triplet State Delocalization in a Conjugated Porphyrin Dimer Probed by Transient Electron Paramagnetic Resonance Techniques. J. Am. Chem. Soc. 2015, 137, 6670–6679. 10.1021/jacs.5b03249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Favereau L.; Cnossen A.; Kelber J. B.; Gong J. Q.; Oetterli R. M.; Cremers J.; Herz L. M.; Anderson H. L. Six-Coordinate Zinc Porphyrins for Template-Directed Synthesis of Spiro-Fused Nanorings. J. Am. Chem. Soc. 2015, 137, 14256–14259. 10.1021/jacs.5b10126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sprafke J. K.; Kondratuk D. V.; Wykes M.; Thompson A. L.; Hoffmann M.; Drevinskas R.; Chen W.-h.; Yong C. K.; Karnbratt J.; Bullock J. E.; et al. Belt-Shaped π-Systems: Relating Geometry to Electronic Structure in a Six-Porphyrin Nanoring. J. Am. Chem. Soc. 2011, 133, 17262–17273. 10.1021/ja2045919. [DOI] [PubMed] [Google Scholar]
- Kasha M.; Rawls H. R.; Ashraf El-Bayoumi M. The Exciton Model in Molecular Spectroscopy. Pure Appl. Chem. 1965, 11, 371–392. 10.1351/pac196511030371. [DOI] [Google Scholar]
- Anderson H. L. Building Molecular Wires from the Colours of Life: Conjugated Porphyrin Oligomers. Chem. Commun. 1999, 2323–2330. 10.1039/a904209a. [DOI] [Google Scholar]
- Ketelaars M.; van Oijen A. M.; Matsushita M.; Köhler J.; Schmidt J.; Aartsma T. J. Spectroscopy on the B850 Band of Individual Light-Harvesting 2 Complexes of Rhodopseudomonas Acidophilia I. Experiments and Monte Carlo Simulations. Biophys. J. 2001, 80, 1591–1603. 10.1016/S0006-3495(01)76132-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valeur B.; Berberan-Santos M. N.. Molecular Fluorescence: Principles and Applications, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2012. [Google Scholar]
- Chang M. H.; Frampton M. J.; Anderson H. L.; Herz L. M. Intermolecular Interaction Effects on the Ultrafast Depolarization of the Optical Emission from Conjugated Polymers. Phys. Rev. Lett. 2007, 98, 027402. 10.1103/PhysRevLett.98.027402. [DOI] [PubMed] [Google Scholar]
- Lakowicz J. R.Principles of Fluorescence Spectroscopy, 3rd ed.; Springer: New York, 2006. [Google Scholar]
- Gong J. Q.; Parkinson P.; Kondratuk D. V.; Gil-Ramírez G.; Anderson H. L.; Herz L. M. Structure-Directed Exciton Dynamics in Templated Molecular Nanorings. J. Phys. Chem. C 2015, 119, 6414–6420. 10.1021/acs.jpcc.5b00210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menelaou C.; Schiphorst J.; Kendhale A. M.; Parkinson P.; Debije M. G.; Schenning A.; Herz L. M. Rapid Energy Transfer Enabling Control of Emission Polarization in Perylene-Bisimide Donor-Acceptor Triads. J. Phys. Chem. Lett. 2015, 6, 1170–1176. 10.1021/acs.jpclett.5b00183. [DOI] [PubMed] [Google Scholar]
- Neuhaus P.; Cnossen A.; Gong J. Q.; Herz L. M.; Anderson H. L. A Molecular Nanotube with Three-Dimensional π-Conjugation. Angew. Chem., Int. Ed. 2015, 54, 7344–7348. 10.1002/anie.201502735. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.