Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2015 Dec 28;49(1):172–181. doi: 10.1021/acs.macromol.5b02385

How Do Spherical Diblock Copolymer Nanoparticles Grow during RAFT Alcoholic Dispersion Polymerization?

E R Jones †, O O Mykhaylyk †, M Semsarilar ‡, M Boerakker ‡, P Wyman ‡, S P Armes †,*
PMCID: PMC4745608  PMID: 26893528

Abstract

graphic file with name ma-2015-02385c_0012.jpg

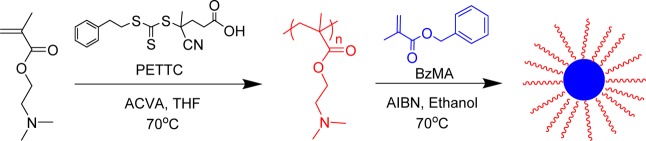
A poly(2-(dimethylamino)ethyl methacrylate) (PDMA) chain transfer agent (CTA) is used for the reversible addition–fragmentation chain transfer (RAFT) alcoholic dispersion polymerization of benzyl methacrylate (BzMA) in ethanol at 70 °C. THF GPC analysis indicated a well-controlled polymerization with molecular weight increasing linearly with conversion. GPC traces also showed high blocking efficiency with no homopolymer contamination apparent and Mw/Mn values below 1.35 in all cases. 1H NMR studies confirmed greater than 98% BzMA conversion for a target PBzMA degree of polymerization (DP) of up to 600. The PBzMA block becomes insoluble as it grows, leading to the in situ formation of sterically stabilized diblock copolymer nanoparticles via polymerization-induced self-assembly (PISA). Fixing the mean DP of the PDMA stabilizer block at 94 units and systematically varying the DP of the PBzMA block enabled a series of spherical nanoparticles of tunable diameter to be obtained. These nanoparticles were characterized by TEM, DLS, MALLS, and SAXS, with mean diameters ranging from 35 to 100 nm. The latter technique was particularly informative: data fits to a spherical micelle model enabled calculation of the core diameter, surface area occupied per copolymer chain, and the mean aggregation number (Nagg). The scaling exponent derived from a double-logarithmic plot of core diameter vs PBzMA DP suggests that the conformation of the PBzMA chains is intermediate between the collapsed and fully extended state. This is in good agreement with 1H NMR studies, which suggest that only 5−13% of the BzMA residues of the core-forming chains are solvated. The Nagg values calculated from SAXS and MALLS are in good agreement and scale approximately linearly with PBzMA DP. This suggests that spherical micelles grow in size not only as a result of the increase in copolymer molecular weight during the PISA synthesis but also by exchange of individual copolymer chains between micelles and/or by sphere–sphere fusion events.

Introduction

Block copolymer self-assembly in solution has been studied for more than 50 years.1−3 Typically, it is conducted at rather low copolymer concentration (<1%) either via a solvent switch,4−6 pH adjustment,7 or by thin film rehydration.8,9 However, such protocols are not amenable for industrial scale-up. This is a significant problem for many potential applications, including the use of block copolymer nanoparticles as colloidal templates,10 for nanostructured films,11 as responsive gels,12 and in nanomedicine.13,14

The development of living radical polymerization (LRP) techniques over the past two decades has undoubtedly revolutionized the synthesis of well-defined functional block copolymers.15−17 In this context, reversible addition–fragmentation chain transfer (RAFT) polymerization has proved to be particularly versatile.18−20 The recent combination of LRP chemistry with polymerization-induced self-assembly (PISA) has enabled the rational design of a wide range of AB diblock copolymer nano-objects.21−36 PISA syntheses can be conducted at relatively high solids without any need for post-polymerization processing, since the desired sterically stabilized nanoparticles are produced directly during the copolymer synthesis. RAFT-mediated dispersion polymerization formulations have been particularly effective.18,35,37−46 Thus, amphiphilic diblock copolymers are readily formed by chain extension of a soluble macromolecular chain transfer agent (macro-CTA) with a second polymer that gradually becomes insoluble, which drives in situ self-assembly. Aqueous dispersion polymerization has been extensively studied.30,42,47 However, there are also many examples of RAFT PISA dispersion formulations conducted in alcoholic media27,33,34,48−54 and n-alkanes,38,55−57 as well as aqueous emulsion polymerization formulations.25,29,58,59 Compared to conventional solution polymerization, such PISA syntheses allow relatively high copolymer concentrations (up to 40–50% solids60,61) to be achieved while maintaining low solution viscosity. Moreover, faster polymerizations are usually observed, since monomer-swollen particles can act as nanoreactors.62,63 Finally, enhanced living character has been observed for RAFT dispersion polymerization compared to solution polymerization.64 In this rather esoteric example the PISA formulation involved a semifluorinated monomer, which conferred the isorefractivity with the ethanolic continuous phase that was required for UV spectroscopy studies of the rate of degradation of the RAFT chain-ends. Nevertheless, it seems likely that this may be a general result, at least for methacrylic monomers.

Various copolymer morphologies can be accessed via PISA, including spheres,34,35,46 worms,24,34,35 vesicles,27,34,35 framboidal vesicles,65 “lumpy rods”,66 and lamellae.39,46,67 As first reported by Israelachvili and co-workers for surfactant amphiphiles,68 the final copolymer morphology often depends on the relative volume fractions of the core-forming block and the stabilizer block. For PISA syntheses, several other parameters can also influence the copolymer morphology. These include the absolute DP of the stabilizer block,30,35 the copolymer concentration (or total solids content),30 the solution temperature,12,69 the choice of solvent,31,70 and, for aqueous syntheses, the solution pH71 and salt concentration.32,72,73 Detailed phase diagrams have been constructed for many PISA formulations, enabling specific copolymer morphologies to be targeted reproducibly. Such a systematic approach is essential to avoid undesirable mixed phases (e.g., spheres plus worms or worms plus vesicles).33−35,56

Dynamic light scattering (DLS)74,75 and transmission electron microscopy (TEM)76 are the most widely used characterization techniques described in the literature for assessing the particle size and morphology of diblock copolymer nano-objects.77 For the former technique, a spherical morphology is assumed and a hydrodynamic diameter is reported. For the latter technique, assessment is often restricted to a few hundred particles, which may not necessarily be representative of the whole particle size distribution. A third, arguably more robust, characterization technique is small-angle X-ray scattering (SAXS).78,79 This is much more statistically robust than TEM, since X-ray scattering is averaged over millions of particles. In principle, determining gradients for X-ray scattering intensity vs scattering vector, q, in the low q (Guinier) regime, enables various copolymer morphologies to be assigned.80 Fitting a SAXS pattern to a core–shell model should allow determination of the mean particle diameter for spherical nanoparticles. However, this simplistic model incorrectly assumes a constant electron density throughout the coronal layer (or shell). If there is a sufficiently large difference in electron density between the two blocks, a more sophisticated spherical micelle model can be used.81−83 This enables physically realistic dimensions for the core and coronal layers to be calculated as well as the mean micelle aggregation number, Nagg. Traditionally, the latter parameter can also be determined using multiangle laser light scattering (MALLS), also known as static light scattering (SLS).84

Recently, we reported an all-methacrylic alcoholic RAFT dispersion polymerization formulation based on chain extension of a poly(2-(dimethylamino)ethyl methacrylate) (PDMA) macro-CTA using benzyl methacrylate (BzMA).34 Substantially higher final monomer conversions were obtained compared to those previously reported for similar PISA formulations in which the core-forming block comprised polystyrene.27,48,85 The RAFT dispersion polymerization of BzMA displayed relatively good pseudo-living character, as judged by GPC analysis. A systematic increase in spherical particle diameter was observed when targeting progressively higher degrees of polymerization (DP) for the core-forming block. When using a relatively short stabilizer block (DP = 31), either spheres, worms, or vesicles could be obtained when targeting longer core-forming blocks. In the present study, we have deliberately selected a significantly longer PDMA stabilizer block (DP = 94). This leads to more effective steric stabilization once initial micellar nucleation has occurred, which prevents further evolution in copolymer morphology and results in kinetically trapped spherical nanoparticles, regardless of the target DP for the core-forming PBzMA block.34 A series of well-defined PDMA94–PBzMAx spheres of varying size have been obtained, which have been characterized by TEM, DLS, SAXS, and MALLS. In particular, the latter two techniques are used to examine the evolution of the mean aggregation number in order to gain mechanistic insights regarding the particle growth mechanism for such PISA syntheses.

Experimental Section

Materials

All reagents were purchased from Sigma-Aldrich (UK) and used as received unless otherwise noted. Either 4,4′-azobis(4-cyanovaleric acid) (ACVA)) or 2,2′-azobis(isobutyronitrile) (AIBN) was used as an initiator. Benzyl methacrylate (96%) was passed through a column of inhibitor remover (also purchased from Sigma) prior to use. Deuterated chloroform (CDCl3), dichloromethane (CD2Cl2), and ethanol (C2D5OD) were purchased from Goss Scientific (Nantwich, UK).

Synthesis of 4-Cyano-4-(2-phenylethanesulfanylthiocarbonyl)sulfanylpentanoic Acid (PETTC)

2-Phenylethanethiol (10.5 g, 76 mmol) was gradually added over 10 min to a stirred suspension of sodium hydride (60% in oil) (3.15 g, 79 mmol) in diethyl ether (150 mL) at 5–10 °C. Vigorous evolution of hydrogen gas was observed, and the grayish suspension was slowly transformed into a white viscous slurry of sodium phenylethanethiolate over 30 min. The reaction mixture was cooled to 0 °C, and carbon disulfide (6.0 g, 79 mmol) was gradually added to produce a thick yellow precipitate of sodium 2-phenylethanetrithiocarbonate, which was collected by filtration after 30 min and subsequently used in the next step without further purification. Solid iodine (6.3 g, 0.025 mol) was gradually added to a suspension of sodium 2-phenylethanetrithiocarbonate (11.6 g, 0.049 mol) in diethyl ether (100 mL). This reaction mixture was then stirred at room temperature for 1 h, and the insoluble white precipitate of sodium iodide was removed by filtration. The yellow–brown filtrate was washed with an aqueous solution of sodium thiosulfate to remove excess iodine, dried over sodium sulfate, and then evaporated to yield bis(2-phenylethanesulfanylthiocarbonyl) disulfide (∼100% yield). A solution of ACVA (2.10 g, 0.0075 mol) and bis(2-phenylethanesulfanylthiocarbonyl) disulfide (2.13 g, 0.005 mol) in ethyl acetate (50 mL) was degassed by nitrogen bubbling and heated at reflux under a dry nitrogen atmosphere for 18 h. After removal of the volatiles under vacuum, the crude product was washed with water (five 100 mL portions). The organic phase was concentrated and purified by silica chromatography using a mixed eluent (initially 7:3 petroleum ether/ethyl acetate, gradually increasing to a 4:6 solvent composition) to afford 4-cyano-4-(2-phenylethanesulfanylthiocarbonyl)sulfanylpentanoic acid as a yellow oil. 1H NMR (400.13 MHz, CD2Cl2, 298 K) δ (ppm) = 1.89 (3H, −CH3), 2.34–2.62 (m, 2H, −CH2), 2.7 (t, 2H, −CH2), 3.0 (t, 2H, −CH2), 3.6 (t, 2H, −CH2), 7.2–7.4 (m, 5H, aromatic). 13C NMR (400.13 MHz, CD2Cl2, 298 K) δ (ppm) = 24.2 (CH3), 29.6 (CH2CH2COOH), 30.1(CH2Ph), 33.1 (CH2 CH2COOH), 39.9 (SCH2CH2Ph), 45.7 (SCCH2), 118.6 (CN), 127.4, 128.8, 129.2, 144.3 (Ph), 177.4 (C=O), 222.2 (C=S).

Synthesis of Poly(2-(dimethylamino)ethyl methacrylate) (PDMA) Macro-CTA via RAFT Solution Polymerization

A round-bottomed flask was charged with 2-(dimethylamino)ethyl methacrylate (DMA; 30.0 g, 191 mmol), PETTC (0.589 g, 1.73 mmol), ACVA (49 mg, 0.173 mmol), and THF (30.0 g) (target DP = 110; macro-CTA/AIBN molar ratio = 10.0). The sealed reaction vessel was purged with nitrogen and placed in a preheated oil bath at 70 °C for 8.5 h. The resulting polymer (DMA conversion = 76%; Mn = 11 800 g mol–1, Mw/Mn = 1.20) was purified by precipitation into excess petroleum ether. The mean degree of polymerization (DP) of this PDMA macro-CTA was calculated to be 94 using 1H NMR spectroscopy by comparing the integrated signals corresponding to the aromatic protons at 7.2–7.4 ppm with those assigned to the methacrylic polymer backbone at 0.4–2.5 ppm.

Synthesis of Poly(2-(dimethylamino)ethyl methacrylate)–Poly(benzyl methacrylate) (PDMA–PBzMA) Diblock Copolymer Nanoparticles via RAFT Dispersion Polymerization in Ethanol

In a typical RAFT dispersion polymerization synthesis conducted at 25% w/w solids, BzMA (2.00 g, 11.4 mmol), PDMA94 macro-CTA (840 mg, 0.057 mmol), and AIBN (1.90 mg, 0.011 mmol; macro-CTA/AIBN molar ratio = 5.0) were dissolved in ethanol (8.53 g). The reaction mixture was sealed in a round-bottomed flask, purged with nitrogen gas for 20 min, and then placed in a preheated oil bath at 70 °C for 24 h. The final monomer conversion was determined by 1H NMR analysis in CDCl3 by integrating the two benzylic protons at 4.9 ppm assigned to PBzMA to the two vinyl protons corresponding to BzMA monomer at 5.2 and 5.4 ppm. In further PDMA–PBzMA diblock copolymer syntheses, the mean DP of the PBzMA block was systematically varied by adjusting the BzMA/PDMA macro-CTA molar ratio.

Copolymer Characterization

Molecular weight distributions of the macro-CTA and the various diblock copolymers were assessed using gel permeation chromatography (GPC). The GPC setup comprised two 5 μm (30 cm) “Mixed C” columns; a WellChrom K-2301 refractive index detector operating at 950 ± 30 nm. THF eluent containing 2.0% v/v triethylamine and 0.05% w/v butylhydroxytoluene (BHT) was used at a flow rate of 1.0 mL min–1. A series of ten near-monodisperse linear poly(methyl methacrylate) standards (Mp ranging from 1280 to 330 000 g mol–1), purchased from Polymer Laboratories (Church Stretton, UK), were employed for calibration using the above refractive index detector. 1H NMR spectra were acquired in either CDCl3 or CD2Cl2 using a Bruker 400 MHz spectrometer (64 scans averaged per spectrum); all chemical shifts are reported in ppm (δ).

DLS measurements were conducted on highly dilute (∼0.10% w/w) copolymer ethanolic dispersions at 20 °C using a Malvern Instruments Zetasizer Nano series instrument equipped with a 4 mW He–Ne laser operating at 633 nm. Scattered light was detected at 173° using an avalanche photodiode detector with high quantum efficiency coupled to an ALV/LSE-5003 multiple tau digital correlator electronics system.

TEM studies were performed at 100 kV using a Phillips CM100 instrument equipped with a Gatan 1 k CCD camera. Initial 25% w/w dispersions were diluted with ethanol at 20 °C to generate 0.20% w/w dispersions. Copper/palladium TEM grids (Agar Scientific, UK) were surface-coated in-house to yield a thin film of amorphous carbon. These grids were then plasma glow-discharged for 30 s to create a hydrophilic surface. Each copolymer dispersion (0.20% w/w, 10 μL) was placed onto a freshly glow-discharged grid for 1 min and then blotted with filter paper to remove excess solution. To stain the deposited nanoparticles, a 0.75% w/w aqueous solution of uranyl formate (10 μL) was placed via micropipet on the sample-loaded grid for 20 s and then carefully blotted to remove excess stain. Each grid was then dried using a vacuum hose.

SAXS data were collected at a synchrotron (Diamond Light Source, station I22, Didcot, UK). A 2D SAXS detector (hybrid photon counting Dectris Pilatus 2M) was used for all experiments. SAXS patterns were recorded over a scattering vector (q) range from 0.025 to 1.65 nm–1 using monochromatic X-ray radiation (wavelength λ = 0.1001 nm), where the length of the scattering vector is given by q = (4π sin θ)/λ and θ is half of the scattering angle. A 2 mm diameter flow-through glass capillary cell was used as a sample holder for all measurements. Scattering data were reduced using Nika SAS data processing macros for Igor Pro (integration, normalization, and background subtraction) and further analyzed using Irena SAS macros within Igor Pro.86 The structural model used for the SAXS data analysis is given in the Supporting Information. This model is based on the analytical expression for a spherical micelle form factor87 and has been reported previously for other PISA formulations.88

Multiangle laser light scattering (MALLS) was used to determine the molecular weight of the PDMA94–PBzMAx diblock copolymer spherical nanoparticles. Measurements were performed at 15°–160° using a DAWN HELIOS II 18 angle laser light scattering instrument (Wyatt Technologies Corp. USA) equipped with a 130 mW linearly polarized GaAs laser operating at 658 nm. Dispersions were diluted with ethanol to afford a copolymer concentration of approximately 0.01% w/v (0.1 mg mL–1) and measured in batch mode. Data were analyzed using ASTRA V software for Windows and extrapolating using the Zimm, Debye and Berry formalisms. Typical plots obtained for PDMA94–PBzMA392 nanoparticles analyzed using each of the three formalisms can be found in the Supporting Information (see Figures S4 and S5).

An Optilab T-rEX differential refractometer was used to determine the dn/dc for dilute copolymer dispersions in ethanol over a concentration range of 0.10–0.50 mg mL–1. Further details are given in the Supporting Information.

Results and Discussion

A PDMA macro-CTA was synthesized by conventional RAFT solution polymerization in THF (see Scheme 1). Following purification, the mean DP of this PDMA macro-CTA was estimated to be 94 by 1H NMR spectroscopy. This PDMA94 macro-CTA was then chain-extended with differing amounts of BzMA via RAFT dispersion polymerization in ethanol at 70 °C to produce a series of PDMA94–PBzMAx diblock copolymer nanoparticles. These syntheses were conducted at 25% w/w solids with the target PBzMA degree of polymerization (DP) (x) being varied between 100 and 1000. Each BzMA polymerization was allowed to proceed for 24 h prior to analysis by 1H NMR, THF GPC, DLS and TEM; the results are summarized in Table 1.

Scheme 1. Synthesis of a Poly(2-(dimethylamino)ethyl methacrylate) (PDMA) Macro-CTA by RAFT Solution Polymerization Followed by Chain Extension with Benzyl Methacrylate (BzMA) via Ethanolic RAFT Dispersion Polymerization To Produce Sterically Stabilized Spherical Nanoparticles.

Scheme 1

Open in a new tab

Table 1. 1H NMR Monomer Conversions, GPC Molecular Weights (Mn), Polydispersities (Mw/Mn), and Intensity-Average Particle Diameters Obtained for PDMA94–PBzMAx Diblock Copolymer Nanoparticles Synthesized at 25% w/w Solids by RAFT Alcoholic Dispersion Polymerization of BzMA Using a PDMA94 Macro-CTA in Ethanol at 70 °C.

target composition BzMA conv (%) actual PBzMA DP Mn Mw/Mn DLS diam (dH)
PDMA94–PBzMA100 100 100 22000 1.34 39.9 (0.02)
PDMA94–PBzMA200 99 198 33200 1.32 47.6 (0.04)
PDMA94–PBzMA300 100 300 44600 1.35 61.5 (0.09)
PDMA94–PBzMA400 98 392 53900 1.34 65.6 (0.02)
PDMA94–PBzMA500 99 495 68300 1.35 73.9 (0.02)
PDMA94–PBzMA600 99 594 75000 1.23 77.9 (0.02)
PDMA94–PBzMA700 95 665 82000 1.28 88.2 (0.07)
PDMA94–PBzMA800 76 608 76900 1.32 83.2 (0.03)
PDMA94–PBzMA900 81 729 88400 1.32 93.2 (0.03)
PDMA94–PBzMA1000 81 810 93900 1.31 98.3 (0.01)
Open in a new tab

Targeting higher PBzMA DPs led to lower BzMA conversions: monomer conversions ≥98% were obtained up to a target DP of 600, but significantly lower conversions were achieved when targeting DPs of 800–1000. In this series of PISA syntheses, the target copolymer concentration was fixed at 25% w/w. Thus, higher DPs for the PBzMA block were targeted by lowering the PDMA macro-CTA concentration relative to the BzMA monomer concentration. Since the macro-CTA/initiator molar ratio was fixed at 5.0, this means that progressively lower initiator concentrations were utilized when targeting longer core-forming blocks. This accounts for the progressively slower rates of BzMA polymerization. THF GPC analyses indicate unimodal molecular weight distributions and minimal contamination of the PDMA94–PBzMAx diblock copolymers with unreacted PDMA94 macro-CTA, which suggests relatively high blocking efficiencies (see Figure 1a). GPC analyses also indicate a monotonic increase in diblock copolymer Mn as higher PBzMA DPs are targeted (see Figure 1b). Furthermore, Mw/Mn values remained below 1.35 in all cases (see Table 1). Representative TEM images recorded for selected dried dispersions are shown in Figure 2. The PDMA94–PBzMAx diblock copolymer nanoparticles invariably exhibited a uniform spherical morphology, as expected given the relatively high stabilizer DP chosen for these syntheses. Mean particle diameters estimated from these TEM images are somewhat smaller than those calculated by DLS. This is partly because the former technique is insensitive to the PDMA stabilizer layer and partly because the latter technique is more biased toward larger particles, since these scatter light much more strongly.

Figure 1.

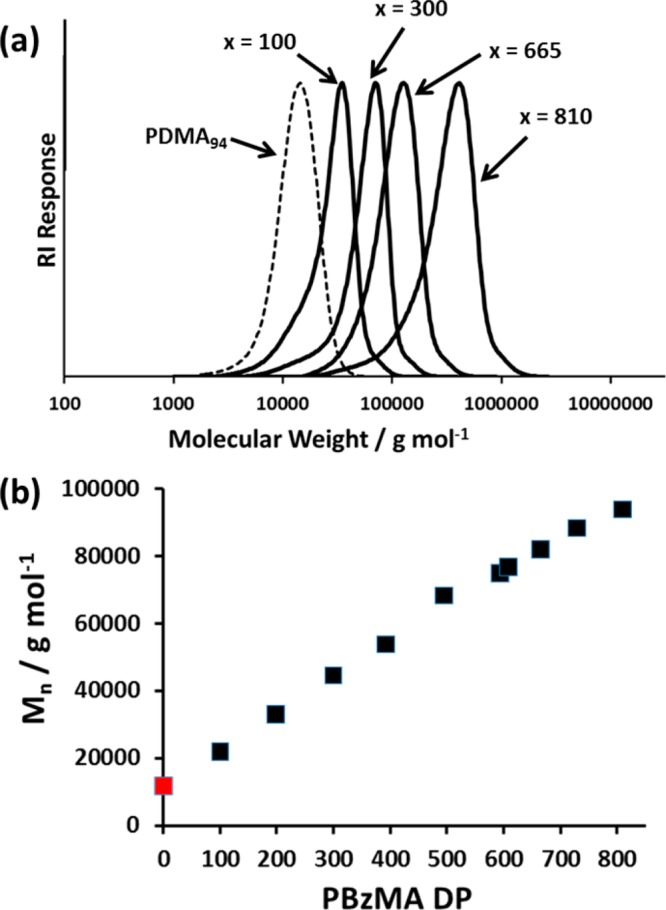
Figure 1

Open in a new tab

(a) THF GPC traces for a series of PDMA94–PBzMAx diblock copolymers showing the increase in molecular weight with increasing PBzMA DP (x). (b) Plot showing the correlation between PDMA94–PBzMAx diblock copolymer Mn (as determined by GPC) and PBzMA DP. The Mn for the PDMA94 macro-CTA (also determined by GPC) is shown in red and explains the nonzero intercept.

Figure 2.

Figure 2

Open in a new tab

Representative TEM images obtained for PDMA94–PBzMAx diblock copolymer nanoparticles prepared at 25% w/w solids via RAFT dispersion polymerization in ethanol at 70 °C. Increasing the target degree of polymerization, x, of the core-forming PBzMA block results in progressively larger spherical nanoparticles. (a) PDMA94–PBzMA100 (b) PDMA94–PBzMA300 (c) PDMA94–PBzMA495 and (d) PDMA94–PBzMA810.

Thus, for any size distribution of finite width, the intensity-average diameter reported by DLS always exceeds the number-average diameter calculated from TEM images. DLS polydispersities remained relatively low (0.01–0.09) in each case, which suggests fairly narrow particle size distributions (see Table 1). Figure 3b shows how hydrodynamic diameter increases during a polymerization by analyzing samples taken during a polymerization targeting a final PBzMA DP of 500.

Figure 3.

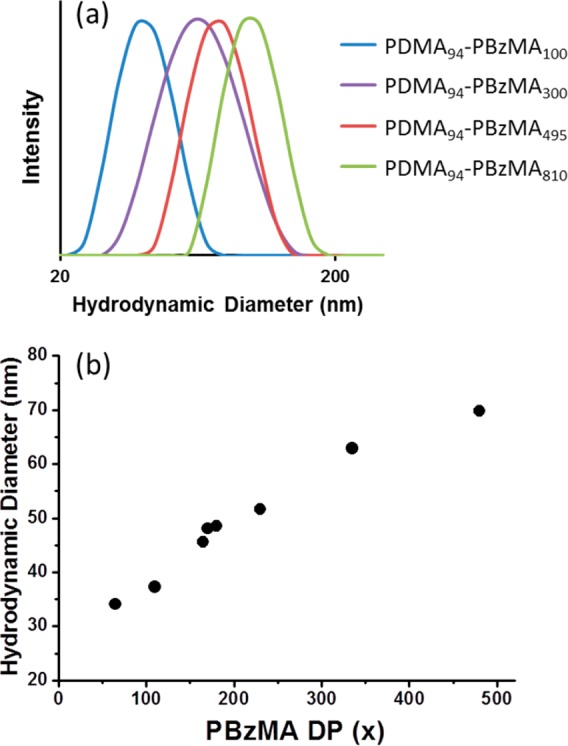
Figure 3

Open in a new tab

(a) Representative DLS curves obtained for PDMA94–PBzMAx diblock copolymer nanoparticles prepared at 25% w/w solids via RAFT dispersion polymerization of BzMA in ethanol at 70 °C. Increasing the target degree of polymerization, x, of the core-forming PBzMA block results in progressively larger spherical nanoparticles. (b) Hydrodynamic diameter of the growing PDMA94–PBzMAx diblock copolymer nanoparticles as determined by DLS measurements conducted on diluted dispersions extracted during a PISA synthesis targeting PDMA94–PBzMA500. The PBzMA DP was determined by 1H NMR analysis of each sample.

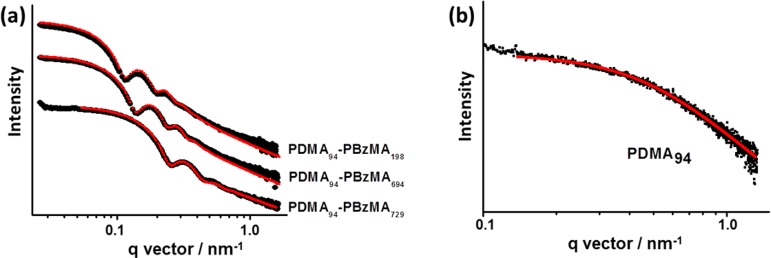
SAXS was utilized to further characterize the series of 10 PDMA94–PBzMAx (x = 100–810) diblock copolymer nanoparticles. Scattering patterns were recorded for 1.0% w/v dispersions in ethanol to minimize interparticle interactions. Representative curves expressed as double-logarithmic plots of I(q) against q are shown for three different PBzMA DPs in Figure 4a; each curve was fitted using a micelle model by assuming a Gaussian particle size distribution (further details are given in the Supporting Information). There are seven parameters in this model: the micelle core radius, Rs, the standard deviation of the core radius σRs, solvent volume fraction in the core, xsol, the radius of gyration of the corona block, Rg, the width of the radial density distribution function of the micelle coronas, s, the weight coefficient of the profile function, a, and the relative copolymer concentration, c. Four of these seven parameters (xsol, Rg, s, and a) were fixed at physically realistic values obtained from independent measurements in order to constrain the fittings. Alternatively, allowing xsol and Rg to vary during fitting led to physically unrealistic (much higher) values for these parameters. Thus, this approach was not explored further. The radius of gyration, Rg, of the PDMA stabilizer block was taken to be 3.2 nm based on SAXS studies of a 1.0% w/v solution of PDMA94 macro-CTA dissolved in ethanol (see Figure 4b). It should be noted that the Rg value obtained for the corona PDMA block is comparable to that calculated assuming theta solvent conditions. The projected contour length of a PDMA monomer is 0.255 nm (two C–C bonds in all-trans conformation). Thus, the total contour length of a PDMA94 block is LPDMA = 94 × 0.255 nm = 24.0 nm. Given a mean Kuhn length of 1.53 nm (based on the known literature value for PMMA89), the PDMA94 radius of gyration is 2.5 nm, Rg = (24.0 × 1.53/6)0.5. Since this estimated Rg is slightly less than the experimental value, this indicates that ethanol is a better-than-theta solvent for PDMA. Assuming that this Rg remains unchanged after chain extension of the macro-CTA with BzMA, the PDMA stabilizer layer thickness is estimated to be s = 2Rg, or 6.4 nm. In practice, the Rg of the PDMA block may well increase somewhat as this stabilizer block adopts a brush-like conformation during the synthesis of the PDMA–PBzMA diblock copolymer nanoparticles, but similar approximations have been previously reported by others to give good model fits.90,91

Figure 4.

Figure 4

Open in a new tab

SAXS patterns recorded for (a) selected PDMA94–PBzMAx spherical nanoparticles in ethanol at 1.0% w/v solids (previously prepared at 25% w/v solids via RAFT dispersion polymerization of BzMA in ethanol at 70 °C using a PDMA94 macro-CTA) and (b) PDMA94 macro-CTA dissolved in ethanol at 1.0% w/v solids. The red lines indicate data fits obtained using (a) a spherical micelle model (eqs S1 and S2) and (b) a Debye function for a Gaussian chain (eq S4).

1H NMR studies of the PDMA94–PBzMAx diblock copolymer nanoparticles diluted in C2D5OD indicated only a very low degree of solvation for the core-forming PBzMA block (5–13%) (see Figure S1 for typical spectra). Thus, when using the SAXS micelle model, the volume fraction of ethanol in the particle core (xsol) was held constant at 0.10 for all copolymer dispersions. The physical significance of the a coefficient is briefly discussed in the Supporting Information. The constrained model with three variable parameters produced good fits to the scattering patterns (see Figure 4a). SAXS analysis indicates that the core radius of the spherical micelles increases when targeting a higher DP for the core-forming PBzMA block (see Table 2). The concomitant increase in the micelle aggregation number is likely to be the result of an increase in the nanoparticle surface area. In this respect, it is noteworthy that the number of chains per unit surface area (Sagg, Table 2) is reduced from an initial value of 0.092 for PDMA94–PBzMA100 to a limiting value of approximately 0.050 when targeting longer PBzMA blocks (x = 495–810). Although not previously reported, both Nagg and Sagg can be calculated from SAXS analysis of PGMA59–(PHPMA91-stat-PDEGMA39)88 and PEG113–PHPMA10092 spheres prepared via PISA. The Sagg values obtained for these two diblock copolymers are 0.08 and 0.07, respectively, which are in close agreement with those observed in the present study.

Table 2. Summary of the Structural Parameters Obtained from SAXS Analysis of PDMA94–PBzMAx Diblock Copolymer Spherical Nanoparticles Prepared via RAFT Dispersion Polymerization of BzMA in Ethanol at 70 °C Using a PDMA94 Macro-CTAa.

copolymer composition Rs (nm) Vmc (nm3) Dtotal (nm) Nagg (chains) Sagg (chains nm–2)
PDMA94–PBzMA100 11.2 36 35.3 145 0.092
PDMA94–PBzMA198 16.4 68 45.5 243 0.072
PDMA94–PBzMA300 21.2 104 55.2 346 0.061
PDMA94–PBzMA392 25.2 133 63.2 452 0.057
PDMA94–PBzMA495 29.0 169 70.8 542 0.051
PDMA94–PBzMA594 31.3 182 75.3 631 0.051
PDMA94–PBzMA608 33.5 195 79.7 723 0.051
PDMA94–PBzMA665 35.9 220 84.5 787 0.049
PDMA94–PBzMA729 38.3 241 89.4 876 0.048
PDMA94–PBzMA810 39.9 266 92.6 899 0.046
Open in a new tab
a

These structural parameters are the micelle core radius (Rs), solvophobic block volume (Vmc), overall particle diameter (Dtotal = Rs + 2Rg), mean aggregation number of copolymer chains per spherical micelle (Nagg), and the number of copolymer chains normalized with respect to the surface area of the spherical nanoparticles [Sagg = Nagg/(4πRs2)]. Further details regarding these SAXS spherical micelle model parameters can be found in the Supporting Information.

The relationship between mean particle diameter (as determined by SAXS, DLS, and TEM) and PBzMA DP (corrected for incomplete monomer conversion, where applicable) is shown in Figure 5. A linear relationship is observed for each technique, and there is a significant difference between the mean diameters reported by SAXS and DLS compared to those estimated from TEM images. Both DLS and SAXS give a diameter ≈10–20 nm larger than TEM, and this difference simply indicates the thickness of the steric stabilizer layer (≈ 2 × 6.4 nm).

Figure 5.

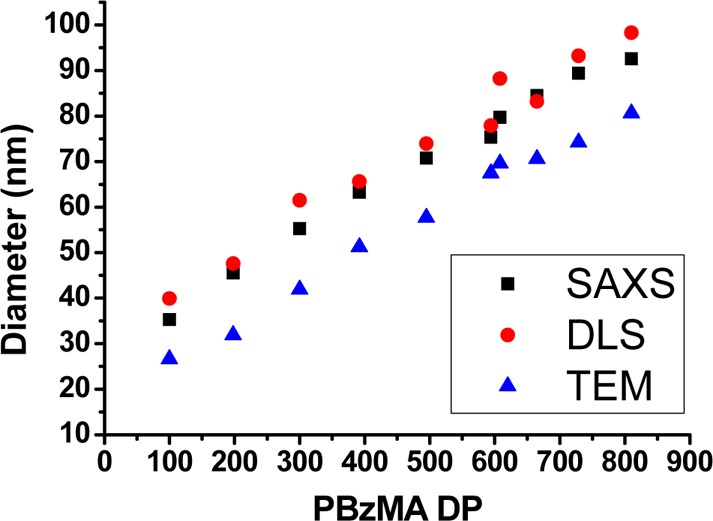
Figure 5

Open in a new tab

Mean particle diameters determined for a series of PDMA94–PBzMAx diblock copolymer nanoparticles as determined by SAXS, DLS, or TEM. Nanoparticles were synthesized at 25% w/w solids via RAFT dispersion polymerization of BzMA at 70 °C in ethanol.

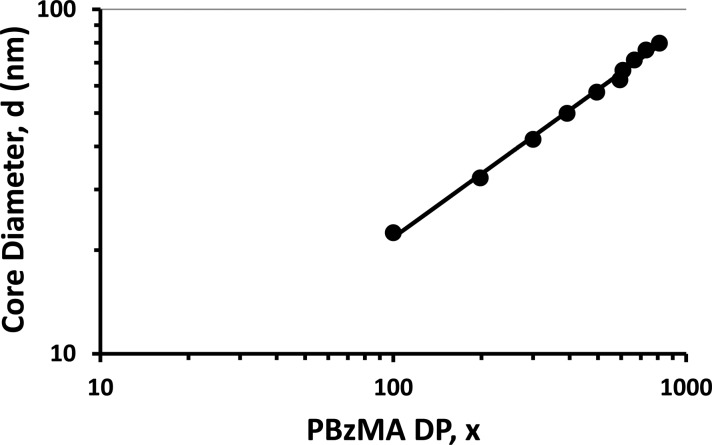
A double-logarithmic plot of the particle core diameter, d, as determined by SAXS, against the mean DP (x) of the core-forming PBzMA block is shown in Figure 6. Using a power law of the form d = kxα enables the exponent α to be determined from the linear gradient. According to the literature,93,94 the value of α indicates how solvated the PBzMA chains are within the particle cores: α = 0.50 for completely collapsed chains and α = 1.00 for fully stretched chains.93−95 From Figure 6 the exponent α is calculated to be 0.62, which suggests that the PBzMA chains are only weakly solvated. This is consistent with 1H NMR studies conducted in C2D5OD and also supports the relatively low solvent volume fraction assumed for the SAXS analysis. Theoretical predictions made for diblock copolymer micelles predict that an α value of 0.66 corresponds to the strong segregation regime.93 Nagarajan and Ganesh96 predicted a system-specific scaling exponent, with α values of 0.70 for polystyrene–polybutadiene block copolymers in n-heptane and 0.73 for poly(ethylene oxide)–poly(propylene oxide) in water. Such values are in relatively good agreement with that calculated for the present PDMA–PBzMA formulation, particularly given that the scaling exponent in this model is known to change depending on the precise nature of the diblock copolymer and solvent.

Figure 6.

Figure 6

Open in a new tab

Relationship between SAXS particle core diameter (d) and PBzMA DP (x) for a series of PDMA94–PBzMAx diblock copolymer nanoparticles. Assuming a power law of the form d = kxα enables an α exponent of 0.62 to be calculated, which suggests a relatively low degree of core solvation and strong segregation between the two blocks.

Multiangle laser light scattering (MALLS) was used to determine the weight-average molecular weight, Mw, of the diblock copolymer nanoparticles. MALLS is the preferred analytical technique for determining the absolute Mw of various soluble polymer chains in solution.97−99 However, this technique requires the differential refractive index (dn/dc) as an input parameter. This was calculated for each diblock composition using a commercial differential refractometer (see Figure S2 for representative raw data and Figure S3 for the corresponding dn/dc values). Some experimental scatter was observed within this dn/dc data set, which may be attributable to varying amounts of residual BzMA monomer in the copolymer dispersions when targeting higher PBzMA DPs (see Table 1). In view of this likely problem, no MALLS analysis was attempted for nanoparticle dispersions containing significant levels of residual BzMA. For the subset of six PDMA94–PBzMAx diblock copolymer nanoparticle syntheses for which at least 98% BzMA conversion was achieved (i.e., for x = 100–600), dn/dc values ranged from 0.1572 to 0.1722 mL g–1 (see Figure S3). This trend was anticipated, since these copolymers contain a progressively greater proportion of PBzMA, which has a higher refractive index than the PDMA block. These dn/dc values were used for the analysis of light scattering data to obtain Mw values for a subset of five PDMA94–PBzMAx diblock copolymer nanoparticle dispersions in ethanol.

The Zimm,100 Debye,101 and Berry102 methods are the most common analytical techniques for determining molecular weights via MALLS. Light scattering data obtained for PDMA94–PBzMAx diblock copolymer nanoparticles were analyzed by each of these three methods; the associated equations can be found in the Supporting Information. It was found that each method gave very similar results for the micelle molecular weight (see Table S1). Taking into consideration the various experimental errors associated with each method,103 it was decided to use the Mw values calculated using the Debye method to determine the corresponding micelle aggregation numbers. The Debye method uses eq 1 to construct a graphical plot of the type shown in Figure 7. Andersson et al. also concluded that this approach was superior to either the Berry or Zimm methods for spheres with mean diameters greater than 50 nm.103

graphic file with name ma-2015-02385c_m001.jpg 1

Here Rθ is the Rayleigh ratio, K is an optical constant, c is the concentration (in mg mL–1) of the scattering species, Mw is the weight-average molecular weight, P(θ) is the particle scattering function, and A2 is the second virial coefficient (in mol mL g–1). Figure 7 shows an example of the data extrapolation using the Debye method to determine Mw from the MALLS data for PDMA94–PBzMA392 (plots for the analysis of the other diblock copolymer nanoparticles can be found in the Supporting Information, see Figure S6).

Figure 7.

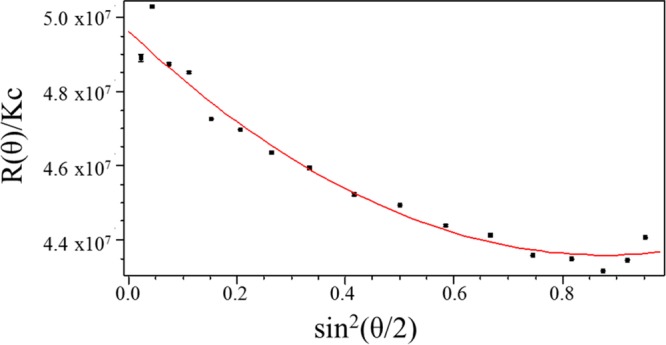
Figure 7

Open in a new tab

Representative MALLS plot using the Debye formalism for light scattering data obtained for PDMA94–PBzMA392 diblock copolymer micelles dispersed in ethanol. The weight-average molecular weight (Mw) of these micelles was determined to be 4.979 × 107 g mol–1, which indicates a micelle aggregation number, Nagg, of 441.

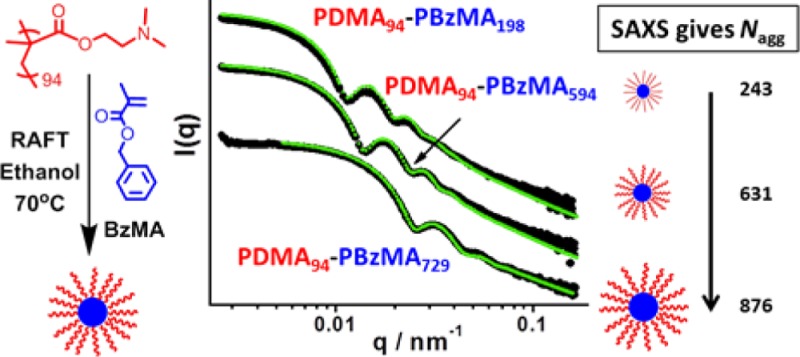
The Mw value for each molecularly dissolved diblock copolymer was determined by multiplying its Mn (determined by end-group analysis by 1H NMR spectroscopy in CDCl3 using the PDMA block as an end-group) by the corresponding Mw/Mn value determined by GPC analysis. The mean aggregation number (Nagg) was then calculated by dividing the Mw determined for the diblock copolymer nanoparticles using MALLS by the Mw calculated for the individual diblock copolymer chains. Both MALLS and SAXS analyses indicate an approximately linear relationship between Nagg and PBzMA DP, with remarkably good agreement being observed between these two techniques (see Figure 8). As far as we are aware, this is the first time that either MALLS or SAXS has been utilized to determine mean aggregation numbers for diblock copolymer nanoparticles prepared via PISA. Inspecting Figure 8, Nagg increases from 145 to 631 as the PBzMA DP is varied from 100 to 594. Conversely, the number of chains per nm2, Sagg, is reduced with increasing PBzMA DP over the same interval, after which it remains fairly constant, whereas Nagg continues to increase (see Table 2). This suggests that immediately after micellar nucleation the stabilizer chains adopt an initial brush-like conformation, but subsequent particle growth leads to a less stretched, mushroom-like conformation as the mean interchain separation distance is gradually increased.

Figure 8.

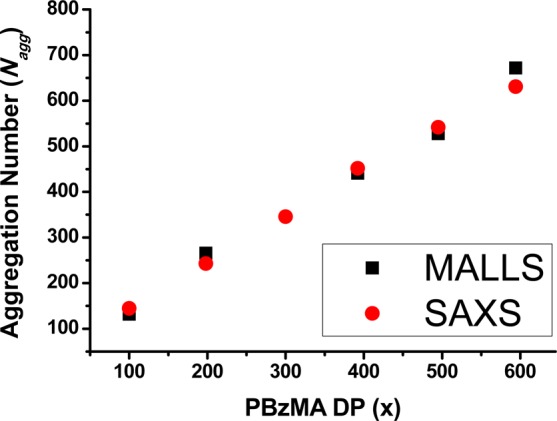
Figure 8

Open in a new tab

Mean aggregation number (Nagg) as determined by either multiangle laser light scattering (MALLS) or small-angle X-ray scattering (SAXS) for a series of PDMA94–PBzMAx diblock copolymer nanoparticles synthesized via RAFT dispersion polymerization of BzMA in ethanol at 70 °C.

In principle, an increase in particle diameter during PISA could be simply the result of an increase in copolymer molecular weight; i.e., the mean aggregation number of the nascent micelles formed during nucleation might remain unchanged throughout the BzMA polymerization. However, Zhang and co-workers have estimated aggregation numbers from a combination of DLS and 1H NMR spectroscopy data obtained during the RAFT dispersion polymerization of styrene conducted in an ethanol/water mixture.104 These results indicate larger aggregation numbers at higher conversions, which suggests that the observed increase in particle size is not simply the result of the linear evolution in copolymer molecular weight that characterizes well-behaved RAFT syntheses. The data shown in Figure 8 were obtained at essentially full conversion for a series of separate PISA syntheses rather than in situ data obtained over a range of monomer conversions. Nevertheless, it suggests that the aggregation number increases during this particular RAFT dispersion polymerization similar to that reported by Zhang and co-workers.104 An increase in Nagg for larger micelles has also been predicted by Nagarajan and Ganesh96 based on the free energy of micellization.

If Nagg does increase during these PISA syntheses, a pertinent question is by which physical mechanism(s) do these diblock copolymer nanoparticles increase their aggregation number? There are two obvious possible mechanisms: (i) exchange of individual copolymer chains between nanoparticles and (ii) sphere–sphere fusion (see Figure 9). Exchange of block copolymer chains between micelles is well-known in the literature, especially for core-forming blocks with low glass transition temperatures (e.g., polybutadiene or Pluronics).105,106 On the other hand, there are various reports of kinetically frozen (non-ergodic) micelles comprising high glass transition temperature blocks such as polystyrene or poly(methyl methacrylate).4,107−111 According to Zhang and co-workers,104 copolymer chain exchange is favored during PISA syntheses because the core-forming block is well-solvated by the unreacted monomer, which should favor high chain mobility. This seems to be a perfectly reasonable hypothesis. Such monomer partitioning has been suggested for various RAFT dispersion polymerization formulations in order to explain the pronounced rate enhancement that is closely correlated with micellar nucleation.56,63,112

Figure 9.

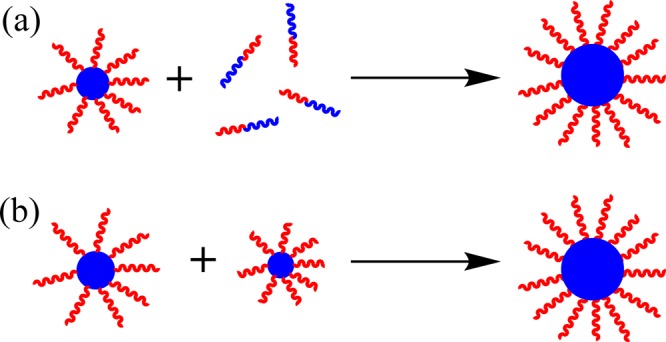
Figure 9

Open in a new tab

Schematic cartoon illustrating the two possible mechanisms proposed for the concomitant increase in micelle diameter and aggregation number during the growth of the core-forming PBzMA block. Mechanism (a) involves exchange of individual copolymer chains between micelles following nucleation, while mechanism (b) involves isotropic sphere–sphere fusion events.

However, Zhang et al. also discount sphere–sphere fusion as a possible mechanism, mainly on the grounds that the DLS size distributions obtained during the PISA synthesis are invariably narrow. We feel that this is a more debatable hypothesis because it is well-known that DLS is a rather low resolution particle size analysis technique.113 The 3D fusion of spheres to produce larger spheres is a widely accepted particle growth mechanism for conventional free radical dispersion polymerization.114 Moreover, we note that a hypothetical sphere–sphere fusion event involving the inelastic collision of two identical spheres each of radius r and mass m to form a single larger sphere of mass 2m only results in a 26% increase in the particle radius. Notwithstanding the argument postulated by Zhang et al.,104 we suggest that isotropic sphere–sphere fusion may well occur during PISA, which would clearly lead to larger nanoparticles with higher Nagg values. After all, it is well-established that anisotropic sphere–sphere fusion occurs if the stabilizer block is relatively short in certain PISA formulations, since this is the mechanism by which diblock copolymer worms are formed.63 More specifically, the latter phenomenon is already known for the PISA synthesis of PDMA31–PBzMAx diblock copolymer worms in ethanol.33 Thus, it does not seem unreasonable that isotropic sphere–sphere fusion events may occur for PDMA94–PBzMAx diblock copolymer formulations, with the longer PDMA stabilizer block ensuring that the final copolymer morphology is restricted to spheres. It is also feasible that both mechanisms shown in Figure 9 may contribute to particle growth during PISA syntheses.

Conclusions

The growth of PDMA94–PBzMAx diblock copolymer nanoparticles prepared via RAFT alcoholic RAFT dispersion polymerization has been studied in detail using a relatively long PDMA macro-CTA as a steric stabilizer. The target DP for the core-forming PBzMA block was varied from 100 to 1000, which enables the final DLS particle diameter to be systematically controlled from 40 to 98 nm. In each case well-defined spherical nanoparticles with narrow size distributions were obtained. Final BzMA conversions were high (>98%) for x = 100–600, but significantly lower conversions were obtained for higher target DPs. SAXS analysis enabled a range of structural parameters to be determined from data fits based on a spherical micelle model, including the overall diameter, the core diameter, the surface area occupied per copolymer chain, and the mean aggregation number (Nagg). A power law plot of core diameter against the DP of the PBzMA block indicated an α exponent of 0.62, which is consistent with the relatively low solvent volume fraction indicated by 1H NMR spectroscopy studies. MALLS was also used to determine Nagg values for selected dispersions, and these data were generally in good agreement with those values calculated from SAXS analysis. For both techniques, Nagg increased linearly with the target DP of the core-forming PBzMA block. This suggests that the particle growth mechanism during PISA involves exchange of individual copolymer chains between monomer-swollen nanoparticles and/or isotropic sphere–sphere fusion events. There is reasonable indirect experimental evidence in the PISA literature to support both mechanisms.

Acknowledgments

DSM Research (Geleen, Netherlands) is thanked for funding a CASE award for E.R.J.’s EPSRC PhD studentship and also for permission to publish this research. S.P.A. acknowledges a five-year ERC Advanced Investigator grant (PISA 320372) and also partial project funding from Stichting Innovatie Alliantie (Foundation Innovation Alliance). The authors are grateful to Diamond Light Source (Didcot, UK) for providing SAXS beam-time and the personnel of I22 station are thanked for help with SAXS experiments.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.macromol.5b02385.

  • Spherical micelle model used for SAXS analysis; differential refractive index measurements; molecular weight determination from MALLS data (PDF)

The authors declare no competing financial interest.

Supplementary Material

ma5b02385_si_001.pdf (747.7KB, pdf)

References

  1. Israelachvili J. N.; Mitchell D. J.; Ninham B. W. J. Chem. Soc., Faraday Trans. 2 1976, 72, 1525. 10.1039/f29767201525. [DOI] [Google Scholar]
  2. Israelachvili J.Intermolecular & Surface Forces, 2nd ed.; Academic Press: London, 1991. [Google Scholar]
  3. Tuzar Z.; Kratochvil P. Adv. Colloid Interface Sci. 1976, 6, 201. 10.1016/0001-8686(76)80009-7. [DOI] [Google Scholar]
  4. Zhang L.; Eisenberg A. Science 1995, 268, 1728. 10.1126/science.268.5218.1728. [DOI] [PubMed] [Google Scholar]
  5. Zhang L.; Eisenberg A. J. Am. Chem. Soc. 1996, 118, 3168. 10.1021/ja953709s. [DOI] [Google Scholar]
  6. Dupont J.; Liu G. J.; Niihara K.; Kimoto R.; Jinnai H. Angew. Chem., Int. Ed. 2009, 48, 6144. 10.1002/anie.200901517. [DOI] [PubMed] [Google Scholar]
  7. Cui H.; Chen Z.; Zhong S.; Wooley K. L.; Pochan D. J. Science 2007, 317, 647. 10.1126/science.1141768. [DOI] [PubMed] [Google Scholar]
  8. Lee J. C. M.; Bermudez H.; Discher B. M.; Sheehan M. A.; Won Y. Y.; Bates F. S.; Discher D. E. Biotechnol. Bioeng. 2001, 73, 135. 10.1002/bit.1045. [DOI] [PubMed] [Google Scholar]
  9. Ghoroghchian P. P.; Frail P. R.; Susumu K.; Blessington D.; Brannan A. K.; Bates F. S.; Chance B.; Hammer D. A.; Therien M. J. Proc. Natl. Acad. Sci. U. S. A. 2005, 102, 2922. 10.1073/pnas.0409394102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Arsenault A. C.; Rider D. A.; Tetreault N.; Chen J. I. L.; Coombs N.; Ozin G. A.; Manners I. J. Am. Chem. Soc. 2005, 127, 9954. 10.1021/ja052483i. [DOI] [PubMed] [Google Scholar]
  11. Chenal M.; Rieger J.; Vechambre C.; Chenal J. M.; Chazeau L.; Creton C.; Bouteiller L. Macromol. Rapid Commun. 2013, 34, 1524. 10.1002/marc.201300410. [DOI] [PubMed] [Google Scholar]
  12. Blanazs A.; Verber R.; Mykhaylyk O. O.; Ryan A. J.; Heath J. Z.; Douglas C. W. I.; Armes S. P. J. Am. Chem. Soc. 2012, 134, 9741. 10.1021/ja3024059. [DOI] [PubMed] [Google Scholar]
  13. Savić R.; Luo L.; Eisenberg A.; Maysinger D. Science 2003, 300, 615. 10.1126/science.1078192. [DOI] [PubMed] [Google Scholar]
  14. Howse J. R.; Jones R. A. L.; Battaglia G.; Ducker R. E.; Leggett G. J.; Ryan A. J. Nat. Mater. 2009, 8, 507. 10.1038/nmat2446. [DOI] [PubMed] [Google Scholar]
  15. Hawker C. J.; Bosman A. W.; Harth E. Chem. Rev. 2001, 101, 3661. 10.1021/cr990119u. [DOI] [PubMed] [Google Scholar]
  16. Matyjaszewski K. Macromolecules 2012, 45, 4015. 10.1021/ma3001719. [DOI] [Google Scholar]
  17. Moad G.; Rizzardo E.; Thang S. H. Aust. J. Chem. 2005, 58, 379. 10.1071/CH05072. [DOI] [Google Scholar]
  18. Moad G.; Rizzardo E.; Thang S. H. Aust. J. Chem. 2012, 65, 985. 10.1071/CH12295. [DOI] [Google Scholar]
  19. Boyer C.; Stenzel M. H.; Davis T. P. J. Polym. Sci., Part A: Polym. Chem. 2011, 49, 551. 10.1002/pola.24482. [DOI] [Google Scholar]
  20. Moad G.; Rizzardo E.; Thang S. H. Aust. J. Chem. 2009, 62, 1402. 10.1071/CH09311. [DOI] [Google Scholar]
  21. Zetterlund P. B.; Aldabbagh F.; Okubo M. J. Polym. Sci., Part A: Polym. Chem. 2009, 47, 3711. 10.1002/pola.23432. [DOI] [Google Scholar]
  22. Li Y.; Armes S. P. Angew. Chem., Int. Ed. 2010, 49, 4042. 10.1002/anie.201001461. [DOI] [PubMed] [Google Scholar]
  23. Charleux B.; D’Agosto F.; Delaittre G. In Hybrid Latex Particles: Preparation With; Van Herk A. M., Landfester K., Eds.; Springer-Verlag: Berlin, 2010; Vol. 233, p 125. [Google Scholar]
  24. Boissé S.; Rieger J.; Belal K.; Di-Cicco A.; Beaunier P.; Li M.-H.; Charleux B. Chem. Commun. 2010, 46, 1950. 10.1039/b923667h. [DOI] [PubMed] [Google Scholar]
  25. Rieger J.; Zhang W.; Stoffelbach F. o.; Charleux B. Macromolecules 2010, 43, 6302. 10.1021/ma1009269. [DOI] [Google Scholar]
  26. Wan W.-M.; Pan C.-Y. Polym. Chem. 2010, 1, 1475. 10.1039/c0py00124d. [DOI] [Google Scholar]
  27. Huang C.-Q.; Pan C.-Y. Polymer 2010, 51, 5115. 10.1016/j.polymer.2010.08.056. [DOI] [Google Scholar]
  28. Zhang X.; Boissé S.; Zhang W.; Beaunier P.; D’Agosto F.; Rieger J.; Charleux B. Macromolecules 2011, 44, 4149. 10.1021/ma2005926. [DOI] [Google Scholar]
  29. Zhang W. J.; D’Agosto F.; Boyron O.; Rieger J.; Charleux B. Macromolecules 2011, 44, 7584. 10.1021/ma201515n. [DOI] [Google Scholar]
  30. Sugihara S.; Blanazs A.; Armes S. P.; Ryan A. J.; Lewis A. L. J. Am. Chem. Soc. 2011, 133, 15707. 10.1021/ja205887v. [DOI] [PubMed] [Google Scholar]
  31. Zhang X.; Rieger J.; Charleux B. Polym. Chem. 2012, 3, 1502. 10.1039/c2py20071f. [DOI] [Google Scholar]
  32. Semsarilar M.; Ladmiral V.; Blanazs A.; Armes S. P. Langmuir 2012, 28, 914. 10.1021/la203991y. [DOI] [PubMed] [Google Scholar]
  33. Semsarilar M.; Jones E. R.; Blanazs A.; Armes S. P. Adv. Mater. 2012, 24, 3378. 10.1002/adma.201200925. [DOI] [PubMed] [Google Scholar]
  34. Jones E. R.; Semsarilar M.; Blanazs A.; Armes S. P. Macromolecules 2012, 45, 5091. 10.1021/ma300898e. [DOI] [Google Scholar]
  35. Blanazs A.; Ryan A. J.; Armes S. P. Macromolecules 2012, 45, 5099. 10.1021/ma301059r. [DOI] [Google Scholar]
  36. Sun J. T.; Hong C. Y.; Pan C. Y. Soft Matter 2012, 8, 7753. 10.1039/c2sm25537e. [DOI] [Google Scholar]
  37. Chiefari J.; Chong Y. K.; Ercole F.; Krstina J.; Jeffery J.; Le T. P. T.; Mayadunne R. T. A.; Meijs G. F.; Moad C. L.; Moad G.; Rizzardo E.; Thang S. H. Macromolecules 1998, 31, 5559. 10.1021/ma9804951. [DOI] [Google Scholar]
  38. Pei Y.; Thurairajah L.; Sugita O. R.; Lowe A. B. Macromolecules 2015, 48, 236. 10.1021/ma502230h. [DOI] [Google Scholar]
  39. Kang Y.; Pitto-Barry A.; Willcock H.; Quan W. D.; Kirby N.; Sanchez A. M.; O’Reilly R. K. Polym. Chem. 2015, 6, 106. 10.1039/C4PY01074D. [DOI] [Google Scholar]
  40. Shi P. F.; Li Q. L.; He X.; Li S. T.; Sun P. C.; Zhang W. Q. Macromolecules 2014, 47, 7442. 10.1021/ma501598k. [DOI] [Google Scholar]
  41. Li Q. L.; Huo F.; Cui Y. L.; Gao C. Q.; Li S. T.; Zhang W. Q. J. Polym. Sci., Part A: Polym. Chem. 2014, 52, 2266. 10.1002/pola.27235. [DOI] [Google Scholar]
  42. Warren N. J.; Armes S. P. J. Am. Chem. Soc. 2014, 136, 10174. 10.1021/ja502843f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Gao C. Q.; Li S. T.; Li Q. L.; Shi P. F.; Shah S. A.; Zhang W. Q. Polym. Chem. 2014, 5, 6957. 10.1039/C4PY01069H. [DOI] [Google Scholar]
  44. Jennings J.; Beija M.; Kennon J. T.; Willcock H.; O’Reilly R. K.; Rimmer S.; Howdle S. M. Macromolecules 2013, 46, 6843. 10.1021/ma401051e. [DOI] [Google Scholar]
  45. Sun J. T.; Hong C. Y.; Pan C. Y. Polym. Chem. 2013, 4, 873. 10.1039/C2PY20612A. [DOI] [Google Scholar]
  46. Mastroianni S. E.; Patterson J. P.; O’Reilly R. K.; Epps T. H. Soft Matter 2013, 9, 10146. 10.1039/c3sm51806j. [DOI] [Google Scholar]
  47. Monteiro M. J.; Cunningham M. F. Macromolecules 2012, 45, 4939. 10.1021/ma300170c. [DOI] [Google Scholar]
  48. Cai W.; Wan W.; Hong C.; Huang C.; Pan C.-Y. Soft Matter 2010, 6, 5554. 10.1039/c0sm00284d. [DOI] [Google Scholar]
  49. Wan W. M.; Sun X. L.; Pan C. Y. Macromol. Rapid Commun. 2010, 31, 399. 10.1002/marc.200900640. [DOI] [PubMed] [Google Scholar]
  50. Pei Y. W.; Dharsana N. C.; Van Hensbergen J. A.; Burford R. P.; Roth P. J.; Lowe A. B. Soft Matter 2014, 10, 5787. 10.1039/C4SM00729H. [DOI] [PubMed] [Google Scholar]
  51. Pei Y. W.; Lowe A. B. Polym. Chem. 2014, 5, 2342. 10.1039/C3PY01719B. [DOI] [Google Scholar]
  52. Gonzato C.; Semsarilar M.; Jones E. R.; Li F.; Krooshof G. J. P.; Wyman P.; Mykhaylyk O. O.; Tuinier R.; Armes S. P. J. Am. Chem. Soc. 2014, 136, 11100. 10.1021/ja505406s. [DOI] [PubMed] [Google Scholar]
  53. Semsarilar M.; Ladmiral V.; Blanazs A.; Armes S. P. Polym. Chem. 2014, 5, 3466. 10.1039/c4py00201f. [DOI] [Google Scholar]
  54. Semsarilar M.; Penfold N. J. W.; Jones E. R.; Armes S. P. Polym. Chem. 2015, 6, 1751. 10.1039/C4PY01664E. [DOI] [Google Scholar]
  55. Houillot L.; Bui C.; Save M.; Charleux B.; Farcet C.; Moire C.; Raust J.-A.; Rodriguez I. Macromolecules 2007, 40, 6500. 10.1021/ma0703249. [DOI] [Google Scholar]
  56. Fielding L. A.; Derry M. J.; Ladmiral V.; Rosselgong J.; Rodrigues A. M.; Ratcliffe L. P. D.; Sugihara S.; Armes S. P. Chemical Science 2013, 4, 2081. 10.1039/c3sc50305d. [DOI] [Google Scholar]
  57. Fielding L. A.; Lane J. A.; Derry M. J.; Mykhaylyk O. O.; Armes S. P. J. Am. Chem. Soc. 2014, 136, 5790. 10.1021/ja501756h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Rieger J.; Stoffelbach F.; Bui C.; Alaimo D.; Jerome C.; Charleux B. Macromolecules 2008, 41, 4065. 10.1021/ma800544v. [DOI] [Google Scholar]
  59. Charleux B.; Delaittre G.; Rieger J.; D’Agosto F. Macromolecules 2012, 45, 6753. 10.1021/ma300713f. [DOI] [Google Scholar]
  60. Cunningham V. J.; Alswieleh A. M.; Thompson K. L.; Williams M.; Leggett G. J.; Armes S. P.; Musa O. M. Macromolecules 2014, 47, 5613. 10.1021/ma501140h. [DOI] [Google Scholar]
  61. Derry M. J.; Fielding L. A.; Armes S. P. Polym. Chem. 2015, 6, 3054. 10.1039/C5PY00157A. [DOI] [Google Scholar]
  62. Valade D.; Jeon Y.; Kessel S.; Monteiro M. J. J. Polym. Sci., Part A: Polym. Chem. 2012, 50, 4762. 10.1002/pola.26300. [DOI] [Google Scholar]
  63. Blanazs A.; Madsen J.; Battaglia G.; Ryan A. J.; Armes S. P. J. Am. Chem. Soc. 2011, 133, 16581. 10.1021/ja206301a. [DOI] [PubMed] [Google Scholar]
  64. Semsarilar M.; Jones E. R.; Armes S. P. Polym. Chem. 2014, 5, 195. 10.1039/C3PY01042B. [DOI] [Google Scholar]
  65. Chambon P.; Blanazs A.; Battaglia G.; Armes S. P. Macromolecules 2012, 45, 5081. 10.1021/ma300816m. [DOI] [Google Scholar]
  66. Sugihara S.; Armes S. P.; Blanazs A.; Lewis A. L. Soft Matter 2011, 7, 10787. 10.1039/c1sm06593a. [DOI] [Google Scholar]
  67. Yang P. C.; Ratcliffe L. P. D.; Armes S. P. Macromolecules 2013, 46, 8545. 10.1021/ma401797a. [DOI] [Google Scholar]
  68. Israelachvili J. N.; Mitchell D. J.; Ninham B. W. J. Chem. Soc., Faraday Trans. 2 1976, 72, 1525. 10.1039/f29767201525. [DOI] [Google Scholar]
  69. Pei Y.; Sugita O. R.; Thurairajah L.; Lowe A. B. RSC Adv. 2015, 5, 17636. 10.1039/C5RA00274E. [DOI] [Google Scholar]
  70. Huo F.; Wang X. H.; Zhang Y. Y.; Zhang X.; Xu J. X.; Zhang W. Q. Macromol. Chem. Phys. 2013, 214, 902. 10.1002/macp.201200640. [DOI] [Google Scholar]
  71. Chaduc I.; Crepet A.; Boyron O.; Charleux B.; D’Agosto F.; Lansalot M. Macromolecules 2013, 46, 6013. 10.1021/ma401070k. [DOI] [Google Scholar]
  72. Semsarilar M.; Ladmiral V.; Blanazs A.; Armes S. P. Langmuir 2013, 29, 7416. 10.1021/la304279y. [DOI] [PubMed] [Google Scholar]
  73. Boissé S.; Rieger J.; Pembouong G.; Beaunier P.; Charleux B. J. Polym. Sci., Part A: Polym. Chem. 2011, 49, 3346. 10.1002/pola.24771. [DOI] [Google Scholar]
  74. Berne B. J.; Pecora R.. Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics; Courier Corporation: 2000. [Google Scholar]
  75. Pecora R.Dynamic Light Scattering: Applications of Photon Correlation Spectroscopy; Springer Science & Business Media: 2013. [Google Scholar]
  76. Reimer L.Transmission Electron Microscopy: Physics of Image Formation and Microanalysis; Springer: 2013; Vol. 36. [Google Scholar]
  77. Patterson J. P.; Robin M. P.; Chassenieux C.; Colombani O.; O’Reilly R. K. Chem. Soc. Rev. 2014, 43, 2412. 10.1039/c3cs60454c. [DOI] [PubMed] [Google Scholar]
  78. Schnablegger H.; Singhthird Y.. The SAXS Guide: Getting Acquainted with the Principles, 3rd ed.; Anton Paar GmbH: 2013. [Google Scholar]
  79. Boldon L.; Laliberte F.; Liu L. Nano Rev. 2015, 10.3402/nano.v6.25661. [DOI] [PMC free article] [PubMed] [Google Scholar]
  80. Guinier A.; Fournet G.. Small-Angle Scattering of X-rays; Wiley: New York, 1955. [Google Scholar]
  81. Pedersen J. S.; Gerstenberg M. C. Macromolecules 1996, 29, 1363. 10.1021/ma9512115. [DOI] [Google Scholar]
  82. Pedersen J. S.; Schurtenberger P. Macromolecules 1996, 29, 7602. 10.1021/ma9607630. [DOI] [Google Scholar]
  83. Forster S.; Burger C. Macromolecules 1998, 31, 879. 10.1021/ma970761v. [DOI] [Google Scholar]
  84. Wyatt P. J. Anal. Chim. Acta 1993, 272, 1. 10.1016/0003-2670(93)80373-S. [DOI] [Google Scholar]
  85. He W. D.; Sun X. L.; Wan W. M.; Pan C. Y. Macromolecules 2011, 44, 3358. 10.1021/ma2000674. [DOI] [Google Scholar]
  86. Ilavsky J.; Jemian P. R. J. Appl. Crystallogr. 2009, 42, 347. 10.1107/S0021889809002222. [DOI] [PMC free article] [PubMed] [Google Scholar]
  87. Pedersen J. S. J. Appl. Crystallogr. 2000, 33, 637. 10.1107/S0021889899012248. [DOI] [Google Scholar]
  88. Cunningham V. J.; Ratcliffe L. P. D.; Blanazs A.; Warren N. J.; Smith A. J.; Mykhaylyk O. O.; Armes S. P. Polym. Chem. 2014, 5, 6307. 10.1039/C4PY00856A. [DOI] [Google Scholar]
  89. Fetters L. J.; Lohse D. J.; Colby R. H. In Physical Properties of Polymers Handbook; Mark J., Ed.; Springer: New York, 2007; p 447. [Google Scholar]
  90. Pedersen J. S.; Gerstenberg M. C. Colloids Surf., A 2003, 213, 175. 10.1016/S0927-7757(02)00511-3. [DOI] [Google Scholar]
  91. Pedersen J. S.; Svaneborg C.; Almdal K.; Hamley I. W.; Young R. N. Macromolecules 2003, 36, 416. 10.1021/ma0204913. [DOI] [Google Scholar]
  92. Warren N. J.; Mykhaylyk O. O.; Mahmood D.; Ryan A. J.; Armes S. P. J. Am. Chem. Soc. 2014, 136, 1023. 10.1021/ja410593n. [DOI] [PMC free article] [PubMed] [Google Scholar]
  93. Leibler L. Macromolecules 1980, 13, 1602. 10.1021/ma60078a047. [DOI] [Google Scholar]
  94. Förster S.; Zisenis M.; Wenz E.; Antonietti M. J. Chem. Phys. 1996, 104, 9956. 10.1063/1.471723. [DOI] [Google Scholar]
  95. Battaglia G.; Ryan A. J. J. Am. Chem. Soc. 2005, 127, 8757. 10.1021/ja050742y. [DOI] [PubMed] [Google Scholar]
  96. Nagarajan R.; Ganesh K. J. Chem. Phys. 1989, 90, 5843. 10.1063/1.456390. [DOI] [Google Scholar]
  97. Tarazona M. P.; Saiz E. J. Biochem. Biophys. Methods 2003, 56, 95. 10.1016/S0165-022X(03)00075-7. [DOI] [PubMed] [Google Scholar]
  98. Burdalo J.; Medrano R.; Saiz E.; Tarazona M. P. Polymer 2000, 41, 1615. 10.1016/S0032-3861(99)00318-3. [DOI] [Google Scholar]
  99. Dayal U.; Mehta S. K. J. Liq. Chromatogr. 1994, 17, 303. 10.1080/10826079408013353. [DOI] [Google Scholar]
  100. Zimm B. H. J. Chem. Phys. 1948, 16, 1099. 10.1063/1.1746740. [DOI] [Google Scholar]
  101. Debye P. J. Phys. Colloid Chem. 1947, 51, 18. 10.1021/j150451a002. [DOI] [PubMed] [Google Scholar]
  102. Berry G. C. J. Chem. Phys. 1966, 44, 4550. 10.1063/1.1726673. [DOI] [Google Scholar]
  103. Andersson M.; Wittgren B.; Wahlund K.-G. Anal. Chem. 2003, 75, 4279. 10.1021/ac030128+. [DOI] [PubMed] [Google Scholar]
  104. Su Y.; Xiao X.; Li S.; Dan M.; Wang X.; Zhang W. Polym. Chem. 2014, 5, 578. 10.1039/C3PY00995E. [DOI] [Google Scholar]
  105. Won Y. Y.; Davis H. T.; Bates F. S. Macromolecules 2003, 36, 953. 10.1021/ma021439+. [DOI] [Google Scholar]
  106. Michels B.; Waton G.; Zana R. Langmuir 1997, 13, 3111. 10.1021/la962084o. [DOI] [Google Scholar]
  107. Tian M. M.; Qin A. W.; Ramireddy C.; Webber S. E.; Munk P.; Tuzar Z.; Prochazka K. Langmuir 1993, 9, 1741. 10.1021/la00031a022. [DOI] [Google Scholar]
  108. Baines F. L.; Armes S. P.; Billingham N. C.; Tuzar Z. Macromolecules 1996, 29, 8151. 10.1021/ma960740l. [DOI] [Google Scholar]
  109. Gao Z. S.; Varshney S. K.; Wong S.; Eisenberg A. Macromolecules 1994, 27, 7923. 10.1021/ma00104a058. [DOI] [Google Scholar]
  110. Schillen K.; Yekta A.; Ni S. R.; Winnik M. A. Macromolecules 1998, 31, 210. 10.1021/ma971289g. [DOI] [Google Scholar]
  111. Gohy J. F.; Willet N.; Varshney S.; Zhang J. X.; Jerome R. Angew. Chem., Int. Ed. 2001, 40, 3214.. [DOI] [PubMed] [Google Scholar]
  112. Semsarilar M.; Ladmiral V.; Blanazs A.; Armes S. P. Langmuir 2012, 28, 914. 10.1021/la203991y. [DOI] [PubMed] [Google Scholar]
  113. Growney D. J.; Fowler P. W.; Mykhaylyk O. O.; Fielding L. A.; Derry M. J.; Aragrag N.; Lamb G. D.; Armes S. P. Langmuir 2015, 31, 8764. 10.1021/acs.langmuir.5b01651. [DOI] [PubMed] [Google Scholar]
  114. Paine A. J. Macromolecules 1990, 23, 3109. 10.1021/ma00214a013. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ma5b02385_si_001.pdf (747.7KB, pdf)

Articles from Macromolecules are provided here courtesy of American Chemical Society

RESOURCES