Bringing Model-Based Prediction to Oncology Clinical Practice: A Review of Pharmacometrics Principles and Applications

Oncology is an area with significant unmet medical needs, with new therapies and more effective use of current therapies needed. Pharmacometrics combines principles from pharmacology, statistics, and computational modeling to support drug development and optimize the use of available drugs. Population models can be often developed using routinely collected medical record data. The application of such models in the clinical setting by close collaboration between physicians and pharmacometricians is encouraged.

Abstract

Despite much investment and progress, oncology is still an area with significant unmet medical needs, with new therapies and more effective use of current therapies needed. The emergent field of pharmacometrics combines principles from pharmacology (pharmacokinetics [PK] and pharmacodynamics [PD]), statistics, and computational modeling to support drug development and optimize the use of already marketed drugs. Although it has gained a role within drug development, its use in clinical practice remains scarce. The aim of the present study was to review the principal pharmacometric concepts and provide some examples of its use in oncology. Integrated population PK/PD/disease progression models as part of the pharmacometrics platform provide a powerful tool to predict outcomes so that the right dose can be given to the right patient to maximize drug efficacy and reduce drug toxicity. Population models often can be developed with routinely collected medical record data; therefore, we encourage the application of such models in the clinical setting by generating close collaborations between physicians and pharmacometricians.

Implications for Practice:

The present review details how the emerging field of pharmacometrics can integrate medical record data with predictive pharmacological and statistical models of drug response to optimize and individualize therapies. In order to make this routine practice in the clinic, greater awareness of the potential benefits of the field is required among clinicians, together with closer collaboration between pharmacometricians and clinicians to ensure the requisite data are collected in a suitable format for pharmacometrics analysis.

Introduction

Pharmacometrics, defined as “the science of developing and applying mathematical and statistical methods to (a) characterize, understand, and predict a drug’s pharmacokinetic and pharmacodynamic behavior, (b) quantify uncertainty of information about that behavior, and (c) rationalize data-driven decision making in drug development process and pharmacotherapy” [1], has evolved substantially in the past four decades. The discipline is focused on the development of pharmacokinetic, pharmacodynamic, and disease progression models and integrates principles from the fields of pharmacology and statistics for a better understanding of the in vivo drug effect supporting drug development and personalized medicine. In vitro and in vivo preclinical and clinical data can be combined in a multiscale pharmacometrics analysis for several purposes, including, among others, drug monitoring, optimizing dose-finding studies, and determination of suitable biomarker endpoints and optimum dose regimens. The use of pharmacometrics in pharmaceutical companies has increased noticeably since the beginning of the field [2]. In addition, regulatory agencies have highlighted the use of pharmacometrics and model-based approaches to improve drug development by reducing the attrition rate [3]. Although pharmacometrics has gained a role within drug development, its use in routine clinical practice remains scarce, and it is still considered a niche discipline. A general awareness is lacking among clinical scientists regarding the field and its potential added value. In a recent opinion article, Bonate argued that pharmacometricians have not sufficiently communicated their message outside of the field [4].

Pharmacometrics has been used in a wide variety of therapeutic areas, including oncology, which has presented unique challenges for the field: (a) the characterization of the dose-response relationship can be difficult because of the ethical requirement to minimize the number of patients dosed at subtherapeutic doses and because cancer therapies generally have narrower therapeutic indexes; (b) regarding the characterization of pharmacodynamic relationships, efficacy studies are complicated by the frequent lack of placebo data; and (c) the quantification of overall survival (reference standard to assess clinical outcomes of late phase clinical trials) requires a large number of patients and long study durations.

The aim of the present work was to bring to the attention of the oncology community the quantitative model-based approach and to consider applying pharmacometrics principles to routinely collected clinical data. To accomplish our goal, we present the quantitative framework in a comprehensive manner, reducing the mathematical and statistical aspects to a minimum. We first present the main concepts and nomenclature in pharmacometrics, pharmacokinetics (PK), and pharmacodynamics (PD). The concepts of disease progression, turnover processes, and how to link biomarkers and tumor size with clinical outcomes are then discussed, under the successful paradigm of model-based drug development. Finally, guidance on data collection is provided to physicians and clinical scientists to enable and facilitate population PK/PD modeling.

Pharmacometrics

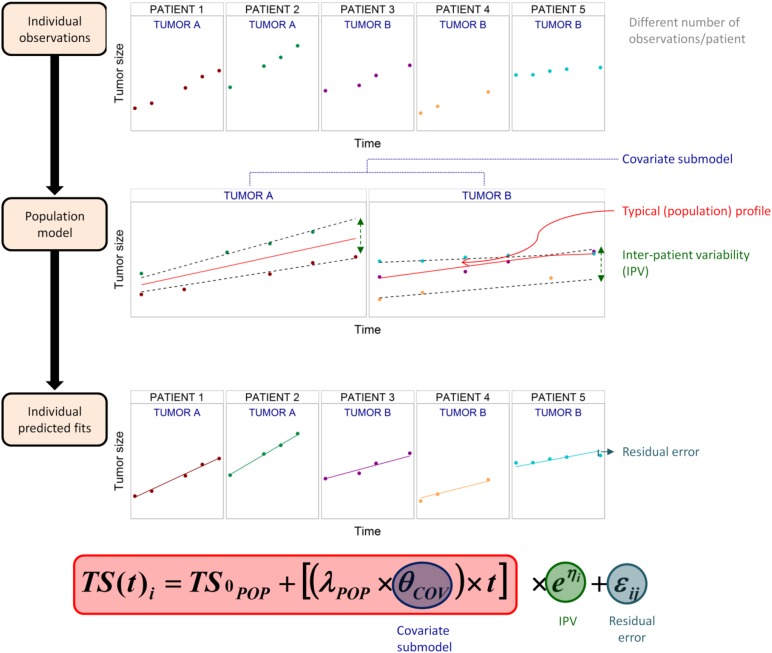
It is well accepted that humans, even with the same disease status and physiological characteristics, can exhibit quite different levels of response to the same treatment, a phenomenon known as interpatient variability (IPV). Thus, population models that can explain and quantify variability in the underlying physiological processes (PK, PD, and/or disease related) would be ideally suited to describe the variation in individual responses. Population models are primarily developed using mixed-effect models, in which the data from all individuals are analyzed simultaneously [5–7]. The term “mixed-effects” means that both fixed effects (i.e., population level trends) and random effects (i.e., individual-level parameters) are described simultaneously. Fixed effects refer to the parameters governing the nonlinear population level trends (i.e., the typical individual), and random effects include IPV (i.e., differences observed between patients), interoccasion variability (i.e., difference observed between study occasions), and residual error (i.e., difference between the observation and the individual prediction). Because these random effects are inferred from the individual data and estimated population level trends, the population approach is especially applicable to sparse data sampling situations. IPV can be, in part, explained by predictors that are specific to each patient. In the pharmacometrics field, such predictors are termed covariates. Covariates can be classified as intrinsic factors, such as age, sex, race, and genetic information (i.e., polymorphisms), or extrinsic factors, such as concomitant medication, smoking status, or primary tumor location, and so forth. Covariates can be continuous (e.g., age), dichotomous (e.g., sex), or categorical (e.g., race). The influence of covariate information on the model is handled via fixed-effects parameters and, as such, a mixed-effect model is composed of a structural model, a random effects model (which includes IPV and residual error), and a covariate model. Figure 1 shows these basic concepts of the population approach described.

Figure 1.

Fundamental principles of the population approach. A population model to describe the typical time course of tumor size and quantify the interpatient variability is built based on infrequent and sparse observations from patients. In this example, the covariate, the tumor type (A or B), was found to explain some of the interpatient variability and therefore was included in population model, leading to one typical population tumor size profile for each type of tumor (θ_COV). The population approach also allows one to describe the individual profiles (η_i represents the deviation from the typical tumor profile and it is assumed to follow a normal distribution with a mean of 0 and variance of ω²) and to quantify the remaining residual error at each j observation for i patient (difference between individual prediction and real observation explained by ε_i, which is a random variable from a normal distribution with a mean of 0 and variance of σ²).

Abbreviations: IPV, interpatient variability; λ_POP, typical value representing disease (tumor) progression; TS_0POP, typical value of tumor size at baseline; TS(t)_i, tumor size at t measurement time for the ith individual.

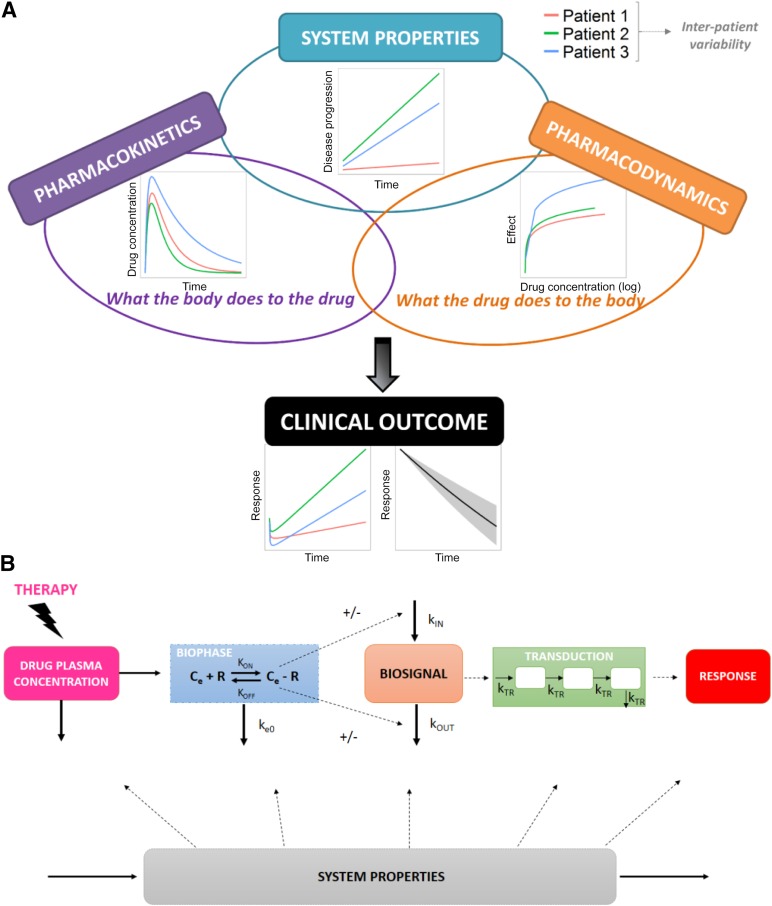
Figure 2A represents the main components of disease progression and PK/PD models, and in Figure 2B, the main components involved in the drug response are presented. In the following sections, we detail the concepts involved in such models and provide different examples of the models applied to oncology.

Figure 2.

Principal data and model components under the context of the pharmacokinetic/pharmacodynamic/disease progression modeling. (A): Schematic representation of the main components involved in disease/pharmacokinetics (PK)/pharmacodynamics (PD) models. (B): Components of PK/PD models, including distribution to a biophase, receptor binding, modulation of the K_in or K_out of a biosignal and transduction of the response. System properties can influence the response by affecting some or all of these processes involved in the dynamics of the in vivo drug response. Adapted from Jusko et al. [92].

Abbreviations: C_e, effect site concentrations; C_e-R, drug-receptor complex; K_in, production; K_off, dissociation rate constant; K_on, association rate constant; K_out, elimination; KTR, rate constant of transit; R, receptor.

Pharmacokinetics

The absorption, distribution, and elimination (metabolism and excretion) (ADME) of a drug is the set of processes describing the movement of the drug through the body. These processes are studied by a branch of pharmacology, namely PK. One of the primary goals of population PK modeling is the characterization of variability in drug exposure, an important driver of the clinical response to a treatment.

Two main approaches are available to analyze PK data: (a) noncompartmental analysis (NCA), in which descriptive statistics, such as the area under the plasma drug concentration versus time curve, maximum drug concentration (C_MAX), or time at which C_MAX is achieved (T_MAX), are summarized directly from observed individual profiles (which implies rich sampling strategies to achieve reliable estimates of the descriptors); and (b) model-based compartmental analysis, in which the parameters governing underlying pharmacokinetic processes are inferred from the data.

NCA does not require any particular interpretation of the data (i.e., model assumptions) and therefore is a quick model-independent method of obtaining summary PK metrics. During the course of studies, such metrics can provide useful measure of approximate exposure; however, this approach presents several limitations. First, because the only output is descriptive statistics of the data, the approach is not suitable for obtaining insights into the underlying physiological processes. Second, the prediction of untested dosing regimens is not generally possible if the PK data are nonlinear or the model or frequency of administration is to be adjusted, because summary statistics will generally only be valid for that particular dose study.

NCA does not require any particular interpretation of the data (i.e., model assumptions) and therefore is a quick model-independent method of obtaining summary PK metrics.

In contrast to NCA, model-based analysis quantifies primary physiologically related parameters (i.e., first order rate constant of absorption, apparent volume of distribution, and total clearance), enabling the use of model-based simulations to predict drug concentrations under different dosing administrations without the need to administer the drug to patients.

Compartmental model-based analysis assumes that the organism is split in one or more compartments, which, in general, does not represent a real body entity. A compartment is considered a simplified representation of regions of the body in which the drug is absorbed, distributed, metabolized, or eliminated. For example, most published PK models include a central compartment, which has been assumed to be representative of systemic drug concentrations and represents system circulation and well-perfused organs with nonrestrictive membranes, and peripheral compartments, which often represent extravascular less-perfused regions with restricted distribution membranes. Typically, the well-mixed assumption is used, which assumes rapid distribution of a drug within a compartment. Absorption, reversible transfer of a drug between compartments, and irreversible loss owing to elimination are processes that generally follow first order kinetics, characterized by the corresponding first order rate constant. Clearly, this approach represents an approximation of the complex processes involved; however, these models have proved sufficient to characterize drug exposure and establish therapeutic dosing regimens for many compounds. In addition, the ability of population PK modeling to explain the variability in PK with intrinsic and extrinsic covariates means that drug exposure can also be predicted in different target populations. Compartmental PK models are, therefore, useful tools to help determine the right dose in the right population.

In some cases, for which a more granular prediction of drug exposure in tissue is required, physiologically based pharmacokinetic (PBPK) models can be used. In these models, compartments are chosen to represent the specific organs and/or tissues involved in all relevant ADME processes. PBPK models can also be useful to predict human PK from preclinical to clinical settings [8]. An oncology-based example is the PBPK model developed by Tsukamoto et al. to describe the kinetics of capecitabine and its metabolites [9]. This model integrated tissue-specific information about metabolic enzyme activity between tumor and normal cells from in vitro data and enabled the prediction of the therapeutic index in terms of exposure in target organs and toxicity in off-target organs (i.e., gastrointestinal tract toxicity). A weakness of this approach is that PBPK models typically involve many more model parameters than can be estimated using data generated in clinical studies. Their wider use has therefore been primarily at the preclinical stage [10].

The classic characterization of the PK of small molecules has generally assumed that binding of the drug to its biological target site (i.e., receptor, enzyme, transporter) will not influence systemic exposure, because the fraction of drug binding to the target is usually small [11]. However, biological compounds (e.g., therapeutic proteins, monoclonal antibodies) bind with higher affinity to their biological target; thus, in many instances, the disposition of the drug-target complex can influence overall the PK of the drug, as first described by Levy in 1994 as “target-mediated drug disposition” (TMDD) [12]. In oncology, therapies based on monoclonal antibodies (mAbs) have noticeably increased in the past 20 years for a wide variety of cancers, which has led to significant improvement in patient outcomes [13]. Generally, mAbs bind with high affinity to their target, exhibiting nonlinear TMDD. In 2001, Mager and Jusko [14] proposed a general mechanistic-based model, which combines classic PK aspects with drug-target binding thermodynamics to characterize the nonlinear PK of three drugs exhibiting TMDD. Since then, this model (either the full model or model approximations) has been applied to a wide range of biological compounds in all therapeutic areas, including oncology, such as with cetuximab in patients with squamous cell carcinoma of the head and neck [15] or with bevacizumab and VEGF₁₆₅ in colorectal cancer patients [16]. As biotechnology techniques evolve and we progress to higher affinity compounds, TMDD will remain an important part of PK characterization.

The use of drug combinations, involving mAbs and/or classic cytotoxic agents, represents a key aspect in therapeutic strategies within oncology, although it also involves additional challenges regarding the optimal dose and schedule. PK/PD models can also be used to guide dose and regimen selection using isobolograms, which relate in vivo exposure to antitumor activity [17].

Pharmacodynamics

Although PK is often defined as “what the body does to the drug,” PD can be defined as “what the drug does to the body” [11]. Derendorf et al. defined PD as “a broad term that is intended to include all of the pharmacological actions, pathophysiological effects, and therapeutic responses, both beneficial and adverse, of the active drug ingredient, therapeutic moiety, and/or its metabolite(s) on various system of the body from subcellular effects to clinical outcomes” [18]. PD models allow us to establish the link between the drug concentration and the response and, therefore, together with PK models, aid us in understanding and predicting the time course of the pharmacological response. Response endpoints can involve biomarkers, surrogate endpoints, and clinical outcomes and can be obtained as continuous measurements, graded categories, or categorical measures, as discussed in the following sections.

Biomarker Models

The Biomarkers Definition Working Group of the NIH has provided a precise definition of a biomarker as “a characteristic that is objectively measured and evaluated as an indicator of normal biologic processes, pathogenic processes, or pharmacologic responses to a therapeutic intervention” [19]. Biomarkers can potentially be used at different phases of drug development (from preclinical to after commercialization) for different purposes.

In oncology, many biomarkers are modulated by the total tumor load, enabling assessment of treatment efficacy and prediction of disease progression. The motivation to find predictive biomarkers has been driven by the need to identify which patients are responding to treatment and which have a high risk of relapse. Once a biomarker has been confirmed to strongly correlate with outcome, it constitutes a powerful tool to support personalized disease monitoring.

Traditionally, the predictive performance of biomarkers has been assessed by conventional statistics (i.e., noninferential statistics), given a single time point, and generally dichotomizing a continuous variable (e.g., baseline value, thresholds above the normal range) [20–22]. However, such an analysis can hide relationships between the biomarker response and clinical outcome by not accounting for indirect and time-dependent relationships, giving the impression of poor predictivity. Recently, the current alternative use of mathematical models to describe biomarker dynamics and their potential utility was reviewed by Almufti et al. [23]. In addition, Almufti et al. advocated the use of nonlinear mixed-effect (NLME) modeling to “standardize biomarker kinetic analysis methodologies to ensure the optimized development of novel serum biomarkers and avoid the pitfalls of traditional markers.”

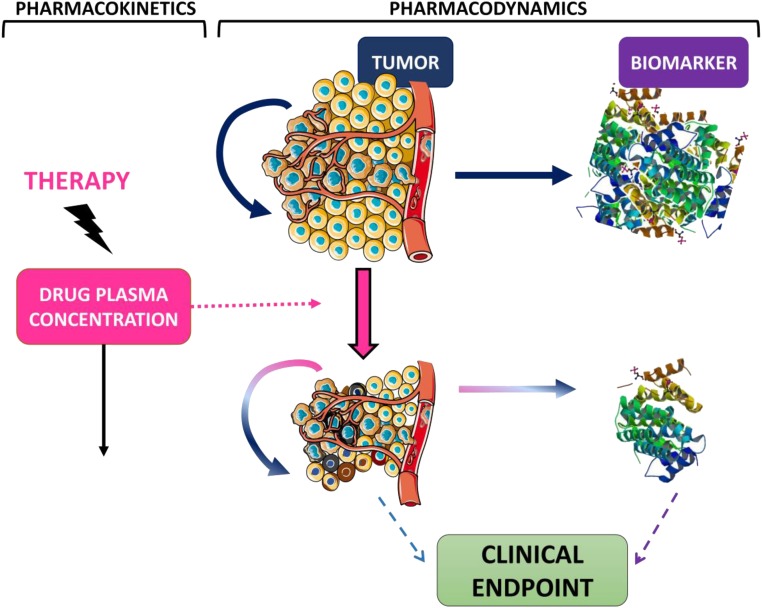
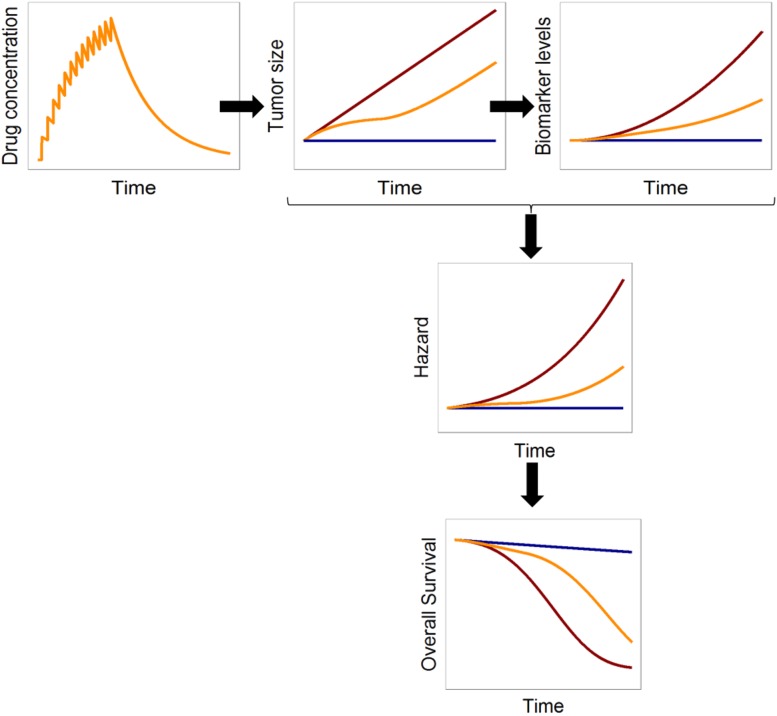
Ideally, the assessment of whether a biomarker can potentially be used as a surrogate biomarker should involve a mechanistic PK/PD/disease progression model to describe the relevant pathways linking the target to the outcome. Such models have typically required multiple tumor size observations, which are often not available. Because the models are mathematical in nature, suitable approximations can be used to describe the main processes (e.g., tumor proliferation, biomarker production and elimination) in those cases in which frequent tumor size measurements are not available. Semimechanistic models to characterize biomarker dynamics are often described using indirect response models [24]. An indirect response model assumes that the synthesis and degradation of the biomarker are governed by a zero and first order rate process, respectively. Modulation of either synthesis or elimination can therefore translate into delays in the response. In oncology, it can be assumed that tumor cells release tumor markers to the circulating blood; therefore, the presence of a tumor in the body will indirectly upregulate biomarker production. In contrast, decreased tumor proliferation in response to target site drug exposure will lead to a potentially delayed decrease in tumor biomarker levels. A schematic representation of these model assumptions is shown in Figure 3. To build intuition in that model, Figure 4 shows the predicted time courses of drug effects, tumor size, and biomarker levels for an example compound. Examples in published studies of similar structural models include a model for cancer antigen (CA)-125 in patients with recurrent ovarian cancer [25]. Wilbaux et al. showed that the model could be used to relate the predicted change in CA-125 to progression-free survival (PFS) and advocated the use of CA-125 as an early predictive biomarker. Although tumor size measurements should always be included, if available, frequently, they are not reported in routinely collected clinical data. In their absence, a model-based framework can describe the total tumor load using an unobserved variable (underlying nonobserved variable). Buil-Bruna et al. used an unobserved variable to describe the tumor size in patients with small-cell lung cancer patients, which upregulated synthesis of lactate dehydrogenase and neuron-specific enolase [26]. Treatment exposure modulated the tumor size, which, in turn, resulted in downregulation of the biomarker levels. They showed that using NLME models to analyze multiple nonvalidated biomarkers could provide sufficient information to predict the disease time course and could be used to identify, at the end of first-line treatment, patients at risk of relapse in follow-up visits [27]. Similarly, Wilbaux et al. used an unobserved variable, influenced by chemotherapy and hormonal therapy, to describe prostate-specific antigen (PSA) and circulating tumor cell dynamics in prostate cancer patients [28]. This approach could be useful when developing semimechanistic models and longitudinal tumor size data are not available. However, care should be taken when using unobserved variables to ensure the model parameters remain identifiable to avoid biased predictions.

Figure 3.

Example of a pharmacokinetics/pharmacodynamics model. Chemotherapy is given by bolus and is assumed to show one-compartment pharmacokinetics. Drug concentrations lead to tumor shrinkage either by inhibiting tumor proliferation or enhancing tumor death. Tumor cells upregulate biomarker synthesis. The tumor and/or biomarker can be predictors of the clinical endpoint (i.e., overall survival). Tumor picture modified from Servier Medical Art, http://www.servier.com, Creative Commons Attribution 3.0 Unported License.

Figure 4.

Example of simulated relationships between time profiles of drug concentration, tumor size, biomarker levels, and hazard (constant) and overall survival in the absence of disease progression (blue lines), presence of disease progression (red lines), and presence of disease progression and treatment (yellow lines). The response model assumes that the biomarker levels are constant over time in the absence of tumor (blue lines). In the presence of tumor, which is assumed to grow linearly (red lines) and to upregulate synthesis of the biomarker, the biomarker levels will increase over time (red lines). With treatment (i.e., drug effect), which we assume decreases the proliferation rate of the tumor, the tumor increases more slowly and therefore the total tumor size is decreased (yellow line). Consequently, synthesis of the biomarker is reduced, and we can observe lower biomarker levels (yellow) compared with those without treatment. The hazard risk is assumed to be constant over time and increased by the ratio between the tumor size and biomarkers levels with respect to baseline. Overall survival is obtained by integrating the hazard over time.

Population biomarker models using NLME have recently been reviewed [23, 29]. The different strategies have included the use of the kinetic modeling of human chorionic gonadotropin as an early predictor of methotrexate resistance in patients with low-risk gestational trophoblastic neoplasia [30], mathematical models to personalize vaccination regimens to stabilize PSA levels [31, 32], and the use of soluble VEGF receptor 3 to monitor adverse events and clinical response in patients with imatinib-resistant gastrointestinal stromal tumors [33, 34].

Tumor Size Models

Tumor size can be considered the reference standard biomarker for clinical outcomes in oncology, because it forms the basis of several clinical endpoints (i.e., disease-free survival, overall response rate, time to progression, PFS, and time to treatment failure) [35]. In the past decade, several population models describing the time course of tumor size have been developed to characterize drug efficacy and predict the long-term clinical outcomes. Two recent studies have reviewed population tumor size modeling [36, 37]. In brief, tumor growth inhibition (TGI) models are based on ordinary differential equations, in which the change in tumor size is explained by net tumor growth minus tumor shrinkage due to drug efficacy. Tumors are often assumed to grow linearly, exponentially, or following a Gompertz function. Tumor shrinkage is related to some measure of drug exposure, such as the drug concentration, area under the curve, or trough drug levels. These models have been used to derive tumor metrics (e.g., change in tumor size 6 or 8 weeks after the start of treatment or the time to tumor growth or regrowth), which are useful to forecast the clinical outcome. For example, Claret et al. showed that estimated tumor size dynamics from a phase II clinical trial was capable of predicting overall survival in a phase III study for colorectal cancer patients [38].

The current research in pharmacometrics applied to tumor growth analysis and its predictive capability for disease progression and/or survival is full of challenges and opportunities, including, for example, (a) analysis of the time course of individual lesions stratified by the affected organ compared with the pooled analysis of all tumor lesions; (b) proper accounting of the appearance of new lesions; and (c) translation of data generated in the preclinical arena to generate useful information in the clinical setting. The latter represents one of the objectives within the Drug and Disease Model Resources (DDMoRe) consortium, which was founded in 2011 by the Innovative Medicines Initiative Joint Undertaking [39] as a “European public-private partnership to address a lack of common tools, languages, and standards for modelling and simulation to improve model-based knowledge integration” [40]. In brief, the DDMoRe consortium has been created to improve the quality, efficiency, and cost-effectiveness of drug development and marketed drugs through the development of an open access library consisting of pharmacometrics models, an interoperability framework, and a training program for pharmacometricians.

Although TGI models rely on continuous longitudinal tumor size measurements, clinical routine practice mainly uses the RECIST criteria to assess clinical efficacy [41]. The use of RECIST has several disadvantages, and several investigators have argued that it should not be the basis of the response assessment [42, 43]. RECIST categorizes continuous tumor size measurements from a limited number of lesions into four different grades, which leads to a loss of information. In addition, RECIST was originally defined mainly for cytotoxic agents, for which drug efficacy has always involved a reduction in tumor size. Therefore, the RECIST criteria currently cannot be considered as the exclusive or most appropriate method to evaluate efficacy in patients receiving immunotherapy, antiangiogenic therapy, or targeted therapy. With such therapies, prolonged stabilization of the disease can be expected. It has been reported that the tumor response obtained with immune checkpoint inhibitors (e.g., ipilimumab, pembrolizumab, nivolumab) can be preceded by initial disease progression according to RECIST [44–49]. Because of these weaknesses, we strongly recommend clinicians to report, in addition to the RECIST category, continuous tumor size measurements from computed tomography scans. Nevertheless, predictive PK/PD models can also be constructed using noncontinuous response variables as demonstrated in the next sections.

Analysis of continuous oncology data (i.e., biomarker measurements, tumor size) often also involves informative withdrawal and censored information; therefore, a simultaneous analysis of continuous and noncontinuous data could be required [50]. Joint analyses have been a scarce practice until recently owing to a lack of software implementation availability and validated techniques for proper evaluation of model performance.

Adverse Event Models

Although targeted agents are aimed to target a specific molecular defect, and, in principle, toxicity is expected to be reduced compared with traditional chemotherapy, it is still common for patients to experience adverse events. Dose reductions to alleviate toxicity risks the occurrence of disease relapse later. Model-based assessment of efficacy and toxicity can provide the quantitative methods to predict and balance the expected risk with the expected benefit.

Model-based assessment of efficacy and toxicity can provide the quantitative methods to predict and balance the expected risk with the expected benefit.

The primary toxicities of concern include hematological and organ-specific toxicities. Regarding hematological toxicities, Friberg et al. [51] developed a model to characterize the time course of myelosuppression, which has been widely used to model this type of toxicity, including neutropenia, leukopenia, and thrombocytopenia [52–60]. This model is considered empirically accurate and physiologically plausible (i.e., semimechanistic) and has been applied to different chemotherapy drugs given alone and in combination. However, discrepancies in the parameter estimates obtained with different administration routes [61] or with different dosing regimens [62] have suggested that some issues regarding the underlying physiological mechanism could be revised. Recently, Mangas-Sanjuan et al. [63] proposed an expanded version of this model by including one additional physiological process resembling cell cycle dynamics (Fig. 5), which allows the description of neutropenic effects after different dosing schedules of diflomotecan. Just as TGI models are insufficiently supported by tumor size measurements categorized according to RECIST, toxicity models should be informed by continuous, rather than categorical, data. Although grade IV toxicities can be life-threatening and, therefore, should be the endpoints to quantify and predict, such predictors can be obtained easily from continuous data (e.g., neutrophil count), and the data set should include all information. Other hematological drug toxic effects that have been characterized and quantified via NLME modeling include pharmacodynamic models to describe the hemoglobin time course (i.e., anemia) [64], alterations in liver enzymes such as alanine aminotransferase [65], and disruptions in blood pressure [33, 66, 67].

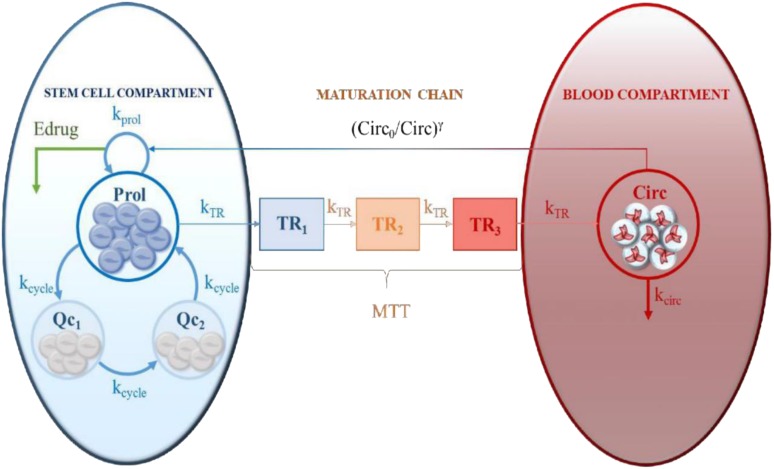
Figure 5.

Semimechanistic cell cycle-based pharmacokinetics/pharmacodynamics model of chemotherapy-induced neutropenic effects. This model assumes that (a) within the stem cell compartment proliferative and quiescent cells coexist, and cell cycle dynamics are described by first order processes governed by k_cycle, (b) quiescent cells comprise two compartments (Qc1 and Qc2), and (c) only cells in the proliferative condition are sensitive to drug effects and capable of following the maturation chain. The rest of the model assumptions are equal to those in the model reported by Friberg et al. [51]. Reprinted from [63] with permission.

Abbreviations: γ, parameter governing the rebound; Circ, circuating neutrophils; Circ₀, circulating neutrophils at baseline; Edrug, drug effects; k_circ, rate constant of neutrophil degradation; k_prol, rate constant of proliferation; k_TR, rate constant of transit; MTT, mean transition time; Prol, proliferative cells; Qc, quiescent cells; TR1-3, transit compartments.

Among organ-specific adverse events, gastrointestinal and cutaneous toxicities are prominent. These findings are often quantified using grades, because objective direct measurement is not always possible. In these cases, NLME models can use discrete data models, for example, logistic regression/proportional odds, in which the probability of a certain grade is correlated with a measure of exposure (e.g., diarrhea grades [68] and asthenia, nausea, and vomiting grades [69]). Additionally, Markov models can be used if the toxicity grades between the nearby time points are correlated, which Hénin et al. illustrated for hand-and-foot syndrome [70]. Because these models are ultimately empirical, caution should be taken when predicting the response to untested dosing regimens.

Clinical Endpoint Models

Traditionally, overall survival (OS) has been characterized using an empirical Kaplan-Meier estimator, in which the Cox proportional hazard test or log-rank test is used to compare different Kaplan-Meier curves (i.e., placebo vs. treatment groups). In the pharmacometrics field, parametric time-to-event (TTE) models are often preferred [71]. These models allow the identification of the underlying hazard function (i.e., the instantaneous event rate), from which the survival function (i.e., probability of remaining in the study) can be easily obtained by integrating the hazard with respect to time [72]. The main advantage of these types of models is that in addition to obtaining hazard ratios between two groups, simulations can be performed in different scenarios, because the underlying hazard distribution is estimated. In addition, both time variant and invariant covariates can be easily introduced in the hazard function to explain some of the variability in OS. Although TTE models are called “overall survival” models, they are also applicable to describing other events, including progression-free survival, time of disease progression occurrence, time to complete response, and time to a toxicity event.

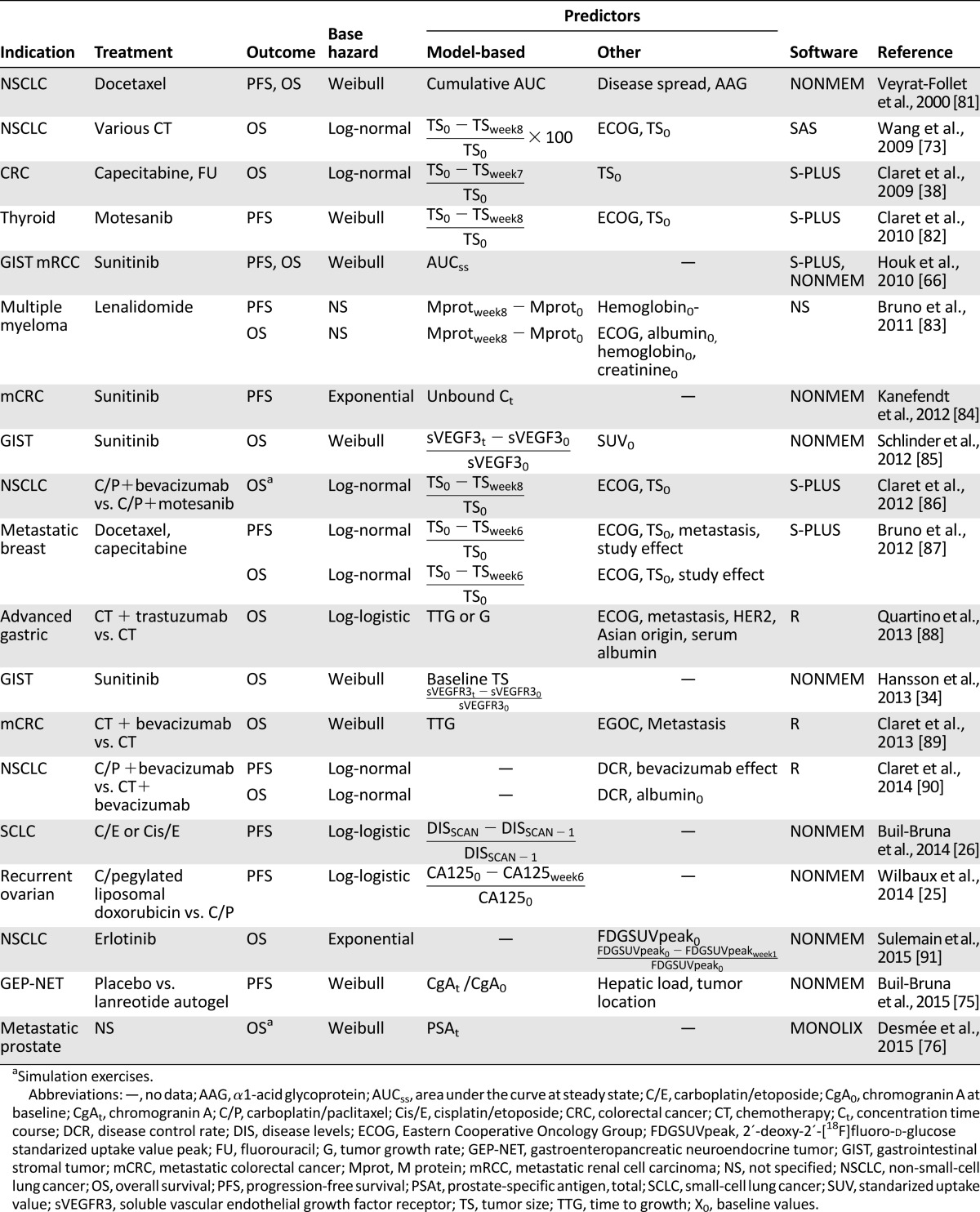
Table 1 shows a representative example of the use of parametric TTE analyses and population PK/PD modeling in several cancer indications under a variety of treatments. As shown in Table 1, the distributions most used to describe the underlying baseline hazard are the Weibull, log-normal, and log-logistic distributions. Since the first published model linking model-based tumor size as a predictor of survival [73], the number of publications including such analyses has increased notably in the past 5 years. Most reported studies used variables based on predefined time points as predictors, such as the change in tumor size after 6–8 weeks of treatment or the time to tumor growth. However, such predictors have some limitations in their ability to accurately predict outcome, as previously discussed by others [36, 74]. In addition, such static early predictors are unlikely to predict PFS and OS outcomes in treatments that involve different timeframes for the onset of effect, such as immune modulators. Therefore, the validity of these predictors needs to be evaluated further in such cases. The use of a predictor’s full-time course to dynamically predict the disease time course and therefore outcome, shown recently for gastrointestinal stromal tumors [34], gastroenteropancreatic neuroendocrine tumors [75], and metastatic prostate cancer [76], has been recommended to overcome some of these limitations and also to enable simulations of different scenarios [74]. However, as discussed in previous sections, the optimal incorporation of the course of time variant predictors into this quantitative framework requires a joint modeling exercise.

Table 1.

Examples of parametric time-to-event models and population PK/PD modeling

Role of PK Information in PK/PD Analysis

The quantification of PK/PD relationships allows us to infer the underlying causal chain among the dose-concentration-effect such that predictions of response in new and existing patients can be made. However, PK samples (i.e., drug concentrations in plasma) are not always collected during clinical practice; therefore, alternative strategies have been developed to overcome that design limitation, allowing the construction of PK/PD models.

Use of Previous Knowledge

During the past decades, population PK models have been developed for most chemotherapy agents. Zandvliet et al. reviewed published clinical population analyses of anticancer drugs [77]. These models can be used to simulate individual profiles for the studied population. Details of the dosing regimen, including dosage amounts and actual times of dosing, are required. Individual covariate information (e.g., serum creatinine, body weight) can also be used to refine the drug time course predictions when the covariates are present in the model.

K_kinetic-PD Model

A K_kinetic-PD model approximates the kinetics of a drug with a one-compartment PK model, with the dosage form treated as a bolus administration. The compartment is treated as an unobserved variable informed only by the pharmacodynamic data. This approach allows PK-driven time dependencies between drug administration and target site exposure to be accounted for empirically and without PK data [78].

Data Sets

Throughout the present review, we have highlighted the importance of obtaining, when possible, longitudinal, continuous data measurements, rather than categories or data summaries. Another aspect that is fundamental and often ignored by nonpharmacometricians is to collect the exact time of dosing administration and exact time of observation. Actual dosing and observation times can differ significantly from the planned times, and this can affect the analysis and interpretation of the results. Similarly, the actual dosage amounts (and durations in the case of infusions) rather than the planned amounts should be recorded for each patient to allow accurate characterization of the dose-exposure-response relationship. One advantage of using NLME models is that the observation times and dosing amounts do not necessarily need to be at the same time for all patients to generate robust models.

In addition, regarding time-to-event models, one point to consider when constructing data sets is that the information should include the actual time of the start of the study and the actual time and nature of the events. Monitored event types that had not occurred in individuals by the end of the study (or observational period) should be recorded as censored information.

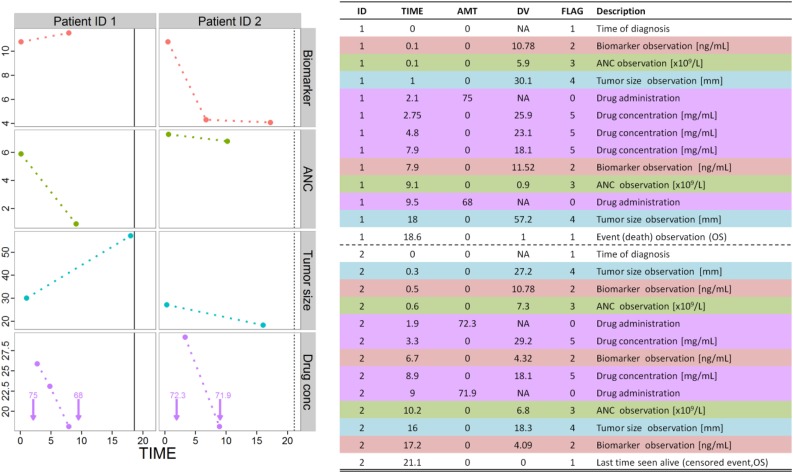
Figure 6 shows an example of a data set compatible with common NLME tools [79, 80], which we hope will provide a template to ensure sufficient information is collected to enable pharmacometrics model building to occur. This example includes data sufficient for a complete PK/PD analysis of biomarker levels, tumor size measurements, and overall survival.

Figure 6.

Example of available data corresponding to patients 1 and 2. Note that the drug amount and frequency of observations differ between the two patients. Models are developed to describe the DV dynamics for each type of observation (i.e., FLAG). Patient 1 had died (DV = 1 and FLAG = 1, vertical solid line in lower panel) and patient 2 was alive at the end of the period studied (DV = 0 and FLAG = 1, vertical dashed line in lower panel). Vertical arrows in the lower panel correspond to the time of drug administration, and numbers indicate the drug amount administered. Abbreviations: AMT, amount (mg); ANC, absolute neutrophil count; DV, dependent variable (i.e., observation); FLAG, identification column; ID, patient identification; NA not applicable; OS, overall survival.

Conclusion

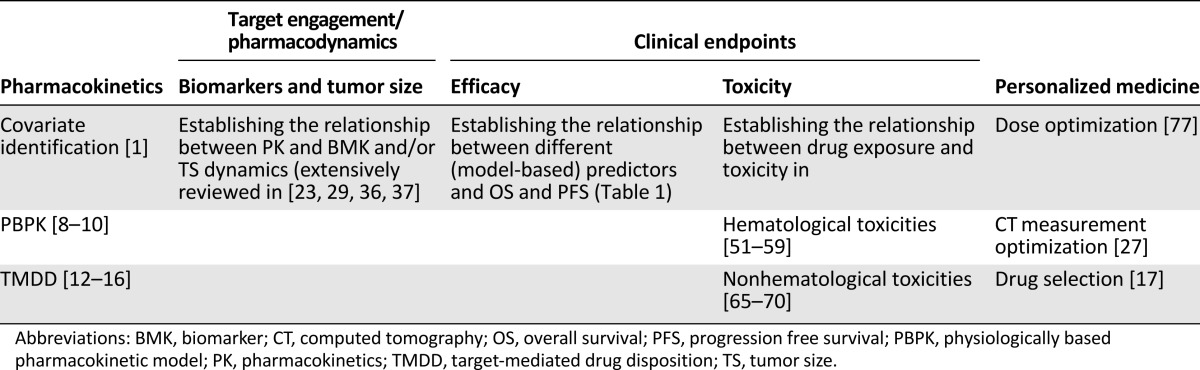
The main objective of the present review was to highlight the potential benefits of pharmacometrics techniques, not only as a valuable component within the current paradigm of model-based drug development, but also as a successful and accessible aid for clinical scientists in the optimization of current oncology therapies. We have discussed the basic concepts and provided examples of existing PK/PD models in use in the field of oncology. These have been summarized in Table 2. Integrated population PK/PD/disease progression models provide a powerful tool to predict outcomes such that the right dose can be given to the right patient to maximize drug efficacy and reduce drug toxicity. As such, pharmacometrics is ideally suited to offering patients “personalized medicine.”

Table 2.

Summary of pharmacometrics applications

We have shown that pharmacometrics tools can be applied using routinely collected medical record data, without the financial burden of a formal study and without compromising a clinician’s primary objective of treating patients. Therefore, we encourage the application of population models in hospitals by generating close collaborations between physicians and pharmacometricians.

Author Contributions

Conception/design: Núria Buil-Bruna, José-María López-Picazo, Salvador Martín-Algarra, Iñaki F. Trocóniz

Data analysis and interpretation: Núria Buil-Bruna, Iñaki F. Trocóniz

Manuscript writing: Núria Buil-Bruna, José-María López-Picazo, Iñaki F. Trocóniz

Final approval of manuscript: Núria Buil-Bruna, José-María López-Picazo, Salvador Martín-Algarra, Iñaki F. Trocóniz

Disclosures

The authors indicated no financial relationships.