Abstract
Huntington disease (HD) is caused by an expanded HTT CAG repeat that leads in a length-dependent, completely dominant manner to onset of a characteristic movement disorder. HD also displays early mortality, so we tested whether the expanded CAG repeat exerts a dominant influence on age at death and on the duration of clinical disease. We found that, as with clinical onset, HD age at death is determined by expanded CAG-repeat length and has no contribution from the normal CAG allele. Surprisingly, disease duration is independent of the mutation’s length. It is also unaffected by a strong genetic modifier of HD motor onset. These findings suggest two parsimonious alternatives. (1) HD pathogenesis is driven by mutant huntingtin, but before or near motor onset, sufficient CAG-driven damage occurs to permit CAG-independent processes and then lead to eventual death. In this scenario, some pathological changes and their clinical correlates could still worsen in a CAG-driven manner after disease onset, but these CAG-related progressive changes do not themselves determine duration. Alternatively, (2) HD pathogenesis is driven by mutant huntingtin acting in a CAG-dependent manner with different time courses in multiple cell types, and the cellular targets that lead to motor onset and death are different and independent. In this scenario, processes driven by HTT CAG length lead directly to death but not via the striatal pathology associated with motor manifestations. Each scenario has important ramifications for the design and testing of potential therapeutics, especially those aimed at preventing or delaying characteristic motor manifestations.
Introduction
Huntington disease (HD [OMIM: 143100]) is a dominantly inherited disorder1, 2 whose characteristic neurological symptoms result from an expanded CAG repeat of greater than 35 units in the huntingtin-encoding sequence of HTT (OMIM: 613004).2, 3, 4, 5 It has long been known that the age of onset of HD motor symptoms is negatively correlated with the length of the expanded HTT CAG repeat,2, 6, 7, 8, 9 but the question of whether the length of the normal CAG allele also plays a role in determining onset remained uncertain until recently. Two publications reported that a complex interaction between the CAG-repeat lengths of the normal and expanded alleles played a significant role in determining an individual’s age at motor onset.10, 11 However, a more comprehensive study recently uncovered issues with the statistical analysis of the correlation between age at onset and the CAG repeat, developed a route to robust statistical analysis of such data, and concluded that the length of the normal CAG allele has no significant impact, either alone or in interaction with the expanded CAG repeat, on age at motor onset.12 Consistent with this conclusion, age at motor onset of HD subjects with two expanded HTT alleles is determined by the longer of their two CAG repeats and is similar to that of subjects with a single mutant allele of comparable size.12 Thus, the expanded HTT CAG repeat triggers HD pathogenesis (defined here as the underlying abnormal process that leads to pathology, defined in turn as disease phenotype), and the length of the mutation largely determines the rate of the pathogenic process that leads to clinical motor signs in a fully dominant fashion. The motor disturbances are thought to result from dysfunction and degeneration of neurons in the striatum, which, according to post-mortem pathological examination of brains, is also correlated with CAG-repeat length.13, 14, 15, 16 The relationship among CAG-repeat length, age at motor onset, and inferred rate of striatal pathology has informed the potential for treatment by HTT silencing, given that the lack of an effect of either the normal allele or an interaction between normal and expanded alleles implies that one can target the single mutant copy of HTT in the striatum to delay onset and worsening of motor symptoms.
Another important HD feature that has been reported to show a strong correlation with expanded CAG-repeat length is age at death.6, 9, 17 Compared to the general population, HD subjects show early mortality,18 but it is not clear whether this reflects a direct or an indirect effect of mutant huntingtin on vital processes. In principle, early mortality in HD could be due to neurodegenerative changes in the regions most associated with HD clinical symptoms or, alternatively, to some other independent effect of mutant huntingtin.16, 19, 20, 21, 22, 23, 24, 25 In order to inform potential treatments for preventing or delaying disease onset and early death of HD subjects, we performed a comprehensive statistical assessment of the impact of the expanded and normal CAG repeats on determining the timing of death and the relationship between this timing and the prior onset of diagnostic motor signs, an interval that we define as “disease duration.” Our findings suggest that the expanded CAG repeat has a dominant effect on age at death, as it does on age at motor onset, and that the normal CAG allele has no impact. However, they also indicate a surprising lack of contribution of either the mutant or the normal HTT allele to the duration of clinical disease from onset to death. We propose two alternative explanations for the relationship between motor onset and death and show that they have quite different implications for designing therapies in HD.
Material and Methods
Study Subjects
We analyzed DNA samples from 4,448 HD heterozygous subjects with either a known age at onset of motor signs and/or age at death: 4,161 subjects had age-at-onset data, 1,165 subjects had age-at-death data, and 878 subjects had both. Subjects with a recorded age at death were primarily identified from HD brain banks: the Harvard Brain Tissue Resource Center (McLean Hospital, Belmont), the New York Brain Bank (Columbia University, New York City), the National Neurological Research Specimen Bank (Department of Veterans Affairs Medical Center, Los Angeles), and the Harvard NeuroDiscovery Center Advanced Tissue Resources Core (Massachusetts General Hospital, Charlestown). HD subjects with a recorded age at onset were described previously.12 The lengths of HTT CAG repeats for each DNA sample were determined by a PCR assay against sequenced-allele size standards as described previously.26 Primary analysis was based on HD subjects who carried one expanded HTT CAG repeat (CAG > 35). The means of expanded and normal CAG-repeat lengths of our study subjects were 45.1 (range = 36–120; median = 44) and 18.45 (range = 9–35; median = 18), respectively. Age at death, age at onset of motor signs, and disease duration (the difference between age at onset and age at death) were the primary dependent variables in the statistical models. Ages at onset were estimated by a clinician rater, reported by a family member, and/or self-reported. When multiple ages at onset were available, priority was given first to the expert rater’s estimate and then to the family member’s report. In addition to analyzing ascertained subjects for onset and/or death, we also independently analyzed observational cohort data from the European Huntington’s Disease Network (EHDN) Registry to construct survival models. CAG repeats of EHDN samples were determined by the same method as above. The familial relationships of our samples were not known because our de-identified data lacked pedigree information. Because related individuals tend to cause statistical inflation, the lack of significant influence in our results would not change dramatically if familial relationships could be included in the model. The study was approved by the Partners HealthCare institutional review board.
Statistical Analysis of Age at Death
We previously described a robust statistical-analysis method for age at onset of motor signs12 and used it in this study for the analysis of age at death. Natural-log-transformed age-at-death data from 1,165 subjects were modeled as a function of (1) expanded CAG length, (2) normal CAG length, and (3) gender (Table 1, model 3). In addition, we performed quality-control (QC) analyses to identify a subset of data that met the requirements of linear-regression modeling, including (1) normality, (2) equal variance, and (3) absence of disproportionately influential observations. First, we evaluated data normality for each CAG-repeat length and found that the distribution of age at death approximated a normal distribution for subjects with 40–52 CAG repeats, representing 90.3% of the samples (Figure S1). Variance in age at death was not constant but rather was larger for subjects with smaller expanded CAG repeats, potentially implicating a greater role for modifiers in this range (Figure S2A). We addressed the non-constant variance by log transformation of the data (as shown in Figure S2B), which also rendered the relationship between expanded CAG-repeat length and age at death close to linear (Figure S2C). Lastly, we identified which outliers to exclude by using a standard interquartile-outlier-identification method (Figure S2C). In brief, for each CAG-repeat size, we sorted age-at-death data to obtain an interquartile value (i.e., the difference between the 75th and 25th percentile data points). Then, 1.5× the interquartile value was added to the 75th percentile data point and subtracted from the 25th percentile data point. Any age-at-death values outside of this range were identified as potential outliers. These procedures resulted in a subset of 1,019 subjects (87.5% of all those with age-at-death data) for a robust analysis of models that included gender along with both expanded and normal CAG length (model 1) and only expanded CAG length (model 2), as summarized in Table 1. In addition, to evaluate the effect of outlier removal, we fitted model 3 to all data without excluding any samples. We evaluated the model behavior by checking (1) residuals versus fitted values, (2) quantile-quantile plots, and (3) residuals versus leverage (Figure S3).
Table 1.
Summary of Statistical Models for Testing Effects of CAG-Repeat Sizes on Age at Death in HD
| Sample Size |
Estimate (p Value) |
Adjusted R2 | |||
|---|---|---|---|---|---|
| Expanded CAG | Normal CAG | Gender (Male) | |||
| Model 1 | 1,019 | −0.056722 (<2E−16) | −0.001636 (0.134840) | −0.026275 (0.000288) | 66.9% |
| Model 2 | 1,019 | −0.056723 (<2E−16) | not tested | −0.026240 (0.000296) | 66.9% |
| Model 3 | 1,165 | −0.0363498 (<2E−16) | −0.00259 (0.06007) | −0.0288 (0.00157) | 74.8% |
Two different statistical models were constructed to test the impact of CAG repeats on age at death of HD subjects by using QC-passed data points. Natural-log-transformed age at death was modeled as a function of expanded CAG, normal CAG, and gender with the use of QC-passed data points (model 1). After the normal CAG was confirmed to have no effect on age at death, model 2 was constructed with only the expanded CAG repeat and gender. Finally, for evaluating the impact of samples excluded in models 1 and 2, model 3 was fitted to data including all HD subjects with age-at-death data. Interaction between expanded and normal CAG repeats was not significant and was therefore excluded from modeling.
We also performed three additional tests to establish the robustness of the conclusion from Table 1. (1) Using the minimal adequate model based on only QC-passed data (Table 1, model 2), we calculated the residual of age at death for all subjects, including outlier subjects, with 40–52 CAGs (total of 1,052 subjects) and subsequently used it as a dependent variable to test the effect of outliers previously excluded via our QC pipeline (Figure S4). (2) We compared the distributions of normal CAG length between HD subjects who represent the top and bottom 10% of residual age-at-death values (105 individuals each; Figure S5). (3) To determine the effects of samples excluded from the model because of repeats longer than 52 CAGs, we constructed an independent model by using only the 97 HD subjects excluded from the analysis (Figure S6). None of these additional tests supported any effect of the normal CAG-repeat length on age at death.
Statistical Analysis of Disease Duration
Eight hundred and seventy-eight HD subjects were fully ascertained for both age at motor onset and age at death. For each subject, we calculated disease duration by subtracting age at onset from age at death. For these fully ascertained subjects, the range, mean, SD, and median of duration values were 0–46, 15.4, 6.8, and 15 years, respectively. Approximately 72.9% of the HD subjects had duration values within 1 SD of the mean (8.6–22.2 years), forming a non-normal distribution with a sharp peak and long tails, indicating positive excess kurtosis and prompting our non-parametric statistical analysis. Because duration values of 10–20 years were highly enriched in the data regardless of the length of expanded CAG repeats, QC analyses that were applied to age-at-death data and age-at-onset data could not identify a subset of data points that were normally distributed (Figures S7 and S8). Therefore, instead of using parametric regression models, we performed non-parametric modeling (i.e., generalized additive model and Spearman’s rank-correlation analysis) to test the significance of CAG-repeat lengths and gender on duration. In addition, we compared disease duration of HD subjects with expanded CAG < 43 to that of HD subjects with expanded CAG > 45 to test whether HD subjects with longer expanded CAG repeats display a shorter duration than do HD subjects with shorter expanded CAG repeats. In a conceptually similar manner, we compared expanded CAG-repeat lengths of HD subjects with the top 10% duration values to those of HD subjects with the bottom 10% of duration values to test whether extreme-duration subjects vary by expanded CAG-repeat length. Finally, we compared disease duration of adult-onset HD subjects (age at onset > 20 years) to that of juvenile-onset HD subjects (age at onset < 21 years) (Mann-Whitney U test).
Survival Analysis of Duration for an Observational Study Cohort and for Fully Ascertained Samples
In addition to non-parametric duration analyses using HD subjects fully ascertained for both onset and death, survival analysis was performed with data from the EHDN Registry observational cohort. In this dataset, 1,314 HD subjects had only a recorded age at onset, and 115 HD subjects had data on both age at onset and age at death. We performed a non-parametric survival analysis using a Cox Proportional Hazards model by setting age at onset as time 0 and duration as time to event. For subjects without a recorded age at death, age at onset subtracted from age at last study visit was used as time to event with a censoring indicator. Duration values were modeled as a function of CAG (continuous variable) and gender with the “coxph” function in the “survival” R package. A similar survival analysis approach (but without censoring) using CAG-repeat size as a continuous predictor variable and gender was applied to the data for 855 fully ascertained HD subjects used for our primary non-parametric analysis. In addition, on the basis of sorted CAG-repeat sizes of fully ascertained samples, two groups of HD subjects with the top or bottom 10% of extreme CAG repeats (85 subjects in each group: 50–63 CAGs or 38–41 CAGs, respectively) were identified to be compared for duration through survival analysis.
Simulation Analysis
The capacity for CAG length to explain duration was not significant in the observed dataset (Figure 3). To estimate whether different levels of explanatory power of the CAG repeat for duration could have been visualized in such data, we first randomly permuted the duration values of the 855 HD subjects. Then, without data replacement, we sampled duration values randomly until the model’s R2 value (model: duration ∼ CAG) reached 20%, 10%, 5%, 2%, or 1%. Once the model based on permuted data generated the pre-specified R2 value, the mean duration for each CAG length based on that simulation set was recorded for plotting against CAG.
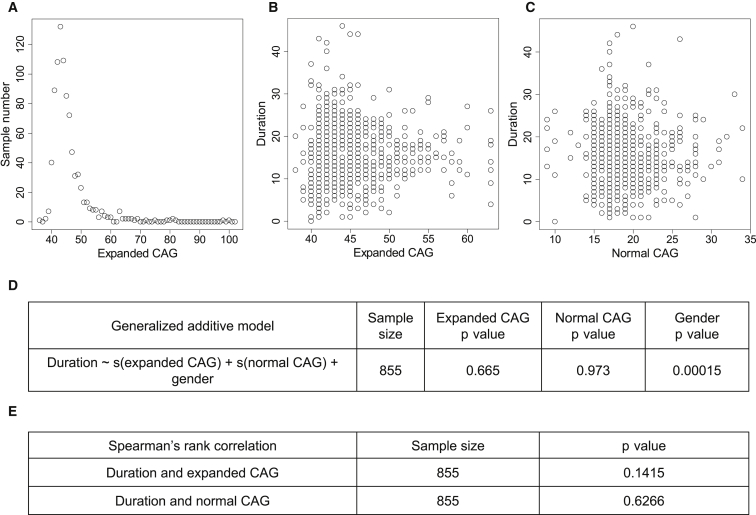
Figure 3.
Non-parametric Analyses to Test Effects of CAG-Repeat Size on Duration
(A) Sample sizes were plotted against expanded CAG repeats for statistical modeling of duration.
(B and C) Duration values were plotted against either expanded CAG (B) or normal CAG (C).
(D) A generalized linear model (GAM) was constructed to test the effects expanded CAG, normal CAG, and gender on duration in the non-normally distributed data. Expanded CAGs with sample sizes greater than 2 (38–63 CAGs) were used. The p values of independent variables are provided.
(E) In addition, Spearman’s rank-correlation analysis was performed for determining whether duration values correlated with the sizes of either expanded or normal CAG repeats.
Software Package for Statistical Analysis
All statistical analyses were performed with R (version 3.0.2).
Results
Age at Death in HD Is Strongly Correlated with the Length of the Expanded HTT CAG Repeat
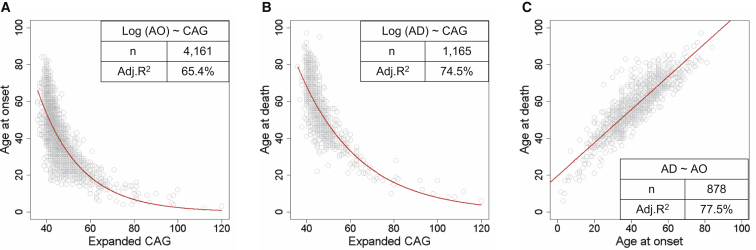
We initially compared the relationships between (1) expanded CAG-repeat length and age at onset of motor signs, (2) expanded CAG-repeat length and age at death, and (3) age at onset and age at death. Consistent with previous findings,6, 9, 12 analysis using all data points showed that age at motor onset (Figure 1A) and age at death (Figure 1B) were both inversely correlated with expanded CAG-repeat length (adjusted R2 = 65.4% and 74.5%, respectively). However, a substantial amount of variance in age at onset and age at death was not explained by the expanded CAG repeat, suggesting that these outcomes are modified by other factors. In addition, age at death was strongly correlated with age at onset (Figure 1C), indicating that the former can be predicted relatively accurately from the latter (adjusted R2 = 77.5%). Interestingly, the correlation between expanded CAG length and age at death appeared stronger, given that age at onset is more variable. This could be because age at onset involves a subjective assessment on the part of an expert clinician, whereas age at death is objectively recorded. It could also be that age at onset is more easily modified by other genetic or environmental factors than is age at death. In any event, the strong correlation between age at death and expanded CAG length indicates that, averaged across the HD population, the length of the mutation is the primary factor determining at what age an individual with HD dies.
Figure 1.
Correlation between Age at Death and the Length of the Expanded HTT CAG Repeat
(A) Age at onset of motor signs plotted against the expanded CAG-repeat length.
(B) Age at death plotted against the expanded CAG-repeat length.
(C) Age at death plotted against age at onset for individuals for whom both are known.
In each panel, each circle represents a unique HD subject. The red trend line represents a statistical model based on all data points prior to QC analysis and describes the relationship between natural-log-transformed age at onset and expanded CAG-repeat length (A), between natural-log-transformed age at death and expanded CAG-repeat length (B), and between age at death and age at onset (C). A summary of a model, including its formula, sample number (n), and adjusted R2 (Adj. R2) value is provided inside each plot. The larger variance in age at onset (A) than in age at death (B) is not due to statistical artifacts related to sample size, given that the R2 values for age-at-onset models based on randomly picked 1,165 subject sample sets (mean = 0.6537) were similar to those of the original model using all data points.
Age at Death Is Not Influenced by the Length of the Normal HTT CAG Repeat
Next, we tested whether variance in age at death in HD is influenced by the normal CAG repeat or gender. The expanded CAG repeats in 1,165 HD subjects ranged from 36 to 120 CAGs; the median of the expanded and normal CAG-repeat lengths was 44 and 18, respectively. We have reported previously on the importance of conforming to data-quality assumptions in parametric statistical analysis of CAG-repeat relationships to avoid spurious results when testing for potentially subtle effects of modifiers, and we have proposed a QC pipeline for robust statistical analysis.12 Among other factors, important requirements that should be confirmed in parametric regression analysis include (1) data normality, (2) equal variance, and (3) absence of disproportionately influential data points. We performed QC analyses, as described in Lee et al.12 and in the Material and Methods (Figures S1 and S2), to generate a dataset that includes 1,019 subjects with 40–52 CAG repeats and conforms to the assumptions of regression analysis (Figure S3). We used this dataset to generate reliable statistical models, model 1 and model 2, which include and exclude the normal CAG repeat, respectively (Table 1). Only the expanded CAG-repeat length and gender explained a significant portion of the variance in age at death (model 1; adjusted R2 = 66.9%) given that omitting the normal CAG-repeat length from the model (model 2; R2 = 66.9%) made no significant difference (ANOVA model comparison, p value = 0.1348). Exclusion of outliers did not change the conclusion given that model 3, fitted to all data without any sample exclusion, also revealed significance only for expanded CAG and gender (Table 1; Figure S3). Similarly, tests involving inclusion of the outliers excluded by the QC pipeline or specific examination of individuals with >52 CAGs failed to reveal any significant impact of the normal CAG-repeat length (Figures S4–S6). Thus, the size of the expanded CAG repeat and gender have predictive power for age at death, but the normal CAG length has no discernible impact.
Relationship between Age at Onset and Age at Death: Disease Duration
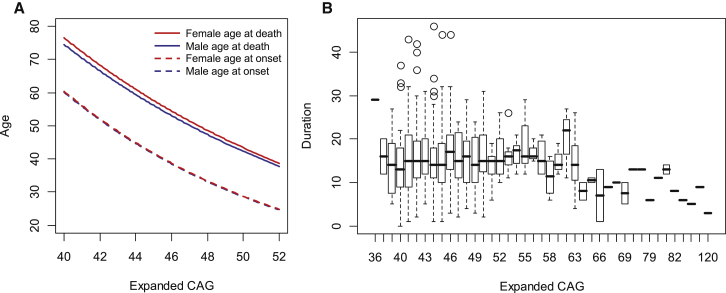
The construction of statistical models relating the expanded CAG repeat length to both age at onset12 and age at death (Table 1, model 2) allowed us to estimate indirectly the average time between the initial presentation of diagnostic motor signs and death in male and female HD subjects. Age at onset was not different between the two genders (Figure 2A, dashed lines), but there was a significant ∼1 year difference between males and females in age at death (Figure 2A, red and blue solid lines). Interestingly, the age-at-death model (solid) and the age-at-onset model (dashed) were largely parallel for CAG ranges associated with onset in adulthood, indicating that the disease duration from diagnosis to death is similar regardless of expanded CAG-repeat size. This implies that gender-associated disease duration is independent of the length of the expanded CAG repeat, which we have suggested previously from a limited post-mortem brain study.5, 9
Figure 2.
Distribution of Disease Duration by CAG-Repeat Length
(A) Models for age at death (Table 1, model 2) and age at onset12 were constructed with normally distributed samples and a gender covariate. For the age-at-onset model, gender was included in the model described previously.12 Blue and red lines represent statistical models for males and females, respectively. Solid and dotted lines represent the CAG age-at-death model and the CAG age-at-onset model, respectively.
(B) The distribution of disease duration for each expanded CAG repeat was plotted in a boxplot format. Open circles are outliers defined by a standard interquartile-outlier-identification method. The top, middle, and bottom of the box represent the 75th percentile (upper quartile), median, and 25th percentile (lower quartile) data points, respectively. The higher and lower whiskers indicate the upper quartile plus 1.5× the interquartile range (IQR) and the lower quartile minus 1.5× the IQR, respectively.
We next used several approaches to test this proposition in the 878 HD subjects for whom disease duration could be measured directly because both age at motor onset and age at death were ascertained, a much larger dataset than analyzed previously. The median of the expanded and normal alleles was 44 and 18 CAGs, respectively. As suggested from the statistical models, although the duration values were highly variable for any given CAG-repeat length, the median of measured disease duration for these HD subjects appeared similar regardless of expanded CAG-repeat length (Figure 2B). It was not possible to construct a reliable parametric linear-regression model relating disease duration and expanded CAG length because the duration values were not normally distributed; instead, they were highly enriched with values between 10 and 20 years, quite different from the distributions of age at onset12 and age at death (Figures S7 and S8). Therefore, as a first analysis, we instead performed non-parametric statistical analysis by using a generalized additive model and Spearman’s rank correlation, which does not require normal distribution of the data, to test whether disease duration is associated with CAG-repeat length. This generalized additive model based on 855 subjects with those CAG sizes represented by at least three HD subjects indicated that gender was a significant predictor of disease duration in that male HD subjects had a slightly shorter duration than did female HD subjects (p value = 0.00015). However, there was no significant association or correlation between disease duration and either the expanded or normal CAG-repeat length (Figure 3).
We also specifically examined duration values for HD subjects with shorter or longer expanded CAG repeats. The median CAG repeat in our duration data was 44, so we excluded three consecutive CAGs bins around the median CAG in order to generate two arbitrary groups of HD subjects with (1) similar sample sizes and (2) distinct CAG-repeat lengths. Disease duration for HD subjects with expanded CAG length < 43 (Figure S9A, blue; 247 subjects) and > 45 (Figure S9A, red; 305 subjects) was not significantly different (Figure S9B; Mann-Whitney U test, p value = 0.484). Furthermore, mutant alleles in HD subjects representing the top 10% (Figure S9C, red; median duration = 27 years; 87 subjects) and bottom 10% (Figure S9C, blue; median duration = 5 years; 87 subjects) of duration values showed similar expanded CAG-repeat sizes (Figure S9D; Mann-Whitney U test, p value = 0.8975). Finally, we determined whether duration values differed between juvenile-onset HD subjects (age at onset < 21 years old; 55 subjects) and adult-onset HD subjects (age at onset > 20 years old; 823 subjects). This analysis revealed the expected significant differences in expanded CAG-repeat lengths, age at onset, and age at death but no difference in median disease duration between adult-onset and juvenile-onset HD subjects (Figure 4D; Mann-Whitney U test, p value = 0.75). In our data, the mean and median duration of those 11 juvenile-onset HD subjects with CAG-repeat size greater than 69 were 9.1 and 9, respectively. Therefore, although disease duration overall in juvenile-onset HD individuals (age at onset < 21 years) is similar to that of adult-onset HD subjects, those with extreme juvenile-onset HD (e.g., age at onset < 10) might have a shorter disease duration.
Figure 4.
HD Subjects with Adult Onset and Juvenile Onset Have Similar Durations
HD subjects with adult age at onset (>20 years; 823 subjects) or juvenile age at onset (<21 years; 55 subjects) were compared for their expanded CAG repeats (A), age at onset (B), age at death (C), and duration (D) with the Mann-Whitney U test. In each panel, a boxplot summarizes the distribution of the test object (left), and a summary-statistics table is provided (right).
Consistent with the lack of an effect of the expanded CAG repeat on disease duration in HD heterozygotes, five additional HD individuals with two expanded CAG-repeat alleles had disease duration within 1 SD (8.6–22.2 years) of the mean. Although this is based on a very small cohort of “HD homozygote” individuals (because of their rarity), it suggests further the lack of a dosage effect of mutant HTT on disease duration.
All of the above comparisons were consistent in supporting the conclusion that in HD, disease duration is independent of the length of the expanded CAG repeat. Because a lack of effect of the disease mutation on the duration of clinical disease is counterintuitive, we were concerned that an actual correlation with CAG length might be obscured by some ascertainment bias. There were two sources of ascertainment for our subjects: (1) cohort studies in which HD subjects were ascertained for age at onset and in which a subset of individuals subsequently died and (2) brain banks where ascertainment was based upon death. Although our ultimate conclusion was derived from individuals from both groups where duration could be measured directly because both parameters were known, it was conceivable that individuals with shorter CAG-repeat lengths and potentially longer duration in observational cohort studies were missed because they have not yet died. Consequently, we performed a survival analysis for our major source of cohort samples with motor onset: 1,426 heterozygous HD individuals from the EHDN Registry study. Survival analysis based on this observational cohort with censoring indications for surviving HD subjects revealed a significant impact on age at death for expanded CAG (p value < 2E−16), but not normal CAG (p value = 0.0926). Using non-parametric Cox’s proportional-hazards analysis, we then tested whether CAG-repeat length and gender influence survival after onset. We found no effect on disease duration for either expanded CAG-repeat length (exponentiated coefficient per one unit of expanded CAG = 1.007; p value = 0.754) or gender (exponentiated coefficient for males = 1.178; p value = 0.385). Tests for proportional-hazards assumption using the “cox.zph” function confirmed that neither CAG-repeat size nor gender violated the assumption; p values for expanded CAG length and gender were 0.504 and 0.680, respectively.
A similar analysis of the 10% extremes of CAG-repeat length from 855 HD subjects from the MA HD Center Without Walls collection and for whom both age at onset and age at death were known showed an influence only of gender (exponentiated coefficient for low-CAG group = 0.8216, p value = 0.22; exponentiated coefficient for males = 1.2582, p value = 0.146). Survival analysis using all 855 ascertained subjects and CAG as a continuous variable also revealed no significant contribution of CAG to duration (p value = 0.665).
Next, we restricted analysis of duration only to those subjects ascertained through death, i.e., obtained from HD brain banks. Like the full set of 878 individuals with a direct measurement of duration, this set of 524 brain-bank-derived individuals showed no significant correlation between CAG-repeat length and the length of time between onset and death (Spearman’s rank correlation, p value = 0.2738; Pearson’s correlation, p value = 0.4529).
Finally, in order to judge the degree to which we had power to visualize an effect of the expanded CAG-repeat length on duration, we performed simulation studies based upon the characteristics of our actual dataset of 855 individuals of known duration (described in the Figure 3 legend). We simulated distributions of the duration data across the CAG-repeat range on the basis that CAG-repeat length explained 1%, 2%, 5%, 10%, or 20% of the variance in duration (Figure S10). In brief, we used a data matrix of true CAG-repeat size and duration to calculate R2 to evaluate how much variance in duration was explained by CAG-repeat length in the observed data (Figure S10A). We then randomly shuffled duration values to obtain the explanatory power of permuted CAG on duration. Although CAG-repeat length accounted for more than 65% of the variance in age at onset and age at death, it had no detectable influence on duration (Figure S10A), whereas these simulations (Figures S10B–S10F) suggest that even a 2% contribution of CAG-repeat length to determining duration could have been detected (Figure S10E).
Impact of HTT Haplotypes and a Genetic Modifier of Age at Onset on Duration
In the absence of an effect of expanded CAG length on HD duration, we next assessed two additional candidate modifiers. We first tested whether common HTT haplotypes, which we have shown do not modify age at onset,27 might instead have an effect on disease duration. HTT haplotypes were defined on the basis of 21 common SNPs that show significant differences in allele frequencies between HD subjects and normal control individuals.27 ANOVA models in which duration was modeled as a function of HTT haplotype, either on the disease chromosome (p value = 0.363) or on the normal chromosome (p value = 0.091), provided no evidence of a significant association between duration and HTT haplotype.
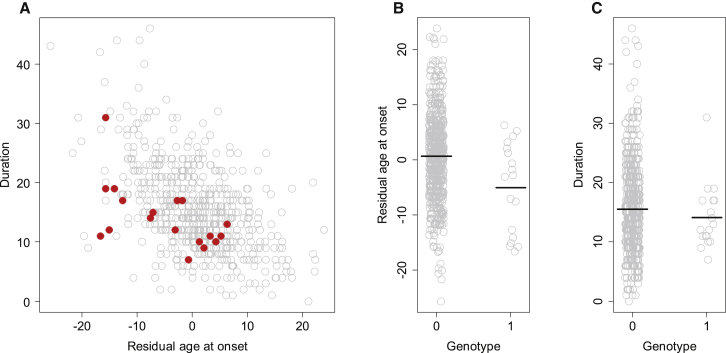
Recently, through a genome-wide association strategy, we discovered genetic loci significantly associated with the difference between observed age at onset of motor signs and that expected on the basis of the CAG-repeat length of the individual subjects. The genome-wide-significant locus with the largest effect size, detected by SNP rs146353869 on chromosome 15, was estimated to accelerate motor onset by ∼6 years, suggesting hastening of HD pathogenesis, at least prior to diagnosis. The same SNP was significantly associated with age at death corrected for CAG-repeat length (p value = 9.3E−5). We therefore evaluated the potential influence of this strong age-at-onset modifier locus on disease duration.28 As expected and shown in Figure 5, HD subjects with a minor allele for rs146353869 had onset significantly earlier than those without such an allele (Mann-Whitney U test, p value = 0.010). However, disease duration was similar between subjects with and without a rs146353869 minor allele (Mann-Whitney U test, p value = 0.370). Thus, the functional variant tagged by rs146353869 modifies CAG-driven HD pathogenesis but does not influence the length of the CAG-independent period between onset and death.
Figure 5.
Duration Is Not Associated with rs146353869
On the basis of recent results from a genome-wide association (GWA) analysis, we tested whether duration is altered by a strong genetic modifier tagged by SNP rs146353869 on chromosome 15. HD subjects with the minor allele of this SNP developed clinical symptoms significantly (∼6 years) earlier than did subjects with a comparable expanded CAG length but without the minor allele of rs146353869.
(A) Among samples used in our GWA analysis aimed at identifying age-at-onset modifiers, 654 individuals had both age-at-onset and age-at-death data. Disease duration (i.e., age at death minus age at onset) was plotted against residual age at onset. Gray (636 subjects) and red (18 subjects) circles represent HD subjects without and with a minor allele for rs146353869, respectively.
(B and C) Residual age at onset (B) and duration (C) of HD subjects without (genotype 0) or with (genotype 1) a minor allele for rs146353869 are plotted. Black horizontal lines represent the mean. Mann-Whitney U tests were performed to compare residual age at death (p value = 0.01) and duration (p value = 0.37) between the two groups of HD subjects differentiated by the rs146353869 genotype.
Discussion
Our robust statistical analysis based on a large dataset firmly establishes that, like age at diagnostic onset, the age at death of HD individuals is determined primarily by the size of their HTT CAG-expansion mutation and is not significantly affected by the normal CAG allele. Indeed, CAG-repeat length is slightly more correlated with age at death than with age at motor onset because of greater variance in the latter, which reflects either the subjectivity of determining onset or its greater susceptibility to modification. It has been suggested from the effects of precise genetic replicas of the CAG mutation in the endogenous mouse ortholog (formerly Hdh, now Htt) and the fact that these “knock-in” alleles rescue the embryonic lethality of a null Htt allele that mutant huntingtin might precipitate pathogenesis by enhancing or dysregulating some normal activity of huntingtin.29 At least some normal activities of human huntingtin vary with changes in CAG length even in the normal size range, revealing the CAG repeat to be a polymorphism with functional consequences.30 Our data with respect to age at motor onset and now age at death indicate that any variations in the activity of normal huntingtin occasioned by changes in the size of the normal allele repeat do not have an effect on the rate of pathogenesis leading to motor onset or death.
Because diagnosis of HD is primarily based upon characteristic motor signs, the length of time that an individual actually displays HD, i.e., the period between motor onset and death, is defined here as disease duration. In the literature, HD disease duration varies greatly (reported ranges of 1–45 years and medians of 16.2–21.4 years), although in some cases, analyses have included individuals ascertained for either onset or death, but not both.16, 31, 32, 33 In our analyses, we were able to focus on individuals for whom both age at motor onset and age at death had been ascertained, permitting a direct assignment of disease-duration values. Across this dataset, disease duration (1) is not correlated with the expanded CAG-repeat length, (2) is similar between HD subjects with low and high CAG expansions, and (3) is comparable between adult-onset and juvenile-onset HD. In addition, expanded CAG lengths are similar between HD subjects with shorter and longer duration. Because our studies were based exclusively on individuals who have already displayed disease onset, it remains formally possible that individuals who have expanded CAG repeats and who are pre-manifest will display a disease duration that is correlated with CAG-repeat length. However, we think that this theoretical possibility is unlikely. The potential bias of studies excluding pre-manifest individuals was first considered in examining the CAG-onset relationship according to a survival model by Langbehn et al.34 The “Langbehn et al. survival model” for CAG-onset relationship is similar to (1) our regression model based on a large cohort of manifest HD subjects (>4,000) (data not shown) and (2) predictions from previously published formulae for the adult-onset CAG-repeat range.35 The similarity between the two models when the regression-model dataset is large indicates that the exclusion of pre-manifest individuals does not substantially bias the estimate of the CAG-onset relationship. We would expect the same to be true of the CAG-death relationship and that our duration estimate based on a large sample of subjects fully ascertained for both onset and death is not likely to be substantially biased by the absence of pre-manifest subjects.
Although sometimes assumed, it has not been clearly demonstrated whether the disease duration of juvenile-onset HD subjects (<21 years of age) is generally different from that of adult-onset individuals (>20 years of age). In one study, disease duration was similar across HD subjects for onset in the juvenile and adult age ranges, and the duration was somewhat shorter for those with onset age over 50 years.32 A second report based on age at onset of first sign and age at death, or on age alone if HD subjects were still living, noted that extremes of onset, either juvenile or elderly, were associated with significantly shorter durations than typical adult onset.33 Juvenile-onset subjects had a 1- to 2-year-shorter duration (median = 20.0 years) than those with typical adult onset between 20 and 49 years (median of 21.3 years for age at onset between 20 and 34 years; 22.1 years for age at onset between 35 and 49 years).33 The lack of consistency in disease duration might be due to different definitions and types of onset. However, breaking down the juvenile-onset category into only the most extreme cases of individuals who have the longest CAG repeats and who developed clinical symptoms before 10 years of age has been reported to reveal a significantly shorter disease duration (range = 2–15 years; mean = 6.6 years) than that of other HD subjects.36, 37
Nevertheless, our data indicate strongly that the duration of the period in which clinical manifestations of HD are expressed, i.e., the period between diagnosis and death, is not altered in the vast majority of HD individuals by the expanded CAG repeat, the normal CAG repeat, HTT haplotype, or a strong age-at-onset modifier. Our statistical confirmation of this seemingly counterintuitive finding argues against the simple scenario in which a toxic CAG-length-determined property of mutant huntingtin drives a single pathogenic process that leads in a sequential manner first to onset and then directly from onset to death. Rather, it suggests two alternative scenarios for the HD disease process, and these should be considered in designing, testing, and interpreting the results of therapeutic interventions, particularly those aimed at silencing the mutant CAG-expanded HTT allele.
It is well established that the rate of the pathogenic process that leads to clinical diagnosis is determined primarily by the length of the expanded CAG tract. The onset of diagnostic motor abnormalities is thought to ensue from the dysfunction and eventual loss of striatal neurons, and it has been estimated that at the time of clinical onset, 30% or more of medium spiny neurons in the striatum have been lost, and the remainder have already compromised38 by a neurodegenerative process that continues as clinical manifestations progressively worsen (commonly referred to as “progression”). Indeed, in studies of post-mortem HD brains, Hadzi et al. have shown that the extent of striatal pathology (pathological grade) is correlated both with CAG-repeat length and with duration.16 The former correlation is consistent with a CAG-driven pathogenic process causing striatal pathology. The latter correlation makes sense because the longer the duration of disease, the longer that CAG-driven process has to act, and consequently the greater the extent of striatal pathology. However, we have shown the lack of correlation between CAG-repeat length and duration, suggesting that the extent of striatal pathology per se is not a determinant of death and that the reasons for correlation between each of these two parameters and striatal pathology are distinct. In our analyses of the 310 brains for which pathological grade was known, we found, like Hadzi et al.,16 that higher pathological grade associates with longer CAG repeats, earlier onset, and earlier death, all of which are consistent with a more rapid rate of HD pathogenesis with increasing mutation size. The higher pathological grade also associates with longer duration in these individuals, reinforcing the conclusion that disease duration is not determined by CAG-repeat length or by the extent of striatal pathology.
Like motor onset, age at onset of cognitive and, to a lesser extent, of psychiatric signs is correlated with the expanded CAG length and might reflect contributions of additional neuropathological changes in cortical regions. A simple view of pathogenesis, whereby the same CAG-driven process in the striatum or in these cortical regions leads to diagnostic onset and then simply continues with worsening manifestations and ultimate death, is not a viable hypothesis because of the CAG independence of disease duration. Instead, we propose two alternative parsimonious explanations for these data.
In the first scenario, the pathogenic process is driven by mutant huntingtin, and motor onset results when the coping capacity of the most vulnerable structures, particularly the striatum, has reached its limit. Around or before motor onset, the damage has so weakened the homeostatic mechanisms of the individual that catastrophic failure of the regions associated with onset enables susceptibility to one or more CAG-independent processes that contribute to causing early death, on average 15 years later. In this “two-stage” scenario, CAG-driven pathological changes, including those affecting other cells and tissues, and consequent worsening of symptoms continue to occur after onset, but these CAG-driven changes are not critical to causing death. Instead, death results from one or more separate CAG-independent processes acting on the background of a critical juncture reached by the initial CAG-dependent pathogenesis. The potential CAG-independent processes that could determine duration are not necessarily limited to intrinsic biological risk factors, given that many external factors (nutrition, medical care, nursing-home care, infectious exposure, etc.) could play a contributory role.
In the second scenario, a pathogenic process is driven by mutant huntingtin independently in multiple cell types in the brain or in other organs, each of which has a distinct coping potential. The striatum is most vulnerable and so succumbs first and produces clinical manifestations that progress over time. However, neither the occurrence of diagnostic symptoms nor their progression due to the underlying CAG-length-dependent pathology determines viability of the individual. Rather, some other cells are critical for viability, and when these essential cells independently reach their coping limit, averaging 15 years after motor onset, the subject dies. In this second scenario, unlike the first, a pathogenic process driven by HTT CAG length leads directly to death in a manner that is not a downstream consequence of the pathology associated with characteristic neurological manifestations.
The leading causes of death of HD subjects as reported in the literature are pneumonia and heart disease.18, 39 Although not directly connected to the brain, each of these causes could occur on the background of physiological changes occasioned by the neuronal dysfunction that becomes evident at the time of HD onset (scenario 1) or could be precipitated by direct effects of mutant huntingtin in peripheral cells, such as immune system components or cardiac muscle (scenario 2). Indeed, HD subjects display a number of peripheral abnormalities that could represent either direct or indirect effects of mutant huntingtin, including abnormal energy metabolism, extreme weight loss, diabetes, and reduced pulmonary function.21, 23, 24, 40, 41, 42 These all suggest that although HD is classified as a neurodegenerative disorder, the overall impact of the HTT CAG expansion is ultimately rather widespread. Given that HD CAG-driven neuropathological changes in symptom-associated brain regions continue after onset, the early mortality in HD might result from effects of the expanded CAG repeat in vital brain regions not associated with early clinical symptoms (scenario 2), CAG-repeat effects outside the brain (scenario 2), or intrinsic or extrinsic factors unrelated to the CAG repeat (scenario 1).
Our findings and the two distinct explanations proposed for them have implications for developing and testing disease-modifying therapeutic modalities in HD. Our results clearly indicate that only the expanded length of the HTT CAG repeat has significant power for predicting both age at onset and age at death but that remaining variance in these measures is unexplained by the CAG mutation and must be due to other causes. One approach that we and others are taking to reveal validated therapeutic targets for HD is to identify genetic modifiers of motor onset in human subjects, i.e., genetic factors that alter the rate of CAG-driven HD pathogenesis and therefore can identify target proteins and processes for the development of traditional small-molecule therapeutics. An example of such a factor is the as yet undefined functional variant tagged by SNP rs146353869, which dramatically hastens motor onset. In both scenarios 1 and 2, drugs based upon modification of CAG-driven processes would be expected to be effective in delaying both onset and death if they are delivered sufficiently prior to onset. In scenario 2, such interventions might also be expected to delay death even if they are delivered after motor onset, whereas in scenario 1 they might alleviate the progression of clinical symptoms without actually delaying death. The CAG independence of disease duration suggests that if the first scenario is correct, an array of modifiers and potential therapeutic targets different from those involved in CAG-dependent processes might be effective in delaying death. Indeed, both alternative scenarios also allow for modifiers that act in a cell- or tissue-specific fashion and have the potential to modify predominantly age at onset or disease duration, but most likely not both.
A fundamentally different route to therapeutic intervention currently being explored is suppression of mutant huntingtin expression through nucleic-acid-based gene-silencing strategies. Planning for initial clinical trials has typically considered delivery of the therapeutic agent to the brains of HD individuals early after clinical diagnosis with the goal of delaying the progression of clinical symptoms and associated neuropathology. In our first scenario, such treatment can be very effective in limiting the progression of clinical symptoms and improving quality of life without necessarily altering disease duration given that the latter is independent of CAG-repeat length. Consequently, although it presents greater regulatory hurdles and difficulties in clinical-trial design, the ideal time to treat with a HTT-suppression strategy is significantly prior to diagnostic onset because an effective treatment would then be expected to delay both onset and death. In the second scenario, treatment of the brain might have no impact on preventing death if the gene-silencing strategy is not being delivered to the cells or organ responsible for maintaining viability. Thus, in either scenario, our findings suggest that a brain HTT-silencing strategy that is successful in reducing the progression of symptoms might improve the quality of life of HD individuals without necessarily preventing their early death.
Although it is not currently possible to distinguish between our two scenarios for HD pathogenesis leading to early death, the CAG independence of disease duration suggests that the results of treatment trials measuring some aspects of clinical progression after onset might not be predictive for the efficacy of the same treatments in preventing motor onset or early death. Fortunately, ongoing large natural-history studies of HD offer a route for more fully exploring the biological basis of early death in HD in order to distinguish between these explanations and to guide therapeutic development. Most importantly, the application of the continuous CAG analysis strategy, applied here to onset and death, to defining and distinguishing other phenotypic measures (molecular, imaging, neurological, etc.) tied to the pathogenic process offers the hope of enabling clinical trials before motor onset, when disease-modifying treatments based upon CAG-length-dependent effects are expected to be most broadly effective.
Acknowledgments
The authors acknowledge and thank the Harvard Brain Tissue Resource Center at McLean Hospital (Dr. Francine Benes, Director), the New York Brain Bank at Columbia University (Dr. Jean-Paul Vonsattel, Director), the National Neurological Research Specimen Bank at the Department of Veterans Affairs Medical Center (Dr. Wallace Tourtellotte, Director), the Neuropathology Core of the MA Alzheimer Disease Research Center (Matt Frosch, Director), and the Harvard NeuroDiscovery Center Advanced Tissue Resources Core at Massachusetts General Hospital (Dr. Charles Vanderburg, Director) for providing Huntington disease post-mortem brain tissues. We also thank Dr. Richard H. Myers (Boston University School of Medicine) for helpful comments on this manuscript. This work was supported by NIH grants NINDS NS16367, U01NS082079, and R01NS091161 and the CHDI Foundation, Inc.
Published: February 4, 2016
Footnotes
Supplemental Data include ten figures and can be found with this article online at http://dx.doi.org/10.1016/j.ajhg.2015.12.018.
Web Resources
The URL for data presented herein is as follows:
OMIM, http://www.omim.org/
Supplemental Data
References
- 1.Huntington G. On chorea. Med. Surg. Rep. 1872;26:320–321. [Google Scholar]
- 2.The Huntington’s Disease Collaborative Research Group A novel gene containing a trinucleotide repeat that is expanded and unstable on Huntington’s disease chromosomes. Cell. 1993;72:971–983. doi: 10.1016/0092-8674(93)90585-e. [DOI] [PubMed] [Google Scholar]
- 3.Cattaneo E., Zuccato C., Tartari M. Normal huntingtin function: an alternative approach to Huntington’s disease. Nat. Rev. Neurosci. 2005;6:919–930. doi: 10.1038/nrn1806. [DOI] [PubMed] [Google Scholar]
- 4.Bates G.P. History of genetic disease: the molecular genetics of Huntington disease - a history. Nat. Rev. Genet. 2005;6:766–773. doi: 10.1038/nrg1686. [DOI] [PubMed] [Google Scholar]
- 5.Gusella J., MacDonald M. No post-genetics era in human disease research. Nat. Rev. Genet. 2002;3:72–79. doi: 10.1038/nrg706. [DOI] [PubMed] [Google Scholar]
- 6.Andrew S.E., Goldberg Y.P., Kremer B., Telenius H., Theilmann J., Adam S., Starr E., Squitieri F., Lin B., Kalchman M.A. The relationship between trinucleotide (CAG) repeat length and clinical features of Huntington’s disease. Nat. Genet. 1993;4:398–403. doi: 10.1038/ng0893-398. [DOI] [PubMed] [Google Scholar]
- 7.Duyao M., Ambrose C., Myers R., Novelletto A., Persichetti F., Frontali M., Folstein S., Ross C., Franz M., Abbott M. Trinucleotide repeat length instability and age of onset in Huntington’s disease. Nat. Genet. 1993;4:387–392. doi: 10.1038/ng0893-387. [DOI] [PubMed] [Google Scholar]
- 8.Snell R.G., MacMillan J.C., Cheadle J.P., Fenton I., Lazarou L.P., Davies P., MacDonald M.E., Gusella J.F., Harper P.S., Shaw D.J. Relationship between trinucleotide repeat expansion and phenotypic variation in Huntington’s disease. Nat. Genet. 1993;4:393–397. doi: 10.1038/ng0893-393. [DOI] [PubMed] [Google Scholar]
- 9.Persichetti F., Srinidhi J., Kanaley L., Ge P., Myers R.H., D’Arrigo K., Barnes G.T., MacDonald M.E., Vonsattel J.P., Gusella J.F. Huntington’s disease CAG trinucleotide repeats in pathologically confirmed post-mortem brains. Neurobiol. Dis. 1994;1:159–166. doi: 10.1006/nbdi.1994.0019. [DOI] [PubMed] [Google Scholar]
- 10.Aziz N.A., Jurgens C.K., Landwehrmeyer G.B., van Roon-Mom W.M., van Ommen G.J., Stijnen T., Roos R.A., EHDN Registry Study Group Normal and mutant HTT interact to affect clinical severity and progression in Huntington disease. Neurology. 2009;73:1280–1285. doi: 10.1212/WNL.0b013e3181bd1121. [DOI] [PubMed] [Google Scholar]
- 11.Djoussé L., Knowlton B., Hayden M., Almqvist E.W., Brinkman R., Ross C., Margolis R., Rosenblatt A., Durr A., Dode C. Interaction of normal and expanded CAG repeat sizes influences age at onset of Huntington disease. Am. J. Med. Genet. A. 2003;119A:279–282. doi: 10.1002/ajmg.a.20190. [DOI] [PubMed] [Google Scholar]
- 12.Lee J.M., Ramos E.M., Lee J.H., Gillis T., Mysore J.S., Hayden M.R., Warby S.C., Morrison P., Nance M., Ross C.A., PREDICT-HD study of the Huntington Study Group (HSG) REGISTRY study of the European Huntington’s Disease Network. HD-MAPS Study Group. COHORT study of the HSG CAG repeat expansion in Huntington disease determines age at onset in a fully dominant fashion. Neurology. 2012;78:690–695. doi: 10.1212/WNL.0b013e318249f683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Guo Z., Rudow G., Pletnikova O., Codispoti K.E., Orr B.A., Crain B.J., Duan W., Margolis R.L., Rosenblatt A., Ross C.A., Troncoso J.C. Striatal neuronal loss correlates with clinical motor impairment in Huntington’s disease. Mov. Disord. 2012;27:1379–1386. doi: 10.1002/mds.25159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Paulsen J.S., Nopoulos P.C., Aylward E., Ross C.A., Johnson H., Magnotta V.A., Juhl A., Pierson R.K., Mills J., Langbehn D., Nance M., PREDICT-HD Investigators and Coordinators of the Huntington’s Study Group (HSG) Striatal and white matter predictors of estimated diagnosis for Huntington disease. Brain Res. Bull. 2010;82:201–207. doi: 10.1016/j.brainresbull.2010.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rosas H.D., Goodman J., Chen Y.I., Jenkins B.G., Kennedy D.N., Makris N., Patti M., Seidman L.J., Beal M.F., Koroshetz W.J. Striatal volume loss in HD as measured by MRI and the influence of CAG repeat. Neurology. 2001;57:1025–1028. doi: 10.1212/wnl.57.6.1025. [DOI] [PubMed] [Google Scholar]
- 16.Hadzi T.C., Hendricks A.E., Latourelle J.C., Lunetta K.L., Cupples L.A., Gillis T., Mysore J.S., Gusella J.F., MacDonald M.E., Myers R.H., Vonsattel J.P. Assessment of cortical and striatal involvement in 523 Huntington disease brains. Neurology. 2012;79:1708–1715. doi: 10.1212/WNL.0b013e31826e9a5d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pekmezovic T., Svetel M., Maric J., Dujmovic-Basuroski I., Dragasevic N., Keckarevic M., Romac S., Kostic V.S. Survival of Huntington’s disease patients in Serbia: longer survival in female patients. Eur. J. Epidemiol. 2007;22:523–526. doi: 10.1007/s10654-007-9157-7. [DOI] [PubMed] [Google Scholar]
- 18.Lanska D.J., Lavine L., Lanska M.J., Schoenberg B.S. Huntington’s disease mortality in the United States. Neurology. 1988;38:769–772. doi: 10.1212/wnl.38.5.769. [DOI] [PubMed] [Google Scholar]
- 19.Morton A.J. Circadian and sleep disorder in Huntington’s disease. Exp. Neurol. 2013;243:34–44. doi: 10.1016/j.expneurol.2012.10.014. [DOI] [PubMed] [Google Scholar]
- 20.Petersén A., Gabery S. Hypothalamic and Limbic System Changes in Huntington’s Disease. J. Huntingtons Dis. 2012;1:5–16. doi: 10.3233/JHD-2012-120006. [DOI] [PubMed] [Google Scholar]
- 21.Reyes A., Cruickshank T., Ziman M., Nosaka K. Pulmonary function in patients with Huntington’s disease. BMC Pulm. Med. 2014;14:89. doi: 10.1186/1471-2466-14-89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Andreassen O.A., Dedeoglu A., Stanojevic V., Hughes D.B., Browne S.E., Leech C.A., Ferrante R.J., Habener J.F., Beal M.F., Thomas M.K. Huntington’s disease of the endocrine pancreas: insulin deficiency and diabetes mellitus due to impaired insulin gene expression. Neurobiol. Dis. 2002;11:410–424. doi: 10.1006/nbdi.2002.0562. [DOI] [PubMed] [Google Scholar]
- 23.Hu Y., Liang J., Yu S. High prevalence of diabetes mellitus in a five-generation Chinese family with Huntington’s disease. J. Alzheimers Dis. 2014;40:863–868. doi: 10.3233/JAD-131847. [DOI] [PubMed] [Google Scholar]
- 24.Djoussé L., Knowlton B., Cupples L.A., Marder K., Shoulson I., Myers R.H. Weight loss in early stage of Huntington’s disease. Neurology. 2002;59:1325–1330. doi: 10.1212/01.wnl.0000031791.10922.cf. [DOI] [PubMed] [Google Scholar]
- 25.Kremer H.P., Roos R.A. Weight loss in Huntington’s disease. Arch. Neurol. 1992;49:349. doi: 10.1001/archneur.1992.00530280029014. [DOI] [PubMed] [Google Scholar]
- 26.Perlis R.H., Smoller J.W., Mysore J., Sun M., Gillis T., Purcell S., Rietschel M., Nöthen M.M., Witt S., Maier W. Prevalence of incompletely penetrant Huntington’s disease alleles among individuals with major depressive disorder. Am. J. Psychiatry. 2010;167:574–579. doi: 10.1176/appi.ajp.2009.09070973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lee J.M., Gillis T., Mysore J.S., Ramos E.M., Myers R.H., Hayden M.R., Morrison P.J., Nance M., Ross C.A., Margolis R.L. Common SNP-based haplotype analysis of the 4p16.3 Huntington disease gene region. Am. J. Hum. Genet. 2012;90:434–444. doi: 10.1016/j.ajhg.2012.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Genetic Modifiers of Huntington’s Disease (GeM-HD) Consortium Identification of Genetic Factors that Modify Clinical Onset of Huntington’s Disease. Cell. 2015;162:516–526. doi: 10.1016/j.cell.2015.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.White J.K., Auerbach W., Duyao M.P., Vonsattel J.P., Gusella J.F., Joyner A.L., MacDonald M.E. Huntingtin is required for neurogenesis and is not impaired by the Huntington’s disease CAG expansion. Nat. Genet. 1997;17:404–410. doi: 10.1038/ng1297-404. [DOI] [PubMed] [Google Scholar]
- 30.Seong I.S., Ivanova E., Lee J.M., Choo Y.S., Fossale E., Anderson M., Gusella J.F., Laramie J.M., Myers R.H., Lesort M., MacDonald M.E. HD CAG repeat implicates a dominant property of huntingtin in mitochondrial energy metabolism. Hum. Mol. Genet. 2005;14:2871–2880. doi: 10.1093/hmg/ddi319. [DOI] [PubMed] [Google Scholar]
- 31.Pridmore S.A. Age of death and duration in Huntington’s disease in Tasmania. Med. J. Aust. 1990;153:137–139. doi: 10.5694/j.1326-5377.1990.tb136831.x. [DOI] [PubMed] [Google Scholar]
- 32.Roos R.A., Hermans J., Vegter-van der Vlis M., van Ommen G.J., Bruyn G.W. Duration of illness in Huntington’s disease is not related to age at onset. J. Neurol. Neurosurg. Psychiatry. 1993;56:98–100. doi: 10.1136/jnnp.56.1.98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Foroud T., Gray J., Ivashina J., Conneally P.M. Differences in duration of Huntington’s disease based on age at onset. J. Neurol. Neurosurg. Psychiatry. 1999;66:52–56. doi: 10.1136/jnnp.66.1.52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Langbehn D.R., Brinkman R.R., Falush D., Paulsen J.S., Hayden M.R., International Huntington’s Disease Collaborative Group A new model for prediction of the age of onset and penetrance for Huntington’s disease based on CAG length. Clin. Genet. 2004;65:267–277. doi: 10.1111/j.1399-0004.2004.00241.x. [DOI] [PubMed] [Google Scholar]
- 35.Langbehn D.R., Hayden M.R., Paulsen J.S., PREDICT-HD Investigators of the Huntington Study Group CAG-repeat length and the age of onset in Huntington disease (HD): a review and validation study of statistical approaches. Am. J. Med. Genet. B. Neuropsychiatr. Genet. 2010;153B:397–408. doi: 10.1002/ajmg.b.30992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Byers R.K., Dodge J.A. Huntington’s chorea in children. Report of four cases. Neurology. 1967;17:587–596. doi: 10.1212/wnl.17.6.587. [DOI] [PubMed] [Google Scholar]
- 37.Nahhas F.A., Garbern J., Krajewski K.M., Roa B.B., Feldman G.L. Juvenile onset Huntington disease resulting from a very large maternal expansion. Am. J. Med. Genet. A. 2005;137A:328–331. doi: 10.1002/ajmg.a.30891. [DOI] [PubMed] [Google Scholar]
- 38.Aylward E.H., Sparks B.F., Field K.M., Yallapragada V., Shpritz B.D., Rosenblatt A., Brandt J., Gourley L.M., Liang K., Zhou H. Onset and rate of striatal atrophy in preclinical Huntington disease. Neurology. 2004;63:66–72. doi: 10.1212/01.wnl.0000132965.14653.d1. [DOI] [PubMed] [Google Scholar]
- 39.Lanska D.J., Lanska M.J., Lavine L., Schoenberg B.S. Conditions associated with Huntington’s disease at death. A case-control study. Arch. Neurol. 1988;45:878–880. doi: 10.1001/archneur.1988.00520320068017. [DOI] [PubMed] [Google Scholar]
- 40.Berent S., Giordani B., Lehtinen S., Markel D., Penney J.B., Buchtel H.A., Starosta-Rubinstein S., Hichwa R., Young A.B. Positron emission tomographic scan investigations of Huntington’s disease: cerebral metabolic correlates of cognitive function. Ann. Neurol. 1988;23:541–546. doi: 10.1002/ana.410230603. [DOI] [PubMed] [Google Scholar]
- 41.Young A.B., Penney J.B., Starosta-Rubinstein S., Markel D., Berent S., Rothley J., Betley A., Hichwa R. Normal caudate glucose metabolism in persons at risk for Huntington’s disease. Arch. Neurol. 1987;44:254–257. doi: 10.1001/archneur.1987.00520150010010. [DOI] [PubMed] [Google Scholar]
- 42.Young A.B., Penney J.B., Starosta-Rubinstein S., Markel D.S., Berent S., Giordani B., Ehrenkaufer R., Jewett D., Hichwa R. PET scan investigations of Huntington’s disease: cerebral metabolic correlates of neurological features and functional decline. Ann. Neurol. 1986;20:296–303. doi: 10.1002/ana.410200305. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.