Magnetic resonance of calcified tissues

Abstract

MRI of the human body is largely made possible by the favorable relaxation properties of protons of water and triacyl glycerides prevalent in soft tissues. Hard tissues – key among them bone – are generally less amenable to measurement with in vivo MR imaging techniques, not so much as a result of the lower proton density but rather due to the extremely short life-times of the proton signal in water bound to solid-like entities, typically collagen, or being trapped in micro-pores. Either mechanism can enhance T2 relaxation by up to three orders of magnitude relative to their soft-tissue counterparts. Detection of these protons requires solid-state techniques that have emerged in recent years and that promise to add a new dimension to the study of hard tissues. Alternative approaches to probe calcified tissues exploit their characteristic magnetic properties. Bone, teeth and extra-osseous calcium-containing biomaterials are unique in that they are more diamagnetic than all other tissues and thus yield information indirectly by virtue of the induced magnetic fields present in their vicinity. Progress has also been made in methods allowing very high-resolution structural imaging of trabecular and cortical bone relying on detection of the surrounding soft-tissues. This brief review, much of it drawn from work conducted in the author’s laboratory, seeks to highlight opportunities with focus on early-stage developments for image-based assessment of structure, function, physiology and mechanics of calcified tissues in humans via liquid and solid-state approaches, including proton, deuteron and phosphorus NMR and MRI.

1. Chemistry, architecture and physiology of bone

Bone is a hierarchically organized biomaterial evolved so as to optimally fulfill its multiple functions ranging from weight-bearing and locomotion to serving as a store for calcium and phosphorus. The major chemical constituents of bone are an organic fraction, consisting predominantly of type-I collagen (~50% by volume), an inorganic or mineral fraction (~35%), made up of poorly mineralized nonstoichiometric calcium hydroxyl apatite with a much smaller and variable fraction of carbonate apatite. The balance is water, with its majority bound to collagen, and a smaller fraction occupying the bone’s pore structure. The mineral crystals are interspersed in the gaps between successive collagen fibrils [1]. The bone’s compressive strength is largely conferred by the material’s inorganic component whereas collagen is responsible for the bone’s tensile strength. On a macrostructural level bone is about 80% compact (or cortical) and 20% trabecular. Cortical bone forms the shell encasing bone marrow and blood vessels, dominating the shaft of the extremities and femoral neck whereas trabecular bone, consisting of a meshwork on interconnected plates and rods, is dominant in the vertebrae, ribs and near the joints where stresses are multidirectional and tensile and torsional loading occurs.

Bone is a living tissue with its own blood supply and ability for self-repair through a process called ‘remodeling’, referring to the interplay of two types of cells: osteoblasts, the bone-forming, and osteoclasts, the bone-resorbing cells. A third type of cells, the osteocytes occupying small cavities on the order of 30 µm in diameter, act as pressure transducers providing signals to osteoblast to induce bone formation. Osteocytes are interconnected with each other through a system of channels, called canaliculi, about 100 nm in diameter. Cortical bone further is permeated by a network of channels, on the order of 50–100 µm in diameter, carrying blood vessels, in contrast to the blood supply to trabecular bone, which is effected through the marrow’s microvascular system.

2. Indirect detection of trabecular and cortical bone microstructure

We refer to ‘indirect detection’ of microarchitecture methods that obviate the need for resolving individual trabecular elements (which are on the order of 100 µm thickness) in trabecular bone or, for example, pore volume fraction in cortical bone (with pore diameters ranging from 10 to several hundred micrometers), thereby obviating the need to resolve individual structural elements. Such approaches entail significant advantages in terms of signal-to-noise (SNR) requirements.

3. Methods exploiting internal magnetic fields for the study of trabecular bone architecture

3.1. Static dephasing regime

The majority of low-resolution MRI studies of bone architecture exploit the bone’s diamagnetic properties. The greater density of higher atomic-number elements in bone mineral (notably calcium and phosphorus) render bone tissue considerably more diamagnetic than bone marrow (by about 3 ppm, S.I.) [2]. Compartmentalization of the two phases (i.e. bone and marrow) leads to induced inhomogeneous magnetic fields near the interface of the two phases [3].

The empirical observation of a rapid decay of the trabecular bone marrow FID or gradient echo thus results from local induced field gradients (also referred to ‘internal magnetic field gradients’ IMFG). The signal S(t) in the presence of a mesoscopic perturber such as a trabecula in a small volume element as, for example, an imaging voxel can be written as

$$S(t)=\int \int {\int }_V{M}_{\perp }(0)\mathrm{ exp}(i\gamma \mathrm{\Delta }{H}_z(x,y,z)·t)dxdydz$$ (1)

where ΔH_z(x, y, z) represents the local induced field, i.e. the offset from the nominal field.

Based on a magnetic surface-charge model, Hwang and Wehrli [4], computed the induced magnetic field from 3D trabecular bone images and showed the local field to result in a distribution whose mean and variance depend on the orientation of the static magnetic field relative to the structure. These findings are, of course, a consequence of the structural anisotropy of trabecular bone, which is known to grow and remodel in response to the stresses to which is subjected (Wolff’s Law). Since the induced magnetic surface charge density scales as the scalar product of the surface normal n and the applied magnetic field H₀ as

$$\sigma \approx {\mu }_0\mathrm{\Delta }\chi {\mathbf{H}}_0·\hat{\mathbf{n}}$$ (2)

(valid as long as for the susceptibility difference between the two materials, |Δχ| ≪ 1 holds), trabecular plates perpendicular to the applied field get magnetized preferentially. There are various approaches to compute the induced field. In [4] the authors resorted to a surface triangulation method by computing the induced field H_induced at location r as the sum of the induced fields from all source locations r′ as

$${\mathbf{H}}_{\mathit{\text{induced}}}=\sum _{p=1}^N{\mathbf{H}}_{\mathit{\text{induced}},p}^{\mathit{\text{triangle}}}=\frac{1}{4\pi {\mu }_0}\sum _{p=1}^N{\int }_{T_p}\sigma (\mathbf{r}\prime )\frac{(\mathbf{r}-\mathbf{r}\prime )}{{|\mathbf{r}-\mathbf{r}\prime |}^3}dA\prime$$ (3)

where N is the number of triangles and the integral represents the induced field from a single source location. The authors showed that the computation is greatly simplified by assuming that each triangular element has constant surface-charge density given by Eq. (2). The expected structural anisotropy is evident from the histograms of the induced magnetic field computed for the three orthogonal directions of the applied magnetic field relative to the major loading axis, shown for a specimen of human trabecular bone from the vertebrae (Fig. 1). The same authors subsequently evaluated their model by field mapping [5]. From the slopes of regression between the experimental and computed fields they obtained the absolute susceptibility of bone as −11.0 × 10⁻⁶ (S.I.), which is in close agreement with a reported value of −11.3 × 10⁻⁶ obtained with powdered bone by means of a spectroscopic susceptibility matching technique referred to previously [2].

Fig. 1.

(a) Orthogonal slices from a 3D image of trabecular bone from a human vertebral body. The superior–inferior axis is in the z direction. (b) P_marrow (h_induced) when H₀ is aligned with the x, y, or z axis (from [4], with permission).

The width of the induced magnetic field distribution over the sample volume (such as an imaging voxel) can be measured, for example with an asymmetric echo technique for which the echo amplitude evolves as $\text{exp}(-2\tau /T_2^{\prime })$ where τ is the echo offset [6]. Other pulse sequences based on combining RF and gradient echoes such as GESFIDE (gradient-echo sampling of FID and echo) [7] or GESSE (gradient-echo sampling of spin echo) [8] yield both T₂ and $T_2^{*}$ and thus $T_2^{\prime }$ as $1/T_2^{*}-1/T_2$. The full width at half maximum, ΔH, of the distribution of the induced field, P(H_induced), then is related to $T_2^{\prime }$ as $T_2^{\prime }=\gamma \mathrm{\Delta }H/2$. Spectroscopic approaches have also been practiced to obtain $T_2^{*}$ from the line width of the marrow water or methylene resonance [9].

Yablonskiy and Haacke had previously developed a theory for magnetically heterogenous materials such as trabecular bone or networks of blood vessels, showing that the concept of an exponential time constant $T_2^{\prime }$ is valid in the static dephasing regime, but only for decay times longer than a critical time t_c [10]. The static dephasing regime essentially implies that dephasing from local inhomogeneous fields is much faster than phase-coherence loss of magnetic moments as they visit sites of different magnetic field during diffusion, a condition that is generally satisfied for fatty bone marrow but, as we shall see, not necessarily in the cellular boundary zone lining the trabecular trabecular bone surface [11]. Yablonskiy and Haacke’s model also showed $R_2^{\prime }(=1/T_2^{\prime })$ to scale with the volume fraction of the perturber (i.e. bone in the present case) and further that it has and angular dependence for anisotropic structures. The latter arrangement, as previously pointed out, is typical of trabecular networks, which preferentially align along the bone’s major loading axis. For an array of mutually perpendicular struts and columns such similar to the trabeculae found in the vertebrae or in the radius (cf. Fig. 1), the model predicts $R_2^{\prime }$ to obey the following relationship [10]:

$$R_2^{\prime }\propto \mathrm{\Delta }\chi H_0\{{\varsigma }_h+({\varsigma }_v-\frac{1}{2}{\varsigma }_h\left){\text{ sin}}^2\vartheta \right\}$$ (4)

where ς_h and ς_v represent the volume fractions of struts and columns and θ is the angle between the magnetic field and the columns. The predictions of Eq. (4) are in good semiquantitative agreement with experimental findings in model structures [12,13], specimens of trabecular bone [14] as well as measurements in vivo in humans [15].

Measurements of $T_2^{*}$ or $T_2^{\prime }$ have allowed discrimination of patients with osteoporotic bone loss and structural degradation of the trabecular bone network at various anatomic sites including the distal radius, vertebrae and hip, all common fracture sites, as well as at surrogate locations such as the calcaneus (for recent reviews of the subject, see, for example [16]). In general, regional relaxation rates were found to parallel apparent density measured by dual-energy X-ray absorptiometry or quantitative computed tomography. Some of this work has shown $T_2^{\prime }$ or $T_2^{*}$ to discriminate patients with from those without fractures as well or better than bone densitometry [9,17]. However, the translational aspects of these methods are of primary interest to the clinical imaging community and are thus somewhat outside the intended scope of this article.

3.2. Diffusion in background magnetic field gradients

There has been recent evidence that the notion of the static dephasing regime, generally assumed to apply to protons in the marrow spaces exposed to the internal magnetic field gradient (IMFG) at the bone–bone-marrow boundary, may not necessarily be valid [18,19]. If the primary interest is the evaluation of the IMFG this can be achieved with a simple field map, obtained, for example from 3D high-resolution trabecular bone images, such as those reported by Hwang and Wehrli [4], yielding both magnitude and direction of the IMFG as ∇H_z(x, y, z) where H_z(x, y, z) is the local induced magnetic field. Of course, such an approach would require imaging at a resolution adequate to resolve individual trabeculae, which is not required for the methods quantifying $T_2^{\prime }$. In fact, Yablonsky’s theory requires operation in the mesoscopic scale where a statistical distribution of the perturber is present in the volume element, i.e. imaging voxel, therefore being applicable to the in vivo resolution regime.

Some of the more recent methods aimed at probing the IMFG in trabecular bone emerged from work in porous media, conceived by Song and colleagues at Schlumberger [20,21]. DDIF (decay of diffusion in internal gradients) is a method based on collecting a stimulated echo, which is modulated by diffusion in IMFGs caused in the pore spaces of heterogenous materials such as rocks. The basic idea is to sample the stimulated echo signal as a function of diffusion time. Laplace inversion of this signal after correction for decay caused by T₁ relaxation yields what has been referred to as a ‘DDIF spectrum’ from which the pore size distribution can be inferred [20]. The basic DDIF pulse sequence for which also imaging implementations were designed [18,19], is shown in Fig. 2. For large pores as in the case of trabecular bone, with pore volume fractions on the order of 80%, the IMFG is confined to a region encompassing tens of micrometers at most. As a result the DDIF parameters are sensitive to the surface-to-volume ratio [18].

Fig. 2.

(a) DDIF pulse sequence; (b) reference pulse sequence yielding T₁. Timing parameters t_e and t_D represent encoding and diffusion time periods, respectively. An echo signal is detected for DDIF, and an FID is detected for the reference sequence. For imaging the RF pulses are made spatially selective and an imaging module is added. (from Ref. [18] with permission).

For small sampling volumes, i.e. imaging voxels smaller than the typical structural length scale the DDIF rate, 1/T_DDIF, is given by [18]

$$1/T_{DDIF}=1/T_{\mathit{\text{back}}}+{\gamma }^2{G}_{\mathit{\text{int}}}^2{t}_e^{2}D$$ (5)

where 1/T_back is the background relaxation rate, essentially the longitudinal relaxation rate and contributions from diffusion attenuation due to the imaging gradients. Hence, the mean square internal gradient can be computed from Eq. (5). In contrast, for large sampling volumes, i.e. voxels more characteristic of the low-resolution imaging regime in which structural elements typically are not resolved, the DDIF signal exhibits multiexponential behavior commensurate with a distribution of G_int.

Fig. 3 shows DDIF data in specimens of trabecular bone from recent work by Sigmund et al. [18] highlighting the characteristically different decay behavior for samples differing in structural makeup. For example, there was a strong correlation between the short decay fraction and the projected surface area. Similar data were subsequently obtained by the same group of authors from images obtained in various resolution regimes illustrating the potential of the method to characterize structural properties [19].

Fig. 3.

(a) Micro-CT images of bovine tibia trabecular bone samples (top: longitudinal section center: transverse section; bottom: volume rendered image). After marrow removal samples were immersed in saline and subjected to the pulse sequences of Fig. 2. (b) DDIF signal versus diffusion time (top) and resulting DDIF spectra after Laplace inversion of T₁-corrected signal (bottom). Particularly notable is the higher spectral weight of the short-decay time region for the very dense sample B. (from [18], with permission).

Common to the work described above is that it is based on specimen data and further that the experiments were performed after bone marrow removal and suspension in water. The key difficulty to overcome in translating the method to studies in vivo are the diffusion characteristics of bone marrow constituents. At many skeletal locations the marrow is predominantly of the yellow type (for example in the distal extremities), with the dominant signalproducing entity being fatty acid glycerides (FAT). Alternatively, such as in the vertebrae, marrow is mixed, i.e. consisting of both yellow and read marrow, with water being the major constituent in the latter. Since the diffusion coefficient of FAT is two to three orders lower than that of tissue water, diffusion attenuation is expected to be far lower for the former. However, very recent work in Silvia Capuani’s laboratory shows that even at locations of predominantly fatty marrow, diffusion of the water in the cellular boundary layer adjoining the bone surface is sensitive to internal gradients (Fig. 4). Their approach to obtain a collective measure of the IMFG differs from the DDIF approach. Instead, de Santis et al. [11] collected a train of CPMG echoes whose amplitude is attenuated due to both T₂ relaxation and diffusion:

$$S(TE)=S_0\text{ exp}[(-TE/T_2^{\mathit{\text{true}}})-{(\gamma G_i)}^2·ADC·{(TE)}^3]$$ (6)

where $T_2^{\mathit{\text{true}}}$ is the true transverse relaxation rate, G_i is an average internal gradient, and ADC is the apparent diffusion coefficient. The authors then separately determined ADC and $T_2^{\mathit{\text{true}}}$ and extracted G_i by curve fitting in experiments on intact calf tibia trabecular bone samples. In their interpretation the latter represents a dynamic average of the IMFG. Experiments were done both in bulk in spectroscopy mode and by fat suppressed imaging at 400 MHz. T₂, ADC, G_i for water and fat are listed in Table 1. Of interest is the inverse dependence of ADC and internal gradient on trabecular density, which is only present for the water component (Table 1a). ADC for the lipid component was found to be two orders of magnitude lower and independent of trabecular architecture, with the internal gradient determined by the fat–water interface. The authors have since extended their work to the study of patients with independently diagnosed osteoporosis or osteopenia and shown at 3 T field strength that the IMFG measured in the calcaneus (the densely trabeculated heel bone) strongly differentiated patients with low bone density from their healthy peers.

Fig. 4.

Trabecular bone specimen MR images from which the data in Table 1 were obtained. Acronyms refer to low, intermediate and high trabecular density (LTD, ITD, HTD). Red mask superimposed on the images marks the water containing boundary zone in which water molecular diffusion is assumed to occur (from [11] with permission).

Table 1.

T₂, ADC, and G_i in three trabecular bone specimens of variable density with native marrow for both water (a) and fat component (b). Notable is the steep decreases in water ADC with trabecular density and commensurate increase in G_i. In contrast lipid ADC is independent of trabecular density (data from [11]).

	Water (%)	T2 ± SD (ms)	ADC ± SD (×10−10 m2 s−1)	Gi ± SD (mT m−1)	$T_2^{\mathit{\text{true}}}$ ± SD (ms)
(a) Water component
LTD	55	17.0 ± 3.0	19.0 ± 0.4	222 ± 131	17.9 ± 1.0
ITD	47	15.0 ± 2.3	7.0 ± 0.4	282 ± 134	15.2 ± 0.5
HTD	97	14.8 ± 0.4	1.6 ± 0.1	803 ± 181	16.0 ± 0.3
(b) Fat component
	Fat (%)	T2 ± SD (ms)	ADC ± SD (×10−10 m2 s−1)	Gi ± SD (mT m−1)	$T_2^{\mathit{\text{true}}}$ ± SD (ms)
LTD	45	42.3 ± 6.2	5.3 ± 0.3	760 ± 195	43.0 ± 4.8
ITD	53	39.7 ± 4.0	5.9 ± 0.3	727 ± 437	44.0 ± 5.3
HTD	3	31.6 ± 6.0	5.4 ± 0.2	904 ± 119	37.5 ± 9.8

4. Assessment of cortical bone composition and structure

4.1. Bone water and collagen

The structural and physiologic organization of cortical bone substantially differs from its trabecular counterpart. With a porosity on the order of 5–20% it is far denser than trabecular bone, which typically has a pore volume fraction of 80% or greater. As pointed out previously, cortical bone is permeated by a network of channels, called Haversian and Volkman’s canals that make up the large majority of the pore volume. Knowledge of pore volume fraction is of interest in that it increases with age [22] and particularly so in osteoporosis [23], thereby causing a significant decline in the bone’s mechanical properties [24]. Water is the dominant chemical constituent present in the bone’s pore space. However, a significant, typically larger, fraction of cortical bone water is collagen bound. Both fractions possess short T₂ and are thus not detectable with conventional spin-echo or gradient-echo methods. However, the emergence of what is now termed “ultra-short echo time (UTE)” MRI during the past decade has made detection [25] and quantification [26] of bone water possible. UTE MRI has generally proven useful to make heavily collagenated connective tissues such as articular cartilage, tendon, ligaments, and bone “visible” [27]. We shall return to this topic following a brief review of the basic properties of the protons in the bone matrix and the insight recent NMR work has provided.

4.2. Spectral and relaxation behavior of bone water and collagen

Bone water is exchangeable with time constants for exchange, observed for example, by immersion in D₂O, on the order of tens of minutes to hours. Fernandez et al. studied the exchange behavior of bone water from which they determined the apparent diffusion coefficient of water using bulk exchange experiments as well as image-based measurements via finite-difference modeling of the diffusion equation [28]. The authors found an apparent diffusion coefficient in rabbit tibia of 7.8 ± 1.5 × 10⁻⁷ cm²/s at 40 °C (close to physiological temperature), which is over two orders of magnitude slower than that of free water. The data are of interest in that they shed some light on diffusive transport of small molecules from the bone vascular system to the osteocytes, suggesting this process to occur within minutes.

The detectability of bone water hinges largely on the FID’s lifetime. Fernandez et al. measured a line width of the proton signal in rabbit cortical bone at 9.4 T of 1 kHz corresponding ($T_2^{*}~300\mathrm{\mu }\mathrm{s}$) [29]. UTE image based measurements by Reichert et al. at 1.5 T in the human tibia yielded values of 400–500 µs [30], similar to those reported later by Techawiboonwong et al. at 3 T field strength [26,31]. The loss of the majority of the proton signal upon immersion in D₂O clearly showed these protons not to pertain to collagen, the major organic constituent of bone. The initial rapid decay of the post-D₂O exchange signal suggested a collagen proton T₂ at 9.4 T on the order of 20–40 µs in rabbit bone [29]. More recently, Horch et al. [32] performed a detailed spectroscopic and relaxometric investigation of the proton NMR signal in human cortical bone of the femur at 4.7 T. T₂ relaxation spectra were obtained from the echo envelope of a CPMG train with 10,000 echoes were collected at 100 µs echo spacing by fitting the echo amplitudes to a weighted sum of exponentials. The authors found two submillisecond components with T₂ values of 57 ± 4 and 416 ± 35 µs, which they assigned to collagen and collagen-bound water, as well as long-lived components ranging from tens to several hundred milliseconds (Fig. 5a). Their assignment of the short components was further supported by 2D T₂ – T₂ relaxation exchange spectroscopy (REXY) [33] (Fig. 5b). From a quantitative analysis the authors concluded about 70% of total water to be collagen-bound. While these results agree at least semiquantitatively with those obtained with other methods [34], the illposedness of the problem, in particular in the presence of noise and an a priori unknown number of relaxation components, remain a concern [35].

Fig. 5.

(a) Proton T₂ spectra from six donors showing two sub-millisecond peaks and a broad envelope covering a band ranging from about 1 ms to 1 s. (b) Two-dimensional REXSY proton spectra showing cross-peaks between the two sub-millisecond signals, suggesting exchange between two pools during the 200-ms REXSY mixing period, indicative of spins exchanging via magnetization transfer mechanisms. Thus, the protons relaxing with T₂ ~ 60 µs and ~400 µs are in thermal contact during the mixing period while remaining isolated from the long-lived protons (from [32], with permission).

A further indication in support of the assignment of the T₂ relaxation-based assignment of the dominant fraction to collagen-bound water are the findings for T₁, which is far shorter than expected if the majority of the water were contained in the pores of the Haversian canal system. Actual values reported range from 140 to 260 ms [30] at 1.5 T in the human tibial cortex, increasing with age. At 3 T somewhat longer values were found at the same anatomic location, averaging 398 ± 7 ms in five donors, ages 57– 79 years. The unusually efficient T₁ relaxation therefore is indicative of significant motional hindrance.

Ong et al. pursued another approach for unambiguous assignment and quantification of collagen-bound and pore water pools via deuterium NMR [34]. It is well known that collagen-bound deuterium oxide in heavily collagenated, motionally rigid, connective tissues such as tendons or articular cartilage, gives rise to quadrupole splittings (see, for example, [36], for a recent review of the subject). The magnitude, ν_Q of the splitting is given by

$${\nu }_Q=\sum _i{\nu }_i{P}_i(3{\text{ cos}}^2{\theta }_i-1)/2$$ (7)

where ν_i and P_i represent the splitting and population of the ith binding site, and θ_I is the angle between the director – typically the direction of the collagen fibers – and the magnetic field. Accordingly, the largest splitting is expected when the osteon is parallel to the B₀. Since osteons in cortical bone are oriented with their axes parallel to the major loading direction, this coincides with the macroscopic axis for bone from the shaft of the tibia or femur. A similar relationship is expected for protons, in which case the origin of the splitting is dipole–dipole coupling. However, the phenomenon is not commonly observed since proton dipolar split water signals are more sensitive to exchange averaging [37]. Further, as a significant fraction of the tissue water is not ordered (i.e. pore water), the splittings may be partially or fully masked by singlet resonances. One solution is to eliminate the undesired signals by double-quantum filtering. There are multiple approaches to this problem but a convenient pulse sequence (for which also imaging implementations have been reported [36]) is the IP-DQF sequence

$$90°-\tau -90°-t_{DQ}-90°-\tau -90°-t_{ZQ}-90°(Acq)$$ (8)

which returns in-phase spectra [37]. Here τ is the creation time, t_DQ and t_ZQ are the double-quantum and zero-quantum evolution times. Setting of the creation time is critical for optimizing the signal amplitude for a particular magnitude of the splitting ν_Q. The signal amplitude scales as sin(πν_Qτ) indicating that the two signal components ought to be 180° out of phase with each prior to application of the second 90° pulse in [8] to yield maximum signal. Fig. 6a–c shows 400 MHz proton spectra of a small specimen of human cortical bone before and after complete D₂O exchange. Of particular relevance are the post-D₂O exchange DPF spectra showing a broad Pake doublet assigned to the methylene protons in collagen with a splitting of approximately 40 kHz, suggesting an order parameter between 0.5 and 1, consistent with the much higher rigidity of the collagen chains in calcified tissue. Of note is also the expected absence of angular dependence, a situation that is quite different for the deuterium quadrupole splittings of the water (Fig. 6d and e). Here, we find the quadrupole splitting to be approximately half of its value with the osteonal axis perpendicular as opposed to parallel to the field (4.3 versus 8.2 kHz), as predicted by Eq. (7).

Fig. 6.

9.4 T proton and deuterium NMR spectra from a lamb tibia cortical bone specimen at 20 °C: (a) ¹H pulse-acquire and IP-DQF (at creation time, t = 25 µs) spectra before ²H₂O immersion; (b and c) same as (a) after ²H₂O immersion with bone parallel (‖) and perpendicular () to the applied field, B₀. Note increased vertical scale relative to panel a to highlight the dipolar splitting. (d and f) ²H pulse-acquire and IP-DQF (t = 200 µs) spectra after ²H₂O immersion with bone ‖ and to B₀ (from [34], modified).

While a direct comparison of the SQ and DQF spectra does not allow quantitative separation of the bound water from the total water pool, one can exploit the much longer T₁ of the pore water for separation by means of inversion nulling. In this manner Ong et al. [34] succeeded in quantifying pore water fraction achieving good agreement with micro-computed tomography (µCT) derived values. In 24 specimens from six donors varying in age from 27 to 83 years, pore volume fraction was found to increase from 2 to almost 40% correlating highly with µCT derived values with a slope close to unity and and near zero intercept. Conversely, bound water fraction correlated negatively with µCT porosity indicating an increase in pore volume fraction to occur at the expense of loss in osteoid and thus bound water. We shall see below that image-based determination of these important structural parameters by proton UTE imaging may be feasible, even in vivo in human subjects.

4.3. Image-based visualization of sub-millisecond protons in calcified tissues

It was recognized early that the most common spatial encoding techniques based of phase encoding in the second dimension as in Cartesian sampling are generally not suited for imaging spins with very short transverse relaxation, such as quadrupolar nuclei or solids, as the delay imparted by the phase-encoding period entails signal losses. Radial acquisition techniques generally meet the requirement for minimizing the delay δ between the end of the RF pulse and beginning of sampling to satisfy $\delta \ll T_2^{*}$. The second requirement is for the RF pulse duration to be short enough so as to minimize coherence losses during the pulse (${\tau }_{RF}<T_2^{*}$) [38]. Third, the sampling frequency bandwidth (BW) ought to be large enough so that for the total sampling time, $T_s\cong T_2^{*}$, as a means to minimize point-spread function (PSF) blurring.

The various methods being practiced for imaging short-T₂ biological materials only partially meet the above criteria, the key impediment in vivo often being specific absorption rate. Methods such as single-point mapping and their derivatives (e.g. SPRITE [39]) provide a relatively benign PSF but are inefficient otherwise. For imaging calcified connective tissues the family of radial 2D and 3D k-space mapping techniques sketched in Fig. 7 have emerged as favorites even though other methods, such as SWIFT [40], reviewed elsewhere in this special issue of the journal, should have merit too for the target applications discussed below.

Fig. 7.

Most common radial imaging techniques practiced in the author’s laboratory for imaging short-T₂ calcified tissues on 1.5, 3 T and 7 T whole-body scanners: (a) 2D UTE with ramp sampling and slice-selective half-pulses; (b) 3D hybrid-UTE method with variable-TE slice-encoding to encode in the third dimension; (c) 3D UTE with ramp sampling following a non-selective excitation pulse; (d) 3D ZTE pulse sequence differing from (c) by the RF pulse being played out in the presence of the radial encoding gradient.

Pulse design, pulse sequences and reconstruction for UTE MRI have recently been reviewed [41], as have methods and applications specific to bone [42]. Therefore, this section will be relatively brief, keeping the focus on quantification and translation from the laboratory to studies in patients. 2D UTE, a radial encoding technique based on half-pulses not requiring slice gradient rephrasing, was first described by Bergin et al. in 1991 [43] but remained little used until “rediscovered” by Robson et al. in 2003 [25]. This group of researchers recognized its potential for visualizing sub-millisecond T₂ tissues, in particular in conjunction with soft-tissue suppression techniques such as echo subtraction or inversion nulling. Since then the field has rapidly evolved both in terms of methodology and applications to the musculoskeletal (see, for instance [27]) and even the neurologic system [44,45].

Fig. 7 displays generic 2D and 3D pulse sequence diagrams for some of the sequences in current use for imaging short-T₂ tissues. Fig. 7a shows the sequence introduced by Robson et al. [25] involving half pulses with RAMP sampling. Notable is the requirement for two acquisitions of each radial line with opposite polarity of the slice-selection gradients. In this manner, the imaginary signal components cancel upon summing of the two signals [46]. Fig. 7b shows a hybrid 3D implementation differing from the former by inclusion of Cartesian sampling in the third dimension [47]. As a means to minimize echo time at k_z = 0 the slice-encoding gradient is stepped in time rather than in amplitude. Lastly, Fig. 7c and d display 3D radial sequences based on non-selective RF pulses with ramp sampling analogous to Fig. 7a (3D UTE) or with RF excitation in the presence of the encoding gradient (also referred to as 3D ZTE [48,49]). Since the latter fails to capture the lowest spatial-frequency signals, alternative means are required to collect the missing samples, such as resampling that portion of k-space at much lower gradient amplitude [50] or by single-point mapping as in PETRA (pointwise encoding time reduction with radial acquisition) [51]. A third option is algebraic reconstruction based on acquisition of pairs of radial projections with opposite polarity [48,52]. Fig. 8 illustrates the potential of ZTE for imaging teeth, the most densely calcified tissue in mammals, suggesting that the method may be sensitive to subtle demineralization defects in carious teeth not detectable by X-ray imaging [48]. While these studies were conducted on extracted teeth ex vivo at 500 MHz, another recent paper highlights the possible applications of UTE MRI for examining teeth in situ in patients [53].

Fig. 8.

Micro-CT (a) and proton ZTE image of extracted molar tooth obtained at 500 MHz in 6 min 55 s (b). The ZTE image displays large demineralized lesion (arrow A) with invasion into enamel, as well as a smaller lesion barely perceptible in the CT image (arrow B) appearing hyperintense in the MR image (from [48], with permission).

4.4. Suppression of soft-tissue signals

Detection of calcified tissues, most typically cortical and trabecular bone, calcified cartilage, teeth or extra-osseous calcifications, studied with the techniques outlined above, is hampered by the signals of the surrounding soft tissues. Not only are the latter’s spin densities far greater, their transverse relaxation times are at least two orders of magnitude longer. The need to selectively suppress the undesired signals has been recognized early and a variety of strategies have been offered. Most exploit the differential life times of the two proton species. In the simplest approach a second echo collected at TE ≫ T_2,short is subtracted from the UTE signal [30] but this method may be sensitive to gradient-induced eddy currents and, of course, sacrifices SNR as all subtraction methods do.

In 1992, Pauly et al. first proposed the use of saturation pulses that are long relative to T₂ of the fast-decaying spins of interest (τ_RF > T_2short) showing that under these conditions only the long-T₂ soft-tissue protons are mutated, leaving the short-T₂ protons largely unaffected [46]. The design criteria and theory were subsequently detailed by Sussman et al. [38] and various embodiments of the method are now in widespread use, including water and fat saturation consisting of successively applied frequency-selective saturation pulses (WASPI [50]) or dual-band saturation pulses [54]. Single and double-inversion nulling have also been practiced. In order to simultaneously suppress soft tissue signals arising from fat and water Du et al. applied adiabatic inversion pulses in succession, first on resonance with water and subsequently with the methylene proton chemical shift of triacyl glyceride (fat) in such a manner as to time the pulses so that the longitudinal magnetization of both components is nulled immediately prior to playing out the excitation half-pulse [55]. In contrast, the short-T₂ protons of the bone water are only saturated by the inversion pulses. Both inversion and saturation soft-tissue suppression methods can be combined with echo subtraction for additional efficiency of long-T₂ signal attenuation, albeit at the expense of an additional factor of $\sqrt{2}$ reduction in SNR. In a recent comparison of the various suppression techniques Li et al. concluded that combination of dual-band saturation UTE with echo subtraction to provide good short-T₂ SNR and CNR, albeit at the expense of greater sensitivity to B1 homogeneity. In distinction, IR-UTE was found to yield lower short-T₂ SNR efficiency while providing highly uniform short-T2 contrast [54]. Fig. 9 illustrates the spatial and T₂ selectivity of an adiabatic inversion preparation with a pulse bandwidth covering both water and fat spectra.

Fig. 9.

Spatial and T₂ relaxation selectivity of adiabatic inversion: (a) inversion profile of 1 kHz-bandwidth hyperbolic secant inversion pulse for T₁ = 1 s, T₂ = 100 ms; (b) longitudinal magnetization as a function of T₂ indicating that protons with T₂ ≤ 1 ms are saturated by the pulse. Also noted is the relative insensitivity of the effect of the pulse to deviations from desired B1 field (dashed and dotted lines). (c) unsuppressed first echo image (TE = 60 µs) at the mid-tibia obtained with a 2D UTE pulse sequence; (d) same with adiabatic inversion preparation; (e) difference image obtained by subtraction of second echo with TE = 4.6 ms. Arrows indicate tibia and Achilles tendon (modified, from Li et al. [54]).

4.5. Quantification of water in calcified tissues

While mere visualization of protons that ordinarily elude detection by spin-echo based conventional imaging strategies is important in its own right as illustrated in the previous section, quantification of the water residing in the pore spaces of bone tissue versus that bound to the organic matrix, can provide new insight into the structural and molecular organization of the tissue [26,31,47,56,57]. Techawiboonwong et al. conceived a method based on calibration of the signal with a reference sample of known proton concentration and similar T₂ relaxation characteristics in specimens of human cortical bone from the tibia and subsequently in patients [26,31]. The transverse magnetization at time t = TE can be written as

$$M_{xy}(TE)=C{\rho }_0{f}_{xy}\frac{1-e^{-TR/T1}}{1-f_z{e}^{-TR/T1}}{e}^{-TR/T_2^{*}}$$ (9)

where f_xy and f_z represent the transverse and longitudinal magnetizations at the end of the RF pulse [38]:

$$f_{xy}=i\text{ exp}(-\tau /2T_2^{*}\gamma B_1\tau ·\text{sin }c[\sqrt{{(\gamma B_1\tau )}^2-{(\tau /2T_2^{*})}^2}]$$ (10)

and

$$f_z=\text{exp }(-\tau /2T_2^{*})\text{ cos }\left[\sqrt{{(\gamma B_1\tau )}^2-{(\tau /2T_2^{*})}^2}\right]+\tau /2T_2^{*}\times \text{sin }c\left[\sqrt{{(\gamma B_1\tau )}^2-{(\tau /2T_2^{*})}^2}\right],$$ (11)

We see that under conditions where $\gamma B_1\gg 1/2T_2^{*}$ the expressions for f_xy and f_z revert to the usual cosine and sine terms of the flip angle γB₁τ. In a second regime, referred to as “critically damped” [38], the two terms balance each other ($\gamma B_1\approx /2T_2^{*}$) and some transverse magnetization that is independent of the nominal flip angle is still generated:

$$f_{xy}=i\text{ exp}(-\tau /2T_2^{*})\tau /2T_2^{*}$$ (10a)

while for the longitudinal mapping function the following is obtained:

$$f_z=\text{exp }(-\tau /2T_2^{*})(1+\tau /2T_2^{*})$$ (11a)

In the third regime, termed “overdamped”, where $\gamma B_1\ll 1/2T_2^{*}$ no excursion of the magnetization from the z-axis occurs, i.e.

$$f_{xy}\approx 0$$ (10b)

and f_z becomes [38]:

$$f_z=\text{exp }(-{(\gamma B_1\tau )}^2/(\tau /T_2^{*}))$$ (10b)

Eqs. (10) and (11) are valid for rectangular pulses but the two quantities need be computed numerically for selective pulses such as half-sinc pulses used in 2D UTE. In this situation, the actual transverse and longitudinal magnetizations deviate more significantly from their nominal values as the pulse duration is an order of magnitude longer than for non-selective pulses.

The authors in [31] validated their method in specimens of human cortical bone by means of deuterium exchange techniques whereby they measured the native water expelled from the bone after prolonged immersion in D₂O in comparison to measurements by UTE. They found the two methods to correlate (r² = 0.99, p < 0.001) but found that even after complete exchange there was a residual signal on the order of about 10%, which was attributed to non-exchangeable protons, likely pertaining to lipids. Further, a pilot study in a small group of pre- and postmenopausal women and patients with renal dystrophy showed bone water measured by UTE MRI in the mid-tibia cortex to be greater by 65% (28.7 ± 1.3 versus 17.4 ± 2.2%, p < 0.001) in the premenopausal than in the postmenopausal group, with the highest bone water concentration (41.4 ± 9.6%) found in the subjects with renal disease. The authors interpreted their findings as reflecting increasing porosity with age and particularly in subjects with end-stage renal disease. We have seen previously, however, that bulk measurements based on T₂ relaxometry [32] and deuterium NMR [34] support the notion that a greater fraction of bone water is collagen bound as opposed to pore-resident. Thus, increased pore water fraction can only occur as a result of a decrease in osteoid volume and thus a decrease in collagen-bound water, thereby suggesting two opposing, potentially mutually canceling effects. However, because of the greater volume density of pore water, a reduction in a given amount of bone tissue will result in a disproportionate gain in pore water. It is for this reason that bulk water fraction was also found to correlate with independently measured pore volume fraction, as observed by Ong et al. [34]. Nevertheless, noninvasive separation of the two water fractions would be desirable as a means to evaluate porosity indirectly, i.e. without the need to resolve individual pores.

Diaz et al. [58] hypothesized that pore water, by virtue of its greater mobility, should have longer $T_2^{*}$. The authors then showed in bovine cortical that the $T_2^{*}$ decay fit a bicomponent model

$$S(T_2^{*})=A_S\text{ exp }(-\frac{t}{T_{2s}^{*}})+A_l\text{ exp }(-\frac{t}{T_{2l}^{*}})$$ (12)

with A_s and A_l being the fractions of the short and long $T_2^{*}$ components, which they found to be on the order of 80% and 20% and 300 µs and 2 ms, respectively, and which they attributed to bound and free water. In subsequent work from the same group, Bae et al. [59] found the two water populations to be correlated with µCT-derived porosity; positively with the free water fraction and negatively with the bound water fraction (both R² = 0.25, p < 0.001), in good qualitative agreement with the work by Ong et al. [34], discussed above. Therefore, the results lend credence to the authors’ assignments suggesting the long-$T_2^{*}$ component to be predominantly composed of free, i.e. pore water, and thus pore volume fraction. Horch et al. questioned the validity of the $T_2^{*}$ relaxometric approach arguing that the pore water NMR line should be inhomogeneously broadened by virtue of the expected large range of resonance frequencies governed by pore-matrix susceptibility and pore geometry [60].

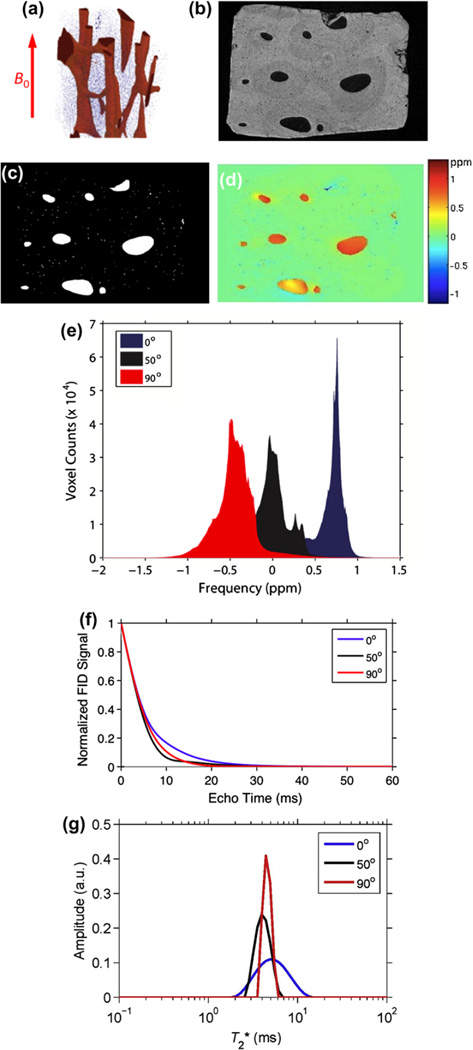
We tested this hypothesis by computing the induced field similar to the approach in [4] for trabecular bone except that much higher-resolution images are required since the pore sizes in cortical bone are one to two orders of magnitude smaller than those of the spaces between adjacent trabeculae. The induced magnetic field ΔB in the pore spaces of the Haversian and lacunar system of cortical bone was computed by means of the fast Fourier approach in k-space (see, for example [61]) as

$$\mathrm{\Delta }B(x,y,z)/B_0=F{T}^{-1}(FT(\mathrm{\Delta }\chi (\mathbf{r}))(\frac{1}{3}-\frac{{(k_z\mathit{\text{cos}}\theta -k_y\mathit{\text{sin}}\theta )}^2}{k_x^2+k_y^2+k_z^2}\left)\right)$$ (13)

where FT is the Fourier operator, (Δχ(r)) is the spatial distribution of the relative magnetic susceptibility at spatial location r(x, y, z) (obtained from the 3D image after segmentation into bone and pore space). The expression $(\frac{1}{3}-\frac{{(k_z\text{cos}\theta -k_y\text{sin}\theta )}^2}{k_x^2+k_y^2+k_z^2})$ is the Fourier transform of the convolution kernel representing the dipole field $d=\frac{1}{4\pi }\frac{3{\text{cos}}^2\theta -1}{{|r|}^3}$ and θ is the angle of the x-axis relative to the applied field B₀. Fig. 10a–d show a 3D rendition of a small volume of cortical bone, along with a map of the induced field. In Fig. 10e, the histogram of the induced field is displayed for three orientations of the specimen axis relative to the magnetic field showing characteristic shifts similar to those predicted previously in trabecular bone [4] and observed experimentally in specimens [14] and humans in vivo [15]. The predicted FID and $T_2^{*}$ relaxation spectrum is shown in Fig. 10f and g. In order to simulate T₂ (as a means toward predicting $T_2^{*}$ as the sum $1/T_2+1/T_2^{*}$) a surface relaxation model was used similar to the one described by Wang et al. to estimate CPMG decays rates in cortical bone [62]. It is based on the concept that 1/T₂ = ρ · S/V where ρ is the surface relaxivity, S is the pore surface and V its volume. Since surface relaxivity is unknown pore water T₂ was assumed to cover a range of 10 ms and the signal s(t) was calculated as the sum of contributions from each pore voxel i as

$$s(t)=\sum _i\text{exp}(-t/T_{2,i}+j2\pi \gamma B_{i}t).$$ (14)

where ΔB_i is the induced field in pore voxel i and summation is over all pore voxels. The two terms in the equation thus represent damping from surface relaxation and static dephasing. Since the voxel is much smaller than the pore size (1 µm versus ≥20 µm) it is reasonable to consider the field to be approximately constant across the voxel. We note the preliminary nature of these data requiring corroboration in other specimens as well as experimental verification. Nevertheless, the predicted $T_2^{*}$ is of the order observed in cortical bone specimens and in vivo by bi-component analysis [59].

Fig. 10.

Induced magnetic field in the pore space of the Haversian system: (a) 3D rendition of a small volume of human cortical bone of the mid-tibia obtained at 1 µm isotropic voxel size; (b) cross-sectional image; (c) segmented image (pore space white); (d) induced magnetic field in the pore spaces computed from Eq. (13) assuming a volume susceptibility Δχ = 4π·0.19, showing section across 3D volume; (e) histogram of induced field for three orientations of the osteonal axis relative to B₀; (f) predicted decay of the UTE signal computed from Eq. (14) for three orientations relative to the magnetic field; (g) $T_2^{*}$ spectra obtained by inversion of the FIDs in (e) (C. Li et al., unpublished).

4.6. Bone mineral

Mineral density is commonly assessed by X-ray based modalities, either dual-energy X-ray absorptiometry or quantitative computed tomography, which provide a density measure expressed in g/cm² or g/cm³, respectively. Both methods use ionizing radiation even though the former’s dose is minimal. The density measurements are non-specific and are apparent in the sense that the resolution is such that reduced tissue mineralization could not be distinguished from bone of greater microporosity. This ambiguity, it has been argued [63], precludes distinction of osteoporosis in which bone becomes porous but is generally normally mineralized, from osteomalacia, a disorder in which the bone is hypomineralized. The same group of authors reasoned that true mineralization density (variably also denoted ‘degree of mineralization of bone’, DMB [64] or ‘extent of bone mineralization’ [65]) could be obtained by quantifying matrix volume (i.e. the fractional volume of bone occupied by bone tissue). Cao et al. [65] achieved this goal by solid-state radial imaging with water and fat suppression (WASPI [50]) in conjunction with a polymer blend of matching relaxation times serving as a calibration standard. Hence, phosphorus density via solid-state ³¹P imaging, whose feasibility was first shown by Wu et al. [66] and matrix volume, would allow derivation of DMB.

While path delineated above toward noninvasive quantification of DMB is plausible, the method is fraught with difficulties. Chief among these are the extremely unfavorable relaxation properties of ³¹P in bone mineral with T₂/T₁ ratios on the order of 10⁻⁵–10⁻⁶ depending on field strength [67] (compared to about 0.02 for protons in soft tissue). Nevertheless, 3D radial ³¹P imaging in animal models has yielded unique information on mineralization in model systems of osteomalacia [68] and response to antiresorptive treatment [69]. The very short T₂ of ³¹P in bone mineral and its further shortening with field strength (reaching 120 µs at 7 T) is likely a consequence of the significant chemical shift anisotropy of hydroxyl apatite (~40 ppm) [70]. Besides adversely affecting SNR, point-spread function blurring limits the effective resolution to a few millimeters. In spite of these adversities Wu et al. [71] recently have been able to acquire ³¹P images of the human wrist in vivo at 3 T field strength on a clinical scanner with a custombuilt birdcage transmit-receive coil (Fig. 11). The critical hurdle to overcome was to shorten the receiver dead-time in the spectrometer’s ³¹P RF chain, which the authors accomplished by mixing the proton transmit pulse frequency with the frequency from an external synthesizer. In this manner they achieved an effective delay from the end of the pulse to the start of data acquisition of 20 µs.

Fig. 11.

In vivo ³¹P 3D radial MRI of bone mineral of the wrist of a healthy 41-year-old male volunteer. (a) Schematic view of the scanned region. (b–d) Posterior–anterior, lateral and transverse image slices; (e) three-dimensional iso-surface rendering of the full dataset. Distal radius and ulna including marrow cavity are clearly visualized (from [71], with permission).

5. Direct detection of trabecular architecture via high-resolution marrow MRI

Much work has been focused on methods for direct visualization and quantification of structure at length scales resolving individual trabeculae. However, in spite of advances in pulse sequence methodology and RF coil design, in vivo structural imaging of trabecular bone architecture largely remains confined to peripheral skeletal locations such as the wrist and ankle. Here, closely coupled receive coils ensure that adequate SNR levels can be attained, currently allowing for voxel volumes as small as 4 × 10⁻³ mm³ at 3 T field strength [72]. Notably, these are one to two orders of magnitude lower than those practiced in structural imaging of the musculoskeletal system. Since much of the technology and applications have been reviewed in recent years (see, for instance, [16,73] and references cited) only the most recent pertinent developments will be discussed. Lastly, it needs to be pointed out that MRI competes with CT as both modalities have demonstrated their ability to yield structural information (see, for instance [74]).

Initially, structure evaluated in terms of scale, topology and orientation of the trabecular networks had been given the most attention as possible surrogates for bone strength and for assessing fracture susceptibility in patients [75]. For example, it is known that bone loss occurring during aging, and at an accelerated pace in osteoporosis, entails perforation of trabecular plates, leading to conversion of plates to rods [76], thereby disproportionately weakening the structure [77]. Since trabeculae orient along the major stress lines, various measures of structural orientation, including mean intercept length [78] and spatial autocorrelation analysis [79] have been applied as a means to mathematically describe structural anisotropy from in vivo MR images [80]. Wald et al., on the basis of in vivo images of the distal tibia, were able to show that bone volume fraction and indices of structural anisotropy predicted the bone’s mechanical competence with high accuracy [81].

More recently, there has been a shift toward exploiting the capabilities of obtaining images representative of partially or fully resolved 3D structural images as input into finite-element (FE) solvers, typically after converting voxels to hexahedral finite elements [82]. Since in spin-echo imaging marrow protons are the signal producing entities while pure bone appears with background intensity (as bone water cannot be detected at typical echo times on the order of several milliseconds), the raw images are processed to yield parametric images in which signal amplitudes represent the fractional voxel occupancy by bone (i.e. bone volume fraction maps) [83]. Full validation of the structural indices would require mechanical testing on specimen images obtained at comparable resolution. However, there is compelling evidence from earlier work based on high-resolution micro-computed tomography that indicates good agreement between FE derived indices and mechanical test results [84] and further, that the predicted mechanical indices obtained in a resolution regime of in vivo imaging are strongly correlated with those derived by high-resolution CT imagery [85].

MR image based FE analysis has shown potential as a means to assess the response to intervention in patients with various disorders of bone mineral homeostasis such as treatment with drugs preventing bone resorption or enhancing bone formation [87,88] or to evaluate the implications of organ transplantation [86]. In [86], the authors showed that 6 months following renal transplantation both cortical and trabecular bone stiffness estimated in the distal tibia decreased, presumably as a result of exposure to large doses of steroids. Fig. 12a–c shows a single image from a 3D image array along with processed bone volume fraction map for FE modeling. Magnified strain energy maps at two time points highlighting local structural and mechanical alterations are displayed in Fig. 12d.

Fig. 12.

(a) Axial view of MR image obtained at the left distal tibia (b, inset) from a 25-year old woman at 137 × 137 × 410 µm³ voxel size. (c) Bone-volume-fraction (BVF) map derived from A representing the fractional occupancy of bone linearly scaled between 0% (pure marrow) and 100% (pure bone) at each voxel. (d) Comparison of strain maps obtained from whole-bone at time of kidney transplantation and 6 months thereafter. Magnified 1 mm × 2 mm × 6 mm regions highlight alterations occurred in the trabecular bone network between the two time points: (A) enlargement of a perforation, (B) thinning of a vertical trabecula, (C) a plate-to-rod conversion, and (D) strain accumulation due to bone loss (from [86], with permission).

FE modeling in the nonlinear regime to predict the bone’s yield and post-yield behavior has also come of age, thanks to algorithmic advances and the unprecedented computing power that has become available with multi-core desktop computers and the ever-decreasing cost of RAM [83]. Recent work in the author’s laboratory shows that fracture toughness (energy required for the bone to fail) obtained as ∫σ(ε)dε where σ and ε represent stress and strain, and integration is to peak strain, is not well predicted by linear indices such as stiffness [89].

MRI based FE methodology is still in its infancy and, except for the wrist, the major fracture sites are the femur and vertebrae, anatomic locations at which high-resolution imaging is more difficult. Much of this work has been performed for compressive loading, which is rarely the failure mechanism that leads to fracture. Further, MRI currently provides only limited information on the intrinsic material properties determined by mineral density and composition, or chemical modification occurring in collagen (e.g. nature and extent of cross-linking, water binding, etc.), some of which have been discussed previously. Lastly, the material modulus is generally assumed to be isotropic even though this is known not to be correct given the highly anisotropic nanostructure of this complex biomaterial.

In summary, some of the work discussed in this article, shows that NMR and MRI can provide unprecedented insight into structure and function of calcified tissues nondestructively, and in many instances, noninvasively, in animals and humans. Further advances are difficult to anticipate just as much of what we now take for granted was entirely unforeseeable a mere two decades ago.