Abstract
Three driving forces control the energy level alignment between transition-metal oxides and organic materials: the chemical interaction between the two materials, the organic electronegativity and the possible space charge layer formed in the oxide. This is illustrated in this study by analyzing experimentally and theoretically a paradigmatic case, the TiO2(110) / TCNQ interface: due to the chemical interaction between the two materials, the organic electron affinity level is located below the Fermi energy of the n-doped TiO2. Then, one electron is transferred from the oxide to this level and a space charge layer is developed in the oxide inducing an important increase in the interface dipole and in the oxide work-function.
Keywords: titanium dioxide, tcnq, DFT, charging energy, band bending, space-charge layer
1. INTRODUCTION
Hybrid materials that contain interfaces between transition metal oxides and organic species exhibit very promising properties for applications in devices like solar cells, light emitting diodes, fuel cells and thin films transistors. In particular, the easy injection of charge between the oxide and the organic, which depends critically on the barriers formed at the interface between the materials, plays a very important role in the good efficiency of those devices.1—6
A large amount of work has been undertaken in an effort to understand the energy level alignment between different metal/organic and organic/organic interfaces.7—9 In contrast, very few studies have analyzed the energy level alignment at the interface between transition metal oxides and organic semiconductors. In a recent work, Greiner et al.10 analyzed a variety of non-reactive oxide/organic interfaces and concluded that the energy level alignment is determined mainly by one driving force: the electron chemical potential equilibration between the oxide Fermi level and the organic ionization energy. On the other hand, Xu et al.11 have conclusively shown that a second driving force is the oxide doping and the concomitant formation of a space-charge layer upon the interaction with the organic material; for strongly n-doped oxides, such as ZnO or TiO2, this mechanism is particularly important when the organic affinity level is located below the oxide Fermi level, as is the case of F4TCNQ physisorbed on a H-saturated ZnO(000-1)surface.11 Recently, other groups6, 12 have also shown the important role that the oxide/organic interface chemistry has in the barrier formation. All this suggests that the injection of charge between transition metal oxides and organic materials depends crucially on the interface barrier that is determined mainly by the relative electronegativity of both materials, the possible space-charge layer formed in the oxide, and the chemical interaction between the oxide and the organic.
In order to understand how the combination of all these effects operates in the formation of the oxide/organic level alignment, we have analyzed in this work the particular case of the TiO2/TCNQ interface; TiO2 is one of the most extensively studied substrates for organic devices,13—14 while TCNQ is an organic molecule, frequently used due to its very electronegative properties,15—18 showing a strong chemical interaction with the substrate. We can expect that an important chemical interaction and charge transfer should appear between the two materials, which should affect the interface barrier formation as well as the creation of a metal oxide space charge layer. In the following we shall show experimentally and theoretically that this charge transfer is significant with one electron being transferred from the oxide to the LUMOTCNQ level which is located below the oxide conduction band edge; our results are also compatible with an important increase in the metal oxide work-function. We shall also show that the chemical interaction between the oxide and this very electronegative organic material plays an important role in the creation of that charge transfer and in the formation of an oxide space charge layer.
In our approach, we first use different spectroscopic techniques (UPS, IPS and XPS) to characterize the electronic properties of the TCNQ/TiO2 interface. A theoretical analysis of these data is a delicate task11 due to the different length scales associated with the oxide space charge layer or with the intimate contact between the organic and the oxide. In our analysis we combine a DFT-LDA calculation of that contact with a classical description of the space charge layer; the connection between these two different regimes is provided by the charging energy of the molecule, which is associated with the charge transfer from the oxide space charge layer to the LUMOTCNQ level.
2. EXPERIMENTAL RESULTS
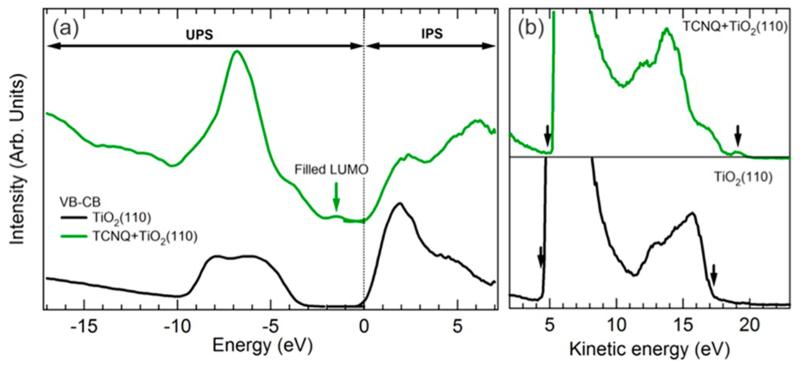
A TiO2(110) single crystal surface prepared in UHV (see Supporting Information for details) and exposed to TCNQ was found to saturate at room temperature to a coverage referred to as monolayer coverage (ML) in the following. The valence and conduction band spectra of the clean and TCNQ-exposed TiO2, measured respectively using ultraviolet and inverse photoemission spectroscopies (UPS and IPS) are displayed in Figure 1(a). On this figure, the zero of energy is defined as the Fermi level, so that the occupied states are characterized with a negative energy and the unoccupied state with a positive energy. The valence band (VB) of the pristine TiO2(110) surface originates mainly from O 2p states, while the conduction band (CB) is composed of Ti 3d states. A linear fit of the sharp band edges to the background of the spectra indicates a valence band maximum at −3.5 eV and a conduction band minimum at 0.1 eV, resulting in a 3.6 eV gap for TiO2. The position of the Fermi level, only 0.1 eV below the conduction band, is indicative of the strong n-doped nature of the TiO2 crystal (see SI for the details of band edges measurements). Upon TCNQ adsorption, molecular states are appearing both in occupied and unoccupied states as seen in Figure 1(a). These molecular states cannot be interpreted in terms of the molecular signature of an intact TCNQ molecule. (In contrast, the VB and CB spectra of a TCNQ multilayer grown at 230 K on a metal substrate, shown in Supporting Information, can be directly compared to the DOS calculated for a TCNQ molecule.) This indicates that TCNQ is strongly affected by the presence of the TiO2 surface. Particularly important for this study, the first occupied molecular states are found in the gap of TiO2, 1.5 eV below the measured Fermi level, as indicated by the arrow in Figure 1(a). In the unoccupied states, broad molecular features, superimposed upon the contribution of the strong Ti 3d state of the TiO2 substrate CB, prevent a clear determination of the unoccupied frontier molecular states.
Figure 1.
(a) Valence and conduction band spectra measured using UPS (He II, hν=40.8 eV) and IPS (E=20.3 eV) respectively, of the clean TiO2(110) surface and of the same surface saturated with TCNQ. The zero of energy is chosen as the position of the Fermi level. (b) Secondary electron cutoff determination using the full width of the emitted photoelectrons (He I, hν=21.1 eV).
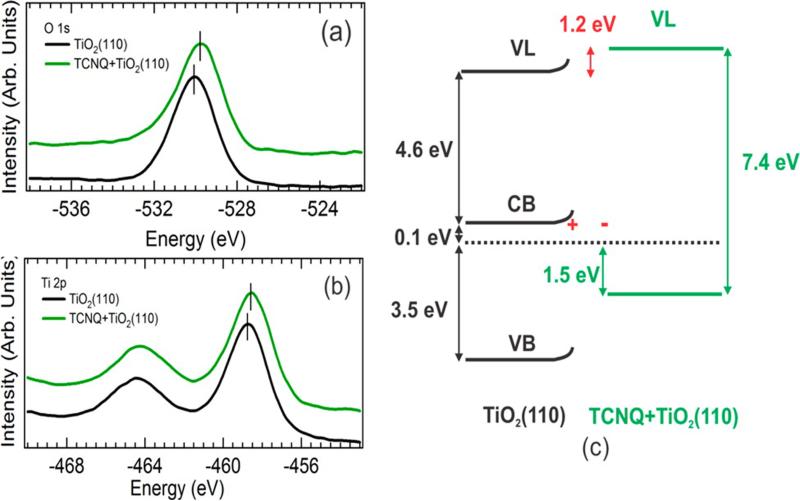
The position of the vacuum level (VL) of the system has also been measured for the clean and TCNQ-exposed TiO2(110) surface, using the position of the secondary electron cutoff (SECO) of the total spectra of emitted photoelectrons shown in Figure 1(b). An energy separation of 13 eV (delimited by the arrows) is measured between the VB edge and the SECO of the clean TiO2(110) surface. With a photon excitation energy of 21.2 eV and a measured gap of 3.6 eV, the electron affinity for the TiO2(110) surface is found to be 4.6 eV. For the TCNQ-saturated TiO2 surface, the distance between the first occupied molecular state and the SECO (delimited by the arrows) is measured to be 13.8 eV, giving a distance of 7.4 eV between that first occupied molecular state and the VL of the molecule (see Figure 2(c)).
Figure 2.
(a) O 1s and (b) Ti 2p core levels of the substrate before and after TCNQ adsorption. A clear peak displacement is observed for both core levels and attributed to upward band bending. (c) Energy diagram obtained from the experimental data shown in Figures 1 and 2.
Figure 2 shows x-ray photoemission spectra measured on the clean and on the subsequently saturated TiO2(110) surface. In Figure S1 (see Supporting Information), large scale survey scans indicate that, as expected, only C 1s and N 1s core levels are added to the initial Ti 2p and O 1s core levels belonging to the surface. The molecular coverage can be evaluated by comparing the relative ratio of C 1s and Ti 2p core levels to no more than a monolayer. Upon TCNQ adsorption, a noticeable shift of the TiO2 surface core levels is observed as shown in panels (a) and (b) of Figure 2. Both the O 1s and Ti 2p core level spectra are found shifted toward the Fermi level by about 0.2 eV after TCNQ adsorption. Such behavior is interpreted as an upward band bending at the surface of the TiO2 substrate, due to charge reorganization at the TCNQ/TiO2 interface. This band bending and the VL (of the TiO2 + 1ML TCNQ system) shift, shown in panel (c) of Figure 2, are indicative of a strong negative charge transfer from the oxide to the molecule. This is analyzed theoretically in the following.
3. THEORETICAL ANALYSIS AND DISCUSSION
The TCNQ/TiO2 interface was analyzed by means of an accurate and efficient local-orbital Density Functional Theory (DFT) approach (see Supporting Information for further details). In a first step, we consider the T=0 K case, and analyze the interface geometry neglecting van der Waals interactions due to the strong chemical bonds between the molecules and the oxide surface, which are partially ionic. In a second step, the electronic properties of the interface, including the TiO2/TCNQ level alignment and charge transfer, are calculated introducing appropriate corrections in the DFT calculation.17—18 Although the intermolecular distance is long, there is an important interaction between molecules related to the electrostatic potential induced by the molecule/oxide charge transfer. Finally, we introduce temperature effects and analyze the space charge layer formation and the charge transfer from the oxide to the LUMOTCNQ level.
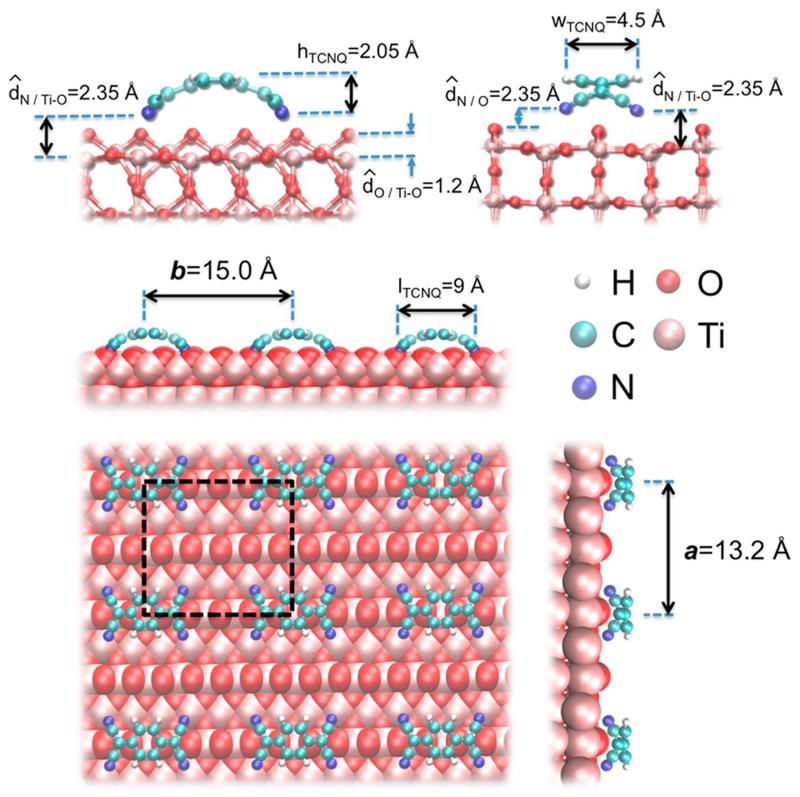
Lattice vectors and unit cell for the periodic DFT calculations are shown in Figure 3 (α=13.2 Å;b=15.0 Å) for a TCNQ monolayer on TiO2(110). The TiO2(110)-surface is represented by a slab with 5 layers and the TCNQ adlayer is placed on one side of the slab; thus, there are in total 360 atoms per unit cell including the TCNQ molecule. The Brillouin zone (BZ) has been sampled by means of 8 special k-points using a Monkhorst-Pack grid,19 guaranteeing a full convergence in energy and density. In our calculations for the interface geometry, we have started with a perfectly flat TCNQ molecule and have applied a dynamical relaxation procedure to obtain the most stable chemisorbed state. Our DFT calculations show that the TCNQ molecule forms strong bonds with the TiO2 surface. After several initial positions of the molecule on the oxide unit cell, we have obtained the relaxed interface geometry shown in Figure 3: TCNQ is deformed by its interaction with the oxide, with the N atoms strongly bonded to O and Ti; while the mean distance from the central part of the molecule to the first layer of oxygen atoms is 3.20 Å, the N—O and N—Ti distances are around 2.80 Å and 2.87 Å, respectively. The unit cell size defining the molecule—molecule distance has been fixed assuming a good matching between the oxide and the adsorbed TCNQ-structure; we stress that these distances are similar to the ones found in other TCNQ-interfaces.20—22
Figure 3.
Surface geometry for the TiO2/TCNQ interface. Notice the pronounced on-surface molecule bending of 2.05 Å, which is the height of the molecule, hTCNQ. Width and length of the molecule, wTCNQ and lTCNQ, are also indicated, as well as the average distances between N atoms and the oxide O-rows, , between the N atoms and the topmost oxide Ti-O plane, , and between the oxide O-rows and the topmost oxide Ti-O plane, . The black-dashed square of size (13.2 × 15.0) Å2 shows the unit cell used in the calculations.
For a careful discussion of the organic/oxide interface electronic properties, one has to introduce some corrections to the standard DFT-calculations due to limitations of this approach: (a) the Kohn-Sham energy levels yield transport gaps that are usually too small;7, 17, 18 (b) although the local-orbital basis set has been optimized in each material to give a reasonable description of the electronic properties of either the oxide or the organic (except for their energy gaps), their initial relative level alignment is not correctly described, a general problem that appears for even well converged LDA-calculations.23
The energy gap for a TCNQ molecule in the gas phase, Eggas, (measured as the energy difference between its electron affinity and ionization potential) is about 5.3 eV, whereas the energy gap between the Kohn-Sham HOMO and LUMO levels in LDA (or in GGA) calculations, EgLDA, is 1.7 eV.20, 24—26 This difference is related to the self-interaction energy, and is described by the molecular charging energy term, Umol, with Umol=Eggas-EgLDA=3.6 eV for TCNQ in gas phase.7
In the case of the organic-oxide interface, additional electron correlation effects reduce the gas phase charging energy, Umol, to U and, consequently, the energy gap of the adsorbed TCNQ molecule. These effects are associated with the image potential induced by the oxide and the other molecules on the electron (LUMO) or the hole (HOMO) of the molecule under consideration. Similar to what has been reported before for organic adsorbates on metal surfaces, U is calculated by analyzing the case of an isolated molecule on the oxide27 (neglecting in this way the effects of the other molecules) and relating U to the electrostatic energy shift introduced in the frontier orbitals of the molecule, eVcharge, by the charge transfer, n (expressed in electron units), between the oxide and the single molecule: eVcharge=nU. In our calculation (see more details below) we find U=1.9 eV leading to a TCNQ energy gap of 1.7 eV+1.9 eV=3.6 eV. We stress that this is the energy gap for any TCNQ-molecule of the organic monolayer, even though we have calculated it for an isolated one; the rationale behind this is that the image potential effects, which are mainly controlled by the effects of the oxide on a single molecule, determine the organic energy gap. Accordingly, we account for those polarization effects on the energy gap by introducing the following operator in the DFT-LDA calculation:27—29
| (1) |
|μ〉 (|ν〉) being the empty (occupied) orbitals of the isolated molecule (with the actual geometry of the molecule on the surface). We stress that once U is determined from the single molecule case, the corresponding scissor-operator is applied for all the molecules of the monolayer; this implies, as already mentioned, neglecting other molecules contributions to the dynamical polarization effects of the system on the organic energy levels.
The misalignment between the initial levels of the oxide and the organic is corrected by introducing the following operator:27—29
| (2) |
where ε fixes the relative between the oxide and the molecule levels. In our calculations, the initial LUMOTCNQ level is chosen 5.0 eV below the vacuum level, a value close to the ones reported for TCNQ multilayers (and by this work within our error bars as shown in Figure S2) if the energy gap is reduced symmetrically around the mid-gap to 3.6 eV.28 For the oxide, the conduction band edge, Ec, is located 4.6 eV below the vacuum level (as shown in Figure 2c). Although in our calculations the oxide energy gap is only 3.0 eV, we expect a good description of the most important charge transfer that takes place at the TCNQ/TiO2(110) interface: the charge transfer from the conduction band of the strongly n-doped oxide to the LUMOTCNQ level. We remark that the corrections introduced in our calculations by means of the operators (1) and (2) are reminiscent of the “shift and stretch” procedure30 used by other groups to correct the DFT-LDA Density of States calculations.
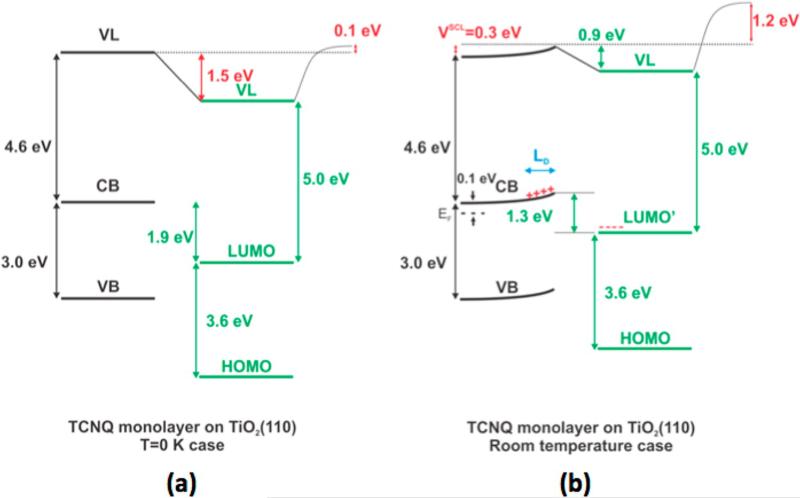
Figure 4(a) shows the energy level alignment obtained at T=0 K for a TCNQ monolayer on TiO2(110). Although before contact (i.e. with vacuum levels aligned), the LUMOTCNQ level was initially located 0.4 eV below the oxide conduction band edge (CB), its final position is now 1.9 eV below CB. This shift originates from two effects: (a) a strong oxide-molecule hybridization resulting in a 1.6 eV shift of the LUMOTCNQ toward higher binding energies, competing with (b) an electrostatic dipole of 0.1 eV moving the LUMO level toward lower binding energies due to charge rearrangement upon hybridization. This electrostatic dipole has two contributions: Vmol, a dipole induced by the distortion of the molecule upon adsorption on the surface (eVmol= −0.50 eV) and Vcharge from charge transfer (eVcharge= 0.60 eV). The result of the hybridization and the total electrostatic dipole is a downward displacement of the LUMO level with respect to its initial position by 1.50 eV, yielding a LUMO that is now found 1.9 eV below CB.
Figure 4.
Energy alignment calculated for the TCNQ/TiO2(110) interface at (a) T=0 K and (b) room temperature. A 0.30 eV band bending is estimated at room temperature for n-doped TiO2.
Given the highly n-doped nature of the TiO2 substrate (for our doping level the Fermi level is found 0.1 eV below the conduction band edge), this energy alignment suggests that, at room temperature, there should be a strong thermally excited charge transfer from the oxide to the LUMOTCNQ. This populated LUMO will be referred to as LUMO’ in the following as it is not formally the lowest unoccupied state of the system anymore. This transfer of charge should create an important electrostatic potential at the interface with two contributions: a surface potential VSCL due to the space charge layer in the oxide extending a distance of a Debye length, LD, into the crystal (as shown in Figure 4b), and an interface potential due to the negative charge (Q in electron unit) in the LUMO’ level and the corresponding opposite positive charge in the oxide (−Q also in electron unit).31
The space-charge (or boundary layer) potential, V(z), can be analyzed using Poisson’s equation:32
| (3) |
where LD2=εkT/4πene (ne being the electron charge density for the n-doped oxide material), z is the direction normal to the interface. In our calculations, we consider ne≈1019 cm−3 and ε≈120 for the oxide (110) direction resulting in LD≈40 Å at room temperature. At the surface of the oxide, the surface potential VSCL can be approximated to VSCL≈4πQeLD/εA, A being the surface area per molecule (around 200 Å2), resulting in an energy shift: eVSCL/Q≈ 0.30 eV. Assuming Q=1, this value is compatible with the 0.2 eV O 1s and Ti 2p core levels shifts measured in photoemission upon TCNQ adsorption (as shown in Figure 2). Consequently, the effect of the space charge layer on the oxide/organic alignment is to displace both the oxide surface layers and the organic levels to lower binding energies.
The strong charge transfer Q from the oxide toward the LUMO’ level that results in the formation of the space charge layer also induces a shift of the molecular levels. We denote this shift by eVS and its value is given by eVS=UeffQ , where Ueff incorporates not only the charging energy of the molecule but also the interaction between molecules; this means that Ueff collects the electrostatic effects created by the monolayer on a single molecule. Similarly to what is done for an isolated molecule, for the monolayer case, Ueff is calculated from the equation: eVMLcharge=UeffnML, where VMLcharge is the electrostatic potential induced on the frontier orbitals of the molecule by the charges of the system (including all the molecules) and nML the oxide-to-TCNQ charge transfer per molecule expressed in electron units. It is convenient to calculate VMLcharge and nML as incremental quantities introducing a fictitious shift, Δ, to the TCNQ molecular levels (using an operator similar to Oshift, equation (2), with Δ instead of ε). Then, eδVMLcharge is obtained from the atomic charges induced in the molecules by the energy shift Δ, and Ueff is calculated from eδVMLcharge=UeffδnML; our calculations yield Ueff=2.2 eV, a value slightly larger than U=1.9 eV (calculated in a similar way for an isolated molecule). Notice that the value of U for the single molecule was used in equation (1) to incorporate the dynamical polarization processes (image potential effects) in the organic energy gap,27 while Ueff is introduced to incorporate the induced electrostatic potential on the organic molecular levels due to the charge transfer from TiO2 to the TCNQ monolayer. For completeness, we also show in figure S4 (see SI) for a TCNQ-monolayer the evolution of the charge transfer, nML, (Ec-LUMO’) and eVMLcharge as a function of Δ.
Once Ueff is established, we analyze how that induced potential, eVS, modifies the oxide/organic alignment, by making use of the previous monolayer calculations for T=0 K. The idea is to introduce an external shift Δ0 to the TCNQ-levels in order to simulate the effect of that charge transfer induced shift eVS. Assuming Q=1, then eVS=Ueff, which implies that one has to apply a shift of Δ=Δ0=2.2 eV to the TCNQ molecular levels and recalculate the resulting oxide/organic realignment.33, 34 The result of this process is shown in Figure 4b. In the energy diagram, the LUMO’ of TCNQ is found 1.3 eV below the oxide’s conduction band edge, to be compared to the experimental value of 1.80 eV, indicating that the charge transfer to TCNQ is about 1 electron. One can see from the upper panel of figure S3 of the supplemental information that a shift from Δ=0 to Δ=2.2 eV induces a change in the charge transfer of about 0.5 electrons from TCNQ to the oxide, which creates a potential shift of 0.5×2.2 eV=1.1eV that opposes the original displacement. Therefore, the room temperature realignment of the LUMO’ level with respect to the oxide band edges is the result of two effects: (a) a strong oxide-molecule hybridization shift of 2.1 eV (toward higher binding energies), 0.5 eV larger than the value found for T=0 K; and (b) a new interface electrostatic dipole of 2.2-1.1=1.1 eV (toward lower binding energies), yielding a total interface electrostatic dipole of 1.2 eV (see figure 4b).
It is important to point out that all these effects also alter the work function of the surface by 1.50 eV, when taking into account the mentioned total interface electrostatic dipole of 1.2 eV and the space charge layer shift of 0.30 eV. This value is in good agreement with the experimentally measured 1.2 eV work function increase upon TCNQ adsorption on the TiO2(110) surface (as shown in Figure 2c). We stress that the main contribution to this work function shift comes from the transfer of charge to the LUMO’ level.
Finally, it is worth mentioning that a second TCNQ layer (or a multilayer) physisorbed on-top of this first monolayer would feel an important realignment with respect to the oxide because the chemical shift of 2.1 eV, associated with the interaction between the oxide and the TCNQ first layer, should disappear. At the same time, we can expect an increase of the TCNQ energy gap to around 5.2 eV, which should also shift the LUMO’ level by 0.8 eV (1/2 of the change in the energy gap) to higher energies. These two effects should dramatically displace the LUMO’ level from 1.3 eV below to 1.6 eV above the conduction band. As a consequence, only the first TCNQ layer would be able to develop a strong accumulation of charge incoming from the oxide.
4. SUMMARY AND CONCLUSIONS
In conclusion, we have shown that there is an important charge transfer between TiO2 and a TCNQ monolayer, with one electron filling the LUMO level of the organic molecule. This is strongly suggested by the experimental evidence showing that, upon the deposition of a TCNQ-monolayer on TiO2, a space charge in the oxide is formed and that an important increase in the work-function of the TiO2 + 1ML TCNQ system appears. Our theoretical analysis based on a combination of a DFT approach and a calculation of the space charge potential, as provided by the molecule charging energy, supports this interpretation, and shows the important role that the oxide/organic interface chemistry as well as their electron-chemical equilibration and the oxide space charge have in the barrier formation. Our results are tantamount to the formation of an electron accumulation layer in the first organic layer; although this strong accumulation of charge can be expected to disappear for successive layers, this effect should be considered as an important ingredient for tuning devices having those components.
Supplementary Material
ACKNOWLEDGEMENTS
SR, CR, and RAB acknowledge support from the National Science Foundation under Grant No NSF-CHE 1213727. JO and FF acknowledge support from Spanish MINECO under project MAT2014-59966-R. JIM acknowledges funding from the CSIC-JAEDOC Fellowship Program, cofunded by the European Social Fund, and ERC Synergy Grant No ERC-2013-SYG-610256 NANOCOSMOS.
Footnotes
The authors declare no competing financial interests.
ASSOCIATED CONTENT
Supporting Information Available
Detailed explanation on experimental methods: spectroscopic methods, sample preparation and surface characterization. Detailed explanation on the general computational framework. Projected Density of States onto TCNQ and a layer of TiO2 after introducing the Δ0-shift in the molecular levels. Details of the pristine TiO2(110) band edges. This information is available free of charge via the Internet at http://pubs.acs.org.
REFERENCES
- (1).Forrest SR. Ultrathin Organic Films Grown by Organic Molecular Beam Deposition and Related Techniques. Chem. Rev. 1997;97:1793–1896. doi: 10.1021/cr941014o. [DOI] [PubMed] [Google Scholar]
- (2).Sessolo M, Bolink HJ. Hybrid Organic-Inorganic Light-Emitting Diodes. Adv. Mat. 2011;23:1829–1845. doi: 10.1002/adma.201004324. [DOI] [PubMed] [Google Scholar]
- (3).O’Regan B, Gratzel M. A Low-cost, High-efficiency Solar Cell Based on Dye-sensitized Colloidal TiO2 Films. Nature. 1991;353:737–740. [Google Scholar]
- (4).Kabra D, Lu LP, Song MH, Snaith HJ, Friend RH. Efficient Single-Layer Polymer Light-Emitting Diodes. Adv. Mat. 2010;22:3194–3198. doi: 10.1002/adma.201000317. [DOI] [PubMed] [Google Scholar]
- (5).Meyer J, Hamwi S, Krger M, Kowalsky W, Riedl T, Kahn A. Transition Metal Oxides for Organic Electronics: Energetics, Device Physics and Applications. Adv. Mat. 2012;24:5408–5427. doi: 10.1002/adma.201201630. [DOI] [PubMed] [Google Scholar]
- (6).Li H, Winget P, Brédas JL. Transparent Conducting Oxides of Relevance to Organic Electronics: Electronic Structures of Their Interfaces with Organic Layers. Chem. Mat. 2014;26:631–646. [Google Scholar]
- (7).Flores F, Ortega J, Vázquez H. Modelling Energy Level Alignment at Organic Interfaces and Density Functional Theory. Phys. Chem. Chem. Phys. 2009;11:8658–8675. doi: 10.1039/b902492c. [DOI] [PubMed] [Google Scholar]
- (8).Cahen D, Kahn A, Umbach E. Energetics of Molecular Interfaces. Mat. Today. 2005;8:32–41. [Google Scholar]
- (9).Koch N. Energy Levels at Interfaces between Metals and Conjugated Organic Molecules. J. Phys.: Condens. Matter. 2008;20:184008. [Google Scholar]
- (10).Greiner MT, Helander MG, Tang WM, Wang ZB, Qiu J, Lu ZH. Universal Energy-level Alignment of Molecules on Metal Oxides. Nat. Mater. 2012;11:76–81. doi: 10.1038/nmat3159. [DOI] [PubMed] [Google Scholar]
- (11).Xu Y, Hofmann OT, Schlesinger R, Winkler S, Frisch J, Niederhausen J, Vollmer A, Blumstengel S, Henneberger F, Koch N, et al. Space-Charge Transfer in Hybrid Inorganic-Organic Systems. Phys. Rev. Lett. 2013;111:226802. doi: 10.1103/PhysRevLett.111.226802. [DOI] [PubMed] [Google Scholar]
- (12).Winget P, Schirra LK, Cornil D, Li H, Coropceanu V, Ndione PF, Sigdel AK, Ginley DS, Berry JJ, Shim J, et al. Defect-Driven Interfacial Electronic Structures at an Organic/Metal-Oxide Semiconductor Heterojunction. Adv. Mater. 2014;26:4711–4716. doi: 10.1002/adma.201305351. [DOI] [PubMed] [Google Scholar]
- (13).Sánchez-Sánchez C, Martínez JI, Lanzilotto V, Biddau G, Gómez-Lor B, Pérez R, Floreano L, López MF, Martín-Gago JA. Chemistry and Temperature-assisted Dehydrogenation of C60H30 Molecules on TiO2(110) Surfaces. Nanoscale. 2013;5:11058–11065. doi: 10.1039/c3nr03706a. [DOI] [PubMed] [Google Scholar]
- (14).Sánchez-Sánchez C, Martínez JI, Lanzilotto V, Méndez J, Martín-Gago JA, López MF. Antiphase Boundaries Accumulation Forming a New C Decoupled 60 Crystallographic Phase on the Rutile TiO2 (110)-(1 × 1) Surface. J. Phys. Chem. C. 2014;118(2):27318–27324. [Google Scholar]
- (15).Ferraris J, Cowan DO, Walatka V, Perlstein JH. Electron Transfer in a New Highly Conducting Donor-acceptor Complex. J. Amer. Chem. Soc. 1973;95:948–949. [Google Scholar]
- (16).Alves H, Molinari AS, Xie H, Morpurgo AF. Metallic Conduction at Organic Charge-transfer Interfaces. Nat. Mater. 2008;7:574–580. doi: 10.1038/nmat2205. [DOI] [PubMed] [Google Scholar]
- (17).Martínez JI, Abad E, Beltrán JI, Flores F, Ortega J. Barrier Height Formation in Organic Blends/metal Interfaces: Case of Tetrathiafulvalene-tetracyanoquinodimethane/Au(111) J. Chem. Phys. 2013;139:214706. doi: 10.1063/1.4836635. [DOI] [PubMed] [Google Scholar]
- (18).Beltrán JI, Flores F, Martínez JI, Ortega J. Energy Level Alignment in Organic–Organic Heterojunctions: The TTF/TCNQ Interface. J. Phys. Chem. C. 2013;117:3888–3894. [Google Scholar]
- (19).Monkhorst HJ, Pack JD. Special Points for Brillouin-zone Integrations. Phys. Rev. B. 1976;13:5188–5192. [Google Scholar]
- (20).Martínez JI, Abad E, Flores F, Ortega J. Simulating the Organic-molecule/metal Interface TCNQ/Au(111) Phys. Stat. Sol. B. 2011;248:2044–2049. [Google Scholar]
- (21).Fernández-Torrente I, Franke KJ, Pascual JI. Structure and Electronic Configuration of Tetracyanoquinodimethane Layers on a Au(111) Surface. Int. J. Mass Spectr. 2008;277:269–273. [Google Scholar]
- (22).Yan H, Li S, Yan C, Chen Q, Wan L. Adsorption of TTF, TCNQ and TTF-TCNQ on Au(111): An in situ ECSTM Study. Sci. China Series B: Chem. 2009;52:559–565. [Google Scholar]
- (23).Kronik L, Fromherz R, Ko E, Gantefor G, Chelikowsky JR. Highest Electron Affinity as a Predictor of Cluster Anion Structures. Nat. Mat. 2003;1:49–53. doi: 10.1038/nmat704. [DOI] [PubMed] [Google Scholar]
- (24).Milian B, Pou-Amerigo R, Viruela R, Orti E. On the Electron Affinity of TCNQ. Chem. Phys. Lett. 2004;391:148–151. [Google Scholar]
- (25).Kanai K, Akaike K, Koyasu K, Sakai K, Nishi T, Kamizuru Y, Nishi T, Ouchi Y, Seki K. Determination of Electron Affinity of Electron Accepting Molecules. Appl. Phys. A. 2009;95:309–313. [Google Scholar]
- (26).Medjanik K, Perkert S, Naghavi S, Rudloff M, Solovyeva V, Chercka D, Huth M, Nepijko SA, Methfessel T, Felser C, et al. Formation of an Intermolecular Charge-transfer Compound in UHV Codeposited Tetramethoxypyrene and Tetracyanoquinodimethane. Phys. Rev. B. 2010;82:245419. [Google Scholar]
- (27).Abad E, González C, Ortega J, Flores F. Charging Energy, Self-interaction Correction and Transport Energy Gap for a Nanogap Organic Molecular Junction. Org. Elec. 2010;11:332–337. [Google Scholar]
- (28).Beltrán J, Flores F, Ortega J. The Role of Charge Transfer in the Energy Level Alignment at the Pentacene/C60 Interface. Phys. Chem. Chem. Phys. 2014;16:4268–4274. doi: 10.1039/c3cp55004d. [DOI] [PubMed] [Google Scholar]
- (29).Abad E, Dappe YJ, Martínez JI, Flores F, Ortega J. C6H6/Au(111): Interface Dipoles, Band Alignment, Charging Energy, and van der Waals Interaction. J. Chem. Phys. 2011;134:044701. doi: 10.1063/1.3521271. [DOI] [PubMed] [Google Scholar]
- (30).Segev L, Salomon A, Natan A, Cahen D, Kronik L, Amy F, Chan CK, Kahn A. Electronic Structure of Si(111)-bound Alkyl Monolayers: Theory and Experiment. Phys. Rev. B. 2006;74:165323. [Google Scholar]
- (31).Fitting the initial LUMO level to 4.4 eV, at a position slightly above EC, would shift the final LUMO or LUMO’ levels by around 0.3 eV closer to EC (see Figure 4).
- (32).Frankl DR. Electrical properties of semiconductor surfaces. Pergamon Press; Oxford: 1967. (International series of monographs on semiconductors) [Google Scholar]
- (33).Schlesinger R, Xu Y, Hofmann OT, Winkler S, Frisch J, Niederhausen J, Vollmer A, Blumstengel S, Henneberger F, Rinke P, et al. Controlling the Work Function of ZnO and the Energy-level Alignment at the Interface to Organic Semiconductors with a Molecular Electron Acceptor. Phys. Rev. B. 2013;87:155311. [Google Scholar]
- (34).In our theoretical approximation we neglect the spin-dependent solution for the organic energy levels (a reasonable approximation for a non-magnetic material), and the new geometry that the corresponding charge transfer might induce in the system. This effect should probably increase the oxide/organic interaction and should modify slightly11 the results of this work without changing its main conclusions.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.