Probabilistic ODF Estimation from Reduced HARDI Data with Sparse Regularization

Abstract

High Angular Resolution Diffusion Imaging (HARDI) demands a higher amount of data measurements compared to Diffusion Tensor Imaging (DTI), restricting its use in practice. We propose to represent the probabilistic Orientation Distribution Function (ODF) in the frame of Spherical Wavelets (SW), where it is highly sparse. From a reduced subset of measurements (nearly four times less than the standard for HARDI), we pose the estimation as an inverse problem with sparsity regularization. This allows the fast computation of a positive, unit-mass, probabilistic ODF from 14–16 samples, as we show with both synthetic diffusion signals and real HARDI data with typical parameters.

1 Introduction

Diffusion Magnetic Resonance Imaging (MRI) provides an unparalleled tool to probe the connectivity of the nerve fibers within the white matter of the brain in vivo. At the core of this technique is the relationship between the signal E(q), acquired by the MRI scanner when a pulsed gradient encoded by the wave-vector q is applied, and the random process P(R) driving the restricted diffusion of water molecules. Such relationship is modeled as the following Fourier transform [1]:

$$P(\mathbf{R})=\int \int {\int }_{{ℝ}^3}|E(\mathbf{q})|\text{exp}(-j2\pi \mathbf{q}·\mathbf{R})d\mathbf{q}.$$ (1)

The obvious way to recover P(R) is to sample E(q) and approximate eq. (1) as a discrete Fourier transform, what is known as Diffusion Spectrum Imaging [2]. The main drawback of this technique is the need to sample the entire space of wave-vectors q, since each of them implies the acquisition of a whole MRI volume. Though it has been recently shown [3] how this amount of data can be drastically reduced using Compressed Sensing (CS, [4]), this approach still requires several hundreds of samples to attain a reliable reconstruction.

High Angular Resolution Diffusion Imaging (HARDI, [5]) permits reduction of the measurements to a sampling of the space of orientations with constant ‖q‖. This is achieved at the expense of losing the radial information in P(R), computing some sort of projection or Orientation Distribution Function (ODF) [2]:

$$\Phi (\mathbf{r})={\int }_{-\infty }^{\infty }P(R\mathbf{r})R^{2}dR=\frac{-1}{8{\pi }^2}\int {\int }_{\perp \mathbf{r}}\Delta E(\mathbf{q})d\mathbf{q}.$$ (2)

There are some other alternative definitions for the orientation function (see [6] for an excellent review on this topic), but eq. (2) has the advantage of being a true probability law [7]. HARDI typically requires 60–100 wave-vectors q, but considerations similar to those in [3] allow relaxation of this requirement to a few tens (16–30) [8, 9], whenever a sparse representation of E(q) may be achieved. This condition is met by representing E(q) in a suitable vector frame, namely Spherical Ridgelets (SR), whose components closely resemble the shape of E(q) at different scales. This frame is adequate in [8] since the object of interest is the diffusion signal. Unfortunately, these plate-like functions do not fit the cigar-shaped appearance of the probabilistic ODF, Φ(r), and cannot be expected to provide a sparse representation of it.

In section 2, we postulate Spherical Wavelets [10] as a suitable frame to sparsely represent the Φ(r) in eq. (2), as depicted in Fig. 1. In section 3 we formulate the estimation of the ODF as an inverse problem, by relating the SW functions to their counterparts in the q-space. We propose two alternative solutions based on either ℓ₁ or ℓ₂ regularization, justifying that non-negative ℓ₂ provides sparse representations analogous to ℓ₁. Finally, the results in section 4 illustrate how positive, unit-mass, probabilistic ODFs can be recovered from as few as 14 gradient directions. With ℓ₂ regularization, the minimization problem can be solved with Newton-like methods, becoming computationally efficient.

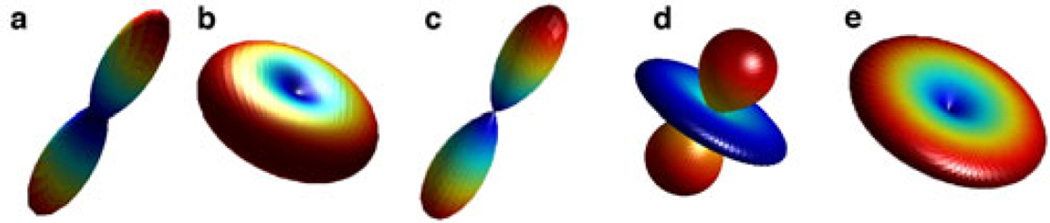
Fig. 1.

Examples of: a) the true Φ(r) when P(R) is Gaussian; b) its corresponding diffusion signal E(q); c) a SW, Ψ_v,j (r). These wavelets aim to sparely represent signals of the type a), which seems quite reasonable; d) the response Ξ(q) to Ψ_v,j (r) in the space of measurements; e) a SR, which in [8] aims to sparsely represent signals of the type b). Note this shape prevents the use of SR to represent ODFs like a).

2 Spherical Wavelets to Sparsely Represent Φ(r)

The shape of the ODF in Fig. 1 implies that a combination of a few Spherical Wavelets (SW, [10]) with different widths and orientations may accurately represent Φ(r) for an arbitrary ensemble of diffusion compartments, i.e. the coefficients of Φ(r) in its SW expansion are sparse. The domain of definition of SW is the set Ω ≡ {r ∈ ℝ³ : ‖r‖ = 1} of unit directions (i.e. diffusion gradients). Their definition is founded on the basis of Spherical Harmonics (SH), for which the following summation formula holds:

$${\sum }_{m=-l}^l{Y}_l^m(\mathbf{u})Y_l^m(\mathbf{v})=\frac{2l+1}{4\pi }{P}_l(\mathbf{u}·\mathbf{v}),$$ (3)

where $Y_l^m$ is the real SH basis function of degree l ≥ 0 and order −l ≤ m ≤ l, and P_l is the Legendre polynomial of degree l. Note P_l(u · v) is a rotation of $Y_l^0(\mathbf{u})$ to an auxiliary system for which the ‘z’ axis is aligned with v. Any symmetric (i.e. f(u) = f(−u)), square-integrable function $f\in {𝕃}_{\text{sym}}^2(\Omega )$, can be written as [10]:

$$f(\mathbf{u})=\int {\int }_{\Omega }f(\mathbf{v})\sum _{l=0,2,\dots }^{\infty }\frac{2l+1}{4\pi }{P}_l(\mathbf{u}·\mathbf{v})d\mathbf{v}=\int {\int }_{\Omega }f(\mathbf{v}){\Theta }_{\mathbf{v}}(\mathbf{u})d\mathbf{v},$$ (4)

where Θ_v(u) is a spherical convolution kernel. To achieve a scale-space representation of f(u), the following scaling kernel K_v,j(u) and semi-discrete frame ${\cup }_{j=-1}^{\infty }{\cup }_{\mathbf{v}\in \Omega }{\Psi }_{\mathbf{v},j}(\mathbf{u})$, that spans ${𝕃}_{\text{sym}}^2(\Omega )$, are introduced in [10]:

$$K_{\mathbf{v},j}(\mathbf{u})=\sum _{l=0,2,\dots }^{\infty }\frac{2l+1}{4\pi }{\kappa }_{\rho }(-2^{-j}l)P_l(\mathbf{u}·\mathbf{v}),$$ (5)

$${\Psi }_{\mathbf{v},j}(\mathbf{u})=\{\begin{array}{cc}\hfill K_{\mathbf{v},0}(\mathbf{u}),\hfill & j=-1;\hfill \\ \hfill K_{\mathbf{v},j+1}(\mathbf{u})-K_{\mathbf{v},j}(\mathbf{u}),\hfill & j\ge 0,\hfill \end{array}$$ (6)

where we choose κ_ρ(x) = e^{−ρx(x + 1)}. When the resolution j → ∞, κ_ρ (2^−j l) → 1 for each l, and we have the exact recovery in eq. (4). When j → −∞, κ_ρ (2^−jl) → 0 for l ≠ 0, and we have the DC component of f(u). This reasoning clarifies the multiscale nature of K_{v, j}, from coarse (j → −∞) to fine details (j → ∞).

3 ODF Reconstruction from Sparse Representations

From the representation provided by SW as described in the previous section, we aim to estimate the ODF, Φ(r), as the sparsest combination of SW that can explain the data acquired in the q-space, E(q). Therefore, we need to compute the q-space response of each SW defined in r ∈ Ω (section 3.1), and then discretize the problem to account for the discrete nature of the measurements (section 3.2).

3.1 Response of SW Ψ_{v, j(r)} in the Space of Wave-Vectors q

We are interested in probabilistic ODF estimators [7], so that the response pursued obeys the following form:

$$\Phi (\mathbf{r})=\frac{1}{4\pi }+\frac{1}{16{\pi }^2}𝒢\{{\Delta }_b\zeta (E(\mathbf{q}))\}(\mathbf{r}),$$ (7)

Among the chances provided in [7], we choose ζ(·) = −E_i(−log(·)) as it seems to be a trade-off between angular resolution and noise sensitivity. Also, the unit-mass constraint comes for free with this model, since the Beltrami operator Δ_b eliminates all DC components so that we keep only the 1/4π factor. We denote by 𝒢 the Funk-Radon Transform (FRT, [5]).

Since SH are eigenfunctions for both 𝒢 and Δ_b, it is straightforward to prove this property holds also for the rotated versions of $Y_l^0(\mathbf{u})$, i.e. P_l(u · v). If we insert eqs. (5) and (6) into (7), we get the following duality between the SW, Ψ_v,j(r), and their counterparts in the q-space, Ξ_v,j(q) (see Fig. 1):

$${\Psi }_{\mathbf{v},j}(\mathbf{r})=\sum _{l=2,4,\dots }^{\infty }\frac{2l+1}{4\pi }{\nu }_{\rho ,j}(l)P_l(\mathbf{r}·\mathbf{v})\iff {\Xi }_{\mathbf{v},j}(\mathbf{q})=\sum _{l=2,4,\dots }^{\infty }\frac{4\pi (2l+1)}{-l(l+1)}\frac{{\nu }_{\rho ,j}(l)}{{\lambda }_l}{P}_l(\mathbf{q}·\mathbf{v}),$$

$${\nu }_{\rho ,j}(l)=\{\begin{array}{cc}\hfill {\kappa }_{\rho }(l),\hfill & \hfill j=-1;\hfill \\ \hfill {\kappa }_{\rho }(2^{-j-1}l)-{\kappa }_{\rho }(2^{-j}l),\hfill & \hfill j\ge 0,\hfill \end{array}$$ (8)

where λ_l and −l(l + 1) are respectively the eigenvalues for 𝒢 and Δ_b. Note we drop the DC term l = 0 from the sums, according to our previous statement.

3.2 Optimization Problem with ℓ_p Regularization

Like in [8], we need a fully discrete version of the frame we use for sparse representation: let ${\{{\mathbf{q}}_n\}}_{n=1}^N$ be the set of wave-vectors in the HARDI data-set; let ${\{{\mathbf{r}}_m\}}_{m=1}^M$ be the set of directions for which the ODF is computed; let ${\{{\mathbf{v}}_{j(k),k}\}}_{k=1}^K$ be a collection of discretizations of Ω for each resolution level −1 ≤ j ≤ J. The estimation of x ≡ Φ(r) is arranged as the ℓ_p inverse problem:

$$\begin{array}{c}\hfill {\text{min}}_{\mathbf{a}}{\Vert \mathbf{a}\Vert }_p,\mathrm{s}.\mathrm{t}.{\Vert A\mathbf{a}-\mathbf{y}\Vert }_2^2<\eta \hfill \\ \hfill \text{with}:\mathbf{x}=B\mathbf{a}+\frac{1}{4\pi }\hfill \end{array}|\begin{array}{c}\hfill A_{n,k}={\Xi }_{{\mathbf{v}}_{j(k),k},j(k)}({\mathbf{q}}_n);{\mathbf{y}}_n=E({\mathbf{q}}_n);\hfill \\ \hfill B_{m,k}={\Psi }_{{\mathbf{v}}_{j(k),k},j(k)}({\mathbf{r}}_m);{\mathbf{x}}_m=\Phi ({\mathbf{r}}_m).\hfill \end{array}$$ (9)

In brief, we discretize the responses Ξ_v,j(q) into a N × K sampling matrix A to find that a best describing the N × 1 vector y ≡ E(q). These coefficients are used to recover x from the discretized M × K sparsifying matrix B. We deliberately choose the same names used in [4], given the formal similarity of eq. (9) with CS for p = 1. Typically, N ≪ K, so that Aa = y is highly underdetermined. This is the reason why a has to be assumed sparse a priori. Though sparsity is only enforced in case p ≤ 1 [4], we also consider here the case p = 2 for the reasons detailed below. Note the ℓ₂ problem has a closed-form solution for eq. (9):

$$\mathbf{a}=A^T{(A{A}^T+\tau (\eta )·I_N)}^{-1}\mathbf{y},$$ (10)

3.3 Positivity Constraints on the Probabilistic ODF

Since Φ(r) is a probability law, it has to be positive for all r. Given a set of directions ${\{{\mathbf{r}}_{m\prime }^{\prime }\}}_{m\prime =1}^{M\prime }$, we add M′ additional linear constraints to eq. (9):

$$B\prime \mathbf{a}+\frac{1}{4\pi }\ge 0,B_{m\prime ,k}={\Psi }_{{\mathbf{v}}_{j(k),k},j(k)}(\mathbf{r}{\prime }_{m\prime }).$$ (11)

Two important remarks arise here regarding the ℓ₂ problem: 1) the solution in eq. (10) no longer holds, but eq. (9) becomes a quadratic program which is still very efficient to solve compared to ℓ₁. 2) Non-negative least squares in fact provide sparse solutions [11], so that we may reasonably hypothesize (see [9]) that the solution of the constrained ℓ₂ will approach that of the constrained ℓ₁.

4 Results

Synthetic Experiments

We generate a two-tensor model simulating two fibers crossing in angles 45°, 60°, or 90°. The results are the average for 300 trials with random rotations of the tensor ensemble, with the diffusion signal generated as:

$$S(\mathbf{u})=\sqrt{{(\frac{1}{2}\text{exp }(-b{\mathbf{u}}^T{\mathbf{D}}_1\mathbf{u})+\frac{1}{2}\text{exp }(-b{\mathbf{u}}^T{\mathbf{D}}_2\mathbf{u})+\sigma ·n_c)}^2+{(\sigma ·n_s)}^2,}$$ (12)

for eigenvalues of D_n: [1.7, 0.3, 0.3] · 10⁻³ mm²/s, b = 2, 000 s/mm², n_c,s ~ 𝒩(0, 1), and Signal to Noise Ratios (SNR): 1/σ =100, 40.

All the methods are coded in MatLab^®, using the ℓ₁-magic library (http://www.acm.caltech.edu/l1magic/) to solve ℓ₁ and quadprog to solve ℓ₂.

The parameters are fixed following the guidelines in [8]: a width ρ = 0.75 of the kernel in eq. (5) is chosen by trial and error for best performance, and so it is the error threshold η in eq. (9) (its value depends on the scenario). For the directions r, r′, and q, we choose regular samplings of Ω in all cases, with respective set sizes M = 214, M′ = 50, and N (the number of HARDI measurements) ranging from 12 to 28. For the discretization of the SW frame, we uniformly sample Ω at each level −1 ≤ j ≤ J, taking (2^j+1m₀ + 1)² evenly spaced samples, with m₀ = 4 and J = 1.

For the sake of comparison, we have adapted the approach in [8] (namely, SR) to interpolate ζ(E), and used eq. (7) to evaluate the probabilistic ODF. We have also adapted the method described in section 3 by alternatively representing the ODF in the basis of SH with l ≤ 4, where Φ(r) is not sparse¹. The comparison is based on the relative Mean Squared Error (rMSE) between the recovered ODF and the ground-truth, computed using eq. (7) over a SH fitting (l ≤ 8) of 214 noise-free q-space samples, see [7, Table 2] for details.

Discussion

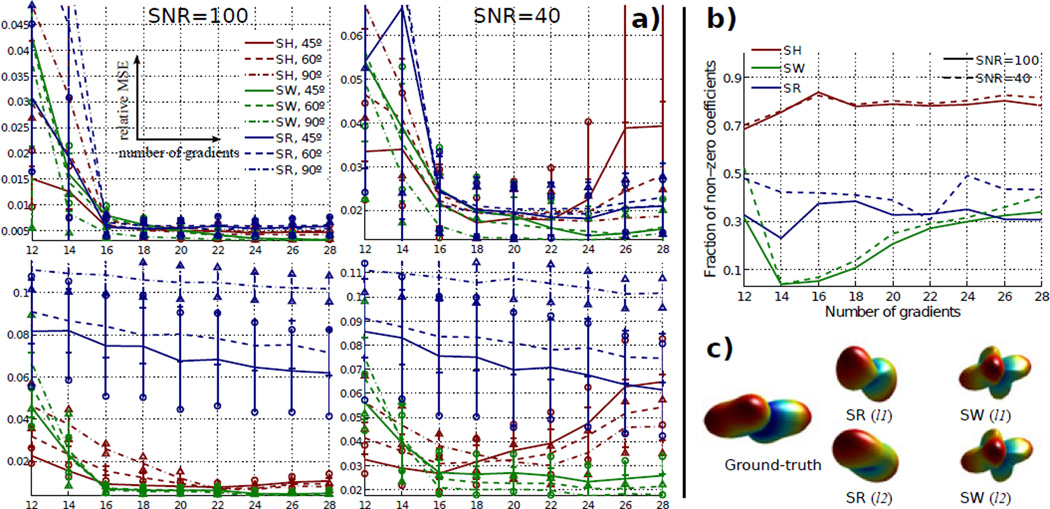
Numerical results are shown in Fig. 2, using the optimal parameters in each case. It is worth to stress the following remarks:

• 1)With ℓ₁ regularization, our approach (SW) provides the lowest reconstruction errors (see Fig. 2.a, top). Though this numeric difference may seem subtle, the ODFs reconstructed in Fig. 2.c suggest it might be critical to correctly resolve the fiber crossings in poor SNR scenarios.
• 2)As the number of gradients acquired increases, the rMSE with SW and SR rapidly decreases, but not with SH. Since the ODFs are not actually sparse in the SH basis (see Fig. 2.b), the a priori sparse behavior does not hold.
• 3)From Fig. 2.a, bottom, our SW approach provides very similar rMSE (and visually identical ODFs, see Fig. 2.c) with either ℓ₁ or ℓ₂ regularization. As stated before, non-negative ℓ₂ yield sparse solutions [11], close to those with ℓ₁ in the space of coefficients. We show in Appendix A that SW, as used here, nearly meet the Parseval property: if the ℓ₁ and ℓ₂ solutions are alike, the Euclidean distance between the corresponding ODFs will also be small. The SR in [8] do not exhibit this feature. Moreover, according to eq (7), a differential operator Δ_b is applied to compute Φ from ζ(E), so the difference in the reconstruction of ζ(E) (which is not bounded by the distance between the ℓ₁ and ℓ₂ solutions) is amplified when computing the ODF. Accordingly, the corresponding errors in Fig. 2.a, bottom (ℓ₂) for [8] are far larger compared to the ℓ₁ case.
• 4)The minimum number of gradients to attain a reliable ODF reconstruction seems to be 14–16 (Fig. 2.a, top and bottom), and below this threshold the rMSE blows. With SW, this range coincides with the minimum number of non-zero coefficients of the solution (see remark 5), so we may hypothesize that a minimum of 3% of the SW coefficients are required to properly describe ODFs.
• 5)Our method, SW, provides also the sparsest solution (Fig. 2.b). As the number of measurements grows, we have more information on the ODF, so the solution may be refined with more SW coefficients and it becomes less sparse.

Fig. 2.

Results obtained with our approach (SW), our adaptation of [8] to estimate ODFs (SR), and an implementation of our method based on SH. a) Mean and variance of the rMSE for ℓ₁ (top row) and ℓ₂ (bottom row). b) Sparsity of the solutions for a 60° crossing. c) Examples of the ODFs reconstructed for SNR=40 and a 60° crossing.

In vivo Experiments

A HARDI data set with 8 unweighted T2 baseline images and 16 evenly spaced gradients (b = 3, 000 s/mm²) is used in this section.

Fig. 3 shows an axial slice intersecting the corpus callosum (red lobes aligned with the ‘x’ axis) and the uppermost part of the cingulum (green lobes, ‘y’ axis).

Fig. 3.

Axial slice of a real data set with 16 gradients. The ODFs field has been recovered with our method. The highlighted regions have been further analyzed with both our method (SW) and the method in [8] (SR), with either ℓ₁ or ℓ₂ regularization.

We are able to correctly resolve the crossings between these structures in the top row, or even the complex three-compartment crossings in the bottom row (blue lobes along the ‘z’ axis correspond to the corona radiata).

While for ℓ₁ the improvement with our method over [8] is not dramatic, the reconstructed ODFs are still sharper (see blue square), according to remark 1.

With ℓ₂ regularization, the method in [8] completely fails, while our method outputs accurate ODFs, and even the three-compartment crossings are better resolved than with ℓ₁ (see green square).

This is in agreement with remark 3. Our final remark is that:

• 6)ℓ₁-based reconstruction takes ~200 s, while ℓ₂-based takes ~1.5 s, for Fig. 3 (the speedup is ~130), which is an additional argument supporting ℓ₂.

5 Conclusion

We have shown that as few as 14–16 diffusion directions suffice to obtain accurate probabilistic ODFs estimates. Positivity constraints, which are not considered in [7], can be easily incorporated into our model. Although sparse regularization has been previously used in [8] to fit the diffusion signal, our approach is, to our knowledge, the very first to use this technique to reconstruct the ODF from HARDI data with reduced measurements. Though we have discussed in the results section a work-around to compute the ODF from the diffusion signal provided by [8], the results with our own approach are clearly better with ℓ₁, and the only usable at all with ℓ₂. This is specially important, since ℓ₂ reconstruction is two orders of magnitude faster than ℓ₁: for this latter approach, the overwhelming duration of the estimation for an entire volume (in the order of 100 days with our Matlab implementation) makes the overall acquisition/reconstruction time unattractive. Our ℓ₂ approach provides virtually identical results as ℓ₁ with reasonable reconstruction times, while allowing an acquisition speedup in the order of 4.

Appendix

A Parseval Property in the Semi-Discrete SW Frame

A frame is said to be tight or Parseval if the projections of a vector f in each frame element conserve the energy of f. If C is the frame bound, $c_l^m$ the coefficient of f(u) for the SH basis function $Y_l^m(\mathbf{u})$, and f_l(u) the orthogonal projection of f(u) in the subspace of SH of degree l, this condition reads:

$$\sum _{j=-1}^{\infty }\int {\int }_{\Omega }{|\langle f(\mathbf{u}),{\Psi }_{\mathbf{v},j}(\mathbf{u})\rangle |}^{2}d\mathbf{v}\stackrel{?}{=}C{\Vert f(\mathbf{u})\Vert }_2^2$$ (13)

for the semi-discrete frame of SW. From its definition in eq. (6), eq. (13) reads:

$$\sum _{j=-1}^{\infty }\int {\int }_{\Omega }^{d\mathbf{v}}{|\langle f(\mathbf{u}),\sum _{l=0,2,\dots }^{\infty }{\nu }_{\rho ,j}(l)\sum _{m=-l}^l{Y}_l^m(\mathbf{u})Y_l^m(\mathbf{v})\rangle |}^2=\sum _{j=-1}^{\infty }\int {\int }_{\Omega }^{d\mathbf{v}}{\left|\sum _{l=0,2,\dots }^{\infty }{\nu }_{\rho ,j}(l)\sum _{m=-l}^l{c}_l^m{Y}_l^m(\mathbf{v})\right|}^2=\sum _{j=-1}^{\infty }\sum _{l,l\prime =0,2,\dots }^{\infty }{\nu }_{\rho ,j}(l){\nu }_{\rho ,j}(l\prime )\sum _{m,m\prime =-l}^l{c}_l^m{c}_{l\prime }^{m\prime }\langle Y_l^m,Y_{l\prime }^{m\prime }\rangle =\sum _{j=-1}^{\infty }\sum _{l=0,2,\dots }^{\infty }{\nu }_{\rho ,j}{(l)}^2\sum _{m=-l}^l{(c_l^m)}^2=\sum _{l=0,2,\dots }^{\infty }{s}_l{\Vert f_l\Vert }_2^2.$$ (14)

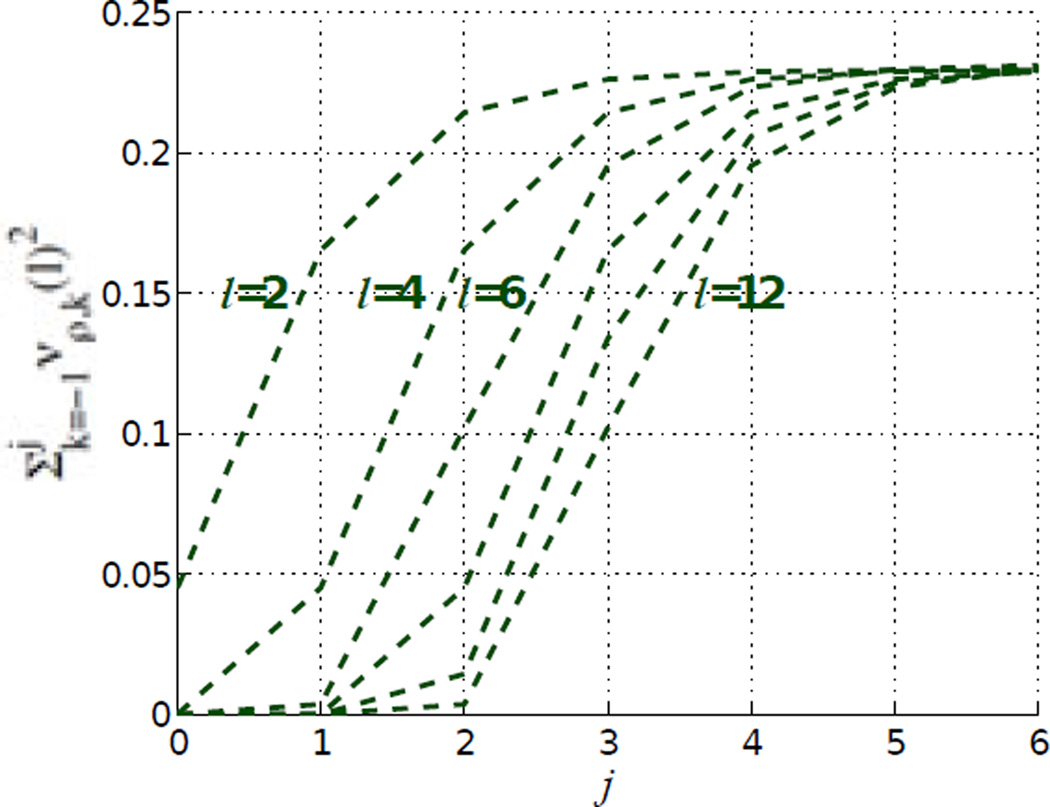
The condition (13) is equivalent to $s_l={\sum }_{j=-1}^{\infty }{\nu }_{\rho ,j}{(l)}^2$ (see eq. (8)) being constant for all l. Fig. 4 shows the partial sums for the first few l. SW are near Parseval (i.e. the curves approach the same value when j → ∞) if l = 0 is ignored, but this is the DC component, unnecessary for our derivations.

Fig. 4.

Partial sums ${\sum }_{k=-1}^J{\nu }_{\rho ,k}{(l)}^2$ for different degrees of l (for l = 0, the curve is a line with constant value 1). We use ρ = 0.75 as in all the experiments throughout the results section (this behavior does not hold for all ρ).