A dose–schedule finding design for phase I–II clinical trials

SUMMARY

Dose-finding methods aiming at identifying an optimal dose of a treatment with a given schedule may be at a risk of misidentifying the best treatment for patients. In this article we propose a phase I/II clinical trial design to find the optimal dose-schedule combination. We define schedule as the method and timing of administration of a given total dose in a treatment cycle. We propose a Bayesian dynamic model for the joint effects of dose and schedule. The proposed model allows us to borrow strength across dose-schedule combinations without making overly restrictive assumptions on the ordering pattern of the schedule effects. We develop a dose-schedule-finding algorithm to sequentially allocate patients to a desirable dose-schedule combination, and select an optimal combination at the end of the trial. We apply the proposed design to a phase I/II clinical trial of a γ-secretase inhibitor in patients with refractory metastatic or locally advanced solid tumours, and examine the operating characteristics of the design through simulations.

1 Introduction

In oncology, a treatment plan usually consists of: 1) the amount of medication to be given to a patient; 2) how the medication will be given and the times when it will be given. The former is known as the dose and the latter is known as the schedule of the treatment. In a dose-schedule-finding trial, the investigators aim to identify an optimal combination of dose and schedule of an investigational drug that is both tolerable and sufficiently active to warrant further testing of its anti-tumour efficacy.

In a motivating trial of a γ-secretase inhibitor as a single agent in patients with refractory metastatic or locally advanced solid tumours conducted at The University of Texas MD Anderson Cancer Center, dose is defined as the total dose of the study drug given to the patients during a 21-day treatment cycle, and schedule is defined by how the fixed total dose will be split and when the split dose will be given within each treatment cycle. The four specific doses of interest are 210 mg, 273 mg, 336 mg, and 395 mg. The three specific schedules of interest are a continuous 3-day administration with a 4-day rest, a continuous 7-day administration with a 14-day rest, and a continuous daily administration. The goal is to identify an optimal combination of dose and schedule that is both tolerable and demonstrates sufficient anti-tumour response based on pre-specified criteria.

Preclinical studies and clinical trials have demonstrated schedule-dependent toxicity and anti-tumour effects of many anti-cancer drugs (Slevin et al., 1989; Blomqvist et al., 1993; Gervais et al., 2005; Hirsh et al., 2007; Shah et al., 2008a; Gyergyay et al., 2009; Lonial et al., 2010; Wagner et al., 2010, among others). For example, the clinical development of dasatinib for treating chronic myelogenous leukemia (CML) initially proceeded using a 70 mg twice-daily dosing schedule due to its relatively short half-life, with the goal of achieving sustained kinase inhibition while avoiding toxicity (Shah et al., 2008b). This dosing regimen was approved by the U.S. Food and Drug Administration in June 2006. However, a phase III trial of dasatinib in 670 chronic phase CML patients later on demonstrated that the clinical benefit of dasatinib was equivalent when dosed once daily, and, importantly, tolerability was superior to the twice-daily schedule, with significantly reduced incidences of key treatment-related adverse events (Shah et al., 2008a). This example highlights the importance of dose-schedule-finding trials and potentially complex schedule effects (e.g., in the sense of contradicting to the physicians’ prior hypotheses). It demonstrates that the conventional dose-finding methods, which focus only on dosage with a pre-specified schedule, may be at risk of prematurely claiming a lack of therapeutic effect or excessive toxicity in the drug development process, or identifying a sub-optimal treatment for the patients in the end.

Despite the importance of the schedule effects on the treatment outcomes, very limited literature exists on the design of dose-schedule-finding trials. Depending on the goal of the trial, two different definitions of schedule have been used in the dose-schedule-finding literature. When the investigators are interested in identifying an optimal number of cycles to treat patients along with the dose given to the patients per cycle, schedule has been defined as the number of treatment cycles (with a pre-specified method of administration of the study medication within each cycle). Under this definition, Braun et al. (2005) proposed a method to determine a maximum-tolerated schedule of a cytotoxic agent, which was further extended to simultaneously optimize dose and schedule (Braun et al., 2007). The other definition of schedule, on which we will focus here, is the method and timing of administration (which in our motivating trial refers to the frequency of and dose per administration) within a cycle with a given total dose per cycle. Based on our experience at MD Anderson Cancer Center, the latter definition of schedule seems more practically relevant in dose-schedule-finding trials. This is because in practice, as long as patients show benefit from the treatment, physicians typically will continue treatment cycles until patients achieve complete remission or experience dose-limiting toxicities (DLTs). What is of more interest to the physicians is how to administer the treatment agent within each treatment cycle to achieve low toxicity and high efficacy. Li et al. (2008) proposed a dose-schedule-finding method to address this issue. However, their method makes a strong assumption that a prolonged administration of the study drug would not increase the rate of DLT in the patients, which may not always hold (Shah et al., 2008a).

The goal of this article is to propose a clinical trial design to find the optimal dose-schedule combination that is safe and has the highest efficacy. We propose a Bayesian dynamic model for a trinary patient outcome in a probit model framework to model the joint effects of dose and schedule. The proposed model allows us to borrow strength across dose-schedule combinations without making overly restrictive assumptions on the ordering pattern of the schedule effects. Specifically, our proposed model centers the parameter associated with each dose-schedule combination in the outcome distribution on that of the next lower dose with the same schedule, when applicable, plus an “average” dose effect, while allowing random variation. We develop a dose-schedule-finding algorithm to sequentially allocate patients to a desirable dose-schedule combination, based on the posterior distribution of toxicity and efficacy at each dose-schedule combination. At the end of the trial, an optimal dose-schedule combination is selected. We examine the operating characteristics of the proposed design through simulations.

The remainder of this article is organized as follows. In Section 2, we present the probability model, including the likelihood, priors, and posteriors. We describe the decision criteria and dose-schedule-finding algorithm in Section 3. In Section 4, we apply the proposed design to the motivating trial and evaluate the operating characteristics of the design through simulation studies as well as sensitivity analyses. We provide concluding remarks in Section 5.

2 Probability Model

Consider a dose-schedule-finding trial with J doses of an investigational drug, d₁ < d₂ < ··· < d_J, and K schedules, denoted as s = 1, …, K. We refer to schedule as the method and timing of administration (e.g., frequency and timing of dosing) with a given total dose during a treatment cycle. In our motivating trial example, each of three different schedules involves a different frequency of administration of the study drug with a fixed total dose during a treatment cycle (see Section 4). We define a dose-schedule combination (j, k) as dose level j (with dose being d_j) administered under schedule k, j = 1, …, J, k = 1, …, K, resulting in a dose-schedule matrix with J rows and K columns. For simplicity, we standardize the dose by dividing it by the maximum dose under investigation, so that all doses fall in the range of (0, 1]. To characterize a patient’s response to the treatment, we collapse the bivariate binary toxicity and efficacy outcomes into a trinary outcome Y, namely: [Y = 0] = [no efficacy and no toxicity], [Y = 1] = [efficacy and no toxicity], and [Y = 2] = [toxicity]. The use of this collapsed trinary outcome is often appropriate in assessing the effect of the drug because DLT is typically unacceptable in practice, making potential efficacy irrelevant in the presence of DLTs.

Let θ_ljk denote the probability of Y = l for a patient treated with dose-schedule combination (j, k), i.e., θ_ljk = pr(Y = l | d_j, s = k) for l = 0, 1, 2. Because ${\sum }_{l=0}^2{\theta }_{\mathit{ijk}}=1$, we only need to model two out of the three probabilities (θ_0jk, θ_1jk, θ_2jk). We here choose to model a transformation of θ_1jk and θ_2jk, namely,

$$\begin{array}{r}{\alpha }_{jk}=\eta ({\theta }_{2jk}),\\ {\beta }_{jk}=\eta ({\theta }_{1jk}+{\theta }_{2jk}),\end{array}$$

where η(·) is a transformation mapping (0, 1) to (−∞,∞), e.g., logit or probit transformation.

To appropriately model α_jk and β_jk, some considerations on the potential pattern of the schedule effects are warranted. We note that although it is generally true that toxicity and efficacy monotonically increase with an increasing dose, the pattern of the effects of schedule on treatment outcomes is complicated. For some agents, given the same total dose, a more frequently administered (or prolonged) schedule is associated with lower toxicity. For example, in treating metastatic breast cancer, Blomqvist et al. (1993) found that the toxicity of the combination of uorouracil, epirubicin and cyclophosphamide (FEC) was reduced when the conventional every-4-week dosing regimen was divided into four weekly doses. The same trend had been observed for doxorubicin in treating the same patient population (Blomqvist et al., 1993). Similarly, when treating metastatic renal cell cancer patients with sunitinib, Gyergyay et al. (2009) showed that a 2-week on and 1-week off schedule is more tolerable than a 4-week on and 2-week off schedule. However, for dasatinib, a prolonged schedule can lead to higher toxicity in treating CP-CML patients (Shah et al., 2008a). The effect of schedule of an anti-cancer agent on efficacy is similarly complex. Clark et al. (1994) suggested that for treating small-cell lung cancer patients, a prolonged exposure to low concentrations of etoposide may improve the therapeutic ratio of this drug, whereas Blomqvist et al. (1993) showed for treating metastatic breast cancer patients with FEC, a prolonged schedule was associated with a lower efficacy.

Based on the above considerations, we propose a exible Bayesian dynamic model for the dose-schedule effect on the trinary treatment outcome Y as follows:

$$\begin{array}{lll}\hfill {\alpha }_{jk}\mid {\alpha }_{j-1,k},\gamma & ~\hfill & N\left({\alpha }_{j-1,k}+\gamma (d_j-d_{j-1}),{\sigma }^2\right),\hfill \\ \hfill {\alpha }_{1k}& ~\hfill & N({\alpha }_{0k},{\sigma }_0^2),\hfill \end{array}$$ (1)

for j = 2, …, J, k = 1, …, K, where γ > 0 represents an “average” dose effect, σ² is a fixed variance, and α_0k and ${\sigma }_0^2$ are hyperparameters. This Bayesian dynamic model is exible in the sense that it specifies the effects of dose-schedule combinations (as represented by α_jk) without making overly restrictive assumptions on the ordering pattern of the schedule effects, in contrast to the monotonicity assumption made in Li et al. (2008). In addition, this model allows us to borrow strength across dose-schedule combinations by centering the parameter in the outcome distribution associated with each dose-schedule combination on that of the next lower dose with the same schedule, plus an “average” dose effect, while allowing certain degree of random variation as characterized by the variance σ². Such random variation, or non-constant α_jk − α_j−1,k − γ(d_j − d_j−1) across schedules, implies a dose-schedule interaction effect, with σ² controlling for the magnitude of the effect. This would be desirable, especially when the compound has slow clearance or a long half-life (Simon, 1997; Legezda and Ibrahim, 2000). By tuning the value of σ² via simulation with pre-specified scenarios, our proposed model can achieve an appropriate level of strength borrowing, and result in desirable operating characteristics of the design. We choose σ² as a tuning parameter because typically the small amount of data from phase I/II trials does not provide sufficient information to reliably estimate σ². Hyperparameters α_0k and ${\sigma }_0^2$ can be determined by consulting with clinical investigators. As α_1k = η(θ_21k), where θ_21k is the probability of toxicity at the lowest dose level of schedule k, and α_0k is the prior mean of α_1k, we can pick α_0k based on the investigators’ best guess of the toxicity probability at the lowest dose of each schedule, while the value of ${\sigma }_0^2$ reflects the uncertainty of this prior guess.

To model β_jk, we follow the spirit of proportional odds model and take

$${\beta }_{jk}=\delta +{\alpha }_{jk}$$ (2)

with δ > 0. Under this model, if a dose-schedule combination increases the probability of toxicity compared to another combination, then it also increases the probability of efficacy or toxicity (thus decreasing the probability of no efficacy and no toxicity). In addition, such increases remain the same after taking a η⁻¹(·) transformation. Note that η⁻¹(α_jk) = θ_2jk = pr(Y > 1 | d_j, s = k) and η⁻¹(β_jk) = θ_1jk + θ_2jk = pr(Y > 0 | d_j, s = k). When η(·) takes a form of the logit transformation, the above model specification leads to the proportional odds model. In this article, we use the probit transformation, i.e., η(·) = Φ⁻¹(·), to facilitate the use of the method of Albert and Chib (1993) to sample the posteriors of unknown parameters.

Suppose n patients have been treated in the trial, with the ith patient being treated at dose-schedule combination (j_i, k_i), i = 1, …, n, yielding data D = (y₁, …, y_n). Let α = {α_jk}. The likelihood is given by

$$L(\mathit{\alpha },\delta ;D)=\prod _{i=1}^n\left\{1(y_i=0)(1-\mathrm{\Phi }(\delta +{\alpha }_{j_i{k}_i}))+1(y_i=1)(\mathrm{\Phi }(\delta +{\alpha }_{j_i{k}_i})-\mathrm{\Phi }({\alpha }_{j_i{k}_i}))+1(y_i=2)\mathrm{\Phi }({\alpha }_{j_i{k}_i})\right\}.$$

Let f(δ) and f(γ) denote the prior distributions of δ and γ, respectively. In our motivating trial example, we take f(δ) and f(γ) to be uniform distributions U(0, U_δ) and U(0, U_γ), respectively, with U_δ and U_γ being hyperparameters. The posterior distribution of θ = (α, δ, γ) is given by

$$f(\mathit{\theta }\mid D)=L(\mathit{\alpha },\delta ;D)\times \prod _{k=1}^K\left(\varphi ({\alpha }_{1,k};{\alpha }_{0k},{\sigma }_0^2)\prod _{j=2}^J\varphi ({\alpha }_{j,k};{\alpha }_{j-1,k}+\gamma (d_j-d_{j-1}),{\sigma }^2)\right)\times f(\delta )\times f(\gamma )$$

where ϕ(x; μ, σ²) represents the density of the normal distribution with mean μ and variance σ². We sample the posteriors using the Gibbs sampler.

3 Dose-Schedule-Finding Algorithm

We propose a design that adaptively allocates patients to dose-schedule combinations that are safe and efficacious. Suppose we treat patients in cohorts of size c. In our trial example we use c = 2. After we observe the efficacy and toxicity outcomes of each cohort of patients, a Gibbs sampler is run to update the posterior distributions of all parameters. Using the updated dose-response curves, a new cohort of patients is assigned to a dose-schedule combination with the estimated toxicity and efficacy probabilities satisfying certain criteria defined below.

Let ${\theta }_E^{★}$ and ${\theta }_T^{★}$ be physician-specified lower limit for efficacy and upper limit for toxicity, respectively. We define a target dose-schedule combination to be the combination (j, k) with the highest efficacy probability θ_1jk among combinations satisfying both ${\theta }_{1jk}\ge {\theta }_E^{★}$ and ${\theta }_{2jk}\le {\theta }_T^{★}$. To find the target combination, we first define acceptable efficacy and toxicity of a combination as follows:

• A combination (j, k) has acceptable efficacy if

  $${\psi }_{jk}^E\equiv Pr({\theta }_{1jk}\ge {\theta }_E^{★})>{\pi }_{1n}$$ (3)
• A combination (j, k) has acceptable toxicity if

  $${\psi }_{jk}^T\equiv Pr({\theta }_{2jk}\le {\theta }_T^{★})>{\pi }_{2n}$$ (4)
  where (π_1n, π_2n) are cutoffs that depend on n, the current number of patients whose efficacy and toxicity outcomes are observed. Because the posterior distribution of {θ_ljk} is much less concentrated, thus less informative at the beginning of the trial when only a small amount of data are available, and becomes increasingly concentrated when more data accumulate over the course of the trial, it is desirable to allow the cutoffs adaptively change with the sample size, such that the criteria are liberal at the beginning of the trial and become more stringent at a later stage of the trial (Cai et al., 2014; Riviere et al., 2015; Guo and Li, 2015). Let M denote the minimal sample size at which we start to apply criteria (3) and (4), N denote the total sample size, and n denote the number of patients currently treated in the trial. We propose the following adaptive cutoffs for toxicity and efficacy

  $${\pi }_{ln}={\pi }_{la}+\frac{n-M}{N-M}({\pi }_{lb}-{\pi }_{la}),$$

  which linearly increases from π_la to π_lb when the current sample size n increases from M to N, where 0 < π_la < π_lb < 1, l = 1, 2.

We say a dose-schedule combination is admissible if it has both acceptable toxicity and efficacy. Let 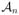denote the set of all admissible dose-schedule combinations at which at least one cohort of patients have been treated. We propose the following adaptive dose-schedule-finding algorithm:

1. During the course of the trial, a dose is never skipped under a given schedule in escalation.

2. Treat one cohort of patients at each combination (1, k), k = 1, …, K, i.e., the lowest dose of each schedule. If for any k = 1, …, K, the lowest dose level is unacceptably toxic, then the trial is terminated. The K cohorts can be randomized to the K combinations in any reasonable manner. For example, each patient can be randomized to one of the combinations (1, k), until c patients are assigned to each combination (1, k), k = 1, …, K. Consistent with this proposed step, we define our minimum trial sample size M to be equal to cK, i.e., the product of the cohort size c and the number of schedules K.

3. 1. If the highest tried doses under all schedules are either J, or have unacceptable toxicity, then the next cohort of patients is treated at the dose-schedule combination in 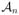that has the largest ${\psi }_{jk}^E$, or the trial is terminated and declared inconclusive if 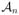is empty.

   2. Otherwise, there are l (1 ≤ l ≤ K) schedules under which the highest tried doses, say combinations (h_k1, k₁), …, (h_kl, k_l), with max(h_k1, …, h_kl) < J, have acceptable toxicity. We will treat the next cohort of patients at combination (h_km + 1, k_m) with probability ${\psi }_{h_{k_m}+1,k_m}^E/{\sum }_{t=1}^l{\psi }_{h_{k_t}+1,k_t}^E$, 1 ≤ m ≤ l. For example, suppose doses 1–3, doses 1–2, and dose 1 have been used to treat at least one cohort of patients under schedules 1, 2, and 3, respectively, and furthermore, all these combinations have acceptable toxicity. Thus, l = 2, and we can define (h_k1, k₁) = (2, 2) and (h_k2, k₂) = (1, 3). Correspondingly, (h_k1 + 1, k₁) = (3, 2) and (h_k2 + 1, k₂) = (2, 3). We will treat the next cohort of patients at combination (3,2) or (2,3) with probability ${\psi }_{3,2}^E/({\psi }_{3,2}^E+{\psi }_{2,3}^E)$ and ${\psi }_{2,3}^E/({\psi }_{3,2}^E+{\psi }_{2,3}^E)$, respectively. Note that in the special case of l = 1, we will treat the next cohort of patients at combination (h_k1 + 1, k₁).

4. The trial is terminated when the maximum sample size N is reached. The dose-schedule combination in 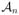with the maximum ${\psi }_{jk}^E$ is selected as the recommended combination.

4 Numerical Studies

4.1 Operating Characteristics

We applied the proposed methodology to the phase I/II metastatic or advanced solid tumour clinical trial described previously. The investigators were interested in identifying an optimal combination of dose and schedule that was both tolerable and showed promising anti-tumour response based on certain pre-specified criteria. The four specific doses of interest were 210 mg, 273 mg, 336 mg, and 395 mg as the total dose during a 21-day treatment cycle. The three specific schedules of interest were a continuous 3-day administration with a 4-day rest, a continuous 7-day administration with a 14-day rest, and a continuous daily administration. The DLTs include non-hematologic toxicity of grade 3 or above according to the National Cancer Institute (NCI)-CTCAE version 3.0, with a few specified exceptions, grade 4 nuetropenia lasting ≥ 7 days, febrile neutropenia and/or documented infection with absolute neutrophil count (ANC) < 1.0 ×10⁹/L, and thrombocytopenia grade 4 or any thrombocytopenia requiring platelet transfusion. The efficacy will be assessed by the Response Evaluation Criteria in Solid tumours (RECIST), and defined by complete remission (CR) or partial remission (PR). The physician-suggested efficacy (i.e., efficacy without toxicity) lower limit and toxicity upper limit were ${\theta }_E^{★}=0.3$ and ${\theta }_T^{★}=0.2$, respectively.

On the basis of the motivating trial, we specified eight scenarios with different true probabilities of toxicity and efficacy across 12 dose-schedule combinations with J = 4 and K = 3. We chose the maximum sample size to be 40 for the simulation studies. Given the small sample size in reference to the number of dose-schedule combinations, we used a cohort size of c = 2. We assigned δ and γ uniform priors δ ~ U(0, U_δ) and γ ~ U(0, U_γ). U_δ = 4 was chosen so that a reasonable range of β_jk (or equivalently, Pr(Y = 1 | d_j, s = k) + Pr(Y = 2 | d_j, s = k)) that might be encountered in practice was covered. For example, when the toxicity probability Pr(Y = 2 | d_j, s = k) = 0.1, the support for Pr(Y = 1 | d_j, s = k) + Pr(Y = 2 | d_j, s = k) is (0.1, 0.99) under this prior. Similarly, we chose U_γ= 8 to reflect a reasonable range of toxicity probability increase between adjacent doses. The results of the sensitivity analysis (see Section 4.2) suggested that the operating characteristics of the design were not sensitive to the choice of U_δ and U_γ. Based on the physicians’ prior knowledge, we set α₀₁ = α₀₂ = α₀₃ = −1 such that the prior average toxicity probability at the lowest dose level of each schedule was about 0.15, and set ${\sigma }_0^2=4$ to reflect the uncertainty of this prior specification. The variance σ² = 0.5 and cutoff probabilities π_la = 0.05 and π_lb = 0.18 for l = 1, 2 were tuned through simulations to obtain desirable operating characteristics of the design.

The 12 scenarios are summarized in Table 1. In any scenario, given the same schedule, the toxicity probability, denoted as “pr(tox)”, increases with an increasing dose, and the probability of efficacy without toxicity, denoted as “pr(eff & no tox)”, either increases or first increases and then decreases with an increasing dose. Some dose-response curves are rather at (e.g., efficacy of schedule 3 in scenario 7) while some are steep (e.g., toxicity of schedule 1 in scenario 3). In the first four scenarios, there is only one target dose-schedule combination. In the next three scenarios, there are two target combinations. In scenario 7, both toxicity probabilities and efficacy probabilities increase across both dose and schedule. The eighth scenario has three target combinations. We considered different situations where the targets are at different locations in the dose-schedule matrix. Therefore, these eight scenarios were constructed only to ensure the diversity of the pattern of the dose and schedule effects and the number and location of the target dose-schedule combinations (rather than constructed based on model (2)). To assess the sensitivity of the performance of the proposed design to the misspecification of model (2), we purposely constructed scenarios 9–11 that violate model (2) (see Table 1 in the Supplementary Material for a demonstration of how these scenarios violate model (2)). Finally, scenario 12 is considered a slight modification of scenario 4 to allow the target dose-schedule combination to have an even lower probability of toxicity. Under each scenario, we simulated 1,000 trials. Posterior inferences were based on 2,000 posterior samples after 1,000 burn-ins.

Table 1.

True probabilities of (1) efficacy and no toxicity and (2) toxicity at each dose-schedule combination for the 12 scenarios. The numbers in boldface correspond to the target dose-schedule combinations (i.e., pr(eff & no tox) ≥ 0.3 and pr(tox) ≤ 0.2).

Dose	Schedule						Schedule
	True pr(eff & no tox)			True pr(tox)			True pr(eff & no tox)			True pr(tox)
	1	2	3	1	2	3	1	2	3	1	2	3
	Scenario 1						Scenario 2
1	0.3	0.28	0.29	0.02	0.01	0.02	0.32	0.38	0.33	0.02	0.03	0.02
2	0.32	0.3	0.31	0.06	0.08	0.13	0.51	0.6	0.51	0.35	0.1	0.35
3	0.53	0.31	0.46	0.1	0.1	0.46	0.46	0.52	0.53	0.5	0.42	0.43
4	0.43	0.32	0.43	0.5	0.15	0.5	0.39	0.46	0.39	0.58	0.52	0.57
	Scenario 3						Scenario 4
1	0.54	0.32	0.32	0.1	0.02	0.02	0.18	0.24	0.33	0.01	0.01	0.01
2	0.56	0.5	0.34	0.31	0.42	0.03	0.23	0.27	0.4	0.01	0.01	0.02
3	0.42	0.38	0.5	0.54	0.58	0.42	0.24	0.33	0.44	0.02	0.02	0.03
4	0.3	0.35	0.39	0.69	0.62	0.58	0.27	0.4	0.6	0.02	0.03	0.1
	Scenario 5						Scenario 6
1	0.28	0.28	0.31	0.02	0.02	0.02	0.3	0.3	0.48	0.01	0.02	0.45
2	0.3	0.34	0.32	0.03	0.05	0.03	0.33	0.56	0.49	0.02	0.1	0.46
3	0.32	0.35	0.52	0.04	0.08	0.12	0.56	0.5	0.46	0.1	0.42	0.5
4	0.52	0.43	0.43	0.12	0.4	0.4	0.54	0.49	0.42	0.4	0.46	0.54
	Scenario 7						Scenario 8
1	0.3	0.32	0.45	0.04	0.05	0.12	0.3	0.3	0.33	0.01	0.02	0.02
2	0.45	0.46	0.47	0.12	0.38	0.4	0.33	0.56	0.36	0.02	0.09	0.03
3	0.46	0.48	0.49	0.38	0.4	0.42	0.56	0.54	0.56	0.09	0.4	0.09
4	0.48	0.5	0.53	0.4	0.45	0.46	0.54	0.49	0.5	0.4	0.46	0.4
	Scenario 9						Scenario 10
1	0.33	0.24	0.11	0.01	0.04	0.01	0.14	0.37	0.36	0.01	0.05	0.02
2	0.35	0.3	0.23	0.03	0.04	0.01	0.47	0.5	0.59	0.34	0.42	0.08
3	0.4	0.56	0.33	0.42	0.14	0.01	0.48	0.49	0.45	0.38	0.46	0.31
4	0.32	0.41	0.36	0.58	0.54	0.02	0.48	0.38	0.41	0.42	0.58	0.34
	Scenario 11						Scenario 12
1	0.4	0.22	0.29	0.42	0.02	0.02	0.18	0.24	0.25	0.01	0.01	0.01
2	0.4	0.28	0.5	0.46	0.03	0.14	0.23	0.27	0.3	0.01	0.01	0.01
3	0.4	0.5	0.39	0.5	0.16	0.54	0.24	0.33	0.35	0.02	0.02	0.02
4	0.37	0.46	0.35	0.58	0.46	0.62	0.27	0.4	0.6	0.02	0.02	0.02

To show the benefits of our proposed design, which borrows strength across schedules, we compared the performance of our design with a design that runs an independent trial for each schedule, using the following proportional odds model (i.e., equation (1) in Thall and Russell, 1998) for the trinary outcome:

$$\begin{array}{r}\text{logit}\{{\gamma }_{1,k}(d)\}={\eta }_{1,k}(d)={\mu }_k+{\alpha }_k+{\beta }_{k}d,\\ \text{logit}\{{\gamma }_{2,k}(d)\}={\eta }_{2,k}(d)={\mu }_k+{\beta }_{k}d,\end{array}$$

where d is dose under a given schedule, γ_j,k(d) = Pr(Y ≥ j | dose = d, schedule = k), α_k > 0, β_k > 0, j = 1, 2, k = 1, 2, 3. We used the following relative vague priors in our implementation: π(α_k) ~ Unif(0, 4), π(β_k) ~ Unif(0, 8), π(μ_k) ~ N(−1.7, 4), k = 1, 2, 3. We assumed a maximum sample size of 14 in each independent trial in this design (hereafter denoted as the TR design), which yielded a larger maximum total sample size than our proposed design (thus favoring the TR approach). For a fair comparison, we used decision criteria in the spirit of our proposed design, yet adapted to the single-schedule settings with appropriately tuned cutoff design parameters through simulations. We recommended a target dose (unless it was inconclusive) for each independent trial. If at least one trial was not inconclusive at the end of the study, we then selected the target dose that corresponded to the largest observed probability of efficacy and no toxicity as the recommended combination. In cases where more than one combination corresponded to the largest observed probability of efficacy and no toxicity, all were selected as the recommended combinations.

The selection percentage and number of patients treated at each dose-schedule combination for the 12 scenarios using both designs are summarized in Table 2. In all scenarios, the percentages of inconclusive trials using the proposed design were very low with a maximum of 3.2% (results not shown). The combination used to treat the highest average number of patients was a target combination in every scenario. In the first four scenarios, the target combinations are at locations (3, 1), (2, 2), (1, 1), and (4, 3), respectively. The selection percentages of the targets were 48.3%, 48.9%, 40.2%, and 63.6%, respectively. The average patient allocations of the targets were 8.2, 9.1, 6.8, and 10.8, respectively. In scenario 5, the selection percentages of the two target combinations (4, 1) and (3, 3) were 17.1% and 44.1%, respectively, with the sum being 61.2%. The numbers of patients treated were 4 and 8.1, respectively. In scenario 6, the selection percentages of the two target combinations (3, 1) and (2, 2) were 39.1% and 45%, respectively, with the sum being 84.1%. The numbers of patients allocated at the two targets were 8.4 and 9.1, respectively. In scenario 7, the two target combinations (2, 1) and (1, 3) were selected 31.5% and 21.1% of the times, respectively, with the sum being 52.6%. The average patient allocations were 6.4 and 4.6. In scenario 8, the selection of each of the three targets ranged from 22.8% to 30.8% with an average allocation of 6.0. In scenarios 9, 10, and 12, the single target combinations are at (3,2), (2,3), and (4,3), respectively, with the selection percentages of 58.8%, 33.7%, and 56.6%, respectively. The numbers of patients treated at these combinations were 9.4, 6.3, and 9.9, respectively. In scenario 11, the two target combinations are at (3,2) and (2,3), with the selection percentages being 40.9% and 42.3% and the patient allocations being 8.8 and 9.2, respectively.

Table 2.

Selection probability and number of patients treated at each dose-schedule combination, with the target dose-schedule combinations in boldface.

Dose	Proposed design						Independent TR design
	Selection percentage			Number of patients			Selection percentage			Number of patients
	Schedule			Schedule			Schedule			Schedule
	1	2	3	1	2	3	1	2	3	1	2	3
	Scenario 1
1	0.3	0	0.9	2	2	2.2	0.5	0.4	2.9	2.2	2.3	3.1
2	4.6	1.5	19.2	2.8	2.2	5.2	5.2	1.2	11.8	3.4	2.4	6.1
3	48.3	4.3	5.3	8.2	2.9	4.4	39.4	5.1	11.6	5.3	2.8	3.3
4	3.2	8.7	0.5	2.8	3.1	1.7	9	11.9	1	2.8	6	1.3
	Scenario 2
1	5.5	3.2	3.9	2.7	2.4	2.6	5	2.9	5.1	5.9	3.3	5.9
2	15.1	48.9	14.2	5.6	9.1	5.6	15.3	34.2	20.2	5.3	6.3	5.1
3	1	5.9	1.5	2.3	3.9	2.5	2.4	11.5	3	2.1	3	2.1
4	0	0.2	0.1	0.9	1.3	1	0.1	0.2	0.1	0.4	1.1	0.5
	Scenario 3
1	40.2	6.5	0	6.8	3	2	25	9.9	0.3	6.1	7.1	2.2
2	19.3	6.9	16.4	6.6	5.1	4.7	20.8	16.4	10.7	4.1	4.6	6.2
3	0.5	0.6	8.6	1.9	2	4.8	0.6	0.2	15.7	1.5	1.7	3.8
4	0	0	0	0.7	0.6	1.6	0	0	0.2	0.4	0.3	1.6
	Scenario 4
1	0.2	0.9	2.9	2.1	2.2	2.5	0	0	0.2	2	2	2.1
2	0.3	0.9	5.1	2.1	2.2	2.8	0	0	0.5	2	2	2.2
3	0.6	1.2	11.8	2.2	2.4	4.2	0	0.2	9.1	2	2.1	3.1
4	1	10.7	63.6	2.5	4	10.8	6.8	20.2	63	7.3	7.5	6.6
	Scenario 5
1	0.1	0.1	0.1	2	2	2	0	0.1	0	2.1	2.2	2.2
2	0.3	1.1	1.9	2.1	2.3	2.6	0.2	1.5	3	2.1	2.6	3.3
3	3	16.6	44.1	2.6	4.5	8.1	2.6	10.4	25.5	2.7	4.8	4.9
4	17.1	7.9	6.8	4	3.8	3.7	35.9	11.3	9.5	6.7	4	3.4
	Scenario 6
1	0	0.4	2.9	2	2.2	3	0	1.1	4.6	2.1	2.9	3.5
2	1.4	45	1.4	2.4	9.1	2.4	3.4	33	1.1	3	6.5	1.1
3	39.1	5.6	0.2	8.4	5	0.9	33.6	10.7	0	5.5	3.2	0.2
4	3.6	0.1	0.1	2.8	1.6	0.3	11.5	0.8	0	3.3	1.2	0.1
	Scenario 7
1	2.1	6.1	21.1	2.3	3	4.6	1.6	5.9	17	3.2	6.2	6.4
2	31.5	11.7	9.8	6.4	5.2	4.7	22.1	15.8	13.3	5.4	4.4	3.6
3	8.9	3.2	2.4	5	2.9	2.3	13.3	3.2	3.1	3.4	2	1.5
4	1.8	0	0	1.7	1	0.8	3.9	0.5	0.1	1.7	0.5	0.4
	Scenario 8
1	0	0.8	0	2	2.1	2	0	0.5	0.1	2.1	2.9	2.1
2	1	30.8	1.1	2.3	6.3	2.3	1.4	20.7	1.8	2.9	6.2	2.9
3	30	7.6	22.6	6.3	4.7	5.4	22.8	12.1	21.9	5.5	3.4	5.4
4	2.2	0.2	3.7	2.5	1.6	2.5	9.5	0.3	8.9	3.3	1.3	3.4
	Scenario 9
1	0.4	0.9	0	2	2.1	2	0.2	0.4	0	2.2	2.2	2
2	13.5	4.7	0.1	4.3	2.9	2	15.2	6	0	6	3.6	2
3	8.9	58.8	0.6	5.3	9.4	2.1	11.8	44.4	0.3	3.9	5.4	2.1
4	0.8	2.8	6.1	2	2.8	2.8	1	3.6	17	1.8	2.5	7.3
	Scenario 10
1	1	8.2	2.3	2.2	3.2	2.3	1.1	12.3	1.5	5	7	2.7
2	15.9	6.3	33.7	5.5	4.5	6.3	15.5	16.7	24.1	5.2	4.2	4.8
3	6.8	1	17.9	3.8	2.1	5.7	6.6	1.2	15.7	2.5	1.6	3.9
4	1	0.4	4.6	1.3	0.8	2.1	0.9	0	4	0.8	0.3	2.4
	Scenario 11
1	6	0	1.2	3.5	2	2.2	4.3	0.1	6.1	3.9	2.1	3.7
2	2.2	2.2	42.3	2.9	2.5	9.2	1.1	5.9	36.7	1.5	3.5	6.5
3	0.3	40.9	1	1.3	8.8	3.1	0	31.8	6.1	0.4	5.2	2.7
4	0	2.1	0.1	1.7	1	0.8	3.9	0.5	0.1	1.7	0.5	0.4
	Scenario 12
1	0.1	2	1.9	2.2	2.4	2.5	0	0	0	2	2	2
2	1.2	1.9	2	2.2	2.3	2.5	0	0	0.1	2	2	2.1
3	1.1	4.8	5	2.2	2.9	3	0	0.3	1.4	2	2.1	2.3
4	4.4	17	56.6	3	4.8	9.9	5.6	20.7	71.8	7.1	7.5	7.5

The performance of the TR design was worse than that of our design in most scenarios, in terms of both the selection percentages and numbers of patients treated at the target combinations. The only exceptions were in scenarios 5 and 12. In scenario 5, the TR design resulted in more balanced selection percentages and patient allocations, being 35.9% and 25.5%, and 6.7 and 4.9 patients, at the two target combinations (4,1) and (3,3), respectively. The total selection percentage of 61.4% and the total number of patients treated of 11.6 across the two target combinations, however, were similar to those of our design. In scenario 12, the TR design selected the target combination 71.8% of the times, higher than 56.6%, the corresponding selection percentage under the proposed design, yet allocated 7.5 patients to the target combination, lower than the 9.9 patients allocated using our proposed design.

4.2 Sensitivity Analysis

We carried out sensitivity analyses to assess the operating characteristics of the proposed design by varying the upper bounds of the prior uniform distributions of δ and γ:

• δ ~ U(0, 6); γ ~ U(0, 6)

• δ ~ U(0, 8); γ ~ U(0, 6)

• δ ~ U(0, 6); γ ~ U(0, 10)

• δ ~ U(0, 8); γ ~ U(0, 10)

The results from these four additional sets of prior distributions are very similar to those in the original simulations. In Table 3, we report the operating characteristics of our approach for scenarios 1–3 under the first set of priors, scenarios 4–6 under the second set of priors, scenarios 7–9 under the third set of priors, and 10–12 under the last set of priors. The rest of the results are shown in Tables 2–5 in the Supplementary Material.

Table 3.

Selection probability and number of patients treated at each dose-schedule combination under various specifications of the upper bounds of the prior uniform distributions for δ and γ. The bolded numbers correspond to the target dose-schedule combinations.

Dose	Selection percentage			Number of patients			Selection percentage			Number of patients
	Schedule			Schedule			Schedule			Schedule
	1	2	3	1	2	3	1	2	3	1	2	3
	δ ~ U(0, 6); γ ~ U(0, 6)						δ ~ U(0, 8); γ ~ U(0, 6)
	Scenario 1						Scenario 4
1	0.3	0.3	0.8	2.1	2.0	2.2	0.1	0.2	2.9	2.1	2.1	2.6
2	3.6	2.6	17.5	2.8	2.4	4.9	0.7	1.6	4.1	2.1	2.3	2.8
3	48.7	5.2	4.1	8.4	2.9	4.3	0.8	2.1	13.5	2.1	2.4	4.4
4	3.7	9.5	1.2	2.8	3.1	1.7	2.4	9.3	62.1	2.5	3.9	10.6
	Scenario 2						Scenario 5
1	4.6	2.9	5.3	2.6	2.5	2.7	0.2	0.2	0.2	2.0	2.0	2.0
2	11.4	48.8	18.4	5.4	8.8	5.7	0.6	3.1	1.9	2.1	2.6	2.5
3	0.7	5.4	1.9	2.3	4.1	2.6	2.8	17.8	41.7	2.6	4.9	7.6
4	0.1	0.2	0.0	0.8	1.4	1.0	16.2	7.3	7.2	3.9	3.8	3.7
	Scenario 3						Scenario 6
1	38.6	7.8	0.4	6.5	3.3	2.0	0.1	1.0	3.2	2.0	2.1	2.9
2	19.7	8.5	15.0	6.4	4.9	4.7	1.7	42.0	1.1	2.4	8.9	2.3
3	0.4	0.2	8.2	1.9	1.9	5.2	39.4	6.1	0.3	8.3	5.1	1.0
4	0.0	0.0	0.1	0.7	0.6	1.7	4.5	0.6	0.0	2.9	1.7	0.4
	δ ~ U(0, 6); γ ~ U(0, 10)						δ ~ U(0, 8); γ ~ U(0, 10)
	Scenario 7						Scenario 10
1	1.3	7.2	20.5	2.3	3.0	4.7	0.8	9.8	1.4	2.2	3.4	2.3
2	28.8	12.4	8.7	6.2	5.2	4.6	16.2	6.4	33.9	5.3	4.2	6.6
3	11.9	3.4	1.9	5.1	3.0	2.2	6.1	0.7	17.1	4.0	2.0	5.6
4	1.8	0.2	0.0	1.7	1.0	0.8	1.0	0.2	5.4	1.4	0.7	2.2
	Scenario 8						Scenario 11
1	0.0	0.1	0.0	2.0	2.0	2.0	5.9	0.2	1.8	3.5	2.0	2.4
2	0.7	31.5	1.3	2.2	6.4	2.4	2.0	2.4	42.3	2.8	2.6	9.2
3	27.3	6.1	27.4	5.8	4.5	6.0	0.4	39.1	1.4	1.2	8.6	3.1
4	2.2	0.2	3.1	2.5	1.6	2.5	0.0	1.9	0.4	0.4	2.6	1.2
	Scenario 9						Scenario 12
1	0.4	0.2	0.0	2.1	2.1	2.0	0.6	1.4	2.0	2.2	2.4	2.3
2	13.5	6.3	0.0	4.4	3.0	2.0	1.1	1.6	1.8	2.2	2.3	2.4
3	10.4	58.4	0.3	5.2	9.8	2.1	1.7	4.0	4.9	2.4	2.8	3.0
4	0.2	2.9	5.5	2.0	2.7	2.6	4.5	17.9	56.6	3.1	4.9	9.9

We carried out additional sensitivity analyses of the effect of the choice of σ² on the performance of our design. The results (summarized in Tables 6 and 7 in the Supplementary Material) suggest that the performance of our design is robust when σ² ranges from 0.2 to 1.

5 Discussion

We have proposed a Bayesian adaptive design for phase I/II clinical trials to identify an optimal dose-schedule combination satisfying both toxicity and efficacy requirements. A probit model is implemented for a trinary patient outcome, and a Bayesian dynamic model is used to borrow strength across dose-schedule combinations. To allow for flexibility, we assume non-monotonic relationships between the probabilities of efficacy and toxicity and schedule. Through simulation studies and sensitivity analyses, we demonstrate that our model can reliably identify the target dose-schedule combinations and allocate a large number of patients to the target combinations.

The Bayesian dynamic model we used for modeling the efficacy and toxicity probabilities at different dose-schedule combinations yields a moderate level of interaction effects between dose and schedule, using an appropriately tuned variance parameter (i.e., σ²). This appears desirable as it is difficult to envision that the dose effect may be dramatically different across schedules in practical scenarios.

The proposed method requires that both efficacy and toxicity outcomes be observed shortly after the initiation of the treatment to allow for adaptive dose and schedule assignment. However, in some phase I studies, either the efficacy or toxicity outcome may need a long time to observe. In the presence of such late-onset toxicity or efficacy, our model would not be appropriate. In that case, we can extend our method by modeling the time-to-event efficacy or toxicity outcome.